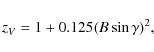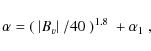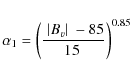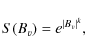| Issue |
A&A
Volume 517, July 2010
|
|
|---|---|---|
| Article Number | A37 | |
| Number of page(s) | 17 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/200913972 | |
| Published online | 29 July 2010 | |
Distribution functions for magnetic fields on the quiet Sun
J. O. Stenflo1,2
1 - Institute of Astronomy, ETH Zurich, 8093 Zurich, Switzerland
2 - Istituto Ricerche Solari Locarno, via Patocchi, 6605 Locarno Monti, Switzerland
Received 26 December 2009 / Accepted 28 April 2010
Abstract
The statistical properties of the highly structured magnetic field
of the quiet Sun are best described in terms of distribution functions,
in particular the probability density functions (PDF) for the flux
densities and the angular distribution for the orientations of the
field vector. They are needed to test the validity of various MHD
simulations, but past determinations have led to contradictory results.
A main reason for these difficulties lies in the circumstance that the
magnetic structuring continues on scales that are much smaller than the
telescope resolution, and that this structuring strongly affects the
quantities averaged over each pixel due to the non-linear relation
between polarization and magnetic field. Here we use a Hinode SOT/SP
data set for the disk center of the quiet Sun to explore the complex
behavior of the polarized 6301-6302 Å line system and identify the
observables that allow the most robust determinations of inclination
angles and flux densities. These observables are then used to derive
the empirical distribution functions. Our Stokes V line
ratio analysis leads us to an unexpected discovery: a magnetic
dichotomy with two distinct populations, representing strong (kG)
and weak fields. This can be understood in terms of the convective
collapse mechanism, which makes the Sun's magnetic flux end up in two
states: collapsed and uncollapsed. With the linear-to-circular
polarization ratio as a robust observable for the inclination angles,
we find that the angular distribution is extremely peaked around the
vertical direction for the largest flux densities, but gradually
broadens as we go to smaller flux densities, to become asymptotically
isotropic at zero flux density. The PDF for the vertical flux density,
after accounting for the smearing effect of measurement noise, is found
to have an extremely narrow core peak centered at zero flux density,
which can be analytically represented by a stretched exponential. The
PDF wings are extended and decline quadratically. The PDFs for the
horizontal and total flux densities have a similar behavior. In
particular we demonstrate that earlier claims that the PDF for the
total flux density increases from small values at zero flux density to
have a maximum significantly shifted from zero is an artefact of
measurement noise.
Key words: Sun: atmosphere - magnetic fields - polarization - Magnetohydrodynamics (MHD)
1 Introduction
Magnetic fields on the quiet Sun are fractal-like and highly structured on a large range of scales, probably all the way down to the magnetic diffusion scale (around 10 m if the Spitzer conductivity is used), where the field ceases to be frozen in (de Wijn et al. 2009). This is about four orders of magnitude below the best spatial resolution in solar observations. Numerical simulations of magneto-convection (e.g. Stein & Nordlund 2006; Schüssler & Vögler 2008) help us understand this structuring, but these theoretical simulations use a variety of different boundary conditions and approximations and therefore need to be tested through comparison with observations. For quantitative constraints on theories of magneto-convection we need to extract the relevant statistical properties of the observed magnetic structure and compare with the corresponding statistical properties of the simulated structures. These statistical properties come in the form of distribution functions for the field strength and field orientation as well as correlations between the magnetic field and the temperature-density structure and dynamics of the solar plasma. The aim of the present paper is to extract such statistical properties from the highest quality data set available for the diagnostics of vector magnetic fields, obtained by the Hinode satellite.
Since the structuring continues on scales far smaller than the Hinode angular resolution of 0.3 arcsec, we are dealing with unresolved observations and must therefore be careful not to use the word ``field strength'' but instead speak about ``flux densities''. Both concepts have the same dimension (we will stick to the commonly used cgs unit G), but previous literature abounds in the confused misuse of them. Flux density represents flux through the resolution element divided by its area. Since the field is not resolved, there are fields both stronger and weaker than this flux density inside the resolution element. There are indications that the distribution functions as extracted on different spatial scales have a high degree of self similarity that is characteristic of a fractal pattern (Janßen et al. 2003; Stenflo & Holzreuter 2003a,2002). If we can derive the scaling laws for the flux density distribution functions and compare with numerical simulations, we may get insights into the behavior of the distributions on subresolution scales. In the limit of the smallest scales, flux density would asymptotically become equivalent to field strength. The present paper is limited in scope to the extraction of distribution functions valid for the Hinode 0.3 arcsec scale, while the pursuit of the scaling laws will be reserved for future work.
The derivation of pixel-averaged flux densities is not a straightforward matter because of the magnetic structuring on subpixel scales (cf. Stenflo 1971; Sánchez Almeida & Lites 2000). The influence of the subresolution structure is much more severe for the linear polarization (transverse Zeeman effect) than for the circular polarization (longitudinal Zeeman effect), because the relation between polarization and magnetic field is much more non-linear for the linear polarization than for the circular polarization. In the weak-field limit the linear polarization is proportional to the square of the transverse field strength, while the circular polarization relates linearly to the longitudinal field strength. When the Zeeman splitting increases to become comparable to the line width a more complicated relation between polarization and field strength develops (cf. Stenflo 1994).
It has been well known since the early 1970s that weak polarization signals on the quiet Sun do not at all imply the absence of strong fields inside the resolution element. Instead the presence of kG field strengths inside the resolution elements (pixels) is commonplace. It has however also been known since the early 1980s from applications of the Hanle effect that there exists, besides the kG fields, another population of flux elements, which represents a spatially unresolved tangled field with typical field strengths of order 10-100 G (Stenflo 1982). We further know that there are subresolution correlations between the magnetic field and the thermodynamic parameters. The polarization signals decrease when the spectral line gets shallower and broader. It is well known that there is a very close correlation between line weakenings and field concentrations (Chapman & Sheeley 1968; Stenflo 1973; Sheeley 1967; Frazier & Stenflo 1978), as we will also see in the Hinode data set used here. This effect cannot simply be calibrated away, since the variations of the profile shape is not directly observable as they occur on subresolution scales. In addition we have strong asymmetries in the Stokes line profiles that are caused by subresolution correlations between the spatial gradients of the velocity fields (Doppler shifts) and the magnetic-field gradients (Sigwarth 2001; Sánchez Almeida & Lites 2000; Stenflo et al. 1984; Steiner 2000). These asymmetries are very difficult to model in any systematic way.
These examples illustrate how the magnetic and thermodynamic effects are intricately and non-linearly entangled in their influence on the Zeeman-effect polarization. It was to disentangle the magnetic effects from the thermodynamic effects that the line-ratio method was introduced (Stenflo 1973). In its ``pure'' version it requires the use of a line pair for which the two lines behave identically in all respects except for their different Landé factors. The only line pair known with these properties consists of the Fe I 5250.22 and 5247.06 Å lines, which have effective Landé factors 3.0 and 2.0, respectively, but are otherwise identical in terms of line strength and excitation potential and belong to the same atomic multiplet. The much used line pair Fe I 6301.51 and 6302.50 Å, which also is used by Hinode, cannot achieve such disentanglement, since the two lines have significantly different line strengths. We will see examples in the present paper how they respond quite differently to the thermodynamic parameters. Still the 6302/6301 line ratio information in the Hinode data provides interesting insights into the field structure, but it has to be used with great care.
With all the complications arising from processes happening in the domain that is not resolved, it is not surprising that earlier attempts to derive empirical probability density functions or PDFs (Stenflo & Holzreuter 2003a; Domínguez Cerdeña et al. 2006; Stenflo & Holzreuter 2002; Khomenko et al. 2003; Martínez González et al. 2008b) have not yet led to a coherent picture. When it comes to the derivation of the angular distribution of field vectors, the results are very contradictory. Thus through analyses of infrared data obtained with TIP on the German VTT Khomenko et al. (2003) find a broad range of inclination angles but with preference for more vertical fields, Martínez González et al. (2008a) conclude that the distribution is isotropic, while Beck & Rezaei (2009) find fields of both small and large inclinations, and conclude that the more vertical fields carry twice as much flux as the strongly inclined fields. In contrast, Orozco Suárez et al. (2007) and Lites et al. (2008) find a very strong predominance of horizontal fields from analysis of Hinode SOT/SP quiet-Sun data using the 6301-6302 Å line pair, while Asensio Ramos (2009) concludes from the same Hinode data that the angular distribution is quasi-isotropic.
The aim of the present paper is to use Hinode data to carefully explore the rich and complex properties of the 6301-6302 Å line system, to expose interpretation pitfalls and identify robust observables that allow the determination of flux densities and inclination angles in a reliable way. Sections 2-5 describe the richly structured behavior of the observed Stokes profiles, revealing the existence of two distinctly different flux populations. The modelling approach and approximations used for the conversion of Stokes profile information to flux densities and field inclination angles are described in Sect. 6, while Sects. 7-9 present the extracted properties of the magnetic field in terms of distribution functions for the field orientations and flux densities. Finally Sect. 10 summarizes the conclusions and presents an outlook.
2 Hinode quiet-Sun data set used
The solar telescope that currently produces high spatial resolution Stokes spectra for Zeeman-effect analysis with the by far best quality is the Hinode Solar Optical Telescope - Spectro-Polarimeter (SOT/SP, cf. Suematsu et al. 2008). Due to the excellent guiding, the spatial resolution does not get degraded by the longer integration times, but remains effectively at 0.3 arcsec (with a pixel spacing of 0.16 arcsec). The SP data contain full Stokes I, Q, U, and V spectra covering a wavelength window around the Fe I 6301.509 and 6302.502 Å lines with 112 pixels and a pixel spacing in the dispersion direction of 21.4 mÅ.
We select a Hinode ``deep mode'' data set recorded at the quiet-Sun disk center on February 27, 2007, because it represents one of the best-quality SP recordings of Hinode, and because it is the identical data set that was used by Lites et al. (2008) in their exploration of horizontal magnetic flux of the quiet Sun. By using the same data set we can better highlight the profound difference that the analysis method makes, as our conclusions are nearly opposite to those of Lites et al. (2008). The data set represents a time series of 727 exposures for a single position of the spectrograph slit at disk center. The integration time is 9.6 s. Each exposure contains 1024 pixels along the slit.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg1.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg18.png)
|
Figure 1:
The solid curves represent normalized mean Stokes V ( top panel) and Q ( bottom panel)
profiles that are representative of weak polarizations (polarization
amplitudes 0.5-3%). The dashed curve in the top panel shows for
comparison the normalized
|
| Open with DEXTER | |
Figure 1 illustrates the average Stokes V and Q profile shapes that are representative for polarization amplitudes between 0.5-3%. Since the average U profile has the same shape as the average Q profile, we do not show it here. We note in particular the strong line asymmetries, which can only arise if there are subresolution correlations between the spatial gradients of the velocity field and the magnetic field. In the absence of such correlations the Stokes V profile would be anti-symmetric around line center while the Q profile would be symmetric. Therefore all models that do not include these subpixel correlations fail to reproduce the observed Stokes profiles, including of course all Milne-Eddington based models. The asymmetries vary strongly from pixel to pixel and are most often very much larger (see below) than the illustrated asymmetries for the mean profiles.
In the weak-field limit Stokes V is proportional to the strength of the line-of-sight component of the magnetic field, to the Landé factor g (which is 1.667 for the 6301 Å line, 2.50 for the 6302 Å line), and to the wavelength gradient of the Stokes I
profile, but only in the absence of correlated spatial gradients along
the line of sight for the magnetic and velocity fields. For this reason
we have for comparison also plotted the normalized function
![]() in Fig. 1 (dashed). Without the mentioned correlations and in the weak-field case (
in Fig. 1 (dashed). Without the mentioned correlations and in the weak-field case (![]() G) we would expect the solid and dashed curves to coincide.
G) we would expect the solid and dashed curves to coincide.
The comparison of the solid and dashed V curves in Fig. 1 reveals two effects: (1) The V6302/V6301 amplitude line ratio is significantly smaller for the solid curve than for the dashed curve, which could be caused by the presence of intrinsically strong fields of order kG on subresolution scales. Such fields produce differential Zeeman saturation between the two lines (differential non-linearity in the polarization-field strength relation); (2) the relative shapes of the blue lobes of the Stokes V profiles agree nearly perfectly with the blue lobes of the Stokes I gradient profiles. In contrast there is very poor agreement between the corresponding red profile lobes. The red Stokes V lobes appear suppressed and broadened in a skewed way.
The asymmetries of the Q and U profiles are even more extreme than those of V.
Also here it is the red profile lobe that appears suppressed and
deformed, being narrower and asymmetrically squeezed towards line
center, while the blue profile lobe has a more ``normal'' shape. For
the Q and U profiles we cannot compare directly with a function derived from Stokes I, as we could for Stokes V (with
![]() ). If both the fields and the spectral lines were weak, then Q and U would be proportional to the square of the transverse field strength times
). If both the fields and the spectral lines were weak, then Q and U would be proportional to the square of the transverse field strength times
![]() ,
but in our case this relation is not useful, since the two iron lines that we use are far from being weak.
,
but in our case this relation is not useful, since the two iron lines that we use are far from being weak.
Another anomalous feature of the illustrated mean Q profiles is the absence of a ![]() component (of opposite sign around line center), in contrast to numerical models without correlated velocity gradients.
component (of opposite sign around line center), in contrast to numerical models without correlated velocity gradients.
In the present paper we have chosen to consistently base all our
derivations of the field parameters (inclination angles and flux
densities) only on the blue ![]() component lobe of the Stokes Q, U, and V profiles.
component lobe of the Stokes Q, U, and V profiles.
3 Extraction of the Stokes profile parameters
Due to the low S/N ratio for most of the pixels we obtain the most
robust determination of the polarized Stokes profile parameters by
applying masks to determine the amplitudes of the ![]() and
and ![]() component lobes. The basic masks are derived from the solid curves in Fig. 1 that represent the average profile shapes.
component lobes. The basic masks are derived from the solid curves in Fig. 1 that represent the average profile shapes.
A mask can be the normalized V, Q, or U profile, or better, an individual ![]() or
or ![]() component lobe, of each of the 6301 and 6302 Å lines. This mask is
multiplied by a scaling factor to obtain an optimum fit to the
corresponding profile observed in a given pixel. The single free
parameter, the scaling factor, is determined by an iterative least
squares fitting procedure. Since there is only one free parameter, the
fit is extremely robust, unique, and converges immediately.
component lobe, of each of the 6301 and 6302 Å lines. This mask is
multiplied by a scaling factor to obtain an optimum fit to the
corresponding profile observed in a given pixel. The single free
parameter, the scaling factor, is determined by an iterative least
squares fitting procedure. Since there is only one free parameter, the
fit is extremely robust, unique, and converges immediately.
The goodness of the fit, the squared standard deviation between the
model (scaled mask) and the observations, is best expressed by the ![]() of the fit. A
of the fit. A ![]() of unity means that the model and the observations are consistent
within the standard errors. The formal standard error in the fit
parameters scales in inverse proportion to
of unity means that the model and the observations are consistent
within the standard errors. The formal standard error in the fit
parameters scales in inverse proportion to ![]() .
If we multiply the parameter errors obtained from the fit procedure with the
.
If we multiply the parameter errors obtained from the fit procedure with the ![]() that results from the fit, then the new, rescaled parameter errors correspond to a fit with a
that results from the fit, then the new, rescaled parameter errors correspond to a fit with a ![]() of unity. These parameter errors are the correct ones to use, since
they reflect not only the errors in the observational input data, but
also systematic errors due to deficiencies in the choice of fitting
model. In this way we find the appropriate 1-
of unity. These parameter errors are the correct ones to use, since
they reflect not only the errors in the observational input data, but
also systematic errors due to deficiencies in the choice of fitting
model. In this way we find the appropriate 1-![]() standard errors in the extracted Stokes profile amplitudes.
standard errors in the extracted Stokes profile amplitudes.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg2.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg25.png)
|
Figure 2: Normalized histogram of the Stokes V blue-lobe amplitudes for the 6301 Å line, in lin-log scale. The inset panel shows the core region in linear scale. |
| Open with DEXTER | |
Due to the greatly variable Stokes asymmetries it is not optimum
to use the full Stokes profile of each line in Fig. 1 as a mask. Instead we cut out the blue and red ![]() lobes of the profiles to be used as individual masks after each of them has been scaled to an amplitude of unity. Since the
lobes of the profiles to be used as individual masks after each of them has been scaled to an amplitude of unity. Since the ![]() component lobes are missing in the Q profiles of Fig. 1, we create
component lobes are missing in the Q profiles of Fig. 1, we create ![]() lobe masks by generating synthetic profiles, then cut out the
lobe masks by generating synthetic profiles, then cut out the ![]() lobe part and scale it to unity. Doppler shifts are accounted for by
referring the observed Stokes profile to the position of the
Stokes I profile of the same pixel.
lobe part and scale it to unity. Doppler shifts are accounted for by
referring the observed Stokes profile to the position of the
Stokes I profile of the same pixel.
Figure 2 shows a normalized histogram of V6301, the amplitude of the blue-lobe component of Stokes V for the 6301 Å line. It illustrates how the quiet Sun is dominated by very weak magnetic fluxes. As seen from the inset panel for the core region, the great majority of pixels have polarization amplitudes below 0.2%. Due to the low S/N ratio for these pixels one needs to develop statistically robust analysis methods to obtain reliable and unbiased distribution functions for the magnetic-field parameters.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg3.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg26.png)
|
Figure 3:
Amplitude-normalized histograms of the Stokes V asymmetry A defined in Eq. (1) for various bins of
|
| Open with DEXTER | |
Fitting with the various masks gives us for each of the
![]() pixels the polarization amplitude, with sign and standard error, of the blue and red
pixels the polarization amplitude, with sign and standard error, of the blue and red ![]() lobes for each of the two lines, and in addition for Q and U the amplitude of the
lobes for each of the two lines, and in addition for Q and U the amplitude of the ![]() component lobe. This data set allows us among other things to explore
the distribution functions for the Stokes asymmetries. Figure 3 illustrates for various bins of the blue
component lobe. This data set allows us among other things to explore
the distribution functions for the Stokes asymmetries. Figure 3 illustrates for various bins of the blue ![]() component amplitude
component amplitude
![]() of the 6301 Å line the histograms for the Stokes V asymmetries, defined as
of the 6301 Å line the histograms for the Stokes V asymmetries, defined as
The broad dashed-triple-dot curve represents the V asymmetries within a
To ease the physical interpretation of the histograms, let us point out that zero asymmetry A means a perfectly anti-symmetric Stokes V profile. ![]() represent single lobe profiles, +1 with only the blue lobe, -1 with
only the red lobe. In the interval [-1,1] the two lobes have opposite
signs, but the blue lobe dominates for positive values, the red lobe
for negative values. A
> 1 represents two lobes of the same sign. When both lobes have the
same amplitude and sign, the asymmetry becomes infinite.
represent single lobe profiles, +1 with only the blue lobe, -1 with
only the red lobe. In the interval [-1,1] the two lobes have opposite
signs, but the blue lobe dominates for positive values, the red lobe
for negative values. A
> 1 represents two lobes of the same sign. When both lobes have the
same amplitude and sign, the asymmetry becomes infinite.
Figure 3 shows that we have a huge spread in the V asymmetries for weak polarization signals, with high occurrence rate for two lobes of the same sign as well as of dominance of the red lobe, similar to earlier results of Sigwarth (2001). As the polarization increases, the spread decreases. For Stokes V amplitudes beyond 10% the spread becomes small and the average asymmetry also decreases, although the average remains positive for all polarization values. The histograms shown are for the 6301 Å line, but those derived for the 6302 Å are almost identical and are therefore not reproduced here.
Physically this means that the subpixel correlations between the magnetic and velociy field gradients have a well-defined geometry in the case of the largest flux densities, but become strongly randomized as we go to small flux densities. This illustrates the intrinsic difficulty of modeling the Stokes profiles in regions with flux densities below a few hundred G, due to the highly individualistic behavior of the mentioned correlations.
4 Dependence of the Stokes I profiles on flux density
In addition to the mask fits of the Q, U, and V profiles we have extracted from the Stokes I data of each pixel the relative line depth
![]() ,
line width w
(half level chord length), line position (as the center of gravity of
the portion of the line profile below the half level chord), line
strength (profile area below the half level chord), and relative
intensity of the continuum. This allows us to use regression analysis
to explore the generally tight correlations between these various
quantities and in particular the Stokes V amplitude.
,
line width w
(half level chord length), line position (as the center of gravity of
the portion of the line profile below the half level chord), line
strength (profile area below the half level chord), and relative
intensity of the continuum. This allows us to use regression analysis
to explore the generally tight correlations between these various
quantities and in particular the Stokes V amplitude.
The main relevant Stokes I parameters influencing the conversion of polarization amplitudes to flux densities are the line depth d and line width w. For weak fields Stokes V scales with the intensity gradient
![]() ,
which in turn scales with the ratio d/w.
While the line depth determines the scale of the intensity variations
within the line, the line width determines the factor by which the line
is stretched relative to the wavelength scale.
,
which in turn scales with the ratio d/w.
While the line depth determines the scale of the intensity variations
within the line, the line width determines the factor by which the line
is stretched relative to the wavelength scale.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg4.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg31.png)
|
Figure 4:
Variation of Stokes I relative line depth d with Stokes V amplitude of the 6301 Å line. Solid curve: 6301 Å. Dashed curve: 6302 Å. The dotted curves represent the
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg5.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg32.png)
|
Figure 5: Same as Fig. 4, but for the Stokes I line widths. |
| Open with DEXTER | |
Both d and w exhibit very tight regression relations with Stokes V amplitude for both spectral lines, as illustrated in Figs. 4 and 5. The variations are huge, of order factor of two for both line depth and line width, as we go from the smallest to the largest polarization values. Thus the lines get shallower and broader with increasing flux density. While this may partly be due to an increase in Zeeman splitting, a major part of the effect is likely caused by intrinsic thermodynamic line weakenings and line broadenings in the spatially unresolved magnetic structures.
If we in the 2-component scenario assume a certain difference in the thermodynamic structure of the magnetic component with respect to its ``non-magnetic'' surroundings, and further assume that this differential line weakening-broadening as well as the intrinsic field strength of the magnetic component are independent of magnetic filling factor, then we would expect to find linear relations between line depth and polarization (since Stokes V would scale with the filling factor). The deviations from linearity indicate that the situation is more complex.
The Zeeman splitting alone would not have much effect on the Stokes I line profiles for Stokes V amplitudes below about 7%. Thus, if Zeeman splitting plays a significant role for the observed line weakenings and broadenings in Figs. 4 and 5, then we have to invoke strong fields, of order 1 kG. As we will see below, the observed Stokes V line ratio indeed demands that most of the observed flux is carried by such strong fields.
Model dependence can often be minimized by making use of ratios between physical quantities rather than the quantities by themselves. In Fig. 6 we illustrate the behavior of the d6302/d6301 line ratio. We find a tight, highly linear relation from a ratio of 0.9 to 0.6 when we go from small to large polarizations. If the two lines of the chosen line pair were identical in their line-formation properties, with the same line strengths and excitation potentials and belonging to the same multiplet, like the 5250-5247 Å line pair, then the d line ratio in Fig. 6 would be unity in the limit of vanishing flux and only begin to deviate from unity for field strengths larger than several hundred G. A deviation from unity would then be direct evidence for strong fields. Since however the 6301 and 6302 Å lines that were selected for the Hinode spectropolarimeter do not form such an ideal pair but have different line strengths and therefore different line-formation properties, the Zeeman saturation and thermodynamic effects become entangled, which enormously complicates the interpretation. This example illustrates the diagnostic superiority of the 5250-5247 Å line pair, for which the variations are exclusively due to differential Zeeman saturation, but unfortunately this line pair was not selected in the Hinode design.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg6.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg33.png)
|
Figure 6:
Observed Stokes I
line depth ratio between the 6302 and 6301 Å lines. Here the
dashed curve represents the observed mean relation, while the solid
line is a straight line fit to demonstrate the high degree of linearity
of the relation. The dotted curves are the |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg7.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg34.png)
|
Figure 7: Synthetic Stokes I line depth ratio vs. field strength for the three model atmospheres illustrated in Fig. 12 (dotted curve: hot flux tube model AYFLUXT; solid curve: facular model FAL-F; dashed curve: quiet Sun model Maltby). The upper (lower) horizontal lines represent the observed d line ratio for the pixels with the smallest (largest) Stokes V amplitudes. |
| Open with DEXTER | |
Still, even for unequal lines like 6301 and 6302 Å, use of line ratios can suppress the model dependence. We have computed synthetic Stokes profiles using three model atmospheres with highly different thermodynamic structures, a hot flux tube model (AYFLUXT), an average facular model (FAL-F), and a quiet Sun model (Maltby), which will be described in Sect. 6.1. For comparison with our observational line-ratio diagram of Fig. 6 we present in Fig. 7 the corresponding theoretical diagram, giving the line depth ratio as a function of field strength for the three model atmospheres (the solid, dashed, and dotted curves). What is most striking is that the three model curves are almost identical, although the individual line depths vary greatly between the models (cf. Fig. 13 below). The thermodynamics thus affects the line depth by approximately the same factor in both lines, with the consequence that the model dependence divides out when forming the ratio.
While the theoretical dependence on field strength in Fig. 7 is highly non-linear, the observed linearity of the relation in Fig. 6 indicates that our apparent flux densities must be much more closely related to varying filling factors than to varying field strengths. This lends general support to the diagnostic validity of the 2-component scenario, although it should be used with care.
The upper dashed horizontal line in Fig. 7 marks the d line ratio observed for the pixels with the smallest Stokes V amplitudes, while the lower dashed horizontal line represents the pixels with the largest Stokes V. The upper line agrees with the theoretical d line ratio for the non-magnetic case, as expected, while the lower line shows that the largest Stokes V amplitudes must represent kG type fields with large filling factors.
5 Magnetic dichotomy: two distinct flux populations
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg8.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg35.png)
|
Figure 8: Scatter plot of the blue lobe Stokes V amplitudes derived for the 6302 Å line vs. the corresponding Stokes V amplitudes for the 6301 Å line. The dashed line with slope s=1.66 represents the regression relation that would be expected for spatially resolved, weak fields. We identify two populations of points: (1) The dominant population that follows a slope that is about 0.7s for small polarizations, decreasing to about 0.6s for larger values. (2) A secondary population that is significant only for Stokes V amplitudes below about 2%, and which almost follows the slope of the dashed line. |
| Open with DEXTER | |
Let us now turn our attention to the Stokes V line ratio, shown in Fig. 8 as a scatter plot of the Stokes V
blue lobe amplitudes in the 6302 and 6301 Å lines. If the Hinode
data with 0.3 arcsec effective resolution would spatially resolve
the solar structures, if there are no velocity gradients along the line
of sight, and if the fields are weaker than a few hundred G,
Stokes V would be proportional to
![]() ,
where g
is the Landé factor. In this case we would expect the points to line up
along the dashed line in the figure, which has the slope
s=b6302/b6301. As the V
amplitude increases the points would be expected to gradually bend away
from this line due to increasing differential Zeeman saturation for
stronger fields. In contrast to such a gradually curved function the
points follow a relation that is nearly a straight line with an almost
constant slope (0.6-0.7 times s) all the way down to the smallest flux densities. The value of the slope s used here is based on the global averages over all the pixels of the amplitudes of
,
where g
is the Landé factor. In this case we would expect the points to line up
along the dashed line in the figure, which has the slope
s=b6302/b6301. As the V
amplitude increases the points would be expected to gradually bend away
from this line due to increasing differential Zeeman saturation for
stronger fields. In contrast to such a gradually curved function the
points follow a relation that is nearly a straight line with an almost
constant slope (0.6-0.7 times s) all the way down to the smallest flux densities. The value of the slope s used here is based on the global averages over all the pixels of the amplitudes of
![]() for each of the two lines. Its value is s=1.66.
for each of the two lines. Its value is s=1.66.
A constant slope indicates that the Zeeman saturation does not vary with flux density. In the framework of a 2-component interpretation model this implies that the intrinsic field strength of the magnetic component is independent of flux density. This means that different flux densities are due to different filling factors rather than to different field strengths. The small scatter of the points around the nearly straight-line relation implies that the spread in the values of the intrinsic field strength is small. For the slope to deviate so much from slope s (the dashed line) one needs field strengths of order 1 kG, in line with earlier conclusions from observations with the 5250-5247 Å line ratio.
A closer look at the densely populated region with polarizations
![]() %
reveals however that there are two distinct populations: (1) The
dominant population with a small slope of about 0.6-0.7 times s, and (2) a less abundant population that follows a slope close to s
(the dashed line), but which vanishes for polarizations well beyond 2%.
Because of its slope the second smaller population may be understood as
representing intrinsically weak fields, while the main population
represents intrinsically strong, kG fields with varying filling
factors. We find no evidence for a continuous transition between the
two populations (see below).
%
reveals however that there are two distinct populations: (1) The
dominant population with a small slope of about 0.6-0.7 times s, and (2) a less abundant population that follows a slope close to s
(the dashed line), but which vanishes for polarizations well beyond 2%.
Because of its slope the second smaller population may be understood as
representing intrinsically weak fields, while the main population
represents intrinsically strong, kG fields with varying filling
factors. We find no evidence for a continuous transition between the
two populations (see below).
We test the conjecture that there are two discrete populations by making histograms of the
V6302/V6301 line ratio for a sequence of narrow bins in
![]() .
If there were only one population, it should be possible to obtain a
good fit to each histogram with a single Gaussian function. If however
there are two populations representing two distinctly different line
ratios (slopes in the V6302 vs. V6301 scatter-plot diagram), then two Gaussians centered around the different line-ratio values would be needed for a good fit.
.
If there were only one population, it should be possible to obtain a
good fit to each histogram with a single Gaussian function. If however
there are two populations representing two distinctly different line
ratios (slopes in the V6302 vs. V6301 scatter-plot diagram), then two Gaussians centered around the different line-ratio values would be needed for a good fit.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg9.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg39.png)
|
Figure 9:
Histogram of the
V6302/V6301 line ratio (normalized to the slope s, which accounts for the factor 0.6=1/s) for a
|
| Open with DEXTER | |
We have therefore done an iterative least squares Gaussian
decomposition of each histogram with a model containing five free
parameters: the amplitudes and positions of two Gaussians, and the
``Doppler'' width (which is assumed to be the same for both Gaussians).
We find excellent fits within the standard errors for all the
histograms. A representative case is illustrated in Fig. 9 for a 0.2% wide
![]() bin centered at 0.95%. An excellent fit is indeed obtained with exactly
two discrete Gaussian components, there is absolutely no need for
additional components or a continuum of components.
bin centered at 0.95%. An excellent fit is indeed obtained with exactly
two discrete Gaussian components, there is absolutely no need for
additional components or a continuum of components.
Notice that while the dominant component is centered around a line-ratio value of 0.64s, the secondary component is not centered around line-ratio unity but around a value of 0.92s in Fig. 9. Taken at face value, the circumstance that 0.92s is significantly smaller than unity could suggest that even this secondary component does not represent truly weak fields but rather fields of some intermediate strength. A more likely explanation, however, is that the secondary population really represents truly weak fields, and that the reason why the normalized line ratio then is not exactly unity has to do with the differential effect of spatially unresolved correlations between the gradients of the magnetic and velocity fields, which also are at the origin of the Stokes V line asymmetries. We will return to this important issue later.
For increasing flux densities the two Gaussians get much better
separated, since the ``Doppler'' width in line-ratio units decreases
with increasing polarization (two regression lines with different
slopes get better separated as we move away from origo). For small
polarizations the Gaussians overlap so much that the decomposition
becomes numerically unstable. We find reliable decompositions only for
![]() %.
%.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg10.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg41.png)
|
Figure 10:
Fraction of points belonging to the weaker-field population (solid curve), surrounded by the 1- |
| Open with DEXTER | |
From decompositions like the one in Fig. 9 we obtain the fit parameters with their error bars as functions of polarization amplitude
![]() .
In Fig. 10
we show the fraction of all the points that belong to the secondary
(weaker-field) population. It decreases from about 30-35% for
Stokes V amplitudes of 0.5-0.6% to less than 2% for
.
In Fig. 10
we show the fraction of all the points that belong to the secondary
(weaker-field) population. It decreases from about 30-35% for
Stokes V amplitudes of 0.5-0.6% to less than 2% for
![]() %. Thus it is only significant for polarizations below about 2%.
%. Thus it is only significant for polarizations below about 2%.
The breakdown in two distinct populations has important consequences for the extraction of inclination angles and corrected flux densities from the data set. While the main population with a small slope should be interpreted in terms of a 2-component model with intrinsically strong (kG-type) magnetic fields, the weak population should rather be interpreted in terms of intrinsically weak fields. Since extraction of inclination angles with the weak-field assumption favors horizontal fields much more as compared with the interpretation model with intrinsically strong fields, and as the great majority of pixels have Stokes V amplitudes well below 0.5% (cf. Fig. 2) we need to make some extrapolation assumption for the relative abundance of the weak population in the polarization range 0-0.5%, where the Gaussian decomposition could not be used reliably.
For this reason we have fit the data with two choices of analytical fit
functions that extend all the way down to zero polarization, as
illustrated by the dotted and dot-dashed curves in Fig. 10.
While the more gentle extrapolation is the lower (dotted) curve that
ends at 37%, we choose to base our analysis in the present paper on the
upper (dot-dashed) curve that goes all the way up to 100%. There are
two main reasons for doing this: (1) Since we will later find that the
quiet-Sun magnetic fields are predominantly vertical, not horizontal,
in contrast to some previous investigations, we want to rule out the
possibility that this conclusion depends on our choice of extrapolation
in Fig. 10. By
choosing the upper curve we give maximum advantage to the horizontal
fields. (2) There is a natural physical scenario that can explain why
there is a dichotomy, why the Sun's magnetic flux ends up in two
distinct populations. The convective collapse mechanism (Unno & Ando 1979; Spruit 1979; Spruit & Zweibel 1979; Parker 1978)
will spontaneously do exactly this job: Flux that is subject to this
instability will quickly end up in the strong-field state, where it
will remain for a time that is long compared to the formation time,
while the remaining, uncollapsed solar flux will stay in the weak state
(with the tendency of being tangled up). It is physically natural to
expect that in the limit of zero flux density all such weak flux is in
the uncollapsed state, so for this reason the extrapolated curve should
reach 100%, as the dot-dashed curve does. It is described by the
function
where
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg11.eps} \vspace*{3mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg45.png)
|
Figure 11:
Line-ratio position (normalized to the resolved weak-field case) of the two Gaussian components vs. Stokes V amplitude
|
| Open with DEXTER | |
The positions of the two Gaussians, in normalized line-ratio units, are plotted vs. polarization amplitude
![]() in Fig. 11.
The line ratio of the weak-field population remains nearly independent
of flux density within the error bars, with a value of 0.92-0.97 (in
units of slope s). The normalized line ratio of the main,
strong-field population on the other hand decreases from about 0.7 for
small polarizations to 0.6 for large polarizations. In the framework of
the 2-component interpretation model this corresponds to a gradual
increase of the intrinsic field strength of the magnetic component as
the filling factor increases.
in Fig. 11.
The line ratio of the weak-field population remains nearly independent
of flux density within the error bars, with a value of 0.92-0.97 (in
units of slope s). The normalized line ratio of the main,
strong-field population on the other hand decreases from about 0.7 for
small polarizations to 0.6 for large polarizations. In the framework of
the 2-component interpretation model this corresponds to a gradual
increase of the intrinsic field strength of the magnetic component as
the filling factor increases.
Note that the error bars for the line ratios in Fig. 11 are so small because a large number of pixels contribute to each determination. The standard errors for the line ratios of the individual pixels are of course very much larger, but this is totally irrelevant here, since we never use these individual line ratios in our analysis. The purpose of determining the line ratios for the two populations as we have done here is to be able to define the procedures for converting Stokes Q, U, and V amplitudes to field inclination angles and flux densities, as described in Sect. 6. The conversion procedure for the main population is qualitatively different from that of the weak population. The conversion results from each procedure are weighted together in proportion to the relative abundances of the two populations, as given by Fig. 10.
We note that the relative amplitude of the weak-field population declines towards zero an order of magnitude faster than the relative filling factor of the ``non-magnetic'' or tangled field component would in a 2-component framework. The filling factor for this component would decrease linearly from unity for zero polarization to reach zero for a polarization value at least as large as the largest observed polarization in our data set, 15%. In contrast, the weak-field population in Fig. 10 declines towards zero over a polarization range of about 2% only. This may be understood as a natural consequence of the convective collapse mechanism. As this instability applies to vertical, laterally optical thick flux regions, much of the weak, tangled fluxes will not be affected, while practically all the larger flux regions will end up in the collapsed state.
It has been common practice in the literature to use the terminology ``network'' and ``internetwork'' magnetic fields for the quiet Sun. Here we have chosen not to refer to these two concepts, because they are poorly defined and therefore not helpful. The network concept has been introduced to describe the pattern of brightness structures on the Sun, and since the magnetic flux is found to correlate well with brightness, the concept of a magnetic network has emerged. However, the correlation between brightness and flux density is a continuous function (cf. Fig. 4), and there is no procedure to tell whether a given weak flux element represents network or internetwork. Since we cannot (in scatter plots like those used for Fig. 4) resolve any dichotomy in the regression relation between brightness and magnetic flux, it is not warranted to associate our newly discovered weak population with the concept of ``internetwork'' fields. Instead one should rather refer to physical concepts like collapsed and uncollapsed flux.
6 Interpretation steps
The great complexity of the 6301-6302 Å line pair system has often been seriously underestimated in the past. The complexity arises from an atmosphere full of subresolution structuring with strong couplings between thermodynamic and magnetic parameters. To optimize the reliability of the interpretation we need to explore the behavior of the 6301-6302 Å system to identify which observables are the most robust. In general the optimum choice of observables comes in the form of ratios, because then the model dependence often divides out to first order.
6.1 Model atmospheres used
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg12.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg46.png)
|
Figure 12: Temperature structure of the three model atmospheres used to explore the behavior of various synthetic observables. Solid line: Quiet-Sun model of Maltby et al. (1986). Dashed line: Facular model FAL-F of Fontenla et al. (1993). Dot-dashed line: Hot flux tube model AYFLUXT of Ayres et al. (1986) and Solanki et al. (1994). |
| Open with DEXTER | |
The first goal is to make the derivation of the field structure insensitive to the thermodynamic structure of the atmosphere. To explore such model dependence we have selected three highly different numerically given model atmospheres, the temperature structures of which are illustrated in Fig. 12. They range from the hot flux tube model AYFLUXT of Ayres et al. (1986) and Solanki et al. (1994) (dot-dashed line) to the facular model FAL-F of Fontenla et al. (1993) (dashed line) and the quiet Sun model MACKKL of Maltby et al. (1986) (solid line). We use them to calculate a variety of synthetic observables of the 6301-6302 Å system.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg13.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg47.png)
|
Figure 13: Comparison between observed and synthetic Stokes I profiles. The microturbulence is zero in all three models. The dotted, dashed, and dot-dashed curves represent the models of Maltby, FAL-F, and AYFLUXT, respectively, while the solid line represents the observations for the central pixel of the data set. |
| Open with DEXTER | |
In Fig. 13 we compare the three synthetic Stokes I profiles with a typical Hinode recording (solid line, here representing the central pixel in the Hinode data set). As expected, the hottest model (AYFLUXT) gives the shallowest profiles, the coolest model (Maltby) the deepest, while the observed profile usually lies in between. The line widths of all models, defined as the full width of the half level chord, agree to within 1% of the corresponding observed width, but only when the microturbulence is set to zero in all the models. The observed profiles are more u-shaped, the theoretical models more v-shaped.
Although there is a large difference between the line depths of the hottest and coolest models, it is interesting to note that the line-depth variations of the observations, as shown by Fig. 4, span a range that is significantly larger than the range spanned by the three models. Although part of the observed line weakenings is due to the large Zeeman splitting of the intrinsically strong fields, this effect is not sufficient to explain the much larger range of the observed line depth variations, as we will see explicitly later. This indicates that even the hot flux tube model AYFLUXT is not hot enough to properly represent the thermodynamic state of the spatially unresolved flux elements.
6.2 Extraction of intrinsic field strengths
The nearly straight-line regression of the main population of points in the V6302 vs. V6301 line-ratio scatter-plot diagram of Fig. 8, combined with the existence of a secondary, weak population that follows a very different slope, is evidence for an underlying flux-tube type structure with intrinsically strong fields (of order kG) as the source of the main population. We know of no other possibility to make sense of the presence of these two distinct slopes, the diagram leaves us no alternative interpretation. The next step is therefore to examine how the observed line ratios that represent the two populations may be used to derive the values of the intrinsic field strengths of the main population.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg14.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg48.png)
|
Figure 14: Stokes V line ratios obtained from Figs. 11 and 8 (dotted, dashed, and dot-dashed curves). The solid curve represents an analytical fit to the main population, while the weak population is characterized by the horizontal level at 1.55. |
| Open with DEXTER | |
In Fig. 11 we derived the line ratio as a function of Stokes V amplitude for the range below 2.3% only, since the amplitude of the weak population vanishes beyond that range. This gives us the dashed and dotted curves in Fig. 14. For the main population the derivation of the line ratio as a function of polarization amplitude can be continued as a single population all the way to the largest observed polarizations. This continuation is represented by the dot-dashed line in Fig. 14.
The dashed and dot-dashed curves can jointly be well fitted by an analytical function given by the solid curve in Fig. 14. For the weak population there is no evidence for significant variations with polarization amplitude beyond the given uncertainties, and if it represents truly weak fields there should not be any variations. We therefore represent it with a horizontal line to be used as a reference level for the line ratio scale. The reason for the need of renormalizing the line ratio scale will be clarified next.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg15.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg49.png)
|
Figure 15: Theoretical Stokes V line ratio vs. field strength, calculated for the three model atmospheres (solid: AYFLUXT, dotted: FAL-F, dot-dashed: Maltby). The agreement between the three curves demonstrates that the line ratio is insensitive to the thermodynamic structure of the atmosphere. |
| Open with DEXTER | |
To convert the observed line ratios in Fig. 14 to intrinsic field strengths we need to compare with the synthetic line ratios as functions of field strength for our three model atmospheres. These theoretical line ratios are given in Fig. 15, with the solid curve representing model AYFLUXT, the dotted FAL-F, and the dot-dashed Maltby. It is highly satisfactory that all three curves almost coincide. This means that the thermodynamic model dependence effectively divides out when forming the Stokes V line ratio.
When we however make a comparison with the observed line ratios of Fig. 14, we immediately notice a serious problem: the observed line ratio for our ``weak'' population is 1.55, which with the theoretical diagram of Fig. 15 would correspond to more than 600 G, suggesting that this population does not represent weak fields at all. Much worse, however, is that the main population, with observed line ratios even below 0.9, would represent unphysical field strengths far beyond the scale of the theoretical diagram of Fig. 15, which reaches its lowest point of only 1.1 for fields of 2000 G. It is thus clear that the use of unnormalized observed line ratios, taken at face value, would lead to unphysical results.
A similar conclusion was reached by Khomenko & Collados (2007), who compared the performance of the 6302/6301 line ratio with that of 5250/5247 as well as with infrared lines through diagnostics of the magnetic-field structure generated by numerical MHD simulations. While the 5250/5247 line ratio and the infrared lines were able to correctly diagnose the field at the respective levels of line formation, the 6302/6301 line ratio was found to produce fictitious, strong kG fields everywhere (where there should not be any). The reason was that the synthetic line ratio was systematically smaller than theoretically expected for a homogeneous 1-D atmosphere, just as we have found here. Khomenko & Collados (2007) identified the origin of this problem as due to the spatially unresolved correlations between the gradients of the velocity field and the magnetic field. This explanation is fully consistent with our findings. We saw in Sect. 3 how severely distorted the Stokes V profiles become because of these subresolution gradient correlations. Since the 6301 and 6302 Å lines are formed at different heights we can expect them to be affected differently by the subpixel correlations. This again illustrates how crucial it is to select a line ratio, for which the two lines behave identically in the absence of magnetic fields, which unfortunately is not the case for the 6302-6301 line pair.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg16.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg50.png)
|
Figure 16: Normalized theoretical Stokes V line ratio for the AYFLUXT model, after applying the 35 mÅ spectral smearing done by Hinode. The normalized observed line ratios of the main population fall within the range marked by the horizontal dotted and dashed lines. |
| Open with DEXTER | |
Assuming that the differential effects from the subresolution velocity-magnetic field gradient correlations lead to an offset of the Stokes V line ratio scale by a fixed factor, and that the weak population represents truly weak fields, we can normalize the observed line ratios in Fig. 14 by 1.55, the level of the weak population, and compare them with the normalized version of the theoretical diagram of Fig. 15. This rather simplistic procedure is justified by the circumstance that the so normalized line ratio gives intrinsic field strengths that are fully consistent with other types of determinations in the literature (see below). Without normalization the results would be unphysical.
In Fig. 16 the solid curve is the normalized theoretical function for the AYFLUXT model (selected because it is expected to represent the flux tubes the best, although the other two models give almost the same curve), after the theoretical V profiles have been smoothed by the 35 mÅ spectral broadening of Hinode (which however has a very minor effect). The observed, normalized V line ratios for the main population in Fig. 14 fall within the range marked by the dotted and dashed horizontal lines in the diagram. We now see that our normalization procedure produces line ratios corresponding to intrinsic field strengths in the range 700-1900 G, which is fully consistent with previous investigations based on the 5250/5247 line ratio and on Zeeman splittings in the infrared.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg17.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg51.png)
|
Figure 17: Field strength representing the magnetic component of the main population vs. Stokes V blue wing polarization amplitude in the 6301 Å line, obtained through a translation of Fig. 14 with the help of Fig. 16. |
| Open with DEXTER | |
With the ``calibration'' curve in Fig. 16 we can now convert the normalized line ratio for the main population in Fig. 14 to intrinsic field strength as a function of polarization amplitude in the blue wing of the 6301 Å line, as shown in Fig. 17. Consistent with many previous 2-component decompositions based on numerous other diagnostic methods (cf. Rüedi et al. 1992), we find for polarization amplitudes above 2% a slow increase of the field strength within the 1-2 kG range. When we go to polarization amplitudes below 2% the field strength rapidly drops to 700 G (at the same time as the weak population starts to take over).
While our normalization procedure gives consistent results in line with previous work, it would be important to have it tested against data produced by numerical MHD simulations, similar to the work of Khomenko & Collados (2007). As they did not have a reference level to normalize their line ratio with (while we here could use the weak population level), they found physically unacceptable results with the 6302/6301 line ratio (which we also would get without normalization). Without the existence of the weak population, no alternative reference level would have been available.
A real test may however require that the MHD simulations reproduce the magnetic dichotomy of the field structure, otherwise the simulations will not generate any reference level to use for the normalization, but the normalization scale factor would have to be introduced as a free parameter.
6.3 Choice of observable for the inclination angles
The field inclination ![]() with respect to the line of sight is found by comparing the relative
magnitudes of the linear and circular polarizations with each other.
While the circular polarization is represented by Stokes V
and is to first order proportional to the line of sight component of
the magnetic field, the linear polarization, represented by
with respect to the line of sight is found by comparing the relative
magnitudes of the linear and circular polarizations with each other.
While the circular polarization is represented by Stokes V
and is to first order proportional to the line of sight component of
the magnetic field, the linear polarization, represented by
![]() ,
depends on the transverse field component in a highly non-linear way.
In the limit of weak fields it is proportional to the square of the
transverse field strength, i.e., to the magnetic energy of the
transverse field.
,
depends on the transverse field component in a highly non-linear way.
In the limit of weak fields it is proportional to the square of the
transverse field strength, i.e., to the magnetic energy of the
transverse field.
To simplify the discussion, let us replace
![]() by the short-hand notation Q, as if we (just for discussion purposes) were in a Stokes reference frame with an azimuth chosen to make Stokes U zero. Then there are two types of ratios that can serve as observables for the derivation of the inclination angles: the Q/V ratio, and the
by the short-hand notation Q, as if we (just for discussion purposes) were in a Stokes reference frame with an azimuth chosen to make Stokes U zero. Then there are two types of ratios that can serve as observables for the derivation of the inclination angles: the Q/V ratio, and the
![]() ratio. We will now explain why the first of these ratios is the optimum
choice for the main population, while the second ratio is the one to
use for the weak population.
ratio. We will now explain why the first of these ratios is the optimum
choice for the main population, while the second ratio is the one to
use for the weak population.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg18.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg54.png)
|
Figure 18:
Q/V ratio divided by
|
| Open with DEXTER | |
Since both Q and V are proportional to filling factor f, the filling factor always divides out when forming the Q/V ratio. Accordingly, uncertainties in the filling factor do not affect the inclination angles. For this reason Q/V is the ratio of choice for the main population, which represents a large variety of filling factors.
In the limit of weak fields, Q is proportional to
![]() ,
while V is proportional to
,
while V is proportional to
![]() .
It is therefore clear that the field strength B does not divide out in the Q/V ratio. However, this is a relatively minor issue, as shown in Fig. 18, where we have plotted vs. field strength for the 6301 Å line the theoretically calculated Q/V divided by
.
It is therefore clear that the field strength B does not divide out in the Q/V ratio. However, this is a relatively minor issue, as shown in Fig. 18, where we have plotted vs. field strength for the 6301 Å line the theoretically calculated Q/V divided by
![]() for the three model atmospheres and for two choices of
for the three model atmospheres and for two choices of ![]() ,
60
,
60![]() and 30
and 30![]() .
We note that the spread between all these 6 curves is minor, and completely insignificant in comparison with the main
.
We note that the spread between all these 6 curves is minor, and completely insignificant in comparison with the main ![]() -dependent factor,
-dependent factor,
![]() ,
which varies by many orders of magnitude.
,
which varies by many orders of magnitude.
Figure 18 demonstrates the advantages of the Q/V ratio. Since Q and V are affected in almost the same way by the thermodynamics, these effects divide out when forming the Q/V ratio. For the extraction of the inclination angles of the main population we select, out of the 6 curves in Fig. 18, the one corresponding to FAL-F and
![]() ,
but the curves are so similar that the choice has no effect on the results.
,
but the curves are so similar that the choice has no effect on the results.
The second alternative observable that carries information on the inclination angles is the
![]() ratio. It has the advantage that the field strength B nearly divides out, since both
ratio. It has the advantage that the field strength B nearly divides out, since both ![]() and V are proportional to B
in the limit of weak fields, but it depends on the square root of the
filling factor. Since we however will assume the filling factor to be
unity for the weak population, neither the filling factor nor the field
strength enter in the determination of the inclination angles. If the
assumption of the filling factor being unity is wrong, then the derived
inclination angles will be larger than they actually are. Our
assumption thus gives maximum advantage to the horizontal fields.
and V are proportional to B
in the limit of weak fields, but it depends on the square root of the
filling factor. Since we however will assume the filling factor to be
unity for the weak population, neither the filling factor nor the field
strength enter in the determination of the inclination angles. If the
assumption of the filling factor being unity is wrong, then the derived
inclination angles will be larger than they actually are. Our
assumption thus gives maximum advantage to the horizontal fields.
Since ![]() scales with
scales with
![]() while V scales with
while V scales with
![]() ,
,
![]() scales with
scales with
![]() .
In Fig. 19 the theoretically calculated
.
In Fig. 19 the theoretically calculated
![]() divided by
divided by
![]() is given as a function of field strength for the three models and the two values of
is given as a function of field strength for the three models and the two values of ![]() ,
60
,
60![]() and 30
and 30![]() .
The spread between the 6 curves is small, demonstrating that also the
.
The spread between the 6 curves is small, demonstrating that also the
![]() ratio is insensitive to the thermodynamics. The spread is indeed very minor in comparison with the main
ratio is insensitive to the thermodynamics. The spread is indeed very minor in comparison with the main ![]() -dependent function,
-dependent function,
![]() .
Since the variation in the 0-100 G range that is relevant to the
weak population is flat, we only need to pick a single value for
.
Since the variation in the 0-100 G range that is relevant to the
weak population is flat, we only need to pick a single value for
![]() divided by
divided by
![]() .
We select 0.16 from Fig. 19
for use in our derivation of inclination angles. It is important to
note that this value refers to the use of percentage units for Q and V.
.
We select 0.16 from Fig. 19
for use in our derivation of inclination angles. It is important to
note that this value refers to the use of percentage units for Q and V.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg19.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg63.png)
|
Figure 19:
|
| Open with DEXTER | |
6.4 Calibration of the flux density scale
The extremely large flux-correlated Stokes I line weakenings that we saw in Fig. 4 indicate that the thermodynamic properties of the subresolution magnetic elements are very different from the average solar atmosphere, and that they must be accounted for to avoid serious errors in the flux density scale. The problem is that the full amount of line weakening is not directly observable, since it occurs on subpixel scales.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg20.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg64.png)
|
Figure 20: Amplitudes of Stokes V (asterisks) and Stokes Q (open squares) for the three model atmospheres AYFLUXT, FAL-F, and Maltby ( from left to right), plotted vs. Stokes I line depth, for the case of a 1000 G field strength and the 6301 Å line. The left vertical line marks the line depth observed for the pixels with the largest Stokes V amplitudes, the right vertical line the observed line depth for the smallest V amplitudes. The dotted horizontal line indicates the highest observed Stokes V in our data set. The solid and dashed curves are second-order polynomial fits through the symbols, used to extrapolate the models to the thermodynamic situation represented by the two vertical lines. |
| Open with DEXTER | |
With our three model atmospheres we can calculate synthetic
Stokes profiles for various field strengths and inclination
angles. These synthetic profiles allow us to examine the relation
between the Stokes V and Q amplitudes and the Stokes I line depth. In Fig. 20 we show this relation for the special case when the field strength is 1000 G. The three asterisks refer to the V amplitude obtained from the three model atmospheres, assuming inclination angle ![]() ,
while the open squares refer to the Stokes Q amplitudes, assuming inclination angle
,
while the open squares refer to the Stokes Q amplitudes, assuming inclination angle ![]() .
In each case the three symbols refer, from left to right, to models
AYFLUXT, FAL-F, and Maltby (the line depth being smallest for the
hottest model).
.
In each case the three symbols refer, from left to right, to models
AYFLUXT, FAL-F, and Maltby (the line depth being smallest for the
hottest model).
For comparison the solid vertical lines mark the observed Stokes I line depths for the pixels with the largest and smallest Stokes V amplitudes, respectively. While the Maltby model agrees rather well with the observed line depth for the smallest magnetic fluxes, the observed maximum line weakening lies significantly outside the range covered by the models, indicating that the ``hot'' AYFLUXT model is not hot enough. Since the observed maximum line weakening is not an outlier but is part of the tight regression relation for the points in Fig. 4, it should be representative of the flux tube population, implying that the intrinsic line weakening in the subresolution flux elements must be at least that large.
In the following analysis we will use this observed maximum line weakening as our best estimate of the intrinsic line weakening. This can be seen as a conservative estimate, since it is very possible that the intrinsic line weakening has not been reached by any pixel in our data set, and that therefore our estimate is rather a lower limit. If the line weakening is underestimated, then the derived flux densities will be too small.
Since the three symbols representing our three model atmospheres can be nicely connected with a second-order polynomial fit curve, we can easily extrapolate this fit curve to determine the values of the Stokes V amplitudes where the curve crosses the two vertical lines. These crossing points represent what the V amplitude would be for a realistic model atmosphere with a thermodynamic structure that would give Stokes I line depths equal to the observed minimum and maximum values, respectively.
The line weakenings are determined jointly by both the thermodynamics and the Zeeman splitting. While Fig. 20
illustrates how the crossing points are determined in the case of a
1000 G field with zero inclination angle in the case of the V
parameter, we have determined them in this way for the whole range of
field strengths from 100 to 2000 G and for the three inclination
angles ![]() 30
30![]() ,
and
,
and ![]() .
The results are shown in Fig. 21. The three solid curves represent the Stokes V amplitudes that correspond to a Stokes I line depth given by the left vertical line in Fig. 20
(our ``conservative'' estimate of the intrinsic line weakening in the
magnetic component) for the three inclination angles, with line
thickness decreasing with increasing inclination angle. Similarly, for
comparison, the three dashed lines represent the Stokes V amplitudes that correspond to the Stokes I line depth in areas with nearly zero flux.
.
The results are shown in Fig. 21. The three solid curves represent the Stokes V amplitudes that correspond to a Stokes I line depth given by the left vertical line in Fig. 20
(our ``conservative'' estimate of the intrinsic line weakening in the
magnetic component) for the three inclination angles, with line
thickness decreasing with increasing inclination angle. Similarly, for
comparison, the three dashed lines represent the Stokes V amplitudes that correspond to the Stokes I line depth in areas with nearly zero flux.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg21.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg68.png)
|
Figure 21:
Stokes V divided by zV and the ``true'' longitudinal flux density
|
| Open with DEXTER | |
To first order Stokes V is proportional to
![]() ,
where f is the filling factor. Therefore V has been divided by this quantity for the plot in Fig. 21. In addition we have divided by a factor that we call zV, which is given by
,
where f is the filling factor. Therefore V has been divided by this quantity for the plot in Fig. 21. In addition we have divided by a factor that we call zV, which is given by
where B should be given in units of kG. Without this factor there would be a
7 Angular distribution functions
Let us now summarize our procedure to determine the inclination angles
from the Hinode data set, in terms of the following steps (where we for
convenience of short-hand notation let Q denote the linear polarization - in reality it is always
![]() that is used): (1) Conversion of the observed Stokes V amplitude to intrinsic field strength for the main population, using the translation curve in Fig. 17; (2) conversion of the Stokes V amplitude to the relative abundance of the weak population, using the upper, analytical dot-dashed fit curve in Fig. 10, as represented by Eq. (2); (3) use of the intrinsic field strength to find the theoretically expected value for the
that is used): (1) Conversion of the observed Stokes V amplitude to intrinsic field strength for the main population, using the translation curve in Fig. 17; (2) conversion of the Stokes V amplitude to the relative abundance of the weak population, using the upper, analytical dot-dashed fit curve in Fig. 10, as represented by Eq. (2); (3) use of the intrinsic field strength to find the theoretically expected value for the
![]() ratio, using the thick FAL-F curve in Fig. 18; (4) comparison of the observed (Q/V) ratio with the theoretical ratio of step (3) to find the value of
ratio, using the thick FAL-F curve in Fig. 18; (4) comparison of the observed (Q/V) ratio with the theoretical ratio of step (3) to find the value of ![]() ,
assuming that the pixel belongs to the main population; (5) similarly, comparison of the observed
,
assuming that the pixel belongs to the main population; (5) similarly, comparison of the observed
![]() ratio with the theoretical
ratio with the theoretical
![]() value of 0.16, to find the value of
value of 0.16, to find the value of ![]() ,
assuming that the pixel belongs to the weak-field population;
(6) averaging the results of steps (4) and (5) with weights
given by the relative abundance of the two populations as found by step
(2), to obtain the final value of
,
assuming that the pixel belongs to the weak-field population;
(6) averaging the results of steps (4) and (5) with weights
given by the relative abundance of the two populations as found by step
(2), to obtain the final value of ![]() .
.
Let us here stress that errors in the determination of the intrinsic
field strength under step (1) do not much affect the inclination
angles, since the completely dominating factor influencing the ![]() determination under step (4) is the
determination under step (4) is the
![]() ratio, which varies over several orders of magnitude. Further, since
the curve determining the relative abundance of the weak population
under step (2) has been chosen in a way that maximally favors the
horizontal flux over the vertical flux, uncertainties in this choice
cannot explain why we later find a predominance of the vertical over
the horizontal flux density.
ratio, which varies over several orders of magnitude. Further, since
the curve determining the relative abundance of the weak population
under step (2) has been chosen in a way that maximally favors the
horizontal flux over the vertical flux, uncertainties in this choice
cannot explain why we later find a predominance of the vertical over
the horizontal flux density.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg22.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg72.png)
|
Figure 22:
Dashed line and pluses: observed angular distribution histogram for
vertical flux densities in the interval 100-120 G. Solid line and
asterisks: least squares model fit with the function
|
| Open with DEXTER | |
With the above procedure we can assign a value for the field inclination ![]() to every single pixel in our data set. The statistical properties of these
to every single pixel in our data set. The statistical properties of these ![]() values can best be represented in terms of the angular distribution functions, given as histograms with binning in terms of
values can best be represented in terms of the angular distribution functions, given as histograms with binning in terms of
![]() .
Only with this choice of binning is an isotropic distribution
represented by a horizontal line. If the distribution gives preference
to the horizontal fields (and thus is more pancake like), then the
histogram function will have a negative slope, while a positive slope
implies a distribution that is peaked around the vertical direction.
.
Only with this choice of binning is an isotropic distribution
represented by a horizontal line. If the distribution gives preference
to the horizontal fields (and thus is more pancake like), then the
histogram function will have a negative slope, while a positive slope
implies a distribution that is peaked around the vertical direction.
Since the angular distribution varies very strongly with flux density,
it can only be explored in a meaningful way if we make separate
histograms for different flux density bins. As an example we show in
Fig. 22
the angular distribution histogram for the vertical flux density bin
100-120 G. The observed distribution function (dashed curve)
clearly has a very steep positive slope, expressing that it is
extremely peaked around the vertical direction. To characterize each
angular distribution by a single free parameter, we use the analytical
fit function
![]() ,
with exponent
,
with exponent ![]() as the free parameter. The fit, with
as the free parameter. The fit, with
![]() ,
is shown as the solid curve in Fig. 22.
,
is shown as the solid curve in Fig. 22.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg23.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg74.png)
|
Figure 23:
Fit parameter |
| Open with DEXTER | |
The determined values of the fit parameter ![]() as a function of vertical flux density (using a sequence of flux density bins) are shown in Fig. 23. Positive values of
as a function of vertical flux density (using a sequence of flux density bins) are shown in Fig. 23. Positive values of ![]() represent distributions that are peaked to various degrees around the
vertical direction, while negative values represent pancake-like
distributions that are dominated by horizontal fields.
represent distributions that are peaked to various degrees around the
vertical direction, while negative values represent pancake-like
distributions that are dominated by horizontal fields. ![]() corresponds to an isotropic distribution. We clearly see how
corresponds to an isotropic distribution. We clearly see how ![]() rapidly increases with flux density (the distribution gets increasingly
peaked around the vertical direction) and is positive everywhere,
except for the smallest flux densities. It starts to become slightly
negative in the flux density bin 5-10 G but gets significantly
negative only for the bin 0-5 G.
rapidly increases with flux density (the distribution gets increasingly
peaked around the vertical direction) and is positive everywhere,
except for the smallest flux densities. It starts to become slightly
negative in the flux density bin 5-10 G but gets significantly
negative only for the bin 0-5 G.
There are two solutions, since we have two choices of extrapolations for the relative abundance of the weak population in Fig. 10. The solid curve with the asterisks in Fig. 23 is based on the upper curve in Fig. 10 (for which the weak population reaches 100% at zero G), while the dot-dashed curve and the pluses are based on the other extrapolation. The dashed curve is a smooth, analytical fit curve (see below).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg24.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg76.png)
|
Figure 24: Angular distribution histograms for the flux density bin 0-5 G. Solid line and asterisks: histogram exclusively due to noise, based on Monte-Carlo simulation using the upper extrapolation for the weak population in Fig. 10. Dashed line and pluses: observations. Similarly the thinner solid curve with the triangles, and the thinner dashed curve with the diamonds, represent the noise simulation and observations, respectively, based on the lower extrapolation for the weak population in Fig. 10. |
| Open with DEXTER | |
A large fraction of all the pixels have vertical flux densities in the range 0-5 G. According to Fig. 23 it appears as if they have a strong preference for a horizontal orientation (since ![]() is so negative). However, as measurement noise has the effect of making
the field look much more horizontal than it is (see below), and as the
0-5 G bin is dominated by noise, we have used the values for the
standard deviations of the actual noise in our data set to derive, via
Monte Carlo simulations, what the histogram would look like in the
0-5 G bin if it were exclusively due to measurement noise. Since
the Monte Carlo generated noise in Q and V
is evaluated according to the same procedure as the real data, we
obtain two solutions corresponding to the two extrapolations for the
weak population abundance in Fig. 10. The results are shown in Fig. 24.
The solutions for the observations are given by the dashed lines, those
for the noise simulations by the solid lines. The thicker lines (with
the asterisk and plus symbols) correspond to the upper extrapolation in
Fig. 10, the other two curves (with the triangle and diamond symbols) to the lower extrapolation.
is so negative). However, as measurement noise has the effect of making
the field look much more horizontal than it is (see below), and as the
0-5 G bin is dominated by noise, we have used the values for the
standard deviations of the actual noise in our data set to derive, via
Monte Carlo simulations, what the histogram would look like in the
0-5 G bin if it were exclusively due to measurement noise. Since
the Monte Carlo generated noise in Q and V
is evaluated according to the same procedure as the real data, we
obtain two solutions corresponding to the two extrapolations for the
weak population abundance in Fig. 10. The results are shown in Fig. 24.
The solutions for the observations are given by the dashed lines, those
for the noise simulations by the solid lines. The thicker lines (with
the asterisk and plus symbols) correspond to the upper extrapolation in
Fig. 10, the other two curves (with the triangle and diamond symbols) to the lower extrapolation.
Figure 24 shows that
there is no significant difference between the histograms for the
observations and those for the noise. Therefore there is no evidence
that there is any preponderance of horizontal over vertical fields for
any of the flux density bins. Because of noise we lack information on
the actual inclination angles for the 0-5 G bin. However, based on
the smooth shape of the derived functional relation between fit
parameter ![]() in Fig. 23 and flux density for flux densities larger than 15 G, we find that
in Fig. 23 and flux density for flux densities larger than 15 G, we find that ![]() asymptotically approaches zero in the limit of zero flux. This
indicates that the angular distribution becomes isotropic in the limit
of zero flux density, and gets increasingly peaked around the vertical
direction as the flux density increases. Already for flux densities
below 100 G it has become very strongly peaked. Such behavior may
be expected, since the buoyancy force that tries to make the field
vertical increases with field strength.
asymptotically approaches zero in the limit of zero flux. This
indicates that the angular distribution becomes isotropic in the limit
of zero flux density, and gets increasingly peaked around the vertical
direction as the flux density increases. Already for flux densities
below 100 G it has become very strongly peaked. Such behavior may
be expected, since the buoyancy force that tries to make the field
vertical increases with field strength.
We have represented the behavior of fit parameter ![]() with a smooth analytical function (dashed in Fig. 23), which has the property of approaching zero for vanishing flux density. It is given by
with a smooth analytical function (dashed in Fig. 23), which has the property of approaching zero for vanishing flux density. It is given by
where
for
The reason why noise distorts the angular distribution to make it more pancake-like with a fictitious predominance of horizontal fields lies in the fundamentally different ways that the transverse and longitudinal Zeeman effects relate polarization and field strength to each other. In the limit of small polarizations, which are most affected by noise, the linear polarization of the transverse Zeeman effect is proportional to B2, while the circular polarization of the longitudinal Zeeman effect is proportional to B. This has the consequence that we need a much larger magnetic field strength to generate a certain amount of linear polarization than we need to generate the same amount of circular polarization.
For the Hinode SOT/SP, the noise in the circular and linear polarizations are of similar magnitudes. In 3-D Poincaré space, spanned by Stokes Q, U, and V, the noise distribution is therefore nearly isotropic. When we however via the Zeeman effect translate the noise distribution in Poincaré space to the magnetic-field distribution in ordinary space, the distribution becomes pancake-like, with much larger apparent field strengths in the transverse plane.
Let us here note that an isotropic distribution of field vectors does
not imply that the average vertical and horizontal fields have the same
strengths. Instead the horizontal field is 1.57 times stronger. The
proof is simple: for a given field strength B, the vertical field is
![]() ,
the horizontal field
,
the horizontal field
![]() .
If we average the absolute value of
.
If we average the absolute value of
![]() over all directions, we get
over all directions, we get ![]() ,
while the average of the absolute value of
,
while the average of the absolute value of
![]() over all directions is 1/2. The ratio between these two numbers is
over all directions is 1/2. The ratio between these two numbers is
![]() .
.
The reason why this ratio differs from unity is that the vertical field component represents the projection of B on a certain axis, while the horizontal field represents the projection of B onto a plane. If we instead would have projected B on the two orthogonal axes in the horizontal plane, then each projection would have the same average as the projection on the vertical axis.
To avoid such confusion one should not refer to the ratio between horizontal and vertical field strengths but instead speak about the angular distribution and compare it with the isotropic distribution.
8 Distribution of vertical flux densities
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg25.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg85.png)
|
Figure 25: Probability density function PDF for the vertical flux densities. Solid curve: observations. Dashed curve: analytical fit function, given by Eq. (10) as explained in the text. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg26.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg86.png)
|
Figure 26: Same as Fig. 25, but with linear scale for the core region of the PDF. The dashed curve is an analytical representation of the noise-free PDF (same as dashed curve in Fig. 25). If one convolves it with the Gaussian noise distribution, the dotted curve is obtained, which is nearly indistinguishable from the solid (observed) curve. |
| Open with DEXTER | |
We now turn our attention to the vertical flux densities Bv, derived with the procedure described in Sect. 6.4, which also makes use of the derived inclination angles ![]() .
Figure 25 shows the resulting histogram as the solid curve in lin-log scale, Fig. 26
as the solid curve for the core region in linear scale. The dashed
curves in the two figures show an analytical function that represents
the histogram in the absence of measurement noise (see below).
.
Figure 25 shows the resulting histogram as the solid curve in lin-log scale, Fig. 26
as the solid curve for the core region in linear scale. The dashed
curves in the two figures show an analytical function that represents
the histogram in the absence of measurement noise (see below).
To derive the flux densities we need to make a choice between the two extrapolated versions of the relative proportion of the weak population, as given in Fig. 10. For all the probability density functions (PDFs) that we present here, we have chosen the upper extrapolation that ends at 100% for zero flux density, because it relates to a physical scenario for the magnetic dichotomy with the Sun's magnetic flux in a collapsed and an uncollapsed state, and this choice in addition maximally favors the horizontal fields. We have also calculated all the PDFs with the other extrapolation choice, but find that the choice of extrapolation does not affect the derived PDFs except in minor quantitative details.
Since to first order the values for the vertical flux densities scale in proportion to Stokes V, and since the noise in V has a centered Gaussian distribution, the influence of noise on the observed PDF for the vertical flux densities can be described in terms of a Gaussian convolution of the ``intrinsic'' PDF. The determined standard deviation for the actual noise in our data represents a Gaussian that is nearly as wide as the core of the observed PDF. This implies that the core of the ``intrinsic'', noise-free PDF must be extremely narrow, otherwise the Gaussian smearing would result in a PDF that is broader than observed.
The intrinsic PDF therefore must have an extremely peaked and narrow
core. A convenient (although not unique) choice of parametrized
analytical representation of such a peaked function is in terms of a
stretched exponential
where Bv is given in G, and k is the free stretching parameter. The dashed curve in Fig. 26 is based on the value k=0.6.
For the PDF wings the stretched exponential does not give a good representation, a better choice is the Lorentzian
A Lorentz function is however symmetric, while the observed histogram shows a pronouced asymmetry between the positive and negative sides. This unbalance between the magnetic polarities of the sampled solar region can be accounted for by the ``anomalous dispersion'' type function
The dashed curves in Figs. 25 and 26 are based on using the function L(Bv)+A(Bv), with the choice
to obtain the PDF distribution P(Bv) as
With the choice of
When convolving P(Bv) with the Gaussian noise distribution we obtain the dotted curve in Fig. 26, which is almost indistinguishable from the observed, solid curve, as expected if the dashed curve is a good representation of the noise-free PDF.
In the far wings in Fig. 25, where the noise-smearing has no practical effect, our simplified choice of analytical representation P(Bv) differs in some important details from the solid curve that represents the observed PDF: for vertical flux densities larger than 600 G there is a histogram excess (a bump in the distribution), which extends almost to the upper cut-off (maximum flux density). For the positive polarity the cut-off occurs near 1200 G, for the negative polarity much earlier. The statistical significance of this bump needs to be tested by extending the statistical sample.
9 Distribution of total and horizontal flux densities
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg27.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg93.png)
|
Figure 27: The solid and dashed curves that are peaked at zero flux density represent noise-free PDFs for the total and horizontal flux densities, respectively, derived from the data with a Monte Carlo technique as described in the text. The dotted curve is half of the symmetric part of the analytical noise-free version of the PDF for the vertical flux density from Fig. 25. The dot-dashed and long-dashed curves are the PDFs for the apparent total and horizontal flux densities, before application of any noise-correction procedure. |
| Open with DEXTER | |
In Fig. 27 we plot the derived PDFs (uncorrected for noise) for the horizontal flux densities as the long-dashed curve, for the total flux density vector as the dot-dashed curve. For reference we also show as the dotted curve the dashed analytical fit curve of Fig. 25, which represents the noise-free PDF for the vertical flux densities.
The solid and short-dashed curves in Fig. 27 represent noise-free versions of the PDFs for the total and horizontal flux densities, respectively, to demonstrate that in the absence of noise all the PDFs are extremely peaked at zero flux density, and that the displacement of the apparent PDF maximum from zero to about 27 G is an artefact of noise. The somewhat elaborate procedure for this noise removal is as follows:
In the case of the PDF for the vertical flux densities the influence of
noise is, to first order, a simple Gaussian convolution. Therefore it
was rather straightforward to find the very peaked, ``intrinsic'' PDF
for the vertical flux densities (dashed curve in Fig. 26).
Since the noise enters in an entirely different and entangled way for
the horizontal and total flux densities, we have made use of the
possibility to derive these PDFs from the known PDF for the vertical
flux densities together with the known angular distribution of field
vectors, as given by the analytical expression for the distribution
parameter ![]() in Eqs. (4) and (5). This derivation uses a Monte Carlo technique (random-number generator), as follows:
in Eqs. (4) and (5). This derivation uses a Monte Carlo technique (random-number generator), as follows:
The starting point is the analytical representation of the noise-free PDF for the vertical flux densities as given by the dashed curve in Fig. 25 and by Eqs. (6) to (10), but we only use the symmetric part, since the PDFs for the horizontal and total flux densities that we want to reconstruct are one-sided. This symmetric vertical-field PDF is sampled 50 million times with a random-number generator (that picks a number between 0 and 1 to randomly select a value for the cumulative, integrated version of the area-normalized PDF, which is then inverted to find the corresponding flux density value that represents the random pick that is governed by the given PDF function). Similarly we use Eqs. (4) and (5) that describe the angular distribution of field vectors as a function of vertical flux density, and with the random-number generator find the inclination angle that is generated by the angular distribution in combination with the already picked vertical flux density. From the generated pair of values for the vertical flux density and inclination angle the corresponding values for the horizontal and total flux densities follow by simple geometrical projection.
With the help of this procedure we find that all the PDFs, also the ones for the horizontal and total flux densities, have their maxima in the form of an extremely narrow peak at zero flux density. The apparent displacement of the maxima away from zero is an artefact of noise. This conclusion is in agreement with the numerical simulations of magneto-convection by Stein & Nordlund (2006), who find PDFs for the total field strength that also have a narrow, extremely peaked maximum at zero field strength.
10 Conclusions and outlook
We find no evidence for any predominance of horizontal fields on the quiet Sun. The angular distribution of the field varies steeply with flux density. For the largest flux densities the distribution is extremely peaked around the vertical direction. As we go to smaller vertical flux densities the distribution widens to become asymptotically isotropic in the limit of zero flux density. The apparent dominance of horizontal fields for flux densities below 5 G is shown to be an artefact of noise.
An unexpected finding is the discovery of a magnetic dichotomy with two distinct populations. It can be understood in terms of the convective collapse mechanism, according to which the flux spontaneously ends up in two states, a collapsed and an uncollapsed state. The existence of a well-defined weak population allows us to renormalize the Stokes V line ratios to correct for a serious scale offset that is due to the differential effects of subpixel correlations between the gradients of the velocity and magnetic fields. With the renormalized line ratios we find that the intrinsic field strengths for the collapsed flux increases from 700 to 1870 G as we go from the smallest to the largest flux densities.
We have identified the Q/V and
![]() ratios as robust observables for determinations of the inclination angle
ratios as robust observables for determinations of the inclination angle ![]() .
Here Q is used as short-hand notation for
.
Here Q is used as short-hand notation for
![]() ,
and Q, U, and V refer to the amplitude of the blue wing
,
and Q, U, and V refer to the amplitude of the blue wing ![]() lobe. We have demonstrated with synthetic spectra that the influence on Q/V and
lobe. We have demonstrated with synthetic spectra that the influence on Q/V and
![]() of the choice of model atmosphere approximately divides out, since the
nominator and denominator are similarly affected by the thermodynamic
parameters.
of the choice of model atmosphere approximately divides out, since the
nominator and denominator are similarly affected by the thermodynamic
parameters.
The Q/V ratio has the great advantage that it is independent of the ill determined filling factor (which divides out). Therefore we apply it to the main population, which has highly varying filling factors. The Q/V ratio however scales with the (intrinsic) field strength, which we retrieve with the help of the renormalized Stokes V line ratio. This procedure gives us field strengths that are consistent with previous determinations from the 5247-5250 line ratio and from infrared diagnostics. For this reason there should not be any significant systematic error in the derived inclination angles.
The
![]() ratio on the other hand is nearly independent of field strength but
scales with the square root of the filling factor. Therefore we use it
for the weak population, for which we cannot use the line ratio to get
any field strength estimates, but for which we instead assume the
filling factor to be unity (spatially resolved fields). As long as this
assumption is valid the
ratio on the other hand is nearly independent of field strength but
scales with the square root of the filling factor. Therefore we use it
for the weak population, for which we cannot use the line ratio to get
any field strength estimates, but for which we instead assume the
filling factor to be unity (spatially resolved fields). As long as this
assumption is valid the
![]() ratio gives us robust inclination angles for the weak population. If
however this assumption is wrong and the actual filling factor is
significantly smaller than unity, then our inclination angles will be
too large. Our assumption that the filling factor is unity gives
maximum advantage to the horizontal fields. Therefore this assumption
is not to blame when we find a predominance of vertical instead of
horizontal fields.
ratio gives us robust inclination angles for the weak population. If
however this assumption is wrong and the actual filling factor is
significantly smaller than unity, then our inclination angles will be
too large. Our assumption that the filling factor is unity gives
maximum advantage to the horizontal fields. Therefore this assumption
is not to blame when we find a predominance of vertical instead of
horizontal fields.
Once we have reliable determinations of the inclination angles and the vertical flux densities, we obtain the horizontal and total flux densities through geometrical projections. The conversion of Stokes V amplitudes to vertical flux densities requires knowledge about the intrinsic thermodynamic line weakenings in the subresolution magnetic elements. From the tight regression relation between Stokes I line depth and Stokes V amplitude we can infer the presence of line weakenings that significantly exceed those expected for the hottest flux tube models in the literature. The inferred line weakenings allow us to obtain the flux density scale from the observed polarization.
The so obtained PDF for the vertical flux densities contains a nearly Gaussian core at zero flux density and extended wings that decline quadratically. As the width of the core region only marginally exceeds that of the Gaussian distribution for the measurement noise, we conclude that the noise-free core region is extremely narrow and peaked at zero flux density, with a shape that can be well represented by a stretched exponential. The PDF wings on the other hand can be better fit with a Lorentz profile plus an anti-symmetric line dispersion function that accounts for the imbalance between the positive and negative magnetic polarities in the sampled solar region. The observed PDF has a bump in excess of the Lorentzian function near kG flux densities, which may reflect the circumstance that most of the collapsed flux is carried by kG fields, and that some fraction of the subresolution flux elements are partially resolved with the Hinode 200 km spatial resolution.
With the analytical representation of the noise-free PDF for the vertical flux densities and the derived angular distribution as a function of vertical flux density we can use Monte Carlo simulations to derive the corresponding noise-free PDFs for the horizontal and total flux densities. We find them also to be strongly peaked at zero flux density and have extended wings. Thereby we demonstrate that the apparent shift of the PDF maximum from zero to about 27 G in the directly determined PDFs is spurious and an artefact of noise.
In the present paper we have tried to make a clear distinction between flux density and field strength, although both are measured in the same units (G). With flux density we mean the flux divided by the spatial resolution element. It thus refers to a certain spatial scale, the resolution scale. All our PDFs in the present paper refer to flux densities at the Hinode resolution scale, and not to field strengths. In the limit of infinite resolution the distinction between flux density and field strength would disappear, but we are of course very far from such a situation.
Eventually we would like to go beyond flux densities to gain insight
into the PDF for the field strengths. We do not think that the
2-component model should be used as the starting point for this
purpose, since by definition it represents an assumed PDF consisting of
two ![]() function peaks, one at zero G, correponding to the
``non-magnetic'' component, and one at a field strength near 1 kG,
representing the magnetic component. Although this cartoon-like
scenario has been useful for a number of diagnostic purposes, it has no
similarity to the field structure obtained from numerical simulations
of magneto-convection, and it is not consistent with the behavior of
the observed Stokes profile amplitudes when the spatial resolution
is varied (Martínez González et al. 2010).
The underlying reality is more likely represented by continuous PDFs.
Our use of the 2-component model in the present paper has been limited
to the task of properly translating the observed Q/V ratios, which are field-strength dependent, to inclination angles, as well as to converting the observed Stokes V,
which depends on intrinsic thermodynamic line weakenings, to vertical
flux densities. We make no other use here of the extracted ``intrinsic
field strengths'', they only serve as an aid to obtain distribution
functions valid for the Hinode resolution scale.
function peaks, one at zero G, correponding to the
``non-magnetic'' component, and one at a field strength near 1 kG,
representing the magnetic component. Although this cartoon-like
scenario has been useful for a number of diagnostic purposes, it has no
similarity to the field structure obtained from numerical simulations
of magneto-convection, and it is not consistent with the behavior of
the observed Stokes profile amplitudes when the spatial resolution
is varied (Martínez González et al. 2010).
The underlying reality is more likely represented by continuous PDFs.
Our use of the 2-component model in the present paper has been limited
to the task of properly translating the observed Q/V ratios, which are field-strength dependent, to inclination angles, as well as to converting the observed Stokes V,
which depends on intrinsic thermodynamic line weakenings, to vertical
flux densities. We make no other use here of the extracted ``intrinsic
field strengths'', they only serve as an aid to obtain distribution
functions valid for the Hinode resolution scale.
Another approach to gain the desired insight into the PDF for the field strengths is to explore the scaling behavior of the PDF for the flux density at different spatial scales. Earlier attempts to do this have indicated a high degree of scale invariance (Stenflo & Holzreuter 2003a; Janßen et al. 2003; Stenflo & Holzreuter 2002; Lawrence et al. 1993; Cadavid et al. 1994; Lawrence et al. 1996; Pietarila Graham et al. 2009), which is characteristic of a multi-fractal. Our discovery of a magnetic dichotomy, however, suggests a scenario in the spatially unresolved domain that has similarity with the idealized 2-component model, with the flux split into two discrete states, a collapsed and an uncollapsed state, each with well separated distribution functions, one concentrated around high field strengths (of order 1 kG), the other peaked at zero field strength. The bump of our observed PDFs near kG flux densities is a hint in this direction.
Earlier suggestions for a magnetic dichotomy have been related to the use of two mutually almost exclusive diagnostic tools, the Zeeman and Hanle effects. The resulting dualistic view of solar magnetism could then be an artefact of the circumstance that the Hanle and Zeeman effects project out distinctly different aspects of an underlying, unified reality (Stenflo & Holzreuter 2003b). In contrast, the magnetic dichotomy discovered in the present paper cannot be such a diagnostic artefact, since it is exclusively based on the Zeeman effect, without any use of the Hanle effect at all. It is interesting to note that the field being diagnosed by the Hanle effect is almost exclusively that of the weak population, since the intrinsic fields of the main (collapsed) population are beyond the Hanle sensitivity range.
The magnetic dichotomy suggests that a break in the approximate scale invariance of the PDF may occur just below the currently resolved scales, near the 100 km scale where the transition between optically thick and thin scales takes place. Below this scale the PDF may break up into separated strong-field and a weak-field regions. No such break has so far been indicated in numerical MHD simulations. If the break is found to be real, it can therefore have important implications for our understanding of the physical processes, on which the MHD simulations are based.
Although the collapsed magnetic structures that may cause the mentioned break in the PDF scaling law are not resolved by Hinode, the theoretical MHD simulations can still be well tested and constrained by the current data. Thus the simulations need to be able to reproduce the empirical PDFs, the observed dependence of the angular distribution on flux density, the histograms of the Stokes V asymmetry and their dependence on flux density, as well as the tight correlations of the line weakenings and broadenings with the flux density. However, the probably most important and biggest challenge for the MHD simulations will be to reproduce our discovery of two distinct populations in the Stokes V scatter plot diagram, which may test how well the convective collapse mechanism is contained and resolved in the numerical simulation models.
AcknowledgementsPart of the present work was carried out during a month-long visit to the Hinode Science Center in Mitaka during November 2009. I am grateful to Saku Tsuneta and his colleagues at NAOJ for their great support and hospitality, and to David Orozco Suarez for many constructive discussions. Further I wish to thank Bruce Lites for having introduced me to the wonderful Hinode SOT/SP data set. Hinode is a Japanese mission developed and launched by ISAS/JAXA, with NAOJ as domestic partner and NASA and STFC (UK) as international partners. It is operated by these agencies in co-operation with ESA and NSC (Norway).
References
- Asensio Ramos, A. 2009, ApJ, 701, 1032 [NASA ADS] [CrossRef] [Google Scholar]
- Ayres, T. R., Testerman, L., & Brault, J. W. 1986, ApJ, 304, 542 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, C., & Rezaei, R. 2009, A&A, 502, 969 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cadavid, A. C., Lawrence, J. K., Ruzmaikin, A. A., & Kayleng-Knight, A. 1994, ApJ, 429, 391 [NASA ADS] [CrossRef] [Google Scholar]
- Chapman, G. A., & Sheeley, Jr., N. R. 1968, Sol. Phys., 5, 442 [NASA ADS] [CrossRef] [Google Scholar]
- de Wijn, A. G., Stenflo, J. O., Solanki, S. K., & Tsuneta, S. 2009, Space Sci. Rev., 144, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Domínguez Cerdeña, I., Sánchez Almeida, J., & Kneer, F. 2006, ApJ, 636, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Fontenla, J. M., Avrett, E. H., & Loeser, R. 1993, ApJ, 406, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Frazier, E. N., & Stenflo, J. O. 1978, A&A, 70, 789 [NASA ADS] [Google Scholar]
- Janßen, K., Vögler, A., & Kneer, F. 2003, A&A, 409, 1127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Khomenko, E., & Collados, M. 2007, ApJ, 659, 1726 [NASA ADS] [CrossRef] [Google Scholar]
- Khomenko, E. V., Collados, M., Solanki, S. K., Lagg, A., & Trujillo Bueno, J. 2003, A&A, 408, 1115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lawrence, J. K., Ruzmaikin, A. A., & Cadavid, A. C. 1993, ApJ, 417, 805 [NASA ADS] [CrossRef] [Google Scholar]
- Lawrence, J. K., Cadavid, A. C., & Ruzmaikin, A. A. 1996, ApJ, 465, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Lites, B. W., Kubo, M., Socas-Navarro, H., et al. 2008, ApJ, 672, 1237 [NASA ADS] [CrossRef] [Google Scholar]
- Maltby, P., Avrett, E. H., Carlsson, M., et al. 1986, ApJ, 306, 284 [Google Scholar]
- Martínez González, M. J., Asensio Ramos, A., López Ariste, A., & Manso Sainz, R. 2008a, A&A, 479, 229 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martínez González, M. J., Collados, M., Ruiz Cobo, B., & Beck, C. 2008b, A&A, 477, 953 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martínez González, M. J., Manso Sainz, R., Asensio Ramos, A., López Ariste, A., & Bianda, M. 2010, ApJ, 711, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Orozco Suárez, D., Bellot Rubio, L. R., del Toro Iniesta, J. C., et al. 2007, ApJ, 670, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1978, ApJ, 221, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Pietarila Graham, J., Danilovic, S., & Schüssler, M. 2009, ApJ, 693, 1728 [Google Scholar]
- Rüedi, I., Solanki, S. K., Livingston, W., & Stenflo, J. O. 1992, A&A, 263, 323 [NASA ADS] [Google Scholar]
- Sánchez Almeida, J., & Lites, B. W. 2000, ApJ, 532, 1215 [NASA ADS] [CrossRef] [Google Scholar]
- Schüssler, M., & Vögler, A. 2008, A&A, 481, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sheeley, Jr., N. R. 1967, Sol. Phys., 1, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Sigwarth, M. 2001, ApJ, 563, 1031 [NASA ADS] [CrossRef] [Google Scholar]
- Solanki, S. K., Livingston, W., & Ayres, T. 1994, Science, 263, 64 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Spruit, H. C. 1979, Sol. Phys., 61, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Spruit, H. C., & Zweibel, E. G. 1979, Sol. Phys., 62, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Stein, R. F., & Nordlund, Å. 2006, ApJ, 642, 1246 [NASA ADS] [CrossRef] [Google Scholar]
- Steiner, O. 2000, Sol. Phys., 196, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Stenflo, J. O. 1971, in Solar Magnetic Fields, ed. R. Howard, IAU Symp., 43, 101 [Google Scholar]
- Stenflo, J. O. 1973, Sol. Phys., 32, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Stenflo, J. O. 1982, Sol. Phys., 80, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Stenflo, J. O. 1994, Solar Magnetic Fields - Polarized Radiation Diagnostics. (Kluwer) [Google Scholar]
- Stenflo, J. O., & Holzreuter, R. 2002, in Proceedings of the Magnetic Coupling of the Solar Atmosphere Euroconference, ed. H. Sawaya-Lacoste, ESA Special Publication, 505, SOLMAG, 101 [Google Scholar]
- Stenflo, J. O., & Holzreuter, R. 2003a, in Current Theoretical Models and Future High Resolution Solar Observations: Preparing for ATST, ed. A. A. Pevtsov, & H. Uitenbroek, ASP Conf. Ser., 286, 169 [Google Scholar]
- Stenflo, J. O., & Holzreuter, R. 2003b, Astron. Nachr., 324, 397 [Google Scholar]
- Stenflo, J. O., Solanki, S., Harvey, J. W., & Brault, J. W. 1984, A&A, 131, 333 [NASA ADS] [Google Scholar]
- Suematsu, Y., Tsuneta, S., Ichimoto, K., et al. 2008, Sol. Phys., 249, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Unno, W., & Ando, H. 1979, Geophys. Astrophys. Fluid Dyn., 12, 107 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg1.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg18.png)
|
Figure 1:
The solid curves represent normalized mean Stokes V ( top panel) and Q ( bottom panel)
profiles that are representative of weak polarizations (polarization
amplitudes 0.5-3%). The dashed curve in the top panel shows for
comparison the normalized
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg2.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg25.png)
|
Figure 2: Normalized histogram of the Stokes V blue-lobe amplitudes for the 6301 Å line, in lin-log scale. The inset panel shows the core region in linear scale. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg3.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg26.png)
|
Figure 3:
Amplitude-normalized histograms of the Stokes V asymmetry A defined in Eq. (1) for various bins of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg4.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg31.png)
|
Figure 4:
Variation of Stokes I relative line depth d with Stokes V amplitude of the 6301 Å line. Solid curve: 6301 Å. Dashed curve: 6302 Å. The dotted curves represent the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg5.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg32.png)
|
Figure 5: Same as Fig. 4, but for the Stokes I line widths. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg6.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg33.png)
|
Figure 6:
Observed Stokes I
line depth ratio between the 6302 and 6301 Å lines. Here the
dashed curve represents the observed mean relation, while the solid
line is a straight line fit to demonstrate the high degree of linearity
of the relation. The dotted curves are the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg7.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg34.png)
|
Figure 7: Synthetic Stokes I line depth ratio vs. field strength for the three model atmospheres illustrated in Fig. 12 (dotted curve: hot flux tube model AYFLUXT; solid curve: facular model FAL-F; dashed curve: quiet Sun model Maltby). The upper (lower) horizontal lines represent the observed d line ratio for the pixels with the smallest (largest) Stokes V amplitudes. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg8.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg35.png)
|
Figure 8: Scatter plot of the blue lobe Stokes V amplitudes derived for the 6302 Å line vs. the corresponding Stokes V amplitudes for the 6301 Å line. The dashed line with slope s=1.66 represents the regression relation that would be expected for spatially resolved, weak fields. We identify two populations of points: (1) The dominant population that follows a slope that is about 0.7s for small polarizations, decreasing to about 0.6s for larger values. (2) A secondary population that is significant only for Stokes V amplitudes below about 2%, and which almost follows the slope of the dashed line. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg9.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg39.png)
|
Figure 9:
Histogram of the
V6302/V6301 line ratio (normalized to the slope s, which accounts for the factor 0.6=1/s) for a
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg10.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg41.png)
|
Figure 10:
Fraction of points belonging to the weaker-field population (solid curve), surrounded by the 1- |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg11.eps} \vspace*{3mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg45.png)
|
Figure 11:
Line-ratio position (normalized to the resolved weak-field case) of the two Gaussian components vs. Stokes V amplitude
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg12.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg46.png)
|
Figure 12: Temperature structure of the three model atmospheres used to explore the behavior of various synthetic observables. Solid line: Quiet-Sun model of Maltby et al. (1986). Dashed line: Facular model FAL-F of Fontenla et al. (1993). Dot-dashed line: Hot flux tube model AYFLUXT of Ayres et al. (1986) and Solanki et al. (1994). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg13.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg47.png)
|
Figure 13: Comparison between observed and synthetic Stokes I profiles. The microturbulence is zero in all three models. The dotted, dashed, and dot-dashed curves represent the models of Maltby, FAL-F, and AYFLUXT, respectively, while the solid line represents the observations for the central pixel of the data set. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg14.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg48.png)
|
Figure 14: Stokes V line ratios obtained from Figs. 11 and 8 (dotted, dashed, and dot-dashed curves). The solid curve represents an analytical fit to the main population, while the weak population is characterized by the horizontal level at 1.55. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg15.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg49.png)
|
Figure 15: Theoretical Stokes V line ratio vs. field strength, calculated for the three model atmospheres (solid: AYFLUXT, dotted: FAL-F, dot-dashed: Maltby). The agreement between the three curves demonstrates that the line ratio is insensitive to the thermodynamic structure of the atmosphere. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg16.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg50.png)
|
Figure 16: Normalized theoretical Stokes V line ratio for the AYFLUXT model, after applying the 35 mÅ spectral smearing done by Hinode. The normalized observed line ratios of the main population fall within the range marked by the horizontal dotted and dashed lines. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg17.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg51.png)
|
Figure 17: Field strength representing the magnetic component of the main population vs. Stokes V blue wing polarization amplitude in the 6301 Å line, obtained through a translation of Fig. 14 with the help of Fig. 16. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg18.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg54.png)
|
Figure 18:
Q/V ratio divided by
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg19.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg63.png)
|
Figure 19:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg20.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg64.png)
|
Figure 20: Amplitudes of Stokes V (asterisks) and Stokes Q (open squares) for the three model atmospheres AYFLUXT, FAL-F, and Maltby ( from left to right), plotted vs. Stokes I line depth, for the case of a 1000 G field strength and the 6301 Å line. The left vertical line marks the line depth observed for the pixels with the largest Stokes V amplitudes, the right vertical line the observed line depth for the smallest V amplitudes. The dotted horizontal line indicates the highest observed Stokes V in our data set. The solid and dashed curves are second-order polynomial fits through the symbols, used to extrapolate the models to the thermodynamic situation represented by the two vertical lines. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg21.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg68.png)
|
Figure 21:
Stokes V divided by zV and the ``true'' longitudinal flux density
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg22.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg72.png)
|
Figure 22:
Dashed line and pluses: observed angular distribution histogram for
vertical flux densities in the interval 100-120 G. Solid line and
asterisks: least squares model fit with the function
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg23.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg74.png)
|
Figure 23:
Fit parameter |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg24.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg76.png)
|
Figure 24: Angular distribution histograms for the flux density bin 0-5 G. Solid line and asterisks: histogram exclusively due to noise, based on Monte-Carlo simulation using the upper extrapolation for the weak population in Fig. 10. Dashed line and pluses: observations. Similarly the thinner solid curve with the triangles, and the thinner dashed curve with the diamonds, represent the noise simulation and observations, respectively, based on the lower extrapolation for the weak population in Fig. 10. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg25.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg85.png)
|
Figure 25: Probability density function PDF for the vertical flux densities. Solid curve: observations. Dashed curve: analytical fit function, given by Eq. (10) as explained in the text. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg26.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg86.png)
|
Figure 26: Same as Fig. 25, but with linear scale for the core region of the PDF. The dashed curve is an analytical representation of the noise-free PDF (same as dashed curve in Fig. 25). If one convolves it with the Gaussian noise distribution, the dotted curve is obtained, which is nearly indistinguishable from the solid (observed) curve. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13972fg27.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13972-09/Timg93.png)
|
Figure 27: The solid and dashed curves that are peaked at zero flux density represent noise-free PDFs for the total and horizontal flux densities, respectively, derived from the data with a Monte Carlo technique as described in the text. The dotted curve is half of the symmetric part of the analytical noise-free version of the PDF for the vertical flux density from Fig. 25. The dot-dashed and long-dashed curves are the PDFs for the apparent total and horizontal flux densities, before application of any noise-correction procedure. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



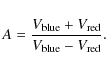
![\begin{displaymath}r_{\rm weak}=\left[~1-(\vert V_{6301}\vert/4.17)^{0.75}~\right]^4,
\end{displaymath}](/articles/aa/full_html/2010/09/aa13972-09/img43.png)