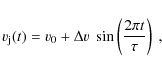EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 517 (July 2010) A&A, 517 (2010) A20 Full HTML
Free Access
Issue
A&A
Volume 517, July 2010
Article Number A20
Number of page(s) 7
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/200913908
Published online 27 July 2010
A&A 517, A20 (2010)

A variable jet model for the H$\alpha $ emission of HH 444

A. C. Raga1 - A. Riera2 - D. I. González-Gómez3

1 - Instituto de Ciencias Nucleares, UNAM, Ap. 70-543, 04510 D. F. México, México
2 - Departament de Física i Enginyeria Nuclear, EUETIB, Universitat Politecnica de Catalunya, Compte d'Urgell 187, 08036 Barcelona, Spain
3 - Instituto de Geofísica, UNAM, 04510 D. F. México, México

Received 18 December 2009 / Accepted 7 March 2010

Abstract
Context. HH 444 is one of the first Herbig-Haro (HH) jets discovered within a photoionized region.
Aims. We re-analyze the H$\alpha $and red [S II] HST images of HH 444, and calculate the width of the jet as a function of distance from the source. We compare the H$\alpha $ image with predictions from variable ejection velocity jet models.
Methods. The determination of the jet's width is done with a non-parametric, wavelet analysis technique. The axisymmetric, photoionized jet simulations are used to predict H$\alpha $ maps that can be directly compared with the observations.
Results. Starting with a thin jet (unresolved at the resolution of the observations), we are able to produce knots with widths and morphologies that generally agree with the H$\alpha $ knots of HH 444. This agreement is only obtained if the jet axis is at a relatively large, ${\sim}45^\circ$ angle with respect to the sky. This agrees with previous spectroscopic observations of the HH 444 bow shock, which imply a relatively large jet axis/plane of the sky angle.
Conclusions. We conclude that the general morphology of the chain of knots close to V510 Ori (the HH 444 source) can be explained with a variable ejection velocity jet model. For explaining the present positions of the HH 444 knots, however, it is necessary to invoke a more complex ejection velocity history than a single-mode, periodic variability.

Key words: circumstellar matter - ISM: jets and outflows - Herbig-Haro objects - ISM: individual objects: HH 444 - stars: formation

1 Introduction

HH 444, a Herbig-Haro (HH) object in the vicinity of $\sigma$ Orionis, is one of the first jets detected within a photoionized region (Reipurth et al. 1998). The NE outflow lobe has a chain of aligned knots extending ${\sim}20''$ away from the source (V510 Ori) and a bow shock structure ${\sim}2'.7$ away from V510 Ori.

Reipurth et al. (1998) presented images and low dispersion spectra of this object. López-Martín et al. (2001) presented two long-slit spectra (of the base of the HH 444 jet, and of the bow shock) and compared the observations with a numerical simulation of an externally photoionized, variable ejection velocity jet. Finally, Andrews et al. (2004) presented a long-slit spectrum of the jet/counterjet system within ${\sim}7''$ from V510 Ori as well as an H$\alpha $ and a [S II] 6716+30 HST image of the outflow (not including the HH 444 bow shock at ${\sim}3'$ from the source, see above).

Since the discovery of HH 444 (Reipurth et al. 1998), a considerable number of HH jets within photoionized regions have been found. For example, Bally & Reipurth (2001) report the discovery of several HH jets within the outskirts of M 42 and in NGC 1333 (also see Bally et al. 2001). Many of these jets show remarkable, curved structures, which have been interpreted as the interaction between the HH outflows and a streaming external medium (which could result e.g. from the expansion of the H II region). This type of curved morphology has been modeled in some detail both analytically (Cantó & Raga 1995) and numerically (Lim & Raga 1998; Masciadri & Raga 2001; Ciardi et al. 2008).

Both its less complex structure and the detailed available observations render HH 444 a candidate for studying whether or not a variable ejection jet model can reproduce the observed knot structures. A similar comparison was previously done e.g. for the DG Tauri microjet (Raga et al. 2001), HH 34 (Raga & Noriega-Crespo 1998), HH 111 (Masciadri et al. 2002) and HH 32 (Raga et al. 2004).

The only externally photoionized jet that was modeled in this way is HH 444. López-Martín et al. (2001) computed 3D, variable jet models from which they obtained predictions of position-velocity diagrams (which they then compare with the observed long-slit spectra of the HH 444 jet base). They studied the effects of having a non-zero initial opening angle for the jet, and of a non-top hat initial cross section.

We first re-analyze the HST images of Andrews et al. (2004). We we use a wavelet analysis technique (Riera et al. 2003) to determine the angular sizes across the outflow axis of the knots in the two outflow lobes (Sect. 2). We then compute a grid of photoionized, single-mode variable ejection velocity, axisymmetric jet models (Sect. 3) from which we obtain H$\alpha $maps that can be directly compared with the H$\alpha $ HST image of HH 444 (Sect. 4). We discuss the time evolution predicted for the H$\alpha $ maps and the effects of having different orientations between the outflow and the plane of the sky. Finally, we discuss a two-mode variable ejection velocity jet model (Sect. 5).

\begin{figure} \par\includegraphics[width=9cm,clip]{13908fig1.eps} \end{figure} Figure 1:

HH 444 H$\alpha $ image ( right, see Sect. 2.1) and characteristic width $a_{x,{\rm m}}$ as a function of position along the jet axis ( left), obtained from the wavelet analysis (see Sect. 2.2). Two successive contours correspond to a factor of 2.

Open with DEXTER

\begin{figure} \par\includegraphics[width=9cm,clip]{13908fig2.eps} \end{figure} Figure 2:

HH 444 [S II] 6716+30 image ( right, see Sect. 2.1) and characteristic width $a_{x,{\rm m}}$ as a function of position along the jet axis ( left), obtained from the wavelet analysis (see Sect. 2.2). Two successive contours correspond to a factor of 2.

Open with DEXTER

2 The H$\alpha $ and [S II] images of HH 444

2.1 HST images

The F656N H$\alpha $ and F673N [S II] Wide Field Planetary Camera 2 (WFPC2) images of HHH 444-445 were retrieved from the HLA[*] archive. The images were obtained on 2000 January 25 with the WFPC2 on HST through the F656N and F673N filters. HH 444 was placed on the WF4 CCD which has a plate scale of $0\hbox{$.\!\!^{\prime\prime}$ }1$ pixel-1. Four exposures were obtained with each filter giving a total exposure time of 5100 s (for H$\alpha $) and 5200 s (for [S II]). These images were originally part of the Cycle 8 proposal 8323 (P.I.: B. Reipurth). For details of the observations see Andrews et al. (2004). The retrieved data were processed with the HST pipeline used at the Canadian Astronomy Data Centre (CADC).

2.2 Morphological analysis

In Figs. 1 and 2 we show the H$\alpha $ and [S II] images of HH 444, where we can see the structure of the jet/counterjet close to the outflow source. The knots were named following the nomenclature used by Reipurth et al. (1998).

As previously reported by Andrews et al. (2004), the [S II] emission displays a chain of compact knots emanating from the outflow source up to 12'' from the stellar centroid. The inner region of the jet (i.e., knot A) is dominated by [S II]. The H$\alpha $ emission of the jet extends up to ${\sim}20''$ from the stellar centroid (i.e., to larger distances than the [S II] emission). The inner part of the H$\alpha $ jet is more diffuse than its [S II] counterpart.

In order to assess the width of the HH 444 jet as a function of distance from the central source, we have applied a wavelet transform analysis. This method for deriving the width of a jet is mathematically more complex than the ``standard'' method of fitting a function (e.g., a Gaussian profile) to the cross section of the jet and then using the characteristic width of this function as an estimate of the jet width (this approach dates back to the papers of Raga & Mateo 1988; Bührke et al. 1988).

We first attempted to fit Gaussians to the cross section of the HH 444 jet in the HST images. We find that this does not produce satisfactory results for two reasons:

  • the signal-to-noise of the images is quite poor (because of this, Andrews et al. 2004 actually show spatially smoothed images),
  • the substraction of the background emission is not straightforward, particularly in the region close to the jet source (in which a strong reflection nebula with a complex morphology is present).
A wavelet analysis technique is more appropriate in this case, since it is based on convolutions with spatially extended functions (which mitigates the signal to noise problem), and automatically separates the emission in different spatial scales (so that no special treatment is necessary for separating the jet from the background emission). We therefore adopt the procedure developed by Riera et al. (2003), who analyzed images of the HH 110 jet with a wavelet technique.

We rotated the H$\alpha $ and [S II] emission maps so that the outflow axis is parallel to the ordinate. On these rotated images, we then carried out a decomposition in a basis of anisotropic wavelets. Following Riera et al. (2003) we used a basis of ``Mexican hat'' wavelets:

g(r) = C(2 - r2)e-r/2 , (1)

where $r=\left[(x/a_x)^2 + (y/a_y)^2\right]^{-1/2}$, $C=\left(a_x^2+a_y^2\right)^{1/2}$, and ax, ay are the scale lengths of the wavelet along the x- and y-axis, respectively. We then chose a range for ax and ay (which are taken to have integer values, from 1 to 30 pixels) and then computed the transform maps Tax,ay(x,y) for the H$\alpha $ and [S II] images.

On the observed intensity map we fixed the position of y and found the value of $x_{\rm m}$, where the intensity map has a local maximum close to the outflow axis. For the positions $(x_{\rm m},y)$, where the intensity $I(x_{\rm m},y)$ has a maximum (along the y-axis), we plotted the 2D spectrum $T_{a_x,a_y}(x_{\rm m},y)$. In each of these spectra we found the peak in the spectral, (ax,ay)-plane, which we denoted $(a_{x,{\rm m}},a_{y,{\rm m}})$. This peak gave us the characteristic size across ( $a_{x,{\rm m}}$) and along ( $a_{y,{\rm m}}$) the outflow axis of the knot structures present at the position $(x_{\rm m},y)$. The width ( $a_{x,{\rm m}}$) as a function of position y along the jet obtained in this way are shown in Figs. 1 and 2 (for H$\alpha $ and [S II], respectively).

We first describe the characteristic widths (sizes across the jet axis) of the jet in the H$\alpha $ image. Figure 1 shows the $a_{x,{\rm m}}$ values as a function of position y (where y increases with distance from the outflow source). Along knot A (i.e., the innermost region) the width of the jet increases more or less monotonically from a value of $0\hbox{$.\!\!^{\prime\prime}$ }2$ (basically unresolved) up to $0\hbox{$.\!\!^{\prime\prime}$ }8$ (for $y=3\to 7''$). At the inner edge of knot B, we see that $a_{x,{\rm m}}$ suddenly grows (adopting values of up to $1\hbox{$.\!\!^{\prime\prime}$ }5$). Along knots B and C ( $y=8''\to 13''$) the width grows from a value of $0\hbox{$.\!\!^{\prime\prime}$ }6$ to $1\hbox{$.\!\!^{\prime\prime}$ }2$. Knot D shows the highest values of $a_{x,{\rm m}}$, with values in the range from $1\hbox{$.\!\!^{\prime\prime}$ }0$ to $2\hbox{$.\!\!^{\prime\prime}$ }0$. The width of the counterjet remains unresolved at the present spatial resolution.

In the red [S II] image (Fig. 2), we obtain widths that are approximately $0\hbox{$.\!\!^{\prime\prime}$ }1$ smaller than the H$\alpha $ widths for knots A, B and C. The width of the counterjet is again unresolved.

Table 1:   Grid of models.

\begin{figure} \par\includegraphics[height=17cm,angle=-90,clip]{13908fig3.eps} \vspace*{2mm} \end{figure} Figure 3:

HH 444 H$\alpha $ image ( left) and H$\alpha $ images predicted from models M1-M6 (labeled on the bottom left of each frame) for a t=375 yr time-integration. The images were computed assuming a $\phi =45^\circ $ orientation angle between the outflow axis and the plane of the sky. The HH 444 image is depicted with the logarithmic scale given at the top of the left frame (in erg s-1sterad-1) and the predicted images are depicted with the scale given at the top of the right frame (in the same units). Both scales cover a dynamic range of 3 orders of magnitude. The displayed domain has an axial (vertical) extent of $12\hbox{$.\!\!^{\prime\prime}$ }6$, corresponding to $8.5\times 10^{16}$ cm at 450 pc.

Open with DEXTER

\begin{figure} \par\includegraphics[height=17cm,angle=-90,clip]{13908fig4.eps} \end{figure} Figure 4:

HH 444 H$\alpha $ image ( left) and a time-series of H$\alpha $ images predicted from model M4 (the corresponding integration times are given at the bottom left of each frame). The images were computed assuming a $\phi =45^\circ $ orientation angle between the outflow axis and the plane of the sky. The HH 444 image is depicted with the logarithmic scale given at the top of the left frame (in erg s-1sterad-1) and the predicted images are depicted with the scale given at the top of the right frame (in the same units). The displayed domain has an axial (vertical) extent of $12\hbox{$.\!\!^{\prime\prime}$ }6$, corresponding to $8.5\times 10^{16}$ cm at 450 pc.

Open with DEXTER

3 The model parameters

López-Martín et al. (2001) found that to model the long-slit spectrum of the HH 444 jet base, a variable ejection velocity jet model with a sinusoidal variability with a mean velocity $v_0 \sim 200$ km s-1, a half-amplitude $\Delta v\sim 50$ km s-1and a period $\tau \sim 100$ yr was appropriate. These authors also deduced an angle $\phi \approx 40^\circ$ between the outflow axis and the plane of the sky (from the maximum and minimum radial velocities observed in the HH 444 bow shock).

In the present work, we study a grid of models with a sinusoidal ejection velocity variability:

\begin{displaymath}v_{\rm j}(t)=v_0+\Delta v~\sin\left({2\pi t\over \tau}\right)~, \end{displaymath} (2)

with mean velocity v0=180 km s-1 and all the combinations of half-amplitudes $\Delta v=30$, 60 km s-1 and periods $\tau=50$, 100, 200 yr. The six resulting models are tabulated in Table 1.

\begin{figure} \par\includegraphics[height=17cm,angle=-90]{13908fig5.eps}\vspace*{1.3mm} \end{figure} Figure 5:

HH 444 H$\alpha $ image ( left) and H$\alpha $ images predicted from model M4 (for a t=425 yr time-integration) assuming different orientation angles $\phi $ between the outflow axis and the plane of the sky. The values of $\phi $ for each image are given at the bottom left of each frame). The HH 444 image is depicted with the logarithmic scale given at the top of the left frame (in erg s-1sterad-1) and the predicted images are depicted with the scale given at the top of the right frame (in the same units). The displayed domain has an axial (vertical) extent of $12\hbox{$.\!\!^{\prime\prime}$ }6$, corresponding to $8.5\times 10^{16}$ cm at 450 pc.

Open with DEXTER

\begin{figure} \par\includegraphics[height=17cm,angle=-90]{13908fig6.eps} \end{figure} Figure 6:

HH 444 H$\alpha $ image ( left) and a time-series of H$\alpha $ images predicted from the two-mode ejection velocity variability model described in Sect. 5 (the corresponding integration times are given at the bottom left of each frame). The images were computed assuming a $\phi =45^\circ $ orientation angle between the outflow axis and the plane of the sky. The HH 444 image is depicted with the logarithmic scale given at the top of the left frame (in erg s-1sterad-1) and the predicted images are depicted with the scale given at the top of the right frame (in the same units). The displayed domain has an axial (vertical) extent of $12\hbox{$.\!\!^{\prime\prime}$ }6$, corresponding to $8.5\times 10^{16}$ cm at 450 pc.

Open with DEXTER

The six jet models have top-hat initial cross sections with a radius $r_{\rm j}=5\times 10^{14}$ cm (corresponding to ${\sim}0\hbox{$.\!\!^{\prime\prime}$ }07$ at a distance of 450 pc), number density $n_{\rm j}=10^5$ cm-3 and temperature $T_{\rm j}=10^4$ K. These parameters give a mean mass-loss rate ${\dot M}_{\rm j}=4.81\times 10^{-8}~M_\odot$ yr-1for the jet. The jet moves into a uniform environment with density $n_{\rm env}=100$ cm-3 and temperature $T_{\rm env}=10^4$ K.

The time-integrations are computed with a cylindrically symmetric version of the ``yguazú-a'' code in a 4-level, binary adaptive grid with a maximum resolution of $1.46\times 10^{14}$ cm along the two axes. A detailed description of the ``yguazú-a'' code is given by Raga et al. (2000a).

We consider that hydrogen is fully ionized throughout the computational grid, and we impose a minimum temperature of 104 K (for higher temperatures, the parametrized cooling function of Raga et al. 2000b is included). This is an approximate way of simulating a fully photoinized jet.

We note that Raga et al. (2000c) estimated that the HH 444 flow would become fully photoionized by the external UV radiation field at a distance of ${\sim}10^{16}$ cm from V510 Ori. Therefore, the approximation of a fully photoionized flow is incorrect for distances smaller than ${\sim}10^{16}$ cm from the outflow source.

The simulations were carried out in a $(15.0,3.75)\times 10^{16}$ cm (axial $\times$ radial) cylindrical grid, with reflection conditions on the symmetry axis and on the jet/counterjet symmetry plane and trasmission conditions in the other grid boundaries. We carried out 500 yr time integrations, in which the leading working surface of the jet leaves the computational domain. At the later integration times we see the emission from the knots close to the outflow source (formed by the ejection velocity variability) without the contribution from the jet's head and its extended bow shock wings.

In the rest of the paper we assume a distance D=450 pc to the HH 444 outflow. This distance is used to scale the model predictions so that they can be directly compared with the observations.

4 The H$\alpha $ maps

4.1 Maps obtained from all models

We now assume that the jet axis lies at a $\phi =45^\circ $ angle with respect to the plane of the sky (consistent with the angle determined for HH 444 by López-Martín et al. 2001), and compute H$\alpha $ maps from the t=375 yr flow stratifications obtained from models M1-M6 (see Table 1). The maps are obtained by integrating the H$\alpha $ emission coefficient (obtained from the H recombination cascade) along lines of sight.

The resulting maps are shown, together with the H$\alpha $ image of HH 444, in Fig. 3. From this figure, it is evident that the models produce a well collimated, narrow H$\alpha $ emitting region close to the source and broad knots at larger distances, qualitatively resembling the emission from the HH 444 jet base and from the knots HH 444B and C.

Models M1 and M2 (with a $\tau=50$ yr variability period, see Table 1) reproduce the separation between knots B and C. However, a well-defined H$\alpha $ knot is seen at ${\sim}4''$ from the source, which does not exist in HH 444. Models M3 and M4 (with $\tau=100$ yr) have two knots, which have a separation a factor of ${\sim}2$ larger than the separation beween HH 444B and C. Finally, models M5 and M6 (with $\tau=100$ yr, see Table 1) have a single knot at the position of HH 444C.

It is clear that while all models have qualitative similarities to the observations, it appears that the H$\alpha $ emission structure of HH 444 cannot be reproduced by a model with a single-mode, periodic ejection variability. In order to obtain the correct knot separations it will be necessary to consider at least a two-mode ejection variability model (like the one explored by Raga & Noriega-Crespo 1998), or possibly a non-periodic ejection variability (like the one recently explored by Yirak et al. 2009). A two-mode ejection variability model is presented in Sect. 5.

It is also clear that in the region close to the source the relative H$\alpha $ emission from the jet base predicted from all models is much stronger than that observed in HH 444. In order to reconcile the observations and model predictions it is therefore necessary to invoke a relatively strong circumstellar extinction close to V510 Ori.

4.2 The time-evolution of the H$\alpha $ maps

We now focus on model M4 (with $\tau=100$ yr and $\Delta v=30$ km s-1, see Table 1) and compute a time-series of H$\alpha $ maps covering a full ejection variability period. The resulting maps are shown in Fig. 4.

In this time-series, we see the formation of a knot at ${\sim}5''$ from the source (in the t=375 yr frame of Fig. 4). This knot travels away from the source and grows in angular size, and in the last two time-frames (t=450, 475 yr) reaches the position of the HH 444B and C knots.

The t=475 yr frame corresponds to a full ejection variability period after the t=375 yr frame (the last and first frames of Fig. 4, respectively). These two H$\alpha $maps are very similar, with the exception that the knot at ${\sim}10''$ from the source is fainter in the t=475 yr frame. This is because the cocoon gas is progressively evacuated from the computational domain, resulting in lower pre-shock densities for the successive bow shocks travelling away from the source.

4.3 The orientation with respect to the plane of the sky

We now consider the t=375 yr frame of model M4 (see Fig. 4), and compute H$\alpha $ maps for different angles $\phi $ between the outflow axis and the plane of the sky. For $\phi=0$we have a knot at ${\sim}10''$ from the source. This knot has a flat, bow-shaped emission structure, which does not resemble the round morphology of the knots HH 444B and C.

As we go to higher values of $\phi $, the simulated knot approaches the source and develops a rounder morphology. For $\phi\geq 30^\circ$ the morphology of the simulated knot resembles the structures of the HH 444B and C knots.

From this we conclude that the morphologies observed for the HH 444B and C knots are consistent with the morphologies found for the emission from internal working surfaces when the outflow axis is at an angle $\phi\geq 30^\circ$ with respect to the plane of the sky. This result is consistent with the $\phi=40^\circ$ angle (between the outflow axis and the plane of the sky) determined by López-Martín et al. (2001) for the HH 444 outflow.

5 A two-mode ejection velocity variability model

5.1 The H$\alpha $ maps

The available observations of HH 444 are not sufficient to constrain a two- or three-mode ejection variability. This was possible in the past for objects in which more extensive kinematic information (i.e., of a spatially more extended region along the outflow axis) as well as proper motions are available. Examples of this are HH 34 and HH 444 (see Raga et al. 2002) and HH 30 (Anglada et al. 2007; Esquivel et al. 2007).

\begin{figure} \par\includegraphics[height=8cm,angle=-90,clip]{13908fig7.eps} \end{figure} Figure 7:

H$\alpha $ images (for a $\phi =45^\circ $ orientation angle between the outflow axis and the plane of the sky) predicted from the two-mode ejection velocity variability model described in Sect. 5 for a t=400 yr integration time. The three maps correspond to three simulations with maximum resolutions $\Delta x=1.46\times 10^{14}$ cm (the ``low'' resolution model), $7.32\times 10^{13}$ cm (``medium'' resolution) and $3.66\times 10^{13}$ cm (``high'' resolution) along the two axes. The images are depicted with the scale given at the top of the right frame (in erg cm-2 s-1 sterad-1). The displayed domain has an axial (vertical) extent of $8.5\times 10^{16}$ cm.

Open with DEXTER

For this reason, we only present one two-mode ejection velocity variability model to illustrate that it is indeed possible to produce knot structures that resemble the HH 444 jet. We choose a model that has a velocity variability with two sinusoidal modes with half-amplitudes $\Delta v_1=30$ km s-1 and $\Delta v_2=60$ km s-1and corresponding periods $\tau_1=50$ yr and $\tau_2=260$ km s-1. The mean velocity v0=180 km s-1, and the remaining parameters of the models are identical to those of models M1-M6 (see Sect. 3). The computation is done (as in models M1-M6, see Sect. 3) in a 4-level, binary adaptive grid with a maximum resolution $\Delta x=1.46\times 10^{14}$ cm (along the two axes).

In Fig. 6 we present a comparison between the H$\alpha $ image of HH 444 and a time-series of H$\alpha $ maps computed from the two-mode ejection velocity variability jet model. It is clear that a number of time-frames (e.g., the maps obtained for t=350, 375, 425, and 600 yr) have knot distributions that qualitatively resembles the HH 444 knot structure.

5.2 Convergence study

We use this two-mode jet model to illustrate the numerical convergence of our simulations. All results presented above were obtained using a 4-level, binary adaptive grid with a maximum resolution $\Delta x=1.46\times 10^{14}$ cm (along the two axes). This implies that the initial jet radius ( $r_{\rm j}=5\times 10^{14}$ cm, see Sect. 3) is only resolved with three grid points. While the resolution of the jet beam improves at larger distances from the source (due to the lateral expansion of the beam), this is indeed a rather low resolution, and one might suspect that the results will change for higher resolutions.

In Fig. 7 we show the t=400 yr H$\alpha $ map obtained from our two-mode jet model computed with three different maximum resolutions: $\Delta x=1.46\times 10^{14}$, $7.32\times 10^{13}$ and $3.66\times 10^{13}$ cm (computed in binary grids with 4, 5 and 6 levels, respectively). From this figure, it is clear that while the general morphology of the predicted H$\alpha $ maps does not change with increasing resolution of the simulation, the fluxes of the knots do change.

\begin{figure} \par\includegraphics[width=9cm,clip]{13908fig8.eps} \end{figure} Figure 8:

Peak H$\alpha $ intensity of the three knots seen in the images predicted from the 2-mode, variable ejection jet model (see Fig. 7) as a function of the maximum resolution of the simulation. The crosses give the H$\alpha $ intensity of the knot closest to the source, the triangles correspond to the second knot, and the circles to the third knot.

Open with DEXTER

\begin{figure} \par\includegraphics[width=9cm,clip]{13908fig9.eps} \end{figure} Figure 9:

H$\alpha $ map ( right) predicted from the two-mode ejection variability model (see Sect. 5) for a t=400 yr time-integration. The map was computed assuming a $\phi =45^\circ $ orientation between the jet axis and the plane of the sky. The left plot shows the jet width vs. position dependence recovered from the predicted H$\alpha $map using the wavelet analysis technique (described in Sect. 2.2). Two successive contours correspond to a factor of 2.

Open with DEXTER

This change in H$\alpha $ intensity as a function of resolution is shown in Fig. 8, in which we plot the peak H$\alpha $intensities of the three knots (seen in the t=400 yr H$\alpha $ maps, see Fig. 7) as a function of maximum resolution $\Delta x$ of the simulations. If we look at the brightest knot, we see that the peak H$\alpha $intensity drops by a factor of ${\sim}3.4$ when going from the $\Delta x=1.46\times 10^{14}$ to the $\Delta x=7.32\times 10^{13}$ cm resolution. Its peak H$\alpha $ intensity again drops when going from the $\Delta x=7.32\times 10^{13}$ to the $\Delta x=3.66\times 10^{13}$ cm resolution, but only by a factor of ${\sim}2.0$. Similar results are found for the other two knots.

These results indicate that at least a partial numerical convergence is obtained for the H$\alpha $ intensity maps when we reach our highest, $\Delta x=3.66\times 10^{13}$ cm resolution. We then use this higher resolution simulation to compute the jet width as a function of position, with relative confidence that the results are quantitatively meaningful. This is described in the following section.

5.3 Width vs. position

Let us now explore whether or not our two-mode jet model results in a width vs. position distribution which resembles the one observed in the HH 444 jet (see Sect. 2.2). For this analysis we consider the t=400 yr H$\alpha $ map computed from our higher resolution simulation (with minimum cell size $\Delta x=3.66\times 10^{13}$ cm, see Sect. 5.2).

When applying the wavelet analysis to this synthetic image, we obtain the width vs. position shown in Fig. 9. From this figure we see that we obtain a region extending to ${\sim}2''$from the source in which the jet width is ${\sim}0\hbox{$.\!\!^{\prime\prime}$ }1$, basically unresolved at the resolution of the HST images. The first knot (at a distance of ${\sim}3\hbox{$.\!\!^{\prime\prime}$ }5$ from the source) has a width of ${\approx}0\hbox{$.\!\!^{\prime\prime}$ }3$, and the second knot (at a distance of ${\sim}7''$ from the source) has a width of ${\approx}0\hbox{$.\!\!^{\prime\prime}$ }6$.

We note the interesting effect seen at ${\sim}5''$from the outflow source (see Fig. 9). In this inter-knot region, the width determined for the jet beam (from the wavelet analysis) blows up, attaining values of several arcseconds. This is probably because in the inter-knot regions the spatial scale of the emission is dominated by the distance to the neighbouring knots. These broadenings in the faint inter-knot regions are generally obtained in width determinations based on wavelet analyses (see Figs. 1 and 2), and a similar effect is also obtained when fitting Gaussian functions to the jet cross-section, provided that data with a high enough signal-to-noise ratio are used (see Raga et al. 1991).

Comparing these results with those obtained from the H$\alpha $ map of HH 444 (see Sect. 2.2 and Fig. 1), we see that though the positions of the knots in the simulated jet do not coincide with those of the HH 444 knots, a general agreement is obtained between the observed and predicted width vs. position. Both show an unresolved jet-width region close to the source, and widths of ${\sim}0\hbox{$.\!\!^{\prime\prime}$ }5$ for the knots.

6 Conclusions

We re-analyzed the HST H$\alpha $ and red [S II] images of HH 444 obtained by Andrews et al. (2004). We applied the non-parametric wavelet analysis technique of Riera et al. (2003) to calculate the width vs. position along the HH 444 jet. From this analysis we found that the jet width is basically unresolved (in both H$\alpha $ and [S II]) close to the source, and grows to widths of ${\sim}0\hbox{$.\!\!^{\prime\prime}$ }6\to 1''$in the well-defined knots B and C.

We computed a grid of jet models with a single-mode, sinusoidal variability for the ejection velocity, with a range of values for the periods and amplitudes that appears to be appropriate for the knots along HH 444 (Sect. 3). H$\alpha $ maps computed from all models (assuming a $\phi =45^\circ $ angle between the outflow axis and the plane of the sky, see Fig. 3) produce knots which qualitatively resemble the HH 444 B and C knots. We studied the effect of changing the angle $\phi $ (between the outflow axis and the plane of the sky, see Fig. 5) and found that the predicted H$\alpha $ knots resemble the HH 444 knots only for $\phi\geq 30^\circ$. This result is consistent with the $\phi\sim 40^\circ$ orientation of the HH 444 outflow estimated by López-Martín et al. (2001).

A systematic difference between the model predictions and the observations is that the models show brighter H$\alpha $ emission close to the outflow source (in a region within ${\sim}3''$ from the source, see Figs. 3-5). This result might be consistent with the fact that the region around $\sigma$ Orionis shows substantial circumstellar emission (possibly including a proplyd tail, see Andrews et al. 2004), indicating the presence of a dense, circumstellar envelope which may be producing a substantial extinction of the jet emission.

However, we find that the single sinusoidal mode variability models cannot explain the knot spacings observed in HH 444. This problem can be solved by proposing a model with a two-mode sinusoidal ejection velocity variability. We illustrate this possibility by computing a two-mode jet model (Sect. 5).

We chose an H$\alpha $ map predicted from this two-mode model for computing the jet width vs. position with the wavelet analysis technique that we used for analyzing the HH 444 images. We find that the jet has an unresolved region close to the source and that the jet width grows as a function of increasing distance from the source. A comparison between the predictions (Fig. 9) and the HH 444 H$\alpha $ observations (Fig. 1) shows a qualitatively good agreement between the predicted and observed width vs. position.

To summarize, we showed that the H$\alpha $ HST image of HH 444 has knots with morphologies that agree with the predictions from a variable ejection velocity jet (if one considers an appropriate orientation angle between the jet axis and the plane of the sky). The knot spacings observed in HH 444, however, require at least a two-mode ejection velocity variability.

The two-mode time-variability that we explored is not well constrained by the present observations, and in principle a more complex variability is probably needed. An indication of the necessity of a more complex variability are the knots at larger distances from the HH 444 source: knots G and H, at distances of 114'' and 154'' (respectively) from the source (Reipurth et al. 1998). These knots can in principle be modeled through the introduction of an extra ejection variability mode (a similar morphology in the HH 34 jet was modeled in this way by Raga & Noriega-Crespo 1998). Instead of a multi-mode variability, a non-periodic variability (see Yirak et al. 2009; Bonito et al. 2010) might be present, but the richness of inter-knot spatial scales that is to be expected from a well-sampled random variability (Raga 1992) does not seem to be present in the HH 444 jet.

Acknowledgements
This work was supported by the CONACyT grants 61547, 101356 and 101975. The work of A.Ri. was supported by the MICINN grant AYA2008-06189-C03 and AYA2008-04211-C02-01 (co-funded with FEDER funds). We acknowledge the support of E. Palacios from the ICN-UNAM computing staff. We thank John Bally (the referee) for several helpful suggestions.

References

  1. Andrews, S. M., Reipurth, B., Bally, J., & Heathcote, S. R. 2004, ApJ, 606, 353 [NASA ADS] [CrossRef] [Google Scholar]
  2. Anglada, G., López, R., Estalella, R., et al. 2007, AJ, 133, 2799 [NASA ADS] [CrossRef] [Google Scholar]
  3. Bally, J., & Reipurth, B. 2001, ApJ, 546, 299 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bally, J., Johnstone, D., Joncas, G., Reipurth, B., & Mallén-Ornelas, G. 2001, AJ, 122, 1508 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bonito, R., Orlando, S., Peres, G., et al. 2010, A&A, 511, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Bührke, T., Mundt, R., & Ray, T. 1988, A&A, 200 99 [NASA ADS] [Google Scholar]
  7. Cantó, J., & Raga, A. C. 1995, MNRAS, 277, 1120 [NASA ADS] [CrossRef] [Google Scholar]
  8. Ciardi, A., Ampleford, D. J., Lebedev, S. V., & Stehle, C. 2008, ApJ, 678, 968 [NASA ADS] [CrossRef] [Google Scholar]
  9. Esquivel, A., Raga, A. C., & De Colle, F. 2007, A&A, 468, 613 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Lim, A. J., & Raga, A. C. 1998, MNRAS, 298, 871 [NASA ADS] [CrossRef] [Google Scholar]
  11. López-Martín, L., Raga, A. C., López, J. A., & Meaburn, J. 2001, A&A, 371, 1118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Masciadri, E., & Raga, A. C. 2001, AJ, 121, 408 [NASA ADS] [CrossRef] [Google Scholar]
  13. Masciadri, E., Velázquez, P. F., Raga, A. C., Cantó, J., & Noriega-Crespo, A. 2002, ApJ, 573, 260 [NASA ADS] [CrossRef] [Google Scholar]
  14. Raga, A. C. 1992, MNRAS, 258, 301 [NASA ADS] [Google Scholar]
  15. Raga, A. C., & Mateo, M. 1988, AJ, 95, 543 [NASA ADS] [CrossRef] [Google Scholar]
  16. Raga, A. C., & Noriega-Crespo, A. 1998, AJ, 116, 2943 [NASA ADS] [CrossRef] [Google Scholar]
  17. Raga, A. C., Mundt, R., & Ray, T. P. 1991, A&A, 252, 733 [NASA ADS] [Google Scholar]
  18. Raga, A. C., Navarro-González, R., & Villagrán-Muniz, M. 2000a, RMxAA, 36, 67 [Google Scholar]
  19. Raga, A. C., Curiel, S., Rodríguez, L. F., & Cantó, J. 2000b, A&A, 364, 763 [NASA ADS] [Google Scholar]
  20. Raga, A. C., López-Martín, L., Binette, L., et al. 2000c, MNRAS, 314, 681 [NASA ADS] [CrossRef] [Google Scholar]
  21. Raga, A. C., Cabrit, S., Dougados, C., & Lavalley, C. 2001, A&A, 367, 959 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Raga, A. C., Velázquez, P. F., Cantó, J., & Masciadri, E. 2002, A&A, 395, 647 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Raga, A. C., Riera, A., Masciadri, E., et al. 2004, AJ, 127, 1081 [NASA ADS] [CrossRef] [Google Scholar]
  24. Reipurth, B., Bally, J., Fesen, R. A., & Devine, D. 1998, Nature, 396 [Google Scholar]
  25. Riera, A., Raga, A. C., Reipurth, B., et al. 2003, AJ, 126, 327 [NASA ADS] [CrossRef] [Google Scholar]
  26. Yirak, K., Frank, A., Cunninghan, A. J., & Mitran, S. 2009, ApJ, 695, 999 [NASA ADS] [CrossRef] [Google Scholar]

Footnotes

... HLA[*]
Based on observations made with the NASA/ESA Hubble Space Telescope, and obtained from the Hubble Legacy Archive, which is a collaboration between the Space Telescope Science Institute (STScI/NASA), the Space Telescope European Coordinating Facility (ST-ECF/ESA) and the Canadian Astronomy Data Centre (CADC/NRC/CSA).

All Tables

Table 1:   Grid of models.

All Figures

  \begin{figure} \par\includegraphics[width=9cm,clip]{13908fig1.eps} \end{figure} Figure 1:

HH 444 H$\alpha $ image ( right, see Sect. 2.1) and characteristic width $a_{x,{\rm m}}$ as a function of position along the jet axis ( left), obtained from the wavelet analysis (see Sect. 2.2). Two successive contours correspond to a factor of 2.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{13908fig2.eps} \end{figure} Figure 2:

HH 444 [S II] 6716+30 image ( right, see Sect. 2.1) and characteristic width $a_{x,{\rm m}}$ as a function of position along the jet axis ( left), obtained from the wavelet analysis (see Sect. 2.2). Two successive contours correspond to a factor of 2.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[height=17cm,angle=-90,clip]{13908fig3.eps} \vspace*{2mm} \end{figure} Figure 3:

HH 444 H$\alpha $ image ( left) and H$\alpha $ images predicted from models M1-M6 (labeled on the bottom left of each frame) for a t=375 yr time-integration. The images were computed assuming a $\phi =45^\circ $ orientation angle between the outflow axis and the plane of the sky. The HH 444 image is depicted with the logarithmic scale given at the top of the left frame (in erg s-1sterad-1) and the predicted images are depicted with the scale given at the top of the right frame (in the same units). Both scales cover a dynamic range of 3 orders of magnitude. The displayed domain has an axial (vertical) extent of $12\hbox{$.\!\!^{\prime\prime}$ }6$, corresponding to $8.5\times 10^{16}$ cm at 450 pc.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[height=17cm,angle=-90,clip]{13908fig4.eps} \end{figure} Figure 4:

HH 444 H$\alpha $ image ( left) and a time-series of H$\alpha $ images predicted from model M4 (the corresponding integration times are given at the bottom left of each frame). The images were computed assuming a $\phi =45^\circ $ orientation angle between the outflow axis and the plane of the sky. The HH 444 image is depicted with the logarithmic scale given at the top of the left frame (in erg s-1sterad-1) and the predicted images are depicted with the scale given at the top of the right frame (in the same units). The displayed domain has an axial (vertical) extent of $12\hbox{$.\!\!^{\prime\prime}$ }6$, corresponding to $8.5\times 10^{16}$ cm at 450 pc.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[height=17cm,angle=-90]{13908fig5.eps}\vspace*{1.3mm} \end{figure} Figure 5:

HH 444 H$\alpha $ image ( left) and H$\alpha $ images predicted from model M4 (for a t=425 yr time-integration) assuming different orientation angles $\phi $ between the outflow axis and the plane of the sky. The values of $\phi $ for each image are given at the bottom left of each frame). The HH 444 image is depicted with the logarithmic scale given at the top of the left frame (in erg s-1sterad-1) and the predicted images are depicted with the scale given at the top of the right frame (in the same units). The displayed domain has an axial (vertical) extent of $12\hbox{$.\!\!^{\prime\prime}$ }6$, corresponding to $8.5\times 10^{16}$ cm at 450 pc.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[height=17cm,angle=-90]{13908fig6.eps} \end{figure} Figure 6:

HH 444 H$\alpha $ image ( left) and a time-series of H$\alpha $ images predicted from the two-mode ejection velocity variability model described in Sect. 5 (the corresponding integration times are given at the bottom left of each frame). The images were computed assuming a $\phi =45^\circ $ orientation angle between the outflow axis and the plane of the sky. The HH 444 image is depicted with the logarithmic scale given at the top of the left frame (in erg s-1sterad-1) and the predicted images are depicted with the scale given at the top of the right frame (in the same units). The displayed domain has an axial (vertical) extent of $12\hbox{$.\!\!^{\prime\prime}$ }6$, corresponding to $8.5\times 10^{16}$ cm at 450 pc.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[height=8cm,angle=-90,clip]{13908fig7.eps} \end{figure} Figure 7:

H$\alpha $ images (for a $\phi =45^\circ $ orientation angle between the outflow axis and the plane of the sky) predicted from the two-mode ejection velocity variability model described in Sect. 5 for a t=400 yr integration time. The three maps correspond to three simulations with maximum resolutions $\Delta x=1.46\times 10^{14}$ cm (the ``low'' resolution model), $7.32\times 10^{13}$ cm (``medium'' resolution) and $3.66\times 10^{13}$ cm (``high'' resolution) along the two axes. The images are depicted with the scale given at the top of the right frame (in erg cm-2 s-1 sterad-1). The displayed domain has an axial (vertical) extent of $8.5\times 10^{16}$ cm.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{13908fig8.eps} \end{figure} Figure 8:

Peak H$\alpha $ intensity of the three knots seen in the images predicted from the 2-mode, variable ejection jet model (see Fig. 7) as a function of the maximum resolution of the simulation. The crosses give the H$\alpha $ intensity of the knot closest to the source, the triangles correspond to the second knot, and the circles to the third knot.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{13908fig9.eps} \end{figure} Figure 9:

H$\alpha $ map ( right) predicted from the two-mode ejection variability model (see Sect. 5) for a t=400 yr time-integration. The map was computed assuming a $\phi =45^\circ $ orientation between the jet axis and the plane of the sky. The left plot shows the jet width vs. position dependence recovered from the predicted H$\alpha $map using the wavelet analysis technique (described in Sect. 2.2). Two successive contours correspond to a factor of 2.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.