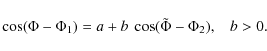| Issue |
A&A
Volume 517, July 2010
|
|
|---|---|---|
| Article Number | A8 | |
| Number of page(s) | 9 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/200913863 | |
| Published online | 23 July 2010 | |
Analyzing X-ray pulsar profiles: geometry and beam pattern of EXO 2030+375
M. Sasaki1 - D. Klochkov1 - U. Kraus2 - I. Caballero3 - A. Santangelo1
1 - Institut für Astronomie und Astrophysik,
Universität Tübingen,
Sand 1,
72076 Tübingen, Germany
2 -
Institut für Physik und Technik,
Universität Hildesheim,
Marienburger Platz 22,
31141 Hildesheim, Germany
3 -
CEA Saclay, DSM/IRFU/SAp - UMR AIM (7158)
CNRS/CEA/Université P. Diderot, 91191 Gif-sur-Yvette, France
Received 14 December 2009 / Accepted 7 April 2010
Abstract
Context. The pulse profiles of the transient Be/X-ray binary
EXO 2030+375 show strong dependence on energy, as well as on its
luminosity state, and are asymmetric in shape.
Aims. We want to identify the emission components of the two
magnetic poles in the pulsed emission to understand the geometry of the
neutron star and its beam pattern.
Methods. We utilize a pulse-profile decomposition method that
enables us to find two symmetric pulse profiles from the magnetic poles
of the neutron star. The symmetry characteristics of these single-pole
pulse profiles give information about the position of the magnetic
poles of the neutron star relative to its rotation axis.
Results. We find a possible geometry for the neutron star in
EXO 2030+375 through the decomposition of the pulse profiles,
which suggests that one pole gets closer to the line of sight than the
other and that, during the revolution of the neutron star, both poles
disappear behind the horizon for a short period of time. A considerable
fraction of the emission arises from a halo while the pole is facing
the observer and from the accretion stream of the other pole while it
is behind the neutron star, but the gravitational line bending makes
the emission visible to us.
Key words: stars: neutron - X-rays: binaries
1 Introduction
EXO 2030+375 is an accreting X-ray pulsar with a pulsation period of
![]() 42 s, which was discovered with EXOSAT in 1985 during a giant outburst
(Parmar et al. 1989b).
A B0 Ve star was found as its counterpart in follow-up observations in the
optical and infrared bands
(Coe et al. 1988; Janot-Pacheco et al. 1988; Motch & Janot-Pacheco 1987).
During the giant outburst, EXO 2030+375 showed a spin-up of
42 s, which was discovered with EXOSAT in 1985 during a giant outburst
(Parmar et al. 1989b).
A B0 Ve star was found as its counterpart in follow-up observations in the
optical and infrared bands
(Coe et al. 1988; Janot-Pacheco et al. 1988; Motch & Janot-Pacheco 1987).
During the giant outburst, EXO 2030+375 showed a spin-up of
![]() yr
(Parmar et al. 1989b) and quasi-periodic oscillations with a frequency
of
yr
(Parmar et al. 1989b) and quasi-periodic oscillations with a frequency
of ![]() 0.2 Hz (Angelini et al. 1989) interpreted as caused by
the formation of an accretion disk. Detailed analyses have shown that
its rate of pulse-period change
0.2 Hz (Angelini et al. 1989) interpreted as caused by
the formation of an accretion disk. Detailed analyses have shown that
its rate of pulse-period change ![]() ,
energy spectrum, and pulse profile
are strongly luminosity dependent
(Reynolds et al. 1993; Parmar et al. 1989a,b).
The orbital period is 46 days (Wilson et al. 2002), and a normal outburst
has been detected for nearly every periastron passage since 1991
(Wilson et al. 2005).
In 2006, EXO 2030+375 underwent the first giant outburst since its discovery in 1985
(Corbet & Levine 2006; Krimm et al. 2006; McCollough et al. 2006),
during which it reached a maximum luminosity of
,
energy spectrum, and pulse profile
are strongly luminosity dependent
(Reynolds et al. 1993; Parmar et al. 1989a,b).
The orbital period is 46 days (Wilson et al. 2002), and a normal outburst
has been detected for nearly every periastron passage since 1991
(Wilson et al. 2005).
In 2006, EXO 2030+375 underwent the first giant outburst since its discovery in 1985
(Corbet & Levine 2006; Krimm et al. 2006; McCollough et al. 2006),
during which it reached a maximum luminosity of
![]() erg s-1 (Klochkov et al. 2008)
and again showed a strong spin-up.
Rossi X-ray Timing Explorer (RXTE) monitored EXO 2030+375 extensively during the
2006 giant outburst (Wilson et al. 2008). The source was also observed
by the INTErnational Gamma Ray Astrophysics Laboratory
(INTEGRAL, Winkler et al. 2003) and Swift
(Gehrels et al. 2004). The spectra indicate a cyclotron
absorption line (Wilson et al. 2008; Klochkov et al. 2007).
Klochkov et al. (2008) have shown that the spectrum of EXO 2030+375 changes
with pulse phase, suggesting a fan beam geometry during the maximum,
while towards the end of the giant outburst, it changes to a
combination of a fan beam and a pencil beam.
erg s-1 (Klochkov et al. 2008)
and again showed a strong spin-up.
Rossi X-ray Timing Explorer (RXTE) monitored EXO 2030+375 extensively during the
2006 giant outburst (Wilson et al. 2008). The source was also observed
by the INTErnational Gamma Ray Astrophysics Laboratory
(INTEGRAL, Winkler et al. 2003) and Swift
(Gehrels et al. 2004). The spectra indicate a cyclotron
absorption line (Wilson et al. 2008; Klochkov et al. 2007).
Klochkov et al. (2008) have shown that the spectrum of EXO 2030+375 changes
with pulse phase, suggesting a fan beam geometry during the maximum,
while towards the end of the giant outburst, it changes to a
combination of a fan beam and a pencil beam.
In X-ray pulsars, a neutron star accretes matter from a companion star via stellar wind or Roche lobe overflow. The accreted matter is channeled along the field lines of the strong magnetic field of the neutron star onto the magnetic poles. X-ray emission from the neutron star is produced in regions around the two magnetic poles. As the magnetic dipole axis is most likely inclined against the rotation axis of the neutron star, a distant observer sees pulsed emission. X-ray pulsars exhibit a wide variety of pulse shapes that differ from source to source. Generally, high-energy pulses have simpler shapes than low-energy pulses (Bildsten et al. 1997; White et al. 1983; Frontera & Dalfiume 1989, and references therein). If one assumes an axially symmetric geometry for the two emission regions of the neutron star in a dipole configuration, the observed pulse profile should be symmetric. However, the observed pulse profiles typically show an asymmetry. To explain the asymmetric shape of the total pulse profile, a distorted magnetic dipole field in which the two magnetic poles are not located opposite each other have been discussed (Riffert et al. 1993; Parmar et al. 1989a; Leahy 1991; Bulik et al. 1995). Kraus et al. (1995) shows that, starting from the observed, asymmetric pulse profile, it is possible to disentangle the contribution of the two emission regions of the neutron star. Once the pulsed emission from each of the poles has been obtained, one can derive the geometry of the neutron star. This again allows us to construct the beam pattern, i.e., the flux distribution from one emission region. Using this pulse-profile decomposition method, Kraus et al. (1996) have analyzed the pulse profiles of Cen X-3 and find indications of both pencil and fan beam. In the case of Her X-1, the results of the pulse-profile decomposition by Blum & Kraus (2000) have not only shed light on the beam pattern of the magnetic poles, but have also confirmed that a warped and tilted accretion disk attenuates the emission from one pole of the neutron star. For A 0535+26, the reconstructed beam pattern suggests that the emission comes from a hollow column plus a halo of scattered radiation on the neutron star surface (Caballero et al. 2010).
In this paper we present the analysis of the energy-resolved pulse profiles of EXO 2030+375 utilizing the decomposition method developed by Kraus et al. (1995). Section 2 gives an overview of the data used for our analysis and Sect. 3 describes the analysis and the results obtained with the pulse-profile decomposition method. The results are discussed in Sect. 4. Section 5 summarizes the possible geometry of the neutron star and the origin of the observed emission.
2 Data
![\begin{figure}
\mbox{\includegraphics[angle=270,width=6cm,origin=rb,clip]{13863f...
...cludegraphics[angle=270,width=6cm,origin=rb,clip]{13863fg1b.eps} }\end{figure}](/articles/aa/full_html/2010/09/aa13863-09/Timg15.png)
|
Figure 1: Pulse profiles of EXO 2030+375 during the rise ( left) and the decay ( right) of the giant outburst in 2006 observed with RXTE. |
| Open with DEXTER | |
EXO 2030+375 experienced a giant outburst in 2006, during which the source was monitored continuously by RXTE and was also observed by INTEGRAL. We have used the pulse profiles obtained with the Joint European X-Ray Monitor (JEM-X, Lund et al. 2003) and the imaging system IBIS/ISGRI (Ubertini et al. 2003) as presented in Figs. 2 and 8 of Klochkov et al. (2008).
2.1 RXTE observations
For better statistics, we also used publicly available archival data
from two observations with RXTE during the rise and the decay of the giant
outburst when EXO 2030+375 showed about half of the maximum luminosity.
The observations took place on June 28 and September 17, 2006
(observation IDs 91089-01-07-00 and 91089-01-19-01) when the luminosity of the
source was
![]() erg s-1 and
erg s-1 and
![]() erg s-1, respectively.
We started from the event files obtained with the Proportional Counter Array
(PCA, Jahoda et al. 1996).
We used the event encoded mode files in oder to have optimum binning. After
filtering good time intervals and applying bitmasks, we created lightcurves with
a time binning of 0.125 s in the following spectral bands: 2-9 keV,
9-14 keV, 14-20 keV, 20-30 keV, and 30-115 keV. After background
subtraction, the lightcurves were corrected to solar barycenter and for orbitary
motion of the binary.
After folding the lightcurves with periods measured for each observation,
we obtained pulse profiles with 128 phase bins. Phase 0.0 was fixed to agree
with the INTEGRAL pulse profiles of Klochkov et al. (2008).
The folded lightcurves from the RXTE observations are shown in Fig. 1.
erg s-1, respectively.
We started from the event files obtained with the Proportional Counter Array
(PCA, Jahoda et al. 1996).
We used the event encoded mode files in oder to have optimum binning. After
filtering good time intervals and applying bitmasks, we created lightcurves with
a time binning of 0.125 s in the following spectral bands: 2-9 keV,
9-14 keV, 14-20 keV, 20-30 keV, and 30-115 keV. After background
subtraction, the lightcurves were corrected to solar barycenter and for orbitary
motion of the binary.
After folding the lightcurves with periods measured for each observation,
we obtained pulse profiles with 128 phase bins. Phase 0.0 was fixed to agree
with the INTEGRAL pulse profiles of Klochkov et al. (2008).
The folded lightcurves from the RXTE observations are shown in Fig. 1.
During the two RXTE observations shown here, the luminosity of EXO 2030+375 was comparable. As can be seen in Fig. 1, the pulse profiles before the maximum and after the maximum of the giant outburst are very similar, corroborating that the shape of the pulse profiles only depends on the luminosity state (Parmar et al. 1989a).
3 The analysis
3.1 The method
A detailed description of the pulse-profile decomposition method, which is based on a backward tracing of the emission, can be found in Kraus et al. (1995). All major steps of our analysis and the criteria applied to obtain the best solution are described in the Appendix.
The basic assumption of the method is that
the magnetic dipole field of the neutron star is
distorted in such a way that the two magnetic poles do not lie on a straight
line through the center of the neutron star.
Therefore, even though the emission from each pole is axisymmetric, the sum
of the emission from both poles results in an asymmetric pulse profile.
Using Fourier analysis, we model the observed asymmetric pulse profiles with
two symmetric functions
f1,2 to search for symmetry points
![]() in the pulse profiles
and their offset
in the pulse profiles
and their offset ![]() (see Appendix for details). For each observation
and energy range, the functions f1 and f2 correspond to the two
single-pole pulse profiles that in total add up to the observed asymmetric
pulse profile.
Each symmetry point corresponds to the pulse phase where the respective pole
is either closest to or most distant from the observer's line of sight.
From the two symmetry
points and functions, we then derive the location of the emission regions and
the beam pattern.
(see Appendix for details). For each observation
and energy range, the functions f1 and f2 correspond to the two
single-pole pulse profiles that in total add up to the observed asymmetric
pulse profile.
Each symmetry point corresponds to the pulse phase where the respective pole
is either closest to or most distant from the observer's line of sight.
From the two symmetry
points and functions, we then derive the location of the emission regions and
the beam pattern.
3.2 Decompositions
![\begin{figure*}
{\hspace{6cm}\footnotesize\sf\mbox{Solution 1}\hspace{10cm}}\\
\includegraphics[width=12.8cm,clip]{13863fg2.eps}
\end{figure*}](/articles/aa/full_html/2010/09/aa13863-09/Timg19.png)
|
Figure 2:
A selection of single-pole pulse profiles ( left) and corresponding
beam patterns ( right) obtained by the decomposition
method for the |
| Open with DEXTER | |
We have a total of 26 pulse profiles from INTEGRAL and RXTE observations.
To perform pulse-profile decomposition, the maximum in each of the 26
pulse profiles is normalized to unity. Thereafter each pulse
profile is modeled with two symmetric functions f1 and f2 based on
Fourier analysis. After applying criteria 1 (positive flux, see
Appendix A.1) and 2 (no ripples),
we obtain a large number of possible values for the parameters ![]() and
and ![]() .
However, after combining the results for all pulse profiles
(criterion 3), only two interesting solution regions remain in the parameter
space of
.
However, after combining the results for all pulse profiles
(criterion 3), only two interesting solution regions remain in the parameter
space of ![]() -
-![]() .
We call these solutions 1 and 2 and perform
further analysis with these two possible solutions.
.
We call these solutions 1 and 2 and perform
further analysis with these two possible solutions.
For each observation and energy band, the functions f1 and f2
correspond to the two single-pole pulse profiles that in total add up to the
observed asymmetric pulse profile. The Fourier analysis finds more than
one possible set of ![]() and
and ![]() within a small region for one
solution. For each total pulse profile, we have to look at the
different sets of the single-pole pulse profiles to decide which one is
consistent with the single-pole pulse profiles at other energies.
The pulse profiles of the different observations are studied separately,
because one should see a correlation between the
different energy bands of one luminosity state, but not necessarily between
two different observations. Figure 2 shows some of the selected
single-pole pulse profiles and the derived beam patterns for each pole
for solution 1. Within one observation, one can see an energy-dependent
evolution of the single-pole pulse profiles.
The values of
within a small region for one
solution. For each total pulse profile, we have to look at the
different sets of the single-pole pulse profiles to decide which one is
consistent with the single-pole pulse profiles at other energies.
The pulse profiles of the different observations are studied separately,
because one should see a correlation between the
different energy bands of one luminosity state, but not necessarily between
two different observations. Figure 2 shows some of the selected
single-pole pulse profiles and the derived beam patterns for each pole
for solution 1. Within one observation, one can see an energy-dependent
evolution of the single-pole pulse profiles.
The values of ![]() and
and ![]() for solutions 1 and 2 are
(65
for solutions 1 and 2 are
(65![]()
![]() < 75
< 75![]() ,
63
,
63![]()
![]() < 70
< 70![]() )
and
(70
)
and
(70![]()
![]() < 80
< 80![]() ,
81
,
81![]()
![]() < 88
< 88![]() ),
respectively.
The parameters for the two solutions are listed in Table 1.
),
respectively.
The parameters for the two solutions are listed in Table 1.
Table 1: Parameters obtained from the decomposition for solutions 1 and 2.
3.3 Overlaying beam patterns
As the neutron star rotates, the angle between the axis through one magnetic
pole and the line of sight ![]() changes with phase, i.e., with
rotation angle
changes with phase, i.e., with
rotation angle ![]() .
The decomposition has provided us with beam patterns as seen by the distant
observer for each emission region as functions of the phase.
Now we compare the two beam patterns derived from the two single-pole pulse
profiles of each observed pulse profile and search for a range
in
.
The decomposition has provided us with beam patterns as seen by the distant
observer for each emission region as functions of the phase.
Now we compare the two beam patterns derived from the two single-pole pulse
profiles of each observed pulse profile and search for a range
in
![]() ,
and thus
,
and thus ![]() ,
in which the two beam patterns
seem to show the same emission (see Appendix A.2).
We try to overlay the two beam patterns by using the relation:
,
in which the two beam patterns
seem to show the same emission (see Appendix A.2).
We try to overlay the two beam patterns by using the relation:
For solution 1 we are not able to find an overlap of the single-pole beam patterns. It is more likely that, in this case, the geometry only allows the observer to see two different parts of the total beam pattern. To assemble the two parts of the beam pattern, we use a = -2.1 and b = 1.0 (see Fig. A.2, upper panel). For solution 2, we find an overlap of the single-pole beam patterns for a = -0.1, b = 1.0, although the beam patterns do not seem to match perfectly.
![\begin{figure*}
{\hspace{55mm}\footnotesize\sf Solution 1\hspace{55mm}}\\ [4mm]
...
...ncludegraphics[angle=270,width=12cm,origin=rb,clip]{13863fg3b.eps}
\end{figure*}](/articles/aa/full_html/2010/09/aa13863-09/Timg25.png)
|
Figure 3:
Asymptotic beam patterns of the plus and minus solutions
of solution 1 seen by the distant observer plotted over the angle |
| Open with DEXTER | |
A total beam pattern can be reconstructed from the
beam patterns calculated from the single-pole pulse profiles.
As shown in Kraus et al. (1995), there is an ambiguity in the
relation between ![]() and
and ![]() ,
as each single-pole pulse profile has two symmetry points
at
,
as each single-pole pulse profile has two symmetry points
at ![]() and
and
![]() .
Therefore, the solutions cannot tell us
which ends of the sections of the beam patterns belong to, e.g., the lower
values of
.
Therefore, the solutions cannot tell us
which ends of the sections of the beam patterns belong to, e.g., the lower
values of ![]() .
For each
set of
.
For each
set of ![]() and
and ![]() we obtain two possible solutions (called
plus and minus) for the total beam pattern. The decomposition
method cannot tell us which one is the real solution. We have to take results
from other measurements of the source into consideration, e.g., luminosities
or spectra that will give insight into the emission processes, to decide which
of the two is the real solution.
The reconstructed asymptotic beam patterns for solution 1 as seen by
the distant observer are shown in Fig. 3.
Here the beam patterns are plotted over the angle
we obtain two possible solutions (called
plus and minus) for the total beam pattern. The decomposition
method cannot tell us which one is the real solution. We have to take results
from other measurements of the source into consideration, e.g., luminosities
or spectra that will give insight into the emission processes, to decide which
of the two is the real solution.
The reconstructed asymptotic beam patterns for solution 1 as seen by
the distant observer are shown in Fig. 3.
Here the beam patterns are plotted over the angle ![]() between the normal
at the first magnetic pole and the line of sight.
between the normal
at the first magnetic pole and the line of sight.
That the beam patterns of the single-pole pulse profiles do not match
in the overlap region of solution 2
might indicate that the emission from the two magnetic poles are not identical
and cannot be described with one local beam pattern. Therefore, we take the mean
of the two beam patterns and model a total averaged beam pattern, which we use
to reconstruct the visible total pulse profile, i.e., assuming equal local
emission pattern for the two poles.
The reconstructed pulse profiles (Fig. A.3) show significant
deviations from the observed profiles.
In addition, this solution yields a very extreme
geometry with the two magnetic poles located near the equator of the neutron star,
forming an angle of ![]() 90
90![]() between each other (see Table 1).
Although, in principle, we cannot rule such a strongly distorted geometry out,
especially not for young neutron stars like those expected in Be/X-ray binary
systems,
as they might have experienced some anisotropic conditions while their birth,
this rather unlikely geometry also suggests that solution 2
is not appropriate for EXO 2030+375. Therefore, in the following, we focus on
the discussion of solution 1.
between each other (see Table 1).
Although, in principle, we cannot rule such a strongly distorted geometry out,
especially not for young neutron stars like those expected in Be/X-ray binary
systems,
as they might have experienced some anisotropic conditions while their birth,
this rather unlikely geometry also suggests that solution 2
is not appropriate for EXO 2030+375. Therefore, in the following, we focus on
the discussion of solution 1.
3.4 Geometry of the neutron star
![\begin{figure}
\par\includegraphics[angle=90,width=8.8cm,clip=]{13863fg4.eps}\vspace{-2mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13863-09/Timg28.png)
|
Figure 4:
Relation between the observing angle
|
| Open with DEXTER | |
To derive the exact geometry of the neutron
star, i.e., to determine the polar angles of the magnetic poles
![]() and
and
![]() as well as the offset angle
as well as the offset angle ![]() ,
we need to know the
inclination angle of the rotation axis of the neutron star. However, this
angle is not known for most of the neutron stars, in particular not for
EXO 2030+375. Figure 4 shows the dependence of the angles
,
we need to know the
inclination angle of the rotation axis of the neutron star. However, this
angle is not known for most of the neutron stars, in particular not for
EXO 2030+375. Figure 4 shows the dependence of the angles
![]() ,
,
![]() ,
and
,
and ![]() on the angle
on the angle
![]() between the rotation axis
of the neutron star and the line of sight of the observer.
To convert the phase parameter
between the rotation axis
of the neutron star and the line of sight of the observer.
To convert the phase parameter
![]() into the angle
into the angle ![]() between the first magnetic pole and the observer, we have to assume an
inclination angle
between the first magnetic pole and the observer, we have to assume an
inclination angle
![]() with respect to the rotation axis.
Here, we use
with respect to the rotation axis.
Here, we use
![]()
![]() ,
corresponding to
,
corresponding to
![]()
![]() ,
,
![]()
![]() (see Fig. 4 and Table 1).
(see Fig. 4 and Table 1).
4 Discussion
In this section we want to further examine the results of the decomposition method and present the possible geometry of the neutron star.
4.1 Disentangling the emission components
For solution 1, there is no overlap between the two beam patterns obtained
from the single-pole pulse profiles as shown in Sect. 3.3.
It means that only a part of the emission is seen from
each pole during the revolution of the neutron star.
By putting the two visible parts
together, we obtain the total beam pattern of the emission around one magnetic
pole. In doing so, we make the assumption that the two magnetic poles have
the same emission pattern.
The plus solution (Fig. 3, upper panel) can be
described as a composition of a forward directed emission (towards 0![]() )
that is more pronounced at higher energies and an extended, relatively soft
emission (
)
that is more pronounced at higher energies and an extended, relatively soft
emission (![]() 80
80![]() -180
-180![]() ). The harder, forward-directed emission
indicates a pencil beam. The relative flux of the softer emission component
is higher in the data from the observation performed near the maximum
compared to the one during the decay and can be
interpreted as a fan beam, in agreement with the largely accepted picture
that an optically thick accretion column is formed during the giant outburst
(White et al. 1983, and references therein).
The minus solution has a soft emission at
). The harder, forward-directed emission
indicates a pencil beam. The relative flux of the softer emission component
is higher in the data from the observation performed near the maximum
compared to the one during the decay and can be
interpreted as a fan beam, in agreement with the largely accepted picture
that an optically thick accretion column is formed during the giant outburst
(White et al. 1983, and references therein).
The minus solution has a soft emission at
![]() 60
60![]() and a
harder emission at
and a
harder emission at
![]() 120
120![]() that increases for larger
that increases for larger ![]() .
As newest calculations by Kraus et al. (2010) have shown, reprocessing of
photons in the upper accretion stream creates a significant emission component
that dominates the beam pattern at higher energies and can be observed while
the pole, hence the accretion column,
is on the other side of the neutron star (``anti-pencil''). In addition,
the emission from a halo that is formed by scattered photons at the bottom
of the accretion column dominates the beam pattern at lower energies and
at lower
.
As newest calculations by Kraus et al. (2010) have shown, reprocessing of
photons in the upper accretion stream creates a significant emission component
that dominates the beam pattern at higher energies and can be observed while
the pole, hence the accretion column,
is on the other side of the neutron star (``anti-pencil''). In addition,
the emission from a halo that is formed by scattered photons at the bottom
of the accretion column dominates the beam pattern at lower energies and
at lower ![]() and is stronger in the data near the maximum of
the giant outburst.
and is stronger in the data near the maximum of
the giant outburst.
| Figure 5: Decomposed single-pole pulse profiles of the data taken near the maximum of the giant outburst for the lowest energy band (same as the upper left diagram of the upper [solution 1] panels in Fig. 2) with proposed emission components derived from the beam patterns of the minus solution (Fig. 3, lower panel). We suggest that the emission from the first pole consists of emission from the halo (diagonally striped component) and from the accretion column (vertically striped). The dominant emission from the second pole seems to have its origin in the scattered photons in the upper accretion stream, which is visible while the second pole is behind the horizon of the neutron star due to gravitational light bending, while there is also a contribution from the accretion column (vertically striped). In this solution, the first pole gets closer to the line of sight than the second. |
|
| Open with DEXTER | |
Figure 5 shows how the emission from the two poles contributes
to the pulse profiles for the decompositions of the low energy band
data taken at the maximum of the giant outburst in the case of the
minus solution.
Let us assume that the first magnetic pole with the polar angle
![]() gets closer to the line of sight than the second magnetic pole, i.e.,
gets closer to the line of sight than the second magnetic pole, i.e.,
![]() .
At phase 0.0, both poles are right behind the horizon of the neutron star:
the first pole is going to reappear, the second pole is turning farther away
from the observer.
At phase
.
At phase 0.0, both poles are right behind the horizon of the neutron star:
the first pole is going to reappear, the second pole is turning farther away
from the observer.
At phase ![]() 0.1 the first pole becomes visible, and from then on the
emission from the halo of the first pole makes the largest contribution until
the pole disappears behind the horizon at
0.1 the first pole becomes visible, and from then on the
emission from the halo of the first pole makes the largest contribution until
the pole disappears behind the horizon at ![]() 0.6. When the first pole,
which is closer to the observer's line of sight, is right at the horizon
of the neutron star and its accretion column is seen from the side, a minimum
is likely to be observed in the pulse profile (see also Sect. 4.4).
At the major maximum at phase 0.15-0.25, the second magnetic pole is
behind the horizon of the neutron star and the scattered and gravitationally
bent photons from the upper accretion stream cause the pronounced increase in
flux.
The second pole that is rotating on a circle farther away from
the line of sight than the first pole comes back to the front side at about
phase 0.45 and is closest to the observer at about phase 0.7. However,
since the line of sight is closer in latitude to the first pole than to the
second pole, the observer never gets as close to the surface normal of
the second pole as to that of the first pole. The main emission seen from the
second pole while it is on this side of the horizon comes directly from the
accretion column.
0.6. When the first pole,
which is closer to the observer's line of sight, is right at the horizon
of the neutron star and its accretion column is seen from the side, a minimum
is likely to be observed in the pulse profile (see also Sect. 4.4).
At the major maximum at phase 0.15-0.25, the second magnetic pole is
behind the horizon of the neutron star and the scattered and gravitationally
bent photons from the upper accretion stream cause the pronounced increase in
flux.
The second pole that is rotating on a circle farther away from
the line of sight than the first pole comes back to the front side at about
phase 0.45 and is closest to the observer at about phase 0.7. However,
since the line of sight is closer in latitude to the first pole than to the
second pole, the observer never gets as close to the surface normal of
the second pole as to that of the first pole. The main emission seen from the
second pole while it is on this side of the horizon comes directly from the
accretion column.
![\begin{figure}
\par\mbox{\includegraphics[angle=270,width=8cm,clip=]{13863fg6a.eps}\includegraphics[angle=270,width=8cm,clip=]{13863fg6b.eps} }
\end{figure}](/articles/aa/full_html/2010/09/aa13863-09/Timg36.png)
|
Figure 6:
Polar diagrams of the intrinsic beam pattern for the minus
solution of solution 1
for the same observations as shown in Fig. 3, for the softest
and the hardest bands for an assumed
|
| Open with DEXTER | |
Parmar et al. (1989a) have modeled the luminosity dependent
pulse profiles from the first observed giant outburst in 1985 by
assuming a fan beam and a pencil beam component for the two magnetic poles
based on a model by Wang & Welter (1981). They obtain a fit
for all ten pulse profiles for different luminosities ranging from
0.1-
![]() erg s-1 with some residuals and find
that the fan beam mainly produces the major peak at phase 0.2, whereas
the peak at phase 0.95 can be ascribed to a pencil beam. The
way they have chosen phase 0.0 is different than in our work, resulting
in a shift by about 0.4. The best-fit parameters of Parmar et al. (1989a)
correspond to
erg s-1 with some residuals and find
that the fan beam mainly produces the major peak at phase 0.2, whereas
the peak at phase 0.95 can be ascribed to a pencil beam. The
way they have chosen phase 0.0 is different than in our work, resulting
in a shift by about 0.4. The best-fit parameters of Parmar et al. (1989a)
correspond to
![]()
![]() ,
,
![]()
![]() ,
and
,
and
![]()
![]() ,
assuming
,
assuming
![]()
![]() .
This result is consistent
with our solution 1 for the case of
.
This result is consistent
with our solution 1 for the case of
![]()
![]() (see
Fig. 4).
(see
Fig. 4).
4.2 Comparison to phase-resolved spectral analysis
Klochkov et al. (2008) analyzed the same INTEGRAL data as used in
this work and performed pulse phase resolved spectroscopy. For the data of the
maximum, they find that the spectrum is harder at the main peak (phase 0.2).
They conclude that the observer might be seeing Compton scattered photons from
the optically thick accretion column.
In the data taken at the end of the decay, a new peak appears at about phase
0.95. At this point, the spectrum is again harder, leading to the conclusion
that the line of sight of the observer is closest to the magnetic field lines.
This picture is in good agreement with the solution 1 of the decomposition,
in which the
emission of the upper accretion stream of the second pole, which
is visible owing to gravitational light bending, has its maximum at
phase ![]() 0.2 while the halo of the first pole also has substantial
emission, thus contributing significantly to the main peak.
At phase
0.2 while the halo of the first pole also has substantial
emission, thus contributing significantly to the main peak.
At phase ![]() 0.95 the scattered emission from
the upper accretion stream of the second pole starts to increase,
while the emission from the accretion column of the first
pole also contributes to the observed emission.
0.95 the scattered emission from
the upper accretion stream of the second pole starts to increase,
while the emission from the accretion column of the first
pole also contributes to the observed emission.
4.3 Intrinsic beam patterns
The observed asymptotic beam pattern differs from the intrinsic local beam
pattern of the emission region because of relativistic light deflection
near the neutron star. Making assumptions on the radius r and mass
m of the neutron star, the asymptotic angle ![]() can be
transformed into the intrinsic angle
can be
transformed into the intrinsic angle ![]() relative to the surface
normal at the first magnetic pole to describe the local emission pattern. We
use the canonical values r = 10 km and
relative to the surface
normal at the first magnetic pole to describe the local emission pattern. We
use the canonical values r = 10 km and
![]() ,
thus the ratio between r and the Schwarzschild radius
,
thus the ratio between r and the Schwarzschild radius ![]() is
is
![]() .
The intrinsic beam patterns of the minus solution
are shown in Fig. 6 in polar diagrams.
As can be seen in these polar diagrams, the range for
the visible angle is
.
The intrinsic beam patterns of the minus solution
are shown in Fig. 6 in polar diagrams.
As can be seen in these polar diagrams, the range for
the visible angle is ![]() 10
10![]() -105
-105![]() if
if
![]()
![]() is
assumed.
is
assumed.
4.4 Possible origin of the emission
In X-ray pulsars, a strong magnetic field funnels matter accreted from the companion star onto the polar caps. The infalling particles deposit their energy in the atmosphere of the neutron star. Heating due to accretion is balanced by radiative cooling through bremsstrahlung emission, Compton scattering, and the so-called cyclotron radiation after collisional excitation of electrons. In low-luminosity states, the accreted matter is decelerated in the atmosphere of the neutron star by Coulomb scattering. Emission can be seen as pencil beams from the hot spots at polar caps (Wang & Welter 1981). In high-luminosity states, however, the accretion rate is higher, and an accretion column is believed to form. Plasma is decelerated by radiation pressure in the column, and a radiative shock forms above the neutron star surface (Davidson 1973; Basko & Sunyaev 1976). Above the radiative shock, plasma is in free fall, while below the discontinuity, there is a region of nearly stagnant plasma from which photons escape from the sides of the column in a fan beam.
In addition, a luminous halo might form around the accretion column (Lyubarskii & Syunyaev 1988; Davidson & Ostriker 1973) and radiation from the polar cap and the halo can also be scattered in the upper accretion stream (Brainerd & Meszaros 1991; Soffel et al. 1985). As the accretion stream is delimited by magnetic field lines of the neutron star, it opens up wide far from the neutron star. Therefore, the emission from the upper part of the accretion stream can dominate the observed flux and can also screen the polar caps and the halo. Due to relativistic light deflection, emission from one pole can be deflected to the antipodal direction (Pechenick et al. 1983; Leahy & Li 1995; Kraus 2001; Riffert & Meszaros 1988). All these effects can modify the local beam pattern and thus have an effect on the pulse profile of the X-ray pulsar. Wang & Welter (1981) have modeled the pulse profiles of X-ray pulsars by assuming hot spots and fan beams, although EXO 2030+375 is not included in their list of selected X-ray pulsars. They show that, in general, sharp minima can be seen in the pulse profiles at the moment when the fan beam rotates behind the horizon of the neutron star and when it reappears on the side of the neutron star facing the observer. This is exactly what seems to be happening in EXO 2030+375 at phases 0.1 and 0.6 as the decomposition method has shown.
Kraus et al. (2010,2003)
have modeled beam patterns and pulse profiles for
medium-luminosity X-ray pulsars assuming an accretion column with
energy-dependent local beaming of radiation, a luminous halo formed by
illumination of the neutron star surface, and magnetic scattering
in the upper accretion stream.
They show that the emission from the upper accretion stream can
dominate the local beam pattern for ![]() 120
120![]() .
Halo emission has
a maximum at
.
Halo emission has
a maximum at
![]() 30
30![]() -60
-60![]() ,
with significant contribution to
the beam pattern for photon energies below
,
with significant contribution to
the beam pattern for photon energies below ![]() 5 keV. If one assumes
isotropic emission from the accretion column below the discontinuity,
the halo emission becomes comparable or negligible relative to the column
emission at
5 keV. If one assumes
isotropic emission from the accretion column below the discontinuity,
the halo emission becomes comparable or negligible relative to the column
emission at ![]() 10 keV. However, if the radiation below the shock is
beamed downwards, the halo remains more luminous than the accretion column
and the upper stream up to
10 keV. However, if the radiation below the shock is
beamed downwards, the halo remains more luminous than the accretion column
and the upper stream up to ![]() 30 keV.
The decomposition has shown that the beam patterns show dominant
soft emission for
30 keV.
The decomposition has shown that the beam patterns show dominant
soft emission for ![]() 60
60![]() ,
which can be interpreted as halo
emission, while the emission
,
which can be interpreted as halo
emission, while the emission ![]() 150
150![]() most likely arises from
the upper accretion stream (see Fig. 3, lower panel).
most likely arises from
the upper accretion stream (see Fig. 3, lower panel).
5 Summary
We performed pulse-profile decomposition with data of EXO 2030+375 taken during the giant outburst of 2006 by RXTE and INTEGRAL. This is the fourth source after Cen X-3, Her X-1, and A 0535+26 to which this method has been applied. Each of the asymmetric pulse profiles of EXO 2030+375 at different luminosities in various energy bands are decomposed in two symmetric pulse profiles that account for emission from the two emission regions of the system.
We find that the magnetic field of the neutron star is moderately
distorted. The observer sees a part of the emission from each of the two
emission regions, but these parts do not overlap.
We suggest that the main peak at phase 0.2 in the observed pulse profiles
can be attributed to harder emission from the upper accretion stream
of the second pole, which can be observed while the pole is on the other side
of the neutron star because of relativistic light bending around the neutron star
(``anti-pencil'').
However, the main peak also has a considerable contribution
from the halo emission of the first pole, which is closer to the line of sight
than the second. Between phases ![]() 0.95 and
0.95 and ![]() 0.1, both poles are located
on the rear side of the neutron star. The sharp minima seen at phases 0.0 and 0.6
are caused when the first pole is about to re- and disappear at the horizon of the
neutron star, and its accretion column is seen from the side.
0.1, both poles are located
on the rear side of the neutron star. The sharp minima seen at phases 0.0 and 0.6
are caused when the first pole is about to re- and disappear at the horizon of the
neutron star, and its accretion column is seen from the side.
Our analysis has disentangled the emission components of the neutron star, which in total lead to the observed asymmetric, energy-, and luminosity-dependent pulse profiles of EXO 2030+375. It will allow us to perform detailed analyses of, e.g., the pulse phase-resolved spectra with reliable interpretation of the differences in the spectral parameters, hence shedding light on the physical processes in the system responsible for the observed emission.
AcknowledgementsThis research is based on observations with INTEGRAL, an ESA project with instruments and science data centre funded by ESA member states (especially the PI countries: Denmark, France, Germany, Italy, Switzerland, Spain), Poland, and with the participation of Russia and the USA. This research has made use of data obtained from the High Energy Astrophysics Science Archive Research Center (HEASARC), provided by NASA's Goddard Space Flight Center. This work was supported by DFG grant SA 1777 1/1.
Appendix A: The decomposition method
![\begin{figure}\par\includegraphics[width=17cm,clip=]{13863fgA1.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13863-09/Timg50.png)
|
Figure A.1: Intrinsic geometry of the neutron star. Figures taken from Kraus et al. (1995). |
| Open with DEXTER | |
![\begin{figure*}{\hspace{60mm}\footnotesize\sf Solution 1\hspace{70mm}}\\
\inclu...
...udegraphics[angle=270,width=12.5cm,origin=rb,clip]{13863fga2b.eps}
\end{figure*}](/articles/aa/full_html/2010/09/aa13863-09/Timg51.png)
|
Figure A.2:
Beam patterns from the two emission regions seen by the observer
plotted over
|
| Open with DEXTER | |
The pulse-profile decomposition method has been developed and first presented by Kraus et al. (1995). Here we quickly summarize the method and the steps in the analysis.
A.1 Decomposition into two single-pole pulse profiles
Let ![]() be the angle between the direction of the line of sight and
the axis through one magnetic pole.
Figure A.1 shows the configuration of the neutron star, showing
the positions of the magnetic poles with respect to the rotation axis.
The polar angles of the two magnetic poles are called
be the angle between the direction of the line of sight and
the axis through one magnetic pole.
Figure A.1 shows the configuration of the neutron star, showing
the positions of the magnetic poles with respect to the rotation axis.
The polar angles of the two magnetic poles are called
![]() and
and
![]() .
As the neutron star rotates,
.
As the neutron star rotates, ![]() changes with rotation angle
changes with rotation angle ![]() .
For the emission of each pole, there are two symmetry points at
.
For the emission of each pole, there are two symmetry points at ![]() and
and
![]() .
For each pole, the relation between
.
For each pole, the relation between ![]() ,
,
![]() ,
and
,
and ![]() can be obtained using the spherical triangle in Fig. A.1 (left):
can be obtained using the spherical triangle in Fig. A.1 (left):
We assume that there is an offset
For an ideal dipole field
| Figure A.3:
Left:
beam patterns from the two emission regions plotted over
|
|
| Open with DEXTER | |
To find the contributions from each magnetic pole, we perform Fourier analysis
of the observed total pulse profiles. We model it as a sum of two symmetric
functions f1 and f2 and search for the values for their symmetry
points ![]() and
and ![]() ,
respectively.
In principle we are able to find a set of f1 and f2 for any chosen
,
respectively.
In principle we are able to find a set of f1 and f2 for any chosen
![]() and
and ![]() .
However, since we deal with functions that describe astronomically
observed emission, the following criteria need to be fulfilled:
.
However, since we deal with functions that describe astronomically
observed emission, the following criteria need to be fulfilled:
- 1.
- Positive flux: The symmetric functions f1 and f2 must not have negative values because they model the flux of an astronomical object.
- 2.
- No ripples: The functions f1 and f2should show no small-scale features that cancel out in the sum. As the two functions correspond to pulse profiles of single-poles that emit independently, they ought not to have features that match exactly. Also, the single-pole pulse profiles are supposedly not more complicated than the total pulse profile.
- 3.
- Same geometry: We have pulse profiles from one source in different energy bands and, ideally, from more than one observation. The observed pulse profiles are energy and luminosity dependent in most cases. Since the emission arises from only one object, the symmetry points must be the same for the decompositions of all available data.
A.2 Reconstruction of the beam pattern
Two beam patterns are obtained from single-pole pulse profiles as
functions of the rotation angles
![]() (for one single-pole pulse profile) and
(for one single-pole pulse profile) and
![]() (for the other single-pole pulse profile).
During one revolution of the neutron star, the angle
(for the other single-pole pulse profile).
During one revolution of the neutron star, the angle ![]() between the
first magnetic pole and the line of sight changes with the phase.
There may be an interval during one phase, i.e., a range of the angle
between the
first magnetic pole and the line of sight changes with the phase.
There may be an interval during one phase, i.e., a range of the angle ![]() ,
in which the observer sees emission from both poles.
The same is true for the second magnetic pole. The range covered by the angle
,
in which the observer sees emission from both poles.
The same is true for the second magnetic pole. The range covered by the angle
![]() is in general different for each pole.
There may, however, be a certain subrange of values of
is in general different for each pole.
There may, however, be a certain subrange of values of ![]() that occur for each of the poles. Then,
at some phase
that occur for each of the poles. Then,
at some phase ![]() ,
the observer looks onto the first pole at angle
,
the observer looks onto the first pole at angle
![]() and at some different phase
and at some different phase
![]() ,
the observer looks onto
the second pole at the same angle
,
the observer looks onto
the second pole at the same angle ![]() .
A simple example would be two antipodal poles that pass through the line
of sight (
.
A simple example would be two antipodal poles that pass through the line
of sight (![]() = 0) at
= 0) at ![]() = 0 and at
= 0 and at
![]() = 0.5, respectively.
If, in addition, the two emission regions of the neutron star have the
same beam pattern, the emission seen at
= 0.5, respectively.
If, in addition, the two emission regions of the neutron star have the
same beam pattern, the emission seen at ![]() from the first pole
(phase
from the first pole
(phase ![]() )
is the same as the emission seen at
)
is the same as the emission seen at ![]() from the second
pole (phase
from the second
pole (phase
![]() ).
This means that the visible beam patterns of
the two poles must have identical parts at different pulse phases.
If we find such parts of the beam patterns of the two single-pole
pulse profiles we can overlay them and get a relation between
).
This means that the visible beam patterns of
the two poles must have identical parts at different pulse phases.
If we find such parts of the beam patterns of the two single-pole
pulse profiles we can overlay them and get a relation between
![]() and
and
![]() .
From this relation,
we can derive the positions of the magnetic poles
.
From this relation,
we can derive the positions of the magnetic poles
![]() and
and
![]() as functions of the direction of the observation
as functions of the direction of the observation
![]() .
The angle
.
The angle
![]() needs to be determined independently
in other studies of the source.
needs to be determined independently
in other studies of the source.
References
- Angelini, L., Stella, L., & Parmar, A. N. 1989, ApJ, 346, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Basko, M. M., & Sunyaev, R. A. 1976, MNRAS, 175, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Bildsten, L., Chakrabarty, D., Chiu, J., et al. 1997, ApJS, 113, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Blum, S., & Kraus, U. 2000, ApJ, 529, 968 [NASA ADS] [CrossRef] [Google Scholar]
- Brainerd, J. J., & Meszaros, P. 1991, ApJ, 369, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Bulik, T., Riffert, H., Meszaros, P., et al. 1995, ApJ, 444, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Caballero, I., Kraus, U., Santangelo, A., Sasaki, M., & Kretschmar, P. 2010, A&A, submitted [Google Scholar]
- Coe, M. J., Payne, B. J., Longmore, A., & Hanson, C. G. 1988, MNRAS, 232, 865 [NASA ADS] [CrossRef] [Google Scholar]
- Corbet, R. H. D., & Levine, A. M. 2006, The Astronomer's Telegram, 843, 1 [Google Scholar]
- Davidson, K. 1973, Nature, 246, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Davidson, K., & Ostriker, J. P. 1973, ApJ, 179, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Frontera, F., & Dalfiume, D. 1989, in Two Topics in X-Ray Astronomy, Vol. 1, X Ray Binaries, Vol. 2, AGN and the X Ray Background, ed. J. Hunt, & B. Battrick, ESA SP, 296, 57 [Google Scholar]
- Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Jahoda, K., Swank, J. H., Giles, A. B., et al. 1996, in SPIE Conf. Ser. 2808, ed. O. H. Siegmund, & M. A. Gummin, 59 [Google Scholar]
- Janot-Pacheco, E., Motch, C., & Pakull, M. W. 1988, A&A, 202, 81 [NASA ADS] [Google Scholar]
- Klochkov, D., Horns, D., Santangelo, A., et al. 2007, A&A, 464, L45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klochkov, D., Santangelo, A., Staubert, R., & Ferrigno, C. 2008, A&A, 491, 833 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kraus, U. 2001, ApJ, 563, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Kraus, U., Nollert, H.-P., Ruder, H., & Riffert, H. 1995, ApJ, 450, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Kraus, U., Blum, S., Schulte, J., Ruder, H., & Meszaros, P. 1996, ApJ, 467, 794 [NASA ADS] [CrossRef] [Google Scholar]
- Kraus, U., Zahn, C., Weth, C., & Ruder, H. 2003, ApJ, 590, 424 [NASA ADS] [CrossRef] [Google Scholar]
- Kraus, U., Zahn, C., & Santangelo, A. 2010, A&A, submitted [Google Scholar]
- Krimm, H., Barthelmy, S., Gehrels, N., et al. 2006, The Astronomer's Telegram, 861, 1 [NASA ADS] [Google Scholar]
- Leahy, D. A. 1991, MNRAS, 251, 203 [NASA ADS] [Google Scholar]
- Leahy, D. A., & Li, L. 1995, MNRAS, 277, 1177 [NASA ADS] [Google Scholar]
- Lund, N., Budtz-Jørgensen, C., Westergaard, N. J., et al. 2003, A&A, 411, L231 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lyubarskii, Y. E., & Syunyaev, R. A. 1988, SvA Lett., 14, 390 [Google Scholar]
- McCollough, M. L., Turler, M., Willis, D., & Shaw, S. E. 2006, The Astronomer's Telegram, 868, 1 [NASA ADS] [Google Scholar]
- Motch, C., & Janot-Pacheco, E. 1987, A&A, 182, L55 [NASA ADS] [Google Scholar]
- Parmar, A. N., White, N. E., & Stella, L. 1989a, ApJ, 338, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Parmar, A. N., White, N. E., Stella, L., Izzo, C., & Ferri, P. 1989b, ApJ, 338, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Pechenick, K. R., Ftaclas, C., & Cohen, J. M. 1983, ApJ, 274, 846 [NASA ADS] [CrossRef] [Google Scholar]
- Reynolds, A. P., Parmar, A. N., & White, N. E. 1993, ApJ, 414, 302 [NASA ADS] [CrossRef] [Google Scholar]
- Riffert, H., & Meszaros, P. 1988, ApJ, 325, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Riffert, H., Nollert, H.-P., Kraus, U., & Ruder, H. 1993, ApJ, 406, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Soffel, M., Herold, H., Ruder, H., & Ventura, J. 1985, A&A, 144, 485 [NASA ADS] [Google Scholar]
- Ubertini, P., Lebrun, F., Di Cocco, G., et al. 2003, A&A, 411, L131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, Y., & Welter, G. L. 1981, A&A, 102, 97 [NASA ADS] [Google Scholar]
- White, N. E., Swank, J. H., & Holt, S. S. 1983, ApJ, 270, 711 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, C. A., Finger, M. H., Coe, M. J., Laycock, S., & Fabregat, J. 2002, ApJ, 570, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, C. A., Fabregat, J., & Coburn, W. 2005, ApJ, 620, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, C. A., Finger, M. H., & Camero-Arranz, A. 2008, ApJ, 678, 1263 [NASA ADS] [CrossRef] [Google Scholar]
- Winkler, C., Courvoisier, T. J.-L., Di Cocco, G., et al. 2003, A&A, 411, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Table 1: Parameters obtained from the decomposition for solutions 1 and 2.
All Figures
![\begin{figure}
\mbox{\includegraphics[angle=270,width=6cm,origin=rb,clip]{13863f...
...cludegraphics[angle=270,width=6cm,origin=rb,clip]{13863fg1b.eps} }\end{figure}](/articles/aa/full_html/2010/09/aa13863-09/Timg15.png)
|
Figure 1: Pulse profiles of EXO 2030+375 during the rise ( left) and the decay ( right) of the giant outburst in 2006 observed with RXTE. |
| Open with DEXTER | |
| In the text | |
![\begin{figure*}
{\hspace{6cm}\footnotesize\sf\mbox{Solution 1}\hspace{10cm}}\\
\includegraphics[width=12.8cm,clip]{13863fg2.eps}
\end{figure*}](/articles/aa/full_html/2010/09/aa13863-09/Timg19.png)
|
Figure 2:
A selection of single-pole pulse profiles ( left) and corresponding
beam patterns ( right) obtained by the decomposition
method for the |
| Open with DEXTER | |
| In the text | |
![\begin{figure*}
{\hspace{55mm}\footnotesize\sf Solution 1\hspace{55mm}}\\ [4mm]
...
...ncludegraphics[angle=270,width=12cm,origin=rb,clip]{13863fg3b.eps}
\end{figure*}](/articles/aa/full_html/2010/09/aa13863-09/Timg25.png)
|
Figure 3:
Asymptotic beam patterns of the plus and minus solutions
of solution 1 seen by the distant observer plotted over the angle |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90,width=8.8cm,clip=]{13863fg4.eps}\vspace{-2mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13863-09/Timg28.png)
|
Figure 4:
Relation between the observing angle
|
| Open with DEXTER | |
| In the text | |
| |
Figure 5: Decomposed single-pole pulse profiles of the data taken near the maximum of the giant outburst for the lowest energy band (same as the upper left diagram of the upper [solution 1] panels in Fig. 2) with proposed emission components derived from the beam patterns of the minus solution (Fig. 3, lower panel). We suggest that the emission from the first pole consists of emission from the halo (diagonally striped component) and from the accretion column (vertically striped). The dominant emission from the second pole seems to have its origin in the scattered photons in the upper accretion stream, which is visible while the second pole is behind the horizon of the neutron star due to gravitational light bending, while there is also a contribution from the accretion column (vertically striped). In this solution, the first pole gets closer to the line of sight than the second. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[angle=270,width=8cm,clip=]{13863fg6a.eps}\includegraphics[angle=270,width=8cm,clip=]{13863fg6b.eps} }
\end{figure}](/articles/aa/full_html/2010/09/aa13863-09/Timg36.png)
|
Figure 6:
Polar diagrams of the intrinsic beam pattern for the minus
solution of solution 1
for the same observations as shown in Fig. 3, for the softest
and the hardest bands for an assumed
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[width=17cm,clip=]{13863fgA1.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13863-09/Timg50.png)
|
Figure A.1: Intrinsic geometry of the neutron star. Figures taken from Kraus et al. (1995). |
| Open with DEXTER | |
| In the text | |
![\begin{figure*}{\hspace{60mm}\footnotesize\sf Solution 1\hspace{70mm}}\\
\inclu...
...udegraphics[angle=270,width=12.5cm,origin=rb,clip]{13863fga2b.eps}
\end{figure*}](/articles/aa/full_html/2010/09/aa13863-09/Timg51.png)
|
Figure A.2:
Beam patterns from the two emission regions seen by the observer
plotted over
|
| Open with DEXTER | |
| In the text | |
| |
Figure A.3:
Left:
beam patterns from the two emission regions plotted over
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.