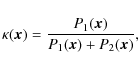EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 517 (July 2010) A&A, 517 (2010) A23 Full HTML
Free Access
Issue
A&A
Volume 517, July 2010
Article Number A23
Number of page(s) 25
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/200913852
Published online 28 July 2010
A&A 517, A23 (2010)

Observations, compositional, and physical characterization of near-Earth and Mars-crosser asteroids from a spectroscopic survey[*]

J. de León1,2 - J. Licandro2 - M. Serra-Ricart2 - N. Pinilla-Alonso3 - H. Campins4

1 - Instituto de Astrofísica de Andalucía-CSIC, Camino Bajo de Huétor 50, 18008 Granada, Spain
2 - Instituto de Astrofísica de Canarias (IAC), C/Vía Láctea s/n, 38205 La Laguna, Spain
3 - NASA Ames Research Center, MS 245-3, Moffett Field, CA 94035-1000, USA
4 - University of Central Florida, PO Box 162385, Orlando, FL 32816.2385, USA

Received 11 December 2009 / Accepted 20 March 2010

Abstract
Aims. We analyse a significantly large sample of spectroscopic data to provide a compositional characterization of the near-Earth asteroid population. We present visible and near-infrared spectra of a total of 74 near-Earth asteroids (NEAs) and Mars-crossers (MCs), covering the wavelength region from 0.5 to 2.5 $\mu $m. Using spectra of NEAs from other databases to enlarge our sample, and compiling two comparison samples of main belt asteroids (MBs) and ordinary chondrites (OCs), we analyse a total of 79 NEAs, 91 MBs, and 103 OCs.
Methods. We obtained our visible and near-infrared spectra using the instruments and the telescopes located at ``El Roque de los Muchachos'' Observatory, in the island of La Palma (Spain). We compute several diagnostic spectral parameters from the reflectance spectra of NEAs, MBs, and OCs, that are used to infer the mineralogical composition. The distribution of the obtained values are analysed in 2 different parameter spaces. We also apply a robust statistical method based on neuronal networks to those spectral parameters, to compare the NEAs with OCs. Space weathering effects and dynamical and physical properties of NEAs and MBs are also studied.
Results. Compositional differences between MBs and NEAs are inferred from the mineralogical analysis. The most remarkable results are: (1) the high olivine content of the NEAs; (2) the compositional similarity between NEAs and a small group of meteorites, the LL ordinary chondrites; and (3) that NEAs are not compositionally similar to OCs, implying that they are not the most likely parent bodies of those meteorites, as has been widely believed. To explain their apparently fresh surfaces (NEAs are on average less red than MBs), a combination of composition and size distribution (NEAs have diameters of some kilometres) should be invoked. Dynamical models applied to our sample of NEAs indicate that most of them originate in the inner part of the main belt, as expected.

Key words: minor planets, asteroids: general - methods: observational - techniques: spectroscopic - surveys

1 Introduction

The population of near-Earth objects (NEOs) is composed of both asteroids and extinct/active comets that have perihelion distances $q \le 1.3$ AU and aphelion distances $Q \ge 0.98$ AU, and whose orbits periodically approach or intersect Earth's orbit. According to their orbital parameters, near-Earth asteroids (NEAs) are subdivided into Apollos ($a \ge 1.0$ AU; $q \le 1.016$ AU), Atens (a < 1.0 AU; $Q \ge 0.983$ AU), and Amors ( 1.016 < q < 1.3 AU). Another population of asteroids that come close to Earth is the Mars-crossers population (MCs), whose orbits approach or intersect the orbit of Mars, and have perihelion distances 1.30 < q < 1.66 AU.

NEOs are objects that have migrated into the interior of the Solar System and have lifetimes of 106-107 years, short compared to the age of the Solar System itself (Morbidelli et al. 2002). This, and that the NEO population is basically stationary in number, implies that this population of objects has to be periodically replenished. Wetherill (1979) and Wisdom (1983) first identified the different gravitational resonances in the Solar System as major sources of near-Earth objects. Current dynamical models have now identified three main transport routes to deliver asteroids from the main belt to near-Earth orbits: the $\nu _6$ secular resonance with Saturn, located in the inner edge of the main asteroid belt; the 3:1 mean motion resonance with Jupiter, located at 2.5 AU, and the region occupied by Mars-crossing asteroids (Froeschlé & Scholl 1987; Farinella et al. 1993; Froeschlé & Morbidelli 1994; Moons 1997; Morbidelli & Nesvorný 1999). There is also a fraction of near-Earth asteroids that come from extinct or dormant comets that have subsequently developed an asteroidal appearance. While Bottke et al. (2002) consider that this contribution varies between 2% and 10% (for absolute magnitudes 13 < H < 22), Fernández et al. (2002) show that the actual NEA population in cometary orbits can be explained by means of dispersed objects from the outer main belt. Binzel et al. (2004) estimate a fraction of between 10% and 18%, and DeMeo et al. (2008) indicate that this percentage varies from 0% to 16%.

Different spectroscopic surveys in the visible region have been used to develop a taxonomical classification of the asteroids, according to differences in their reflectance spectra[*]. Those surveys have also revealed that the NEA population is dominated by objects belonging to the taxonomic classes S and Q: Binzel et al. (2004) found that 40% of the NEAs are S-type asteroids, while 25% of the NEAs can be classified as Q-type asteroids. When corrected for discovery biases, about 40% of the NEA population belong to one of these two taxonomic classes. In the case of Mars-crossers, 65% of the population belongs to the S class. In the main belt, these taxonomic types are concentrated in the inner and central regions, between 2.0 and 2.5 AU. Those classes are characterized by a reflectance spectrum that shows prominent absorption bands centred on 1 and 2 $\mu $m. These absorption bands are crystal field absorptions produced by transition metal cations (Fe2+, Mg2+,Ca2+,Al2+, etc.) located in specific crystallographic coordination sites in mafic silicates, mainly pyroxenes, feldspars, and olivine (Burns 1970). Mafic minerals are also the most abundant in all chondrites and in the majority of achondrites, and so are also present in the spectra of the most abundant class of meteorites (80% of all the falls), the ordinary chondrites (OCs). Therefore, given the dominance of S-type or ``rocky'' asteroids among the NEA population and the ordinary chondrites among the meteorites, it has been generally and widely assumed that they are connected, and that NEAs are the most likely parent bodies of the OCs. It is therefore crucial to obtain spectra in the near-infrared region for this group of asteroids, if we wish to characterize with greater accuracy their mineralogy and their connection with the ordinary chondrites.

The SMASS survey (Xu et al. 1995; Bus & Binzel 2002a,b) and the S3OS2 (Lazzaro et al. 2004) are two of the most comprehensive and largest spectroscopic surveys that have been undertaken up to now. However, they both focus only on the visible region, from 0.45 to 0.92 $\mu $m approximately, and basically observed main belt asteroids. The SMASS survey has a near-infrared extension, the SMASSIR (Binzel et al. 2001; Burbine & Binzel 2002), but this only covers the spectra up to 1.6 $\mu $m. Therefore, the absence of spectroscopic surveys in the near-infrared region and the necessity for data at these wavelengths to permit a proper mineralogical characterization, motivated us to start an observational program in 2002 to obtain visible and near-infrared spectra of NEAs, creating the survey presented in this work. Besides near-Earth asteroids, this survey includes visible and near-infrared spectra of several Mars-crossers, which are also presented in this paper. During the execution of this observational program that finished in 2007, we also observed a group of asteroids in cometary orbits (ACOs), and some D-type main belt asteroids, Hildas and one Trojan as a comparison sample, that were published and analysed in Licandro et al. (2006,2008). Both databases are available at our web page[*]. Today, there are another two ongoing surveys similar to this one: the SINEO survey (Lazzarin et al. 2004, 2005), which started in 2000 and currently has spectra of 64 objects available at its web page[*]; and the MIT-UH-IRTF NEO reconnaissance program[*], which acquires only near-infrared spectra.

In Sect. 2, we describe the technical details of the instruments and the telescopes employed to obtain the visible and near-infrared spectra of the asteroids of this survey, together with the observational conditions and setup and the data reduction process. Section 3 describes our compilation of spectra from different databases to enlarge our sample of NEAs and perform the mineralogical analysis. In Sect. 4, we apply the ``classical'' method of mineralogical analysis (Cloutis et al. 1986; Cloutis & Gaffey 1991; Gaffey et al. 1993), based on the computation of different diagnostic spectral parameters, to a sample of NEAs, main belt asteroids (MBs) and ordinary chondrites (OCs). In Sect. 5, we apply a statistical method, based on neural network techniques to confirm one of the main results inferred from the mineralogical analysis. The contribution of space weathering effects and dynamics on the results are discussed in Sects. 6 and 7, respectively.

2 Survey description and data reduction

\begin{figure} \par {\hspace*{2cm}\includegraphics[width=4.5cm,clip]{13852f1a.ep... ...2cm}}\vspace*{3mm} \includegraphics[width=8.5cm,clip]{13852f1b.eps} \end{figure} Figure 1:

Distribution of the observational characteristics of this survey, from top and counter-clockwise: airmass, solar phase angle, and apparent visual magnitude. Mean value $\pm $1$\sigma $ deviation of each quantity are shown in brackets.

Open with DEXTER

Visible and near-infrared spectra of 74 NEAs and MCs covering the 0.5-2.5 $\mu $m spectral region were obtained during a total of 28 nights, as part of an observational campaign started in August 2002, using two telescopes at the ``El Roque de los Muchachos'' Observatory (Canary Islands, Spain). The list of observed objects and their observational parameters are shown in Appendix A, Table A.1. This table includes the type of orbit of the object, the starting UT, the airmass, the distance to the Sun (r) and to the Earth ($\Delta$), the phase angle ($\alpha$) and the visual magnitude mV at the time the observation was made, the number of exposures, and the total on-object exposure time. Whenever possible, objects were observed close to their meridian, when their airmass was near its minimum. Figure 1 shows the distribution of the airmass, the phase angle, and the visual magnitude of the observations. Mean values are shown within brackets.

Table 1:   Solar analogue stars used to obtain the reflectance spectra of the asteroids of this survey.

\begin{figure} \par\includegraphics[width=8.5cm,clip]{13852f2.eps} \end{figure} Figure 2:

Distribution of the observed solar analogue stars in this survey. Each star is labelled with a number, as in Table A.1. The observation frequency depends both on the stars visibility during each night and the distribution of the observing nights during the year.

Open with DEXTER

\begin{figure} \par\includegraphics[width=8cm,clip]{13852f3.eps} \end{figure} Figure 3:

Different solar analogue stars are used to obtain the reflectance spectrum of asteroid (433) Eros in the visible region. The top panel shows the spectrum of the asteroid and three solar analogues, with an offset in vertical axis for the sake of clarity. In the bottom panel, we can see the three resultant reflectance spectra of the asteroid. The uncertainty in the slope, computed between 0.5 and 0.7 $\mu $m is about 3%/1000 Å. For the majority of the asteroids, the uncertainties will be smaller that this value.

Open with DEXTER

To correct for telluric absorption and obtain the relative reflectance of each asteroid, several solar analogue stars (SAs) were observed during the same night at the same airmass. Apart from Hyades 64, widely accepted to be a solar analogue (Hardorp 1978), several stars from the list of Landolt (1992), with spectral types ranging from F8 to G2.5, were observed in previous nights and checked carefully against the solar analogue star P330E (Colina & Bohlin 1997), which exhibited a regular behaviour as solar analogue in both the visible and the near-infrared region. The complete list of SAs used in this survey can be seen in Table 1. Star coordinates and spectral types were obtained from the SIMBAD database[*]. Values of J, H, and K magnitudes were extracted from the 2MASS database (Skrutskie et al. 2006), while V magnitude and B-V colour were taken from different Landolt catalogues (Landolt 1973, 1983, 1992). We can also see in Table 1 the values for the solar analogue star P330E, as well as an average value for Hardorp's class 1 solar analogues, compiled by Campins et al. (1985). Values for the Sun were compiled from different papers (Hardorp 1980; Campins et al. 1985; Colina et al. 1996; Hainaut & Delsanti 2002). As can be seen from Table 1, all the stars used as SAs have colours that are similar to those of the Sun, from visible to near-infrared wavelengths. Figure 2 shows the observation frequencies of the solar analogues for this survey, as labelled in Appendix A, Table A.1. We note that the solar analogue star Hyades 64 was used only twice during the near-infrared observations, because of its high brightness. The observation frequency depends on both the star's visibility during each night and the distribution of the observation nights during each year.

2.1 Visible observations

Visible spectra were obtained with the 2.5 m Nordic Optical Telescope (NOT) using Andalucia Faint Object Spectrograph (ALFOSC). Observations before September 2003 were made with CCD#7, a 2048 $\times$ 2048 backside illuminated detector with a plate scale of 0.188''/pixel. After that, a new CCD with similar dimensions and a plate scale of 0.190''/pixel was installed (CCD#8). The new detector is affected by fringe levels that are typically twice as high as for CCD#7 (10%). We used a grism disperser that covers the 0.32-0.91 $\mu $m range, with a dispersion of 3 Å/pixel (300 lines per mm, blazed at 0.48 $\mu $m with $R \sim 700$). To avoid a second-order spectral image being superimposed on the red half of the first-order spectrum (approximately 20% of light absorption above 5900 Å), we used a second order blocking filter at 0.475 $\mu $m. A 1.3'' slit was employed, oriented in the parallactic angle to correct for differential refraction effects. The tracking was at the asteroid's proper motion, extracted from the corresponding ephemeris. The objects were identified as moving objects at the predicted position and with the predicted proper motion. To increase the quality of the spectra, three acquisitions, offsetting the object 5'' in-between in the slit direction, were obtained and subsequently averaged.

Visible data reduction was performed using the Image Reduction and Analysis Facility (IRAF) standard procedures (Tody 1993). Preprocessing of the CCD images included bias and flat field correction. An averaged bias frame taken at the telescope at the beginning of each observing night was used to perform bias subtraction. Flat field images were obtained for each object using calibration lamps, just before or after observing the object, to minimize the effects of telescope and instrument bending. We followed this same procedure for the wavelength calibration lamps. The extraction of 1D spectra from 2D images was carried out together with the sky background subtraction. Wavelength calibration was applied using Ne and Ar lamp spectra.

To obtain the reflectance spectra, we observed a minimum of 2 and a maximum of 4 solar analogue stars during each night (see Table A.1). After the extraction and wavelength calibration procedures, we divided each star spectrum by the remaining stellar spectra and checked that none of the ratios obtained exhibited slope variations greater than 3% per 1000 Å (this value is slightly higher than that for the near-infrared region). Each object's spectrum was then divided by the spectra of all the solar analogues, confirming that the resulting reflectance spectra were similar within the noise level. An example of this procedure can be seen in Fig. 3, where we have plotted the spectra of asteroid (433) Eros and three solar analogues. The resultant reflectance spectra of the asteroid are slightly different, with uncertainties in the computed slope of about 3%/1000 Å. The majority of the asteroids in our database have uncertainties lower than this value. Finally, a final reflectance spectrum of each object was obtained by averaging these individual reflectance spectra after a uniformly rebinning to a dispersion of 21 Å (a factor of 7), to increase the S/N, and normalized to unity at 0.55 $\mu $m.

2.2 Near-infrared spectra

Low resolution near-infrared spectra were taken with the 3.6 m Telescopio Nazionale Galileo (TNG) using the low resolution mode of NICS (Near Infrared Camera Spectrograph), a multi-mode instrument based on a HgCdTe Hawaii $1024 \times 1024$ array. All spectroscopic modes use the large field camera (LF), which has a plate scale of 0.25''/pixel. The large field camera has a quite large field of view (4.2' $\times$ 4.2') with a pixel scale small enough to properly sample the images under normal seeing conditions. We employed a 1.5'' slit, corresponding to a spectral resolving power R $\approx$ 34 quasi-constant along the spectra, and the Amici prism disperser. The Amici disperser consists of two low-dispersion (BaF2) and one high-dispersion (IRG2) prisms arranged in a configuration that disperses the light without deviating from the central wavelength (Oliva 2000; Baffa et al. 2001). The most remarkable feature of this system is its throughput: 88% average and 82% minimum transmission over the 0.8-2.5 $\mu $m spectral range. As in the case of visible observations, the slit was oriented in the parallactic angle, and the tracking was at the asteroid proper motion. Some images through the $J_{\rm s}$ filter were previously taken to identify the object in the field of view and to place the slit over the object. The acquisition consisted of a series of short exposure images in one position of the slit (position A), then an offset of the telescope by 10'' in the direction of the slit (position B), and the acquisition of another series of images. This process was repeated and a number of ABBA cycles were acquired. The total on-object exposure time is listed in Table A.1.

The observational method and reduction procedure followed Licandro et al. (2001, 2002). Standard bias and flat correction were applied to the images, the latter providing a 3% improvement in the pixel-to-pixel variation. Nevertheless, since the objects occupy the same pixels in the detector in all images, this variation mostly disappears when we divide by the spectra of the solar analogue stars. The reduction of the spectra was done by subtracting consecutive A and B images. With this procedure, we obtain two 2D images from each ABBA cycle. The extraction of the 1D spectra followed the same procedure as in the case of the visible data, with the exception of the sky subtraction step.

Owing to the low resolution of the Amici prism, virtually all the Ar/Xe lines of the calibrations lamps appear blended and cannot be easily used for standard reduction procedures. For this reason, wavelength calibration was performed using a look-up table based on the theoretical dispersion predicted by ray-tracing and adjusted to best fit the observed spectra of calibration sources and telluric absorptions. The spectra of the asteroids were divided by the spectra of the solar analogue stars. Sub-pixel offsetting was applied when dividing the spectra to correct for errors in the wavelength calibrations due to instrumental flexure. We compared the reflectance spectra of the same asteroid obtained with different solar analogues to ensure that the uncertainty in the slope is smaller than 1%/1000 Å. The individual spectra were finally averaged to obtain the final reflectance spectrum of each object, which was normalized to unity at 1.6 $\mu $m for convention.

2.3 Visible and near-infrared spectra

Once we have the reflectance spectra of the objects in the visible and near-infrared region, the final step is to merge the two regions, using the common interval 0.8-0.92 $\mu $m. The method of compositional analysis that we use to extract the mineralogical information about the objects in this survey is quite sensitive to the way we join the visible and the near-infrared part of the spectra. As an example, one of the spectral parameters that is commonly computed and used to infer mineralogy, is the wavelength position of the centre of the absorption bands present in the spectra. To measure these positions, we have to first remove the continuum contribution from the spectra, i.e., to compute the tangents to the spectral curve at the shoulders of the absorption bands and to divide the spectrum by those tangents. The first absorption band, normally centred around 1 $\mu $m, is formed when the two spectral regions are merged, so its tangent is especially sensitive to the way we carry out this step. For this reason, we carefully merged visible and near-infrared spectra for each individual object by means of least squares fitting.

The final reflectance spectra in the visible and near-infrared are shown in Appendix B, Fig. B.1. For single wavelength region observations, we used spectra from other surveys to complement our data and be able to perform the subsequent mineralogical analysis. In particular, as described in the introduction, we gathered spectra from the SMASS database (Bus & Binzel 2002a,b), including the ongoing observational program MIT-UH-IRTF NEO reconnaissance program, and the SINEO database (Lazzarin et al. 2004, 2005).

3 Data compilation

To apply the method of mineralogical analysis, we must select only asteroids in our database that meet two requirements: a complete reflectance spectrum in the visible and near-infrared range, and the presence of typical absorption bands associated with silicates (i.e., the asteroid belonging to S-complex). Besides the objects that belong to the ACO group (Asteroids in Cometary Orbits), our database includes some asteroids with ``featureless'' spectra, some of which have been specifically observed, as is the case of (3200) Phaethon (Licandro et al. 2007). Other objects had poor S/N or a spectrum for only one of the spectral ranges. As pointed out in the previous section, we use spectra from other databases to complete our own data. Furthermore, to increase our sample and make the analysis statistically more meaningful, we included complete visible and near-infrared spectra of other NEAs from those databases (mainly SMASS and MIT-UH-IRTF). Considering therefore the spectra from other surveys, we analyse a total of 79 NEAs and MCs.

As shown in the introduction, NEAs originate primarily in two main source regions located in the main asteroid belt, the $\nu _6$ and the 3:1 gravitational resonances (Bottke et al. 2002). Therefore, we perform a similar mineralogical analysis for a statistically significant number of main-belt asteroids (MBs), using the reflectance spectra from the surveys SMASS, S3OS2 (Lazzaro et al. 2004), and 52-color asteroid survey (Bell et al. 1995). As an observational sub-program of this survey, we are currently obtaining near-infrared spectra of main-belt asteroids located in the main source regions of NEAs (Main Belt Objects near-Infrared Spectroscopic Survey, or MBOISS). We have reduced part of these data, and we included some in the sample of MBs analysed here. Finally, we used all the available reflectance spectra of ordinary chondrites, basaltic achondrites, and olivine-rich meteorites, mainly from the RELAB[*] database and also from Gaffey (1976), to compile a comparison sample. We gathered data for a total of 91 MB asteroids and 103 ordinary chondrites for our analysis.

4 Mineralogical analysis

The ``classical'' method is based on different parameters that can be extracted from the reflectance spectra of the object. Each parameter provides information about the relative proportions of mineral phases that are present on the surface of the object, their modal abundances, and the size of the grains. Although previous works mentioned some of those parameters and carried out several laboratory calibrations (Adams 1974; Singer 1981; Gaffey 1984), it was not until the paper of Edward Cloutis in 1986 that all the diagnostic parameters were compiled and properly described.

4.1 Computation of spectral parameters

Cloutis (1986) reviewed all the possible diagnostic spectral parameters and their relationship with the abundances of specific minerals on the surface of asteroids, as well as the most important laboratory calibrations that are used nowadays. Those parameters had been previously mentioned by some authors. Adams (1974) measured the variation in the position of the centres of pyroxene absorption bands at 1 and 2 $\mu $m as a function of its composition, while Singer (1981) studied mixtures of different silicates and iron oxides and their relation with the variation in the position of the absorption bands. The most important spectral parameters defined by Cloutis et al. (1986) are the following. First, the wavelength positions of the reflectance minima at 1 and 2 $\mu $m are computed. Using the wavelength and reflectance at the two maxima, around 0.7 and 1.4-1.7 $\mu $m, and the end of the spectrum, around 2.4-2.5 $\mu $m, we compute two linear continuum, tangential to the spectral curve, and their corresponding spectral slopes. The reflectance curve is then divided by this continuum to remove it, and after that, several parameters are computed: the wavelength position of the band minima (band centres), the band depths, and the ratio of the areas of the second to the first absorption band, or band area ratio (BAR).

The wavelength position of the band maxima and band minima are derived from nth order polynomial fits to the spectral curve in a varying region around each maximum or minimum. The order of the polynomial fit ranged from 3 to 8, and the best fit was selected to produce the smallest least square residual. The band areas were computed following a simple but effective trapezoid method. The computed parameters with their corresponding errors are shown in Tables A.2 and A.3 for our sample of NEAs and MBs, respectively. The 2 space parameters in which we analyse the mineralogy of the samples are the band II-band I centres and the BAR-band I centre.

4.2 Band II centre versus band I centre

\begin{figure} \par\includegraphics[width=15.5cm,clip]{13852f4.eps} \vspace*{7mm} \end{figure} Figure 4:

Wavelength position of the centres of the two absorption bands computed for MBs (blue squares) and NEAs (red circles). The mean error bars associated to each group of data are shown in the upper left region of each plot. Filled black and empty circles correspond to ortho (OPX) and clinopyroxenes (CPX) from Cloutis & Gaffey (1991). The regions enclosed with green, blue, and red lines correspond to the band centres computed for the H, L, and LL ordinary chondrites, respectively. Note the abundance of asteroids located up and far from the OPX-CPX tendency line (blue arrow) in the case of MBs.

Open with DEXTER

The first spectral parameter space in which we are comparing the NEA and MB population is the one defined by the wavelength position of the centres of the absorption bands of the terrestrial pyroxenes, first used by Adams (1974) and later modified by Cloutis & Gaffey (1991). This space is shown in Fig. 4. Those objects whose surface is mainly composed of pyroxene are located along the tendency line that define terrestrial pyroxenes in the plot, where black dots correspond to orthopyroxenes (OPX) and white dots correspond to clinopyroxenes (CPX) (band centres shift to longer wavelengths with increasing Fe2+ and Ca2+ content, respectively). If both types of pyroxenes or any additional mineral phase is present on the surface of the asteroid, the object will lie outside the tendency line. In particular, the presence of olivine translates into vertical displacements in the graph (type-A clinopyroxenes can also produce vertical shifts, although on a smaller scale). Figure 4 shows the position of the centres computed for the two absorption bands of NEAs (red circles) and MBs (blue squares). The mean error bars associated with each group of asteroids are shown in the upper left region of each plot. Several differences between the two asteroid populations can be seen in the graph. Most obviously, a larger number of asteroids composed mainly of olivine[*] can be seen among the MB population (blue arrow). This overabundance of olivine asteroids in the main belt will be more clearly seen in the parameter space of BAR versus band I centre. We point out that, although olivine asteroids are classified as A-type asteroids, this taxonomy is based only on their visible spectra; it can therefore be misleading, as it is reflected in the variety of spectral classes of the MBs that lie in the olivine region of the plot (blue arrow).

Another clear difference is that MBs that occupy the pyroxene tendency line seem to be more concentrated in the region associated with the orthopyroxenes, while NEAs are more dispersed, from Fe-rich orthopyroxene to clinopyroxenes with medium Ca-content. Finally, about 35% of the MBs[*] deviate from the tendency line, compared to 55% of NEAs, indicating that, on average, the NEA population is more olivine-rich than the MBs.

The regions enclosed by continuous lines correspond to the values computed for our sample of ordinary chondrites: green line for H chondrites, blue line for L chondrites, and red line for LL chondrites. According to their well-known composition from laboratory analysis and in agreement with their position in the plot, Fe and olivine content decrease and increase, respectively, in the series H-L-LL. Furthermore, on the basis of their location relative to the OPX-CPX tendency line, ordinary chondrites are composed mainly of orthopyroxene and olivine, with only minor contributions of clinopyroxene.

4.3 Spectral parameters for the meteorite sample

Before we begin studying the distribution of the data in the second parameter space, the BAR vs. band I centre plot, we explain some changes in the regions associated with the meteorite sample. As previously shown in Duffard et al. (2005), the BAR parameter increases with increasing grain size. In the case of the basaltic achondrites employed to define their new BA region, the authors used samples with a grain size smaller than 25 $\mu $m, as most of the available reflectance spectra of basaltic achondrites in the RELAB database were limited to that grain size. When they studied the increase in the BAR parameter with grain size, observed a mean ``shift'' of $\sim$0.57 for an increase in grain size from 25 to 500 $\mu $m. Applying this shift to the region defined by Duffard et al. (2005), the region corresponding to the basaltic achondrites will appear as that shown in Fig. 5 with a continuous line and labelled as BA. This new region encloses the original one (dashed-line) defined by Gaffey et al. (1993) using a sample of 40 basaltic achondrites (bulk samples, not powders), and accounts also for the V-type asteroids present in our sample of objects (both NEAs and MBs). In the case of the ordinary chondrites, the new region is quite similar to the one defined by Gaffey et al. (1993), as we have simply used a larger sample of meteorites.

4.4 Band area ratio (BAR) versus band I centre

\begin{figure} \par\includegraphics[width=15.5cm,clip]{13852f5.eps} \end{figure} Figure 5:

Band area ratio (BAR) versus band I centre for MBs (blue squares) and NEAs (red circles). The regions enclosed by continuous lines correspond to the values computed for basaltic achondrites (BA), ordinary chondrites (OC) and olivine-rich meteorites (Ol). Those enclosed by dashed lines were computed by Gaffey et al. (1993). The red dashed line in the upper left part of the plots encloses asteroids composed exclusively/mainly of olivine.

Open with DEXTER

The compositional differences that can be inferred from the previous parameter space are also evident in the BAR vs. Band I centre calibration plot (Fig. 5), first studied by Gaffey et al. (1993). In this graph, the regions enclosed by continuous lines correspond to the values computed for our sample of ordinary chondrites (OC), basaltic achondrites (BA, see Sect. 4.3) and olivine-rich meteorites (Ol). As in Fig. 4, MBs are plotted as blue squares and NEAs are plotted as red circles. The red dashed line region defined in the upper-left part of the plot encloses the asteroids composed exclusively/mainly of olivine. As was observed in the previous parameter space, there are more of this A-type asteroids among the MB population. This apparent deficit of A-type NEAs was noted by previous spectroscopic surveys: from a total of 400 NEAs analysed by Binzel et al. (2004), only 4 are A-types, and 3 of them are Mars-crossers. From the 371 asteroids classified using the new DeMeo et al. (2007) taxonomy extended to the near-infrared, only 6 are A-types, and all of them are MBs. Therfore, as Fig. 5 shows for our sample, there is a larger number of asteroids composed exclusively/mainly of olivine among the MBs than among the NEAs.

The second conclusion that can be extracted from Fig. 5, is that NEAs seem to be concentrated into lower values of BAR and higher values of band I centre than MBs, indicated by the ellipses in the graph. This translates into a more significant presence of olivine among the NEA population, as also inferred from the previous calibration space. This higher olivine content was first pointed out by de León et al. (2007), and subsequently confirmed by Vernazza et al. (2008). In their paper, the authors illustrated the high olivine content of LL chondrites. Applying a radiative transfer model, they concluded that the NEA population is olivine-rich, and that its composition is well correlated with the LL group of OCs. The concentration of our NEAs in the upper part of the OC region in Fig. 5, mostly occupied by LL chondrites, supports this connection.

This higher olivine content for the NEA population is also obtained when we apply the method described in the following section.

5 Statistical analysis

We now apply a statistical method to compare the NEA population with the OC group, to see if we obtain the same compositional behaviour as those shown above for the other spectral parameter spaces. The problem, from a statistical point of view, is to compare two data sets answering a single question: are the two samples drawn from the same distribution function? We assume that we have two sample sets with ``m1'' (i.e. NEA data) and ``m2'' (i.e. OC data) independent observations, and we wish to test the hypothesis that both samples can be described by the same probability distribution

\begin{displaymath}P_1(\vec x) = P_2(\vec x). \end{displaymath}

If the data is described by only one parameter (one dimensional data), several tests can be performed, such as the Pearson's $\chi ^2$ test or the Kolmogorov-Smirnov test (KS). The difference between both methods is that, while in the former it is necessary to bin the observations, the latest is free of binning.

When the data is multi-dimensional, there is no equivalent to the unbinned KS test in one dimension, and a normal procedure would be to bin the multi-dimensional space and perform a $\chi ^2$ test. The volume of the bins can vary but a common accepted criteria for determining it is that the number of expected events per bin is greater than 5. In our case, we consider two-dimensional data, so if 10 bins are selected we need about 500 data points to perform a $\chi ^2$ test of statistical significance. However, our samples only have a maximum of 100 data points, so alternative methods are needed. Garrido et al. (1994) presented a new method, based on neural network techniques, which transforms a complicated test in the multi-dimensional input space into a simple test in a one-dimensional space, without losing sensitivity. The astronomical reliability of the method was demonstrated by Serra-Ricart et al. (1996). Thus, we apply this statistical method to our sample of NEAs and OCs.

5.1 Neural network implementation

As mentioned above, the proposed method transforms a difficult $\chi ^2$ test in the original multi-dimensional space of the variables, which requires large amounts of data, into a $\chi ^2$ test in one-dimensional space, using a suitable projection, the ``$\kappa $ projection''. This procedure significantly reduces the amount of observational data needed. The new variable $\kappa $ is defined as

\begin{displaymath}% \kappa(\vec x) = \frac{P_1(\vec x)}{P_1(\vec x)+P_2(\vec x)}, \end{displaymath} (1)

where $\vec x$ are the variables chosen to describe our observations, and P1 and P2 are the probability density functions of the observational data samples. Using this relation, any pair of sample data, $\vec x$, can be described by $\kappa $.

As demonstrated by Garrido et al. (1994), we have the same statistical sensitivity in the final one-dimensional $\kappa $ space as in the original multi-dimensional space of the $\vec x$ variables, which allows the Pearson's test to be applied in the $\kappa $ instead of the $\vec x$ space. The problem arises from  $P_1(\vec x)$ and  $P_2(\vec x)$, not being known a priori, so it seems that the projection is unrealistic. However, Garrido et al. (1994) proposed a technique, based on artificial neural networks, to obtain the $\kappa $ projection.

The basic idea is to train a layered feed-forward neural net to distinguish the two data sets, minimizing a quadratic error function (see Serra-Ricart et al. 1996, for details). The input of this net contains n neurons that are activated by the quantities of the n relevant variables to the problem, and the output is only one neuron, for which the desired activation is 1 for sample 1 (i.e., NEA data) and 0 for sample 2 (i.e., OC data). After the training step, during which a sample containing a mixture of two data sets is presented to the net, we obtain a function $f(\vec x):R^n \rightarrow R$, which maps the n-dimensional space of the input variables to $[0,1] \in R $ and is  ${\approx}\kappa$. The goodness of the approximation depends upon the architecture of the net, the ability to escape from local minima during the training step and the existence of adequate data.

\begin{figure} \par\includegraphics[width=8cm,clip]{13852f6a.eps}\par\includegraphics[width=8cm,clip]{13852f6b.eps} \end{figure} Figure 6:

Top: distribution of 20 000 synthetic points (red dots) in the BAR vs. Band I centre space, generated from seeds containing the original computed data for NEA population (black diamonds), considering error bars (1-$\sigma $) and following a normal distribution. It can be seen how the synthetic points are more dispersed for the seeds with larger error bars. Bottom: optimum $\kappa $ projection for the NEAs, OCs, and the three subgroups of ordinary chondrites (H, L and LL). This plot has been chosen to help visualize one of the results listed in Table 2. It is clearly seen that the shape of the projections for the NEAs (black line) and OCs (green line) are completely different.

Open with DEXTER

We therefore created sets of synthetic data from seeds that contain the original data (in this case the computed values of BAR and band I centre), considering a normal distribution and 1$\sigma $ dispersion obtained from the error bars of the original data (errors for each of the spectral parameters computed for the NEAs are listed in Table A.2). As an example, Fig. 6 in its top panel shows what a set of 20 000 synthetic data looks like for a single population. Red dots are the synthetic points randomly generated from the corresponding seeds (black diamonds, original data) and following a normal distribution. It is evident that the points are more dispersed for the seeds that exhibit higher error bars. We therefore mix the two samples we wish to compare, i.e., the NEAs and the OCs, and proceed in the same manner to generate the input for the neural net.

Table 2:   Values of $\chi ^2$ test obtained for each pair of datasets used as the input to the neuronal net.

The results obtained can be seen in Table 2. The first and second column indicate each of the ``inputs'' that we used (the populations we compare), while the third column shows the value of the $\chi ^2$ resulting for each pair. The lower the value of the $\chi ^2$, the more similar the datasets usually are. We can therefore conclude that, within the significance level: a) the two groups that are ``less different'' are the NEAs and the LLs (the subgroup of ordinary chondrites with the highest olivine content), which agrees with the results obtained from the mineralogical analysis; b) the two groups that are ``less similar'' are the NEAs and the OCs. This last result is visualized in the bottom panel of Fig. 6, where the optimum $\kappa $ projection for all the samples is represented: the shape of the projections for the NEAs (black line) and OCs (green line) are completely different.

After performing the mineralogical analysis for our sample of asteroids, we study in the following sections other mechanisms that could have some influence on the obtained results, such as the effects of the space weathering or the dynamical properties of the objects.

6 Space weathering effects

\begin{figure} \par\includegraphics[width=12cm,clip]{13852f7.eps} \end{figure} Figure 7:

Distributions of the computed spectral slope (SI, measured between the two maxima of the spectra) for the NEAs, MBs, and ordinary chondrites. The mean spectral slope for each group is indicated in brackets. We show also the size-frequency distributions (SFDs) of both populations.

Open with DEXTER

The exposure of the surfaces of airless bodies to the cosmic and solar wind ion irradiation, and to the bombardment of micrometeorites is known as space weathering. The effects of these two processing mechanisms have been widely studied, and include spectral darkening, reddening and subdued absorption bands (Pieters et al. 1993; Chapman 1996; Pieters et al. 2000; Hiroi & Sasaki 2001; Hapke 2001). Brunetto & Strazzulla (2005) and Strazzulla et al. (2005) carried out different experiments of ion irradiation, bombarding samples of ordinary chondrites and silicates with a variety of ions (H+, He+, Ar+, Ar2+) and energies (60-400 keV). They found that ordinary chondrite samples exhibit a progressive reddening that is similar to the spread of spectra observed for S-type near-Earth asteroids. The timescales for inducing the same effects in space as those obtained in laboratory are estimated to be 104-106 years. On the other hand, experiments simulating micrometeorite bombardment by means of nanopulse laser irradiation, indicate that the reddening timescale in the near-Earth space is about 108-109 years (Sasaki et al. 2001; Brunetto et al. 2006).

The distribution of the computed spectral slopes for the NEAs, MBs, and OCs studied in this work is shown in Fig. 7. As can be seen, the two asteroid populations exhibit similar distributions, alghough MBs are on average ``redder'' than NEAs. We recall that the spectral slope is computed to be the line tangent to the asteroid spectra at the two maxima, around 0.7 $\mu $m and 1.4-1.7 $\mu $m, and is used to remove the continuum (see Sect. 4.1). The mean values and the 1$\sigma $ deviation for each group is indicated in brackets[*]. The mean spectral slopes obtained for our sample of MBs (0.400 $\pm $ 0.270) and NEAs (0.283 $\pm $ 0.171) are in good agreement with those obtained by Marchi et al. (2005) for a total of 52 MBs (0.300 $\pm $ 0.201) and 31 NEAs (0.318 $\pm $ 0.178) and are consistent with the timescale associated with ion irradiation, 104-106 years, according to Strazzulla et al. (2005). This demonstrates that the ion irradiation caused by the solar wind is the main process acting in both cases. Marchi et al. (2006a) also find a relationship between the reddening of asteroid's surfaces and their distance to the Sun, concluding that space weathering is mainly due to Sun-related effects.

The classical scenario where redder spectra was associated with older surfaces was revisited by Vernazza et al. (2009). They demonstrate the need to account for composition when evaluating weathering effectiveness, as olivine is more sensitive to space weathering than orthopyroxene (Brunetto et al. 2006; Marchi et al. 2005). Therefore, olivine-rich surfaces would be affected by higher amounts of reddening, and one would expect a higher mean spectral slope for the NEA population. However, we have to take into account the different size distributions of both populations. As shown in Fig. 7, near-Earth asteroids are kilometre-sized objects, while the mean diameter of main belt asteroids is tens of kilometres, even hundreds, a difference that affects the way space weathering acts on their surfaces. A combination of both composition and size must therefore be considered when explaining the effects of space weathering on the surfaces of NEAs. One possibility is that these small asteroids may have lost their regolith during the collisional event that is most likely to have created them, and been unable to either develop or retain a new regolith, thus preserving preferentially larger grains on their surfaces (de León et al. 2010). This is consistent with a ``bluer'' spectral slope, as some experiments in the laboratory with meteorite samples find that reflectance spectra are darker and bluer for coarser grain sizes (Johson & Fanale 1973), and also that smaller asteroids have higher thermal inertia (Delbo et al. 2007). Another possibility, raised by Marchi et al. (2006b) and Vernazza et al. (2009), is that small near-Earth asteroids might be affected by tidal shaking caused by planetary encounters that frequently exposes fresh, unaltered material (Nesvorný et al. 2006).

7 Correlation with dynamics

\begin{figure} \par\includegraphics[width=8cm,clip]{13852f8.eps} \end{figure} Figure 8:

Location of the NEAs (red circles) and MBs (blue squares) analysed in the orbital parameter space a-e ( top panel) and a-i ( bottom panel). NEAs have perihelia q $\le $ 1.3 AU and aphelia Q $\ge $ 0.983 AU. The q < 1.66 AU dashed line defines the boundary between objects on Mars-crossing orbits and those in the main belt. Several mean motion resonances are shown as dashed vertical lines. The $i = 0^{\circ }$ position of the $\nu _6$ secular resonance is also shown as a dashed vertical line in the top panel and a continuous line in the bottom panel. Here we also indicate the IMC region (intermediate source Mars-crossing asteroid) and the OB1-OB5 regions, defined following Bottke et al. (2002). The position of the Hungaria (Hung) and Phocaea (Phoc) groups is also indicated.

Open with DEXTER

The physical properties and orbital elements of the near-Earth asteroids analysed in this paper are shown in Appendix A, Table A.4. As can be seen in Fig. 7, the distribution of diameters in our sample of NEAs is the usual one: most of the objects are kilometre-sized. In contrast, the main belt asteroids are much larger, typically tens of kilometres. Both distributions are typical of those obtained from the detection surveys, so we are not biased towards any particular size range. As stated in the introduction, different studies indicate that one of the main source regions for the NEA population is the main asteroid belt. There is also an undetermined percentage of NEAs that are dead or dormant comets, which can vary between 0 and 18% (Fernández et al. 2002; Demeo & Binzel 2008).

To determine the source regions of the NEAs analysed in this paper, we used the dynamical model by Bottke et al. (2002). These authors define different regions and classify them as primary or secondary sources, according to their higher or lower contribution to the NEA population. Following their criteria, the 3:1 mean motion resonance at 2.5 AU, the $\nu _6$ secular resonance with Saturn, the intermediate source Mars-crossing region (IMC), the Jupiter Family Comets (JFC) region, and the outer main belt (OB) are considered as primary sources; the regions occupied by Hungaria or Phocaea asteroids are examples of secondary sources. Figure 8 shows the distribution of the NEAs (red circles) and MBs (blue squares) in the orbital parameter space. We have indicated in the plot some of the source regions mentioned above. To determine if a MB asteroid is located ``at'' or ``close to'' one of the main zones defined by Bottke et al. (2002), i.e., the 3:1, the $\nu _6$ resonances and the IMC region, we apply the following criteria:

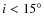  • 3:1 resonance: those asteroids with 2.4 < a < 2.6 AU, e < 0.35, $i < 15^{\circ}$.

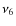  • $\nu _6$ resonance: those asteroids whose orbital parameters place them in the continuous line defined by the resonance in the a-i space (Fig. 8, bottom panel), 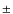$\pm $0.1 AU (dashed lines).

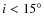  • IMC region: those asteroids with 2.06 < a < 2.48 or 2.52 < a < 2.8 AU; 1.30 < q < 1.82 AU; $i < 15^{\circ}$.

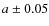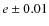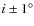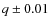    Asteroids with orbital parameters $a \pm 0.05$ AU, $e \pm 0.01$, $i \pm 1^{\circ}$, $q \pm 0.01$ AU, are considered to be located ``close to'' the main source regions.

According to these criteria, from our sample of 91 MBs analysed, about 20 asteroids are located at or close to the $\nu _6$ resonance, 40 asteroids the 3:1 resonance and fewer than 10 the IMC region. Just a few asteroids are located in the outer belt. It is interesting to note that some of the MB asteroids analysed are concentrated in the region associated with the Flora family, located close to the $\nu _6$ resonance. This family accounts for 15-20% of the asteroids residing in the inner main belt region, and is expected to contribute substantially to the population of NEAs (Nesvorný et al. 2002; Vernazza et al. 2008).

Therefore, by using the orbital parameters of our NEAs as input to the dynamical model, we estimated the relative probability that they originate in a given source (A. Morbidelli, personal communication). The probability values for each object are computed to have a total probability of 1. The results obtained for the 5 primary source regions are: 51% for the $\nu _6$ resonance [37%]; 27% for the IMC region [25%]; 13% for the 3:1 resonance [23%]; 4% for the outer belt (OB) [8%]; and 1% for the JFC region [6%]. For the secondary source regions, a 8% corresponds to the Hungaria group and a 2% to the Phocaea group. The values shown in brackets correspond to the computed NEO orbital distributions by Bottke et al. (2002), valid for absolute magnitudes H < 22. Following these results, the majority of our NEAs come from the $\nu _6$ resonance, followed by the IMC[*] and the 3:1 resonance, in good agreement with the predictions by Bottke et al. (2002). Unfortunately, this is not the case for our sample of MBs, which are primarily located in the 3:1 mean motion resonance. This illustrates the importance of obtaining spectral data from main belt asteroids located in the $\nu _6$, to improve the results from the mineralogical comparison with the NEA population. Our currently ongoing MBOISS survey, mentioned in Sect. 3, will contribute significantly to this purpose.

8 Conclusions

The survey that we have presented is one of the largest database of visible and near-infrared spectra of near-Earth and Mars-crosser asteroids, consisting of a total of 74 objects. It represents consistency in the way that all the observations were obtained and subsequently reduced, and the particular care taken in the extraction, calibration, and merge steps. We have used other existing databases to complete some of our data for the compositional analysis and those spectra perfectly matched. This is a strong indication of the goodness of our results: the spectrum of an object obtained with different instrumental set-ups and characteristics matches our spectrum of the same object.

All the data from this survey have been analysed, as well as visible and near-infrared spectra of NEAs from other databases. We have also analysed two datasets of reflectance spectra to perform a compositional and a dynamical correlation with the results obtained from the NEA population: a sample of main belt asteroids, collected from different surveys and a group of meteorites, including ordinary chondrites (OCs), basaltic achondrites, and olivine-rich meteorites. As the NEAs have always been understood to be the most likely parent bodies of the OCs, and the MBs are the principal source of NEAs, we have studied the mineralogy of these three groups of objects to understand their connection more clearly.

Several conclusions can be extracted from the analysis presented in this paper:

1.
The location of the computed spectral parameters for our NEAs in the two calibration plots used to interpret their mineralogical composition, reflects the high content of olivine among this asteroid population. From a visual inspection and a comparison with the region occupied by ordinary chondrites in the same parameter spaces, it seems that the NEAs have closer agreement with a subgroup of OCs, the LLs, also rich in olivine. The statistical analysis of these two populations by means of a neural net confirms this result: NEAs and OCs follow different distributions, while NEAs have a higher probability of originating in the same distribution as the LLs.

2.
Analysing the effects of the space weathering on the spectral parameters we have computed for our sample of NEAs and MBs, we conclude that the slope distributions of both populations are similar, although on average, MBs have redder surfaces than NEAs. A combination of their mineralogical composition, the NEAs being more olivine-rich than the MBs, and their size distributions, the NEAs being smaller that the MBs, should be invoked to explain this result. The slope values obtained for all the asteroids give exposure timescales of 104-106 years, implying that the solar wind is the most efficient mechanism of weathering.

3.
The source region probabilities computed for our sample of NEAs indicates that about 50% of the asteroids come from the 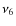$\nu _6$ region, located in the inner main belt. This result shows that our sample of NEAs is not biased against any particular region of the main belt, as it is in good agreement with the percentages predicted by the dynamical model used to compute the probabilities. Furthermore, it may be likely that the Flora family is the dominant source of NEAs and LL chondrites, as pointed out by other authors.

Acknowledgements
We gratefully acknowledge support from the Spanish ``Ministerio de Ciencia e Innovación'' projects AYA2005-07808-C03-02 and AYA2008-06202-C03-02. This paper is based on observations made with the Nordic Optical Telescope, operated on the island of La Palma jointly by Denmark, Finland, Iceland, Norway, and Sweden, and on observations made with the Italian Telescopio Nazionale Galileo (TNG) operated on the island of La Palma by the Centro Galileo Galilei of the INAF (Instituto Nazionale di Astrofisica), both telescopes located at the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofisica de Canarias. Part of the data utilized in this publication were obtained and made available by the The MIT-UH-IRTF Joint Campaign for NEO Reconnaissance. The IRTF is operated by the University of Hawaii under Cooperative Agreement No. NCC 5-538 with the National Aeronautics and Space Administration, Office of Space Science, Planetary Astronomy Program. The MIT component of this work is supported by the National Science Foundation under Grant No. 0506716.

References

  1. Adams, J. B. 1974, J. Geophys. Res., 79, 4829 [NASA ADS] [CrossRef] [Google Scholar]
  2. Baffa, C., Comoretto, G., Gennari, S., et al. 2001, A&A, 378, 722 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Bell, J. F., Owensby, P. D., Hawke, B. R., et al. 1995, 52-color Asteroid Survey, NASA Planetary Data System [Google Scholar]
  4. Binzel, R. P., Harris, A. W., Bus, S. J., & Burbine, T. H. 2001, Icarus, 151, 139 [NASA ADS] [CrossRef] [Google Scholar]
  5. Binzel, R. P., Rivkin, A. S., Stuart, J. S., et al. 2004, Icarus, 170, 259 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bottke, W. F., Morbidelli, A., Jedicke, R., et al. 2002, Icarus, 156, 399 [NASA ADS] [CrossRef] [Google Scholar]
  7. Brunetto, R., & Strazzulla, G. 2005, Icarus, 179, 265 [NASA ADS] [CrossRef] [Google Scholar]
  8. Brunetto, R., Romano, F., Blanco, A., et al. 2006, Icarus, 180, 546 [NASA ADS] [CrossRef] [Google Scholar]
  9. Brunetto, R., de León, J., & Licandro, J. 2007, A&A, 472, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Burbine, T. H., & Binzel, R. P. 2002, Icarus, 159, 468 [NASA ADS] [CrossRef] [Google Scholar]
  11. Burns, R. G. 1970, Mineralogical Applications of Crystal Field Theory (Cambridge: Cambridge University Press), 576 [Google Scholar]
  12. Bus, S. J., & Binzel, R. 2002a, Icarus, 158, 106 [CrossRef] [Google Scholar]
  13. Bus, S. J., & Binzel, R. 2002b, Icarus, 158, 146 [NASA ADS] [CrossRef] [Google Scholar]
  14. Campins, H., Rieke, G. H., & Lebofsky, M. J. 1985, AJ, 90, 896 [NASA ADS] [CrossRef] [Google Scholar]
  15. Champan, C. R. 1996, Meteorit. Planet. Sci., 31, 699 [NASA ADS] [CrossRef] [Google Scholar]
  16. Cloutis, E. A., & Gaffey, M. J. 1991, J. Geophys. Res., 96, 22809 [NASA ADS] [CrossRef] [Google Scholar]
  17. Cloutis, E. A., Gaffey, M. J., Jackowski, T. L., & Reed, K. L. 1986, J. Geophys. Res., 91, 11641 [Google Scholar]
  18. Colina, L., & Bohlin, R. 1997, AJ, 113, 1138 [NASA ADS] [CrossRef] [Google Scholar]
  19. Colina, L., Bohlin, R. C., & Castelli, F. 1996, AJ, 112, 307 [NASA ADS] [CrossRef] [Google Scholar]
  20. Delbo, M., dell'Oro, A., Harris, A. W., et al. 2007, Icarus, 190, 236 [NASA ADS] [CrossRef] [Google Scholar]
  21. de León, J., Licandro, J., & Pinilla-Alonso, N. 2007, BAAS, 38, 481 [NASA ADS] [Google Scholar]
  22. de León, J., Campins, H., Tsiganis, K., Morbidelli, A., & Licandro, J. 2010, A&A, 513, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. DeMeo, F., & Binzel, R. P. 2008, Icarus, 194, 436 [NASA ADS] [CrossRef] [Google Scholar]
  24. DeMeo, F. E., Binzel, R. P., Silvan, S. M., & Bus, S. J. 2009, Icarus, 202, 160 [NASA ADS] [CrossRef] [Google Scholar]
  25. Duffard, R., Lazzaro, D., Licandro, J., et al. 2004, Icarus, 171, 120 [NASA ADS] [CrossRef] [Google Scholar]
  26. Duffard, R., Lazzaro, D., Licandro, J., et al. 2005, Meteorit. Planet. Sci., 40, 361 [Google Scholar]
  27. Farinella, P., Froeschlé, Ch., & Gonczi, R. 1993, Cel. Mech. Dyn. Astron., 62, 87 [Google Scholar]
  28. Fernández, J. A., Gallardo, T., & Brunini, A. 2002, Icarus, 159, 358 [NASA ADS] [CrossRef] [Google Scholar]
  29. Froeschlé, Ch., & Scholl, H. 1987, A&A, 179, 294 [NASA ADS] [Google Scholar]
  30. Froeschlé, Ch., & Morbidelli, A. 2004, in Asteroids, comets, meteors 1993, ed. A. Milani, M. Di Martino, & A. Cellino (Kluwer Academic Publishers), Proc. IAU Symp., 160, 189 [Google Scholar]
  31. Gaffey, M. J. 1976, J. Geophys. Res., 81, 905 [NASA ADS] [CrossRef] [Google Scholar]
  32. Gaffey, M. J., 1984, Icarus, 60, 83 [NASA ADS] [CrossRef] [Google Scholar]
  33. Gaffey, M. J., Burbine, T. H., Piatek, J. L., et al. 1993, Icarus, 106, 573 [NASA ADS] [CrossRef] [Google Scholar]
  34. Gaffey, M. J., Cloutis, E. A., Kelley, M. S., & Reed, K. L. 2002, in Asteroids III, ed. W. F. Bottke Jr., A. Cellino, P. Paolicchi, & R. P. Binzel (Tucson: University of Arizona Press), 183 [Google Scholar]
  35. Garrido, Ll., Gaitan, V., & Serra-Ricart, M. 1994, Comput. Phys. Commun., 84, 297 [NASA ADS] [CrossRef] [Google Scholar]
  36. Hainaut, O. R., & Delsanti, A. C. 2002, A&A, 389, 641 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Hapke, B. 2001, J. Geophys. Res., 106, 10039 [NASA ADS] [CrossRef] [Google Scholar]
  38. Hardorp, J. 1978, A&A, 63, 383 [NASA ADS] [Google Scholar]
  39. Hardorp, J. 1980, A&A, 88, 334 [NASA ADS] [Google Scholar]
  40. Hiroi, T., & Sasaki, S. 2001, Meteorit. Planet. Sci., 36, 1587 [Google Scholar]
  41. Johnson, T. V., & Fanale, F. 1973, JGR, 78, 8507 [NASA ADS] [CrossRef] [Google Scholar]
  42. Krugly, Y. N., Gaftonyuk, N. M., Belskaya, I. N., et al. 2007, in Near Earth Objects, our Celestial Neighbors: Opportunity and Risk, ed. G. B. Valsecchi, D. Vokrouhlický, & A. Milani (Cambridge: Cambridge University Press), Proc. IAU Symp., 236, 385 [Google Scholar]
  43. Landolt, A. U. 1973, AJ, 78, 959 [NASA ADS] [CrossRef] [Google Scholar]
  44. Landolt, A. U. 1983, AJ, 88, 439 [NASA ADS] [CrossRef] [Google Scholar]
  45. Landolt, A. U. 1992, AJ, 104, 340 [NASA ADS] [CrossRef] [Google Scholar]
  46. Lazzarin, M., Marchi, S., Barucci, M. A., et al. 2004, Icarus, 169, 373 [NASA ADS] [CrossRef] [Google Scholar]
  47. Lazzarin, M., Marchi, S., Magrin, S., & Licandro, J. 2005, MNRAS, 359, 1575 [NASA ADS] [CrossRef] [Google Scholar]
  48. Lazzaro, D., Angeli, C. A., Carvano, J. M., et al. 2004, Icarus, 172, 179 [CrossRef] [Google Scholar]
  49. Licandro, J., Oliva, E., & Di Martino, M. 2001, A&A, 373, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Licandro, J., Ghinassi, F., & Testi, L. 2002, A&A, 388, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Licandro, J., de León, J., Pinilla-Alonso, N., & Serra-Ricart, M. 2006, Adv. Space Res., 38, 1991 [NASA ADS] [CrossRef] [Google Scholar]
  52. Licandro, J., Campins, H., Mothé-Diniz, T., et al. 2007, A&A, 461, 751 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Licandro, J., Alvarez-Candal, A., de León, J., et al. 2008, A&A, 481, 861 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Marchi, S., Brunetto, R., Magrin, S., et al. 2005, A&A, 443, 769 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Marchi, S., Paolicchi, P., Lazzarin, M., & Magrin, S. 2006a, AJ, 131, 1138 [NASA ADS] [CrossRef] [Google Scholar]
  56. Marchi, S., Magrin, S., Nesvorný, D., et al. 2006b, MNRAS, 368, L39 [NASA ADS] [Google Scholar]
  57. Moons, M. 1997, in The Dynamical Behaviour of our Planetary System, ed. R. Dvorak, & J. Henrard (Kulwer Academic Publishers) 175 [Google Scholar]
  58. Morbidelli, A., & Nesvorný, D. 1999, Icarus, 139, 295 [NASA ADS] [CrossRef] [Google Scholar]
  59. Morbidelli, A., Bottke, Jr. W. F., Froeschlé, C., & Michel, P. 2002, in Asteroids III, ed. W. F. Bottke Jr., A. Cellino, P. Paolicchi, & R. P. Binzel (Tucson: University of Arizona Press), 409 [Google Scholar]
  60. Nesvorný, D., Morbidelli, A., Vokrouhlický, D., et al. 2002, Icarus, 157, 155 [NASA ADS] [CrossRef] [Google Scholar]
  61. Nesvorný, D., Jedicke, R., Whiteley, R. J., & Ivezic, . 2006, Icarus, 173, 132 [Google Scholar]
  62. Oliva, E. 2000, Mem. Soc. Astron. Ital., 71, 861 [Google Scholar]
  63. Pieters, C. M., Fischer, E. M., Rode, O., & Basu, A. 1993, J. Geophys. Res., 98, 20817 [Google Scholar]
  64. Pieters, C. M., Taylor, L. A., Noble, S. K., et al. 2000, Meteorit. Planet. Sci., 35, 1101 [NASA ADS] [CrossRef] [Google Scholar]
  65. Pravec, P., Scheirich, P., Kusnirák, P., et al. 2006, Icarus, 181, 63 [NASA ADS] [CrossRef] [Google Scholar]
  66. Reddy, V., Gaffey, M. J., Abell, P. A., & Hardersen, P. S. 2006, in 37th Annual Lunar and Planetary Institute Conference Abstracts, 39, 1746 [Google Scholar]
  67. Sasaki, S., Nakamura, K., Hamabe, Y., et al. 2001, Nature, 410, 555 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  68. Serra-Ricart, M., Aparicio, A., Garrido, Ll., & Gaitan, V. 1996, ApJ, 462, 221 [NASA ADS] [CrossRef] [Google Scholar]
  69. Singer, R. B. 1981, J. Geophys. Res., 86, 7967 [NASA ADS] [CrossRef] [Google Scholar]
  70. Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
  71. Strazzulla, G., Dotto, E., Binzel, R., et al. 2005, Icarus, 174, 31 [NASA ADS] [CrossRef] [Google Scholar]
  72. Tholen, D. J. 1984, Ph.D. Thesis, AA (Tucson: Arizona University) [Google Scholar]
  73. Tody, D. 1993, in Astronomical Data Analysis Software and Systems II, ed. R. J. Hanisch, R. J. V. Brissenden, & J. Barnes (San Francisco: Astron. Soc. of the Pacific), 173 [Google Scholar]
  74. Vernazza, P., Binzel, R. P., Thomas, C. A., et al. 2008, Nature, 454, 858 [NASA ADS] [CrossRef] [Google Scholar]
  75. Vernazza, P., Binzel, R. P., Rossi, A., et al. 2009, Nature, 458, 993 [NASA ADS] [CrossRef] [Google Scholar]
  76. Warner, B. D., & Fitzsimmons, A. 2005, IAU Circ., 8578 [Google Scholar]
  77. Warner, B. D., Pravec, P., Kusnirák, P., et al. 2006, Minor Planet Bulletin, 33, 21 [NASA ADS] [Google Scholar]
  78. Wetherill, G. W. 1979, Icarus, 37, 96 [NASA ADS] [CrossRef] [Google Scholar]
  79. Wisdom, J. 1983, Icarus, 56, 51 [NASA ADS] [CrossRef] [Google Scholar]
  80. Xu, S., Binzel, R. P., Burbine, T. H., & Bus, S. J. 1995, Icarus, 115, 1 [NASA ADS] [CrossRef] [Google Scholar]

Online Material

Appendix A: Tables

In the tables here, we present the observational conditions, computed spectral parameters and physical and dynamical properties of the NEAs and MCs analysed in this paper. Table A.1 shows information about the observations of the objects: r is the distance to the Sun, $\Delta$ is the distance to the Earth, $\alpha$ is the object phase angle and mV is the apparent visual magnitude. Computed spectral parameters of NEAs and MCs are listed in Table A.2, including in blue text colour asteroids from other surveys, to work with a statistical meaningful sample of objects. We compute the position of the first maxima, band minima, slopes, band centres and band area ratios. See text for more details. For some objects, we have not been able to compute some of the parameters due to the low S/N. The same parameters have also been computed for the sample of MBs and are shown in Table A.3. Finally, physical and orbital parameters of the analysed NEAs and MCs are shown in Table A.4. We show the semi-major axis, the eccentricity, and the inclination of the orbit, as well as the perihelion distance and the Tisserand parameter as the dynamical information, while the diameter D, the geometric albedo $p_{\rm v}$, and the absolute visual magnitude H are physical parameters. The taxonomical classification follows Bus & Binzel (2002a,b).

Table A.1:   Observational circumstances of the NEAs and MCs that make up this survey.

Table A.2:   Spectral parameters computed following Cloutis et al. (1986) for the sample of NEAs and MCs studied in this paper.

Table A.3:   Spectral parameters computed following Cloutis et al. (1986) for the sample of MBs.

Table A.4:   Physical and dynamical parameters of the analysed NEAs and MCs.

Appendix B: Asteroid reflectance spectra

Final reduced visible and near-infrared spectra of 74 NEAs and MCs that form part of this survey. All spectra are normalised to unity at 0.55 $\mu $m, with the exception of (1951) Lick and near-infrared spectra, which are normalised to unity at 1.6 $\mu $m. We gathered visible or near-infrared spectra from other databases to complete our survey: red spectra are from SMASS survey, while blue spectra are from SINEO.

\begin{figure} \par\includegraphics[width=16.5cm,clip]{13852f9a.eps} \end{figure} Figure B.1:

Asteroid spectra.

Open with DEXTER

\begin{figure} \par\includegraphics[width=16.5cm,clip]{13852f9b.eps} \end{figure} Figure B.1:

continued.

Open with DEXTER

\begin{figure} \par\includegraphics[width=16.5cm,clip]{13852f9c.eps} \end{figure} Figure B.1:

continued.

Open with DEXTER

Footnotes

... survey[*]
Appendices are only available in electronic form at http://www.aanda.org
... spectra[*]
Although the taxonomic types cannot be used to infer the mineralogical composition of the objects, they help constrain mineral species that may be present on the surface of the asteroid.
... page[*]
http://www.iac.es/proyecto/pcssolar/pages/en/objectives/data.php
... page[*]
http://www.astro.unipd.it/planets/sineo.html
... program[*]
http://smass.mit.edu/minus.html
... database[*]
http://simbad.u-strasbg.fr/simbad/
... RELAB[*]
http://www.planetary.brown.edu/relab
... olivine[*]
These spectra need some residual second absorption band in order to appear in the graph.
... MBs[*]
We have not included the V-type asteroids from Duffard et al. (2004) to compute this percentage, to avoid a compositional bias, as they are composed of pyroxene and lie along the tendency line. We also did not consider objects with a band I centre above 1.05 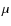$\mu $m, composed mainly of olivine.
... brackets[*]
We have not included the high slope of asteroid (1951) Lick to compute the mean value for NEAs, as it is an extreme case (Brunetto et al. 2007).
... IMC[*]
We have to point out here that the IMC result presents some contamination, as there are a number of Mars-crossers in our sample of NEAs.

All Tables

Table 1:   Solar analogue stars used to obtain the reflectance spectra of the asteroids of this survey.

Table 2:   Values of $\chi ^2$ test obtained for each pair of datasets used as the input to the neuronal net.

Table A.1:   Observational circumstances of the NEAs and MCs that make up this survey.

Table A.2:   Spectral parameters computed following Cloutis et al. (1986) for the sample of NEAs and MCs studied in this paper.

Table A.3:   Spectral parameters computed following Cloutis et al. (1986) for the sample of MBs.

Table A.4:   Physical and dynamical parameters of the analysed NEAs and MCs.

All Figures

  \begin{figure} \par {\hspace*{2cm}\includegraphics[width=4.5cm,clip]{13852f1a.ep... ...2cm}}\vspace*{3mm} \includegraphics[width=8.5cm,clip]{13852f1b.eps} \end{figure} Figure 1:

Distribution of the observational characteristics of this survey, from top and counter-clockwise: airmass, solar phase angle, and apparent visual magnitude. Mean value $\pm $1$\sigma $ deviation of each quantity are shown in brackets.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{13852f2.eps} \end{figure} Figure 2:

Distribution of the observed solar analogue stars in this survey. Each star is labelled with a number, as in Table A.1. The observation frequency depends both on the stars visibility during each night and the distribution of the observing nights during the year.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13852f3.eps} \end{figure} Figure 3:

Different solar analogue stars are used to obtain the reflectance spectrum of asteroid (433) Eros in the visible region. The top panel shows the spectrum of the asteroid and three solar analogues, with an offset in vertical axis for the sake of clarity. In the bottom panel, we can see the three resultant reflectance spectra of the asteroid. The uncertainty in the slope, computed between 0.5 and 0.7 $\mu $m is about 3%/1000 Å. For the majority of the asteroids, the uncertainties will be smaller that this value.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=15.5cm,clip]{13852f4.eps} \vspace*{7mm} \end{figure} Figure 4:

Wavelength position of the centres of the two absorption bands computed for MBs (blue squares) and NEAs (red circles). The mean error bars associated to each group of data are shown in the upper left region of each plot. Filled black and empty circles correspond to ortho (OPX) and clinopyroxenes (CPX) from Cloutis & Gaffey (1991). The regions enclosed with green, blue, and red lines correspond to the band centres computed for the H, L, and LL ordinary chondrites, respectively. Note the abundance of asteroids located up and far from the OPX-CPX tendency line (blue arrow) in the case of MBs.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=15.5cm,clip]{13852f5.eps} \end{figure} Figure 5:

Band area ratio (BAR) versus band I centre for MBs (blue squares) and NEAs (red circles). The regions enclosed by continuous lines correspond to the values computed for basaltic achondrites (BA), ordinary chondrites (OC) and olivine-rich meteorites (Ol). Those enclosed by dashed lines were computed by Gaffey et al. (1993). The red dashed line in the upper left part of the plots encloses asteroids composed exclusively/mainly of olivine.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13852f6a.eps}\par\includegraphics[width=8cm,clip]{13852f6b.eps} \end{figure} Figure 6:

Top: distribution of 20 000 synthetic points (red dots) in the BAR vs. Band I centre space, generated from seeds containing the original computed data for NEA population (black diamonds), considering error bars (1-$\sigma $) and following a normal distribution. It can be seen how the synthetic points are more dispersed for the seeds with larger error bars. Bottom: optimum $\kappa $ projection for the NEAs, OCs, and the three subgroups of ordinary chondrites (H, L and LL). This plot has been chosen to help visualize one of the results listed in Table 2. It is clearly seen that the shape of the projections for the NEAs (black line) and OCs (green line) are completely different.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=12cm,clip]{13852f7.eps} \end{figure} Figure 7:

Distributions of the computed spectral slope (SI, measured between the two maxima of the spectra) for the NEAs, MBs, and ordinary chondrites. The mean spectral slope for each group is indicated in brackets. We show also the size-frequency distributions (SFDs) of both populations.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13852f8.eps} \end{figure} Figure 8:

Location of the NEAs (red circles) and MBs (blue squares) analysed in the orbital parameter space a-e ( top panel) and a-i ( bottom panel). NEAs have perihelia q $\le $ 1.3 AU and aphelia Q $\ge $ 0.983 AU. The q < 1.66 AU dashed line defines the boundary between objects on Mars-crossing orbits and those in the main belt. Several mean motion resonances are shown as dashed vertical lines. The $i = 0^{\circ }$ position of the $\nu _6$ secular resonance is also shown as a dashed vertical line in the top panel and a continuous line in the bottom panel. Here we also indicate the IMC region (intermediate source Mars-crossing asteroid) and the OB1-OB5 regions, defined following Bottke et al. (2002). The position of the Hungaria (Hung) and Phocaea (Phoc) groups is also indicated.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=16.5cm,clip]{13852f9a.eps} \end{figure} Figure B.1:

Asteroid spectra.

Open with DEXTER
In the text

 \begin{figure} \par\includegraphics[width=16.5cm,clip]{13852f9b.eps} \end{figure} Figure B.1:

continued.

Open with DEXTER
In the text

 \begin{figure} \par\includegraphics[width=16.5cm,clip]{13852f9c.eps} \end{figure} Figure B.1:

continued.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.