| Issue |
A&A
Volume 517, July 2010
|
|
|---|---|---|
| Article Number | A6 | |
| Number of page(s) | 13 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/200913730 | |
| Published online | 23 July 2010 | |
Abundance analysis for long period variables
Velocity effects studied with O-rich dynamic model atmospheres
T. Lebzelter1 - W. Nowotny1 - S. Höfner2 - M. T. Lederer1 - K. H. Hinkle3 - B. Aringer1,4
1 - University of Vienna, Department of Astronomy, Türkenschanzstraße 17, 1180 Wien, Austria
2 -
Department of Physics and Astronomy, Division of Astronomy and Space Physics, Uppsala University,
Box 515, 75120 Uppsala, Sweden
3 -
National Optical Astronomy Observatories![]() , 950 N. Cherry Avenue, Tucson, Arizona 85726, USA
, 950 N. Cherry Avenue, Tucson, Arizona 85726, USA
4 -
Osservatorio Astronomico di Padova - INAF, vicolo dell'Osservatorio 5, 35122 Padova, Italy
Received 24 November 2009 / Accepted 31 March 2010
Abstract
Context. Measuring the surface abundances of AGB stars is an
important tool for studying the effects of nucleosynthesis and mixing
in the interior of low- to intermediate mass stars during their final
evolutionary phases. The atmospheres of AGB stars can be strongly
affected by stellar pulsation and the development of a stellar wind,
though, and the abundance determination of these objects should
therefore be based on dynamic model atmospheres.
Aims. We investigate the effects of stellar pulsation and mass
loss on the appearance of selected spectral features (line profiles,
line intensities) and on the derived elemental abundances by performing
a systematic comparison of hydrostatic and dynamic model atmospheres.
Methods. High-resolution synthetic spectra in the near infrared
range were calculated based on two dynamic model atmospheres (at
various phases during the pulsation cycle) as well as a grid of
hydrostatic COMARCS models with effective temperatures
![]() and surface gravities log g
over an adequate range. Equivalent widths of a selection of atomic and
molecular lines (Fe, OH, CO) were derived in both cases and compared
with each other.
and surface gravities log g
over an adequate range. Equivalent widths of a selection of atomic and
molecular lines (Fe, OH, CO) were derived in both cases and compared
with each other.
Results. In the case of the dynamic models, the equivalent
widths of all investigated features vary over the pulsation cycle. A
consistent reproduction of the derived variations with a set of
hydrostatic models is not possible, but several individual phases and
spectral features can be reproduced well with the help of specific
hydrostatic atmospheric models. In addition, we show that the
variations in equivalent width that we found on the basis of the
adopted state-of-the-art dynamic model atmospheres agree qualitatively
with observational results for the Mira R Cas over its light
cycle.
Conclusions. The findings of our modelling form a starting point
to deal with the problem of abundance determination in strongly dynamic
AGB stars (i.e., long-period variables). Our results illustrate that
some quantities such as the C/O ratio can probably still be determined
to a reasonable accuracy, but the measurement of other quantities will
be hampered by the dynamics. The qualitative agreement with
observations of R Cas opens promising possibilities for a
forthcoming quantitative comparison of our synthetic spectra with
observed ones of AGB variables in the globular cluster 47 Tuc.
Key words: stars: late-type - stars: AGB and post-AGB - stars: atmospheres - stars: abundances - line: profiles
1 Introduction
Measurements of abundances in atmospheres of highly evolved red giants contribute to the understanding of two major astrophysical aspects, namely the processes inside red giant stars such as nucleosynthesis and mixing, and, secondly, the enrichment of the interstellar medium by freshly produced elements due to the mass loss of these stars. The determination of accurate element abundances is complicated by the large number of spectral lines from neutral atoms and molecules that give rise to heavy blending, especially in the optical range of the spectrum. The problem is less severe in the near infrared range, which has become increasingly important for this kind of analysis.
When a low or intermediate mass star evolves to the asymptotic giant branch (AGB) phase, a second major problem occurs concerning the spectral analysis. Stars in this part of the HRD exhibit large amplitude radial pulsations. Being members of the variability class of so-called long period variables (LPVs), these objects change their visual brightnesses by up to several magnitudes over a few hundred days. The pulsating stellar interiors lead to complex velocity fields in the stellar atmospheres (e.g., Nowotny et al. 2010) and subsequently to phase-dependent line profile variations (asymmetric and split lines or emission features) as seen in observed spectra of these stars (e.g. Hinkle et al. 1982). Thus, a hydrostatic description of these objects is inappropriate. However, it is this evolutionary phase where major nucleosynthesis and mixing processes take place, and therefore great interest in measuring stellar abundances exists.
In the past, a few attempts have been made to investigate the complicated profiles of individual lines observed in spectra of variable AGB stars on the basis of model calculations. Using the dynamic models for pulsating red giants without mass loss of Bessell & Scholz (1989), Scholz (1992) showed how velocity fields in Mira photospheres distort line profiles of different species and affect measurements of equivalent widths and curves of growth for abundance analyses from these spectra. This fundamental paper, also referencing earlier works in this field, investigated the possibility to ``predict accurately the equivalent width of lines which are little affected by outflow/infall velocities by means of a conventional hydrostatic model in place of a dynamical model'' (Scholz 1992). He found that lines formed in deep layers below the arising shock fronts may be accessible to a classical curve of growth study, but that in some cases this approach seriously fails, so that abundance determination for large amplitude red variables remains a difficult problem.
In this context, a major challenge for dynamic model atmospheres was to reproduce the line profile variations observable in spectra of Mira type variables. First results concerning this were presented by Bessell et al. (1996), who calculated synthetic line profiles (CO, Fe I) based on the models of Bessell & Scholz (1989). They could qualitatively reproduce some of the observed line profile characteristics (asymmetries, shifted, or doubled lines).
McSaveney et al. (2007) attempted to derive abundances from high resolution spectra of pulsating AGB stars in the Magellanic Clouds by using the same type of model atmospheres. They succeeded in fitting the spectra of some stars at selected phases during the pulsation cycle. However, they had to restrict themselves to cases of relatively smooth atmospheric velocity fields. They were unable to derive abundances for model phases with complex atmospheric structures (shock waves), which cause distortions in the line profiles (emission components, line splitting).
While the Australia-Heidelberg model atmospheres (e.g., Bessell & Scholz 1989; Bessell et al. 1996; Hofmann et al. 1998) represent pulsating red giants without mass loss, the Berlin models (e.g. Fleischer et al. 1992; Winters et al. 1997, 2000) describe the optically thick dusty outflows of evolved C-rich AGB stars with high mass-loss rates. Based on the latter, Winters et al. (2000) presented synthetic fundamental and first overtone CO line profiles. By comparing reasonably with observed ones for the obscured C-rich Mira IRC+10216, these spectral lines can be used to investigate the radial structure and the temporal variation in the dusty envelope of these objects.
The non-grey dynamic model atmospheres of Höfner et al. (2003) represent a combination of both approaches and describe the outer layers of an AGB star from the pulsating deep photosphere (piston driven), to the dust forming region where the stellar wind is triggered and beyond to the region of the steady outflow (Nowotny et al. 2005a). Keeping in mind the work of Scholz (1992), we conducted a similar exercise to investigate the problem of deriving abundances for LPVs by utilising the advanced dynamic models of Höfner et al. (2003).
The major aim of the work presented here was to study the effect of atmospheric dynamics (pulsation, stellar wind) on the intensity of spectral lines for typical AGB stars. For this purpose, we compared selected spectral features in synthetic spectra computed on the basis of the aforementioned dynamic atmospheric models (Sect. 4) with the corresponding results based on hydrostatic model atmospheres (Sect. 3). In a second step, we investigate observed high-resolution spectra of a typical Mira to see if the effects we found by the modelling are also recognisable in the observational data (Sect. 5).
2 Methods
The starting point for the calculations are atmospheric structures,
either from hydrostatic or dynamic models. Based on this, we calculate
synthetic spectra and derive equivalent widths for a selection of
atomic and molecular features. In our study, we follow the approach of
an observational abundance study: to have a starting point for fitting
an observed spectrum with a synthetic one, basic quantities such as
effective temperature are derived from observed colours and
subsequently the observed target is compared with the corresponding
model. In our case, we also use a typical colour, (J-K), as an indicator of
![]() .
That is, we investigate how line intensities deviate in the dynamical
case from the hydrostatic model, both related by a given colour. In
doing so, we assume that (J-K) correlates with
.
That is, we investigate how line intensities deviate in the dynamical
case from the hydrostatic model, both related by a given colour. In
doing so, we assume that (J-K) correlates with
![]() ,
keeping in mind that the term effective temperature may become
questionable for the very evolved AGB stars featuring strong pulsations
and mass loss (Baschek et al. 1991; Nowotny et al. 2005b).
,
keeping in mind that the term effective temperature may become
questionable for the very evolved AGB stars featuring strong pulsations
and mass loss (Baschek et al. 1991; Nowotny et al. 2005b).
2.1 Model atmospheres
The guideline for the parameters of our model atmospheres was a typical
globular cluster LPV, namely the variable V3 in the well studied
cluster 47 Tuc. This metal poor, short period mira was observed in
the past by different authors (cf. Lebzelter & Wood 2005; Lebzelter et al. 2005, 2006, and references therein)![]() . The reason for choosing this object (and the corresponding models) was (i) the availability of spectroscopic data
. The reason for choosing this object (and the corresponding models) was (i) the availability of spectroscopic data![]() , and (ii) the parameters characterizing the star (comparably high
, and (ii) the parameters characterizing the star (comparably high
![]() ,
lower metallicity) to reduce the confusing effect of line blending.
,
lower metallicity) to reduce the confusing effect of line blending.
For our simulations, we used the dynamic model atmospheres of Höfner et al. (2003). These represent a combined and self-consistent solution of hydrodynamics, frequency-dependent radiative transfer![]() and - at least in the carbon-rich case - a detailed time-dependent
treatment of dust formation and evolution. Being well suited to
describing pulsating, mass-losing red giants, these models were able to
reproduce observational results such
as low-resolution spectra of C-rich stars (Gautschy-Loidl et al. 2004), line profile variations in high- resolution IR spectra (Nowotny et al. 2005a,b, 2010), or interferometric data (Paladini et al. 2009) reasonably well. The parameters of the atmospheric models (see Table 1)
were chosen to resemble our reference globular cluster mira. Starting
with the same hydrostatic initial model, we ended up with two different
dynamic models - P and PM - due to the altered piston velocity
amplitude
and - at least in the carbon-rich case - a detailed time-dependent
treatment of dust formation and evolution. Being well suited to
describing pulsating, mass-losing red giants, these models were able to
reproduce observational results such
as low-resolution spectra of C-rich stars (Gautschy-Loidl et al. 2004), line profile variations in high- resolution IR spectra (Nowotny et al. 2005a,b, 2010), or interferometric data (Paladini et al. 2009) reasonably well. The parameters of the atmospheric models (see Table 1)
were chosen to resemble our reference globular cluster mira. Starting
with the same hydrostatic initial model, we ended up with two different
dynamic models - P and PM - due to the altered piston velocity
amplitude
![]() of the varying inner boundary (cf. Eqs. (1) and (2) in Nowotny et al.
2010). While the first one
represents a pulsating dust-free atmosphere, we encounter in the second
case the development of a stellar wind on top of the pulsating
photosphere. Plots of moving mass shells and the corresponding
atmospheric structures during a pulsation cycle for similar models of
both types can be found in Höfner et al. (2003) or Nowotny et al. (2010).
We note that in the case of oxygen-rich chemistry the physics of dust
formation and mass loss of AGB stars is not yet fully understood (e.g.
Woitke 2006;
Höfner 2007, 2008). For M-type models such as those used here
of the varying inner boundary (cf. Eqs. (1) and (2) in Nowotny et al.
2010). While the first one
represents a pulsating dust-free atmosphere, we encounter in the second
case the development of a stellar wind on top of the pulsating
photosphere. Plots of moving mass shells and the corresponding
atmospheric structures during a pulsation cycle for similar models of
both types can be found in Höfner et al. (2003) or Nowotny et al. (2010).
We note that in the case of oxygen-rich chemistry the physics of dust
formation and mass loss of AGB stars is not yet fully understood (e.g.
Woitke 2006;
Höfner 2007, 2008). For M-type models such as those used here![]() the dust-driven wind is therefore induced by a simple parametrised description of the dust opacity first introduced by Bowen (1988) and described in detail in Höfner et al. (2003; Eq. (19)). We applied a maximum dust mass absorption coefficient of
the dust-driven wind is therefore induced by a simple parametrised description of the dust opacity first introduced by Bowen (1988) and described in detail in Höfner et al. (2003; Eq. (19)). We applied a maximum dust mass absorption coefficient of
![]() = 5 cm2 g-1 to generate such an artificial wind for model PM
= 5 cm2 g-1 to generate such an artificial wind for model PM![]() .
.
Table 1: Characteristics of the dynamic atmospheric models used for the modelling (P = pulsating, PM = pulsating and mass-losing).
Table 2: Effective temperatures and surface gravities (ranges, stepwidths) of the grid of hydrostatic atmospheric models (COMARCS) used.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{13730f01.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13730-09/Timg29.png)
|
Figure 1:
Overview of the spectral features studied. Synthetic spectra based on
three different COMARCS models (hydrostatic, i.e., no velocity effects)
with log g = 0.0 are shown, for
|
| Open with DEXTER | |
Since we wish to study the influence of atmospheric dynamics on
spectral lines, we also computed a reference grid of hydrostatic model
atmospheres. We thereby followed the approach described in detail by
Aringer et al. (2009).
Being guided again by 47 Tuc-V3, a grid of COMARCS models was
calculated with the aim of covering the full colour range of the
dynamic models, as illustrated in Figs. 2 and 3. The parameter ranges of the two subgrids with different C/O ratios are given in Table 2. Other model parameters were kept constant according to values found in the literature for 47 Tuc-V3: ![]() = 0.6
= 0.6 ![]() (Lebzelter & Wood 2005), [Fe/H] = -0.7 dex (Carretta & Gratton 1997),
(Lebzelter & Wood 2005), [Fe/H] = -0.7 dex (Carretta & Gratton 1997), ![]() = 2.5 km s-1 (Nowotny et al. 2010). For the isotopic ratio 12C/13C, we chose a typical AGB value of 30 (cf. Lebzelter et al. 2008).
= 2.5 km s-1 (Nowotny et al. 2010). For the isotopic ratio 12C/13C, we chose a typical AGB value of 30 (cf. Lebzelter et al. 2008).
2.2 Synthetic spectra and photometry
For the spectral synthesis, we followed an approach that had already been applied very successfully in the past, for details we refer to e.g. Nowotny et al. (2005a, 2010), Aringer et al. (2002, 2009), Lebzelter et al. (2008), or Gautschy-Loidl et al. (2004).
Based on a given radial atmospheric structure (temperature-pressure)
and the assumptions of chemical equilibrium as well as conditions of
LTE, opacities for all necessary sources were calculated by using the
COMA code (described in detail by Aringer 2000; Aringer et al. 2009; Lederer & Aringer 2009).
Element abundances for the spectral synthesis were used consistent with
the hydrodynamic models. We adopted the values for solar composition
from Anders & Grevesse (1989), except for C, N, and O where we took the data from Grevesse & Sauval (1994). To obtain the correct metallicity (cf. Table 1), the abundances of all elements heavier
than H and He were then scaled by the same factor of 0.2 (as [Fe/H] = -0.7 dex corresponds to
![]() ).
The C/O ratios were subsequently adapted by increasing the amount of
carbon (without changing the rest of the composition). Following the
descriptions given in Nowotny et al. (2010), Doppler profiles were assumed for molecular lines and the corresponding absorption coefficients were computed with the help
of line lists by Goorvitch & Chackerian (1994) for CO and by Rothman et al. (2005; HITRAN database) for OH. For the atomic Fe lines, we followed the method of Lederer & Aringer (2009) and adopted full Voigt profiles with line data taken from the VALD database (Kupka et al. 2000). All sources of the continuum opacity listed in Lederer & Aringer (2009) were taken into account. In addition, we included
absorption of H2O
where necessary. Spectral features of water are present across the
whole near-IR range and can severely influence the spectra for low
effective temperatures and mass-losing objects as illustrated in
Fig. 1. However, most of the existing H2O line lists show considerable differences in the positions of lines (Aringer et al. 2008)
when compared with observed spectra. Therefore, we accounted for water
in a pseudo-continuous way in order not to introduce uncertainties
related to the studied line profiles (blending). The water absorption
was calculated by using the (low-resolution) OS data from the SCAN data
base (Jørgensen 1997), a detailed description of which can be found in Jørgensen et al. (1993, 2001). Spline fits through minimum values of appropriately grouped data points were then applied to determine the
contribution of H2O
to the actual high-resolution wavelength grid. This method ensures that
the opacities are not overestimated (cf. Fig. 2.5 in Nowotny 2005) and infers lower limits to the quasi-continuous contributions.
).
The C/O ratios were subsequently adapted by increasing the amount of
carbon (without changing the rest of the composition). Following the
descriptions given in Nowotny et al. (2010), Doppler profiles were assumed for molecular lines and the corresponding absorption coefficients were computed with the help
of line lists by Goorvitch & Chackerian (1994) for CO and by Rothman et al. (2005; HITRAN database) for OH. For the atomic Fe lines, we followed the method of Lederer & Aringer (2009) and adopted full Voigt profiles with line data taken from the VALD database (Kupka et al. 2000). All sources of the continuum opacity listed in Lederer & Aringer (2009) were taken into account. In addition, we included
absorption of H2O
where necessary. Spectral features of water are present across the
whole near-IR range and can severely influence the spectra for low
effective temperatures and mass-losing objects as illustrated in
Fig. 1. However, most of the existing H2O line lists show considerable differences in the positions of lines (Aringer et al. 2008)
when compared with observed spectra. Therefore, we accounted for water
in a pseudo-continuous way in order not to introduce uncertainties
related to the studied line profiles (blending). The water absorption
was calculated by using the (low-resolution) OS data from the SCAN data
base (Jørgensen 1997), a detailed description of which can be found in Jørgensen et al. (1993, 2001). Spline fits through minimum values of appropriately grouped data points were then applied to determine the
contribution of H2O
to the actual high-resolution wavelength grid. This method ensures that
the opacities are not overestimated (cf. Fig. 2.5 in Nowotny 2005) and infers lower limits to the quasi-continuous contributions.
On the basis of the opacities
![]() for all depth and wavelengths points determined in this way, the
radiative transfer is solved in spherical geometry. As we wish to
investigate the influence of the complex atmospheric velocity fields on
spectral lines, a radiative transfer code was applied that takes into
account the effects of macroscopic gas velocities. This code follows
the algorithm described by Yorke (1988) and has
been used successfully in the past (e.g. Nowotny et al. 2005a, 2010).
Our aim was to study the behaviour of the individual line profiles.
Thus, we computed synthetic spectra containing the spectral features
chosen for our abundance studies (Table 3) with a high resolution of R = 300 000. Rebinning to R = 70 000
led to spectra with resolutions comparable to observations with
state-of-the-art IR spectrographs (FTS, CRIRES, Phoenix). The latter
were then used for measuring equivalent widths (Sect. 2.3). Sample spectra based on hydrostatic COMARCS models (thus no velocity effects) are shown in Fig. 1.
for all depth and wavelengths points determined in this way, the
radiative transfer is solved in spherical geometry. As we wish to
investigate the influence of the complex atmospheric velocity fields on
spectral lines, a radiative transfer code was applied that takes into
account the effects of macroscopic gas velocities. This code follows
the algorithm described by Yorke (1988) and has
been used successfully in the past (e.g. Nowotny et al. 2005a, 2010).
Our aim was to study the behaviour of the individual line profiles.
Thus, we computed synthetic spectra containing the spectral features
chosen for our abundance studies (Table 3) with a high resolution of R = 300 000. Rebinning to R = 70 000
led to spectra with resolutions comparable to observations with
state-of-the-art IR spectrographs (FTS, CRIRES, Phoenix). The latter
were then used for measuring equivalent widths (Sect. 2.3). Sample spectra based on hydrostatic COMARCS models (thus no velocity effects) are shown in Fig. 1.
In addition to these high-resolution spectra containing the line profiles, we also computed low-resolution spectra and synthetic photometry following the approach of Aringer et al. (2009). Opacity sampling spectra covering the near-IR with resolutions of R = 10 000 were calculated on the basis of several atmospheric models. By convolving these spectra with filter transmission curves and applying adequate zeropoints, we obtained synthetic photometry. The resulting (J-K) colours (subsequently used to correlate different models) for the dynamic model atmospheres during the pulsation cycle and for the grid of hydrostatic COMARCS models, are shown in Figs. 2 and 3, respectively.
Table 3: Spectral features investigated.
2.3 Measurement of equivalent widths
Elemental abundances in the atmospheres of stars can be derived from the intensity of spectral features since the number of absorbers will directly affect the depth of a line (except for saturated lines) apart from effects of temperature and electron density. Since we wish to investigate the effect of atmospheric dynamics on the derived abundances, we have to look for a quantity describing the line intensity. The standard concept in the context of abundance measurement is the equivalent width of a line, which is related to the abundance of the parent element by the curve of growth (e.g. Castelli & Hack 1990). The spectra of cool giants with their severe blending of adjacent molecular lines would certainly favour the application of a full spectral comparison to study the abundances of the elements on the surface (see e.g. Lebzelter et al. 2008). However, as we see below, stellar pulsation leads to considerable modifications of the line profile with the appearance of emission or doubled absorption components (cf. Nowotny et al. 2005a, 2010). Therefore, a complete fit of a spectrum of a mira-like variable in a particular spectral range with hydrostatic model spectra will fail anyway (at least during a good portion of the pulsation cycle). This makes a comparison of hydrostatic and dynamic models difficult. With the help of the equivalent width, we can at least measure the amount by which the total line intensity is changed by pulsation.
We obtained equivalent widths for a selection of spectral
features of various species. For this, we first imported the synthetic
spectra into IRAF. To allow for an automatic and objective measurement,
we removed all velocity shifts from the dynamical spectra by shifting
the investigated features to zero velocity (while retaining the
Doppler- modified line profiles). For this shift, we used the line core
as a reference point, except in cases of line doubling,
where we used instead a mean value between the two components. For the
shifted spectra, we afterwards verified that the complete feature falls
within our range of measurement and corrected the shift if necessary.
All spectra were normalized to the local pseudo-continuum instead of
the model continuum![]() to resemble an observer's approach as realistically as possible. The
pseudo-continuum was defined by placing a straight line through the
highest points in the spectrum excluding obvious emission peaks (as
present in the case of the dynamic models). The equivalent widths were
then measured using the IRAF tasks splot and bplot.
to resemble an observer's approach as realistically as possible. The
pseudo-continuum was defined by placing a straight line through the
highest points in the spectrum excluding obvious emission peaks (as
present in the case of the dynamic models). The equivalent widths were
then measured using the IRAF tasks splot and bplot.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13730f02.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13730-09/Timg38.png)
|
Figure 2: (J-K) colour variation versus bolometric phase for the dynamic models with (PM, filled symbols) and without (P, open symbols) wind. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13730f03.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13730-09/Timg39.png)
|
Figure 3:
Relation between
|
| Open with DEXTER | |
For our study, we selected lines in the H- and K-band. These wavelength ranges have played a key role in the study of photospheres of AGB stars since the development of high resolution near-infared spectrographs. Within this wavelength range, we chose a combination of strong and weak lines, and atomic and molecular features including a molecular band head for our analysis. Many of the selected lines had already been used in the abundance analysis of red giants (e.g. Smith et al. 2002; Lebzelter et al. 2008). For each feature we measured the same area around the central wavelength in all spectra. The borders are listed in Table 3. Examples illustrating the measured range are shown in Fig. 1.
A few uncertainties in this kind of measurement have to be considered.
First, variable line asymmetries as well as a limited number of points
in the pseudo-continuum can introduce small inconsistencies in the
handling from one spectrum to another. We ran some tests and found
possible deviations below 2% of the measured equivalent width. A second
and more severe problem is blending, although we tried to avoid
strongly blended lines in our selection of spectral features. The
problem emerges mainly for cool stars (
![]() K) with the appearance of H2O
and CN lines in the spectrum. We return to this point below. For the
dynamic models, the occurrence of line doubling and emission components
is a problem. The former can lead to significant broadening of the
feature requiring us to measure a wider range about the central
wavelength. This, however, leads to an inclusion of any (typically
blueshifted) emission component reducing the equivalent width of the
feature at other phases. When measuring a line in an observed stellar
spectrum, one may deliberately exclude this emission component provided
the spectral resolution is high enough. This would lead to qualitative
and phase-dependent differences between our model results and
observations. Emission components close to the line core do not require
special consideration since any measurement in observed spectra would
not be able to distinguish them either.
K) with the appearance of H2O
and CN lines in the spectrum. We return to this point below. For the
dynamic models, the occurrence of line doubling and emission components
is a problem. The former can lead to significant broadening of the
feature requiring us to measure a wider range about the central
wavelength. This, however, leads to an inclusion of any (typically
blueshifted) emission component reducing the equivalent width of the
feature at other phases. When measuring a line in an observed stellar
spectrum, one may deliberately exclude this emission component provided
the spectral resolution is high enough. This would lead to qualitative
and phase-dependent differences between our model results and
observations. Emission components close to the line core do not require
special consideration since any measurement in observed spectra would
not be able to distinguish them either.
3 Dependence of hydrostatic line sensitivities on stellar parameters
We describe the dependency of the intensity of various spectral features on (i) effective
temperature (
![]() ); (ii) surface gravity (log g); (iii) C/O ratio, and (iv) 12C/13C
ratio as derived from synthetic spectra based on hydrostatic models.
The results are grouped by the element or molecule producing the
feature.
); (ii) surface gravity (log g); (iii) C/O ratio, and (iv) 12C/13C
ratio as derived from synthetic spectra based on hydrostatic models.
The results are grouped by the element or molecule producing the
feature.
As can be seen from Fig. 3, the roughly linear relation between
![]() and (J-K)
stops at a temperature of 3200 K. For lower temperatures, the
near-infrared colour becomes almost constant and even shows a slight
linear trend towards lower values. This phenomenon has also been found
for carbon rich stars by Aringer et al. (2009)
and is caused by the behaviour of different molecular features in the
region of the filters. For the same reason - but of course due to
different molecular species (mainly H2O) - a similar trend
is seen in the oxygen-rich models. However, AGB stars in this
low-temperature range are subject to mass-loss processes and the effect
induced on the colour by the subsequent circumstellar reddening may be
much larger than the one caused by the aforementioned behaviour of
molecular features. This is especially true for C-rich stars and high
mass-loss rates (Aringer et al. 2009).
and (J-K)
stops at a temperature of 3200 K. For lower temperatures, the
near-infrared colour becomes almost constant and even shows a slight
linear trend towards lower values. This phenomenon has also been found
for carbon rich stars by Aringer et al. (2009)
and is caused by the behaviour of different molecular features in the
region of the filters. For the same reason - but of course due to
different molecular species (mainly H2O) - a similar trend
is seen in the oxygen-rich models. However, AGB stars in this
low-temperature range are subject to mass-loss processes and the effect
induced on the colour by the subsequent circumstellar reddening may be
much larger than the one caused by the aforementioned behaviour of
molecular features. This is especially true for C-rich stars and high
mass-loss rates (Aringer et al. 2009).
As shown below, the intensities of the spectral features also continue
to increase below 3200 K (except for the iron lines, which
decrease in strength with decreasing
![]() ). This results in a turnaround in the equivalent width curves at the high (J-K) values. We decided to plot the relations versus the near infared colour for two reasons. First, the (J-K)
colour is a quantity that is directly measurable. It is thus easier to
compare the modelling results with observations (see below). Second,
the comparison with dynamic models (performed in the next section)
requires the use of a global parameter such as the colour, because the
concept of an effective temperature is questionable for extended
dynamical structures.
). This results in a turnaround in the equivalent width curves at the high (J-K) values. We decided to plot the relations versus the near infared colour for two reasons. First, the (J-K)
colour is a quantity that is directly measurable. It is thus easier to
compare the modelling results with observations (see below). Second,
the comparison with dynamic models (performed in the next section)
requires the use of a global parameter such as the colour, because the
concept of an effective temperature is questionable for extended
dynamical structures.
3.1 Fe lines
Two iron lines were selected for the analysis to investigate the
behaviour of lines typically used to derive stellar metallicities (e.g.
Smith et al. 2002). The two lines originate in the same excitation level (5.642 eV). Accordingly, both lines show a similar trend with
![]() and log g, there being a clear dependence of the equivalent widths on both parameters as illustrated for one of the lines in Fig. 4.
The line at 15 536 Å is only mildly affected by blending,
although a CN feature becomes strong for the lowest temperatures
studied. The second Fe line close to 15 538 Å, which behaves
qualitatively identically, is blended with a nearby CN line producing
the asymmetric line profile clearly visble in Fig. 1. A neighbouring OH line mildly affects the red wing of the line profile. As can be seen from Fig. 1,
a large fraction of the observed decrease in the line strengths at low
temperatures is caused by a depression of the overall continuum.
and log g, there being a clear dependence of the equivalent widths on both parameters as illustrated for one of the lines in Fig. 4.
The line at 15 536 Å is only mildly affected by blending,
although a CN feature becomes strong for the lowest temperatures
studied. The second Fe line close to 15 538 Å, which behaves
qualitatively identically, is blended with a nearby CN line producing
the asymmetric line profile clearly visble in Fig. 1. A neighbouring OH line mildly affects the red wing of the line profile. As can be seen from Fig. 1,
a large fraction of the observed decrease in the line strengths at low
temperatures is caused by a depression of the overall continuum.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13730f04.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13730-09/Timg41.png)
|
Figure 4: Equivalent widths in [Å] of the Fe line at 15 536 Å measured from synthetic spectra based on hydrostatic model atmospheres against the corresponding (J-K) values. Same line style coding for various log g values as in Fig. 3. Details of the range in wavelength used around the line centre are listed in Table 3 and illustrated in Fig. 1. |
| Open with DEXTER | |
3.2 OH lines
Lines of the OH molecule produce very prominent features in the H-band spectra of cool giants. We selected two lines from the 2-0 transition and one line from the 3-1 transition for our study. In addition, we included a blend of OH lines across the same wavelength region in our analysis. A CN line is located in the blue wing of this blend. The blue end for measuring the equivalent width was defined to include the complete blend also in the dynamical case, but this means that most of the CN line is also covered (see Fig. 1).
All these lines behave identically. They show a strong dependency on (J-K), i.e.
![]() ,
while the change in the line intensity with log g is comparably small. This is shown for two of the lines in Figs. 5 and 6. The OH blend (Fig. 5)
including also a CN line does not behave differently, the feature being
dominated by OH. We also derived equivalent widths for a model with
log g = 0.0 and C/O = 0.25 to study the
effect of a change in the C/O ratio. The other parameters were left
unchanged. The result is plotted as a dash-dotted line in the figures.
The effect is visible for the OH 2-0 line at 15 576 Å, but it
is rather small. In this context, we note that for our modelling -
simulating the change caused by third dredge up - the C/O ratio is
changed by increasing or decreasing the carbon abundance, while the
oxygen abundance remains constant.
,
while the change in the line intensity with log g is comparably small. This is shown for two of the lines in Figs. 5 and 6. The OH blend (Fig. 5)
including also a CN line does not behave differently, the feature being
dominated by OH. We also derived equivalent widths for a model with
log g = 0.0 and C/O = 0.25 to study the
effect of a change in the C/O ratio. The other parameters were left
unchanged. The result is plotted as a dash-dotted line in the figures.
The effect is visible for the OH 2-0 line at 15 576 Å, but it
is rather small. In this context, we note that for our modelling -
simulating the change caused by third dredge up - the C/O ratio is
changed by increasing or decreasing the carbon abundance, while the
oxygen abundance remains constant.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13730f05.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13730-09/Timg42.png)
|
Figure 5: Equivalent widths in [Å] of the OH blend at 15 570 Å measured from synthetic spectra based on hydrostatic model atmospheres against the corresponding (J-K) values. Same line style coding for various log g values as in Fig. 3. The dash-dotted line indicates the relation for C/O = 0.25 (standard value: 0.48). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13730f06.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13730-09/Timg43.png)
|
Figure 6: Same as Fig. 5 for the OH line at 15 576 Å. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13730f07.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13730-09/Timg44.png)
|
Figure 7: Equivalent widths in [Å] of the 12CO 3-0 band head (measured between 15 581 Å and 15 585.7 Å) measured from synthetic spectra based on hydrostatic model atmospheres against the corresponding (J-K) values. See Fig. 1 for the wavelength range covered. Same line style coding for various log g values as in Fig. 3. The dash-dotted line indicates the relation for C/O = 0.25 (standard value: 0.48). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13730f08.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13730-09/Timg45.png)
|
Figure 8: Equivalent widths in [Å] of the 12CO line at 23 137 Å measured from synthetic spectra based on hydrostatic model atmospheres versus the corresponding (J-K) values. Same line style coding for various log g values as in Fig. 3. The dash-dotted line indicates the relation for 12C/13C = 10 (standard value: 30). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13730f09.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13730-09/Timg46.png)
|
Figure 9: Same as Fig. 8 for the 13CO line at 23 660 Å. |
| Open with DEXTER | |
3.3 CO features
Features of CO with its well expressed band structure can be easily identified in the H- and K-band spectra of stars of spectral type K or later. They are frequently used to derive stellar parameters and abundances or to study the atmospheric dynamics (e.g. Hinkle et al. 1982; Lebzelter 1999). The three CO features selected here represent different spectral signatures of this molecule: the (3-0) band head of 12CO located in the H-band; a strong single 12CO line in the K-band; and finally a line from 13CO in the same wavelength range.
As in all other cases, the equivalent widths of the three features were derived for various
![]() and log g (Figs. 7 to 9). In addition, the CO band head was also measured for a model with log g=0.0
and reduced C/O = 0.25. To investigate the effect of a change
in the carbon isotopic ratio, we also calculated synthetic spectra with
12C / 13C = 10 instead of 30 (log g=0.0).
and log g (Figs. 7 to 9). In addition, the CO band head was also measured for a model with log g=0.0
and reduced C/O = 0.25. To investigate the effect of a change
in the carbon isotopic ratio, we also calculated synthetic spectra with
12C / 13C = 10 instead of 30 (log g=0.0).
The strength of the CO band head (Fig. 7) depends on all three parameters
![]() ,
log g,
and C/O. As one would expect from simple considerations concerning
molecule formation, for the star investigated here the intensity of the
C/O bands increases with the C/O ratio. Quite a different behaviour can
be seen for the 12CO line at 23137 Å. The equivalent width is almost constant for a wide range of (J-K), but below 3400 K a strong dependency on
,
log g,
and C/O. As one would expect from simple considerations concerning
molecule formation, for the star investigated here the intensity of the
C/O bands increases with the C/O ratio. Quite a different behaviour can
be seen for the 12CO line at 23137 Å. The equivalent width is almost constant for a wide range of (J-K), but below 3400 K a strong dependency on
![]() is observed. We note that, in contrast to the situation around 1.5
is observed. We note that, in contrast to the situation around 1.5 ![]() m, the line strengths of the features at 2.3
m, the line strengths of the features at 2.3 ![]() m are not affected
by a change in the continuum level. The 12CO line investigated is almost independent of log g.
An exception is the model with the lowest surface gravity, which seems
to be offset from the other models. The reason for that behaviour is
unclear, but a weakening of the lines due to sphericity effects
occurring in very extended atmospheres is a likely explanation (Aringer
et al. 2009). Finally, the 13CO line again shows a trend of increasing line strenghts with
m are not affected
by a change in the continuum level. The 12CO line investigated is almost independent of log g.
An exception is the model with the lowest surface gravity, which seems
to be offset from the other models. The reason for that behaviour is
unclear, but a weakening of the lines due to sphericity effects
occurring in very extended atmospheres is a likely explanation (Aringer
et al. 2009). Finally, the 13CO line again shows a trend of increasing line strenghts with
![]() and a mild dependency on the log g value (especially for log g<0.0, see Fig. 9). The change with
and a mild dependency on the log g value (especially for log g<0.0, see Fig. 9). The change with
![]() seems to be intensified by a neighbouring line of CN, which appears at
the lower end of the temperature range studied. A change in the carbon
isotopic ratio has a strong impact on the intensity of the studied 13CO line.
seems to be intensified by a neighbouring line of CN, which appears at
the lower end of the temperature range studied. A change in the carbon
isotopic ratio has a strong impact on the intensity of the studied 13CO line.
4 Comparing dynamical and hydrostatic line intensities
We summarize our findings for hydrostatic models as follows:
- Most features are sensitive to changes in
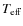 .
The only exception is the 12CO
line at 23 137 Å, which becomes temperature sensitive for low
temperatures only. The two studied lines of Fe are also less sensitive
to
.
The only exception is the 12CO
line at 23 137 Å, which becomes temperature sensitive for low
temperatures only. The two studied lines of Fe are also less sensitive
to
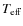 changes for higher temperatures.
changes for higher temperatures.
- The dependency on
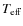 is a combination of a change in both the line intensity and the level of the pseudo-continuum due to H2O.
is a combination of a change in both the line intensity and the level of the pseudo-continuum due to H2O.
- At the lowest temperatures, we observed CN line blending for most of the features studied.
- A change in surface gravity has on average a smaller influence on the feature strengths. The most pronounced changes in this parameter were found for the CO 3-0 band head and the iron lines.
4.1 Fe lines
We first note here the overall behaviour of dynamic models in the (J-K) versus equivalent width plane, which is already clearly visible for the Fe lines in Figs. 10 and 11: for a given (J-K) value, the line intensity is different for the falling and rising branch of the light curve. As a result, the model values loop through the diagram. This loop is more pronounced in the case of the model with mass loss (PM) than for the model without mass loss (P). Small changes are visible between the pulsation cycles calculated, but the general behaviour remains the same.
In the dynamcial case, the (J-K) - equivalent width relations for the iron lines show a similar arc-like shape as in the hydrostatic case. The maximum line intensity is reached at neither maximum nor minimum light. However, the two iron lines clearly differ in their behaviour. Fe 15 538 Å seems to vary in a way similar to that in the hydrostatic models. The variation in line intensity over the pulsation cycle for model PM may be described by a combination of a hydrostatic model of log g=0.0 for the first half of the light curve and a hydrostatic model of somewhat lower surface gravity for the second half of the light variation. Model P is offset to somewhat higher line strengths.
The Fe 15536 Å line (Fig. 10) shows a trend clearly different from the other iron line and from the hydrostatic reference case. Here the line strenghts are weaker than in the COMARCS model and would correspond to a higher surface gravity. In addition, the shape of the relation is different. Model P again exhibits stronger lines at a given (J-K) than model PM. For (J-K) >1.2, model P approaches the hydrostatic relation.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13730f10.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13730-09/Timg49.png)
|
Figure 10:
Change in the intensity of the Fe line at 15 536 Å over the calculated pulsation cycles versus (J-K)
for two dynamic models. The model with mass loss (PM) is shown with
solid symbols, while the model without mass loss (P) is marked with
open symbols. Data points are connected to illustrate the path of the
change over the pulsation cycle. Two cycles are plotted for
model PM and four for model P. The small arrow indicates the
direction of the path and starts at the maximum bolometric phase (
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13730f11.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13730-09/Timg50.png)
|
Figure 11: Same as Fig. 10 for the Fe line at 15 538 Å. |
| Open with DEXTER | |
4.2 OH lines
All four OH lines investigated exhibit similar behaviour over the pulsation cycle. As for the iron lines, the model produces a loop in the diagram over one pulsation cycle. The dynamic model P again exhibits stronger lines than model PM. The difference between the two models changes from line to line.
Both dynamic models have similar dependences on (J-K), i.e.
![]() ,
as our hydrostatic reference models (Figs. 12 to 14).
During half of the pulsation cycle, we can see an offset between
model PM and the hydrostatic case. As the hydrostatic line
intensity is almost independent of the surface gravity (cf. Figs. 5 and 6), this offset cannot be compensated for by choosing a different log g
value as in the case of the iron lines. To bring the dynamic model in
alignment with a series of hydrostatic models, one would be inveigled
to change the C/O ratio. However, the OH line at 15 540 Å
(Fig. 12)
shows a deviation from the hydrostatic case towards the opposite side
of the other OH lines, therefore requiring an inverse change of C/O.
,
as our hydrostatic reference models (Figs. 12 to 14).
During half of the pulsation cycle, we can see an offset between
model PM and the hydrostatic case. As the hydrostatic line
intensity is almost independent of the surface gravity (cf. Figs. 5 and 6), this offset cannot be compensated for by choosing a different log g
value as in the case of the iron lines. To bring the dynamic model in
alignment with a series of hydrostatic models, one would be inveigled
to change the C/O ratio. However, the OH line at 15 540 Å
(Fig. 12)
shows a deviation from the hydrostatic case towards the opposite side
of the other OH lines, therefore requiring an inverse change of C/O.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13730f12.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13730-09/Timg51.png)
|
Figure 12: Same as Fig. 10 for the OH line at 15540 Å. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13730f13.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13730-09/Timg52.png)
|
Figure 13: Same as Fig. 10 for the OH blend at 15570 Å. Compare with Fig. 5. |
| Open with DEXTER | |
The different slope seems to be a result of a complex mixture of
various components of the investigated lines, which are difficult or
even impossible to distinguish in the measurement. One obvious feature
is the appearance of an emission component between
![]() and 0.41 (corresponding to the lower branch of the loop between (J-K) = 1.1 and 1.28; see Fig. 14)
on the blue wing of the OH 15573 and OH 15576 Å lines. This
emission component is not excluded from the measurement of the
equivalent width and may be responsible for at least part of the
depression of the line intensity measured.
and 0.41 (corresponding to the lower branch of the loop between (J-K) = 1.1 and 1.28; see Fig. 14)
on the blue wing of the OH 15573 and OH 15576 Å lines. This
emission component is not excluded from the measurement of the
equivalent width and may be responsible for at least part of the
depression of the line intensity measured.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13730f14.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13730-09/Timg54.png)
|
Figure 14: Same as Fig. 10 for the OH line at 15576 Å. Compare with Fig. 6. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13730f15.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13730-09/Timg55.png)
|
Figure 15: Same as Fig. 10 for the 12CO 3-0 band head. Compare with Fig. 7. |
| Open with DEXTER | |
4.3 CO features
The most remarkable loops in the diagram EW versus (J-K) corresponding to model PM are found for the features of CO. For the CO band head (Fig. 15), model P (no outflow) and part of the pulsation cycle of model PM show a very similar relation of band strength with (J-K) as the hydrostatic models. Owing to the high sensitivity of the CO band head to the surface gravity (note the different scale on the y-axis in Fig. 7), the whole loop made by model PM can be reproduced by a change in log g of 0.25. A modification of the C/O ratio from 0.48 to 0.25 has an about three times larger effect on the band strength than the changes during the pulsation cycle.
For the two individual CO lines studied in the K-band, the situation is completely different, especially for model PM (with outflow). For the 12CO line at 23 137 Å, we find only very short parts of the pulsation cycle where the derived line intensity is in a similar range as that found for the hydrostatic models. This deviation from the hydrostatic case is caused by the occurrence of line doubling over most of the pulsation cycle. However, this does not lead to a simple broadening. As can be seen from Fig. 16, the line intensity at some phases is also weaker than in the hydrostatic case. This is caused by an emission component that is visible on the blue side of the line profile for almost half the light cycle. For illustration, we compare in Fig. 17 the corresponding line profile of this CO line derived from a hydrostatic model and from two phases of model PM at similar (J-K). The two chosen phases represent the two branches of the bolometric light curve.
Model P resembles the hydrostatic case more closely. Line doubling is observed less often, but again a blue-shifted emission component can be seen. Here the differences between hydrostatic and dynamic models are greatest at minimum light.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13730f16.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13730-09/Timg56.png)
|
Figure 16: Same as Fig. 10 for the 12CO line at 23137 Å. Compare with Fig. 8. |
| Open with DEXTER | |
![\begin{figure}
\par\hspace*{0.5mm}\includegraphics[width=7.1cm,clip]{13730a17.ep...
...s}\par\hspace*{4mm}\includegraphics[width=7.4cm,clip]{13730c17.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13730-09/Timg57.png)
|
Figure 17:
Comparison of the line profile of 12CO 23 137 in a hydrostatic model (
|
| Open with DEXTER | |
Line profile variations such as those havee frequently been reported in the literature (e.g. Hinkle et al. 1982; Lebzelter et al. 1999; Nowotny et al. 2005a,b). The low excitation 2-0 transitions of 12CO are strong lines that form over a large part of the stellar atmospheres and also in the outflow of AGB stars. This makes the difference between line intensity variations in models P and PM understandable because the latter model has a larger extension and introduces an additional redshifted component to the line profile.
For the 13CO line studied, we also find a behaviour deviating from the hydrostatic case (Fig. 18). Model P shows a trend very similar to the hydrostatic models over a large fraction of the pulsation cycle. The line intensity in model PM follows the hydrostatic relation for about half the pulsation cycle, but for the other half the lines are much weaker. This cannot be accounted for by a change in log g alone and would require an enormous change in the isotopic ratio. The occurrence of an emission component in the line profile is responsible for this weakening as in the case of the 12CO line. The emission is visible at several phases as a separate component, but is probably hidden by a general weakening of the line during a much larger part of the pulsation cycle. If we take out the emission component by artificially setting all values above the pseudo-continuum to the continuum level, the loop becomes less extended in the lower right corner of Fig. 18. Contrary to the case of model P, a flattening of the loop cannot be achieved in this way.
In Fig. 18, we also see noticeable cycle-to-cycle differences, especially in the case of model PM. This is an interesting result keeping in mind that our model atmosphere is modulated by a strictly sinusoidal variation in the inner boundary. This behaviour was previously noted for other output quantities (e.g. degree of dust condensation) from this kind of models (Nowotny et al. 2005a,b). For models based on self-excitation pulsation or real stars (see next section), even larger cycle-to-cycle differences can be expected (Lebzelter et al. 2001).
5 Results from observations
It is naturally it is a critical question whether the behaviour found for various lines in the dynamic models are also visible in observations. For the hydrostatic case, a number of successful comparisons between observed and synthetic photometry and spectra exist (e.g. Loidl et al. 2001; Aringer et al. 2002; Lebzelter et al. 2008). For the dynamical case, it could also be shown that the models reproduce observations of C-rich stars reasonably well (e.g. Gautschy-Loidl et al. 2004; Nowotny et al. 2005b).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13730f18.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13730-09/Timg58.png)
|
Figure 18: Same as Fig. 10 for the 13CO line at 23 660 Å. Compare with Fig. 9. |
| Open with DEXTER | |
Long time series of high resolution spectra of LPVs are rare. Here we use a time series of FTS spectra in the H- and K-band of the mira R Cas. This object is a typical mira variable in the solar neighbourhood with a period of 431![]() and a visual brightness amplitude up to 9 magnitudes. At minimum light, the star reaches a spectral type of M10 (Lockwood 1970; Wyckoff & Wehinger 1971). Its dusty envelope has been used to derive
a mass-loss rate of a few 10-7
and a visual brightness amplitude up to 9 magnitudes. At minimum light, the star reaches a spectral type of M10 (Lockwood 1970; Wyckoff & Wehinger 1971). Its dusty envelope has been used to derive
a mass-loss rate of a few 10-7 ![]() yr-1 (Schutte & Tielens 1989; Weigelt & Yudin 2001). This agrees with an older mass-loss rate derived from thermal circumstellar CO emission (Loup et al. 1993). The atmospheric kinematics of R Cas was described by Hinkle et al. (1984).
These authors note that around minimum light the near infrared CO line
profiles investigated by them seem to be strongly affected by blending
of the CO lines with H2O lines. Strong water absorption bands were also reported by Truong-Bach et al. (1999) and Aringer et al. (2002)
in the mid-infrared range. Clearly R Cas is described by
parameters quite different from our models, and we wish to explicitly
state that the dynamic model atmospheres (Table 1)
were not designed to resemble this specific object. We did not attempt
to reproduce the spectrum of R Cas. The main goal of this study is
to identify the basic problems and features of abundance analysis in
dynamical atmospheres. Our comparison shall be made on a qualitative
basis only. The main reason for choosing this set of spectra is that to
our knowledge it is the most extensive time series of high-resolution
near-infrared spectra of an M-type mira available.
yr-1 (Schutte & Tielens 1989; Weigelt & Yudin 2001). This agrees with an older mass-loss rate derived from thermal circumstellar CO emission (Loup et al. 1993). The atmospheric kinematics of R Cas was described by Hinkle et al. (1984).
These authors note that around minimum light the near infrared CO line
profiles investigated by them seem to be strongly affected by blending
of the CO lines with H2O lines. Strong water absorption bands were also reported by Truong-Bach et al. (1999) and Aringer et al. (2002)
in the mid-infrared range. Clearly R Cas is described by
parameters quite different from our models, and we wish to explicitly
state that the dynamic model atmospheres (Table 1)
were not designed to resemble this specific object. We did not attempt
to reproduce the spectrum of R Cas. The main goal of this study is
to identify the basic problems and features of abundance analysis in
dynamical atmospheres. Our comparison shall be made on a qualitative
basis only. The main reason for choosing this set of spectra is that to
our knowledge it is the most extensive time series of high-resolution
near-infrared spectra of an M-type mira available.
Our time series was obtained by one of us (KH) between August 1983 and September 1986 with the FTS spectrometer at the Kitt Peak National Observatory 4 m Mayall telescope (Hall et al. 1979). It covers two complete light cycles of this star. A standard data analysis described extensively in previous papers (e.g. Hinkle et al. 1982, 1984) was applied to the spectra. Additional analysis was performed within IRAF using the same procedures as in the case of the synthetic spectra.
Phases within the pulsation cycle were attributed to the individual observations by using the AAVSO lightcurve (Fig. 21). The figure clearly indicates that by chance our time series covers an untypical behaviour of the star with an outstandingly bright maximum during the first cycle and an unusually weak maximum in the second. The third maximum plotted represents the typical amplitude observed for this star. That this behaviour is reflected in an untypical atmospheric dynamics was demonstrated by Lebzelter et al. (2001). This has to be kept in mind when discussing the line behaviour in R Cas.
(J-K) values obtained parallel to our time series do not exist. The atypical light change during that time does not allow us to use near-infrared light curves obtained during some other pulsation cycle (e.g. Kerschbaum et al. 2001; Nadzhip et al. 2001). The only quantity directly available is the visual brightness from the AAVSO light curve. Assuming that (J-K) changes approximately in phase with the visual brightness, we use this indicator in our investigation. The V value was derived from a polynomial fit to all AAVSO data. No correction for the difference between visual measurements and photometric V-band magnitudes was applied, but the effect on the shape of the light curve should be very small.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13730f19.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13730-09/Timg61.png)
|
Figure 19:
FTS spectrum of R Cas around the OH lines obtained at JD 2 445 575 (corresponding to
|
| Open with DEXTER | |
We attempted to measure spectral features in the R Cas data in a similar way (i.e. using the same width to determine the equivalent widths of lines) as in the synthetic spectra. We naturally had some difficulties in this case: the definition of the continuum is far more complicated in the observations than in the synthetic spectra, where emission peaks can be easily identified from the nominal continuum level. We illustrate our definition of the continuum in Fig. 19. As for the synthetic spectra (Sect. 2.3), the observed spectra were shifted in wavelength (while preserving the Doppler-modified profiles) to allow an automatic measurement of equivalent widths. For comparison, we chose features that are only slightly contaminated by telluric absorption and assume that the influence of the Earth's atmosphere is negligible. Finally, our data are slightly affected by the instrument profile for which we also did not apply any corrections.
The most remarkable features in the case of the synthetic spectra are certainly the loops derived from the dynamic models, especially those models that produce an outflow of material. For a given near-infrared colour, two line strengths are found depending on the star being on the rising or falling part of the light change. R Cas is obviously also a mira with a substantial mass loss. In Fig. 20, we show the behaviour of the OH line at 15 570 Å versus visual brightness. Consecutive data points in the light cycle are connected by lines. Altering the continuum level by 2 % changes the measured equivalent width by about 0.03 Å. Other spectral features checked by ourselves show a similar behaviour.
For an easier comparison, we also show the behaviour of the equivalent width with visual brightness derived from our models P and PM. The absolute visual magnitudes predicted by the models were shifted to roughly coincide with the V-brightness of R Cas. It is clear that the observed behaviour in R Cas is in qualitative agreement with that found in our study using synthetic spectra. However, we note that the loop over the light cycle goes in the inverse direction (see the arrow in Fig. 20). At the moment, the reason for this difference is not clear. Figure 21 shows a strong correlation between the feature intensity and the visual brightness. The difference between the first and the second observed light cycle mentioned above is therefore clearly reflected in a corresponding change in the equivalent width. As a consequence, the loops resulting from these two light cycles (Fig. 20) have different extensions.
The occurrence of loops in a digram of equivalent width versus either (J-K) or V corresponds to a different relation between the two quantities on the rising and the falling branch of the light cycle. This can be seen in both Fig. 22 for the model case and Fig. 21 for the observations.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13730f20.eps}\vspace{3mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13730-09/Timg62.png)
|
Figure 20: Equivalent widths in [Å] of the OH blend at 15 570 Å measured from our time series of FTS spectra of the mira R Cas (triangles) against the corresponding V values taken from the AAVSO light curve. The small arrow indicates the path from the first visual light maximum to minimum. For comparison, we also added the results from model P (open circles) and model PM (filled circles). Note that the model parameters are very different from the parameters of R Cas. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13730f21.eps}\vspace{3mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13730-09/Timg63.png)
|
Figure 21: Equivalent widths in [Å] of the OH blend at 15 570 Å (large dots, left y-axis) and the AAVSO light curve (small dots, right y-axis) for R Cas against time expressed in JD. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13730f22.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13730-09/Timg64.png)
|
Figure 22: Equivalent widths in [Å] of the OH blend at 15570 Å (solid symbols, left y-axis) and (J-K) colour (solid line, right y-axis) for model PM against the bolometric phase. Phase 0 has been assigned to the light maximum. |
| Open with DEXTER | |
6 Conclusions and outlook
The aim of our study has been to explore the possibilities and caveats of deriving stellar abundances from observed spectra of AGB stars that are strongly affected by pulsation and mass loss. We can summarise our findings as follows:
- There is not a single phase, neither for model P nor for model PM, where all investigated features would be in agreement with a single hydrostatic model at the same time. This suggests that there is a fundamental problem in fitting the complete spectrum of a dynamical star with one hydrostatic model.
- For several features, the dynamic models, especially model PM, touch areas in the (J-K) versus equivalent width plane that seem to be unreachable by hydrostatic models even when modifying the chemical composition. Further tests are necessary to test the effects of e.g. metallicity on this finding.
- Spectral peculiarities due to stellar dynamics seem to be less significant in the H-band than in the K-band.
- For dynamic atmospheres with mass loss (represented by model PM), the rising, post-minimum branch seems to be more promising for deriving element abundances with the help of hydrostatic models. This is, however, untrue for some of the features studied (namely the iron lines, OH 15540 and 12CO 23137).
- For dynamical atmospheres without mass loss (model P), the loops are less extended and the detected trends of equivalent width with colour seem to resemble the hydrostatic case in many respects. For several features, we find an offset between the relation for model P and the hydrostatic reference case with log g=-0.25. This offset, however, is not the same for all features.
- Including the emission lines in the measurement of the strength of a spectral feature leads to an extension of the loop completed in the colour versus equivalent width plane. For high resolution spectroscopy, it is therefore better to exclude any clearly separated emission component when deriving the stellar abundance. If low resolution spectra were used, in which the emission component cannot be detected separately, we expect to see extensive loops such as those found in this study.
- Our results are qualitatively similar to the findings of Scholz (1992) and others.
Deriving stellar abundances for pulsating stars without an outflow
(simulated in this study by model P with a bolometric light
amplitude of 0.86
![]() )
may well be possible if we take into account a set of offsets that
still need to be determined. Abundance determinations for these kind of
stars performed so far are probably affected by systematic error,
depending on the feature used.
)
may well be possible if we take into account a set of offsets that
still need to be determined. Abundance determinations for these kind of
stars performed so far are probably affected by systematic error,
depending on the feature used.
If we wish to derive stellar abundances from dynamic atmospheres, we have to search for features that are far more sensitive to changes in the chemical composition than to dynamical effects. An example would be the 12CO 3-0 band head. As described above, the loop (Fig. 15) covers a range in the colour vs. equivalent width diagram similar to a change in log g by 0.5. This is clearly less than the change from C/O = 0.48 to C/O = 0.25 (Fig. 7). Therefore we have a good chance of determining whether, e.g., the surface abundances of an AGB star have already been modified from the first dredge-up composition by the third dredge-up (e.g. Lattanzio & Wood 2004). Having measurements of different phases would naturally help us to improve the accuracy of the result.
We emphasize that our approach includes some simplifications that need to be explored in more detail. We did not test the effect of a variation in metallicity. Furthermore, a change in C/O may have a more complex effect on dynamic atmospheres than known from the hydrostatic case. Finally, a comparison with observed time series of a mira reveals that some features are in common with the model (e.g. the occurrence of loops), while other aspects are different (e.g. the dependency on phase). At present, it is not clear if this is due to a general problem in the models or a dependence of these characteristics on the parameters of the model (note that R Cas is very different from the models we used in our analysis). However, we point out that the values found for the equivalent widths in R Cas are in good agreement with what we would expect from an extension of the detected trends towards redder colours.
In a forthcoming paper, we will continue our comparison of high resolution synthetic spectra from dynamical and hydrostatic model atmospheres to identify the most well-suited features for measuring stellar parameters and abundances for cool large amplitude variables. We also plan to extend the study to dynamic models with different composition. Finally, we intend to directly compare the observed spectra of AGB variables in the globular cluster 47 Tuc with the results of hydrostatic and dynamic model atmospheres.
AcknowledgementsThis work has been supported by the Austrian Science Fund (P18171-02, P18939-N16, P20046-N16 and P21988-N16). B.A. acknowledges funding by the contract ASI-INAF I/016/07/0. We acknowledge with thanks the variable star observations from the AAVSO International Database contributed by observers worldwide and used in this research.
References
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- Aringer, B. 2000, Ph.D. Thesis, University of Vienna, Austria [Google Scholar]
- Aringer, B., Höfner, S., Wiedemann, G., et al. 1999, A&A, 342, 799 [NASA ADS] [Google Scholar]
- Aringer, B., Kerschbaum, F., & Jørgensen, U. G. 2002, A&A, 395, 915 [Google Scholar]
- Aringer, B., Nowotny, W., & Höfner, S. 2008, in Perspectives in Radiative Transfer and Interferometry, ed. S. Wolf, F. Allard, & Ph. Stee, EAS Publ. Ser., 28, 67 [Google Scholar]
- Aringer, B., Girardi, L., Nowotny, W., Marigo, P., & Lederer, M. T. 2009, A&A, 503, 913 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baschek, B., Scholz, M., & Wehrse, R. 1991, A&A, 246, 374 [NASA ADS] [Google Scholar]
- Bessell, M. S., & Scholz, M. 1989, in Evolution of Peculiar Red Giants, ed. H. R. Johnson, & B. Zuckerman (Cambridge University Press), IAU Coll., 106, 67 [Google Scholar]
- Bessell, M. S., Scholz, M., & Wood, P. R. 1996, A&A, 307, 481 [NASA ADS] [Google Scholar]
- Bowen, G. H. 1988, ApJ, 329, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Carretta, E., & Gratton, R. G. 1997, A&AS, 121, 95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castelli, F., & Hack, M. 1990, Mem. Soc. Astron. Ital., 61, 595 [Google Scholar]
- Cristallo, S., Straniero, O., Lederer, M. T., & Aringer, B. 2007, ApJ, 667, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Fleischer, A. J., Gauger, A., & Sedlmayr, E. 1992, A&A, 266, 321 [NASA ADS] [Google Scholar]
- Gautschy-Loidl, R., Höfner, S., Jørgensen, U. G., & Hron, J. 2004, A&A, 422, 289 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goorvitch, D., & Chackerian, C. Jr. 1994, ApJS, 91, 483 [NASA ADS] [CrossRef] [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1994, in Molecules in the Stellar Environment, ed. U. G. Jørgensen, Lecture Notes in Physics, 428 (Springer), IAU Coll., 146, 196 [Google Scholar]
- Hall, D. N. B., Ridgway, S. T., Bell, E. A., & Yarborough, J. M. 1979, Proc. SPIE, 172, 121 [Google Scholar]
- Hinkle, K. H., Hall, D. N. B., & Ridgway, S. T. 1982, ApJ, 252, 697 [NASA ADS] [CrossRef] [Google Scholar]
- Hinkle, K. H., Scharlach, W. W. G., & Hall, D. N. B. 1984, ApJS, 56, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Hofmann, K.-H., Scholz, M., & Wood, P. R. 1998, A&A, 339, 846 [NASA ADS] [Google Scholar]
- Höfner, S. 2007, in Why Galaxies Care About AGB Stars, ed. F. Kerschbaum, C. Charbonnel, & B. Wing., ASP Conf. Ser., 378, 145 [Google Scholar]
- Höfner, S. 2008, A&A, 491, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Höfner, S., Gautschy-Loidl, R., Aringer, B., & Jørgensen, U. G. 2003, A&A, 399, 589 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jørgensen, U. G. 1997, in Molecules in Astrophysics: Probes and Processes, ed. E. F. van Dishoek, IAU Symp., 178, 441 [Google Scholar]
- Jørgensen, U. G., & Jensen, P. 1993, J. Mol. Spectrosc., 161, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Jørgensen, U. G., Jensen, P., Sørensen, G. O., & Aringer, B. 2001, A&A, 372, 249 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kerschbaum, F., Lebzelter, T., & Lazaro, C. 2001, A&A, 375, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kupka, F. G., Ryabchikova, T. A., Piskunov, N. E., et al. 2000, BaltA, 9, 590 [Google Scholar]
- Lattanzio, J. C., & Wood, P. R. 2004, in Asymptotic Giant Branch Stars, ed. H. J. Habing, & H. Olofsson (New York: Springer), 23 [Google Scholar]
- Lebzelter, T. 1999, A&A, 351, 664 [Google Scholar]
- Lebzelter, T., & Wood, P. R. 2005, A&A, 441, 1117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lebzelter, T., Hinkle, K. H., & Hron, J. 1999, A&A, 341, 224 [NASA ADS] [Google Scholar]
- Lebzelter, T., Hinkle, K. H., & Aringer, B. 2001, A&A, 377, 617 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lebzelter, T., Wood, P. R., Hinkle, K. H., Joyce, R. R., & Fekel, F. C. 2005, A&A, 432, 207 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lebzelter, Th., Posch, Th., Hinkle, K., et al. 2006, ApJ, 653, L145 [NASA ADS] [CrossRef] [Google Scholar]
- Lebzelter, T., Lederer, M. T., Cristallo, S., et al. 2008, A&A, 486, 511 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lederer, M. T., & Aringer, B. 2009, A&A, 494, 403 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Loidl, R., Lancon, A., & Jørgensen, U. G. 2001, A&A, 371, 1065 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lockwood, G. W. 1970, ApJ, 160, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Loup, C., Foreville, T., Omont, A., & Paul, J. F. 1993, A&AS, 99, 271 [NASA ADS] [Google Scholar]
- McSaveney, J. A., Wood, P. R., Scholz, M., et al. 2007, MNRAS, 578, 1089 [NASA ADS] [CrossRef] [Google Scholar]
- Nadzhip, A. E., Tatarnikov, A. M., Shenavrin, V. I., et al. 2001, Astron. Lett., 27, 376 [CrossRef] [Google Scholar]
- Nowotny, W. 2005, The Dynamic Atmospheres of Red Giant Stars. Spectral Synthesis in High Resolution, Ph.D. Thesis, University of Vienna, Austria [Google Scholar]
- Nowotny, W., Aringer, B., Höfner, S., Gautschy-Loidl, R., & Windsteig, W. 2005a, A&A, 437, 273 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nowotny, W., Lebzelter, T., Hron, J., & Höfner, S. 2005b, A&A, 437, 285 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nowotny, W., Höfner, S., & Aringer, B. 2010, A&A, 514, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paladini, C., Aringer, B., Hron, J., et al. 2009, A&A, 501, 1073 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rothman, L. S., Jacquemart, D., Barbe, A., et al. 2005, J. Quant. Spec. Radiat. Transf., 96, 139 [Google Scholar]
- Scholz, M. 1992, A&A, 253, 203 [NASA ADS] [Google Scholar]
- Smith, V. V., Hinkle, K. H., Cunja, K., et al. 2002, ApJ, 124, 3241 [Google Scholar]
- Schutte, W. A., & Tielens, A. G. G. M. 1989, ApJ, 343, 369 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Truong-Bach, Sylvester, R. J., Barlow, M. J., et al. 1999, A&A, 345, 925 [NASA ADS] [Google Scholar]
- Weigelt, G., & Yudin, B. F. 2001, Astron. Rep., 45, 510 [NASA ADS] [CrossRef] [Google Scholar]
- Winters, J. M., Fleischer, A. J., Le Bertre, T., & Sedlmayr, E. 1997, A&A, 326, 305 [NASA ADS] [Google Scholar]
- Winters, J. M., Keady, J. J., Gauger, A., & Sada, P. V. 2000, A&A, 359, 651 [NASA ADS] [Google Scholar]
- Woitke, P. 2006, A&A, 460, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wyckoff, S., & Wehinger, P. 1971, ApJ, 164, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Yorke, H. W. 1988, in Radiation in moving gaseous media, ed. Y. Chmielewski, & T. Lanz, 18th Advanced Course of the Swiss Society of Astrophysics and Astronomy (Saas-Fee Course), 193 [Google Scholar]
Footnotes
- ... Observatories
![[*]](/icons/foot_motif.png)
- Operated by the Association of Universities for Research in Astronomy, Inc. under cooperative agreement with the National Science Foundation.
- ... therein)
![[*]](/icons/foot_motif.png)
- Approximate values found for V3 are: L = 4592
 ,
,
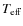 = 3565 K, P = 192 d,
= 3565 K, P = 192 d, 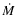 = 10-7-10-6
= 10-7-10-6 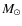 yr-1.
yr-1.
- ... data
![[*]](/icons/foot_motif.png)
- To be presented in a follow-up paper.
- ... transfer
![[*]](/icons/foot_motif.png)
- The radiative transfer is solved at 64 frequency points and based on opacity sampling data of molecular opacities.
- ... here
![[*]](/icons/foot_motif.png)
- For the C/O ratios, the solar value of 0.48 was assumed, dynamic models for other C/O ratios <1 are currently under development.
- ... model PM
![[*]](/icons/foot_motif.png)
- The critical value (i.e. corresponding to
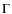 =
=
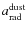 /
/
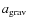 = 1) of
= 1) of
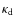 for the chosen set of stellar parameters (Table
1) is 2 cm2 g-1 and the chosen
for the chosen set of stellar parameters (Table
1) is 2 cm2 g-1 and the chosen
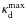 may
appear to be a little high. Still, this is probably not an unrealistic
assumption and comparable to what can be estimated for silicates in the
context of dust-driven winds (see, e.g., Höfner 2008). Test calculations of another dynamic model with a reduced
may
appear to be a little high. Still, this is probably not an unrealistic
assumption and comparable to what can be estimated for silicates in the
context of dust-driven winds (see, e.g., Höfner 2008). Test calculations of another dynamic model with a reduced
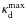 of 3 cm2 g-1
(but higher piston velocity amplitude)
led to a quite similar behaviour of an outflow strongly driven by
radiative pressure. Moreover, not only is the dust absorption relevant
for the wind, but also the effect of pulsation - simulated by the
piston - providing kinetic energy input and leading to enhanced
densities in the cool outer layers. It should indeed be possible to
obtain a stellar wind with
an even smaller
of 3 cm2 g-1
(but higher piston velocity amplitude)
led to a quite similar behaviour of an outflow strongly driven by
radiative pressure. Moreover, not only is the dust absorption relevant
for the wind, but also the effect of pulsation - simulated by the
piston - providing kinetic energy input and leading to enhanced
densities in the cool outer layers. It should indeed be possible to
obtain a stellar wind with
an even smaller
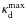 for a higher
for a higher
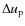 .
.
- ... continuum
![[*]](/icons/foot_motif.png)
- In contrast to the pseudo-continuum approach usually applied
by observational studies, modelling offers the possibility to normalize
the synthetic spectra relative to a computation for which only the
continuous opacity was taken into account (F/
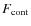 ;
cf. Fig. 1).
;
cf. Fig. 1).
All Tables
Table 1: Characteristics of the dynamic atmospheric models used for the modelling (P = pulsating, PM = pulsating and mass-losing).
Table 2: Effective temperatures and surface gravities (ranges, stepwidths) of the grid of hydrostatic atmospheric models (COMARCS) used.
Table 3: Spectral features investigated.
All Figures
![\begin{figure}
\par\includegraphics[width=12cm,clip]{13730f01.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13730-09/Timg29.png)
|
Figure 1:
Overview of the spectral features studied. Synthetic spectra based on
three different COMARCS models (hydrostatic, i.e., no velocity effects)
with log g = 0.0 are shown, for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13730f02.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13730-09/Timg38.png)
|
Figure 2: (J-K) colour variation versus bolometric phase for the dynamic models with (PM, filled symbols) and without (P, open symbols) wind. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13730f03.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13730-09/Timg39.png)
|
Figure 3:
Relation between
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13730f04.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13730-09/Timg41.png)
|
Figure 4: Equivalent widths in [Å] of the Fe line at 15 536 Å measured from synthetic spectra based on hydrostatic model atmospheres against the corresponding (J-K) values. Same line style coding for various log g values as in Fig. 3. Details of the range in wavelength used around the line centre are listed in Table 3 and illustrated in Fig. 1. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13730f05.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13730-09/Timg42.png)
|
Figure 5: Equivalent widths in [Å] of the OH blend at 15 570 Å measured from synthetic spectra based on hydrostatic model atmospheres against the corresponding (J-K) values. Same line style coding for various log g values as in Fig. 3. The dash-dotted line indicates the relation for C/O = 0.25 (standard value: 0.48). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13730f06.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13730-09/Timg43.png)
|
Figure 6: Same as Fig. 5 for the OH line at 15 576 Å. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13730f07.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13730-09/Timg44.png)
|
Figure 7: Equivalent widths in [Å] of the 12CO 3-0 band head (measured between 15 581 Å and 15 585.7 Å) measured from synthetic spectra based on hydrostatic model atmospheres against the corresponding (J-K) values. See Fig. 1 for the wavelength range covered. Same line style coding for various log g values as in Fig. 3. The dash-dotted line indicates the relation for C/O = 0.25 (standard value: 0.48). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13730f08.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13730-09/Timg45.png)
|
Figure 8: Equivalent widths in [Å] of the 12CO line at 23 137 Å measured from synthetic spectra based on hydrostatic model atmospheres versus the corresponding (J-K) values. Same line style coding for various log g values as in Fig. 3. The dash-dotted line indicates the relation for 12C/13C = 10 (standard value: 30). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13730f09.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13730-09/Timg46.png)
|
Figure 9: Same as Fig. 8 for the 13CO line at 23 660 Å. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13730f10.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13730-09/Timg49.png)
|
Figure 10:
Change in the intensity of the Fe line at 15 536 Å over the calculated pulsation cycles versus (J-K)
for two dynamic models. The model with mass loss (PM) is shown with
solid symbols, while the model without mass loss (P) is marked with
open symbols. Data points are connected to illustrate the path of the
change over the pulsation cycle. Two cycles are plotted for
model PM and four for model P. The small arrow indicates the
direction of the path and starts at the maximum bolometric phase (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13730f11.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13730-09/Timg50.png)
|
Figure 11: Same as Fig. 10 for the Fe line at 15 538 Å. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13730f12.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13730-09/Timg51.png)
|
Figure 12: Same as Fig. 10 for the OH line at 15540 Å. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13730f13.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13730-09/Timg52.png)
|
Figure 13: Same as Fig. 10 for the OH blend at 15570 Å. Compare with Fig. 5. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13730f14.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13730-09/Timg54.png)
|
Figure 14: Same as Fig. 10 for the OH line at 15576 Å. Compare with Fig. 6. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13730f15.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13730-09/Timg55.png)
|
Figure 15: Same as Fig. 10 for the 12CO 3-0 band head. Compare with Fig. 7. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13730f16.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13730-09/Timg56.png)
|
Figure 16: Same as Fig. 10 for the 12CO line at 23137 Å. Compare with Fig. 8. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\hspace*{0.5mm}\includegraphics[width=7.1cm,clip]{13730a17.ep...
...s}\par\hspace*{4mm}\includegraphics[width=7.4cm,clip]{13730c17.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13730-09/Timg57.png)
|
Figure 17:
Comparison of the line profile of 12CO 23 137 in a hydrostatic model (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13730f18.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13730-09/Timg58.png)
|
Figure 18: Same as Fig. 10 for the 13CO line at 23 660 Å. Compare with Fig. 9. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13730f19.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13730-09/Timg61.png)
|
Figure 19:
FTS spectrum of R Cas around the OH lines obtained at JD 2 445 575 (corresponding to
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13730f20.eps}\vspace{3mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13730-09/Timg62.png)
|
Figure 20: Equivalent widths in [Å] of the OH blend at 15 570 Å measured from our time series of FTS spectra of the mira R Cas (triangles) against the corresponding V values taken from the AAVSO light curve. The small arrow indicates the path from the first visual light maximum to minimum. For comparison, we also added the results from model P (open circles) and model PM (filled circles). Note that the model parameters are very different from the parameters of R Cas. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13730f21.eps}\vspace{3mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13730-09/Timg63.png)
|
Figure 21: Equivalent widths in [Å] of the OH blend at 15 570 Å (large dots, left y-axis) and the AAVSO light curve (small dots, right y-axis) for R Cas against time expressed in JD. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13730f22.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13730-09/Timg64.png)
|
Figure 22: Equivalent widths in [Å] of the OH blend at 15570 Å (solid symbols, left y-axis) and (J-K) colour (solid line, right y-axis) for model PM against the bolometric phase. Phase 0 has been assigned to the light maximum. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


