| Issue |
A&A
Volume 517, July 2010
|
|
|---|---|---|
| Article Number | A54 | |
| Number of page(s) | 23 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/200913366 | |
| Published online | 04 August 2010 | |
A deep survey of the AKARI north ecliptic pole field
I. WSRT 20 cm radio survey description, observations and data reduction
G. J. White1,2 - C. Pearson2,3,1 - R. Braun4 - S. Serjeant 1 - H. Matsuhara5 - T. Takagi5 - T. Nakagawa5 - R. Shipman6 - P. Barthel7 - N. Hwang8 - H. M. Lee9 - M. G. Lee9 - M. Im9 - T. Wada5 - S. Oyabu5 - S. Pak9 - M.-Y. Chun9 - H. Hanami10 - T. Goto11,8 - S. Oliver12
1 - Department of Physics and Astronomy, The Open University, Walton
Hall, Milton Keynes, MK7 6AA, UK
2 - Space Science and Technology Department, STFC Rutherford Appleton
Laboratory, Chilton, Didcot, Oxfordshire, OX11 0QX, UK
3 - Institute for Space Imaging Science, University of Lethbridge,
Lethbridge, Alberta, T1K 3M4, Canada
4 - CSIRO Astronomy and Space Science, Australia Telescope National
Facility, CSIRO, Marsfield NSW 2122, Australia
5 - Institute of Space and Astronautical Science, JAXA, Yoshino-dai
3-1-1, Sagamihara, Kanagawa 229-8510, Japan
6 - SRON Netherlands Institute for Space Research, PO Box 800, 9700 AV
Groningen, The Netherlands
7 - Kapteyn Astronomical Institute, University of Groningen, PO Box
800, 9700 AV Groningen, The Netherlands
8 - National Astronomical Observatory of Japan, Osawa, Mitaka, Tokyo
181-8588, Japan
9 - Astronomy Program, Department of Physics and Astronomy, Seoul
National University, Seoul 151-747, Korea
10 - Physics Section, Faculty of Humanities and Social Sciences, Iwate
University, Morioka 020-8550, Japan
11 - Institute for Astronomy, University of Hawaii, 2680 Woodlawn
Drive, Honolulu, HI 96822, USA
12 - Department of Physics & Astronomy, School of Science and
Technology, University of Sussex, Falmer, Brighton BN1 9QH, UK
Received 28 September 2009 / Accepted 26 April 2010
Abstract
Aims. The Westerbork Radio Synthesis Telescope, ![]() ,
has been used to make a deep radio survey of an
,
has been used to make a deep radio survey of an ![]() 1.7 degree2
field coinciding with the AKARI north ecliptic pole deep field. The
observations, data reduction and source count analysis are presented,
along with a description of the overall scientific objectives.
1.7 degree2
field coinciding with the AKARI north ecliptic pole deep field. The
observations, data reduction and source count analysis are presented,
along with a description of the overall scientific objectives.
Methods. The survey consisted of
10 pointings, mosaiced with enough overlap to maintain a
similar sensitivity across the central region that reached as low as
21 ![]() Jy beam-1
at 1.4 GHz.
Jy beam-1
at 1.4 GHz.
Results. A catalogue containing 462 sources detected
with a resolution of 17.0
![]()
![]() 15.5
15.5
![]() is presented. The differential source counts calculated from the
is presented. The differential source counts calculated from the ![]() data
have been compared with those from the shallow
data
have been compared with those from the shallow ![]() survey
of Kollgaard et al. 1994, and show a pronounced excess for
sources fainter than
survey
of Kollgaard et al. 1994, and show a pronounced excess for
sources fainter than ![]() 1 mJy,
consistent with the presence of a population of star forming galaxies
at sub-mJy flux levels.
1 mJy,
consistent with the presence of a population of star forming galaxies
at sub-mJy flux levels.
Conclusions. The AKARI north ecliptic pole deep
field is the focus of a major observing campaign conducted across the
entire spectral region. The combination of these data sets, along with
the deep nature of the radio observations will allow unique studies of
a large range of topics including the redshift evolution of the
luminosity function of radio sources, the clustering environment of
radio galaxies, the nature of obscured radio-loud active galactic
nuclei, and the radio/far-infrared correlation for distant galaxies.
This catalogue provides the basic data set for a future series of paper
dealing with source identifications, morphologies, and the associated
properties of the identified radio sources.
Key words: galaxies: active - radio continuum: galaxies - surveys - catalogs - cosmology: observations
1 Introduction
Deep radio and far-infrared (far-IR) surveys are useful to study the
global properties of extragalactic source populations in the early
Universe; to measure the evolution of AGN's and starburst
galaxies at early epochs; and to understand the cosmic history of star
formation. Recently, the Japanese AKARI infrared satellite has
made deep surveys close to the north and the south ecliptic poles.
These regions have relatively low line of sight extinction
(to the distant Universe) and low hydrogen column densities,
which are important if objects at large distances are to be detectable
at optical and infrared wavelengths. To support the AKARI
north ecliptic pole (![]() ) survey
(Matsuhara et al. 2006;
Wada et al. 2008),
this region has been observed using the Westerbork Radio Synthesis
Telescope (
) survey
(Matsuhara et al. 2006;
Wada et al. 2008),
this region has been observed using the Westerbork Radio Synthesis
Telescope (
![]() ).
).
The observational results of the ![]() survey will be presented in three papers: a) the present paper
presents the basic radio survey, source catalogues, radio source counts
and statistics; b) a second paper will report the
results from cross-correlation between the
survey will be presented in three papers: a) the present paper
presents the basic radio survey, source catalogues, radio source counts
and statistics; b) a second paper will report the
results from cross-correlation between the ![]() radio observations and the infrared source catalogue from the AKARI NEP
survey; and c) the third paper will present optical
identifications from a cross-correlation between the
radio observations and the infrared source catalogue from the AKARI NEP
survey; and c) the third paper will present optical
identifications from a cross-correlation between the ![]() radio
survey and deep optical imaging made using the Canada France Hawaii
3.6 m (CFHT) and SUBARU 8 m telescopes, and will
address the more global objectives of the survey stated above.
radio
survey and deep optical imaging made using the Canada France Hawaii
3.6 m (CFHT) and SUBARU 8 m telescopes, and will
address the more global objectives of the survey stated above.
2 Multi-wavelength observations
The two ecliptic poles are amongst the deepest exposure regions that
have been observed by many infrared satellite missions, and provide a
wealth of data about the distant source populations, for example the
surveys of IRAS (Hacking et al. 1987; Aussel
et al. 2000),
ISO (Stickel et al. 1998;
Aussel et al. 2000),
COBE (Bennett et al. 1996),
and ROSAT (Mullis et al. 2001,
2003). Other
surveys of this region at radio wavelengths have been made with the ![]() (Kollgaard et al. 1994;
Brinkmann et al. 1999,
at 20 and 91 cm); Westerbork: Rengelink
et al. (1997);
Effelsberg 100 m telescope (Loiseau et al. 1988); and in
2.7 GHz surveys by Condon & Broderick (1985, 1986) and Loiseau
et al. (1988);
at optical/IR wavelengths (Gaidos et al. 1993; and K
(Kollgaard et al. 1994;
Brinkmann et al. 1999,
at 20 and 91 cm); Westerbork: Rengelink
et al. (1997);
Effelsberg 100 m telescope (Loiseau et al. 1988); and in
2.7 GHz surveys by Condon & Broderick (1985, 1986) and Loiseau
et al. (1988);
at optical/IR wavelengths (Gaidos et al. 1993; and K
![]() mmel et al. 2000, 2001); and at X-ray
wavelengths using ROSAT by Henry et al. (2001) and Mullis
et al. (2001).
The area around the
mmel et al. 2000, 2001); and at X-ray
wavelengths using ROSAT by Henry et al. (2001) and Mullis
et al. (2001).
The area around the ![]() has a moderate/low level of HI emission
has a moderate/low level of HI emission ![]() 4.3
4.3 ![]() 1020 cm-2 (Elvis
et al. 1994).
This corresponds to a line of sight extinction Av
1020 cm-2 (Elvis
et al. 1994).
This corresponds to a line of sight extinction Av ![]() 0.2-0.5 mag, favouring very deep optical and near-infrared
observations because of the low level of foreground extinction
(Zickgraf et al. 1997).
Optical and infrared surveys provide key information to help to
understand the source populations of the
0.2-0.5 mag, favouring very deep optical and near-infrared
observations because of the low level of foreground extinction
(Zickgraf et al. 1997).
Optical and infrared surveys provide key information to help to
understand the source populations of the ![]() region,
in particular the AKARI mission and its supporting ancillary
programmes have included two deep 2.4-24
region,
in particular the AKARI mission and its supporting ancillary
programmes have included two deep 2.4-24 ![]() m wavelength
surveys at the North Ecliptic Pole (
m wavelength
surveys at the North Ecliptic Pole (![]() ): a) covering
a 0.4 deg2 circular area
(known as
): a) covering
a 0.4 deg2 circular area
(known as ![]() -Deep -
see Matsuhara et al. 2006);
and b) a wide and shallow 2.4-24
-Deep -
see Matsuhara et al. 2006);
and b) a wide and shallow 2.4-24 ![]() m survey
covering a 5.8 deg2 circular
area surrounding the
m survey
covering a 5.8 deg2 circular
area surrounding the ![]() -Deep
field (also known as
-Deep
field (also known as ![]() -Wide -
Lee et al. 2009).
-Wide -
Lee et al. 2009).
Optical, radio, X-ray and infrared surveys provide essential
support to the interpretation of deep extragalactic radio surveys.
A shallow ![]() 20 cm survey of the
20 cm survey of the ![]() region was made by Kollgaard et al. (1994), which covered
an area of 29.3 deg2. The Kollgaard
survey reported 2435 radio sources with flux densities ranging
from 0.3-1000 mJy, observed with a 20
region was made by Kollgaard et al. (1994), which covered
an area of 29.3 deg2. The Kollgaard
survey reported 2435 radio sources with flux densities ranging
from 0.3-1000 mJy, observed with a 20
![]() beam and 1
beam and 1![]() noise
noise
![]() 60
60 ![]() Jy per beam
at the centre of the survey field. A comparison between this
radio survey and the NASA Extragalactic database, and with other
catalogues (including the ROSAT X-ray catalogue), resulted in the
identification of
Jy per beam
at the centre of the survey field. A comparison between this
radio survey and the NASA Extragalactic database, and with other
catalogues (including the ROSAT X-ray catalogue), resulted in the
identification of ![]() 20
20![]() of the sources, with
of the sources, with ![]() 6
6![]() of the sources found to be extended with diameters
of the sources found to be extended with diameters ![]() 30
30
![]() .
A 2.7 GHz survey of the region was made by Condon
& Broderick (1985,
1986).
Between 1 and 150 mJy, the slope of the log N - log S relationship
was 0.68
.
A 2.7 GHz survey of the region was made by Condon
& Broderick (1985,
1986).
Between 1 and 150 mJy, the slope of the log N - log S relationship
was 0.68 ![]() 0.03.
An even larger area of 570 degrees2
was observed at 325 MHz using the
0.03.
An even larger area of 570 degrees2
was observed at 325 MHz using the ![]() telescope by Rengelink et al. (1997) in the
telescope by Rengelink et al. (1997) in the ![]() survey (beam size 54
survey (beam size 54
![]() ), which resulted in the
detection of more than 11 000 sources. The source
populations have already in this region include galaxy clusters (Gioia
et al. 2003,
2004; Hwang
et al. 2007;
Goto et al. 2008),
radio galaxy clusters (Branchesi et al. 2006), stars
(Pretorious et al. 2007;
Micela et al. 2007;
Affer et al. 2008),
X-ray sources (Voges et al. 2001; Henry
et al. 2001,
2006) and
infrared sources (K
), which resulted in the
detection of more than 11 000 sources. The source
populations have already in this region include galaxy clusters (Gioia
et al. 2003,
2004; Hwang
et al. 2007;
Goto et al. 2008),
radio galaxy clusters (Branchesi et al. 2006), stars
(Pretorious et al. 2007;
Micela et al. 2007;
Affer et al. 2008),
X-ray sources (Voges et al. 2001; Henry
et al. 2001,
2006) and
infrared sources (K
![]() mmel et al. 2000).
mmel et al. 2000).
3 WSRT Observations
The radio observations presented in this paper were observed during
2004 with the ![]() operated at 20 cm wavelength. The array included fourteen
25 m telescopes arranged in a 2.7 km east-west
configuration, with signals processed using a digital continuum 2-bit
back end consisting of eight 20 MHz bandwidth sub-bands across
the frequency range 1301-1461 MHz. The
operated at 20 cm wavelength. The array included fourteen
25 m telescopes arranged in a 2.7 km east-west
configuration, with signals processed using a digital continuum 2-bit
back end consisting of eight 20 MHz bandwidth sub-bands across
the frequency range 1301-1461 MHz. The ![]() observations were interleaved with observations of the intensity,
polarisation and phase calibration sources 3C 147
and 3C 286, which past experience suggested should
lead to a flux density calibration accuracy of better than 5
observations were interleaved with observations of the intensity,
polarisation and phase calibration sources 3C 147
and 3C 286, which past experience suggested should
lead to a flux density calibration accuracy of better than 5![]() .
The survey mosaic was made from 10 discrete pointings that
were positioned on an hexagonal grid, with beam spacings at the 70
.
The survey mosaic was made from 10 discrete pointings that
were positioned on an hexagonal grid, with beam spacings at the 70![]() point
of the 36.2
point
of the 36.2![]() primary
beam full width half maximum (FWHM) diameter, each observed as a full
12 h track. This observing strategy was adopted to provide a
relatively uniform noise background of less than
primary
beam full width half maximum (FWHM) diameter, each observed as a full
12 h track. This observing strategy was adopted to provide a
relatively uniform noise background of less than ![]() 10
10![]() over the most sensitive part of the surveyed area (see Prandoni
et al. 2006)
for a full treatment of mosaicing strategies, who show that this
results in mosaiced noise variations of
over the most sensitive part of the surveyed area (see Prandoni
et al. 2006)
for a full treatment of mosaicing strategies, who show that this
results in mosaiced noise variations of ![]() 5
5![]() ),
where a 1
),
where a 1![]() source
detection sensitivity of point sources as low as 21
source
detection sensitivity of point sources as low as 21 ![]() Jy per beam
was achieved. The J2000 coordinate system is used throughout
this paper. Experience at the WSRT suggests that the interpolation and
coplanarity (also known as faceting) processing in the mosaicing step
should not introduce errors in excess of 0.1 arcsec for a
relatively small mosaic of this size.
Jy per beam
was achieved. The J2000 coordinate system is used throughout
this paper. Experience at the WSRT suggests that the interpolation and
coplanarity (also known as faceting) processing in the mosaicing step
should not introduce errors in excess of 0.1 arcsec for a
relatively small mosaic of this size.
![\begin{figure}
\par\includegraphics[angle=90,width=15cm,clip]{13366fg1.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13366-09/Timg25.png)
|
Figure 1:
The central 1 square degree area of the |
| Open with DEXTER | |
The observations were reduced and calibrated using standard tasks in
the ![]() software package. The data sets were uniformly of high quality, with
only a few percent of the visibilities having to be flagged out, mostly
due to low level radio interference. Each pointing was mapped onto a
regular grid with 4
software package. The data sets were uniformly of high quality, with
only a few percent of the visibilities having to be flagged out, mostly
due to low level radio interference. Each pointing was mapped onto a
regular grid with 4
![]() pixels using a
multi-frequency synthesis approach to minimise bandwidth smearing.
Adjacent pointings were co-added to the FWHM point (Condon
et al. 1998;
Huynh et al. 2005).
After a first iteration, model components with a flux density of more
than
pixels using a
multi-frequency synthesis approach to minimise bandwidth smearing.
Adjacent pointings were co-added to the FWHM point (Condon
et al. 1998;
Huynh et al. 2005).
After a first iteration, model components with a flux density of more
than ![]() 1 mJy beam-1
were used for phase and amplitude self-calibration, to correct
for residual phase and amplitude errors. The data were then re-imaged
and cleaned with
1 mJy beam-1
were used for phase and amplitude self-calibration, to correct
for residual phase and amplitude errors. The data were then re-imaged
and cleaned with ![]() 2000 clean
components, at which point the side lobes of most of the strong sources
were found to be below the noise level. There was however a particular
problem toward the central position in the mosaic where the prominent
galactic planetary nebula, the Cat's Eye Nebula (NGC 6543)
lies close to the field centre. Since this is slightly extended at
radio wavelengths, it presented a particular challenge to the data
reduction and cleaning, and ultimately limited the rms noise
level achievable in the immediate vicinity to be several times the
thermal limit. However, the number of pixels affected was very
small (
2000 clean
components, at which point the side lobes of most of the strong sources
were found to be below the noise level. There was however a particular
problem toward the central position in the mosaic where the prominent
galactic planetary nebula, the Cat's Eye Nebula (NGC 6543)
lies close to the field centre. Since this is slightly extended at
radio wavelengths, it presented a particular challenge to the data
reduction and cleaning, and ultimately limited the rms noise
level achievable in the immediate vicinity to be several times the
thermal limit. However, the number of pixels affected was very
small (![]() 0.1
0.1![]() of the total), and a correction for this was made during the
differential source count calculation presented
in Sect. 7.
of the total), and a correction for this was made during the
differential source count calculation presented
in Sect. 7.
After reduction of the individual pointings, the maps were
individually intensity corrected using a model of the primary beam, and
then mosaiced together into a final image using the ![]() task
task ![]() ,
to make a linearly combined mosaic, correcting for the
individual primary beam patterns, and optimizing the signal to noise
ratio. The pixels at the edges of the mosaiced region have higher noise
uncertainties compared to those at the centre of the merged field
because of the primary beam profile, and the mosaicing strategy. The
mosaiced, primary beam corrected image of the high sensitivity region
of the
,
to make a linearly combined mosaic, correcting for the
individual primary beam patterns, and optimizing the signal to noise
ratio. The pixels at the edges of the mosaiced region have higher noise
uncertainties compared to those at the centre of the merged field
because of the primary beam profile, and the mosaicing strategy. The
mosaiced, primary beam corrected image of the high sensitivity region
of the ![]() image is shown in Fig. 1.
image is shown in Fig. 1.
Several automated source extraction and cataloging routines
were tested, including the ![]() task
task ![]() and the
and the ![]() tasks
tasks ![]() and
and ![]() (Sault et al. 1995),
but the latter task was eventually adopted as the extraction task of
choice for reasons that will be discussed in Sect. 4.
A quantitative comparison between
(Sault et al. 1995),
but the latter task was eventually adopted as the extraction task of
choice for reasons that will be discussed in Sect. 4.
A quantitative comparison between ![]() ,
,
![]() ,
,
![]() ,
and
,
and ![]() has already been presented by Hopkins et al. (2002) to which the
reader is referred for a rigorous treatment of noise and error
estimates relevant to this paper.
has already been presented by Hopkins et al. (2002) to which the
reader is referred for a rigorous treatment of noise and error
estimates relevant to this paper.
The final restored beam size in the mosaic after all of the
associated processing steps was 17.0
![]()
![]() 15.5
15.5
![]() at position angle 0 degrees. The most sensitive part of the
survey field had a 1
at position angle 0 degrees. The most sensitive part of the
survey field had a 1![]() rms sensitivity of 21
rms sensitivity of 21 ![]() Jy beam-1 in the
centre of the map, increasing to
Jy beam-1 in the
centre of the map, increasing to ![]() 100
100 ![]() Jy beam-1 toward
the edges of the field, because of the primary beam attenuation
correction. It was therefore not possible to use the same
detection threshold across the whole of the mosaiced region.
Furthermore, flux densities measured toward the image edges were
increasingly affected by uncertainties in the primary beam model, and
consequently the image analysis was restricted to those sources which
lie in regions where the theoretical sensitivity is below 60
Jy beam-1 toward
the edges of the field, because of the primary beam attenuation
correction. It was therefore not possible to use the same
detection threshold across the whole of the mosaiced region.
Furthermore, flux densities measured toward the image edges were
increasingly affected by uncertainties in the primary beam model, and
consequently the image analysis was restricted to those sources which
lie in regions where the theoretical sensitivity is below 60 ![]() Jy beam-1
for noise considerations, and to mitigate other biases such as
bandwidth smearing so as not to affect the source intensities by more
than a few percent. To measure the noise, estimates of the rms
errors were estimated using
Jy beam-1
for noise considerations, and to mitigate other biases such as
bandwidth smearing so as not to affect the source intensities by more
than a few percent. To measure the noise, estimates of the rms
errors were estimated using ![]() ,
and separately using the
,
and separately using the ![]() task
task ![]() .
The detection sensitivity is shown in Fig. 2, with similar
results being obtained in
.
The detection sensitivity is shown in Fig. 2, with similar
results being obtained in ![]() and in
and in ![]() .
.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13366fg2.ps}\vspace*{3mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13366-09/Timg33.png)
|
Figure 2:
The horizontal axis shows the typical 1 |
| Open with DEXTER | |
4 Source catalogue
The ![]() mosaic has a non-uniform and continuously varying noise level, a
complex mosaicing strategy, and locally elevated noise levels around
the few bright sources such as the Cat's Eye Nebula, and it is clear
that source detection using an uniform flux threshold over the whole
primary beam corrected image is not the optimal approach. Source
detection in this case is better determined using locally determined
noise levels - an approach that has already been used in other
studies to improve the efficacy of their source detection catalogues
(e.g. Morganti et al. 2004).
mosaic has a non-uniform and continuously varying noise level, a
complex mosaicing strategy, and locally elevated noise levels around
the few bright sources such as the Cat's Eye Nebula, and it is clear
that source detection using an uniform flux threshold over the whole
primary beam corrected image is not the optimal approach. Source
detection in this case is better determined using locally determined
noise levels - an approach that has already been used in other
studies to improve the efficacy of their source detection catalogues
(e.g. Morganti et al. 2004).
The source catalogue in this paper was built using the ![]() task
task ![]() .
This is a method for identifying source pixels, where the detected
sources are drawn from a distribution of pixels with a robustly known
chance of being falsely drawn from the background (see Hopkins
et al. 1999,
2002; and
Morganti et al. 2004)
for a complete description justifying the adoption of this technique.
.
This is a method for identifying source pixels, where the detected
sources are drawn from a distribution of pixels with a robustly known
chance of being falsely drawn from the background (see Hopkins
et al. 1999,
2002; and
Morganti et al. 2004)
for a complete description justifying the adoption of this technique. ![]() robustly characterises the fraction of expected pixels more rigorously
than from a traditional sigma-clipping criterion - which is
known to suffer limitations at lower signal-to-noise levels. Noise
estimation is implemented in the image plane by dividing the image into
small square regions within which the mean and rms noise level
are estimated by fitting a Gaussian to the pixel histogram in each
region. The image is then normalised by subtracting the mean and
dividing by the rms within each region, resulting in an image where
pixel values are specified in units of the local rms noise
level
robustly characterises the fraction of expected pixels more rigorously
than from a traditional sigma-clipping criterion - which is
known to suffer limitations at lower signal-to-noise levels. Noise
estimation is implemented in the image plane by dividing the image into
small square regions within which the mean and rms noise level
are estimated by fitting a Gaussian to the pixel histogram in each
region. The image is then normalised by subtracting the mean and
dividing by the rms within each region, resulting in an image where
pixel values are specified in units of the local rms noise
level ![]() .
.
![]() uses a
statistical technique, the false discovery rate (FDR), which assigns a
threshold based on an acceptable rate of false detections (Hopkins
et al. 2002).
We followed Hopkins et al. (2002)
by adopting an FDR value of 2
uses a
statistical technique, the false discovery rate (FDR), which assigns a
threshold based on an acceptable rate of false detections (Hopkins
et al. 2002).
We followed Hopkins et al. (2002)
by adopting an FDR value of 2![]() .
Each of the sources identified by
.
Each of the sources identified by ![]() were visually inspected to remove any obvious mis-identifications.
Comparison with independent catalogues derived using the
were visually inspected to remove any obvious mis-identifications.
Comparison with independent catalogues derived using the ![]() task
task ![]() (with a 7
(with a 7![]() clip),
and with one derived using
clip),
and with one derived using ![]() with a locally defined background rms were almost identical with the
with a locally defined background rms were almost identical with the ![]() catalogue.
catalogue.
A sample from the final source catalogue is presented in Table 1.
The positional accuracy listed in the Table 1 is relative to the self-calibrated and
bootstrapped reference frame described in Sect. 3,
after mitigating the various effects mentioned above. Several other
effects that can affect the positions include the mosaicing process
(which we have discussed in Sect. 3; the
signal-to-noise of the detected sources (presented in Table 1; and other observational effects that
bias the positions or sizes of sources, which are discussed in
Sect. 5.
We also present an estimate of source dimensions estimated by
deconvolving the measured sizes from the synthesized beam, reporting
those more than double the synthesised beam size. Although is possible
to model the source sizes in a more exact way (for example
following the approach of Oosterbaan (1978), we only use
the present source size data as a guide to whether the sources are
either extended, or likely to be multi-component sources.
A more detailed discussion of the WSRT source sizes will be
made in a future paper that combines the present data set with higher
resolution observations of the ![]() field with the GMRT Telescope (Sedgwick et al. 2009).
To test the accuracy of the radio reference frame, WSRT
sources with a peak signal to noise ratio
field with the GMRT Telescope (Sedgwick et al. 2009).
To test the accuracy of the radio reference frame, WSRT
sources with a peak signal to noise ratio ![]() 10 which could be identified with compact optical
galaxies from a deep SUBARU image (referenced from HST Guide Star
positions) were found to have positional offsets within
10 which could be identified with compact optical
galaxies from a deep SUBARU image (referenced from HST Guide Star
positions) were found to have positional offsets within ![]() 2
2
![]() of each other, randomly distributed around the nominal radio position.
Further quantitative discussion of the optical identifications, and the
radio-optical frame registration determined from a larger selection of
optically identified sources will be presented in Paper 2,
which is dedicated to the optical/infrared identifications from this
survey (White et al., in preparation).
of each other, randomly distributed around the nominal radio position.
Further quantitative discussion of the optical identifications, and the
radio-optical frame registration determined from a larger selection of
optically identified sources will be presented in Paper 2,
which is dedicated to the optical/infrared identifications from this
survey (White et al., in preparation).
5 Flux accuracy and error estimates
The observations from a radio synthesis array must be corrected for various instrumental effects: a) the primary beam response of the antenna elements; b) time-average smearing due to the finite integration time; c) chromatic aberration resulting from the finite bandwidth (Bridle & Schwab 1989; Cotton 1989); and d) incompleteness at low signal to noise levels. We briefly describe the approach we have taken, below.
5.1 Time-average smearing
The data were observed using integration times of 60 s, which
was estimated to lead to a reduction in the flux of point sources of no
more than ![]() 1
1![]() for a point source 10
for a point source 10![]() from the field centre, and it is believed that this does not play a
dominant effect in determining source sizes.
from the field centre, and it is believed that this does not play a
dominant effect in determining source sizes.
5.2 Chromatic aberration
To correct for bandwidth smearing, the radio analog of optical
chromatic aberration, we inserted 500 artificial point source
models into the uv-data with peak values from 5-50![]() using the
using the ![]() task
task ![]() .
This data were processed in a similar way to the
.
This data were processed in a similar way to the ![]() field,
and
field,
and ![]() was used to recover the source intensities and measure the noise
uncertainties. There was no evidence significant variation of the
source intensities with position in the mosaic, which is similar to the
conclusion of Prandoni et al. (2000b) for a
similar set of
was used to recover the source intensities and measure the noise
uncertainties. There was no evidence significant variation of the
source intensities with position in the mosaic, which is similar to the
conclusion of Prandoni et al. (2000b) for a
similar set of ![]() data.
data.
5.3 Clean bias
Radio surveys can be affected by a ``clean bias'' effect, where a
systematic under estimation of the peak and total source fluxes (Becker
et al. 1995;
White et al. 1997;
Condon et al. 1998)
is a consequence of redistribution of the flux from point sources to
noise peaks in the image. Prandoni et al. (2000a,b) show that
it is possible to mitigate this bias if the ![]() ing process
is stopped well before the maximum residual flux has reached the
theoretical noise level. Following Garrett et al. (2000), we set the
cleaning limit at 5 times the theoretical noise to mitigate
against this effect.
ing process
is stopped well before the maximum residual flux has reached the
theoretical noise level. Following Garrett et al. (2000), we set the
cleaning limit at 5 times the theoretical noise to mitigate
against this effect.
5.4 Resolution bias
Resolution bias is an effect in which the peak flux densities of weak
extended sources fall below the chosen detection limit, yet still have
total integrated flux densities that are above the survey limit. In
other studies, a 3![]() correction
was required for source counts below 1 mJy (Moss
et al. 2007;
Garn et al. 2008),
although no resolution correction was applied to brighter sources. This
effect reduces the number of faint sources in differential source
counts (see for example Hopkins et al. 2002), and we do not
consider that it has a significant effect on our data reduction
methodology.
correction
was required for source counts below 1 mJy (Moss
et al. 2007;
Garn et al. 2008),
although no resolution correction was applied to brighter sources. This
effect reduces the number of faint sources in differential source
counts (see for example Hopkins et al. 2002), and we do not
consider that it has a significant effect on our data reduction
methodology.
5.5 Eddington bias
Since the source counts rise strongly with decreasing flux density,
more sources will have their true fluxes ``boosted'' by the effect of
noise, than those that are ``reduced'' at higher flux densities
(see discussion in Coppin et al. 2006).
To examine the effect of this, a population of
``test'' point sources were added into a single field, uncorrected for
the primary beam response using the ![]() task ``
task ``
![]() '', and processed and
extracted in the same way as the un-mosaiced survey data, with the
difference between the detected counts, and those inputs, providing an
estimate of the net amount of up-scattering. The effect of this was
only significant in the lowest flux bin, and led to an overestimate of
the source count by 16
'', and processed and
extracted in the same way as the un-mosaiced survey data, with the
difference between the detected counts, and those inputs, providing an
estimate of the net amount of up-scattering. The effect of this was
only significant in the lowest flux bin, and led to an overestimate of
the source count by 16![]() (the boundaries of the lowest flux bin were
(the boundaries of the lowest flux bin were ![]() 5
5![]() above the formal survey limit. This value should be compared with the
value estimated by Moss et al. (2007) of 21
above the formal survey limit. This value should be compared with the
value estimated by Moss et al. (2007) of 21![]() ,
which goes slightly closer to their formal survey limit. Consequently
in later analysis the counts in the lowest flux bin (110-125
,
which goes slightly closer to their formal survey limit. Consequently
in later analysis the counts in the lowest flux bin (110-125 ![]() Jy were
``de-boosted'' by 16
Jy were
``de-boosted'' by 16![]() .
This correction has a negligible effect for fluxes above this limit,
and it is safe to ignore it.
.
This correction has a negligible effect for fluxes above this limit,
and it is safe to ignore it.
5.6 Component extraction
In the terminology of this paper a radio component is described as a region of radio emission represented by a Gaussian shaped object in the map. Close radio doubles are represented by two Gaussians and are deemed to consist of two components, which make up a single source. A clear case of a very extended radio source is shown in Fig. 3, and a selection of other sources with multiple components is shown in Fig. 4.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13366fg3.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13366-09/Timg38.png)
|
Figure 3:
The extended radio source centred on the |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=90,width=15.7cm,clip]{13366fg4.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13366-09/Timg39.png)
|
Figure 4: Regions showing complex or extended structure. The vertical scale is Declination. The contours are at 0.0001, 0.0003, 0.0005, 0.001, 0.003, 0.006, 0.012, 0.024, 0.048 and 0.096 Jy beam-1 respectively. |
| Open with DEXTER | |
5.7 Resolved sources
Although it may seem relatively straightforward to calculate the
density of sources as a function of the flux density, the distribution
of angular sizes as a function of the flux density may also bias the
results. It was assumed that the median sizes below 1 mJy
remain approximately constant as a function of the flux density with
those at higher flux levels. Fomalont et al. (2006) find that
8 ![]() 4
4![]() of the
of the ![]() Jy sources
have sizes greater than 4
Jy sources
have sizes greater than 4
![]() .
For low signal-to-noise ratio detections, Gaussian fitting routines may
be significantly affected by noise spikes, leading to errors in the
estimated widths and flux densities of the sources (Moss
et al. 2007).
This is one of the reasons for adopting the
.
For low signal-to-noise ratio detections, Gaussian fitting routines may
be significantly affected by noise spikes, leading to errors in the
estimated widths and flux densities of the sources (Moss
et al. 2007).
This is one of the reasons for adopting the ![]() source extraction methodology in this paper. The ratio
source extraction methodology in this paper. The ratio ![]() /
/
![]() = (
= (![]()
![]()
![]()
![]() )/(
)/(
![]()
![]() )
where
)
where ![]() and
and ![]() are the major and minor axes of the detected source and
are the major and minor axes of the detected source and ![]() and
and ![]() are the major and minor axes of the restoring beam. The flux density
ratio may be used to discriminate between unresolved sources and those
which are much larger than the beam (see Prandoni et al. 2006).
In Fig. 5,
the ratio of the flux densities to the signal-to-noise ratio (
are the major and minor axes of the restoring beam. The flux density
ratio may be used to discriminate between unresolved sources and those
which are much larger than the beam (see Prandoni et al. 2006).
In Fig. 5,
the ratio of the flux densities to the signal-to-noise ratio (
![]() /
/![]()
![]() )
is plotted for all sources above a 6
)
is plotted for all sources above a 6![]() local threshold. The biases introduced by using different thresholds
have been modelled by Prandoni et al. (2000a,b), Owen
et al. (2008) and Fomalont et al. (2006), which suggest
that the biases are most prevalent below an
local threshold. The biases introduced by using different thresholds
have been modelled by Prandoni et al. (2000a,b), Owen
et al. (2008) and Fomalont et al. (2006), which suggest
that the biases are most prevalent below an ![]() 5-6
5-6![]() (sigma-clip) threshold. To identify sources for which
(sigma-clip) threshold. To identify sources for which ![]()
![]() /
/![]()
![]() < 1,
a functional form of the curve f(x) =
1.0
< 1,
a functional form of the curve f(x) =
1.0 ![]() 3.22/x was plotted in Fig. 5 to define the
point where 90
3.22/x was plotted in Fig. 5 to define the
point where 90![]() of the
of the ![]() 6
6![]() detections with
detections with ![]() /
/
![]() < 1
lie above the curve (this is similar to the ratio adopted by
Prandoni et al. 2000a,b).
Reflecting this curve about
< 1
lie above the curve (this is similar to the ratio adopted by
Prandoni et al. 2000a,b).
Reflecting this curve about ![]() /
/
![]() = 1 shows
those sources which lie between the two curves, and which are
considered to be unresolved.
= 1 shows
those sources which lie between the two curves, and which are
considered to be unresolved.
In Fig. 5
the flux ratio is shown as a function of the signal-to-noise for all
the sources (or source components) in the ![]() catalogue.
catalogue.
The flux density ratio shows a skewed distribution, where the
tail toward high flux ratios is due to the presence of extended
sources. Values for ![]() result from the effect of noise in affecting the source sizes
(see Sect. 4). To establish a criterion for
extension, such noise errors have to be taken into account. The lower
envelope of the flux ratio distribution (the curve containing
90
result from the effect of noise in affecting the source sizes
(see Sect. 4). To establish a criterion for
extension, such noise errors have to be taken into account. The lower
envelope of the flux ratio distribution (the curve containing
90![]() of the sources) was determined, and mirrored it on its side (upper
envelope in Fig. 5),
so that unresolved sources should lie below the upper envelope. The
upper envelope can be characterised by the equation from Huynh
et al. (2005)
that was found to characterise the 90
of the sources) was determined, and mirrored it on its side (upper
envelope in Fig. 5),
so that unresolved sources should lie below the upper envelope. The
upper envelope can be characterised by the equation from Huynh
et al. (2005)
that was found to characterise the 90![]() envelope of sources where
envelope of sources where ![]()
![]()
![]() ,
and a 5
,
and a 5![]() cut off to the peak fluxes was adopted:
cut off to the peak fluxes was adopted:
![\begin{displaymath}%
\frac{{S_{\rm total} }}{{S_{\rm peak} }} = 1 + \left[ {\fra...
...S_{\rm peak} /\sigma _{\rm fit} } \right)^{3} }}} \right]\cdot
\end{displaymath}](/articles/aa/full_html/2010/09/aa13366-09/img53.png)
|
(1) |
It is worth noting that the envelope does not converge to unity at large signal-to-noise values. This is due to the radial smearing effect which systematically reduces the ``peak'' fluxes, leading to larger
Radio sources are often made up of multiple components, as
seen earlier in Fig. 4. The
source counts need to be corrected for this, so that the fluxes of
physically related components are summed together, rather than being
treated as separate sources. Magliocchetti et al. (1998) have proposed
criteria to identify the double and compact source populations,
by plotting the separation of the nearest neighbour of a
source against the summed flux of the two sources, and selecting for
objects where the ratio of their fluxes, f1
and f2 is in the
range 0.25 ![]() f1 / f2
f1 / f2 ![]() 4.
In Fig. 6
the sum of the fluxes of nearest neighbours are plotted against their
separation.
4.
In Fig. 6
the sum of the fluxes of nearest neighbours are plotted against their
separation.
The dashed line marks the boundary satisfying the separation
criterion defined by Huynh et al. (2005):
![\begin{displaymath}%
\theta = 100\left[ {\frac{{S_{\rm total} ({\rm mJy}) }}{{10}}} \right]^{0.5}
\end{displaymath}](/articles/aa/full_html/2010/09/aa13366-09/img55.png)
|
(2) |
where
5.8 Positional accuracy
Noise fluctuations limit the rms positional uncertainty in each of the
fitted sky coordinates (![]() RA or
RA or ![]() Dec) of a
faint point source with an rms brightness fluctuation
Dec) of a
faint point source with an rms brightness fluctuation
![]() and FWHM resolution
and FWHM resolution
![]() to (following Rengelink et al. 1997):
to (following Rengelink et al. 1997):
The positions listed in the Table 1 are those estimated from the external calibration sources and are internally consistent within Table 1. Further discussion of the positional alignment to the optical and infrared reference planes will be given in the second paper of this series.
5.9 Noise flux accuracy
The accuracy of flux estimates in radio interferometer data has been
discussed by a number of authors, for example Rengelink
et al. (1997).
The accuracy of flux recovery with specific reference to the ![]() technique adopted for this paper has been presented in Hopkins
et al. (2003),
and will not be repeated in detail here. However, for completeness, we
will repeat the Hopkins et al. (2003) equations
using the terminology in the present paper, which reduce to those
presented by Rengelink et al. (1997).
For point sources, Hopkins et al. (2003) show that the
total relative uncertainty in the integrated flux density is
given by:
technique adopted for this paper has been presented in Hopkins
et al. (2003),
and will not be repeated in detail here. However, for completeness, we
will repeat the Hopkins et al. (2003) equations
using the terminology in the present paper, which reduce to those
presented by Rengelink et al. (1997).
For point sources, Hopkins et al. (2003) show that the
total relative uncertainty in the integrated flux density is
given by:
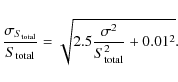
|
(4) |
The reader is referred to the papers listed above for more detailed analysis of this, where the treatments of both papers reduce to similar relationships for both extended and for point sources.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13366fg5.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13366-09/Timg61.png)
|
Figure 5:
Ratio of the integrated flux |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13366fg6.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13366-09/Timg62.png)
|
Figure 6:
This figure shows the sum of the flux densities of the nearest
neighbours between sources from the detection catalogue. Following
Magliocchetti et al. (1998)
near neighbour pairs to the left of the line are considered as possible
double sources. The double sources can be further constrained by adding
the second constraint that the fluxes of the two components f1
and f2 should be in
the range 0.25 |
| Open with DEXTER | |
5.10 Comparison with the VLA flux density scaling
We initially compared the WSRT radio fluxes with those reported in the
Kollgaard et al. (1994)
paper. This showed that the ![]() fluxes below
fluxes below ![]() 10 mJy
appear to be too bright, initially giving some concern about the
calibration efficacy of the
10 mJy
appear to be too bright, initially giving some concern about the
calibration efficacy of the ![]() data compared to Kollgaard's survey. However, from comparison between
the integrated fluxes of the Kollgaard et al. (1994) survey and the
NVSS catalogue, it appears that the former study may
systematically overestimate the radio fluxes below about
10 mJy, as shown in Fig. 7.
data compared to Kollgaard's survey. However, from comparison between
the integrated fluxes of the Kollgaard et al. (1994) survey and the
NVSS catalogue, it appears that the former study may
systematically overestimate the radio fluxes below about
10 mJy, as shown in Fig. 7.
It therefore appears that the Kollgaard et al. (1994) fluxes may be
unreliable in the flux range appropriate to the ![]() survey, and that we should instead rely on NVSS fluxes to assess the
efficacy of the present data.
survey, and that we should instead rely on NVSS fluxes to assess the
efficacy of the present data.
To consider whether the differential source plots are affected
by an incorrectly applied completeness correction, or are truly
representative of astrophysical the source populations, such as an
under-density of sources, or showing evidence for cosmic
variance or clustering, we carried out a further series of tests.
Firstly, a comparison was made between the fluxes of sources
in common between the ![]() and
and ![]() observations is shown in Fig. 8.
observations is shown in Fig. 8.
To check the efficacy of the ![]()
![]() data, the
flux densities of components measured in the
data, the
flux densities of components measured in the ![]() survey were compared with those reported by Kollgaard et al. (1994),
as shown in Fig. 8.
survey were compared with those reported by Kollgaard et al. (1994),
as shown in Fig. 8.
The two plots show reasonably good agreement between the two
independent data sets, with the ![]() peak fluxes of Kollgaard et al. (1994) systematically
lying a little above the
peak fluxes of Kollgaard et al. (1994) systematically
lying a little above the ![]() peak fluxes above
peak fluxes above ![]() 50 mJy,
but being consistent with the
50 mJy,
but being consistent with the ![]() fluxes below that. For the integrated fluxes, there is some evidence
that the
fluxes below that. For the integrated fluxes, there is some evidence
that the ![]() fluxes are systematically higher than the
fluxes are systematically higher than the ![]() fluxes by
fluxes by ![]() 2-30
2-30![]() at fluxes below 20 mJy, although consistent at higher flux
densities. It is difficult to directly compare these, because
of the different observational characteristics, and data reduction
steps, and there is no a priori reason to favour one
calibration over another. However, this test does show that at least at
the level of a few tens of percent, and down to
at fluxes below 20 mJy, although consistent at higher flux
densities. It is difficult to directly compare these, because
of the different observational characteristics, and data reduction
steps, and there is no a priori reason to favour one
calibration over another. However, this test does show that at least at
the level of a few tens of percent, and down to ![]() 1 mJy,
the two data sets are broadly consistent with each other.
It is however difficult to know whether or not this holds at
lower flux densities, because of the lack of the lower sensitivity of
the
1 mJy,
the two data sets are broadly consistent with each other.
It is however difficult to know whether or not this holds at
lower flux densities, because of the lack of the lower sensitivity of
the ![]() survey, or due to the slightly elliptical beams noted for some
parts of the
survey, or due to the slightly elliptical beams noted for some
parts of the ![]() field by Kollgaard et al. (1994),
which makes direct comparison difficult, differing
field by Kollgaard et al. (1994),
which makes direct comparison difficult, differing ![]() coverage,
or due to intrinsic radio source variability. It is also
notable that Becker et al. (1995)
report that one effect of
coverage,
or due to intrinsic radio source variability. It is also
notable that Becker et al. (1995)
report that one effect of ![]() bias on
bias on ![]() observations is to reduce the flux. On the basis of this,
there appears to be no reason to suspect that the measured
observations is to reduce the flux. On the basis of this,
there appears to be no reason to suspect that the measured ![]() integrated fluxes lead to the apparent deficit of sub-mJy sources
suggested in Fig. 11.
integrated fluxes lead to the apparent deficit of sub-mJy sources
suggested in Fig. 11.
A search was then made to count how many sources were detected
by the Kollgaard et al. (1994)
![]() survey to a
given flux level in comparison to those detected in the
survey to a
given flux level in comparison to those detected in the ![]() survey. Restricting this analysis to the central 0.5 degree
diameter area of the
survey. Restricting this analysis to the central 0.5 degree
diameter area of the ![]() mosaic (where the rms peak flux is below
mosaic (where the rms peak flux is below ![]() 30
30 ![]() Jy per beam,
the
Jy per beam,
the ![]() observations recover 307 sources with fluxes above
2 mJy, whereas the
observations recover 307 sources with fluxes above
2 mJy, whereas the ![]() catalogue contains 53 sources, and an unpublished
610 MHz GMRT image (Sirothia et al.,
in prep.) recovers about 312 sources (after making
approximate flux scaling corrections assuming that the flux to first
order follows a
catalogue contains 53 sources, and an unpublished
610 MHz GMRT image (Sirothia et al.,
in prep.) recovers about 312 sources (after making
approximate flux scaling corrections assuming that the flux to first
order follows a
![]() relationship).
It therefore appears that there are some unexplained
discrepancies between the
relationship).
It therefore appears that there are some unexplained
discrepancies between the ![]() survey of Kollgaard and the
survey of Kollgaard and the ![]() results, although in term of raw source numbers, the
results, although in term of raw source numbers, the ![]() and GMRT data appear to be more consistent, particularly bearing in
mind the approximations assumed about spectral indices. Despite these
apparent differences, the check carried out and presented here
provide no evidence to support the presence of a systematic bias to the
and GMRT data appear to be more consistent, particularly bearing in
mind the approximations assumed about spectral indices. Despite these
apparent differences, the check carried out and presented here
provide no evidence to support the presence of a systematic bias to the
![]() differential
number counts presented in Figs. 10
and 11,
and in the absence of further reasons to be concerned about the
differential
number counts presented in Figs. 10
and 11,
and in the absence of further reasons to be concerned about the ![]() counts, it will be assumed that the differences shown in
Fig. 11
are most likely due to cosmic variance.
counts, it will be assumed that the differences shown in
Fig. 11
are most likely due to cosmic variance.
Assuming that faint radio sources have the same correlation
length as mJy sources from the ![]() and
and ![]() surveys (r
surveys (r ![]() 5 Mpc;
Overzier et al. 2003),
and that they sample the redshift interval
5 Mpc;
Overzier et al. 2003),
and that they sample the redshift interval ![]() = 1
= 1 ![]() 0.5,
the rms uncertainty to the differential source counts in a
given flux bin from cosmic variance is estimated to be
0.5,
the rms uncertainty to the differential source counts in a
given flux bin from cosmic variance is estimated to be ![]() 9 per cent
(Peacock & Dodds 1994;
Eq. (3) of Somerville et al. 2004; Simpson
et al. 2006),
which is comparable with the error spread seen at the lower flux
levels.
9 per cent
(Peacock & Dodds 1994;
Eq. (3) of Somerville et al. 2004; Simpson
et al. 2006),
which is comparable with the error spread seen at the lower flux
levels.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13366fg7.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13366-09/Timg66.png)
|
Figure 7:
Cross correlation of the integrated fluxes from the Kollgaard
et al. (1994)
and the NVSS surveys, with 2 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13366fg8.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13366-09/Timg68.png)
|
Figure 8:
Comparison of the integrated fluxes of isolated radio sources in common
between the |
| Open with DEXTER | |
5.11 Summary of flux density corrections for systematic effects
As discussed in the previous subsections, various systematic effects
have been taken into account to estimate the ![]() flux densities, including the clean bias and the bandwidth smearing
effects. The corrected flux densities reported in Table
flux densities, including the clean bias and the bandwidth smearing
effects. The corrected flux densities reported in Table ![]() , (
, (
![]() )
have been corrected for the various effects described as follows
(following Prandoni et al. 2000b):
)
have been corrected for the various effects described as follows
(following Prandoni et al. 2000b):
where
The clean bias correction is taken into account by the term in
the square brackets. As discussed by Prandoni et al. (2000b) the
importance of the clean bias effect varies across mosaiced images
depending on the average number of clean components. For the present
data the average number of clean components was 2121, and on
the basis of the simulations reported in Sect. 5.3 we
adopt (a,b) =
(0.07, 0.82). Applying Eq. (5) correctly
leads to a good correlation between the ![]() and
and ![]() fluxes shown in Fig. 8
(where the
fluxes shown in Fig. 8
(where the ![]() fluxes were corrected using these parameters).
fluxes were corrected using these parameters).
6 Comparison with other observations
Cross identification with optical data obtained from deep
3.6 m ![]() MEGACAM imaging and IR images from the AKARI survey will be included in
the next of this series of papers on the NEP Deep Field.
An indicative overlay between the radio and
MEGACAM imaging and IR images from the AKARI survey will be included in
the next of this series of papers on the NEP Deep Field.
An indicative overlay between the radio and ![]() -band images
for the spiral galaxy CGCG 322-021 is shown in Fig. 9. Under seeing
conditions of 0.87
-band images
for the spiral galaxy CGCG 322-021 is shown in Fig. 9. Under seeing
conditions of 0.87
![]() the limiting magnitude in this filter was
the limiting magnitude in this filter was ![]() 23.5.
Further details of the data collection and reduction has been given by
Hwang et al. (2007).
23.5.
Further details of the data collection and reduction has been given by
Hwang et al. (2007).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13366fg9.eps}\vspace*{3mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13366-09/Timg76.png)
|
Figure 9:
Overlay between the |
| Open with DEXTER | |
7 Differential counts
In Fig. 10
the differential radio source counts are shown from the ![]() field, normalised to a static Euclidean Universe (dN/dS S2.5 (sr-1 mJy1.5)).
These source counts are broadly consistent with previous results at
1.4 GHz (e.g. the compilation of Windhorst
et al. 1993;
the PHOENIX Deep Survey, Hopkins et al. 2003; and the
shallow
field, normalised to a static Euclidean Universe (dN/dS S2.5 (sr-1 mJy1.5)).
These source counts are broadly consistent with previous results at
1.4 GHz (e.g. the compilation of Windhorst
et al. 1993;
the PHOENIX Deep Survey, Hopkins et al. 2003; and the
shallow ![]() survey of Kollgaard et al. 1994).
survey of Kollgaard et al. 1994).
The data from Fig. 10 are
given in Table 1,
where the flux bins and mean flux for each of the bin centres are
listed in Cols. (1 and 2),
the number of sources corrected for clean and resolution bias
a discussed in Appendix A are shown in Col. (3), and
the number of sources corrected for the area coverage and double
sources in Col. 4 (note that because of these correction
factors, ![]() may be less than N0),
and in Col. (5) we show the differential source counts and the
error. The relationship for calculating the numbers in Col. 5
is the same as that presented by Kollgaard et al. (1994).
may be less than N0),
and in Col. (5) we show the differential source counts and the
error. The relationship for calculating the numbers in Col. 5
is the same as that presented by Kollgaard et al. (1994).
To model the observed source counts a two component model was
used that was made of a classical bright radio loud population and a
fainter star-forming population. It is well established that
classical bright radio galaxies require strong evolution in order to
fit the observed source counts at radio wavelengths (Longair 1966; Rowan-Robinson
1970). The
source counts above 10 mJy are dominated by giant radio
galaxies and QSOs (powered by accretion onto black holes, commonly
joined together in the literature under the generic term AGN). Radio
loud sources dominate the source counts down to levels of ![]() 1 mJy,
however, at the sub-mJy level the normalised source counts
flatten as a new population of faint radio sources emerge (Windhorst
et al. 1985).
The dominance of starburst galaxies in the sub-mJy population is
already well established (Gruppioni et al. 2008), where the
number of blue galaxies with star-forming spectral signatures is seen
to increase strongly. Rowan-Robinson et al. (1993), Hopkins
et al. (1998),
and others have concluded that the source counts at these faintest
levels require two populations, AGNs and starburst galaxies. This
latter population can best be modelled as a dusty star-forming
population, under the assumption that they are the higher redshift
analogues of the IRAS star-forming population (Rowan-Robinson
et al. 1993;
Pearson & Rowan-Robinson 1996).
In this scenario, the radio emission originates from the
non-thermal synchrotron emission from relativistic electrons
accelerated by supernovae remnants in the host galaxies.
1 mJy,
however, at the sub-mJy level the normalised source counts
flatten as a new population of faint radio sources emerge (Windhorst
et al. 1985).
The dominance of starburst galaxies in the sub-mJy population is
already well established (Gruppioni et al. 2008), where the
number of blue galaxies with star-forming spectral signatures is seen
to increase strongly. Rowan-Robinson et al. (1993), Hopkins
et al. (1998),
and others have concluded that the source counts at these faintest
levels require two populations, AGNs and starburst galaxies. This
latter population can best be modelled as a dusty star-forming
population, under the assumption that they are the higher redshift
analogues of the IRAS star-forming population (Rowan-Robinson
et al. 1993;
Pearson & Rowan-Robinson 1996).
In this scenario, the radio emission originates from the
non-thermal synchrotron emission from relativistic electrons
accelerated by supernovae remnants in the host galaxies.
To represent the radio loud population the luminosity function
of Dunlop & Peacock (1990)
was used to model the local space density with an assumption that the
population evolves in luminosity with increasing redshift. The assumed
luminosity evolution then follows a power law with redshift
of
(1+z)3.1,
broadly consistent with both optically and X-ray selected quasars
(Boyle et al. 1987).
The spectrum of the radio loud quasar population was modelled from
Elvis et al. (1994),
assuming a steep radio spectrum source of (
![]() ,
,
![]() ).
).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13366fg10.ps}
\vspace*{3mm}\end{figure}](/articles/aa/full_html/2010/09/aa13366-09/Timg80.png)
|
Figure 10:
Differential counts determined from the AKARI |
| Open with DEXTER | |
Table 1: 20 cm differential source counts for the WSRT-AKARI-NEP survey.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13366fg11.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13366-09/Timg82.png)
|
Figure 11: A compilation of the differential source counts of a number of deep 20 cm radio surveys taken from: SWIRE Owen & Morrison (2008); COSMOS Bondi et al. (2008); SSA13 Fomalont et al. (2006); SXDF Simpson et al. (2006); HDF-N, LOCKMAN and ELAIS N2 Biggs & Ivison (2006), HDF-S Huynh et al. (2005). The solid curve is the best fit to the present data taken as described in Fig. 10. There are however differences in the instrumental and systematic corrections that have been made for the different survey results shown here (see detailed discussion by Prandoni et al. 2000b), that make quantitative comparison at the faintest flux levels somewhat uncertain. |
| Open with DEXTER | |
To model the faint sub-mJy population the IRAS
60 ![]() m
luminosity function of Saunders et al. (2000) was used as a
starting point, with the parameters for the star-forming population,
segregated by warmer 100
m
luminosity function of Saunders et al. (2000) was used as a
starting point, with the parameters for the star-forming population,
segregated by warmer 100 ![]() m/60
m/60 ![]() m IRAS colour, given in
Pearson (2005,
in prep). To convert the infrared luminosity function to radio
wavelengths, the well known correlation between the
60
m IRAS colour, given in
Pearson (2005,
in prep). To convert the infrared luminosity function to radio
wavelengths, the well known correlation between the
60 ![]() m
far-IR and radio flux emission of
m
far-IR and radio flux emission of ![]() (Helou et al. 1985;
Yun et al. 2001;
Appleton et al. 2004;
White et al. 2009) was assumed. To model the
star-forming population the spectral template of the archetypical
starburst galaxy of M 82 from the models of Efstathiou
et al. (2000)
was adopted. The radio and far-infrared fluxes are correlated due to
the presence of hot OB stars in giant molecular clouds that
heat the surrounding dust producing the infrared emission. These stars
subsequently end their lives as supernovae with the radio emission
powered by the synchrotron emission from their remnants. The radio
spectrum is characterised by a power law of (
(Helou et al. 1985;
Yun et al. 2001;
Appleton et al. 2004;
White et al. 2009) was assumed. To model the
star-forming population the spectral template of the archetypical
starburst galaxy of M 82 from the models of Efstathiou
et al. (2000)
was adopted. The radio and far-infrared fluxes are correlated due to
the presence of hot OB stars in giant molecular clouds that
heat the surrounding dust producing the infrared emission. These stars
subsequently end their lives as supernovae with the radio emission
powered by the synchrotron emission from their remnants. The radio
spectrum is characterised by a power law of (
![]() ,
,
![]() ).
).
It was assumed that the star-forming population evolves in
luminosity as a power law ![]() .
This infrared representation of the star-forming population was
preferred over using the radio luminosity function directly, since it
creates a phenomenological link between the radio emission and the
infrared which is responsible for the bulk of the emission in the
star-forming population. Note that Huynh et al. (2005) used the radio
luminosity function of Condon et al. (2002) and derived a
best fitting evolution parameterisation
.
This infrared representation of the star-forming population was
preferred over using the radio luminosity function directly, since it
creates a phenomenological link between the radio emission and the
infrared which is responsible for the bulk of the emission in the
star-forming population. Note that Huynh et al. (2005) used the radio
luminosity function of Condon et al. (2002) and derived a
best fitting evolution parameterisation ![]() ,
slightly lower than the work presented here although the values are
broadly consistent and differences can be due to the assumed SED and
luminosity function. Hopkins (2004)
and Hopkins et al. (1998)
used radio and infrared luminosity functions respectively obtaining
evolution in the sub-mJy population
,
slightly lower than the work presented here although the values are
broadly consistent and differences can be due to the assumed SED and
luminosity function. Hopkins (2004)
and Hopkins et al. (1998)
used radio and infrared luminosity functions respectively obtaining
evolution in the sub-mJy population ![]() and
and ![]() .
It does however appear that the counts measured in this study
lie at the lower end of the emerging picture on excess sub-mJy radio
counts, as shown in Fig. 11.
.
It does however appear that the counts measured in this study
lie at the lower end of the emerging picture on excess sub-mJy radio
counts, as shown in Fig. 11.
8 Conclusions
A deep radio survey has been made of an ![]() 1.7 square degree
area around the North Ecliptic Pole field using the
1.7 square degree
area around the North Ecliptic Pole field using the ![]() at 20 cm wavelength. The maximum sensitivity of the survey was
21
at 20 cm wavelength. The maximum sensitivity of the survey was
21 ![]() Jy
beam-1, with a synthesised beam of 17.0
Jy
beam-1, with a synthesised beam of 17.0 ![]() 15.5
15.5
![]() .
The analysis methodology was carefully chosen to mitigate the various
effects that can affect the efficacy of radio synthesis array
observations, resulting in a final catalogue of 462 radio
emitting sources, with the faintest integrated fluxes at about the
100
.
The analysis methodology was carefully chosen to mitigate the various
effects that can affect the efficacy of radio synthesis array
observations, resulting in a final catalogue of 462 radio
emitting sources, with the faintest integrated fluxes at about the
100 ![]() Jy
level. The differential source counts calculated from the
Jy
level. The differential source counts calculated from the ![]() data show a pronounced excess for sources fainter than
data show a pronounced excess for sources fainter than ![]() 1 mJy,
consistent with a population of faint star forming galaxies. Comparison
between the Kollgaard et al. (1994) survey and the
NVSS catalogue shows a systematic difference in this flux range,
suggesting that one or the other may suffer from a slight
mis-calibration. The present
1 mJy,
consistent with a population of faint star forming galaxies. Comparison
between the Kollgaard et al. (1994) survey and the
NVSS catalogue shows a systematic difference in this flux range,
suggesting that one or the other may suffer from a slight
mis-calibration. The present ![]() catalogue of radio sources will form the basis for two further papers
reporting cross correlation against extant AKARI and deep optical
imaging. A further paper reporting the radio spectral indices
of the sources utilising
catalogue of radio sources will form the basis for two further papers
reporting cross correlation against extant AKARI and deep optical
imaging. A further paper reporting the radio spectral indices
of the sources utilising ![]() data will be reported elsewhere.
data will be reported elsewhere.
This work is based on observations with AKARI, aproject with the participation of ESA. We thank Andrew Hopkins for helping us to understand the operation of
, Niruj Mohan for discussions on source detection algorithms, and Sandeep Sirothia for discussions about the GMRT 610 MHz NEP survey. We also express our thanks to The Netherlands Institute for Radio Astronomy,
, for the substantial allocation of observing time; the staff of the Westerbork Observatory for technical support; and the UK Science and Technology Facilities Council,
and its forerunner,
, for manpower and travel support. The UK-Japan AKARI Consortium has also received funding awards from the Sasakawa Foundation, The British Council, and the DAIWA Foundation, which facilitated travel and exchange activities, and for which we are very grateful. T.G. acknowledges financial support from the Japan Society for the Promotion of Science (JSPS) through JSPS Research Fellowships for Young Scientists. M.I. was supported by the Korea Science and Engineering Foundation (KOSEF) grant No. 2009-0063616, funded by the Korea government (MEST). HML was supported by National Research Foundation through grant No. 2006-341-C00018.
References
- Affer, L., Micela, G., & Morel, T. 2008, A&A, 483, 801
- Appleton, P. N., Fadda, D. T., Marleau, F. R., et al. 2004, ApJS, 154, 147
- Aussel, H., Coia, D., Mazzei, P., et al. 2000, A&AS, 141, 257
- Becker, R. H., White, R. L., & Helfand, D. J. 1995, ApJ, 450, 559
- Bennett, C. L., Banday, A. J., Gorski, K. M., et al. 1996, ApJ, 464, 1
- Biggs, A. D., & Ivison, R. J. 2006, MNRAS, 371, 963
- Bondi, M., Ciliegi, P., Zamorani, G., et al. 2003, A&AS, 403, 857
- Bondi, M., Ciliegi, P., Schinnerer, E., et al. 2008, ApJ, 681, 1129
- Boyle, B. J., Fong, R., Shanks, T., et al. 1987, MNRAS, 227, 717
- Branchesi, M., Gioia, I. M., Fanti, C., et al. 2006, A&A, 446, 97
- Bridle, A. H., & Schwab, F. R. 1989, in Synthesis Imaging in Radio Astronomy, ed. R. A. Perley, F. R Schwab, & A. H. Bridle, ASP Conf. Ser., 6, 247
- Brinkmann, W., Chester, M., Kollgaard, R., et al. 1999, A&AS, 134, 221; and VizieR On-line Data Catalog: J/A+AS/134/221
- Condon, J. J., & Broderick, J. J. 1985, AJ, 90, 2540
- Condon, J. J., & Broderick, J. J. 1986, AJ, 91, 1051
- Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693
- Condon, J. J., Cotton, W. D., & Broderick, J. J. 2002, AJ, 124, 675
- Coppin, K., Chapin, E. L., Mortier, A. M. J., et al. 2006, MNRAS, 372, 1621
- Cotton, W. H. 1989, in Synthesis Imaging in Radio Astronomy, ed. R. A. Perley, F. R. Schwab, & A. H. Bridle, ASP Conf. Ser., 6, 233
- de Vries, W. H., Morganti, R., R
 ttgering, H. J. A., et al.
2002, AJ, 1231, 1784
ttgering, H. J. A., et al.
2002, AJ, 1231, 1784
- Dunlop, J. S., & Peacock, J. A. 1990, MNRAS, 247, 19
- Efstathiou, A., Rowan-Robinson, M., & Siebenmorgen, R. 2000, MNRAS, 313, 734
- Elvis, M., Lockman, F. J., & Fassnacht, C. 1994, ApJS, 95, 413
- Fomalont, E. B., Kellermann, K. I., Cowie, L. L., et al. 2006, ApJS, 167, 103
- Gaidos, E. J., Magnier, E. A., Schechter, P. L., et al. 1993, PASP, 105, 1294
- Garn, T., Green, D. A., Riley, J. M., & Alexander, P. 2008, MNRAS, 383, 75
- Garrett, M. A., de Bruyn, A. G., Giroletti, M., Baan, W. A., & Schilizzi, R. T. 2000, A&A, 361, 41
- Gioia, I. M., Henry, J. P., Mullis, C. R., et al. 2003, ApJS, 149, 29
- Gioia, I. M., Wolter, A., Mullis, C. R., et al. 2004, A&A, 428, 867
- Goto, T., Hanami, H., Im, M., et al. 2008, PASJ, 60, 531
- Gruppioni, C., Pozzi, F., Polletta, M., et al. 2008, MNRAS, 684, 136
- Hacking, P., Condon, J. J., & Houck, J. R. 1987, ApJ, 316, L15
- Helou, G., Soifer, T. T., & Rowan-Robinson, M. 1985, ApJ, 298, 7
- Henry, J. P., Gioia, I. M., Mullis, C. R., et al. 2001, ApJ, 553, 109
- Henry, J. P., Mullis, C. R., Voges, W., et al. 2006, ApJS, 162, 304
- Hopkins, A. M. 2004, ApJ, 615, 209
- Hopkins, A. M., Mobasher, B., Cram, L., et al. 1998, MNRAS, 296, 839
- Hopkins, A., Afonso, J., Cram, L., et al. 1999, ApJ, 519, L59
- Hopkins, A. M., Miller, C. J., Connolly, A. J., et al. 2002, AJ, 123, 1086
- Hopkins, A. M., Afonso, J., Chan, B., et al. 2003, AJ, 125, 465
- Huynh, M. T., Jackson, C. A., Norris, R. P., et al. 2005, AJ, 130, 1388
- Hwang, N., Lee, H.-M., Im, M., et al. 2007, ApJS, 172, 583
- Kaper, H. G., Smiths, D. W., Schwartz, U., et al. 1966, BAN, 18, 465
- Kollgaard, R. I., Brinkmann, W., Chester, M. M., et al. 1994, ApJS, 93, 145
- K
 mmel, M. W., & Wagner,
S. J. 2000, A&A, 353, 867
mmel, M. W., & Wagner,
S. J. 2000, A&A, 353, 867
- K
 mmel, M. W., & Wagner,
S. J. 2001, A&A, 370, 384
mmel, M. W., & Wagner,
S. J. 2001, A&A, 370, 384
- Lee, H. M., Kim, S. J., Im, M., et al. 2009, PASJ, 61, 375
- Loiseau, N., Reich, W., Wielebinski, R., et al. 1988, A&AS, 75, 67
- Longair, M. S. 1966, MNRAS, 133, 421
- Magliocchetti, M., Maddox, S. J., Lahav, O., et al. 1998, MNRAS, 300, 257
- Matsuhara, H., Wada, T., Matsuura, S., et al. 2006, PASJ, 58, 673
- Micela, G., Affer, L., Favata, F., et al. 2007, A&A, 461, 977
- Morganti, R., Garrett, M. A., Chapman, S., et al. 2004, A&A, 424, 371
- Moss, D., Seymour, N., McHardy, I., et al. 2007, MNRAS, 378, 995
- Mullis, C. R., Henry, J. P., Gioia, I. M., et al. 2001, ApJ, 553, 115
- Mullis, C. R., McNamara, B. R., Quintana, H., et al. 2003, ApJ, 594, 154
- Owen, F. R., & Morrison, G. E. 2008, AJ, 136, 1889
- Oosterbaan, C. E. 1978, A&A, 69, 235
- Overzier, R. A., Rottgering, H. J. A., Rengelink, R. B., et al. 2003, A&A, 405, 53
- Pearson, C. P. 2005, MNRAS, 358, 1417
- Pearson, C. P., & Rowan-Robinson, M. 1996, MNRAS, 283, 174
- Peacock, J. A., & Dodds, S. J. 1994, MNRAS, 267, 1020
- Prandoni, I., Gregorini, L., Parma, P., et al. 2000a, A&AS, 146, 31
- Prandoni, I., Gregorini, L., Parma, P., et al. 2000b, A&AS, 146, 41
- Prandoni, I., Gregorini, L., Parma, P., et al. 2001, A&A, 365, 392
- Prandoni, I., Parma, P., Wieringa, M. H., et al. 2006, A&A, 457, 517
- Pretorius, M. L., Knigge, C., & O'Donoghue, D. 2007, MNRAS, 382, 1279
- Rengelink, R. B., Tang, Y., de Bruyn, A. G., et al. 1997, A&AS, 124, 259
- Rowan-Robinson, M. 1970, MNRAS, 149, 365
- Rowan-Robinson, M., Benn, C. R., Lawrence, A., et al. 1993, MNRAS, 263, 192
- Sault, R. J., Teuben, P. J., & Wright, M. C. H. 1995, Astronomical Data Analysis Software and Systems IV, ed. R. Shaw, H. E. Payne, & J. J. E. Hayes, ASP Conf. Ser., 77, 433
- Saunders, W., Sutherland, W. J., Maddox, S. J., et al. 2000, MNRAS, 317, 55
- Sedgwick, C., Serjeant, S., Sirothia, S., et al. 2009, in ASP Conf. Ser., ed. T. Onaka, G. J. White, T. Nakagawa, & I. Yamamura, 418, 519
- Simpson, C., Martinez-Sansigre, A., Rawlings, S., et al. 2006, MNRAS, 372, 741
- Somerville, R. S., Lee, K., Ferguson, H. C., et al. 2004, ApJ, 600, L171
- Stickel, M., Bogun, S., Lemke, D., et al. 1998, A&A, 336, 116
- Voges, W., Henry, J. P., Briel, U. G., et al. 2001, ApJ, 553, 119
- Wada, T., Matsuhara, H., Oyabu, S., et al. 2008, PASJ, 60, 517
- White, R. L., Becker, R. H., Helfand, D. J., et al. 1997, ApJ, 475, 479
- Windhorst, R. A., Miley G. K., Oweb, F. N., et al. 1985, ApJ, 289, 494
- Windhorst, R. A., Fomalont, E. B., Partridge, R. B., et al. 1993, ApJ, 405, 498
- Yun, M. S., Reddy, N. A., & Condon, J. J. 2001, ApJ, 554, 803
- Zickgraf, F., Thiering, I., Krautter, J., et al. 1997, A&AS, 123, 103
Table 2: The source catalogue.
All Tables
Table 1: 20 cm differential source counts for the WSRT-AKARI-NEP survey.
Table 2: The source catalogue.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



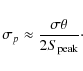
![\begin{displaymath}%
S_{\rm corr} = \frac{{S_{\rm meas}}}{{k~\left[ {a\;{\rm log}\left( {\frac{{S_{\rm meas}}}{\sigma }} \right) + b} \right]}}
\end{displaymath}](/articles/aa/full_html/2010/09/aa13366-09/img70.png)