| Issue |
A&A
Volume 517, July 2010
|
|
|---|---|---|
| Article Number | A28 | |
| Number of page(s) | 43 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/200913239 | |
| Published online | 28 July 2010 | |
VLT-VIMOS integral field spectroscopy of luminous and ultraluminous infrared galaxies
II. Evidence for shock ionization caused by tidal forces in the
extra-nuclear regions of interacting and merging LIRGs![[*]](/icons/foot_motif.png) ,
,![[*]](/icons/foot_motif.png)
A. Monreal-Ibero1 - S. Arribas2 - L. Colina2 - J. Rodríguez-Zaurín2 - A. Alonso-Herrero2 - M. García-Marín3
1 - European Organisation for Astronomical Research in the Southern
Hemisphere (ESO); Karl-Schwarzschild-Strasse 2, 85748 Garching bei München, Germany
2
- Departamento de Astrofísica Molecular e Infrarroja (DAMIR), Instituto
de Estructura de la Materia (IEM/CSIC); c/ Serrano 121, 28996 Madrid,
Spain
3 -
I. Physikalisches Institut, Universität zu Köln Zülpicher Strasse 77, 50937 Köln, Germany
Received 30 September 2009 / Accepted 15 April 2010
Abstract
Context. Luminous infrared galaxies (LIRGs) are an important class of objects in the low-z
universe bridging the gap between normal spirals and the strongly
interacting and starbursting ultraluminous infrared galaxies (ULIRGs).
Since a large fraction of the stars in the Universe have been formed in
these objects, LIRGs are also relevant in a high-z context. Studies of the two-dimensional physical properties of LIRGs are still lacking.
Aims. We aim to understand the nature and origin of the
ionization mechanisms operating in the extra-nuclear regions of LIRGs
as a function of the interaction phase and infrared luminosity.
Methods. This study uses optical integral field spectroscopy
(IFS) data obtained with VIMOS. Our analysis is based on over
25 300 spectra of 32 LIRGs covering all types of
morphologies (isolated galaxies, interacting pairs, and advanced
mergers), and the entire
![]() infrared luminosity range.
infrared luminosity range.
Conclusions. We found strong evidence for shock ionization, with
a clear trend with the dynamical status of the system. Specifically, we
quantified the variation with interaction phase of several line ratios
indicative of the excitation degree. While the [N II]![]() 6584/H
6584/H![]() ratio does not show any significant change, the [S II]
ratio does not show any significant change, the [S II]
![]() 6717,6731/H
6717,6731/H![]() and [O I]
and [O I]![]() 6300/H
6300/H![]() ratios
are higher for more advanced interaction stages. Velocity dispersions
are higher than in normal spirals and increase with the interaction
class (medians of 37, 46, and 51 km s-1
for class 0-2, respectively). We constrained the main mechanisms
causing the ionization in the extra-nuclear regions (typically for
distances ranging from
ratios
are higher for more advanced interaction stages. Velocity dispersions
are higher than in normal spirals and increase with the interaction
class (medians of 37, 46, and 51 km s-1
for class 0-2, respectively). We constrained the main mechanisms
causing the ionization in the extra-nuclear regions (typically for
distances ranging from ![]() 0.2-2.1 kpc to
0.2-2.1 kpc to ![]() 0.9-13.2 kpc)
using diagnostic diagrams. Isolated systems are mainly consistent with
ionization caused by young stars. Large fractions of the extra-nuclear
regions in interacting pairs and more advanced mergers are consistent
with ionization caused by shocks of
0.9-13.2 kpc)
using diagnostic diagrams. Isolated systems are mainly consistent with
ionization caused by young stars. Large fractions of the extra-nuclear
regions in interacting pairs and more advanced mergers are consistent
with ionization caused by shocks of
![]() km s-1.
This is supported by the relation between the excitation degree and the
velocity dispersion of the ionized gas, which we interpret as evidence
for shock ionization in interacting galaxies and advanced mergers but
not in isolated galaxies. This relation does not show any dependence
with the infrared luminosity (i.e. the level of star formation).
All this indicates that tidal forces play a key role in the origin of
the ionizing shocks in the extra-nuclear regions. We also showed for
the first time what appears to be a common
km s-1.
This is supported by the relation between the excitation degree and the
velocity dispersion of the ionized gas, which we interpret as evidence
for shock ionization in interacting galaxies and advanced mergers but
not in isolated galaxies. This relation does not show any dependence
with the infrared luminosity (i.e. the level of star formation).
All this indicates that tidal forces play a key role in the origin of
the ionizing shocks in the extra-nuclear regions. We also showed for
the first time what appears to be a common ![]() ([O I]
([O I]![]() 6300/H
6300/H![]() ) -
) -
![]() relation for the extranuclear ionized gas in interacting (U)LIRGs (i.e. covering the entire
relation for the extranuclear ionized gas in interacting (U)LIRGs (i.e. covering the entire
![]() luminosity range). This preliminary result needs to be investigated further with a larger sample of ULIRGs.
luminosity range). This preliminary result needs to be investigated further with a larger sample of ULIRGs.
Key words: galaxies: active - galaxies: interactions - galaxies: starburst - infrared: galaxies
1 Introduction
Luminous and ultraluminous infrared galaxies (LIRGs and ULIRGs) are defined as those objects with an infrared luminosity of
![]() and
and
![]() ,
respectively (see Sanders & Mirabel 1996; Lonsdale et al. 2006, for a review). They are systems which contain large amounts of gas and dust (e.g. Evans et al. 2002) and which are undergoing an intense star-formation episode in their (circum)nuclear regions (e.g. Alonso-Herrero et al. 2006; Scoville et al. 2000). This activity is the main cause of their huge luminosity in about
,
respectively (see Sanders & Mirabel 1996; Lonsdale et al. 2006, for a review). They are systems which contain large amounts of gas and dust (e.g. Evans et al. 2002) and which are undergoing an intense star-formation episode in their (circum)nuclear regions (e.g. Alonso-Herrero et al. 2006; Scoville et al. 2000). This activity is the main cause of their huge luminosity in about ![]() 80% of these systems, although some contribution from an AGN is present and even dominant in some cases
(e.g. Genzel et al. 1998; Risaliti et al. 2006; Farrah et al. 2007; Nardini et al. 2008).
80% of these systems, although some contribution from an AGN is present and even dominant in some cases
(e.g. Genzel et al. 1998; Risaliti et al. 2006; Farrah et al. 2007; Nardini et al. 2008).
These systems usually present some degree of interaction whose
importance increases with luminosity. While the majority of local LIRGs
can be classified as isolated spirals or interacting pairs
(e.g. Arribas et al. 2004; Sanders & Ishida 2004; Alonso-Herrero et al. 2006), most of the ULIRGs show signs of a clear merging process (e.g. Clements et al. 1996; Borne et al. 2000; Veilleux et al. 2002; Cui et al. 2001; Bushouse et al. 2002).
While (U)LIRGs are an oddity in the local Universe, recent mid-infrared
and submillimeter surveys show how they present a strong evolution with
redshift, increasing their number by two orders of magnitude at
![]() (Elbaz et al. 2002).
Indeed they are the dominant population of the infrared selected
galaxies at high redshift, making a significant contribution to the
star-formation rate density at
0.5 < z < 2 (Le Floc'h et al. 2005; Rampazzo et al. 2005).
(Elbaz et al. 2002).
Indeed they are the dominant population of the infrared selected
galaxies at high redshift, making a significant contribution to the
star-formation rate density at
0.5 < z < 2 (Le Floc'h et al. 2005; Rampazzo et al. 2005).
The study of the ionization properties of the gas in these objects is relevant for two main reasons. On the one hand, the ionization is important to investigate the nature (i.e. starburst, AGN) of the dominant source that causes the huge luminosity in the infrared. In the optical, this has mainly been done via long-slit observations of the nuclear regions of large samples of (U)LIRGs (e.g. Veilleux et al. 1999; Kim et al. 1995, and references therein). These studies established trends with the luminosity and interaction stage, and found an increase in the frequency of AGN-dominated systems with luminosity. These results have been recently revisited using the new optical classifications provided by the use of Sloan Digital Sky Survey (SDSS) data (Yuan et al. 2010). They show that most of the (U)LIRGs previously classified as Low-ionization nuclear emission-line region (LINER), now are classified as starburst-AGN composite galaxies. The presence of an obscured AGN has been also revealed by the detection of ionization cones with integral field spectroscopy (IFS) data (e.g. Arp 299, García-Marín et al. 2006).
On the other hand, the ionization structure helps to understand how the interaction/merger process as well as the release of energy and material from the central source and/or starbursts are affecting the extended structure of the galaxies in general and its interstellar medium in particular. In that sense, the presence of Super Galactic Winds (SGWs) in (U)LIRGs has been suggested using emission (Lehnert & Heckman 1996; Heckman et al. 1990) and absorption (Rupke et al. 2002; Heckman et al. 2000; Rupke et al. 2005a,b) lines. Tidally induced forces associated with the interaction process itself have been also suggested as the cause for the ionization of the gas (Colina et al. 2005; McDowell et al. 2003). Given the complex structure of these systems, where the selection of a preferential direction is specially difficult, these studies would benefit from IFS data thanks to which it is possible to obtain homogeneous two-dimensional spectral information.
Using this technique Monreal-Ibero et al. (2006, hereafter MAC06)
have studied a sample of six ULIRGs (nine galaxies), and found that
wide areas of the extra-nuclear extended regions presented line ratios
typical of LINERs according to the diagnostic diagrams of Veilleux & Osterbrock (1987).
In addition, it was shown that the velocity dispersion is
positively correlated with the degree of ionization supporting the
idea that shocks are the main cause of the ionization in these areas.
However, these results were based on a relatively small sample, which
covered a restricted range in luminosity (
![]() )
and interaction phase.
)
and interaction phase.
In this paper we extend that study to a larger sample of 32 systems, which cover the entire
![]() luminosity
range (i.e. the LIRGs range), and the different interaction types
(i.e., isolated galaxies, interaction pairs, and mergers
remnants).
luminosity
range (i.e. the LIRGs range), and the different interaction types
(i.e., isolated galaxies, interaction pairs, and mergers
remnants).
The present study is part of a wider project devoted to the study of the internal structure and kinematics of a representative sample of low-redshift LIRGs and ULIRGs using optical and near-IR IFS facilities (Arribas et al. 2008). Specifically we used the INTEGRAL+WYFFOS facility (Bingham et al. 1994; Arribas et al. 1998) and the Potsdam Multi-Aperture Spectrograph, PMAS (Roth et al. 2005) in the Northern Hemisphere, and VIMOS (Le Fèvre et al. 2003) and SINFONI (Eisenhauer et al. 2003) in the southern one. The corresponding catalogs for the PMAS, INTEGRAL and VIMOS samples can be found in Alonso-Herrero et al. (2009), García-Marín et al. (2009) and Rodríguez-Zaurín et al. (2010), respectively.
The paper is structured as follows: in Sect. 2 we describe the sample used in this work as well as the characteristics of the instrumental configuration and technical details regarding data reduction and analysis; Sect. 3 quantifies how the ionization degree varies with interaction stage and constrains the possible mechanisms that cause the ionization of the gas. Finally, a comparison with the previous results for ULIRGs and a discussion about the origin of the ionization produced by shocks in terms of the star formation and the interaction process are presented.
Throughout the paper, a cosmology with 70 km s-1 Mpc-1,
![]() and
and
![]() is assumed.
is assumed.
2 The data
2.1 The sample
The present sample is drawn from the VIMOS IFS sample of (U)LIRGs presented in Arribas et al. (2008, hereafter, Paper I). Specifically, it includes all the LIRGs listed in that paper, except for IRAS F10173+0828, for which no emission lines were detected. That implies 32 systems, of which 13 were isolated, 11 interacting systems (9 pairs and 2 triple), and 8 advanced mergers (i.e. classes 0-2, respectively, according to Paper I terminology). The methodology followed to perform the morphological classification is described below.
Figure 1
summarizes the distribution in luminosity, distance, and interaction
type of the systems in our final sample. The mean distance of the
sample is 87 Mpc, which leads to a mean linear scale of ![]() 400 pc arcsec-1. Taking into account the VIMOS spaxel size of 0
400 pc arcsec-1. Taking into account the VIMOS spaxel size of 0
![]() 67, this translates into a mean linear spatial sampling of the source of
67, this translates into a mean linear spatial sampling of the source of ![]() 270 pc spaxel-1. We refer the reader to Table 1 in Paper I for the basic properties of the individual systems.
270 pc spaxel-1. We refer the reader to Table 1 in Paper I for the basic properties of the individual systems.
![\begin{figure}
\par\mbox{\includegraphics[width=8.5cm,clip]{13239fg1a.eps}\hspac...
...
\includegraphics[width=8.4cm,clip]{13239fg1b.eps} }\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg33.png)
|
Figure 1: Histograms showing the luminosity ( left) and distance ( right) distributions of the systems in the sample. Light, intermediate and dark gray areas indicate the total number of isolated galaxies (class 0), interacting systems (class 1), and merger remnants (class 2), respectively (see text for a more detailed definition of the different morphological types). |
| Open with DEXTER | |
2.2 Morphological classification
Our morphological/merging classification is a simplified version of that proposed by Veilleux et al. (2002) for ULIRGs, who divided their sample in five classes (and four sub-classes). We only considered three main classes (i.e. ``isolated'': 0, ``interacting'': 1, ``merger'': 2) to reduce uncertainties associated with sorting. In particular, the different morphological classes considered are
- Class 0: objects that appear to be single isolated galaxies, with a relatively symmetric morphology and without evidence for strong past or ongoing interaction.
- Class 1: objects in a pre-coalescence phase with two well differentiated nuclei separated by a projected distance of D > 1.5 kpc. For those objects classified as 1, it is still possible to identify the individual merging galaxies and their corresponding tidal structures due to the interaction. The limit of 1.5 kpc was chosen because theoretical models predict a fast coalescence phase after the nuclei become closer than that distance (e.g. Naab et al. 2006; Mihos & Hernquist 1996).
- Class 2: objects with a relatively asymmetric morphology
suggesting a post-coalescence merging phase. They may have two nuclei
separated a projected distance of D
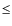 1.5 kpc. For objects classified as 2, it is not possible to identify the interacting galaxies individually.
1.5 kpc. For objects classified as 2, it is not possible to identify the interacting galaxies individually.
The classification was primarily based on the Digital Sky Survey (DSS) images, which are available for all the sources on the NASA Extragalactic database (NED). In most of the cases these images are sufficient to classify the objects of the present sample. However, for seven objects (less than 25% of the sample), the DSS images were not conclusive. In these cases (IRAS 08355-4944, IRAS F08520-6850, IRAS F10038-3338, IRAS F12116-5610, IRAS F13001-2339, IRAS F17138-1017 and IRAS F21453-3511) high-resolution HST images were used as supplementary information, mainly from program ID:10582 (IP: Evans). For another six objects the HST images just confirm the morphological classification derived using the DSS images. In Fig. 14 (on-line) we present the images used for the classification. In some cases the dynamic range is large and the different relevant features appear at quite different intensity levels, so we recommend the reader interested in a particular case to directly download and display the images.
In order to estimate the uncertainty associated with this classification process, we thrice classified the whole sample independently. The level of agreement was higher than 90%. However, there were intrinsically difficult cases for which we agreed they have an uncertain classification. These cases are: IRAS 09437+0317 (IC 563/IC 564) (1/0), IRAS F12116-5615 (2/0), IRAS F13001-2339 (2/1), and IRAS F17138-1017 (2/0), and they will not be considered later when analyzing the global behavior of the different classes.
Further details on the morphology of these objects may be found in Rodríguez-Zaurín et al. (2010).
2.3 Observations and instrumental set-up
A detailed description of the observations is provided in Paper I. Here we briefly recall the observational set-up and characteristics of the data.
Table 1: VIMOS LIRG sample: for each pointing, the total number of data points, mean value and standard deviation for the different line ratios and velocity dispersion are given.
The data were obtained in service mode with the VIMOS-IFU at VLT during semesters 76, 78, and 81.
We used the HR-Orange configuration, which covers the
5250-7400 Å spectral range with a resolution of 3400. It provides a field-of-view of
![]()
![]()
![]() with 0
with 0
![]() 67 per spatial element (spaxel)
making a total of 1600 spectra per pointing. Each galaxy was
observed using a 4-pointing dither pattern with a relative off-set
of 2
67 per spatial element (spaxel)
making a total of 1600 spectra per pointing. Each galaxy was
observed using a 4-pointing dither pattern with a relative off-set
of 2
![]() 7 (i.e. four spaxels) to minimize the effect of dead fibers and thus, providing an effective field-of-view of about
7 (i.e. four spaxels) to minimize the effect of dead fibers and thus, providing an effective field-of-view of about
![]()
![]()
![]() .
Details about data reduction and line fitting can be found in Paper I.
.
Details about data reduction and line fitting can be found in Paper I.
2.4 Emission line data
We used in our analysis the [O I]![]() 6300, H
6300, H![]() ,
[N II]
,
[N II]
![]() 6548,6584, and [S II]
6548,6584, and [S II]
![]() 6717,6730 emission lines, which were fitted to a single Gaussian component. For some galaxies, small areas of the H
6717,6730 emission lines, which were fitted to a single Gaussian component. For some galaxies, small areas of the H![]() emission
showed evidence for two or more kinematically distinct components.
These particular areas of double components are generally associated
with nuclear regions (i.e. IRAS F08520-6850,
IRAS F13229-2934, the eastern member of
IRAS F14544-4255 and IRAS 21453-3511)
which are not used in the present analysis (see below).
In some cases these also affect small areas in the extra-nuclear
regions (IRAS F06592-6313,
IRAS F07160-6215, IRAS F10409-4556,
IRAS F13229-2934, IRAS 08424-3130,
IC 564, the western member of
IRAS F14544-4255, the northern and central members
of IRAS 18093-5744,
IRAS F04315-0840, IRAS 10257-4338,
IRAS 17138-1017 and IRAS 21453-3511).
For a given galaxy, these regions represent typically less
than 5% of the data. In those cases where the two components
were clearly distinguishable, the dominant
component was used in the present analysis, while in those of strong
blending we used the results from the one-profile fit. A more
detailed analysis of the regions where multiple components are
identified is out of the scope of the present paper and will be
presented with the full kinematic analysis in a future paper.
emission
showed evidence for two or more kinematically distinct components.
These particular areas of double components are generally associated
with nuclear regions (i.e. IRAS F08520-6850,
IRAS F13229-2934, the eastern member of
IRAS F14544-4255 and IRAS 21453-3511)
which are not used in the present analysis (see below).
In some cases these also affect small areas in the extra-nuclear
regions (IRAS F06592-6313,
IRAS F07160-6215, IRAS F10409-4556,
IRAS F13229-2934, IRAS 08424-3130,
IC 564, the western member of
IRAS F14544-4255, the northern and central members
of IRAS 18093-5744,
IRAS F04315-0840, IRAS 10257-4338,
IRAS 17138-1017 and IRAS 21453-3511).
For a given galaxy, these regions represent typically less
than 5% of the data. In those cases where the two components
were clearly distinguishable, the dominant
component was used in the present analysis, while in those of strong
blending we used the results from the one-profile fit. A more
detailed analysis of the regions where multiple components are
identified is out of the scope of the present paper and will be
presented with the full kinematic analysis in a future paper.
Thus a measure of the flux in the different emission lines as well as
one independent measurement of the central wavelength and FWHM (full
width at half maximum) is obtained for each spectrum. The FWHM has been
corrected from the instrumental width measured with the strong [O I]![]() 6300 Å
sky line, and then translated into velocity dispersions. For the VIMOS
configuration used, the spectral resolution translates into an
instrumental width
6300 Å
sky line, and then translated into velocity dispersions. For the VIMOS
configuration used, the spectral resolution translates into an
instrumental width
![]()
![]() 8 km s-1. The corresponding values for the weaker [O I]
8 km s-1. The corresponding values for the weaker [O I]![]() 6363 Å sky line are
6363 Å sky line are
![]()
![]() 10 km s-1. Therefore, the profiles of the emission lines will be considered as resolved if their observed
profile is wider than 50 km s-1 (
10 km s-1. Therefore, the profiles of the emission lines will be considered as resolved if their observed
profile is wider than 50 km s-1 (
![]() ). In general the [O I]
). In general the [O I]![]() 6300, [S II]
6300, [S II]
![]() 6717,6731, [N II]
6717,6731, [N II]
![]() 6584,
and H
6584,
and H![]() emission lines define a sequence of increasing S/N and, therefore, the [N II]
emission lines define a sequence of increasing S/N and, therefore, the [N II]![]() 6584/H
6584/H![]() maps cover a larger area than those generated with the other line
ratios. While uncertainties in the line flux for the strongest emission
lines (H
maps cover a larger area than those generated with the other line
ratios. While uncertainties in the line flux for the strongest emission
lines (H![]() )
in high surface-brightness regions are about 10%, weaker lines like [S II]
)
in high surface-brightness regions are about 10%, weaker lines like [S II]
![]() 6717,6731 and [O I]
6717,6731 and [O I]![]() 6300
can have large uncertainties due to the lower S/N. However,
no lines with flux uncertainties larger than 30% are used in
the analysis presented in this paper. So, the typical
uncertainties in the line ratios varies from about 15% for
high S/N lines to about 30% for low surface brightness and
when a weak line is involved.
6300
can have large uncertainties due to the lower S/N. However,
no lines with flux uncertainties larger than 30% are used in
the analysis presented in this paper. So, the typical
uncertainties in the line ratios varies from about 15% for
high S/N lines to about 30% for low surface brightness and
when a weak line is involved.
Similarly to MAC06, we only used the extra-nuclear regions of our
galaxies for the analysis in this paper. To do so, we excluded the
nuclear regions, defined as those within the central 3 spaxel ![]() 3 spaxel (
3 spaxel (
![]()
![]()
![]() )
where, in addition to the complex line profiles mentioned above,
contamination due to a dust enshrouded AGN could affect the results.
For the typical distances of our sample of LIRGs, this corresponds
to a region of about
)
where, in addition to the complex line profiles mentioned above,
contamination due to a dust enshrouded AGN could affect the results.
For the typical distances of our sample of LIRGs, this corresponds
to a region of about ![]() 800 pc
800 pc ![]() 800 pc in size. For the particular case of
IRAS F04315-0840, where the two galaxies are coalescing,
the area with emission lines presenting double components was a bit
larger than the standard 3 spaxel
800 pc in size. For the particular case of
IRAS F04315-0840, where the two galaxies are coalescing,
the area with emission lines presenting double components was a bit
larger than the standard 3 spaxel ![]() 3 spaxel one. Because here the one Gaussian approach did not
properly reproduce the line profiles, we we made an exception and also
masked
the corresponding spaxels (see Fig. 2).
3 spaxel one. Because here the one Gaussian approach did not
properly reproduce the line profiles, we we made an exception and also
masked
the corresponding spaxels (see Fig. 2).
The final total number of available data points, mean and standard
deviation for each individual pointing for the three line ratio used as
well as the velocity dispersion inferred from H![]() are shown in Table 1.
are shown in Table 1.
3 Results and discussion
3.1 General characteristics of the excitation maps
Figure 2 presents the [N II]![]() 6584/H
6584/H![]() ,
[S II]
,
[S II]
![]() 6717,6731/H
6717,6731/H![]() ,
and [O I]
,
and [O I]![]() 6300/H
6300/H![]() line ratio maps for each individual VIMOS pointing. Although these maps
only represent one axis of the classical BPT diagrams (Veilleux & Osterbrock 1987; Baldwin et al. 1981), they are good tracers of the excitation when studying the general properties
of the extra-nuclear ionized regions of LIRGs. In fact, in the X-[O III]
line ratio maps for each individual VIMOS pointing. Although these maps
only represent one axis of the classical BPT diagrams (Veilleux & Osterbrock 1987; Baldwin et al. 1981), they are good tracers of the excitation when studying the general properties
of the extra-nuclear ionized regions of LIRGs. In fact, in the X-[O III]![]() 5007/H
5007/H![]() diagnostic diagrams (where X is any of the above line ratios), the
boundaries distinguishing regions mainly photo-ionized by stars
(i.e. H II-like) and those of LINER type are nearly vertical for the expected values of
diagnostic diagrams (where X is any of the above line ratios), the
boundaries distinguishing regions mainly photo-ionized by stars
(i.e. H II-like) and those of LINER type are nearly vertical for the expected values of ![]() ([O III]
([O III]![]() 5007/H
5007/H![]() )
in these extra-nuclear regions (
)
in these extra-nuclear regions (
![]() ,
see below). Figure 2 also shows the H
,
see below). Figure 2 also shows the H![]() surface
brightness maps. These maps are presented here mainly as a reference
for the excitation maps, and they will be discussed in detail elsewhere
(Rodríguez-Zaurín et al. 2010). The different area covered by the
excitation maps is a direct consequence of the different
signal-to-noise (S/N) of the involved lines. The [N II]
surface
brightness maps. These maps are presented here mainly as a reference
for the excitation maps, and they will be discussed in detail elsewhere
(Rodríguez-Zaurín et al. 2010). The different area covered by the
excitation maps is a direct consequence of the different
signal-to-noise (S/N) of the involved lines. The [N II]![]() 6584/H
6584/H![]() map encompasses the largest area in all the cases, reaching areas of low H
map encompasses the largest area in all the cases, reaching areas of low H![]() surface brightness where no good S/N data are available for the [O I]
surface brightness where no good S/N data are available for the [O I]![]() 6300 and [S II]
6300 and [S II]
![]() 6717,6731 lines.
6717,6731 lines.
![\begin{figure}
\par\includegraphics[width=16.8cm,clip]{13239fg2a.ps}
\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg50.png)
|
Figure 2:
Maps for H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.8cm,clip]{13239fg2b.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg51.png)
|
Figure 2: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13239fg2c.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg52.png)
|
Figure 2: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.8cm,clip]{13239fg2d.ps}\vspace*{-3mm}\vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg53.png)
|
Figure 2: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13239fg2e.ps}
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg54.png)
|
Figure 2: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13239fg2f.ps}\vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg55.png)
|
Figure 2: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{13239fg2g.ps}
\vspace*{6.5mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg56.png)
|
Figure 2: continued. |
| Open with DEXTER | |
The star-forming regions of relatively low excitation are well identified in the maps. These are generally high H![]() surface
brightness regions associated with large scale structures like spiral
arms (e.g. IRAS F13229-2934), rings (e.g.
IRAS F11255-4120), or tidal tails
(e.g. IRAS 06076-2139). However, knots of star
formation are also found in isolated external regions
(e.g. IRAS F12115-4656,
IRAS F07027-6011 S). In some cases these
external regions define a chain suggestive of star formation along
tidal tails (e.g. IRAS F11506-3851,
IRAS 06076-2139, Paper I).
surface
brightness regions associated with large scale structures like spiral
arms (e.g. IRAS F13229-2934), rings (e.g.
IRAS F11255-4120), or tidal tails
(e.g. IRAS 06076-2139). However, knots of star
formation are also found in isolated external regions
(e.g. IRAS F12115-4656,
IRAS F07027-6011 S). In some cases these
external regions define a chain suggestive of star formation along
tidal tails (e.g. IRAS F11506-3851,
IRAS 06076-2139, Paper I).
Galaxies in double or triple systems may have quite different excitation conditions, indicating that the interstellar medium of the individual objects have different properties. For instance, while the external regions of the central and southern component of IRAS F06259-4708 are dominated by star formation, for the northern galaxy these regions show higher excitation (similarly for IRAS F06076-2139).
Interestingly the external regions associated to diffuse low surface brightness H![]() emission
have relatively high excitation. In these regions the line ratios
could, in principle, be affected by an underlying absorption
spectrum. Indeed, preliminary results for our PMAS sample of LIRGs
(Alonso-Herrero et al. 2009) show that for spectra with EW(H
emission
have relatively high excitation. In these regions the line ratios
could, in principle, be affected by an underlying absorption
spectrum. Indeed, preliminary results for our PMAS sample of LIRGs
(Alonso-Herrero et al. 2009) show that for spectra with EW(H
![]() Å, the line ratio can decrease
Å, the line ratio can decrease ![]() 0.2 dex once the contribution of an old stellar population has been taken into account (Alonso-Herrero et al. 2010). In order to quantify the effect of a possible component in absorption, we created maps including a correction of
0.2 dex once the contribution of an old stellar population has been taken into account (Alonso-Herrero et al. 2010). In order to quantify the effect of a possible component in absorption, we created maps including a correction of
![]() Å. [S II]
Å. [S II]
![]() 6717,6731/H
6717,6731/H![]() and [O I]
and [O I]![]() 6300/H
6300/H![]() line ratios are affected by about 0.2 dex for only a handful (
line ratios are affected by about 0.2 dex for only a handful (![]() %) of spaxels, and by less than 0.1 dex, for most of the data. For the [N II]
%) of spaxels, and by less than 0.1 dex, for most of the data. For the [N II]![]() 6584/H
6584/H![]() line ratio, this effect could reach
line ratio, this effect could reach ![]() dex
in the very low surface brightness areas, but does not change in any
case the observed ionization structure that we describe here. These
regions of low H
dex
in the very low surface brightness areas, but does not change in any
case the observed ionization structure that we describe here. These
regions of low H![]() surface
brightness and relatively high excitation are found in all kind of
objects: structured systems with rings (IRAS 10567-4310)
and spiral
(IRAS F04315-0840) morphologies, highly disturbed
systems (the central member of IRAS F07160-5744),
and galaxies with relatively round/ elliptical shape
(IRAS F11506-3851). In objects with round
morphologies this transition from low to high excitation translates
into the appearance of external rings of high excitation
(IRAS F11506-3851, IRAS F12115-4656). The
transition from low to high excitation is also observed in the triple
system IRAS 18093-5744 where an extension (tidal tail?)
from the main body of the central galaxy towards the northern galaxy is
identified. In some cases the high-excitation regions are found
close to the nucleus and/or along preferential directions, and defining
structures suggestive of cones. Some examples are
IRAS F10409-4556, ESO 297-G012 or the
southern member of IRAS 12042-3140.
surface
brightness and relatively high excitation are found in all kind of
objects: structured systems with rings (IRAS 10567-4310)
and spiral
(IRAS F04315-0840) morphologies, highly disturbed
systems (the central member of IRAS F07160-5744),
and galaxies with relatively round/ elliptical shape
(IRAS F11506-3851). In objects with round
morphologies this transition from low to high excitation translates
into the appearance of external rings of high excitation
(IRAS F11506-3851, IRAS F12115-4656). The
transition from low to high excitation is also observed in the triple
system IRAS 18093-5744 where an extension (tidal tail?)
from the main body of the central galaxy towards the northern galaxy is
identified. In some cases the high-excitation regions are found
close to the nucleus and/or along preferential directions, and defining
structures suggestive of cones. Some examples are
IRAS F10409-4556, ESO 297-G012 or the
southern member of IRAS 12042-3140.
For the rest of the paper we will focus on the study of the extra-nuclear excitation conditions using the presented line ratios as well as the velocity dispersions.
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{13239fg3.eps}
\vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg61.png)
|
Figure 3:
Distributions of the different LIRG subsamples according to [N II] |
| Open with DEXTER | |
Table 2: Median, standard deviation, and number of data points for the distributions of the different groups and line ratios.
3.2 Dependence of the excitation conditions of the extra-nuclear ionized gas with the interaction class
In order to investigate possible changes in the excitation properties
of the ionized gas as a consequence of interactions and mergers,
the distribution of the emission line ratios for the entire sample
of LIRGs was divided into three main groups according to their
morphology: isolated, interacting, and merger remnants. The [N II]![]() 6584/H
6584/H![]() ,
[S II]
,
[S II]
![]() 6717,6731/H
6717,6731/H![]() ,
and [O I]
,
and [O I]![]() 6300/H
6300/H![]() emission line ratio distributions for these classes of galaxies as well as for the entire sample are shown in Fig. 3. Galaxies with dubious classification (see Table 1)
were excluded from the histograms or the individual groups. The number
of data points as well as the median and standard deviation of these
distributions are indicated in Table 2. We also indicate in each panel the boundaries between ionization caused by stars and by other mechanisms in the Baldwin et al. (1981, hereafter BPT) diagrams according to the boundaries proposed by different authors.
The original boundaries (Veilleux & Osterbrock 1987) were empirically determined using a sample that includes extragalactic H II regions,
and nuclear (or integrated) data for starburst galaxies and
different kinds of active galaxies (i.e. Seyfert 2, LINERs,
narrow-line radio galaxies and what would be called today
``intermediate objects''). Despite a recent new discussion about the
location of these boundaries, we considered that they provide valuable
information because i) they are the only set of empirical boundaries for the three
BPT diagnostic diagrams ii) they facilitate a possible
comparison of the line ratios presented here with those in previous
works. The other complete set of three boundaries is the one proposed
by Kewley et al. (2001b). Using a
combination of photo-ionization and stellar populations synthesis
models they determined the extreme cases under which line ratios can be
explained via photo-ionization caused by stars. Recently,
the empirical borders associated to the [N II]
emission line ratio distributions for these classes of galaxies as well as for the entire sample are shown in Fig. 3. Galaxies with dubious classification (see Table 1)
were excluded from the histograms or the individual groups. The number
of data points as well as the median and standard deviation of these
distributions are indicated in Table 2. We also indicate in each panel the boundaries between ionization caused by stars and by other mechanisms in the Baldwin et al. (1981, hereafter BPT) diagrams according to the boundaries proposed by different authors.
The original boundaries (Veilleux & Osterbrock 1987) were empirically determined using a sample that includes extragalactic H II regions,
and nuclear (or integrated) data for starburst galaxies and
different kinds of active galaxies (i.e. Seyfert 2, LINERs,
narrow-line radio galaxies and what would be called today
``intermediate objects''). Despite a recent new discussion about the
location of these boundaries, we considered that they provide valuable
information because i) they are the only set of empirical boundaries for the three
BPT diagnostic diagrams ii) they facilitate a possible
comparison of the line ratios presented here with those in previous
works. The other complete set of three boundaries is the one proposed
by Kewley et al. (2001b). Using a
combination of photo-ionization and stellar populations synthesis
models they determined the extreme cases under which line ratios can be
explained via photo-ionization caused by stars. Recently,
the empirical borders associated to the [N II]![]() 6584/H
6584/H![]() line ratio have been up-dated by using the Sloan Digital Sky
Survey (hereafter SDSS, York et al. 2000) data (Stasinska et al. 2006; Kauffmann et al. 2003). There is no similar up-date for the diagnostic diagrams involving the [S II]
line ratio have been up-dated by using the Sloan Digital Sky
Survey (hereafter SDSS, York et al. 2000) data (Stasinska et al. 2006; Kauffmann et al. 2003). There is no similar up-date for the diagnostic diagrams involving the [S II]
![]() 6717,6731/H
6717,6731/H![]() and the [O I]
and the [O I]![]() 6300/H
6300/H![]() line ratios.
line ratios.
In order to locate the ionization type boundaries in Fig. 3 we assumed a ![]() ([O III]
([O III]![]() 5007/H
5007/H![]() ) = -0.2. This is the median observed value for the sample of LIRGs sample presented inAlonso-Herrero et al. (2009). Individual values range between -0.6 and 0.1
) = -0.2. This is the median observed value for the sample of LIRGs sample presented inAlonso-Herrero et al. (2009). Individual values range between -0.6 and 0.1![]() (excluding NGC 7469, which is known to host a luminous
Seyfert 1 nucleus that largely affects its integrated spectrum).
As is illustrated in Fig. 3 with gray bands, the boundaries change very little in this [O III]
(excluding NGC 7469, which is known to host a luminous
Seyfert 1 nucleus that largely affects its integrated spectrum).
As is illustrated in Fig. 3 with gray bands, the boundaries change very little in this [O III]![]() 5007/H
5007/H![]() range (typically
range (typically ![]() 0.1 dex for the empirical boundaries of Veilleux & Osterbrock 1987; Stasinska et al. 2006; and Kauffmann et al. 2003; and
0.1 dex for the empirical boundaries of Veilleux & Osterbrock 1987; Stasinska et al. 2006; and Kauffmann et al. 2003; and ![]() 0.2 dex for the theoretical boundaries of Kewley et al. 2001b) making this
0.2 dex for the theoretical boundaries of Kewley et al. 2001b) making this ![]() ([O III]
([O III]![]() 5007/H
5007/H![]() ) = -0.2, a reasonable assumption for establishing the mean borders.
) = -0.2, a reasonable assumption for establishing the mean borders.
The line ratio distributions for the whole sample (Fig. 3,
upper row) are not symmetrical around a mean value, but show a
significant wing towards high values. This suggests
that a fraction of regions have a relatively high ionization
(i.e. LINER-like). According to the Veilleux & Osterbrock
boundaries, the percentage of data presenting
a LINER spectrum corresponds to 19%, 31%, and 35%
when using the [N II]![]() 6584/H
6584/H![]() ,
[S II]
,
[S II]
![]() 6717,6731/H
6717,6731/H![]() ,
and [O I]
,
and [O I]![]() 6300/H
6300/H![]() ,
respectively. Using the boundaries proposed by Kewley et al. (2001b),
the number of spaxels that cannot be explained as purely ionized
by stars is significantly smaller (4%, 2%, and 25%, for the
[N II]
,
respectively. Using the boundaries proposed by Kewley et al. (2001b),
the number of spaxels that cannot be explained as purely ionized
by stars is significantly smaller (4%, 2%, and 25%, for the
[N II]![]() 6584/H
6584/H![]() ,
[S II]
,
[S II]
![]() 6717,6731/H
6717,6731/H![]() ,
and [O I]
,
and [O I]![]() 6300/H
6300/H![]() line
ratios, respectively). The significant differences in the percentages
when comparing the three line ratios could be due to the fact that
these distributions do not come from exactly the same regions
(i.e. set of spectra). Indeed, the [O I]
line
ratios, respectively). The significant differences in the percentages
when comparing the three line ratios could be due to the fact that
these distributions do not come from exactly the same regions
(i.e. set of spectra). Indeed, the [O I]![]() 6300/H
6300/H![]() and [S II]
and [S II]
![]() 6717,6731/H
6717,6731/H![]() data points are restricted to a smaller region than the [N II]
data points are restricted to a smaller region than the [N II]![]() 6584/H
6584/H![]() ones because the [O I] and [S II] lines have on average lower S/N than
the [N II] line.
However, when these distributions are generated with data points from
the same regions for the three lines (not shown), we find similar
differences between the percentages when using the Kewley et al.
boundaries (1%, 1% and 13%) and even larger ones when using the
Veilleux & Osterbrock boundaries (7%, 21% and 22% for the
[N II]
ones because the [O I] and [S II] lines have on average lower S/N than
the [N II] line.
However, when these distributions are generated with data points from
the same regions for the three lines (not shown), we find similar
differences between the percentages when using the Kewley et al.
boundaries (1%, 1% and 13%) and even larger ones when using the
Veilleux & Osterbrock boundaries (7%, 21% and 22% for the
[N II]![]() 6584/H
6584/H![]() ,
[S II]
,
[S II]
![]() 6717,6731/H
6717,6731/H![]() ,
and [O I]
,
and [O I]![]() 6300/H
6300/H![]() line ratios, respectively). This confirms that the [O I]
line ratios, respectively). This confirms that the [O I]![]() 6300/H
6300/H![]() distribution has a higher percentage of data points with high ionization than the other two distributions. That the [S II]
distribution has a higher percentage of data points with high ionization than the other two distributions. That the [S II]
![]() 6717,6731 and [O I]
6717,6731 and [O I]![]() 6300 emission is enhanced by shocks and therefore the [S II]
6300 emission is enhanced by shocks and therefore the [S II]
![]() 6717,6731/H
6717,6731/H![]() and, especially, [O I]
and, especially, [O I]![]() 6300/H
6300/H![]() ratio are better tracers of shock-induced ionization (e.g. Dopita & Sutherland 1995)
suggests a significant presence of this type of ionization in the
extra-nuclear extended regions of LIRGs. This will be explored in more
detail below.
ratio are better tracers of shock-induced ionization (e.g. Dopita & Sutherland 1995)
suggests a significant presence of this type of ionization in the
extra-nuclear extended regions of LIRGs. This will be explored in more
detail below.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{13239fg4a.ps}\vspace*{1mm}
\par\includegraphics[width=6.5cm,clip]{13239fg4b.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg62.png)
|
Figure 4:
Percentage of data for the different interaction classes classified as LINERs using the Veilleux & Osterbrock (1987) line ratio boundaries (up) and Kewley et al. (2001b) ones (down) and assuming [O III] |
| Open with DEXTER | |
A clear distinction emerges in the excitation properties, i.e. in
the distributions of the emission line ratios, when LIRGs are separated
according to their interaction class (Fig. 3). While the [N II]![]() 6584/H
6584/H![]() line ratio distributions are similar with a median ratio of
line ratio distributions are similar with a median ratio of
![]()
![]() 0.18 dex, typical of H II, the [S II]
0.18 dex, typical of H II, the [S II]
![]() 6717,6731/H
6717,6731/H![]() line
ratio shows on average higher values, i.e. higher excitation, in
the more dynamically perturbed systems (class 1 and 2).
Indeed, median (
line
ratio shows on average higher values, i.e. higher excitation, in
the more dynamically perturbed systems (class 1 and 2).
Indeed, median (![]() standard deviation) values of -0.55
standard deviation) values of -0.55 ![]() 0.13, -0.49
0.13, -0.49 ![]() 0.16, and -0.48
0.16, and -0.48 ![]() 0.17 are found for classes 0-2, respectively. Similar values are
found after assuming a correction for a H
0.17 are found for classes 0-2, respectively. Similar values are
found after assuming a correction for a H![]() component in absorption with an equivalent width of 2 Å.
component in absorption with an equivalent width of 2 Å.
A more extreme change is evident in the [O I]![]() 6300/H
6300/H![]() ratio (i.e. shock tracer) with median values of -1.56
ratio (i.e. shock tracer) with median values of -1.56 ![]() 0.28, -1.43
0.28, -1.43 ![]() 0.33, and -1.35
0.33, and -1.35 ![]() 0.35
for classes 0-2, respectively. In addition, LIRGs belonging
to both classes 1 and 2 seem to have a double-peak
distribution, with values around -1.4 (i.e. H II-like)
and -0.9 (LINER-like). In all the cases, the
Kolmogorov-Smirnoff test allows us to reject the possibility that these
distributions come from the same parent distribution even in the case
of the [N II]
0.35
for classes 0-2, respectively. In addition, LIRGs belonging
to both classes 1 and 2 seem to have a double-peak
distribution, with values around -1.4 (i.e. H II-like)
and -0.9 (LINER-like). In all the cases, the
Kolmogorov-Smirnoff test allows us to reject the possibility that these
distributions come from the same parent distribution even in the case
of the [N II]![]() 6584/H
6584/H![]() line ratio.
line ratio.
Moreover, when using the Veilleux & Osterbrock boundaries the percentage of data points with [S II]
![]() 6717,6731/H
6717,6731/H![]() and [O I]
and [O I]![]() 6300/H
6300/H![]() line
ratios in the LINER range increases by factors of two and three with
the interaction class with respect to the isolated galaxies
(class 0), representing about
line
ratios in the LINER range increases by factors of two and three with
the interaction class with respect to the isolated galaxies
(class 0), representing about ![]() 17% and
17% and ![]() 33%
of the regions in class 1 and 2 galaxies, respectively. When
using the Kewley et al. boundaries, only the percentage for the
[O I]
33%
of the regions in class 1 and 2 galaxies, respectively. When
using the Kewley et al. boundaries, only the percentage for the
[O I]![]() 6300/H
6300/H![]() line ratio shows a significant increase (see Fig. 4).
line ratio shows a significant increase (see Fig. 4).
As shown in Table 1,
the number of data points associated with a galaxy can range from a few
tens to a few thousands, depending on the line ratio. Given this range
of two orders of
magnitude, one might wonder if the distributions presented in Fig. 3
are biased due to the contribution of a few galaxies. To check
this possibility, we generated the distributions for the three line
ratios and the different morphological groups, but without the pointing
with the largest number of spaxels. These were
IRAS F22132-3705 for class 0,
ESO 297-G011 for class 1, and
IRAS 10257-4338 for class 2. In this way, the
remaining pointings contribute in a similar manner to the distribution
(i.e. with several hundreds of data points for the [N II]![]() 6584/H
6584/H![]() line ratio in most of the cases and with many tens - a few hundreds for the [S II]
line ratio in most of the cases and with many tens - a few hundreds for the [S II]
![]() 6717,6731/H
6717,6731/H![]() and [O I]
and [O I]![]() 6300/H
6300/H![]() line
ratios). The distributions (not shown here) were similar to those for
the whole sample, with differences between the medians
line
ratios). The distributions (not shown here) were similar to those for
the whole sample, with differences between the medians ![]() 0.05 dex. Moreover, we checked how the median of the
average line ratios per galaxy changes with the interaction class. This is shown in Fig. 5.
In this way, every pointing contributes with one data point per
line ratio. As was found for the data distributions, this figure
shows how, while the [N II]
0.05 dex. Moreover, we checked how the median of the
average line ratios per galaxy changes with the interaction class. This is shown in Fig. 5.
In this way, every pointing contributes with one data point per
line ratio. As was found for the data distributions, this figure
shows how, while the [N II]![]() 6584/H
6584/H![]() line ratio remains constant with the interaction class, the [S II]
line ratio remains constant with the interaction class, the [S II]
![]() 6717,6731/H
6717,6731/H![]() and, especially, the [O I]
and, especially, the [O I]![]() 6300/H
6300/H![]() line ratio increases with the degree of interaction.
line ratio increases with the degree of interaction.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{13239fg5.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg64.png)
|
Figure 5: Variation of the median of the average line ratio per galaxy with the interaction class. We use the same line and color code as in Fig. 4 to distinguish among the emission line ratios. |
| Open with DEXTER | |
| Figure 6:
Same as Fig. 3 for NGC 5194 (only [N II] |
|
| Open with DEXTER | |
Although it would have been interesting to compare the present line
ratio distributions with those obtained for other kinds of galaxies
(e.g. normal spirals, less powerful starbursts), there is a clear
lack of data comparable to those presented here. In particular,
a meaningful comparison requires galaxies with line ratios
measured at similar spatial scales as those sampled here.
For example, line ratios derived for the SDSS![]() ,
the largest extragalactic survey up to date, were derived from
spectra obtained through 3-arcsec diameter fibers. For galaxies at
similar redshift like the present sample, this would be representative
of the ionization in the nuclear regions, and thus, not
directly comparable with our analysis on the external areas.
For galaxies at larger distances - say,
0.04< z<0.10 - the spatial sampling in the SLOAN galaxies would be much larger (
,
the largest extragalactic survey up to date, were derived from
spectra obtained through 3-arcsec diameter fibers. For galaxies at
similar redshift like the present sample, this would be representative
of the ionization in the nuclear regions, and thus, not
directly comparable with our analysis on the external areas.
For galaxies at larger distances - say,
0.04< z<0.10 - the spatial sampling in the SLOAN galaxies would be much larger (
![]() kpc)
and thus again not directly comparable. The only galaxy with published
data comparable to those presented here is the spiral NGC 5194
(also known as Whirlpool Galaxy, Blanc et al. 2009), a spiral galaxy interacting with a dwarf galaxy. At its distance (
kpc)
and thus again not directly comparable. The only galaxy with published
data comparable to those presented here is the spiral NGC 5194
(also known as Whirlpool Galaxy, Blanc et al. 2009), a spiral galaxy interacting with a dwarf galaxy. At its distance (![]() 8 Mpc) and with the size of the VIRUS-P fibers (
8 Mpc) and with the size of the VIRUS-P fibers (
![]() )
the spatial sampling is comparable with that for our sample within a factor of
)
the spatial sampling is comparable with that for our sample within a factor of ![]() 3. Figure 6 shows the distribution for the two available line ratios for this galaxy. While the [N II]
3. Figure 6 shows the distribution for the two available line ratios for this galaxy. While the [N II]![]() 6584/H
6584/H![]() distributions for the LIRGs and NGC 5194 are similar, LIRGs have larger [S II]
distributions for the LIRGs and NGC 5194 are similar, LIRGs have larger [S II]
![]() 6717,6731/H
6717,6731/H![]() ratios.
Because this comparison was done only with one galaxy, this result
needs to be revised when line ratios in the external areas of larger
samples of spiral galaxies at similar linear spatial resolution become
available.
ratios.
Because this comparison was done only with one galaxy, this result
needs to be revised when line ratios in the external areas of larger
samples of spiral galaxies at similar linear spatial resolution become
available.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13239fg7.eps}
\vspace*{3.5mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg68.png)
|
Figure 7:
Relation between the H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{13239fg8.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg70.png)
|
Figure 8:
[S II]
|
| Open with DEXTER | |
3.3 Anti-correlation between excitation and H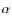 luminosity
luminosity
Maps presented in Sect. 3.1 (Fig. 2) display an increase on the line ratio in those areas with low H![]() surface brightness. Similar results have been observed in other environments, like our Galaxy (Reynolds et al. 1999; Madsen et al. 2006), or other spiral galaxies (Miller & Veilleux 2003; Blanc et al. 2009; Collins & Rand 2001)
in the so-called diffuse ionized gas (DIG) or warm interstellar medium
(WIM). In this section we further explore this result by looking
at the relation between the ionization degree and surface brightness
for the different interaction groups. This is shown in Fig. 7, where each data point represents the information from an individual spaxel.
As can be seen in the figure, while the [N II]
surface brightness. Similar results have been observed in other environments, like our Galaxy (Reynolds et al. 1999; Madsen et al. 2006), or other spiral galaxies (Miller & Veilleux 2003; Blanc et al. 2009; Collins & Rand 2001)
in the so-called diffuse ionized gas (DIG) or warm interstellar medium
(WIM). In this section we further explore this result by looking
at the relation between the ionization degree and surface brightness
for the different interaction groups. This is shown in Fig. 7, where each data point represents the information from an individual spaxel.
As can be seen in the figure, while the [N II]![]() 6584/H
6584/H![]() covers almost three orders of magnitude in H
covers almost three orders of magnitude in H![]() surface brightness, the [S II]
surface brightness, the [S II]
![]() 6717,6731/H
6717,6731/H![]() and the [O I]
and the [O I]![]() 6300/H
6300/H![]() line ratios are restricted to only about two. Also, low values of [S II]
line ratios are restricted to only about two. Also, low values of [S II]
![]() 6717,6731/H
6717,6731/H![]() and [O I]
and [O I]![]() 6300/H
6300/H![]() are only found at high H
are only found at high H![]() surface
brightness. We estimated our observational limit by looking at the
typical values and uncertainties measured for our [N II]
surface
brightness. We estimated our observational limit by looking at the
typical values and uncertainties measured for our [N II]![]() 6584/H
6584/H![]() line
ratio. Then we allowed for a maximum uncertainty in the logarithm of
the line ratios of 0.4 and assumed that the S/N scales with the
root square of the signal. The derived observational limit is shown in
Fig. 7 which shows how these effects are caused by the sensitivity limit of the data, as was pointed out in Sect. 3.1. That is, the relatively low S/N of the [S II]
line
ratio. Then we allowed for a maximum uncertainty in the logarithm of
the line ratios of 0.4 and assumed that the S/N scales with the
root square of the signal. The derived observational limit is shown in
Fig. 7 which shows how these effects are caused by the sensitivity limit of the data, as was pointed out in Sect. 3.1. That is, the relatively low S/N of the [S II]
![]() 6717,6731 and [O I]
6717,6731 and [O I]![]() 6300 emission lines in the outer parts prevent us from measuring low [S II]
6300 emission lines in the outer parts prevent us from measuring low [S II]
![]() 6717,6731/H
6717,6731/H![]() and [O I]
and [O I]![]() 6300/H
6300/H![]() line ratios at low H
line ratios at low H![]() surface brightness. Figure 7
shows that independently of the line ratio, high
values are found at low surface brightness as it happened in our Galaxy
and other spiral galaxies. Moreover, typical distances where the high
line ratios are found (from
surface brightness. Figure 7
shows that independently of the line ratio, high
values are found at low surface brightness as it happened in our Galaxy
and other spiral galaxies. Moreover, typical distances where the high
line ratios are found (from ![]() 400 pc up to
400 pc up to ![]() 6 kpc)
are comparable with the distances where this anti-correlation between
excitation and surface brightness has been found (up to
6 kpc)
are comparable with the distances where this anti-correlation between
excitation and surface brightness has been found (up to ![]() 8 kpc Miller & Veilleux 2003; Collins & Rand 2001).
8 kpc Miller & Veilleux 2003; Collins & Rand 2001).
The figure also shows the ranges of [N II]![]() 6584/H
6584/H![]() and [S II]
and [S II]
![]() 6717,6731/H
6717,6731/H![]() line ratios measured in a sample of H II regions and DIGs areas in our Galaxy by Madsen et al. (2006), as well as for extragalactic DIG (Miller & Veilleux 2003). Part of the [N II]
line ratios measured in a sample of H II regions and DIGs areas in our Galaxy by Madsen et al. (2006), as well as for extragalactic DIG (Miller & Veilleux 2003). Part of the [N II]![]() 6584/H
6584/H![]() and [S II]
and [S II]
![]() 6717,6731/H
6717,6731/H![]() line ratios are compatible with those expected for H II regions.
However, there is a large number of spaxels with line ratios similar to
what it is observed in the DIGs areas.
line ratios are compatible with those expected for H II regions.
However, there is a large number of spaxels with line ratios similar to
what it is observed in the DIGs areas.
H II regions are generally understood as
photo-ionized by the young stellar populations within them. On the
other hand, DIGs seem more difficult to explain only via
photo-ionization (e.g. Miller & Veilleux 2003). If they are interpreted only as photo-ionization areas, there is a need for extra heating (Reynolds et al. 1999; Mathis 2000) and even with this extra heating, it is difficult to reach [N II]![]() 6584/H
6584/H![]()
![]() 1 line
ratios. Another possibility would be that these line ratios are the
composite effect of photo-ionization and shocks or turbulent mixing
layers (TML, Miller & Veilleux 2003; Collins & Rand 2001).
In the next section we will explore the role of these different
ionization mechanisms by comparing our measured line ratios with the
predictions of the models.
1 line
ratios. Another possibility would be that these line ratios are the
composite effect of photo-ionization and shocks or turbulent mixing
layers (TML, Miller & Veilleux 2003; Collins & Rand 2001).
In the next section we will explore the role of these different
ionization mechanisms by comparing our measured line ratios with the
predictions of the models.
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{13239fg9.ps}
\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg72.png)
|
Figure 9:
[O I] |
| Open with DEXTER | |
3.4 Ionization mechanisms in the extra-nuclear ionized regions: young stars and shocks
To investigate the nature of the ionization mechanisms present in the extended extra-nuclear regions, the [S II]
![]() 6717,6731/H
6717,6731/H![]() vs. [N II]
vs. [N II]![]() 6584/H
6584/H![]() and [O I]
and [O I]![]() 6300/H
6300/H![]() vs. [N II]
vs. [N II]![]() 6584/H
6584/H![]() diagnostic diagrams for (thousands) of data points sampling these regions were compared with model predictions for H II regions, shocks and AGNs. State-of-the-art models for evolving H II regions (Dopita et al. 2006), shocks (Allen et al. 2008), TML (Slavin et al. 1993) and dusty AGNs (Groves et al. 2004)
covering a wide range of physical parameters (ionization, density,
stellar ages, shock velocity, etc.) and metallicities were considered.
The results for the galaxies were separated according to their
interaction class, and set of models best representing the data are
given in Figs. 8 and 9 for the
[S II]
diagnostic diagrams for (thousands) of data points sampling these regions were compared with model predictions for H II regions, shocks and AGNs. State-of-the-art models for evolving H II regions (Dopita et al. 2006), shocks (Allen et al. 2008), TML (Slavin et al. 1993) and dusty AGNs (Groves et al. 2004)
covering a wide range of physical parameters (ionization, density,
stellar ages, shock velocity, etc.) and metallicities were considered.
The results for the galaxies were separated according to their
interaction class, and set of models best representing the data are
given in Figs. 8 and 9 for the
[S II]
![]() 6717,6731/H
6717,6731/H![]() vs. [N II]
vs. [N II]![]() 6584/H
6584/H![]() and [O I]
and [O I]![]() 6300/H
6300/H![]() vs. [N II]
vs. [N II]![]() 6584/H
6584/H![]() diagnostic diagrams, respectively. Galaxies with dubious
classification (see Table 1) were excluded. The data associated with each individual pointing have been attached as On-line Material.
diagnostic diagrams, respectively. Galaxies with dubious
classification (see Table 1) were excluded. The data associated with each individual pointing have been attached as On-line Material.
From these diagrams it is clear that although the ionization properties
of most of the extended, extra-nuclear regions are consistent with
those of H II regions,
there is a trend with the interaction class. As the interaction
progresses (e.g. moving from class 0 to class 2),
a larger fraction of extra-nuclear regions shows a clear shift
towards an increased excitation, as traced by the increment of the
[S II]
![]() 6717,6731 and, in particular, [O I]
6717,6731 and, in particular, [O I]![]() 6300 emission with respect to H
6300 emission with respect to H![]() (see Figs. 8 and 9).
(see Figs. 8 and 9).
Although individual galaxies within an interaction class or regions within galaxies can behave differently, a direct comparison of all the available data (represented by thousands of points in the diagrams of Figs. 8 and 9) with the model predictions allow us to obtain some general conclusions about the ionization mechanisms playing the main role in the extra-nuclear regions of LIRGs.
The first conclusion that can be drawn from a comparison of Figs. 8 and 9
is that TML are not playing a major role in the ionization of the
extra-nuclear regions of this sample. Models can marginally reproduce
the observed [N II]![]() 6584/H
6584/H![]() vs. [S II]
vs. [S II]
![]() 6717,6731/H
6717,6731/H![]() ,
but clearly under-predict the [O I]
,
but clearly under-predict the [O I]![]() 6300/H
6300/H![]() line ratio for a given [N II]
line ratio for a given [N II]![]() 6584/H
6584/H![]() .
.
Instead, most of the regions are consistent with ionization by young
stellar populations with ages of 3 Myr or less and metallicities
twice solar. The measured H![]() emission
line equivalent widths in these regions are in the 40 to
300 Å range (Rodríiguez-Zaurín et al., in prep.), and
therefore do not correspond with the strong H
emission
line equivalent widths in these regions are in the 40 to
300 Å range (Rodríiguez-Zaurín et al., in prep.), and
therefore do not correspond with the strong H![]() lines (equivalent widths of 1000 to 2000 Å) expected in very young (
lines (equivalent widths of 1000 to 2000 Å) expected in very young (![]() 3 Myr) stellar clusters (STARBURST99, Leitherer et al. 1999). This apparent discrepancy is likely due to contamination by evolved
stellar populations (see Alonso-Herrero et al. 2010). Because the physical scale of each resolution element (determined by a seeing of
3 Myr) stellar clusters (STARBURST99, Leitherer et al. 1999). This apparent discrepancy is likely due to contamination by evolved
stellar populations (see Alonso-Herrero et al. 2010). Because the physical scale of each resolution element (determined by a seeing of
![]() )
would be about 480 pc, the measured equivalent widths are
likely the result of different stellar populations where the old stars
present in these regions contribute to the optical continuum, but not
to the emission lines. Moreover, typical sizes
for giant H II regions would be
)
would be about 480 pc, the measured equivalent widths are
likely the result of different stellar populations where the old stars
present in these regions contribute to the optical continuum, but not
to the emission lines. Moreover, typical sizes
for giant H II regions would be ![]() 400 pc (e.g. Kennicutt 1984; Alonso-Herrero et al. 2002).
Because our typical resolution is slightly higher, a single spaxel
can sample both pure DIG and regions of very young star formation. This
implies that measured line ratios, specially the [N II]
400 pc (e.g. Kennicutt 1984; Alonso-Herrero et al. 2002).
Because our typical resolution is slightly higher, a single spaxel
can sample both pure DIG and regions of very young star formation. This
implies that measured line ratios, specially the [N II]![]() 6584/H
6584/H![]() one, are higher than those for pure H II regions and thus a comparison with models suggests too young stellar populations.
one, are higher than those for pure H II regions and thus a comparison with models suggests too young stellar populations.
For regions showing a ![]() ([S II]
([S II]
![]() 6717,6731/H
6717,6731/H![]() )
) ![]() -0.6, the model predictions considering ionization mechanisms different
from the TML's ones overlap and therefore no firm conclusions can be
made based on the [S II]
-0.6, the model predictions considering ionization mechanisms different
from the TML's ones overlap and therefore no firm conclusions can be
made based on the [S II]
![]() 6717,6731/H
6717,6731/H![]() vs. [N II]
vs. [N II]![]() 6584/H
6584/H![]() alone (see Fig. 8). However, much of this overlap disappears when the [O I]
alone (see Fig. 8). However, much of this overlap disappears when the [O I]![]() 6300/H
6300/H![]() ratio is considered. In particular regions showing
ratio is considered. In particular regions showing ![]() ([O I]
([O I]![]() 6300/H
6300/H![]() )
) ![]() -1.6 are best explained by the presence of shocks with velocities of less than 200 km s-1 and metallicities 1-2 solar (see Fig. 9).
-1.6 are best explained by the presence of shocks with velocities of less than 200 km s-1 and metallicities 1-2 solar (see Fig. 9).
We note that a detailed comparison of our data with the models in Figs. 8 and 9 may lead to some inconsistencies. For instance, the [S II]
![]() 6717,6731/H
6717,6731/H![]() - [N II]
- [N II]![]() 6584/H
6584/H![]() diagram presents less data points in the area of shocks of
diagram presents less data points in the area of shocks of
![]() km s-1 than the [O I]
km s-1 than the [O I]![]() 6300/H
6300/H![]() - [N II]
- [N II]![]() 6584/H
6584/H![]() diagram. These disagreements may be due to the intrinsic difficulty in modeling some emission (e.g. [O I]
diagram. These disagreements may be due to the intrinsic difficulty in modeling some emission (e.g. [O I]![]() 6300 line, Dopita & Sutherland 1995)
as well as possible observational effects. The areas sampled by a given
spaxel include both star-forming regions and diffuse ionized gas, which
affect the line ratios differently. In any case, these figures
should be read looking for general behaviors rather than for detailed
comparisons.
6300 line, Dopita & Sutherland 1995)
as well as possible observational effects. The areas sampled by a given
spaxel include both star-forming regions and diffuse ionized gas, which
affect the line ratios differently. In any case, these figures
should be read looking for general behaviors rather than for detailed
comparisons.
Taking this into account, we considered the [O I]![]() 6300/H
6300/H![]() - [N II]
- [N II]![]() 6584/H
6584/H![]() diagram
as our main indicator to establish the most important ionization
mechanism for individual galaxies in Table 3. In some cases this was complemented with other indicators, especially for the galaxies with
no [O I]
diagram
as our main indicator to establish the most important ionization
mechanism for individual galaxies in Table 3. In some cases this was complemented with other indicators, especially for the galaxies with
no [O I]![]() 6300 detections.
6300 detections.
Elevated line ratios can in principle be explained by both shocks and
AGN. This is evident from the models presented in Figs. 8 and 9, as well as from integrated data from the literature (Kewley et al. 2006).
Indeed, four of the 32 galaxies are classified as Seyfert
(the northern member of IRAS F07027-6011,
IRAS F13229-2934, and the western member of
IRAS 14544-4255 and IRAS 21453-3511, see
footnotes in Table 3). The
northern member of IRAS F07027-6011 should not pose a
problem, because most of its line ratios are typical of young stars.
However, as stated in Table 3,
some areas with elevated line ratios could be caused by the nuclear
AGN. The galaxy IRAS 13229-3934 contains a central AGN
which causes an ionization cone in the north-south direction (Bedregal et al. 2009). However, our measured line ratios are associated to wide areas in the inter-arms
zone, not coincident with the direction of the ionization cone, and
thus difficult to be explained by the central AGN. Finally, for the
western member IRAS 14544-4255 and
IRAS 21453-3511, it is not possible to discern with
the present information whether the ionization in the external areas is
caused by shocks or the central
AGN. However, an indirect argument allows us to favor shocks
against AGN as the mechanisms responsible of the observed line ratios.
As was shown for Arp 299, a very nearby LIRG,
the extra-nuclear area with an excitation caused by the AGN
(as seen by the [O III]![]() 5007/H
5007/H![]() line
ratio) is very small and restricted to specific directions defined by
the ionization cone (see detailed analysis for this system in García-Marín et al. 2006).
Also, nuclear regions, where one could expect the largest influence of
an AGN, were removed from our analysis (see Sect. 2.4).
line
ratio) is very small and restricted to specific directions defined by
the ionization cone (see detailed analysis for this system in García-Marín et al. 2006).
Also, nuclear regions, where one could expect the largest influence of
an AGN, were removed from our analysis (see Sect. 2.4).
It is worth mentioning that the metallicities (solar to twice solar) of the models (H II and shocks) that best fit the range of data are underabundant by a factor of
![]() with respect to what is expected from the mass-metallicity relation for galaxies (Tremonti et al. 2004). This relation predicts metallicities of
with respect to what is expected from the mass-metallicity relation for galaxies (Tremonti et al. 2004). This relation predicts metallicities of
![]()
![]() for galaxies with masses as those expected in typical LIRGs (
for galaxies with masses as those expected in typical LIRGs (
![]() ,
e.g., Väisänen et al. 2008a,b; Hinz & Rieke 2006). Similar findings for the nuclear region of these kinds of galaxies have been reported by Rupke et al. (2008).
,
e.g., Väisänen et al. 2008a,b; Hinz & Rieke 2006). Similar findings for the nuclear region of these kinds of galaxies have been reported by Rupke et al. (2008).
Table 3: Ionization in the extra-nuclear ionized regions of LIRGs.
In summary, the ionization of the extended, extra-nuclear regions in
isolated galaxies (class 0), is mostly explained as due to
young stars like in H II regions. Systems showing some degree
of interaction (class 1 and 2) present a large and increasing fraction of regions which are better
explained by shocks. This is particularly evident when using the [O I]![]() 6300/H
6300/H![]() vs. [N II]
vs. [N II]![]() 6584/H
6584/H![]() diagnostic
diagram. In particular cases (e.g. IRAS 21453-3511), an
AGN also could explain the observed high line ratios. In order to
explore the precise relevance of a putative AGN, other additional
observables than those utilized here (e.g. flux in the [O III]
diagnostic
diagram. In particular cases (e.g. IRAS 21453-3511), an
AGN also could explain the observed high line ratios. In order to
explore the precise relevance of a putative AGN, other additional
observables than those utilized here (e.g. flux in the [O III]![]() 5007
emission line) would be needed. Further evidence for the presence and
relevance of shocks as ionizing sources can be found through the gas
velocity dispersions and their correlations with the emission line
ratios. This is presented in the next section.
5007
emission line) would be needed. Further evidence for the presence and
relevance of shocks as ionizing sources can be found through the gas
velocity dispersions and their correlations with the emission line
ratios. This is presented in the next section.
3.5 The relation between excitation and gas velocity dispersion: further evidence for the importance of shocks
![\begin{figure}
\par\includegraphics[width=16.8cm,clip]{13239fg10.eps}
\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg85.png)
|
Figure 10:
Relation between the velocity dispersion and the [N II] |
| Open with DEXTER | |
Table 4: Linear Pearson correlation coefficients r and 1-degree polynomial fits for the different morphological groups considered here.
The presence and relevance of shocks in (U)LIRGs has already been
suggested by a positive relation between the ionized gas velocity
dispersion and its ionization degree as traced by the [S II]
![]() 6717,6731/H
6717,6731/H![]() ratio in a sample of about 30 galaxies (Dopita & Sutherland 1995; Veilleux et al. 1995; Armus et al. 1989).
These studies were based on long-slit observations and were therefore
dominated by the contribution from the high-surface brightness nuclear
regions in a large number of cases. Also, the slit was positioned along
a given orientation and therefore the results of these studies do not
necessarily represent the excitation and kinematics of the ionized gas
in the extra-nuclear extended (several kpc) regions. Instead, for the
detailed study of the excitation conditions in the extended regions it
is more appropriate to use the two-dimensional information provided by
IFS data once the nuclear regions are removed, as already
discussed for a small sample of ULIRGs (Monreal-Ibero et al. 2006). We performed a similar study with the present sample of LIRGs, limiting the analysis to the data with [N II]
ratio in a sample of about 30 galaxies (Dopita & Sutherland 1995; Veilleux et al. 1995; Armus et al. 1989).
These studies were based on long-slit observations and were therefore
dominated by the contribution from the high-surface brightness nuclear
regions in a large number of cases. Also, the slit was positioned along
a given orientation and therefore the results of these studies do not
necessarily represent the excitation and kinematics of the ionized gas
in the extra-nuclear extended (several kpc) regions. Instead, for the
detailed study of the excitation conditions in the extended regions it
is more appropriate to use the two-dimensional information provided by
IFS data once the nuclear regions are removed, as already
discussed for a small sample of ULIRGs (Monreal-Ibero et al. 2006). We performed a similar study with the present sample of LIRGs, limiting the analysis to the data with [N II]![]() 6584/H
6584/H![]() ,
[S II]
,
[S II]
![]() 6717,6731/H
6717,6731/H![]() ,
and [O I]
,
and [O I]![]() 6300/H
6300/H![]() higher than -0.7, -0.8, -1.8, respectively (i.e. line ratios in
the range expected for shocks according to the models discussed in the
previous section). In particular, Fig. 10
presents the relation between the excitation degree (here represented
by our three line ratios) and the gas velocity dispersion for the
entire sample (upper panels) and according interaction class (three
lower panels). The relations for each individual pointing have been
appended in the On-line only version (see Fig. 17).
higher than -0.7, -0.8, -1.8, respectively (i.e. line ratios in
the range expected for shocks according to the models discussed in the
previous section). In particular, Fig. 10
presents the relation between the excitation degree (here represented
by our three line ratios) and the gas velocity dispersion for the
entire sample (upper panels) and according interaction class (three
lower panels). The relations for each individual pointing have been
appended in the On-line only version (see Fig. 17).
Several conclusions are already evident from these results. Firstly, the ionized gas in the extra-nuclear regions of LIRGs has typically velocity dispersions between 32 km s-1 (lower limit given by our spectral resolution) and 125 km s-1, with very few regions having velocities above this value, independently of the morphology and infrared luminosity.
Secondly, the velocity dispersion of the ionized gas is larger in
galaxies with some degree of
interaction, i.e. class C1 and C2. While galaxies
identified as isolated have a median velocity dispersion of
37 km s-1, class C1 and C2 have values of 46 km s-1 and 51 km s-1,
respectively. Moreover, the velocity dispersions of class 0
galaxies (i.e. isolated) tend to be
concentrated in the low velocity range, while classes 1 and 2
have a relevant fraction of regions with high velocities. This means
that only 5% of the data points for class 0 galaxies present
velocity dispersions larger than 80 km s-1, while 28% and 16% of those for classes 1 and 2
respectively do when considering, for example, the [O I]![]() 6300/H
6300/H![]() line
ratio. These values are much higher than the median velocity
dispersions measured in the extranuclear ionized regions of normal
galaxies with velocities in the 20 to 30 km s-1 range (Epinat et al. 2010).
This is a clear indication that the ionized interstellar medium in
LIRGs in general, and even more in interacting LIRGs,
is dynamically hotter than the quiescent ISM of normal galaxies
due to the strong shocks produced by the tidal forces and by stellar
winds in the powerful nuclear starbursts.
line
ratio. These values are much higher than the median velocity
dispersions measured in the extranuclear ionized regions of normal
galaxies with velocities in the 20 to 30 km s-1 range (Epinat et al. 2010).
This is a clear indication that the ionized interstellar medium in
LIRGs in general, and even more in interacting LIRGs,
is dynamically hotter than the quiescent ISM of normal galaxies
due to the strong shocks produced by the tidal forces and by stellar
winds in the powerful nuclear starbursts.
Thirdly, there is a clear correlation between the excitation
degree and the velocity dispersion in interacting galaxies
(class 1) and mergers (class 2), while the evidence of
correlation in isolated galaxies (class 0) is poor and restricted
to the relation involving the [N II]![]() 6584/H
6584/H![]() line ratio.
line ratio.
To obtain a more quantitative analysis of the degree of the correlation, the linear Pearson correlation coefficient, r,
is used. This coefficient quantifies the degree of correlation
between two given quantities that are assumed to follow a linear
relation. It varies from -1 to +1,
where +1(-1) means a perfect correlation(anti-correlation) and
0 means no-correlation. The Pearson coefficient for the ![]() ([S II]
([S II]
![]() 6717,6731/H
6717,6731/H![]() ) -
) -
![]() in the Armus et al. (1989) sample
(see
also Fig. 8 in Dopita & Sutherland 1995) has a value of r=0.4.
Hereafter we consider that a positive relation exists between the
excitation conditions and velocity dispersion in the ionized gas only
if r is higher than 0.4. The computed r coefficient
for the different groups as well as the polynomial coefficients
obtained from a least-square one-degree polynomial fit to the mean of
the data in 0.2 dex bins in the velocity dispersion appear in
Table 4. For the
individual pointings, the direct fits to the data are included in the
lower right corner of the corresponding panel in Fig. 17 in the On-line only version.
in the Armus et al. (1989) sample
(see
also Fig. 8 in Dopita & Sutherland 1995) has a value of r=0.4.
Hereafter we consider that a positive relation exists between the
excitation conditions and velocity dispersion in the ionized gas only
if r is higher than 0.4. The computed r coefficient
for the different groups as well as the polynomial coefficients
obtained from a least-square one-degree polynomial fit to the mean of
the data in 0.2 dex bins in the velocity dispersion appear in
Table 4. For the
individual pointings, the direct fits to the data are included in the
lower right corner of the corresponding panel in Fig. 17 in the On-line only version.
![\begin{figure}
\par\includegraphics[width=5.8cm,clip]{13239fg11.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg86.png)
|
Figure 11: Variation of the r coefficient (up) and percentage of galaxies with a confidence level higher than 90% showing correlation (down) with the interaction types (0 = isolated, 1 = interacting pairs, 2 = merger remnants) for the three emission line ratios. We used the same line and color code as in Fig. 4 to distinguish among the emission line ratios. |
| Open with DEXTER | |
The confidence level of the different relations was estimated by means
of the t-Student test. All relations corresponding to the different
groups present a confidence level higher than 99.9%.
For individual pointings, the [N II]![]() 6584/H
6584/H![]() -
- ![]() show a larger degree of confidence than those for the [S II]
show a larger degree of confidence than those for the [S II]
![]() 6717,6731/H
6717,6731/H![]() -
- ![]() and [O I]
and [O I]![]() 6300/H
6300/H![]() -
- ![]() relations, because the S/N limits the number of points.
All relations involving the [N II]
relations, because the S/N limits the number of points.
All relations involving the [N II]![]() 6584/H
6584/H![]() line
ratio except the southern member of IRAS 18093-5744
present a level of confidence higher than 95%. For the other
line ratios the level of confidence is in general lower. For the
[S II]
line
ratio except the southern member of IRAS 18093-5744
present a level of confidence higher than 95%. For the other
line ratios the level of confidence is in general lower. For the
[S II]
![]() 6717,6731/H
6717,6731/H![]() line
ratio, 11 out of 36 pointings (i.e. 30%) did not reach
a 90% of confidence level. These are
IRAS F06295-1735, IRAS F11255-4120,
IRAS F11506-3851, IRAS F01159-4443,
ESO 297-G012, IC 563, both pointings for
IC 564, the northern and central member of
IRAS 18093-5744 and IRAS 12596-1529.
In the case of the relation involving the [O I]
line
ratio, 11 out of 36 pointings (i.e. 30%) did not reach
a 90% of confidence level. These are
IRAS F06295-1735, IRAS F11255-4120,
IRAS F11506-3851, IRAS F01159-4443,
ESO 297-G012, IC 563, both pointings for
IC 564, the northern and central member of
IRAS 18093-5744 and IRAS 12596-1529.
In the case of the relation involving the [O I]![]() 6300/H
6300/H![]() line
ratio 22% of the pointings (i.e. 6 out of 27) did
not reach a 90% confidence level. They are the southern member of
IRAS F07027-6011, ESO 297-G011,
ESO 297-G012, IRAS 08424-3130, the
central member of IRAS 18093-5744 and
IRAS 12596-1529.
line
ratio 22% of the pointings (i.e. 6 out of 27) did
not reach a 90% confidence level. They are the southern member of
IRAS F07027-6011, ESO 297-G011,
ESO 297-G012, IRAS 08424-3130, the
central member of IRAS 18093-5744 and
IRAS 12596-1529.
The variation of the Pearson coefficient (r) with the interaction class is summarized in the upper part of Fig. 11. The percentage of galaxies in each group showing a correlation coefficient r>0.4 and a level of confidence higher than 90% is summarized in the lower part of Fig. 11.
The quantitative analysis emphasizes the main differences according to
the interaction class already mentioned above. The degree of
correlation between the excitation properties and the velocity
dispersion of the ionized gas when the [S II]
![]() 6717,6731/H
6717,6731/H![]() and [O I]
and [O I]![]() 6300/H
6300/H![]() line ratios are considered increases with the degree of interaction. In particular, the [O I]
line ratios are considered increases with the degree of interaction. In particular, the [O I]![]() 6300/H
6300/H![]() ratio
is the best tracer of shocks as already shown in the previous section.
When using this ratio, the Pearson correlation coefficient for the
class 0 galaxies is r= 0.30, indicating no correlation.
This result supports the idea that shocks are not playing an important
role in the ionization of the external areas of this group of LIRGs and
agrees well with our previous findings that young stars are the main
cause for the ionization. On the other hand, the mean r values
for classes 1 and 2 (0.48 and 0.61, respectively) are
well above the 0.4 criterion, which we considered necessary for a
good positive relation. This quantitative result clearly supports a
direct cause-effect relation
between the dynamical status of the gas, i.e. turbulence and
shocks traced by the velocity dispersion, and its excitation
conditions.
ratio
is the best tracer of shocks as already shown in the previous section.
When using this ratio, the Pearson correlation coefficient for the
class 0 galaxies is r= 0.30, indicating no correlation.
This result supports the idea that shocks are not playing an important
role in the ionization of the external areas of this group of LIRGs and
agrees well with our previous findings that young stars are the main
cause for the ionization. On the other hand, the mean r values
for classes 1 and 2 (0.48 and 0.61, respectively) are
well above the 0.4 criterion, which we considered necessary for a
good positive relation. This quantitative result clearly supports a
direct cause-effect relation
between the dynamical status of the gas, i.e. turbulence and
shocks traced by the velocity dispersion, and its excitation
conditions.
In summary, there are two clear differences between LIRGs classified as class 0 (i.e. isolated), and those classified as class 1 (mostly pairs), and class 2 (mergers). The ionized gas in classes 1 and 2 is characterized by covering a wide range in velocity dispersion with an extension towards higher values than class 0 galaxies. Moreover, the dynamical status of the gas, turbulence and shocks, plays an important role in the excitation of the gas mainly in LIRGs classified as interacting pairs or evolved mergers.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13239fg12.eps}
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg87.png)
|
Figure 12: Same as Fig. 10 but for class 1 and 2 systems grouped in four luminosity bins. |
| Open with DEXTER | |
Table 5: Linear Pearson correlation coefficients r and linear fits for for the class 1 and 2 LIRGs distributed in luminosity groups spanning the entire luminosity range.
3.6 Tidal forces as the origin of shocks in the extra-nuclear regions?
It was shown above that the importance of shocks in large extended regions increases with the interaction class. What is the origin of these shocks? Are the shocks caused by the tidal forces due to the interaction process itself? Or are the shocks produced in stellar superwinds associated with the intense starbursts generated in the nuclear regions?
To answer these questions, we investigated how the relation between the
excitation conditions and gas velocity dispersion varies with the total
infrared luminosity of the system. In the sample considered here,
only four objects were classified as Seyfert - and thus harboring
an AGN- according to their nuclear spectra (Corbett et al. 2003; Kewley et al. 2001b) (see Table 3).
Thus the total infrared luminosity is considered in general a direct
tracer of the intensity of the star formation, because the infrared
luminosity in these galaxies scales linearly with the star-formation
rate
(e.g. Kennicutt 1998). Figure 12 presents similar relations to those
in Fig. 10
for those classes with some degree of interaction (class 1
and 2) but this time binned in four luminosity ranges covering the
entire luminosity range of LIRGs (i.e. from 1011 to 10
![]() ).
).
Contrary to what happens with the interaction class there is no evidence for a dependence of the correlation coefficient with the luminosity bin,
independently of the utilized line ratio.
Assuming star-formation dominates the energy output in these galaxies
(see above), the range in infrared luminosity covered by the
sample represents a change of a factor ten in the star-formation rate
(see Kennicutt 1984,
for the specific relation). Therefore the radiative and mechanical
energy released in the surrounding ISM due to supernovae explosions and
stellar winds produced in young massive stars would increase linearly
with the rate of star formation (see e.g. Colina et al. 1991).
These linear relations in the mass, momentum and energy deposition have
already been measured in the cool, neutral gas traced by the Na I line (Rupke et al. 2005b). However, these studies do show some evidence for a flattening of these relationships for star-formation rates above 10 ![]() yr-1 (i.e. LIRG and ULIRG range). It is unclear whether these results would apply to the ionized gas traced by the H
yr-1 (i.e. LIRG and ULIRG range). It is unclear whether these results would apply to the ionized gas traced by the H![]() line.
The momentum and energy release in the cool, neutral gas is usually a
small fraction of the energy in the warm ionized and hot X-ray emitting
gas. Moreover, the nonlinear relation between the outflow velocity of
the cool gas and the SFR (
line.
The momentum and energy release in the cool, neutral gas is usually a
small fraction of the energy in the warm ionized and hot X-ray emitting
gas. Moreover, the nonlinear relation between the outflow velocity of
the cool gas and the SFR (![]() SFR0.35, Martin 2005)
could indicate a saturation in the mechanical energy liberated into the
more dense neutral gas, but not necessarily in the other phases of the
ISM. In addition, the velocity gradients measured in several
outflows detected in ULIRGs are inconsistent with the expected gaseous
radial flows produced by nuclear (size of 200-300 pc)
starbursts (Martin 2006). These gradients could
indeed still be consistent with more extended starbursts on scales
of kpc, or shocks generated by tidal forces during the
interaction process (Martin 2006). Our H
SFR0.35, Martin 2005)
could indicate a saturation in the mechanical energy liberated into the
more dense neutral gas, but not necessarily in the other phases of the
ISM. In addition, the velocity gradients measured in several
outflows detected in ULIRGs are inconsistent with the expected gaseous
radial flows produced by nuclear (size of 200-300 pc)
starbursts (Martin 2006). These gradients could
indeed still be consistent with more extended starbursts on scales
of kpc, or shocks generated by tidal forces during the
interaction process (Martin 2006). Our H![]() IFS of (U)LIRGs indicates that the H
IFS of (U)LIRGs indicates that the H![]() emission is more concentrated than that of the stellar continuum. In particular, the fraction of H
emission is more concentrated than that of the stellar continuum. In particular, the fraction of H![]() emission within the central 2 kpc is higher than that of the continuum for about 80% of the cases. However,
emission within the central 2 kpc is higher than that of the continuum for about 80% of the cases. However, ![]() 60% of the objects have more than half of their H
60% of the objects have more than half of their H![]() emission outside the central 2 kpc (see Rodríguez-Zaurín et al. 2010 for details).
emission outside the central 2 kpc (see Rodríguez-Zaurín et al. 2010 for details).
Therefore, if the detected evidence of shocks were due to star formation, it would be reasonable to expect a more turbulent gas with stronger outflows and shocks. This could be traced by higher excitation conditions and velocity dispersions in the ionized gas as well as higher correlation degrees. No evidence for any of this is observed in the present data that sample large extra-nuclear regions of several hundreds of pc to several kpc in size, outside the circumnuclear regions.
The comparison between Figs. 10 and 12
indicates that the presence and relevance of shocks are more strongly
correlated with the interaction/merging
class of a system than with its star formation activity. Indeed, our
sample of class 0 galaxies shows on average a level of star
formation activity (i.e. infrared luminosity) similar to or
slightly lower than that of classes 1 and 2 (
![]() for
class 0 against 11.51 and 11.60 for classes 1
and 2, respectively). Note that this statement is valid for our
particular sample, which was selected in order to cover all the
interaction types and luminosity ranges in a more or less uniform way.
However, it does not apply to complete samples of LIRGs, because
they show a much higher percentage of interaction/merging systems at
higher luminosities (e.g. Sanders & Ishida 2004).
These results point to tidal forces associated with the
interaction/merging
process as the origin for the shock ionization in the extended,
extra-nuclear regions. A similar result was found by MAC06, who
concluded that the more likely explanation for shocks in five out of
the six ULIRGs studied there were tidally induced large scale gas flows
caused by the merging process.
for
class 0 against 11.51 and 11.60 for classes 1
and 2, respectively). Note that this statement is valid for our
particular sample, which was selected in order to cover all the
interaction types and luminosity ranges in a more or less uniform way.
However, it does not apply to complete samples of LIRGs, because
they show a much higher percentage of interaction/merging systems at
higher luminosities (e.g. Sanders & Ishida 2004).
These results point to tidal forces associated with the
interaction/merging
process as the origin for the shock ionization in the extended,
extra-nuclear regions. A similar result was found by MAC06, who
concluded that the more likely explanation for shocks in five out of
the six ULIRGs studied there were tidally induced large scale gas flows
caused by the merging process.
Detailed studies of the nearest ULIRG Arp 220 (Colina et al. 2003; McDowell et al. 2003)
have also suggested that large extended regions in this system arise
purely from merger dynamics and collisional shock heating of the gas.
At the same time, footprints associated with starburst superwinds
have also been detected (Heckman et al. 1990; Arribas et al. 2001).
In Arp 220, the ionized gas plumes that could be
associated with superwinds generated in the nuclear starburst form an
elongated structure up to a distance of about 2 kpc from the
nucleus. However, for the present sample of LIRGs, which show a
significant lower star-forming activity based on their
![]() but similar dynamical mass (Väisänen et al. 2008a; Hinz & Rieke 2006; Väisänen et al. 2008b) and hence similar escape velocity, a smaller area of influence of the stellar superwinds should be expected.
but similar dynamical mass (Väisänen et al. 2008a; Hinz & Rieke 2006; Väisänen et al. 2008b) and hence similar escape velocity, a smaller area of influence of the stellar superwinds should be expected.
Thus our results indicate that the tidal forces during the interaction process are the mechanism producing the ionizing shocks in the extended extra-nuclear regions in LIRGs. This is still compatible with the existence of SGWs produced in nuclear starbursts at distances closer to the nucleus (i.e. radius of 1 to 2 kpc), or AGN ionizing cones along particular orientations (e.g. Arp 299, García-Marín et al. 2006).
3.7 Interacting LIRGs and ULIRGs. Towards a common
log([O I] 6300/H
6300/H )
- log(
)
- log(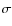 )
relation?
)
relation?
In previous sections we showed that our IFS data indicate that shocks produced by the tidal forces in interacting and merging LIRGs play a relevant role in the excitation of the extended ionized regions, without any clear relation with the intensity of the star formation. Because ULIRGs are the extreme cases of interactions and mergers, one may wonder how the LIRGs situation compares with that for the ULIRGs. For that purpose, we compared our results with those presented in MAC06. The relatively small sample of MAC06 (i.e. six ULIRGs systems, nine galaxies) was made out of three class 1 systems (IRAS 08572+3915, IRAS 12112+0305, IRAS 14348-1447) and three class 2 systems (IRAS 15206+3342, IRAS 15250+3609, IRAS 17208-0014). We found that in all the systems but IRAS 17208-0014 the extra-nuclear extended regions were well explained by ionization due to fast shocks with velocities of 150-500 km s-1. Because none of the systems in the MAC06's ULIRGs sample is classified as isolated (class 0), we present in Fig. 13 (second row) the line ratio vs. velocity dispersion only for LIRGS of classes 1 and 2.
Considering the best shock tracer, the [O I]![]() 6300/H
6300/H![]() line ratio, the similarity of the
line ratio, the similarity of the ![]() ([O I]
([O I]![]() 6300/H
6300/H![]() ) -
) -
![]() correlation found independently for LIRGs and ULIRGs is remarkable. Because the average infrared luminosity (
correlation found independently for LIRGs and ULIRGs is remarkable. Because the average infrared luminosity (
![]() )
of the ULIRG sample is 12.24, this extends the previous
result found for class 1 and class 2 LIRGs, where a similar
linear relation exists for the entire LIRG luminosity range,
independent of the luminosity beam selected. Although the number of
ULIRGs in the MAC06 sample is small, the combined results
suggest a common
relation between the excitation and dynamical properties of the ionized
gas in interacting and merging (U)LIRGs over the entire infrared
luminosity range of
)
of the ULIRG sample is 12.24, this extends the previous
result found for class 1 and class 2 LIRGs, where a similar
linear relation exists for the entire LIRG luminosity range,
independent of the luminosity beam selected. Although the number of
ULIRGs in the MAC06 sample is small, the combined results
suggest a common
relation between the excitation and dynamical properties of the ionized
gas in interacting and merging (U)LIRGs over the entire infrared
luminosity range of
![]() covered by these two samples. This relation is best traced by the direct proportionality (slope of
covered by these two samples. This relation is best traced by the direct proportionality (slope of ![]() 1.0) between
1.0) between ![]() ([O I]
([O I]![]() 6300/H
6300/H![]() )
and
)
and
![]() (see Tables 4 and 6
for the specific slopes). A larger sample of about 20 ULIRGs
with available optical integral field spectroscopy is currently under
study (García-Marín et al., in preparation) to further
investigate the reality of the relation for both LIRGs and ULIRGs and
its physical interpretation.
(see Tables 4 and 6
for the specific slopes). A larger sample of about 20 ULIRGs
with available optical integral field spectroscopy is currently under
study (García-Marín et al., in preparation) to further
investigate the reality of the relation for both LIRGs and ULIRGs and
its physical interpretation.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13239fg13.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg96.png)
|
Figure 13: Upper row: same as Fig. 10, but for all systems in MAC06 but IRAS 17208-0014. This is similar to the first row of Fig. 4 of MAC06 but we plotted the same ranges in the axes as in Fig. 10 for a better comparison with the results in the present paper. Lower row: same as Fig. 10 for the combined class 1 + class 2 group. |
| Open with DEXTER | |
Table 6: Linear Pearson correlation coefficients r and linear fits for all C1 and C2 LIRGs and ULIRGs.
4 Conclusions
The two-dimensional ionization structure of the extended (few to
several kpc) ionized gas in a representative sample of 32 low-z LIRGs (i.e.
![]() luminosity range) was investigated with the VIMOS integral field
spectrograph. The sample covers isolated galaxies, as well as
interacting galaxies and systems in an advanced stage of the merger.
This paper investigates the nature and origin of the main ionization
mechanisms operating in the extra-nuclear regions of these systems
based on several thousands of independent measurements of the emission
line ratios (up to 24 000 for [N II]
luminosity range) was investigated with the VIMOS integral field
spectrograph. The sample covers isolated galaxies, as well as
interacting galaxies and systems in an advanced stage of the merger.
This paper investigates the nature and origin of the main ionization
mechanisms operating in the extra-nuclear regions of these systems
based on several thousands of independent measurements of the emission
line ratios (up to 24 000 for [N II]![]() 6584/H
6584/H![]() )
and velocity dispersions.
)
and velocity dispersions.
The present study is part of a larger project devoted to the study of the two-dimensional structure for the stars and ionized gas as well as its kinematics and ionization conditions in representative samples of LIRGs and ULIRGs using optical IFS. The main results of this study can be summarized as follows:
- 1.
- The distribution of the [N II]
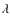 6584/H
6584/H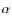 line
ratio does not show any significant variations with the interaction
class, with most regions presenting a ratio typical of H II regions. The [S II]
line
ratio does not show any significant variations with the interaction
class, with most regions presenting a ratio typical of H II regions. The [S II]
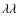 6717,6731/H
6717,6731/H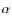 and [O I]
and [O I]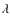 6300/H
6300/H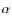 line
ratios do however show a change in their distribution with an extension
towards higher excitation (i.e. LINER-like excitation) for
galaxies classified as interacting pairs and advanced mergers. This
change is more pronounced for the [O I]
line
ratios do however show a change in their distribution with an extension
towards higher excitation (i.e. LINER-like excitation) for
galaxies classified as interacting pairs and advanced mergers. This
change is more pronounced for the [O I]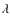 6300/H
6300/H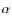 ratio.
ratio.
- 2.
- There is an anti-correlation between the ionization degree and the H
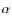 surface
brightness independently of the interaction type and similar to what
occurs in our Galaxy or in the so-called DIG in other spiral galaxies.
Most of the observed line ratios are similar to those found in H II regions in our Galaxy, but there is a relatively large percentage of line ratios similar to those for DIGs.
surface
brightness independently of the interaction type and similar to what
occurs in our Galaxy or in the so-called DIG in other spiral galaxies.
Most of the observed line ratios are similar to those found in H II regions in our Galaxy, but there is a relatively large percentage of line ratios similar to those for DIGs.
- 3.
- The nature of the ionization sources was investigated comparing the measured [S II]
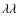 6717,6731/H
6717,6731/H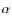 vs. [N II]
vs. [N II]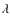 6584/H
6584/H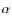 and [O I]
and [O I]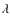 6300/H
6300/H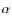 vs. [N II]
vs. [N II]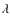 6584/H
6584/H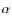 line ratios with the predictions of ionization due to stars (H II regions),
TML, shocks (DIGs) and power-law (AGN) spectra. Turbulent Mixing Layers
do not seem to play a major role in the ionization of the extra-nuclear
regions. Line ratios in LIRGs classified as isolated can mostly be
explained as caused by ionization due to young stars. On the other
hand, the ionization in a large fraction of the regions in systems
with some degree of interaction cannot be due to
stars but is better explained by high velocity shocks. This is
particularly evident when using the best shock tracer, i.e. the
[O I]
line ratios with the predictions of ionization due to stars (H II regions),
TML, shocks (DIGs) and power-law (AGN) spectra. Turbulent Mixing Layers
do not seem to play a major role in the ionization of the extra-nuclear
regions. Line ratios in LIRGs classified as isolated can mostly be
explained as caused by ionization due to young stars. On the other
hand, the ionization in a large fraction of the regions in systems
with some degree of interaction cannot be due to
stars but is better explained by high velocity shocks. This is
particularly evident when using the best shock tracer, i.e. the
[O I]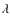 6300/H
6300/H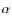 vs. [N II]
vs. [N II]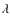 6584/H
6584/H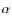 diagram.
Independently of the ionization mechanisms, only models with
metallicity between solar and twice solar are able to explain the
observed line ratios.
diagram.
Independently of the ionization mechanisms, only models with
metallicity between solar and twice solar are able to explain the
observed line ratios.
- 4.
- Local velocity dispersions increase with the interaction degree, with medians of 37, 46, and 51 km -1 for class 0-2 respectively, and are higher than those typically found in normal spirals (
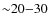 km s-1, Epinat et al. 2010).
This indicates that the ionized ISM in LIRGs is dynamically hotter than
the quiescent ISM of normal galaxies due to strong shocks produced by
tidal forces and stellar winds associated to the nuclear starburst.
km s-1, Epinat et al. 2010).
This indicates that the ionized ISM in LIRGs is dynamically hotter than
the quiescent ISM of normal galaxies due to strong shocks produced by
tidal forces and stellar winds associated to the nuclear starburst.
- 5.
- There is a positive relation between the degree of excitation
(as traced by the emission line ratios) and the velocity
dispersion of the ionized gas in LIRGs classified as interacting
systems, and mergers, while this relation is not observed in isolated
systems. This relation is better seen when using the [O I]
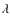 6300/H
6300/H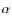 and [S II]
and [S II]
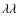 6717,6731/H
6717,6731/H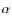 line
ratios, and supports the scenario where the relevance of shocks as
ionizing sources in the extranuclear extended regions of LIRGs
increases when there is some degree of interaction.
line
ratios, and supports the scenario where the relevance of shocks as
ionizing sources in the extranuclear extended regions of LIRGs
increases when there is some degree of interaction. - 6.
- The relation between the degree of excitation and the velocity dispersion of the ionized gas in interacting and merging LIRGs does not clearly improve with the infrared luminosity (i.e. star formation rate) of the systems. Thus the interaction process itself rather than superwinds caused by the star formation seems to be the main origin of the shocks in the extended extra-nuclear regions, assuming that the release of energy into the ISM is proportional to the SFR. This result is still compatible with stellar superwinds in the internal regions of these systems, and/or along certain preferential directions associated with AGN-related outflows.
- 7.
- A comparison between the sub-sample of interacting/merging
LIRGs and a small sample of ULIRGs suggests the existence of a common
positive
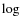 ([O I]
([O I]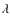 6300/H
6300/H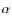 ) -
) -
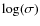 relation.
If confirmed, these results will provide further evidence for the
tidal origin of shocks in these galaxies over the entire LIRG and ULIRG
luminosity range. A study with a larger sample of ULIRGs is under
way to confirm the result.
relation.
If confirmed, these results will provide further evidence for the
tidal origin of shocks in these galaxies over the entire LIRG and ULIRG
luminosity range. A study with a larger sample of ULIRGs is under
way to confirm the result.
We thank J. Alfonso-Garzón for her help in the initial stages of this project. We also thank the anonymous referee for his/her careful and detailed review of the manuscript that helped to greatly improve this paper. Based on observations collected at the European Organisation for Astronomical Research in the Southern Hemisphere, Chile (ESO Programs 076.B-0479(A), 078.B-0072(A) and 081.B-0108(A)). A.M.-I. is grateful for the hospitality of the Instituto de Estructura de la Materia where part of this work was performed. This paper uses the plotting package jmaplot, developed by Jesús Maíz-Apellániz, http://dae45.iaa.csic.es:8080/ jmaiz/software. This research made use of the NASA/IPAC Extragalactic Database (NED), which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. This work has been supported by the Spanish Ministry for Education and Science under grants PNE2005-01480 and ESP2007-65475-C02-01. A.M.-I. is supported by the Spanish Ministry of Science and Innovation (MICINN) under the program ``Specialization in International Organisms'', Ref. ES2006-0003. M.G.-M. is supported by the German federal department for education and research (BMBF) under the project numbers: 50OS0502 & 50OS0801.
References
- Allen, M. G., Groves, B. A., Dopita, M. A., Sutherland, R. S., & Kewley, L. J. 2008, ApJS, 178, 20 [Google Scholar]
- Alonso-Herrero, A., Rieke, G. H., Rieke, M. J., & Scoville, N. Z. 2002, AJ, 124, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Alonso-Herrero, A., Rieke, G. H., Rieke, M. J., et al. 2006, ApJ, 650, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Alonso-Herrero, A., García-Marín, M., Monreal-Ibero, A., et al. 2009, A&A, 506, 1541 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alonso-Herrero, A., García-Marín, M., Rodríguez-Zaurín, J., et al. 2010, A&A, accepted [Google Scholar]
- Armus, L., Heckman, T. M., & Miley, G. K. 1989, ApJ, 347, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Arribas, S., Carter, D., Cavaller, L., et al. 1998, in SPIE Conf. Ser. 3355, ed. S. D'Odorico, 821 [Google Scholar]
- Arribas, S., Colina, L., & Clements, D. 2001, ApJ, 560, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Arribas, S., Bushouse, H., Lucas, R. A., Colina, L., & Borne, K. D. 2004, AJ, 127, 2522 [NASA ADS] [CrossRef] [Google Scholar]
- Arribas, S., Colina, L., Monreal-Ibero, A., et al. 2008, A&A, 479, 687 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., Allende Prieto, C., & Kiselman, D. 2004, A&A, 417, 751 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baldwin, J. A., Phillips, M. M., & Terlevich, R. 1981, PASP, 93, 5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bedregal, A. G., Colina, L., Alonso-Herrero, A., & Arribas, S. 2009, ApJ, 698, 1852 [NASA ADS] [CrossRef] [Google Scholar]
- Bingham, R. G., Gellatly, D. W., Jenkins, C. R., & Worswick, S. P. 1994, in SPIE Conf. Ser. 2198, ed. D. L. Crawford, & E. R. Craine, 56 [Google Scholar]
- Blanc, G. A., Heiderman, A., Gebhardt, K., Evans, N. J., & Adams, J. 2009, ApJ, 704, 842 [NASA ADS] [CrossRef] [Google Scholar]
- Borne, K. D., Bushouse, H., Lucas, R. A., & Colina, L. 2000, ApJ, 529, L77 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bushouse, H. A., Borne, K. D., Colina, L., et al. 2002, ApJS, 138, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Clements, D. L., Sutherland, W. J., McMahon, R. G., & Saunders, W. 1996, MNRAS, 279, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Colina, L., Lípari, S., & Macchetto, F. 1991, ApJ, 379, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Colina, L., González Delgado, R., Mas-Hesse, J. M., Leitherer, C., & Jiménez Bailón, E. 2003, ApJ, 582, 1269 [NASA ADS] [CrossRef] [Google Scholar]
- Colina, L., Arribas, S., & Monreal-Ibero, A. 2005, ApJ, 621, 725 [NASA ADS] [CrossRef] [Google Scholar]
- Collins, J. A., & Rand, R. J. 2001, ApJ, 551, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Corbett, E. A., Kewley, L., Appleton, P. N., et al. 2003, ApJ, 583, 670 [NASA ADS] [CrossRef] [Google Scholar]
- Cui, J., Xia, X.-Y., Deng, Z.-G., Mao, S., & Zou, Z.-L. 2001, AJ, 122, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Dopita, M. A., & Sutherland, R. S. 1995, ApJ, 455, 468 [NASA ADS] [CrossRef] [Google Scholar]
- Dopita, M. A., Pereira, M., Kewley, L. J., & Capaccioli, M. 2002, ApJS, 143, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Dopita, M. A., Fischera, J., Sutherland, R. S., et al. 2006, ApJS, 167, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenhauer, F., Abuter, R., Bickert, K., et al. 2003, in SPIE Conf. Ser. 4841, ed. M. Iye, & A. F. M. Moorwood, 1548 [Google Scholar]
- Elbaz, D., Cesarsky, C. J., Chanial, P., et al. 2002, A&A, 384, 848 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Epinat, B., Amram, P., Balkowski, C., & Marcelin, M. 2010, MNRAS, 401, 2113 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, A. S., Mazzarella, J. M., Surace, J. A., & Sanders, D. B. 2002, ApJ, 580, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Farrah, D., Bernard-Salas, J., Spoon, H. W. W., et al. 2007, ApJ, 667, 149 [NASA ADS] [CrossRef] [Google Scholar]
- García-Marín, M., Colina, L., Arribas, S., Alonso-Herrero, A., & Mediavilla, E. 2006, ApJ, 650, 850 [NASA ADS] [CrossRef] [Google Scholar]
- García-Marín, M., Colina, L., Arribas, S., & Monreal-Ibero, A. 2009, A&A, 505, 1319 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Genzel, R., Lutz, D., Sturm, E., et al. 1998, ApJ, 498, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Groves, B. A., Dopita, M. A., & Sutherland, R. S. 2004, ApJS, 153, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Heckman, T. M., Armus, L., & Miley, G. K. 1990, ApJS, 74, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Heckman, T. M., Lehnert, M. D., Strickland, D. K., & Armus, L. 2000, ApJS, 129, 493 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Hinz, J. L., & Rieke, G. H. 2006, ApJ, 646, 872 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, G., Heckman, T. M., Tremonti, C., et al. 2003, MNRAS, 346, 1055 [Google Scholar]
- Kennicutt, Jr., R. C. 1984, ApJ, 287, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, Jr., R. C. 1998, ARA&A, 36, 189 [Google Scholar]
- Kewley, L. J., Dopita, M. A., Sutherland, R. S., Heisler, C. A., & Trevena, J. 2001a, ApJ, 556, 121 [Google Scholar]
- Kewley, L. J., Heisler, C. A., Dopita, M. A., & Lumsden, S. 2001b, ApJS, 132, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., Groves, B., Kauffmann, G., & Heckman, T. 2006, MNRAS, 372, 961 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, D.-C., Sanders, D. B., Veilleux, S., Mazzarella, J. M., & Soifer, B. T. 1995, ApJS, 98, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Le Fèvre, O., Saisse, M., Mancini, D., et al. 2003, in SPIE Conf. Ser. 4841, ed. M. Iye, & A. F. M. Moorwood, 1670 [Google Scholar]
- Le Floc'h, E., Papovich, C., Dole, H., et al. 2005, ApJ, 632, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Lehnert, M. D., & Heckman, T. M. 1996, ApJ, 462, 651 [NASA ADS] [CrossRef] [Google Scholar]
- Leitherer, C., Schaerer, D., Goldader, J. D., et al. 1999, ApJS, 123, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Lonsdale, C. J., Farrah, D., & Smith, H. E. 2006, Ultraluminous Infrared Galaxies, ed. J. W. Mason (Springer Verlag), 285 [Google Scholar]
- Madsen, G. J., Reynolds, R. J., & Haffner, L. M. 2006, ApJ, 652, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, C. L. 2005, ApJ, 621, 227 [Google Scholar]
- Martin, C. L. 2006, ApJ, 647, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S. 2000, ApJ, 544, 347 [NASA ADS] [CrossRef] [Google Scholar]
- McDowell, J. C., Clements, D. L., Lamb, S. A., et al. 2003, ApJ, 591, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Mihos, J. C., & Hernquist, L. 1996, ApJ, 464, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, S. T., & Veilleux, S. 2003, ApJ, 592, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Monreal-Ibero, A., Arribas, S., & Colina, L. 2006, ApJ, 637, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Moshir, M., et al. 1990, in IRAS Faint Source Catalogue, version 2.0 [Google Scholar]
- Naab, T., Jesseit, R., & Burkert, A. 2006, MNRAS, 372, 839 [NASA ADS] [CrossRef] [Google Scholar]
- Nardini, E., Risaliti, G., Salvati, M., et al. 2008, MNRAS, 385, L130 [NASA ADS] [Google Scholar]
- Pérez-González, P. G., Rieke, G. H., Egami, E., et al. 2005, ApJ, 630, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Rampazzo, R., Plana, H., Amram, P., et al. 2005, MNRAS, 356, 1177 [NASA ADS] [CrossRef] [Google Scholar]
- Reynolds, R. J., Haffner, L. M., & Tufte, S. L. 1999, ApJ, 525, L21 [Google Scholar]
- Risaliti, G., Maiolino, R., Marconi, A., et al. 2006, MNRAS, 365, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Rodríguez-Zaurín, J., Arribas, S., Monreal-Ibero, A., et al. 2010, A&A,submitted [Google Scholar]
- Roth, M. M., Kelz, A., Fechner, T., et al. 2005, PASP, 117, 620 [NASA ADS] [CrossRef] [Google Scholar]
- Rupke, D. S., Veilleux, S., & Sanders, D. B. 2002, ApJ, 570, 588 [NASA ADS] [CrossRef] [Google Scholar]
- Rupke, D. S., Veilleux, S., & Sanders, D. B. 2005a, ApJS, 160, 87 [Google Scholar]
- Rupke, D. S., Veilleux, S., & Sanders, D. B. 2005b, ApJS, 160, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Rupke, D. S. N., Veilleux, S., & Baker, A. J. 2008, ApJ, 674, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, D. B., & Mirabel, I. F. 1996, ARA&A, 34, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, D., & Ishida, C. 2004, in The Neutral ISM in Starburst Galaxies, ed. S. Aalto, S. Huttemeister, & A. Pedlar, ASP Conf. Ser., 320, 230 [Google Scholar]
- Sanders, D. B., Mazzarella, J. M., Kim, D.-C., Surace, J. A., & Soifer, B. T. 2003, AJ, 126, 1607 [Google Scholar]
- Scoville, N. Z., Evans, A. S., Thompson, R., et al. 2000, AJ, 119, 991 [NASA ADS] [CrossRef] [Google Scholar]
- Slavin, J. D., Shull, J. M., & Begelman, M. C. 1993, ApJ, 407, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Stasinska, G., Cid Fernandes, R., Mateus, A., Sodré, L., & Asari, N. V. 2006, MNRAS, 371, 972 [NASA ADS] [CrossRef] [Google Scholar]
- Tremonti, C. A., Heckman, T. M., Kauffmann, G., et al. 2004, ApJ, 613, 898 [NASA ADS] [CrossRef] [Google Scholar]
- Väisänen, P., Mattila, S., Kniazev, A., et al. 2008a, MNRAS, 384, 886 [NASA ADS] [CrossRef] [Google Scholar]
- Väisänen, P., Ryder, S., Mattila, S., & Kotilainen, J. 2008b, ApJ, 689, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Veilleux, S., & Osterbrock, D. E. 1987, ApJS, 63, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Veilleux, S., Kim, D.-C., Sanders, D. B., Mazzarella, J. M., & Soifer, B. T. 1995, ApJS, 98, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Veilleux, S., Kim, D.-C., & Sanders, D. B. 1999, ApJ, 522, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Veilleux, S., Kim, D.-C., & Sanders, D. B. 2002, ApJS, 143, 315 [NASA ADS] [CrossRef] [Google Scholar]
- York, D. G., Adelman, J., Anderson, Jr., J. E., et al. 2000, AJ, 120, 1579 [Google Scholar]
- Yuan, T.-T., Kewley, L. J., & Sanders, D. B. 2010, MNRAS, 709, 884 [Google Scholar]
- Zhou, S., Wynn-Williams, C. G., & Sanders, D. B. 1993, ApJ, 409, 149 [NASA ADS] [CrossRef] [Google Scholar]
Online Material
![\begin{figure}
\par\includegraphics[width=14cm,clip]{13239fg14a.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg99.png)
|
Figure 14: Panel showing the images utilized for the morphological classification. The left column contains details about the size and scale for the displayed images, as well as relevant morphological features and final classification. The central and right columns display the Digital Sky Survey and HST images, respectively. Orientation is north up, east to the left. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{13239fg14b.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg100.png)
|
Figure 14: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{13239fg14c.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg101.png)
|
Figure 14: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{13239fg14d.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg102.png)
|
Figure 14: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{13239fg14e.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg103.png)
|
Figure 14: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{13239fg14f.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg104.png)
|
Figure 14: continued. |
| Open with DEXTER | |
| Figure 14: continued. |
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13239fg15a.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg106.png)
|
Figure 15:
[S II]
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13239fg15b.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg107.png)
|
Figure 15: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13239fg16a.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg108.png)
|
Figure 16:
[O I] |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13239fg16b.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg109.png)
|
Figure 16: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13239fg17a.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg110.png)
|
Figure 17: Line ratios vs. velocity dispersions relation for the individual pointings. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13239fg17b.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg111.png)
|
Figure 17: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13239fg17c.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg112.png)
|
Figure 17: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13239fg17d.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg113.png)
|
Figure 17: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13239fg17e.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg114.png)
|
Figure 17: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13239fg17f.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg115.png)
|
Figure 17: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13239fg17g.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg116.png)
|
Figure 17: continued. |
| Open with DEXTER | |
Footnotes
- ... LIRGs
![[*]](/icons/foot_motif.png)
- Based on observations collected at the European Organisation for Astronomical Research in the Southern Hemisphere, Chile (ESO Programs 076.B-0479(A), 078.B-0072(A) and 081.B-0108(A)).
- ...
![[*]](/icons/foot_motif.png)
- Figures 14-17 are only available in electronic form at http://www.aanda.org
- ... and 0.1
![[*]](/icons/foot_motif.png)
- These ratios have not been corrected for the underlying stellar absorption in H
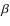 .
Such an absorption could typically decrease the [O III]
.
Such an absorption could typically decrease the [O III]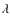 5007/H
5007/H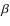 line ratio by
line ratio by  0.0-0.2 dex (see Alonso-Herrero et al. 2009, for details).
0.0-0.2 dex (see Alonso-Herrero et al. 2009, for details).
- ... SDSS
![[*]](/icons/foot_motif.png)
- See http://www.mpa-garching.mpg.de/SDSS/
- ...
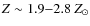
![[*]](/icons/foot_motif.png)
- We have employed
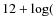 O/H
O/H
 ,
from Asplund et al. (2004).
,
from Asplund et al. (2004).
All Tables
Table 1: VIMOS LIRG sample: for each pointing, the total number of data points, mean value and standard deviation for the different line ratios and velocity dispersion are given.
Table 2: Median, standard deviation, and number of data points for the distributions of the different groups and line ratios.
Table 3: Ionization in the extra-nuclear ionized regions of LIRGs.
Table 4: Linear Pearson correlation coefficients r and 1-degree polynomial fits for the different morphological groups considered here.
Table 5: Linear Pearson correlation coefficients r and linear fits for for the class 1 and 2 LIRGs distributed in luminosity groups spanning the entire luminosity range.
Table 6: Linear Pearson correlation coefficients r and linear fits for all C1 and C2 LIRGs and ULIRGs.
All Figures
![\begin{figure}
\par\mbox{\includegraphics[width=8.5cm,clip]{13239fg1a.eps}\hspac...
...
\includegraphics[width=8.4cm,clip]{13239fg1b.eps} }\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg33.png)
|
Figure 1: Histograms showing the luminosity ( left) and distance ( right) distributions of the systems in the sample. Light, intermediate and dark gray areas indicate the total number of isolated galaxies (class 0), interacting systems (class 1), and merger remnants (class 2), respectively (see text for a more detailed definition of the different morphological types). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16.8cm,clip]{13239fg2a.ps}
\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg50.png)
|
Figure 2:
Maps for H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16.8cm,clip]{13239fg2b.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg51.png)
|
Figure 2: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13239fg2c.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg52.png)
|
Figure 2: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16.8cm,clip]{13239fg2d.ps}\vspace*{-3mm}\vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg53.png)
|
Figure 2: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13239fg2e.ps}
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg54.png)
|
Figure 2: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13239fg2f.ps}\vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg55.png)
|
Figure 2: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{13239fg2g.ps}
\vspace*{6.5mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg56.png)
|
Figure 2: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{13239fg3.eps}
\vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg61.png)
|
Figure 3:
Distributions of the different LIRG subsamples according to [N II] |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{13239fg4a.ps}\vspace*{1mm}
\par\includegraphics[width=6.5cm,clip]{13239fg4b.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg62.png)
|
Figure 4:
Percentage of data for the different interaction classes classified as LINERs using the Veilleux & Osterbrock (1987) line ratio boundaries (up) and Kewley et al. (2001b) ones (down) and assuming [O III] |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{13239fg5.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg64.png)
|
Figure 5: Variation of the median of the average line ratio per galaxy with the interaction class. We use the same line and color code as in Fig. 4 to distinguish among the emission line ratios. |
| Open with DEXTER | |
| In the text | |
| |
Figure 6:
Same as Fig. 3 for NGC 5194 (only [N II] |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13239fg7.eps}
\vspace*{3.5mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg68.png)
|
Figure 7:
Relation between the H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{13239fg8.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg70.png)
|
Figure 8:
[S II]
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{13239fg9.ps}
\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg72.png)
|
Figure 9:
[O I] |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16.8cm,clip]{13239fg10.eps}
\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg85.png)
|
Figure 10:
Relation between the velocity dispersion and the [N II] |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=5.8cm,clip]{13239fg11.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg86.png)
|
Figure 11: Variation of the r coefficient (up) and percentage of galaxies with a confidence level higher than 90% showing correlation (down) with the interaction types (0 = isolated, 1 = interacting pairs, 2 = merger remnants) for the three emission line ratios. We used the same line and color code as in Fig. 4 to distinguish among the emission line ratios. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13239fg12.eps}
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg87.png)
|
Figure 12: Same as Fig. 10 but for class 1 and 2 systems grouped in four luminosity bins. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13239fg13.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg96.png)
|
Figure 13: Upper row: same as Fig. 10, but for all systems in MAC06 but IRAS 17208-0014. This is similar to the first row of Fig. 4 of MAC06 but we plotted the same ranges in the axes as in Fig. 10 for a better comparison with the results in the present paper. Lower row: same as Fig. 10 for the combined class 1 + class 2 group. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{13239fg14a.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg99.png)
|
Figure 14: Panel showing the images utilized for the morphological classification. The left column contains details about the size and scale for the displayed images, as well as relevant morphological features and final classification. The central and right columns display the Digital Sky Survey and HST images, respectively. Orientation is north up, east to the left. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{13239fg14b.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg100.png)
|
Figure 14: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{13239fg14c.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg101.png)
|
Figure 14: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{13239fg14d.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg102.png)
|
Figure 14: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{13239fg14e.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg103.png)
|
Figure 14: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{13239fg14f.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg104.png)
|
Figure 14: continued. |
| Open with DEXTER | |
| In the text | |
| |
Figure 14: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13239fg15a.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg106.png)
|
Figure 15:
[S II]
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13239fg15b.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg107.png)
|
Figure 15: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13239fg16a.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg108.png)
|
Figure 16:
[O I] |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13239fg16b.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg109.png)
|
Figure 16: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13239fg17a.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg110.png)
|
Figure 17: Line ratios vs. velocity dispersions relation for the individual pointings. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13239fg17b.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg111.png)
|
Figure 17: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13239fg17c.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg112.png)
|
Figure 17: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13239fg17d.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg113.png)
|
Figure 17: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13239fg17e.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg114.png)
|
Figure 17: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13239fg17f.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg115.png)
|
Figure 17: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13239fg17g.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13239-09/Timg116.png)
|
Figure 17: continued. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


