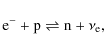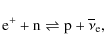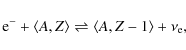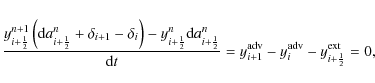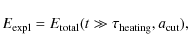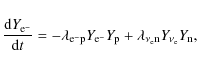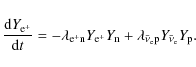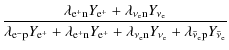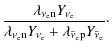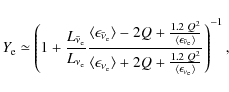| Issue |
A&A
Volume 517, July 2010
|
|
|---|---|---|
| Article Number | A80 | |
| Number of page(s) | 25 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/200913106 | |
| Published online | 11 August 2010 | |
Protoneutron star evolution and the neutrino-driven wind in general relativistic neutrino radiation hydrodynamics simulations
T. Fischer1 - S. C. Whitehouse1 - A. Mezzacappa2 - F.-K. Thielemann1,3 - M. Liebendörfer1
1 - Department of Physics, University of Basel, Klingelbergstrasse 82, 4056 Basel, Switzerland
2 -
Physics Division, Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831-1200, USA
3 -
GSI Helmholtzzentrum für Schwerionenforschung GmbH, Planckstrasse1, 64291 Darmstadt, Germany
Received 11 August 2009 / Accepted 28 March 2010
Abstract
Massive stars end their lives in explosions with kinetic energies on the order of 1051 erg.
Immediately after the explosion has been launched, a region of low
density and high entropy forms behind the ejecta, which is continuously
subject to neutrino heating. The neutrinos emitted from the remnant at
the center, the protoneutron star (PNS), heat the material above
the PNS surface. This heat is partly converted into kinetic
energy, and the material accelerates to an outflow that is known as the
neutrino-driven wind. For the first time we simulate the collapse,
bounce, explosion, and the neutrino-driven wind phases consistently
over more than 20 s. Our numerical model is based on spherically
symmetric general relativistic radiation hydrodynamics using spectral
three-flavor Boltzmann neutrino transport. In simulations where no
explosions are obtained naturally, we model neutrino-driven explosions
for low- and intermediate-mass Fe-core progenitor stars by enhancing
the charged current reaction rates. In the case of a special progenitor
star, the 8.8 M![]() O-Ne-Mg-core, the explosion in spherical symmetry was obtained without
enhanced opacities. The post-explosion evolution is in qualitative
agreement with static
steady-state and parametrized dynamic models of the neutrino-driven
wind. On the other hand, we generally find lower neutrino luminosities
and mean neutrino energies, as well as a different evolutionary
behavior of the neutrino luminosities and mean neutrino energies. The
neutrino-driven wind is proton-rich for more than 10 s and the
contraction of the PNS differs from the assumptions made for the
conditions at the inner boundary in previous neutrino-driven wind
studies.
Despite the moderately high entropies of about 100
O-Ne-Mg-core, the explosion in spherical symmetry was obtained without
enhanced opacities. The post-explosion evolution is in qualitative
agreement with static
steady-state and parametrized dynamic models of the neutrino-driven
wind. On the other hand, we generally find lower neutrino luminosities
and mean neutrino energies, as well as a different evolutionary
behavior of the neutrino luminosities and mean neutrino energies. The
neutrino-driven wind is proton-rich for more than 10 s and the
contraction of the PNS differs from the assumptions made for the
conditions at the inner boundary in previous neutrino-driven wind
studies.
Despite the moderately high entropies of about 100 ![]() /baryon and the fast expansion timescales, the conditions found in our models are unlikely to favor r-process
nucleosynthesis.
The simulations are carried out until the neutrino-driven wind settles
down to a quasi-stationary state. About 5 s after the bounce,
the peak temperature inside the PNS already starts to decrease because
of the continued deleptonization. This moment determines the beginning
of a cooling phase dominated by the emission of neutrinos. We discuss
the physical conditions of the quasi-static PNS evolution and take
the effects of deleptonization and mass accretion from early fallback
into account.
/baryon and the fast expansion timescales, the conditions found in our models are unlikely to favor r-process
nucleosynthesis.
The simulations are carried out until the neutrino-driven wind settles
down to a quasi-stationary state. About 5 s after the bounce,
the peak temperature inside the PNS already starts to decrease because
of the continued deleptonization. This moment determines the beginning
of a cooling phase dominated by the emission of neutrinos. We discuss
the physical conditions of the quasi-static PNS evolution and take
the effects of deleptonization and mass accretion from early fallback
into account.
Key words: hydrodynamics - neutrinos - radiative transfer - relativistic processes
1 Introduction
Stars more massive than 8 M![]() run
into gravitational collapse at the end of their evolution, due to
pressure loss via the photodisintegration of heavy nuclei and electron
captures.
The collapse halts at nuclear density, typically 2-4
run
into gravitational collapse at the end of their evolution, due to
pressure loss via the photodisintegration of heavy nuclei and electron
captures.
The collapse halts at nuclear density, typically 2-4 ![]() 1014 g/cm3
depending on the equation of state (EoS). However,
the supersonically infalling material from the outer core
continues to fall into the center. The core overshoots its equilibrium
configuration and bounces back. A dynamic shock wave forms, which
propagates outwards and continuously loses energy owing to the
dissociation of heavy nuclei. As soon as the shock reaches the
neutrinospheres, i.e. the neutrino energy and flavor dependent
spheres of last scattering, additional electron captures emit a large
amount of electron neutrinos. This burst of electron neutrinos, known
as the deleptonization burst, carries away energy of several 1053 erg/s
on a timescale of 10-20 ms. This energy loss turns the
expanding shock into a standing accretion shock (SAS) already about
5 ms after bounce. Due to the high energy in the neutrino
radiation field, neutrino heating between the neutrinospheres and the
SAS has long been investigated as a possible source of reviving the SAS
and for triggering neutrino-driven explosions (Janka 2001; Bethe & Wilson 1985; Janka et al. 2005; Mezzacappa et al. 2006).
1014 g/cm3
depending on the equation of state (EoS). However,
the supersonically infalling material from the outer core
continues to fall into the center. The core overshoots its equilibrium
configuration and bounces back. A dynamic shock wave forms, which
propagates outwards and continuously loses energy owing to the
dissociation of heavy nuclei. As soon as the shock reaches the
neutrinospheres, i.e. the neutrino energy and flavor dependent
spheres of last scattering, additional electron captures emit a large
amount of electron neutrinos. This burst of electron neutrinos, known
as the deleptonization burst, carries away energy of several 1053 erg/s
on a timescale of 10-20 ms. This energy loss turns the
expanding shock into a standing accretion shock (SAS) already about
5 ms after bounce. Due to the high energy in the neutrino
radiation field, neutrino heating between the neutrinospheres and the
SAS has long been investigated as a possible source of reviving the SAS
and for triggering neutrino-driven explosions (Janka 2001; Bethe & Wilson 1985; Janka et al. 2005; Mezzacappa et al. 2006).
Up to now, neutrino-driven explosions in spherical symmetry have only been obtained for the low-mass 8.8 M![]() O-Ne-Mg-core by Kitaura et al. (2006) and for low- and intermediate-mass Fe-core
progenitor stars by Sagert et al. (2009)
assuming a hadron-quark phase transition during the early post-bounce
phase. On the other hand, multi-dimensional core collapse models with
spectral neutrino transport have only recently become available. They
demonstrate the complexity of the underlying physical phenomena such as
rotation and the development of fluid instabilities. Such models have
been shown to increase the neutrino heating efficiency (see for
example
Miller et al. 1993; Janka & Müller 1996; Herant et al. 1994; Burrows et al. 1995) and help to understand aspherical explosions (see for example Bruenn et al. 2006; Marek & Janka 2009).
For a review of axially-symmetric neutrino-driven explosions, see also Janka et al. (2008).
O-Ne-Mg-core by Kitaura et al. (2006) and for low- and intermediate-mass Fe-core
progenitor stars by Sagert et al. (2009)
assuming a hadron-quark phase transition during the early post-bounce
phase. On the other hand, multi-dimensional core collapse models with
spectral neutrino transport have only recently become available. They
demonstrate the complexity of the underlying physical phenomena such as
rotation and the development of fluid instabilities. Such models have
been shown to increase the neutrino heating efficiency (see for
example
Miller et al. 1993; Janka & Müller 1996; Herant et al. 1994; Burrows et al. 1995) and help to understand aspherical explosions (see for example Bruenn et al. 2006; Marek & Janka 2009).
For a review of axially-symmetric neutrino-driven explosions, see also Janka et al. (2008).
The following dynamical evolution of the PNS and hence the properties of the neutrino spectra emitted is determined by the mass accretion and the EoS. On a timescale of several seconds after the explosion has been launched, the region between the expanding explosion shock, and the PNS at the center is subject to the formation of the neutrino-driven wind as follows. Neutrinos continuously diffuse out of the hot PNS and heat the material on top of the PNS surface before they reach the neutrinospheres. We define the PNS surface to be the radius of the energy-integrated electron-neutrinosphere. The dominant neutrino heating contributions are given by the captures of electron-neutrinos and electron-antineutrinos at free nucleons. Matter is heated by neutrinos and the thermal energy is converted into kinetic energy, which accelerates material on top of the PNS surface to positive velocities. This matter outflow is known as the neutrino-driven wind.
In this context, two particular studies are of special importance. The properties of the neutrino-driven wind as described in Woosley et al. (1994) are based on the detailed radiation
hydrodynamics simulation of a 20 M![]() Fe-core progenitor applying the numerical model from Wilson & Mayle (1993).
The simulation was carried until about 18 s after bounce. Another
state-of-the-art model of that time was the explosion of the
O-Ne-Mg-core by Mayle & Wilson (1988).
Both investigations were milestones in the research of core collapse
supernovae and are based on detailed neutrino input physics including
neutrino transport, developed by J. R. Wilson. The results
obtained, in particular the properties of the ejecta and the
neutrino observables such as luminosities and energies, were considered
the standard reference for more than 10 years.
Neutrino-driven wind studies used the results as parameters, where the
conditions found indicated the possible site for the production of
heavy elements via the r-process. In the simulations discussed in the present paper, we follow a similar approach as Woosley et al. (1994) and Mayle & Wilson (1988), where we apply the neutrino input physics based on Bruenn (1985).
Although the previous work is in qualitative agreement with our
findings, in particular the explosion phase, significant
differences occur in several properties of the neutrino-driven wind.
The entropies per baryon are lower by a factor of 2-3 and the wind
stays proton-rich for more than 10 s for all our models.
In addition, the neutrino luminosities and mean energies are
generally lower. The mean neutrino energies decrease with time, where
they
remain almost constant in the simulation of Woosley et al. (1994).
The largest difference arises in the decreasing difference between the
mean electron neutrino and antineutrino energies found
in our simulations, i.e. the neutrino spectra become more similar
with respect to time. The difference in the neutrino spectra in Woosley et al. (1994) remains large and even increases with time. Using the results from Woosley et al. (1994) as reference, Qian & Woosley (1996)
analyzed the neutrino-driven wind and formulated approximate analytical
expressions for various properties of the neutrino-driven wind,
e.g. the neutrino heating rate, the electron fraction,
the entropy per baryon and the mass outflow rate.
Fe-core progenitor applying the numerical model from Wilson & Mayle (1993).
The simulation was carried until about 18 s after bounce. Another
state-of-the-art model of that time was the explosion of the
O-Ne-Mg-core by Mayle & Wilson (1988).
Both investigations were milestones in the research of core collapse
supernovae and are based on detailed neutrino input physics including
neutrino transport, developed by J. R. Wilson. The results
obtained, in particular the properties of the ejecta and the
neutrino observables such as luminosities and energies, were considered
the standard reference for more than 10 years.
Neutrino-driven wind studies used the results as parameters, where the
conditions found indicated the possible site for the production of
heavy elements via the r-process. In the simulations discussed in the present paper, we follow a similar approach as Woosley et al. (1994) and Mayle & Wilson (1988), where we apply the neutrino input physics based on Bruenn (1985).
Although the previous work is in qualitative agreement with our
findings, in particular the explosion phase, significant
differences occur in several properties of the neutrino-driven wind.
The entropies per baryon are lower by a factor of 2-3 and the wind
stays proton-rich for more than 10 s for all our models.
In addition, the neutrino luminosities and mean energies are
generally lower. The mean neutrino energies decrease with time, where
they
remain almost constant in the simulation of Woosley et al. (1994).
The largest difference arises in the decreasing difference between the
mean electron neutrino and antineutrino energies found
in our simulations, i.e. the neutrino spectra become more similar
with respect to time. The difference in the neutrino spectra in Woosley et al. (1994) remains large and even increases with time. Using the results from Woosley et al. (1994) as reference, Qian & Woosley (1996)
analyzed the neutrino-driven wind and formulated approximate analytical
expressions for various properties of the neutrino-driven wind,
e.g. the neutrino heating rate, the electron fraction,
the entropy per baryon and the mass outflow rate.
Based on the static wind equations, the results obtained in parameter studies (see e.g.
Thompson et al. 2001; Hoffman et al. 1997; Duncan et al. 1986; Thompson & Burrows 2001)
became known as static steady-state wind models, where Woosley & Baron (1992), Woosley et al. (1994), Takahashi et al. (1994) and Witti et al. (1994)
described the neutrino-driven wind in a radiation-hydrodynamics
context. Of special importance for the neutrino-driven wind
investigations is the impact to the nucleosynthesis. Most interesting
is the possibility to explain the production of heavy elements via the r-process due to the high entropies per baryon, the fast expansion timescales and the low electron fraction of
![]() in the wind. Otsuki et al. (2000)
explored general relativistic effects of the neutrino-driven wind and
investigated the possible impact to the nucleosynthesis. Recently,
Wanajo (2006a) and Wanajo (2006b) investigated the neutrino-driven wind with respect to
the r- and rp-processes.
in the wind. Otsuki et al. (2000)
explored general relativistic effects of the neutrino-driven wind and
investigated the possible impact to the nucleosynthesis. Recently,
Wanajo (2006a) and Wanajo (2006b) investigated the neutrino-driven wind with respect to
the r- and rp-processes.
The possibility of supersonic wind velocities has been explored in most of the references. The supersonically expanding material in the wind collides with the much slower expanding and denser explosion ejecta. The material decelerates and a reverse shock forms which is known as the neutrino-driven wind termination shock (first observed by Burrows et al. 1995; Janka & Müller 1995). Recently, Arcones et al. (2007) examined the post-bounce phase of core collapse supernovae of several massive progenitor stars. Their models were launched from massive progenitor stars that were previously evolved through the core collapse, bounce and early post-bounce phases using sophisticated radiation hydrodynamics based on spectral neutrino transport in spherical symmetry. The simulations were then continued applying a simplified radiation hydrodynamics description (see Scheck et al. 2006), assuming high luminosities to trigger neutrino-driven explosions in spherical symmetry. The neutrino-driven wind develops supersonic outflow and the wind termination shock appears in all their models. Like most of the present neutrino-driven wind studies, an interior boundary was assumed instead of simulating the PNS interior for the PNS contraction and the diffusion of neutrinos out of the PNS. However, steady-state wind studies could not predict the important dynamical features from the presence of the neutrino-driven wind termination shock, especially the deceleration of the wind material and the consequent entropy as well as density and temperature increase during the deceleration. In this respect, the investigation from Arcones et al. (2007) was a milestone in modeling the neutrino-driven wind consistently. On the other hand, they were focusing on parameters (luminosities and mean neutrino energies) in agreement with the simulations of Bethe & Wilson (1985) and Woosley et al. (1994). Although the dynamics is in general agreement, several properties of the neutrino-driven wind as well as the neutrino spectra emitted differ significantly from our findings.
The present paper follows a different approach. We simulate
consistently the dynamical evolution
of the collapse, bounce and post-bounce phases until the
neutrino-driven wind phase for more than 20 s. The
simulations are launched from the 8.8 M![]() O-Ne-Mg-core from Nomoto (1984,1983,1987) and the 10.8 and 18 M
O-Ne-Mg-core from Nomoto (1984,1983,1987) and the 10.8 and 18 M![]() Fe-core progenitors
from Woosley et al. (2002).
Our numerical model is based on general relativistic radiation
hydrodynamics with spectral three-flavor Boltzmann neutrino transport
in spherical symmetry. The explosion mechanism of massive Fe-core
progenitors is an active subject of research. To model
neutrino-driven explosions for such progenitors in spherical symmetry,
we enhance the electronic charged current reaction rates artificially
which increases the neutrino energy deposition and revives
the SAS. The mechanism including the tuned neutrino reaction rates
will be further discussed in Sects. 2 and 3. Such explosion
models were investigated with respect to the nucleosynthesis by Fröhlich et al. (2006a-c).
Here, we report on the formation of the neutrino-driven wind and the
possibility of the wind developing supersonic velocities and hence the
formation of the wind termination shock. In addition, we will also
illustrate the explosion and the neutrino-driven wind for the O-Ne-Mg
core, where the explosion is
obtained in spherical symmetry applying the standard neutrino
opacities. The results are in qualitative agreement with those of Mayle & Wilson (1988) and Kitaura et al. (2006),
who used a different EoS.
Fe-core progenitors
from Woosley et al. (2002).
Our numerical model is based on general relativistic radiation
hydrodynamics with spectral three-flavor Boltzmann neutrino transport
in spherical symmetry. The explosion mechanism of massive Fe-core
progenitors is an active subject of research. To model
neutrino-driven explosions for such progenitors in spherical symmetry,
we enhance the electronic charged current reaction rates artificially
which increases the neutrino energy deposition and revives
the SAS. The mechanism including the tuned neutrino reaction rates
will be further discussed in Sects. 2 and 3. Such explosion
models were investigated with respect to the nucleosynthesis by Fröhlich et al. (2006a-c).
Here, we report on the formation of the neutrino-driven wind and the
possibility of the wind developing supersonic velocities and hence the
formation of the wind termination shock. In addition, we will also
illustrate the explosion and the neutrino-driven wind for the O-Ne-Mg
core, where the explosion is
obtained in spherical symmetry applying the standard neutrino
opacities. The results are in qualitative agreement with those of Mayle & Wilson (1988) and Kitaura et al. (2006),
who used a different EoS.
We find that for low progenitor masses, the neutrino-driven wind termination shock will develop, using the tuned neutrino reaction rates. When the neutrino reaction rates are switched back to the standard opacities given in Bruenn (1985), the neutrino-driven wind develops only a subsonic matter outflow. For intermediate progenitor masses, the neutrino-driven wind remains subsonic even with the artificially enhanced neutrino emission and absorption rates. Since the neutrino-driven wind depends sensitively on the emitted neutrino spectra at the neutrinospheres, we believe accurate neutrino transport and general relativity in the presence of strong gravitational fields are essential in order to describe the dynamical evolution. Furthermore, the accurate modeling of the electron fraction in the wind is essential for nucleosynthesis calculations, which can only be obtained solving the neutrino transport equation. In addition, it is beyond the present computational capabilities to carry multi-dimensional simulations with neutrino transport to several seconds after bounce. Hence, our investigations are performed in spherical symmetry where we simulate the entire PNS interior rather than approximating an interior boundary. We find significant discrepancies in comparison with the assumptions made in previous wind studies. Material is found to be proton-rich for more than 10 s, where most wind models assume luminosities and mean neutrino energies such that the neutrino-driven wind becomes neutron-rich. We question the validity of the approximations made in such wind studies. We believe that the accurate and consistent modeling of the physical conditions in the neutrino-driven wind is essential, especially in order to be able to draw conclusions with respect to the nucleosynthesis.
The paper is organized as follows. In Sect. 2, we will
present our spherically symmetric core collapse model. Section 3
is devoted to the explosion phase of neutrino-driven explosions in
spherical symmetry. We examine the 8.8 M![]() progenitor model from Nomoto (1984,1983,1987) using the standard neutrino opacities and the 10.8 and 18 M
progenitor model from Nomoto (1984,1983,1987) using the standard neutrino opacities and the 10.8 and 18 M![]() progenitor models from Woosley et al. (2002)
using artificially enhanced neutrino reaction rates. In Sect. 4 we
discuss the conditions for the formation of the neutrino-driven wind
and the possibility for the wind to develop supersonic velocities. We
discuss in Sect. 5 the electron fraction approximation used in the
literature. Since a generally neutron-rich neutrino-driven wind is
found in many previous and present wind studies, we illustrate the
differences and investigate why we find a generally proton-rich wind.
Section 6 is dedicated to the long term post-bounce evolution for
more than 20 s. In Sect. 7 we discuss the results
and emphasize the main differences of the present investigation to
previous wind studies. Finally we close with a summary
in Sect. 8.
progenitor models from Woosley et al. (2002)
using artificially enhanced neutrino reaction rates. In Sect. 4 we
discuss the conditions for the formation of the neutrino-driven wind
and the possibility for the wind to develop supersonic velocities. We
discuss in Sect. 5 the electron fraction approximation used in the
literature. Since a generally neutron-rich neutrino-driven wind is
found in many previous and present wind studies, we illustrate the
differences and investigate why we find a generally proton-rich wind.
Section 6 is dedicated to the long term post-bounce evolution for
more than 20 s. In Sect. 7 we discuss the results
and emphasize the main differences of the present investigation to
previous wind studies. Finally we close with a summary
in Sect. 8.
2 The model
Our core collapse model, AGILE-BOLTZTRAN, is based on general
relativistic radiation hydrodynamics in spherical symmetry, using
three-flavor (anti)neutrino Boltzmann transport. For details see Mezzacappa & Bruenn (1993a-c), Mezzacappa & Messer (1999), Liebendörfer et al. (2001a,b) and Liebendörfer et al. (2004). For this study we include the neutrino input physics based on Bruenn (1985). The charged current reactions considered
are electron and positron captures at free nucleons as well as electron captures at nuclei. The nuclei are characterized by an average atomic mass and charge

where
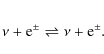
The classical neutrino pair process is electron-positron annihilation,
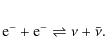
The standard neutrino energy E dependent emissivity j(E) and absorptivity
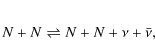
has been implemented into our model according to Thompson & Burrows (2001) and is also taken into account. The emission of (

as well as contributions from nucleon-recoil and weak magnetism as studied in Horowitz (2002) are investigated in Fischer et al. (2009) and are not taken into account in the present study of the neutrino-driven wind.
2.1 Recent improvements of the adaptive grid
Long-term simulations of the supernova post-bounce phase with
AGILE-BOLTZTRAN lead to a very large contrast of densities, reaching
from
![]() g/cm3 at the center of the protoneutron star (PNS) to densities on the order of g/cm3 and lower in the outer layers. The version of AGILE described in Liebendörfer et al. (2002) is not able to resolve such large density contrasts. If the enclosed mass a
is large and the density in one zone very low, then the evaluation of
the mass contained in the zone according to Eq. (39) in Liebendörfer et al. (2002),
g/cm3 at the center of the protoneutron star (PNS) to densities on the order of g/cm3 and lower in the outer layers. The version of AGILE described in Liebendörfer et al. (2002) is not able to resolve such large density contrasts. If the enclosed mass a
is large and the density in one zone very low, then the evaluation of
the mass contained in the zone according to Eq. (39) in Liebendörfer et al. (2002),
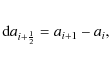
is subject to large cancellation so that truncation errors inhibit the convergence of the Newton-Raphson scheme in the implicitly finite differenced time step. However, the problem can be avoided by a simple modification that was first explored in Fisker (2004, priv. comm.). The state vector of AGILE-BOLTZTRAN is given by the following set of quantities
| (4) |
with enclosed baron mass a, radius r, velocity u, gravitational mass m, baryon density
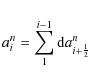
becomes the derived quantity.
The form of the generic Eq. (30) in Liebendörfer et al. (2002) applies to the continuity equation, the momentum equation and the energy equation. If we define
![]() as the difference of the enclosed mass ai between time tn and tn+1, Eq. (30) in Liebendörfer et al. (2002) becomes
as the difference of the enclosed mass ai between time tn and tn+1, Eq. (30) in Liebendörfer et al. (2002) becomes
where the relative velocity between the fluid and the grid in the advection term
The cancellation of large numbers during the Newton-Raphson iterations of the implicit time step is avoided if the time shifts
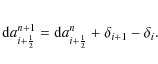
This leads to satisfactory convergence of the Newton-Raphson iterations even in the presence of large density contrasts.
2.2 The equation of state
For the present investigation of the neutrino-driven wind, the baryon EoS from Shen et al. (1998)
for hot and dense nuclear matter has been implemented for matter in
nuclear statistical equilibrium (NSE). For temperatures below T=0.5 MeV
where NSE does not apply, the baryon EoS combines an ideal gas
approximation for a distribution of nuclei, based on Timmes & Arnett (1999)
(including ion-ion-correlations), and a nuclear reaction network using
the composition given by the progenitor model. Details of the reaction
network are given in Thielemann et al. (2004) and references therein. The nuclear abundances are included in the state vector of AGILE-BOLTZTRAN, which reads as follows
| (7) |
For all these quantities, including the nuclear abundances Y1, ..., YN, the corresponding advection equations are solved as described in Liebendörfer et al. (2002) Sect. 3, but with an improved second order accurate total variation diminishing advection scheme. The nuclear reaction network is used in an operator-split manner in order to calculate the abundance changes due to the source terms which in turn depend on employed reaction rates.
Due to computational limitations, we restrict ourselves to N=19. We consider the free nucleons and the 14 symmetric nuclei, from 4He to 56Ni. In order to model matter with
![]() to some extent, we additionally include 53Fe, 54Fe and 56Fe.
The network calculates the composition dynamically from the progenitor
stage until the simulations are stopped. It is used for an
accurate internal energy evolution. In addition, we can
approximately reflect the composition of the PNS surface for more
than 20 s after bounce,
where nuclei that have been previously in NSE are freezing out of NSE
as the temperature drops rapidly below 0.5 MeV already
about 1 s after bounce and reach below 0.01 MeV at
about 10 s post-bounce. In previous studies the
simplification of an ideal gas of Si-nuclei was used for matter which
is not in NSE. This leads to an increasing inaccurate internal
energy evolution after 500 ms post-bounce when the explosion
shock reaches the Si-layer of the progenitor and simplifications could
not be extended beyond 1 s post-bounce time. The
implementation of the nuclear reaction network now makes it possible to
include more mass (up to and including a large fraction of the
He-layer, depending on the progenitor model) into the physical domain
and follow the dynamical evolution of the explosion by one order of
magnitude longer.
to some extent, we additionally include 53Fe, 54Fe and 56Fe.
The network calculates the composition dynamically from the progenitor
stage until the simulations are stopped. It is used for an
accurate internal energy evolution. In addition, we can
approximately reflect the composition of the PNS surface for more
than 20 s after bounce,
where nuclei that have been previously in NSE are freezing out of NSE
as the temperature drops rapidly below 0.5 MeV already
about 1 s after bounce and reach below 0.01 MeV at
about 10 s post-bounce. In previous studies the
simplification of an ideal gas of Si-nuclei was used for matter which
is not in NSE. This leads to an increasing inaccurate internal
energy evolution after 500 ms post-bounce when the explosion
shock reaches the Si-layer of the progenitor and simplifications could
not be extended beyond 1 s post-bounce time. The
implementation of the nuclear reaction network now makes it possible to
include more mass (up to and including a large fraction of the
He-layer, depending on the progenitor model) into the physical domain
and follow the dynamical evolution of the explosion by one order of
magnitude longer.
The baryon EoSs for NSE and for non-NSE are coupled to an electron-positron EoS (including photons), developed by Timmes & Arnett (1999).
2.3 Enhanced neutrino emissivity and opacity
By our choice of a spherically symmetric approach, we implement the explosion mechanism of massive Fe-core progenitor stars artificially to trigger neutrino-driven explosions during the post-bounce evolution after the deleptonization burst has been launched. Neutrino heating between the neutrinospheres and the SAS transfers energy from the radiation field into the fluid. A part of this energy is converted into thermal energy which revives the SAS and launches the explosion. The revival of the SAS and hence the neutrino-driven explosions take place on a timescale of several 100 ms.
During the post-bounce evolution, heavy nuclei continue to fall
onto the SAS and dissociate into free nucleons. These free nucleons
accrete onto the PNS surface. Hence the dominant neutrino heating
contributions behind the SAS are due to the electronic charged current
reactions, expressions (1) and (2).
To trigger explosions in spherically symmetric core collapse
simulations of massive Fe-core progenitors, we enhance the
emissivity j and absorptivity ![]() by a certain factor (typically 5-7) in the region between the SAS
and the neutrinospheres. This corresponds to matter with entropies
above
by a certain factor (typically 5-7) in the region between the SAS
and the neutrinospheres. This corresponds to matter with entropies
above
![]() /baryon and baryon densities below 1010 g/cm3.
The entropies ahead of the shock are lower and the central densities of
the PNS are higher, such that the artificial heating only
applies to the region between the neutrinospheres and the SAS. The
artificially enhanced reaction rates do not change the neutrino
luminosities and mean neutrino energies significantly for the
electron-neutrinos and electron-antineutrinos. Furthermore,
/baryon and baryon densities below 1010 g/cm3.
The entropies ahead of the shock are lower and the central densities of
the PNS are higher, such that the artificial heating only
applies to the region between the neutrinospheres and the SAS. The
artificially enhanced reaction rates do not change the neutrino
luminosities and mean neutrino energies significantly for the
electron-neutrinos and electron-antineutrinos. Furthermore, ![]() -equilibrium
is fulfilled since the reverse reaction rates are obtained via the
detailed balance. However, the timescale for weak-equilibrium to
be established is reduced and hence the electron fraction changes on a
shorter timescale. In combination with the increased neutrino
energy deposition, this leads to a deviation of the thermodynamic
variables in comparison to simulations using the standard opacities
given in Bruenn (1985), which will be
further discussed in Sect. 7. The weak neutrino-driven explosions
obtained have explosion energies of 6.5
-equilibrium
is fulfilled since the reverse reaction rates are obtained via the
detailed balance. However, the timescale for weak-equilibrium to
be established is reduced and hence the electron fraction changes on a
shorter timescale. In combination with the increased neutrino
energy deposition, this leads to a deviation of the thermodynamic
variables in comparison to simulations using the standard opacities
given in Bruenn (1985), which will be
further discussed in Sect. 7. The weak neutrino-driven explosions
obtained have explosion energies of 6.5 ![]() 1050 erg and 2
1050 erg and 2 ![]() 1050 erg for the 10.8 and the 18 M
1050 erg for the 10.8 and the 18 M![]() progenitor model respectively.
progenitor model respectively.
2.4 Explosion energy and mass cut
The explosion energy estimate is a quantity which changes during the
dynamical evolution of the system. It is given by the total
specific energy of the fluid in the laboratory frame
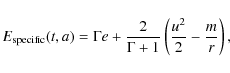
|
(8) |
which in turn is the sum of the specific internal energy e
gives the total mass-integrated energy, at a given time t0 outside a given mass a0. The expression (9) is negative during the collapse, bounce and the early post-bounce phases because the progenitor and central Fe-core are gravitationally bound. At some time after bounce, expression (9) becomes positive in the region between the shock and the neutrinospheres. It stays negative at large distances and close to the deep gravitational potential of the PNS, because the outer layers of the progenitor and the PNS continue to be gravitationally bound. While the emission of neutrinos cools the PNS interior, neutrino absorption deposits energy on the timescale
On a suggestion by S. Bruenn, we consider the mass cut as follows

|
(10) |
The material outside of
at late times (
From the time post-bounce when the shock reaches low enough densities and temperatures such that neutrinos decouple from matter completely, neutrino heating and cooling does not affect the explosion energy estimate anymore. The additional energy deposition from the neutrino-driven wind, which will be discussed further below, might affect the explosion estimate at later times. We will illustrate in particular the effect of the formation of a supersonic neutrino-driven wind and the wind termination shock to the explosion energy estimate. Only after the neutrino-driven wind disappears, the final value of the explosion energy can be obtained.
2.5 The neutrino observables
The neutrino radiation hydrodynamics equations are a coupled system
which combines the evolution of the matter properties given by the
state vector y and the radiation field, as documented in Liebendörfer et al. (2004) and references therein. The neutrino radiation field is taken into account via the phase-space distribution function
![]() for each neutrino flavor
for each neutrino flavor
![]() .
In spherical symmetry, it depends on the time t, the enclosed baryon mass a as well as on the neutrino energy E and the cosine of the propagation angle
.
In spherical symmetry, it depends on the time t, the enclosed baryon mass a as well as on the neutrino energy E and the cosine of the propagation angle
![]() .
The evolution of the neutrino radiation field is taken into account by
solving the Boltztran transport equation for massless fermions.
It determines the phase-space derivative of the specific
distribution function
.
The evolution of the neutrino radiation field is taken into account by
solving the Boltztran transport equation for massless fermions.
It determines the phase-space derivative of the specific
distribution function
![]() ,
i.e. the distribution function divided by the matter density
,
i.e. the distribution function divided by the matter density ![]() ,
in a co-moving frame (see for example Eq. (8) of Liebendörfer et al. 2005) and due to neutrino-matter interactions such as emission and
absorption as well as scattering and pair reactions.
,
in a co-moving frame (see for example Eq. (8) of Liebendörfer et al. 2005) and due to neutrino-matter interactions such as emission and
absorption as well as scattering and pair reactions.
In order to compare simulation results, neutrino observables can
be defined. Commonly used are the neutrino number-luminosities, which
is given by the phase-space integration of the neutrino distribution
function as follows
![\begin{eqnarray*}L_n\left([t_0,t_1],a\right) = 4\pi r^2 \rho \frac{2\pi c}{(hc)^...
...1} {\rm d}\mu \int_{0}^{\infty} E^2~{\rm d}E~~ F_\nu(t,a,\mu,E),
\end{eqnarray*}](/articles/aa/full_html/2010/09/aa13106-09/img66.png)
which is the number of neutrinos
![\begin{eqnarray*}L_{\rm e}\left([t_0,t_1],a\right) &\equiv& L_\nu\left([t_0,t_1]...
...mu~{\rm d}\mu \int_{0}^{\infty} E^3~{\rm d}E~~ F_\nu(t,a,\mu,E),
\end{eqnarray*}](/articles/aa/full_html/2010/09/aa13106-09/img68.png)
for each neutrino flavor, i.e.
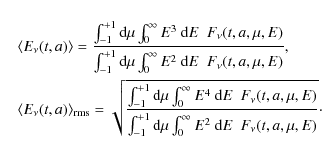
We will use these observables, i.e. the energy-luminosities and the mean and root-mean-squared energies, to illustrate the dynamical evolution of the radiation field as well as for comparisons with previous studies.
2.6 The electron fraction
The proton-to-baryon ratio is essential for the composition of the
ejecta, which is obtained via detailed post processing nucleosynthesis
calculations. In the absence of muons or tauons,
the proton-to-baryon ratio is given by the electron fraction
as follows
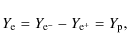
|
(12) |
which is equal to the number of protons and defines the total number of charges per baryon. The change of the electron fraction is given by the balance of emitted and absorbed electrons (positrons) and electron-neutrinos (antineutrinos) at free nucleons and nuclei. Weak-equilibrium is achieved if
| (13) |
| (14) |
where
where
3 Explosions in spherical symmetry
Progenitor stars more massive than 9 M![]() develop extended Fe-cores at the end of stellar evolution. The
explosion mechanism of such Fe-core progenitors is an active subject of
research. In the following section, we will investigate the
neutrino-driven explosions of the 10.8 and 18 M
develop extended Fe-cores at the end of stellar evolution. The
explosion mechanism of such Fe-core progenitors is an active subject of
research. In the following section, we will investigate the
neutrino-driven explosions of the 10.8 and 18 M![]() Fe-core progenitors from Woosley et al. (2002)
in spherical symmetry by enhancing the electronic charged current
reaction rates artificially. Further below, we will investigate the
explosion phase of the 8.8 M
Fe-core progenitors from Woosley et al. (2002)
in spherical symmetry by enhancing the electronic charged current
reaction rates artificially. Further below, we will investigate the
explosion phase of the 8.8 M![]() O-Ne-Mg-core from Nomoto (1984,1983,1987), where the explosion is obtained using the standard neutrino opacities as introduced in Sect. 2.
O-Ne-Mg-core from Nomoto (1984,1983,1987), where the explosion is obtained using the standard neutrino opacities as introduced in Sect. 2.
3.1 Neutrino-driven explosions of Fe-core progenitors
The dynamical behavior of the explosion energy estimate and the shock position are illustrated in Figs. 1a
and b respectively with respect to time after bounce. The figures
illustrate the explosion phase and the long term evolution up to
10 s after bounce. After achieving a convergent value between
600 ms and 2 s post-bounce of 4.5 ![]() 1050 erg, the explosion energy estimate is lifted slightly to about 6.5
1050 erg, the explosion energy estimate is lifted slightly to about 6.5 ![]() 1050 erg.
This effect coincides with the additional mass outflow obtained
in the neutrino-driven wind and the appearance of the reverse shock,
which will be discussed further below. In simulations with a less
intense (subsonic) neutrino-driven wind, this effect is negligible and
the explosion energy can be obtained already after about 1 s
post-bounce.
1050 erg.
This effect coincides with the additional mass outflow obtained
in the neutrino-driven wind and the appearance of the reverse shock,
which will be discussed further below. In simulations with a less
intense (subsonic) neutrino-driven wind, this effect is negligible and
the explosion energy can be obtained already after about 1 s
post-bounce.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13106fig01.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13106-09/Timg90.png)
|
Figure 1:
Explosion energy estimate and shock position with respect to time after bounce for the 10.8 M |
| Open with DEXTER | |
The neutrino luminosities and the mean as well as rms neutrino energies are shown in Fig. 2 for the 10.8 (middle panel) and the 18 (right panel) M![]() progenitor model with respect to time after bounce. Note that the more compact PNS of the 18 M
progenitor model with respect to time after bounce. Note that the more compact PNS of the 18 M![]() progenitor
model results in generally higher neutrino luminosities. The
oscillating shock position and the consequent contracting and expanding
neutrinospheres during the neutrino heating phase of the 10.8 and
18 M
progenitor
model results in generally higher neutrino luminosities. The
oscillating shock position and the consequent contracting and expanding
neutrinospheres during the neutrino heating phase of the 10.8 and
18 M![]() progenitor models on a timescale of several 100 ms are reflected
in the electron-flavor neutrino luminosities, which correspondingly
increase and decrease respectively. During the heating phase, the mean
neutrino energies of the electron-(anti)neutrinos increase from about
8 (10) MeV after bounce to about 12 (14) MeV until
the explosion is launched. The mean neutrino energy of the (
progenitor models on a timescale of several 100 ms are reflected
in the electron-flavor neutrino luminosities, which correspondingly
increase and decrease respectively. During the heating phase, the mean
neutrino energies of the electron-(anti)neutrinos increase from about
8 (10) MeV after bounce to about 12 (14) MeV until
the explosion is launched. The mean neutrino energy of the (![]() )-neutrinos
remains constant at about 18 MeV during the heating phase. The
mean neutrino energies are generally lower than the rms-energies but
follow the same behavior. The explosions for both models are launched
after about 350 ms post-bounce, which defines the neutrino heating
timescale for the energy deposition in the gain region to revive the
SAS. Matter is accelerated to positive velocities and the SAS turns
into the dynamic explosion shock. The resulting neutrino spectra from
these artificially induced explosions in spherical symmetry are in
general agreement with the neutrino spectra from axially-symmetric
neutrino-driven core collapse supernova models that explode without
artificially modified reaction rates (see Marek & Janka 2009).
The explosion shock continuously propagates through the remaining
domain of the progenitor star.
After the explosions have been launched, the electron flavor neutrino
luminosities decay exponentially. Furthermore the jumps in the neutrino
energies after 350 ms post-bounce for the 10.8 and 18 M
)-neutrinos
remains constant at about 18 MeV during the heating phase. The
mean neutrino energies are generally lower than the rms-energies but
follow the same behavior. The explosions for both models are launched
after about 350 ms post-bounce, which defines the neutrino heating
timescale for the energy deposition in the gain region to revive the
SAS. Matter is accelerated to positive velocities and the SAS turns
into the dynamic explosion shock. The resulting neutrino spectra from
these artificially induced explosions in spherical symmetry are in
general agreement with the neutrino spectra from axially-symmetric
neutrino-driven core collapse supernova models that explode without
artificially modified reaction rates (see Marek & Janka 2009).
The explosion shock continuously propagates through the remaining
domain of the progenitor star.
After the explosions have been launched, the electron flavor neutrino
luminosities decay exponentially. Furthermore the jumps in the neutrino
energies after 350 ms post-bounce for the 10.8 and 18 M![]() progenitor models are due to the shock propagation over the position of
500 km, where the observables are measured in a co-moving
reference frame.
progenitor models are due to the shock propagation over the position of
500 km, where the observables are measured in a co-moving
reference frame.
![\begin{figure}
\par\mbox{\includegraphics[width=6cm,clip]{13106fig02.eps}\hspace...
...\includegraphics[width=6cm,clip]{13106fig04.eps} }\vspace*{7.5mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13106-09/Timg91.png)
|
Figure 2:
Neutrino luminosities and energies with respect to time after bounce for the 8.8 M |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{13106fig05.eps}\par\include...
...ar\includegraphics[width=14cm,clip]{13106fig07.eps}
\vspace*{5.5mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13106-09/Timg92.png)
|
Figure 3:
Evolution of the 8.8 M |
| Open with DEXTER | |
3.2 The O-Ne-Mg-core
A special star is the 8.8 M![]() progenitor model from Nomoto (1984,1983,1987). The central thermodynamic conditions at the end of stellar evolution are such that only a tiny fraction of about 0.15 M
progenitor model from Nomoto (1984,1983,1987). The central thermodynamic conditions at the end of stellar evolution are such that only a tiny fraction of about 0.15 M![]() of Fe-group nuclei are produced, where nuclear statistical equilibrium (NSE) applies (see Fig. 3a top panel). Instead, the central composition is dominated by 16O, 20Ne and 24Mg nuclei.
Because temperature and density increase during the collapse, these
nuclei are burned into Fe-group nuclei and the NSE regime
increases (see Fig. 3 middle panel). The core continues to deleptonize, which can be identified at the decreasing
of Fe-group nuclei are produced, where nuclear statistical equilibrium (NSE) applies (see Fig. 3a top panel). Instead, the central composition is dominated by 16O, 20Ne and 24Mg nuclei.
Because temperature and density increase during the collapse, these
nuclei are burned into Fe-group nuclei and the NSE regime
increases (see Fig. 3 middle panel). The core continues to deleptonize, which can be identified at the decreasing ![]() in Fig. 3. We use our nuclear reaction network as described in Sect. 2.2 to calculate the dynamically changing composition,
based on the abundances provided by the progenitor model. The size of the bouncing core of
in Fig. 3. We use our nuclear reaction network as described in Sect. 2.2 to calculate the dynamically changing composition,
based on the abundances provided by the progenitor model. The size of the bouncing core of
![]() M
M![]() is significantly larger in comparison with the previous studies by Kitaura et al. (2006) and Liebendörfer (2004), illustrated in Fig. 4 (left panel) at different velocity profiles before and at bounce.
This is because we do not take the improved electron capture rates from Hix et al. (2003) and Langanke et al. (2003)
into account, which are based on the capture of electrons at the
distribution of heavy nuclei. It results in a lower central
electron fraction at bounce and a consequently more compact bouncing
core of about
is significantly larger in comparison with the previous studies by Kitaura et al. (2006) and Liebendörfer (2004), illustrated in Fig. 4 (left panel) at different velocity profiles before and at bounce.
This is because we do not take the improved electron capture rates from Hix et al. (2003) and Langanke et al. (2003)
into account, which are based on the capture of electrons at the
distribution of heavy nuclei. It results in a lower central
electron fraction at bounce and a consequently more compact bouncing
core of about
![]() M
M![]() ,
in comparison to the standard rates given in Bruenn (1985). The remaining difference is most likely due to the large asymmetry energy of the EoS from Shen et al. (1998) applied to the present study.
,
in comparison to the standard rates given in Bruenn (1985). The remaining difference is most likely due to the large asymmetry energy of the EoS from Shen et al. (1998) applied to the present study.
This progenitor is not only a special case due to the incomplete
nuclear burning at the end of stellar evolution but also due to the
steep density gradient which separates the dense core from the He- and
H-rich envelope at 1.376 M![]() ,
see Fig. 3c. There, the density drops over 13 orders of magnitude which makes it difficult to handle numerically.
,
see Fig. 3c. There, the density drops over 13 orders of magnitude which makes it difficult to handle numerically.
| Figure 4:
Radial velocity profiles at selected times with respect to the
baryon mass (left panel) before and at bounce and with respect to the radius (right panel) after bounce, for the 8.8 M |
|
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\includegraphics[width=5.2cm,clip]{13106fig10.eps}\incl...
...3106fig14.eps}\includegraphics[width=5.2cm,clip]{13106fig15.eps} }\end{figure}](/articles/aa/full_html/2010/09/aa13106-09/Timg96.png)
|
Figure 5:
Heating (>0) and cooling (<0) rates for the 8.8 M |
| Open with DEXTER | |
The low density of the mass outside the O-Ne-Mg-core makes it possible
to obtain the explosion in spherical symmetry supported via neutrino
heating. Neutrino cooling in the region of dissociated nuclear matter
causes the expanding shock front to turn into the SAS with no
significant matter outflow.
![]() -cooling dominates over
-cooling dominates over
![]() -heating
by one order of
magnitude. Only at the dissociation line of infalling heavy nuclei, the
neutrino energy deposition drives the SAS slowly to larger radii,
for illustration see the heating(cooling) rates and velocity
profile in Fig. 5 (left panel) at 20 ms post-bounce. However, the cooling of
-heating
by one order of
magnitude. Only at the dissociation line of infalling heavy nuclei, the
neutrino energy deposition drives the SAS slowly to larger radii,
for illustration see the heating(cooling) rates and velocity
profile in Fig. 5 (left panel) at 20 ms post-bounce. However, the cooling of
![]() still contributes to a large amount at 25 ms post-bounce over the heating of
still contributes to a large amount at 25 ms post-bounce over the heating of
![]() and
and
![]() in Fig. 5
(middle panel) behind the SAS. Only directly at the shock a low
net-heating rate remains. Hence the influence of the neutrinos to the
explosion itself is of minor importance. More important is the region
of C-O-burning which produces Ne and Mg. The hydrodynamic feedback
to this thermodynamic transition
can be identified already during the collapse phase of the progenitor
core at the velocity profiles in Fig. 4 (left panel) at about
1.35-1.374 M
in Fig. 5
(middle panel) behind the SAS. Only directly at the shock a low
net-heating rate remains. Hence the influence of the neutrinos to the
explosion itself is of minor importance. More important is the region
of C-O-burning which produces Ne and Mg. The hydrodynamic feedback
to this thermodynamic transition
can be identified already during the collapse phase of the progenitor
core at the velocity profiles in Fig. 4 (left panel) at about
1.35-1.374 M![]() .
As material is shock heated post-bounce, the transition layer
where Ne and Mg nuclei are burned into NSE propagates together
with the expanding shock wave outwards. In other words, the
Ne-Mg-layer of the progenitor
is converted directly into NSE. Furthermore, the transition
(discontinuity) from C-O-burning is falling quickly towards the SAS.
It was found to be at about 350 km at 20 ms post-bounce
and at about 200 km at 25 ms post-bounce, illustrated at the
velocity profiles (bottom) in
Fig. 5
(left-right panels). At about 30 ms post-bounce,
the entire Ne-Mg-layer is converted into NSE due to the
temperature increase obtained via shock heating.
Hence, C and O nuclei are burned directly into NSE.
.
As material is shock heated post-bounce, the transition layer
where Ne and Mg nuclei are burned into NSE propagates together
with the expanding shock wave outwards. In other words, the
Ne-Mg-layer of the progenitor
is converted directly into NSE. Furthermore, the transition
(discontinuity) from C-O-burning is falling quickly towards the SAS.
It was found to be at about 350 km at 20 ms post-bounce
and at about 200 km at 25 ms post-bounce, illustrated at the
velocity profiles (bottom) in
Fig. 5
(left-right panels). At about 30 ms post-bounce,
the entire Ne-Mg-layer is converted into NSE due to the
temperature increase obtained via shock heating.
Hence, C and O nuclei are burned directly into NSE.
In contrast to more massive Fe-core progenitors where O-burning produced an extended Si-S-layer, the amount of 28Si and 32S is less than ![]() at the end of nuclear burning
for the O-Ne-Mg-core discussed here (see Fig. 3a
middle panel). This low fraction of Si and S is already converted into
NSE during the initial collapse phase, due to the rapid density and
temperature increase of the contracting core. Hence, C- and O-nuclei
are burned directly into NSE during the post-bounce evolution. This
sharp transition is related to a jump in the density and the
thermodynamic variables. As the SAS propagates over this
transition along the decreasing density, the shock accelerates to
positive velocities (see Fig. 5
right panel). The consequent explosion is hence driven due to the shock
propagation over the infalling transition between two different
thermonuclear regimes rather than by pure neutrino heating, illustrated
at the velocity profiles in Fig. 4 (right panel).
Although Kitaura et al. (2006)
approximated nuclear reactions during the evolution of the O-Ne-Mg-core
progenitor, the results of their explosion dynamics are in
qualitative agreement with our findings.
at the end of nuclear burning
for the O-Ne-Mg-core discussed here (see Fig. 3a
middle panel). This low fraction of Si and S is already converted into
NSE during the initial collapse phase, due to the rapid density and
temperature increase of the contracting core. Hence, C- and O-nuclei
are burned directly into NSE during the post-bounce evolution. This
sharp transition is related to a jump in the density and the
thermodynamic variables. As the SAS propagates over this
transition along the decreasing density, the shock accelerates to
positive velocities (see Fig. 5
right panel). The consequent explosion is hence driven due to the shock
propagation over the infalling transition between two different
thermonuclear regimes rather than by pure neutrino heating, illustrated
at the velocity profiles in Fig. 4 (right panel).
Although Kitaura et al. (2006)
approximated nuclear reactions during the evolution of the O-Ne-Mg-core
progenitor, the results of their explosion dynamics are in
qualitative agreement with our findings.
The more massive Fe-core progenitors show the same thermo- and hydrodynamic features as discussed above for the O-Ne-Mg-core due to the transition between different thermonuclear regimes. However, the differences are smaller because C-O-burning produces an extended layer composed of 28Si and 32S. The transition of Si-burning into NSE is much smoother than the transition of C-O-burning into NSE. Furthermore, due to the more massive Si-S and C-O-layers for the Fe-core progenitors, the transitions take more time on the order of seconds to fall onto the SAS. The presence of neutrino heating becomes important for the more massive Fe-core progenitors to drive the SAS to large radii on a longer timescale. The effects of the shock propagation across the transition between different thermonuclear regimes has been pointed out in Bruenn et al. (2006) with respect to the explosion dynamics in axially-symmetric simulations of massive Fe-core progenitors. In our spherically symmetric models, we cannot confirm the driving force of explosions of Fe-core progenitors to be the shock propagation across different thermonuclear regimes. We find that the explosions are initiated due to the deposition, although enhanced, of neutrino energy. The shock is accelerated additionally when crossing different thermonuclear regimes due to the density jumps at the transitions.
3.3 Comparison of the neutrino spectra
Striking is the agreement in the mean neutrino energies between all
different progenitor models (including the O-Ne-Mg-core and the Fe-core
progenitors) during the explosion phase, although the neutrino
emissivities and opacities are enhanced for the Fe-core progenitor
models (see Fig. 2).
The explosion phase for the O-Ne-Mg-core lasts only until about
40 ms post-bounce, which is significantly shorter in comparison to
the more massive Fe-core progenitors. Furthermore,
the luminosities are also lower by a factor of 2.
For all models, the electron antineutrino luminosity is
higher than the electron neutrino luminosity on a timescale of
200 ms after the explosions have been launched. This slight
difference reduces again at later times where the electron neutrino
luminosity becomes again higher than the electron antineutrino
luminosity. However, after the explosions have been launched the
behaviors of the luminosities are in qualitative agreement for all
models. The same holds for the mean neutrino energies which increase
continuously during the neutrino heating phase. The electron
(anti)neutrinos have rms energies of about 12 (14) MeV where
as after the explosions have been launched, rms energies of about
11 (13) MeV are obtained. The values remain constant on the
timescale of 1 s post-bounce. The (![]() )-neutrinos
have rms energies of about 18 MeV during the neutrino heating
phase and about 15 MeV after the explosion has been launched.
These differences in the mean neutrino energies and luminosities during
the neutrino heating, initial and proceeding explosion phases are in
correspondence with the electron fraction of the material, as will
be illustrated in the following section.
)-neutrinos
have rms energies of about 18 MeV during the neutrino heating
phase and about 15 MeV after the explosion has been launched.
These differences in the mean neutrino energies and luminosities during
the neutrino heating, initial and proceeding explosion phases are in
correspondence with the electron fraction of the material, as will
be illustrated in the following section.
3.4 The electron fraction of the early ejecta
During the neutrino heating phase, the neutrino spectra are mainly
determined by mass accretion at the neutrinospheres. Neutron-rich
nuclei from the progenitor star with an electron fraction of
![]() are falling onto the oscillating SAS and dissociate into free nucleons and light nuclei, see Fig. 6d.
These nucleons accrete then slowly onto the PNS surface at the
center. Due to the increased electron-degeneracy behind the SAS in
Fig. 6c, weak-equilibrium is established at a lower value of the electron fraction of
are falling onto the oscillating SAS and dissociate into free nucleons and light nuclei, see Fig. 6d.
These nucleons accrete then slowly onto the PNS surface at the
center. Due to the increased electron-degeneracy behind the SAS in
Fig. 6c, weak-equilibrium is established at a lower value of the electron fraction of
![]() .
.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13106fig16.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13106-09/Timg102.png)
|
Figure 6:
Selected hydrodynamic variables during the initial explosion
phase at three different post-bounce times for the
|
| Open with DEXTER | |
As soon as the SAS is revived and propagates outward, see the velocity and density profiles in Figs. 6a and b, the electron degeneracy behind the expanding shock
is reduced and weak-equilibrium is established at a higher value of the electron fraction of
![]()
![]() .
The capture rates for electron-neutrinos at neutrons are favored over
electron-antineutrino captures at protons. This slight difference
results in an electron and hence proton excess. Consequently the
explosion ejecta are found to be initially proton-rich. This behavior
of the electron fraction was found for all our explosion models, for
the 10.8 and
.
The capture rates for electron-neutrinos at neutrons are favored over
electron-antineutrino captures at protons. This slight difference
results in an electron and hence proton excess. Consequently the
explosion ejecta are found to be initially proton-rich. This behavior
of the electron fraction was found for all our explosion models, for
the 10.8 and
![]() Fe-core progenitors with artificially enhanced opacities and for the
O-Ne-Mg-core using the standard opacities. Such explosion models were
investigated with respect to the nucleosynthesis in general and with
respect to the
Fe-core progenitors with artificially enhanced opacities and for the
O-Ne-Mg-core using the standard opacities. Such explosion models were
investigated with respect to the nucleosynthesis in general and with
respect to the ![]() -process by Fröhlich et al. (2006a-c).
-process by Fröhlich et al. (2006a-c).
One of the main goals of the present investigation is to determine the behavior of the electron fraction for the initially proton-rich ejecta on a long timescale on the order of 10 s, in a consistent manner. We explore the question if the material ejected in the neutrino-driven wind becomes neutron-rich and which are the conditions (e.g. entropy per baryon, expansion timescale) obtained in the neutrino-driven wind. These aspects are of special relevance for the composition of the ejecta, which is determined via explosive nucleosynthesis analysis, in particular in order to be able to draw conclusions with respect to a possible site for the production of heavy elements via the r-process. Therefore, the continued expansion of the explosion ejecta must be simulated, for which the inclusion of a large physical domain of the progenitor up to the He-layer is required. Furthermore, since the electronic charged current reaction rates and the neutrino fluxes determine the electron fraction, the PNS contraction at the center and hence the contraction of the neutrinospheres are essential.
4 The neutrino-driven wind
In this section we investigate the post explosion evolution with
special focus on the properties of the ejecta, in particular the
electron fraction. We explore the problem if the initially proton-rich
ejecta become neutron-rich at later times on the order
of 10 s and if the conditions might indicate a possible site
for the nucleosynthesis of heavy nuclei via the r-process.
This has been assumed in static steady-state as well as parametrized
dynamic wind models, based on the results obtained by Woosley et al. (1994).
The ejected material in their simulations does never become
proton-rich, the electron fraction was found to continuously
decrease with time after the explosion has been launched. Thus,
the ejecta were investigated in a region where the conditions are
favorable for the r-process. The stellar models applied to the present investigation of the neutrino driven wind are the
![]() O-Ne-Mg-core and the 10.8 and
O-Ne-Mg-core and the 10.8 and
![]() Fe-core progenitors, where for the latter two cases the explosions are
obtained using the artificially enhanced opacities as described
in Sect. 2.3.
Fe-core progenitors, where for the latter two cases the explosions are
obtained using the artificially enhanced opacities as described
in Sect. 2.3.
After the explosions have been launched, the region between the
expanding explosion shock and the neutrinospheres cools rapidly and the
density decreases continuously as illustrated in Figs. 7 and 8d and h. In order to determine the evolution of the electron fraction ![]() ,
the non-local neutrino fluxes are as important as the local
neutrino reaction rates. Since the PNS and hence the neutrinospheres
contract continuously due to the deleptonization, the degeneracy
increases and matter at the PNS surface is found to be extremely
neutron-rich with
,
the non-local neutrino fluxes are as important as the local
neutrino reaction rates. Since the PNS and hence the neutrinospheres
contract continuously due to the deleptonization, the degeneracy
increases and matter at the PNS surface is found to be extremely
neutron-rich with
![]() (see Figs. 7 and 8d and f).
(see Figs. 7 and 8d and f).
![\begin{figure}
\par\includegraphics[width=16cm,clip]{13106fig17.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13106-09/Timg109.png)
|
Figure 7:
Selected hydrodynamic variables during the formation of the
neutrino-driven wind at three different post-bounce times for the
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{13106fig18.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13106-09/Timg110.png)
|
Figure 8:
The same configuration as Fig. 7 for the
|
| Open with DEXTER | |
Independent of the progenitor model, the region on top of the
PNS surface is continuously subject to neutrino heating during the
post explosion phase. The dominant heating sources are the absorption
of electron-(anti)neutrinos at free nucleons, due to the high
fraction of free nucleons (dissociated nuclear matter) present in the
region on top of the PNS, as shown in Fig. 9.
The neutrino pair production and thermalization processes have a
negligible contribution to the heating outside the neutrinospheres.
In order to compare the heating and cooling rates in Fig. 9, we plot the quantities with respect to the baryon density. While neutrino cooling is still dominantly present at ![]() ms post-bounce (thin lines in Fig. 9), at later times after
ms post-bounce (thin lines in Fig. 9), at later times after ![]() s post-bounce (thick lines in Fig. 9) neutrino cooling vanishes and only heating is found in the density
domain of interest, i.e. between
107-1012 g/cm3. Figures 7d and 8d
show the conditions for the contracting PNSs at the center via the
radial baryon density profiles and the electron-neutrinospheres. The
region of interest where the neutrino-driven wind develops corresponds
to the density domain of
10 7-1011 g/cm3. The degeneracy of the early ejecta favors proton-rich matter where a high electron fraction of
s post-bounce (thick lines in Fig. 9) neutrino cooling vanishes and only heating is found in the density
domain of interest, i.e. between
107-1012 g/cm3. Figures 7d and 8d
show the conditions for the contracting PNSs at the center via the
radial baryon density profiles and the electron-neutrinospheres. The
region of interest where the neutrino-driven wind develops corresponds
to the density domain of
10 7-1011 g/cm3. The degeneracy of the early ejecta favors proton-rich matter where a high electron fraction of
![]() is obtained. Hence, the absorption of electron-antineutrinos at
free protons dominates over electron-neutrino absorption at free
neutrons. The corresponding radial neutrino luminosities and rms
energies are shown in Figs. 7 and 8e
and g. In addition, for the first time we were able to
follow the deleptonization burst from core bounce for several seconds
over a large physical domain including several 105 km of the progenitor star. The outrunning luminosity peak can be identified in the luminosities in Figs. 7 and 8e at 0.6 s after bounce at a distance between 5
is obtained. Hence, the absorption of electron-antineutrinos at
free protons dominates over electron-neutrino absorption at free
neutrons. The corresponding radial neutrino luminosities and rms
energies are shown in Figs. 7 and 8e
and g. In addition, for the first time we were able to
follow the deleptonization burst from core bounce for several seconds
over a large physical domain including several 105 km of the progenitor star. The outrunning luminosity peak can be identified in the luminosities in Figs. 7 and 8e at 0.6 s after bounce at a distance between 5 ![]() 104 and 105 km, leaving the computational domain between 1-2 s post-bounce.
104 and 105 km, leaving the computational domain between 1-2 s post-bounce.
After the explosions have been launched, the continued energy transfer
from the neutrino radiation field into the fluid outside the
neutrinospheres as illustrated in Fig. 9
drives the matter entropies to high values, shown in Figs. 7 and 8c. The heat deposition at the PNS surface accelerates matter to positive velocities, see Figs. 7 and 8a, after ![]() s
post-bounce. This matter outflow is known as the neutrino-driven wind,
which proceeds adiabatically at larger radii. This is consistent with
the constant radial entropy per baryon profiles in the graphs (c).
Furthermore, the rapidly decreasing luminosities reach values
below 5
s
post-bounce. This matter outflow is known as the neutrino-driven wind,
which proceeds adiabatically at larger radii. This is consistent with
the constant radial entropy per baryon profiles in the graphs (c).
Furthermore, the rapidly decreasing luminosities reach values
below 5 ![]() 1051 erg/s already 1 s after bounce (see Figs. 7 and 8e). The luminosities continue to decrease and reach values below 1
1051 erg/s already 1 s after bounce (see Figs. 7 and 8e). The luminosities continue to decrease and reach values below 1 ![]() 1051 erg/s
at 10 s after bounce. The mean neutrino energies also decrease
constantly where values below 10 MeV for the electron-flavor
neutrinos and below 12 MeV for the (
1051 erg/s
at 10 s after bounce. The mean neutrino energies also decrease
constantly where values below 10 MeV for the electron-flavor
neutrinos and below 12 MeV for the (![]() )-neutrinos are obtained
(see Figs. 7 and 8g).
)-neutrinos are obtained
(see Figs. 7 and 8g).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13106fig19.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13106-09/Timg114.png)
|
Figure 9:
Heating and cooling rates with respect to the baryon density
at three different post-bounce times 0.5 s (thin lines), 1 s (intermediate lines), 5 s (thick lines) for the
|
| Open with DEXTER | |
Several previous wind studies achieved supersonic matter outflow
velocities for the neutrino-driven wind due to assumed high
luminosities. In any case, the accelerated material of the
neutrino-driven wind collides with the slower and subsonically
expanding explosion ejecta. Comparing Figs. 7 and 8, the more compact wind region of the
![]() progenitor model produces a less pronounced neutrino-driven wind in comparison to the
progenitor model produces a less pronounced neutrino-driven wind in comparison to the
![]() progenitor model. The densities of the wind region are higher up to two
orders of magnitude and the temperatures are higher by a factor
of 2. The resulting velocities of the neutrino-driven wind outflow
are lower by a factor of 2 and stay below 104 km s-1. Hence, the neutrino-driven wind remains subsonic for all times for the
progenitor model. The densities of the wind region are higher up to two
orders of magnitude and the temperatures are higher by a factor
of 2. The resulting velocities of the neutrino-driven wind outflow
are lower by a factor of 2 and stay below 104 km s-1. Hence, the neutrino-driven wind remains subsonic for all times for the
![]() progenitor model (see Fig. 8a) where the wind develops supersonic velocities for the
progenitor model (see Fig. 8a) where the wind develops supersonic velocities for the
![]() progenitor model (see Fig. 7a).
In the case of a supersonic neutrino-driven wind, this leads to
the formation of the reverse shock known as the wind termination shock.
The formation of the wind termination shock of the
progenitor model (see Fig. 7a).
In the case of a supersonic neutrino-driven wind, this leads to
the formation of the reverse shock known as the wind termination shock.
The formation of the wind termination shock of the
![]() progenitor model is illustrated in Fig. 10
and will be discussed in the following paragraph. In order to
analyze the dynamical evolution and the consequences of the formation
of the reverse shock, steady-state wind models cannot be used.
Radiation hydrodynamics is required in order to describe the dynamical
effects consistently. Our results, obtained using general relativistic
radiation hydrodynamics
based on spectral three-flavor Boltzmann neutrino transport, are in
qualitative agreement with the detailed parametrized investigation by Arcones et al. (2007).
progenitor model is illustrated in Fig. 10
and will be discussed in the following paragraph. In order to
analyze the dynamical evolution and the consequences of the formation
of the reverse shock, steady-state wind models cannot be used.
Radiation hydrodynamics is required in order to describe the dynamical
effects consistently. Our results, obtained using general relativistic
radiation hydrodynamics
based on spectral three-flavor Boltzmann neutrino transport, are in
qualitative agreement with the detailed parametrized investigation by Arcones et al. (2007).
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{13106fig20.eps}
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13106-09/Timg116.png)
|
Figure 10:
Evolution of selected mass elements in the neutrino-driven wind
(as listed in graph a) from
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{13106fig21.eps}
\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13106-09/Timg118.png)
|
Figure 11:
Evolution of selected mass shells in the neutrino-driven wind
(as listed in graph a) from
|
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\includegraphics[width=8.35cm,clip]{13106fig22.eps}\includegraphics[width=8.35cm,clip]{13106fig23.eps} }\vspace*{5.5mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13106-09/Timg119.png)
|
Figure 12:
Selected radial mass fraction profiles during the neutrino driven wind phase for the
|
| Open with DEXTER | |
During the initial and subsonic wind expansion, the matter entropies in Fig. 10c increase slowly from 4 to
![]() /baryon
and the densities in Fig. 10b and temperatures in Fig. 10e
decrease on a long timescale over several seconds. Furthermore,
the reduced degeneracy in the wind increases the electron fraction
shown in Fig. 10d slowly on the same timescale. When the material is accelerated supersonically with velocities of several 104 km s-1 up to radii of a several 103 km
(see Figs. 10a and f), the entropies increase from s
/baryon
and the densities in Fig. 10b and temperatures in Fig. 10e
decrease on a long timescale over several seconds. Furthermore,
the reduced degeneracy in the wind increases the electron fraction
shown in Fig. 10d slowly on the same timescale. When the material is accelerated supersonically with velocities of several 104 km s-1 up to radii of a several 103 km
(see Figs. 10a and f), the entropies increase from s ![]()
![]() /baryon to s
/baryon to s ![]()
![]() /baryon
on a short timescale of the order of 100 ms. During this
rapid expansion, the density and temperature decrease drastically
from 1010 g/cm3 to
104-102 g/cm3 and from 3 MeV to
0.1-0.01 MeV respectively (see Figs. 10b
and e). It also corresponds to a rapid decrease of the
degeneracy which in turn is reflected in a rapid increase of the
electron fraction of the accelerated material on top of the
PNS surface, from
/baryon
on a short timescale of the order of 100 ms. During this
rapid expansion, the density and temperature decrease drastically
from 1010 g/cm3 to
104-102 g/cm3 and from 3 MeV to
0.1-0.01 MeV respectively (see Figs. 10b
and e). It also corresponds to a rapid decrease of the
degeneracy which in turn is reflected in a rapid increase of the
electron fraction of the accelerated material on top of the
PNS surface, from
![]() to
to
![]() (see Fig. 10d).
Furthermore, the supersonically expanding neutrino-driven wind
collides with the explosion ejecta as can bee seen in Fig. 10a (solid red line) at radii of several 104 km.
Consequently, the previously accelerated material decelerates
behind the explosion ejecta as can be seen in the velocities in
Fig. 10f. This
phenomenon becomes significant after about 2 s post-bounce
and corresponds to the formation of the reverse shock, i.e. the
wind termination shock. (See Fig. 10a dashed red line at radii of several 103 km.) It causes an additional entropy increase to the final values of s
(see Fig. 10d).
Furthermore, the supersonically expanding neutrino-driven wind
collides with the explosion ejecta as can bee seen in Fig. 10a (solid red line) at radii of several 104 km.
Consequently, the previously accelerated material decelerates
behind the explosion ejecta as can be seen in the velocities in
Fig. 10f. This
phenomenon becomes significant after about 2 s post-bounce
and corresponds to the formation of the reverse shock, i.e. the
wind termination shock. (See Fig. 10a dashed red line at radii of several 103 km.) It causes an additional entropy increase to the final values of s ![]()
![]() /baryon.
During the rapid deceleration on the same short timescale on the order
of 100 ms, the densities in Fig. 10b and temperatures in Fig. 10e increase again slightly, where the degeneracy increases and hence the electron fraction reduces slightly to values of
/baryon.
During the rapid deceleration on the same short timescale on the order
of 100 ms, the densities in Fig. 10b and temperatures in Fig. 10e increase again slightly, where the degeneracy increases and hence the electron fraction reduces slightly to values of
![]() .
The following dynamical evolution is given by the subsonic and
adiabatic expansion of the explosion ejecta on a longer timescale on
the order of seconds. The density and temperature decrease slowly where
the entropies of s
.
The following dynamical evolution is given by the subsonic and
adiabatic expansion of the explosion ejecta on a longer timescale on
the order of seconds. The density and temperature decrease slowly where
the entropies of s ![]()
![]() /baryon and the electron fraction of about
/baryon and the electron fraction of about
![]() remain constant. The latter aspects are essential for the
nucleosynthesis analysis of the ejecta. It can be understood in
the sense that the neutrino reaction rates freeze out and the matter
conditions correspond to the neutrino free streaming regime.
remain constant. The latter aspects are essential for the
nucleosynthesis analysis of the ejecta. It can be understood in
the sense that the neutrino reaction rates freeze out and the matter
conditions correspond to the neutrino free streaming regime.
Note that the strong neutrino-driven wind for the
![]() progenitor
model is obtained using the enhanced opacities as introduced in
Sect. 2.3. We additionally illustrate selected properties of the
neutrino-driven wind for the
progenitor
model is obtained using the enhanced opacities as introduced in
Sect. 2.3. We additionally illustrate selected properties of the
neutrino-driven wind for the
![]() progenitor model in Fig. 11 where a strong neutrino-driven wind was obtained using the standard emissivities and opacities given in Bruenn (1985).
This is due to the low density of the region between the
neutrinospheres at the PNS surface and the expanding explosion
shock, where neutrino heating via the standard rates and energy from
nuclear burning are sufficient to drive a strong supersonic matter
outflow. Matter entropies increase to
progenitor model in Fig. 11 where a strong neutrino-driven wind was obtained using the standard emissivities and opacities given in Bruenn (1985).
This is due to the low density of the region between the
neutrinospheres at the PNS surface and the expanding explosion
shock, where neutrino heating via the standard rates and energy from
nuclear burning are sufficient to drive a strong supersonic matter
outflow. Matter entropies increase to
![]() /baryon
during the initial acceleration of the wind and the densities and
temperatures decrease slowly on a timescale of seconds. The properties
during the initial acceleration observed are similar
to those of the more massive
/baryon
during the initial acceleration of the wind and the densities and
temperatures decrease slowly on a timescale of seconds. The properties
during the initial acceleration observed are similar
to those of the more massive
![]() Fe-core progenitor. The same holds for the acceleration to supersonic
velocities. The timescale is reduced to 100 ms where the entropies
increase rapidly to
Fe-core progenitor. The same holds for the acceleration to supersonic
velocities. The timescale is reduced to 100 ms where the entropies
increase rapidly to
![]() /baryon (see Fig. 11c)
and due to the reduced degeneracy the electron fraction increases from
/baryon (see Fig. 11c)
and due to the reduced degeneracy the electron fraction increases from
![]() at the PNS surface to
at the PNS surface to
![]() (see Fig. 11d). Density and temperature decrease to 10-100 g/cm3 and 0.001 MeV respectively (see Figs. 11b and e). The difference to the more massive
(see Fig. 11d). Density and temperature decrease to 10-100 g/cm3 and 0.001 MeV respectively (see Figs. 11b and e). The difference to the more massive
![]() Fe-core progenitor is due to the lower mass enclosed between the
PNS surface and the expanding explosion ejecta. For the more
massive
Fe-core progenitor is due to the lower mass enclosed between the
PNS surface and the expanding explosion ejecta. For the more
massive
![]() Fe-core progenitor in Fig. 10f,
the previously accelerated material collides with the explosion
ejecta already after a few 100 ms. Here the supersonic
wind expands on a much longer timescale up to several seconds before it
collides with the explosion ejecta (see Fig. 11f).
During this adiabatic expansion, entropy and electron fraction remain
constant. The fast material collides with the much slower expanding
explosion ejecta so that the material is decelerated and the reverse
shock appears. This is again similar to the formation of the reverse
shock for the more massive
Fe-core progenitor in Fig. 10f,
the previously accelerated material collides with the explosion
ejecta already after a few 100 ms. Here the supersonic
wind expands on a much longer timescale up to several seconds before it
collides with the explosion ejecta (see Fig. 11f).
During this adiabatic expansion, entropy and electron fraction remain
constant. The fast material collides with the much slower expanding
explosion ejecta so that the material is decelerated and the reverse
shock appears. This is again similar to the formation of the reverse
shock for the more massive
![]() Fe-core progenitor as discussed above. Matter entropies increase to
Fe-core progenitor as discussed above. Matter entropies increase to
![]() /baryon (see Fig. 11c), density and temperature increase sightly (see Figs. 11b and e) and the electron fraction reduces slightly to
/baryon (see Fig. 11c), density and temperature increase sightly (see Figs. 11b and e) and the electron fraction reduces slightly to
![]() due to the increased degeneracy
(see Fig. 11d).
The following evolution is determined by the adiabatic expansion of the
explosion ejecta during which the entropy and electron fraction remain
constant.
due to the increased degeneracy
(see Fig. 11d).
The following evolution is determined by the adiabatic expansion of the
explosion ejecta during which the entropy and electron fraction remain
constant.
In the following paragraph, we will discuss the composition of
the neutrino-driven wind region to some extent. This is possible due to
the recently implemented nuclear reaction network. It includes the
free nucleons and the symmetric nuclei from 4He to 56Ni plus 53Fe, 54Fe and 56Fe. The initial composition is given by the progenitor model. Mostly 28Si and 30S
are shock-heated and burned to Fe-group nuclei due to the temperature
and density jump during the initial expansion of the explosion shock
(see Fig. 12 and compare with Figs. 7
and 8d
and f). The high fraction of these Fe-group nuclei reduces behind
the explosion shock due to photodisintegration, indicated by the region
of low density and high entropy in Figs. 7 and 8b and c.
This produces a high fraction of ![]() -particles, which in our model represent light nuclei.
The region of
-particles, which in our model represent light nuclei.
The region of ![]() -particle domination behind the expanding explosion shock increases with time. This behavior is illustrated in Fig. 12
for both Fe-core progenitor models under investigation. The position of
the explosion shock coincides with the maximum of the mass fraction of
Fe-group nuclei (in particular 56Ni).
In addition, density and temperature of the neutrino-driven wind
on top of the PNS surface decrease continuously with time. The low
temperatures and densities in that region do not justify the assumption
of NSE beyond
-particle domination behind the expanding explosion shock increases with time. This behavior is illustrated in Fig. 12
for both Fe-core progenitor models under investigation. The position of
the explosion shock coincides with the maximum of the mass fraction of
Fe-group nuclei (in particular 56Ni).
In addition, density and temperature of the neutrino-driven wind
on top of the PNS surface decrease continuously with time. The low
temperatures and densities in that region do not justify the assumption
of NSE beyond ![]() s
after bounce, where temperatures reach values below 0.5 MeV.
Instead, our nuclear reaction network is used to determine the
composition in that region. The decreasing density and temperature and
the presence of a high fraction of free nucleons favor the freeze out
of light nuclei. Finally, the entire region between the expanding
explosion shock and the PNS surface is found to be dominated in our
simulations by
s
after bounce, where temperatures reach values below 0.5 MeV.
Instead, our nuclear reaction network is used to determine the
composition in that region. The decreasing density and temperature and
the presence of a high fraction of free nucleons favor the freeze out
of light nuclei. Finally, the entire region between the expanding
explosion shock and the PNS surface is found to be dominated in our
simulations by ![]() -particles. In Fig. 12,
the radii of the NSE to non-NSE transitions are indicated by vertical
lines. The slight mismatch between the abundances between the heavy
``Fe''-group nuclei (the representative heavy nucleus with average
atomic mass and charge in NSE) and 56Ni (non-NSE) as well as between the
-particles. In Fig. 12,
the radii of the NSE to non-NSE transitions are indicated by vertical
lines. The slight mismatch between the abundances between the heavy
``Fe''-group nuclei (the representative heavy nucleus with average
atomic mass and charge in NSE) and 56Ni (non-NSE) as well as between the ![]() 's
is due to the different nuclear models used for the two regimes. While
in NSE the EoS for hot and dense nuclear matter assumes 56Fe as the most stable nucleus due to the lowest mass per nucleon
for low temperatures and densities, the nuclear reaction network applied in non-NSE calculates the
composition dynamically based on tabulated reaction rates.
's
is due to the different nuclear models used for the two regimes. While
in NSE the EoS for hot and dense nuclear matter assumes 56Fe as the most stable nucleus due to the lowest mass per nucleon
for low temperatures and densities, the nuclear reaction network applied in non-NSE calculates the
composition dynamically based on tabulated reaction rates.
5 Comparison with previous wind studies
5.1 The proton-to-baryon ratio of the wind
The most fundamental approximations made in previous wind studies is the simplified description of the radiation-hydrodynamics equations, see for example Duncan et al. (1986) and Qian & Woosley (1996). More crucial is the absence of neutrino transport. Neutrino heating and cooling is calculated based on parametrized neutrino luminosities and mean energies. Hence, such models explore the neutrino-driven wind by varying the neutrino luminosities and energies, where the simplified radiation-hydrodynamics equations are solved (see for example Thompson et al. 2001). Since neutrino transport is neglected, the evolution equation for the electron fraction Eq. (15) cannot be solved consistently because the neutrino distribution functions are unknown. In the following paragraph, we will discuss the assumptions made for the evolution of the electron fraction in the neutrino-driven wind which go back to Qian & Woosley (1996).
![\begin{figure}% latex2html id marker 1025\par\mbox{\subfigure[Different electr...
...mean energy.]{ \includegraphics[width=7cm,clip]{13106fig25.eps} }}\end{figure}](/articles/aa/full_html/2010/09/aa13106-09/Timg134.png)
|
Figure 13:
The Electron fraction approximations at a distance of 10 km outside the electron-neutrinosphere for the
|
| Open with DEXTER | |
Applying the theory of weak interactions based on the reaction rates
![]() for the reaction partners (i,j),
i.e. electron and positron as well as electron neutrino and
antineutrino captures, the evolution equations for the electron
and positron fractions
can be written as follows
for the reaction partners (i,j),
i.e. electron and positron as well as electron neutrino and
antineutrino captures, the evolution equations for the electron
and positron fractions
can be written as follows
These expressions can be combined to calculate the evolution of the total number of charges, using the relations
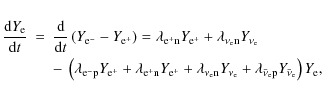
assuming fully dissociated nuclear matter. This expression is approximated in a crucial but powerful way (Qian & Woosley 1996, Eq. (73)), ignoring contributions from electron and positron captures as well as the decoupling of radiation from matter and the angular dependency of the neutrino distribution function on the distance from the energy-dependent neutrinospheres, as follows
This approximation of the electron fraction was further simplified and expressed in terms of the neutrino luminosities
which is used in previous static steady-state and parametrized dynamic studies of the neutrino-driven wind.
Figure 13a compares the electron fraction behavior at a distance of 10 km outside the electron-neutrinosphere, from Boltzmann neutrino transport (solid line) with the approximations Eq. (19) based on the neutrino capture rates (dashed line) and Eq. (20) based on the luminosities and mean neutrino energies (dash-dotted lines). The approximations are in qualitative agreement with Boltzmann transport. The differences on the longer timescale are most likely due to the presence of light and heavy nuclei which are not taken into account explicitly in the approximations. They change the number of free nucleons available for the reactions in Eqs. (16) and (17). All descriptions agree qualitatively in the prediction of a generally proton-rich material in the wind, based on the neutrino spectra obtained via Boltzmann transport.
5.2 The neutrino observables in the wind
Comparing the neutrino spectra in Fig. 14 with the spectra assumed in previous static steady-state and dynamic wind studies (see for example Thompson et al. 2001; and Arcones et al. 2007), we find two major differences: One, the neutrino luminosities and mean neutrino energies assumed are significantly higher than those we find and two, the assumed behavior with respect to time is different.
![\begin{figure}
\par\mbox{\includegraphics[width=6cm,clip]{13106fig26.eps}\hspace...
...}
\includegraphics[width=6cm,clip]{13106fig28.eps} }
\vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13106-09/Timg149.png)
|
Figure 14:
Neutrino luminosities and mean energies with respect to time after bounce for the
|
| Open with DEXTER | |
The commonly used assumptions made in static steady-state and
parametrized dynamic wind studies go back to the detailed investigation
from Woosley et al. (1994),
who performed core collapse simulations based on sophisticated input
physics. They investigated the neutrino-driven explosion of a
![]() progenitor
star and followed the evolution for 18 s post-bounce into the
neutrino-driven wind phase. In their simulations the electron
(anti)neutrino luminosities decreased from initially 4
progenitor
star and followed the evolution for 18 s post-bounce into the
neutrino-driven wind phase. In their simulations the electron
(anti)neutrino luminosities decreased from initially 4 ![]() 1052 (3
1052 (3 ![]() 1052) erg/s at the onset of
the explosion to 6
1052) erg/s at the onset of
the explosion to 6 ![]() 1051 (7.5
1051 (7.5 ![]() 1050) erg/s at 10 s after bounce, where strictly
1050) erg/s at 10 s after bounce, where strictly
![]() after the onset of the explosion. The difference between the neutrino
and antineutrino luminosities remained small and constant with respect
to time up to 3 s post-bounce and increased only significantly
after 4-5 s post-bounce, after which the difference reached its
maximum of 1.5
after the onset of the explosion. The difference between the neutrino
and antineutrino luminosities remained small and constant with respect
to time up to 3 s post-bounce and increased only significantly
after 4-5 s post-bounce, after which the difference reached its
maximum of 1.5 ![]() 1050 erg/s at the end of the simulation at about 18 s post-bounce.
The electron flavor neutrino luminosities in our models follow a different behavior. They reach 1
1050 erg/s at the end of the simulation at about 18 s post-bounce.
The electron flavor neutrino luminosities in our models follow a different behavior. They reach 1 ![]() 1051 erg/s at about 5, 6 and 8 s post-bounce for the 8.8, 10.8 and
1051 erg/s at about 5, 6 and 8 s post-bounce for the 8.8, 10.8 and
![]() progenitor models respectively. The higher electron flavor neutrino
luminosities for the more massive progenitors are in correlation with
the more massive PNSs and the hence larger number of neutrinos emitted.
However, the difference between electron-neutrino and
electron-antineutrino luminosities found in the present investigation
is significantly lower
than the difference in Woosley et al. (1994).
During the initial explosion phase until about 300 ms after
the onset of the explosion, the electron antineutrino luminosity is
slightly higher than the electron neutrino luminosity by about 1
progenitor models respectively. The higher electron flavor neutrino
luminosities for the more massive progenitors are in correlation with
the more massive PNSs and the hence larger number of neutrinos emitted.
However, the difference between electron-neutrino and
electron-antineutrino luminosities found in the present investigation
is significantly lower
than the difference in Woosley et al. (1994).
During the initial explosion phase until about 300 ms after
the onset of the explosion, the electron antineutrino luminosity is
slightly higher than the electron neutrino luminosity by about 1 ![]() 1050 erg/s which in
our models explains the electron fraction of
1050 erg/s which in
our models explains the electron fraction of
![]() of the early explosion ejecta. After about 900 ms post-bounce, the
luminosities can hardly be distinguished where during the initial
neutrino-driven wind phase after about 1 s after bounce the
electron neutrino luminosity becomes higher than the electron
antineutrino luminosity by about 1
of the early explosion ejecta. After about 900 ms post-bounce, the
luminosities can hardly be distinguished where during the initial
neutrino-driven wind phase after about 1 s after bounce the
electron neutrino luminosity becomes higher than the electron
antineutrino luminosity by about 1 ![]() 1050 erg/s.
This difference reduces again at later times at about 6 s
post-bounce and the electron flavor neutrino luminosities become more
and more similar (see Fig. 14).
1050 erg/s.
This difference reduces again at later times at about 6 s
post-bounce and the electron flavor neutrino luminosities become more
and more similar (see Fig. 14).
Even more different are the values and the behavior of the mean neutrino energies, see Fig. 14 and compare with Fig. 2 of Woosley et al. (1994). They found (![]() )-neutrino
energies of about 35 MeV which remained constant with respect to
time.
Their electron-antineutrino energies increased slightly from
about 20 MeV to 22 MeV where the electron-neutrino
energies decrease from 14 MeV to 12 MeV. This
increasing difference between the electron neutrino and antineutrino
spectra favored neutron-rich material, which was consistent with their
findings of
)-neutrino
energies of about 35 MeV which remained constant with respect to
time.
Their electron-antineutrino energies increased slightly from
about 20 MeV to 22 MeV where the electron-neutrino
energies decrease from 14 MeV to 12 MeV. This
increasing difference between the electron neutrino and antineutrino
spectra favored neutron-rich material, which was consistent with their
findings of
![]() for the material ejected in the neutrino-driven
wind in Woosley et al. (1994).
We cannot confirm these results for the mean neutrino energies
nor the evolution of the spectra. In contrast, all mean neutrino
energies decrease with respect to time for all our models. This is a
consequence of lepton number and energy loss of the central
PNS where the neutrinos diffuse out. The electron (anti)neutrino
energies decrease from about 10 (12) MeV at the onset of
the explosion to about 8.5 (9) MeV and the (
for the material ejected in the neutrino-driven
wind in Woosley et al. (1994).
We cannot confirm these results for the mean neutrino energies
nor the evolution of the spectra. In contrast, all mean neutrino
energies decrease with respect to time for all our models. This is a
consequence of lepton number and energy loss of the central
PNS where the neutrinos diffuse out. The electron (anti)neutrino
energies decrease from about 10 (12) MeV at the onset of
the explosion to about 8.5 (9) MeV and the (![]() )-neutrino
energies decrease from 16 MeV to 10 MeV at the end of the
simulations. Hence, not only the mean energies decrease also the
difference between
the electron flavor neutrino spectra decreases. The reason for the
neutrino spectra to become more similar with respect to time is related
to the evolution of the thermodynamic properties at the
neutrinospheres, and will be discussed in the following subsection.
)-neutrino
energies decrease from 16 MeV to 10 MeV at the end of the
simulations. Hence, not only the mean energies decrease also the
difference between
the electron flavor neutrino spectra decreases. The reason for the
neutrino spectra to become more similar with respect to time is related
to the evolution of the thermodynamic properties at the
neutrinospheres, and will be discussed in the following subsection.
| Figure 15:
Evolution of the neutrinosphere radii in graph a) and temperature, density and electron fraction at the corresponding neutrinospheres in graphs b), c) and d) respectively for the
|
|
| Open with DEXTER | |
| Figure 16:
Radial PNS profiles at two different post-bounce times (thick lines: 2 s, thin lines: 10 s), for the
|
|
| Open with DEXTER | |
5.3 The PNS contraction
The behavior of the neutrino spectra and hence the evolution and the
properties of the neutrinospheres is related to the
PNS contraction. The contraction is caused by a continuous
deleptonization and translates to a continued steepening of the density
gradient at the PNS surface.
Hence, the neutrinosphere radii for the electron flavor neutrinos
move closer together with time.
The evolution of the neutrinosphere radii for both electron neutrino
and antineutrino are illustrated in Fig. 15a for the
![]() progenitor model. Their difference reduces from 740 m at about
1 s post-bounce to 370 m at about 5 s
post-bounce and further to 260 m at about 10 s
post-bounce.
progenitor model. Their difference reduces from 740 m at about
1 s post-bounce to 370 m at about 5 s
post-bounce and further to 260 m at about 10 s
post-bounce.
This contraction behavior has consequences for the neutrino
spectra, which are determined during the neutrino-driven wind phase by
diffusion rather than by mass accretion. Hence, the electron
flavor neutrino luminosities can be determined as follows
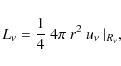
|
(21) |
where
Since this difference is small in our simulations, with initially
![]() MeV and
MeV and
![]() MeV
(at about 1 s post-bounce) and only
MeV
(at about 1 s post-bounce) and only
![]() MeV
and
MeV
and
![]() MeV (at later times at 10 s post-bounce), the values found for the electron fraction of
MeV (at later times at 10 s post-bounce), the values found for the electron fraction of
![]() (solid line in Fig. 13b for the
(solid line in Fig. 13b for the ![]() -approximation
based on the luminosity and mean neutrino energies) clearly illustrate
that the accelerated matter in the neutrino driven wind stays
proton-rich for more than 10 s. This is in qualitative
agreement with Boltzmann transport
as discussed above and shown in Fig. 13a. Hence we find Eq.( 20)
to be a good approximation to model the electron fraction in the wind.
On the other hand, most of the previous studies select the
neutrino luminosities and mean energies to investigate a neutron-rich
neutrino driven wind. In order to test the appearance of
-approximation
based on the luminosity and mean neutrino energies) clearly illustrate
that the accelerated matter in the neutrino driven wind stays
proton-rich for more than 10 s. This is in qualitative
agreement with Boltzmann transport
as discussed above and shown in Fig. 13a. Hence we find Eq.( 20)
to be a good approximation to model the electron fraction in the wind.
On the other hand, most of the previous studies select the
neutrino luminosities and mean energies to investigate a neutron-rich
neutrino driven wind. In order to test the appearance of
![]() under such conditions,
we increase the difference between the mean neutrino and antineutrino energies by hand. We evaluate expression (20) shown in Fig. 13b
at 10 km outside the electron-neutrinosphere for 1.2
(dashed line) and 1.5 (dash-dotted line) times larger
electron-antineutrino mean energies. For the first value,
under such conditions,
we increase the difference between the mean neutrino and antineutrino energies by hand. We evaluate expression (20) shown in Fig. 13b
at 10 km outside the electron-neutrinosphere for 1.2
(dashed line) and 1.5 (dash-dotted line) times larger
electron-antineutrino mean energies. For the first value, ![]() decreases
but matter remains slightly proton-rich, where for the latter value
matter becomes neutron-rich. Indeed, the larger the difference
between neutrino and antineutrino spectra are, the lower becomes
the electron fraction in the wind. Note that the luminosities and
electron-neutrino energies
remained unmodified for this experiment. Such an increase of the energy
difference between neutrinos and antineutrinos could perhaps be related
to the uncertainty of the EoS for nuclear matter, which will be
discussed in the following paragraph.
decreases
but matter remains slightly proton-rich, where for the latter value
matter becomes neutron-rich. Indeed, the larger the difference
between neutrino and antineutrino spectra are, the lower becomes
the electron fraction in the wind. Note that the luminosities and
electron-neutrino energies
remained unmodified for this experiment. Such an increase of the energy
difference between neutrinos and antineutrinos could perhaps be related
to the uncertainty of the EoS for nuclear matter, which will be
discussed in the following paragraph.
The assumed PNS radii in previous wind studies reach about 10 km shortly (![]() s)
after the onset of the explosion. We define the radius of the PNS as
the position of the electron-neutrinosphere at the steep density
gradient at the PNS surface. The approximated inner boundary of
the physical domain in most wind models is close to but still inside
this radius.
The position of the neutrinospheres and the contraction of the PNSs
found in the present paper differ significantly from the assumptions
made in most previous wind studies. We find PNS radii of about
40 km at the time of the explosion and 20 km at
about 2 s after bounce (see Fig. 15a).
During the later evolution, the PNS contraction slows down.
The PNS profile and hence the position of the neutrinospheres
as well as the contraction behavior itself is given implicitly by the
EoS for hot and dense nuclear matter as well as the
PNS deleptonization. For the stiff EoS from Shen et al. (1998) and both the 10.8 and
s)
after the onset of the explosion. We define the radius of the PNS as
the position of the electron-neutrinosphere at the steep density
gradient at the PNS surface. The approximated inner boundary of
the physical domain in most wind models is close to but still inside
this radius.
The position of the neutrinospheres and the contraction of the PNSs
found in the present paper differ significantly from the assumptions
made in most previous wind studies. We find PNS radii of about
40 km at the time of the explosion and 20 km at
about 2 s after bounce (see Fig. 15a).
During the later evolution, the PNS contraction slows down.
The PNS profile and hence the position of the neutrinospheres
as well as the contraction behavior itself is given implicitly by the
EoS for hot and dense nuclear matter as well as the
PNS deleptonization. For the stiff EoS from Shen et al. (1998) and both the 10.8 and
![]() progenitors, the PNSs reach radii of 14.5-15 km only at about 10 s after bounce (see Fig. 15).
The larger radii of the neutrinospheres result in lower neutrino
luminosities and mean energies and a lower difference between neutrino
and antineutrino spectra in comparison to the assumptions made in most
previous wind models. This is in agreement with Arcones et al. (2007)
who additionally assume PNS radii of 15 km and find
conditions that differ more from previous wind studies. They obtained
significantly higher values for the electron fraction.
To summarize, this effects and the different behavior of the
neutrino spectra assumed in the previous wind studies leads to
different matter properties of the neutrino-driven wind.
A detailed comparison study of fast and slow contracting PNSs with
respect to the neutrino-driven wind, e.g. applying EoSs with
different compressibilities and asymmetry energies, would be necessary
in the context of radiation hydrodynamics simulations using spectral
Boltzmann neutrino transport.
progenitors, the PNSs reach radii of 14.5-15 km only at about 10 s after bounce (see Fig. 15).
The larger radii of the neutrinospheres result in lower neutrino
luminosities and mean energies and a lower difference between neutrino
and antineutrino spectra in comparison to the assumptions made in most
previous wind models. This is in agreement with Arcones et al. (2007)
who additionally assume PNS radii of 15 km and find
conditions that differ more from previous wind studies. They obtained
significantly higher values for the electron fraction.
To summarize, this effects and the different behavior of the
neutrino spectra assumed in the previous wind studies leads to
different matter properties of the neutrino-driven wind.
A detailed comparison study of fast and slow contracting PNSs with
respect to the neutrino-driven wind, e.g. applying EoSs with
different compressibilities and asymmetry energies, would be necessary
in the context of radiation hydrodynamics simulations using spectral
Boltzmann neutrino transport.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{13106fig31.eps}
\vspace*{6.5mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13106-09/Timg166.png)
|
Figure 17:
Radial profiles of selected hydrodynamic variables
for the
|
| Open with DEXTER | |
6 Long term post-bounce evolution
During the neutrino-driven wind phase, the neutrino luminosities and
mean neutrino energies decrease continuously, which leads to a constant
decrease in the net-heating rates. At luminosities below 1051 erg/s (see Fig. 14), the supersonic matter outflow for the
![]() progenitor model descends into a subsonic expansion. The wind
termination shock turns again into a subsonic neutrino-driven wind.
At later times, the neutrino-driven wind settles down to a
quasi-stationary state with no significant matter outflow, illustrated
at the example of the
progenitor model descends into a subsonic expansion. The wind
termination shock turns again into a subsonic neutrino-driven wind.
At later times, the neutrino-driven wind settles down to a
quasi-stationary state with no significant matter outflow, illustrated
at the example of the
![]() progenitor model in Fig. 17a.
The explosion shock continues to expand and the material enclosed
inside the mass cut accretes onto the PNS at the center.
In combination with the deleptonization, this leads to the
continuous PNS contraction. However, the contraction proceeds
on a timescale of seconds and hence the PNS can be considered in a
quasi-stationary state. The dense and still hot and lepton-rich PNS at
the center is surrounded by a low density and high entropy atmosphere,
composed of light and heavy nuclei. See for example the abundances
of the
progenitor model in Fig. 17a.
The explosion shock continues to expand and the material enclosed
inside the mass cut accretes onto the PNS at the center.
In combination with the deleptonization, this leads to the
continuous PNS contraction. However, the contraction proceeds
on a timescale of seconds and hence the PNS can be considered in a
quasi-stationary state. The dense and still hot and lepton-rich PNS at
the center is surrounded by a low density and high entropy atmosphere,
composed of light and heavy nuclei. See for example the abundances
of the
![]() progenitor for the post-bounce time of 22 s in Fig. 17e.
The region at sub-saturation densities where light nuclei are present
belongs to the inhomogeneous matter phase where clusters, known as
pasta-
and spaghetti-phases, are predicted to dominate the EoS. However,
the EoS from Shen et al. (1998) approximates these effects by the presence of light nuclei represented in our model by
progenitor for the post-bounce time of 22 s in Fig. 17e.
The region at sub-saturation densities where light nuclei are present
belongs to the inhomogeneous matter phase where clusters, known as
pasta-
and spaghetti-phases, are predicted to dominate the EoS. However,
the EoS from Shen et al. (1998) approximates these effects by the presence of light nuclei represented in our model by ![]() -particles.
-particles.
The internal temperature profile of the PNS is not constant. The
central region of the PNS did not experience shock heating immediately
after the Fe-core bounce, since the initial shock forms at the edge of
the bouncing core. Its mass scales roughly with
![]() and is typically around values of
and is typically around values of
![]() for
low- and intermediate-mass Fe-core progenitors. Hence, the central
temperature after bounce is given by the thermodynamic conditions at
bounce. The temperature changes only during the post-bounce evolution
due to compressional heating and the diffusion of neutrinos. The shock
heated material inside the PNS shows significantly higher temperatures
than at the center. The temperature decreases again towards the PNS
surface where the matter is less dense (for the illustration of
the radial temperature profile inside the PNS as well as the dynamical
evolution of temperature and density, see Figs. 17f
and b at selected post-bounce times between 5-22 s). The
neutrinos diffuse continuously out of the PNS and carry away energy.
The central electron fraction reduces from
for
low- and intermediate-mass Fe-core progenitors. Hence, the central
temperature after bounce is given by the thermodynamic conditions at
bounce. The temperature changes only during the post-bounce evolution
due to compressional heating and the diffusion of neutrinos. The shock
heated material inside the PNS shows significantly higher temperatures
than at the center. The temperature decreases again towards the PNS
surface where the matter is less dense (for the illustration of
the radial temperature profile inside the PNS as well as the dynamical
evolution of temperature and density, see Figs. 17f
and b at selected post-bounce times between 5-22 s). The
neutrinos diffuse continuously out of the PNS and carry away energy.
The central electron fraction reduces from
![]() at the onset of the explosion to
at the onset of the explosion to
![]() at 22 s after bounce (see Fig. 17d).
It relates to a temperature decrease from about 35 MeV
initially (at 3 s post-bounce) to 23 MeV at
about 22 s post-bounce. This corresponds to the initial and
neutrino dominated cooling phase. Unfortunately the achieved
temperatures are not representative since important neutrino reactions,
such as the direct and modified Urca processes, are not yet taken
into account.
at 22 s after bounce (see Fig. 17d).
It relates to a temperature decrease from about 35 MeV
initially (at 3 s post-bounce) to 23 MeV at
about 22 s post-bounce. This corresponds to the initial and
neutrino dominated cooling phase. Unfortunately the achieved
temperatures are not representative since important neutrino reactions,
such as the direct and modified Urca processes, are not yet taken
into account.
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{13106fig32.eps}\par\includegraphics[width=16.5cm,clip]{13106fig33.eps}
\vspace*{7mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13106-09/Timg171.png)
|
Figure 18:
Comparing selected hydrodynamic variables using the standard
reactions rates based on Bruenn (1985) (solid lines) and the artificially enhanced rates (dashed lines) for the
|
| Open with DEXTER | |
7 Discussion
The neutrino-driven wind was found to occur in all three progenitor models under investigation,
the
![]() O-Ne-Mg-core and the 10.8 and
O-Ne-Mg-core and the 10.8 and
![]() Fe-core
progenitor models.
Because the neutrino-driven explosions for the Fe-core progenitors are
launched using artificially enhanced neutrino reaction rates, one may
ask about the impact of these modified rates to the neutrino-driven
wind. Therefore we performed additional runs for which we switch back
to the
standard opacities given in Bruenn (1985)
after the explosions have been launched. The times when we switch back
is about 500 ms after bounce, chosen such that the dynamics of the
explosion ejecta does not change anymore significantly due to neutrino
heating. However, the lower opacities translate to a significantly
lower net-heating by a factor of 5-6 in the region on top of the
PNS where the neutrino-driven wind develops. The energy deposition is
still sufficient to drive the neutrino-driven wind but the matter
velocities are lower by a factor of 2-5 in comparison to the wind
velocities using the enhanced reaction rates (see Fig. 18a).
The main effect of the artificially enhanced reaction rates and the
hence increased neutrino heating to the dynamics is clearly the
stronger neutrino-driven wind. For the
Fe-core
progenitor models.
Because the neutrino-driven explosions for the Fe-core progenitors are
launched using artificially enhanced neutrino reaction rates, one may
ask about the impact of these modified rates to the neutrino-driven
wind. Therefore we performed additional runs for which we switch back
to the
standard opacities given in Bruenn (1985)
after the explosions have been launched. The times when we switch back
is about 500 ms after bounce, chosen such that the dynamics of the
explosion ejecta does not change anymore significantly due to neutrino
heating. However, the lower opacities translate to a significantly
lower net-heating by a factor of 5-6 in the region on top of the
PNS where the neutrino-driven wind develops. The energy deposition is
still sufficient to drive the neutrino-driven wind but the matter
velocities are lower by a factor of 2-5 in comparison to the wind
velocities using the enhanced reaction rates (see Fig. 18a).
The main effect of the artificially enhanced reaction rates and the
hence increased neutrino heating to the dynamics is clearly the
stronger neutrino-driven wind. For the
![]() progenitor model and with the enhanced heating, the wind even
develops supersonic velocities (as discussed above in
Sect. 4) in Fig. 18a
(top panel). The supersonic wind collides with the explosion ejecta
where matter decelerates and hence the reverse shock forms, which
additionally increases the entropy in the wind (see Fig. 18c,
top panel).
This additional entropy increase is absent in the simulations using the
standard opacities, where the wind stays subsonic. This is also the
case for the
progenitor model and with the enhanced heating, the wind even
develops supersonic velocities (as discussed above in
Sect. 4) in Fig. 18a
(top panel). The supersonic wind collides with the explosion ejecta
where matter decelerates and hence the reverse shock forms, which
additionally increases the entropy in the wind (see Fig. 18c,
top panel).
This additional entropy increase is absent in the simulations using the
standard opacities, where the wind stays subsonic. This is also the
case for the
![]() progenitor model (Fig. 18,
bottom panel), with and without the enhanced opacities. The
neutrino-driven wind of the O-Ne-Mg-core is illustrated in Fig. 11 using the standard rates based on Bruenn (1985).
The formation of a supersonic neutrino-driven wind could be confirmed
including the formation of the wind termination shock. Hence, one may
speculate whether only low-mass progenitors develop strong
neutrino-driven winds, while for more massive progenitors the influence
of the winds to the matter properties of the ejecta becomes small. The
progenitor dependency of the neutrino-driven wind is related to the
density of the envelope surrounding the PNS after the explosion has
been launched, which is significantly higher for more massive
progenitors and hence the neutrino-driven wind is weaker.
progenitor model (Fig. 18,
bottom panel), with and without the enhanced opacities. The
neutrino-driven wind of the O-Ne-Mg-core is illustrated in Fig. 11 using the standard rates based on Bruenn (1985).
The formation of a supersonic neutrino-driven wind could be confirmed
including the formation of the wind termination shock. Hence, one may
speculate whether only low-mass progenitors develop strong
neutrino-driven winds, while for more massive progenitors the influence
of the winds to the matter properties of the ejecta becomes small. The
progenitor dependency of the neutrino-driven wind is related to the
density of the envelope surrounding the PNS after the explosion has
been launched, which is significantly higher for more massive
progenitors and hence the neutrino-driven wind is weaker.
The agreement of the time evolution of the mean neutrino
energies between all three progenitor models under investigation (using
the enhanced and standard opacities) in Fig. 14
is striking. The impact of the artificial heating to the neutrino
observables and hence to the electron fraction in the wind is less
pronounced. The influence on the composition of the wind is illustrated
via the electron fraction in Fig. 18d. Using the standard rates, the wind stays slightly more proton-rich. Increasing the charged current reaction rates allows ![]() -equilibrium
to be established on a shorter timescale. In addition, matter
stays slightly more proton-rich for the less intense neutrino-driven
wind, which develops for the Fe-core progenitors using the standard
neutrino opacities. The additional electron fraction decrease in the
neutrino-driven wind for the models using the enhanced neutrino
reactions is found due to the higher degeneracy obtained in the
stronger deceleration behind the explosion ejecta, and is therefore a
dynamic effect. However, the findings of generally proton-rich
ejecta as well as the generally proton-rich neutrino-driven wind does
not change. The corresponding densities and entropies per baryon in the
wind are shown in Figs. 18b
and c. The effects of the artificial heating are slightly lower
entropies per baryon. The higher matter outflow velocities in the wind
region using the artificial heating results additionally in lower
densities, shown in Fig. 18b.
-equilibrium
to be established on a shorter timescale. In addition, matter
stays slightly more proton-rich for the less intense neutrino-driven
wind, which develops for the Fe-core progenitors using the standard
neutrino opacities. The additional electron fraction decrease in the
neutrino-driven wind for the models using the enhanced neutrino
reactions is found due to the higher degeneracy obtained in the
stronger deceleration behind the explosion ejecta, and is therefore a
dynamic effect. However, the findings of generally proton-rich
ejecta as well as the generally proton-rich neutrino-driven wind does
not change. The corresponding densities and entropies per baryon in the
wind are shown in Figs. 18b
and c. The effects of the artificial heating are slightly lower
entropies per baryon. The higher matter outflow velocities in the wind
region using the artificial heating results additionally in lower
densities, shown in Fig. 18b.
The artificially increased charged current reaction rates cannot be justified by physical uncertainties of the rates themselves. Similar to the high luminosities assumed in Arcones et al. (2007), they could be seen as a lowest order attempt to take the effects of multi-dimensional phenomena into account. For example, known fluid instabilities increase the neutrino energy deposition efficiency. Convection allows matter to stay for a longer time in the neutrino heating region (see Herant et al. 1994; Janka & Müller 1996). Present axially symmetric core collapse models of massive Fe-core progenitor stars (even non-rotating) predict bipolar explosions (see Janka et al. 2008). The deviation from a spherical description and hence the deformation of the SAS due to fluid instabilities takes place during the neutrino heating phase on a timescale of several 100 ms after bounce. In multi-dimensional models, the luminosities are powered by a significantly higher mass accretion because the up-streaming neutrino heated matter is accompanied by large down-streams of cold material. These higher luminosities may power a strong (even supersonic) neutrino-driven wind behind the explosion ejecta, while the neutrino-driven wind may remain absent in the angular directions of the accreting material which will not be ejected.
![\begin{figure}
\par\includegraphics[width=15cm,clip]{13106fig34.eps}\par\include...
...ar\includegraphics[width=15cm,clip]{13106fig36.eps}
\vspace*{5.2mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13106-09/Timg172.png)
|
Figure 19:
Mass accretion rate, timescales and entropy in the wind for the three progenitor models under investigation,
|
| Open with DEXTER | |
Previous wind models have long been investigated as a possible site for the production of heavy elements via the r-process,
motivated by the expectation of the ejection of neutron-rich material,
the high entropies per baryon in the neutrino-driven wind and the short
timescale of the neutrino-driven wind expansion (see Hoffman et al. 2007; Panov & Janka 2009; and references therein). The relevant quantities are shown in Figs. 10 and 11 for the
![]() and
and
![]() progenitor models respectively. Illustrated are several selected mass
shells that are part of the region where the neutrino-driven wind
develops in our radiation hydrodynamics model based on spectral
three-flavor Boltzmann neutrino transport. The inclusion of neutrino
transport in a dynamical model is essential in order to obtain
consistent neutrino spectra which determine the evolution of the
electron fraction and the PNS contraction due to deleptonization
and mass accretion. In comparison to previous static steady-state
and dynamic wind models - where these ingredients were
assumed - we confirm several properties of the accelerated
material in the neutrino-driven wind, such as the fast expansion
and the high matter outflow rate shown in Fig. 19, the high velocities in the Figs. 10f and 11f and the
rapidly decreasing density and temperature of the accelerated material in Figs. 10b and c respectively. The expansion timescale in Fig. 19 is given by the following expression
progenitor models respectively. Illustrated are several selected mass
shells that are part of the region where the neutrino-driven wind
develops in our radiation hydrodynamics model based on spectral
three-flavor Boltzmann neutrino transport. The inclusion of neutrino
transport in a dynamical model is essential in order to obtain
consistent neutrino spectra which determine the evolution of the
electron fraction and the PNS contraction due to deleptonization
and mass accretion. In comparison to previous static steady-state
and dynamic wind models - where these ingredients were
assumed - we confirm several properties of the accelerated
material in the neutrino-driven wind, such as the fast expansion
and the high matter outflow rate shown in Fig. 19, the high velocities in the Figs. 10f and 11f and the
rapidly decreasing density and temperature of the accelerated material in Figs. 10b and c respectively. The expansion timescale in Fig. 19 is given by the following expression
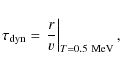
evaluated at the surface of constant temperature of T=0.5 MeV, compared with an alternative definition of the dynamic timescale which has been introduced in Thompson et al. (2001)
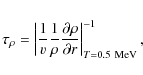
as well as a timescale approximation which has been derived in Qian & Woosley (1996) Eq. (61)
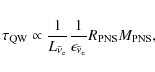
where additionally approximations for the mass outflow rate and the entropy per baryon are derived as follows
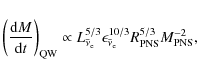
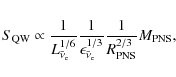
where
However, the wind entropies of
![]() found
(initially driven due to neutrino heating and additionally due to the
deceleration in the reverse shock) are significantly smaller than often
assumed in the literature and the previously accelerated matter does
not become neutron-rich as the neutrino-driven wind decelerates behind
the explosion ejecta but stays slightly
proton-rich where
found
(initially driven due to neutrino heating and additionally due to the
deceleration in the reverse shock) are significantly smaller than often
assumed in the literature and the previously accelerated matter does
not become neutron-rich as the neutrino-driven wind decelerates behind
the explosion ejecta but stays slightly
proton-rich where
![]() for more than 10 s. This, in combination with the much
slower PNS contraction illustrated via the neutrinospheres in
Fig. 15
in comparison to static steady-state and dynamic wind models suggest
that the assumptions made in previous wind studies should be carefully
reconsidered.
With respect to Woosley et al. (1994) (e.g. Fig. 3),
we find generally smaller mean neutrino energies which decrease with
respect to time after bounce. This results in a decreasing difference
between the electron flavor neutrino mean energies, while in Woosley et al. (1994) this difference increases. This fact in combination with the different PNS properties found in Woosley et al. (1994), enabled a strong neutrino-driven wind where high entropies up to
for more than 10 s. This, in combination with the much
slower PNS contraction illustrated via the neutrinospheres in
Fig. 15
in comparison to static steady-state and dynamic wind models suggest
that the assumptions made in previous wind studies should be carefully
reconsidered.
With respect to Woosley et al. (1994) (e.g. Fig. 3),
we find generally smaller mean neutrino energies which decrease with
respect to time after bounce. This results in a decreasing difference
between the electron flavor neutrino mean energies, while in Woosley et al. (1994) this difference increases. This fact in combination with the different PNS properties found in Woosley et al. (1994), enabled a strong neutrino-driven wind where high entropies up to
![]() /baryon and a low electron fraction of
/baryon and a low electron fraction of
![]() was obtained. These properties of the neutrino-driven wind differ
quantitatively from our results, where lower entropies per baryon are
obtained and matter stays proton-rich for more than 10 s.
was obtained. These properties of the neutrino-driven wind differ
quantitatively from our results, where lower entropies per baryon are
obtained and matter stays proton-rich for more than 10 s.
8 Summary and outlook
For the first time, spherically symmetric core collapse supernova
simulations based on general relativistic radiation hydrodynamics and
three-flavor Boltzmann neutrino transport are performed consistently
for more than 20 s. We follow the dynamical evolution of low-
and intermediate-mass progenitors through the collapse, bounce,
post-bounce, explosion and neutrino-driven wind phases. The explosions
of Fe-core progenitors of 10.8 and
![]() are modeled using artificially enhanced opacities, while the explosion of the
are modeled using artificially enhanced opacities, while the explosion of the
![]() O-Ne-Mg-core
is obtained using the standard opacities. For all models under
investigation, we confirm the formation and illustrate the conditions
for the appearance of the neutrino-driven wind during the dynamical
evolution after the explosions have been launched. For the O-Ne-Mg-core
and the
O-Ne-Mg-core
is obtained using the standard opacities. For all models under
investigation, we confirm the formation and illustrate the conditions
for the appearance of the neutrino-driven wind during the dynamical
evolution after the explosions have been launched. For the O-Ne-Mg-core
and the
![]() Fe-core progenitor models, the supersonic neutrino-driven wind
collides with the slower expanding explosion ejecta where due to the
deceleration the neutrino-driven wind termination shock appears. We
discuss the impact of the reverse shock for several properties of the
ejecta and find general agreement with Arcones et al. (2007).
Fe-core progenitor models, the supersonic neutrino-driven wind
collides with the slower expanding explosion ejecta where due to the
deceleration the neutrino-driven wind termination shock appears. We
discuss the impact of the reverse shock for several properties of the
ejecta and find general agreement with Arcones et al. (2007).
The comparison with approximate and static steady-state as well as
parametrized dynamic wind models leads to a discrepancy in the obtained
physical properties of the neutrino-driven wind. Although the evolution
of the hydrodynamic variables are in general agreement, we find smaller
neutrino luminosities and a different behavior of the mean neutrino
energies. In particular, the differences between the neutrino
and antineutrino luminosities and mean neutrino energies are smaller.
These differences reduce with time as the PNSs contract, which
results in generally proton-rich neutrino-driven winds over more
than 10 s for all our models. Hence, the suggestion that
the physical conditions in the neutrino-driven wind could be favorable
for the nucleosynthesis of heavy elements via the r-process
could not be confirmed. For the accurate determination of the
yields of the neutrino-driven wind, detailed nucleosynthesis analysis
based on a large nuclear reaction network, taking the r-, p- and ![]() -processes
into account, is required. In order to further support the
robustness, improvements of the input physics such as weak magnetism
and nucleon-nucleon recoil (following e.g. Horowitz 2002),
taking the presence of light
and heavy clusters of nuclei into account as well as different EoSs
with respect to different PNS contraction behaviors, should be
considered. These may have a strong influence on the properties of the
neutrino spectra at the neutrinospheres and may therefore modify some
of the results found in the present study of the neutrino-driven wind.
-processes
into account, is required. In order to further support the
robustness, improvements of the input physics such as weak magnetism
and nucleon-nucleon recoil (following e.g. Horowitz 2002),
taking the presence of light
and heavy clusters of nuclei into account as well as different EoSs
with respect to different PNS contraction behaviors, should be
considered. These may have a strong influence on the properties of the
neutrino spectra at the neutrinospheres and may therefore modify some
of the results found in the present study of the neutrino-driven wind.
Our simulations are carried out until the neutrino-driven wind settles down to a quasi-stationary state leading to the initial and neutrino dominated PNS cooling phase. There, the simulations have to be stopped because important neutrino cooling processes like the direct and modified URCA processes are not taken into account yet. However, a smooth connection to isolated neutron or protoneutron star cooling studies comes into reach for future work (Henderson & Page 2007).
The authors would like to thank A. Arcones and G. Martínez-Pinedo for discussions and helpful comments. The project was funded by the Swiss National Science Foundation grant numbers PP002-106627/1, PP00P2-124879 and 200020-122287. The authors are additionally supported by CompStar, a research networking program of the European Science Foundation, and the Scopes project funded by the Swiss National Science Foundation grant. No. IB7320-110996/1. A. Mezzacappa is supported at the Oak Ridge National Laboratory, which is managed by UT-Battelle, LLC for the US Department of Energy under contract DE-AC05-00OR22725.
References
- Arcones, A., Janka, H.-Th., & Scheck, L. 2007, A&A, 467, 1227 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arcones, A., Martínez-Pinedo, G., O'Conner, E., et al. 2008, Phys. Rev. C, 78, 015806 [NASA ADS] [CrossRef] [Google Scholar]
- Bethe, H. A., & Wilson, J. R. 1985, ApJ, 295, 14 [Google Scholar]
- Bruenn, S. W. 1985, ApJS, 58, 771 [NASA ADS] [CrossRef] [Google Scholar]
- Bruenn, S. W., Dirk, C. J., Mezzacappa, A., et al. 2006, J. Phys. Conf. Ser., 46, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Burrows, A., Hayes, J., & Fryxell, B. A. 1995, ApJ, 450, 830 [NASA ADS] [CrossRef] [Google Scholar]
- Duncan, R. C., Shapiro, S. L., & Wasserman, I. 1986, ApJ, 309, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Fischer, T., Whitehouse, S. C., Mezzacappa, A., Thielemann, F.-K., & Liebendörfer, M. 2009, A&A, 499, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fröhlich, C., Hauser, P., Liebendörfer, M., et al. 2006a, ApJ, 637, 415 [Google Scholar]
- Fröhlich, C., Hix, W. R., Martínez-Pinedo, G., et al. 2006b, New Astron. Rev., 50, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Fröhlich, C., Martínez-Pinedo, G., Liebendörfer, M., et al. 2006c, Phys. Rev. Lett., 96 (14), 142502 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Henderson, J. A., & Page, D. 2007, Ap&SS, 308, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Herant, M., Benz, W., Hix, W. R., Fryer, C. L., & Colgate, S. A. 1994, ApJ, 435, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Hix, W. R., Messer, O. B. E., Mezzacappa, A., et al. 2003, Phys. Rev. Lett., 91, 201102 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hoffman, R. D., Woosley, S. E., & Qian, Y. Z. 1997, ApJ, 482, 951 [NASA ADS] [CrossRef] [Google Scholar]
- Hoffman, R. D., Pruet, J., Fisker, J. L., et al. 2007, unpublished [arXiv:0712.2847] [Google Scholar]
- Horowitz, C. J. 2002, Phys. Rev. D, 65, 043001 [NASA ADS] [CrossRef] [Google Scholar]
- Janka, H.-Th. 2001, A&A, 368, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Janka, H.-Th., & Müller, E. 1995, ApJ, 448, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Janka, H.-Th., & Müller, E. 1995, A&A, 306, 167 [Google Scholar]
- Janka, H.-Th., Buras, R., Kitaura Joyanes, F. S., et al. 2005, Nuclear Physics A, 758, 19 [Google Scholar]
- Janka, H.-Th., Marek, A., Müller, B., & Scheck, L. 2008, In 40 Years of Pulsars: Millisecond Pulsars, Magnetars and More, ed. C. Bassa, Z. Wang, A. Cumming, & V. M. Kaspi, AIP Conf. Ser., 983, 369 [Google Scholar]
- Kitaura, F. S., Janka, H.-Th., & Hillebrandt, W. 2006, A&A, 450, 345 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kotake, K., Sato, K., & Takahashi, K. 2006, Rep. Prog. Phys., 69, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Langanke, K., Martínez-Pinedo, G., Sampaio, J. M., et al. 2003, Phys. Rev. Lett., 90, 241102 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Liebendörfer, M. 2004, Proceedings of the 12th Workshop on Nuclear Astrophysics, Rep. No. MPA/P14, 143 [arXiv:astro-ph/0405029] [Google Scholar]
- Liebendörfer, M., Mezzacappa, A., Thielemann, F.-K., et al. 2001a, Phys. Rev. D, 63, 103004 [NASA ADS] [CrossRef] [Google Scholar]
- Liebendörfer, M., Mezzacappa, A., & Thielemann, F.-K. 2001b, Phys. Rev. D, 63, 104003 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Liebendörfer, M., Rosswog, S., & Thielemann, F.-K. 2002, ApJS, 141, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Liebendörfer, M., Messer, O. E. B., Mezzacappa, A., et al. 2004, ApJS, 150, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Liebendörfer, M., Ramp, M., Janka, H.-Th., & Mezzacappa, A. 2005, ApJ, 620, 840 [NASA ADS] [CrossRef] [Google Scholar]
- Marek, A., & Janka, H.-Th. 2009, ApJ, 694, 664 [NASA ADS] [CrossRef] [Google Scholar]
- Mayle, R., & Wilson, J. R. 1988, ApJ, 334, 909 [NASA ADS] [CrossRef] [Google Scholar]
- Mezzacappa, A., & Bruenn, S. W. 1993a, ApJ, 405, 637 [NASA ADS] [CrossRef] [Google Scholar]
- Mezzacappa, A., & Bruenn, S. W. 1993b, ApJ, 405, 669 [NASA ADS] [CrossRef] [Google Scholar]
- Mezzacappa, A., & Bruenn, S. W. 1993c, ApJ, 410, 740 [NASA ADS] [CrossRef] [Google Scholar]
- Mezzacappa, A., & Messer, O. E. B. 1999, J. Comput. Appl. Math., 109, 281 [Google Scholar]
- Mezzacappa, A., Blondin, J. M., Messer, O. E. B., & Bruenn, S. W. 2006, In Origin of Matter and Evolution of Galaxies, AIP Conf. Ser., 847, 179 [Google Scholar]
- Miller, D. S., Wilson, J. R., & Mayle, R. W. 1993, ApJ, 415, 278 [NASA ADS] [CrossRef] [Google Scholar]
- Misner, C. W., & Sharp, D. H. 1964, Phys. Rev., 136, 571 [Google Scholar]
- Nomoto, K. 1983, IAU Symp., 101, 139 [NASA ADS] [Google Scholar]
- Nomoto, K. 1984, ApJ, 277, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Nomoto, K. 1987, ApJ, 322, 206 [NASA ADS] [CrossRef] [Google Scholar]
- Otsuki, K., Tagoshi, H., Kajino, T., & Wanajo, S. Y. 2000, ApJ, 533, 424 [NASA ADS] [CrossRef] [Google Scholar]
- Panov, I. V., & Janka, H.-Th. 2009, A&A, 494, 829 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Qian, Y. Z., & Woosley, S. E. 1996, ApJ, 471, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Sagert, I., Fischer, T., Hempel, M., et al. 2009, Phys. Rev. Lett., 102 (8), 081101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Scheck, L., Kifondis, K., Janka, H.-T., & Müller, E. 2006, A&A, 457, 963 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schinder, P. J., & Shapiro, S. L. 1982, ApJS, 50, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, H., Toki, H., Oyamatsu, K., & Sumiyoshi, K. 1989, Prog. Theor. Phys., 100, 1013 [Google Scholar]
- Takahashi, K., Witti, J., & Janka, H.-Th. 1994, A&A, 286, 857 [NASA ADS] [Google Scholar]
- Thielemann, F.-K., Brachwitz, F., Höflich, P., Martinez-Pinedo, G., & Nomoto, K. 2004, New Astron. Rev., 48, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, T. A., & Burrows, A. 2001, Nucl. Phys. A, 688, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, T. A., Burrows, A., & Meyer, B. S. 2001, ApJ, 562, 887 [NASA ADS] [CrossRef] [Google Scholar]
- Timmes, F. X., & Arnett, D. 1999, ApJS, 125, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Wanajo, S. 2006a, ApJ, 647, 1323 [Google Scholar]
- Wanajo, S. 2006b, ApJ, 650, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, J. R., & Mayle, W. R. 1993, Phys. Rep., 227, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Witti, J., Janka, H.-Th., & Takahashi, K. 1994, A&A, 286, 841 [NASA ADS] [Google Scholar]
- Woosley, S. E., & Baron, E. 1992, ApJ, 391, 228 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., Wilson, J. R., Mathews, G. J., Hoffman, R. D., & Meyer, B. S. 1994, ApJ, 433, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., Heger, A., & Weaver, T. A. 2002, Rev. Mod. Phys., 74, 1015 [NASA ADS] [CrossRef] [Google Scholar]
- Yueh, W. R., & Buchler, J. R. 1976, Ap&SS, 41, 221 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ...e
![[*]](/icons/foot_motif.png)
- The baryon contribution to the internal energy is composed
of a thermal and nuclear part, i.e.
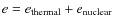 .
In NSE, e is given implicitly via
the EoS of hot and dense nuclear matter.
In non-NSE,
.
In NSE, e is given implicitly via
the EoS of hot and dense nuclear matter.
In non-NSE,  is
the binding energy of the nuclear composition used in the reaction
network.
is
the binding energy of the nuclear composition used in the reaction
network.
- ... neutrinos
![[*]](/icons/foot_motif.png)
- The integration with respect to
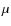 is performed
separately for in- and out-ward direction, according to the transport
coefficients.
is performed
separately for in- and out-ward direction, according to the transport
coefficients.
- ...
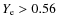
![[*]](/icons/foot_motif.png)
- The EoS from Shen
et al. (1998) is limited to a maximum electron
fraction of
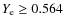 .
The EoS has been extended by Gögelein (2007, priv. comm.) to
model asymmetric nuclear matter with an electron fraction
above 0.564. We assume an ideal gas of free nucleons and light
nuclei, which is a sufficient assumption for the conditions found in
the region of the extremely proton-rich ejecta.
.
The EoS has been extended by Gögelein (2007, priv. comm.) to
model asymmetric nuclear matter with an electron fraction
above 0.564. We assume an ideal gas of free nucleons and light
nuclei, which is a sufficient assumption for the conditions found in
the region of the extremely proton-rich ejecta.
All Figures
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13106fig01.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13106-09/Timg90.png)
|
Figure 1:
Explosion energy estimate and shock position with respect to time after bounce for the 10.8 M |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=6cm,clip]{13106fig02.eps}\hspace...
...\includegraphics[width=6cm,clip]{13106fig04.eps} }\vspace*{7.5mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13106-09/Timg91.png)
|
Figure 2:
Neutrino luminosities and energies with respect to time after bounce for the 8.8 M |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{13106fig05.eps}\par\include...
...ar\includegraphics[width=14cm,clip]{13106fig07.eps}
\vspace*{5.5mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13106-09/Timg92.png)
|
Figure 3:
Evolution of the 8.8 M |
| Open with DEXTER | |
| In the text | |
| |
Figure 4:
Radial velocity profiles at selected times with respect to the
baryon mass (left panel) before and at bounce and with respect to the radius (right panel) after bounce, for the 8.8 M |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=5.2cm,clip]{13106fig10.eps}\incl...
...3106fig14.eps}\includegraphics[width=5.2cm,clip]{13106fig15.eps} }\end{figure}](/articles/aa/full_html/2010/09/aa13106-09/Timg96.png)
|
Figure 5:
Heating (>0) and cooling (<0) rates for the 8.8 M |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13106fig16.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13106-09/Timg102.png)
|
Figure 6:
Selected hydrodynamic variables during the initial explosion
phase at three different post-bounce times for the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{13106fig17.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13106-09/Timg109.png)
|
Figure 7:
Selected hydrodynamic variables during the formation of the
neutrino-driven wind at three different post-bounce times for the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{13106fig18.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13106-09/Timg110.png)
|
Figure 8:
The same configuration as Fig. 7 for the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13106fig19.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa13106-09/Timg114.png)
|
Figure 9:
Heating and cooling rates with respect to the baryon density
at three different post-bounce times 0.5 s (thin lines), 1 s (intermediate lines), 5 s (thick lines) for the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{13106fig20.eps}
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13106-09/Timg116.png)
|
Figure 10:
Evolution of selected mass elements in the neutrino-driven wind
(as listed in graph a) from
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{13106fig21.eps}
\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13106-09/Timg118.png)
|
Figure 11:
Evolution of selected mass shells in the neutrino-driven wind
(as listed in graph a) from
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=8.35cm,clip]{13106fig22.eps}\includegraphics[width=8.35cm,clip]{13106fig23.eps} }\vspace*{5.5mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13106-09/Timg119.png)
|
Figure 12:
Selected radial mass fraction profiles during the neutrino driven wind phase for the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}% latex2html id marker 1025\par\mbox{\subfigure[Different electr...
...mean energy.]{ \includegraphics[width=7cm,clip]{13106fig25.eps} }}\end{figure}](/articles/aa/full_html/2010/09/aa13106-09/Timg134.png)
|
Figure 13:
The Electron fraction approximations at a distance of 10 km outside the electron-neutrinosphere for the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=6cm,clip]{13106fig26.eps}\hspace...
...}
\includegraphics[width=6cm,clip]{13106fig28.eps} }
\vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13106-09/Timg149.png)
|
Figure 14:
Neutrino luminosities and mean energies with respect to time after bounce for the
|
| Open with DEXTER | |
| In the text | |
| |
Figure 15:
Evolution of the neutrinosphere radii in graph a) and temperature, density and electron fraction at the corresponding neutrinospheres in graphs b), c) and d) respectively for the
|
| Open with DEXTER | |
| In the text | |
| |
Figure 16:
Radial PNS profiles at two different post-bounce times (thick lines: 2 s, thin lines: 10 s), for the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{13106fig31.eps}
\vspace*{6.5mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13106-09/Timg166.png)
|
Figure 17:
Radial profiles of selected hydrodynamic variables
for the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{13106fig32.eps}\par\includegraphics[width=16.5cm,clip]{13106fig33.eps}
\vspace*{7mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13106-09/Timg171.png)
|
Figure 18:
Comparing selected hydrodynamic variables using the standard
reactions rates based on Bruenn (1985) (solid lines) and the artificially enhanced rates (dashed lines) for the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{13106fig34.eps}\par\include...
...ar\includegraphics[width=15cm,clip]{13106fig36.eps}
\vspace*{5.2mm}
\end{figure}](/articles/aa/full_html/2010/09/aa13106-09/Timg172.png)
|
Figure 19:
Mass accretion rate, timescales and entropy in the wind for the three progenitor models under investigation,
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.