| Issue |
A&A
Volume 517, July 2010
|
|
|---|---|---|
| Article Number | A81 | |
| Number of page(s) | 27 | |
| Section | Galactic structure, stellar clusters, and populations | |
| DOI | https://doi.org/10.1051/0004-6361/200912572 | |
| Published online | 12 August 2010 | |
The second and third parameters of the horizontal branch in globular
clusters![[*]](/icons/foot_motif.png)
R. G. Gratton1 - E. Carretta2 - A. Bragaglia2 - S. Lucatello1,3 - V. D'Orazi1
1 - INAF - Osservatorio Astronomico di Padova, Vicolo dell'Osservatorio 5, 35122 Padova, Italy
2 -
INAF - Osservatorio Astronomico di Bologna, via Ranzani 1, 40127 Bologna, Italy
3 -
Excellence Cluster Universe, Technische Universität München, Boltzmannstr. 2, 85748 Garching, Germany
Received 26 May 2009 / Accepted 17 April 2010
Abstract
Context. The second parameter (the first being metallicity)
defining the distribution of stars on the horizontal branch (HB) of
globular clusters (GCs) has long been one of the major open issues in
our understanding of the evolution of normal stars. Large photometric
and spectroscopic databases are now available: they include large and
homogeneous sets of colour-magnitude diagrams, cluster ages, and
homogeneous data about chemical compositions from our FLAMES survey.
Aims. We use these databases to re-examine this issue.
Methods. We use the photometric data to derive median and
extreme (i.e., the values including 90% of the distribution) colours
and magnitudes of stars along the HB for about a hundred GCs. We
transform these into median and extreme masses of stars on the HB,
using the models developed by the Pisa group, and taking into account
evolutionary effects. We compare these masses with those expected at
the tip of the red giant branch (RGB) to derive the total mass lost by
the stars.
Results. We find that a simple linear dependence on metallicity
of this total mass lost describes quite well the median colours of
HB stars. Assuming this mass loss law to be universal, we find
that age is the main second parameter, determining many of the most
relevant features related to HBs. In particular, it allows us
to explain the Oosterhoff dichotomy as a consequence of the peculiar
age-metallicity distribution of GCs in our Galaxy, although both
Oosterhoff groups have GCs spanning a rather wide range of ages.
However, at least an additional - third - parameter is
clearly required. The most likely candidate is the He abundance, which
might be different in GC stars belonging to the different stellar
generations whose presence was previously derived from the Na-O and
Mg-Al anticorrelations. Variations in the median He abundance allow us
to explain the extremely blue HB of GCs like NGC 6254 (=M 10)
and NGC 1904 (=M 79); such variations are found to be
(weakly) correlated with the values of the R-parameter (that is
the ratio of the number of stars on the HB and on the RGB). We also
show that suitable He abundances allow deriving ages from the HB
which are consistent with those obtained from the Main Sequence. Small
corrections to these latter ages are then proposed. We find that a very
tight age-metallicity relation (with a scatter below 4%) can be
obtained for GCs kinematically related to the disk and bulge, once
these corrections are applied. Furthermore, star-to-star variations in
the He content, combined with a small random term, explain very
well the extension of the HB. There is a strong correlation between
this extension and the interquartile of the Na-O anticorrelation,
strongly supporting the hypothesis that the third parameter for GC HBs
is He. Finally, there are strong indications that the main driver for
these variations in the He-content within GCs is the total cluster
mass. There are a few GCs exhibiting exceptional behaviours (including
NGC 104=47 Tuc and in less measure NGC 5272=M 3);
however, they can be perhaps accommodated in a scenario for the
formation of GCs that relates their origin to cooling flows generated
after very large episodes of star formation, as proposed by Carretta
et al. (2009d).
Key words: globular clusters: general - stars: abundances
1 Introduction
Sandage & Wallerstein (1960)
noticed that the distribution with colour/temperature of stars on the
horizontal branch (HB) of globular clusters (GCs) is roughly correlated
with their metal content.
A few years later, this observation was explained by the first
successful models of HB stars describing the effect of metal
content on the efficiency of H-shell burning in low mass stars where He
is burning in the core (Faulkner 1966). However, soon after this important theoretical achievement, van den Bergh (1967) and Sandage & Wildey (1967)
pointed out that the correlation between colour/temperature and
metallicity had several exceptions, a difficulty that has become
known as the second parameter problem. In the following forty
years, a large number of tentative explanations for this
discrepancy appeared in the literature, but no overall satisfactory
scenario has yet been found. A proof of the large interest raised by
this issue is that entering ``globular cluster'' and ``second
parameter'' in the ADS data base![]() resulted in 231 abstracts (24 since 2006) with
6031 citations on a query made on April 15th, 2009.
Of course, this search is probably incomplete, because there are
many related issues, e.g., the Oosterhoff dichotomy in the mean periods
of RR Lyrae in galactic GCs (Oosterhoff 1944; Sandage 1982), the UV upturn in the spectra of bulges and elliptical galaxies (Code 1969), the ages and the He abundances of GCs (Iben 1968),
the mass loss law for low mass stars, which use different keywords. The
second parameter problem is certainly one of the major open issues in
our understanding of the evolution of normal stars. For reviews of
this topic, we refer to Moehler (2001) and Catelan (2009a).
resulted in 231 abstracts (24 since 2006) with
6031 citations on a query made on April 15th, 2009.
Of course, this search is probably incomplete, because there are
many related issues, e.g., the Oosterhoff dichotomy in the mean periods
of RR Lyrae in galactic GCs (Oosterhoff 1944; Sandage 1982), the UV upturn in the spectra of bulges and elliptical galaxies (Code 1969), the ages and the He abundances of GCs (Iben 1968),
the mass loss law for low mass stars, which use different keywords. The
second parameter problem is certainly one of the major open issues in
our understanding of the evolution of normal stars. For reviews of
this topic, we refer to Moehler (2001) and Catelan (2009a).
There are various reasons why the second parameter issue has been insofar so difficult to solve. The most important is that there is most likely more than a single second parameter. The colour of HB stars is very sensitive to several physical stellar quantities in the age and metallicity regime typical of GCs (see e.g., Rood 1973; Renzini 1977; Freeman & Norris 1981; Fusi Pecci et al. 1993). Zinn (1980) and many authors after him convincingly showed that younger ages might explain the red colours of the HB of several of the outer halo GCs (see Dotter et al. 2008, for a similar line of thought). However, progress in the determination of the (relative) ages of GCs (e.g., Stetson et al. 1996; Rosenberg et al. 1999; De Angeli et al. 2005; Marín-Franch et al. 2009) demonstrated that this cannot be the only second parameter. The same result had previously been obtained even more directly from the broad distribution in colours of HB stars within some individual GCs (see e.g., Ferraro et al. 1990).
Since a change in the mass of stars on the HB may well cause even large variations in their colours (Rood 1973), a special mass-loss law has become a popular explanation (see Dotter 2008, for an example of this approach). Unfortunately, the physics of mass loss is very poorly known at present (see e.g., Willson 2000; Mészáros et al. 2009; Dupree et al. 2009). Many different mechanisms may affect mass loss (see e.g., Rich et al. 1997; Green et al. 1997; Soker & Harpaz 2000) and empirical evidence is inadequate for fully constraining them (see e.g., Peterson 1982; Origlia et al. 2007, 2008). Given these limitations, it is not yet possible to build an ab-initio model for the estimation of mass loss from GC stars. Hence we prefer to carefully restrict our assumptions: we looked for solutions with a mass loss law based on as few simple parameters as possible, for which we may obtain constraints from independent observations.
Additional second parameters considered included He abundances, the ratio of CNO to Fe abundances, stellar rotation or binarity (see e.g., Freeman & Norris 1981), and cluster concentration (Fusi Pecci et al. 1993). However, all of these explanations were found to be unsatisfactory overall. In the most successful cases, they might explain some groups of stars with anomalous colours on the HB (e.g., most field O-B subdwarfs are binaries, see e.g., Maxted et al. 2001; Napiwotzki et al. 2004; Han et al. 2003; however most of these in GCs seem to be single stars, see e.g., Moni Bidin et al. 2006). In the least successful cases, they are inconsistent with the data (CNO abundances: see the case of the second parameter pair NGC 362 and NCC 288: Shetrone & Keane 2000; and Catelan et al. 2001). The situations for rotation and He abundances are more complicated. For rotation, after the initial enthusiasm triggered by the pioneering observations of Peterson (1982), the problem was found to be less straightforward. More extensive data sets (Deliyannis et al. 1989; Behr et al. 2000a,b; Behr 2003; Recio-Blanco et al. 2002) revealed an intricate pattern, so that it seems difficult to use direct observations of rotation along the HB to confirm its rôle in the second parameter issue. While these observations do not rule out the possibility that rotation is indeed important, we cannot avoid concluding that the evidence for and against remains poor (see e.g., Sweigart 2002). We discuss the case of He abundances in subsequent sections.
Over the years, an enormous wealth of observational data has been collected, not only in terms of the distribution of stars along the HB with colour, but also the chemical composition, the period distribution of RR Lyrae, and other properties of GCs. Several authors (see e.g., Fusi Pecci et al. 1993; Catelan et al. 2001; Recio-Blanco et al. 2006; Carretta et al. 2007) pointed out the existence of correlations between global cluster parameters (such as luminosity, concentration, or Galactic orbit) and phenomena related to the second parameter. However, the mechanism connecting these global properties to the evolution of individual stars remained elusive until a few years ago.
A revised approach to the problem of the second parameter can now be developed. It is based on what was initially considered to be a separate characteristic of GCs, that is the abundance anomalies observed for GCs in the light elements CNO, Na, Mg, and Al (see Kraft 1994; and Gratton et al. 2004, for reviews of this topic). Early suggestions that there might be a correlation between these two sets of observations were made by Norris (1981), and more recently by Kraft (1994) and Catelan & de Freitas Pacheco (1995) and several other authors after them. However, the exact mechanism linking the two phenomena remained unclear. The two innovative steps taken subsequently were:
- the recognition that typical GCs host at least two generations of stars: this is required to explain the abundance anomalies observed for main sequence (MS) stars by Gratton et al. (2001) and Cohen et al. (2002). These observations contradicted the paradigm of GCs as single stellar populations, and opened a new view on GC formation and evolution that we are now only beginning to explore (see Gratton et al. 2004, for early results);
- the understanding by D'Antona et al. (2002)
that (large) variations in the abundance of He, which are expected to
be correlated with the variations in Na and O and other elements, might
result in large differences in the turn-off (TO) masses of stars of
similar age: this is because He-rich stars evolve faster than He-poor
ones and thus, at a given age, He-rich stars at TO are less massive
![[*]](/icons/foot_motif.png) .
Therefore, similar mass losses along the red giant branch (RGB) would
lead to HB stars of very different masses, and hence colours. Not
all authors estimated
variations in the He abundances as large as those proposed by
D'Antona et al. (2002; see for instance Marcolini et al. 2009).
We note however that these small spreads in He abundance (which
are
usually justified on the basis of chemical evolution models) have
difficulties in reproducing the observed spread in masses along the HB
and the splitting of the MS of NGC 2808 (Lee et al. 2005; Piotto et al. 2007).
.
Therefore, similar mass losses along the red giant branch (RGB) would
lead to HB stars of very different masses, and hence colours. Not
all authors estimated
variations in the He abundances as large as those proposed by
D'Antona et al. (2002; see for instance Marcolini et al. 2009).
We note however that these small spreads in He abundance (which
are
usually justified on the basis of chemical evolution models) have
difficulties in reproducing the observed spread in masses along the HB
and the splitting of the MS of NGC 2808 (Lee et al. 2005; Piotto et al. 2007).
While these observations are extremely interesting, they are rather limited in number: the data discussed insofar only concern a handful of massive GCs. A more comprehensive study of a large set of GCs, analysed in a homogeneous way, was lacking until recently. Such an analysis is now possible, thanks to the large databases of colour magnitude diagrams (CMD) and accurate ages provided by ground (Rosenberg et al. 2000a,b) and space observations (e.g., Piotto et al. 2002), and the extensive data on the Na-O anticorrelation from our FLAMES survey (Carretta et al. 2009a,b, and references therein), complemented by literature data. In this paper, we present an exploration of these unprecedented databases. In the first part of the paper, we consider the evidence provided by extensive photometric datasets, from both ground-based and HST observations for a sample of almost a hundred GCs, deriving the properties of HBs as defined by their median values and extension, and examining their correlations with metallicity and age. This analysis produces a simple mass-loss law, that explains the median colours of HB stars. However, as found by several authors before, an additional parameter is needed to explain the HB colours of GCs with an extreme blue HB (BHB) and the spread of colours in many other cases. In the second part of the paper, we consider variations in the He content as a possible explanation of these discrepancies, we derive the He abundance variations required explaining the observed properties of the HBs, and discuss the implications for MS photometry. In the third part of the paper, we search for additional evidence that He is indeed the additional parameter required to explain the HB morphology. In particular, we explore the correlations with other chemical anomalies, namely the Na-O anticorrelation. For this purpose, we consider a smaller but still quite large sample of 24 GCs, including classical second parameter cases (NGC 288 and NGC 362; NGC 5272 and NGC 6205), a list of blue HB clusters (such as NGC 1904 or NGC 6752), and the very extended HB cases (such as NGC 2808, NGC 6388 and NGC 6441). The aim of our discussion is to convince the reader that a combination of age and He abundance variations, the latter being related to multiple generations of stars within each GC, is a promising scenario to clarify most of the so far unexplained characteristics of the second parameter issue. We emphasise that we do consider that additional effects (e.g., binarity) may affect the colour of stars along the HB, but the rôles played by the age and He abundance variations are probably dominant.
2 Median and extreme colours of stars along the HB
Several authors have suggested that age is the (main) second parameter determining the colour of HB stars (e.g., Zinn 1985; Demarque et al. 1989; Lee et al. 1994). In this section, we present a revised evaluation of this issue, performing an extensive comparison between observations and models. We exploit the large databases of globular cluster photometry available on the web and the latest age and metallicity estimates.
Table 1:
Basic parameters for globular clusters considered in this paper (
![]() and
and
![]() are in solar masses).
are in solar masses).
2.1 Observational data
The first step of our procedure was to derive the median and range
of colours and magnitudes (hereinafter the range including 90% of the
stars) along the HB. We derived these quantities from the databases of
ground-based and HST (snapshot) observations presented by Rosenberg
et al. (2000a,b) and Piotto et al. (2002),
respectively. These databases were selected because they are publicly
available and include a large number of clusters analysed with very
homogeneous methods. The HST-ACS survey (Sarajedini et al. 2007)
is providing new, very high quality data, which will largely supersede
those older catalogues; unfortunately, this data set is not publicly
available yet![]() .
However, as we will see, the older photometry is of excellent
quality, with only a few caveats. The ground database includes V and I CMDs
and photometric tables for 52 GCs, from which we dropped E3,
which is too scarcely populated for the present purposes, and
.
However, as we will see, the older photometry is of excellent
quality, with only a few caveats. The ground database includes V and I CMDs
and photometric tables for 52 GCs, from which we dropped E3,
which is too scarcely populated for the present purposes, and ![]() Cen,
whose spread in metal abundance makes the interpretation of data far
more complicated than for the remaining clusters. The HST database
contains F439W and F555W CMDs and photometric tables for 71 GCs. In the following, we considered B and V colours obtained from the HST photometry through the transformations given by Piotto et al. (2002). There are 23 clusters in common between the two samples, so data are available for a total of 98 GCs.
Cen,
whose spread in metal abundance makes the interpretation of data far
more complicated than for the remaining clusters. The HST database
contains F439W and F555W CMDs and photometric tables for 71 GCs. In the following, we considered B and V colours obtained from the HST photometry through the transformations given by Piotto et al. (2002). There are 23 clusters in common between the two samples, so data are available for a total of 98 GCs.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig1.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg20.png)
|
Figure 1: Observed CMD for NGC 5904. RGB and HB stars are marked with red and blue points, respectively, while the green boxes represent the selection region of each component. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig2.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg21.png)
|
Figure 2:
Comparison between the number of HB and RGB stars that are within |
| Open with DEXTER | |
Table 1 gives basic
parameters for the clusters. Metallicities [Fe/H] are from our
re-analysis of GC metallicity (Carretta et al. 2009c; note that we adopted a metallicity of [Fe/H] = -1.35 for NGC 6256, from Stephens & Frogel 2004), while apparent distance moduli (m-M)V, reddenings E(B-V), absolute magnitudes ![]() ,
and HBR are from the Harris catalogue (1996). Relative ages are from the compilation of Carretta et al. (2009d), and are mainly from Marín-Franch et al. (2009) and De Angeli et al. (2005,
this last modified to be on the same scale), corrected to have values
consistent with the metallicities by Carretta et al. (2009c). Masses at both the turn-off (
,
and HBR are from the Harris catalogue (1996). Relative ages are from the compilation of Carretta et al. (2009d), and are mainly from Marín-Franch et al. (2009) and De Angeli et al. (2005,
this last modified to be on the same scale), corrected to have values
consistent with the metallicities by Carretta et al. (2009c). Masses at both the turn-off (
![]() )
and the tip of the RGB (
)
and the tip of the RGB (
![]() )
were computed as explained in Sect. 2.4. IQR values are the interquartile of the Na-O, and Mg-Al (anti-)correlations and come from Carretta et al. (2009b), with a few additional data from literature (Shetrone & Keane 2000, for NGC 362; Sneden et al. 2004; and Cohen & Melendez 2005, for NGC 5272 and NGC 6205; Marino et al. 2008, 2009, for NGC 6121 and NGC 6656, respectively; and Yong et al. 2005, for NGC 6752). Finally,
)
were computed as explained in Sect. 2.4. IQR values are the interquartile of the Na-O, and Mg-Al (anti-)correlations and come from Carretta et al. (2009b), with a few additional data from literature (Shetrone & Keane 2000, for NGC 362; Sneden et al. 2004; and Cohen & Melendez 2005, for NGC 5272 and NGC 6205; Marino et al. 2008, 2009, for NGC 6121 and NGC 6656, respectively; and Yong et al. 2005, for NGC 6752). Finally,
![]() (HB) is the maximum temperature
of HB stars, from Recio-Blanco et al. (2006), complemented by data for a few clusters evaluated by Carretta et al. (2009d).
For each cluster, we first identified the region covered by the
HB, as well as that occupied by RGB stars that are within
(HB) is the maximum temperature
of HB stars, from Recio-Blanco et al. (2006), complemented by data for a few clusters evaluated by Carretta et al. (2009d).
For each cluster, we first identified the region covered by the
HB, as well as that occupied by RGB stars that are within ![]() mag of the mean magnitude of the HB V(HB), taken from the on line version of the Harris catalogue of GCs (Harris 1996). Figure 1 shows an example of the selection of HB and RGB stars.
mag of the mean magnitude of the HB V(HB), taken from the on line version of the Harris catalogue of GCs (Harris 1996). Figure 1 shows an example of the selection of HB and RGB stars.
Completeness of the photometry can be an issue in a statistical study
such as the present one. HST-based observations are generally complete
to magnitude
![]() (with some exceptions on both the brighter and fainter side), which is
much fainter than the HB level at the RR Lyrae colour in the
vast majority of GCs of this sample. We tested the completeness of the
HB in the HST photometry by checking whether the number of HB
stars is not unexpectedly small compared to the number of
RGB stars that are within
(with some exceptions on both the brighter and fainter side), which is
much fainter than the HB level at the RR Lyrae colour in the
vast majority of GCs of this sample. We tested the completeness of the
HB in the HST photometry by checking whether the number of HB
stars is not unexpectedly small compared to the number of
RGB stars that are within ![]() mag of V(HB) (see Fig. 2). On average, this ratio is 0.934
mag of V(HB) (see Fig. 2). On average, this ratio is 0.934 ![]() 0.020
for GCs with HST data. The only cluster for which there is a clear
deficiency of observed HB stars (a value smaller than the
average one by more than twice the standard deviation,
as estimated by Poisson statistics) is the farthest one
(NGC 2419: Harris et al. 1996), for which this ratio is
0.56
0.020
for GCs with HST data. The only cluster for which there is a clear
deficiency of observed HB stars (a value smaller than the
average one by more than twice the standard deviation,
as estimated by Poisson statistics) is the farthest one
(NGC 2419: Harris et al. 1996), for which this ratio is
0.56 ![]() 0.09. The next smallest value is for NGC 6624, for which the value is 0.70
0.09. The next smallest value is for NGC 6624, for which the value is 0.70 ![]() 0.14,
which is only 1.6 standard deviation below the average value.
However, the ground-based observations are shallower, with typical
limiting magnitudes in the range 19-20. For this reason, extreme HB
stars are sometimes missing from these data; we then generally give
preference to the HST snapshot data in our discussion. However, the
ground-based data provide very useful information about a number of
nearby GCs missing in the Piotto et al. (2002) database
0.14,
which is only 1.6 standard deviation below the average value.
However, the ground-based observations are shallower, with typical
limiting magnitudes in the range 19-20. For this reason, extreme HB
stars are sometimes missing from these data; we then generally give
preference to the HST snapshot data in our discussion. However, the
ground-based data provide very useful information about a number of
nearby GCs missing in the Piotto et al. (2002) database![]() .
.
![\begin{figure}
\par\includegraphics[width=14cm,clip]{12572fig3.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg24.png)
|
Figure 3:
Two examples of the application of the statistical field subtraction used in this paper ( top: NGC 3201; bottom: NGC 6779); both cases are based on ground-based photometry. The left panels give the original photometry; the central panels
give the CMD of field stars appropriate for the direction and reddening
of the GCs, from the TRILEGAL model of the Milky Way (Girardi
et al. 2005; Vanhollebeke et al. 2009); the right panels are the field-subtracted HB (red points) and RGB (blue points). The RGB stars are only those within |
| Open with DEXTER | |
Particular care was devoted to the separation between the HB and the RGB, which is difficult for very metal-rich GCs when differential reddening is large. We also tried to minimize the impact of contamination by field stars, which may significantly affect the determination of the colour extremes, but only marginally affect the determination of median colours and magnitudes, which are robust estimators. Unfortunately, while very extensive and homogeneous, the databases that we used include neither comparison fields allowing a (statistical) subtraction of field contaminants, nor a full membership study. Our procedure was to first estimate those field stars expected to fall within the region of the CMD that we identified with the HB (Col. 3 of Table 2) and the RGB, based on the galactic model TRILEGAL (Girardi et al. 2005; Vanhollebeke et al. 2009). We then subtracted from the CMD the star closest to each field star (weighting differences in colours five times more than differences in magnitudes); the numbers of HB and RGB stars given in this paper are those after this subtraction. This procedure introduces some uncertainty in our results, in particular in cases of strongly contaminated fields. However, eye inspection of the colour-magnitude diagrams obtained using this procedure shows that it worked satisfactorily. Figure 3 shows a couple of examples of this decontamination.
We typically identified a few hundred HB stars, and a similar number of RGB stars. However, in a few cases we identified only a few tens of stars belonging to the two sequences. In these cases, larger uncertainties are associated with the extreme values, while the median is still quite robust (see however Sect. 6).
We fitted each observed HB with a polynomial (using the colour as an independent variable), whose degree varied (between 1 and 4) from cluster-to-cluster, depending on the extension of the HB. For each star, we then replaced the observed colour and magnitude with that corresponding to the closest position along the polynomial. The metrics that we considered weight differences in colours five times more than those in magnitudes. This procedure reduces the impact of outliers. We then ordered the stars in terms of either increasing colour or magnitude, and determined the median as well as the colours and magnitudes that include the central 90% of the distribution.
In the case of the RGB, we determined the average colour of the sequence at the magnitude of the HB by fitting a straight line through the points corresponding to the RGB-selected stars; in this case, we used the magnitude as an independent variable.
Values of observed colours and magnitudes are given in Tables 2 and 3 for HST and ground-based data, respectively. Error bars are only those from statistics. They do not include systematic errors, which are due to incompleteness at faint magnitudes (most relevant for ground-based observations), incorrect separation of the different sequences (sometimes possible for most metal-rich clusters with differential reddening), or uncertainties in decontamination by field stars.
Table 2: Photometric data from the HST-snapshot (Piotto et al. 2002).
Table 3: Photometric data from ground-based data (Rosenberg et al. 2000a,b).
2.2 From observed to intrinsic colours
Observed colours and magnitudes differ from intrinsic ones for
mainly three reasons: (i) errors in photometric calibration and
transformation to the standard system (colour and magnitude);
(ii) distance to the stars; and (iii) interstellar absorption
and reddening. To reduce the impact of these uncertainties, we
used the difference between observed and predicted colours of the RGB
at the HB level (
![]() and
and
![]() for
HST and ground-based observations, respectively) to estimate the offset
in colours appropriate for each cluster, and then corrected the median
and the extreme colours of the HB for these offsets.
To a first approximation, errors in reddening and photometric
calibration should cancel out when determining these quantities.
However,
for
HST and ground-based observations, respectively) to estimate the offset
in colours appropriate for each cluster, and then corrected the median
and the extreme colours of the HB for these offsets.
To a first approximation, errors in reddening and photometric
calibration should cancel out when determining these quantities.
However,
![]() and
and
![]() both depend on metallicity. To estimate this dependence, we fitted
with polynomials the relations obtained for clusters with only moderate
reddening (
E(B-V)<0.25), using reddening from Harris (1996) and metallicities from Carretta et al. (2009c). We obtained the relations
both depend on metallicity. To estimate this dependence, we fitted
with polynomials the relations obtained for clusters with only moderate
reddening (
E(B-V)<0.25), using reddening from Harris (1996) and metallicities from Carretta et al. (2009c). We obtained the relations
and
for HST (33 clusters, rms = 0.026 mag) and ground-based data (29 clusters, rms = 0.039 mag), respectively (see Fig. 4).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig4.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg42.png)
|
Figure 4:
Run of (B-V)
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig5.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg43.png)
|
Figure 5: Median and extreme colours as a function of metallicity for clusters observed with HST. Filled (red) triangles and (blue) dots indicate GCs older and younger than a relative age parameter of 0.92, respectively; clusters for which an age estimate is not available are marked with (black) empty squares. Points representing a few interesting clusters are marked. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig6.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg44.png)
|
Figure 6: Same as Fig. 5 but for ground-based sample. |
| Open with DEXTER | |
Inspection of the upper panel of Fig. 4 reveals that there is a systematic trend in which
![]() values
for highly reddened metal-rich GCs are systematically below the
calibration curve, when using the HST photometry. This discrepancy
might have either of three causes (or a combination of them):
(i) metallicity or (ii) reddening for these clusters are
overestimated; or (iii) the colour transformation at very red
colours ((B-V)>1.5) is incorrect, producing
too red colours for these stars. Errors in reddening have no impact in
our analysis, since the procedure we adopted should cancel their
effect. The impacts of errors in the metallicity scale and colour
transformations are more difficult to trace throughout the analysis.
However, in general they would lead to a small underestimate of
the masses of HB stars in these clusters; this would reduce
the sensitivity to metallicity of the mass-loss law we derive later,
but should have no other major impact on our analysis.
values
for highly reddened metal-rich GCs are systematically below the
calibration curve, when using the HST photometry. This discrepancy
might have either of three causes (or a combination of them):
(i) metallicity or (ii) reddening for these clusters are
overestimated; or (iii) the colour transformation at very red
colours ((B-V)>1.5) is incorrect, producing
too red colours for these stars. Errors in reddening have no impact in
our analysis, since the procedure we adopted should cancel their
effect. The impacts of errors in the metallicity scale and colour
transformations are more difficult to trace throughout the analysis.
However, in general they would lead to a small underestimate of
the masses of HB stars in these clusters; this would reduce
the sensitivity to metallicity of the mass-loss law we derive later,
but should have no other major impact on our analysis.
We estimated intrinsic colours by adding the offsets from the mean relations (for
![]() and
and
![]() )
to the observed colours. Median and extreme of the colours are plotted against metallicity in Figs. 5 and 6,
for HST and ground-based data, respectively. Different symbols are used
for clusters of different relative ages (see Carretta et al. 2009d).
In particular, we note that old clusters define a tight, unique
(although quite complex) relation between metallicity and median colour
of the HB. This indicates that the median location of the HB is
uniquely determined by age and metallicity. The relation between
colours and masses of HB stars is however not linear, with the
well-known, very strong sensitivity of colours on metallicities for the
metallicity range -1.6 < [Fe/H] < -1.1. This is more
clearly explained in the next subsection. Younger clusters typically
have redder median colours than older ones at a given metallicity,
as expected. Finally, clusters with no age determination roughly
occupy the same region identified by the other clusters, but they seem
to have a larger scatter. This is not unexpected, since data for these
GCs are of poorer quality, and this is the reason why they lack an age
estimate. We note also that much larger scatters are obtained for both
minimum and maximum colours. We return to this point in the following.
)
to the observed colours. Median and extreme of the colours are plotted against metallicity in Figs. 5 and 6,
for HST and ground-based data, respectively. Different symbols are used
for clusters of different relative ages (see Carretta et al. 2009d).
In particular, we note that old clusters define a tight, unique
(although quite complex) relation between metallicity and median colour
of the HB. This indicates that the median location of the HB is
uniquely determined by age and metallicity. The relation between
colours and masses of HB stars is however not linear, with the
well-known, very strong sensitivity of colours on metallicities for the
metallicity range -1.6 < [Fe/H] < -1.1. This is more
clearly explained in the next subsection. Younger clusters typically
have redder median colours than older ones at a given metallicity,
as expected. Finally, clusters with no age determination roughly
occupy the same region identified by the other clusters, but they seem
to have a larger scatter. This is not unexpected, since data for these
GCs are of poorer quality, and this is the reason why they lack an age
estimate. We note also that much larger scatters are obtained for both
minimum and maximum colours. We return to this point in the following.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig7.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg45.png)
|
Figure 7: Median colours versus HBR ratio for HST ( upper panel) and ground-based ( lower panel) clusters. Different symbols denote different ages (see Fig. 5). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig8.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg46.png)
|
Figure 8:
Run of minimum colours and maximum magnitudes with the maximum temperatures
|
| Open with DEXTER | |
In the case of magnitudes, we simply corrected the observed values for the apparent distance moduli given in Harris (1996).
Table 4: Intrinsic HB photometric parameters for GCs with HST data.
Table 5: Intrinsic HB photometric parameters for GCs with ground-based data.
We note that the plot of the median colour with metallicity is conceptually similar to a Lee-Zinn diagram (Lee & Zinn 1990), since the median colours are very well correlated with the HBR parameter used in this diagram (see Fig. 7; for a definition of HBR, see Zinn 1985).
The only exception to this close correlation is NGC 2808, when
using HST (but not ground-based) data.
This is due to the multi-modal distribution of stars along the HB of
this cluster, and to the incompleteness of the ground-based photometry,
which was used to derive the value of the HBR parameter. On the
other hand, minimum colours and maximum absolute magnitudes along the
HB are obviously well correlated with the maximum temperatures
![]() (HB) determined by Recio-Blanco et al. (2006, see Fig. 8),
which were derived from the same HST photometry. The few
discrepant cases are either GCs with poor statistics or CMDs that are
heavily contaminated with field stars, and for which different
assumptions about the impact of contaminants were adopted here with
respect to Recio-Blanco et al. (2006).
(HB) determined by Recio-Blanco et al. (2006, see Fig. 8),
which were derived from the same HST photometry. The few
discrepant cases are either GCs with poor statistics or CMDs that are
heavily contaminated with field stars, and for which different
assumptions about the impact of contaminants were adopted here with
respect to Recio-Blanco et al. (2006).
Values of intrinsic colours and magnitudes are given in Tables 4 and 5 for HST and ground-based data, respectively.
2.3 From intrinsic colours to masses
Our next step was to transform observed colours into masses of stars
along the HB. The masses were obtained by comparing the observed
colours and magnitudes with predictions from HB evolutionary models.
For this purpose, we used the database of models computed by the
Pisa evolutionary group (Castellani et al. 2003; Cariulo et al. 2004)![]() ,
which are particularly useful here since they provide a grid of HB
evolutionary sequences for different masses and metallicities. We first
derived the masses appropriate for ZAHB stars of the same
colours/magnitudes of the observed loci on the HB, and then applied
corrections appropriate to taking into account the evolution of the
stars away from the ZAHB.
,
which are particularly useful here since they provide a grid of HB
evolutionary sequences for different masses and metallicities. We first
derived the masses appropriate for ZAHB stars of the same
colours/magnitudes of the observed loci on the HB, and then applied
corrections appropriate to taking into account the evolution of the
stars away from the ZAHB.
For the first step, we derived transformations from the evolutionary tracks given by
| |
= | ![$\displaystyle 0.5254 \!-\! 0.0650~{\rm [Fe/H]} \!-\! 0.1181~{\rm [Fe/H]}(B-V)$](/articles/aa/full_html/2010/09/aa12572-09/img58.png)
|
|
| + 0.1425 (B-V) - 0.6560 (B-V)2 | |||
| (3) |
and
| |
= | ![$\displaystyle 0.5271 \!-\! 0.0629~{\rm [Fe/H]} \!-\! 0.0851~{\rm [Fe/H]}(V-I)$](/articles/aa/full_html/2010/09/aa12572-09/img60.png)
|
|
| + 0.1399 (V-I) - 0.6490 (V-I)2 | |||
| (4) |
which are valid in the range
| |
= | ![$\displaystyle 0.5544 \!-\! 0.07286~{\rm [Fe/H]} \!+\! 0.005228~{\rm [Fe/H]}~M_V^2$](/articles/aa/full_html/2010/09/aa12572-09/img63.png)
|
|
| (5) |
which is valid for
The evolutionary corrections were obtained by deriving masses from
median and extreme colours of synthetic HB diagrams, obtained by
taking into account evolution, with respect to the values appropriate
for the same set of stars when on the ZAHB. We obtained the correcting
formulae
| |
= | ||
| (6) |
| |
= | ||
| (7) |
and
| |
= | ||
| (8) |
for minimum, median, and maximum mass, respectively.
In practice, we estimated masses from: (i) colours whenever these were redder than (B-V)0>0.1 (or (V-I)0>0.2); (ii) magnitudes whenever colours were bluer than (B-V)0=(V-I)0<-0.1; and (iii) by a weighted average of the values obtained from magnitudes and colours when they were in an intermediate range.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig9.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg76.png)
|
Figure 9: Differences between maximum and minimum masses along the HB, compared to differences between median and minimum masses, for clusters observed with HST. Filled (red) triangles and (blue) dots indicate GCs older and younger than a relative age parameter of 0.92, respectively; clusters for which an age estimate is not available are marked with (black) empty squares. |
| Open with DEXTER | |
Not unexpectedly, there is a good correlation between the differences
![]() and
and
![]() (see Fig. 9), the regression line (for HST data) being
(see Fig. 9), the regression line (for HST data) being
![]() with a linear regression coefficient of r=0.82
(74 clusters). We note, however, that the estimate of the maximum
mass is of much larger uncertainty than that of the median mass,
because of the large evolutionary effects and the impact of smaller
statistics. Furthermore, the median mass is on average much closer to
the maximum than to the minimum mass, because of the difference between
these two values is mainly due to a nearly constant offset of about
0.03-0.04
with a linear regression coefficient of r=0.82
(74 clusters). We note, however, that the estimate of the maximum
mass is of much larger uncertainty than that of the median mass,
because of the large evolutionary effects and the impact of smaller
statistics. Furthermore, the median mass is on average much closer to
the maximum than to the minimum mass, because of the difference between
these two values is mainly due to a nearly constant offset of about
0.03-0.04 ![]() .
In only a few
extreme cases (e.g., NGC 2808) is the difference between
.
In only a few
extreme cases (e.g., NGC 2808) is the difference between
![]() and
and
![]() sufficiently large to really affect the arguments made in the remainder of this paper. Hereinafter we thus do not refer to
sufficiently large to really affect the arguments made in the remainder of this paper. Hereinafter we thus do not refer to
![]() in our discussion.
in our discussion.
We note that the lowest mass HB models considered here have a mass of 0.52 ![]() ,
the corresponding absolute magnitude predicted for these stars being
,
the corresponding absolute magnitude predicted for these stars being
![]() .
However, there are a few GCs for which the maximum absolute magnitude of HB stars is
.
However, there are a few GCs for which the maximum absolute magnitude of HB stars is
![]() .
In these cases, the masses given by our equations may be lower than the
core masses at the He-flash for these models (Cassisi et al. 1998). While this might be indicative of either a different origin or a late He-flash for these stars (see e.g., D'Cruz et al. 1996),
we note that in these cases our mass estimates are inferred from an
extrapolation outside the range covered by the stellar models, and may
therefore have a larger uncertainty. The value of the minimum mass
along the HB for these GCs is certainly small, although probably not as
small as indicated by our formulae.
.
In these cases, the masses given by our equations may be lower than the
core masses at the He-flash for these models (Cassisi et al. 1998). While this might be indicative of either a different origin or a late He-flash for these stars (see e.g., D'Cruz et al. 1996),
we note that in these cases our mass estimates are inferred from an
extrapolation outside the range covered by the stellar models, and may
therefore have a larger uncertainty. The value of the minimum mass
along the HB for these GCs is certainly small, although probably not as
small as indicated by our formulae.
Statistical errors in the mass estimates can be obtained by
combining statistical errors in the colours with the errors in the
metallicities. Errors in colours cause an uncertainty of about
0.007 ![]() in the masses, while masses change by -0.005
in the masses, while masses change by -0.005 ![]() if metallicity is increased by +0.1 dex in [Fe/H].
if metallicity is increased by +0.1 dex in [Fe/H].
The comparison between HST and ground-based results is as follows:
- minimum mass: ground-HST = 0.025
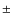
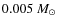 (rms 0.024
(rms 0.024 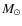 ,
27 clusters), where the scatter is mainly caused by GCs
(NGC 2808, NGC 5986, and NGC 6266 = M 62) with
,
27 clusters), where the scatter is mainly caused by GCs
(NGC 2808, NGC 5986, and NGC 6266 = M 62) with
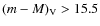 and with BHB tails that are fainter than the limiting magnitude of
the ground-based photometry. When these three clusters are eliminated, the offset is
0.019
and with BHB tails that are fainter than the limiting magnitude of
the ground-based photometry. When these three clusters are eliminated, the offset is
0.019 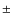 0.003
0.003 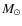 (rms 0.016
(rms 0.016 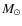 ,
24 clusters);
,
24 clusters);
- median mass: ground-HST = 0.019
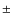 0.003
0.003 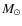 (rms = 0.019
(rms = 0.019 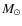 ,
28 clusters). The only clear outlier is NGC 2808. The offset is 0.016
,
28 clusters). The only clear outlier is NGC 2808. The offset is 0.016 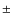 0.003
0.003 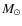 (rms = 0.015
(rms = 0.015 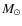 ,
27 clusters) if this cluster is eliminated. This confirms that the
median mass is far less sensitive to outliers and photometric errors
than the minimum mass. The case of NGC 2808 is very peculiar,
because the distribution along the HB is very discontinuous and clumpy.
If the extreme blue tail were neglected (as in the case of the
ground based photometry), the median would jump from the blue HB
to the red HB, with a change in mass of about 0.04
,
27 clusters) if this cluster is eliminated. This confirms that the
median mass is far less sensitive to outliers and photometric errors
than the minimum mass. The case of NGC 2808 is very peculiar,
because the distribution along the HB is very discontinuous and clumpy.
If the extreme blue tail were neglected (as in the case of the
ground based photometry), the median would jump from the blue HB
to the red HB, with a change in mass of about 0.04 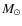 .
.
Table 6: Masses on HB for GCs with HST data.
Table 7: Masses on HB for GCs with ground-based data.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{12572fig10.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg88.png)
|
Figure 10: Median and minimum masses vs. [Fe/H] for HST and ground based samples. Symbol legend is given in Fig. 5. A few points relative to interesting clusters are marked. |
| Open with DEXTER | |
Figure 10 illustrates the run of median and minimum masses with metallicity [Fe/H], from HST and ground-based data, respectively. As for colours, we indicate with different symbols clusters of different relative ages. If we consider only the old clusters, the plots with median masses show a quite simple (although not linear) relation with metallicity, with a very small scatter about the mean line. Younger clusters scatter above the relation defined by the old ones, as expected. Again, clusters with no age estimates occupy a similar locus, but with a considerable scatter.
As noted in the case of colours, when we also consider minimum masses the scatter is much larger than obtained for the median. We underline that in spite of some uncertainties in our mass derivations this scatter is real, corresponding to a large variation in the appearance of the HBs: we note for instance the low minimum masses that are obtained for the GCs with very extended blue tails, such as NGC 2808 or NGC 7078. We return to this point in Sect. 6.
Values for the minimum, median, and maximum masses obtained following the previous procedure are given in Tables 6 and 7, for HST and ground-based data, respectively.
2.4 Mass-loss law
The tight relation between median HB mass and metallicity for old GCs
obtained in the previous subsection suggests that the median location
of stars along the HB of a GC can be determined using a combination of
metallicity, age, and a relatively simple and uniform mass-loss law. To
show that this is indeed the case, we first estimated the original
masses of stars currently on the HB. To determine this value, we
first consider masses at TO (
![]() ), which can be obtained
from their age, chemical composition, and He content, by using appropriate models. In practice, we used the relation
), which can be obtained
from their age, chemical composition, and He content, by using appropriate models. In practice, we used the relation
that closely follows the isochrones of the Pisa group when Y=0.25, over the range of parameters (age, metallicity) appropriate for GC stars. We note that Age in this formula is the relative age parameter of Carretta et al. (2009d), and we assumed that Age = 1 corresponds to an isochrone age of 12.5 Gyr. We then corrected this value to those appropriate for stars at the tip of the RGB (neglecting mass loss, hence assuming the mass of the stars to be identical to those at the beginning of their evolution), using the formula
which again fits the Pisa group isochrones.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{12572fig11.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg93.png)
|
Figure 11: Median mass loss as a
function of metallicity for GCs older (triangles) and younger (dots)
than 0.92. The solid line is the best-fit relation to the HST
data, while the dashed one is just shifted by 0.02 |
| Open with DEXTER | |
We then assume that the original mass of stars at the tip of the RGB is
equal to that of stars currently on the HB (on average, it should
be slightly lower, but this difference can be neglected in our
discussion). The median mass lost by the stars before reaching the HB
can then be obtained by comparing their current mass
![]() (as determined in the previous paragraph) with
(as determined in the previous paragraph) with
![]() .
The precise evolutionary phase (before ZAHB) at which mass loss occurs
is not important in our approach. It would of course play an
important rôle in the comparison with mass loss laws. The values of the
median mass loss for stars in each cluster are plotted against
metallicity in Fig. 11
for clusters with HST (upper panel) and ground-based data (bottom
panel). As usual, we used different symbols for old and young
clusters (age is required when deriving this estimate of the mass loss,
so that clusters with no age estimates cannot be plotted here).
Mass losses obtained from the two sets of data are quite similar, with
a small offset of about 0.020
.
The precise evolutionary phase (before ZAHB) at which mass loss occurs
is not important in our approach. It would of course play an
important rôle in the comparison with mass loss laws. The values of the
median mass loss for stars in each cluster are plotted against
metallicity in Fig. 11
for clusters with HST (upper panel) and ground-based data (bottom
panel). As usual, we used different symbols for old and young
clusters (age is required when deriving this estimate of the mass loss,
so that clusters with no age estimates cannot be plotted here).
Mass losses obtained from the two sets of data are quite similar, with
a small offset of about 0.020 ![]() between them. The best-fit straight line through the HST data is
between them. The best-fit straight line through the HST data is
which has a highly significant correlation coefficient of r=0.91 over 45 clusters. The scatter of points relative to each cluster around this mean line is small (rms of 0.021 and 0.027
At first look, this small scatter appears to be compatible with errors
in metallicity and ages that are used in this derivation. For instance,
in the case of the metal-rich cluster NGC 6441, changing the
assumed values of the metallicity [Fe/H] and age parameter by 0.10
would cause variations in the values estimated for the mass loss by
0.014 and 0.031 ![]() (larger mass losses are obtained if metallicity and ages are
increased). Sensitivities to these parameters are smaller for more
metal-poor clusters; e.g., in the case of NGC 7078, similar
changes in the assumed values of metallicity and age would cause
variations in the mass loss of 0.007 and 0.022
(larger mass losses are obtained if metallicity and ages are
increased). Sensitivities to these parameters are smaller for more
metal-poor clusters; e.g., in the case of NGC 7078, similar
changes in the assumed values of metallicity and age would cause
variations in the mass loss of 0.007 and 0.022 ![]() .
In conclusion, a simple unique mass-loss law, combined with
metallicity and age, seems able to define quite well the median mass
and colours of HB stars for the whole sample of clusters considered in
this analysis. However, as we will show in Sect. 4, the deviations of
individual points from the mean relation are caused mostly by true physical effects.
.
In conclusion, a simple unique mass-loss law, combined with
metallicity and age, seems able to define quite well the median mass
and colours of HB stars for the whole sample of clusters considered in
this analysis. However, as we will show in Sect. 4, the deviations of
individual points from the mean relation are caused mostly by true physical effects.
We may compare this estimate for the total mass lost along the RGB with
predictions by mass-loss laws in the literature. A compilation of
these predictions is given in Table 1 and Fig. 4 of Catelan (2009a).
The present estimate of the mass lost is generally much higher than the
values given by these predictions; only a small fraction (0.002 ![]() )
of this difference can be attributed to the identification of the mass
of HB stars with that of stars at the tip of the RGB. The observed run
compares quite well with a simple or modified Reimers (1975a,b) laws, or the law by VandenBerg et al. (2000), provided that the efficiency parameter is roughly doubled. On the other hand, other mass-loss laws (Mullan 1978; Goldberg 1979; Judge & Stencel 1991) provide a total mass lost along the RGB that changes too fast with metallicity to reproduce current results.
)
of this difference can be attributed to the identification of the mass
of HB stars with that of stars at the tip of the RGB. The observed run
compares quite well with a simple or modified Reimers (1975a,b) laws, or the law by VandenBerg et al. (2000), provided that the efficiency parameter is roughly doubled. On the other hand, other mass-loss laws (Mullan 1978; Goldberg 1979; Judge & Stencel 1991) provide a total mass lost along the RGB that changes too fast with metallicity to reproduce current results.
Origlia et al. (2007)
proposed a mass-loss law based on mid-IR Spitzer observations of red
giants in globular cluster. According to this mass-loss law, GCs star
should lose about 0.23 ![]() while ascending the RGB, nearly independent of their metallicity. While
this average value roughly corresponds to what is needed to explain the
HB of GCs of intermediate metallicity, our analysis indicates that the
total mass lost along the RGB should depend on metallicity.
while ascending the RGB, nearly independent of their metallicity. While
this average value roughly corresponds to what is needed to explain the
HB of GCs of intermediate metallicity, our analysis indicates that the
total mass lost along the RGB should depend on metallicity.
We note that the assumption of a particular age-metallicity
relation (the one by Marin-Franch et al.) is implicit in our
analysis. Had we adopted a different age-metallicity relation, the
metallicity-mass-lost relation would be different. For instance, if the
(relative) ages of disk-inner halo clusters were independent of
metallicity (rather than with a slope of
![]() as adopted throughout this paper), the slope of the mass-loss law with metallicity would
be reduced by
as adopted throughout this paper), the slope of the mass-loss law with metallicity would
be reduced by
![]() ,
from
,
from
![]() to
to
![]() .
This would not modify significantly any of the main results
of the paper.
.
This would not modify significantly any of the main results
of the paper.
3 RR Lyrae
RR Lyrae variables are HB stars within the classical instability strip. Properties of the pulsating stars may be used to constrain several basic properties, including mass, radius, and chemical composition. An in-depth star-by-star comparison, while very illuminating, requires a considerable effort, because individual HB stars may be within the instability strip at various phases of their HB evolution. This comparison then requires a synthesis of populations, such as those performed by Marconi et al. (2003), Di Criscienzo et al. (2004), Caloi & D'Antona (2007, 2008), and D'Antona & Caloi (2008). We defer this analysis to forthcoming papers; here we briefly examine only a few features.
3.1 Data
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig12.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg99.png)
|
Figure 12: RR Lyrae richness parameter, S(RR), as a function of the RR Lyrae fraction for both HST (upper panel) and ground-based sample (lower panel). |
| Open with DEXTER | |
Table 8: Properties of the RR Lyrae variables for each cluster.
Because of the uncertainty related to evolution, we focus only on those
clusters where the RR Lyrae population is dominated by stars still
close to the ZAHB in the CMD. Since most of the lifetime of
HB stars is spent close to their ZAHB location, we may be
reasonably sure that this occurs for GCs that contain a large
population of RR Lyrae. To identify these clusters, we
consider the RR Lyrae richness parameter S(RR) as tabulated in the Harris (1996) catalogue, which is the number of RR Lyrae per unit cluster luminosity![]() . In Fig. 12,
we compared this parameter with the number of stars in the instability
strip that we may obtain from the photometric catalogues considered in
Sect. 2. We derived the number of RR Lyrae in each cluster
by assuming that all HB stars whose dereddened (B-V)0 colour is
. In Fig. 12,
we compared this parameter with the number of stars in the instability
strip that we may obtain from the photometric catalogues considered in
Sect. 2. We derived the number of RR Lyrae in each cluster
by assuming that all HB stars whose dereddened (B-V)0 colour is
![]() are RR Lyrae (see Marconi et al. 2003; and Di Criscienzo et al. 2004).
are RR Lyrae (see Marconi et al. 2003; and Di Criscienzo et al. 2004).
In Table 8, we report for each cluster the S(RR) values
(Col. 2) as well as the number and the fraction of RR Lyrae
stars from both HST and ground-based samples (Cols. 3-6). In
Col. 7, we list the f(RR) estimates derived whenever possible from S(RR) values, or otherwise from f(RR), while the mean period (
![]() )
and the corresponding number of stars (n(RR
)
and the corresponding number of stars (n(RR![]() )) are reported in Cols. 8 and 9, respectively. These last two values are from Clement et al. (2001).
)) are reported in Cols. 8 and 9, respectively. These last two values are from Clement et al. (2001).
We note that the photometry considered throughout this paper is based
on only a few, not even simultaneously acquired images in each filter.
Hence, individual RR Lyrae will have nominal colours and
magnitudes that can differ substantially from their mean values, and
may even locate them out of our definitions of both the instability
strip and the HB locus. However, we might expect that, provided
that photometric errors are not too large, there should be a
correlation between the number of stars that according to the
photometric catalogues are within the instability strip, and the true
number of RR Lyrae. This appears to be the case: the correlation
between the fraction of HB stars that are nominally within the
instability strip, and the RR Lyrae richness parameter listed by
Harris, is quite good for HST data which have smaller photometric
errors. It is somewhat poorer, but still fairly good for
ground-based data. This correlation allows us to (i) calibrate the
richness parameter in terms of the fraction of HB stars that are
actually RR Lyrae f(RR) (we found that this is represented by the mean relation
![]() ); and (ii) complement the RR Lyrae richness parameter with data obtained from the photometry of those few
clusters where this datum was missing.
); and (ii) complement the RR Lyrae richness parameter with data obtained from the photometry of those few
clusters where this datum was missing.
Table 9: Comparison of median and maximum masses with the masses for RR Lyrae variables derived by Di Criscienzo et al. (2004).
To estimate the separation between clusters whose RR Lyrae population
is dominated by ZAHB objects rather than evolved ones, we considered in
more detail a few interesting cases using synthetic HBs. We found that
using parameters that provide an accurate distribution of stars along
the HB, the fraction of RR Lyrae stars that were within the
instability strip also when they were on the ZAHB is 0.67 for
NGC 4590 (f(RR) = 0.23), 0.45 for NGC 7078 (f(RR) = 0.10), and close to zero for NGC 4833 (f(RR) = 0.04). We note however that the values of f(RR)
are quite uncertain, and that synthetic HBs need several parameters to
reproduce various aspects of the colour distribution. The fractions
cited above are then uncertain and should only be taken as indicative
of a decreasing ratio of stars close to the ZAHB to the total of
RR Lyrae variables with decreasing specific frequency; and that a
value in the range of f(RR) ![]() 0.04-0.1 roughly corresponds to the transition between a population of
RR Lyrae variables dominated by ZAHB stars to a population
dominated by evolved objects.
0.04-0.1 roughly corresponds to the transition between a population of
RR Lyrae variables dominated by ZAHB stars to a population
dominated by evolved objects.
![\begin{figure}
\par\includegraphics[width=11.9cm,clip]{12572fig13.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg110.png)
|
Figure 13: Median mass and age as function of metallicity; different symbols in this case are for GCs with different RR Lyrae fractions (black: f(RR) > 0.10, grey: 0.04 < f(RR) < 0.10) and HBR ratios (blue triangles: HBR > 0, red squares: HBR < 0). The shaded area is the strip containing GCs rich in RR Lyrae. |
| Open with DEXTER | |
Hereafter, we assume that all clusters for which
![]() > 0.10 (that is
> 0.10 (that is
![]() > 19.7)
have an RR Lyrae population dominated by stars that are still
close to their ZAHB location. While as mentioned this limit is rather
arbitrary, we found very similar results with other values in the range
0.04-0.10.
> 19.7)
have an RR Lyrae population dominated by stars that are still
close to their ZAHB location. While as mentioned this limit is rather
arbitrary, we found very similar results with other values in the range
0.04-0.10.
After identifying GCs for which we may assume that most RR Lyrae remain close to the ZAHB, we can perform a sanity check of the minimum, median, and maximum masses that we adopted for HB stars by comparing them with those derived from pulsational properties. Table 9 lists the different mass values for the GCs analysed by Di Criscienzo et al. (2004). We found that masses derived from pulsational properties are very similar to the median masses for the metal-rich clusters (which typically have an HB extending on both sides of the instability strip), and closer to the maximum masses for metal-poor clusters, which have predominantly blue HBs. While this result is unsurprising because we use the same HB evolutionary models as Di Criscienzo et al. (2004), who performed a similar comparison, at least it shows that there are no gross errors in the way we applied these models.
3.2 Discussion
One of the most intriguing characteristics of HBs is the dichotomy in
the distribution of the GCs in terms of the mean periods of variables
pulsating in the fundamental mode (RRab), discovered by Oosterhoff (1944).
We note that while the Oosterhoff dichotomy applies not only to GCs,
but also to field stars in our Galaxy (e.g., Szczygiel et al. 2009),
populations of RR Lyrae sampled in other (smaller) galaxies such
as the Magellanic Clouds or the dSphs have mean periods that are
intermediate between the two Oosterhoff groups (Oo I and Oo II, e.g., Pritzl et al. 2004; Catelan 2009a).
A quite extensive discussion of various properties of GCs in
relation to the Oosterhoff dichotomy can be found in Sect. 6 of
Catelan (2009a). The information
collectively is quite difficult to interpret, because of significant
uncertainties in many of the basic parameters considered
(in particular, ages, but also metallicities), of small number
statistics, and because average periods within a cluster depend on a
complex combination of factors, mainly related to RR Lyrae
possibly belonging to different evolutionary phases. In spite of
this, many authors have searched for a simple explanation of the
Oosterhoff dichotomy, and several of them suggested that this might be
caused by a combination of ages and metallicities, the OoII group being
attributable to old, metal-poor GCs, and the OoI to a population
of young, metal-intermediate clusters (see e.g., Lee & Carney 1999).
We used our data to test whether this interpretation of the Oosterhoff
dichotomy is consistent with the HB scenario we consider in this
paper. We first replotted (upper panel of Fig. 13) the metallicity-median mass diagram of Fig. 10, but this time using different symbols for GCs that are either rich or poor in RR Lyrae: black and grey circles are for f ![]() 0.10 and 0.04
0.10 and 0.04 ![]() f < 0.10, respectively. The GCs with f < 0.04
are divided according to the HBR ratios, (blue) triangles and
(red) squares representing HBR greater and smaller than 0,
respectively. Not unexpectedly, RR Lyrae-rich GCs occupy a well
defined locus in this diagram, roughly represented by a diagonal strip;
GCs below this strip have blue HBs, while those above the strip have
red HBs. We note that the anomalous behaviour of NGC 6535, being a
BHB cluster with very low RR Lyrae fraction and located
within the instability strip (shaded box) probably reflects a small
amount of data in the CMD of this cluster.
f < 0.10, respectively. The GCs with f < 0.04
are divided according to the HBR ratios, (blue) triangles and
(red) squares representing HBR greater and smaller than 0,
respectively. Not unexpectedly, RR Lyrae-rich GCs occupy a well
defined locus in this diagram, roughly represented by a diagonal strip;
GCs below this strip have blue HBs, while those above the strip have
red HBs. We note that the anomalous behaviour of NGC 6535, being a
BHB cluster with very low RR Lyrae fraction and located
within the instability strip (shaded box) probably reflects a small
amount of data in the CMD of this cluster.
As shown by Fig. 10, this diagram is essentially an age-metallicity diagram (with some caveats that are described more clearly in the next section). Given the distribution of GCs in age and metallicity, there are very few galactic GCs with young ages and -2 < [Fe/H] < -1.6. This lack of GCs with suitable parameters divides the galactic population of RR Lyrae rich GCs into two ensembles, which can be identified with the Oosterhoff groups, confirming what had already been proposed by many other authors. However, ages of both groups have a much larger spread than given by this simple consideration. This is because of two results: (i) the diagonal strip defined by the RR Lyrae-rich clusters has a considerable width, much larger than that caused simply by the range in colour of the instability strip itself; this indicates that there is an intrinsic spread in the masses of ZAHB stars, which is a basic property of HBs that we exploit throughout this paper. This is important in particular for the case of metal-poor clusters, which are able to produce an RR Lyrae rich population over a rather wide range of ages. (ii) Given the interplay between the original mass and the mass-loss variation with metallicity, the strip occupied by RR Lyrae-rich clusters overlaps twice with the locus occupied by old GCs in the metallicity-median mass diagram. This implies that there are old RR Lyrae-rich GCs that are either metal-poor (the classical Oo II clusters), or in a restricted range of metallicity around [Fe/H] = -1. Hence, the most metal-rich among the Oo I GCs belong to the old population, and are actually as old as the most metal-poor Oo II clusters. This is clearly shown in the age-metallicity diagram shown in the bottom panel of Fig. 13, where again we plotted with different symbols clusters that are either rich or poor in RR Lyrae.
This description only refers to those GCs that are very rich in RR Lyrae. There are many GCs with only a few RR Lyrae: as mentioned above, in these cases (generally metal-poor clusters with predominantly BHB) most variables can be identified with stars that have evolved off the ZAHB. In these cases, we should expect long mean periods, and the cluster to be identified as Oo II (e.g., Lee et al. 1990). Furthermore, there are peculiar cases (including e.g., NGC 6388 and NGC 6441) where the RR Lyrae are actually HB stars with masses much lower than expected for their metallicity and age (see next section). All these cases complicate the simple picture described above, as discussed by Catelan (2009a).
To summarise, although the Oosterhoff dichotomy indeed depends on the peculiar distribution of galactic GCs in the age-metallicity plane, and most of the Oo II clusters are old while most of the Oo I clusters are young, it is not possible to identify tout-court the Oosterhoff groups with groups of GCs having different ages (a similar conclusion was drawn by Catelan 2009a).
4 Ages from median HB colours
After demonstrating that the median colour of the HB is determined mainly by cluster metallicity and age, provided a suitable mass-loss law is adopted, we attempt to derive ages for GCs from their median HB colour. This procedure is almost identical to that considered by several authors (e.g., Lee et al. 1994), but it is now applied to a large database of GCs in a uniform way.Table 10:
Clusters' ages from main sequence fitting and from HB both for HST and ground based data-set.
![]() is given in Table 12.
is given in Table 12.
These ages can be obtained by simply adding to the median mass of the
HB stars the mass lost during the previous evolution (Eq. (11)), then subtracting the mass difference between stars at the tip of the RGB and the TO (Eq. (10)), and finally inverting the age-metallicity-TO mass relation (Eq. (9)).
Of course, since the mean mass-loss law adopted throughout this
paper
(a linear dependence on [Fe/H]) was obtained by comparing median
masses on the HB with those at the tip of the RGB, where mass loss is
neglected, on average the two sets of ages should agree. However,
any difference in the ages derived from the HB and RGB for a given GC
indicates peculiarities for that GC. Taking an extreme view, were not
age the main parameter affecting the HB morphology, we might have
no correlation (or even an anticorrelation) between MS and
HB ages, only their mean values being in agreement. The derivation
of ages from HB is then crucial to understanding the second parameter
issue. These ages (expressed in our usual relative scale) are listed in
Cols. 3 and 4 of Table 10 for HST and ground-based data, respectively. We compared these
two age estimates in Fig. 14.
The two sets of ages agree very well each other, with the exception of
NGC 2808, for which the ground-based HB age is underestimated
because the limiting magnitude of the relevant photometry is too bright
to include the faint end of the HB. Once this cluster is dropped,
the mean difference is 0.003 ![]() 0.009 (rms = 0.046); assuming the same error in both age
estimates, this implies an internal error of 0.032 for each of
them. In the following, we adopt as our most robust estimates of
the HB ages those determined from HST data, whenever
available, otherwise we use values obtained from ground-based data.
0.009 (rms = 0.046); assuming the same error in both age
estimates, this implies an internal error of 0.032 for each of
them. In the following, we adopt as our most robust estimates of
the HB ages those determined from HST data, whenever
available, otherwise we use values obtained from ground-based data.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig14.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg113.png)
|
Figure 14: Comparison of ages derived from HB for HST and ground-based samples. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig15.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg114.png)
|
Figure 15:
Comparison of ages from HB and from main sequence for both HST and
ground based samples; filled squares and circles are GCs with |
| Open with DEXTER | |
In Fig. 15, we compare
these HB ages with those determined from the main sequence. The
agreement is fairly good: the rms of the difference in ages from
HB and from the main sequence is 0.094 for HST and 0.105 for
ground-based data respectively: this is approximately equivalent
to 1 Gyr. While this agreement may appear satisfactory,
it is actually much larger than internal error bars![]() .
.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig16.ps}\vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg115.png)
|
Figure 16: Dereddened HST CMDs for stars on the HB of NGC 6934 and NGC 1904. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig17.ps}
\vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg116.png)
|
Figure 17: Comparison of ages from HB and from main sequence for the whole sample (HST+ground based); typical error bars are shown at bottom right corner of each panel. The thick (black) arrows show the impact of a 0.02 variation in the assumed He content, while the thin (red) ones represent the consequence of a 0.1 dex error in [Fe/H]. |
| Open with DEXTER | |
There are various ways to convince ourselves that this is indeed the case. First, we compared in Fig. 16
the HBs of two GCs (NGC 1904 and NGC 6934) that have very
similar metallicities ([Fe/H] = -1.58 and
[Fe/H] = -1.56, respectively) and relative ages from MS
(0.89 and 0.88). It is clear that their HBs are vastly
different. The median mass values we obtain are 0.606 ![]() 0.003 and 0.671
0.003 and 0.671 ![]() 0.008 for NGC 1904 and NGC 6934, respectively. The two clusters
also have a very different frequency of RR Lyrae, i.e., f(RR) = 0.02 and 0.38.
0.008 for NGC 1904 and NGC 6934, respectively. The two clusters
also have a very different frequency of RR Lyrae, i.e., f(RR) = 0.02 and 0.38.
Second, as shown by Fig. 15,
the scatter of ages from MS and from HB is much larger for GCs of
intermediate luminosity and smaller for both brighter and fainter
clusters. Furthermore, there is a clear trend of this scatter with
metallicity. This is shown in Fig. 17,
where GCs of different metallicity are plotted separately in the three
panels. In this figure, we also plotted the typical error bars as well
as arrows showing the impact of errors in the assumed metallicity and
He content. These errors take consistently into consideration the
impact of the He content on the MS colour, the TO point,
and the HB. While the uncertainties in the assumed metallicity have a
relatively moderate impact on these age estimates, those in the
He content very significantly affect the age estimates from HB.
This effect is particularly large at intermediate metallicity, which is
where we found the largest discrepancies between the two sets of ages.
This suggests that the He content might be responsible for these
discrepancies (although we cannot exclude that other terms, e.g., the
total CNO abundances, might contribute). We also note that the
errors in the ages from MS and HB due to He are anticorrelated with
each other: if the true He abundances are higher than we assumed,
the MS ages are underestimated, while the HB ages are
overestimated. This result could be exploited to simultaneously derive
the values of
![]() and age for each cluster, by ensuring agreement between these two age derivations. The age values, Age(Y), obtained by applying this procedure are listed in the last column of Table 10. Age(Y) values
are typically close to MS ages, the largest differences being
for a few clusters with very blue HBs, such as NGC 6254 and
NGC 1904.
and age for each cluster, by ensuring agreement between these two age derivations. The age values, Age(Y), obtained by applying this procedure are listed in the last column of Table 10. Age(Y) values
are typically close to MS ages, the largest differences being
for a few clusters with very blue HBs, such as NGC 6254 and
NGC 1904.
In principle, errors in Age(Y) should be obtained by
quadratically summing the internal errors in MS and HB ages; the
mean quadratic value determined in this way is 0.063. To confirm
the reliability of this uncertainty estimate, we plot the
age-metallicity relation for different groups of GCs in Fig. 18:
outer halo GCs, inner halo GCs, disk/bulge GCs, and GCs associated with
dSphs (for the classification of the GCs in these different
populations see Carretta et al. 2009d). Briefly, we replot the same age-metallicity diagram, as previously done in Carretta et al. (2009d) but with the new age values, i.e. Age(Y):
we found that for the disk/bulge GCs the relation becomes tighter, with
an rms around a least squares fit of 0.036 with respect to 0.042
previously derived (note that assuming the age values directly
retrieved from Marín-Franch et al. 2009, the scatter around the fit line is ![]() 0.050).
This improvement also supports the identification of this third
parameter with variations in the median He abundances.
Furthermore, the very small dispersion, well within the above cited
error of 0.063, suggests that the observational uncertainties in the
ages from MS's were most likely overestimated. We consider these Age(Y) values
to be the most robust estimates of the relative ages currently
available: they incorporate updated photometric data and metallicities,
and take into account cluster-to-cluster variations in the
He content. We however postpone to a future paper a full
discussion of the age-metallicity relation for the different Galactic
populations of GCs.
0.050).
This improvement also supports the identification of this third
parameter with variations in the median He abundances.
Furthermore, the very small dispersion, well within the above cited
error of 0.063, suggests that the observational uncertainties in the
ages from MS's were most likely overestimated. We consider these Age(Y) values
to be the most robust estimates of the relative ages currently
available: they incorporate updated photometric data and metallicities,
and take into account cluster-to-cluster variations in the
He content. We however postpone to a future paper a full
discussion of the age-metallicity relation for the different Galactic
populations of GCs.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig18.ps}\vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg117.png)
|
Figure 18: Age-metallicity relation for different groups of globular clusters: outer halo clusters (green pentagons), inner halo clusters (blue circles), disk/bulge clusters (red squares). Magenta circles are GCs associated with dSphs. Different symbol sizes are used for clusters of different luminosity. |
| Open with DEXTER | |
5 He from HB and R-parameter
Are there other arguments supporting the idea that the third parameter
required to explain the median colours and masses of HB stars is
indeed the He content? Is there any available evidence on
variations in the median He content between different GCs? The
most classical derivation of He abundances for GCs is obtained
using the so-called R-parameter method (Iben 1968). The R-parameter is the ratio of the number of HB stars,
We note that the statistical error in the R parameter can in principle be reduced by adopting a different definition. With the usual definition, on average ![]() ,
there are more stars on the HB than on the RGB brighter than the HB, which is then a major contributor to the random noise.
However, we may use a different definition of R,
where the error caused by the small number of stars on the RGB is
substantially reduced, but has a similar dependence on the helium
content than the R-parameter. In practice, we may define
,
there are more stars on the HB than on the RGB brighter than the HB, which is then a major contributor to the random noise.
However, we may use a different definition of R,
where the error caused by the small number of stars on the RGB is
substantially reduced, but has a similar dependence on the helium
content than the R-parameter. In practice, we may define
![]() ,
where
,
where
![]() is the number of stars on the RGB brighter than
is the number of stars on the RGB brighter than
![]() .
Roughly,
.
Roughly,
![]() is twice the value of
is twice the value of
![]() ,
so that
,
so that
![]() .
It is then clear that the statistical errors in R' are smaller than in R. Furthermore, checks of the stellar models of Bertelli et al. (2008) indicate that R' has roughly the same (fractional) dependence on Y as R, with only one important modification: the RGB bump is brighter than
.
It is then clear that the statistical errors in R' are smaller than in R. Furthermore, checks of the stellar models of Bertelli et al. (2008) indicate that R' has roughly the same (fractional) dependence on Y as R, with only one important modification: the RGB bump is brighter than
![]() in all GCs considered in this paper. Hence, R' has a simpler (roughly linear) dependence on [Fe/H], unlike R. We then decided to repeat the test using Y values inferred from R', rather than R.
in all GCs considered in this paper. Hence, R' has a simpler (roughly linear) dependence on [Fe/H], unlike R. We then decided to repeat the test using Y values inferred from R', rather than R.
Table 11: R' parameter as derived from both HST and ground based data (note the different definition with respect to the usual R parameter).
Table 11 gives the values of R' deduced from HST and ground-based data; since completeness is more of a concern for this second set of photometry, we give preference to the HST values, whenever possible. When making this derivation, we simply used the HB level listed by Harris (1996). The errors related to individual entries of Table 11 are simply those from statistics, and do not include the effects of uncertainties in decontamination by field stars, differential reddening, and photometric limits. In a few cases, these effects are known and can be taken into consideration. On this basis, we exclude from our estimates the ground-based observations for NGC 2808, NGC 5986, and NGC 6266, and the HST data for NGC 2419, where the photometry is not deep enough to reach the extreme hot/faint tail of the HB. For NGC 5927, the ground-based photometry is also not good enough to discriminate between HB and RGB stars. The R' values are underestimated in these cases, and we did not consider them in our discussion.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig19.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg127.png)
|
Figure 19: The R' values plotted against the R values from Salaris et al. (2004); filled and empty squares are for GCs with [Fe/H] larger and smaller than -1.0 dex, respectively. Note the different definitions of R' and R (see text). |
| Open with DEXTER | |
In Fig. 19, we compare the average values of R' with the values of R obtained by Salaris et al. (2004). There is a good correlation between these two sets of data, which improves if we consider the offset between metal-rich and metal-poor clusters caused by the luminosity of the RGB bump; however, we recall that this new determination is not completely independent of the Salaris et al. one, since both use the HST snapshot photometry. A reasonable good correlation is also obtained with the older determinations of R by Sandquist et al. (2000) and Zoccali et al. (2000).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig20.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg128.png)
|
Figure 20: The R' values plotted against [Fe/H]; filled and open symbols are GCs with or without age estimate, respectively. The solid lines correspond to Y=0.225, 0.250, 0.275. |
| Open with DEXTER | |
The last column of Table 11 gives the value of Y that we could derive from these R'. These were obtained by scaling the calibration of Cassisi et al. (2003) for the ratio of
![]() to
to
![]() ,
and taking into account that the RGB bump is brighter than
,
and taking into account that the RGB bump is brighter than
![]() in all GCs, while being fainter than V(HB) for GCs with [Fe/H] > -1.1. In Fig. 20 we have plotted the values of R'
against the metallicity [Fe/H], and compared them with the
calibrations we used. We note the absence of an obvious bump at
[Fe/H]
in all GCs, while being fainter than V(HB) for GCs with [Fe/H] > -1.1. In Fig. 20 we have plotted the values of R'
against the metallicity [Fe/H], and compared them with the
calibrations we used. We note the absence of an obvious bump at
[Fe/H] ![]() -1.1, which is present in the case of the R-parameter.
-1.1, which is present in the case of the R-parameter.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig21.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg129.png)
|
Figure 21:
The values of
|
| Open with DEXTER | |
In Fig. 21, we plotted the values of Y(R') obtained following this procedure against the median He abundance
![]() required by placing ages estimated from the HB in agreement with those
determined from the MS. There is some correlation between the two
determinations of Y (linear correlation coefficient r=0.23
over 64 GCs, which is significant at a level of confidence of
>95%). The scatter is clearly not negligible, as expected based
on the rather large errors in Y(R'). However, we note that the meaning of these two quantities is not necessarily the same.
To show this, we note that the strongest contribution to a
required by placing ages estimated from the HB in agreement with those
determined from the MS. There is some correlation between the two
determinations of Y (linear correlation coefficient r=0.23
over 64 GCs, which is significant at a level of confidence of
>95%). The scatter is clearly not negligible, as expected based
on the rather large errors in Y(R'). However, we note that the meaning of these two quantities is not necessarily the same.
To show this, we note that the strongest contribution to a ![]() test
performed by comparing the two sets of He determinations is from
NGC 6388 and NGC 6441; in both these clusters, Y(R') is far larger than
test
performed by comparing the two sets of He determinations is from
NGC 6388 and NGC 6441; in both these clusters, Y(R') is far larger than
![]() than the (statistical) errors. The large value of Y(R')
is explained by HB at the RR Lyrae colour being very bright in
these clusters (and indeed the RR Lyrae have anomalously long
periods: Pritzl et al. 2002, 2003).
On the other hand, the RR Lyrae are most likely in the tail of the
distribution of high He abundances in these clusters, whose HB is
predominantly red. In these cases, Y(R') is then expected to be larger than
than the (statistical) errors. The large value of Y(R')
is explained by HB at the RR Lyrae colour being very bright in
these clusters (and indeed the RR Lyrae have anomalously long
periods: Pritzl et al. 2002, 2003).
On the other hand, the RR Lyrae are most likely in the tail of the
distribution of high He abundances in these clusters, whose HB is
predominantly red. In these cases, Y(R') is then expected to be larger than
![]() ,
as is indeed observed. We also note that a much stronger correlation exists between Y(R') and the average of
,
as is indeed observed. We also note that a much stronger correlation exists between Y(R') and the average of
![]() and
and
![]() .
In this case, the correlation coefficient is r=0.294 for the same 64 GCs, which is significant at a level of confidence of
.
In this case, the correlation coefficient is r=0.294 for the same 64 GCs, which is significant at a level of confidence of ![]() %.
%.
We conclude that the hypothesis that the He abundances obtained by matching ages from MS and HB is compatible with current estimates of the He abundances from the R-method, but that more extensive data sets and more careful comparisons (taking into consideration other possible indication of the He abundance, see e.g., Catelan et al. 2009-c) are needed to definitively settle this issue.
6 The colour and mass spread along the HB
6.1 Observational data
The previous discussion suggests that at least three parameters (metallicity, age, and most likely helium content) are required to provide a detailed explanation of the median colours of the HBs. We intend to demonstrate that this selection of parameters successfully explains the extension of the HBs.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig22.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg132.png)
|
Figure 22:
Observed CMDs for NGC 4833 and NGC 5024 ( upper panels) and synthetic diagrams lower panels), obtained with a Gaussian-like distribution mass loss with standard
deviation of 0.02 |
| Open with DEXTER | |
To illustrate our approach, in Fig. 22 we compare the BV colour
magnitude diagrams of NGC 4833 and NGC 5024. These two
clusters have very similar ages (1.01 and 1.04, respectively) and
metallicity ([Fe/H] = -1.89 and -2.06 respectively), similar
values of both median colour and mass of stars on the HB
(0.655 versus 0.658 ![]() ),
but yet very different HBs. The main difference between these two
clusters is in the minimum mass of stars along the HB (0.561 vs.
0.649
),
but yet very different HBs. The main difference between these two
clusters is in the minimum mass of stars along the HB (0.561 vs.
0.649 ![]() ).
We can explain the short HB of NGC 5024 in terms of a small
star-to-star scatter in mass loss (see e.g., Rood et al. 1973, and
many others since). The bottom left panel of Fig. 22 shows a synthetic HB obtained by assuming that the mass lost during
the RGB phase is distributed like a Gaussian, with a standard deviation of 0.02
).
We can explain the short HB of NGC 5024 in terms of a small
star-to-star scatter in mass loss (see e.g., Rood et al. 1973, and
many others since). The bottom left panel of Fig. 22 shows a synthetic HB obtained by assuming that the mass lost during
the RGB phase is distributed like a Gaussian, with a standard deviation of 0.02 ![]() (this
is the minimum value required to reproduce the shortest HBs). While this synthetic
HB matches well the one observed in NGC 5024, it is clearly a poor match to that of
NGC 4833, because it fails to describe its very extended faint tail. The difference between
the two clusters is not simply in terms of the spread of mass loss. This is shown in the
bottom right panel of Fig. 22, where we plotted a synthetic HB obtained assuming a
mass loss spread of 0.07
(this
is the minimum value required to reproduce the shortest HBs). While this synthetic
HB matches well the one observed in NGC 5024, it is clearly a poor match to that of
NGC 4833, because it fails to describe its very extended faint tail. The difference between
the two clusters is not simply in terms of the spread of mass loss. This is shown in the
bottom right panel of Fig. 22, where we plotted a synthetic HB obtained assuming a
mass loss spread of 0.07 ![]() ,
required for an HB extending as faint as the
observed one for NGC 4833. However, this synthetic HB has by far too many red stars, as
shown by a comparison of the cumulative distributions in colours (see Fig. 23)
,
required for an HB extending as faint as the
observed one for NGC 4833. However, this synthetic HB has by far too many red stars, as
shown by a comparison of the cumulative distributions in colours (see Fig. 23)![]() .
A Kolmogorov-Smirnov test shows that the observed colour
distribution disagrees with that of the synthetic HB (at about
98% level of confidence). In contrast, a much better
agreement is obtained between the observed and synthetic HBs for
NGC 5024. We may conclude that at least in the case of the pair
NGC 4833-NGC 5024, a third parameter other than age and
metallicity is required, and that this parameter mainly affects the
minimum mass along the HB.
.
A Kolmogorov-Smirnov test shows that the observed colour
distribution disagrees with that of the synthetic HB (at about
98% level of confidence). In contrast, a much better
agreement is obtained between the observed and synthetic HBs for
NGC 5024. We may conclude that at least in the case of the pair
NGC 4833-NGC 5024, a third parameter other than age and
metallicity is required, and that this parameter mainly affects the
minimum mass along the HB.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig23.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg133.png)
|
Figure 23: Cumulative distribution of (B-V) colours from colour-magnitude (dashed) and synthetic (solid) diagrams for NGC 5024 and NGC 4833; the resulting probabilities from Kolmogorov-Smirnov (KS) test are also shown. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig24.ps}\vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg134.png)
|
Figure 24:
Same as Fig. 22, but for the GCs NGC 6171 and NGC 6723. The
synthetic diagrams ( lower panels) were obtained with a Gaussian-like distribution
mass loss with standard deviation of 0.03 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig25.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg135.png)
|
Figure 25: As for Fig. 23, cumulative distributions and KS values for NGC 6171 and NGC 6723. |
| Open with DEXTER | |
A similar comparison can be made using more metal-rich clusters.
For this purpose, we selected the pair
NGC 6171-NGC 6723, which also have very similar metallicities
and ages ([Fe/H] = -1.03 and -1.10, Age = 0.99 and 1.01,
respectively), similar median mass on the HB (0.650 and 0.644 ![]() ), but again vastly different HB, due to a very different value for the minimum mass (0.629 vs. 0.558
), but again vastly different HB, due to a very different value for the minimum mass (0.629 vs. 0.558 ![]() ). We can reproduce the observed HB of NGC 6171 by a synthetic HB with a small Gaussian spread of 0.03
). We can reproduce the observed HB of NGC 6171 by a synthetic HB with a small Gaussian spread of 0.03 ![]() in the mass lost (see Fig. 24).The shape of the colour distribution of NGC 6171 is not perfectly reproduced, again because the synthetic
diagram predicts too many red stars, as shown by Fig. 25:
however, given the small size of the sample, the result of the
Kolmogorov-Smirnov test returns a 32.7% probability that observed
and synthetic HBs are drawn from the same population, which is not
significant. On the other hand, the distribution of colours of HB stars
along the HB of NGC 6723 is clearly bimodal (see also Rood &
Crocker 1985), and there is no
way of reproducing it assuming a Gaussian distribution of mass lost. In
this case, the result of the Kolmogorov-Smirnov test is that the
probability that a Gaussian distribution (with a dispersion of
0.07
in the mass lost (see Fig. 24).The shape of the colour distribution of NGC 6171 is not perfectly reproduced, again because the synthetic
diagram predicts too many red stars, as shown by Fig. 25:
however, given the small size of the sample, the result of the
Kolmogorov-Smirnov test returns a 32.7% probability that observed
and synthetic HBs are drawn from the same population, which is not
significant. On the other hand, the distribution of colours of HB stars
along the HB of NGC 6723 is clearly bimodal (see also Rood &
Crocker 1985), and there is no
way of reproducing it assuming a Gaussian distribution of mass lost. In
this case, the result of the Kolmogorov-Smirnov test is that the
probability that a Gaussian distribution (with a dispersion of
0.07 ![]() )
reproduces observations is 0.2%. Hence, the case of the pair NGC 4833-NGC 5024 is not alone.
)
reproduces observations is 0.2%. Hence, the case of the pair NGC 4833-NGC 5024 is not alone.
6.2 The correlation between mass spread and absolute magnitude
We propose that the cases discussed in the previous subsection,
extracted from several decades of discussions, convincingly show the
need for a third parameter in addition to metallicity and age to
explain the blue extension of the HBs. Hereinafter, we quantify the
spread in mass loss by the
difference between the minimum and median mass of stars along the HB,
and call this quantity ![]() M
M![]() . We note that
. We note that ![]() M has been estimated by assuming a constant He abundance, hence it cannot be used directly to derive the spread
in He within the cluster.
M has been estimated by assuming a constant He abundance, hence it cannot be used directly to derive the spread
in He within the cluster.
It has long been known that GCs with a large spread of masses along the HB are bright and massive (Fusi Pecci et al. 1993). Recio-Blanco et al. (2006) obtained a good correlation between the highest effective temperature along the HB and the cluster absolute magnitude ![]() .
Given that the highest effective temperature along the HB is well
(anti-)correlated with the minimum mass of HB stars, we should expect a
good anti-correlation between
.
Given that the highest effective temperature along the HB is well
(anti-)correlated with the minimum mass of HB stars, we should expect a
good anti-correlation between ![]() M and
M and ![]() .
In Fig. 26, we show the run of
.
In Fig. 26, we show the run of ![]() M with
M with ![]() (
(![]() values were taken directly from the Harris 1996
catalogue), for both the HST and ground-based data sets. There is
indeed a very significant anti-correlation between these two
quantities: large values of
values were taken directly from the Harris 1996
catalogue), for both the HST and ground-based data sets. There is
indeed a very significant anti-correlation between these two
quantities: large values of ![]() M
are only found among bright clusters. The correlation is much cleaner
if we restrict ourselves only to those GCs with age estimates, which
have the highest quality colour-magnitude diagrams. Hereinafter, we use
these GCs only, and combined ground-based and HST data. However,
by comparing the two data sets, we noted that the anti-correlation
between
M
are only found among bright clusters. The correlation is much cleaner
if we restrict ourselves only to those GCs with age estimates, which
have the highest quality colour-magnitude diagrams. Hereinafter, we use
these GCs only, and combined ground-based and HST data. However,
by comparing the two data sets, we noted that the anti-correlation
between ![]() M and
M and ![]() is stronger when HST data are used (r=0.68 for 45 clusters) than if ground-based data are considered (r=0.54
for 46 clusters). This stronger correlation occurs because the
extreme BHB stars are sometimes below the detection limit of the
ground-based observations. Hence, when considering the two samples
(whenever possible), we give preference to the HST data.
is stronger when HST data are used (r=0.68 for 45 clusters) than if ground-based data are considered (r=0.54
for 46 clusters). This stronger correlation occurs because the
extreme BHB stars are sometimes below the detection limit of the
ground-based observations. Hence, when considering the two samples
(whenever possible), we give preference to the HST data.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig26.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg137.png)
|
Figure 26:
Absolute magnitudes ( |
| Open with DEXTER | |
For this whole sample of 65 GCs (making up almost half of the total
number of Galactic GCs), the linear relation between ![]() M and
M and ![]() is
is
| (12) |
with an extremely significant correlation coefficient of r=0.63. The rms scatter of individual points along this mean relation (0.026
6.3 He variations required explaining the HB width
In the remainder of this section, we examine the possibility that
the additional parameter (to both metallicity and age) determining
the spread in mass for stars along the HB is the variation in the He
abundance, related to various stellar generations in GCs, which
combines with a small (
![]()
![]() )
random spread in mass loss. This last value was adopted because
it is roughly the value required to explain those GCs with the minimum
spread in mass for stars along the HB. In principle, this value may
vary from cluster to cluster, depending e.g., on cluster concentration
(see e.g., Fusi Pecci et al. 1993). However, we wish at present to keep our assumptions to a minimum.
)
random spread in mass loss. This last value was adopted because
it is roughly the value required to explain those GCs with the minimum
spread in mass for stars along the HB. In principle, this value may
vary from cluster to cluster, depending e.g., on cluster concentration
(see e.g., Fusi Pecci et al. 1993). However, we wish at present to keep our assumptions to a minimum.
To test the hypothesis presented above, we first derived the spread in He required to explain the observed spread in colours and masses along the HB. In the next section, we discuss the evidence provided by chemical abundances that might support this hypothesis. When deriving the spread in He, we should take into account that variations in He abundances have important effects on our analysis.
The first step of our procedure is quite simple. Since we assumed that an intrinsic spread in the mass loss equal to 0.02 ![]() is
a universal phenomenon, we corrected the observed mass spread for this
effect by subtracting this value in quadrature from the observed
is
a universal phenomenon, we corrected the observed mass spread for this
effect by subtracting this value in quadrature from the observed ![]() M. In those few cases where
M. In those few cases where ![]() M<0.02,
we simply assumed that the corrected value is 0. The corrected
spread is then attributed to a variation in the He abundance,
assuming that the same mass-loss law is applicable to all stars.
M<0.02,
we simply assumed that the corrected value is 0. The corrected
spread is then attributed to a variation in the He abundance,
assuming that the same mass-loss law is applicable to all stars.
However, to derive the variation in He, we should take into account
that the masses derived for HB stars are themselves functions of the
adopted He abundance. Unfortunately, the Pisa evolutionary tracks were
computed for a single (not constant) value of the He abundance for each
value of the metal abundance, and cannot then be used to estimate this
correction. We therefore used instead the isochrones by Bertelli
et al. (2008),
which while assuming a unique value for the mass loss along the RGB
(preventing its use to derive the relation between masses and colours
along the HB), do however provide data for different He
abundances. We then combined the two sets of models to produce the
following correction formula for ![]() M
M
![\begin{displaymath}%
\Delta {M(Y)} = \Delta {M}\!-\!\Delta {Y}(1.976\!+\!1.982{\rm [Fe/H]}\!+\!0.562{\rm [Fe/H]}^2).
\end{displaymath}](/articles/aa/full_html/2010/09/aa12572-09/img140.png)
|
(13) |
In this equation,
![\begin{displaymath}%
\Delta {Y} = \Delta {M(Y)}/(1.245+30.747~Z_\odot 10^{({[m/H]})}),
\end{displaymath}](/articles/aa/full_html/2010/09/aa12572-09/img144.png)
|
(14) |
where
Table 12 lists the values of
![]() ,
,
![]() ,
and
,
and ![]() Y =
Y =
![]() obtained by this procedure for each cluster. We recall that in some cases
obtained by this procedure for each cluster. We recall that in some cases
![]() values might overestimate the minimum Y in the cluster, and then underestimate
values might overestimate the minimum Y in the cluster, and then underestimate ![]() Y.
The highest He abundances found using this procedure is
Y.
The highest He abundances found using this procedure is
![]() = 0.347 for NGC 6273. The value we find for NGC 2808 is
= 0.347 for NGC 6273. The value we find for NGC 2808 is
![]() = 0.333; this value is discussed in the following section.
= 0.333; this value is discussed in the following section.
Table 12: Spread in He and mass required explaining the HB.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig27.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg151.png)
|
Figure 27:
Absolute magnitudes vs.
|
| Open with DEXTER | |
In Fig. 27, we plotted the
![]() values against the absolute magnitude
values against the absolute magnitude ![]() .
As expected, the correlation is good, yielding
.
As expected, the correlation is good, yielding
| (15) |
with a very significant correlation coefficient of r=0.49 for 65 clusters.
6.4 Colour spread along the main sequence
The spread in helium required to explain the spread in masses along the
HB should cause a broadening of the MS. We estimated this expected
colour spread in the MS at absolute magnitude
![]() ,
by using the following formulae we derived by fitting data from the Bertelli et al. (2008)
isochrones
,
by using the following formulae we derived by fitting data from the Bertelli et al. (2008)
isochrones
| (16) |
and
| (17) |
The colour spreads in B-V and V-I for each cluster are given in Cols. 6 and 7 of Table 12, respectively. Again, we recall that in some cases these spreads may be underestimated, because
Most GCs have not yet been scrutinised in enough detail, but in a few
cases we may compare these predictions with observations. For instance,
in the case of NGC 2808, Piotto et al. (2007) found a spread of ![]() mag in the
mag in the
![]() colour from very high quality ACS data. Since we expect that
colour from very high quality ACS data. Since we expect that
![]() ,
the spread we predict from our analysis of the HB is
,
the spread we predict from our analysis of the HB is
![]() ,
which is roughly half the spread indeed observed. Part of this
difference can be attributed to the median colour of the HB of
NGC 2808 (
,
which is roughly half the spread indeed observed. Part of this
difference can be attributed to the median colour of the HB of
NGC 2808 (
![]() )
not corresponding to the red HB, but rather to the BHB, and in our
framework is then interpreted as a moderately He enriched population (Y=0.273). The He-poor population is however present, corresponding to the red HB, which makes up almost 40% of the cluster HB
population. The total spread in colour along the MS is then expected to be larger than given simply by
)
not corresponding to the red HB, but rather to the BHB, and in our
framework is then interpreted as a moderately He enriched population (Y=0.273). The He-poor population is however present, corresponding to the red HB, which makes up almost 40% of the cluster HB
population. The total spread in colour along the MS is then expected to be larger than given simply by
![]() ;
a more appropriate estimate of the expected colour spread is
;
a more appropriate estimate of the expected colour spread is
![]() and
and
![]() .
While this is still somewhat smaller than observed, the discrepancy is
now small, and could be justified by some additional source of scatter
(differential reddening, binaries, photometric errors) for MS colours
or an incorrect calibration of the HB.
.
While this is still somewhat smaller than observed, the discrepancy is
now small, and could be justified by some additional source of scatter
(differential reddening, binaries, photometric errors) for MS colours
or an incorrect calibration of the HB.
Anderson et al. (2009)
found that some spread in colour is also present in 47 Tuc, from a
very comprehensive analysis of extensive archive HST data. This spread
is small, roughly
![]() ,
and could only be identified thanks to the exceptional quality of the
data, and the very careful procedures used to analyse them. However,
the HB of 47 Tuc is very short
,
and could only be identified thanks to the exceptional quality of the
data, and the very careful procedures used to analyse them. However,
the HB of 47 Tuc is very short![]() , so that our estimate for the He spread is only
, so that our estimate for the He spread is only
![]() (based on the assumption that the small residual spread in masses could
be explained by random star-to-star variations in the mass loss adopted
throughout this paper), and we then expect no widening of the MS due to
He. A careful study of the HB of 47 Tuc by Di Criscienzo
et al. (2009) is work in progress; early results suggest that it
may be more accurately represented by assuming that there is a very
small spread in Y (
(based on the assumption that the small residual spread in masses could
be explained by random star-to-star variations in the mass loss adopted
throughout this paper), and we then expect no widening of the MS due to
He. A careful study of the HB of 47 Tuc by Di Criscienzo
et al. (2009) is work in progress; early results suggest that it
may be more accurately represented by assuming that there is a very
small spread in Y (
![]() ).
By itself, this is not enough to justify the spread in colours of
the MS. However, Di Criscienzo et al. also found that variations
in the total CNO abundances might possibly explain both the small
spread in colour of the MS and the far more evident split in the SGB,
also found by Anderson et al. (2009; see however Bergbush & Stetson 2009,
for a different interpretation of this observation). While this
comparison on the whole supports our result of a small spread in He in
47 Tuc, it also indicates that more careful examinations using
synthesis of populations, taking into account the distribution in both
colours and magnitudes of the stars on the HB, may provide additional
important information about the properties of GCs. Extension of this
careful analysis to many other GCs would be very helpful.
).
By itself, this is not enough to justify the spread in colours of
the MS. However, Di Criscienzo et al. also found that variations
in the total CNO abundances might possibly explain both the small
spread in colour of the MS and the far more evident split in the SGB,
also found by Anderson et al. (2009; see however Bergbush & Stetson 2009,
for a different interpretation of this observation). While this
comparison on the whole supports our result of a small spread in He in
47 Tuc, it also indicates that more careful examinations using
synthesis of populations, taking into account the distribution in both
colours and magnitudes of the stars on the HB, may provide additional
important information about the properties of GCs. Extension of this
careful analysis to many other GCs would be very helpful.
7 He and GC chemistry
7.1 Light elements anti-correlations
Additional evidence that the spread in colours along the HB of GCs is
caused by variations in the He abundances can be obtained by
considering correlations with similar spreads in the abundances of
light elements such as Na and O, Mg and Al. As mentioned in the
introduction, these spreads are
caused by different generations of stars in GCs, the ejecta from the
earliest one having polluted the material from which the later
generation(s) of stars formed. While p-captures
at high temperatures are clearly required to produce Na and Al, and
destroy O and Mg, we do not yet have a satisfactory detailed model, and
even its astrophysical basis is currently debated (either fast rotating
massive stars or massive AGB stars, experiencing hot bottom burning, or
massive binaries: see Decressin et al. 2007; Ventura et al. 2001;
De Mink et al. 2009). We are unable to derive the exact mass range
of the polluting stars. This is an important concern, because the
production of He has probably a different dependence on the mass of the
polluters than both the production of Na and the destruction of O.
For instance, if we consider the massive AGB scenario, He is
mainly produced in the previous MS phase, and it is far more abundant
in the ejecta of the most massive polluters (mass
![]() ).
On the other hand, a very significant production of Na and depletion of
O can be obtained even within stars of lower mass. Hence, the ratio of
He to Na production might change from cluster-to-cluster, provided that
the mass range of polluters changes. With this caveat in mind, we can
then examine current evidence.
).
On the other hand, a very significant production of Na and depletion of
O can be obtained even within stars of lower mass. Hence, the ratio of
He to Na production might change from cluster-to-cluster, provided that
the mass range of polluters changes. With this caveat in mind, we can
then examine current evidence.
In principle, the original He content should be attainable from
direct measurements for each HB star. However, this datum is neither
available nor can be easily obtained, save possibly for a restricted
temperature range at
![]() K (Villanova et al. 2009; He is heavily depleted by
sedimentation in warmer HB stars: see e.g., Behr et al. 2000b; Behr 2003).
Furthermore, even O and Na abundances are not available for most HB
stars (for a possible exception, see again Villanova et al. 2009),
although in this last case abundances could in principle be obtained
for stars on the RHB, within the instability strip, and on the coolest
part of the BHB. Because of this shortage of data, we use values
provided by RGB stars. Of course, the implication is that only
statistical properties of the distributions, not individual values can
be studied. In practice, we only consider extreme values, with the
assumption, consistent with our approach, that the bluest (i.e., less
massive) HB stars are the progeny of the most He-rich TO-stars, and the
reddest ones of the most He-poor ones; in a future paper, we plan to
consider in more detail other characteristics of these distributions.
K (Villanova et al. 2009; He is heavily depleted by
sedimentation in warmer HB stars: see e.g., Behr et al. 2000b; Behr 2003).
Furthermore, even O and Na abundances are not available for most HB
stars (for a possible exception, see again Villanova et al. 2009),
although in this last case abundances could in principle be obtained
for stars on the RHB, within the instability strip, and on the coolest
part of the BHB. Because of this shortage of data, we use values
provided by RGB stars. Of course, the implication is that only
statistical properties of the distributions, not individual values can
be studied. In practice, we only consider extreme values, with the
assumption, consistent with our approach, that the bluest (i.e., less
massive) HB stars are the progeny of the most He-rich TO-stars, and the
reddest ones of the most He-poor ones; in a future paper, we plan to
consider in more detail other characteristics of these distributions.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12572fig28.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg170.png)
|
Figure 28:
|
| Open with DEXTER | |
In the present discussion, we considered a subset of the GCs with
extensive enough data on the Na-O and Mg-Al anticorrelations. Most of
the GCs considered here are from the very extensive study by Carretta
et al. (2009a,b); we complement this data set with a few GCs from the literature (Shetrone & Keane 2000, for NGC 362; Sneden et al. 2004; and Cohen & Melendez 2005, for NGC 5272 and NGC 6205; Sneden et al. 1991, 2000, for NGC 6341; Marino et al. 2008, for NGC 6121; Marino et al. 2009, for NGC 6656; and Yong et al. 2005, for NGC 6752). The relevant data are given in
Table 1.
We note that we prefer to use the inter-quartile IQR of the
distributions (either directly taken from the literature, or obtained
from abundances for individual stars![]() ),
rather than the corresponding values for 90% of the distribution, as we
did for the extension of the HB. The IQR is indeed a more robust
indicator, which is less sensitive to small number statistics and to
many upper limits to the abundance determinations. This last problem
remains an important concern. In general, we may consider the IQR
determinations as lower limits for
those GCs with metallicity [Fe/H] < -1.5. Figure 28
illustrates the correlations between the spread in He abundances
obtained from the colour spread of the HB, and the IQR values for both
the [Na/O] and the [Al/Mg] anticorrelations. As can be seen, fairly
tight correlations exist, the strongest being between
),
rather than the corresponding values for 90% of the distribution, as we
did for the extension of the HB. The IQR is indeed a more robust
indicator, which is less sensitive to small number statistics and to
many upper limits to the abundance determinations. This last problem
remains an important concern. In general, we may consider the IQR
determinations as lower limits for
those GCs with metallicity [Fe/H] < -1.5. Figure 28
illustrates the correlations between the spread in He abundances
obtained from the colour spread of the HB, and the IQR values for both
the [Na/O] and the [Al/Mg] anticorrelations. As can be seen, fairly
tight correlations exist, the strongest being between ![]() Y
and IQR([Na/O]), which are based on more extensive data sets than the
IQR([Al/Mg]). This correlation strongly supports the current
interpretation that the extent of the HB is determined by the spread in
He content within each GC. However, we note
that at least for
Y
and IQR([Na/O]), which are based on more extensive data sets than the
IQR([Al/Mg]). This correlation strongly supports the current
interpretation that the extent of the HB is determined by the spread in
He content within each GC. However, we note
that at least for
![]() ,
the relation has an offset, where
,
the relation has an offset, where ![]() Y is significantly larger than 0 only for clusters with IQR([Na/O] > 0.6).
Y is significantly larger than 0 only for clusters with IQR([Na/O] > 0.6).
7.2 Comparison with a dilution model
We may compare these results with the prediction of a simple universal mechanism for the production of the Na-O correlation, that has only one class of polluters, and for which the composition of second generation stars differ only in terms of the different dilution of polluted gas by primordial material. A similar dilution model has been successfully used to explain many features of the Na-O anti-correlation (see discussion in Prantzos & Charbonnel 2006), including its shape and the residual observed Li abundances in stars severely depleted in O in NGC 6752 (Pasquini et al. 2005). Once the compositions of the pristine and processed material are set (e.g., by the extremes of the observed distributions), the dilution factor may be determined for each star (either from O or Na abundances), and the helium production can be inferred, save for a constant factor.
In this model, the logarithmic abundance of an element [X] for a given dilution factor dil is given by
![\begin{displaymath}%
[X] = \log{[(1-dil)~10^{[X_{\rm o}]} + dil~10^{[X_{\rm p}]}]},
\end{displaymath}](/articles/aa/full_html/2010/09/aa12572-09/img172.png)
|
(18) |
where [
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12572fig29.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg176.png)
|
Figure 29:
Run of [Na/Fe]
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12572fig30.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg177.png)
|
Figure 30: Run of [Na/Fe] vs. [O/Fe] expected for different values of dil from our dilution model. The insert shows the run of [Na/Fe] with [O/Fe] for stars in our FLAMES survey (Carretta et al. 2009a). |
| Open with DEXTER | |
In Fig. 30, we
compare the expected run of [O/Fe] vs. [Na/Fe] according to this
dilution model, with observations for the ensemble of stars observed
within our project (Carretta et al. 2009a).
It is important to notice that within this approach the production
of Na (and of He) saturates at large values of the dilution parameter dil. This has two important implications: (i) most reliable estimate of the maximum value of dil
is given by the O abundances; and (ii) that similar He abundances
are obtained for a rather wide range of [O/Fe]. On the other hand, the
minimum value of dil is most accurately given by Na abundances,
because similar values of [O/Fe] are obtained for small values of dil. Minimum and maximum values of O and Na abundances measured in each cluster are given in Cols. 2-5 of Table 13.
We note that while Na and O maximum abundances listed in this table are
somewhat different from the values adopted in our dilution model, this
has no consequences on our discussion because minimum and maximum
values of the dil parameter (Cols. 6 and 7 of Table 13) are obtained from the minimum abundances of Na and O, respectively. Both minimum and maximum values of dil
contain some uncertainty, because only upper limits to O and Na
abundances can be obtained in extreme cases; this caveat is stronger
for metal-poor stars, and for the smallest GCs, where most of the
observed stars are quite warm. For instance, we suspect that the
minimum Na abundance is overestimated in
the case of M 15, which is a very metal-poor GC, and that for this
reason we underestimate the ![]() dil
range appropriate for this cluster. Finally, the differences between
the maximum and the minimum dilution are given in the last column of
Table 13. Within this model, these values should be proportional to
dil
range appropriate for this cluster. Finally, the differences between
the maximum and the minimum dilution are given in the last column of
Table 13. Within this model, these values should be proportional to ![]() Y.
Y.
Table 13: Minimum and maximum values for [Na/Fe] and [O/Fe] (see text for references).
We note that while this simple dilution model predicts quite uniform values of
![]() ,
and then
,
and then ![]() ,
the values we derived from the HB exhibit large variations from
cluster-to-cluster. As a consequence, the correlation for individual
clusters is poor. We may also remind that this simple model, which uses
a universal polluter, also predicts that the Na-O and Mg-Al
anticorrelations should closely resemble each other, which is not
observed (see Carretta et al. 2009b).
,
the values we derived from the HB exhibit large variations from
cluster-to-cluster. As a consequence, the correlation for individual
clusters is poor. We may also remind that this simple model, which uses
a universal polluter, also predicts that the Na-O and Mg-Al
anticorrelations should closely resemble each other, which is not
observed (see Carretta et al. 2009b).
We conclude that while a second generation of stars polluted by some stars of an earlier generation exists in all GCs, the composition of the polluters is not universal. In some clusters (such as NGC 2808), the polluters produce large amounts of He (most likely with similarly large amounts of Al), and very efficiently destroy O and Mg; while in others (like NGC 6121) practically no fresh He (and Al) is present in the material that produced the second generation stars. On the other hand, all these polluters produce similar amounts of Na. Independent of the polluter, we should be able to reproduce these observations, within a viable scenario for cluster formation and early evolution.
7.3 The impact of cluster luminosity
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12572fig31.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg179.png)
|
Figure 31:
Run of |
| Open with DEXTER | |
The previous discussion suggests that the spread in the He content
within stars in GCs are the most important factor determining the
extension of the HBs. It is important however to understand the
basic physical property of GCs causing this spread in He. The existence
of a good correlation between the maximum temperature of the HB and the
cluster luminosity (Recio-Blanco et al. 2006) suggests that the total cluster mass determines its ability to have stars of very different He
contents, assuming that the present cluster luminosity is a good proxy for its original mass. In Fig. 31 we show the correlation that we find between the spread in He abundance (as represented by ![]() Y) and cluster luminosity
Y) and cluster luminosity ![]() ,
here a proxy for the total mass. There is a clear strong trend of an increase in
,
here a proxy for the total mass. There is a clear strong trend of an increase in ![]() Y with decreasing
Y with decreasing ![]() (that is an increase in luminosity). The linear correlation coefficient
is 0.56 for a total of 65 clusters, which is significant at a
level of more than 99.99%. The mean regression line is
(that is an increase in luminosity). The linear correlation coefficient
is 0.56 for a total of 65 clusters, which is significant at a
level of more than 99.99%. The mean regression line is
| (19) |
Although the correlation between the spread in He abundances (derived from the width of the HB) and luminosity is very good, there are a few clear exceptions, which are massive clusters with very short HBs (and hence small values of
We finally recall that D'Ercole et al. (2008) and Carretta et al. (2009d) presented a scenario for the formation of GCs in which the correlation between cluster luminosity and extension of its HB may occur naturally. According to that scenario, the formation of a GC is the final act of a series of events that begins from the violent onset of star formation in a very large original cloud. Star formation in this cloud continues until the kinetic energy injected by SNe and massive star winds causes dissipation of the remaining gas. In this scenario, this early population is not compact enough for the formation of a stable cluster, and should dissipate after the violent relaxation produced by the loss of the remaining gas and the ejecta of the most massive stars. However, once this very violent initial phase terminates, a much quieter situation follows, where there is no longer a strong injection of energy in the ISM; the slow winds from stars of intermediate mass may then lead to the onset of a cooling flow, and a formation of a very dense and kinematically cold cloud, from which the present GC may form, mainly composed by second generation stars (the I and E populations of Carretta et al. 2009a). Part of the primordial stellar population remains trapped in the current GCs, and forms what Carretta et al. (2009a) called the P-population. In this scenario, it is quite natural to expect that the onset of star formation within the cooling flow should occur earlier in more massive clusters; it will also probably stop earlier, because of the kinetic energy injected by the massive stars of this second generation. Therefore, we may expect that the delay of the second generation, hence the typical polluter mass, is roughly determined by the mass of the GC itself. A few exceptions may be easily accommodated in this scenario as objects characterised by a prolonged phase of formation of the primordial population, e.g., caused by the presence of a very extended region of star formation or companion clusters, as often observed among LMC populous clusters.
This scenario is clearly constructed on the hypothesis of massive AGB stars being polluters. Were rotating massive stars the polluters, some important modifications would be required, because these stars lose most of their mass in the epoch of core-collapse SNe explosions, and it would be very difficult to produce the required cooling flow. Reproducing the trends considered in this paper would clearly be a challenge for this alternative scenario.
8 The M 3-M 13 pair
Since the paper by Van den Bergh (1967), the pair M 3-M 13 (=NGC 5272 and NGC 6205) has played a very special rôle in the second parameter issue. This pair has been repeatedly studied to search for evidence of He-abundance variations (see Caloi & D'Antona 2005; and Catelan et al. 2009-c). They are bright, massive and amongst the easiest GCs observable from the northern hemisphere. M 3, with its large population of RR Lyrae, has often been considered the archetype of Oo I GCs, while M 13 is considered to play the same rôle amongst the clusters with very blue HB. It is interesting to revisit them within the scenario outlined in this paper.
According to the basic parameters defined in this series of
papers, M 3 and M 13 might not be so close twins, after all.
While the metal abundance is quite similar ([Fe/H] = -1.50 and
-1.58), the ages might be different. Without considering the correction
for the different He abundance, the relative ages we considered are
0.88 and 1.02 (see Table 1).
After this correction is
taken into account, this difference becomes even a bit larger (0.875
and 1.033). It is then possible that M 3 is younger then
M 13, a result found in some careful determinations (see
Rosenberg et al. 1999; and De Angeli et al. 2005), but not in others (Marín-Franch et al. 2009; Dotter et al. 2010).
This by itself might explain why the median colour of the HB of
M 13 is much bluer than that of M 3, without any need for a
very large difference in
![]() (we actually obtained values of 0.249 for M 3 and 0.260 for M 13).
(we actually obtained values of 0.249 for M 3 and 0.260 for M 13).
However, it has for a long time been known that these two GCs
also have a large difference in the extension of their HBs. According
to our analysis, the spread in mass along the HB of M 3 is small.
Assuming a constant helium abundance, we obtain minimum, median and
maximum masses of 0.624 ![]() 0.003, 0.670
0.003, 0.670 ![]() 0.001, and 0.716
0.001, and 0.716 ![]() ,
respectively. Apart from a general offset of about 0.02
,
respectively. Apart from a general offset of about 0.02 ![]() (which resembles the overall offset of masses derived from HST and
ground-based data in our analysis), these values are quite similar to those obtained in the analysis of Valcarce & Catelan (2008),
although it is possible that some very blue/faint stars considered by
these authors were actually not studied by the Rosenberg et al. (2000a)
photometry. As discussed by several authors, the distribution of masses
along the HB is probably not Gaussian (see Castellani et al. 2005; and Valcarce & Catelan 2008).
If the interpretation that we give for the mass spread along the HB in
terms of variations in the He content is correct, we would correct the
offset between median and minimum mass to 0.030
(which resembles the overall offset of masses derived from HST and
ground-based data in our analysis), these values are quite similar to those obtained in the analysis of Valcarce & Catelan (2008),
although it is possible that some very blue/faint stars considered by
these authors were actually not studied by the Rosenberg et al. (2000a)
photometry. As discussed by several authors, the distribution of masses
along the HB is probably not Gaussian (see Castellani et al. 2005; and Valcarce & Catelan 2008).
If the interpretation that we give for the mass spread along the HB in
terms of variations in the He content is correct, we would correct the
offset between median and minimum mass to 0.030 ![]() ,
and the corresponding spread in helium would be
,
and the corresponding spread in helium would be
![]() Y = 0.023. Catelan et al. (2009-c)
argued that such a small spread in He in M 3 would be detectable
from Strömgren photometry and spectroscopy of the blue HB stars, and
concluded that a uniform He abundance more closely matches the
observations for this cluster. This might suggest that small spreads in
He such as the one we derived for M 3 might be an artifact of a
non-Gaussian random mass-loss distribution. However, since the bluest HB stars (
Y = 0.023. Catelan et al. (2009-c)
argued that such a small spread in He in M 3 would be detectable
from Strömgren photometry and spectroscopy of the blue HB stars, and
concluded that a uniform He abundance more closely matches the
observations for this cluster. This might suggest that small spreads in
He such as the one we derived for M 3 might be an artifact of a
non-Gaussian random mass-loss distribution. However, since the bluest HB stars (
![]() K, consisting of some 5% of the whole HB population of M 3) could not be analyzed by Catelan et al.,
it is not entirely clear that there is no real spread in helium within M 3.
K, consisting of some 5% of the whole HB population of M 3) could not be analyzed by Catelan et al.,
it is not entirely clear that there is no real spread in helium within M 3.
On the other hand, M 13 has a very wide range of both colours and masses along the HB. The spread in mass and Y abundances we obtained using
![]() are
are ![]() M = 0.082
M = 0.082 ![]() and
and ![]() Y = 0.065. Had we instead used
Y = 0.065. Had we instead used
![]() ,
scaled down by 0.02
,
scaled down by 0.02 ![]() to take into account the random term in mass lost, we would have got
to take into account the random term in mass lost, we would have got ![]() M = 0.107
M = 0.107 ![]() and
and ![]() Y = 0.083. We expect then a detectable spread in colours for the MS of M 13: [
Y = 0.083. We expect then a detectable spread in colours for the MS of M 13: [
![]() mag and possibly as much as
mag and possibly as much as
![]() mag, if
mag, if
![]() were adopted,
assuming that the minimum Y value is smaller than
were adopted,
assuming that the minimum Y value is smaller than
![]() .
This colour spread could possibly be detected in the future by a careful analysis of HST photometry.
.
This colour spread could possibly be detected in the future by a careful analysis of HST photometry.
As noticed by several authors, this huge difference in the width of the
HB between M 3 and M 13 is quite unexpected, since M 3
is a luminous cluster (
![]() ), even more luminous than M 13 (
), even more luminous than M 13 (
![]() ).
As the discussion in Sect. 6.4 shows, we should indeed expect a
more extended HB for a luminous cluster like M 3. As a matter of
fact, M 3 (and moreover 47 Tuc and NGC 5024) appears
peculiar with respect to the other GCs, while M 13 appears to be
similar to the majority of GCs in this respect. Within the scenario we
described in the previous section (see also Carretta et al. 2009d),
we are tempted to invoke a delayed cooling flow to explain the
peculiarity of M 3 and 47 Tuc. This might explain other
differences between M 3 and 47 Tuc on the one hand, and the
other massive GCs on the other, such as the small values of IQR[Na/O].
However, we admit that without any further information, this hypothesis
might look rather ad hoc
).
As the discussion in Sect. 6.4 shows, we should indeed expect a
more extended HB for a luminous cluster like M 3. As a matter of
fact, M 3 (and moreover 47 Tuc and NGC 5024) appears
peculiar with respect to the other GCs, while M 13 appears to be
similar to the majority of GCs in this respect. Within the scenario we
described in the previous section (see also Carretta et al. 2009d),
we are tempted to invoke a delayed cooling flow to explain the
peculiarity of M 3 and 47 Tuc. This might explain other
differences between M 3 and 47 Tuc on the one hand, and the
other massive GCs on the other, such as the small values of IQR[Na/O].
However, we admit that without any further information, this hypothesis
might look rather ad hoc![]() .
Thus, ironically, while the present approach seems to explain most of
the observations relate to the second parameter effect, its application
to the most classical couple M 3-M 13 still encounters
difficulties.
.
Thus, ironically, while the present approach seems to explain most of
the observations relate to the second parameter effect, its application
to the most classical couple M 3-M 13 still encounters
difficulties.
9 Conclusions and suggestions for further work
As we have seen, our reanalysis of public extensive photometric databases of GCs demonstrates that age is the main second parameter
affecting the HB morphology. This hypothesis is able to explain quite
well most of the observables related to median HB stars of GCs, when
coupled with a simple mass-loss law that is a linear function of
[Fe/H]. Among the many observables that are successfully explained, we
note the Oosterhoff dichotomy that we attribute to the peculiar
age-metallicity distribution of Galactic GCs. Oo II clusters are mostly old, while Oo I are predominantly young, although young Oo II and old Oo I GCs exist. However, at least a third parameter is required
(and possibly even others) to fully explain the median colours of HBs
(in particular those with very blue HBs) as well as their
extension. There are various reasons to identify this third parameter
with variations in the He content. These include the variation in the scatter with metallicity, some correlation with the R-parameter,
and the clear links with chemical anomalies observed in GCs. This
result is strongly indicative of a possible link between the colours of
the stars on the HB and their original composition, in a multiple
generation scenario for the formation and early evolution of GCs.
Self-pollution in GCs is possibly responsible for a large variety of
the second parameter features, and may be in part described using the
Na-O anticorrelation, although some modulation according to cluster
luminosity is required![]() .
.
A combination of age and He variation therefore appears to be an explanation of the long-standing problem of the second parameter, although we do not exclude additional parameters such as the CNO abundances or the presence of binaries (e.g., of the progeny of blue stragglers) possibly playing some rôle. However, this issue is still far from being completely settled. We need to make some progress in developing models, and a number of observational tests. A short list includes:
- Understanding the nature of the polluters. This requires advances in the modeling of AGB stars and rotating massive stars. Furthermore, detailed spectroscopic data for stars in massive and very young clusters, such as RSGC1 and RSGC2 (Davies et al. 2007), or intermediate age clusters in the LMC, where multiple MS TO's have been observed (Mackey et al. 2008; Milone et al. 2009), may provide a crucial test of this scenario.
- The present discussion has focused on He, Na and O, but the abundances of other elements may also play an important rôle. For instance, Al might be a proxy for He that is more reliable than Na. Unfortunately, our data for Al are not as extensive as those for Na and O, but the relation between the production of He (which most likely occurred within MS stars), and the proton capture processes (which might have occurred in the same main sequence stars, if massive and fast rotating, or later during the AGB phase, if the stars were of intermediate mass) must be clarified.
- A number of confirmations of this scenario are required. These include (i) direct determinations of He, Na, and O in HB stars, which were shown to be possible in at least some cases by Villanova et al. (2009); and (ii) a discussion of the luminosity of the RGB bump that we defer to another paper currently in preparation.
- In addition, we ask: do properties of RR Lyrae variables agree with expectations? Are anti-correlations found where expected (important clusters such as M 54 and NGC 1851 do not yet have adequate data)? Are multiple sequences observed where they are expected? We note here that while the connections between multiple MSs and variations in the He abundance is quite clear, the case of multiple sub-giant branches (SGB) is more ambiguous. SGB splitting measured using visual-red-near infrared colours (see e.g., Milone et al. 2008) might be due to a variation either in age or most likely total CNO content (see e.g., D'Antona et al. 2009; and Cassisi et al. 2008), or even [Fe/H] (in this case however some spread in the MS and RGB is also expected). Interpretation of splitting is even more ambiguous when considering ultraviolet colours, which are sensitive to N excesses. Variations in He abundances are only marginally effective in these cases, because sequences differing only in Y are very close each other on the SGB (D'Antona et al. 2002). Variations in total CNO content can be most likely attributed to the contribution of thermally pulsing AGB stars (Cassisi et al. 2008), which have a rather low mass and probably do not contribute much to He abundance variations. It is then unclear that there should be any correlation between the SGB splitting and large spreads on the HBs. In fact, NGC 2808 has a quite narrow SGB (Piotto et al. 2007). SGB splitting has been detected using visual-red-near infrared colours in 47 Tuc (Anderson 2009), NGC 1851 (Milone et al. 2008), and NGC 6388 (Moretti et al. 2009). These clusters have very different HB morphologies, ranging from very short (47 Tuc), to bimodal (NGC 1851), to very extended (NGC 6388). We obtain very different estimates of the He spread (0 for 47 Tuc; 0.048 for NGC 1851, a possibly too large value compared with those determined by Salaris et al. 2008; and Catelan et al. 2010; 0.037 for NGC 6388). This lack of correlation suggests that the two phenomena are somewhat different, as expected if the mass range of the polluters changes from cluster-to-cluster.
- The scenario requires a number of refinements. All analytic dependencies adopted throughout this discussion should be reviewed, and possibly replaced by a comparison with synthetic HBs. This may allow us to detect additional effects, e.g., a variation in total CNO abundances, not included in the present analysis.
- Finally, hydrodynamical simulations of the formation and early evolution of massive star clusters are urgently needed. There are aspects of the present scenario that are necessary to explain observations, but should be understood more clearly. The most intriguing is the existence of a pool of gas from which second generation stars formed, which is composed of material processed through H-burning at high temperature diluted with pristine gas. How this pool of gas is generated, and how the stars form from it within the potential well of the young GC, while other stars of the original population evolve, remains unclear. Some explorative results were obtained by D'Ercole et al. (2008) which while very promising should be placed on a sounder basis.
The authors wish to thank the anonymous referee for insightful and useful comments which lead to a significant improvement of the paper. L. Girardi for having provided the results of the TRILEGAL simulations used for field decontamination. F. D'Antona and S. Cassisi deserve to be acknowledged for a critical reading of the manuscript and for the very valuable suggestions. Finally, we thank Mariangela Bonavita for help in the preparation of the figures, and the Italian MUR for financial support through PRIN 20075TP5K9. This research has made use of NASA's Astrophysics Data System.
References
- Anderson, J., Piotto, G., King, I. R., Bedin, L. R., & Guhathakurta, P. 2009, ApJ, 697, L58 [NASA ADS] [CrossRef] [Google Scholar]
- Balser, D. S. 2006, AJ, 132, 2326 [NASA ADS] [CrossRef] [Google Scholar]
- Bedin, L., Piotto, G., Anderson, J., et al. 2004, ApJ, 605, L125 [NASA ADS] [CrossRef] [Google Scholar]
- Behr, B. B. 2003, ApJS, 149, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Behr, B. B., Djorgovski, S. G., Cohen, J. G., et al. 2000a, ApJ, 528, 849 [NASA ADS] [CrossRef] [Google Scholar]
- Behr, B. B., Cohen, J. G., & McCarthy, J. K. 2000b, ApJ, 531, L37 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bergbusch, P. A., & Stetson, P. B. 2009, AJ, 138, 1455 [NASA ADS] [CrossRef] [Google Scholar]
- Bertelli, G., Girardi, L., Marigo, P., & Nasi, E. 2008, A&A, 484, 815 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buonanno, R., Corsi, C. E., Zinn, R., et al. 1998, ApJ, 501, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Caloi, V., & D'Antona, F. 2005, A&A, 435, 987 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caloi, V., & D'Antona, F. 2007, A&A, 463, 949 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caloi, V., & D'Antona, F. 2008, ApJ, 673, 847 [NASA ADS] [CrossRef] [Google Scholar]
- Cariulo, P., Degl'Innocenti, S., & Castellani, V. 2004, A&A, 421, 1121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Recio-Blanco, A., Gratton, R. G., Piotto, G., & Bragaglia, A. 2007, ApJ, 671, L125 [NASA ADS] [CrossRef] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2009a, A&A, 505, 117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., & Lucatello, S. 2009b, A&A, 505, 139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., D'Orazi, V., & Lucatello, S. 2009c, A&A, 508, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2009d, A&A, accepted [Google Scholar]
- Casagrande, L., Flynn, C., Portinari, L., Girardi, L., & Jimenez, R. 2007, MNRAS, 382, 1516 [NASA ADS] [CrossRef] [Google Scholar]
- Cassisi, S., Castellani, V., degl'Innocenti, S., & Weiss, A. 1998, A&AS, 129, 267 [Google Scholar]
- Cassisi, S., Salaris, M., & Irwin, A. W. 2003, ApJ, 588, 862 [NASA ADS] [CrossRef] [Google Scholar]
- Cassisi, S., Salaris, M., Pietrinferni, A., et al. 2008, ApJ, 672, L115 [NASA ADS] [CrossRef] [Google Scholar]
- Castellani, V., Degl'Innocenti, S., Marconi, M., Prada Moroni, P. G., & Sestito, P. 2003, A&A, 404, 645 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castellani, M., Castellani, V., & Cassisi, S. 2005, A&A, 437, 1017 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Catelan, M. 2009a, Resolved Stellar Populations, ASP Conf. Ser., ed. D. Valls-Gabaud, & M. Chavez, Ap&SS, 320, 261 [Google Scholar]
- Catelan, M. 2009b, in The Ages of Stars: The horizontal branch, IAU Symp., 258, 209 [Google Scholar]
- Catelan, M., & de Freitas Pacheco, J. A. 1995, A&A, 297, 345 [NASA ADS] [Google Scholar]
- Catelan, M., Borissova, J., Sweigart, A. V., & Spassova, N. 1998, ApJ, 494, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Catelan, M., Bellazzini, M., Landsman, W. B., et al. 2001, AJ, 122, 3171 [NASA ADS] [CrossRef] [Google Scholar]
- Catelan, M., Grundahl, F., Sweigart, A. V., Valcarce, A. A. R., & Cortés, C. 2009, ApJ, 695, 97 [Google Scholar]
- Catelan, M., Valcarce, A. A. R., Sweigart, A. V. 2010, in Star clusters: basic galactic building blocks throughout time and space, IAU Symp., 266, 281 [Google Scholar]
- Chiosi, C., & Matteucci, F. 1982, A&A, 105, 140 [NASA ADS] [Google Scholar]
- Clement, C. M., Muzzin, A., Dufton, Q., et al. 2001, AJ, 122, 2587 [NASA ADS] [CrossRef] [Google Scholar]
- Code, A. D. 1969, PASP, 81, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, J. G., & Melendez, J. 2005, AJ, 129, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, J. G., Briley, M. M., & Stetson, P. B. 2002, AJ, 123, 2525 [NASA ADS] [CrossRef] [Google Scholar]
- Contreras, R., Catelan, M., Smith, H. A., Pritzl, B. J., & Borissova, J. 2005, ApJ, 623, L117 [NASA ADS] [CrossRef] [Google Scholar]
- Corwin, T. M., Catelan, M., Borissova, J., & Smith, H. A. 2004, A&A, 421, 667 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D'Antona, F., & Caloi, V. 2004, ApJ, 611, 871 [NASA ADS] [CrossRef] [Google Scholar]
- D'Antona, F., & Caloi, V. 2008, MNRAS, 390, 693 [NASA ADS] [CrossRef] [Google Scholar]
- D'Antona, F., Caloi, V., Montalban, J., Ventura, P., & Gratton, R. 2002, A&A, 395, 69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D'Antona, F., Bellazzini, M., Caloi, V., et al. 2005, ApJ, 631, 868 [NASA ADS] [CrossRef] [Google Scholar]
- D'Antona, F., Stetson, P. B., & Ventura, P. 2009, MNRAS, 399, 151 [Google Scholar]
- Davies, B., Figer, D. F., Kudritzki, R.-P., et al. 2007, ApJ, 671, 781 [NASA ADS] [CrossRef] [Google Scholar]
- D'Cruz, N. L., Dorman, D., Rood, R. T., & O'Connell, R. W. 1996, ApJ, 466, 359 [NASA ADS] [CrossRef] [Google Scholar]
- de Angeli, F., Piotto, G., Cassisi, S., et al. 2005, AJ, 130, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Decressin, T., Meynet, G., Charbonnel, C., Prantzos, N., & Ekstrm, S. 2007, A&A, 464, 1029 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deliyannis, C. P., Demaruqe, P., & Pinsonneault, M. H. 1989, ApJ, 347, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Demarque, P., Lee, Y.-W., Zinn, R., & Green, E. M. 1989, IAU Meeting JCM 5 and CM 37/3, The abundance spread within globular clusters: spectroscopy of individual stars, 97 [Google Scholar]
- De Minck, S. E., Pols, O. R., Langer, N., & Izzard, R. G. 2009, A&A, 507, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D'Ercole, A., Vesperini, E., D'Antona, F., McMillan, S. L. W., & Recchi, S. 2008, MNRAS, 391, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Di Criscienzo, M., Marconi, M., & Caputo, F. 2004, ApJ, 612, 1092 [NASA ADS] [CrossRef] [Google Scholar]
- Dotter, A. 2008, ApJ, 687, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Dotter, A., Sarajedini, A., & Yang, S. C. 2008, AJ, 136, 1407 [NASA ADS] [CrossRef] [Google Scholar]
- Dotter, A., Sarajedini, A., Anderson, J., et al. 2010, ApJ, 708, 698 [NASA ADS] [CrossRef] [Google Scholar]
- Dupree, A. K., Smith, G. H., Strader, J., et al. 2009, AJ, 138, 1485 [NASA ADS] [CrossRef] [Google Scholar]
- Faulkner, J. 1966, ApJ, 144, 978 [NASA ADS] [CrossRef] [Google Scholar]
- Ferraro, F. R., Clementini, G., Fusi Pecci, F., Buonanno, R., & Alcaino, G. 1990, A&AS, 84, 59 [NASA ADS] [Google Scholar]
- Freeman, K. C., & Norris, J. 1981, ARA&A, 19, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Fusi Pecci, F., Ferraro, F. R., Bellazzini, M., et al. 1993, AJ, 105, 1145 [NASA ADS] [CrossRef] [Google Scholar]
- Fusi Pecci, F., Bellazzini, M., Cacciari, C., & Ferraro, F. R. 1995, AJ, 110, 1664 [NASA ADS] [CrossRef] [Google Scholar]
- Girardi, L., Groenewegen, M. A. T., Hatziminaoglou, E., & da Costa, L. 2005, A&A, 436, 895 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldberg, L. 1979, QJRAS, 20, 36 [Google Scholar]
- Gratton, R. G., Bonifacio, P., Bragaglia, A., et al. 2001, A&A, 369, 87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gratton, R. G., Sneden, C., & Carretta, E. 2004, ARA&A, 42, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Green, et al. 1997, in Third Conference on Faint Blue Stars, 271 [Google Scholar]
- Han, Z., Podsiadlowski, P., Maxted, P. F. L., & Marsh, T. R. 2003, MNRAS, 341, 669 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, W. E. 1996, AJ, 112, 1487 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, W. E., Bell, R. A., Vandenberg, D. A., et al. 1997, AJ, 114, 1030 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, I., Jr. 1968, Nature, 220, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, I., Jr, & Rood, R. T. 1970, ApJ, 159, 605 [CrossRef] [Google Scholar]
- Judge, P. G., & Stencel, R. E. 1991, ApJ, 371, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Kraft, R. P. 1994, PASP, 106, 553 [NASA ADS] [CrossRef] [Google Scholar]
- Lane, R. R., Brewer, B. K., Kiss, L. L., et al. 2010, ApJ, 711, L122 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, Y.-W., & Zinn, R. 1990, in Confrontation between Stellar Pulsation and Evolution, ed. C. Cacciari, & G. Clementin (San Francisco: ASP), ASP Conf. Ser., 11, 26 [Google Scholar]
- Lee, J.-W., & Carney, B. 1999, AJ, 118, 1373 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, Y.-W., Demarque, P., & Zinn, R. 1990, ApJ, 350, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, Y.-W., Demarque, P., & Zinn, R. 1994, ApJ, 423, 248 [Google Scholar]
- Lee, Y.-W., Joo, S.-J., & Han, S.-I. 2005, ApJ, 621, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Mackey, A. D., Broby Nielsen, P., Ferguson, A. M. N., & Richardson, J. C. 2008, ApJ, 681, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Marcolini, A., Gibson, B. K., Karakas, A. I., & Sanchez-Blazquez, P. 2009, MNRAS, 395, 719 [NASA ADS] [CrossRef] [Google Scholar]
- Marconi, M., Caputo, F., Di Criscienzo, M., & Castellani, M. 2003, ApJ, 596, 299 [Google Scholar]
- Marín-Franch, A., Aparicio, A., Piotto, G., et al. 2009, ApJ, 694, 1498 [NASA ADS] [CrossRef] [Google Scholar]
- Marino, A. F., Villanova, S., Piotto, G., et al. 2008, A&A, 490, 625 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marino, A. F., Milone, A., Piotto, G., et al. 2009, A&A, 505, 1099 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maxted, P. F. L., Heber, U., Marsh, T. R., & North, R. C. 2001, MNRAS, 326, 1391 [NASA ADS] [CrossRef] [Google Scholar]
- Mészáros, Sz., Avrett, E. H., & Dupree, A. K. 2009, AJ, 138, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Milone, A. P., Bedin, L. R., Piotto, G., Anderson, J., & King, I. R. 2008, ApJ, 673, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Milone, A. P., Bedin, L. R., Piotto, G., & Anderson, J. 2009, ApJ, 497, 755 [Google Scholar]
- Milone, A. P., Piotto, G., King, I. R., et al. 2010, ApJ, 709, 1183 [NASA ADS] [CrossRef] [Google Scholar]
- Moehler, S. 2001, PASP, 113, 1162 [NASA ADS] [CrossRef] [Google Scholar]
- Moehler, S., Landsman, W. B., & Dorman, B. 2000, A&A, 361, 937 [NASA ADS] [Google Scholar]
- Moni Bidin, C., Moehler, S., Piotto, G., et al. 2006, A&A, 451, 499 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moretti, A., Piotto, G., Arcidiacono, C., et al. 2009, A&A, 539, 546 [Google Scholar]
- Mullan, D. J. 1978, ApJ, 226, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Napiwotzki, R., Karl, C. A., Lisker, T., et al. 2004, Ap&SS, 291, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, J. E. 1981, ApJ, 248, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, J. E. 2004, ApJ, 612, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Oosterhoff, P. Th. 1944, BAN, 10, 550 [Google Scholar]
- Origlia, L., Rood, R. T., Fabbri, S., et al. 2007, ApJ, 667, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Origlia, L., et al. 2008, MSAIt, 79, 432 [Google Scholar]
- Pasquini, L., Bonifacio, P., Molaro, P., et al. 2005, A&A, 441, 549 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peterson, R. 1982, ApJ, 258, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Piotto, G., King, I. R., Djorgovski, S. G., et al. 2002, A&A, 391, 945 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piotto, G., Villanova, S., Bedin, L. R., Gratton, R., & Cassisi, S. 2005, ApJ, 621, 777 [NASA ADS] [CrossRef] [Google Scholar]
- Piotto, G., Bedin, L. R., Anderson, J., et al. 2007, ApJ, 661, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Prantzos, N., & Charbonnel, C. 2006, A&A, 458, 135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pritzl, B. J., Smith, H. A., Catelan, M., & Sweigart, A. V. 2002, AJ, 124, 949 [NASA ADS] [CrossRef] [Google Scholar]
- Pritzl, B. J., Smith, H. A., Stetson, P. B., et al. 2003, AJ, 126, 1381 [NASA ADS] [CrossRef] [Google Scholar]
- Pritzl, B. J., Armandroff, T. E., Jacoby, G. H., & Da Costa, G. S. 2004, AJ, 127, 318 [NASA ADS] [CrossRef] [Google Scholar]
- Recio-Blanco, A., Piotto, G., Aparicio, A., & Renzini, A. 2002, ApJ, 572, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Recio-Blanco, A., Aparicio, A., Piotto, G., de Angeli, F., & Djorgovski, S. G. 2006, A&A, 452, 875 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reimers, D. 1975a, in Problems in Stellar Atmospheres and Envelopes, ed. B. Baschek, W. H. Kegel, & G. Traving (Berlin: Springer), 229 [Google Scholar]
- Reimers, D. 1975b, Mem. Soc. R. Sci. Liège 6 Ser., 8, 369 [Google Scholar]
- Renzini, A. 1977, in Advanced Stages in Stellar Evolution, ed. P. Bouvier, & A. Maeder, Obs. de Geneve, Geneve, 151 [Google Scholar]
- Rich, M. R., Sosin, C., Djorgovski, S. G., et al. 1997, ApJ, 484, L25 [Google Scholar]
- Rood, R. T. 1973, ApJ, 184, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Rood, R. T., & Crocker, D. A. 1985, in Horizontal-branch and UV-bright stars, 99 [Google Scholar]
- Rosenberg, A., Saviane, I., Piotto, G., & Aparicio, A. 1999, AJ, 118, 2306 [NASA ADS] [CrossRef] [Google Scholar]
- Rosenberg, A., Piotto, G., Saviane, I., & Aparicio, A. 2000a, A&AS, 144, 5 [Google Scholar]
- Rosenberg, A., Aparicio, A., Saviane, I., & Piotto, G. 2000b, A&AS, 145, 451 [Google Scholar]
- Salaris, M., Riello, M., Cassisi, S., & Piotto, G. 2004, A&A, 420, 911 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salaris, M., Cassisi, S., & Pietrinferni, A. 2008, ApJ, 678, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Sandage, A. R. 1982, ApJ, 252, 553 [NASA ADS] [CrossRef] [Google Scholar]
- Sandage, A., & Wallerstein, G. 1960, ApJ, 131, 598 [NASA ADS] [CrossRef] [Google Scholar]
- Sandage, A., & Wildey, R. 1967, ApJ, 150, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Sandquist, E. L., Taam, R. E., & Burkert, A. 2000, ApJ, 533, 984 [NASA ADS] [CrossRef] [Google Scholar]
- Sarajedini, A., Bedin, L. R., Chaboyer, B., et al. 2007, AJ, 133, 1658 [NASA ADS] [CrossRef] [Google Scholar]
- Shetrone, M. D., & Keane, M. J. 2000, AJ, 119, 840 [NASA ADS] [CrossRef] [Google Scholar]
- Sneden, C., Kraft, R. P., Prosser, C. F., & Langer, G. E. 1991, AJ, 102, 2001 [NASA ADS] [CrossRef] [Google Scholar]
- Sneden, C., Pilachowski, C. A., & Kraft, R. P. 2000, AJ, 120, 1351 [NASA ADS] [CrossRef] [Google Scholar]
- Sneden, C., Kraft, R. P., Guhathakurta, P., Peterson, R. C., & Fulbright, J. P. 2004, AJ, 127, 2162 [NASA ADS] [CrossRef] [Google Scholar]
- Soker, N., & Harpaz, A. 2000, MNRAS, 317, 861 [NASA ADS] [CrossRef] [Google Scholar]
- Spergel, D. N., Bean, R., Dorè, O., et al. 2007, ApJ, 170, 377 [NASA ADS] [Google Scholar]
- Stephens, A. W., & Frogel, J. A. 2004, AJ, 127, 925 [NASA ADS] [CrossRef] [Google Scholar]
- Stetson, P. B., Vandenberg, D. A., & Bolte, M. 1996, PASP, 108, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Sweigart, A. V. 2002, Highlights in Astronomy, 12, 292 [Google Scholar]
- Sweigart, A. V., & Gross, P. G. 1976, ApJS, 32, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Szczygiel, D. M., Pojmanski, G., & Pilecki, B. 2009, AcA, 59, 137 [Google Scholar]
- Valcarce, A. A. R., & Catelan, M. 2008, A&A, 487, 185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van den Bergh, S. 1967, AJ, 72, 70 [NASA ADS] [CrossRef] [Google Scholar]
- VandenBerg, D. A., Swenson, F. J., Rogers, F. J., Iglesias, C. A., & Alexander, D. R. 2000, ApJ, 532, 430 [NASA ADS] [CrossRef] [Google Scholar]
- Vanhollebeke, E., Groenewegen, M. A. T., & Girardi, L. 2009, A&A, 498, 95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ventura, P., D'Antona, F., Mazzitelli, I., & Gratton, R. 2001, ApJ, 550, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Villanova, S., Piotto, G., & Gratton, R. G. 2009, A&A, 499, 755 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Willson, L. A. 2000, ARA&A, 38, 573 [NASA ADS] [CrossRef] [Google Scholar]
- Yong, D., Grundahl, F., Nissen, P. E., Jensen, H. R., & Lambert, D. L. 2005, A&A, 438, 875 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zinn, R. 1980, ApJ, 241, 602 [NASA ADS] [CrossRef] [Google Scholar]
- Zinn, R. 1985, ApJ, 293, 424 [Google Scholar]
- Zoccali, M., Cassisi, S., & Bono, G. 2000, ApJ, 538, 289 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ... clusters
![[*]](/icons/foot_motif.png)
- Tables 1-8 and 10-12 are only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/517/A81
- ... base
![[*]](/icons/foot_motif.png)
- http://adsabs.harvard.edu/
- ... massive
![[*]](/icons/foot_motif.png)
- As pointed out by the referee, the knowledge that He abundance variations lead to variations in turn-off masses is much older (see Iben & Rood 1970). However, D'Antona et al. were the first to relate variations in Na, O, and other light elements to variations in He abundances, and then TO masses. This created the link between abundance anomalies on the RGB and the second parameter issue.
- ... yet
![[*]](/icons/foot_motif.png)
- An analysis of the ages of GCs and median colours of the HB based on these ACS data has been published after this paper was written (Dotter et al. 2010). A complete comparison with our results would require a long section. However, we note that there are very tight correlations between the V-I colours from ACS data, and the B-V and V-I ones of this paper. The ages by Dotter et al. also agree fairly well, at least in a statistical sense, with those considered in this paper. Not surprisingly, there is also agreement at least in the first major conclusion: age is the main second parameter. However, Dotter et al. suggest cluster concentration as third parameter, while we propose absolute magnitudes, on turn related to the He content. We note that Dotter et al. did not examine the extension of the HB, limiting their study to the median colours. We argue that it is not easy to discuss this third parameter using this approach. Furthermore, there is some correlation between luminosity and concentration for GCs, which may justify their result. However, our analysis of the extension of the HB shows that this is much more strongly correlated with the cluster absolute magnitudes, rather than their concentration.
- ... database
![[*]](/icons/foot_motif.png)
- The databases we considered actually also include entries for variable stars (on the HB mainly RR Lyrae). These entries are very inaccurate, since usually data at very few epochs are available, and photometry in different bands is not based on data acquired simultaneously. However, while inaccurate, these data still have some statistical meaning; for this reason, they are considered throughout our analysis.
- ...2004)
![[*]](/icons/foot_motif.png)
- http://astro.df.unipi.it/SAA/PEL/Z0.html
- ... luminosity
![[*]](/icons/foot_motif.png)
- As pointed out by the referee, the value of S(RR) listed in the Harris catalogue are underestimated for some GCs. A couple of examples are NGC 2808 (see Corwin et al. 2004) and M 62 (Contreras et al. 2005).
- ... bars
![[*]](/icons/foot_motif.png)
- This indicates that the scatter about the mean mass-loss relation in Fig. 11 is indeed real, as mentioned in Sect. 2.4, and not simply due to observational errors.
- ...)
![[*]](/icons/foot_motif.png)
- Small excesses of red stars along the HB - much smaller than found for NGC 4833 - are found often in our comparisons with synthetic HBs. This same problem was found by other similar analysis (see the discussion in Castellani et al. 2005). It might indicate either a deficiency of the adopted HB models, or a non-Gaussian distribution of the random terms of the mass loss, perhaps because it would be more appropriate to consider a Gaussian distribution in the mass-loss efficiency parameter (D'Cruz et al. 1996).
- ...M
![[*]](/icons/foot_motif.png)
- In principle,
 should give a more correct estimate of the spread in mass along the HB.
However, we preferred to use
should give a more correct estimate of the spread in mass along the HB.
However, we preferred to use  in our discussion for the reasons explained in Sect. 2.3, even
though in some cases it may systematically underestimate the mass
corresponding to stars with primordial He abundances
in our discussion for the reasons explained in Sect. 2.3, even
though in some cases it may systematically underestimate the mass
corresponding to stars with primordial He abundances
- ... short
![[*]](/icons/foot_motif.png)
- 47 Tuc actually contains a few very blue HB stars (Moehler
et al. 2000);
they make up
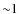 %
of the HB stars in the HST colour-magnitude diagram we are considering.
These stars are so rare that they do not affect our definition of
%
of the HB stars in the HST colour-magnitude diagram we are considering.
These stars are so rare that they do not affect our definition of 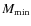 ,
which excludes the lowest 5% of the distribution. Indeed, this
case underlines that there most likely are stars at the extremes of the
HB whose origin is not related to their extreme values of the
He abundance.
,
which excludes the lowest 5% of the distribution. Indeed, this
case underlines that there most likely are stars at the extremes of the
HB whose origin is not related to their extreme values of the
He abundance.
- ... stars
![[*]](/icons/foot_motif.png)
- We thank A. F. Marino for providing the unpublished data for the individual stars in NGC 6656.
- ... ad hoc
![[*]](/icons/foot_motif.png)
- After the first draft of this paper was written, Lane et al. (2010) suggested that 47 Tuc might have formed by the merging of a binary cluster. This suggestion comes from a completely different line of thought, being based on the internal kinematics. As mentioned in the previous section, it is possible to speculate on a possible connection between such an origin of 47 Tuc and its anomalously short HB.
- ... required
![[*]](/icons/foot_motif.png)
- The scenario we propose should of course not only explain
the Milky Way GCs, but e.g., those of Fornax
(Buonanno et al. 1998).
This case is quite puzzling, since clusters 1, 3,
and 5 are nearly coeval, and have similar metallicity, and
still have very different HB's. We did not quantify these variations in
terms of mean colours and magnitudes as done for the Milky Way
GCs considered in the present paper, hence we cannot provide any
quantitative analysis. We only note that the ranking of HBR ratios for
the three coeval clusters of similar metallicity (1, 3,
and 5: -0.2, 0.50, and 0.44) is the same as the ranking in
absolute magnitude
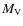 (-5.32, -7.66, -6.82). A quantitative analysis is required to
settle this issue.
(-5.32, -7.66, -6.82). A quantitative analysis is required to
settle this issue.
All Tables
Table 1:
Basic parameters for globular clusters considered in this paper (
![]() and
and
![]() are in solar masses).
are in solar masses).
Table 2: Photometric data from the HST-snapshot (Piotto et al. 2002).
Table 3: Photometric data from ground-based data (Rosenberg et al. 2000a,b).
Table 4: Intrinsic HB photometric parameters for GCs with HST data.
Table 5: Intrinsic HB photometric parameters for GCs with ground-based data.
Table 6: Masses on HB for GCs with HST data.
Table 7: Masses on HB for GCs with ground-based data.
Table 8: Properties of the RR Lyrae variables for each cluster.
Table 9: Comparison of median and maximum masses with the masses for RR Lyrae variables derived by Di Criscienzo et al. (2004).
Table 10:
Clusters' ages from main sequence fitting and from HB both for HST and ground based data-set.
![]() is given in Table 12.
is given in Table 12.
Table 11: R' parameter as derived from both HST and ground based data (note the different definition with respect to the usual R parameter).
Table 12: Spread in He and mass required explaining the HB.
Table 13: Minimum and maximum values for [Na/Fe] and [O/Fe] (see text for references).
All Figures
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig1.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg20.png)
|
Figure 1: Observed CMD for NGC 5904. RGB and HB stars are marked with red and blue points, respectively, while the green boxes represent the selection region of each component. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig2.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg21.png)
|
Figure 2:
Comparison between the number of HB and RGB stars that are within |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{12572fig3.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg24.png)
|
Figure 3:
Two examples of the application of the statistical field subtraction used in this paper ( top: NGC 3201; bottom: NGC 6779); both cases are based on ground-based photometry. The left panels give the original photometry; the central panels
give the CMD of field stars appropriate for the direction and reddening
of the GCs, from the TRILEGAL model of the Milky Way (Girardi
et al. 2005; Vanhollebeke et al. 2009); the right panels are the field-subtracted HB (red points) and RGB (blue points). The RGB stars are only those within |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig4.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg42.png)
|
Figure 4:
Run of (B-V)
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig5.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg43.png)
|
Figure 5: Median and extreme colours as a function of metallicity for clusters observed with HST. Filled (red) triangles and (blue) dots indicate GCs older and younger than a relative age parameter of 0.92, respectively; clusters for which an age estimate is not available are marked with (black) empty squares. Points representing a few interesting clusters are marked. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig6.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg44.png)
|
Figure 6: Same as Fig. 5 but for ground-based sample. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig7.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg45.png)
|
Figure 7: Median colours versus HBR ratio for HST ( upper panel) and ground-based ( lower panel) clusters. Different symbols denote different ages (see Fig. 5). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig8.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg46.png)
|
Figure 8:
Run of minimum colours and maximum magnitudes with the maximum temperatures
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig9.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg76.png)
|
Figure 9: Differences between maximum and minimum masses along the HB, compared to differences between median and minimum masses, for clusters observed with HST. Filled (red) triangles and (blue) dots indicate GCs older and younger than a relative age parameter of 0.92, respectively; clusters for which an age estimate is not available are marked with (black) empty squares. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{12572fig10.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg88.png)
|
Figure 10: Median and minimum masses vs. [Fe/H] for HST and ground based samples. Symbol legend is given in Fig. 5. A few points relative to interesting clusters are marked. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{12572fig11.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg93.png)
|
Figure 11: Median mass loss as a
function of metallicity for GCs older (triangles) and younger (dots)
than 0.92. The solid line is the best-fit relation to the HST
data, while the dashed one is just shifted by 0.02 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig12.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg99.png)
|
Figure 12: RR Lyrae richness parameter, S(RR), as a function of the RR Lyrae fraction for both HST (upper panel) and ground-based sample (lower panel). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=11.9cm,clip]{12572fig13.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg110.png)
|
Figure 13: Median mass and age as function of metallicity; different symbols in this case are for GCs with different RR Lyrae fractions (black: f(RR) > 0.10, grey: 0.04 < f(RR) < 0.10) and HBR ratios (blue triangles: HBR > 0, red squares: HBR < 0). The shaded area is the strip containing GCs rich in RR Lyrae. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig14.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg113.png)
|
Figure 14: Comparison of ages derived from HB for HST and ground-based samples. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig15.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg114.png)
|
Figure 15:
Comparison of ages from HB and from main sequence for both HST and
ground based samples; filled squares and circles are GCs with |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig16.ps}\vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg115.png)
|
Figure 16: Dereddened HST CMDs for stars on the HB of NGC 6934 and NGC 1904. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig17.ps}
\vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg116.png)
|
Figure 17: Comparison of ages from HB and from main sequence for the whole sample (HST+ground based); typical error bars are shown at bottom right corner of each panel. The thick (black) arrows show the impact of a 0.02 variation in the assumed He content, while the thin (red) ones represent the consequence of a 0.1 dex error in [Fe/H]. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig18.ps}\vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg117.png)
|
Figure 18: Age-metallicity relation for different groups of globular clusters: outer halo clusters (green pentagons), inner halo clusters (blue circles), disk/bulge clusters (red squares). Magenta circles are GCs associated with dSphs. Different symbol sizes are used for clusters of different luminosity. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig19.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg127.png)
|
Figure 19: The R' values plotted against the R values from Salaris et al. (2004); filled and empty squares are for GCs with [Fe/H] larger and smaller than -1.0 dex, respectively. Note the different definitions of R' and R (see text). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig20.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg128.png)
|
Figure 20: The R' values plotted against [Fe/H]; filled and open symbols are GCs with or without age estimate, respectively. The solid lines correspond to Y=0.225, 0.250, 0.275. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig21.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg129.png)
|
Figure 21:
The values of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig22.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg132.png)
|
Figure 22:
Observed CMDs for NGC 4833 and NGC 5024 ( upper panels) and synthetic diagrams lower panels), obtained with a Gaussian-like distribution mass loss with standard
deviation of 0.02 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig23.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg133.png)
|
Figure 23: Cumulative distribution of (B-V) colours from colour-magnitude (dashed) and synthetic (solid) diagrams for NGC 5024 and NGC 4833; the resulting probabilities from Kolmogorov-Smirnov (KS) test are also shown. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig24.ps}\vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg134.png)
|
Figure 24:
Same as Fig. 22, but for the GCs NGC 6171 and NGC 6723. The
synthetic diagrams ( lower panels) were obtained with a Gaussian-like distribution
mass loss with standard deviation of 0.03 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig25.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg135.png)
|
Figure 25: As for Fig. 23, cumulative distributions and KS values for NGC 6171 and NGC 6723. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig26.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg137.png)
|
Figure 26:
Absolute magnitudes ( |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12572fig27.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg151.png)
|
Figure 27:
Absolute magnitudes vs.
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12572fig28.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg170.png)
|
Figure 28:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12572fig29.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg176.png)
|
Figure 29:
Run of [Na/Fe]
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12572fig30.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg177.png)
|
Figure 30: Run of [Na/Fe] vs. [O/Fe] expected for different values of dil from our dilution model. The insert shows the run of [Na/Fe] with [O/Fe] for stars in our FLAMES survey (Carretta et al. 2009a). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12572fig31.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa12572-09/Timg179.png)
|
Figure 31:
Run of |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\begin{displaymath}%
(B-V)_{\rm RGB,0} = 1.235 + 0.4397~{\rm [Fe/H]} + 0.0927~{\rm [Fe/H]}^2,
\end{displaymath}](/articles/aa/full_html/2010/09/aa12572-09/img40.png)
![\begin{displaymath}%
(V-I)_{\rm RGB,0} = 1.154 + 0.2066~{\rm [Fe/H]} + 0.0400~{\rm [Fe/H]}^2
\end{displaymath}](/articles/aa/full_html/2010/09/aa12572-09/img41.png)