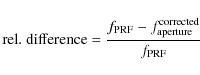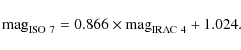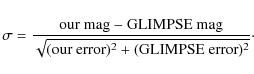Galactic bulge giants: probing stellar and galactic evolution

S. Uttenthaler; M. Stute; R. Sahai; J. A. D. L. Blommaert; M. Schultheis; K. E. Kraemer; M. A. T. Groenewegen; S. D. Price

doi:10.1051/0004-6361/200912232

Free Access

Issue		A&A Volume 517, July 2010


Article Number		A44
Number of page(s)		15
Section		Catalogs and data
DOI		https://doi.org/10.1051/0004-6361/200912232
Published online		03 August 2010

A&A 517, A44 (2010)

I. Catalogue of Spitzer IRAC and MIPS sources

S. Uttenthaler¹ - M. Stute^2,3,4 - R. Sahai² - J. A. D. L. Blommaert¹ - M. Schultheis⁵ - K. E. Kraemer⁶ - M. A. T. Groenewegen⁷ - S. D. Price⁶

1 - Instituut voor Sterrenkunde, K. U. Leuven, Celestijnenlaan 200D, 3001 Leuven, Belgium
2 - Jet Propulsion Laboratory, California Institute of Technology, 4800 Oak Grove Drive, Pasadena, CA 91109, USA
3 - IASA and Section of Astrophysics, Astronomy and Mechanics, Department of Physics, University of Athens, Panepistimiopolis, 157 84 Zografos, Athens, Greece
4 - Dipartimento di Fisica Generale ``A. Avogadro'', Universita degli Studi di Torino, via Pietro Giuria 1, 10125 Torino, Italy
5 - Observatoire de Besançon, 41bis avenue de l'Observatoire, 25000 Besançon, France
6 - Air Force Research Laboratory, Space Vehicles Directorate, 29 Randolph Rd., Hanscom AFB, MA 01731, USA
7 - Royal Observatory of Belgium, Ringlaan 3, 1180 Brussels, Belgium

Received 30 March 2009 / Accepted 15 January 2010

Abstract
Aims. We aim at measuring mass-loss rates and the luminosities of a statistically large sample of Galactic bulge stars at several galactocentric radii. The sensitivity of previous infrared surveys of the bulge has been rather limited, thus fundamental questions for late stellar evolution, such as the stage at which substantial mass-loss begins on the red giant branch and its dependence on fundamental stellar properties, remain unanswered. We aim at providing evidence and answers to these questions.
Methods. To this end, we observed seven $15\times15$ arcmin² fields in the nuclear bulge and its vicinity with unprecedented sensitivity using the IRAC and MIPS imaging instruments on-board the Spitzer Space Telescope. In each of the fields, tens of thousands of point sources were detected.
Results. In the first paper based on this data set, we present the observations, data reduction, the final catalogue of sources, and a detailed comparison to previous mid-IR surveys of the Galactic bulge, as well as to theoretical isochrones. We find in general good agreement with other surveys and the isochrones, supporting the high quality of our catalogue.

Key words: Galaxy: bulge - galaxies: stellar content - infrared: stars - stars: late-type - stars: mass-loss - stars: AGB and post-AGB

1 Introduction

The Galactic bulge (GB), an important dynamical and morphological component of our Galaxy, offers an environment distinct from the Galactic disk for study of stellar populations, stellar evolution, and the mass-loss processes that accompany and, in the end, control the last. Understanding and calibrating the physical processes whereby mass ejected by evolved stars into the bulge environment is recycled back into new generations of stars requires a statistical knowledge of mass loss as a function of fundamental stellar parameters in this region. Because of the limited sensitivity of previous surveys of the bulge, fundamental questions for late stellar evolution, such as the stage at which substantial mass-loss begins on the red giant branch (RGB), and its dependence on fundamental stellar properties, remain unanswered. The GB is an ideal laboratory for addressing these issues, providing a very large sample of stars at an almost identical distance.

We therefore observed seven $15\times15$ arcmin² fields that sample a range of distances from the Galactic centre with unprecedented sensitivity using the Infrared Array Camera (IRAC; Fazio et al. 2004) and the Multiband Imaging Photometer for Spitzer (MIPS; Rieke et al. 2004), the imaging instruments on-board the Spitzer Space Telescope (Werner et al. 2004), in order to determine mass-loss rates and luminosities of a statistically large sample of stars at several galactocentric radii. These data enable us to detect stars with very low mass-loss rates through their infrared excess, determine the dependence of the mass-loss rate on luminosity and effective temperature along the giant branches, and conduct a census of mass-losing stars at different rates. The observations, together with existing studies that probe higher mass-loss rate stars, will enable us to infer the total rate of mass loss in the bulge, a key input to evolutionary models of the bulge. The data have already led to the discovery of mid-IR $\log P$ vs. magnitude relations (Glass et al. 2009). In this paper we present the observations, the data reduction, and the source catalogue. We also compare the data to previous mid-IR surveys of the bulge and to theoretical isochrones.

The outline of this paper is as follows. In Sect. 2, we describe the observations, the data reduction, the different steps of point source extraction, and how the catalogues were created. We then proceed in Sect. 3 with checking our photometric data against other mid-IR surveys of the Galactic bulge. Further checks are presented in Sect. 4, where colour-magnitude diagrams (CMDs) are compared to theoretical isochrones. Finally, Sect. 5 draws conclusions on the catalogues and the data quality.

2 Observations and data reduction

2.1 Field selection and observations

The locations of the observed fields were chosen to sample the bulge on a variety of scales, to measure how the mix of stellar populations varies with Galactic latitude. They were also chosen to avoid the relative intense, saturating emission from near the Galactic plane. Our innermost fields are within the central stellar cusp, which presumably contains stars of various ages (c.f. Blum et al. 2003; Figer et al. 2004). Because the stars within this domain are believed to have formed within the central molecular zone and then to have diffused into an increasingly thicker distribution as a result of scattering off molecular clouds (Kim & Morris 2001), we expect a vertical segregation of stellar ages. Thus, inasmuch as the luminosities and mass-loss rates of red giants and asymptotic giant branch (AGB) stars depend on their masses, hence their ages, the radial distributions of the different kinds of evolved stellar objects can be used to model the star formation and dynamical history of this region.

$\begin{figure} \par\includegraphics[width=8cm,clip]{12232fg1.ps} \end{figure}$	Figure 1: Map of the seven fields observed in this campaign with the labels used throughout this paper.
Open with DEXTER

Table 1: Main characteristics of the seven fields towards the GB observed with Spitzer as part of programme 2345.

Two fields were selected to sample the nuclear bulge at $(l,b)=(0\hbox{$.\!\!^\circ$ }00,-1\hbox{$.\!\!^\circ$ }00)$ and $(l,b)=(0\hbox{$.\!\!^\circ$ }63,-0\hbox{$.\!\!^\circ$ }36)$ , namely N 1 and N 2, both of which were observed by ISOGAL (project for imaging part of the Galaxy using ISO, the Infrared Space Observatory; Omont et al. 2003) at 7 and 15 $\mu$ m. Five fields were selected beyond the nuclear bulge in areas where they overlap the Optical Gravitational Lensing Experiment III (OGLE-III; Udalski et al. 2000) micro-lensing survey. Four of these are located below the Galactic plane along a radial vector that subtends the minor axis of the Galaxy at an angle of about 13 $.\!\!^\circ$ 5, and terminates at the well-studied field in Baade's window at $(l,b)=(1\hbox{$.\!\!^\circ$ }03,-3\hbox{$.\!\!^\circ$ }83)$ , containing the globular cluster NGC 6522 (e.g. Glass et al. 1999). The three fields inside this are located at $(l,b)=(0\hbox{$.\!\!^\circ$ }30,-1\hbox{$.\!\!^\circ$ }42)$ , $(0\hbox{$.\!\!^\circ$ }56,-2\hbox{$.\!\!^\circ$ }23)$ , and $(0\hbox{$.\!\!^\circ$ }76,-3\hbox{$.\!\!^\circ$ }07)$ . The fifth field is positioned above the plane at $(l,b)=(2\hbox{$.\!\!^\circ$ }87,0\hbox{$.\!\!^\circ$ }35)$ . All fields are approximately rectangular in right ascension (RA) and declination (Dec) coordinates. Figure 1 shows the location of the seven observed fields with respect to the Galactic centre, and Table 1 summarises some of their main characteristics. The range in RA and Dec (J2000) given in Table 1 refers to where there is full overlap between MIPS and all four IRAC bands. Particularly in IRAC we do have some coverage outside the given range.

Observations of the GB fields were performed using the IRAC instrument in all four channels at 3.6, 4.5, 5.8, and 8.0 $\mu$ m, and the MIPS instrument in the 24 $\mu$ m channel on board the Spitzer Space Telescope within the programme 2345. Bulge field N 2 was observed only with MIPS in our programme, because this field was covered by IRAC observations within the general observer (GO) programme 3677 (principal investigator: Stolovy; Ramírez et al. 2008). The IRAC observations were carried out on 2005 March 30 and 31, and the MIPS observations between 2005 April 08 and 13.

With IRAC, observations were done in the full-array read out-mode, one frame per pointing with 2 s integration time per frame - the shortest full-array integration time was used to minimise the effects of saturation and resulting latency problems. The mapping was done in a $6\times6$ rectangular grid with step size 260 $^{\prime\prime}$ , with five dither positions, and a medium scale factor, giving a total exposure time of 10 s per pixel. The MIPS observations were obtained using the photometry/raster mode with 10 s integration time and full-array read-out mode, $3 \times 3$ rectangular grid and two cycles, giving a total integration time of 331 s per pixel.

The fields of view of IRAC channels 1 and 3, 2 and 4, as well as MIPS did not fully overlap. Nevertheless, the MIPS field of view is fully contained in all four IRAC fields of view.

2.2 Data reduction

We corrected the IRAC basic calibrated data (bcd) files to mitigate artifacts such as muxbleed or column pulldown with the tools provided by Carey at the Spitzer Science Center (SSC). Post-bcd processing was then conducted on the corrected bcd files using the MOsaicker and Point source EXtractor (MOPEX) software and its subsystem APEX (version 18.2.0, Markovoz & Marleau 2005).

2.2.1 Step 1: point source detection and extraction

Before further processing, mosaics were created by MOPEX for each field and channel from the corrected bcd frames. In this step, the pipeline interpolates the input images onto the output grid, taking geometric distortion into account. An outlier detection scheme flags bad pixels and any pixels affected by cosmic ray hits or moving objects, and these pixels are re-computed before co-addition. Finally, the interpolated images are co-added to one mosaic image. After mosaicking, APEX determines the background by calculating the median in a $45\times45$ pixel box around each pixel, and subtracts it from the image. These background-subtracted images were used in the detection step. Then, background fluctuations in the images were estimated and noise images derived, which were used for signal-to-noise ratio (SNR) estimation and the generation of point source probability images. With those, the detection table was compiled. We chose a detection threshold of $2.3 \sigma$ above the background. We used both the point response function (PRF) fitting capability and the aperture photometry functionality with circular apertures with radii of 2, 3, and 4 pixels. Larger apertures were not applicable owing to the crowding in the fields. The tiles used for PRF fitting also had to be chosen to be very small ( $3 \times 3$ pixels). We used the most up-to-date mean PRFs as provided by the SSC, and set the PRF normalisation radius accordingly.

$\begin{figure} \par\includegraphics[width=8cm,clip]{12232fg2_1.ps}\\ [1.3mm] \in... ...] \includegraphics[width=8.25cm,clip]{12232fg2_3.ps} \vspace*{-2mm} \end{figure}$

Figure 2:

Comparison of the fluxes resulting from PRF fitting and aperture photometry for the IRAC 1 observations of the NGC 6522 field. Top: PRF fitting fluxes and aperture photometry for the aperture with a radius of 2 pixels; middle: the same as top panel, but for the aperture with a radius of 3 pixels; bottom: relative difference between the measured fluxes (3 pixels aperture radius) versus the PRF flux for all sources. The dotted lines in the bottom panel mark relative differences of $\pm$ 7%. In the upper and middle panels, the dashed line is a linear least squares fit to the sources with $\chi ^{2} < 5$ , and the solid horizontal and vertical lines mark the lower and saturation limits of Table 2 used for quality grade labelling.

Open with DEXTER

The measured $\chi^2$ values in our data seem to be very high, even for successfully fitted sources, e.g. in the least-crowded field NGC 6522, they are between 2.5 and 3.3 in the IRAC channels 1 and 2, between 1.4 and 1.8 in IRAC 3, and only in IRAC 4 at the perfect value of 1. This may stem from confusion noise, which is not included in the provided uncertainty images and/or from the high source density. Confusion noise is created by the amplitude variations from PRFs of closely spaced sources (Hacking & Houck 1987; Rieke et al. 1995). Modelling the confusion noise has not improved the resulting $\chi^2$ values. This has consequences for the reliability of automatic de-blending procedures, which were not working properly in this field. We thus had to disable the active and passive de-blending capabilities of APEX (see Appendix A).

In all MIPS fields, we first detected bright sources, removed the Airy rings of these sources to do the source detection on the residual images, and performed the point source extraction on the original images. The southern half of the field N 2 has strong diffuse emission. In that area, the detection threshold is certainly higher than in areas with low diffuse background emission, as is also evident from the histograms of magnitudes in Appendix B.

2.2.2 Step 2: assigning quality grades to the sources

Three different effects can be seen when plotting the flux obtained by PRF fitting versus that found with aperture photometry for all the extracted sources (Fig. 2). The first effect is present when we use a large aperture with a radius of 3 or 4 pixels. At very low PRF fluxes, there are several sources that show disproportionately large aperture fluxes, i.e. are above the dashed line. These sources are faint sources close to a bright source. In case of the larger aperture, we therefore already get a significant contribution in the aperture from the bright source. The second effect is relevant for some bright sources, whose PRF fluxes are smaller than the aperture fluxes. These sources are super-saturated; i.e., the radial intensity profile has a dip in the centre and so it shows a double peak structure. In a few cases, depending on the depth of the central valley, these two peaks are identified as two individual sources that are each fitted with a fainter PRF; i.e., both sources lie above the dashed line. In other cases, the fitted PRF ends up with a central flux between that of the central valley and that of the wings, meaning PRF fitting underestimates the total flux, so these sources are also shifted to the left in Fig. 2.

The SSC homepage provides values of the maximum flux of unsaturated point sources as a function of integration time. Table 2 presents the flux values interpolated to a frame exposure time of 1.2 s, along with a lower flux limit. This lower flux limit was adopted on subjective grounds for the quality grade labelling (see below). We thus have to be cautious with sources brighter than about 320 mJy in IRAC 1. Consistent with this warning is a third slight effect that seems to set in at fluxes close to this value and affects all brighter sources: the PRF fluxes increase disproportionately compared to the aperture fluxes, leading to a bending to the right, away from the dashed line in Fig. 2 (top). Aperture photometry thus measures the saturated plateau of the PRF, while PRF fitting seems to ignore the missing flux that would be present beyond the plateau and fits the wings. The individual source then lies below the dashed line, with a larger PRF flux than the aperture flux.

If dividing the aperture flux by the linear least squares fit to sources with $\chi ^{2} < 5$ , the fluxes measured with both ways are almost identical for many of the sources with $\chi ^{2} < 5$ . The slope of this fit is not the aperture correction factor, to be derived in Sect. 2.2.3. Except for the sources affected by the three aforementioned effects, the relative difference calculated as

$\begin{displaymath}{\rm rel.\ difference} = \frac{{f}_{\rm PRF} - {f}_{\rm aperture}^{\rm corrected}}{{f}_{\rm PRF}} \end{displaymath}$

(1)

scatters around 7% (Fig. 2, bottom). The superscript ``corrected'' in Eq. (1) indicates that the aperture flux has been divided by the linear fit to sources with $\chi ^{2} < 5$ . Sources that are within this range are considered as quality grade A. This test is performed first, therefore grade A sources span the whole range of fluxes, from faint to almost saturated sources.

Faint sources with fluxes smaller than a certain lower limit (Table 2) and outside the 7% range are classified as quality grade B. Sources whose fluxes are above the saturation limit are classified as quality grade C. They would have to be treated differently with dedicated tools. However, since these sources are probably mostly foreground stars, they are not of prime interest to the science goals, thus we decided not to invest more time in their flux determination. The interested reader is invited to download and analyse the mosaics, which will be made available as on-line material at the Centre de Données astronomiques de Strasbourg (CDS).

Sources that failed all of the above criteria are classified as quality grade D. These are blended sources for which the PRFs overlap such that even the aperture with the smallest radius includes both peaks; i.e., no reliable flux measurement is available for these sources. This effect is the same as the first one mentioned above related to the larger aperture with a radius of 3 pixels or larger.

The statistics of grades for all seven fields and all five bands are given in Table 3. The percentage given for grades A and B is relative to the total number of sources in the catalogue for the respective field that is given in the last column. The seventh column gives the number of sources not detected in the respective channel, but detected in at least one of the other bands plus in the reference catalogues (see Sect. 2.2.4).

2.2.3 Step 3: determination of the aperture corrections

Since we do not use a larger aperture to estimate the background, which would give unreliable photometry in the crowded fields, but do aperture photometry on the background-subtracted images instead, the aperture corrections are expected to be different from the standard values given in the instrument handbooks.

To derive aperture corrections, we created point spread functions with stinytim2.0 (Krist 2006) for all five bands. We then inserted artificial sources with known flux in our mosaicked, background-subtracted images and compared the resulting fluxes given by APEX with the initial fluxes with which we had created the sources. The slope of a linear least squares fit to the initial vs. measured flux gives the aperture correction factors. The derived aperture corrections for the aperture with two pixels radius are given in Table 4, along with their statistical error as derived from the linear fit. Also given in the table are the values as recommended by the SSC, for a 2 pixel radius on source and a 10-20 pixel radius background annulus in the case of IRAC, and a 3 $.\!\!^{\prime\prime}$ 5 on source aperture without any background annulus in the case of MIPS. The SSC recommended values are not directly comparable to our aperture correction factors, so they are only given for illustrative purposes. Despite the high value of the aperture correction factor for MIPS 24, we adopted the small aperture with 2 pixels radius because i) our observations are not photon noise limited, thus a larger aperture would not reduce the error estimate; ii) there is a ``population'' of blended sources whose flux increases disproportionally with growing aperture because more of the neighbouring source's flux is measured with larger aperture; iii) the SSC lists aperture corrections for an even smaller aperture, so our value is not an extreme. We also corrected the PRF fluxes with the photometric correction factors as recommended by the SSC.

Table 2: Flux limits applied for assigning quality grades.

Table 3: Statistics of sources with their grades for all seven fields and five bands.

Besides the aperture correction and the photometric correction for the PRF fluxes, we did not apply any other correction factors such as the colour correction. According to the IRAC data handbook, the colour correction factor for blackbody spectra with temperatures between 2000 and 5000 K is around 1%, except for IRAC 4, where it can reach as much as 2.7% for the hotter stars. Since the colour correction is small and we do not know a priori the nature and spectrum of our objects, we did not apply these corrections.

2.2.4 Step 4: creating the point source catalogue

We finally decided to adopt only the PRF fluxes for the final catalogue on the basis of comparison with other catalogues and with isochrones in CMDs. With this choice, we find, on the one hand, slightly better agreement with other catalogues, and on the other, somewhat reduced scatter at the faint end of CMDs. See Sects. 3 and 4 for a comparison with other catalogues and isochrones.

The last step is the cross-identification, for each field, of the extraction tables of all five bands among each other and with other reference catalogues. As reference catalogues we adopt the Deep Near Infrared Survey (DENIS; Epchtein et al. 1997), the 2 Micron All Sky Survey (2MASS; Skrutskie et al. 2006), the Midcourse Space Experiment (MSX) catalogue, and the Infra-Red Astronomical Satellite (IRAS) point source catalogue. We applied the following criteria to include a source in the final catalogue. We identified individual sources by their RA and Dec position and allowed for an error margin of 1 $.\!\!^{\prime\prime}$ 6, i.e. slightly more than one pixel size, for the cross-identification among our five bands. Sources that are detected in at least two of our five bands are included in any case in the final catalogue. A cross-identification is made for these sources with a search radius of 3 $.\!\!^{\prime\prime}$ 0 with DENIS and 2MASS, and 30 $.\!\!^{\prime\prime}$ 0 for identification with an MSX or IRAS counterpart. The information about these counterparts is included in the catalogue. Sources that are detected in only one of our five bands are only included in the final catalogue if they also have a counterpart in at least one of the reference catalogues, with the same search radii applied as for the sources with two or more Spitzer detections. This procedure was followed to include as many of the sources in the final catalogue that were only detected in MIPS 24. These might very well be real objects, albeit extremely red (i.e. not detected with IRAC). Additionally, by following this procedure, more of the sources that are located in the areas that are not sampled by all five bands will be included in the catalogue. These areas are also included in the final catalogue. The least reliable sources in our catalogue are those with detection in only one IRAC band and no MIPS detection, and with: (i) either no 2MASS and DENIS counterpart (depending on the field, between 3.1% and 6.7% of the sources); or (ii) a DENIS and 2MASS counterpart at a distance between 1.6 and 3 arcsec (depending on the field, between 0.4% and 1.0% of the sources).

Table 4: Aperture correction factors.

Table 5 gives ten lines of the band-merged catalogue of the Bulge N 1 field as an example. The entire table will be made available for download from CDS. A portion is shown here for guidance regarding its form and content.

Table 5: Sample table of the band-merged catalogue of the N 1 field.

The columns of our point source catalogue are explained as follows.

Column 1:: Source identification, IAU-conform identifier.
Column 2:: Right ascension in degrees (J2000).
Column 3:: Declination in degrees (J2000).
Column 4:: PRF flux in IRAC 1 (in $\mu$ Jy), set to ``-9.99999e+99'' if not detected.
Column 5:: PRF flux in IRAC 2 (in $\mu$ Jy), set to ``-9.99999e+99'' if not detected.
Column 6:: PRF flux in IRAC 3 (in $\mu$ Jy), set to ``-9.99999e+99'' if not detected.
Column 7:: PRF flux in IRAC 4 (in $\mu$ Jy), set to ``-9.99999e+99'' if not detected.
Column 8:: PRF flux in MIPS 24 (in $\mu$ Jy), set to ``-9.99999e+99'' if not detected.
Column 9:: Quality flags of the IRAC 1, 2, 3, 4, and MIPS 24 channels (see Sect. 2.2.2), set to ``-'' if not detected.
Column 10:: Uncertainty of the PRF flux in IRAC 1 (in $\mu$ Jy), set to ``-9.99999e+99'' if not detected.
Column 11:: Uncertainty of the PRF flux in IRAC 2 (in $\mu$ Jy), set to ``-9.99999e+99'' if not detected.
Column 12:: Uncertainty of the PRF flux in IRAC 3 (in $\mu$ Jy), set to ``-9.99999e+99'' if not detected.
Column 13:: Uncertainty of the PRF flux in IRAC 4 (in $\mu$ Jy), set to ``-9.99999e+99'' if not detected.
Column 14:: Uncertainty of the PRF flux in MIPS 24 (in $\mu$ Jy), set to ``-9.99999e+99'' if not detected.
Column 15:: Observation flag. The first four bits state if the position of the source was in the field of view of the IRAC bands (``1'') or not (``0''), the fifth bit is for MIPS 24.
-
Column 16:: Distance to closest DENIS source (arcsec; only < $3\hbox{$.\!\!^{\prime\prime}$ }0$ ), set to ``-'' if no counterpart.
Column 17:: DENIS I-band magnitude, set to ``-'' if no counterpart or the counterpart has no I-band measurement.
Column 18:: DENIS J-band magnitude, set to ``-'' if no counterpart or the counterpart has no J-band measurement.
Column 19:: DENIS K-band magnitude, set to ``-'' if no counterpart or the counterpart has no K-band measurement.
-
Column 20:: Distance to closest 2MASS source (arcsec; only < 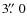$3\hbox{$.\!\!^{\prime\prime}$ }0$ ), set to ``-'' if no counterpart. Only sources with quality flags A, B, C, or D in at least one 2MASS filter have been considered.
Column 21:: 2MASS J-band magnitude, set to ``-'' if no counterpart within 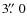$3\hbox{$.\!\!^{\prime\prime}$ }0$ was found, or ``-9.999'' if the counterpart has no measured J-band magnitude available or too low quality flag.
Column 22:: 2MASS H-band magnitude, set to ``-'' if no counterpart within 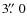$3\hbox{$.\!\!^{\prime\prime}$ }0$ was found, or ``-9.999'' if the counterpart has no measured H-band magnitude available or too low quality flag.
Column 23:: 2MASS K-band magnitude, set to ``-'' if no counterpart within 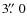$3\hbox{$.\!\!^{\prime\prime}$ }0$ was found, or ``-9.999'' if the counterpart has no measured K-band magnitude available or too low quality flag.
Column 24:: 2MASS quality flags, set to ``-'' if no counterpart or too low quality flag.
-
Column 25:: Distance to closest IRAS source (arcsec; only < 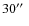$30\hbox{$^{\prime\prime}$ }$ ), set to ``-'' if no counterpart. Only sources with quality flags 2 or 3 in at least one IRAS band have been considered.
Column 26:: IRAS 12 $\mu$ m flux (Jy), set to ``-'' if no counterpart, and to ``-9.9e+99'' if the counterpart has no measured flux in the 12 $\mu$ m band or too low quality flag.
Column 27:: IRAS 12 $\mu$ m quality flag, set to ``-'' if no counterpart or too low quality flag.
Column 28:: IRAS 25 $\mu$ m flux (Jy), set to ``-'' if no counterpart, and to ``-9.9e+99'' if the counterpart has no measured flux in the 25 $\mu$ m band or too low quality flag.
Column 29:: IRAS 25 $\mu$ m quality flag, set to ``-'' if no counterpart or too low quality flag.
Column 30:: IRAS 60 $\mu$ m flux (Jy), set to ``-'' if no counterpart, and to ``-9.9e+99'' if the counterpart has no measured flux in the 60 $\mu$ m band or too low quality flag.
Column 31:: IRAS 60 $\mu$ m quality flag, set to ``-'' if no counterpart or too low quality flag.
Column 32:: IRAS 100 $\mu$ m flux (Jy), set to ``-'' if no counterpart, and to ``-9.9e+99'' if the counterpart has no measured flux in the 100 $\mu$ m band or too low quality flag.
Column 33:: IRAS 100 $\mu$ m quality flag, set to ``-'' if no counterpart or too low quality flag.
-
Column 34:: Distance to closest MSX source (arcsec; only < 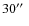$30\hbox{$^{\prime\prime}$ }$ ), set to ``-'' if no counterpart. Only sources with quality flags 2, 3, or 4 in at least one MSX band have been considered.
Column 35:: MSX B1 band flux (Jy), set to ``-'' if no counterpart, and to ``-9.999e+99'' if the counterpart has no measured flux in the B1 band or too low B1 band quality flag.
Column 36:: MSX B1 band quality flag, set to ``-'' if no counterpart or too low quality flag.
Column 37:: MSX B2 band flux (Jy), set to ``-'' if no counterpart, and to ``-9.999e+99'' if the counterpart has no measured flux in the B2 band or too low B2 band quality flag.
Column 38:: MSX B2 band quality flag, set to ``-'' if no counterpart or too low quality flag.
Column 39:: MSX A band flux (Jy), set to ``-'' if no counterpart, and to ``-9.999e+99'' if the counterpart has no measured flux in the A band or too low A band quality flag.
Column 40:: MSX A band quality flag, set to ``-'' if no counterpart or too low quality flag.
Column 41:: MSX C band flux (Jy), set to ``-'' if no counterpart, and to ``-9.999e+99'' if the counterpart has no measured flux in the C band or too low C band quality flag.
Column 42:: MSX C band quality flag, set to ``-'' if no counterpart or too low quality flag.
Column 43:: MSX D band flux (Jy), set to ``-'' if no counterpart, and to ``-9.999e+99'' if the counterpart has no measured flux in the D band or too low D band quality flag.
Column 44:: MSX D band quality flag, set to ``-'' if no counterpart or too low quality flag.
Column 45:: MSX E band flux (Jy), set to ``-'' if no counterpart, and to ``-9.999e+99'' if the counterpart has no measured flux in the E band or too low E band quality flag.
Column 46:: MSX E band quality flag, set to ``-'' if no counterpart or too low quality flag.

3 Comparison with other missions and catalogues

Our observations overlap with a number of other mid-IR surveys. These are:

1.: ISOGAL: Survey with the ISO Camera (ISOCAM) on-board the ISO satellite, combined with DENIS IJK_S photometry.
2.: Galactic Legacy Infrared Mid-Plane Survey Extraordinaire II (GLIMPSE-II), a Spitzer/IRAC survey of the area $\pm$ $1\hbox{$^\circ$ }$ around the Galactic plane and the Galactic centre (Benjamin et al. 2003).
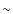
3.: GALactic CENtre (GALCEN), a Spitzer/IRAC survey of the inner 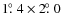$\sim$ $1\hbox{$.\!\!^\circ$ }4 \times 2\hbox{$.\!\!^\circ$ }0$ of the Galaxy (Ramírez et al. 2008).
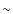
4.: A Spitzer/MIPS survey of the inner 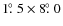$\sim$ $1\hbox{$.\!\!^\circ$ }5 \times 8\hbox{$.\!\!^\circ$ }0$ of the Galaxy (Hinz et al. 2008).

3.1 Comparison with ISOGAL

ISOGAL (Omont et al. 2003) is a survey with the ISOCAM instrument on-board the ISO satellite in two bands at 7 and 15 $\mu$ m, combined with $IJK_{\rm {S}}$ photometry from the DENIS project (Epchtein et al. 1997). The 7 $\mu$ m LW2 band of ISOCAM ( $\sim$ 5.0-8.5 $\mu$ m, central wavelength 6.75 $\mu$ m) overlaps in wavelength with the IRAC 4 channel ( $\sim$ 6.4-9.4 $\mu$ m, nominal wavelength 7.844 $\mu$ m; Hora et al. 2008). For IRAC 4, we have overlap with ISOGAL in the fields Bulge 2, Bulge 4, N 1, and NGC 6522. The number of sources in common (with less than $2\hbox{$.\!\!^{\prime\prime}$ }0$ positional offset) is 163 for Bulge 2, 335 for Bulge 4, 288 for N 1, and 264 in NGC 6522. We present here a brief comparison for the NGC 6522 field, because the ISO 7 $\mu$ m photometry goes deepest in that field (least crowding and diffuse background emission). The results for the other fields are very similar.

$\begin{figure} \par\includegraphics[width=8cm,clip]{12232fg3.ps} \end{figure}$	Figure 3: Magnitude difference between the Spitzer IRAC 4 band and the ISO 7 $\mu$ m LW2 band for 264 sources in common in the NGC 6522 field. The dotted line marks the identity relation, the dashed line is a linear least squares fit through the data points, excluding those sources fainter than 9 $.\!\!^{\rm m}$ 3 in either of the data sets to avoid Malmquist bias.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=13.8cm,clip]{12232fg4.ps} \end{figure}$	Figure 4: Magnitude differences between our and the GLIMPSE-II catalogue for the sources in common in the N 1 field. Sources with quality flag A in our catalogue are represented by black dots, all other quality flags by red dots.
Open with DEXTER

Figure 3 shows the magnitude difference between the Spitzer IRAC 4 band and the ISO LW2 band for the NGC 6522 field. The data points do not scatter randomly around zero. Rather, faint sources tend to be brighter in the ISO 7 $\mu$ m band, whereas bright sources tend to be brighter in the IRAC 4 band. The relation found to convert between the two bands is

$\begin{displaymath}\mbox{mag}_{\rm {ISO}~7} = 0.866 \times \mbox{mag}_{\rm {IRAC}~4} + 1.024. \end{displaymath}$

(2)

The slopes and zero points of this linear fit are similar for all fields, with a cross-over (Spitzer IRAC 4 equal to ISO 7 $\mu$ m magnitude) between $6\hbox{$.\!\!^{\rm m}$ }0$ and $7\hbox{$.\!\!^{\rm m}$ }7$ . The trend might be a reflection of a dependence of the strength of the SiO fundamental band at $\sim$ 7.5 $\mu$ m and/or a water band at $\sim$ 5.5 $\mu$ m on the brightness of the star. At least the SiO first overtone band at $\sim$ 4.0 $\mu$ m has been found to decrease in strength from semi-regular variables to Mira-like variables (Aringer et al. 1999). On top of that, instrumental effects in one or both missions cannot be excluded.

$\begin{figure} \par\includegraphics[width=13.8cm,clip]{12232fg5.ps} \end{figure}$	Figure 5: Distribution of sigma-factors (Eq. (3)) for all IRAC channels in the field N 1 in the magnitude range $7\hbox{$.\!\!^{\rm m}$ }0{-}10\hbox{$.\!\!^{\rm m}$ }0$ . The solid line is a Gaussian fit to the distribution. The dotted line indicates a Gaussian of width 1 and the same area under the graph, the ideal case of correctly estimated errors.
Open with DEXTER

3.2 Comparison with GLIMPSE-II

The Galactic Legacy Infrared Mid-Plane Survey Extraordinaire (GLIMPSE-II; Benjamin et al. 2003), is a Spitzer Legacy Science Programme of most of the inner Galactic disk using the IRAC instrument. Our programme has overlaps the GLIMPSE-II survey in the fields Bulge 1, Bulge 2, Bulge 4, and Bulge N 1. A comparison with this large data set is especially interesting because the same instrument and the same filter bands have been used, though the observing strategies and data reduction techniques are different.

In Fig. 4 we show the magnitude differences between our and the GLIMPSE-II catalogue for all four IRAC channels for the Bulge N 1 field, since there is a large number of sources in common in this field (31 191). These plots look very similar for the other fields with overlap.

In general, the agreement between our and the GLIMPSE-II catalogue is good in the bright to medium brightness range. However, at the faint end, starting at around $10^{\rm {m}}{-}11^{\rm {m}}$ , we notice a strong trend such that the magnitudes become increasingly fainter in our catalogue than in the GLIMPSE-II catalogue. This is not only true for the flag B sources (most of the red dots at faint magnitudes in Fig. 4), but also for flag A sources fainter than this magnitude limit, and for all filters. The same trend is revealed in a comparison between the GLIMPSE-II catalogue and the one of Ramírez et al. (2008, see next section). According to Babler of the GLIMPSE-II team (private communication, 2008), this trend at the faint magnitude limit arises because of GLIMPSE-II's limitation to ``single frame'' photometry. GLIMPSE-II does photometry only on single bcd frames instead of mosaics, because each patch of the sky is observed only twice. This strategy may cause a Malmquist bias, such that GLIMPSE-II magnitudes will be increasingly too bright the closer a source is to the faint limit. Thus, for sources at the faint limit, our magnitudes are likely more accurate than GLIMPSE-II magnitudes. Finally, we also notice some saturation effects above $\sim$ $6\hbox{$.\!\!^{\rm m}$ }5$ in IRAC 1, and a few sources that are significantly fainter in the GLIMPSE-II catalogue than in our catalogue that can be found at all magnitudes.

Due to the large number of sources in common with the GLIMPSE-II survey, we are able to check whether or not the combined errors are of realistic magnitude. To do so, we inspect the sigma-factor, which is also discussed in the aforementioned comparison between the GLIMPSE-II and Ramírez et al. (2008) catalogues:

$\begin{displaymath}\sigma = \frac{\rm {our~mag} - \rm {GLIMPSE~mag}}{\sqrt{(\rm {our~error})^2 + (\rm {GLIMPSE~error})^2}}\cdot \end{displaymath}$

(3)

If the combined errors are close to the magnitude differences, the sigma-factor will have a Gaussian distribution of width 1. If the errors are underestimated, the distribution will be broader than that and narrower if the error estimates are too large. Figure 5 displays the sigma distribution for all four IRAC channels for the field Bulge N 1, along with a Gaussian fit to the data. Also plotted is a Gaussian for a ``perfect'' distribution with the same area under the graph, i.e. when magnitude differences and combined error are on average of the same size ( $\sigma = 1$ ). The source selection was restricted to the magnitude range $7\hbox{$.\!\!^{\rm m}$ }0{-}10\hbox{$.\!\!^{\rm m}$ }0$ to avoid the tail of faint sources with a Malmquist bias (see above). We see that the distributions are centred on zero, but there is a surplus of negative sigma values, because of the sources with negative magnitude difference, as noted above. The actual distributions for IRAC 1 and 2 are only slightly broader than what would be expected if the errors were correctly estimated. This means that the combined errors for these channels are only slightly underestimated. For IRAC 3 and 4, the distributions are definitely broader than in the ideal case. For these channels we have to assume that the combined errors are underestimated by factor of 1.8 to 2.2. Indeed, our error estimates are on average smaller than the ones estimated by GLIMPSE-II, but this is mostly due to the longer exposure time per pixel in our survey, and we are doing the photometry on the mosaicked images. If we used two times the error as given by GLIMPSE-II in Eq. (3), the sigma distribution would have the perfect width of 1.0 for IRAC 1, would be slightly too narrow for IRAC 2 (too large errors), and would still be too broad for IRAC 3 and 4 (too small errors). We therefore conclude that our error estimates for IRAC 1 and 2 are probably only slightly too small, and too small by a somewhat larger amount for IRAC 3 and 4. The GLIMPSE-II errors, on the other hand, are probably correctly estimated for IRAC 1, slightly too large for IRAC 2, and slightly underestimated for IRAC 3 and 4. Table 6 summarises the width, centre, and peak values of the Gaussian fits to the sigma distributions of Fig. 5.

3.3 Comparison with Ramírez et al. (2008)

The overlap with the GALCEN survey of Ramírez et al. (2008) is limited to the Bulge N 1 field. The reason for this is that the Spitzer time allocation committee tried to avoid redundant observations of the same fields of sky within GO programmes (GLIMPSE-II, on the other hand, is a legacy survey). A comparison between our own and the GALCEN observations is useful, because for our N 2 field we will have to use the IRAC observations of GALCEN. Nevertheless, because IRAC channels 1 and 3 are seeing a patch of the sky neighbouring that of channels 2 and 4, we got a small overlap with Ramírez et al. (2008) in our Bulge N 1 field in order to fully sample that field in all bands. Adopting a stringent 1 $.\!\!^{\prime\prime}$ 0 search radius, there are 5172 sources in common in any one of the four IRAC bands. In the Bulge N 2 field, 337 sources detected with MIPS 24 have a counterpart in Ramírez et al. (2008), adopting a less stringent 3 $.\!\!^{\prime\prime}$ 0 search radius because of the less precise MIPS coordinates.

$\begin{figure} \par\includegraphics[width=14cm,clip]{12232fg6.ps} \end{figure}$	Figure 6: Magnitude differences between our photometry and that of Ramírez et al. (2008) for the small overlap in field N 1. Symbols as in Fig. 4.
Open with DEXTER

Figure 6 shows the magnitude differences found for the sources in common with Ramírez et al. (2008) in the Bulge N 1 field. The agreement in the IRAC 1 and 2 bands is very good. In the IRAC 3 band, the GALCEN magnitudes (of flag A sources in the medium brightness range $7\hbox{$.\!\!^{\rm m}$ }0{-}10\hbox{$.\!\!^{\rm m}$ }0$ ) are on average $\sim$ $0\hbox{$.\!\!^{\rm m}$ }05$ fainter than our magnitudes. In the IRAC 4 band, a ``knee'' appears for sources brighter than $8\hbox{$.\!\!^{\rm m}$ }2$ . Since the same effect is found in the aforementioned comparison between GLIMPSE-II and GALCEN data, the origin of this ``knee'' most probably comes from an underestimation of fluxes for sources brighter than $\sim$ $8\hbox{$.\!\!^{\rm m}$ }2$ in IRAC 4 by GALCEN. We will have to consider these differences between our IRAC photometry and that of Ramírez et al. (2008) when comparing the results for Bulge N 2 to those of other fields.

The differences between our reduction and that of GALCEN, on the one hand, and GLIMPSE-II, on the other, should be noted. While in our reduction the background is determined for each pixel in a $45\times45$ pixel box centred on that pixel and subtracted prior to the photometric measurements, GALCEN uses the local background determined by PRF fitting and subtracts it from the corresponding aperture flux of each detected source. For the fitting, PRFs pre-defined by the SSC are used. GALCEN uses the aperture corrections as recommended by the SSC, but adopts the PRF fluxes for their final catalogue (except for sources where the ratio between PRF flux and aperture flux exceeds 1.5; for those sources the aperture flux is adopted). We adopted the PRF flux in our catalogue, derived from the most recent mean PRFs provided by the SSC. GLIMPSE-II, on the other hand, performs photometry on individual bcd frames, not on mosaics. A combination of PRF fitting and aperture photometry called ``tweaking'' is used to measure the flux of a source. PRFs dynamically determined from each individual frame are fitted to the sources and subtracted from the image. On the residual image, aperture photometry was performed around the positions where PRFs had been subtracted in the previous step. If the resultant aperture flux is substantially positive or negative, the source has been under- or over-subtracted. This residual aperture flux is then subtracted from or added to the PRF flux to compensate for the under- or over-subtraction. However, tweaking was applied rather sparingly and only in the IRAC 1 and IRAC 2 bands of the GLIMPSE-II observations. These differences in reduction have to be kept in mind, just as for the comparison between GALCEN and GLIMPSE-II.

Table 6: Width, centre, and peak values of the sigma distributions.

3.4 Comparison of MIPS 24 measurements with Hinz et al. (2008)

A catalogue of Spitzer/MIPS 24 $\mu$ m sources towards the region of $\sim$ $1\hbox{$.\!\!^\circ$ }5 \times 8\hbox{$.\!\!^\circ$ }0$ around the Galactic centre has recently been presented by Hinz et al. (2008). With this survey, we have 371 sources in common (i.e. unique counterparts within a one physical pixel = 2 $.\!\!^{\prime\prime}$ 55 search radius) in our Bulge 4 field, 280 in the Bulge N 1 field, and 129 in the Bulge N 2 field. Thanks to the longer exposure time of our observations (331 s per pixel compared to 15 s per pixel in the fast scan mode used by Hinz et al.), our catalogue reaches much fainter flux levels.

For the N 1 field, we only have a small overlap with the survey of Hinz et al. (2008). In the N 2 field there is strong diffuse galactic emission, and a small fraction of the sources might actually be false detections. We thus concentrate on the Bulge 4 field for a comparison with the Hinz et al. (2008) catalogue. This is also the field with the most sources in common. In Fig. 7 we show the magnitude differences between our measurements and that of Hinz et al. (2008) as a function of the source magnitude in our catalogue. There might be a general offset of $\sim$ $0\hbox{$.\!\!^{\rm m}$ }15$ in the sense that our magnitudes are on average fainter, but the scatter is considerable. At least there seems to be no trend at the faint magnitude end.

As for the comparison with GLIMPSE-II, we also checked the error estimates of the MIPS 24 data by investigating the distribution of sigma-factors (Eq. (3)). The result of this exercise is that the combined errors are too small by a factor of six or more. Even adopting twice the error estimate of Hinz et al. (2008), which is somewhat larger than ours, instead of a combination of the errors, gives a sigma distribution that is wider by a factor of four than what is expected from a correct estimate. We thus conclude that the errors are still largely underestimated in both catalogues, and that the uncertainty due to crowding and strong background radiations renders a precise flux determination in the vicinity of the Galactic centre impossible. Some part of the found differences, however, may be explained by a real variability, since many of the bright sources are expected to be AGB variables in the bulge (Glass et al. 2009). At a wavelength of 20 $\mu$ m, a full amplitude of up to 0 $.\!\!^{\rm m}$ 7 is found for C-rich pulsating AGB variables in the solar neighbourhood (see e.g. Fig. 7 of Le Bertre 1992).

4 Colour-magnitude diagrams and comparison with theoretical isochrones

A final check on the quality of our data reduction are colour-magnitude diagrams (CMDs) in combination with theoretical isochrones. If the flux measurement has no systematic error (and also the isochrones are producing realistic colours), the observed giant branch will be described well by the isochrone. This check is restricted to the IRAC bands, since for many sources the MIPS 24 band will be affected by dust emission, which is very difficult to model accurately in isochrones. We chose to use the most recent isochrones from Marigo et al. (2008). A web-form can be used for computing these isochrones with different parameters. We computed an isochrone with an age of 10 Gyr, metallicity Z = 0.019 (solar metallicity), and no dust formation. In the mid-IR, the isochrones are not very sensitive to the precise choice of the parameters such as age, metallicity, and dust formation.

To disentangle possible systematic errors in the IRAC channels, we want to include a flux measurement that is independent of our reduction method in the comparison with the isochrone. Since all our fields are covered by 2MASS, which can be regarded as a reliable source of $K_{\rm {S}}$ magnitudes, we decided to construct dereddened $K_{\rm {S,0}}$ vs. $(K_{\rm {S}} - \rm {IRAC})_0$ CMDs.

Most of the fields towards the Galactic bulge suffer from strong extinction. Thus, it is necessary to correct the photometric measurements for this extinction before comparing them to the theoretical isochrone. Several extinction maps for the Galactic centre region have been published. Schultheis et al. (1999) derived the extinction from the shift of the giant branch in the $K_{\rm {S}}$ vs. $(J - K_{\rm {S}})$ CMD based on DENIS data. The extinction values published in that work are given in the V band. Another map of A_Vvalues towards fields in the Galactic bulge is presented by Sumi (2004). These are based on the extinction measured on red clump giants in fields of the OGLE-II survey (Udalski et al. 2000). Finally, the map of Dutra et al. (2003) uses the same technique as Schultheis et al. (1999) and applies it to 2MASS data. That map gives the reddening value in the $K_{\rm {S}}$ band. Its spatial resolution is lower than that of the other maps, but it is the only one that fully covers all of our Spitzer fields.

Table 7 summarises the coverage of our seven fields by these extinction maps, and the median extinction in the V band is given. The NGC 6522 field is the only one that is covered by all three extinction maps. Since this field also has the lowest extinction of all our Spitzer fields so that uncertainties in the extinction determination should play a minor role, it serves here as a ``fiducial'' field for the comparison with theoretical isochrones in CMDs. We used the average values for the diffuse inter-stellar medium determined by Indebetouw et al. (2005) for the extinction in the IRAC bands: $A_{K,\rm {S}} : A_{3.6} : A_{4.5} : A_{5.8} : A_{8.0} = 1 : 0.56 : 0.43 : 0.43 : 0.43$ , as well as $A_V : A_{K,\rm {S}} = 1 : 0.089$ . Using the somewhat different values found by other studies (e.g. Nishiyama et al. 2009; Flaherty et al. 2007) has only a negligible impact on the results. Figure 8 shows CMDs of the NGC 6522 field involving the 2MASS $K_{\rm {S}}$ magnitude and the magnitudes of the four IRAC bands.

$\begin{figure} \par\includegraphics[width=8cm,clip]{12232fg7.ps} \end{figure}$	Figure 7: Magnitude differences between our MIPS 24 magnitudes and Hinz et al. (2008), for our Bulge 4 field.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=13cm,clip]{12232fg8.ps} \end{figure}$	Figure 8: Colour-magnitude diagrams of the field NGC 6522 involving the 2MASS $K_{\rm {S}}$ and different IRAC magnitudes. For this version, the extinction map of Schultheis et al. (1999) has been used. A theoretical isochrone from Marigo et al. (2008) is included as a blue line (see text for details). Symbols are as in Fig. 4.
Open with DEXTER

Table 7: Coverage of our fields by different extinction maps of the Galactic centre region.

The following observations can be made from these CMDs. At the faint end, the distribution in colour is quite broad since the errors become quite large for these faint sources, and some of the objects probably are background galaxies. There are also a small number of objects with extremely red or extremely blue colours. Possibly, false identifications are involved in some cases (we include only sources with a 2MASS counterpart within 2 $.\!\!^{\prime\prime}$ 0 search radius for the comparison with CMDs). At intermediate brightnesses, the distribution in colour is much narrower, and only very few outliers can be found. At the bright end, the number of sources far from the isochrone locus increases again. This is partly due to saturated sources, e.g. in IRAC 1 (blue ``sequence'' at the bright end), and to dust emission that already shows up at IRAC 4 wavelengths. In general we find good agreement between the observed and the predicted location of the giant branch in the CMDs. In the $(K_{\rm {S}}{-}\rm {IRAC~1})_0$ CMD (upper left panel of Fig. 8), the tip of the giant branch in the isochrone is somewhat bluer than the observed tip. In the $(K_{\rm {S}} - \rm {IRAC~3})_0$ CMD (lower left panel), the theoretical isochrone is bluer than the observed giant branch by about 0 $.\!\!^{\rm m}$ 1 over the whole brightness range. In this filter, the agreement with the GLIMPSE-II survey is very good, but the GALCEN magnitudes are fainter than our magnitudes. Thus, by adopting the GALCEN magnitude scale, the shift of the isochrone would be somewhat alleviated, but not all catalogues and the isochrone can be made agree. We do not find any trends in magnitude in the IRAC 1 filter in the comparison with any of the other surveys, thus we assume that the difference is related to a small problem with the isochrone in the $(K_{\rm {S}}{-}\rm {IRAC~1})_0$ colour. The same might be suspected for the $(K_{\rm {S}} - \rm {IRAC~3})_0$ colour.

The comparison with the isochrones also allows for a check on how deep our Spitzer photometry goes. We find that in all IRAC bands, we reach sources down to the beginning of the He-core burning (horizontal branch), although probably with a reduced detection probability and less accurate photometry. The He-core burning phase is covered until its end, hence also the whole AGB evolution. However, the sensitivity of the present observations is still far too low to reach the beginning of the RGB phase, and our investigations will be limited to the brighter half of the RGB. The MIPS photometry does not reach down to the horizontal arm. The faintest sources that are detected with MIPS in the NGC 6522 field are roughly $3\hbox{$.\!\!^{\rm m}$ }5$ fainter than the RGB tip of the isochrones.

As for the colour dependence on the used extinction map, we find that for individual sources the de-reddened $K_{\rm {S}} - \rm {IRAC}$ colour may vary by a few 0 $.\!\!^{\rm m}$ 01. However, no general trend is observed when different extinction maps are applied. Thus, though the fine structure of the extinction varies somewhat from map to map, the average magnitude of the extinction is very similar among the maps.

5 Summary and conclusions

We present a catalogue of Spitzer IRAC/MIPS observations of seven fields towards the Galactic bulge, sampling a range of galactocentric radii. These observations allow us, amongst other things, to study the mass loss of a large and homogeneous sample of RGB and AGB stars down to lower luminosities and mass-loss rates than previously achieved.

In this first paper, we present the observations, the data reduction procedure, and comparisons to other mid-IR surveys of the Galactic bulge. In general, we find good agreement with other surveys. The comparison between the Spitzer IRAC 4 band and the ISOGAL LW2 band shows good agreement, but reveals a slight trend with magnitude. GLIMPSE-II magnitudes are in good agreement with our magnitudes in the bright-to-medium brightness range, but a strong trend is present at the faint end. This trend is probably related to a Malmquist bias in the GLIMPSE-II data set. The error estimates of GLIMPSE-II and our IRAC photometry are reasonable in the IRAC 1 and 2 bands, but somewhat too small in the IRAC 3 and 4 bands. In the comparison with GALCEN, we find on average $\sim$ $0\hbox{$.\!\!^{\rm m}$ }05$ brighter magnitudes in the IRAC 3 band. The source of the discrepancy at the bright end of the IRAC 4 band is probably not related to our catalogue. A comparison with the MIPS 24 catalogue of Hinz et al. (2008) reveals that our magnitudes are probably brighter at the level of $\sim$ $0\hbox{$.\!\!^{\rm m}$ }15$ , although with larger scatter. We also find good agreement between our data and recent isochrones in colour-magnitude diagrams for at least three of the four IRAC bands. The $\sim$ $0\hbox{$.\!\!^{\rm m}$ }1$ offset from isochrones involving IRAC 3 deserves some more attention. We thus may assume that the observations and data reduction are accurate on the level of $\sim$ $0\hbox{$.\!\!^{\rm m}$ }1$ or better, as well as precise on the level of $\lesssim$ $0\hbox{$.\!\!^{\rm m}$ }1$ , except for faint sources with quality grade B. The science exploitation of the data will follow in subsequent papers.

Acknowledgements

We thank Sean Carey for providing the artifact correction tools used for this work. This research made use of Tiny Tim/Spitzer, developed by John Krist for the Spitzer Science Center. The Center is managed by the California Institute of Technology under a contract with NASA. The research described in this publication was partly carried out at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with the National Aeronautics and Space Administration. This work is based on observations made with the Spitzer Space Telescope, which is operated by the Jet Propulsion Laboratory, California Institute of Technology under a contract with NASA. Support for this work was provided by NASA through an award issued by the JPL/Caltech. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by NASA and the National Science Foundation. S.U. acknowledges support from the Fund for Scientific Research of Flanders (FWO) under grant number G.0470.07. MSt has been supported by the European Community's Marie Curie Actions - Human Resource and Mobility within the JETSET (Jet Simulations, Experiments and Theory) network under contract MRTN-CT-2004 005592.

References

Aringer, B., Höfner, S., Wiedemann, G., Hron, J., Jørgensen U. G., et al. 1999, å 342, 799 [Google Scholar]
Benjamin, R. A., Churchwell, E., Babler, B. L., et al. 2003, PASP, 115, 953 [NASA ADS] [CrossRef] [Google Scholar]
Blum, R. D., Ramírez, S. V., Sellgren, K., et al. 2003, ApJ, 597, 323 [NASA ADS] [CrossRef] [Google Scholar]
Dutra, C. M., Santiago, B. X., Bica, E. L. D., et al. 2003, MNRAS, 338, 253 [NASA ADS] [CrossRef] [Google Scholar]
Epchtein, N., de Batz, B., Capoani, L., et al. 1997, Messenger, 87, 27 [NASA ADS] [Google Scholar]
Fazio, G. G., Hora, J. L., Allen, L. E., et al. 2004, ApJS, 154, 10 [NASA ADS] [CrossRef] [Google Scholar]
Figer, D. F., Rich, R. M., Kim, S. S., Morris, M., & Serabyn, E. 2004, ApJ, 601, 319 [NASA ADS] [CrossRef] [Google Scholar]
Flaherty, K. M., Pipher, J. L., Megeath, S. T., et al. 2007, ApJ, 663, 1069 [NASA ADS] [CrossRef] [Google Scholar]
Glass, I. S., Ganesh, S., Alard, C., et al. 1999, MNRAS, 308, 127 [NASA ADS] [CrossRef] [Google Scholar]
Glass, I. S., Schultheis, M., Blommaert, J. A. D. L., et al. 2009, MNRAS, 395, L11 [NASA ADS] [CrossRef] [Google Scholar]
Hacking, P., & Houck, J. R. 1987, ApJS, 63, 311 [NASA ADS] [CrossRef] [Google Scholar]
Hinz, J. L., Rieke, G. H., Yusef-Zadeh, F., et al. 2008, ApJS, 181, 227 [NASA ADS] [CrossRef] [Google Scholar]
Hora, J. L., Carey, S., Surace, J., et al. 2008, PASP, 120, 1233 [NASA ADS] [CrossRef] [Google Scholar]
Indebetouw, R., Mathis, J. S., Babler, B. L., et al. 2005, ApJ, 619, 931 [NASA ADS] [CrossRef] [Google Scholar]
Kim, S. S., & Morris, M. 2001, ApJ 554, 1059 [NASA ADS] [CrossRef] [Google Scholar]
Krist, J. 2006, PSF modeling for MIPS imaging: STinyTIM, the Spitzer version of the TinyTIM, STinyTIM manual, http://ssc.spitzer.caltech.edu/archanaly/contributed/stinytim/index.html [Google Scholar]
Le Bertre, T. 1992, A&AS, 94, 377 [NASA ADS] [Google Scholar]
Marigo, P., Girardi, L., Bressan, A., et al. 2008, å, 482, 883 [Google Scholar]
Makovoz, D., & Marleau, F. R. 2005, PASP, 117, 1113 [NASA ADS] [CrossRef] [Google Scholar]
McNamara, D. H., Madsen, J. B., Barnes, J., et al. 2000, PASP, 112, 202 [NASA ADS] [CrossRef] [Google Scholar]
Nishiyama, S., Tamura, M., Hatano, H., et al. 2009, ApJ 696, 1407 [NASA ADS] [CrossRef] [Google Scholar]
Omont, A., Gilmore, G. F., Alard, C., et al. 2003, å, 403, 975 [Google Scholar]
Ramírez, S. V., Arendt, R. G., Sellgren, K., et al. 2008, ApJS, 175, 147 [NASA ADS] [CrossRef] [Google Scholar]
Rieke, G. H., Young, E. T., & Gautier, T. N. 1995, Space Sci. Rev., 74, 17 [NASA ADS] [CrossRef] [Google Scholar]
Rieke, G. H., Young, E. T., Engelbracht, C. W., et al. 2004, ApJS, 154, 25 [NASA ADS] [CrossRef] [Google Scholar]
Sahai, R., & Trauger, J. T. 1998, AJ, 116, 1357 [NASA ADS] [CrossRef] [Google Scholar]
Schultheis, M., Ganesh, S., Simon, G., et al. 1999, å, 349, 69 [Google Scholar]
Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
Sumi, T. 2004, MNRAS, 349, 193 [NASA ADS] [CrossRef] [Google Scholar]
Udalski, A., Zebrun, K., Szymanski, M., et al. 2000, Acta Astron., 50, 1 [NASA ADS] [Google Scholar]
Werner, M. W., Roellig, T. L., Low, F. J., et al. 2004, ApJS, 154, 1 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: De-blending or not de-blending?

We tested the comparability of the fluxes derived by PRF fitting and those resulting from aperture photometry for the IRAC 3.6 $\mu$ m channel and for the field NGC 6522 using the two de-blending capabilities in APEX. The first method is passive de-blending, where already during the detection process multiple peaks in a cluster of pixels are found and this information is used in the PRF fitting module to simultaneously fit all the peaks. The second method is active de-blending, i.e. the number of assumed sources is iteratively increased during PRF fitting to decrease the final $\chi^2$ .

Table A.1: Detected and extracted sources.

$\begin{figure} \par\includegraphics[height=7cm,angle=-90]{12232fgA1.ps}\includeg... ...]{12232fgA7.ps}\includegraphics[height=7cm,angle=-90]{12232fgA8.ps} \end{figure}$	Figure A.1: Comparison of the fluxes resulting from PRF fitting and aperture photometry without de-blending (first row), with passive de-blending (second row), with active de-blending (third row), and with both (last row) for the apertures with radii of 2 pixels ( left) and 3 pixels ( right) for the field NGC 6522 and IRAC 1.
Open with DEXTER

We use the point source probability images in the detection process and filter the raw extraction table with the criterion that SNR is greater than 5 and that APEX has not flagged the source as a point source outside the fitting area. This excludes very weak sources, sources covered by only one image, and sources whose position is not correctly identified. The numbers of detected and extracted sources for the runs also shown in Fig. A.1 are given in Table A.1, along with the number of sources filtered by the two criteria.

The active de-blending procedure relies on the $\chi^2$ values to decide whether de-blending is necessary or not, which results in heavy de-blending activity, even for sources whose PRF and aperture fluxes are consistent. We therefore disabled active de-blending in the final data reduction.

Passive de-blending uses the information from the detection process about whether different entries in the detection table belong to the same cluster of pixels above the detection threshold. If yes, APEX fits the cluster simultaneously, if not, the single sources one after the other. The first effect of switching on passive de-blending is that the number of faint sources that lie below an SNR value of 5, hence the number of sources rejected by the first criterion, increases (see Table A.1). Since the positions of the detected sources are also varied to fit the complete cluster, the number of sources whose pointing is outside of the tile used for PRF fitting increases, too (Table A.1). The number of extracted sources is thus less than in the first run when passive de-blending is not activated. Also brighter sources are affected, when there are other stars within 5-10 pixels. Then the independent stars belong to the same cluster and are fitted simultaneously, although the PRF of one star does not contribute at all to the flux in the small tile of another star used for PRF fitting. This again changes the position of the centroid of the central bright star in the cluster and also the flux measured by PRF fitting. Since the displacements are smaller than the pixel size, the aperture flux does not change as much as the PRF flux. The result is that the bright star moves away from the line of good agreement in the $f_{\rm PRF}$ - $f_{\rm aperture}$ -plane (Fig. A.1), so the scatter around this line is increased. The same effect occurs for saturated and super-saturated sources with a double peak leading to the observed spreading of sources in the top-left part of Fig. A.1. Thus the results of the run with passive de-blending are not as reliable as the results of the run without any de-blending.

Appendix B: Magnitude histograms of the seven bulge fields

$\begin{figure} \par\includegraphics[width=7.9cm,clip]{12232fgB1.ps} \end{figure}$	Figure B.1: Histogram of magnitudes for the Bulge 1 field. The bin size is 0 $.\!\!^{\rm m}$ 2.
Open with DEXTER

$\begin{figure}\includegraphics[width=7.9cm,clip]{12232fgB2.ps} \end{figure}$	Figure B.2: Histogram of magnitudes for the Bulge 2 field. The bin size is 0 $.\!\!^{\rm m}$ 2.
Open with DEXTER

$\begin{figure}\par\includegraphics[width=7.9cm,clip]{12232fgB3.ps} \end{figure}$	Figure B.3: Histogram of magnitudes for the Bulge 3 field. The bin size is 0 $.\!\!^{\rm m}$ 2.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=7.9cm,clip]{12232fgB4.ps}\par \end{figure}$	Figure B.4: Histogram of magnitudes for the Bulge 4 field. The bin size is 0 $.\!\!^{\rm m}$ 2.
Open with DEXTER

$\begin{figure}\par\includegraphics[width=7.9cm,clip]{12232fgB5.ps} \end{figure}$	Figure B.5: Histogram of magnitudes for the Bulge N 1 field. The bin size is 0 $.\!\!^{\rm m}$ 2.
Open with DEXTER

$\begin{figure}\includegraphics[width=7.9cm,clip]{12232fgB6.ps} \end{figure}$	Figure B.6: Histogram of magnitudes for the NGC 6522 field. The bin size is 0 $.\!\!^{\rm m}$ 2.
Open with DEXTER

$\begin{figure}\includegraphics[width=3.4cm,clip]{12232fgB7.ps} \end{figure}$	Figure B.7: Histogram of magnitudes for the Bulge N 2 field. The bin size is 0 $.\!\!^{\rm m}$ 2.
Open with DEXTER

Footnotes

... sources: Full Table 5 as well as the fits mosaics are only available in electronic form at the CDS via anonymous ftp to
cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/517/A44
... comparison: http://www.astro.wisc.edu/sirtf/glm2_galcen_comparison.pdf
... ``tweaking'': http://www.astro.wisc.edu/sirtf/glimpse_photometry_v1.0.pdf
... parameters: http://stev.oapd.inaf.it/cgi-bin/cmd_2.1

All Tables

Table 1: Main characteristics of the seven fields towards the GB observed with Spitzer as part of programme 2345.

Table 2: Flux limits applied for assigning quality grades.

Table 3: Statistics of sources with their grades for all seven fields and five bands.

Table 4: Aperture correction factors.

Table 5: Sample table of the band-merged catalogue of the N 1 field.

Table 6: Width, centre, and peak values of the sigma distributions.

Table 7: Coverage of our fields by different extinction maps of the Galactic centre region.

Table A.1: Detected and extracted sources.

All Figures

$\begin{figure} \par\includegraphics[width=8cm,clip]{12232fg1.ps} \end{figure}$	Figure 1: Map of the seven fields observed in this campaign with the labels used throughout this paper.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{12232fg2_1.ps}\\ [1.3mm] \in... ...] \includegraphics[width=8.25cm,clip]{12232fg2_3.ps} \vspace*{-2mm} \end{figure}$	Figure 2: Comparison of the fluxes resulting from PRF fitting and aperture photometry for the IRAC 1 observations of the NGC 6522 field. Top: PRF fitting fluxes and aperture photometry for the aperture with a radius of 2 pixels; middle: the same as top panel, but for the aperture with a radius of 3 pixels; bottom: relative difference between the measured fluxes (3 pixels aperture radius) versus the PRF flux for all sources. The dotted lines in the bottom panel mark relative differences of $\pm$ 7%. In the upper and middle panels, the dashed line is a linear least squares fit to the sources with $\chi ^{2} < 5$ , and the solid horizontal and vertical lines mark the lower and saturation limits of Table 2 used for quality grade labelling.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{12232fg3.ps} \end{figure}$	Figure 3: Magnitude difference between the Spitzer IRAC 4 band and the ISO 7 $\mu$ m LW2 band for 264 sources in common in the NGC 6522 field. The dotted line marks the identity relation, the dashed line is a linear least squares fit through the data points, excluding those sources fainter than 9 $.\!\!^{\rm m}$ 3 in either of the data sets to avoid Malmquist bias.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=13.8cm,clip]{12232fg4.ps} \end{figure}$	Figure 4: Magnitude differences between our and the GLIMPSE-II catalogue for the sources in common in the N 1 field. Sources with quality flag A in our catalogue are represented by black dots, all other quality flags by red dots.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=13.8cm,clip]{12232fg5.ps} \end{figure}$	Figure 5: Distribution of sigma-factors (Eq. (3)) for all IRAC channels in the field N 1 in the magnitude range $7\hbox{$.\!\!^{\rm m}$ }0{-}10\hbox{$.\!\!^{\rm m}$ }0$ . The solid line is a Gaussian fit to the distribution. The dotted line indicates a Gaussian of width 1 and the same area under the graph, the ideal case of correctly estimated errors.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=14cm,clip]{12232fg6.ps} \end{figure}$	Figure 6: Magnitude differences between our photometry and that of Ramírez et al. (2008) for the small overlap in field N 1. Symbols as in Fig. 4.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{12232fg7.ps} \end{figure}$	Figure 7: Magnitude differences between our MIPS 24 magnitudes and Hinz et al. (2008), for our Bulge 4 field.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=13cm,clip]{12232fg8.ps} \end{figure}$	Figure 8: Colour-magnitude diagrams of the field NGC 6522 involving the 2MASS $K_{\rm {S}}$ and different IRAC magnitudes. For this version, the extinction map of Schultheis et al. (1999) has been used. A theoretical isochrone from Marigo et al. (2008) is included as a blue line (see text for details). Symbols are as in Fig. 4.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[height=7cm,angle=-90]{12232fgA1.ps}\includeg... ...]{12232fgA7.ps}\includegraphics[height=7cm,angle=-90]{12232fgA8.ps} \end{figure}$	Figure A.1: Comparison of the fluxes resulting from PRF fitting and aperture photometry without de-blending (first row), with passive de-blending (second row), with active de-blending (third row), and with both (last row) for the apertures with radii of 2 pixels ( left) and 3 pixels ( right) for the field NGC 6522 and IRAC 1.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=7.9cm,clip]{12232fgB1.ps} \end{figure}$	Figure B.1: Histogram of magnitudes for the Bulge 1 field. The bin size is 0 $.\!\!^{\rm m}$ 2.
Open with DEXTER
In the text

$\begin{figure}\includegraphics[width=7.9cm,clip]{12232fgB2.ps} \end{figure}$	Figure B.2: Histogram of magnitudes for the Bulge 2 field. The bin size is 0 $.\!\!^{\rm m}$ 2.
Open with DEXTER
In the text

$\begin{figure}\par\includegraphics[width=7.9cm,clip]{12232fgB3.ps} \end{figure}$	Figure B.3: Histogram of magnitudes for the Bulge 3 field. The bin size is 0 $.\!\!^{\rm m}$ 2.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=7.9cm,clip]{12232fgB4.ps}\par \end{figure}$	Figure B.4: Histogram of magnitudes for the Bulge 4 field. The bin size is 0 $.\!\!^{\rm m}$ 2.
Open with DEXTER
In the text

$\begin{figure}\par\includegraphics[width=7.9cm,clip]{12232fgB5.ps} \end{figure}$	Figure B.5: Histogram of magnitudes for the Bulge N 1 field. The bin size is 0 $.\!\!^{\rm m}$ 2.
Open with DEXTER
In the text

$\begin{figure}\includegraphics[width=7.9cm,clip]{12232fgB6.ps} \end{figure}$	Figure B.6: Histogram of magnitudes for the NGC 6522 field. The bin size is 0 $.\!\!^{\rm m}$ 2.
Open with DEXTER
In the text

$\begin{figure}\includegraphics[width=3.4cm,clip]{12232fgB7.ps} \end{figure}$	Figure B.7: Histogram of magnitudes for the Bulge N 2 field. The bin size is 0 $.\!\!^{\rm m}$ 2.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.