| Issue |
A&A
Volume 517, July 2010
|
|
|---|---|---|
| Article Number | A64 | |
| Number of page(s) | 4 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/200912103 | |
| Published online | 06 August 2010 | |
Interferometric radius and limb darkening of the asteroseismic
red giant 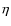 Serpentis with the CHARA Array
Serpentis with the CHARA Array
(Research Note)
A. Mérand1,![]() - P. Kervella2 -
C. Barban2 - E. Josselin3 - T. A. ten
Brummelaar4 - H. A. McAlister4 -
V. Coudé du Foresto2 - S. T. Ridgway5 -
N. Turner4 - J. Sturmann4 - L. Sturmann4 - P. J. Goldfinger4 - C. Farrington4
- P. Kervella2 -
C. Barban2 - E. Josselin3 - T. A. ten
Brummelaar4 - H. A. McAlister4 -
V. Coudé du Foresto2 - S. T. Ridgway5 -
N. Turner4 - J. Sturmann4 - L. Sturmann4 - P. J. Goldfinger4 - C. Farrington4
1 - European Organisation for Astronomical Research in the
Southern Hemisphere (ESO) Alonso de Córdova 3107, Casilla 19001,
Santiago 19, Chile
2 -
LESIA, Observatoire de Paris, CNRS UMR 8109, UPMC, Université Paris Diderot, 5 Place Jules
Janssen, 92195 Meudon, France
3
- Groupe de Recherche en Astronomie et Astrophysique du Languedoc
(GRAAL), Université Montpellier II, CNRS UMR 5024, 34095
Montpellier Cedex 05, France
4 -
Center for High Angular Resolution Astronomy, Georgia State University, PO Box
3965, Atlanta, Georgia 30302-3965, USA
5 -
National Optical Astronomy Observatories, 950 North Cherry Avenue, Tucson, AZ 85719, USA
Received 18 March 2009 / Accepted 4 May 2010
Abstract
Context. The radius of a star is a very important constraint
to evolutionary models, particularly when combined with
asteroseismology. Diameters can now be measured interferometrically
with great precision (better than 1%), but the center-to-limb darkening
(CLD) remains a potential source of bias. Measuring this bias is
possible by completely resolving the star using long-baseline
interferometry, and has only been achieved for a handful of stars.
Aims. The red giant ![]() Ser
(K0III-IV) is a particularly interesting target, as asteroseismic
oscillations have recently been detected in this star by spectroscopy.
We aim to measure its radius with high accuracy, debiased from limb
darkening, in order to bring new constraints to its models.
Ser
(K0III-IV) is a particularly interesting target, as asteroseismic
oscillations have recently been detected in this star by spectroscopy.
We aim to measure its radius with high accuracy, debiased from limb
darkening, in order to bring new constraints to its models.
Methods. We obtained interferometric observations of ![]() Ser
in the near-infrared using the CHARA/FLUOR instrument, in particular in
the so-called second lobe of visibility in order to constrain the CLD
and debias our diameter estimation.
Ser
in the near-infrared using the CHARA/FLUOR instrument, in particular in
the so-called second lobe of visibility in order to constrain the CLD
and debias our diameter estimation.
Results. The limb darkened angular diameter of ![]() Ser is
Ser is
![]() mas (using spherical photosphere models PHOENIX and MARCS for the limb darkening), that converts into a radius of
mas (using spherical photosphere models PHOENIX and MARCS for the limb darkening), that converts into a radius of
![]() with the Hipparcos parallax. Thanks to a precise visibility measurement in the second lobe of the visibility function of
with the Hipparcos parallax. Thanks to a precise visibility measurement in the second lobe of the visibility function of ![]() Ser
and a one-parameter limb-darkened visibility profile, we were able to
show that the photosphere models have the best agreement possible.
Ser
and a one-parameter limb-darkened visibility profile, we were able to
show that the photosphere models have the best agreement possible.
Conclusions. Our limb darkening measurement of ![]() Ser
is in agreement with existing atmosphere models of this star, with a
slightly better agreement for models using spherical geometry. This is
a strong indication that interferometric angular diameter measurements
for red giants, corrected for the CLD using models, are unbiased at a
very small level (a fraction of 1%). In particular, this strengthens
our confidence in the existing catalogues of calibrator stars for
interferometry that are based on giant stars similar to
Ser
is in agreement with existing atmosphere models of this star, with a
slightly better agreement for models using spherical geometry. This is
a strong indication that interferometric angular diameter measurements
for red giants, corrected for the CLD using models, are unbiased at a
very small level (a fraction of 1%). In particular, this strengthens
our confidence in the existing catalogues of calibrator stars for
interferometry that are based on giant stars similar to ![]() Ser. The high accuracy of our measurement brings a new and strong constraint for the asteroseismic modeling of this star.
Ser. The high accuracy of our measurement brings a new and strong constraint for the asteroseismic modeling of this star.
Key words: stars: individual: ![]() Serp - stars: evolution - stars:
fundamental parameters - techniques: interferometric - stars:
oscillations
Serp - stars: evolution - stars:
fundamental parameters - techniques: interferometric - stars:
oscillations
1 Introduction
It is well known that direct measurements of stellar radii are a
powerful tool in discriminating between different numerical stellar
models (see for example 2007 and 2007),
particularly when combined with asteroseismology. In this context, we
present in Sect. 2 a new interferometric measurement
of the angular diameter of ![]() Ser. This star has recently been
the subject of an asteroseismic investigation showing oscillations
with a period of
Ser. This star has recently been
the subject of an asteroseismic investigation showing oscillations
with a period of ![]() 2.1 h (Barban et al. 2004; and
Hekker et al. 2006, for references). The reported
interferometric measurements will provide useful constraints for
future modeling efforts on this star. In the following work care was
taken to ensure that the high precision result (0.3%) was not
affected by biases, in particular any bias due to the correction for
limb darkening. Using measurements obtained in the second lobe of
visibility, we estimate the exponent of the power-law limb darkening
model of this star and, in Sect. 4, we compare the
predictions of several existing model atmospheres with the observed
limb darkening of
2.1 h (Barban et al. 2004; and
Hekker et al. 2006, for references). The reported
interferometric measurements will provide useful constraints for
future modeling efforts on this star. In the following work care was
taken to ensure that the high precision result (0.3%) was not
affected by biases, in particular any bias due to the correction for
limb darkening. Using measurements obtained in the second lobe of
visibility, we estimate the exponent of the power-law limb darkening
model of this star and, in Sect. 4, we compare the
predictions of several existing model atmospheres with the observed
limb darkening of ![]() Ser.
Ser.
2 Interferometric observations
We observed ![]() Ser (HD 168723, HR 6869,
HIP 89962) in July 2006 at the CHARA Array (ten Brummelaar et al. 2005) using FLUOR, the Fiber Linked Unit for
Optical Recombination (Coudé du Foresto et al. 2003;
Mérand et al. 2006a). This instrument is equipped with a
near infrared K' band filter (
Ser (HD 168723, HR 6869,
HIP 89962) in July 2006 at the CHARA Array (ten Brummelaar et al. 2005) using FLUOR, the Fiber Linked Unit for
Optical Recombination (Coudé du Foresto et al. 2003;
Mérand et al. 2006a). This instrument is equipped with a
near infrared K' band filter (
![]() ).
).
We extracted the visibilities from the raw data using the FLUOR data
reduction software (Coudé du Foresto et al. 1997; Kervella
et al. 2004a; Mérand et al. 2006a). For the
reported observations, we used the CHARA baselines S2-W2 and E2-S1,
with ground lengths of 177 and 279 m, respectively. The calibrator
stars were chosen from the catalogue compiled by Mérand et al. (2005), using criteria defined by these authors (Table 1). They were observed immediately before
and/or after ![]() Ser in order to monitor the interferometric
transfer function of the instrument.
Ser in order to monitor the interferometric
transfer function of the instrument.
All our results were obtained using visibility models that take into
account bandwith smearing, as described in Aufdenberg et al. (2006). Since the optical filter for FLUOR is quite
wide, it is extremely important to take band width smearing in
account, especially if one collects data near a visibility null where
the visibility varies substantially inside the waveband. We shall not
fully describe this method in this paper, as it is very specific to
the instrument and filter details. These details are available,
however, directly from the authors. For visual comparison, we plot in
Fig. 1 the monochromatic visibility for
![]() microns.
microns.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{12103fg1.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa12103-09/Timg7.png)
|
Figure 1:
Squared visibilities and adjusted two-parameter limb darkened
disk visibility model of |
| Open with DEXTER | |
Table 1:
Calibrators used for the observations of ![]() Ser.
Ser.
Table 2:
Calibrated squared visibility measurements of ![]() Ser.
Ser.
Table 3: Results of the fits to the data for different models.
3 Angular diameter
3.1 Limb darkening model comparison
In order to estimate the angular diameter from the measured visibilities (Table 2) it is necessary to know the intensity distribution of the light on the stellar disk, that is the limb darkening (LD). In this Section, we present the results of two approaches based on an assumed intensity distribution:
- 1.
- adjust a simple uniform disk model to the V2 measurements. The uniform disk (UD) model, although unphysical, is a useful tool for interferometry when the stars are marginally resolved since it is a single parameter model;
- 2.
- assume a limb darkened profile from existing atmosphere models.
Here we use the stellar parameters derived recently for
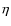 Ser by
Hekker & Meléndez (2007):
Ser by
Hekker & Meléndez (2007):
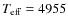 K,
K,
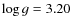 ,
[Fe/H] = -0.21,
,
[Fe/H] = -0.21,
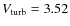 km s-1. For
the computation of the intensity profile of the star, three
models are used: the classical ATLAS9 and PHOENIX models, approximated using
Claret's (2000) four-parameter laws in the K band, and
the MARCS model (Gustafsson et
al. 2008)
km s-1. For
the computation of the intensity profile of the star, three
models are used: the classical ATLAS9 and PHOENIX models, approximated using
Claret's (2000) four-parameter laws in the K band, and
the MARCS model (Gustafsson et
al. 2008)![[*]](/icons/foot_motif.png) ,
using intensities computed using TURBOSPECTRUM (Alvarez & Plez
1998), with spherical (``-sph'') and plane-parallel
geometries (``-pp'').
,
using intensities computed using TURBOSPECTRUM (Alvarez & Plez
1998), with spherical (``-sph'') and plane-parallel
geometries (``-pp'').
Note that the presence of circum-stellar material might bias the angular diameter estimates. We will investigate this possibility in Sect. 3.5.
3.2 Parametrized power-law limb darkening fit
As shown in Fig. 1, two of the data points
were obtained in the second lobe of the visibility
function. The star is therefore fully resolved by the
interferometer, and these data can be used to investigate the limb darkening,
relatively independently from the angular diameter estimate. However, as there
are only two V2 points, we cannot measure the actual shape of the
intensity distribution. Hestroffer (1997) showed that
a power law
![]() (with
(with
![]() and
and
![]() )
is a good approximation to stellar limb
darkening profiles. Such an approximation presents two advantages: it
requires only one more free parameter compared to a simple angular diameter fit
(the
)
is a good approximation to stellar limb
darkening profiles. Such an approximation presents two advantages: it
requires only one more free parameter compared to a simple angular diameter fit
(the ![]() exponent); and it gives an analytical expression of the
visibility function, thus simplifying the visibility curve
modeling. By definition, this model leads to a stellar radius defined
as
exponent); and it gives an analytical expression of the
visibility function, thus simplifying the visibility curve
modeling. By definition, this model leads to a stellar radius defined
as ![]() .
For
.
For ![]() Ser, the two-parameter model fitting gives:
Ser, the two-parameter model fitting gives:
| (1) |
| (2) |
The two parameters in this fit are correlated, and so the derived value of
In Fig. 1, we did not overplot the ATLAS9, PHOENIX and both MARCS models because at the scale of this plot, they would overlap.
3.3 Comparison between power law CLD and photospheric models
It is important to understand the limitations of the
power-law fitting performed above.
We do not claim that the star actually has a power
law CLD profile. However, the visibility profiles of the other
models can be approximated by the power law CLD.
The visibility of the ATLAS9 model
corresponds to the visibility given by a power law
![]() ,
the
MARCS-pp model gives
,
the
MARCS-pp model gives
![]() .
Conversely, the spherical models
PHOENIX and MARCS-sph correspond to
.
Conversely, the spherical models
PHOENIX and MARCS-sph correspond to
![]() and
and
![]() respectively. In other words, our fitted value of
respectively. In other words, our fitted value of ![]() is
statistically compatible with the ATLAS9, PHOENIX and both MARCS
models and at this level of precision, the data do not allow us to
distinguish between the models. It does however, seem that models using
the spherical geometry (PHOENIX and MARCS-sph) give slightly better
agreement than models using the plane-parallel geometry (ATLAS9 and MARCS-pp).
is
statistically compatible with the ATLAS9, PHOENIX and both MARCS
models and at this level of precision, the data do not allow us to
distinguish between the models. It does however, seem that models using
the spherical geometry (PHOENIX and MARCS-sph) give slightly better
agreement than models using the plane-parallel geometry (ATLAS9 and MARCS-pp).
3.4 Limb darkened disk angular (unbiased) diameter
Based on the results of the comparison in setout in Sect. 3.1 and
our two-parameter fit in Sect. 3.2, the best estimate of the
photospheric angular size of ![]() Ser was choosen to be the
value given by the spherical models (an average of PHOENIX and
MARCS-sph). This corresponds to a fit on all
the data set with a power law of
Ser was choosen to be the
value given by the spherical models (an average of PHOENIX and
MARCS-sph). This corresponds to a fit on all
the data set with a power law of
![]() resulting in
resulting in
| (3) |
with a reduced
| (4) |
3.5 On the possibility of the presence photometric excess
Another source of bias of the interferometric measurement of angular
diameters is the presence of fully resolved circumstellar material,
being seen as a photometric excess. This will lead to a measured
visibility apparently not converging to unity as the baseline
decreases. We tested this possibility with a fit of the diameter and
such excess in the first lobe which lead to
![]() with an uncorrelated flux of
with an uncorrelated flux of
![]() of stellar flux. In the second lobe, this leads to
of stellar flux. In the second lobe, this leads to
![]() with an
uncorrelated flux of
with an
uncorrelated flux of
![]() .
In other words, our first
lobe data are not very sensitive to the effect because we are close to
the first null and one needs measurements at very short baselines,
as discussed in Mérand et al. (2006b). On
the other hand, including the second lobe data rules out the presence
of such a bias, at the 1% level in terms of photometric precision, and
we are confident that even in the presence of a photometric
bias of 1%, our final angular diameter estimate remains unbiased.
.
In other words, our first
lobe data are not very sensitive to the effect because we are close to
the first null and one needs measurements at very short baselines,
as discussed in Mérand et al. (2006b). On
the other hand, including the second lobe data rules out the presence
of such a bias, at the 1% level in terms of photometric precision, and
we are confident that even in the presence of a photometric
bias of 1%, our final angular diameter estimate remains unbiased.
4 Linear radius and discussion
The comparison of our different fits to the data points in the second lobe
showed that the limb darkening power law is in good agreement
with the photospheric models.
As a comparison with the angular diameter values derived in
Sect. 3, ![]() Ser is present in Bordé et al.'s (2002) catalogue of interferometric
calibrator stars, where its angular diameter was estimated from its
spectral energy distribution to be
Ser is present in Bordé et al.'s (2002) catalogue of interferometric
calibrator stars, where its angular diameter was estimated from its
spectral energy distribution to be
![]() ,
within 1.1
,
within 1.1![]() of our measurement, but three
times less precise. Considering the V and K magnitudes of
of our measurement, but three
times less precise. Considering the V and K magnitudes of
![]() Ser of
Ser of
![]() and
and
![]() (Morel
& Magnenat 1978, with typical uncertainties), the [V,
V-K] surface brightness-color relation calibrated by Kervella et al. (2004b) predicts an angular diameter of
(Morel
& Magnenat 1978, with typical uncertainties), the [V,
V-K] surface brightness-color relation calibrated by Kervella et al. (2004b) predicts an angular diameter of
![]() mas, in excellent agreement with our
CHARA/FLUOR measurement. Finally, the spectral energy
distribution fitting code developed for the work presented in
Kervella et al. (2009) based on photospheric modeling of
wide band photometric measurements (
B, V, J, H, K), gives an
angular diameter of
mas, in excellent agreement with our
CHARA/FLUOR measurement. Finally, the spectral energy
distribution fitting code developed for the work presented in
Kervella et al. (2009) based on photospheric modeling of
wide band photometric measurements (
B, V, J, H, K), gives an
angular diameter of
![]() mas and an effective
temperature of
mas and an effective
temperature of ![]() K.
K.
The linear radius of ![]() Ser, can be calculated based on a parallax from
the reprocessed Hipparcos catalogue by van
Leeuwen (2007a,b) of
Ser, can be calculated based on a parallax from
the reprocessed Hipparcos catalogue by van
Leeuwen (2007a,b) of
![]() This value, while more precise, is in good agreement with, van Altena et al. (1995) and the initial Hipparcos value
(ESA 1997). The photospheric linear radius is therefore
This value, while more precise, is in good agreement with, van Altena et al. (1995) and the initial Hipparcos value
(ESA 1997). The photospheric linear radius is therefore
| (5) |
5 Conclusion
Our results show that the limb darkening of ![]() Ser is modeled
well by the existing spherical models PHOENIX and MARCS, and to a
smaller extent by plane-parallel ATLAS. This reinforces the already
widely accepted belief that for simple case such as non-pulsating
stars, photospheric models can be used to debias an
interferometrically determined angular diameter. In particular, it
confirms that the interferometric calibrator catalogues from Bordé
et al. (2002) and Mérand et al. (2005) are not
affected by a systematic bias due to the assumed limb darkening
model. They contain mostly K giants of similar spectral types as
Ser is modeled
well by the existing spherical models PHOENIX and MARCS, and to a
smaller extent by plane-parallel ATLAS. This reinforces the already
widely accepted belief that for simple case such as non-pulsating
stars, photospheric models can be used to debias an
interferometrically determined angular diameter. In particular, it
confirms that the interferometric calibrator catalogues from Bordé
et al. (2002) and Mérand et al. (2005) are not
affected by a systematic bias due to the assumed limb darkening
model. They contain mostly K giants of similar spectral types as
![]() Ser. The derived radius of
Ser. The derived radius of ![]() Ser (
Ser (
![]() )
is among the most accurate of such measurements
available, and will be a valuable constraint for the modeling of this
star when combined with asteroseismic data, as demonstrated by our
measurement of the diameter of a G giant,
)
is among the most accurate of such measurements
available, and will be a valuable constraint for the modeling of this
star when combined with asteroseismic data, as demonstrated by our
measurement of the diameter of a G giant, ![]() Oph, and the
successful modeling of its detected asteroseismic frequencies (Mazumdar
et al. 2009).
Oph, and the
successful modeling of its detected asteroseismic frequencies (Mazumdar
et al. 2009).
The authors would like to thank the CHARA Array and Mount Wilson Observatory day-time and night-time technical and administrative staff for their support. The CHARA Array was constructed with funding from Georgia State University, the National Science Foundation, the W. M. Keck Foundation, and the David and Lucile Packard Foundation. The CHARA Array is operated by Georgia State University with support from the College of Arts and Sciences, and from the National Science Foundation under NSF Grant AST 0606958. This work also received the support of PHASE, the high angular resolution partnership between ONERA, Observatoire de Paris, CNRS and University Denis Diderot Paris 7. This research took advantage of the SIMBAD and VIZIER databases at the CDS, Strasbourg (France), and NASA's Astrophysics Data System Bibliographic Services.
References
- Alvarez, R., & Plez, B. 1998, A&A, 330, 1109 [NASA ADS] [Google Scholar]
- Aufdenberg, J. P., Mérand, A., & Coudé du Foresto, V. 2006, ApJ, 645, 664 [NASA ADS] [CrossRef] [Google Scholar]
- ; Erratum 2006, ApJ, 651, 617 [NASA ADS] [CrossRef] [Google Scholar]
- Barban, C., de Ridder, J., Mazumdar, A., et al. 2004, Proc. SOHO 14/GONG 2004 Workshop (ESA SP-559), Helio- and Asteroseismology: Towards a Golden Future, 12-16 July, New Haven, Connecticut, USA, ed. D. Danesy, 113 [Google Scholar]
- Bordé, P., Coudé du Foresto, V., Chagnon, G., & Perrin, G. 2002, A&A, 393, 183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A. 2000, A&A, 363, 1081 [NASA ADS] [Google Scholar]
- Coudé du Foresto, V., Ridgway, S., & Mariotti, J.-M. 1997, A&AS, 121, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coudé du Foresto, V., Bordé, P., Mérand, A., et al. 2003, Proc. SPIE, 4838, 280 [NASA ADS] [CrossRef] [Google Scholar]
- Creevey, O. L., Monteiro, M. J. P. F. G., Metcalfe, T. S., et al. 2007, ApJ, 659, 616 [NASA ADS] [CrossRef] [Google Scholar]
- Cunha, M. S., Aerts, C., Christensen-Dalsgaard, J., et al. 2007, A&AR, 14, 217 [Google Scholar]
- ESA 1997, The Hipparcos and Tycho Catalogues, ESA SP-1200 [Google Scholar]
- Gustafsson, B., Edvardsson B., Eriksson K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hekker, S., & Meléndez, J. 2007, A&A, 475, 1003 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hekker, S., Aerts, C., De Ridder, J., & Carrier, F. 2006, A&A, 458, 931 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hestroffer, D. 1997, A&A, 327, 199 [NASA ADS] [Google Scholar]
- Kervella, P., Ségransan, D., & Coudé du Foresto, V. 2004a, A&A, 425, 1161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kervella, P., Thévenin F., Di Folco, E., & Ségransan, D. 2004b, A&A, 426, 297, K04 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kervella, P., Mérand, A., & Gallenne, A. 2009, A&A, 498, 425 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mazumdar, A., Merand, A., Demarque, P., et al. 2009, A&A, 503, 521 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mérand, A., Bordé, P., & Coudé du Foresto, V. 2005, A&A, 433, 1155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mérand, A., Coudé du Foresto, V., Kellerer, A., et al. 2006a, Proc. SPIE, 6268, 46 [NASA ADS] [Google Scholar]
- Mérand, A., Kervella, P., Coudé Du Foresto, V., et al. 2006a, A&A, 453, 155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morel, M., & Magnenat, P. 1978, A&AS, 34, 477 [NASA ADS] [Google Scholar]
- Perrin, G. 2003, A&A, 400, 1173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- ten Brummelaar, T. A., McAlister, H. A., Ridgway, S. T., et al. 2005, ApJ, 628, 453 [NASA ADS] [CrossRef] [Google Scholar]
- van Altena, W. F., Lee, J. T., & Hoffleit, E. D. 1995, The General Catalogue of Trigonometric Stellar Parallaxes, 4th edition, Yale University Observatory [Google Scholar]
- van Leeuwen, F. 2007a, Hipparcos, the New Reduction of the Raw Data, Astrophysics and Space Science Library, Vol. 350 (Springer) [Google Scholar]
- van Leeuwen, F. 2007b, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Footnotes
- ...
![[*]](/icons/foot_motif.png)
- Formerly a research associate at the CHARA Array, during which period most of the research presented here has been carried out.
- ...2008)
![[*]](/icons/foot_motif.png)
- http://www.marcs.astro.uu.se/
All Tables
Table 1:
Calibrators used for the observations of ![]() Ser.
Ser.
Table 2:
Calibrated squared visibility measurements of ![]() Ser.
Ser.
Table 3: Results of the fits to the data for different models.
All Figures
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{12103fg1.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa12103-09/Timg7.png)
|
Figure 1:
Squared visibilities and adjusted two-parameter limb darkened
disk visibility model of |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


