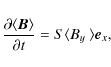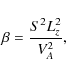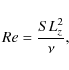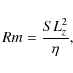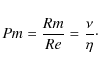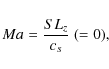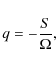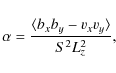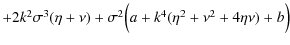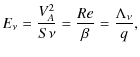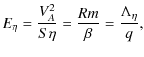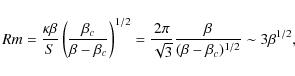| Issue |
A&A
Volume 516, June-July 2010
|
|
|---|---|---|
| Article Number | A51 | |
| Number of page(s) | 11 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201014093 | |
| Published online | 24 June 2010 | |
MRI-driven turbulent transport: the role of dissipation, channel modes and their parasites
P.-Y. Longaretti1 - G. Lesur2
1 - Laboratoire d'Astrophysique, UJF CNRS, BP 53, 38041 Grenoble Cedex 9, France
2
- Department of Applied Mathematics and Theoretical Physics, University
of Cambridge, Centre for Mathematical Sciences, Wilberforce Road,
Cambridge CB3 0WA, UK
Received 18 January 2010 / Accepted 8 April 2010
Abstract
Context. In the recent years, MRI-driven turbulent transport has been found to depend in a significant way on fluid viscosity ![]() and resistivity
and resistivity ![]() through the magnetic Prandtl number
through the magnetic Prandtl number
![]() .
In particular, the transport decreases with decreasing Pm;
if persistent at very large Reynolds numbers, this trend may lead
to question the role of MRI-turbulence in YSO disks, whose Prandtl
number is usually very small.
.
In particular, the transport decreases with decreasing Pm;
if persistent at very large Reynolds numbers, this trend may lead
to question the role of MRI-turbulence in YSO disks, whose Prandtl
number is usually very small.
Aims. In this context, the principal objective of the present
investigation is to characterize in a refined way the role of
dissipation. Another objective is to characterize the effect of linear
(channel modes) and quasi-linear (parasitic modes) physics in the
behavior of the transport.
Methods. These objectives are addressed with the help of a
number of incompressible numerical simulations. The horizontal extent
of the box size has been increased in order to capture all relevant
(fastest growing) linear and secondary parasitic unstable modes.
Results. The major results are the following: i- the
increased accuracy in the computation of transport averages shows that
the dependence of transport on physical dissipation exhibits two
different regimes: for ![]() ,
the transport has a power-law dependence on the magnetic Reynolds number rather than on the Prandtl number; for Pm > 1, the data are consistent with a primary dependence on Pm for large enough (
,
the transport has a power-law dependence on the magnetic Reynolds number rather than on the Prandtl number; for Pm > 1, the data are consistent with a primary dependence on Pm for large enough (
![]() ) Reynolds
numbers. ii- The transport-dissipation correlation is not clearly or
simply related to variations of the linear modes growth rates. iii- The
existence of the transport-dissipation correlation depends neither on
the number of linear modes captured in the simulations, nor on the
effect of the parasitic modes on the saturation of the linear modes
growth. iv- The transport is usually not dominated by axisymmetric
(channel) modes.
) Reynolds
numbers. ii- The transport-dissipation correlation is not clearly or
simply related to variations of the linear modes growth rates. iii- The
existence of the transport-dissipation correlation depends neither on
the number of linear modes captured in the simulations, nor on the
effect of the parasitic modes on the saturation of the linear modes
growth. iv- The transport is usually not dominated by axisymmetric
(channel) modes.
Key words: accretion, accretion disks - turbulence - magnetohydrodynamics (MHD)
1 Introduction
Disks evolve on time-scales that are orders of magnitudes smaller than
expected from microphysical transport processes, and various
suggestions have been made over the years to explain this discrepancy.
Turbulent transport, in particular, has figured among the leading
candidates since the inception of the ![]() -disk
paradigm, and a number of hydrodynamic and MHD turbulent transport
mechanisms have been proposed in the literature.
-disk
paradigm, and a number of hydrodynamic and MHD turbulent transport
mechanisms have been proposed in the literature.
On the hydrodynamic side, subcritical turbulence (Richard & Zahn 1999, and references therein), if present, is apparently too inefficient (Ji et al. 2006; Lesur & Longaretti 2005). Convection was up to now found too inefficient and to transport angular momentum in the wrong direction (Stone & Balbus 1996; Cabot 1996), but a recent reinvestigation of the problem indicates that this might be an artifact of these simulations being performed too close to the stability threshold (Lesur & Ogilvie 2010). Two-dimensional weak turbulence driven by small-scale, incoherent gravitational instabilities (density waves) is an option (Gammie 1996). Alternatively, the baroclinic instability (Klahr & Bodenheimer 2003) may generate vorticity, and transport through the coupling with density waves, but its conditions of existence are still controversial (Petersen et al. 2007; Johnson & Gammie 2006), although Lesur & Papaloizou (2010) have probably identified the root of this debate by pointing out the nonlinear nature of the instability; also the resulting vortices would be subject to 3D instabilities (Lesur & Papaloizou 2009).
Balbus & Hawley (1991) have proposed that the magnetorotational instability (MRI) is a potentially efficient source of turbulent transport in the nonlinear regime, an expectation soon borne out in numerical simulations. This instability provides by now the most extensively studied transport mechanism, through local unstratified (Hawley et al. 1995), stratified (Stone et al. 1996), and global (Hawley 2000) 3D disk simulations. These initial simulations as well as the numerous ones following them have shown that MRI turbulence is an efficient way to transport angular momentum, in the presence or absence of a mean vertical or toroidal field, with an overall transport efficiency depending on the field configuration and strength. However, the significant role played by microphysical dissipation in the resolutions accessible to date had largely been underestimated (Lesur & Longaretti 2007; Fromang et al. 2007).
By now, both the field strength and dissipation dependence of the
simulated turbulent transport have been studied to some extent
(and only in unstratified local shearing box settings for the
latter one). The dependence of the Shakura-Sunyaev ![]() parameter has been characterized very early on by Hawley et al. (1995) who showed that momentum transport
parameter has been characterized very early on by Hawley et al. (1995) who showed that momentum transport
![]() both for a net vertical or toroidal field
both for a net vertical or toroidal field![]() (albeit with very different efficiencies in the two configurations),
a scaling further confirmed in later simulations,
as summarized in Pessah et al. (2007).
(albeit with very different efficiencies in the two configurations),
a scaling further confirmed in later simulations,
as summarized in Pessah et al. (2007).
Until recently, the effect of physical viscosity (![]() )
and resistivity (
)
and resistivity (![]() )
on the transport had been neglected, under the implicit assumption that these should not matter too much once
inertial turbulent scales are resolved in the simulations. However, Lesur & Longaretti (2007)
have shown that, in the presence of a mean vertical field, the
MRI-driven turbulent transport did exhibit a substantial dependence on
the magnetic Prandtl number
)
on the transport had been neglected, under the implicit assumption that these should not matter too much once
inertial turbulent scales are resolved in the simulations. However, Lesur & Longaretti (2007)
have shown that, in the presence of a mean vertical field, the
MRI-driven turbulent transport did exhibit a substantial dependence on
the magnetic Prandtl number
![]() ,
with no clear trends with respect to either viscosity of resistivity alone
,
with no clear trends with respect to either viscosity of resistivity alone![]() . Recently, Simon & Hawley (2009) found similar results in shearing boxes with a mean toroidal field instead of a mean vertical one.
. Recently, Simon & Hawley (2009) found similar results in shearing boxes with a mean toroidal field instead of a mean vertical one.
When the mean magnetic flux vanishes, the transport behavior is more complex. The initial investigation by Hawley et al. (1996) concluded that the transport was converging to a finite value, but Gardiner & Stone (2005) found that the transport efficiency was dependent on the simulation resolution. More recently, the role of the magnetic Prandtl number Pm has been identified in this setting (Fromang et al. 2007): turbulence exists only for magnetic Prandtl numbers larger than about 2, which requires the explicit inclusion of viscous and resistive terms in the fluid equations for numerical simulations to correctly capture the physics of the problem. The disappearance of turbulence at low Pm, as well as the need of large enough amplitudes in the initial conditions at Pm > 2, indicate that the zero net flux magnetized shearing box is a subcritical system rather than a linearly unstable one (Lesur & Ogilvie 2008b,a).
Thus it appears that in all configurations explored to date, the magnetic Prandtl number plays a significant role on the existence and/or efficiency of the turbulent transport, at least at the resolutions accessible on present day computers (or equivalently, the accessible Reynolds and magnetic Reynolds numbers). This raises a number of issues.
For one, the exact role played by channel modes and parasitic modes is unclear. Although they exist only when a mean vertical field is present, they are simpler to analyze and their behavior may provide insight into the generic mechanism responsible for saturation of the linear instability. Channel modes are the axisymmetric unstable modes of the MRI (Pessah & Chan 2008; Balbus & Hawley 1991), and are often observed both in 2D and 3D simulations with a mean vertical field; their name derives from their vertically layered characteristic channel-like radial flow. They were quickly recognized to be also nonlinear solution of the problem by Goodman & Xu (1994); the same authors found them to be unstable with respect to a secondary instability (parasitic modes). A few recent papers have focused on the possibility that the saturation of the channel mode by this parasitic instability might be the mechanism explaining the magnitude of the turbulent transport in MRI simulations, with diverging conclusions (Pessah & Goodman 2009; Latter et al. 2009).
In relation to this, the role of the aspect ratio of the simulations has probably been underestimated in the past. Boxes with an aspect ratio R:Z=1:1 do not allow for the fastest parasitic modes to grow, and Bodo et al. (2008) pointed out that narrow boxes tend to overemphasize the role of the channel modes with respect to more horizontally extended boxes. This calls for a reassessment of the Prandtl number dependence of MRI-driven transport in horizontally extended simulation boxes with a mean vertical field.
More generally, it is still unclear whether this dependence of the transport on physical dissipation is a consequence of the limited Reynolds numbers that can be achieved on present day computers. In particular, none of the published simulations has been able to capture the existence of a significant inertial range in the kinetic or magnetic energy spectrum, which makes it difficult to address this issue. The question here revolves mostly around the direction and locality of transfers and fluxes in Fourier space, and will be addressed elsewhere.
For the time being, we focus the potential role of the channel and parasitic modes in the efficiency of turbulent transport. This is explored by numerical simulations in the shearing sheet limit, with a net vertical magnetic flux, and with horizontally extended simulation boxes. The paper is organized in the following way. Our numerical method, setup, and run parameters are described in Sect. 2. Relevant aspects of the theory of channel modes are summarized in Sect. 3. Section 4 is the core of this paper, and discusses our numerical results; the issues bearing on the resolved linear and secondary modes are also discussed there. The implications of these results are presented in the final section along with some possible future lines of work.
2 Numerical model
2.1 Shearing box model and equations
Following the initial investigation of 3D MRI turbulent properties by Hawley et al. (1995), we base our simulations on the shearing sheet local approximation and the related shearing box model. Most if not all local studies of disk turbulence have been performed in this framework. Local simulations are unescapable to examine in any detail the structure and transport properties of MRI turbulence; indeed, even within a local model, present day computers are still too limited to reach the resolutions required to understand the magnetic Prandtl issue summarized in the introduction, and it is certainly hopeless to tackle this problem directly in global simulations.
To some extent, a shearing box biases the role of the channel mode in turbulent transport, e.g. through the correlations introduced by the periodic boundary conditions. Note however, that, in purely hydrodynamic turbulence, the shearing box seems to capture some of the correct physical properties of actual experimental systems, such as the transition Reynolds number to turbulence as a function of rotation (see, Lesur & Longaretti 2005). In any case, it is very difficult to formulate a well-posed local problem that does not rely on the shearing box framework. The reader is referred to Hawley et al. (1995), Balbus (2003) and Regev & Umurhan (2008) for more detailed discussions of the properties and limitations of this model.
MHD turbulence in discs is essentially subsonic, and we will work in the incompressible approximation, which allows us to eliminate local and transient density fluctuations as well as sound waves and density waves from the problem. Density waves are excited in shearing box turbulence (Heinemann & Papaloizou 2009b), but they appear to have little impact on the turbulent transport (Heinemann & Papaloizou 2009a). This has been confirmed by direct comparison between incompressible and compressible simulations (Fromang et al. 2007). As a consequence, we feel reasonably justified to assume incompressibility. Explicit molecular viscosity and resistivity are included.
The shearing box equations are well-known; we reproduce them
here to introduce our notations. We chose a Cartesian box centered at r=R0, rotating with the disc at angular velocity
![]() and having dimensions
(Lx,Ly,Lz) with
and having dimensions
(Lx,Ly,Lz) with
![]() .
By convention here,
.
By convention here,
![]() and
r-R0 = -y, leading to the following form of the shearing sheet equations:
and
r-R0 = -y, leading to the following form of the shearing sheet equations:
where the magnetic field is measured in units of Alfvén speed. The mean shear
The steady-state solution to these equations is the local Keplerian profile U0=Syex. Our code computes the (turbulent) deviations from this Keplerian profile. Defining v=U-U0, and b=B-B0, one obtains the following equations for v and b:
The boundary conditions associated with this system are periodic in the x and z direction and shearing-periodic in the ydirection (Hawley et al. 1995) (for v and b).
Following Hawley et al. (1995), one can integrate the induction Eq. (6) over the volume of the box, leading to:
where
The numerical resolution makes use of a spectral Galerkin representation of Eqs. (5)-(8) in the sheared frame (see Lesur & Longaretti 2005). In this frame, the shearing-sheet boundary conditions are transformed into perfectly periodic boundary conditions, and Fourier transforms can be used in all three directions. Moreover, this decomposition allows us to conserve magnetic flux to machine precision (the total magnetic flux created during one simulation is typically 10-11). Equations (7) and (8) are enforced to machine precision using a spectral projection (Peyret 2002). The nonlinear terms are computed with a pseudospectral method, and aliasing is prevented using the 3/2 rule.
The sheared frame representation of the spectral domain would
eventually produce a mismatch between the computed Fourier components
and the physically relevant ones. To circumvent this problem, we
use a remap method similar to the one described by Umurhan & Regev (2004). This routine redefines the sheared frame every
![]() ,
and none of the results presented here seems to be related to this time
scale. Spectral methods are very little dissipative by nature;
numerical dissipation is kept to very small values, as can be seen by
computing the total energy budget at each time step (see Lesur & Longaretti 2005, for a discussion of this procedure).
,
and none of the results presented here seems to be related to this time
scale. Spectral methods are very little dissipative by nature;
numerical dissipation is kept to very small values, as can be seen by
computing the total energy budget at each time step (see Lesur & Longaretti 2005, for a discussion of this procedure).
2.2 Dimensionless numbers
All our simulations are performed in horizontally extended boxes, with aspect ratio Lx:Ly:Lz = 4:4:1, with a non vanishing mean vertical field of varying strength.
Our shearing box set up is characterized by a number of dimensionless numbers. Our simulations explore the dependence of the turbulent transport with respect to three of them
- The magnitude of the imposed mean vertical field measured by
where is the Alfvén speed due to this mean field. This definition mimics the usual plasma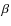 in vertically stratified disk obeying the vertical hydrostatic equilibrium constraint
in vertically stratified disk obeying the vertical hydrostatic equilibrium constraint
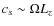 .
.
- The Reynolds number,
comparing the nonlinear advection term to the viscous dissipation. - The magnetic Reynolds number,
comparing magnetic field advection to the Ohmic resistivity. - Alternatively to one of the two Reynolds numbers, the magnetic Prandtl number
- The Mach number
(vanishing for our incompressible simulations). - A Rossby-like number q defined by
which is fixed at the keplerian value (3/2). The sign of q indicates the flow cyclonicity.
Our dimensionless transport coefficient ![]() is defined as
is defined as
where the average is taken over the volume of the simulation box. Within a factor of order unity, this is analogous to the more common prescription for the turbulent viscosity
3 Channel mode physics: a summary of relevant information
As recalled in the introduction, it has been noted in a number of earlier MRI simulations in a shearing box with a mean vertical field that channel modes constitute somewhat recurrent patterns of the turbulent flow, and appear to be more prominent at the maxima in the fluctuations of the turbulent transport. Channel modes do transport angular momentum with roughly the right order of magnitude if their amplitude is comparable to the rms fluctuation in the field close to a maximum of the transport.
This has suggested a picture of turbulent transport in shearing boxes with a mean vertical field that is sketched in Fig. 1.
| Figure 1: Cartoon of the process that may be at the origin of the saturation of the transport in shearing box simulations of MRI with a net vertical field (see text). |
|
| Open with DEXTER | |
According to this picture, the channel modes linearly grow from random noise; at some amplitude, their growth is halted by a secondary instability (parasitic mode) which destroys the channel mode. Presumably, the parasitic modes themselves decay into small scale turbulence, which may then produce the seed for the random fluctuations out of which the channel mode grows in the first place. In this scenario, the channel mode(s) would be responsible for most of the transport, in particular near maxima of the transport fluctuations.
One of the objectives of this paper is to examine the relevance of this picture of MRI turbulence. Even if such a scenario is not generic (it depends directly on the presence of a mean vertical field), if confirmed, it might provide an interesting lead to analyze different situations. Another related objective it to assess the relevance of this scenario to the question of the Prandtl number dependence of MRI-driven transport. To this effect, we gather here the relevant pieces of information on the physics of channel modes that is required in order to analyze the simulations presented in the next section.
3.1 Dispersion relation
The physics of viscous and resistive channel modes has been examined in Lesur & Longaretti (2007) and their properties have been characterized in detail in Pessah & Chan (2008) (Sano & Miyama 1999, have also explored the role of resistivity on MRI in the absence of viscosity). Since non axisymmetric MRI modes are transiently growing structures in non ideal MHD (Balbus & Hawley 1992), the axisymmetric modes give a good grasp of the linear stability properties of the shearing box.
We recall here the dispersion relation of theses modes and a number of other features that will be of use in the next section.
Looking for solutions of the linearized equations of motions in the form
![]() and
and
![]() leads to the following
fourth order dispersion relation:
leads to the following
fourth order dispersion relation:
with
| a = 2kz2VA2, | (18) | |
| (19) | ||
| (20) |
and where
This equation is used later on to compute the channel mode growth
rates in the conditions of our numerical simulations. It is most
conveniently solved in dimensionless form, with S as unit of
time and VA/S as unit of length. We introduce
![]() ,
,
![]() ,
k*=VA k/S; defining the viscous (
,
k*=VA k/S; defining the viscous (![]() )
and resistive (
)
and resistive (![]() )
Elsasser-like numbers by
)
Elsasser-like numbers by
one has
3.2 Stability limits
In the dissipation-free limit, the dispersion relation can be solved
exactly. The magnetic tension stabilizes the instability for
![]() .
In a box of
finite vertical extent Lz, the vertical modes wavelengths are multiple of
.
In a box of
finite vertical extent Lz, the vertical modes wavelengths are multiple of
![]() .
Axisymmetric MRI modes are therefore stabilized when kc <
.
Axisymmetric MRI modes are therefore stabilized when kc <
![]() ,
which translates into
,
which translates into
![]() .
The maximum growth rate in the dissipation-free regime,
.
The maximum growth rate in the dissipation-free regime,
![]() ,
is achieved for a wavenumber
,
is achieved for a wavenumber
![]() .
.
Resistivity and viscosity modify the marginal stability limit in the (Re, Rm, ![]() ) space. Numerical investigation indicates that only one of the four roots is unstable for q < 2, so that
the marginal stability limits obtains when the
) space. Numerical investigation indicates that only one of the four roots is unstable for q < 2, so that
the marginal stability limits obtains when the ![]() -independent term of the dispersion relation is equal to zero. Also, as shown by Lesur & Longaretti (2007), for
-independent term of the dispersion relation is equal to zero. Also, as shown by Lesur & Longaretti (2007), for
![]() and
and ![]() (two conditions that are satisfied in the present investigation), the marginal stability limit is nearly independent
of the Reynolds number. This leads to the following expression of the marginal stability limit
(two conditions that are satisfied in the present investigation), the marginal stability limit is nearly independent
of the Reynolds number. This leads to the following expression of the marginal stability limit
where the second equality applies for keplerian flows. The last approximation holds only when
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{14093fig2.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14093-10/Timg95.png)
|
Figure 2:
Maximal growth rate
|
| Open with DEXTER | |
The maximum growth rate achieved by the instability is modified when
viscosity and resistivity become important, i.e. when either ![]() or
or ![]()
![]() 1. Pessah & Chan (2008) give an asymptotic
form of the growth rate in the dissipation regime for small or of order unity Pm (see their Fig. 5 and their Eq. (91)); it reads
1. Pessah & Chan (2008) give an asymptotic
form of the growth rate in the dissipation regime for small or of order unity Pm (see their Fig. 5 and their Eq. (91)); it reads
![]() where
where
![]() is the dissipation-free growth rate. The range of
is the dissipation-free growth rate. The range of ![]() and Pm
examined in this work spans the transition from a dissipative to a non
dissipative regime for the linear instability. The corresponding
variation of maximum growth rate with both
and Pm
examined in this work spans the transition from a dissipative to a non
dissipative regime for the linear instability. The corresponding
variation of maximum growth rate with both ![]() and
and ![]() (through the Prandtl number) is shown in Fig. 2, along with the asymptotic expressions just
recalled.
(through the Prandtl number) is shown in Fig. 2, along with the asymptotic expressions just
recalled.
![\begin{figure}
\par\includegraphics[angle=-90,width=17cm,clip]{14093fig3.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14093-10/Timg99.png)
|
Figure 3:
The dimensionless turbulent transport |
| Open with DEXTER | |
4 Numerical results
In order to explore a significant range of parameters, most of our runs are performed at a standard resolution (Nr, ![]() , Nz) = (256, 128, 64) in real space. All simulations have an
aspect ratio
, Nz) = (256, 128, 64) in real space. All simulations have an
aspect ratio
![]() ;
as argued earlier, this aspect ratio allows us to capture the fastest
growing channel and parasitic modes. Three simulations have been
performed at a resolution twice as large (512, 256, 128)
in order to reach a higher Reynolds number (
Re=20 000), and lower Prandtl numbers (down to Pm=1/16).
Note that spectral codes are intrinsically more resolved than finite
difference codes with the same number of points;
as a consequence, one needs to adopt resolutions larger by a
factor
;
as argued earlier, this aspect ratio allows us to capture the fastest
growing channel and parasitic modes. Three simulations have been
performed at a resolution twice as large (512, 256, 128)
in order to reach a higher Reynolds number (
Re=20 000), and lower Prandtl numbers (down to Pm=1/16).
Note that spectral codes are intrinsically more resolved than finite
difference codes with the same number of points;
as a consequence, one needs to adopt resolutions larger by a
factor ![]() in all directions in a finite difference code such as ZEUS, Athena or
RAMSES to obtain the same results, a point to bear in mind when
comparing our conclusions with those published in the literature with
finite difference codes (see e.g. Fromang et al. 2007, for
an explicit comparison).
in all directions in a finite difference code such as ZEUS, Athena or
RAMSES to obtain the same results, a point to bear in mind when
comparing our conclusions with those published in the literature with
finite difference codes (see e.g. Fromang et al. 2007, for
an explicit comparison).
The simulations performed in this work are in the large Reynolds number limit ( 400 < Re < 20 000). The relevant marginal stability limit depends only on Rm and is precisely given by Eq. (23). When the magnetic Reynolds number is too close to this limit, nonaxisymmetric perturbations damp out, and the flow becomes nearly identical to an axisymmetric one. We have checked that none of the simulations discussed below is affected by this issue.
With our adopted standard resolution, we can confidently resolve the dissipative scales up to Reynolds numbers
![]() .
Consequently, we have explored Reynolds numbers in the range
400-6400 and magnetic Reynolds numbers in the range
400-12 800. The magnetic Prandtl number of the simulations is either 1/4, 1 or 4. A smaller value (Pm=1/16) has also been
reached with one of our higher resolution runs with Re=20 000.
.
Consequently, we have explored Reynolds numbers in the range
400-6400 and magnetic Reynolds numbers in the range
400-12 800. The magnetic Prandtl number of the simulations is either 1/4, 1 or 4. A smaller value (Pm=1/16) has also been
reached with one of our higher resolution runs with Re=20 000.
We have performed simulations for three different vertical field strengths:
![]() ,
103, and 104.
This range is constrained by two considerations. On the low end
(large field),
one must stay away from the marginal stability limit due to the
magnetic tension. Indeed, when the incompressible MRI works too
close to this stability threshold, the flow is strongly biased by
the presence of channel modes (an effect that incompressible
simulations are more prone to capture, as exemplified in Lesur & Longaretti 2007).
On the large end (weak field), one is limited by the fact that at
some point, the flow is going to be dominated by the zero flux
transport process, whose dependence on the viscous and resistive
dissipation might be sensibly different. If one simply assumes
that one shifts from one regime to the other when the efficiency of the
transport processes are equal, one finds that the transition
between the mean field and zero net field regimes should be in the
range
,
103, and 104.
This range is constrained by two considerations. On the low end
(large field),
one must stay away from the marginal stability limit due to the
magnetic tension. Indeed, when the incompressible MRI works too
close to this stability threshold, the flow is strongly biased by
the presence of channel modes (an effect that incompressible
simulations are more prone to capture, as exemplified in Lesur & Longaretti 2007).
On the large end (weak field), one is limited by the fact that at
some point, the flow is going to be dominated by the zero flux
transport process, whose dependence on the viscous and resistive
dissipation might be sensibly different. If one simply assumes
that one shifts from one regime to the other when the efficiency of the
transport processes are equal, one finds that the transition
between the mean field and zero net field regimes should be in the
range
![]() ;
this limit applies to
;
this limit applies to ![]() (as the zero net flux transport vanishes for lower Prandtl number values), and should be somewhat dependent on Pm. As discussed later on, for our weakest field (
(as the zero net flux transport vanishes for lower Prandtl number values), and should be somewhat dependent on Pm. As discussed later on, for our weakest field (
![]() )
and smallest Prandtl (Pm=4), the flow also tends to become bidimensional for low enough Reynolds number.
)
and smallest Prandtl (Pm=4), the flow also tends to become bidimensional for low enough Reynolds number.
4.1 Transport time histories and standard deviation
Figure 3 displays the behavior of the turbulent transport for the runs we have performed at
![]() .
The simulations are typically run for 500 shear times, and the
transport average is based on the last 400. In our
horizontally extended simulation boxes, the transport fluctuations are
substantially reduced with respect to narrower boxes. Typically,
fluctuations of a factor of
.
The simulations are typically run for 500 shear times, and the
transport average is based on the last 400. In our
horizontally extended simulation boxes, the transport fluctuations are
substantially reduced with respect to narrower boxes. Typically,
fluctuations of a factor of ![]() are observed, whereas in
r:z =1:1 boxes, fluctuations of an order of
magnitude or more are common. This reduction provides more precise
averages for the transport, even though the averaging time is somewhat
smaller than what is used for boxes with a
R:Z=1:1 aspect ratio. This aspect ratio dependence is
related to the prominence of channel modes in the large transport
bursts observed in the narrow boxes (Bodo et al. 2008),
a feature related to the fact that width of the narrow box is
comparable to the correlation length of turbulent fluctuations in the
horizontal direction (Guan et al. 2009).
are observed, whereas in
r:z =1:1 boxes, fluctuations of an order of
magnitude or more are common. This reduction provides more precise
averages for the transport, even though the averaging time is somewhat
smaller than what is used for boxes with a
R:Z=1:1 aspect ratio. This aspect ratio dependence is
related to the prominence of channel modes in the large transport
bursts observed in the narrow boxes (Bodo et al. 2008),
a feature related to the fact that width of the narrow box is
comparable to the correlation length of turbulent fluctuations in the
horizontal direction (Guan et al. 2009).
![\begin{figure}
\par\includegraphics[width=7cm,clip]{14093fig4.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14093-10/Timg107.png)
|
Figure 4:
Transport standard deviation as a function of the time interval |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{14093fig5.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14093-10/Timg108.png)
|
Figure 5:
The dimensionless turbulent radial momentum transport |
| Open with DEXTER | |
The transport time history can be used to quantify the error in the determination of ![]() in the following way. From the raw time history, one can define a series of binned time histories, with a binning time
in the following way. From the raw time history, one can define a series of binned time histories, with a binning time ![]() ranging from 1 to 100 shear times
ranging from 1 to 100 shear times![]() . From these binned time histories, one can define a transport standard deviation in the usual way, i.e.,
. From these binned time histories, one can define a transport standard deviation in the usual way, i.e.,
![]() where N is the number of bins,
where N is the number of bins, ![]() itself being the average value of the transport in bin i. The resulting dependence
itself being the average value of the transport in bin i. The resulting dependence
![]() is shown in Fig. 4 for one of our runs. Two regimes can be distinguished. For
is shown in Fig. 4 for one of our runs. Two regimes can be distinguished. For
![]() ,
the deviation decreases sharply with
,
the deviation decreases sharply with ![]() ;
this is seen directly in Fig. 3, where the transport typical variation time scale is precisely in this range. For large values of
;
this is seen directly in Fig. 3, where the transport typical variation time scale is precisely in this range. For large values of ![]() ,
the transport is less and less correlated with
itself. Consequently, one expects that it should behave more or
less as a random walk, so that the standard deviation should scale
like
,
the transport is less and less correlated with
itself. Consequently, one expects that it should behave more or
less as a random walk, so that the standard deviation should scale
like
![]() .
A fit of this type is performed in Fig. 4, and appears to represent reasonably well the trend, in spite of the crudeness of the approximation.
.
A fit of this type is performed in Fig. 4, and appears to represent reasonably well the trend, in spite of the crudeness of the approximation.
From this approximation we find that the relative error in the
computation of the transport over 400 shear times is in the range ![]() .
There is no clear tendency for the larger values of the relative error
to correspond to higher transport, and no clear trend with either the
magnetic Prandtl or magnetic Reynolds number. On average,
.
There is no clear tendency for the larger values of the relative error
to correspond to higher transport, and no clear trend with either the
magnetic Prandtl or magnetic Reynolds number. On average,
![]() .
.
4.2 Physical dissipation and transport
The dependence of the transport on the dissipation for various field strengths is presented in Fig. 5 for all our standard resolution runs. This figure significantly extends the results reported in (Lesur & Longaretti 2007). Several trends can be observed:
- For a given field strength, the dependence on the magnetic Prandtl number Pm
seems to follow an approximate power law. For comparison with
our previous work, power-law fits are computed. The exponents are
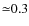 , 0.7 and 0.8 for the three values of
, 0.7 and 0.8 for the three values of 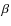 ,
in increasing order.
,
in increasing order.
- The three more resolved runs confirm this trend:
the transport is substantially larger than other runs at the same
field strength (
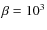 ), but the Pm dependence is consistent
with the other runs at the same
), but the Pm dependence is consistent
with the other runs at the same 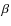 ;
this Pm dependence does not seem to saturate even though a lower Prandtl number has been achieved (1/16).
;
this Pm dependence does not seem to saturate even though a lower Prandtl number has been achieved (1/16).
- At a given Prandtl number, the transport is decreasing with decreasing field strength (increasing
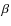 ). This trend is expected from the scaling
). This trend is expected from the scaling
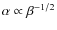 that was
first pointed out in the initial work of Hawley et al. (1995).
However, the variation of the index of the Prandtl number
dependence with field strength just discussed induces deviations from
this scaling.
that was
first pointed out in the initial work of Hawley et al. (1995).
However, the variation of the index of the Prandtl number
dependence with field strength just discussed induces deviations from
this scaling.
- There is a weaker, but systematic and significant increase of the transport with increasing Reynolds number at any given field strength and Prandtl number. This effect is real: for most of our runs, this increase is larger than the standard deviation in the transport, as quantified in the previous subsection. It is also larger for the smaller Prandtl number values. This indicates that the Prandtl number does not capture all the physics of the correlation between transport and physical dissipation; this point is further discussed below.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{14093fig6.eps}\hspace*{2cm}
\includegraphics[width=7cm,clip]{14093fig7.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14093-10/Timg120.png)
|
Figure 6:
The dimensionless transport |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{14093fig8.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14093-10/Timg121.png)
|
Figure 7:
Composite figures showing the dimensionless growth rate |
| Open with DEXTER | |
For the lowest Prandtl number (1/4) and lowest field strength (
![]() ), only one point is reported in the graph. Our other runs for this parameter have lower Reynolds numbers, and are too
close to the linear stability threshold of Eq. (23)
to sustain full 3D turbulent motions. These runs show 2D or
quasi-2D behavior, with very different transport efficiency and
behavior.
The data point we have retained might still be weakly affected by
such effects.
), only one point is reported in the graph. Our other runs for this parameter have lower Reynolds numbers, and are too
close to the linear stability threshold of Eq. (23)
to sustain full 3D turbulent motions. These runs show 2D or
quasi-2D behavior, with very different transport efficiency and
behavior.
The data point we have retained might still be weakly affected by
such effects.
As pointed out above, Fig. 5
indicates that the spread with Reynolds number at a given Prandtl
number increases with decreasing Prandtl number. In fact, two
different regimes can be
noted, one for ![]() and one for Pm =4.
and one for Pm =4.
At Pm=4, the transport seems to be only weakly dependent on Re (or Rm), at least for large enough Reynolds number: the transport increases by ![]() to
to ![]() (depending on
(depending on ![]() )
while the Reynolds number is multiplied by a factor of 4. This trend can also be found in the work of Simon & Hawley (2009), where the MRI turbulent transport in presence of a toroidal field is investigated with more emphasis on the Pm > 1 regime. Their Figs. 6 and 7 show that, for Pm=2 and 4 at least (the only ones with enough data in the Pm > 1 regime), the transport increases steadily with the Reynolds number for
)
while the Reynolds number is multiplied by a factor of 4. This trend can also be found in the work of Simon & Hawley (2009), where the MRI turbulent transport in presence of a toroidal field is investigated with more emphasis on the Pm > 1 regime. Their Figs. 6 and 7 show that, for Pm=2 and 4 at least (the only ones with enough data in the Pm > 1 regime), the transport increases steadily with the Reynolds number for
![]() and much more weakly for
and much more weakly for
![]() .
.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{14093fig9.eps}\hspace*{2cm}
\includegraphics[width=7cm,clip]{14093fig10.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14093-10/Timg127.png)
|
Figure 8:
The relation between dimensionless turbulent radial momentum transport |
| Open with DEXTER | |
On the contrary, the spread in Reynolds number for ![]() is substantial, and systematic. Such a spread was not
detected in our earlier investigation, due to the larger fluctuations
in transport related to the box aspect ratio, as discussed
earlier. In fact, this dispersion seems to be an effect of
the magnetic Reynolds number. To illustrate this point,
the transport is represented in Fig. 6 as a function of Rm (left panel) and Re (right panel), for
is substantial, and systematic. Such a spread was not
detected in our earlier investigation, due to the larger fluctuations
in transport related to the box aspect ratio, as discussed
earlier. In fact, this dispersion seems to be an effect of
the magnetic Reynolds number. To illustrate this point,
the transport is represented in Fig. 6 as a function of Rm (left panel) and Re (right panel), for ![]() ;
the colors describe different field strengths (
;
the colors describe different field strengths (
![]() to 104 from top to bottom). The statistics in the number of points at any given Re or Rm
is rather low; however, it appears quite clearly that the
dispersion of the points at any given Reynolds number is substantially
larger
in Re (with varying Rm) than in Rm (with varying Re). The largest Reynolds number data strongly support this conclusion. Furthermore, the fits
to 104 from top to bottom). The statistics in the number of points at any given Re or Rm
is rather low; however, it appears quite clearly that the
dispersion of the points at any given Reynolds number is substantially
larger
in Re (with varying Rm) than in Rm (with varying Re). The largest Reynolds number data strongly support this conclusion. Furthermore, the fits![]() of the transport as a function of Rm indicate the Rm dependence of the transport for
of the transport as a function of Rm indicate the Rm dependence of the transport for ![]() is very similar to its Pm dependence as shown in Fig. 5. This strongly suggests that the Pm dependence observed on this figure is in fact mostly a Rm dependence for
is very similar to its Pm dependence as shown in Fig. 5. This strongly suggests that the Pm dependence observed on this figure is in fact mostly a Rm dependence for ![]() .
Including the Pm=4
data destroys this correlation, which strengthens the idea that there
are two regimes, depending on the Prandtl number (a feature that
may be related to the existence of a transition around Pm=2 in zero net flux shearing box simulations). The relevant results of Simon & Hawley (2009); although less detailed, are consistent with these findings (see their Fig. 7).
.
Including the Pm=4
data destroys this correlation, which strengthens the idea that there
are two regimes, depending on the Prandtl number (a feature that
may be related to the existence of a transition around Pm=2 in zero net flux shearing box simulations). The relevant results of Simon & Hawley (2009); although less detailed, are consistent with these findings (see their Fig. 7).
5 Role of channel and parasitic modes
5.1 Linear physics and turbulent transport
Lesur & Longaretti (2007) concluded that there was no direct connection between the Prandtl dependence of MRI-driven turbulent transport and the linear growth rate of channel modes. However, the transport was substantially less precisely determined than in the present investigation, and the issue is worth reinvestigating.
To this effect, one needs to compute the linear instability growth rates for the various runs we have performed. We focus on the growth rate of the channel mode; for one thing, it is a guideline for the stability behavior of all unstable modes, and for another, there is a particular interest in the behavior of this specific mode. The resulting growth rates are numerically computed from the dispersion relation recalled in Sect. 3.1 and represented in Fig. 7. The important features to note from this figure are the following:
- The largest growth rate in the continuum limit is always represented or very nearly represented in the simulation, in spite of the discreteness imposed by the vertical boundary condition (the corresponding modes are shown by crosses on the figure). This ensures that the fastest growing channel mode is always present in our simulations.
- For the largest field strength (
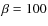 ), the growth rates of all our simulations is very close to the ideal MHD limit (
), the growth rates of all our simulations is very close to the ideal MHD limit (
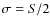 ). This is especially true of the two largest Reynolds numbers (Re=3200 and Re=6400). Note in particular for these runs that the growth rate changes by at most
). This is especially true of the two largest Reynolds numbers (Re=3200 and Re=6400). Note in particular for these runs that the growth rate changes by at most  while the transport varies by a factor of more than 3 (see left panel of Fig. 8). As a consequence the existence of the Prandtl and magnetic Reynolds
number dependences of the transport is not related to the variation of the growth rate with physical dissipation.
while the transport varies by a factor of more than 3 (see left panel of Fig. 8). As a consequence the existence of the Prandtl and magnetic Reynolds
number dependences of the transport is not related to the variation of the growth rate with physical dissipation.
- For
 ,
and for the two largest Prandtl numbers (Pm=1 and Pm=4) and largest Reynolds numbers (Re=3200 and Re=6400), the growth rate is again almost independent of the
dissipation. As there is only one captured channel mode for the
,
and for the two largest Prandtl numbers (Pm=1 and Pm=4) and largest Reynolds numbers (Re=3200 and Re=6400), the growth rate is again almost independent of the
dissipation. As there is only one captured channel mode for the 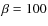 vs. four or five for
vs. four or five for
 ,
the Pm,Rm dependence is not related to the number of captured channel modes in the simulation.
,
the Pm,Rm dependence is not related to the number of captured channel modes in the simulation.
5.2 Quasi-linear physics and turbulent transport:
As indicated in the introduction and in Sect. 3, it is often assumed that the channel mode is responsible for most of the MRI-driven turbulent transport in the presence of a net vertical magnetic field. In particular Pessah & Goodman (2009) argue that the saturation of the channel mode by its parasites may help us to understand the transport. In this section, we make use of our numerical results to investigate these issues.![\begin{figure}
\par\includegraphics[width=8.15cm,clip]{14093fig11.eps}\hspace*{1cm}
\includegraphics[width=8.5cm,clip]{14093fig12.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14093-10/Timg129.png)
|
Figure 9:
One-dimensional spectrum of the transport, in the azimuthal direction,
as a function of the wavenumber |
| Open with DEXTER | |
We first disprove the first statement: the channel mode does not
clearly dominate transport, especially at the maxima of the transport,
as should in the scheme depicted in Fig. 1. This is shown explicitly in Fig. 9.
A one-dimensional Fourier transform of both the Maxwell and
Reynolds stress along the azimuthal direction is shown in this figure.
These transforms are performed at a typical minimum and maximum of
transport in the transport history of two of our runs, namely the runs
with
Re=Rm=6400 at ![]() and
and
![]() ,
respectively. The
transform is shown in terms of the wavenumber
,
respectively. The
transform is shown in terms of the wavenumber
![]() ;
n=0 corresponds to the transport due to the axisymmetric modes
(channel modes) present in the simulations, for the various
captured kz. The other wavenumbers (
;
n=0 corresponds to the transport due to the axisymmetric modes
(channel modes) present in the simulations, for the various
captured kz. The other wavenumbers (![]() )
correspond to non-axisymmetric modes. Channel modes dominate over other individual wavenumbers for
)
correspond to non-axisymmetric modes. Channel modes dominate over other individual wavenumbers for ![]() .
However, the cumulated contribution of non-axisymmetric modes is dominant by a factor
.
However, the cumulated contribution of non-axisymmetric modes is dominant by a factor ![]() at the maximum of transport for this
at the maximum of transport for this ![]() ,
and does not exceed the non-axisymmetric contribution by more than
,
and does not exceed the non-axisymmetric contribution by more than
![]() at minimum transport. For
at minimum transport. For
![]() ,
the cumulated non-axisymmetric are always dominant by a factor
,
the cumulated non-axisymmetric are always dominant by a factor ![]() .
For
.
For
![]() (not shown), the situation is somewhat intermediate between
the two extreme values presented in the figure, but the
non-axisymmetric contribution is again always dominant by a factor
several.
(not shown), the situation is somewhat intermediate between
the two extreme values presented in the figure, but the
non-axisymmetric contribution is again always dominant by a factor
several.
In summary, except for minimum transport for the largest field
strength where axisymmetric and non-axisymmetric contributions to the
transport are comparable, the non-axisymmetric contribution is
always larger by a factor ![]() .
As a result, it seems necessary at least to include
non-axisymmetric modes in the process sketched in Fig. 1.
.
As a result, it seems necessary at least to include
non-axisymmetric modes in the process sketched in Fig. 1.
Furthermore, the analysis of Pessah & Goodman (2009)
is inconsistent with our results, both from a qualitative and
quantitative point of view. Our simulations always capture the fastest
growing channel mode,
or very nearly so (see Fig. 7).
Due to the choice of aspect ratio, the fastest growing
parasitic modes are always captured as well. Finally, for ![]() and Re=3200 and 6400 (even 1600 for the two larger Pm values), the variation of the transport with Pm is quite substantial, whereas Pessah & Goodman (2009) conclude that in these conditions, the transport is independent of dissipation (see the left plot in Fig. 2
of their paper; the three Reynolds numbers values mentioned
correspond to the three largest Elsasser numbers of their graph).
and Re=3200 and 6400 (even 1600 for the two larger Pm values), the variation of the transport with Pm is quite substantial, whereas Pessah & Goodman (2009) conclude that in these conditions, the transport is independent of dissipation (see the left plot in Fig. 2
of their paper; the three Reynolds numbers values mentioned
correspond to the three largest Elsasser numbers of their graph).
6 Discussion and conclusion
Perhaps the most significant new result of this work, disclosed in Figs. 5 and 6, is the existence of a double regime separated by a critical magnetic Prandtl number
![]() .
For Pm < Pmc, at a given field strength, the transport correlates mostly with Rm; for Pm > Pmc, the transport seems to depend mostly on Pm and only weakly on either Re or Rm (once
.
For Pm < Pmc, at a given field strength, the transport correlates mostly with Rm; for Pm > Pmc, the transport seems to depend mostly on Pm and only weakly on either Re or Rm (once
![]() ), although a larger number of Pm values need to be probed on this issue. It is tempting to assume
), although a larger number of Pm values need to be probed on this issue. It is tempting to assume
![]() ,
as this is the critical value for the zero mean field problem,
but this identification requires further work to be substantiated.
The identification of this double dissipation regime was made possible
by the increased accuracy, with respect to our previous work,
in the determination of the transport averages. In the small
Prandtl regime, in contrast to the large one, our most resolved
simulations show no sign of convergence with respect to dissipation,
although values of Rm up to 20 000 have been reached.
,
as this is the critical value for the zero mean field problem,
but this identification requires further work to be substantiated.
The identification of this double dissipation regime was made possible
by the increased accuracy, with respect to our previous work,
in the determination of the transport averages. In the small
Prandtl regime, in contrast to the large one, our most resolved
simulations show no sign of convergence with respect to dissipation,
although values of Rm up to 20 000 have been reached.
The role of linear physics and parasitic modes on transport properties has also been investigated, and the major results on these questions can be summarized as follows:
- The existence of the dependence of turbulent transport on dissipation is not related to the role of dissipation on linear modes growth rates.
- The existence of the correlation of transport with dissipation is not related to the number of channel modes captured in the simulations.
- Saturation of the channel modes growth by parasitic modes is not the responsible for correlation of transport with dissipation. This is hardly surprising as both the channel and parasitic modes are large scale modes, that are expected to be little affected by dissipation, whereas the trends of the transport with dissipation are substantial.
- Furthermore, the transport is usually not dominated by axisymmetric modes; these modes contribute at most at the same level as non-axisymmetric modes for the strongest fields investigated, and have negligible contributions for the weakest fields.
It is worth pointing out that our results do not totally disqualify a saturation of the unstable linear modes by the parasitic modes; only the relevance of this process to the relation between transport and physical dissipation has been disproved.
The role of the Prandtl number disclosed in this investigation
makes more physical sense than a direct dependence of the transport
on Pm. Indeed, it is very likely that the critical value Pmc relates to the switching of the magnetic and kinetic dissipations scales ![]() and
and ![]() in Fourier space: for Pm < Pmc (resp. Pm > Pmc),
in Fourier space: for Pm < Pmc (resp. Pm > Pmc),
![]() (resp.
(resp.
![]() ). For
). For ![]() ,
,
![]() ,
the flow at scales k > or
,
the flow at scales k > or
![]() in Fourier space is therefore purely hydrodynamic. As information flows from small k to large k in this scale range, the flow should be independent of Re, so that in this regime
in Fourier space is therefore purely hydrodynamic. As information flows from small k to large k in this scale range, the flow should be independent of Re, so that in this regime
![]() is expected. The transport may even become independent of Rm at large enough Rm
in the absence of backreaction of the small scales on the large ones,
and if energy exchanges are not strongly nonlocal in Fourier space. We
merely note here that in the context of homogeneous, isotropic,
incompressible MHD turbulence, all energy transfers are direct
(from small k to large k); exchanges between magnetic and kinetic energy are nonlocal in Fourier space (Alexakis et al. 2007), although this nonlocality seems to be of finite (albeit large) extent (Aluie & Eyink 2010).
The situation is more complex in the large Prandtl regime,
as non-local transfers and small scale dynamo action might take
place at scales smaller than the viscous dissipation scale, and further
investigations are required to characterize the properties of the small
dissipation limit, in particular concerning the locality
of transfers.
is expected. The transport may even become independent of Rm at large enough Rm
in the absence of backreaction of the small scales on the large ones,
and if energy exchanges are not strongly nonlocal in Fourier space. We
merely note here that in the context of homogeneous, isotropic,
incompressible MHD turbulence, all energy transfers are direct
(from small k to large k); exchanges between magnetic and kinetic energy are nonlocal in Fourier space (Alexakis et al. 2007), although this nonlocality seems to be of finite (albeit large) extent (Aluie & Eyink 2010).
The situation is more complex in the large Prandtl regime,
as non-local transfers and small scale dynamo action might take
place at scales smaller than the viscous dissipation scale, and further
investigations are required to characterize the properties of the small
dissipation limit, in particular concerning the locality
of transfers.
The behavior of MRI-driven turbulence with respect to these
various issues will be reported elsewhere, through the analysis of
energy transfers in Fourier space. More generally, investigating
the possible independence of transport with respect to dissipation in
the
![]() or
or
![]() limits requires to achieve a double scale separation: one must first
separate in Fourier
space the smallest injection scales (the scales which contribute
to the Reynolds and Maxwell stresses) from the largest dissipation
scales, and then the two dissipation scales themselves. This is
extremely demanding in terms of resolution. Our simulations in the
small Prandtl regime are consistent with a separation of dissipation
scales nearly achieved. As a first step at small Prandtl
(the most critical regime for YSO disks), one can achieve one
or the other of the two scales separation. Such investigations are
underway and will be reported elsewhere.
limits requires to achieve a double scale separation: one must first
separate in Fourier
space the smallest injection scales (the scales which contribute
to the Reynolds and Maxwell stresses) from the largest dissipation
scales, and then the two dissipation scales themselves. This is
extremely demanding in terms of resolution. Our simulations in the
small Prandtl regime are consistent with a separation of dissipation
scales nearly achieved. As a first step at small Prandtl
(the most critical regime for YSO disks), one can achieve one
or the other of the two scales separation. Such investigations are
underway and will be reported elsewhere.
These questions are critical for astrophysical disk dynamics, where the Reynolds numbers are always very large (
![]() ,
while the Prandtl number spans very small (
,
while the Prandtl number spans very small (
![]() ,
YSO disks) to very large values (
,
YSO disks) to very large values (
![]() ,
AGN disks). Addressing these issues requires to overcome a number
of limitations in the simulations. Besides the questions of scale
separation and nonlocality of transfers in Fourier space just
mentioned, the role of compressibility and vertical stratification on
these results must be quantified. These questions can certainly be
investigated in shearing boxes, but global simulations are
probably still largely out of reach, due to the resolution demand.
Also (and probably as much importantly), different dissipation
regimes must be analyzed in the context of YSOs, namely the
ambipolar and Hall regime, which are known to have substantial effect
on the linear development of the MRI, while being relevant for large
fractions of YSO disks.
,
AGN disks). Addressing these issues requires to overcome a number
of limitations in the simulations. Besides the questions of scale
separation and nonlocality of transfers in Fourier space just
mentioned, the role of compressibility and vertical stratification on
these results must be quantified. These questions can certainly be
investigated in shearing boxes, but global simulations are
probably still largely out of reach, due to the resolution demand.
Also (and probably as much importantly), different dissipation
regimes must be analyzed in the context of YSOs, namely the
ambipolar and Hall regime, which are known to have substantial effect
on the linear development of the MRI, while being relevant for large
fractions of YSO disks.
The simulations presented in this work have been performed on the French national supercomputing center at IDRIS. PYL acknowledges the hospitality of the Isaac Newton Institute in Cambridge where most of the data analysis has been done. GL acknowledges support from STFC. The authors thank Sébastien Fromang and an anonymous referee for their comments on a first version of this work.
References
- Alexakis, A., Mininni, P. D., & Pouquet, A. 2007, New J. Phys., 9, 298 [NASA ADS] [CrossRef] [Google Scholar]
- Aluie, H., & Eyink, G. L. 2010, Phys. Rev. Lett., 104, 081101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Balbus, S. A. 2003, ARA&A, 41, 555 [NASA ADS] [CrossRef] [Google Scholar]
- Balbus, S. A., & Hawley, J. F. 1991, ApJ, 376, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Balbus, S. A., & Hawley, J. F. 1992, ApJ, 400, 610 [CrossRef] [Google Scholar]
- Bodo, G., Mignone, A., Cattaneo, F., Rossi, P., & Ferrari, A. 2008, A&A, 487, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cabot, W. 1996, ApJ, 465, 874 [NASA ADS] [CrossRef] [Google Scholar]
- Fromang, S., Papaloizou, J., Lesur, G., & Heinemann, T. 2007, A&A, 476, 1123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gammie, C. F. 1996, ApJ, 457, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Gardiner, T. A., & Stone, J. M. 2005, J. Comput. Phys., 205, 509 [Google Scholar]
- Goodman, J., & Xu, G. 1994, ApJ, 432, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Guan, X., Gammie, C. F., Simon, J. B., & Johnson, B. M. 2009, ApJ, 694, 1010 [NASA ADS] [CrossRef] [Google Scholar]
- Hawley, J. F. 2000, ApJ, 528, 462 [NASA ADS] [CrossRef] [Google Scholar]
- Hawley, J. F., Gammie, C. F., & Balbus, S. A. 1995, ApJ, 440, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Hawley, J. F., Gammie, C. F., & Balbus, S. A. 1996, ApJ, 464, 690 [NASA ADS] [CrossRef] [Google Scholar]
- Heinemann, T., & Papaloizou, J. C. B. 2009a, MNRAS, 397, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Heinemann, T., & Papaloizou, J. C. B. 2009b, MNRAS, 397, 64 [Google Scholar]
- Ji, H., Burin, M., Schartman, E., & Goodman, J. 2006, Nature, 444, 343 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Johnson, B. M., & Gammie, C. F. 2006, ApJ, 636, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Klahr, H. H., & Bodenheimer, P. 2003, ApJ, 582, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Latter, H. N., Lesaffre, P., & Balbus, S. A. 2009, MNRAS, 394, 715 [NASA ADS] [CrossRef] [Google Scholar]
- Lesur, G., & Longaretti, P.-Y. 2005, A&A, 444, 25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lesur, G., & Longaretti, P.-Y. 2007, MNRAS, 378, 1471 [NASA ADS] [CrossRef] [Google Scholar]
- Lesur, G., & Ogilvie, G. I. 2008a, MNRAS, 391, 1437 [NASA ADS] [CrossRef] [Google Scholar]
- Lesur, G., & Ogilvie, G. I. 2008b, A&A, 488, 451 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lesur, G., & Papaloizou, J. C. B. 2009, A&A, 498, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lesur, G., & Ogilvie, G. I. 2010, MNRAS, 404, L64 [NASA ADS] [Google Scholar]
- Lesur, G., & Papaloizou, J. C. B. 2010, A&A, 513, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pessah, M. E., & Chan, C.-k. 2008, ApJ, 684, 498 [NASA ADS] [CrossRef] [Google Scholar]
- Pessah, M. E., & Goodman, J. 2009, ApJ, 698, L72 [NASA ADS] [CrossRef] [Google Scholar]
- Pessah, M. E., Chan, C.-k., & Psaltis, D. 2007, ApJ, 668, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Petersen, M. R., Stewart, G. R., & Julien, K. 2007, ApJ, 658, 1252 [NASA ADS] [CrossRef] [Google Scholar]
- Peyret, R. 2002, Spectral Methods for Incompressible Viscous Flow (Springer) [Google Scholar]
- Regev, O., & Umurhan, O. M. 2008, A&A, 481, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Richard, D., & Zahn, J. 1999, A&A, 347, 734 [NASA ADS] [Google Scholar]
- Sano, T., & Miyama, S. M. 1999, ApJ, 515, 776 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, J. B., & Hawley, J. F. 2009, ApJ, 707, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Stone, J. M., & Balbus, S. A. 1996, ApJ, 464, 364 [NASA ADS] [CrossRef] [Google Scholar]
- Stone, J. M., Hawley, J. F., Gammie, C. F., & Balbus, S. A. 1996, ApJ, 463, 656 [NASA ADS] [CrossRef] [Google Scholar]
- Umurhan, O. M., & Regev, O. 2004, A&A, 427, 855 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Footnotes
- ... field
![[*]](/icons/foot_motif.png)
- The definition of
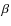 (ratio of gas to magnetic field pressure) is based on the mean field,
a conserved quantity in the settings used in these simulations.
(ratio of gas to magnetic field pressure) is based on the mean field,
a conserved quantity in the settings used in these simulations.
- ... alone
![[*]](/icons/foot_motif.png)
- The linear stability dependence on viscosity and resistivity is totally different.
- ... field
![[*]](/icons/foot_motif.png)
- We measure the magnetic field in units of Alfvén speed.
- ... times
![[*]](/icons/foot_motif.png)
- For
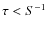 ,
the transport statistics depends very little on the binning time, while for
,
the transport statistics depends very little on the binning time, while for
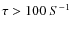 ,
the statistics is too poor to be meaningful.
,
the statistics is too poor to be meaningful.
- ... fits
![[*]](/icons/foot_motif.png)
- The Re=20 000 data points have not been included in this fit to make the comparison between the two dependences in the same conditions.
All Figures
| |
Figure 1: Cartoon of the process that may be at the origin of the saturation of the transport in shearing box simulations of MRI with a net vertical field (see text). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{14093fig2.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14093-10/Timg95.png)
|
Figure 2:
Maximal growth rate
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=17cm,clip]{14093fig3.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14093-10/Timg99.png)
|
Figure 3:
The dimensionless turbulent transport |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{14093fig4.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14093-10/Timg107.png)
|
Figure 4:
Transport standard deviation as a function of the time interval |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{14093fig5.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14093-10/Timg108.png)
|
Figure 5:
The dimensionless turbulent radial momentum transport |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{14093fig6.eps}\hspace*{2cm}
\includegraphics[width=7cm,clip]{14093fig7.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14093-10/Timg120.png)
|
Figure 6:
The dimensionless transport |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{14093fig8.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14093-10/Timg121.png)
|
Figure 7:
Composite figures showing the dimensionless growth rate |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{14093fig9.eps}\hspace*{2cm}
\includegraphics[width=7cm,clip]{14093fig10.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14093-10/Timg127.png)
|
Figure 8:
The relation between dimensionless turbulent radial momentum transport |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.15cm,clip]{14093fig11.eps}\hspace*{1cm}
\includegraphics[width=8.5cm,clip]{14093fig12.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14093-10/Timg129.png)
|
Figure 9:
One-dimensional spectrum of the transport, in the azimuthal direction,
as a function of the wavenumber |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.