| Issue |
A&A
Volume 516, June-July 2010
|
|
|---|---|---|
| Article Number | A79 | |
| Number of page(s) | 8 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201014057 | |
| Published online | 19 July 2010 | |
The reaction between NH3+ and CH3COOH: a possible process for the formation of glycine precursors in the interstellar medium
L. Largo - P. Redondo - V. M. Rayón - A. Largo - C. Barrientos
Computational Chemistry Group, Universidad de Valladolid, Departamento de Química Física Facultad de Ciencias, 47005 Valladolid, Spain
Received 13 January 2010 / Accepted 22 March 2010
Abstract
Context. The formation of glycine is strongly relevant to
our understanding of the interstellar medium and is most accuretely
studied computationally.
Aims. We carry out a theoretical study of the reactions between the radical cation of ammonia and CH3COOH/CH2COOH as possible processes leading to glycine derivatives.
Methods. The gas-phase reactions were theoretically studied
using ab initio methods. We employed the second-order Moller-Plesset
level in conjunction with the cc-pVTZ basis set. In addition, the
electronic energies were refined by means of single-point calculations
at the CCSD(T) level on the MP2/cc-pVTZ geometries with the aug-cc-pVTZ
basis set.
Results. We report accurate potential energy surfaces for the
reactions considered in this work. The different intermediate species
as well as the most relevant transition states for these reactions are
characterized.
Conclusions. Formation of protonated glycine from the reaction of NH3+
with acetic acid is an exothermic (-9.15 kcal/mol at CCSD(T)
level) barrier free process. However, the results obtained indicate
that the hydrogen-transfer process forming NH4+ and CH2COOH
is clearly the dominating path, in agreement with the experimental
evidence. The formation of ionized glycine from the reaction of product
CH2COOH with NH3+ is a
quasi-isoenergetic (2.03 kcal/mol at CCSD(T) level) barrier free
process that leads to a highly stable intermediate: protonated glycine.
Key words: astrochemistry - astrobiology - molecular processes - molecular data - methods: numerical
1 Introduction
There has been an increasing fascination with the complexity of interstellar chemistry and the existence of interstellar molecules of biological interest. In particular, the formation of biomolecules in space constitutes an open question about the origin of life. It has been argued that interstellar amino acid formation could precede the syntheses of more complex systems in space (Wincel et al. 2000). Astrochemical models, laboratory experiments, and theoretical studies have aided in understanding the formation of different organic molecules in interstellar clouds, the regions where stars and planetary systems could be formed. If organic matter were to have been formed in the interstellar regions by gas phase reactions or reactions catalyzed by dust grains, interstellar bodies might have deposited this matter on Earth in the pre-life era which would indicate that these bodies play an essential role in the formation of life. Among the biologically important molecules the amino acids, as key building blocks of proteins and peptides, deserve special attention. The presence of amino acids in the interstellar medium would be of crucial importance to understanding the possible pathways in the origin of life in the Universe. Nevertheless, after more than two decades of continuous searches in space no convincing detection of even the simplest amino acid, glycine, has been reported (Brown et al. 1979; Hollis et al. 1980; Snyder et al. 1983; Combes et al. 1996; Ceccarelli et al. 2000; Kuan et al. 2003; Hollis et al. 2003a,b; Snyder et al. 2005; Guélin et al. 2008).
The observational difficulties associated with the detection of amino acids in line-rich, compact, hot molecular cores can be summarized in two points:
- amino acids have limited photostability (Ehrenfreund et al. 2001). Amino acids in the gas phase will probably be destroyed during the lifetime of a typical interstellar cloud, even when exposed to ultraviolet photons of relatively low energy. However, this does not preclude the amino acids in meteorites having formed in the interstellar medium; it only requires that amino acids be shielded from UV in protected environments, such as dense molecular clouds and hot cores (star-forming regions);
- amino acids constitute relatively large molecules and their rotational spectrum contains weak lines due to large molecular partition functions and contamination of the target transitions by emission from many other molecules in the hot molecular cores and their accompanying extended molecular envelopes (Combes et al. 1996).
Different reaction pathways leading to glycine have been proposed involving relatively abundant interstellar organic molecules. Hoyle & Wickramasinghe (1976) suggested the formation of glycine from the reaction of methanimine (HNCH2) and formic acid (HCOOH) since these compounds had been observed in dense molecular clouds of comparable abundance. In this context, Basiuk & Bogillo (2000), Basiuk (2001), and Basiuk & Kobayashi (2002) carried out a theoretical study of amino-acid-precursor formation in the interstellar medium considering different pathways that include the participation of methanimine and methanimine-related cations, HNCH+ and H2NCH2+. Their studies demonstrated that although the reactions considered are exothermic they are not feasible under the interstellar conditions because of the high energy transition states and the possibility of competitive formation of side products.
Based on the Miller experiment (Miller 1953),
involving the synthesis of amino acids under conditions that simulated
primitive Earth's atmosphere from simple organic molecules, Maeda &
Ono (2004) considered a two-step
synthetic route of glycine with no activation barriers. The route is
composed of an addition reaction of ammonia with singlet methylene
yielding ammonium ylide (NH3 + CH2
![]() H2CNH3) followed by carboxilation of the ylide with carbon dioxide (H2CNH3 + CO2
H2CNH3) followed by carboxilation of the ylide with carbon dioxide (H2CNH3 + CO2
![]() H2NCH2COOH).
H2NCH2COOH).
Other authors (Bernstein et al. 2002) have reported a laboratory demonstration that amino acids can be naturally formed from ultraviolet photolysis of icy interstellar grains containing small amounts of materials such as methanol, ammonia, and hydrogen cyanide. The study suggests that at least some meteoritic amino acids are the result of interstellar photochemistry rather than formation in liquid water on an early Solar System body. In addition, different theoretical works (Woon 2001, 2002a,b) have been devoted to the study of the viability of various pathways in forming amino acids in astrophysical ices.
The possibility of synthesizing amino acids from simple interstellar species by means of gas-phase ion-molecule reactions initiated by cosmic and ultraviolet radiation was discussed by Herbst (2001) in his work about the chemistry of interstellar space.
In this context, different synthetic means of producing glycine and alanine have been proposed (Blagojevic et al. 2003; Snow et al. 2007; Jackson et al. 2005a,b)
involving the joining of amine and carboxyl functional groups. In
particular, theoretical and experimental works (Blagojevic et al. 2003; Snow et al. 2007)
have dealt with the study of gas-phase synthesis of amino acids from
smaller molecules found in the space. From these studies, the formation
of both ionized/protonated glycine and ![]() -alanine in the interstellar medium was inferred to occur by means of the reactions of ionized/protonated hydroxylamine, NH2,3OH+ with acetic and propanoic acids, respectively. However, we note that NH2,3OH+ has not yet been detected in the interstellar medium.
-alanine in the interstellar medium was inferred to occur by means of the reactions of ionized/protonated hydroxylamine, NH2,3OH+ with acetic and propanoic acids, respectively. However, we note that NH2,3OH+ has not yet been detected in the interstellar medium.
To seek a viable formation pathway for producing amino acids from interstellar molecules, Jackson et al. (2005a,b)
carried out a selected ion flow tube (SIFT) study of two types of
ion-molecule reactions: a) reactions between a sequence of ions such as
N+, N2+, HCOOH2+, CH3COOH2+![]() with neutral amine species, CH3NH2 and CH3CH2NH2 (Jackson et al.2005a,b); and b) reactions of positively charged ammonia and amine ion fragments, NH2+, NH3+, and HCNH+ with neutral species, HCOOH, CH3COOH, and CH3OCHO (Jackson et al. 2005b).
with neutral amine species, CH3NH2 and CH3CH2NH2 (Jackson et al.2005a,b); and b) reactions of positively charged ammonia and amine ion fragments, NH2+, NH3+, and HCNH+ with neutral species, HCOOH, CH3COOH, and CH3OCHO (Jackson et al. 2005b).
We performed a preliminary theoretical study of possible ion-molecule reactions leading to precursors of interstellar glycine (Largo et al. 2004), including predictions of their reaction enthalpies at different levels of theory. One of our main conclusions was that the reactions between both NH2+ and NH3+ with acetic acid were promising because the formation of glycine precursors (ionized and protonated glycine, respectively) were exothermic. For these exothermic processes, and to ascertain whether energetic barriers are present, a full exploration of the potential energy surface was required. To complete our early study, we carried out a theoretical study of the reaction of NH2+ with acetic acid considering both the singlet and triplet potential energy surfaces (Largo et al. 2008). Our work suggests that the formation of ionized glycine from the route considered is a feasible process under interstellar conditions (exothermic and barrier free). However, we found two more favourable channels, namely proton transfer and the formation of NH3 + CH2COOH+.
The reaction between the radical cation of ammonia and acetic acid was previously studied by selected ion flow tube experiments (Jackson et al. 2005b). The authors concluded that NH3+ reacts with CH3COOH via H atom abstraction giving NH4+ + CH2COOH, this product being more thermodynamically stable than the CH3COO radical. In this work, we consider whether the radicals generated by the NH3+ abstraction reaction, CH2COOH, play a role in forming interstellar amino acids. On the other hand, Blagojevic et al. (2003) argued that the reaction of NH3+ with CH3COOH does not produce ionized glycine but instead the acetohydroximic acid cation, CH3CONHOH+.
Following on from our previous studies (Largo et al. 2004, 2008), we focused on the reaction of the radical cation of ammonia with acetic acid as a possible gas-phase reaction that could produce interstellar protonated glycine. In addition, to address previous experimental suggestions (Jackson et al. 2005b), we considered the reaction between NH3+ and the CH2COOH radical. We present estimations of the geometries of the different species involved in both reactions and reaction enthalpies for the possible products. We also carried out a detailed analysis of the corresponding potential energy surfaces. We note that the reactants considered in this study have been identified in the interstellar medium. Acetic acid was detected in one core source within the giant molecular cloud complex Sagitarius B2 (Mehringher et al. 1997) and hot cores are rich in ammonia (Ehrenfreund 2000). Theoretical studies in the field of the interstellar chemistry are especially suitable because the conditions of the molecular clouds are appropriate for the application of theoretical methods.
2 Computational methods
The geometries and harmonic vibrational frequencies of the minima and transitions states involved in the reactions of NH3+ with CH3COOH or CH2COOH were computed at the second-order Moller-Plesset level in conjunction with the cc-pVTZ (correlation-consistent polarized valence triple-zeta) basis set developed by Dunning (1989). The nature of each optimized structure on the corresponding potential surfaces was checked by calculating vibrational frequencies; these computations also allow us to estimate zero-point vibrational energy (ZPVE) corrections.
Electronic energies were refined by means of single-point calculations at the CCSD(T) level (coupled cluster single and double excitation model augmented with a non-iterative treatment of triple excitations) (Raghavachari et al. 1989) on the MP2/cc-pVTZ geometries with the aug-cc-pVTZ basis set, which also includes diffuse functions. In this case, ZPVE corrections were included at the MP2/cc-pVTZ level.
The intrinsic reaction coordinate (IRC) technique (Gonzalez & Schelegel 1989, 1990) was used to check the connections between transition-state structures and adjacent minima.
All calculations were performed with the Gaussian-98 program package (Frisch at al. 1998).
3 Results and discussion
3.1 Reaction of NH3+ with CH3COOH
Given the multiplicity of the reactants, NH3+ (2A
![]() ), CH3COOH (1A
), CH3COOH (1A![]() ),
the reaction takes place on the doublet potential energy surface; we
therefore characterized the possible intermediate species as well as
the relevant transition states in this potential energy surface. For
systems involving polyatomic molecules of the present level, building
an explicit potential energy surface, is difficult because of a large
number of possible competitive processes, which are difficult to
account for. Consequently, we limited our study to the search for the
most important stationary points and estimates of energetic feasibility
for some selected reactions.
),
the reaction takes place on the doublet potential energy surface; we
therefore characterized the possible intermediate species as well as
the relevant transition states in this potential energy surface. For
systems involving polyatomic molecules of the present level, building
an explicit potential energy surface, is difficult because of a large
number of possible competitive processes, which are difficult to
account for. Consequently, we limited our study to the search for the
most important stationary points and estimates of energetic feasibility
for some selected reactions.
![\begin{figure}
\par\includegraphics[width=4.8cm,angle=-90]{14057fg1a.ps} \includegraphics[width=6.1cm,angle=-90]{14057fg1b.ps}
\end{figure}](/articles/aa/full_html/2010/08/aa14057-10/Timg8.png)
|
Figure 1: MP2/cc-pVTZ optimized geometries for the different (NO2C2H7)+ minima. Distances are given in angstroms and angles in degrees. |
| Open with DEXTER | |
Figure 1 depicts the optimized geometrical parameters, at the MP2/cc-pVTZ level of theory, of the (NO2C2H7)+ isomers that are relevant to the reaction of NH3+ with CH3COOH. The relative energies, including zero-point vibrational energy differences (MP2/cc-pVTZ level), at both MP2/cc-pVTZ//MP2/cc-pVTZ and CCSD(T)/aug-cc-pVTZ//MP2/cc-pVTZ levels, are collected in Table 1. All the intermediates shown in this table present real vibrational frequencies and are therefore true minima on the potential surface.
From the examination of the different structures shown in Fig. 1, it can be inferred that isomer I1 is obtained from the direct approach of the hydrogen atom of the NH3 group to the carbonylic oxygen of acetic acid. On the other hand, isomer I2 results from the interaction of the hydrogen atom of NH3+ with the carbonylic oxygen of CH3COOH and abstraction of the hydrogen atom of the methyl group to the nitrogen atom. Isomer I5 is produced by the approach of one hydrogen atom of NH3+ to the hydroxylic oxygen of acetic acid. Isomers I6 and I7 correspond to the interaction between the nitrogen atom of NH3+ and the carbonylic oxygen of CH3COOH. Finally, isomers I3 and I4 are produced by the approach of the nitrogen atom of the NH3+ ion to the carbon atom of methyl group of acetic acid and abstraction of hydrogen atom of the methyl group to carbonylic oxygen.
Analyzing the optimized geometries from a quantitative viewpoint, we can see that, apart from isomer I2, all intermediates depicted in Fig. 1 have similar C-C bond distances (in the range of 1.486 Å to 1.493 Å), which are typical of carbon-carbon single bonds. The C-C bond distance in isomer I2, 1.445 Å, suggests a certain degree of double character.
Table 1: Relative energies (kcal/mol) for the relevant intermediates.
In term of energetics, Table 1
shows that the two levels of theory employed predict similar stability
order for the different intermediates. The CCSD(T)/aug-cc-pVTZ level
tends to predict slightly lower relative energies than the MP2/cc-pVTZ
level. At both MP2/cc-pVTZ and CCSD(T)/aug-cc-pVTZ levels of theory,
the global minimum is predicted to be clearly isomer I2. The stability
order of the different isomers is (>means more stable than)
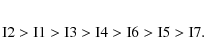
In principle, acetic acid may react with the radical cation of ammonia to produce protonated glycine, although other different products could be formed:
|
|
![$\left\{ \begin{array}{lr}
\rm NH_{3}CH_{2}COOH^{+} (c1) + H & [A] \\
\rm NH_...
...{3}COOH^{+} & [I]\\
\rm NH_{4} + CH_{2}COOH^{+} & [J].\\
\end{array}\right.$](/articles/aa/full_html/2010/08/aa14057-10/img14.png)
|
As we previously mentioned, because of the typical conditions reigning in the interstellar medium (basically low density and low temperature), only reactions that are exothermic and barrier free may play a significant role in interstellar chemistry. Accordingly, we first will calculate the reaction energies for the different processes considered.
Table 2: Relative energies (kcal/mol) for the possible products.
In Table 2, we collected
the relative energies with respect to reactants, at
MP2/cc-pVTZ//MP2/cc-pVTZ and CCSD(T)/aug-cc-pVTZ//MP2/cc-pVTZ levels of
theory, of the possible products that can be formed in the reaction
between NH3+ and CH3COOH. Zero-point
vibrational energy differences were included (MP2/cc-pVTZ level). In
some cases, two possible conformations (referred to as a quasi cis
conformer) and t- (a quasi trans conformer) are considered. The
optimized geometries for reactants and products are given, as Online
Material, in Fig. A.1.
Examination of the energetics showed in Table 2
allows us to infer that the formation of protonated glycine, through
channels A and B, leading, respectively, to the lowest
conformation c1 (consisting of an intramolecular hydrogen bond between
a hydrogen atom of NH3 and the carbonylic oxygen) and to the
second most stable conformer c2 (where the hydrogen bond is connected
to the less basic hydroxilic oxygen) of protonated glycine are
exothermic processes. However, the most favorable process, from
thermodynamical arguments, is the formation of ammonium cation and CH2COOH (channel C) in consonance with the SIFT experiments (Jackson et al. 2005b). In this case, we emphasize that the reaction may also form the CH3COO
radical via extraction of the carboxylic H, although this was reported
to be less thermodynamically and structurally stable (Schalley et al. 1998; Butkovskaya et al. 2004).
Our results for this process are in agreement with this assertion. The
relative energy with respect to the reactants for the formation of NH4+ + CH3COO is
![]() kcal/mol at CCSD(T) level and -6.95 kcal/mol at MP2 level. On the other hand, the reaction between NH3+ + CH3COOH
to produce ionized glycine (Channel D) is a slightly exothermic process
(quasi-isoenergetic). Following the comment of Blagojevic et al. (2003), we also considered the formation of acetohydroximic acid cation CH3CONHOH+ and CH3CONH2OH+ produced by inserting NH3+ into the C-OH bond and the subsequent elimination of H2 or H, respectively (channels E and H). Nevertheless, these reactions clearly seem endothermic at both levels of theory (
kcal/mol at CCSD(T) level and -6.95 kcal/mol at MP2 level. On the other hand, the reaction between NH3+ + CH3COOH
to produce ionized glycine (Channel D) is a slightly exothermic process
(quasi-isoenergetic). Following the comment of Blagojevic et al. (2003), we also considered the formation of acetohydroximic acid cation CH3CONHOH+ and CH3CONH2OH+ produced by inserting NH3+ into the C-OH bond and the subsequent elimination of H2 or H, respectively (channels E and H). Nevertheless, these reactions clearly seem endothermic at both levels of theory (
![]() kcal/mol
and 48.62 kcal/mol respectively at CCSD(T) level). Charge transfer
products and the remaining processes studied are endothermic.
kcal/mol
and 48.62 kcal/mol respectively at CCSD(T) level). Charge transfer
products and the remaining processes studied are endothermic.
![\begin{figure}
\par\includegraphics[width=4.8cm,angle=-90]{14057fg2a.ps} \includegraphics[width=5.7cm,angle=-90]{14057fg2b.ps} \vspace*{2.5mm}
\end{figure}](/articles/aa/full_html/2010/08/aa14057-10/Timg17.png)
|
Figure 2:
MP2/cc-pVTZ optimized geometries for the relevant transition states involved in the reaction of NH3+ (2A
|
| Open with DEXTER | |
The exothermicity is a necessary, but not a sufficient argument for a reaction to be plausible under interstellar conditions. In addition to this energetic requirement, interstellar reactions should be barrier free. We therefore carried out a full exploration of the potential surface, to analyze the feasibility of the reactions studied as a source of precursors of glycine in the interstellar medium.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{14057fg3.ps}
\end{figure}](/articles/aa/full_html/2010/08/aa14057-10/Timg18.png)
|
Figure 3:
Energy profile, in kcal/mol, for the reaction of NH3+ (2A
|
| Open with DEXTER | |
Figure 2 shows the geometries of the more relevant transition states, whereas the energy profile for the NH3+ + CH3COOH reaction is represented in Fig. 3.
As already mentioned, the MP2 and CCSD(T) energetics are in good agreement. Reaction between NH3+
and the acetic acid starts with the barrierless approximation of the
radical cation of ammonia to the carbonyl oxygen atom in CH3COOH giving rise to a rather stable intermediate I1 (
![]() kcal/mol at CCSD(T) level)
kcal/mol at CCSD(T) level)
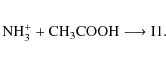
The exothermic formation of intermediate I1 produces an energy reservoir that is used as the reaction proceeds toward the products. After forming the intermediate I1, different processes can take place. Intermediate I1 can proceed to the most stable conformer of protonated glycine through an exothermic and barrier free path, a.1:
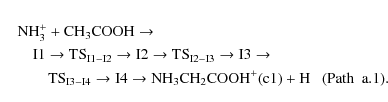
Once structure I1 is obtained, the hydrogen atom migration from the carbon atom to the nitrogen one, through the transition state TSI1-I2, leads to the most stable intermediate I2 (
Protonated glycine can also be obtained from other two different paths. One of them, path a.2, involves the approach of the NH3 group to the carbon atom and simultaneous H atom elimination from carbon through transition state TS1:
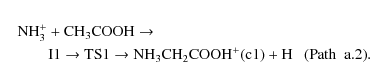
This process has a significant activation barrier (36.64 kcal/mol at CCSD(T) level of theory). The third path (a.3), which also leads to the formation of the most stable conformer of protonated glycine, involves one isomerization process from isomer I1 to I2, also considered in path a.1, followed by hydrogen atom elimination from nitrogen and subsequent migration of NH3 from oxygen atom to carbon one through transition state TS2:
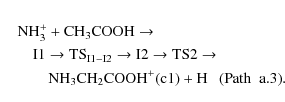
Again, transition state TS2 is clearly located (56.96 kcal/mol at CCSD(T) level of theory) above the reactants in the potential energy surface. In conclusion, none of the paths a.2 and a.3 is energetically feasible under the interstellar conditions.
![\begin{figure}
\par\includegraphics[width=11cm]{14057fg4.ps}
\end{figure}](/articles/aa/full_html/2010/08/aa14057-10/Timg25.png)
|
Figure 4:
Energy profile, in kcal/mol, for the reaction of NH3+ (2A
|
| Open with DEXTER | |
The second most stable conformer of protonated glycine, NH3CH2COOH+ (c2), could be formed through the following path
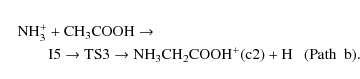
The reaction starts with the approach of the ammonia radical cation to the hydroxilic oxygen of acetic acid giving intermediate I5. Once I5 is obtained, the migration of the NH3 group from oxygen to carbon through the transition state TS3 and the subsequent elimination of a hydrogen atom from carbon, produces protonated glycine (c2). This path has a significant activation barrier (39.14 kcal/mol at CCSD(T) level) and consequently should not be relevant under interstellar conditions.
Finally, we must consider another channel originating from the most
stable intermediate, I2, and subsequent fragmentation into ammonium
cation and CH2COOH
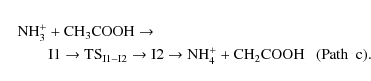
As can be seen from Fig. 3, path c constitutes the most favourable process from both thermodynamic and kinetic arguments. Our theoretical calculations are in agreement with the previous results obtained from SIFT experiments for this reaction (Jackson et al. 2005b). As mentioned before, the formation of ionized glycine (channel C) is a slightly exothermic process. However, we were not able to identify paths that form this product, since all our attempts led to the formation of protonated glycine.
3.2 Reaction of NH3+ with CH2COOH
Following the suggestion of Jackson et al. (2005b) and to check whether the radical generated by the NH3+
atom abstraction reaction could play a role in forming glycine
derivatives, we considered the formation of ionized glycine from the
reaction of the most favourable product of the previous reaction (CH2COOH) with NH3+:
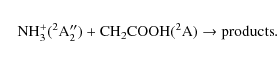
Given the multiplicity of the reactants, NH3+ (2A
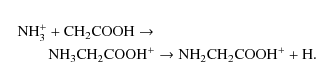
From inspection of Fig. 4, we can conclude that the reaction between NH3+ and the radical CH2COOH is a quasi-isoenergetic barrier free process. We note that the high stability of the intermediate of the reaction, protonated glycine, indicates that it could be a long-lived species given its relative energy with respect to the products. This reaction takes place on the same potential energy surface as the previously studied NH2+ + CH3COOH reaction (Largo et al. 2008). It can be seen that the other possible channels are not feasible under interstellar conditions (see Fig. 4 in Largo et al. 2008).
4 Conclusions
We have performed a theoretical study of the reactions between the radical cation of ammonia and CH3COOH/CH2COOH to investigate whether they are processes that can produce glycine derivatives. The different intermediate species and the most relevant transition states for these reactions have been characterized. The second-order Moller-Plesset level with the cc-pVTZ (correlation-consistent polarized valence triple-zeta) basis set was used. Energetic data were refined at the CCSD(T) level (coupled cluster single and double excitation model augmented with a non-iterative treatment of triple excitations) on the MP2/cc-pVTZ geometries with the aug-cc-pVTZ basis set. The two levels of theory employed in the present study provide energy predictions that are in good agreement. The most stable species of the (NO2C2H7)+ system was found to be isomer I2 (-48.24 kcal/mol below reactants at the CCSD(T) level). This species results from the interaction between the hydrogen atom of NH3+ and the carbonylic oxygen of CH3COOH and abstraction of the hydrogen atom of the methyl group to the nitrogen atom. The analysis of the potential energy surface corresponding to the reaction between NH3+ and acetic acid suggests that path a.1 leading to protonated glycine is a feasible process in the interstellar medium (exothermic and barrier free). However, the dominating path is clearly the hydrogen transfer process giving NH4+ and CH2COOH in agreement with the experimental evidence. In considering whether the formation of the acetohydroximic acid cation from the reaction of NH3+ with CH3COOH is possible, our theoretical study shows that this process is by far endothermic and therefore not be viable under interstellar conditions. The formation of ionized glycine from the subsequent reaction of the CH2COOH radical with NH3+, is a quasi-isoenergetic (2.03 kcal/mol at CCSD(T) level) barrier free process, which leads to a highly stable intermediate, protonated glycine. Our results suggest that the reaction between the radical cation of ammonia and both CH3COOH and CH2COOH leading to glycine derivatives could take place under interstellar conditions but there are other competitive channels that are more favorable. Our theoretical study provides a reasonable interpretation of the experiments that have been performed to date.
AcknowledgementsFinantial support from the Ministerio de Educación y Ciencia of Spain through Grant No. CTQ2007-67234-C02-02) and the Junta de Castilla y León (Spain) through Grant No. VA 040A09 is acknowledged.
References
- Basiuk, V. A., & Bogillo, V. I. 2000, Adv. Space Res., 30, 1439 [Google Scholar]
- Basiuk, V. A. 2001, J. Phys. Chem. A, 105, 4252 [CrossRef] [Google Scholar]
- Basiuk, V. A., & Kobayashi, K. 2002, J. Viva Origino, 30, 54 [Google Scholar]
- Bernstein, M. P., Dworkin, J. P., Sandford, S. A., Cooper, G. W., & Allamandola, L. J. 2002, Nature 416, 401 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Blagojevic, V., Petrie, S., & Bohme, D. K. 2003, MNRAS, 339, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, R. D., Godfrey, P. D., Storey, J. W. V. et al. 1979, MNRAS, 186, 5P [NASA ADS] [CrossRef] [Google Scholar]
- Butkovskaya, N. I., Kukui, A., Pouvesle, N., & Le Bras, G. 2004, J. Phys. Chem. A, 108, 7021 [CrossRef] [Google Scholar]
- Ceccarelli, C., Loinard, L., Castets, A., Faure, A., & Leffloch, B. 2000, A&A, 362, 1122 [NASA ADS] [Google Scholar]
- Combes, F., Nguyen Q.-R., & Wlodarczak, G. 1996, A&A, 308, 618 [NASA ADS] [Google Scholar]
- Dunning, T. H. 1989, J. Chem. Phys., 90, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Ehrenfreund, P., & Charnley, S. B. 2000, ARA&A, 38, 427 [Google Scholar]
- Ehrenfreund, P., Bernstein, M., Dworkin, J. P., Sandford, S. A., & Allamandola, L. 2001, ApJ, 550, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Frisch, M. J., Trucks, G. W., Schlegel, H. B. et al. 1998, Gaussian 98, Pittsburgh, PA: Gaussian Inc. [Google Scholar]
- Gonzalez, C., & Schelegel, H. B. 1989, J. Chem. Phys., 90, 2154 [NASA ADS] [CrossRef] [Google Scholar]
- Gonzalez, C., & Schelegel, H. B. 1990, J. Phys. Chem., 94, 5523 [CrossRef] [Google Scholar]
- Guélin, M., Brouillet, N., Cernicharo, J., Combes F., & Wooten, A. 2008, Ap&SS, 313, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Herbst, E. 2001, Chem. Soc. Rev., 30, 168 [CrossRef] [MathSciNet] [Google Scholar]
- Hollis, J. M., Snyder, L. E., Suenram, R. D., & Lovas, F. J. 1980, ApJ, 241, 1001 [NASA ADS] [CrossRef] [Google Scholar]
- Hollis, J. M., Pedelty, J. A., Boboltz, D. A., et al. 2003a, ApJ, 596, L235 [NASA ADS] [CrossRef] [Google Scholar]
- Hollis, J. M., Pedelty, J. A., Snyder, L. E., et al. 2003b, ApJ, 588, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Hoyle F., & Wickramasinghe, N. C. 1976, Nature, 264, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Jackson, D. M., Stibrich, N. J., Adams, N. G., & Babcock, L. M. 2005a, Int. Mass. Spectrom., 243, 115 [CrossRef] [Google Scholar]
- Jackson, D. M., Stibrich, N. J., McLain, J. L., et al. 2005b, Int. Mass. Spectrom., 247, 55 [CrossRef] [Google Scholar]
- Kuan, Y.-J., Charnley, S. B., Huang, H.-C., Tseng W.-L., & Kisiel, Z. 2003, ApJ, 593, 848 [NASA ADS] [CrossRef] [Google Scholar]
- Largo, A., Redondo, P., & Barrientos, C. 2004, Int. J. Quantum Chem., 98, 355 [Google Scholar]
- Largo, L., Rayón, V. M., Barrientos, C., Largo A., & Redondo P. 2008, J. Chem. Theory Comput., 4, 2085 [CrossRef] [Google Scholar]
- Maeda, S., & Ohno, K. 2004, Chem. Phys. Lett., 398, 240 [NASA ADS] [CrossRef] [Google Scholar]
- Mehringher, D. M., Snyder, L. E., & Miao, Y. 1997, ApJ, 480, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, S. L. 1953, Science, 117, 528 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Raghavachari, K., Trucks, G. W., Pople, J. A., & Head-Gordon, M. 1989, Chem. Phys. Lett., 157, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Schalley, C. A., Hornung, G., Shroder, D., & Schwarz, H. 1998, Int J. Mass Spectrom., 172, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Snow, J. L., Orlova, G., Blagojevic, V., & Bohme, D. K. 2007, J. Am. Chem. Soc., 129, 9910 [CrossRef] [PubMed] [Google Scholar]
- Snyder, L. E., Hollis, J. M., Suenram, R. D., et al. 1983, ApJ, 268, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Snyder, L. E., Lovas, F. J., Hollis, J. M., et al. 2005, ApJ, 619, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Wincel, H., Fockkens, R. H., & Nibbering, N. M. M. 2000, Rapid Commun. Mass Spectrom., 14, 135 [CrossRef] [PubMed] [Google Scholar]
- Woon, D. E. 2001, J. Phys. Chem. A, 105, 9478 [CrossRef] [Google Scholar]
- Woon, D. E. 2002a, ApJ, 571, L177 [NASA ADS] [CrossRef] [Google Scholar]
- Woon, D. E. 2002b, Int. J. Quantum Chem., 88, 226 [Google Scholar]
Appendix A
![\begin{figure}
\par\includegraphics[width=9cm,angle=-90,clip]{14057fgs1.ps}\par\includegraphics[width=9cm,angle=-90,clip]{14057fgs2.ps}
\end{figure}](/articles/aa/full_html/2010/08/aa14057-10/Timg30.png)
|
Figure A.1:
MP2/cc-pVTZ optimized geometries for the reactants and products involved in the reaction of NH3+ (2A
|
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=3.7cm,angle=-90,clip]{14057fgs3.ps}\par...
...\includegraphics[width=11.5cm,clip]{14057fgs4.eps}\hspace*{1.2cm}}\end{figure}](/articles/aa/full_html/2010/08/aa14057-10/Timg31.png)
|
Figure A.1: continued. |
| Open with DEXTER | |
All Tables
Table 1: Relative energies (kcal/mol) for the relevant intermediates.
Table 2: Relative energies (kcal/mol) for the possible products.
All Figures
![\begin{figure}
\par\includegraphics[width=4.8cm,angle=-90]{14057fg1a.ps} \includegraphics[width=6.1cm,angle=-90]{14057fg1b.ps}
\end{figure}](/articles/aa/full_html/2010/08/aa14057-10/Timg8.png)
|
Figure 1: MP2/cc-pVTZ optimized geometries for the different (NO2C2H7)+ minima. Distances are given in angstroms and angles in degrees. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=4.8cm,angle=-90]{14057fg2a.ps} \includegraphics[width=5.7cm,angle=-90]{14057fg2b.ps} \vspace*{2.5mm}
\end{figure}](/articles/aa/full_html/2010/08/aa14057-10/Timg17.png)
|
Figure 2:
MP2/cc-pVTZ optimized geometries for the relevant transition states involved in the reaction of NH3+ (2A
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{14057fg3.ps}
\end{figure}](/articles/aa/full_html/2010/08/aa14057-10/Timg18.png)
|
Figure 3:
Energy profile, in kcal/mol, for the reaction of NH3+ (2A
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=11cm]{14057fg4.ps}
\end{figure}](/articles/aa/full_html/2010/08/aa14057-10/Timg25.png)
|
Figure 4:
Energy profile, in kcal/mol, for the reaction of NH3+ (2A
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,angle=-90,clip]{14057fgs1.ps}\par\includegraphics[width=9cm,angle=-90,clip]{14057fgs2.ps}
\end{figure}](/articles/aa/full_html/2010/08/aa14057-10/Timg30.png)
|
Figure A.1:
MP2/cc-pVTZ optimized geometries for the reactants and products involved in the reaction of NH3+ (2A
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[width=3.7cm,angle=-90,clip]{14057fgs3.ps}\par...
...\includegraphics[width=11.5cm,clip]{14057fgs4.eps}\hspace*{1.2cm}}\end{figure}](/articles/aa/full_html/2010/08/aa14057-10/Timg31.png)
|
Figure A.1: continued. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


