EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 516 (June-July 2010) A&A, 516 (2010) A8 Full HTML
Free Access
Issue
A&A
Volume 516, June-July 2010
Article Number A8
Number of page(s) 10
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/201014038
Published online 16 June 2010
A&A 516, A8 (2010)

X-raying the AU Microscopii debris disk

P. C. Schneider - J. H. M. M. Schmitt

Hamburger Sternwarte, Universität Hamburg, Gojenbergsweg 112, 21029 Hamburg, Germany

Received 11 January 2010 / Accepted 24 March 2010

Abstract
AU Mic is a young, nearby X-ray active M-dwarf with an edge-on debris disk. Debris disk are the successors to the gaseous disks usually surrounding pre-main sequence stars which form after the first few Myrs of their host stars' lifetime, when - presumably - also the planet formation takes place. Since X-ray transmission spectroscopy is sensitive to the chemical composition of the absorber, features in the stellar spectrum of AU Mic caused by its debris disk can in principle be detected. The upper limits we derive from our high resolution Chandra LETGS X-ray spectroscopy are on the same order as those from UV absorption measurements, consistent with the idea that AU Mic's debris disk possesses an inner hole with only a very low density of sub-micron sized grains or gas.

Key words: circumstellar matter - stars: individual: AU Microscopii - stars: coronae - X-rays: stars - protoplanetary disks

1 Introduction

The disks around young stars undergo dramatic changes during the first $\sim$10 Myr after their host stars' birth, when the gas content of the disk largely disappears (Hernández et al. 2006; Alexander 2008; Meyer et al. 2007), leaving behind a so-called debris disk. The Kuiper belt and the asteroid belt are the solar system's analogs of stellar debris disks. The main components of an optically thin debris disk are small grains with about sub-micrometer sizes, larger bodies in the cm range and, possibly, planets, which are thought to form in the same time-span. The initial composition of the material in the debris disks after the transition phase is not well known. Collisions of already formed smaller bodies replenish the dust in the ``older'' debris disks, while it is not clear, whether this is also the source of the initial dust in the debris disk or whether it is remnant proto-planetary dust.

1.1 AU Mic and its activity

AU Mic is a 12+8-4 Myr old M1 dwarf at a distance of about 10 pc, which belongs to the $\beta$ Pic moving group (e.g. Barrado y Navascués et al. 1999; Zuckerman et al. 2001). AU Mic is one of the brightest nearby X-ray emitters ( $\log L_{\rm X} \approx29.3$) and shows strong flaring activity, making AU Mic a valuable target for flare studies as shown by e.g. UV observations (Robinson et al. 2001).

At X-ray wavelengths AU Mic has been observed many times. The first Chandra  observation provided the highest resolution spectrum, but was limited to the wavelength range below $\sim$25 Å  (Linsky et al. 2002). The XMM-Newton  observation of AU Mic in 2000 was simultaneous with UV and VLA observations revealing several flares (Ness et al. 2003; Mitra-Kraev et al. 2005; Smith et al. 2005, for line fluxes). Furthermore, AU Mic was the target of FUSE and Hubble Space Telescope STIS observations (e.g. Pagano et al. 2000; Del Zanna et al. 2002; Robinson et al. 2001), aiming at the determination of the temperature structure of its chromosphere and corona.

1.2 AU Mic and its debris disk

The first indications for cold material around AU Mic go back to IRAS data, which exhibit excess emission at 60 $\mu$m (Song et al. 2002; Mathioudakis & Doyle 1991). A clear infrared excess at 850 $\mu$m in the spectral energy distribution (SED) of AU Mic was detected by Liu et al. (2004), clearly pointing to the existence of a debris disk. By assuming an optical thin disk at a single temperature, Liu et al. (2004) derived a mass of 0.01 $M_\oplus$ and a temperature of 40 K for the disk. These values have been confirmed by Rebull et al. (2008) from Spitzer data (see also Chen et al. 2005). Metchev et al. (2005) also confirmed the dust mass of about 0.01 $M_\oplus$ composed of grains in the submicron regime by modelling the optical, near-IR and SED data.

Optical observations by Kalas et al. (2004), initiated shortly after Liu et al. (2004), clearly showed the presence of a debris disk around AU Mic with a radial extent of at least 210 AU and almost perfectly edge-on. The disk has then been subsequently studied at optical wavelengths with, e.g., the Hubble Space Telescope (HST) and adaptive optics, making it one of the most well studied debris disks. The models derived by Krist et al. (2005) from their HST observation restrict the disk inclination to $i \gtrsim 89^\circ$; they also confirmed the small-scale brightness variations detected by Kalas et al. (2004). These disk inhomogeneities can be readily explained by the existence of orbiting planets, however, no clear signatures of a planet have been found to date (Metchev et al. 2005; Hebb et al. 2007).

Two studies aimed at the detection of circum-stellar gas in the AU Mic disk. By their non-detection of far-UV H2 absorption, Roberge et al. (2005) derived an upper limit on the gas column density along the line of sight of $N_{{\rm H}_2} < 10^{19}$ cm-2. The detection of H2 in fluorescence enabled France et al. (2007) to derive a column density of $3\times10^{15}~ {\rm cm}^{-2} < N_{{\rm H}_2} < 2\times10^{17}~ {\rm cm}^{-2}$ ( $T_{{\rm H}_2}=800$ K and 2000 K, respectively). Comparing their H2 value with the the CO results of Liu et al. (2004), they conclude that H2 contributes less than about 1/30th to the total disk mass. The H absorption mainly traces interstellar rather than circum-stellar material and has a column of $N_{\rm H} = 2.3\times10^{18}$ cm-2 (Wood et al. 2005), thus corresponding to within a factor of five to the Mg  II absorption measurements of Redfield & Linsky (2002, )math10#$N_{\rm Mg} = 1.6\times10^{13}$ cm-2#, assuming solar abundances and Mg  II to be the dominant Mg species (Slavin & Frisch 2002).

1.3 Disk models

Krist et al. (2005) used three-dimensional models of the scattering cross-section densities throughout the disk to interpret their HST images. They find that in the inner disk region (12 AU <r< 49 AU) the observations can be explained by a relatively uniform scattering cross-section density (forward scattering particles with an albedo of 0.5) in approximate correlation with the non-flaring disk model of Metchev et al. (2005). Augereau & Beust (2006) inverted the visible and near-IR scattered light profiles to study the grain properties and find that the scattered light is reflected at grains with sizes mainly between 0.1 $\mu$m and 1 $\mu$m. However, they require only about 1/20th of the total disk mass to account for the scattered light.

The dynamics of the grains were included by Strubbe & Chiang (2006) into their models and led them to explain the observations with a ``birth ring'' at about 40 AU, where larger planetesimals of about decimetre size are located. By collisions of these planetesimals the submicron sized grains are produced, which then, depending on their size, the radiation pressure, the gas content of the disk and the stellar wind, are expelled from the system or dragged into AU Mic. Strubbe & Chiang (2006) conclude that AU Mic's debris disk is dominated by destructive grain-grain collisions and that the inner part of the disk is largely void of submicron sized grains. These small grains mainly populate the outer part of the disk and result in the blueish appearance of a debris disk relative to the star, since submicron sized grains provide the largest fraction of the scattered light (Metchev et al. 2005). In contrast to the scattered light, the IR excess is caused by larger bodies because the mass of the submicron sized grains is too low to account for the observed emission (Fitzgerald et al. 2007). Augereau & Beust (2006) already noticed the need to increase their disk mass derived from the scattered light to reproduce the SED. The void of small grains in the inner part of the disk is consistent with the polarisation data of Graham et al. (2007) and the near-IR data of Fitzgerald et al. (2007), who derived an upper limit on the mass of submicron sized grains in the inner zone of the disk of $10^{-4}~M_\oplus$.

\begin{figure} \par\includegraphics[width=8cm,clip]{14038fg1.ps} \end{figure} Figure 1:

X-ray transmission curves for different absorbers using bamabs from the PINTofALE-package based on the data of Balucinska-Church & McCammon (1992). Top: Absorption by cold gas with solar abundances. Middle panel: Gaseous carbon absorption. Bottom: Absorption by carbon grains. The individual curves are slightly shifted along the x-direction to maintain clarity. The C-K edge is located at 43.6 Å. For the grain absorption, the column density gives the total number of carbon atoms along the line of sight. Therefore, the number of grains in the line of sight depends on the grain-size, i.e., varies between the transmission curves for a fixed column density. For comparison, the dashed line in the gas absorption panel describes the transmission of carbon grains with $N_{\rm C} = 3\times10^{18}~\mbox{cm}^{-2}$.

Open with DEXTER

2 The role of X-rays

The disk models strongly suggest that AU Mic is directly shining through its disk, therefore, absorption features related to the disk should in principle be present in the observed spectrum. AU Mic 's strong X-ray emission make this system a prime target to search for X-ray absorption features from a circum-stellar disk. The dominance of dust lets us expect a substantial amount of carbon in AU Mic 's disk, and thus we examine the influence of carbon on an X-ray transmission spectrum.

2.1 X-ray transmission in the disk of AU Mic 

X-ray transmission spectra contain absorption features directly related to individual elements and, therefore, can be used to probe the elemental composition of an absorber (e.g. Nicastro et al. 2005; Williams et al. 2007). In particular, X-ray transmission spectroscopy allows an assessment of the carbon column density in the disk of AU Mic $\!$. In Fig. 1 we therefore illustrate the effects of X-ray absorption on the transmission curves for different column densities and the resulting soft X-ray spectrum near the carbon K-edge and out to 200 Å , i.e., in the band pass exclusively accessible to the Chandra LETGS. We specifically consider the case of cold gas absorption with solar abundances (Fig. 1, top panel), the case of a pure carbon absorber with various column densities (Fig. 1, middle panel), and the case of carbon absorbers locked up in various grain sizes (Fig. 1, bottom panel); clearly, for an absorber significantly composed of grains, self-shielding within the grains becomes important for the calculation of its transmission properties (see Appendix A, in Wilms et al. 2000). From Fig. 1 (bottom panel) it is clear that graphite grains with sizes around 0.1$~\mu$m are ideal to derive column densities from the carbon absorption edge, because they are so small that self-shielding is unimportant; the derived column density represents (almost) the number column density of carbon. With increasing grain sizes, the absorption features approach that of grey absorbers and grains with sizes in excess of $10~\mu$m are virtually completely grey at X-ray wavelengths with only a marginal reduction of transmission. Therefore, the correspondence of absorption edge depth and column density holds strictly only for gas and small grains, while it breaks down for unknown grain sizes (in particular for sizes $\ga$0.3 $\mu$m).

Figure 1 also illustrates that it is virtually impossible to reconstruct the elemental composition of an absorber from the reduced transmission outside the absorption edges. The shape of the reduced transmission at longer wavelengths can be mimicked by choosing appropriate column densities for almost every composition, e.g., the differences in transmission between a pure oxygen or a pure helium absorber in the Chandra LETGS wavelength range longwards of 50 Å  is less than 10%. Note that only very few narrow absorption lines are available in the case of (low ionised) disks. In particular the 1s-2p transitions of oxygen (23.5 Å) and carbon ($\sim$44.8 Å, estimated from the K$\alpha$ energy) are available (Wilms et al. 2000; Henke et al. 1993).

In the case of an absorber with solar abundances the absorption due to H, He and O reduces strongly the transmission around the absorption edge of C, however, the flux ratio between both sides of the edge depends only on the actual carbon column density. For a column density of $N_{\rm H} = 10^{21}$ cm-2 assuming cold gas with solar abundances, the transmission is reduced by a factor of 20, but the transmission at the low energy side of the C-K edge is about twice that of the high energy side, yet the resulting low flux level makes it virtually impossible to measure the depth of the C-K edge. Therefore, using the carbon absorption edge requires carbon to be strongly enhanced in the absorber so that it contributes significantly to the absorption without the overall reduced transmission by other elements.

2.2 The mass column density of AU Mic 

The range of possible disk masses and hence column densities for AU Mic is relatively narrow. The different methods independently point to a total disk mass of $0.01~M_\oplus$ ($\approx$ $ 6\times10^{25}$ g, cf., Sect. 4.1 in Fitzgerald et al. 2007; France et al. 2007), however, the distribution of this disk mass between small grains and larger bodies and their locations are not particularly well constrained. The most recent disk models including the grain dynamics attribute less than a tenth of the total mass to small grains, while most of the mass is stored in larger bodies with sizes up to $\sim$10 cm. In order to test these scenarios we calculate the mass column density by distributing 0.01 $M_\oplus$ uniformly within the inner zone of the Krist et al. (2005) model (10 AU-50 AU, $h\approx 2$ AU), i.e., the zone where the dust causing the infrared excess should be located. The mass column density $\sigma$ is given by

                     $\displaystyle \sigma = \frac{M}{V}d$ = $\displaystyle \frac{M}{\pi h(r_{\rm o}^2-r_{\rm i}^2)}\cdot (r_{\rm o} - r_{\rm i}) = \frac{M}{\pi h(r_{\rm o}+r_{\rm i})}$ (1)
  $\textstyle \approx$ $\displaystyle 7\times10^{-4} {\rm g}/{\rm cm}^2~ ,$  

where M is total disk mass within 50 AU, V is the volume occupied by the disk, d is the line of sight and $r_{\rm o}$ and $r_{\rm i}$ are the outer and inner radii of the considered region, assuming no significant contribution of larger bodies.

As discussed above, the associated X-ray absorption features depend on the chemical composition of the disk and the grain sizes and shapes. Although Roberge et al. (2006) found that in the $\beta$ Pic disk the chemical composition might deviate from solar by factors of a few with carbon being overabundant, we assume for the AU Mic disk that H and He are virtually absent and that the mass is stored in the remaining elements with solar abundances. This implies that $\sim$15% of the mass is stored in carbon atoms. The number density of carbon atoms in the line of sight is then

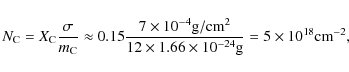
\begin{displaymath}N_{\rm C} = X_{\rm C}\frac{\sigma}{m_{\rm C}} \approx 0.15\fr... ...es 1.66\times 10^{-24}{\rm g}} = 5\times 10^{18}{\rm cm}^{-2}, \end{displaymath} (2)

where $X_{\rm C}$ is the mass-fraction of carbon (15%) and $m_{\rm C}$ is the mass of a carbon atom.

From Fig. 1 it is clear that such column densities should impose strong feature on the transmission spectrum detectable with a Chandra  LETGS observation.

\begin{figure} \par\includegraphics[width=8.5cm,clip]{14038fg2.ps} \end{figure} Figure 2:

LETGS zeroth order X-ray lightcurve of AU Mic. Time represents the time after the start of the observation (MJD = 54643.506).

Open with DEXTER

3 Observations, data reduction and immediate results

3.1 Observation and data reduction

Au Mic was observed on 30 June 2008 with the Chandra LETGS (Obs-ID 8894). The total exposure time was 50 ksec and the data reduction was carried out using CIAO 4 (Fruscione et al. 2006). The photon detector of the LETGS is the HRC-S, a micro-channel plate, which does not provide sufficient energy resolution to separate the individual diffraction orders superposed on the same detector area. Therefore, to allow an analysis of the data with standard tools like XSPEC (Arnaud 1996), we constructed new response matrices including up to ninth diffraction order contributions following the instructions given in the CIAO threads[*] (see Appendix A). Line fluxes were obtained using CORA which accounts for the Poisson character of the data (Ness & Wichmann 2002).

We experimented with the ``standard'' filters (light, medium and heavy) and with the new Gain Map and Pulse-Height filter[*]. Around the carbon edge, the difference in the background fraction is only a few percent between the light and medium filter while significant for the new filter; we list the corresponding values in Table 2. The figures and numbers given in the text pertain to the standard light filter, unless otherwise noted.

\begin{figure} \par\includegraphics[width=14cm,clip]{14038fg3.ps} \end{figure} Figure 3:

The measured spectrum in the spectral range relevant for the analysis. Shown is the sum of the positive and the negative diffraction order.

Open with DEXTER

3.2 Global plasma properties

In Fig. 2 we show the zeroth order X-ray count rate of AU Mic vs. time; obviously, the light curve is more or less constant during the first 40 ksec of the observations, afterwards there is a small flare-like increase. We do not treat this increase separately but analyse the observation in total. In Fig. 3 we show the recorded LETGS spectrum up to 120 Å; sub-regions will be shown individually in the next sections. AU Mic 's X-ray spectrum is typical of an active star, showing the strong Ne emission features and a strong OVIII Ly$_{\alpha}$ line; the carbon Ly$_{\alpha}$ line is also quite strong. The OVII triplet between 21.6 and 22.1 Å as well the Fe XVII feature at 15.03 Å are relatively weak as well as all features attributable to N; we do point out the emission lines between 90 and 120 Å attributable to highly ionised iron. We used XSPEC to fit the X-ray spectrum using a combination of three APED models (variable abundances, Smith et al. 2001) with one absorption component. The increasing background at longer wavelengths make these bins less useful for the spectral analysis. We therefore restrict the wavelength range to values between 5 Å  and 35 Å. Using the full wavelength range does not influence the two low temperature components; only the best fit temperature of the high temperature component doubles. This is mainly driven by a single, somewhat strangely shaped Fe XX line at 132.85 Å. Furthermore, the abundances of Mg, Al, Ca and Ni (low FIP) were coupled to that of Fe in order to decrease the number of free parameters. The thus obtained fit results (listed in Table 1) show the inverse FIP effect usually found in M-dwarfs (Robrade & Schmitt 2005). The temperature structure and the abundances compare well with a fit performed with the XMM-Newton RGS-data of AU Mic (Obs-ID 0111420101).

Table 1:   Coronal properties of AU Mic .

4 Absorption at the carbon edge

The carbon K-edge at 43.6 Å  (284 eV, i.e., the energy needed to expell a K-shell electron from an isolated carbon atom) is a promising absorption feature in the Chandra  LETGS wavelength band. In this region, the line emission is relatively small compared to continuum emission. The oxygen edge, located at 23.1 Å  (536 eV), is also a good candidate, but with an enhanced line-to-continuum ratio. This increases the errors since the prediction of the line emission is not possible with the required precision. Unfortunately, the UV/Ion shield of the HRC-S also contains a large amount of carbon ( $N_{\rm C} \approx 10^{18}~$cm-2) leading to an instrumental feature very similar to that of expected interstellar/circum-stellar carbon absorption. Still, the high continuum fraction of the first order emission around the C-K edge makes this region more promising than the O-K edge.

Table 2:   Contributions at the C-K edge (summed continuum and line emission).

4.1 The model

As is obvious from Fig. 1 the height of the C edge does depend sensitively on the carbon column density (and on the grain sizes). Therefore our basic idea to measure the height of that edge is as follows: We divide the wavelength range around the C edge into a low (44-48 Å) and a high energy band (30-43 Å) and sum up the counts in these two bands to increase the signal. By comparing these two count numbers with models containing specific amounts of carbon absorption the best fit carbon column density can be found.

We do not extend the wavelength range to longer wavelengths since these longer wavelength bins are close to the detector gap at 50 Å  of the negative diffraction order, where the data is less reliable. We also exclude the immediate region around the edge and around the 1s-2p carbon absorption line ($\sim$44.8 Å) because of the relatively little known fine-structure of the carbon absorption edge. Exclusion of a larger wavelength region around the edge does not change the results significantly (see Fig. 7). Increasing the amount of carbon in the line of sight, changes the flux-ratio between the low and high band; since the the change in transmission in the low energy band is comparably small, we normalise our model to match the low energy band. Therefore we carry out only a differential analysis.

For our modelling of the recorded spectrum above and below the carbon edge we consider the following four components as contributors to the counts around the C-K edge.

1.
The continuum emission.
2.
The superimposed line emission.
3.
The higher diffraction orders which cannot be filtered out due to the low intrinsic energy resolution of the photon detector (HRC-S).
4.
The enhanced background of the LETGS due to a wiring error of the micro-channel plate detector.
In the following we describe our modelling of the individual components and discuss their accuracy; the given errors pertain to the higher energy side of the edge while the numbers in brackets correspond to the lower energy side. Since the models are normalised to match the low energy side of the edge, an error at this side will also influence the number of predicted counts at the high energy side of the edge (by roughly the same amount). Figure 4 shows the complete model and the individual model contributions are shown in Fig. 5.

\begin{figure} \par\includegraphics[width=8.5cm,clip]{14038fg4.ps} \end{figure} Figure 4:

Model and data around the C-K edge (sum of both diffraction orders).

Open with DEXTER

\begin{figure} \par\includegraphics[width=8.5cm,clip]{14038fg5.ps} \end{figure} Figure 5:

The different contributions to the measured counts around the C-K edge. Top: First order emission. middle: Higher order contribution. bottom: Background.

Open with DEXTER

The continuum is the simplest component since its shape around the C-K edge does not change noticeably for reasonable changes in the plasma properties. The main spectral components are known from our global spectral modelling, but changing, for example, the temperature by about 50%, changes the number of counts left of the carbon edge by less than 2% (50 cts), while preserving the counts at the right side of the edge by choosing an appropriate normalisation.

\begin{figure} \par\includegraphics[width=8.8cm,clip]{14038fg6.ps} \end{figure} Figure 6:

Data and model for the sum of the positive and the negative diffraction order. Note that the model is not based on a physical model (except for the continuum and the absorption).

Open with DEXTER

The treatment of emission lines is less straightforward. We estimate that contribution of the first diffraction order emission lines is not predictable with a better than 10% accuracy. Therefore, a region of 0.2 Å  around each strong line (based on our XSPEC/APED emission model) was excluded from the two energy bands thus removing $\sim$98% of the line flux of these strong lines. Only 65% and 73% of the available bins are therefore used in the 30-43 Å  and 44-48 Å  range, respectively. As a consequence, the ratio between line and continuum emission is below 10% in the high and low band. In addition, the remaining counts from unresolved lines are predicted from the emission model and are added to the model as a correction; these numbers turn out to be 50 and 35, respectively. Taking this numbers as a conservative estimate of the error, the impact of these lines on the derived carbon column density is quite small, therefore, also the influence of ``unknown'' lines ought to be small.

The third diffraction order of the LETGS is the strongest higher order contribution to the region around the C-K edge, since the second diffraction order is suppressed by the grating design. Unfortunately, AU Mic being an active star, the Ne IX and Ne X lines are quite strong, and their third order components are easily discernible in our LETGS spectrum (cf. middle panel in Fig. 5). However, first and third order are always measured simultaneously, thus, by fitting the stronger (identifiable) lines independently in the wavelength range shorter than the C-K edge provides the desired description of the higher order contamination. The selection of the lines is based on the APED model (see Sect. 3), the Chandra HETGS spectrum of AU Mic   and on the lines visible in the Capella spectrum (Capella is a calibration target of the LETGS, thus providing about 400 ks of data and has an approximately comparable temperature structure as AU Mic). Note that this method is unaffected by the uncertainties of the spectral model. Figure 6 shows the model of the wavelength range which provides the strongest contamination at the carbon edge; 97% of the photons in this range are included in the model. Taking the remaining 3% as a measure for the accuracy of the higher order model, these 3% correspond to only 12 (4) photons not contained in the higher order model between 30 Å  and 48 Å. We can therefore neglect this effect on the derived carbon column density compared to the other factors like the statistical noise or a potential error in the higher order diffraction efficiencies, which would for a 10% error[*] result in an error on the 30 count level (6 cts).

The last component to consider is the background. Fortunately, the background is relatively uniform in the wavelength range between 30 Å  and 48 Å. Since the bins in the ``line-free'' regions are all summed up, the impact of the short-scale variation should be further reduced. The largest problem of the background in this analysis is the enlarged count number leading to an increased statistical uncertainty which amounts to about 50 (30) counts. Since the models are tuned to match the longer wavelength side of the edge, the combined statistical error is $\sim$75 counts at the high energy side of the edge.

\begin{figure} \par\includegraphics[width=8.5cm,clip]{14038fg7.ps} \end{figure} Figure 7:

Number of missing (positive count number) or overpredicted photons (negative count number) as a function of the assumed carbon absorption column density in the model. The flattening of the curves indicates that the flux will, eventually, be completely absorbed in the considered wavelengths range for even higher column densities. The dashed line is the average of the positive and negative order using the new Gain Map and Pulse-Height filtering. The dashed-dotted line is the result using the wavelength ranges 30-42 Å  and 45-48 Å. The statistical errors reflects only first order errors. For a discussion of the errors see Sect. 4.2.

Open with DEXTER

4.2 The influence of carbon absorption

Varying the absorbing carbon column density changes the transmission curve in the whole wavelength range (see Fig. 1). Therefore, it is necessary to re-adjust the continuum-level and the amplitudes of the emission lines for the higher order contribution to construct a new best fit model. The influence of the carbon absorption on the low-energy side of the edge is relatively small (cf. Fig. 1), therefore, we tuned the models so that this region matches the data by varying the continuum normalisation of the model. The normalisations of the models with zero absorption and $N_{\rm C}=2\times10^{18}~$cm-2 differ by about 20%. Due to the strong line emission (there are not many wavelength regions without line emission at shorter wavelengths) and the refitting of these lines, this does not noticeably change the fit-quality in the shorter wavelength region. Having thus fixed our model to account for the number of counts at the low-energy side of the carbon edge, we can compute the model counts on the high energy side of the carbon edge as a function of the assumed carbon column density and hence, by comparison with the observation, the missing model counts, since increasing the carbon column density leads to a more and more relatively reduced model count number below the edge. The dependence of this number of missing counts in the model on the assumed carbon absorption is graphically displayed in Fig. 7. Depending on the accepted accuracy of our model we can read off the maximum number of carbon atoms along the line of sight assuming gaseous absorption (i.e. no self-shielding). If grains cause the absorption, a larger number of carbon atoms in the line of sight is required to produce the same number of missing counts. Explaining gaseous absorption with $N_{\rm C}=10^{18}$ cm-2 requires a 1.3 times higher number of carbon atoms in the line of sight for 0.1 $\mu$m sized grains, a 1.9 times higher number for 0.3 $\mu$m and an almost 5 times higher number for 1.0 $\mu$m grains.

Collecting the errors attached to the individual model components, we estimate an overall error of approximately 200 (80) counts. We cannot simply add the error of both sides of the edge, since it is rather unlikely that the same error-source results in an erroneously increased number of counts at one side of the edge while, at the same time, underestimating the counts at the other side of the edge. Therefore, we conclude that a robust estimate of the error is about 200 counts or $N_{\rm C} \lesssim 10^{18}$ cm-2 (for pure carbon gas).

The result shown in Fig. 7 suggests only a small amount of carbon-atoms along the line of sight ( $N_{\rm C}\sim 10^{17}~$cm-2), which might be supported by a slight deficit in counts around the carbon 1s-2p absorption line. However, this is probably only a statistical effect since this effect is reduced by using the stronger Gain Map and Pulse-Height background filtering (see dashed line in Fig. 7).

5 Constraining the total absorption

The method described above offers the ability to directly constrain the column density of carbon in the line of sight. It is, on the other hand, not useful to set tight contrains on the ``total'' absorbing column density since only a narrow wavelength range is inspected. Emission lines located at largely different wavelengths better utilise the large wavelength coverage of the LETGS. Usage of a single element and ionisation stage reduces the dependence on the reconstruction of the abundances and the temperature structure of the corona.

A good candidate for such a study is Fe XVIII with lines at 14.21 Å  (blend of 14.2060 and 14.2085 Å), 16.08 Å  (blend of 16.0760 and 16.0913 Å), 93.92 Å  and 103.94 Å. Assuming that all these lines are produced in the same environment, the relative fluxes of these ions depend only weakly on the temperature structure; the dependence on the density is virtually negligible for densities around $n_{\rm e} \sim 10^{10}$ cm-3 as usually found in stellar coronae (e.g. Ness et al. 2002). Unfortunately the stronger Fe XVIII lines at shorter wavelength are blended. While the 14.21 Å  lines do posses only small contributions from the 14.17 Å Fe XXI line and the Fe XVIII doublet at 14.26 Å, the 16.08 Å  is blended by the strong O VIII doublet at 16.00 Å  and a Fe XIX line at 16.11 Å, which amounts to about a fourth of the Fe XVIII emission for the temperatures in question. The derived fluxes of the short wavelength lines are comparable to the available HETGS data (Obs-ID 17).

The Chianti package (Dere et al. 1997; Landi et al. 2006) was used to predict relative line fluxes. To investigate the temperature dependence of the relative fluxes, a Gaussian fit of the emission measure distribution (EMD) of Appendix C was performed. The line ratios were then calculated for Gaussian EMDs with different peak temperatures and widths, e.g. the peak temperature was changed up to $\Delta \log (T) = 0.4$ (see Fig. 8). The measured fluxes (sum of both LETGS orders) of the above lines together with predicted ratios (the 14.21 Å  line normalised to 1.0) are listed in Table 3.

Table 3:   Strong Fe XVIII lines and measured fluxes.

\begin{figure} \par\includegraphics[width=8.5cm,clip]{14038fg8.ps} \end{figure} Figure 8:

Ratio of the line-fluxes to the Fe XVIII 14.21 Å  line using Gaussian-like emission measure distributions with a width of $\log (T/{\rm K}) = 0.5$.

Open with DEXTER

From the difference between predicted and measured counts the required hydrogen column density (assuming solar abundances) can be calculated. The resulting ranges are listed in Table 3, they include the uncertainty in the reconstruction of the temperature and the statistical error. The influence of the adopted temperature structure is small compared to the statistical errors. Comparison of the line fluxes from the standard filtering and that of the new Gain Map and Pulse-Height filtering shows that both values agree well. However, the upper limits from these fluxes are higher than that from the light filtered data since their line fluxes at longer wavelength are lower ( $N_{\rm H}<11\times10^{18}~$cm-2).

Summing the line fluxes of the short wavelengths lines and combining the upper limits of the two long wavelength lines improves the upper limit to $N_{\rm H}<4\times10^{18}~$cm $^{-2}~(1\sigma)$. Instead of using one single ion, we checked the ratio of the two strongest Fe lines at short and long wavelengths (Fe XVII 15.02 Å and Fe XX 132.85 Å). Their ratio depends more strongly on the temperature structure with predicted ratios (132.85 Å/15.02 Å) between 1.0 ( $\log~T=6.5$) and 2.0 ( $\log~T=7.3$) for a shallow EMD ( $\Delta T=0.5$). However, their resulting upper limit is only slightly higher ( $N_{\rm H}<6\times10^{18}$ cm-2) than that from the Fe XVIII lines.

The X-ray absorption at wavelengths of around 100 Å  is caused mainly by He atoms. The upper limit on He from the observed line fluxes is $N_{\rm He}<6\times10^{18}~$cm-2 assuming that the absorption is caused exclusively by He and $N_{\rm H}<14\times10^{18}~$cm-2 for a pure Hydrogen absorber. Similarly, upper limits on the abundance of other absorbing elements can be derived under the assumption that they are the only absorbing species.

The analysis of the absorption towards Capella by Gu et al. (2006) using a comparable method has an error of about a factor of five lower which is consistent with the larger data base available for Capella which is a calibration target of the Chandra  LETGS.

6 Discussion

Neither the edge based method nor the line based method are able to find significant absorption along the line of sight towards AU Mic. For both methods, the statistical error overwhelms the error caused by the incomplete models. This is clear by inspection of Table 3 for the line based method but is also true for the edge analysis. The detectable carbon column density from an analysis of the edge height is $5\dots50\times10^{17}\;$cm-2 for artificial stars with X-ray fluxes within a range of five around that of AU Mic (50 ks LETGS exposure). This value decreases only slowly for even higher X-ray fluxes and ``saturates'' at $N_{\rm C}\approx3\times10^{17}\;$cm-2 due to the potential error in the higher order contribution (see Appendix B). The edge-method provides a direct upper limit on the carbon content of the disk without any assumption on the absorber. Its limit is about that provided by the line based method assuming that only carbon is in disk, i.e., calculating the maximum carbon column density allowing the detection of the line-flux from the long wavelengths Fe XVIII lines.

Two measurements of H (atomic and molecular) restrict the total hydrogen column density in the line of sight towards AU Mic to $N_{\rm H}\lesssim 4\times10^{19}~$cm-2 (mainly H2, Roberge et al. 2005). From this value, only $2\times10^{18}~$cm-2 are atomic hydrogen (Wood et al. 2005). Note that the conversion of molecular hydrogen to $N_{\rm H}$ in stellar disks is uncertain (e.g., Kamp et al. 2007), while molecular hydrogen is orders of magnitude less abundant than atomic hydrogen in the nearby interstellar medium (d<200 pc; Lehner et al. 2003). The location of the fluorescent H2 detected by France et al. (2007) is not necessarily along the line of sight and leaves space for an additional H2 not contributing to the fluorescent H2 emission.

X-rays are sensitive to both, atomic and molecular, hydrogen. H2 absorption is about 2.8 times stronger than that of a single H atom (Wilms et al. 2000). Furthermore, the X-ray absorption is insensitive to the excitation state of H2. Therefore, the 5$\sigma$ upper limit from the UV measurement ( $N_{{\rm H}_2}<17\times10^{18}~$cm-2) corresponds to about $N_{\rm H}\lesssim50\times10^{18}~$cm-2 in soft X-rays; the same order as the upper limit derived from the line fluxes assuming a pure hydrogen absorber. The X-ray upper limit on H also includes H2 in the line of sight located in the inner and outer part of the disk which might have different excitation stages and therefore complements the upper limit of Roberge et al. (2005). Furthermore, the detected line fluxes at $\lambda\ga 100~$Å  can be translated to upper limits on other elements restricting the gas / small grain content of the disk, e.g., that of carbon in gaseous form and small grains ( $s\lesssim 0.3~\mu\mbox{m}$, see Table 3).

7 Summary

We analysed the impact of absorption caused by AU Mic's debris disk on its observed X-ray spectrum resulting in three upper limits on the column densities for hydrogen, helium and carbon:

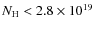  • $N_{\rm H}<2.8\times10^{19}~$cm-2 (pure H absorption)
  • $N_{\rm He}<1.2\times10^{18}~$cm-2 (pure He absorption)
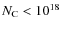  • $N_{\rm C}<10^{18}~$cm-2 (pure C absorption).
Assuming an absorber with solar abundances, the upper limit is $N_{\rm H}<10^{19}$ cm-2, which is about a factor of five higher than the pure interstellar value. The statistical error caused by counting statistics and the high background prevents to set lower limits, while the presented methods are in principle more sensitive.

Both upper limits are consistent with the idea that the AU Mic disk is optically thin in the radial direction as proposed by recent analyses from optical and infrared measurements, and in line with current disk models, which assume that the inner part of the disk is almost void of small grains. The debris of the collisions of planetesimals in the ``birth-ring'' populate mainly the outer part of the disk, where their density is so low that they escape a detection in this X-ray observation. In the inner part of the disk larger grains hold the mass as predicted by birth-ring scenarios.

Roberge et al. (2005) state that they find weak signs of H2 absorption on the order of 1018 cm-2 in their UV data. To reach this level with the Chandra LETGS setup, longer integration times are required. For Capella, a calibration target of the LETGS, the $N_{\rm H} \sim 10^{18}$ cm-2 range is accessable. However, it seems unlikely to reach down to $N_{\rm H} \sim 10^{17}$ cm-2 with the present instrumentation as would be required to safely distinguish a hypothetical circum-stellar H2 component in the $N_{\rm H}\sim10^{18}~$cm-2 range from the interstellar atomic H absorption.

Appendix A: Higher order response matrices for XSPEC

The response matrices contain the probabilities describing how the detector will respond on a photon with a given energy. Including the higher diffraction orders therefore requires to add additional probabilities at two, or more times the rest wavelength. Since the resolution grows with the order number, the energy grid needs to be refined accordingly. The FITS-specification for response files (CAL/GEN/92-002) already includes the concept of wavelength groups which are ideal to reduce the size of the final response matrix.

Appendix B: Carbon detectability

To estimate the detectability of carbon absorption from the edge height, we need to quatify the different error contributions as a function of the source count-rate. Concerning the error due to unknown unresolved first order emission lines and uncertainties in the temperature structure, we regard a correlation with the statistical error as realistic, since better data quality enables a more precise temperature reconstruction and, in turn, a better model for the emission lines around the carbon edge. However, the detailed dependence on the source count-rate might be more complicated. The higher order contribution scales with the source flux; therefore, its error scales also linearly with the first order flux since calibration uncertainties dominate the error. Figure B.1 shows the minimum detectable carbon column density for different source fluxes assuming a pure carbon disk. It shows that column densities below $3\times10^{17}\;$cm-2 can only be achieved for stars that are at least one order of magnitude X-ray brighter than AU Mic and with a hypothetical 500 ks observation. However, the existence of other elements in the disk increases the detectable column density due to the absorption of the first order flux around the carbon edge. Furthermore, without knowing the composition of the disk, the extra absorption changes the continuum slope around the carbon edge and therefore increased the uncertainty in the carbon column density.

\begin{figure} \par\includegraphics[width=8.5cm,clip]{14038fg9.ps} \end{figure} Figure B.1:

The detectable carbon column density by measuring the jump height at the carbon edge as a function of the X-ray flux (0.1 keV-2.0 keV). Here, a pure carbon disk is assumed. The two lines represent a 50 ks and a 500 ks exposure with the LETGS. The same temperature structure as AU Mic is assumed which determines the higher order contribution around the carbon edge. The vertical dotted line indicates the X-ray flux of AU Mic.

Open with DEXTER

Appendix C: The emission measure distribution

Table C.1:   Strong lines and measured fluxes.

The large wavelength coverage of the LETGS offers the ability to quantify the emission measure distribution (EMD) in the corona. Using the lines listed in Table C.1, we reconstructed the EMD using the PintOfAle (Kashyap & Drake 2000) package. Our result compares well with the result obtained using the line fluxes measured in the UV wavelength range by Del Zanna et al. (2002). We also experimented with the Chianti package (Dere et al. 1997; Landi et al. 2006) and found that the results are strongly influenced by numerical problems due to the shallow temperature coverage of the observed lines. However, both methods give rather similar results.

It is clear, that most of the emission is produced in the temperature range $6.4 < \log (T / {\rm K} ) < 7.2$. We also show in Fig. C.1 the location of the three temperature components from the XSPEC fit with APEC models (variable abundances). For an estimate of the error in the relative linefluxes in Sect. 5 we fitted the emission measure distribution with a single Gaussian. We can then change the centroid and the width of the Gaussian to analyse the impact of an error in the reconstructed temperature distribution on the relative linefluxes.

\begin{figure} \par\includegraphics[width=8.5cm,clip]{14038fg10.ps} \end{figure} Figure C.1:

The reconstructed emission measure distribution. The dotted line indicates the Gaussian fit to the EMD.

Open with DEXTER

Acknowledgements
We thank Dr. P. Predehl (MPE) for kindly providing the opportunity to observe AU Mic with the Chandra LETGS. This work has made use of data obtained from the Chandra  and XMM-Newton  data archives. CHIANTI is a collaborative project involving the NRL (USA), RAL (UK), MSSL (UK), the Universities of Florence (Italy) and Cambridge (UK), and George Mason University (USA). PCS acknowledges support from the DLR under grant 50OR703.

References

  1. Alexander, R. 2008, New Astron. Rev., 52, 60 [NASA ADS] [CrossRef] [Google Scholar]
  2. Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, ed. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [Google Scholar]
  3. Augereau, J.-C., & Beust, H. 2006, A&A, 455, 987 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
  5. Balucinska-Church, M., & McCammon, D. 1992, ApJ, 400, 699 [NASA ADS] [CrossRef] [Google Scholar]
  6. Barrado y Navascués, D., Stauffer, J. R., Song, I., & Caillault, J. 1999, ApJ, 520, L123 [NASA ADS] [CrossRef] [Google Scholar]
  7. Chen, C. H., Patten, B. M., Werner, M. W., et al. 2005, ApJ, 634, 1372 [NASA ADS] [CrossRef] [Google Scholar]
  8. Del Zanna, G., Landini, M., & Mason, H. E. 2002, A&A, 385, 968 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Dere, K. P., Landi, E., Mason, H. E., Monsignori Fossi, B. C., & Young, P. R. 1997, A&AS, 125, 149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Fitzgerald, M. P., Kalas, P. G., Duchêne, G., Pinte, C., & Graham, J. R. 2007, ApJ, 670, 536 [NASA ADS] [CrossRef] [Google Scholar]
  11. France, K., Roberge, A., Lupu, R. E., Redfield, S., & Feldman, P. D. 2007, ApJ, 668, 1174 [NASA ADS] [CrossRef] [Google Scholar]
  12. Fruscione, A., McDowell, J. C., Allen, G. E., et al. 2006, in SPIE Conf. Ser., 6270 [Google Scholar]
  13. Graham, J. R., Kalas, P. G., & Matthews, B. C. 2007, ApJ, 654, 595 [NASA ADS] [CrossRef] [Google Scholar]
  14. Gu, M. F., Gupta, R., Peterson, J. R., Sako, M., & Kahn, S. M. 2006, ApJ, 649, 979 [NASA ADS] [CrossRef] [Google Scholar]
  15. Hebb, L., Petro, L., Ford, H. C., et al. 2007, MNRAS, 379, 63 [NASA ADS] [CrossRef] [Google Scholar]
  16. Henke, B. L., Gullikson, E. M., & Davis, J. C. 1993, Atomic Data and Nuclear Data Tables, 54, 181 [Google Scholar]
  17. Hernández, J., Briceño, C., Calvet, N., et al. 2006, ApJ, 652, 472 [NASA ADS] [CrossRef] [Google Scholar]
  18. Kalas, P., Liu, M. C., & Matthews, B. C. 2004, Science, 303, 1990 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  19. Kamp, I., Freudling, W., & Chengalur, J. N. 2007, ApJ, 660, 469 [NASA ADS] [CrossRef] [Google Scholar]
  20. Kashyap, V., & Drake, J. J. 2000, Bull. Astron. Soc. India, 28, 475 [NASA ADS] [EDP Sciences] [Google Scholar]
  21. Krist, J. E., Ardila, D. R., Golimowski, D. A., et al. 2005, AJ, 129, 1008 [NASA ADS] [CrossRef] [Google Scholar]
  22. Landi, E., Del Zanna, G., Young, P. R., et al. 2006, ApJS, 162, 261 [NASA ADS] [CrossRef] [Google Scholar]
  23. Lehner, N., Jenkins, E. B., Gry, C., et al. 2003, ApJ, 595, 858 [NASA ADS] [CrossRef] [Google Scholar]
  24. Linsky, J. L., Ayres, T. R., Brown, A., & Osten, R. A. 2002, Astron. Nachr., 323, 321 [NASA ADS] [CrossRef] [Google Scholar]
  25. Liu, M. C., Matthews, B. C., Williams, J. P., & Kalas, P. G. 2004, ApJ, 608, 526 [NASA ADS] [CrossRef] [Google Scholar]
  26. Mathioudakis, M., & Doyle, J. G. 1991, A&A, 244, 433 [NASA ADS] [Google Scholar]
  27. Metchev, S. A., Eisner, J. A., Hillenbrand, L. A., & Wolf, S. 2005, ApJ, 622, 451 [NASA ADS] [CrossRef] [Google Scholar]
  28. Meyer, M. R., Backman, D. E., Weinberger, A. J., & Wyatt, M. C. 2007, in Protostars and Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil, 573 [Google Scholar]
  29. Mitra-Kraev, U., Harra, L. K., Güdel, M., et al. 2005, A&A, 431, 679 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Ness, J.-U., Schmitt, J. H. M. M., Audard, M., Güdel, M., & Mewe, R. 2003, A&A, 407, 347 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Ness, J.-U., Schmitt, J. H. M. M., Burwitz, V., et al. 2002, A&A, 394, 911 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Ness, J.-U., & Wichmann, R. 2002, Astron. Nachr., 323, 129 [NASA ADS] [CrossRef] [Google Scholar]
  33. Nicastro, F., Mathur, S., Elvis, M., et al. 2005, ApJ, 629, 700 [NASA ADS] [CrossRef] [Google Scholar]
  34. Pagano, I., Linsky, J. L., Carkner, L., et al. 2000, ApJ, 532, 497 [NASA ADS] [CrossRef] [Google Scholar]
  35. Rebull, L. M., Stapelfeldt, K. R., Werner, M. W., et al. 2008, ApJ, 681, 1484 [NASA ADS] [CrossRef] [Google Scholar]
  36. Redfield, S., & Linsky, J. L. 2002, ApJSS, 139, 439 [NASA ADS] [CrossRef] [Google Scholar]
  37. Roberge, A., Weinberger, A. J., Redfield, S., & Feldman, P. D. 2005, ApJ, 626, L105 [NASA ADS] [CrossRef] [Google Scholar]
  38. Roberge, A., Feldman, P. D., Weinberger, A. J., Deleuil, M., & Bouret, J.-C. 2006, Nature, 441, 724 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  39. Robinson, R. D., Linsky, J. L., Woodgate, B. E., & Timothy, J. G. 2001, ApJ, 554, 368 [NASA ADS] [CrossRef] [Google Scholar]
  40. Robrade, J., & Schmitt, J. H. M. M. 2005, A&A, 435, 1073 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Slavin, J. D., & Frisch, P. C. 2002, ApJ, 565, 364 [NASA ADS] [CrossRef] [Google Scholar]
  42. Smith, K., Güdel, M., & Audard, M. 2005, A&A, 436, 241 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Smith, R. K., Brickhouse, N. S., Liedahl, D. A., & Raymond, J. C. 2001, ApJ, 556, L91 [NASA ADS] [CrossRef] [Google Scholar]
  44. Song, I., Weinberger, A. J., Becklin, E. E., Zuckerman, B., & Chen, C. 2002, AJ, 124, 514 [NASA ADS] [CrossRef] [Google Scholar]
  45. Strubbe, L. E., & Chiang, E. I. 2006, ApJ, 648, 652 [NASA ADS] [CrossRef] [Google Scholar]
  46. Williams, R. J., Mathur, S., Nicastro, F., & Elvis, M. 2007, ApJ, 665, 247 [NASA ADS] [CrossRef] [Google Scholar]
  47. Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [NASA ADS] [CrossRef] [Google Scholar]
  48. Wood, B. E., Redfield, S., Linsky, J. L., Müller, H.-R., & Zank, G. P. 2005, ApJS, 159, 118 [NASA ADS] [CrossRef] [Google Scholar]
  49. Zuckerman, B., Song, I., Bessell, M. S., & Webb, R. A. 2001, ApJ, 562, L87 [NASA ADS] [CrossRef] [Google Scholar]

Footnotes

... threads[*]
http://cxc.harvard.edu/ciao/threads/hrcsletg_orders/
... filter[*]
http://cxc.harvard.edu/contrib/letg/GainFilter/
... error[*]
http://asc.harvard.edu/cal/

All Tables

Table 1:   Coronal properties of AU Mic .

Table 2:   Contributions at the C-K edge (summed continuum and line emission).

Table 3:   Strong Fe XVIII lines and measured fluxes.

Table C.1:   Strong lines and measured fluxes.

All Figures

  \begin{figure} \par\includegraphics[width=8cm,clip]{14038fg1.ps} \end{figure} Figure 1:

X-ray transmission curves for different absorbers using bamabs from the PINTofALE-package based on the data of Balucinska-Church & McCammon (1992). Top: Absorption by cold gas with solar abundances. Middle panel: Gaseous carbon absorption. Bottom: Absorption by carbon grains. The individual curves are slightly shifted along the x-direction to maintain clarity. The C-K edge is located at 43.6 Å. For the grain absorption, the column density gives the total number of carbon atoms along the line of sight. Therefore, the number of grains in the line of sight depends on the grain-size, i.e., varies between the transmission curves for a fixed column density. For comparison, the dashed line in the gas absorption panel describes the transmission of carbon grains with $N_{\rm C} = 3\times10^{18}~\mbox{cm}^{-2}$.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{14038fg2.ps} \end{figure} Figure 2:

LETGS zeroth order X-ray lightcurve of AU Mic. Time represents the time after the start of the observation (MJD = 54643.506).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=14cm,clip]{14038fg3.ps} \end{figure} Figure 3:

The measured spectrum in the spectral range relevant for the analysis. Shown is the sum of the positive and the negative diffraction order.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{14038fg4.ps} \end{figure} Figure 4:

Model and data around the C-K edge (sum of both diffraction orders).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{14038fg5.ps} \end{figure} Figure 5:

The different contributions to the measured counts around the C-K edge. Top: First order emission. middle: Higher order contribution. bottom: Background.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{14038fg6.ps} \end{figure} Figure 6:

Data and model for the sum of the positive and the negative diffraction order. Note that the model is not based on a physical model (except for the continuum and the absorption).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{14038fg7.ps} \end{figure} Figure 7:

Number of missing (positive count number) or overpredicted photons (negative count number) as a function of the assumed carbon absorption column density in the model. The flattening of the curves indicates that the flux will, eventually, be completely absorbed in the considered wavelengths range for even higher column densities. The dashed line is the average of the positive and negative order using the new Gain Map and Pulse-Height filtering. The dashed-dotted line is the result using the wavelength ranges 30-42 Å  and 45-48 Å. The statistical errors reflects only first order errors. For a discussion of the errors see Sect. 4.2.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{14038fg8.ps} \end{figure} Figure 8:

Ratio of the line-fluxes to the Fe XVIII 14.21 Å  line using Gaussian-like emission measure distributions with a width of $\log (T/{\rm K}) = 0.5$.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{14038fg9.ps} \end{figure} Figure B.1:

The detectable carbon column density by measuring the jump height at the carbon edge as a function of the X-ray flux (0.1 keV-2.0 keV). Here, a pure carbon disk is assumed. The two lines represent a 50 ks and a 500 ks exposure with the LETGS. The same temperature structure as AU Mic is assumed which determines the higher order contribution around the carbon edge. The vertical dotted line indicates the X-ray flux of AU Mic.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{14038fg10.ps} \end{figure} Figure C.1:

The reconstructed emission measure distribution. The dotted line indicates the Gaussian fit to the EMD.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.