EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 516 (June-July 2010) A&A, 516 (2010) A36 Full HTML
Free Access
Issue
A&A
Volume 516, June-July 2010
Article Number A36
Number of page(s) 13
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/200913758
Published online 23 June 2010
A&A 516, A36 (2010)

A self-consistent approach to the hard and soft states of 4U 1705-44[*]

A. D'Aì1 - T. Di Salvo1 - D. Ballantyne2 - R. Iaria1 - N. R. Robba1 - A. Papitto3,4 - A. Riggio3,4 - L. Burderi3 - S. Piraino5,6 - A. Santangelo5 - G. Matt7 - M. Dovciak8 - V. Karas8

1 - Dipartimento di Scienze Fisiche ed Astronomiche, Università di Palermo, Italy
2 - Center for Relativistic Astrophysics, School of Physics, Georgia Institute of Technology, Atlanta, GA 30332, USA
3 - Università degli Studi di Cagliari, Dipartimento di Fisica, SP Monserrato-Sestu, KM 0.7, 09042 Monserrato, Italy
4 - INAF - Osservatorio Astronomico di Cagliari, Poggio dei Pini, Strada 54, 09012 Capoterra (CA), Italy
5 - IAAT, University of Tubingen, Sand 1, 72076 Tubingen, Germany
6 - INAF IASF di Palermo, via Ugo La Malfa 153, 90146 Palermo, Italy
7 - Dipartimento di Fisica, Università degli Studi Roma Tre, via della Vasca Navale 84, 00146 Roma, Italy
8 - Astronomical Institute, Academy of Sciences of the Czech Republic, Bocni II 1401a, 14131 Prague, Czech Republic

Received 27 November 2009 / Accepted 25 February 2010

Abstract
Context. High-resolution spectroscopy has recently revealed in many low-mass X-ray binaries hosting a neutron star that the shape of the broad iron line observed in the 6.4-6.97 keV range is consistently well-fitted by a relativistically smeared line profile.
Aims. The presence of other broad features, besides the iron line, together with a high S/N of the spectra offer the possibility of testing a self-consistent approach to the overall broadband reflection spectrum and evaluating the impact of the reflection component in the formation of the broadband X-ray spectra.
Methods. We analyzed two XMM-Newton observations of the bright atoll source 4U 1705-44, which can be considered a prototype of the class of the persistent NS LMXBs showing both hard and soft states. The first observation was performed when the source was in a hard low flux state, the second during a soft, high-flux state. Both the spectra show broad iron emission lines. We fit the spectra using a two-component model, together with a reflection model specifically suited to the case of a neutron star, where the incident spectrum has a blackbody shape.
Results. In the soft state, the reflection model, convolved with a relativistic smearing component, consistently describes the broad features present in the spectrum, and we find a clear relation between the temperature of the incident flux and the temperature of the harder X-ray component that we interpret as the boundary layer emission. In this state we find converging evidence that the boundary layer outer radius is $\sim $2 times the neutron star radius. In the low flux state, we observe a change in the continuum shape of the spectrum with respect to the soft state. Still, the broad local emission features can be associated with a disk reflecting matter, but in a lower ionization state, and possibly produced in an accretion disk truncated at greater distance.
Conclusions. Our analysis provides strong evidence that the reflection component in soft states of LMXBs comes from to hard X-ray thermal irradiation, which we identify with the boundary layer emission, also present in the continuum model. In the hard state, the broad iron line if also produced by reflection, and the continuum disk emission can be self-consistently accounted if the disk is truncated at a greater distance than the soft state.

Key words: line: formation - X-rays: binaries - radiation mechanisms: general - X-rays: bursts

1 Introduction

In last few years, the Epic-pn instrument onboard the XMM-Newton satellite has allowed deep investigation of the nature of the broad emission lines observed in the iron K$\alpha$ region of bright accreting neutron star (NS) low-mass X-ray binaries (LMXBs) (Bhattacharyya & Strohmayer 2007; Cackett et al. 2008; Pandel et al. 2008; Papitto et al. 2009; Iaria et al. 2009; Di Salvo et al. 2009; D'Aì et al. 2009). The authors of these works have focused their attention on the shape and origin of the broad iron line, and they agreed on the interpretation of the line broadness being the result of to special and general relativistic effects arising in the disk reflecting matter at a few gravitational radii from the compact object. This interpretation is supported by theoretical expectations and by general agreement between the fitting model and X-ray (1-10 keV) data.

However, if this interpretation is correct, the reflected spectrum should encompass a variety of other disk reflection features, because there are other low-Z, but abundant, emitting ion metals in the low-energy band. The good spectral resolution and the high S/N of the spectra has effectively shown in many cases a more complex pattern of features, besides the broad iron line. D'Aì et al. (2009) found in the spectrum of the bright Z-source GX 340+0 a broad emission line of Ca XIX and an absorbing edge of highly ionized iron; Iaria et al. (2009) found in the spectrum of the Z-source GX 349+2 three broad lines, besides the iron line, identified as Ca XIX, Ar XVIII and a blending of L-shell transitions of moderately ionized iron. Di Salvo et al. (2009) identified in the bright atoll 4U 1705-44 resonant emission lines of Ca XIX, Ar XVIII and S XVI, and an Fe XXV iron edge, which appears broad and redshifted with respect to the expected rest-frame energy. It has been therefore suggested that all these features, and not only the broad iron line, originate in the reflection component. To support this interpretation, it has been shown that the smearing components of the broad iron line (i.e., the smearing parameters of the reflection component, the inner and outer radii, inclination angle of the system, and the emissivity index, which measures the dependence of the emissivity power-law profile from the distance to the source of the irradiating photons) consistently describe the shape and the broadness of all the observed emission lines (Iaria et al. 2009; Di Salvo et al. 2009; D'Aì et al. 2009).

In this work, we perform a detailed analysis of two XMM-Newton observations of the bright atoll source 4U 1705-44. In the first observation, the source was in a low flux state, while in the second the source was in a bright soft state. First results, using a phenomenological approach to model the reflection component of the latter observation have been presented in Di Salvo et al. (2009). Here, we focus on the spectral changes that occurred between these two observations using a self-consistent reflection model.

The angular dependence of the reflected component formed by a constant-density partially-ionized medium was originally studied by Zycki et al. (1994), Zycki & Czerny (1994), and Matt et al. (2003). Reprocessing in a medium in hydrostatic equilibrium was then modeled by Raymond (1993), Nayakshin et al. (2000), Ballantyne et al. (2001), Ballantyne & Ross (2002), and Rózanska et al. (2002). Furthermore, Nayakshin & Kazanas (2002) examined the photoionized accretion discs via a novel time-dependent approach. A hot layer forms at the top of the disk atmosphere, roughly at the inverse Compton temperature, followed by a steep transition to colder, less ionized layers.

We use the reflection table model described in Ballantyne (2004). First application of this table model to consistently fit the X-ray spectrum of an NS LMXB can be found in Ballantyne & Strohmayer (2004). This reflection model (hereafter refbb) is calculated for an optically thick atmosphere, irradiated by a blackbody incident spectrum of $kT_{\rm ion}$temperature. The model gives the reflected spectrum according to the ionization parameter $\xi$, and the relative abundance of iron with respect to the other metals. In addition to fully-ionized species, the following ions are included in the calculations: C III-C VI, N III-N VII, O III-O VIII, Ne III-Ne X, Mg III-Mg XII, Si IV-Si XIV, S IV-S XVI, and Fe VI-Fe XXVI. The ionization parameter, log $\xi$, can vary between 1 and 4, with the density nH of the illuminated slab constant at 1018 cm-3. The constant density prescription can be considered a good diluted approximation of the actual hydrostatic structure in the disk for the 1.0-10.0 keV energy range (Ballantyne et al. 2001).

The $kT_{\rm ion}$ temperature can vary between 1 keV and 5 keV. All the metals abundances are fixed at the solar value, except for iron for which models were calculated for 0.1, 0.3, 1.0, 3, and 10 times the solar value. The space parameters of this model covers, therefore, a wide range of possible spectral solutions. In particular, this is one of the few available reflection models in which the primary incident spectrum is a soft thermal spectrum, and, also on the basis of the results already shown in Di Salvo et al. (2009), it is the most suitable for fitting the soft states of NS LMXBs.

We show that, within the available energy range, the continuum emission can be simply accounted for a three-component model composed of thermal disk emission, a saturated/unsaturated Comptonized harder emission, and a reflection component. The last one arises from the disk reflecting matter, where the impinging radiation field is the hard X-ray emission. We study the chemical abundances of the reflecting disk matter, the accretion flow in the two states, and possible scenarios for explaining the spectral differences in the two states.

\begin{figure} \par\includegraphics[angle=-90,width=9cm,clip]{13758f1.eps} \end{figure} Figure 1:

Long term X-ray light curve of 4U 1705-44. Data from the All Sky Monitor (2-10 keV range) onboard the Rossi XTE, from 1 January 2006 (MJD 53736) to 1 January 2009 (MJD 54832). The two arrows in the figure mark the day when the SoftObs (right arrow) and the HardObs (left arrow) took place.

Open with DEXTER

1.1 4U 1705-44

The source is a persistently bright, accreting LMXB located in the direction of the Galactic bulge (Forman et al. 1978), hosting an NS. It shows type-I X-ray bursts, with recurrence times dependent on the accretion state (Gottwald et al. 1989; Galloway et al. 2008; Langmeier et al. 1987). From the peak luminosity of bursts that exhibited episodes of photospheric radius expansions, which are thought to happen at the Eddington luminosity and are, therefore, used as standard candles, Haberl & Titarchuk (1995) derived a distance of 7.4 -1.1+0.8 kpc, later confirmed by Galloway et al. (2008). The companion source has still not been identified, although a near-infrared counterpart, most probably originated by X-ray reprocessing by the outer accretion disk and/or the companion star, has recently been found by Homan et al. (2009).

4U 1705-44 shows a secular trend toward alternating high- and low-flux periods (see e.g., Fig. 1) on a variable timescale of months. The spectral variability, on the contrary, can be much faster, of days (Barret & Olive 2002). Classified by Hasinger & van der Klis (1989) as an Atoll source, it was later shown that its spectral and temporal states are intermediate between the classic Atoll and the Z-sources division (Barret & Olive 2002). In particular, broadband X-ray data have shown that the switch between hard and soft states can be explained using a two-component model of a Comptonized inner emission and a soft thermal emission. Barret & Olive (2002) and Olive et al. (2003) interpreted the alternate hard and soft state transitions as caused by different truncation radii of the accretion disk. During hard states the disk is truncated at a large distance from the compact object and a hot corona with high electron temperatures and low optical depth forms around the NS. During the hard to soft state transitions, the inner disk approaches the NS; this causes an increase in its flux, thus providing a more efficient Compton cooling for the hot electrons and softer spectra. This scenario is supported by spectral modeling and by the timing analysis of the power-density spectra where the characteristic frequencies of the band-limited noise and of the low-frequency noise components are strongly correlated with the position of the source in the hardness-intensity diagram. High frequency quasi-periodic oscillations (QPOs) are also observed, usually in pairs (so-called kiloHerzt QPOs, kHzQPOs), with the highest reported peak at 1160 Hz (Ford et al. 1998; Wijnands et al. 1998).

Spectral analysis with the Chandra high-resolution gratings revealed, superimposed to the continuum, a set of local features, the most prominent of which was an unambigous, intrinsically broad ( ${\it FWHM} \sim 1.2$ keV) fluorescent iron line (Di Salvo et al. 2005). However, it was not possible to distinguish among different broadening mechanisms on the basis of the goodness of the spectral fit. This motivated the need for new observations with the XMM-Newton satellite, given the much larger collecting area in the iron region of the Epic-pn CCDs. A first XMM-Newton observation caught the source in a low state, and the S/N was rather poor in the iron range. A second observation, performed as a target of opportunity when the source returned to a high-intensity soft period was successful in disclosing the asymmetry in the iron line shape, which Di Salvo et al. (2009) interpreted as the result of reflection on a disk surface, very close to the NS, of hard coronal photons. A similar scenario has also been proposed for BeppoSAX broad band data in Piraino et al. (2007), and a claim was also made, using INTEGRAL high energy data, of a signature of a Compton bump in Fiocchi et al. (2007). Recently, Reis et al. (2009) using broad band SUZAKU data also shows that the asymmetry of the iron profile are naturally described by a disk reflection scenario.

2 Observation and data reduction

The XMM-Newton Observatory (Jansen et al. 2001) includes three 1500 cm2X-ray telescopes each with an European Photon Imaging Camera (Epic, 0.1-15 keV) at the focus. Two of the Epic imaging spectrometers use MOS CCDs (Turner et al. 2001), and one uses pn CCDs (Strüder et al. 2001). Reflection grating spectrometers (RGS, 0.35-2.5 keV, den Herder et al. 2001) are located behind two of the telescopes.

XMM-Newton observed 4U 1705-44 on two occasions. The most recent observation was performed on 24 August 2008 from 02:57:04 to 17:13:35 UTC (Obs. ID 0551270201, hereafter SoftObs) for a duration of 51.390 ks and an effective exposure of 45.170 ks (owing to telemetry overflow during some part of the observation), the second observation took place on 26 August 2006 from 05:04:54 to 14:55:38 UTC (Obs. ID 0402300201, hereafter HardObs), with an exposure total time of 36.733 ks.

On both occasions, the Epic-pn operated in timing mode with medium filter. In this mode only one central CCD is read out with a time resolution of 0.03 ms. This provides a one-dimensional image of the source with the second spatial dimension being replaced by timing information. RGSs operated in spectroscopy mode.

Figure 1 shows the long-term X-ray variability of the source as seen from the All Sky Monitor (ASM) of the Rossi XTE, from 1 January 2006 to 1 January 2009, the period when SoftObs and HardObs were performed is marked in the light curve. HardObs took place when the source activity was in a relatively low state (ASM count rate $\sim $5 count/s), while SoftObs was performed almost at the peak of one of the months lasting active state (ASM count rate $\sim $35 count/s). During the HardObs the source showed a type-I X-ray burst, while no bursts were present in the SoftObs. In Fig. 2, we show the Epic-pn light curves of the two observations. In HardObs the countrate variability, excluding the burst interval (see Sect. 4), is around a 10% level from the average of 33.4 counts/s, while SoftObs has an average of 870 counts/s and a similar variability spread.

\begin{figure} \par\includegraphics[angle=-90,width=8cm,clip]{13758f2a.eps} \includegraphics[angle=-90,width=8cm,clip]{13758f2b.eps} \end{figure} Figure 2:

Light curves for SoftObs ( upper panel) and for HardObs ( lower panel). In HardObs, a type I X-ray burst is present at $\sim $11 ks after the beginning of the observation (see Sect. 4 for details.)

Open with DEXTER

In Fig. 3, we show the color-color diagram for the two observations. The soft color is defined as the ratio of the counts in the 1-3/3-6 keV band and the hard color as the ratio in the 3-6/6-10 keV band. The source shows very little variability during HardObs, while SoftObs is more variable, but always softer than HardObs.

\begin{figure} \par\includegraphics[angle=-90,width=9cm,clip]{13758f3.eps} \end{figure} Figure 3:

Color-color diagram that shows the relative positions of the two observations. Each point represents a time segment of 500 s. SoftObs data in red, HardObs data in green.

Open with DEXTER

For spectral analysis we used Xspec version 12.5.0 (Arnaud 1996). The interstellar absorption (phabs component in Xspec) is calculated using the cross-section table of Verner et al. (1996) and the metal abundances table of Wilms et al. (2000). We used the Science Analysis System (SAS) version 9.0 for the reprocessing of XMM-Newton data, with the epproc pipeline for generating the Epic-pn scientific products and the rgsproc pipeline for the RGS ones.

We used standard SAS tools for data selection, masks generation, ancillary and response matrices. Spectra were filtered according to the $PATTERN \leq 4$ and FLAG=0 criteria. Background spectra above 12 keV were inspected to check for periods of high solar background. Background spectra were extracted using the same filtering criteria of source spectra in the RAWX 3-10 columns. Source spectra were extracted in the RAWX 28-46 columns. We used the Epic-pn spectra grouped to have 5 energy channels per resolution element and at least 25 counts per energy channel. This choice avoids an excessive oversampling of the data, without loss of important spectral information. RGS data were also grouped by adopting the 25 counts per energy channel criterion.

By testing different choices of channels binning, we observed a change in the value of the reduced $\chi^2$ of the best-fitting models, but still the best-fitting parameters are not significantly dependent on this choice.

3 Spectral analysis

3.1 SoftObs the soft state

SoftObs was analyzed in Di Salvo et al. (2009); here we present a self-consistent approach to the spectrum modeling using a broadband reflection model. In Di Salvo et al. (2009), the main focus was on the determination and the nature of the broad emission lines seen in the energy spectrum from 2.5 keV to 11 keV. It was shown that the reflection scenario, including the relativistic effects, is the most physically and statistically favored solution for interpreting the broad emission features.

We analyzed these data again, using a slightly different extraction mask for the Epic-pn, namely excluding the brightest CCD column (RAWX = 37), in order to obtain a complete pile-up free spectrum. We used the epatplot tool of the SAS package to check the distribution of single vs. double event pattern distribution. This tool shows the theoretical normalized fractional distribution of these events and the real data distribution. A mismatch between the data and the theoretical predicted curves indicates possible pile-up. The XMM-Newton data of 4U 1705-44, including the brightest CCD row, deviate from the theoretical curves for energies less than 2.5 keV (which indeed were excluded from the analysis published by Di Salvo et al. 2009) and above 9 keV. The exclusion of the brightest row of the Epic-pn CCD significantly reduces this problem (e.g. the gap between data and theoretical curve passes from 0.02 to 0, from 0.03 to <0.01, from 0.04 to <0.02 at 3 keV, 6 keV, 9 keV, respectively).

We also used RGS1 data in the 1.0-2.0 keV energy range, while RGS2 data have been discarded since they are severely pile-up affected[*]. Epic-pn data were first used in the broad energy range between 0.6-12.0 keV. This range, however, revealed (as in HardObs) some very large systematic features around the Au and Si instrumental edges that are difficult to reconcile with any plausible physical scenario (see also Papitto et al. 2009; Boirin & Parmar 2003). Also, a mismatch between the RGS and PN spectrum in the 1.0-2.0 keV range is indicative of calibration uncertainties that affect the determination of the soft band. In Fig. 4, we show the Epic-pn spectrum for clarity, when the 2.0-11 keV band is used for deriving the best-fitting model, and then the 0.6-2.0 keV channels are noticed. The broad feature at 1.7 keV is also present in HardObs, and we found that this spectral shape can be well-fitted using a simple broad Gaussian line. These Gaussian parameters are consistent in the two datasets. At very low energies, the spectrum shows a clear flux excess, which, however, is ruled out by the simultaneous RGS1 dataset. We therefore excluded the PN energy range below 2 keV in order to get rid of any systematic problem that could affect our analysis, and used only the RGS1 data to constrain the softest band.

\begin{figure} \par\includegraphics[angle=-90,width=9cm,clip]{13758f4.eps} \end{figure} Figure 4:

Residuals, in units of $\sigma $, in the broad 0.6-12 keV energy range, of the Epic-pn spectrum when the 2.0-12.0 keV best-fitting model is used (Table 1). A broad feature at 1.7 keV is clearly visible together with soft residual emission below 1.0 keV.

Open with DEXTER

\begin{figure} \par\mbox{\includegraphics[angle=-90,width=8cm,clip]{13758f5a.eps} \includegraphics[angle=-90,width=8cm,clip]{13758f5b.eps} } \end{figure} Figure 5:

Data and best-fitting model with individual components separately shown (top panels), together with residuals in units of sigma (lower panels). Left panel: the best-fitting model without the Ar XVIII and Ca XIX emission lines. Right panel: data and residuals using the best-fitting model of Table 1.

Open with DEXTER

In analyzing these data, Di Salvo et al. (2009) decomposed the continuum emission into the sum of a soft blackbody component and a harder, optically thick, Comptonized component. In the present work, we used a slightly different but physically and statistically similar continuum model. We replaced the soft blackbody component by a multicolored disk component (diskbb model in Xspec, Makishima et al. 1986), while the Comptonized emission could be approximated well with a simpler hard blackbody component. Having an additional continuum component at energies above 7 keV from the reflection continuum gives, in fact, a Comptonization optical depth over 10, while, at the same time, seed-photon temperature and electron temperature get very near to each other ( $\Delta E < 0.5 $ keV), so that the blackbody approximation is reasonably justified (Iaria et al. 2009; D'Aì et al. 2009). Moreover, instead of a number of local disklines and a smeared absorption edge, in this work we use a self-consistent table reflection model (Ballantyne 2004), convolved with the rdblur component (Fabian et al. 1989) to consider the relativistic effects in a Schwarzschild space-time (i.e. relativistic Doppler boosting, light bending, and lensing effect of the disk irradiated matter). The degree of smearing is set by the disk's inner and outer radius (in units of gravitational radii $R_{\rm g} = GM/c^{2} \sim 2$ km for a 1.4 solar mass NS), the inclination angle of the disk, and the emissivity law profile, assumed to only depend on the distance of the source of the impinging photons ( $\epsilon (r) = r^{-q}$). These parameters are well constrained by the fitting, except for the disk outer radius, which is poorly constrained ( $R_{\rm out} = 10_{-6}^{+100}\times 10^3$ $R_{\rm g}$), so that we choose to keep it frozen at 104 $R_{\rm g}$, given its much larger uncertainty with respect to the other spectral parameters.

We tested that the $kT_{\rm ion}$, the temperature of the irradiating flux is perfectly consistent with the same temperature of the hard blackbody component, and we set the two spectral parameters tied together during the fitting procedure.

This model adequately describes the continuum and the shape of the iron line, and also takes the emission features of Si XIV and S XVI into account, although some residuals are still present at $\sim $2.6 keV probably due to an overabundance of this metal with respect to the other elements. There are still two broad features at $\sim $3.9 keV and $\sim $3.32 keV that stand out in the residuals (see Fig. 5, left panel). Following the interpretation of Di Salvo et al. (2009), which ascribes these features to resonant emission lines of He-like calcium and H-like argon ions, we added two Gaussians to account for these residuals profiles, given that our reflection model lacks, in fact, the relative emission lines for these elements. These lines are kept with 0 keV frozen width and are convolved with the rdblur kernel, with the smearing parameters identical to the refbb model. The reduced $\chi^2$, with the introduction of these two additional smeared lines varies from 1.70 (710 d.o.f.) to 1.30 (706 d.o.f.), and the residuals at the 3.3 keV and 3.9 keV energies are reasonably well fitted (Fig. 5, right panel). These two lines have a similar equivalent width (between 8 and 10 eV), and the line positions are well constrained and in agreement with the expected rest-frame emission line energies (the Ar XVIII at $3.30 \pm 0.02$ keV and the Ca XIX at $3.90 \pm 0.02$ keV).

Given the high quality of the spectrum, we also tried to evaluate the fraction of iron abundance with respect to the other metals. Setting the iron fraction overabundant with respect to other metals by a factor of 3 provides a worsening of the fit with respect to the assumed solar values ( $\Delta \chi^2 = 10, F$ statistic value 9.7 and probability 0.2%), and the same happens when the iron fraction is assumed to be underabundant for the same factor ( $\Delta \chi^2 = 12, F$ statistic value 11.7 and probability 0.06%). We concluded that the iron fraction is well constrained by the reflection model, and it is relatively consistent with the assumed solar abundance values within a factor of 3.

Although this model is formally not satisfactory ( $\chi^2_{\rm red} \sim 1.3$ with 706 d.o.f.), there is no evidence in the residuals of other local features, and the residuals are so randomly distributed around the best-fitting model that no other continuum component is required. The most probable explanation for this high $\chi^2$ is that, at this very high count rate (>400 cts s-1), the statistical errors in the channels becomes too small compared with the relative uncertainty of the response matrix, giving an overall underestimation of the systematic error to be attributed to the energy channels. Adding a 0.8% systematic error to the best-fitting model, we find a value of $\chi^2\sim 1.0$. This error is added in quadrature in order to self-consistently evaluate the error to be associated to the spectral parameters, which are reported in Table 1. We also report the unabsorbed fluxes of each spectral component in the 1-10 keV range, and in the extrapolated 0.1-100.0 keV range. The blackbody radius and inner disk radius are calculated assuming a distance to the source of 7.4 kpc and a disk inclination of 35$^{\circ}$.

The observed 1.0-10.0 keV absorbed flux in this observation is $5.6 \times 10^{-9}$ erg cm-2 s-1, while the unabsorbed flux is $1.2 \times 10^{-8}$ erg cm-2 s-1. Extrapolation of this model from 0.1 keV to 100 keV results in a bolometric unabsorbed flux of $1.6 \times 10^{-8}$ erg cm-2 s-1. The inferred X-ray luminosity in this state corresponds to $\sim $ $1 \times 10^{38}$ erg s-1. Figure 6 shows the contribution of disk thermal emission, hard thermal emission, and reflection component to the absorbed 0.5-50 keV flux (left panel) and to the unabsorbed 0.1-50 keV flux (right panel). The contribution of the reflection component is dominant at very low energies, below 1 keV, while, because of the very soft nature of the incident spectrum, it falls off very rapidly beyond the iron line region.

Table 1:   Best-fitting values of the parameters obtained for the soft state of 4U 1705-44.

\begin{figure} \par\mbox{\includegraphics[angle=-90,width=8cm,clip]{13758f6a} \includegraphics[angle=-90,width=8cm,clip]{13758f6b} } \end{figure} Figure 6:

Best fitting model in the $E \times f(E)$ representation of the soft state of 4U 1705-44. Red line is the thermal disk emission, green line the black body thermal emission, blue line the reflection component. Left panel shows the ISM absorbed model, right panel shows the unabsorbed model.

Open with DEXTER

3.2 HardObs the hard state

In this section we describe the spectral analysis of the persistent emission of HardObs, excluding the data close to the type-I X-ray burst (from 15 s before the burst peak to 200 s after the burst peak). We first used Epic-pn data in the broad energy range from 0.6 keV to 12.0 keV, RGS1, and RGS2 data in the 1.0-2.0 keV energy range. A single absorbed power-law model fails to describe the data ( $\chi^2_{\rm red}\sim 4.07, 826$ d.o.f.); a power law with exponential cut-off provides a better fit, but still unsatisfactory ( $\chi^2_{\rm red} \sim 2.82, 825$ d.o.f.); replacing the exponentially cut-off power law with a physical Comptonization model (comptt in Xspec, Titarchuk 1994) again improves the fit significantly ( $\chi^2_{\rm red}\sim 1.61, 824$ d.o.f.). Residuals at low energies, however, require the addition of an additional soft component. A blackbody component or multicolored disk emission (diskbb in Xspec) is able to satisfactorily model the continuum emission, although from a statistical point of view, we are not able to distinguish between a single thermal temperature and the multicolored model ( $\chi^2_{\rm red}\sim 1.40, 822$ d.o.f. for both models), and we discuss different physical scenarios. The still high $\chi^2$ stems from the presence of a broad local emission line in the iron range and to an S-shaped pattern in the residuals at softer energies, which could be fitted by a broad Gaussian at energies $\sim $1.7 keV. This broad line is, however, not easily identified with any physically reasonable bound-bound transition so we discuss a possible instrumental origin. In fact, the residuals pattern between 1.0 and 2.0 keV is mostly guided by the Epic-pn channels, given the much larger collecting area compared to the RGSs. Fitting the RGS datasets alone, we obtain a relatively good fit (reduced $\chi^2 = 0.99$) using either an absorbed power-law model or blackbody model as continuum. RGS data alone indicate a higher $N_{\rm H}$ than the Epic-pn data ($N_{\rm H}$ $3.0\pm0.4 \times 10^{22}$ cm-2 for power-law continuum, $2.2\pm0.3 \times 10^{22}$ cm-2 for blackbody emission).

\begin{figure} \par\mbox{\includegraphics[angle=-90,width=8.2cm,clip]{13758f7a.e... ...raphics[angle=-90,width=8.2cm,clip]{13758f7b.eps} } \vspace*{2mm} \end{figure} Figure 7:

Left panel: data and residuals at the soft energies (0.6-3.0 keV), using an absorbed blackbody component. Residuals clearly display an S-shaped pattern in the Epic-pn data (black data) between 1.5 keV and 2.0 keV and a general mismatch between RGS data (green and red data) and Epic-pn data at softer energies. Data have been rebinned for clarity. Right panel: residuals in the iron range, when data 4.0-9.0 keV are fitted with Model 1 and the iron line is subtracted from the data.

Open with DEXTER

Table 2:   Best-fitting values and associated errors for different modelization used to fit the hard state data of 4U 1705-44.

On the contrary, in the restricted 0.6-2.0 keV Epic-pn band, we clearly observe large residuals that cannot be ascribed to the shape of the continuum emission (see Fig. 7, left panel). Inclusion of a broad line at 1.7 keV makes the model acceptable; however, this line is not required in the RGSs spectrum, for which we get only an upper limit on the line normalization of $8 \times 10^{-5}$ photons cm-2 s-1 (90% confidence level), which not compatible with the lower limit of the Epic-pn spectrum ( $2.9 \times 10^{-4}$ photons cm-2 s-1 , 90% confidence level). This led us to conclude that the line is probably an artifact due to incorrect modelization of the instrumental K Si and M Au edges of the Epic-pn. Moreover, as mentioned above, the Epic-pn data require a much lower value of the $N_{\rm H}$ ( $1.3~\pm~ 0.2 ~\times~ 10^{22}$ cm-2), which does not match by far the high value as derived from the RGSs and the Epic-pn data above 2 keV or the $N_{\rm H}$value of SoftObs, nor the $N_{\rm H}$ value as derived from the burst analysis. This implies either an usual underabundance of light Z metals (e.g., oxygen, neon, magnesium) with respect to high Z metals or the presence of additional soft X-ray emission, or a soft flux miscalibration of the instruments. The first hypothesis appears the least probable. The second hypothesis can be, in principle, correct and it is not difficult to image other physical mechanisms that can play an important role at these very soft X-ray energies (X-ray reprocessing in the outer disk or at the surface of the companion star), but our experience has shown that other XMM-Newton observations in timing mode of moderately absorbed bright sources are affected by such soft excesses (Iaria et al. 2009; D'Aì et al. 2009), often in the form of strong and very broad emission lines at 1.0 keV. Although possibly hiding a physical origin, such excesses can introduce strong biases in the determination of the correct physical model and physical conclusions. In view of the above-mentioned considerations, we chose not to consider Epic-pn data below 2 keV, in analogy with data reduction of SoftObs, and to rely on the RGS data for the rest of our analysis.

RGS data, however, have fewer statistics than the Epic-pn data, and we noted that the determination of the soft component is strongly correlated with the $N_{\rm H}$ value. We chose to use results of the soft state analysis to derive better constraints for this observation, and we froze the $N_{\rm H}$ value to the best-fitting value of Table 1. Adopting the value of $2.44\times 10^{22}\times$ cm-2 derived from the burst analysis (see Sect. 4) does not significantly change the determination of the spectral components, or our conclusions.

The broad $\sim $6.4 keV line can be identified as a fluorescence emission line of iron in a low ionization state (see Model 1 in Table 2). The line is intrinsically broad, given that its width is much greater than the energy resolution of the Epic-pn in this energy band.

We present in Table 2 the results of three different spectral decompositions. The models mostly differ in the choice of the soft component and of the reflection model, but share the use of a Comptonized component for the hard-energy part of the spectrum. However, because the spectrum is only covered up to 12 keV and the Comptonized emission extends well above this energy, we found a strong correlation, in all the models, in parameter space, between the electron temperature and the optical depth of this component. In this state, the source has been previously observed many times with the Rossi XTE satellite, whose higher energy coverage allows for much better constraints. In Barret & Olive (2002), the optical depth of the Comptonized component, in this hard state, shows a nearly constant value at 5.5. We chose, therefore, to keep this parameter frozen at this value, to reduce the uncertainties in the determination of all the other spectral parameters, after having checked that this value is, however, within the parameter error bar, if this is set free to vary in the fitting procedure.

In Model 1, we use a thermal blackbody for the soft component and a Comptonization for the hard component (Gierlinski & Done 2002; Barret & Olive 2002). The iron line is fitted using a Gaussian line. In Model 2, we use a multicolored disk emission, with disk normalization N fixed to 70 (this value corresponds to an inner edge located at $\sim $1.2  $R_{\rm NS}$) and the refbb reflection model convolved with rdblur smearing kernel. The use of the refbb model can be considered a good first-order approximation, within the 1-12 keV available band, of the actual reflection spectrum, although the impinging radiation spectrum now departs from a saturated blackbody-like spectrum. The reflection model is mainly used to reproduce the broad iron fluorescence line as we have no other prominent feature available to constrain other reflection models. The temperature of the blackbody incident spectrum, the ionization parameter, and the component normalization are left free to vary. In this way, the reflection model provides the same information on the ionization state of the disk reflecting matter, on the 1-10 keV reflection flux, and on the hardness of the impinging radiation source, as would be derived with other reflection models. In Model 3, we force a spectral solution with disk normalization N fixed to 1200 (corresponding to an inner radius of $\sim $5  $R_{\rm NS}$, or $\sim $30 $R_{\rm g}$). For both Model 2 and Model 3, the smearing of the reflection component is strongly required by the fit ( $\Delta \chi^2 > 50$, without any smearing), although the smearing parameters, when left free to vary, were strongly correlated and uncertain. We chose to keep the inclination angle and the emissivity index of the rdblur component frozen to the best-fitting values of the soft state fit (see Table 1), because these parameters are not physically expected to vary between the two states. In Model 2 we left the inner and outer radii free to vary. As can be noted, they are not very well constrained. The inner radius is required to be less than 90 $R_{\rm g}$, with a best fitting value of 30 $R_{\rm g}$. In Model 3, these two parameters are unconstrained as well, and we chose to freeze the inner radius at a reference value of 30 $R_{\rm g}$ (matching it with the inner disk edge value of the continuum component diskbb), while the outer radius is frozen at 1000 $R_{\rm g}$.

In Fig. 8 we show the data and the residuals with respect to the best-fitting models, together with the best-fitting unabsorbed model in the extrapolated 0.1-100.0 keV range. Best-fitting values of the spectral components and corresponding fluxes, calculated in the unabsorbed 1.0-10.0 keV range and in the extrapolated 0.1-100.0 keV range, are reported in Table 2. As observed, irrespective of the model we used to fit the data, the bulk of the emission is in the Comptonized component and the fluxes do not differ substantially from one model to the next.

\begin{figure} \par\includegraphics[angle=-90,width=8.2cm]{13758f8a.eps}\hspace*... ...cludegraphics[angle=-90,width=8.3cm]{13758f8f.eps} \vspace*{1.5mm} \end{figure} Figure 8:

Right panels: XMM-Newton data and residuals in units of $\sigma $ with respect to the best-fitting models for the hard state. Left panels: the theoretical unabsorbed model in the 0.1-100 keV range (in blue the iron line/reflection component, in green the Comptonized component, in red the thermal soft disk emission).

Open with DEXTER

4 Burst analysis

In HardObs, the source showed a type I X-ray burst. The peak of the burst was observed 10.844 s after the beginning of the observation and lasted approximately for 100 s. The light curve profile during the decay phase is well-fitted by an exponential curve with a decay time $\tau$of 10.4 s. The spectral evolution of the burst is similar to what is observed in other sources. We used the source spectrum 15 s before the onset of the burst as background file, and then we extracted a source spectrum every 5 s, after the burst peak. The burst spectrum is well-fitted by an absorbed blackbody spectrum and does not show any other spectral feature, also because the low statistics and the short exposure times. In Table 3, we show the variation in the burst flux and the decreasing temperature of the continuum component as a function of time. The burst does not show photospheric radius expansion.

Table 3:   Time-resolved spectral evolution of the burst emission.

The study of this burst allows, for the first time in this source, to independently constrain the value of the interstellar absorption towards the source direction. Past studies, in fact, relied on the Rossi XTE data, where the spectra started from 3.0 keV and gave nearly no constraint on the $N_{\rm H}$. We fitted the six datasets using a common fit, with the $N_{\rm H}$ tied for each dataset. The reduced $\chi^2$ of the fit is acceptable, 1.03 for 472 dof, and we derived a value for the $N_{\rm H}$ parameter = $2.46\pm 0.22 \times 10^{22}$ cm-2 ( $2.46\pm0.35 \times 10^{22}$ cm-2 for 99% confidence level). Using the once common wabs interstellar absorption component, we get $N_{\rm H} = 1.70\pm0.15 \times 10^{22}$ cm-2. We further checked that this global $N_{\rm H}$ value is within the error bars, when this parameter is independently free to vary for each spectrum. We report in Table 3 the best-fitting blackbody parameters (blackbody radius calculated assuming a distance of 7.4 kpc) for the six time intervals and in Figs. 9 and 10 the burst light curve and the data with the residuals in units of $\sigma $for the common fit.

The evolution of this isolated burst is similar to some of the bursts reported for this source in the RXTE burst catalog (Galloway et al. 2008).

5 Discussion

5.1 The soft state

The two XMM-Newton observations of 4U 1705-44 offer the opportunity of testing a self-consistent model for the 1.0-12.0 keV energy band and, using spectral fitting, probing the different accretion states in this source. During SoftObs the source was in a high-flux, soft state. The bolometric luminosity of the source was at $\sim $50% of the Eddington limit, with most of the X-ray emission within the observed 1-12 keV band ($\sim $70%). This state corresponds to one of the softest states ever observed for this source. Because most of the flux, theoretically limited by the Eddington rate, is radiated at soft energies (E<10 keV), we expect that the spectrum is relatively weak in hard X-rays, (Barret & Olive 2002). Even considering the possible presence of a nonthermal hard tail, which was reported when the source luminosity corresponded to $4 \times 10^{37}$ erg s-1(Piraino et al. 2007), this characterization remains valid as the hard tail flux amounted to only $\sim $10% of the total source luminosity.

The spectrum can be well-fitted by the sum of two thermal components together with the reflection component. This model accounts for the energetics and spectral distribution between the different continuum components, if we associate the blackbody hard emission with the boundary layer (BL) emission (Done et al. 2002; Revnivtsev & Gilfanov 2006; Gilfanov et al. 2003). The boundary layer should, in fact, occupy a very small region between the inner disk radius and the surface of the NS, and theoretically, it should Comptonize seed photons from the disk and the surface of the NS in an optically thick corona in these high-accretion states (Popham & Sunyaev 2001), resulting in a saturated single-temperature Comptonization.

\begin{figure} \par\includegraphics[angle=-90,width=9cm,clip]{13758f9.eps} \vspace*{-2mm} \end{figure} Figure 9:

Light curve of the burst observed during HardObs, the start time of the first time interval used for spectral analysis is time = 20 s in this plot.

Open with DEXTER

\begin{figure} \par\includegraphics[angle=-90,width=9cm,clip]{13758f10.eps} \vspace*{-2mm} \end{figure} Figure 10:

Data and residual with respect to the best-fitting model of the six time selected spectra of Table 3.

Open with DEXTER

The blackbody radius of the hard component is 5.5 km, a value that is remarkably in agreement with the asymptotic value that we derived from the analysis of the burst emission. Taking general relativistic effects into account and the hardening of the spectrum (Shimura & Takahara 1995), this radius is compatible with an emission region of size comparable to the NS surface. The disk and the BL have comparable fluxes with a luminosity ratio $L_{\rm BL}/L_{\rm disk} = 1.67$ (assuming a spherical isotropic emission for the BL and neglecting the reflection contribution) or 2.0 (considering the sum of the reflection emission and the hard component).

We can express the ratio of these two components in terms of the outer boundary layer radius, which can be written in units of the NS radius as $b R_{\rm NS}$, and of the spin frequency of the NS, which can be written as a fraction of the breakup spin frequency, $f \equiv \nu_{\rm spin}/\nu_{\rm break}$ (Popham & Sunyaev 2001),

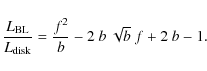
\begin{displaymath}\frac{L_{\rm BL}}{L_{\rm disk}} = \frac{f^2}{b} - 2\phantom{.}b\phantom{.}\sqrt{b}\phantom{.}f + 2\phantom{.} b - 1. \end{displaymath} (1)

The spin frequency of the NS is not known; however, the difference between the upper and the lower kHz QPOs is, in some sources, near the true spin frequency (see Méndez & Belloni 2007; van der Klis 2004). In 4U 1705-44, this difference is $\sim $330 Hz (Ford et al. 1998), which translates into a f value between 0.13-0.2 depending on the equation of state adopted for the NS. A ratio of 2, as we found, constrains the b value in a very narrow range between 1.8 and 2.1, which agrees with theoretical expectations for such a high accretion rate, of the outer radius of the boundary layer (Popham & Sunyaev 2001). In some sources the difference in kHzQPOs peaks is near half the spin frequency. If this were the case, on the contrary, we would obtain b values above 2.6, contradicting both the theory and the inner disk radius obtained from the reflection component.

The thermal disk component normalization N is related to the inner disk radius by the simple expression $R_{\rm col} = D \sqrt[2]{N/\cos \theta}$, where D is the distance expressed in units of 10 kpc and $\theta$is the inclination angle. Using a distance of 7.4 kpc and an inclination angle of 35$^{\circ}$, we obtain a best-fitting value of 11.4 km. However, this value is generally considered an underestimation of the true inner radius by a factor of $\sim $2 (Merloni et al. 2000). Taking these corrective factors into account, we derive an inner disk radius of $\sim $10 $R_{\rm g}$, consistent with the smearing factor of the reflection component and with our estimate of the outer boundary layer radius as derived by the ratio of the continuum fluxes (D'Aí et al. 2007; D'Aì et al. 2009).

The reflection component in this state is remarkably strong, and the reprocessed flux at the disk surface is about 30% of the total Comptonized component. Although most clearly determined by the shape of the broad iron line, the reflection component, gives its strongest contribution in the very soft X-ray band (below 1 keV there is 62% of the overall bolometric flux of the component, with the dominant H-like lines of oxygen and neon), where it can be as competitive as the disk emission, as already noted by Ballantyne (2004). In the 1-10 keV range, the relative contribution is 33%, while above 10 keV, there is only a 5% flux, owing to the very soft nature of the incident flux. We calculated the reflection fraction ( $R = \Omega / 2 \pi$) for this model to be 0.23 $\pm$ 0.01, a value that is consistent with our proposed geometry of a compact illuminating source.

The disk approaches the NS, and we obtain accurate constraints from the relativistically broadened reflection features, which set the inner disk radius to less than 13 $R_{\rm g}$. After comparing our best-fitting model with the results of Di Salvo et al. (2009), we note that the blurring parameters agree quite well, with a difference only in the outer radius, which in our model is found larger and in the inclination angle, which is required to be somewhat lower (although still compatible at 3$\sigma $ level). These differences are, however, impressively small if we consider that we adopted here a different continuum model and a self-consistent broadband reflection model instead of local disklines.

5.2 The hard state

Bright Z-sources accreting very close to the Eddington limit, do not show significant variation in the luminosity ratio between disk and coronal emission when they move along their Z-track on a color-color diagram, and the evolution of the spectral parameters is smooth, without jumps (e.g. D'Aí et al. 2007; Di Salvo et al. 2002; Agrawal & Sreekumar 2003).

Atoll sources, in contrast, resemble the spectral decomposition of bright Z-sources when they are in their soft state (also called banana state), but strongly differ when they move into the hard state (also called island state). In this state a very soft component is occasionally detected (di Salvo et al. 2004; Barret et al. 2000), although the inferred emission radii are of a few kms, and some authors identify this soft emission directly with the NS surface/BL emission (Gierlinski & Done 2002; Barret et al. 2003). The luminosity is dominated by a Comptonized spectrum, with moderate optical depth ( $1 < \tau < 6$) and high-energy cut-offs between 30 and 100 keV. There is no general agreement about what causes these state transitions, although it is certain that the soft-hard and the hard-soft transitions are switched at different luminosities giving rise to a hysteresis pattern (Meyer-Hofmeister et al. 2005). The difference in the switch luminosity is not, however, universal, and 4U 1705-44 displays a small, or null, hysteresis (Gladstone et al. 2007). The luminosity that we derived using the models 1-3 is within 2- $4 \times 10^{36}$ erg s-1, which is slightly below the threshold that Gladstone et al. (2007) quotes for the state transition of 4U 1705-44.

Comparing these results with the models proposed for the soft state, we note the very small contribution of the soft component to the overall energy emission. The source accretes at levels less than 1% $L_{\rm Edd}$, so that the disk is theoretically expected to closely approach the NS surface (at 1.1-1.2 R$_{\rm NS}$), because it has a flux contribution higher, or similar, to the Comptonized component (Popham & Sunyaev 2001). But, as can be seen in Table 2, any soft component would make only $\sim $1/10 of the overall total contribution. This aspect is well known as are the difficulties in the spectral decomposition (see Lin et al. 2007, for a complete discussion).

We showed the best-fitting parameters in Table 2, and the residuals and the extrapolated models for three different modelizations, which are able to describe the 1-10 keV energy spectrum in Fig. 8. The model with the lowest $\chi^2$ is Model 1, although the two other models cannot be a priori ruled out, as the difference in $\chi$ is not significant and is given to tighter constraints imposed on Models 2 and 3. We discuss hereafter the physical implications of the three models, focusing on the combined broadband continuum and line broadening mechanisms.

5.2.1 Model 1

This model provides a very good fit to the data, and is also proposed in Barret & Olive (2002) for RXTE spectral analysis of the same source and in Gierlinski & Done (2002) for the atoll source 4U 1608-52. It closely resembles the so-called Birmingham Model (Church & Baucinska-Church 2004; Church & Balucinska-Church 2001), where the spectral decomposition is resolved into a soft blackbody emission, ascribed to the boundary layer, and a Comptonized emission that takes place in an extended corona (coronal radius $\gg $109 cm) caused by disk evaporation. The inferred blackbody radius is rather small ($14 \pm 5$ km), but it can be still consistent with a surface physically associated with the BL. We derive good constraints for the Comptonized component on the seed photon temperature and the thermal temperature of the electron cloud. When comparing our results with Barret & Olive (2002), we observe that the soft blackbody component has a much lower temperature (0.3 keV against 1 keV), while the electron temperature is well consistent with the RXTE results. The discrepancy is, however, explicable considering the much better low energy coverage of the spectrum offered by XMM-Newton, while the RXTE data start only from 3 keV, not allowing any distinction between the Comptonized curvature at the seed-photon temperature and the contribution of any other soft thermal component. (In Barret & Olive 2002, the seed-photon temperature is, in fact, kept frozen to a reference value of 0.4 keV because not constrained by the fit.)

We note, however, that the blackbody temperature is too low to be associated with the reprocessed emission from the NS surface, while it is physically implausible to observe seed photons for the Comptonized component more energetic than the emitted photons for the BL or the NS surface. We find it more reasonable, on the basis of the results of the soft state, to consider that the continuum soft component still needs to be associated with the thermal disk emission, while the Comptonized emission continues between the inner edge of the accretion disk and the surface of the NS.

5.2.2 Model 2

In analogy with soft state, this model ascribes the softer continuum component to thermal disk emission and the harder component to Comptonized emission. We tried two spectral solutions to check, at least as a first order approximation, that the iron line broadness could still be interpreted in terms of disk reflection. An optically thick, geometrically thin disk must, therefore, be present, so we tried in Model 2 to fit the low-energy X-ray band with a disk emission, whose inner radius would match an $R_{\rm in} \sim 1.2$  $R_{\rm NS}$, as is theoretically expected (Popham & Sunyaev 2001). This corresponds to fixing the normalization of the diskbb component to 70, a value we found to lie within the error box, if the parameter is left free to vary. The reflection component requires a $kT_{\rm ion}$ temperature between 1.5 keV and 2.1 keV.

The degree of smearing, given by the constraints imposed on the rdblur component are sufficient to adequately describe the iron line broadness. In this case, the reflection has a lower subtended angle with respect to SoftObs, and the percentage ratio of the extrapolated fluxes between the corona and the reflection component is $\sim $4%, which can physically correspond to a geometrical shrinking of the area of the BL, which from a quasi-spherical shape around the NS in the soft state, is expected to decrease its area to an equatorial belt of a few kilometers diameter (Inogamov & Sunyaev 1999). Half of the reflected energy is absorbed and re-emitted at energies less than 1 keV, while a higher fraction, about 20%, with respect to the soft state, emerges above 10 keV.

This modelization has, however, the main flaw of unexplaining the strong difference in the fluxes of the two components (more than a factor of 10). A similar spectral decomposition is also possible for black hole sources in their low/hard states, where a very soft component, together with a reflection component arising in an untruncated accretion disk, is claimed to be present by some authors (Miller et al. 2006b,a; Rykoff et al. 2007), but it is rejected by others (Done & Gierlinski 2006; Gierlinski et al. 2008; D'Angelo et al. 2008; Cabanac et al. 2009; Hiemstra et al. 2009). However, in black holes, there is no balance required in the energetics of the components that make up the overall X-ray emission, as the quantity of energy advected beyond the event horizon is an unknown variable. In contrast, in X-ray systems harboring a neutron star, all the accretion energy must be dissipated and released as visible electromagnetic radiation (excluding any strong beaming effect that could arise in a state, but not in an another). Because the spectral solution that we envisioned for SoftObs is perfectly consistent with the presence of a standard accretion disk truncated at $\sim $2  $R_{\rm NS}$, from an energetic distribution between the spectral components, we conclude that, although statistically consistent, Model 2 lacks a correspondingly coherent physical scenario. It is, therefore, possible that the disk structure strongly departs from the standard Shakura-Sunyaev $\alpha$-disk model, becoming less energetically efficient or losing its thinness (Maccarone & Coppi 2003; Meyer-Hofmeister et al. 2005; Dullemond & Spruit 2005).

Recently, Taam et al. (2008) explored this scenario for the low/hard states of black holes, finding that at luminosities of a few percent of the Eddington limit, a cool, underfed, disk can be formed by condensation of coronal matter onto the disk. This disk would be under-luminous with respect to a standard $\alpha$-disk and still act as a reflecting medium for coronal photons. However, the shape of the reflection component would be strongly influenced by Compton-scattering in the corona, if its optical thickness is much higher than 1, as observed in the hard state of this source, and the line should be strongly smeared and practically undetectable (see the discussion in Di Salvo et al. 2005). We are therefore led to consider a different scenario, where still we have a standard accretion disk, but truncated at some distance from the neutron star by an unknown physical switch (magnetic pressure of the B-field of the NS or change in the accretion flow or evaporation or a still unknown physical mechanism).

5.2.3 Model 3

This model revisits Model 2 by forcing a spectral solution consisting of a truncated accretion disk, Comptonized boundary layer emission, and reflection component. The model is adequate for describing the shape of the line, and it is only marginally statistically less favored than the two other models. The diskbb normalization is set to correspond to a truncated disk at 30 $R_{\rm g}$ and the inner radius of the reflection component is also frozen at the same value. We are not interested, here, in evaluating where exactly the disk is truncated, as we do not have the necessary statistical constraints for it, but rather, we are interested in showing a representative spectral solution, which is physically motivated and still statistically acceptable.

Constraining the normalization of the diskbb component to a higher value than for Model 2 produces in the best-fit a lower disk temperature (from 0.4 keV to 0.2 keV) and a lower Compton seed-photon temperature while it has no effect on the determination of the hard part of the spectrum and on the shape of the reflection component.

We observe a large change in the ionization parameter of the irradiated disk when we compare the reflection component in the hard and soft states. The $\xi$ parameter, defined:

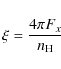
\begin{displaymath}\xi = \frac{4 \pi F_x}{n_{\rm H}} \end{displaymath} (2)

can be used to compare the changes in the impinging flux, assuming that density and distance do not strongly differ in the two observations.

From $\xi_1 / \xi_2 \simeq F_{1x}/F_{2x} $ and the results quoted in Tables 1 and 2, we would expect a change in the fluxes of an order of magnitude, which corresponds to the flux ratio of the hard blackbody component of the soft state and the Comptonized flux of HardObs. We also calculated the reflection fraction for this hard state. However, because the hard continuum component in this state is a thermal Comptonized component and not a blackbody, we measured the reflection fraction only in the restricted energy band (5.5-8 keV), where we approximated the continuum emission with a blackbody-like spectrum. We obtained a value consistent with the reflection fraction in the soft state (0.2 $\pm$ 0.1), but with a larger uncertainty. This value indicates that the geometry has not noticeably changed and that the scenario of a compact illuminating source is still valid.

5.3 The reflection scenario in the hard and soft states

The analysis of the XMM-Newton data in the soft state of 4U 1705-44 presented in this work confirms the results of Di Salvo et al. (2009) regarding the reflection origin of the local emission and absorption features and their relativistic broadening. Our re-analysis excludes any possible influence of pile-up on the spectral modeling of the continuum and of the broad emission lines. Still, the quality of the data allows for tight constraints on the main spectral parameters that are at the origin of the broadening.

In Di Salvo et al. (2009), the spectrum shows also a broad feature in absorption seen at 8-8.5 keV, which has been interpreted as a gravitationally red-shifted smeared K$\alpha$ absorption edge of He-like iron ions. The presence and the degree of this smearing, however, becomes very significant only when the central row of the Epic-pn CCD is considered. In our re-analysis (that reduces the statistics of a factor of 2 with respect to a spectrum extracted including the central row), the absorption edge is detected at a weaker confidence ( $\Delta \chi^2 = -30$, with 3 d.o.f. more, than for the same spectral model of Di Salvo et al. (2009) without the smeared edge), but the best-fitting spectral parameters remain consistent with the values reported in Di Salvo et al. (2009). In our re-analysis both the absorption and the emission processes are consistently described by a smeared broadband reflection model that has a blackbody prescription for the irradiating source photons.

Suzaku data of 4U 1705-44 also support the reflection scenario interpretation for the observed broad features (Reis et al. 2009). Although the spectral decomposition is different, both the present work and the analysis of the Suzaku data clearly indicate that the reflection component can vary according to the accretion state of the source, that the source is seen at an intermediate inclination angle (30 $\pm$ 1 deg in the Suzaku fits), that relativistic effects dominate because they arise from an accretion disk extremely close to the compact object ( $R_{\rm in} = 10.5_{+1.0}^{-1.7}$ $R_{\rm g}$ in the Suzaku fits), and that the ionization degree of the disk reflecting matter strongly depends from the accretion state of the source (with ionization parameter values ranging from 10 to 3500 erg cm2 s-1 in the Suzaku fits). The model of the present paper shows, however, some important differences with respect to the model adopted in Reis et al. (2009): the continuum thermal disk emission is consistent with a thermally hot accretion disk, close to the NS surface; the reflection model has a different prescription regarding the spectral shape of the disk illuminating primary source; i.e., we propose that, during the soft state, the Comptonized component approaches a blackbody-like spectrum and this is the source of the primary impinging radiation on the disk, whereas in Reis et al. (2009), the reflionx table model (Ross & Fabian 2005) has been used, which assumes a power-law spectral distribution of the irradiating flux. We showed that the interpretation of a thermalized source for the disk's illuminating source is justified both by theory and by good model-to-data fitting for the soft state.

This assumption may not be true for hard states, because the Comptonized component is no longer optically thick, and the spectrum substantially hardens, with most of its flux above 10 keV. Therefore, to test both the continuum model and the shape of the reflected component, a coverage of the hard X-ray spectrum (above 10 keV) is essential. If the nature of the disk's impinging radiation is still quite soft, with a low ionizing temperature (less than 3 keV), then no reflection Compton curvature is expected at higher energies, while a Compton bump should be present, together with the fluorescence emission lines, in the case of an extended power-law impinging spectrum. A claim of a detected reflection Compton bump has been made by Fiocchi et al. (2007) using INTEGRAL data; however, the strength of the Compton bump was not correlated with the iron line flux, and this would contradict a common physical origin.

6 Conclusions

We have examined and compared two XMM-Newton observations of the Atoll source 4U 1705-44, in a soft and in a hard spectral state. The soft state is characterized by three main spectral components: a multicolored thermal disk emission, a harder, blackbody-like, boundary layer emission, and a relativistically smeared reflection component. A self-consistent model of reflection has been successfully applied to fit the data, where the incident spectrum is assumed to have a blackbody shape. We have shown that the temperature of this thermal irradiating flux is consistent with the thermal boundary layer temperature and found from independent constraints that the inner disk radius, coincident with the outer boundary layer radius is located at a distance of $\sim $2  $R_{\rm NS}$. The second observation, taken when the source is in the hard state, is also characterized by a broad emission feature in the iron range, although its physical origin appears less constrained because of the much lower statistics and lack of high-energy response. We applied different modelizations, and with the constraints obtained in the analysis of the soft observation, we showed and discussed three possible spectral decompositions. The scenario that appears more successful in data fitting and in its physical implications is a model of very soft thermal disk emission, with an inner edge truncated at relatively large distance from the NS (between 20 $R_{\rm g}$ and 90 $R_{\rm g}$) and a thermal Comptonized emission. The width of the iron line in this state, can still be explained within the reflection scenario, even with a truncated accretion disk. Although the line is intrinsically broad, it does not show any evidence of asymmetry, because of the lower statistics with respect to the soft state observation and because relativistic effects are strongly reduced if the disk is truncated at a greater distance from the NS. To address the nature of the reflection component in the hard states, we still need good spectral coverage of the overall X-ray emission, in the soft (less than 1 keV) range to better constrain the continuum disk emission, in the iron range to resolve the shape of the iron line, and in the hard (above 10 keV) range to constrain the reflection Compton-scattered continuum.



Note added in proof. During the peer review process of the present manuscript, we become aware of a similar and related work appeared on the arxiv.org pages by Cackett et al. (2009).

References

  1. Agrawal, V. K., & Sreekumar, P. 2003, MNRAS, 346, 933 [NASA ADS] [CrossRef] [Google Scholar]
  2. Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, ed. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [Google Scholar]
  3. Ballantyne, D. R. 2004, MNRAS, 351, 57 [NASA ADS] [CrossRef] [Google Scholar]
  4. Ballantyne, D. R., & Ross, R. R. 2002, MNRAS, 332, 777 [NASA ADS] [CrossRef] [Google Scholar]
  5. Ballantyne, D. R., & Strohmayer, T. E. 2004, ApJ, 602, L105 [NASA ADS] [CrossRef] [Google Scholar]
  6. Ballantyne, D. R., Ross, R. R., & Fabian, A. C. 2001, MNRAS, 327, 10 [NASA ADS] [CrossRef] [Google Scholar]
  7. Barret, D., & Olive, J.-F. 2002, ApJ, 576, 391 [NASA ADS] [CrossRef] [Google Scholar]
  8. Barret, D., Olive, J. F., Boirin, L., et al. 2000, ApJ, 533, 329 [NASA ADS] [CrossRef] [Google Scholar]
  9. Barret, D., Olive, J. F., & Oosterbroek, T. 2003, A&A, 400, 643 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Bhattacharyya, S., & Strohmayer, T. E. 2007, ApJ, 664, L103 [NASA ADS] [CrossRef] [Google Scholar]
  11. Boirin, L., & Parmar, A. N. 2003, A&A, 407, 1079 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Cabanac, C., Fender, R. P., Dunn, R. J. H., & Körding, E. G. 2009, MNRAS, 396, 1415 [NASA ADS] [CrossRef] [Google Scholar]
  13. Cackett, E. M., Miller, J. M., Bhattacharyya, S., et al. 2008, ApJ, 674, 415 [NASA ADS] [CrossRef] [Google Scholar]
  14. Cackett, E. M., Miller, J. M., Ballantyne, D. R., et al. 2009, ApJ, submitted [arXiv:0908.1098] [Google Scholar]
  15. Church, M. J., & Balucinska-Church, M. 2001, A&A, 369, 915 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Church, M. J., & Ba▯ucinska-Church, M. 2004, MNRAS, 348, 955 [NASA ADS] [CrossRef] [Google Scholar]
  17. D'Aì, A., Iaria, R., Di Salvo, T., Matt, G., & Robba, N. R. 2009, ApJ, 693, L1 [NASA ADS] [CrossRef] [Google Scholar]
  18. D'Aí, A., Zycki, P., Di Salvo, T., et al. 2007, ApJ, 667, 411 [NASA ADS] [CrossRef] [Google Scholar]
  19. D'Angelo, C., Giannios, D., Dullemond, C., & Spruit, H. 2008, A&A, 488, 441 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. den Herder, J. W., Brinkman, A. C., Kahn, S. M., et al. 2001, A&A, 365, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Di Salvo, T., D'Aí, A., Iaria, R., et al. 2009, MNRAS, 398, 2022 [NASA ADS] [CrossRef] [Google Scholar]
  22. Di Salvo, T., Farinelli, R., Burderi, L., et al. 2002, A&A, 386, 535 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Di Salvo, T., Iaria, R., Méndez, M., et al. 2005, ApJ, 623, L121 [NASA ADS] [CrossRef] [Google Scholar]
  24. di Salvo, T., Santangelo, A., & Segreto, A. 2004, Nucl. Phys. B Proc. Suppl., 132, 446 [NASA ADS] [CrossRef] [Google Scholar]
  25. Done, C., & Gierlinski, M. 2006, MNRAS, 367, 659 [NASA ADS] [CrossRef] [Google Scholar]
  26. Done, C., Zycki, P. T., & Smith, D. A. 2002, MNRAS, 331, 453 [NASA ADS] [CrossRef] [Google Scholar]
  27. Dullemond, C. P., & Spruit, H. C. 2005, A&A, 434, 415 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Fabian, A. C., Rees, M. J., Stella, L., & White, N. E. 1989, MNRAS, 238, 729 [NASA ADS] [CrossRef] [Google Scholar]
  29. Fiocchi, M., Bazzano, A., Ubertini, P., & Zdziarski, A. A. 2007, ApJ, 657, 448 [NASA ADS] [CrossRef] [Google Scholar]
  30. Ford, E. C., van der Klis, M., van Paradijs, J., et al. 1998, ApJ, 508, L155 [NASA ADS] [CrossRef] [Google Scholar]
  31. Forman, W., Jones, C., Cominsky, L., et al. 1978, ApJS, 38, 357 [NASA ADS] [CrossRef] [Google Scholar]
  32. Galloway, D. K., Muno, M. P., Hartman, J. M., Psaltis, D., & Chakrabarty, D. 2008, ApJS, 179, 360 [NASA ADS] [CrossRef] [Google Scholar]
  33. Gierlinski, M., & Done, C. 2002, MNRAS, 331, L47 [NASA ADS] [CrossRef] [Google Scholar]
  34. Gierlinski, M., Done, C., & Page, K. 2008, MNRAS, 388, 753 [NASA ADS] [CrossRef] [Google Scholar]
  35. Gilfanov, M., Revnivtsev, M., & Molkov, S. 2003, A&A, 410, 217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Gladstone, J., Done, C., & Gierlinski, M. 2007, MNRAS, 378, 13 [NASA ADS] [CrossRef] [Google Scholar]
  37. Gottwald, M., Haberl, F., Langmeier, A., et al. 1989, ApJ, 339, 1044 [NASA ADS] [CrossRef] [Google Scholar]
  38. Haberl, F., & Titarchuk, L. 1995, A&A, 299, 414 [NASA ADS] [Google Scholar]
  39. Hasinger, G., & van der Klis, M. 1989, A&A, 225, 79 [NASA ADS] [Google Scholar]
  40. Hiemstra, B., Soleri, P., Méndez, M., et al. 2009, MNRAS, 394, 2080 [NASA ADS] [CrossRef] [Google Scholar]
  41. Homan, J., Kaplan, D. L., van den Berg, M., & Young, A. J. 2009, ApJ, 692, 73 [NASA ADS] [CrossRef] [Google Scholar]
  42. Iaria, R., D'Aí, A., di Salvo, T., et al. 2009, A&A, 505, 1143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Inogamov, N. A., & Sunyaev, R. A. 1999, Astron. Lett., 25, 269 [NASA ADS] [Google Scholar]
  44. Jansen, F., Lumb, D., Altieri, B., et al. 2001, A&A, 365, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Langmeier, A., Sztajno, M., Hasinger, G., Truemper, J., & Gottwald, M. 1987, ApJ, 323, 288 [NASA ADS] [CrossRef] [Google Scholar]
  46. Lin, D., Remillard, R. A., & Homan, J. 2007, ApJ, 667, 1073 [NASA ADS] [CrossRef] [Google Scholar]
  47. Maccarone, T. J., & Coppi, P. S. 2003, MNRAS, 338, 189 [NASA ADS] [CrossRef] [Google Scholar]
  48. Makishima, K., Maejima, Y., Mitsuda, K., et al. 1986, ApJ, 308, 635 [NASA ADS] [CrossRef] [Google Scholar]
  49. Matt, G., Guainazzi, M., & Maiolino, R. 2003, MNRAS, 342, 422 [NASA ADS] [CrossRef] [Google Scholar]
  50. Méndez, M., & Belloni, T. 2007, MNRAS, 381, 790 [NASA ADS] [CrossRef] [Google Scholar]
  51. Merloni, A., Fabian, A. C., & Ross, R. R. 2000, MNRAS, 313, 193 [NASA ADS] [CrossRef] [Google Scholar]
  52. Meyer-Hofmeister, E., Liu, B. F., & Meyer, F. 2005, A&A, 432, 181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Miller, J. M., Homan, J., & Miniutti, G. 2006a, ApJ, 652, L113 [NASA ADS] [CrossRef] [Google Scholar]
  54. Miller, J. M., Homan, J., Steeghs, D., et al. 2006b, ApJ, 653, 525 [NASA ADS] [CrossRef] [Google Scholar]
  55. Nayakshin, S., & Kazanas, D. 2002, ApJ, 567, 85 [NASA ADS] [CrossRef] [Google Scholar]
  56. Nayakshin, S., Kazanas, D., & Kallman, T. R. 2000, ApJ, 537, 833 [NASA ADS] [CrossRef] [Google Scholar]
  57. Olive, J.-F., Barret, D., & Gierlinski, M. 2003, ApJ, 583, 416 [NASA ADS] [CrossRef] [Google Scholar]
  58. Pandel, D., Kaaret, P., & Corbel, S. 2008, ApJ, 688, 1288 [NASA ADS] [CrossRef] [Google Scholar]
  59. Papitto, A., Di Salvo, T., D'Aì, A., et al. 2009, A&A, 493, L39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Piraino, S., Santangelo, A., di Salvo, T., et al. 2007, A&A, 471, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Popham, R., & Sunyaev, R. 2001, ApJ, 547, 355 [NASA ADS] [CrossRef] [Google Scholar]
  62. Raymond, J. C. 1993, ApJ, 412, 267 [NASA ADS] [CrossRef] [Google Scholar]
  63. Reis, R. C., Fabian, A. C., & Young, A. J. 2009, MNRAS, 399, L1 [NASA ADS] [CrossRef] [Google Scholar]
  64. Revnivtsev, M. G., & Gilfanov, M. R. 2006, A&A, 453, 253 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  65. Ross, R. R., & Fabian, A. C. 2005, MNRAS, 358, 211 [NASA ADS] [CrossRef] [Google Scholar]
  66. Rózanska, A., Dumont, A., Czerny, B., & Collin, S. 2002, MNRAS, 332, 799 [NASA ADS] [CrossRef] [Google Scholar]
  67. Rykoff, E. S., Miller, J. M., Steeghs, D., & Torres, M. A. P. 2007, ApJ, 666, 1129 [NASA ADS] [CrossRef] [Google Scholar]
  68. Shimura, T., & Takahara, F. 1995, ApJ, 445, 780 [NASA ADS] [CrossRef] [Google Scholar]
  69. Strüder, L., Briel, U., Dennerl, K., et al. 2001, A&A, 365, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Taam, R. E., Liu, B. F., Meyer, F., & Meyer-Hofmeister, E. 2008, ApJ, 688, 527 [NASA ADS] [CrossRef] [Google Scholar]
  71. Titarchuk, L. 1994, ApJ, 434, 570 [NASA ADS] [CrossRef] [Google Scholar]
  72. Turner, M. J. L., Abbey, A., Arnaud, M., et al. 2001, A&A, 365, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  73. van der Klis, M. 2004, ArXiv Astrophysics e-prints [Google Scholar]
  74. Verner, D. A., Ferland, G. J., Korista, K. T., & Yakovlev, D. G. 1996, ApJ, 465, 487 [NASA ADS] [CrossRef] [Google Scholar]
  75. Wijnands, R., van der Klis, M., Mendez, M., et al. 1998, ApJ, 495, L39 [NASA ADS] [CrossRef] [Google Scholar]
  76. Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [NASA ADS] [CrossRef] [Google Scholar]
  77. Zycki, P. T., & Czerny, B. 1994, MNRAS, 266, 653 [NASA ADS] [CrossRef] [Google Scholar]
  78. Zycki, P. T., Krolik, J. H., Zdziarski, A. A., & Kallman, T. R. 1994, ApJ, 437, 597 [NASA ADS] [CrossRef] [Google Scholar]

Footnotes

... 1705-44[*]
Based on observations obtained with XMM-Newton, an ESA science mission with instruments and contributions directly funded by ESA Member States and NASA.
... affected[*]
The RGS2 frame time is double with respect to the RGS1 CCDs caused by an instrumental failure occurred in August 2007; the longer frame time makes the RGS2 CCDs more easily subject to pile-up.

All Tables

Table 1:   Best-fitting values of the parameters obtained for the soft state of 4U 1705-44.

Table 2:   Best-fitting values and associated errors for different modelization used to fit the hard state data of 4U 1705-44.

Table 3:   Time-resolved spectral evolution of the burst emission.

All Figures

  \begin{figure} \par\includegraphics[angle=-90,width=9cm,clip]{13758f1.eps} \end{figure} Figure 1:

Long term X-ray light curve of 4U 1705-44. Data from the All Sky Monitor (2-10 keV range) onboard the Rossi XTE, from 1 January 2006 (MJD 53736) to 1 January 2009 (MJD 54832). The two arrows in the figure mark the day when the SoftObs (right arrow) and the HardObs (left arrow) took place.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=-90,width=8cm,clip]{13758f2a.eps} \includegraphics[angle=-90,width=8cm,clip]{13758f2b.eps} \end{figure} Figure 2:

Light curves for SoftObs ( upper panel) and for HardObs ( lower panel). In HardObs, a type I X-ray burst is present at $\sim $11 ks after the beginning of the observation (see Sect. 4 for details.)

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=-90,width=9cm,clip]{13758f3.eps} \end{figure} Figure 3:

Color-color diagram that shows the relative positions of the two observations. Each point represents a time segment of 500 s. SoftObs data in red, HardObs data in green.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=-90,width=9cm,clip]{13758f4.eps} \end{figure} Figure 4:

Residuals, in units of $\sigma $, in the broad 0.6-12 keV energy range, of the Epic-pn spectrum when the 2.0-12.0 keV best-fitting model is used (Table 1). A broad feature at 1.7 keV is clearly visible together with soft residual emission below 1.0 keV.

Open with DEXTER
In the text

  \begin{figure} \par\mbox{\includegraphics[angle=-90,width=8cm,clip]{13758f5a.eps} \includegraphics[angle=-90,width=8cm,clip]{13758f5b.eps} } \end{figure} Figure 5:

Data and best-fitting model with individual components separately shown (top panels), together with residuals in units of sigma (lower panels). Left panel: the best-fitting model without the Ar XVIII and Ca XIX emission lines. Right panel: data and residuals using the best-fitting model of Table 1.

Open with DEXTER
In the text

  \begin{figure} \par\mbox{\includegraphics[angle=-90,width=8cm,clip]{13758f6a} \includegraphics[angle=-90,width=8cm,clip]{13758f6b} } \end{figure} Figure 6:

Best fitting model in the $E \times f(E)$ representation of the soft state of 4U 1705-44. Red line is the thermal disk emission, green line the black body thermal emission, blue line the reflection component. Left panel shows the ISM absorbed model, right panel shows the unabsorbed model.

Open with DEXTER
In the text

  \begin{figure} \par\mbox{\includegraphics[angle=-90,width=8.2cm,clip]{13758f7a.e... ...raphics[angle=-90,width=8.2cm,clip]{13758f7b.eps} } \vspace*{2mm} \end{figure} Figure 7:

Left panel: data and residuals at the soft energies (0.6-3.0 keV), using an absorbed blackbody component. Residuals clearly display an S-shaped pattern in the Epic-pn data (black data) between 1.5 keV and 2.0 keV and a general mismatch between RGS data (green and red data) and Epic-pn data at softer energies. Data have been rebinned for clarity. Right panel: residuals in the iron range, when data 4.0-9.0 keV are fitted with Model 1 and the iron line is subtracted from the data.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=-90,width=8.2cm]{13758f8a.eps}\hspace*... ...cludegraphics[angle=-90,width=8.3cm]{13758f8f.eps} \vspace*{1.5mm} \end{figure} Figure 8:

Right panels: XMM-Newton data and residuals in units of $\sigma $ with respect to the best-fitting models for the hard state. Left panels: the theoretical unabsorbed model in the 0.1-100 keV range (in blue the iron line/reflection component, in green the Comptonized component, in red the thermal soft disk emission).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=-90,width=9cm,clip]{13758f9.eps} \vspace*{-2mm} \end{figure} Figure 9:

Light curve of the burst observed during HardObs, the start time of the first time interval used for spectral analysis is time = 20 s in this plot.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=-90,width=9cm,clip]{13758f10.eps} \vspace*{-2mm} \end{figure} Figure 10:

Data and residual with respect to the best-fitting model of the six time selected spectra of Table 3.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.