| Issue |
A&A
Volume 516, June-July 2010
|
|
|---|---|---|
| Article Number | A102 | |
| Number of page(s) | 21 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/200913499 | |
| Published online | 22 July 2010 | |
Physical structure of the envelopes of intermediate-mass protostars
N. Crimier1 - C. Ceccarelli1 - T. Alonso-Albi2 - A. Fuente2 - P. Caselli3 - D. Johnstone4,5 - C. Kahane1 - B. Lefloch1 - S. Maret1 - R. Plume6 - J. R. Rizzo7 - M. Tafalla2 - E. van Dishoeck8 - F. Wyrowski9
1 - Laboratoire d'Astrophysique de l'Observatoire de Grenoble,
BP 53, 38041 Grenoble Cedex 9, France
2 - Observatorio Astronómico Nacional (OAN, IGN), Apdo 112, 28803 Alcalá de Henares, Spain
3 - School of Physics & Astronomy, E.C. Stoner Building, The University of Leeds, Leeds LS2 9JT, UK
4 - National Research Council of Canada, Herzberg Institute of
Astrophysics, 5071, West Saanich Road, Victoria, BC, V9E 2E7, Canada
5 - Department of Physics & Astronomy, University of Victoria, Victoria, BC, V8P 1A1, Canada
6 - Department of Physics and Astronomy, University of Calgary, Calgary, T2N 1N4, AB, Canada
7 - Centro de Astrobiología (CSIC/INTA), Laboratory of Molecular
Astrophysics, Ctra. Ajalvir km. 4, 28850 Torrejón de Ardoz, Spain
8 - Leiden Observatory, PO Box 9513, 2300 RA Leiden, The Netherlands
9 - Max-Planck-Institut fur Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
Received 19 October 2009 / Accepted 27 March 2010
Abstract
Context. Intermediate mass protostars provide a bridge
between low- and high-mass protostars. Furthermore, they are an
important component of the UV interstellar radiation field. Despite
their relevance, little is known about their formation process.
Aims. We present a systematic study of the physical structure of
five intermediate mass, candidate Class 0 protostars. Our two goals are
to shed light on the first phase of intermediate mass star formation
and to compare these protostars with low- and high-mass sources.
Methods. We derived the dust and gas temperature and density
profiles of the sample. We analysed all existing continuum data on each
source and modelled the resulting SED with the 1D radiative transfer
code DUSTY. The gas temperature was then predicted by means of a
modified version of the code CHT96.
Results. We found that the density profiles of five out of six
studied intermediate mass envelopes are consistent with the predictions
of the ``inside-out'' collapse theory. We compared several physical
parameters, like the power law index of the density profile, the size,
the mass, the average density, the density at 1000 AU and the
density at 10 K of the envelopes of low-, intermediate, and
high-mass protostars. When considering these various physical
parameters, the transition between the three groups appears smooth,
suggesting that the formation processes and triggers do not
substantially differ.
Key words: stars: formation
1 Introduction
Stars are usually catalogued in three groups according to their mass:
low-mass (
![]() 2
2 ![]() ), intermediate mass (IM) and high-mass
(
), intermediate mass (IM) and high-mass
(
![]() 8
8 ![]() ). The high-mass stars are usually found to form
in tight clusters (e.g. Hillenbrand & Hartmann 1998), including many low-mass
stars as well. Low-mass stars on their own can be
formed in isolation or in loose groups of a few objects per cubic parsec
(Gomez et al. 1993).
While there is reasonable consensus on the overall process leading
to the formation of isolated, low-mass stars (see e.g. Shu & Adams 1987),
the situation for high-mass star formation is much more
confusing. The major problem is that a central object with
). The high-mass stars are usually found to form
in tight clusters (e.g. Hillenbrand & Hartmann 1998), including many low-mass
stars as well. Low-mass stars on their own can be
formed in isolation or in loose groups of a few objects per cubic parsec
(Gomez et al. 1993).
While there is reasonable consensus on the overall process leading
to the formation of isolated, low-mass stars (see e.g. Shu & Adams 1987),
the situation for high-mass star formation is much more
confusing. The major problem is that a central object with
![]() produces a radiative pressure stronger than the
gravitational pressure, which should stop the accretion. Therefore
stars with a mass greater than
produces a radiative pressure stronger than the
gravitational pressure, which should stop the accretion. Therefore
stars with a mass greater than ![]() 8
8 ![]() cannot be formed in a
simple-minded fully gravitationally driven process and other
mechanisms need to be considered. Studying the differences in observed
environments, several authors have proposed that high-mass stars are
formed by the coalescence of lower-mass stars, while other authors
favor ``monolithic'' formation (see for example the recent
review by Beuther et al. 2007), where turbulence or winds/outflows can play a major role (McKee & Tan 2003; Krumholz et al. 2005).
cannot be formed in a
simple-minded fully gravitationally driven process and other
mechanisms need to be considered. Studying the differences in observed
environments, several authors have proposed that high-mass stars are
formed by the coalescence of lower-mass stars, while other authors
favor ``monolithic'' formation (see for example the recent
review by Beuther et al. 2007), where turbulence or winds/outflows can play a major role (McKee & Tan 2003; Krumholz et al. 2005).
The differences between low- and high-mass protostars are not only restricted to the dynamics of the formation mechanism. Notable differences also exist when it comes to the chemistry. Bottinelli (2006) compared the abundances of O-bearing complex organic molecules (COMs) present in Hot Cores surrounding high-mass protostars and in Hot Corinos around low-mass protostars. They concluded that the abundances of the O-bearing COMs, compared to methanol or formaldehyde, are about one order of magnitude higher in Hot Corinos than Hot Cores. In addition, significant differences in the abundances of molecules constituting the grain mantles (H2O, CO, CO2,CH3OH, OCN-) were observed between low- and high-mass protostars (Boogert et al. 2004). Finally, in contrast to high-mass star forming regions, low-mass protostars present an extremely enhanced molecular deuteration, the so-called Super-Deuteration (e.g. Ceccarelli et al. 2007), not observed in high-mass star forming regions.
Table 1: The coordinates, the distances and the bolometric luminosities of the sources of the sample.
The IM stars, namely stars whose mass lies in the 2 to 8 ![]() range, are crucial in studies of star formation because they
provide the link between low- and high-mass stars
(Mannings & Sargent 1997,2000; Di Francesco et al. 1997) and therefore
can help to determine whether different formation processes are required.
IM stars are also found in clusters
(e.g. Fuente et al. 2007; Testi & Sargent 1998; Neri et al. 2007), with a smooth
transition towards the low-mass star, loose cluster regime for star
masses around 3.5
range, are crucial in studies of star formation because they
provide the link between low- and high-mass stars
(Mannings & Sargent 1997,2000; Di Francesco et al. 1997) and therefore
can help to determine whether different formation processes are required.
IM stars are also found in clusters
(e.g. Fuente et al. 2007; Testi & Sargent 1998; Neri et al. 2007), with a smooth
transition towards the low-mass star, loose cluster regime for star
masses around 3.5 ![]() (Testi et al. 1999). These authors also
conclude that IM stars mark the transition from the low-density
aggregates of
(Testi et al. 1999). These authors also
conclude that IM stars mark the transition from the low-density
aggregates of
![]() 10 stars per cubic parsec of T Tauri stars to
the dense clusters of
10 stars per cubic parsec of T Tauri stars to
the dense clusters of ![]() 103 stars per cubic parsec associated
with massive stars. Finally, IM stars are among the most dominant sources for the
interstellar FUV field (e.g. Habing 1968; Gondhalekar & Wilson 1975),
which regulates the phases of the ISM in the Galaxy and, in turn, the
overall Galaxy star formation process and history.
In this context, the study of the formation of the IM stars is not only
interesting in itself, but it can also greatly help the debate on
the formation of high-mass stars. Indeed, due to their intermediate
position, the study of IM protostars provides crucial information
about the transition between the two formation regimes, as well as on the
limits of the low-mass and high-mass formation scenarios.
103 stars per cubic parsec associated
with massive stars. Finally, IM stars are among the most dominant sources for the
interstellar FUV field (e.g. Habing 1968; Gondhalekar & Wilson 1975),
which regulates the phases of the ISM in the Galaxy and, in turn, the
overall Galaxy star formation process and history.
In this context, the study of the formation of the IM stars is not only
interesting in itself, but it can also greatly help the debate on
the formation of high-mass stars. Indeed, due to their intermediate
position, the study of IM protostars provides crucial information
about the transition between the two formation regimes, as well as on the
limits of the low-mass and high-mass formation scenarios.
Despite their importance, very little is known about the formation and
first evolutionary stages of IM stars. Although some individual IM protostars have been studied in detail (Fuente et al. 2007; Hogerheijde et al. 1999; Neri et al. 2007; Schreyer et al. 2002), the situation is so bad that to date we neither have a satisfying sample of Class 0 IM objects, namely
objects representing the first phases of stellar formation where the
protostar is embedded in its envelope and its luminosity is dominated
by the accretion luminosity, nor a systematic study of their physical
structure, as in the case for low-mass and high-mass protostars.
On the contrary, several previous studies have considered samples of low-
and high-mass protostars. Relevant similar studies to the present
IM one are those reported by Jørgensen et al. (2002) and Shirley et al. (2002),
who targeted 7 and 11 low-mass Class 0 protostars respectively,
and the systematic studies by Mueller et al. (2002), Hatchell & van der Tak (2003),
Williams et al. (2005) and Van der Tak et al. (2000), who
targeted 31, 10, 32, and 9 high-mass protostars respectively. These
authors derived the physical structure of the envelope for each protostar
using continuum observations coupled with a radiative transfer code
assuming a 1D spherical model. Combined, these studies cover a luminosity
range of
![]() ,
and
,
and
![]() for low- and high-mass protostars respectively,
leaving a significant gap in luminosity and knowledge.
for low- and high-mass protostars respectively,
leaving a significant gap in luminosity and knowledge.
This paper aims to fill this gap, providing a systematic study of the physical structure of the envelopes of a sample of five IM protostars. In addition, this study will provide a valuable input for future work on the chemical structure of IM protostars (e.g. Alonso-Albi et al. 2010). The present work follows the method presented in Crimier et al. (2009) to study the IM protostars OMC2-FIR4. Namely, the combination of sub-millimeter to infrared observations with radiative transfer codes are used to derive the physical structure of each envelope. We selected a sample of five representative candidate Class 0 IM protostars: CB3-mm, Cep E-mm, IC1396 N BIMA 2, NGC7129 FIRS 2, and Serpens FIRS 1. These sources were selected using the following criteria:
- the luminosity is in the 30 to 1000
 range (corresponding to a
range (corresponding to a 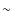 3 to 9
3 to 9 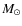 of ZAMS stars);
of ZAMS stars);
- the continuum maps at submillimetre and/or millimetre wavelengths are available;
- the source is closer than 2.5 kpc to the Sun and
isolated, namely no source of similar brightness in the submillimetre
within an angular distance of
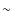 100''.
100''.
Table 2: Continuum fluxes integrated over the envelope of each source and used in the SED analysis.
This article is organised as follows. Section 2 describes the observations used and the method and tools employed to derive the dust and gas density and temperature profiles. Section 3 first summarises the general results obtained toward the IM protostar sample. Next, for each source, background information, data available, and the results obtained are presented. In Sect. 4, the physical structure of the envelopes of IM protostars obtained in this study are compared with those obtained in previous studies of low- and high-mass protostar envelopes. In this section we also discuss the limitations of our modeling method. Finally, Sect. 5 concludes the article.
2 General method
In this section we present the general method used to derive the dust density and temperature profiles by modelling the continuum maps of each region, plus the Spectral Energy Distribution (SED) from the millimetre to the Mid-Infrared (MIR). We first describe the observations used in the analysis and how the brightness profiles and the SED are derived (Sect. 2.1), and then we present the modelling (Sect. 2.2).
2.1 Continuum emission: observational data
In our analysis we used the maps of the continuum emission at 850 and
450 ![]() m obtained at the 15 m James Clerk Maxwell Telescope (JCMT). In
addition, we took into account the SED of each source from 24
m obtained at the 15 m James Clerk Maxwell Telescope (JCMT). In
addition, we took into account the SED of each source from 24 ![]() m to 1300
m to 1300 ![]() m
data obtained with the Spitzer, IRAS, JCMT and IRAM telescopes. Note
that specific details (datasets, pipeline, uncertainties, contamination
... etc.) are given separately for each source in Sect. 3.
m
data obtained with the Spitzer, IRAS, JCMT and IRAM telescopes. Note
that specific details (datasets, pipeline, uncertainties, contamination
... etc.) are given separately for each source in Sect. 3.
- a) Continuum brightness profiles
For each source we retrieved from the JCMT Science Archive![[*]](/icons/foot_motif.png) the 450
the 450  m and 850
m and 850  m maps obtained by the focal-plane instrument SCUBA (Submillimetre Common-User
Bolometer Array). The data were reduced
with the JCMT pipelines SURF V1.6-13, and KAPPA 1.9-7. When multiple
observations were available in the archive, we used the most sensitive
ones. The angular resolution of the maps is approximately 7.5
m maps obtained by the focal-plane instrument SCUBA (Submillimetre Common-User
Bolometer Array). The data were reduced
with the JCMT pipelines SURF V1.6-13, and KAPPA 1.9-7. When multiple
observations were available in the archive, we used the most sensitive
ones. The angular resolution of the maps is approximately 7.5
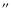 and 14.8
and 14.8
 at 450
and 850
at 450
and 850  m respectively
(see Sect. 2.2 for more details).
Based on the many previous JCMT published
observations, the calibration uncertainty and noise levels are
m respectively
(see Sect. 2.2 for more details).
Based on the many previous JCMT published
observations, the calibration uncertainty and noise levels are
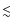 10% and 0.04 Jy beam-1 at 850
10% and 0.04 Jy beam-1 at 850  m and
m and
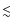 30% and 0.3 Jy beam-1 at 450
30% and 0.3 Jy beam-1 at 450  m,
respectively. To evaluate
the continuum brightness profile (the brightness as a function of the
distance from the envelope centre), we averaged the observed flux over
annuli with the same distance from the centre of the source. The final
uncertainties were evaluated taking into account the calibration
uncertainty, the noise levels of the used maps, and the non-sphericity
of the source. The non-sphericity of the source is taken into account
via the computation of the standard deviation relative to the azimuthal
average for each averaged flux of the brightness profile.
m,
respectively. To evaluate
the continuum brightness profile (the brightness as a function of the
distance from the envelope centre), we averaged the observed flux over
annuli with the same distance from the centre of the source. The final
uncertainties were evaluated taking into account the calibration
uncertainty, the noise levels of the used maps, and the non-sphericity
of the source. The non-sphericity of the source is taken into account
via the computation of the standard deviation relative to the azimuthal
average for each averaged flux of the brightness profile.
- b) SED
The SED points at 850 m and 450
m and 450  m were obtained integrating the
continuum flux profiles previously derived over the full envelope. We
also considered the integrated flux at 24
m were obtained integrating the
continuum flux profiles previously derived over the full envelope. We
also considered the integrated flux at 24  m and 70
m and 70  m extracted from
the Spitzer Space Telescope Multiband Imaging Photometer (MIPS)
maps. To this end, we retrieved the observations from the Spitzer
Science archive
m extracted from
the Spitzer Space Telescope Multiband Imaging Photometer (MIPS)
maps. To this end, we retrieved the observations from the Spitzer
Science archive![[*]](/icons/foot_motif.png) . The
data reduction was performed using the pipeline S16.1.0. The
evaluation of the fluxes was done with the same method employed for
the maps at 850
. The
data reduction was performed using the pipeline S16.1.0. The
evaluation of the fluxes was done with the same method employed for
the maps at 850  m and 450
m and 450  m,
namely deriving the brightness
profiles from the maps and integrating over each annuli. We evaluated
the uncertainties according to the instrument uncertainties and
varying the outer radius of the envelope to account for the
uncertainty in the envelope size. To do this we first set the outer
radius equal to where the flux profile becomes flat (because dominated
by the noise or the flux of the parent cloud) and varied this value up
to 100%. In general, the uncertainties remain relatively constant
for variations larger than 30-50%. Note that we checked
a posteriori that our adopted radius and variation range is
constitent with the outer radius obtained after the modelling. Finally,
we also considered the IRAS
fluxes at 60
m,
namely deriving the brightness
profiles from the maps and integrating over each annuli. We evaluated
the uncertainties according to the instrument uncertainties and
varying the outer radius of the envelope to account for the
uncertainty in the envelope size. To do this we first set the outer
radius equal to where the flux profile becomes flat (because dominated
by the noise or the flux of the parent cloud) and varied this value up
to 100%. In general, the uncertainties remain relatively constant
for variations larger than 30-50%. Note that we checked
a posteriori that our adopted radius and variation range is
constitent with the outer radius obtained after the modelling. Finally,
we also considered the IRAS
fluxes at 60  m and 100
m and 100  m, respectively, taken from the literature
or the IRAS Point Source Catalog v2.0
m, respectively, taken from the literature
or the IRAS Point Source Catalog v2.0![[*]](/icons/foot_motif.png) . The SED fluxes of each source and their uncertainties are reported in
Table 2.
. The SED fluxes of each source and their uncertainties are reported in
Table 2.
2.2 Continuum emission: modelling
To derive the dust temperature and density profiles of the envelope, we used the 1D radiative transfer code DUSTY
(Ivezic & Elitzur 1997). Briefly, giving as input the temperature and size of the
central object and a dust density profile, DUSTY self-consistently computes
the dust temperature profile and the dust
emission. The comparison between the computed 450 ![]() m, 850
m, 850 ![]() m and 1300
m and 1300 ![]() m brightness profiles (namely the brightness versus the distance from
the centre of the envelope) and integrated SED against the observed brightness
profiles and integrated SED (see previous paragraph) allows one to
constrain the density profile and, consequently, the temperature
profile of the envelope.
m brightness profiles (namely the brightness versus the distance from
the centre of the envelope) and integrated SED against the observed brightness
profiles and integrated SED (see previous paragraph) allows one to
constrain the density profile and, consequently, the temperature
profile of the envelope.
To be compared against the observations, the theoretical emission must be
convolved with the beam pattern of each telescope. Following the
recommendations for the JCMT, the beam is assumed to be a combination of
three Gaussian curves: at 850 ![]() m we used HPBWs of 14.5
m we used HPBWs of 14.5
![]() ,
60
,
60
![]() ,
and 120
,
and 120
![]() ,
with amplitudes of 0.976, 0.022, and 0.002 respectively;
at 450
,
with amplitudes of 0.976, 0.022, and 0.002 respectively;
at 450 ![]() m the HPBWs are 8
m the HPBWs are 8
![]() ,
30
,
30
![]() ,
and 120
,
and 120
![]() .
with amplitude ratios of 0.934, 0.06, and 0.006, respectively (Sandell & Weintraub 2001).
.
with amplitude ratios of 0.934, 0.06, and 0.006, respectively (Sandell & Weintraub 2001).
In all sources we assumed that the envelope density follows a single
index power law
where the power law index,
In summary, the output of DUSTY depends on four free parameters: ![]() ,
n0,
,
n0,
![]() and
and
![]() .
In practice, the DUSTY input parameters
are the power law index,
.
In practice, the DUSTY input parameters
are the power law index, ![]() ,
the optical thickness at 100
,
the optical thickness at 100 ![]() m,
m,
![]() ,
the ratio between the inner and outer radius, Y (=
,
the ratio between the inner and outer radius, Y (=
![]() /
/
![]() )
and the temperature at the inner radius
)
and the temperature at the inner radius
![]() .
The optical thickness is, in turn, proportional to the dust
column density which depends on n0 and the physical thickness of
the envelope. Note that because the beam sizes of the available maps are
relatively large (
.
The optical thickness is, in turn, proportional to the dust
column density which depends on n0 and the physical thickness of
the envelope. Note that because the beam sizes of the available maps are
relatively large (![]() 7.5
7.5
![]() ,
which corresponds to a radius of
,
which corresponds to a radius of ![]() 3250 AU for a source at a distance of 1000 pc), the inner regions of
the envelopes are relatively unconstrained by the available
observational data. Finally, as explained in Ivezic & Elitzur (1997), DUSTY
gives scaleless results (which make it very powerful because the same
grid of models can be applied to many different sources).
To compare the DUSTY output with actual observations it is necessary
to scale the output by the source bolometric luminosity,
3250 AU for a source at a distance of 1000 pc), the inner regions of
the envelopes are relatively unconstrained by the available
observational data. Finally, as explained in Ivezic & Elitzur (1997), DUSTY
gives scaleless results (which make it very powerful because the same
grid of models can be applied to many different sources).
To compare the DUSTY output with actual observations it is necessary
to scale the output by the source bolometric luminosity,
![]() ,
and
the distance to the source. Note that the bolometric luminosity
is estimated by integrating the emission across the full spectrum.
By definition, this can only be done when the entire SED is known. This is
exactly one of the outputs of the modelling. Therefore, we
re-evaluate the luminosity of each source iteratively from the best-fit model,
by minimising the
,
and
the distance to the source. Note that the bolometric luminosity
is estimated by integrating the emission across the full spectrum.
By definition, this can only be done when the entire SED is known. This is
exactly one of the outputs of the modelling. Therefore, we
re-evaluate the luminosity of each source iteratively from the best-fit model,
by minimising the ![]() .
.
We ran a grid of models to cover the parameter space as reported in Table 3.
Table 3: Range of the input parameters to DUSTY covered in the present study.
The best-fit model is found by minimising the ![]() with an
iterated two-steps procedure. First, we used the observed brightness
profiles at 450
with an
iterated two-steps procedure. First, we used the observed brightness
profiles at 450 ![]() m and 850
m and 850 ![]() m to constrain
m to constrain ![]() and Y, assuming
a value for
and Y, assuming
a value for
![]() .
The
.
The
![]() computed during this first step are reported as
computed during this first step are reported as
![]() -maps in Table 4. Second, we constrain the optical thickness
-maps in Table 4. Second, we constrain the optical thickness
![]() by comparing the computed and observed SED, assuming the
by comparing the computed and observed SED, assuming the
![]() and Y of the previous step. The new
and Y of the previous step. The new
![]() is used for
the next iteration and the process is repeared. The
is used for
the next iteration and the process is repeared. The
![]() computed during this second step are reported as
computed during this second step are reported as
![]() -SED in Table 4.
In practice, the iteration converges in two
steps. This occurs because the normalised brightness profiles are only
very weakly dependent on
-SED in Table 4.
In practice, the iteration converges in two
steps. This occurs because the normalised brightness profiles are only
very weakly dependent on
![]() ,
while they are very dependent
on the sizes of the envelope and on the slope of the density profile
(see also Jørgensen et al. 2002; Schöier et al. 2002; Crimier et al. 2009). On
the contrary, the optical thickness depends mostly on the absolute
column density of the envelope, which is constrained by the SED.
,
while they are very dependent
on the sizes of the envelope and on the slope of the density profile
(see also Jørgensen et al. 2002; Schöier et al. 2002; Crimier et al. 2009). On
the contrary, the optical thickness depends mostly on the absolute
column density of the envelope, which is constrained by the SED.
2.3 Gas temperature profile: model description
Table 4: Summary of the dust radiative transfer analysis for the five IM protostars.
Ceccarelli et al. (1996), Crimier et al. (2009) and Doty & Neufeld (1997)
showed that the gas can be thermally decoupled from the dust in the
inner regions of low-, intermediate and high-mass protostellar
envelopes. The decoupling occurs mainly in the inner part of the envelopes: for example whereas
![]() K at 200 AU,
K at 200 AU,
![]() K. Note that in the outer envelope, where
K. Note that in the outer envelope, where
![]() K, gas and dust temperature only differ by a few percents (see discussion in Crimier et al. 2009). The reason for this decoupling is the high water
abundance in the gas phase caused by the sublimation of grain
mantles. We therefore explicitly computed the gas temperature
profile of the envelope surrounding each source by finding the
equilibrium temperature obtained by equating the gas cooling and heating
terms at each radius. Following the method described by
Ceccarelli et al. (1996), we considered heating from the gas compression
(due to the collapse), dust-gas collisions, photo-pumping of H2O
and CO molecules by the IR photons emitted by the warm dust close to
the centre, and cosmic rays ionisation which is a minor heating term in
protostellar envelopes. The cooling is mainly due to the
rotational lines from H2O
and CO, plus the fine structure lines
from O. The gas temperature therefore depends on the abundance of
these three species. In practice, only the water abundance is
an important parameter of the model, because the CO and O lines
are
optically thick and LTE populated in the range of CO and
O abundances typical of
protostellar envelopes, while the water levels are sub-thermally
populated (non-LTE). In the non-LTE regime the water levels are excited
by collisional processes and de-excited by radiation while in LTE
regime the levels are mainly excited and de-excited by collisions.
Therefore, a photon emitted in LTE regime in an optically thick region
will be absorbed and then the absorber will be de-excited by collisions
while in non-LTE regime the absorbed photon will possibly be
re-emitted. In this case we say that the water lines are effectively
optically thin. For this reason we computed two cases for the
water abundance, as it is generally poorly constrained in protostellar
envelopes and totally unconstrained in intermediate mass
protostars. We adopted a step function for the water abundance profile
to simulate the jump caused by ice sublimation. The jump is
assumed to occur at 100 K. We considered the H2O abundance (with
respect to H2) X(H2O)
K, gas and dust temperature only differ by a few percents (see discussion in Crimier et al. 2009). The reason for this decoupling is the high water
abundance in the gas phase caused by the sublimation of grain
mantles. We therefore explicitly computed the gas temperature
profile of the envelope surrounding each source by finding the
equilibrium temperature obtained by equating the gas cooling and heating
terms at each radius. Following the method described by
Ceccarelli et al. (1996), we considered heating from the gas compression
(due to the collapse), dust-gas collisions, photo-pumping of H2O
and CO molecules by the IR photons emitted by the warm dust close to
the centre, and cosmic rays ionisation which is a minor heating term in
protostellar envelopes. The cooling is mainly due to the
rotational lines from H2O
and CO, plus the fine structure lines
from O. The gas temperature therefore depends on the abundance of
these three species. In practice, only the water abundance is
an important parameter of the model, because the CO and O lines
are
optically thick and LTE populated in the range of CO and
O abundances typical of
protostellar envelopes, while the water levels are sub-thermally
populated (non-LTE). In the non-LTE regime the water levels are excited
by collisional processes and de-excited by radiation while in LTE
regime the levels are mainly excited and de-excited by collisions.
Therefore, a photon emitted in LTE regime in an optically thick region
will be absorbed and then the absorber will be de-excited by collisions
while in non-LTE regime the absorbed photon will possibly be
re-emitted. In this case we say that the water lines are effectively
optically thin. For this reason we computed two cases for the
water abundance, as it is generally poorly constrained in protostellar
envelopes and totally unconstrained in intermediate mass
protostars. We adopted a step function for the water abundance profile
to simulate the jump caused by ice sublimation. The jump is
assumed to occur at 100 K. We considered the H2O abundance (with
respect to H2) X(H2O)![]() in the inner envelope, where
in the inner envelope, where
![]() K, equal to 10-5 and 10-6, fixing the water
abundance in the outer region, X(H2O)
K, equal to 10-5 and 10-6, fixing the water
abundance in the outer region, X(H2O)
![]() ,
at 10-7. The CO
and O abundances were fixed at the standard values found in molecular clouds, i.e.
,
at 10-7. The CO
and O abundances were fixed at the standard values found in molecular clouds, i.e.
![]() (Frerking et al. 1982) and
(Frerking et al. 1982) and
![]() (Vastel et al. 2000; Caux et al. 1999),
respectively. Note that because the O and CO lines are mostly optically
thick the exact value of their abundance is not important. To
compute the cooling from the lines we used the code described in
Ceccarelli et al. (1996,2003) and Parise et al. (2005).
Briefly, the line cooling is computed with an escape
probability method, which takes into account the dust level pumping and
the line optical depths at each point of the envelope by integrating
over the solid angle. A recent description of the code is reported in
Crimier et al. (2010,2009). The same code has been used in several past
studies, whose results have been substantially confirmed by other
groups (e.g. the analysis on IRAS16293-2422 by Schöier et al. 2002).
(Vastel et al. 2000; Caux et al. 1999),
respectively. Note that because the O and CO lines are mostly optically
thick the exact value of their abundance is not important. To
compute the cooling from the lines we used the code described in
Ceccarelli et al. (1996,2003) and Parise et al. (2005).
Briefly, the line cooling is computed with an escape
probability method, which takes into account the dust level pumping and
the line optical depths at each point of the envelope by integrating
over the solid angle. A recent description of the code is reported in
Crimier et al. (2010,2009). The same code has been used in several past
studies, whose results have been substantially confirmed by other
groups (e.g. the analysis on IRAS16293-2422 by Schöier et al. 2002).
For the collisional coefficients of water with hydrogen molecules, we
used the data by Faure et al. (2007) and Faure & Josselin (2008) available for the temperature range 20-5000 K. Because the ortho-to-para conversion process of H2 is chemical rather than radiative, the Ortho-to-Para Ratio (OPR) H2,
which the water population depends on, is highly uncertain. The recent
analysis of H2CO observations towards a cold molecular cloud by
Troscompt et al. (2009) confirms theoretical estimates (e.g. Flower et al. 2006)
that in molecular clouds the H2 OPR is lower than 1. Lacking specific observations towards protostars, here we assume
that H2 OPR is in Local Thermal Equilibrium and therefore follows
the Boltzmann distribution
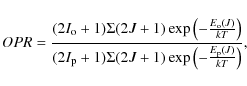
|
(2) |
where
2.4 Water line observations
In order to constrain the water abundance, which is very important for computing the
gas temperature, we considered observations obtained by the Long
Wavelength Spectrometer (LWS) aboard the Infrared Space Observatory
(ISO) in the 45 ![]() m to 200
m to 200 ![]() m range, where several water lines emit.
All sources excepted CB3 were observed with the LWS. In two sources,
Cep E-mm and Serpens FIRS 1, several water lines were detected and their
analysis has been reported by Moro-Martín et al. (2001) and Larsson et al. (2002),
respectively. As discussed by these authors, given the
relatively large beam of the LWS, the water line fluxes are due to the
combination of many components along the line of sight:
outflows, multiple sources and Photo-Dissociation Regions.
The measured H2O line fluxes are thus upper limits
to the fluxes from the envelopes and we checked that our predictions do
not exceed the observed fluxes. For two other sources, IC1396 N BIMA 2
and NGC7129 FIRS 2, we retrieved the LWS grating spectra (spectral
resolution
m range, where several water lines emit.
All sources excepted CB3 were observed with the LWS. In two sources,
Cep E-mm and Serpens FIRS 1, several water lines were detected and their
analysis has been reported by Moro-Martín et al. (2001) and Larsson et al. (2002),
respectively. As discussed by these authors, given the
relatively large beam of the LWS, the water line fluxes are due to the
combination of many components along the line of sight:
outflows, multiple sources and Photo-Dissociation Regions.
The measured H2O line fluxes are thus upper limits
to the fluxes from the envelopes and we checked that our predictions do
not exceed the observed fluxes. For two other sources, IC1396 N BIMA 2
and NGC7129 FIRS 2, we retrieved the LWS grating spectra (spectral
resolution
![]() )
from the ISO Data Archive
)
from the ISO Data Archive![]() and extracted the upper limits to the flux of the brightest H2O lines. Table 5 summarises the water line ISO observations for each source.
and extracted the upper limits to the flux of the brightest H2O lines. Table 5 summarises the water line ISO observations for each source.
Table 5:
The brightest water lines predicted by the our model
considering X(H2O)
![]() and X(H2O)
and X(H2O)
![]() compared with the ISO LWS observations. The upper limits refer to 3
compared with the ISO LWS observations. The upper limits refer to 3![]() .
All fluxes are in 10-12 erg s-1 cm-2 units.
.
All fluxes are in 10-12 erg s-1 cm-2 units.
3 Results : Dust and gas density and temperature profiles
The general results of our analysis are:
- The continuum brightness profiles and the SEDs at wavelengths
larger than 60
 m for the five IM-protostars of our sample can be
reproduced by spherical, single index, power law density models. On the
contrary, in all sample sources, this class of models fails to
reproduce the 24
m for the five IM-protostars of our sample can be
reproduced by spherical, single index, power law density models. On the
contrary, in all sample sources, this class of models fails to
reproduce the 24  m flux, underestimating it by 1 to 3 orders of
magnitude. The possible causes and implications of this failure are
discussed in detail in Sect. 4. The
m flux, underestimating it by 1 to 3 orders of
magnitude. The possible causes and implications of this failure are
discussed in detail in Sect. 4. The
 -maps and
-maps and
 -SED obtained for each source are reported in Table 4. The
-SED obtained for each source are reported in Table 4. The
 -maps ranges from 0.11 to 0.55 for the sources modelled in this paper. The
-maps ranges from 0.11 to 0.55 for the sources modelled in this paper. The
 -SED ranges from 0.8 to 4.4 for the sources modeled in this paper. Note that because the flux at 24
-SED ranges from 0.8 to 4.4 for the sources modeled in this paper. Note that because the flux at 24  m is underestimated by several orders of magnitude, the
m is underestimated by several orders of magnitude, the
 -SED value is mainly driven by this point.
-SED value is mainly driven by this point.
- The power law index for the five sample sources varies between 1.2 and 2.2, with an average value equal to 1.6.
- The envelope radius varies between 6000 AU for the lowest
luminosity and closest source, Serpens FIRS 1, and
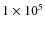 AU
for the brightest and farthest source, CB3-mm.
AU
for the brightest and farthest source, CB3-mm.
- The radius where
 K lies between 100 (Serpens FIRS 1)
and 700 (CB3-mm) AU.
K lies between 100 (Serpens FIRS 1)
and 700 (CB3-mm) AU.
- The density at
 K varies, from 0.4
to
K varies, from 0.4
to
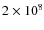 cm-3.
cm-3.
- The envelope mass ranges from 5
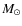 (Serpens FIRS 1) to 120 (CB3-mm)
(Serpens FIRS 1) to 120 (CB3-mm) 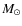 .
.
- The mass of the central object is estimated to be between 0.1
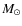 (Serpens FIRS 1) and 6 (CB3-mm)
(Serpens FIRS 1) and 6 (CB3-mm) 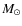 .
.
- The gas and the dust are thermally coupled across the envelope in three of our sources, with temperature differences lower than 5 K. For IC1396 N BIMA 2 (Sect. A.3) and NGC7129 FIRS 2 (Sect. A.4) the difference can reache 40 K.
- The predicted H2O lines are consistent with the ISO upper limits of Sect. 2.4.
The appendix describes in detail the source background, the data included in the analysis, and the derived physical structure (gas and dust density and temperature profiles) for each source.
4 Discussion
4.1 The link between low- and high-mass protostars
One of the major goals of this work is to verify whether intermediate mass protostars provide a link between low- and high-mass star formation. In this section, we analyse whether the parameters describing the protostellar envelope structure (power law index, dust temperature at a given distance, envelope mass...) depend on the luminosity, and hence the mass, of the future central star.
Figure 1 plots key parameters of the envelope
structure (the power law index of the density profile, ![]() ,
the
total mass,
,
the
total mass,
![]() ,
the outer radius,
,
the outer radius,
![]() ,
and the average
density,
,
and the average
density,
![]() of the envelope) for low-, intermediate, and high-mass
protostars as a function on the bolometric luminosity of each
source. The ensemble of the plotted sources covers six orders of
magnitude in luminosity, from about 1
of the envelope) for low-, intermediate, and high-mass
protostars as a function on the bolometric luminosity of each
source. The ensemble of the plotted sources covers six orders of
magnitude in luminosity, from about 1 ![]() to
to ![]()
![]() .
The plotted data are from the present study
(Table 4) and Crimier et al. (2009) for the
intermediate mass protostars, Jørgensen et al. (2002), Shirley et al. (2002)
and Crimier et al. (2010) for the low-mass protostars, and Van der Tak et al. (2000),
Hatchell & van der Tak (2003), Williams et al. (2005) and
Mueller et al. (2002) for the high-mass protostars.
Note that Jørgensen et al. (2002), Williams et al. (2005), Hatchell & van der Tak (2003),
and Crimier et al. (2010,2009),
as well as the present study, use the DUSTY code in the
analysis. The correlation coefficients and probability for a chance
correlation between the pair of parameters considered in Fig. 1 are reported in Table 6. The plots and quantities shown in Fig. 1 and Table 6, respectively, lead to the
following remarks.
.
The plotted data are from the present study
(Table 4) and Crimier et al. (2009) for the
intermediate mass protostars, Jørgensen et al. (2002), Shirley et al. (2002)
and Crimier et al. (2010) for the low-mass protostars, and Van der Tak et al. (2000),
Hatchell & van der Tak (2003), Williams et al. (2005) and
Mueller et al. (2002) for the high-mass protostars.
Note that Jørgensen et al. (2002), Williams et al. (2005), Hatchell & van der Tak (2003),
and Crimier et al. (2010,2009),
as well as the present study, use the DUSTY code in the
analysis. The correlation coefficients and probability for a chance
correlation between the pair of parameters considered in Fig. 1 are reported in Table 6. The plots and quantities shown in Fig. 1 and Table 6, respectively, lead to the
following remarks.
![\begin{figure}
\par\includegraphics[width=15cm,angle=0]{13499f01.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa13499-09/Timg113.png)
|
Figure 1:
Plot of physical quantities within the envelopes surrounding low-,
intermediate, and high-mass protostars as a function of their
bolometric luminosity. Each symbol represents a different group of
sources as follows: crosses: Jørgensen et al. (2002); filled
squares: Shirley et al. (2002); stars:
this study and Crimier et al. (2010,2009);
diamonds: Williams et al. (2005); filled diamonds: Van der Tak et al. (2000); triangles: Hatchell & van der Tak (2003); filled
triangles: Mueller et al. (2002).
Symbols with arrows represent upper/lower limits. The solid line
represents the linear fit of the points obtained when the correlation
is significant (Table 6). The dashed line and the dotted line on panel f) represent the angular resolution of the SCUBA maps at 850 and 450 |
| Open with DEXTER | |
Density power law index ![]() :
:
The density power law index ![]() is similar for low, intermediate
and high-mass protostars. In all three cases the average
is similar for low, intermediate
and high-mass protostars. In all three cases the average ![]() is
1.5. We find that about 60% of the protostars are well modelled by
envelopes with
is
1.5. We find that about 60% of the protostars are well modelled by
envelopes with
![]() .
This indicates that
60% of the protostar envelopes are consistent with the standard
model of free-fall collapse from an initially singular isothermal
sphere, the so-called inside-out model (Shu 1977). However, it appears
that 35% of the sample are reproduced by envelopes with much smaller
indexes, namely
.
This indicates that
60% of the protostar envelopes are consistent with the standard
model of free-fall collapse from an initially singular isothermal
sphere, the so-called inside-out model (Shu 1977). However, it appears
that 35% of the sample are reproduced by envelopes with much smaller
indexes, namely
![]() .
The theoretical
interpretation of theses low
.
The theoretical
interpretation of theses low ![]() values is not straightforward. The
phenomenon was already noted in previous studies of low-mass
protostars (e.g. Andre et al. 1993; Chandler et al. 1998; Motte & André 2001).
Various hypotheses to explain theses low
values is not straightforward. The
phenomenon was already noted in previous studies of low-mass
protostars (e.g. Andre et al. 1993; Chandler et al. 1998; Motte & André 2001).
Various hypotheses to explain theses low ![]() values have been
evoked in the literature. One possibility is that the
envelopes with low
values have been
evoked in the literature. One possibility is that the
envelopes with low ![]() are described by the collapse of an
initially logotropic sphere, rather than a singular isothermal
sphere (Lizano & Shu 1989; McLaughlin & Pudritz 1996; Andre et al. 2000; McLaughlin & Pudritz 1997).
Basically, the logotropic model assumes that
the gas pressure across the initial condensation depends
logarithmically on the density, giving rise to a flatter density
profile in the static part and at the infall/static interface of the
envelope. Because the structure of prestellar cores is well described
by a flat density profile in the inner region (
are described by the collapse of an
initially logotropic sphere, rather than a singular isothermal
sphere (Lizano & Shu 1989; McLaughlin & Pudritz 1996; Andre et al. 2000; McLaughlin & Pudritz 1997).
Basically, the logotropic model assumes that
the gas pressure across the initial condensation depends
logarithmically on the density, giving rise to a flatter density
profile in the static part and at the infall/static interface of the
envelope. Because the structure of prestellar cores is well described
by a flat density profile in the inner region (
![]() )
and a
power law index of
)
and a
power law index of ![]() 2 in the outer part (Visser et al. 2002; Andre et al. 2000),
it has been mentioned in the past that a lower value of
2 in the outer part (Visser et al. 2002; Andre et al. 2000),
it has been mentioned in the past that a lower value of ![]() could probe a
younger protostar. However, later systematic studies have not supported this
interpretation (e.g. Jørgensen et al. 2002).
Another possible explanation is that the envelope is flattened for example because of the presence of a magnetic field (e.g. Hennebelle & Fromang 2008; Li & Shu 1996).
However, testing this hypothesis is not trivial as it requires to solve
the radiative transfer in a 2D geometry. A simple toy model which
assumes constant temperature and optically thin emission suggests that
could probe a
younger protostar. However, later systematic studies have not supported this
interpretation (e.g. Jørgensen et al. 2002).
Another possible explanation is that the envelope is flattened for example because of the presence of a magnetic field (e.g. Hennebelle & Fromang 2008; Li & Shu 1996).
However, testing this hypothesis is not trivial as it requires to solve
the radiative transfer in a 2D geometry. A simple toy model which
assumes constant temperature and optically thin emission suggests that ![]() cannot be lower than 1 even in the extreme case of a flattened structure with axis ratio of 1:10 seen face-on.
The few cases with
cannot be lower than 1 even in the extreme case of a flattened structure with axis ratio of 1:10 seen face-on.
The few cases with
![]() 2 are easier to explain and may be due to the presence of one or more high-density structures, like discs (Jørgensen et al. 2007), embedded within
the envelope.
2 are easier to explain and may be due to the presence of one or more high-density structures, like discs (Jørgensen et al. 2007), embedded within
the envelope.
Envelope mass
![]() :
:
It is very clear from Fig. 1 that more luminous sources
have larger envelope mass. Hatchell & van der Tak (2003) report the mass of the envelopes within 1 pc (empty triangles in Fig. 1). Therefore, the envelope masses from Hatchell & van der Tak (2003) are considered as lower limits for
![]() ,
and are not taken into account in the correlation coefficient
computation. The correlation coefficient is 0.96 with a probability for
a chance correlation of
,
and are not taken into account in the correlation coefficient
computation. The correlation coefficient is 0.96 with a probability for
a chance correlation of ![]() 10-20, pointing out a strong relation between the two variables. Assuming that the luminosity is entirely
due to the gravitational energy released, the luminosity-envelope mass
relation suggests that a similar relation exists between the mass
accretion rate and the mass of the envelope. However, while the
result that more luminous sources
have larger envelope mass agrees with theoretical expectations, it should be
considered with caution. Indeed, the observed correlation between two
quantities does not necessarily imply a physical correlation.
The envelope-mass-derivation differs between
studies. Furthermore, uncertainties in the distance to sources,
particularly in the high-mass cases (uncertainties of several kpc),
and resolution limits of distant objects can introduce errors and
significant observational bias.
10-20, pointing out a strong relation between the two variables. Assuming that the luminosity is entirely
due to the gravitational energy released, the luminosity-envelope mass
relation suggests that a similar relation exists between the mass
accretion rate and the mass of the envelope. However, while the
result that more luminous sources
have larger envelope mass agrees with theoretical expectations, it should be
considered with caution. Indeed, the observed correlation between two
quantities does not necessarily imply a physical correlation.
The envelope-mass-derivation differs between
studies. Furthermore, uncertainties in the distance to sources,
particularly in the high-mass cases (uncertainties of several kpc),
and resolution limits of distant objects can introduce errors and
significant observational bias.
Envelope radius
![]() :
:
Similar to
![]() ,
the outer radius of the envelope
,
the outer radius of the envelope
![]() increases with increasing luminosity, varying from
increases with increasing luminosity, varying from ![]() 104 AU for
low-mass protostars to
104 AU for
low-mass protostars to ![]() 106 AU for high-mass protostars. The
correlation coefficient between
106 AU for high-mass protostars. The
correlation coefficient between
![]() and the luminosity is very
high, 0.90, with a probability for a chance correlation of 10-22.
Note that we checked that the relation is real and not simply due
to the distance to the source combined to the angular resolution
limits. This point is illustrated by the plot of the measured angular
size,
and the luminosity is very
high, 0.90, with a probability for a chance correlation of 10-22.
Note that we checked that the relation is real and not simply due
to the distance to the source combined to the angular resolution
limits. This point is illustrated by the plot of the measured angular
size, ![]() ,
of the sources as function of the luminosity in Fig. 1 (panel f). The figure shows that
,
of the sources as function of the luminosity in Fig. 1 (panel f). The figure shows that ![]() is not decreasing with luminosity, which excludes the possibility of an
observational bias due to the limited angular resolution of the
observations.
is not decreasing with luminosity, which excludes the possibility of an
observational bias due to the limited angular resolution of the
observations.
Average density
![]() :
:
The average density
![]() in the envelope is derived from
in the envelope is derived from
![]() and
and
![]() for each source. Unfortunately,
for each source. Unfortunately,
![]() could be derived
only for intermediate and some high-mass sources, giving an average of
about
could be derived
only for intermediate and some high-mass sources, giving an average of
about
![]() and
and
![]() cm-3, respectively,
over a spread in luminosity of about four orders of magnitude. Although
the average
cm-3, respectively,
over a spread in luminosity of about four orders of magnitude. Although
the average
![]() is one order of magnitude higher in high-mass protostars
versus intermediate mass protostars, the correlation coefficient between
is one order of magnitude higher in high-mass protostars
versus intermediate mass protostars, the correlation coefficient between
![]() and the luminosity is only 0.55. The lower limits for low-mass and
the highest mass protostars do not allow any firm conclusion,
but it seems that there is little difference in the average
density of these envelopes.
and the luminosity is only 0.55. The lower limits for low-mass and
the highest mass protostars do not allow any firm conclusion,
but it seems that there is little difference in the average
density of these envelopes.
Density at 1000 AU:
There is an apparent increase of the density at 1000 AU with
increasing luminosity, going from about ![]() 106 to
106 to ![]() 108 cm-3 for source luminosity varying from 1 to
108 cm-3 for source luminosity varying from 1 to ![]()
![]() .
There are, however, some exceptions on the high-mass
side. Indeed, the increase of the density at a given distance is
consistent with the finding of an increasing envelope radius and
approximately constant average density for the envelope (see the two
items above).
.
There are, however, some exceptions on the high-mass
side. Indeed, the increase of the density at a given distance is
consistent with the finding of an increasing envelope radius and
approximately constant average density for the envelope (see the two
items above).
Density
![]() at 10 K:
at 10 K:
For a smaller sample, formed by low- and intermediate mass protostars
only, it is possible to compare the density
![]() at 10 K, which
is an indication of the density of the parental cloud (the gas shielded by UV photons).
Figure 2 shows that
at 10 K, which
is an indication of the density of the parental cloud (the gas shielded by UV photons).
Figure 2 shows that
![]() is between
is between
![]() and
and
![]() cm-3. This quantity, however, is not correlated with the
source luminosity (varying by three orders of magnitude). Therefore there is no
evidence that the outer density plays a large role in the
determination of the final star mass, a rather important and
surprising result, which needs further confirmation.
cm-3. This quantity, however, is not correlated with the
source luminosity (varying by three orders of magnitude). Therefore there is no
evidence that the outer density plays a large role in the
determination of the final star mass, a rather important and
surprising result, which needs further confirmation.
Summary:
To summarise, the major result of this section is that the protostar
luminosity (namely the mass of the final star) seems preferentially
linked to the size (or mass) of the envelope, rather than to
the parental cloud density, and that most of the envelope ends up
having a centrally condensed, free-fall density distribution.
Furthermore, and maybe even more important, there is a continuity in
the parameters of the envelopes, going from low- to high-mass
protostars. It appears that there is no important difference to the
trigger or process of star formation for these two mass regimes. The
intermediate mass protostars have allowed a bridge between the
low- and high-mass sources, with no apparent observational discontinuity.
However, one has to keep in mind that these results are based on single
dish observations and are therefore driven mainly by the outer region
of the envelopes (![]() 10''). A more accurate analysis of the smaller
scale structure ( cavities, density power law index changes...) will require
interferometric observations.
10''). A more accurate analysis of the smaller
scale structure ( cavities, density power law index changes...) will require
interferometric observations.
![\begin{figure}
\par\includegraphics[width=6.8cm,angle=90,clip]{13499f02.ps}
\vspace*{7mm}
\end{figure}](/articles/aa/full_html/2010/08/aa13499-09/Timg125.png)
|
Figure 2: Plot of the density at 10 K as function of the bolometric luminosity of a sample of low- and intermediate mass protostars. Data are from Jørgensen et al. (2002), (crosses), and the present study, (stars). |
| Open with DEXTER | |
Table 6: Linear correlation coefficients and probability for a chance correlation between the pair of parameters plotted in Figs. 1 and 2.
4.2 The problem of the underestimated 24  m flux
m flux
As mentioned in the previous sections, our modelling fails to reproduce
the observed flux at 24 ![]() m by several orders of magnitude.
This is certainly not due to a numerical problem in the computation but
is rather a real problem: our model misses some key element. A possibility
evoked in the literature is the presence of a large spherical cavity within
the envelope (Jørgensen et al. 2005) which could significantly
reduce the optical thickness at 24
m by several orders of magnitude.
This is certainly not due to a numerical problem in the computation but
is rather a real problem: our model misses some key element. A possibility
evoked in the literature is the presence of a large spherical cavity within
the envelope (Jørgensen et al. 2005) which could significantly
reduce the optical thickness at 24 ![]() m.
m.
![\begin{figure}
\par\mbox{\includegraphics[width=4.5cm,angle=90]{13499f03.eps}\in...
...\includegraphics[width=4.5cm,angle=90]{13499f07.eps}\hspace*{3cm}}\end{figure}](/articles/aa/full_html/2010/08/aa13499-09/Timg130.png)
|
Figure 3:
Cep E-mm physical structure, brightness profiles, and SED from the best-fit model (black solid lines) and
after adding an 1800 AU radius cavity to the best-fit model (red dashed-dotted lines). The dust temperature and H2 density profiles are reported in the upper left panel and upper right panel, respectively. The observed
brightness profiles at 450 |
| Open with DEXTER | |
To check this hypothesis, we carried out a few tests
using Cep E-mm as a representative case. The results
of the tests are shown in Fig. 3. First, we added a
1800 AU radius cavity to the best-fit model of
Table 4. As expected, the emission at 24 ![]() m
is increased by several orders of magnitude. However, this model badly
fails to reproduce the brightness profiles (as shown in the
figure). When a correct procedure is carried out that takes into
account the variation in the brightness profiles, namely a minimisation of the
m
is increased by several orders of magnitude. However, this model badly
fails to reproduce the brightness profiles (as shown in the
figure). When a correct procedure is carried out that takes into
account the variation in the brightness profiles, namely a minimisation of the
![]() varying all the envelope parameters, the situation returns
to the original (best-fit) underestimation of the 24
varying all the envelope parameters, the situation returns
to the original (best-fit) underestimation of the 24 ![]() m flux. In
fact, the introduction of a cavity leads to an increase of the
density power law index,
m flux. In
fact, the introduction of a cavity leads to an increase of the
density power law index, ![]() ,
to compensate for the resulting
flattening of the model brightness profiles. As a result, the mass
found in the outer envelope is lower so that the the overall
dust optical depth must be increased to reproduce the integrated
sub-millimetre fluxes. The dust opacity at 24
,
to compensate for the resulting
flattening of the model brightness profiles. As a result, the mass
found in the outer envelope is lower so that the the overall
dust optical depth must be increased to reproduce the integrated
sub-millimetre fluxes. The dust opacity at 24 ![]() m again becomes
large and very little emission is able to escape at these wavelengths.
These tests suggest that to solve the 24
m again becomes
large and very little emission is able to escape at these wavelengths.
These tests suggest that to solve the 24 ![]() m flux problem it is
necessary to have a low-opacity escape route for the 24
m flux problem it is
necessary to have a low-opacity escape route for the 24 ![]() m photons
and a thick enough envelope to fit the brightness profiles: a simple cavity does not suffice.
m photons
and a thick enough envelope to fit the brightness profiles: a simple cavity does not suffice.
Larsson et al. (2000,2002) similarly found that the 24 ![]() m
flux is underestimated toward Serpens-FIRS1, using different tools and
observations. In their first study, Larsson et al. used a 1D
radiative
transfer code assuming a spherical envelope model with a single power
law density to reproduce the SED (similar to our approach). Their model
underestimates the observed flux near 24
m
flux is underestimated toward Serpens-FIRS1, using different tools and
observations. In their first study, Larsson et al. used a 1D
radiative
transfer code assuming a spherical envelope model with a single power
law density to reproduce the SED (similar to our approach). Their model
underestimates the observed flux near 24 ![]() m
by several orders of
magnitude. In their second study, they modelled the envelope with a
2D radiative transfer code, including a biconical cavity. This
model
reproduces fairly well the SED from the mid-IR to millimetre
wavelengths, but again underestimates the observed flux at 24
m
by several orders of
magnitude. In their second study, they modelled the envelope with a
2D radiative transfer code, including a biconical cavity. This
model
reproduces fairly well the SED from the mid-IR to millimetre
wavelengths, but again underestimates the observed flux at 24 ![]() m
by about a factor 3-10. The biconical cavity treatment alleviates but does not resolve the missing flux problem.
Systematic studies of high-mass protostars by Van der Tak et al. (2000)
and Williams et al. (2005) have led to similar results.
Williams et al. (2005) modelled 36 high-mass protostellar
objects at 850
m
by about a factor 3-10. The biconical cavity treatment alleviates but does not resolve the missing flux problem.
Systematic studies of high-mass protostars by Van der Tak et al. (2000)
and Williams et al. (2005) have led to similar results.
Williams et al. (2005) modelled 36 high-mass protostellar
objects at 850 ![]() m, using DUSTY, as in the present study.
The majority of their best-fits fail to reproduce the flux around 24
m, using DUSTY, as in the present study.
The majority of their best-fits fail to reproduce the flux around 24 ![]() m.
They discuss the possibility of the contribution of high accretion
rates, which would significantly increase the near-IR flux density
(Osorio et al. 1999). Another contribution could come from the
presence of circumstellar disks or the stochastic heating of small grains,
which would alter the emission of the envelope and produce more short
wavelength photons (e.g. Sellgren et al. 1983; Draine & Li 2001).
However, the envelope is optically thick at these wavelengths, making
the emission very sensitive to deviations from the assumed spherical
shape. These additional processes still require a low-opacity
escape route to exists (also mentioned by Van der Tak et al. 2000) to explain
the missing 24
m.
They discuss the possibility of the contribution of high accretion
rates, which would significantly increase the near-IR flux density
(Osorio et al. 1999). Another contribution could come from the
presence of circumstellar disks or the stochastic heating of small grains,
which would alter the emission of the envelope and produce more short
wavelength photons (e.g. Sellgren et al. 1983; Draine & Li 2001).
However, the envelope is optically thick at these wavelengths, making
the emission very sensitive to deviations from the assumed spherical
shape. These additional processes still require a low-opacity
escape route to exists (also mentioned by Van der Tak et al. 2000) to explain
the missing 24 ![]() m flux, for example a biconical cavity
excavated by the outflow. Note
that all the intermediate mass protostars studied here are associated
with outflows, except OMC2-FIR4 for which the model indeed fits the
observed flux at 24
m flux, for example a biconical cavity
excavated by the outflow. Note
that all the intermediate mass protostars studied here are associated
with outflows, except OMC2-FIR4 for which the model indeed fits the
observed flux at 24 ![]() m (see Crimier et al. 2009). Finally, Van Der
Tak et al. also suggest the possible evaporation of grain ice
mantles close to the star, which would decrease the 20
m (see Crimier et al. 2009). Finally, Van Der
Tak et al. also suggest the possible evaporation of grain ice
mantles close to the star, which would decrease the 20 ![]() m optical
depth by 30% (Ossenkopf & Henning 1994) in the
m optical
depth by 30% (Ossenkopf & Henning 1994) in the
![]() K
region.
K
region.
5 Conclusions
We have derived the physical structure of the envelopes of five IM
protostars, with luminosities between 30 to 1000 ![]() .
The
envelope dust density and temperature profiles were determined
by means of the 1D radiative transfer code DUSTY,
using all continuum observations from the literature. The analysis assumed
that the density profiles follow a single index power law and obtained
self-consistently the temperature profile. The best-fit
envelope models well reproduce the observations, namely the
sub-millimetre radial brightness profiles and the SED
between
.
The
envelope dust density and temperature profiles were determined
by means of the 1D radiative transfer code DUSTY,
using all continuum observations from the literature. The analysis assumed
that the density profiles follow a single index power law and obtained
self-consistently the temperature profile. The best-fit
envelope models well reproduce the observations, namely the
sub-millimetre radial brightness profiles and the SED
between ![]() 60
60 ![]() m and 1.3 mm, for each source.
However, the model underestimates the
24
m and 1.3 mm, for each source.
However, the model underestimates the
24 ![]() m
emission by several orders of magnitude. We ran test models to better
understand what ingredient is missing and conclude that a ``simple''
cavity is not enough to reproduce the 24
m
emission by several orders of magnitude. We ran test models to better
understand what ingredient is missing and conclude that a ``simple''
cavity is not enough to reproduce the 24 ![]() m
observations. Apparently, the missing ingredient is a low-opacity
escape route plus a warm dust contribution inside the envelope
(circumstellar disc, warm outflow-excavated cavity...).
m
observations. Apparently, the missing ingredient is a low-opacity
escape route plus a warm dust contribution inside the envelope
(circumstellar disc, warm outflow-excavated cavity...).
The gas density and temperature profiles were derived by assuming a constant dust-to-gas ratio and by computing the gas thermal balance at each point within the envelope. Because the gas equilibrium temperature strongly depends on the water abundance in the interiors of the envelopes, we also computed the expected water emission for each source. We found that the gas and dust are thermally coupled across the envelope with differences less than 5 K in three out of five sources. In IC1396 N BIMA 2 and NGC7129 FIRS 2 the gas is colder than the dust by at most 40 K, in a small region just where the icy mantles are predicted to sublimate. The predicted water line fluxes are consistent with the upper limits derived by the ISO observations.
One of the major goals of the present study was to ``use'' the IM
protostars as a bridge between the low- and high-mass protostars with
the hope that this will aid our understanding of the star formation
process at either end. When comparing the characteristics derived by
the modelling of the envelopes of low-, intermediate, and high-mass
protostars, it appears that there is a smooth transition between the
various groups. This suggests that there are basically no different
triggers or processes between these mass regimes. The
power law index ![]() is similar in all three groups of objects. The
majority of the sources have
is similar in all three groups of objects. The
majority of the sources have ![]() between 1.5 and 2. This is
consistent with the theory of isothermal collapse from an initially
singular isothermal sphere, the so-called inside-out expansion-wave
collapse (Shu 1977). Regardless of the mass
group, a few sources have
between 1.5 and 2. This is
consistent with the theory of isothermal collapse from an initially
singular isothermal sphere, the so-called inside-out expansion-wave
collapse (Shu 1977). Regardless of the mass
group, a few sources have ![]() lower than 1.5, pointing perhaps to the collapse of an initially
logotropic, virialised sphere (Lizano & Shu 1989, McLaughlin 96,
and McLaughlin 97). Finally, the luminosity (mass) of the star
depends on the size of the envelope, but does not depend on the density
at a given temperature (for example at 10 K or 100 K).
lower than 1.5, pointing perhaps to the collapse of an initially
logotropic, virialised sphere (Lizano & Shu 1989, McLaughlin 96,
and McLaughlin 97). Finally, the luminosity (mass) of the star
depends on the size of the envelope, but does not depend on the density
at a given temperature (for example at 10 K or 100 K).
We warmly thank Patrick Hennebelle for helpful discussions. One of us (N.Crimier) is supported by a fellowship of the Ministère de l'Enseignement Supérieur et de la Recherche. We acknowledge the financial support by PPF and the Agence Nationale pour la Recherche (ANR), France (contract ANR-08-BLAN-0225). The James Clerk Maxwell Telescope is operated by the Joint Astronomy Centre on behalf of the Science and Technology Facilities Council of the United Kingdom, the Netherlands Organisation for Scientific Research, and the National Research Council of Canada. This paper has been partially supported by MICINN, within the programme CONSOLIDER INGENIO 2010, under grant ``Molecular Astrophysics: The Herschel and Alma Era - ASTROMOL'' (ref.: CSD2009-00038) Doug Johnstone is supported by a Natural Sciences and Engineering Research Council of Canada (NSERC) Discovery Grant.
Appendix A: Results for individual sources
A.1 CB3-mm
A.1.1 Source background
The CB3 Bok globule is located at ![]() 2.5 kpc (Launhardt & Henning 1997; Wang et al. 1995)
on the near side of the Perseus
arm of the Galaxy. Using ISO data, Launhardt et al. (1998) carried out a
multi-wavelength study of the CB3 globule and derived a total mass
and bolometric luminosity of the order of 400
2.5 kpc (Launhardt & Henning 1997; Wang et al. 1995)
on the near side of the Perseus
arm of the Galaxy. Using ISO data, Launhardt et al. (1998) carried out a
multi-wavelength study of the CB3 globule and derived a total mass
and bolometric luminosity of the order of 400
![]() and
and ![]() 1000
1000
![]() ,
respectively, for the entire globule. The globule hosts
,
respectively, for the entire globule. The globule hosts
![]() 40 NIR sources, 22 of which are likely low- and intermediate mass
protostars in different stages of evolution (Yun & Clemens 1995,1994; Launhardt et al. 1998).
CB3-mm, the brightest millimetre source
in the globule, was first detected by Launhardt & Henning (1997) and
subsequently observed in the sub-millimetre by Huard et al. (2000).
The high luminosity of the source evaluated by Launhardt & Henning (1997),
40 NIR sources, 22 of which are likely low- and intermediate mass
protostars in different stages of evolution (Yun & Clemens 1995,1994; Launhardt et al. 1998).
CB3-mm, the brightest millimetre source
in the globule, was first detected by Launhardt & Henning (1997) and
subsequently observed in the sub-millimetre by Huard et al. (2000).
The high luminosity of the source evaluated by Launhardt & Henning (1997),
![]() ,
suggests that CB3-mm is an intermediate mass
object. A recent interferometric study by Fuente et al. (2007) showed
that CB3-mm contains two compact cores at 3 mm separated by 0.3 pc
(
,
suggests that CB3-mm is an intermediate mass
object. A recent interferometric study by Fuente et al. (2007) showed
that CB3-mm contains two compact cores at 3 mm separated by 0.3 pc
(![]() 0.43
0.43
![]() ). Yun & Clemens (1994) also detected a molecular
bipolar outflow in CO, elongated in the northeast-southwest direction,
associated with H2O masers (de Gregorio-Monsalvo et al. 2006). This
outflow has been mapped in various molecular lines by Codella & Bachiller (1999),
who concluded that it originates from CB3-mm. The same authors
concluded that CB3-mm is probably a Class 0 source. In the present
study we re-evaluated the luminosity of this object,
). Yun & Clemens (1994) also detected a molecular
bipolar outflow in CO, elongated in the northeast-southwest direction,
associated with H2O masers (de Gregorio-Monsalvo et al. 2006). This
outflow has been mapped in various molecular lines by Codella & Bachiller (1999),
who concluded that it originates from CB3-mm. The same authors
concluded that CB3-mm is probably a Class 0 source. In the present
study we re-evaluated the luminosity of this object,
![]() ,
making CB3-mm an intermediate mass protostar.
,
making CB3-mm an intermediate mass protostar.
A.1.2 Analysis
The continuum maps used for the CB3-mm analysis are presented in
Fig. A.1. The maps at 450 ![]() m and 850
m and 850 ![]() m were
obtained on 1997 December 18 as a part of project m96bi28 and
on 1998 August 10 as a part of project m98bc21,
respectively. The flux profiles obtained at each wavelength are shown
in Fig. A.2. The Spitzer observations were obtained on the
20th September 2004 as part of the programme ``Comparative Study of
Galactic and Extragalactic HII Regions'' (AOR: 63, PI: James
R. Houck). The integrated fluxes used for the analysis are reported in
Table 2 and in Fig. A.2. The fluxes at
70
m were
obtained on 1997 December 18 as a part of project m96bi28 and
on 1998 August 10 as a part of project m98bc21,
respectively. The flux profiles obtained at each wavelength are shown
in Fig. A.2. The Spitzer observations were obtained on the
20th September 2004 as part of the programme ``Comparative Study of
Galactic and Extragalactic HII Regions'' (AOR: 63, PI: James
R. Houck). The integrated fluxes used for the analysis are reported in
Table 2 and in Fig. A.2. The fluxes at
70 ![]() m, 450
m, 450 ![]() m and 850
m and 850 ![]() m were obtained by integration over a
m were obtained by integration over a ![]() 50
50
![]() radius. The uncertainty ellipse position of the IRAS
observations are reported on the 450
radius. The uncertainty ellipse position of the IRAS
observations are reported on the 450 ![]() m maps in
Fig. A.1. Note that the map at 24
m maps in
Fig. A.1. Note that the map at 24 ![]() m presents two
sources separated by
m presents two
sources separated by ![]() 12
12
![]() ,
centred on the sub-millimetre
source emission (see Fig. A.1). Therefore, the flux
,
centred on the sub-millimetre
source emission (see Fig. A.1). Therefore, the flux
![]() Jy at 24
Jy at 24 ![]() m was obtained by adding the integrated
flux over the two sources separately. We also report on the SED the
lower limits from Plateau de Bure (PdB) interferometric fluxes at 1.3 mm
and 3 mm (Fuente et al. 2007).
m was obtained by adding the integrated
flux over the two sources separately. We also report on the SED the
lower limits from Plateau de Bure (PdB) interferometric fluxes at 1.3 mm
and 3 mm (Fuente et al. 2007).
![\begin{figure}
\par\includegraphics[width=6cm,angle=270]{13499f08.eps}\includegr...
...0]{13499f10.eps}\includegraphics[width=6cm,angle=270]{13499f11.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa13499-09/Timg135.png)
|
Figure A.1:
Continuum emission maps around CB3-mm at 24 |
| Open with DEXTER | |
A.1.3 Best-fit
![\begin{figure}
\par\mbox{\includegraphics[width=5cm,angle=90]{13499f12.eps}\incl...
...m}\includegraphics[width=5cm,angle=90]{13499f14.eps}\hspace*{3cm}}\end{figure}](/articles/aa/full_html/2010/08/aa13499-09/Timg136.png)
|
Figure A.2:
Observed brightness profiles at 450 |
| Open with DEXTER | |
Table 4 presents the set of parameters ![]() ,
Y, and
,
Y, and
![]() ,
which best reproduce the observations, and
summarises some relevant physical quantities of the model. Figure
A.2 shows the best derived brightness profiles and SED
against the observed ones, while Fig. A.3 shows the
,
which best reproduce the observations, and
summarises some relevant physical quantities of the model. Figure
A.2 shows the best derived brightness profiles and SED
against the observed ones, while Fig. A.3 shows the
![]() contour plots. The dust density and temperature profiles of
the best-fit model are reported in Fig. A.4. Although the
observed flux profiles and SED fluxes from 60
contour plots. The dust density and temperature profiles of
the best-fit model are reported in Fig. A.4. Although the
observed flux profiles and SED fluxes from 60 ![]() m to 850
m to 850 ![]() m are well
reproduced by the model, the observed flux at 24
m are well
reproduced by the model, the observed flux at 24 ![]() m is
underestimated by about two orders of magnitude. The model
agrees well with the lower limits from Plateau de Bure
interferometric fluxes at 1.3 mm and 3 mm (Fuente et al. 2007), however.
m is
underestimated by about two orders of magnitude. The model
agrees well with the lower limits from Plateau de Bure
interferometric fluxes at 1.3 mm and 3 mm (Fuente et al. 2007), however.
The best-fit model, obtained with an ![]() of 2.2,
is the steepest among the five sources modelled in the paper and
leads to a strong gradient in the density profile, from
of 2.2,
is the steepest among the five sources modelled in the paper and
leads to a strong gradient in the density profile, from ![]() 109 to
109 to ![]() 103 cm-3 with a density and radius at 100 K of
103 cm-3 with a density and radius at 100 K of
![]() cm-3 and 700 AU, respectively.
cm-3 and 700 AU, respectively.
Although CB3-mm is the largest and brightest of the five sources
investigated in this paper, its distance of 2500 pc makes it the
least resolved source. Indeed, the brightness
profiles at each wavelength
presented in Fig. A.2 are close to the beam
patterns of the telescope, showing that the source
is barely resolved. Consequently, the value of the envelope radius
![]() suffers a relatively large uncertainty. Considering the
suffers a relatively large uncertainty. Considering the
![]() contour at 10% of the minimum
contour at 10% of the minimum
![]() (see Fig. A.3) in order to estimate the uncertainty, we obtain
(see Fig. A.3) in order to estimate the uncertainty, we obtain
![]() AU. On the
contrary, the envelope column density is quite insensitive to
AU. On the
contrary, the envelope column density is quite insensitive to
![]() ,
due to the high power law index of the density
profile. Finally, in minimising the
,
due to the high power law index of the density
profile. Finally, in minimising the
![]() ,
we also varied
the source luminosity from 800
,
we also varied
the source luminosity from 800 ![]() to 1200
to 1200 ![]() and found that the
best-fit is obtained with source luminosity equal to 1000
and found that the
best-fit is obtained with source luminosity equal to 1000 ![]() .
.
A.2 Cep E-mm
A.2.1 Source background
Located in the Cepheus OB3 association at a distance of 730 pc
(Sargent 1977; Crawford & Barnes 1970), Cepheus E is the second
most massive and dense clump of this region (Few & Cohen
1983). Cepheus E hosts the source IRAS 23011+6126, which is
associated with Cep E-mm, catalogued as a Class 0 protostar by Lefloch et al. (1996).
Targeted by several continuum and lines studies, Cep E-mm
has been observed with IRAS (Palla et al. 1993), IRAM 30m
(Lefloch et al. 1996; Chini et al. 2001), SCUBA (Chini et al. 2001),
ISO (Froebrich et al. 2003), and Spitzer (Noriega-Crespo et al. 2005). All these
studies confirm the Class 0 status of Cep E-mm and constrain
the total mass and bolometric luminosity of the source to 7-25
![]() and
and ![]() 80-120
80-120
![]() ,
respectively. Finally, a bipolar
molecular outflow, first reported by Fukui et al. (1989), is associated with
Cep E-mm. The properties of the outflow have been thoroughly analysed
by Eislöffel et al. (1996), Ayala et al. (2000), Moro-Martín et al. (2001), and
Smith et al. (2003). The H2 and [FeII] study by Eislöffel et al. (1996)
shows a quadrapolar outflow morphology,
suggesting that the driving source is a binary. This outflow
morphology has been confirmed by sub-mm and near-IR observations
(Ladd & Hodapp 1997), and by Spitzer observations (Noriega-Crespo et al. 2005).
,
respectively. Finally, a bipolar
molecular outflow, first reported by Fukui et al. (1989), is associated with
Cep E-mm. The properties of the outflow have been thoroughly analysed
by Eislöffel et al. (1996), Ayala et al. (2000), Moro-Martín et al. (2001), and
Smith et al. (2003). The H2 and [FeII] study by Eislöffel et al. (1996)
shows a quadrapolar outflow morphology,
suggesting that the driving source is a binary. This outflow
morphology has been confirmed by sub-mm and near-IR observations
(Ladd & Hodapp 1997), and by Spitzer observations (Noriega-Crespo et al. 2005).
A.2.2 Analysis
The continuum maps used for the Cep E-mm analysis are presented in
Fig. A.5. The maps at 450 ![]() m and 850
m and 850 ![]() m were
obtained in August 1997 as a part of the project m97bu87 and the observations
are described in detail by Chini et al. (2001). The flux profiles
obtained at each wavelength are shown in Fig. A.6. The
Spitzer observations were obtained on the 2003 September 29 as part of
the programme ``MIPS/IRAC imaging of protostellar jet HH 212'' (AOR:
1063, PI: Alberto Noriega-Crespo) and are described in detail by
Noriega-Crespo & Garnavich (2001). The integrated fluxes at 450
m were
obtained in August 1997 as a part of the project m97bu87 and the observations
are described in detail by Chini et al. (2001). The flux profiles
obtained at each wavelength are shown in Fig. A.6. The
Spitzer observations were obtained on the 2003 September 29 as part of
the programme ``MIPS/IRAC imaging of protostellar jet HH 212'' (AOR:
1063, PI: Alberto Noriega-Crespo) and are described in detail by
Noriega-Crespo & Garnavich (2001). The integrated fluxes at 450 ![]() m, 850
m, 850 ![]() m, and
1300
m, and
1300 ![]() m were retrieved from the literature (Chini et al. 2001).
The uncertainty ellipse position of the IRAS observation is reported on the 450
m were retrieved from the literature (Chini et al. 2001).
The uncertainty ellipse position of the IRAS observation is reported on the 450
![]() m map in Fig. A.5. The fluxes at 24
m map in Fig. A.5. The fluxes at 24 ![]() m and 70
m and 70 ![]() m
were obtained by integration over a
m
were obtained by integration over a ![]() 30
30
![]() and
and ![]() 60
60
![]() radius, respectively. Note that to compute the flux uncertainties, we
varied the integration radius of about 50% and found variations of
radius, respectively. Note that to compute the flux uncertainties, we
varied the integration radius of about 50% and found variations of
![]() 30%. The integrated fluxes used for the analysis
are reported in Table 2 and in Fig. A.6.
30%. The integrated fluxes used for the analysis
are reported in Table 2 and in Fig. A.6.
| Figure A.3:
|
|
| Open with DEXTER | |
A.2.3 Best-fit
Table 4 presents the set of parameters ![]() ,
Y, and
,
Y, and
![]() ,
which best reproduce the observations, and
summarises some relevant physical quantities of the model. Figure A.6 shows the derived brightness profiles and SED
against the observations. The dust density and temperature profiles
of the best-fit model are reported in Fig. A.7. Although
the observed flux profiles and SED fluxes from 60
,
which best reproduce the observations, and
summarises some relevant physical quantities of the model. Figure A.6 shows the derived brightness profiles and SED
against the observations. The dust density and temperature profiles
of the best-fit model are reported in Fig. A.7. Although
the observed flux profiles and SED fluxes from 60 ![]() m to 1300
m to 1300 ![]() m are
well reproduced by the model, the observed flux at 24
m are
well reproduced by the model, the observed flux at 24 ![]() m is
underestimated by about
m is
underestimated by about ![]() 3 orders of magnitude.
Similarly to CB3-mm, the envelope model derived
for Cep E-mm with an
3 orders of magnitude.
Similarly to CB3-mm, the envelope model derived
for Cep E-mm with an ![]() of 1.9 is very peaked, leading to
a strong gradient in the density profile, from
of 1.9 is very peaked, leading to
a strong gradient in the density profile, from ![]() 109 to
109 to ![]() 104 cm-3 with a density and radius at 100 K of
104 cm-3 with a density and radius at 100 K of
![]() cm-3 and 223 AU, respectively. Considering the
cm-3 and 223 AU, respectively. Considering the
![]() contour at 10% of the minimum
contour at 10% of the minimum
![]() in order to
estimate the uncertainty, we obtained
in order to
estimate the uncertainty, we obtained
![]() AU. Finally, in minimising the
AU. Finally, in minimising the
![]() ,
we
also varied the source luminosity from 70
,
we
also varied the source luminosity from 70 ![]() to 130
to 130 ![]() and
found the best-fit for a source luminosity equal to 100
and
found the best-fit for a source luminosity equal to 100 ![]() .
.
A.3 IC1396 N BIMA 2
A.3.1 Source background
IC1396 N is a bright globule located 750 pc (Matthews 1979) from the Sun, near the border of the IC1396 extended HII region (Weikard et al. 1996; Osterbrock 1957)
and at a projected distance of 11 pc north of the O6.5 star
HD 206267 which ionises the region. IC1396 N is associated
with the source
IRAS21391+5802. Its strong submillimetre and millimetre
continuum emission (Codella et al. 2001; Wilking et al. 1993; Sugitani et al. 2000),
high-density gas (Codella et al. 2001; Beltrán et al. 2004; Cesaroni et al. 1999; Serabyn et al. 1993),
and water maser emission (Patel et al. 2000; Felli et al. 1992; Tofani et al. 1995) reveal that IC1396 N is an active site of star formation. The bolometric luminosity
is estimated to range from 235
![]() (Saraceno et al. 1996) to 440
(Saraceno et al. 1996) to 440
![]() (Sugitani et al. 2000).
(Sugitani et al. 2000).
![\begin{figure}
\par\includegraphics[width=5.5cm,angle=90]{13499f16.eps}\includegraphics[width=5.5cm,angle=90]{13499f17.eps}
\vspace*{3mm}
\end{figure}](/articles/aa/full_html/2010/08/aa13499-09/Timg141.png)
|
Figure A.4:
CB3-mm dust temperature ( left panel) and H2 density ( right panel) profiles from the best-fit model. The dashed line
represents the difference between the dust and gas temperature
derived using X(H2O)
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6cm,angle=270]{13499f18.eps}\includegr...
...s}\includegraphics[width=6cm,angle=270]{13499f21.eps}
\vspace*{3mm}
\end{figure}](/articles/aa/full_html/2010/08/aa13499-09/Timg142.png)
|
Figure A.5:
Continuum emission maps around Cep E-mm at 24 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=5cm,angle=90]{13499f22.eps}\includegra...
...\includegraphics[width=5cm,angle=90]{13499f24.eps}\hspace*{3.5cm}}\end{figure}](/articles/aa/full_html/2010/08/aa13499-09/Timg143.png)
|
Figure A.6:
Observed brightness profiles at 450 |
| Open with DEXTER | |
| Figure A.7:
Cep E-mm dust temperature ( left panel) and H2 density ( right panel) profiles from the best-fit model. The dashed line represents the difference between the dust and gas temperature
derived using X(H2O)
|
|
| Open with DEXTER | |
Using BIMA interferometric millimetre observations, Beltrán et al. (2002)
detected three sources (BIMA 1, BIMA 2 and BIMA 3) deeply
embedded in the globule. BIMA 2 has the strongest millimetre emission
and is also the most massive object. The authors concluded that BIMA 2 is
most likely an IM protostar, while BIMA 1, and BIMA 3, located at
![]() 15
15
![]() west and south-east respectively, are less massive and/or
more evolved. The recent studies by Neri et al. (2007) and Fuente et al. (2007),
using Plateau de Bure interferometric observations, provide a detailed
study of BIMA 2 and showed that BIMA 2 contains at least
three dense cores separated by
west and south-east respectively, are less massive and/or
more evolved. The recent studies by Neri et al. (2007) and Fuente et al. (2007),
using Plateau de Bure interferometric observations, provide a detailed
study of BIMA 2 and showed that BIMA 2 contains at least
three dense cores separated by ![]() 1
1
![]() .
.
Finally, the region presents an extended (![]() 3 arcmin) CO bipolar
outflow (Sugitani et al. 1989) which has been mapped by Codella et al. (2001). The
study by Nisini et al. (2001), revealed several
H2 jets inside the region. A more recent analysis (Beltrán et al. 2002,2004)
shows that BIMA 1 and BIMA 2 are associated with
north-south and east-west bipolar molecular outflows, respectively.
3 arcmin) CO bipolar
outflow (Sugitani et al. 1989) which has been mapped by Codella et al. (2001). The
study by Nisini et al. (2001), revealed several
H2 jets inside the region. A more recent analysis (Beltrán et al. 2002,2004)
shows that BIMA 1 and BIMA 2 are associated with
north-south and east-west bipolar molecular outflows, respectively.
A.3.2 Analysis
The continuum maps used for the IC1396 N BIMA 2 analysis are presented in
Fig. A.8. The SCUBA maps were obtained in March 2002
as a part of the project m02au07. The brightness profiles (see
Fig. A.9) are derived excluding the regions
contaminated by the presence of BIMA 1 and BIMA 3 (dashed regions in
Fig. A.8). The Spitzer observations were obtained in
October 2004 as part of the programme ``Star Formation in Bright Rimmed
Clouds'' (AOR: 202, PI: Giovanni Fazio). The integrated fluxes used
for the analysis are reported in Table 2 and in
Fig. A.9. The integrated fluxes at 450 ![]() m and 850
m and 850 ![]() m
were obtained by integration over a
m
were obtained by integration over a ![]() 35
35
![]() .
We varied the
integration radius from 20
.
We varied the
integration radius from 20
![]() to 90
to 90
![]() ,
and found variations on the
fluxes
,
and found variations on the
fluxes
![]() 30%. The large uncertainty in the integrated flux
at 24
30%. The large uncertainty in the integrated flux
at 24 ![]() m is due to the proximity of BIMA 3 (see 24
m is due to the proximity of BIMA 3 (see 24 ![]() m map in
Fig. A.8). Note that due to the large IRAS beams at 60
m map in
Fig. A.8). Note that due to the large IRAS beams at 60 ![]() m
and 100
m
and 100 ![]() m, BIMA 3 introduces significant spurious signal.
We thus used the IRAS and 70
m, BIMA 3 introduces significant spurious signal.
We thus used the IRAS and 70 ![]() m Spitzer fluxes as upper
limits on the SED (Fig A.9).
m Spitzer fluxes as upper
limits on the SED (Fig A.9).
![\begin{figure}
\par\includegraphics[width=6.2cm,angle=270]{13499f27.eps}\include...
...ncludegraphics[width=6.2cm,angle=270]{13499f30.eps}
\vspace*{4.5mm}
\end{figure}](/articles/aa/full_html/2010/08/aa13499-09/Timg145.png)
|
Figure A.8:
Continuum emission maps around IC1396 N BIMA 2 at 24 |
| Open with DEXTER | |
A.3.3 Best-fit
![\begin{figure}
\par\includegraphics[width=5cm,angle=90]{13499f31.eps}\includegra...
...cs[width=5cm,angle=90]{13499f33.eps}\hspace*{3.5cm}}\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/08/aa13499-09/Timg146.png)
|
Figure A.9:
Observed brightness profiles at 450 |
| Open with DEXTER | |
| Figure A.10:
IC1396 N BIMA 2 dust temperature ( left panel) and H2 density
( right panel) profiles from the best-fit model. The dashed line
represents the difference between the dust temperature and the gas
temperature derived using X(H2O)
|
|
| Open with DEXTER | |
Finally, contrary to the previous sources, the gas temperature profile
obtained for IC1396 N BIMA 2 is slightly decoupled from the dust
temperature in the inner region (see Fig. A.10). The origin
of this thermal decoupling is discussed in detail in Crimier et al. (2009).
Briefly, the decoupling is due to a competition between the water
abundance (the main coolant of the gas in the inner region) and the
dust
density, which mainly regulates the balance energy in the inner part
of the envelope. This thermal decoupling is stronger in IC1396 N
BIMA 2 (and NGC7129 FIRS 2) than in the other sources because
of the lower
density in the inner region. The thermal decoupling reaches
a maximum value of about 40 K (![]() 15% of
15% of
![]() )
for an
abundance of X(H2O)
)
for an
abundance of X(H2O)
![]() and about 10 K for
an abundance of X(H2O)
and about 10 K for
an abundance of X(H2O)
![]() .
.
A.4 NGC7129 FIRS 2
A.4.1 Source background
NGC7129 is a reflection nebula located in a complex and active
molecular cloud (Hartigan & Lada 1985; Miranda et al. 1993) and
estimated to be at a distance of
![]() pc (Shevchenko & Yakubov 1989) from the Sun. The region contains several Herbig AeBe stars, which
illuminate the nebula. NGC7129 FIRS 2 has been detected in the
far-infrared by Bechis et al. (1978) and Harvey et al. (1984). FIRS 2
is not detected at optical or near-infrared wavelengths. Its position
coincides with a 13CO column density peak (Bechis et al. 1978) and
a high-density NH3 cloudlet (Guesten & Marcaide 1986). It
is also close to an H2O maser (Rodriguez et al. 1980). NGC7129 FIRS 2
has been classified as an IM Class 0 source by Eiroa et al. (1998), who
carried out a multi-wavelength study of the continuum emission from 25
pc (Shevchenko & Yakubov 1989) from the Sun. The region contains several Herbig AeBe stars, which
illuminate the nebula. NGC7129 FIRS 2 has been detected in the
far-infrared by Bechis et al. (1978) and Harvey et al. (1984). FIRS 2
is not detected at optical or near-infrared wavelengths. Its position
coincides with a 13CO column density peak (Bechis et al. 1978) and
a high-density NH3 cloudlet (Guesten & Marcaide 1986). It
is also close to an H2O maser (Rodriguez et al. 1980). NGC7129 FIRS 2
has been classified as an IM Class 0 source by Eiroa et al. (1998), who
carried out a multi-wavelength study of the continuum emission from 25 ![]() m
to 2000
m
to 2000 ![]() m. These authors estimate a total mass and bolometric luminosity
of
m. These authors estimate a total mass and bolometric luminosity
of ![]() 6
6
![]() and
and ![]() 430
430
![]() ,
respectively. In addition, Edwards & Snell (1983) detected a
bipolar CO outflow associated with FIRS 2. The interferometric study
of Fuente et al. (2001) has confirmed this bipolar
outflow and pointed out a quadrapolar morphology to the flow. This
quadrapolar morphology seems to be due to the superposition of two
flows, FIRS 2-out 1 and FIRS 2-out 2, likely associated with FIRS 2
and a more evolved star (FIRS 2-IR), respectively. Finally, Fuente et al. (2005a,b)
carried out an extensive chemical study of FIRS 2 providing the
first detection of a hot core in an IM Class 0. Based on all these
studies, FIRS 2 is considered the youngest IM object known at
present.
,
respectively. In addition, Edwards & Snell (1983) detected a
bipolar CO outflow associated with FIRS 2. The interferometric study
of Fuente et al. (2001) has confirmed this bipolar
outflow and pointed out a quadrapolar morphology to the flow. This
quadrapolar morphology seems to be due to the superposition of two
flows, FIRS 2-out 1 and FIRS 2-out 2, likely associated with FIRS 2
and a more evolved star (FIRS 2-IR), respectively. Finally, Fuente et al. (2005a,b)
carried out an extensive chemical study of FIRS 2 providing the
first detection of a hot core in an IM Class 0. Based on all these
studies, FIRS 2 is considered the youngest IM object known at
present.
A.4.2 Analysis
All the data and continuum maps used for the NGC7129 FIRS 2 analysis
are reported in Table 2 and Fig. A.11. The maps at 450 ![]() m and 850
m and 850 ![]() m were obtained on the
1998 August 26 as a part of the project M98BU24. We also used the
flux profile and the integrated flux at 1300
m were obtained on the
1998 August 26 as a part of the project M98BU24. We also used the
flux profile and the integrated flux at 1300 ![]() m extracted from the
single dish map at 1300
m extracted from the
single dish map at 1300 ![]() m, presented in Fuente et al. (2001).
Following Greve et al. (1998), the beam at 1300
m, presented in Fuente et al. (2001).
Following Greve et al. (1998), the beam at 1300 ![]() m
is assumed to be a combination
of three Gaussian curves, with HPBWs of 11
m
is assumed to be a combination
of three Gaussian curves, with HPBWs of 11
![]() ,
125
,
125
![]() ,
and 180
,
and 180
![]() ,
with amplitude ratios of 0.975, 0.005, and 0.001, respectively.
The Spitzer observations were obtained on the 2003 September 19 as
part of
the programme ``Protostars and Proto-Brown Dwarfs in a Nearby Dark
Cloud'' (AOR: 34, PI: Tom Megeath).
The integrated fluxes reported in Table 2 and in
Fig. A.12 were obtained by integration over a
,
with amplitude ratios of 0.975, 0.005, and 0.001, respectively.
The Spitzer observations were obtained on the 2003 September 19 as
part of
the programme ``Protostars and Proto-Brown Dwarfs in a Nearby Dark
Cloud'' (AOR: 34, PI: Tom Megeath).
The integrated fluxes reported in Table 2 and in
Fig. A.12 were obtained by integration over a ![]() 40
40
![]() radius. The IRAS integrated fluxes at 60
radius. The IRAS integrated fluxes at 60 ![]() m and 100
m and 100 ![]() m were taken
from Eiroa et al. (1998).
m were taken
from Eiroa et al. (1998).
![\begin{figure}
\par\includegraphics[width=6cm,angle=270]{13499f36.eps}\includegr...
...includegraphics[width=6cm,angle=270]{13499f40.eps}\hspace*{3.3cm}}\end{figure}](/articles/aa/full_html/2010/08/aa13499-09/Timg151.png)
|
Figure A.11:
Continuum emission maps around NGC7129 FIRS 2 at 24 |
| Open with DEXTER | |
A.4.3 Best-fit
![\begin{figure}
\par\includegraphics[width=4.8cm,angle=90]{13499f41.eps}\includeg...
...]{13499f43.eps}\includegraphics[width=4.8cm,angle=90]{13499f44.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa13499-09/Timg152.png)
|
Figure A.12:
Observed brightness profiles at 450 |
| Open with DEXTER | |
| Figure A.13:
NGC7129 FIRS 2 dust temperature ( left panel) and H2 density
( right panel) profiles from the best-fit model. The dashed line
represents the difference between the dust and gas temperature
derived using X(H2O)
|
|
| Open with DEXTER | |
Finally, similarly to IC1396 N BIMA 2, the gas temperature profile obtained in NGC7129 FIRS 2 is slightly decoupled from the dust temperature in the inner part (see Fig. A.13).
A.5 Serpens FIRS 1
A.5.1 Source background
Since its recognition as a very active star forming region (Strom et al. 1974),
the Serpens molecular cloud has been the target of many
observational studies. Several studies have been dedicated to evaluate
the distance of this cloud from the Sun, yielding a range of
distances from ![]() 210
to 440 pc. Following the review by Eiroa et al. (2008),
which reports and compares the distance results from all the different
studies, we adopt a distance of
210
to 440 pc. Following the review by Eiroa et al. (2008),
which reports and compares the distance results from all the different
studies, we adopt a distance of ![]()
![]() pc. Serpens is a
young protocluster whose members are in many different evolutionary
stages. About 100 embedded YSO, protostars, and prestellar clumps
(Eiroa & Casali 1992; Strom et al. 1976; Hurt & Barsony 1996; Giovannetti et al. 1998; Testi & Sargent 1998; Kaas 1999; Casali et al. 1993),
as well as molecular outflows (Williams & Myers 2000; Wolf-Chase et al. 1998; White et al. 1995)
and H2 emission (e.g. Eiroa et al. 1997; Hodapp 1999; Herbst et al. 1997)
have been detected in this region.
pc. Serpens is a
young protocluster whose members are in many different evolutionary
stages. About 100 embedded YSO, protostars, and prestellar clumps
(Eiroa & Casali 1992; Strom et al. 1976; Hurt & Barsony 1996; Giovannetti et al. 1998; Testi & Sargent 1998; Kaas 1999; Casali et al. 1993),
as well as molecular outflows (Williams & Myers 2000; Wolf-Chase et al. 1998; White et al. 1995)
and H2 emission (e.g. Eiroa et al. 1997; Hodapp 1999; Herbst et al. 1997)
have been detected in this region.
Serpens FIRS 1 is located near the centre of the
Serpens main core and is the most luminous object embedded in the
cloud. Several continuum studies classify it as Class 0 source
with a bolometric luminosity estimated to range from 46
![]() to
84
to
84
![]() (Larsson et al. 2000; Hurt & Barsony 1996; Harvey et al. 1984; Casali et al. 1993).
The latest estimation of its luminosity suggests
that Serpens FIRS 1 is on the low/intermediate mass protostar
border. The envelope physical structure of Serpens FIRS 1 has been
modelled by Hogerheijde et al. (1999) using millimetre interferometric observations of the continuum and molecular line observations.
The Serpens FIRS 1 SED was first modelled by means of a
spherical envelope 1D radiative transfer code by Larsson et al. (2000).
Subsequently, Larsson et al. (2002) used a 2D radiative
transfer code and a torus model to reproduce the SED and line
observations from ISO. FIRS1 drives a molecular outflow, which is
orientated at a position angle of 50 degrees, coincident with a triple radio
source with symmetric lobes (Rodriguez et al. 1989).
(Larsson et al. 2000; Hurt & Barsony 1996; Harvey et al. 1984; Casali et al. 1993).
The latest estimation of its luminosity suggests
that Serpens FIRS 1 is on the low/intermediate mass protostar
border. The envelope physical structure of Serpens FIRS 1 has been
modelled by Hogerheijde et al. (1999) using millimetre interferometric observations of the continuum and molecular line observations.
The Serpens FIRS 1 SED was first modelled by means of a
spherical envelope 1D radiative transfer code by Larsson et al. (2000).
Subsequently, Larsson et al. (2002) used a 2D radiative
transfer code and a torus model to reproduce the SED and line
observations from ISO. FIRS1 drives a molecular outflow, which is
orientated at a position angle of 50 degrees, coincident with a triple radio
source with symmetric lobes (Rodriguez et al. 1989).
A.5.2 Analysis
The continuum maps used for the Serpens FIRS 1 analysis are presented
in Fig. A.14. The SCUBA maps were obtained in January 1998
as a part of the project m97bc30. The flux profiles (see
Fig. A.15) are derived excluding the dashed regions in
Fig. A.14 to avoid the non-spherical extended emission. The
Spitzer observations were obtained in October 2004 as part of the
programme ``From Molecular Cores to Planets, continued'' (AOR: 174, PI:
Neal Evans). The integrated fluxes used for the analysis are reported
in Table 2 and in Fig. A.15. The
integrated fluxes from 70 ![]() m to 850
m to 850 ![]() m were obtained by integration
over a
m were obtained by integration
over a ![]() 40
40
![]() .
We also report on the SED the lower limits from
Plateau de Bure (PdB) interferometric fluxes at 1.3 mm and 3 mm
(Fuente et al. 2007).
.
We also report on the SED the lower limits from
Plateau de Bure (PdB) interferometric fluxes at 1.3 mm and 3 mm
(Fuente et al. 2007).
![\begin{figure}
\par\includegraphics[width=6.5cm,angle=270]{13499f47.eps}\include...
...{13499f49.eps}\includegraphics[width=6.5cm,angle=270]{13499f50.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa13499-09/Timg156.png)
|
Figure A.14:
Continuum emission maps around Serpens FIRS 1 at 24 |
| Open with DEXTER | |
A.5.3 Best-fit
![\begin{figure}
\par\includegraphics[width=5cm,angle=90]{13499f51.eps}\includegra...
...\includegraphics[width=5cm,angle=90]{13499f53.eps}\hspace*{3.8cm}}\end{figure}](/articles/aa/full_html/2010/08/aa13499-09/Timg157.png)
|
Figure A.15:
Observed brightness profiles at 450 |
| Open with DEXTER | |
![\begin{figure}
\par\vspace{2mm}
\includegraphics[width=5.4cm,angle=90]{13499f54....
...includegraphics[width=5.4cm,angle=90]{13499f55.eps}
\vspace*{4.5mm}
\end{figure}](/articles/aa/full_html/2010/08/aa13499-09/Timg158.png)
|
Figure A.16:
Serpens FIRS 1 dust temperature ( left panel) and H2 density ( right panel) profiles from the best-fit model. The
dashed line represents the difference between the dust temperature
and the gas temperature derived using X(H2O)
|
| Open with DEXTER | |
Table 4 presents the set of parameters ![]() ,
Y, and
,
Y, and
![]() ,
which best reproduce the observations, and
summarises some relevant physical quantities of the model. Figure A.15 shows the relevant derived brightness profiles and SED
against the observations. The dust density and temperature profiles
of the best-fit model are reported in Fig. A.16. The model
well reproduces the observed flux profiles and SED fluxes from 70
,
which best reproduce the observations, and
summarises some relevant physical quantities of the model. Figure A.15 shows the relevant derived brightness profiles and SED
against the observations. The dust density and temperature profiles
of the best-fit model are reported in Fig. A.16. The model
well reproduces the observed flux profiles and SED fluxes from 70 ![]() m to
850
m to
850 ![]() m and agrees well with the lower limits from Plateau
de Bure interferometric fluxes at 1.3 mm and 3 mm (Fuente et al. 2007).
In minimising the
m and agrees well with the lower limits from Plateau
de Bure interferometric fluxes at 1.3 mm and 3 mm (Fuente et al. 2007).
In minimising the
![]() ,
we also varied the source
luminosity from 20
,
we also varied the source
luminosity from 20 ![]() to 60
to 60 ![]() and found the best-fit for a source luminosity equal to 33
and found the best-fit for a source luminosity equal to 33 ![]() .
Note that the estimated value of
the bolometric luminosity is much lower than the values derived in
previous studies toward this source (Larsson et al. 2000; Hurt & Barsony 1996; Harvey et al. 1984; Casali et al. 1993).
This is due to the adopted smaller distance to the source. Considering the
.
Note that the estimated value of
the bolometric luminosity is much lower than the values derived in
previous studies toward this source (Larsson et al. 2000; Hurt & Barsony 1996; Harvey et al. 1984; Casali et al. 1993).
This is due to the adopted smaller distance to the source. Considering the
![]() contour at 10% of the minimum
contour at 10% of the minimum
![]() to estimate the uncertainty, we obtained
to estimate the uncertainty, we obtained
![]() AU.
AU.
Hogerheijde et al. (1999) studied the envelope physical structure of Serpens FIRS 1 using interferometric continuum observations at OVRO![]() at
at
![]() mm and single-dish line observations from JCMT and CSO
mm and single-dish line observations from JCMT and CSO![]() . They adopted a bolometric luminosity of 77
. They adopted a bolometric luminosity of 77 ![]() and fixed the outer radius of the envelope
and fixed the outer radius of the envelope
![]() AU for a distance of 400 pc. Hogerheijde et al. (1999) derived an envelope with density profile index
AU for a distance of 400 pc. Hogerheijde et al. (1999) derived an envelope with density profile index
![]() in good agreement with our results. By scaling their results to the
same distance adopted here (230 pc) their adopted luminosity,
in good agreement with our results. By scaling their results to the
same distance adopted here (230 pc) their adopted luminosity, ![]() 25
25 ![]() ,
and the envelope radius
,
and the envelope radius
![]() ,
,
![]() 4600 AU, are relatively consistant with our results (Table 4):
4600 AU, are relatively consistant with our results (Table 4):
![]() ,
,
![]() AU. Also their derived gas temperature profile slightly differs from ours: for example they obtained
AU. Also their derived gas temperature profile slightly differs from ours: for example they obtained
![]() K at 200 AU while we obtained
K at 200 AU while we obtained
![]() K. Larsson et al. (2000) studied the SED of Serpens FIRS 1, derived from the ISO LWS maps and photometric data between
K. Larsson et al. (2000) studied the SED of Serpens FIRS 1, derived from the ISO LWS maps and photometric data between ![]() 1 and 105
1 and 105 ![]() m retrieved from the literature. These authors used i) a
single temperature/optically thin approximation; and ii) a radiative
transfer model to analyse the SED. In their models they adopted a
distance of 310 pc, a source diameter of 7
m retrieved from the literature. These authors used i) a
single temperature/optically thin approximation; and ii) a radiative
transfer model to analyse the SED. In their models they adopted a
distance of 310 pc, a source diameter of 7
![]() and a power law density
profile index,
and a power law density
profile index,
![]() .
They succeeded in reproducing the SED between
40
.
They succeeded in reproducing the SED between
40 ![]() m and 3 mm. By scaling their results to the same distance adopted here
(230 pc), they obtain a luminosity of
m and 3 mm. By scaling their results to the same distance adopted here
(230 pc), they obtain a luminosity of ![]() 40
40 ![]() ,
against our estimate of 33
,
against our estimate of 33 ![]() ,
and an envelope mass of 1.1-3.3
,
and an envelope mass of 1.1-3.3 ![]() ,
against our estimate of 5
,
against our estimate of 5 ![]() .
However, as noticed by the authors themselves, their mass estimate is
rather a lower limit, given the optically thin approximation they used.
.
However, as noticed by the authors themselves, their mass estimate is
rather a lower limit, given the optically thin approximation they used.
Finally, the observed flux at 24 ![]() m is underestimated by about two
orders of magnitude. This phenomenon is also observed in the Larsson et al. (2000,2002) studies. We discuss the situation at 24
m is underestimated by about two
orders of magnitude. This phenomenon is also observed in the Larsson et al. (2000,2002) studies. We discuss the situation at 24 ![]() m in more detail in the the following section, Sect. 4.
m in more detail in the the following section, Sect. 4.
References
- Alonso-Albi et al. 2010, A&A, accepted, 2 [Google Scholar]
- Andre, P., Ward-Thompson, D., & Barsony, M. 1993, ApJ, 406, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Andre, P., Ward-Thompson, D., & Barsony, M. 2000, Protostars and Planets IV, 59 [Google Scholar]
- Ayala, S., Noriega-Crespo, A., Garnavich, P. M., et al. 2000, AJ, 120, 909 [NASA ADS] [CrossRef] [Google Scholar]
- Bechis, K. P., Harvey, P. M., Campbell, M. F., & Hoffmann, W. F. 1978, ApJ, 226, 439 [NASA ADS] [CrossRef] [Google Scholar]
- Beltrán, M. T., Girart, J. M., Estalella, R., Ho, P. T. P., & Palau, A. 2002, ApJ, 573, 246 [NASA ADS] [CrossRef] [Google Scholar]
- Beltrán, M. T., Girart, J. M., Estalella, R., & Ho, P. T. P. 2004, A&A, 426, 941 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beuther, H., Churchwell, E. B., McKee, C. F., & Tan, J. C. 2007, in Protostars and Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil, 165 [Google Scholar]
- Boogert, A. C. A., Pontoppidan, K. M., Lahuis, F., et al. 2004, ApJS, 154, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Bottinelli, S. 2006, Ph.D. Thesis, University of Hawai'i at Manoa [Google Scholar]
- Casali, M. M., Eiroa, C., & Duncan, W. D. 1993, A&A, 275, 195 [NASA ADS] [Google Scholar]
- Caux, E., Ceccarelli, C., Castets, A., et al. 1999, A&A, 347, L1 [NASA ADS] [Google Scholar]
- Ceccarelli, C., Caselli, P., Herbst, E., Tielens, A. G. G. M., & Caux, E. 2007, in Protostars and Planets V, ed. B. Reipurth, & D. Jewitt, & K. Keil, 47 [Google Scholar]
- Ceccarelli, C., Hollenbach, D. J., & Tielens, A. G. G. M. 1996, ApJ, 471, 400 [Google Scholar]
- Ceccarelli, C., Maret, S., Tielens, A. G. G. M., Castets, A., & Caux, E. 2003, A&A, 410, 587 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cesaroni, R., Felli, M., & Walmsley, C. M. 1999, A&AS, 136, 333 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chandler, C. J., Barsony, M., & Moore, T. J. T. 1998, MNRAS, 299, 789 [NASA ADS] [CrossRef] [Google Scholar]
- Chini, R., Ward-Thompson, D., Kirk, J. M., et al. 2001, A&A, 369, 155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Codella, C., & Bachiller, R. 1999, A&A, 350, 659 [NASA ADS] [Google Scholar]
- Codella, C., Bachiller, R., Nisini, B., Saraceno, P., & Testi, L. 2001, A&A, 376, 271 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crimier, N., Ceccarelli, C., Lefloch, B., & Faure, A. 2009, A&A, 506, 1229 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crimier, N., Ceccarelli, C., Maret, S., et al. 2010, A&A, accepted [Google Scholar]
- de Gregorio-Monsalvo, I., Gómez, J. F., Suárez, O., et al. 2006, AJ, 132, 2584 [NASA ADS] [CrossRef] [Google Scholar]
- Di Francesco, J., Evans, II, N. J., Harvey, P. M., et al. 1997, ApJ, 482, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Doty, S. D., & Neufeld, D. A. 1997, ApJ, 489, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Li, A. 2001, ApJ, 551, 807 [NASA ADS] [CrossRef] [Google Scholar]
- Eiroa, C., & Casali, M. M. 1992, A&A, 262, 468 [NASA ADS] [Google Scholar]
- Eiroa, C., Palacios, J., Eisloffel, J., Casali, M. M., & Curiel, S. 1997, in Herbig-Haro Flows and the Birth of Stars, ed. B. Reipurth & C. Bertout, IAU Symp., 182, 103 [Google Scholar]
- Eiroa, C., Palacios, J., & Casali, M. M. 1998, A&A, 335, 243 [NASA ADS] [Google Scholar]
- Eiroa, C., Djupvik, A. A., & Casali, M. M. 2008, The Serpens Molecular Cloud, ed. B. Reipurth, 693 [Google Scholar]
- Eislöffel, J., Smith, M. D., Davis, C. J., & Ray, T. P. 1996, AJ, 112, 2086 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, II, N. J., Rawlings, J. M. C., Shirley, Y. L., & Mundy, L. G. 2001, ApJ, 557, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Faure, A., & Josselin, E. 2008, A&A, 492, 257 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Faure, A., Crimier, N., Ceccarelli, C., et al. 2007, A&A, 472, 1029 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Felli, M., Palagi, F., & Tofani, G. 1992, A&A, 255, 293 [NASA ADS] [Google Scholar]
- Flower, D. R., Pineau Des Forêts, G., & Walmsley, C. M. 2006, A&A, 449, 621 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frerking, M. A., Langer, W. D., & Wilson, R. W. 1982, ApJ, 262, 590 [NASA ADS] [CrossRef] [Google Scholar]
- Froebrich, D., Smith, M. D., Hodapp, K.-W., & Eislöffel, J. 2003, MNRAS, 346, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Fuente, A., Neri, R., Martín-Pintado, J., et al. 2001, A&A, 366, 873 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fuente, A., Neri, R., & Caselli, P. 2005a, A&A, 444, 481 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fuente, A., Rizzo, J. R., Caselli, P., Bachiller, R., & Henkel, C. 2005b, A&A, 433, 535 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fuente, A., Ceccarelli, C., Neri, R., et al. 2007, A&A, 468, L37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fukui, Y., Iwata, T., Mizuno, A., Ogawa, H., & Takaba, H. 1989, Nature, 342, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Giovannetti, P., Caux, E., Nadeau, D., & Monin, J.-L. 1998, A&A, 330, 990 [NASA ADS] [Google Scholar]
- Gomez, M., Hartmann, L., Kenyon, S. J., & Hewett, R. 1993, AJ, 105, 1927 [NASA ADS] [CrossRef] [Google Scholar]
- Gondhalekar, P. M., & Wilson, R. 1975, A&A, 38, 329 [NASA ADS] [Google Scholar]
- Greve, A., Kramer, C., & Wild, W. 1998, A&AS, 133, 271 [Google Scholar]
- Guesten, R., & Marcaide, J. M. 1986, A&A, 164, 342 [NASA ADS] [Google Scholar]
- Habing, H. J. 1968, BAIN, 19, 421 [Google Scholar]
- Hartigan, P., & Lada, C. J. 1985, ApJS, 59, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Harvey, P. M., Wilking, B. A., & Joy, M. 1984, ApJ, 278, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Hatchell, J., & van der Tak, F. F. S. 2003, A&A, 409, 589 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hennebelle, P., & Fromang, S. 2008, A&A, 477, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Herbst, T. M., Beckwith, S. V. W., & Robberto, M. 1997, ApJ, 486, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Hillenbrand, L. A., & Hartmann, L. W. 1998, ApJ, 492, 540 [NASA ADS] [CrossRef] [Google Scholar]
- Hodapp, K. W. 1999, AJ, 118, 1338 [NASA ADS] [CrossRef] [Google Scholar]
- Hogerheijde, M. R., van Dishoeck, E. F., Salverda, J. M., & Blake, G. A. 1999, ApJ, 513, 350 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Huard, T. L., Weintraub, D. A., & Sandell, G. 2000, A&A, 362, 635 [NASA ADS] [Google Scholar]
- Hurt, R. L., & Barsony, M. 1996, ApJ, 460, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Ivezic, Z., & Elitzur, M. 1997, MNRAS, 287, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Jørgensen, J. K., Schöier, F. L., & van Dishoeck, E. F. 2002, A&A, 389, 908 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jørgensen, J. K., Lahuis, F., Schöier, F. L., et al. 2005, ApJ, 631, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Jørgensen, J. K., Bourke, T. L., Myers, P. C., et al. 2007, ApJ, 659, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Kaas, A. A. 1999, AJ, 118, 558 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., McKee, C. F., & Klein, R. I. 2005, ApJ, 618, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Ladd, E. F., & Hodapp, K.-W. 1997, ApJ, 474, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Larsson, B., Liseau, R., Men'shchikov, A. B., et al. 2000, A&A, 363, 253 [NASA ADS] [Google Scholar]
- Larsson, B., Liseau, R., & Men'shchikov, A. B. 2002, A&A, 386, 1055 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Launhardt, R., & Henning, T. 1997, A&A, 326, 329 [NASA ADS] [Google Scholar]
- Launhardt, R., Evans, II, N. J., Wang, Y., et al. 1998, ApJS, 119, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Lefloch, B., Eisloeffel, J., & Lazareff, B. 1996, A&A, 313, L17 [NASA ADS] [Google Scholar]
- Li, Z., & Shu, F. H. 1996, ApJ, 472, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Lizano, S., & Shu, F. H. 1989, ApJ, 342, 834 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mannings, V., & Sargent, A. I. 1997, ApJ, 490, 792 [NASA ADS] [CrossRef] [Google Scholar]
- Mannings, V., & Sargent, A. I. 2000, ApJ, 529, 391 [NASA ADS] [CrossRef] [Google Scholar]
- Matthews, H. I. 1979, A&A, 75, 345 [NASA ADS] [Google Scholar]
- McKee, C. F., & Tan, J. C. 2003, ApJ, 585, 850 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- McLaughlin, D. E., & Pudritz, R. E. 1996, ApJ, 469, 194 [NASA ADS] [CrossRef] [Google Scholar]
- McLaughlin, D. E., & Pudritz, R. E. 1997, ApJ, 476, 750 [NASA ADS] [CrossRef] [Google Scholar]
- Miranda, L. F., Eiroa, C., & Gomez de Castro, A. I. 1993, A&A, 271, 564 [NASA ADS] [Google Scholar]
- Moro-Martín, A., Noriega-Crespo, A., Molinari, S., et al. 2001, ApJ, 555, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Motte, F., & André, P. 2001, A&A, 365, 440 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mueller, K. E., Shirley, Y. L., Evans, II, N. J., & Jacobson, H. R. 2002, ApJS, 143, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Neri, R., Fuente, A., Ceccarelli, C., et al. 2007, A&A, 468, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nisini, B., Massi, F., Vitali, F., et al. 2001, A&A, 376, 553 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noriega-Crespo, A., & Garnavich, P. M. 2001, AJ, 122, 3317 [NASA ADS] [CrossRef] [Google Scholar]
- Noriega-Crespo, A., Moro-Martin, A., Carey, S., et al. 2005, in ESA SP 577, ed. A. Wilson, 453 [Google Scholar]
- Osorio, M., Lizano, S., & D'Alessio, P. 1999, ApJ, 525, 808 [NASA ADS] [CrossRef] [Google Scholar]
- Osterbrock, D. E. 1957, ApJ, 125, 622 [NASA ADS] [CrossRef] [Google Scholar]
- Ossenkopf, V., & Henning, T. 1994, A&A, 291, 943 [NASA ADS] [Google Scholar]
- Palla, F., Cesaroni, R., Brand, J., et al. 1993, A&A, 280, 599 [NASA ADS] [Google Scholar]
- Parise, B., Ceccarelli, C., & Maret, S. 2005, A&A, 441, 171 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Patel, N. A., Greenhill, L. J., Herrnstein, J., et al. 2000, ApJ, 538, 268 [NASA ADS] [CrossRef] [Google Scholar]
- Rodriguez, L. F., Moran, J. M., Ho, P. T. P., & Gottlieb, E. W. 1980, ApJ, 235, 845 [NASA ADS] [CrossRef] [Google Scholar]
- Rodriguez, L. F., Curiel, S., Moran, J. M., et al. 1989, ApJ, 346, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Sandell, G., & Weintraub, D. A. 2001, ApJS, 134, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Saraceno, P., Ceccarelli, C., Clegg, P., et al. 1996, A&A, 315, L293 [NASA ADS] [Google Scholar]
- Schöier, F. L., Jørgensen, J. K., van Dishoeck, E. F., & Blake, G. A. 2002, A&A, 390, 1001 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schreyer, K., Henning, T., van der Tak, F. F. S., Boonman, A. M. S., & van Dishoeck, E. F. 2002, A&A, 394, 561 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sellgren, K., Werner, M. W., & Dinerstein, H. L. 1983, ApJ, 271, L13 [CrossRef] [Google Scholar]
- Serabyn, E., Guesten, R., & Mundy, L. 1993, ApJ, 404, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Shevchenko, V. S., & Yakubov, S. D. 1989, SvA, 33, 370 [Google Scholar]
- Shirley, Y. L., Evans, II, N. J., & Rawlings, J. M. C. 2002, ApJ, 575, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, F. H. 1977, ApJ, 214, 488 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, F. H., & Adams, F. C. 1987, in Circumstellar Matter, ed. I. Appenzeller, & C. Jordan, IAU Symp., 122, 7 [Google Scholar]
- Smith, M. D., Froebrich, D., & Eislöffel, J. 2003, ApJ, 592, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Stahler, S. W., Palla, F., & Salpeter, E. E. 1986, ApJ, 302, 590 [NASA ADS] [CrossRef] [Google Scholar]
- Strom, S. E., Grasdalen, G. L., & Strom, K. M. 1974, ApJ, 191, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Strom, S. E., Vrba, F. J., & Strom, K. M. 1976, AJ, 81, 638 [NASA ADS] [CrossRef] [Google Scholar]
- Sugitani, K., Fukui, Y., Mizuni, A., & Ohashi, N. 1989, ApJ, 342, L87 [NASA ADS] [CrossRef] [Google Scholar]
- Sugitani, K., Matsuo, H., Nakano, M., Tamura, M., & Ogura, K. 2000, AJ, 119, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Testi, L., & Sargent, A. I. 1998, ApJ, 508, L91 [NASA ADS] [CrossRef] [Google Scholar]
- Testi, L., Palla, F., & Natta, A. 1999, A&A, 342, 515 [NASA ADS] [Google Scholar]
- Tofani, G., Felli, M., Taylor, G. B., & Hunter, T. R. 1995, A&AS, 112, 299 [NASA ADS] [Google Scholar]
- Troscompt, N., Faure, A., Wiesenfeld, L., Ceccarelli, C., & Valiron, P. 2009, A&A, 493, 687 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van der Tak, F. F. S., van Dishoeck, E. F., Evans, II, N. J., Bakker, E. J., & Blake, G. A. 1999, ApJ, 522, 991 [NASA ADS] [CrossRef] [Google Scholar]
- Van der Tak, F. F. S., van Dishoeck, E. F., Evans, II, N. J., & Blake, G. A. 2000, ApJ, 537, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Vastel, C., Caux, E., Ceccarelli, C., et al. 2000, A&A, 357, 994 [NASA ADS] [Google Scholar]
- Visser, A. E., Richer, J. S., & Chandler, C. J. 2002, AJ, 124, 2756 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Y., Evans, II, N. J., Zhou, S., & Clemens, D. P. 1995, ApJ, 454, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Weikard, H., Wouterloot, J. G. A., Castets, A., Winnewisser, G., & Sugitani, K. 1996, A&A, 309, 581 [NASA ADS] [Google Scholar]
- White, G. J., Casali, M. M., & Eiroa, C. 1995, A&A, 298, 594 [NASA ADS] [Google Scholar]
- Wilking, B., Mundy, L., McMullin, J., Hezel, T., & Keene, J. 1993, AJ, 106, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, J. P., & Myers, P. C. 2000, ApJ, 537, 891 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, S. J., Fuller, G. A., & Sridharan, T. K. 2005, A&A, 434, 257 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wolf-Chase, G. A., Barsony, M., Wootten, H. A., et al. 1998, ApJ, 501, L193 [NASA ADS] [CrossRef] [Google Scholar]
- Young, C. H., Shirley, Y. L., Evans, II, N. J., & Rawlings, J. M. C. 2003, ApJS, 145, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Yun, J. L., & Clemens, D. P. 1994, AJ, 108, 612 [NASA ADS] [CrossRef] [Google Scholar]
- Yun, J. L., & Clemens, D. P. 1995, AJ, 109, 742 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ... Archive
![[*]](/icons/foot_motif.png)
- http://www.jach.hawaii.edu/JCMT/archive/
- ... archive
![[*]](/icons/foot_motif.png)
- http://ssc.spitzer.caltech.edu/archanaly/
- ... v2.0
![[*]](/icons/foot_motif.png)
- http://irsa.ipac.caltech.edu/cgi-bin/Gator/nph-dd?catalog=iraspsc
- ... Archive
![[*]](/icons/foot_motif.png)
- http://iso.esac.esa.int/ida/
- ... OVRO
![[*]](/icons/foot_motif.png)
- Owens Valley Radio Observatory.
- ... CSO
![[*]](/icons/foot_motif.png)
- Caltech Submillimetre Observatory.
All Tables
Table 1: The coordinates, the distances and the bolometric luminosities of the sources of the sample.
Table 2: Continuum fluxes integrated over the envelope of each source and used in the SED analysis.
Table 3: Range of the input parameters to DUSTY covered in the present study.
Table 4: Summary of the dust radiative transfer analysis for the five IM protostars.
Table 5:
The brightest water lines predicted by the our model
considering X(H2O)
![]() and X(H2O)
and X(H2O)
![]() compared with the ISO LWS observations. The upper limits refer to 3
compared with the ISO LWS observations. The upper limits refer to 3![]() .
All fluxes are in 10-12 erg s-1 cm-2 units.
.
All fluxes are in 10-12 erg s-1 cm-2 units.
Table 6: Linear correlation coefficients and probability for a chance correlation between the pair of parameters plotted in Figs. 1 and 2.
All Figures
![\begin{figure}
\par\includegraphics[width=15cm,angle=0]{13499f01.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa13499-09/Timg113.png)
|
Figure 1:
Plot of physical quantities within the envelopes surrounding low-,
intermediate, and high-mass protostars as a function of their
bolometric luminosity. Each symbol represents a different group of
sources as follows: crosses: Jørgensen et al. (2002); filled
squares: Shirley et al. (2002); stars:
this study and Crimier et al. (2010,2009);
diamonds: Williams et al. (2005); filled diamonds: Van der Tak et al. (2000); triangles: Hatchell & van der Tak (2003); filled
triangles: Mueller et al. (2002).
Symbols with arrows represent upper/lower limits. The solid line
represents the linear fit of the points obtained when the correlation
is significant (Table 6). The dashed line and the dotted line on panel f) represent the angular resolution of the SCUBA maps at 850 and 450 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.8cm,angle=90,clip]{13499f02.ps}
\vspace*{7mm}
\end{figure}](/articles/aa/full_html/2010/08/aa13499-09/Timg125.png)
|
Figure 2: Plot of the density at 10 K as function of the bolometric luminosity of a sample of low- and intermediate mass protostars. Data are from Jørgensen et al. (2002), (crosses), and the present study, (stars). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=4.5cm,angle=90]{13499f03.eps}\in...
...\includegraphics[width=4.5cm,angle=90]{13499f07.eps}\hspace*{3cm}}\end{figure}](/articles/aa/full_html/2010/08/aa13499-09/Timg130.png)
|
Figure 3:
Cep E-mm physical structure, brightness profiles, and SED from the best-fit model (black solid lines) and
after adding an 1800 AU radius cavity to the best-fit model (red dashed-dotted lines). The dust temperature and H2 density profiles are reported in the upper left panel and upper right panel, respectively. The observed
brightness profiles at 450 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6cm,angle=270]{13499f08.eps}\includegr...
...0]{13499f10.eps}\includegraphics[width=6cm,angle=270]{13499f11.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa13499-09/Timg135.png)
|
Figure A.1:
Continuum emission maps around CB3-mm at 24 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=5cm,angle=90]{13499f12.eps}\incl...
...m}\includegraphics[width=5cm,angle=90]{13499f14.eps}\hspace*{3cm}}\end{figure}](/articles/aa/full_html/2010/08/aa13499-09/Timg136.png)
|
Figure A.2:
Observed brightness profiles at 450 |
| Open with DEXTER | |
| In the text | |
| |
Figure A.3:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=5.5cm,angle=90]{13499f16.eps}\includegraphics[width=5.5cm,angle=90]{13499f17.eps}
\vspace*{3mm}
\end{figure}](/articles/aa/full_html/2010/08/aa13499-09/Timg141.png)
|
Figure A.4:
CB3-mm dust temperature ( left panel) and H2 density ( right panel) profiles from the best-fit model. The dashed line
represents the difference between the dust and gas temperature
derived using X(H2O)
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6cm,angle=270]{13499f18.eps}\includegr...
...s}\includegraphics[width=6cm,angle=270]{13499f21.eps}
\vspace*{3mm}
\end{figure}](/articles/aa/full_html/2010/08/aa13499-09/Timg142.png)
|
Figure A.5:
Continuum emission maps around Cep E-mm at 24 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=5cm,angle=90]{13499f22.eps}\includegra...
...\includegraphics[width=5cm,angle=90]{13499f24.eps}\hspace*{3.5cm}}\end{figure}](/articles/aa/full_html/2010/08/aa13499-09/Timg143.png)
|
Figure A.6:
Observed brightness profiles at 450 |
| Open with DEXTER | |
| In the text | |
| |
Figure A.7:
Cep E-mm dust temperature ( left panel) and H2 density ( right panel) profiles from the best-fit model. The dashed line represents the difference between the dust and gas temperature
derived using X(H2O)
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.2cm,angle=270]{13499f27.eps}\include...
...ncludegraphics[width=6.2cm,angle=270]{13499f30.eps}
\vspace*{4.5mm}
\end{figure}](/articles/aa/full_html/2010/08/aa13499-09/Timg145.png)
|
Figure A.8:
Continuum emission maps around IC1396 N BIMA 2 at 24 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=5cm,angle=90]{13499f31.eps}\includegra...
...cs[width=5cm,angle=90]{13499f33.eps}\hspace*{3.5cm}}\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/08/aa13499-09/Timg146.png)
|
Figure A.9:
Observed brightness profiles at 450 |
| Open with DEXTER | |
| In the text | |
| |
Figure A.10:
IC1396 N BIMA 2 dust temperature ( left panel) and H2 density
( right panel) profiles from the best-fit model. The dashed line
represents the difference between the dust temperature and the gas
temperature derived using X(H2O)
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6cm,angle=270]{13499f36.eps}\includegr...
...includegraphics[width=6cm,angle=270]{13499f40.eps}\hspace*{3.3cm}}\end{figure}](/articles/aa/full_html/2010/08/aa13499-09/Timg151.png)
|
Figure A.11:
Continuum emission maps around NGC7129 FIRS 2 at 24 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=4.8cm,angle=90]{13499f41.eps}\includeg...
...]{13499f43.eps}\includegraphics[width=4.8cm,angle=90]{13499f44.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa13499-09/Timg152.png)
|
Figure A.12:
Observed brightness profiles at 450 |
| Open with DEXTER | |
| In the text | |
| |
Figure A.13:
NGC7129 FIRS 2 dust temperature ( left panel) and H2 density
( right panel) profiles from the best-fit model. The dashed line
represents the difference between the dust and gas temperature
derived using X(H2O)
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.5cm,angle=270]{13499f47.eps}\include...
...{13499f49.eps}\includegraphics[width=6.5cm,angle=270]{13499f50.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa13499-09/Timg156.png)
|
Figure A.14:
Continuum emission maps around Serpens FIRS 1 at 24 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=5cm,angle=90]{13499f51.eps}\includegra...
...\includegraphics[width=5cm,angle=90]{13499f53.eps}\hspace*{3.8cm}}\end{figure}](/articles/aa/full_html/2010/08/aa13499-09/Timg157.png)
|
Figure A.15:
Observed brightness profiles at 450 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\vspace{2mm}
\includegraphics[width=5.4cm,angle=90]{13499f54....
...includegraphics[width=5.4cm,angle=90]{13499f55.eps}
\vspace*{4.5mm}
\end{figure}](/articles/aa/full_html/2010/08/aa13499-09/Timg158.png)
|
Figure A.16:
Serpens FIRS 1 dust temperature ( left panel) and H2 density ( right panel) profiles from the best-fit model. The
dashed line represents the difference between the dust temperature
and the gas temperature derived using X(H2O)
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



