EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 516 (June-July 2010) A&A, 516 (2010) A16 Full HTML
Free Access
Issue
A&A
Volume 516, June-July 2010
Article Number A16
Number of page(s) 5
Section Astrophysical processes
DOI https://doi.org/10.1051/0004-6361/200913447
Published online 17 June 2010
A&A 516, A16 (2010)

Jet precession driven by neutrino-cooled disk for gamma-ray bursts

T. Liu1 - E.-W. Liang2 - W.-M. Gu3 - X.-H. Zhao4,5 - Z.-G. Dai1 - J.-F. Lu3

1 - Department of Astronomy, Nanjing University, Nanjing, Jiangsu 210093, PR China
2 - Department of Physics, Guangxi University, Nanning, Guangxi, 530004, PR China
3 - Department of Physics and Institute of Theoretical Physics and Astrophysics, Xiamen University, Xiamen, Fujian 361005, PR China
4 - National Astronomical Observatories/Yunnan Observatory, Chinese Academy of Sciences, Kunming, Yunnan, 650011, PR China
5 - Key Laboratory for the Structure and Evolution of Celestial Bodies, Chinese Academy of Sciences, Kunming, Yunnan, 650011, PR China

Received 10 Octobre 2009 / Accepted 12 March 2010

Abstract
Aims. A model of jet precession driven by a neutrino-cooled disk around a spinning black hole is presented to explain the temporal structure and spectral evolution of gamma-ray bursts (GRBs).
Methods. The differential rotation of the outer part of a neutrino-dominated accretion disk may result in precession of the inner part of the disk and the central black hole, hence driving a precessed jet via neutrino annihilation around the inner part of the disk.
Results. Both analytic and numeric results for our model are presented. Our calculations show that a black-hole, accretion-disk system with the black hole mass $M \simeq 3.66~M_\odot$, accretion rate $\dot{M} \simeq 0.54~ ~M_\odot ~\rm s^{-1}$, spin parameter a=0.9, and viscosity parameter $\alpha = 0.01$ may drive a precessed jet with period P=1 s and luminosity L=1051 erg s-1, corresponding to the scenario for long GRBs. A precessed jet with P=0.1 s and L=1050 erg s-1 may be powered by a system with $M \simeq 5.59 ~M_\odot$, $\dot{M} \simeq 0.74 ~M_\odot~ \rm s^{-1}$, a=0.1, and $\alpha = 0.01$, and is possibly responsible for the short GRBs. Both the temporal and spectral evolution in GRB pulse may be explained with our model.
Conclusions. GRB central engines most likely power a precessed jet driven by a neutrino-cooled disk. The global GRB lightcurves thus could be modulated by the jet precession during the accretion timescale of the GRB central engine. Both the temporal and spectral evolution in GRB pulse may stem from a viewing effect of the jet precession.

Key words: accretion: accretion disks - black hole physics - gamma ray burst: general

1 Introduction

Internal shock models have been extensively discussed for gamma-ray bursts (GRBs) (Rees & Mészáros 1992; Mészáros & Rees 1993; Zhang & Mészáros 2004), in which an individual shock episode of two collision shells gives rise to a pulse, and random superposition of pulses results in the observed complexity of GRB lightcurves (e.g., Daigne & Mochkovitch 1998; Kobayashi et al. 1999). The observed flux rapidly increases in the dynamic timescale of a two-shell collision, then decays due to the delayed photons from high latitudes with respect to the line of sight upon the abrupt cessation of emission after the shock crossing timescale, shaping the observed fast-rise-exponential-decay (FRED) pulses. However, some well-separated GRB pulses show symmetric structure, and their peak energy of the $\nu F_\nu$ spectrum ($E_{\rm p}$) traces the lightcurve behavior (Liang & Kargatis 1996; Liang & Nishimura 2004; Lu & Liang 2009; Peng et al. 2009). Both the temporal and spectral properties of these symmetric pulses are difficult to be explained with internal shocks. In addition, the observed $E_{\rm iso}-E_{\rm p}$ relation (Amati et al. 2002) or $L_{\rm iso}-E_{\rm p}$ relation (Wei & Gao 2003; Liang et al. 2004; Yonetoku et al. 2004) also challenge the internal shock models (e.g., Zhang & Mészáros 2002).

Quasi-periodic feature observed in some GRB lightcurves motivated ideas that the GRB jet may be precessed (Blackman et al. 1996; Fargion 1999; Portegies Zwart et al. 1999; Portegies Zwart & Totani 2001; Reynoso et al. 2006; Lei et al. 2007). It is generally believed that the progenitors of short and long GRBs are the mergers of two compact objects (Eichler et al. 1989; Paczynski 1991; Narayan et al. 1992; see recent review by Nakar 2007) and core collapsars of massive stars (Woosley 1993; Paczynski 1998; see reviews by Woosley & Bloom 2006), respectively. Although the progenitors of the two types of GRBs are different, the models for their central engines are similar, and essentially all can be simply classed as a rotating black hole with a rapidly hyper-accreting process of a debris torus surrounding the central black hole. Such a black hole-disk system drives an ultra-relativistic outflow to produce both the prompt gamma rays and afterglows in lower energy bands.

The most popular one is neutrino-dominated accretion flows (NDAFs), involving a black hole of $2\sim10 ~M_\odot$ and a hyper-critical rate in the range of $0.01 \sim 10 ~M_\odot ~{\rm s}^{-1}$ (Popham et al. 1999; Narayan et al. 2001; Kohri & Mineshige 2002; Di Matteo et al. 2002; Kohri et al. 2005, 2007; Lee et al. 2005; Gu et al. 2006; Chen & Beloborodov 2007; Liu et al. 2007, 2008, 2010; Kawanaka & Mineshige 2007; Janiuk et al. 2007). The different direction of angular momentum of two compact objects and the anisotropic fall-back mass in collapsar may conduct precession between black hole and disk. In this scenario, the inner part of the disk is driven by the black hole during the accretion process. The differential rotation between the inner and outer parts may result in precession of the inner part of the disk and the central black hole, hence drive a precessed jet produced by neutrino annihilation around the inner part of the disk, forming an S- or Z-shaped jet as observed in many extragalactic radio sources (see, e.g. Florido et al. 1990). A tilted accretion disk surrounding a black hole would also lead to the precession of the black hole and result in an S-shaped jet as observed in SS 433 (Sarazin et al. 1980; Lu 1990; Lu & Zhou 2005), although the angle between angular momentum of black hole and disk is small because of evolution of a two-compact-object system may decrease the angle between them in mergers or the anisotropic fall-back mass cannot produce a large angle between black hole and fall-back mass in collapsars.

In this paper, we propose a model of jet precession driven by a neutrino-cooled disk around a spinning black hole to explain the temporal structure and spectral evolution of GRBs. In our model, the global profile of a GRB lightcurve may be modulated by the jet procession. The temporal structure and spectral evolution may signal an on-axis/off-axis cycle of the light of sight (LOS) to a precessed jet axis, as proposed by some authors to explain the nature of low-luminosity GRBs 980425 and 031203 (Nakamura 1998; Eichler & Levinson 1999; Waxman 2004; Ramirez-Ruiz et al. 2005) or to present a unified model for GRBs and X-ray flashes (Yamazaki et al. 2003) and the observed spectral lag in long GRBs (Norris 2002; Salmonson & Galama 2002).

We present both analytic and numerical analyse of jet precession driven by a neutrino-cooled disk around a spinning black hole in Sects. 2 and 3. Simplifying the jet emission surface as a point source, we demonstrate the profile and evolution of a GRB pulse in Sect. 4. Conclusions and discussion are shown in Sect. 5.

\begin{figure} \par\includegraphics[width=8.5cm]{13447f1.eps} \end{figure} Figure 1:

Schematic picture of a precessing system.

Open with DEXTER

2 Model

An accretion disk is warped by its precession (Sarazin et al. 1980). We consider a spinning black hole surrounding a tilted accretion disk that its rotation axis is misaligned with that of the black hole, as shown in Fig. 1. Its angular momentum is $J_\ast = aG M^2 /c$, where M is the black hole mass, and a (0<a<1) is the dimensionless specific angular momentum. Since d $J = 2 \pi r^2 \Sigma v_\phi {\rm d}r$ for a ring at radius r in the disk with width dr, we get $J(r) = {\rm d}J/{\rm d}(\ln r) = 2 \pi r^3 \Sigma v_\phi$, where $\Sigma$ and $v_\phi$ are the disk surface density and rotational velocity. Due to the Lense-Thirring effect (Lense & Thirring 1918), the disk material inside a critical radius rp, which is defined as $J(r_p) = J_\ast$, will be aligned with the equatorial plane of the black hole. The outer portion of the disk ($r \ga r_p$) with sufficiently large angular momentum keeps its orientation. This makes the black hole precess along with the inner disk (Bardeen & Petterson 1975). A jet dominated by the ejections of neutrino annihilation around the inner part of the disk thus would be precessed (Popham et al. 1999; Liu et al. 2007). The precession rate $\Omega$ of the central black hole and the inner disk is given by $\Omega=2GJ(r)/c^2 r^3 $ (Sarazin et al. 1980). Regions with $r \ga r_p$ in the disk should contribute to the precession. The $\Omega$decreases as r increases, so one cannot expect a period behavior in an observed lightcurve from our model.

With the continuity equation

$\displaystyle \dot{M}=-2 \pi r \Sigma v_r,$   (1)

the precession period P then can be expressed as
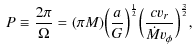
$\displaystyle \ P \equiv \frac{2 \pi} {\Omega} = (\pi M)\Big(\frac{a}{G}\Big )^{\frac{1}{2}} \Big(\frac{c v_r }{\dot{M}v_\phi} \Big )^{\frac{3}{2}},$   (2)

where $\dot{M}$ is the accretion rate and vr the radial inflow velocity of the disk material. Assuming that the angular velocity is approximately Keplerian, we have $v_\phi = r \Omega_{\rm K}$, and the vertical scale height of the flow can be written as $H=c_s / \Omega_{\rm K}$, where $\Omega_{\rm K}= (GM/r^3)^{1/2}$ is the Keplerian angular velocity and cs the sound speed. The vr can be estimated as $v_r \sim \alpha c_s (H / r)$ (Kato et al. 2008), where $\alpha $ is the constant viscosity parameter of the disk. Substituting the expressions of $v_\phi$ and vr into Eq. (3), we have
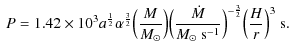
$\displaystyle \ P = 1.42 \times 10^{3} a^{\frac{1}{2}} \alpha^{\frac{3}{2}}\Big... ...t{M}}{M_\odot ~\rm s^{-1}}}\Big)^{-\frac{3}{2}} \Big(\frac{H}{r}\Big)^3~ \rm s.$   (3)

It is found that P is sensitive to $\alpha $, $\dot{M}$, and H/r. These parameters are time-dependent in the GRB phenomenon, so the precession period should evolve with time. Regions with $r \ga r_p$ in the disk should contribute to the precession, and the evolution of the hyper-accretion process would increase the mass and the angular momentum of black hole (Belczynski et al. 2008; Janiuk et al. 2008), leading to the evolution of the precession period. In addition, the nutation in the accretion system even complicates the observed profile. Therefore, one cannot expect clear period information in the GRB lightcurves. If the periods are shorter than the accretion timescale, the observed lightcurve may be composed of some pulses. Occasionally, the lightcurves may show a quasi-periodic feature, as observed in BATSE trigger 1425 (Portegies Zwart et al. 1999). If the periods are longer than the accretion timescale, the global lightcurve may be a broad pulse. This is different from for SS433 (Sarazin et al. 1983), in which it is assumed that the precession periods are shorter than the viscous timescale without rapidly evolving with time, so that the periodic lightcurve is a natural consequence in SS 433.

3 Numerical results

Equation (3) shows an explicit dependence of P on a, $\alpha $, $\dot{M}$, M, and H/r. However, the thickness of NDAF also depends on M, $\dot{M}$, a, and $\alpha $. Similar to P, the injected neutrino annihilation luminosity L is also a function of these parameters. To illustrate both the dependences of P and Lon these parameters, we present numerical calculation with the method by Riffert & Herold (1995). This method defines general relativistic correction factors to simulate the precession period related to the spin of a black hole. They are written as
                                      A = $\displaystyle 1-\frac{2GM}{c^2 r}+\Big(\frac{a G M}{c^2 r}\Big)^2,$ (4)
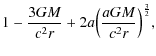
B = $\displaystyle 1- \frac{3GM}{c^2 r}+2a \Big(\frac{a G M}{c^2 r}\Big)^{\frac{3}{2}},$ (5)
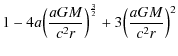
C = $\displaystyle 1- 4a \Big(\frac{a G M}{c^2 r}\Big)^{\frac{3}{2}}+3\Big(\frac{a G M}{c^2 r}\Big)^2$ (6)
D = $\displaystyle \int_{r_{ms}}^{r}\displaystyle \frac{\frac{x^2 c^4}{2G^2}-\frac{3... ...}- \frac{3xMc^2}{G}+2 (\frac{x a^2 M^3 c^2}{G})^{\frac{1}{2}}\right]} {\rm d}x,$ (7)

where rms is the inner boundary of the disk. The equation of conservation of mass remains valid, while hydrostatic equilibrium in the vertical direction leads to a corrected expression for the half thickness of the disk (Riffert & Herold 1995),
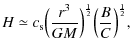
$\displaystyle H \simeq c_{\rm s}\Big(\frac{ r^3}{G M}\Big)^{\frac{1}{2}}\Big(\frac{B}{C}\Big)^{\frac{1}{2}},$   (8)

where $c_{\rm s}=(p/\rho)^{1/2}$, p and $\rho$ are the total pressure and density of the disk, respectively. The viscous shear $T_{r \phi}$ is also corrected as
$\displaystyle \ T_{r \phi} = - \alpha p\Big(\frac{A}{BC}\Big)^{\frac{1}{2}},$   (9)

and the angular momentum equation can be simplified as (Riffert & Herold 1995; Lei et al. 2009)
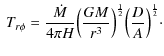
$\displaystyle \ T_{r \phi} = \frac{\dot{M}}{4\pi H}\Big(\frac{GM}{r^3}\Big)^{\frac{1}{2}} \Big(\frac{D}{A}\Big)^{\frac{1}{2}}\cdot$   (10)

The equation of state is
$\displaystyle \ p = p_{\rm gas} + p_{\rm rad} + p_{\rm e} + p_\nu,$   (11)

where $p_{\rm gas}$, $p_{\rm rad}$, $p_{\rm e}$, and $p_\nu$ are the gas pressure from nucleons, radiation pressure of photons, degeneracy pressure of electrons, and radiation pressure of neutrinos, respectively (see, e.g. Di Matteo et al. 2002; Liu et al. 2007). The energy equation is written as
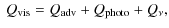
$\displaystyle \ Q_{\rm vis} = Q_{\rm adv} + Q_{\rm photo} + Q_\nu,$     (12)

where $Q_{\rm vis}$, $Q_{\rm adv}$, $Q_{\rm photo}$, and $Q_\nu$ are the viscous heating rate, the advective cooling rate, the cooling rate due to photodisintegration of $\alpha $-particles and the cooling due to the neutrino radiation, respectively (see, e.g. Di Matteo et al. 2002; Liu et al. 2007). The heating rate $Q_{\rm vis}$ is expressed as
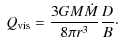
$\displaystyle \ Q_{\rm vis} =\frac{3GM \dot{M}}{8 \pi r^3} \frac{D}{B}\cdot$   (13)

The equation system consisting of Eqs. (1), (2), (4)-(13) is closed for an unknown precession period P. It can be numerically solved for a given parameter set of M, $\dot{M}$, a, and $\alpha $. We show P as a function of $\dot{M}$ for the parameter sets (a=0.9, $M = 3 ~M_\odot$, $\alpha = 0.01$), (a=0.9, $M = 3 ~M_\odot$, $\alpha=0.1$), (a=0.1, $M = 3 ~M_\odot$, $\alpha=0.1$), and (a=0.1, $M = 3 ~M_\odot$, $\alpha = 0.01$) in Fig. 2. It is found that P varies from tens of milliseconds to 10 ks, if $\dot{M}=0.01\sim 10$ $M_\odot$/s, $\alpha=0.01\sim 0.1$, and $a=0.1\sim 0.9$. It can approach the timescale of lightcurve or be longer than the accretion timescale that provides a couple of possibilities for the lightcurve. In collapsar scenario, the central black hole would be rapidly rotates, i.e., $a\gtrsim 0.9$. For the compact object mergers, the spin of the black hole is not strictly as high as in the collapsar scenario (e.g., van Putten et al. 2001). Assuming that the global GRB lightcurves are modulated by the jet precession during the accretion timescale of the GRB central engine, the profile of a pulse duration may be comparable to P. Statistical analysis shows that the typical durations of long and short GRB pulses are $\sim $1 and 0.1 s, respectively (Liang et al. 2002; Nakar & Piran 2002). From Fig. 2, we find that the case of ( $\alpha=0.1$, a=0.9) yields a P value much higher than 1 s in the range of $\dot{M}=0.01\sim 10 ~M_\odot$. For the case of ( $\alpha = 0.01$, a=0.9), we get $P=0.1\sim 1$ s for $\dot{M}=0.4\sim 10 ~M_\odot$. This is consistent with the observed pulse durations for long GRBs. To explain the duration of short GRB pulses, our model requires lower a and $\alpha $, as well as higher $\dot{M}$ than for the long GRBs, indicating that the short-duration GRBs may be powered by a more violent accretion process than the long ones.

\begin{figure} \par\includegraphics[width=7cm,clip]{13447f2.eps} \end{figure} Figure 2:

Illustration of numerical results for P as a function of $\dot{M}$ using different parameter sets as marked in the plot.

Open with DEXTER

\begin{figure} \par\includegraphics[width=7cm,clip]{13447f3.eps} \end{figure} Figure 3:

$\dot{M}$ as a function of M for different parameter sets as marked in the plot. The viscosity parameter is adopted as $\alpha = 0.01$. The two interaction points A nd B indicate estimates of Mand $\dot{M}$ for a given set of (P, L, a, $\alpha $).

Open with DEXTER

The observed luminosity of prompt gamma rays may also place constraints on our model parameters. We assume that the observed gamma-ray luminosity is comparable to the injected neutrino annihilation luminosity L. Similar to $P=P(M, \dot{M}, a, \alpha)$, L is a function of M, $\dot{M}$, a, and $\alpha $, written as $L=L(M, \dot{M}, a, \alpha)$. It can be calculated following the approach of Ruffert et al. (1997), Popham et al. (1999), Rosswog et al. (2003), and Liu et al. (2007). Since the calculation of L (or P) as a function of these parameters is very time-consuming, we calculated only for typical L values and present our results with $\dot{M}$ as a function of M, a, $\alpha $ for a given L (or P). We take L=1051 erg s-1for long GRBs and L=1050 erg s-1 for short GRBs. Based on our analysis above, we also calculated $\dot{M}$ as a function of M for P=1 s and P=0.1 s for the parameter set (L, a, $\alpha $) = (1051 erg s-1, 0.9, 0.01) and (L, a, $\alpha $) = (1050 erg s-1, 0.1, 0.01). We show $\dot{M}$ as a function of M for different parameter sets in Fig. 3. It is found that for a given luminosity, $\dot{M}$ as a function of Mgreatly depends on the rotation of the black hole (see the dotted lines in Fig. 3). The accretion rate $\dot{M}$ does not significantly increase with M for a=0.1.

\begin{figure} \par\includegraphics[width=8cm,clip]{13447f4a.eps}\hspace*{2mm} \includegraphics[width=8.7cm,clip]{13447f4b.eps} \end{figure} Figure 4:

Predicted flux F (the solid line) and Ep (the dashed line) with our model for a symmetric pulse (panel a) and a FRED pulse (panel b) with comparisons to the observations (insets).

Open with DEXTER
However, it rapidly increases with M for a=0.9. The behavior of the function $\dot{M}(M)$ varies for different P (see the solid lines in Fig. 3). As shown in Fig. 3, $\dot{M}$ slightly increases with M if P=1 s; however, it even decreases with M for P=0.1 s. This conflicts with what is shown in the explicit form of P (see Eq. (3)). The reason is that the thickness of NDAF depends on M, $\dot{M}$, a, and $\alpha $ (see Fig. 9 in Liu et al. 2007). One cannot expect an explicit dependence between $\dot{M}$ and Mfor any given P. The intersections between the lines are estimates of M and $\dot{M}$ for a given set of (P, L, a, $\alpha $). We find that $M \simeq 3.66~M_\odot$ and $\dot{M} \simeq 0.54~ M_\odot~ \rm s^{-1}$ for P=1 s, L=1051 erg s-1, and a=0.9, corresponding to the scenario for long GRBs. For P=0.1s, L=1050 erg s-1, and a=0.1, we get $M \simeq 5.59 ~M_\odot$ and $\dot{M} \simeq 0.74 ~M_\odot~ \rm s^{-1}$, corresponding to the scenario for short GRBs. These solutions are generally consistent with the requirements of GRB productions in simulations for collapsars (e.g. MacFadyen & Woosley 1999) and for binary coalescence of a neutron star and a black hole or two neutron stars (e.g. Kluzniak & Lee 1998).

4 Temporal profile and spectral evolution of a GRB pulse from a precessing jet

As discussed above, in the framework of our model one cannot expect period information from the observed lightcurves since the precession period is time-dependent. Since the period is a function of some time-dependent parameters, as mentioned above, the temporal profile and spectral evolution of pulses in GRB lightcurves may be direct information about jet precession since the jet precession may conduct an on-axis/off-axis cycle during a precession period for a given observer.

As discussed in Sect. 1, the $E_{\rm p}$-tracing-flux spectral evolution feature is observed in some GRB pulses (e.g. Liang et al. 1996; Peng et al. 2009; Lu & Liang 2009). The profiles of these pulses are generally FRED, and are occasionally symmetrical. These temporal and spectral features can be explained with our model. We just illustrate the lightcurve and the spectral evolution for a point source with arbitrary radiation intensity in the axis with an arbitrary precession period with ultra-relativistic velocity in the jet axis. As shown by Granot et al. (2002), by assuming the emitting region as a point source in the jet axis, the calculation can give reasonable results without any assumption on the jet structure. Therefore, we adopt the point source assumption in our calculations. We just illustrate the lightcurve and the spectral evolution for a point source with arbitrary radiation intensity in the axis with an arbitrary precession period for an observer (on-axis and off-axis) at the rest frame in Sect. 4. If the emitting region is a shell of the jet with a given opening angle, the peak of the pulse would be flattened for a uniformed jet. Our calculation is followed by the one in Granot et al. (2002).

The observed flux F and $E_{\rm p}$ would be amplified by the Doppler effect, $F= F_0(1-\beta)^3/(1-\beta \rm cos \Psi) ^3$, $E_{\rm p}= E_{p0}(1-\beta)/(1-\beta \rm cos \Psi) $. The observed timescale would be $t= t_0 (1-\beta \rm cos \Psi)/(1-\beta)$, where the subscript 0 means the ``on-axis'' quantities, $\Psi$ is the view angle between the jet axis and the LOS and $\beta= (\Gamma^2-1)^{1/2}/\Gamma$, and $\Gamma$ is the Lorentz factor. From Fig. 1, we have

$\displaystyle {\rm cos} \Psi = {\rm cos} \theta_{\rm jet} {\rm cos} \theta_{\rm... ...\rm jet} {\rm sin} \theta_{\rm obs}{\rm cos} (\phi_{\rm jet} - \phi_{\rm obs}),$   (14)

where $\phi_{\rm jet} = \phi_{\rm jet, 0} +2 \pi t_1/P$ (t1 is the time in the rest frame of the central engine) and z-axis in Fig. 1 is the direction of angular momentum of the outer part. We assume $\Gamma=300$ in our calculations. We computed the observed flux and peak energy of the $\nu F_\nu$ spectrum in a precession period corresponding to an observed pulse. Figure 4 demonstrates the initial ``off-axis'' and initial ``on-axis'' lightcurves and corresponding $E_{\rm p}$ evolutions for a point source with arbitrary flux intensity and spectral hardness in the jet with arbitrary precession period P. The adopted parameters are $\theta_{\rm obs}=1^\circ$, $\phi_{\rm obs} = 90^\circ$, $\theta_{\rm jet} = 4^\circ$, and $\phi_{\rm jet, 0} = 0^\circ$ for initial ``off-axis'' observer and $\theta_{\rm obs}=1^\circ$, $\phi_{\rm obs} = 90^\circ$, $\theta_{\rm jet} = 2^\circ$, and $\phi_{\rm jet, 0} = 0^\circ$ for initial ``on-axis'' observers. Two samples of the observations are also shown in Fig. 4 for comparison. It is found that our model can reproduce both FRED and symmetric pulses with $E_{\rm p}$-tracing-flux behavior, depending on the initial on-axis of off-axis observations.

5 Conclusions

We have suggested that the differential rotation of the outer part of a neutrino-dominated accretion disk may result in precession of the central black hole and the inner part of the disk, so may power a precessed jet via neutrino annihilation around the inner part of the disk. Both analytic and numeric results are present. Our calculations show that for a black hole-accretion disk system with $M \simeq 3.66~M_\odot$, $\dot{M} \simeq 0.54~ M_\odot~ \rm s^{-1}$, a=0.9 and $\alpha = 0.01$ may drives a precessed jet with P=1 s and L=1051 erg s-1, corresponding to the scenario for long GRBs. A precessed jet with P=0.1s and L=1050 erg s-1 may be powered by a system with $M \simeq 5.59 ~M_\odot$, $\dot{M} \simeq 0.74 ~M_\odot~ \rm s^{-1}$, a=0.1, and $\alpha = 0.01$, possibly being responsible for the short GRBs. These results are generally consistent with simulations for long and short GRB productions from collapsars and from mergers of compact stars. Both temporal and spectral features observed in GRB pulses may be explained with our model.

The correlation between $E_{\rm iso}$ (or $L_{\rm iso}$) and Epin the burst frame (Amati et al. 2002; Liang et al. 2004) are difficult to explain in the framework of internal shock scenarios. Our model suggests an Ep-tracing-flux behavior within a GRB pulse caused by the on-axis/off-axis effect for a given observer, similar to that proposed by Yamazaki et al. (2004). The $E_{\rm p}$-tracing-flux behavior would give rise to the observed correlations between $E_{\rm iso}$ ( $L_{\rm iso}$) and $E_{\rm p}$ in the burst frame.

Acknowledgements
We thank the anonymous referee for very useful comments. We also thank Bing Zhang, Shuang-Nan Zhang, Li-Xin Li, and Wei-Hua Lei for beneficial discussions. This work was supported by the China Postdoctoral Science Foundation funded project 20080441038 (T.L.), the National Natural Science Foundation of China under grants 10778711 (W.M.G.), 10833002 (J.F.L. and W.M.G.), 10873002 (E.W.L.), 10873009 (Z.G.D.), the National Basic Research Program (973 Program) of China under Grant 2009CB824800 (E.W.L., W.M.G., and J.F.L.). E.W.L. also acknowledges the support from Guangxi SHI-BAI-QIAN project (Grant 2007201), the Guangxi Science Foundation (2010GXNSFC013011), the program for 100 Young and Middle-aged Disciplinary Leaders in Guangxi Higher Education Institutions, and the research foundation of Guangxi University (M30520).

References

  1. Amati, L., Frontera, F., Tavani, M., et al. 2002, A&A, 390, 81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Bardeen, J. M., & Petterson, J. A. 1975, ApJ, 195, L65 [NASA ADS] [CrossRef] [Google Scholar]
  3. Belczynski, K., Taam, R. E., Rantsiou, E., & van der Sluys, M. 2008, ApJ, 682, 474 [NASA ADS] [CrossRef] [Google Scholar]
  4. Blackman, E. G., Yi, I., & Field, G. B. 1996, ApJ, 473, L79 [NASA ADS] [CrossRef] [Google Scholar]
  5. Chen, W.-X., & Beloborodov, A. M. 2007, ApJ, 657, 383 [NASA ADS] [CrossRef] [Google Scholar]
  6. Daigne, F., & Mochkovitch, R. 1998, MNRAS, 296, 275 [Google Scholar]
  7. Di Matteo, T., Perna, R., & Narayan, R. 2002, ApJ, 579, 706 [NASA ADS] [CrossRef] [Google Scholar]
  8. Eichler, D., & Levinson, A. 1999, ApJ, 521, L117 [NASA ADS] [CrossRef] [Google Scholar]
  9. Eichler, D., Livio, M., Piran, T., & Schramm, D. N. 1989, Nature, 340, 126 [NASA ADS] [CrossRef] [Google Scholar]
  10. Fargion, D. 1999, A&AS, 138, 507 [Google Scholar]
  11. Florido, E., Battaner, E., & Sanchez-Saavedra, M. L. 1990, Ap&SS, 164, 131 [NASA ADS] [CrossRef] [Google Scholar]
  12. Granot, J., Panaitescu, A., Kumar, P., & Woosley, S. E. 2002, ApJ, 570, 61 [Google Scholar]
  13. Gu, W.-M., Liu, T., & Lu, J.-F. 2006, ApJ, 643, L87 [NASA ADS] [CrossRef] [Google Scholar]
  14. Janiuk, A., Yuan, Y.-F., Perna, R., & Di Matteo, T. 2007, ApJ, 664, 1011 [NASA ADS] [CrossRef] [Google Scholar]
  15. Janiuk, A., Moderski, R., & Proga, D. 2008, ApJ, 687, 433 [NASA ADS] [CrossRef] [Google Scholar]
  16. Kato, S., Fukue, J., & Mineshige, S. 2008, Black-Hole Accretion Disks (Kyoto: Kyoto Univ. Press) [Google Scholar]
  17. Kawanaka, N., & Mineshige, S. 2007, ApJ, 662, 1156 [NASA ADS] [CrossRef] [Google Scholar]
  18. Kluzniak, W., & Lee, W. H. 1998, ApJ, 494, L53 [NASA ADS] [CrossRef] [Google Scholar]
  19. Kobayashi, S., Piran, T., & Sari, R. 1999, ApJ, 513, 669 [NASA ADS] [CrossRef] [Google Scholar]
  20. Kohri, K., & Mineshige, S. 2002, ApJ, 577, 311 [NASA ADS] [CrossRef] [Google Scholar]
  21. Kohri, K., Narayan, R., & Piran, T. 2005, ApJ, 629, 341 [NASA ADS] [CrossRef] [Google Scholar]
  22. Kohri, K., Ohsuga, K., & Narayan, R. 2007, MNRAS, 381, 1267 [NASA ADS] [CrossRef] [Google Scholar]
  23. Lee, W. H., Ramirez-Ruiz, E., & Page, D. 2005, ApJ, 632, 421 [NASA ADS] [CrossRef] [Google Scholar]
  24. Lei, W. H., Wang, D. X., Gong, B. P., & Huang, C. Y. 2007, A&A, 468, 563 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Lei, W. H., Wang, D. X., Zhang, L., et al. 2009, ApJ, 700, 1970 [NASA ADS] [CrossRef] [Google Scholar]
  26. Lense, J., & Thirring, H. 1918, Phys. Z., 19, 156 [Google Scholar]
  27. Liang, E., & Kargatis, V. 1996, Nature, 381, 49 [NASA ADS] [CrossRef] [Google Scholar]
  28. Liang, E., & Nishimura, K. 2004, Phys. Rev. Lett., 92, 175005 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  29. Liang, E.-W., Xie, G.-Z., & Su, C.-Y. 2002, PASJ, 54, 1 [NASA ADS] [Google Scholar]
  30. Liang, E.-W., Dai, Z.-G., & Wu, X.-F. 2004, ApJ, 606, L29 [NASA ADS] [CrossRef] [Google Scholar]
  31. Liu, T., Gu, W.-M., Xue, L., & Lu J.-F. 2007, ApJ, 661, 1025 [NASA ADS] [CrossRef] [Google Scholar]
  32. Liu, T., Gu, W.-M., Xue, L., Weng, S.-S., & Lu J.-F. 2008, ApJ, 676, 545 [NASA ADS] [CrossRef] [Google Scholar]
  33. Liu, T., Gu, W.-M., Dai, Z.-G., & Lu, J.-F. 2010, ApJ, 709, 851 [NASA ADS] [CrossRef] [Google Scholar]
  34. Lu J.-F. 1990, A&A, 229, L424 [NASA ADS] [Google Scholar]
  35. Lu J.-F., & Zhou, B.-Y. 2005, ApJ, 635, L17 [NASA ADS] [CrossRef] [Google Scholar]
  36. Lu, R.-J., & Liang, E.-W. 2009, Science in China, submitted [Google Scholar]
  37. MacFadyen, A. I., & Woosley,S. E. 1999, ApJ, 524, 262 [NASA ADS] [CrossRef] [Google Scholar]
  38. Mészáros, P., & Rees, M. J. 1993, ApJ, 405, 278 [Google Scholar]
  39. Nakamura, T. 1998, Prog. Theor. Phys., 100, 921 [NASA ADS] [CrossRef] [Google Scholar]
  40. Nakar, E. 2007, Phys. Rep., 442, 166 [NASA ADS] [CrossRef] [Google Scholar]
  41. Nakar, E., & Piran, T. 2002, MNRAS, 331, 40 [NASA ADS] [CrossRef] [Google Scholar]
  42. Narayan, R., Paczynski, B., & Piran, T. 1992, ApJ, 395, L83 [NASA ADS] [CrossRef] [Google Scholar]
  43. Narayan, R., Piran, T., & Kumar, P. 2001, ApJ, 557, 949 [NASA ADS] [CrossRef] [Google Scholar]
  44. Norris, J. P. 2002, ApJ, 579, 386 [NASA ADS] [CrossRef] [Google Scholar]
  45. Paczynski, B. 1991, , 41, 257 [Google Scholar]
  46. Paczynski, B. 1998, ApJ, 494, L45 [NASA ADS] [CrossRef] [Google Scholar]
  47. Peng, Z.-Y., Ma, L., Zhao, X.-H., et al. 2009, ApJ, 698, 417 [NASA ADS] [CrossRef] [Google Scholar]
  48. Popham, R., Woosley, S. E., & Fryer, C. 1999, ApJ, 518, 356 [NASA ADS] [CrossRef] [Google Scholar]
  49. Portegies Zwart, S. F., Lee, C. H., & Lee, H. K. 1999, ApJ, 529, 666 [NASA ADS] [CrossRef] [Google Scholar]
  50. Portegies Zwart, S. F., & Totani, T. 2001, ApJ, 328, 951 [NASA ADS] [Google Scholar]
  51. Ramirez-Ruiz, E., Granot, J., Kouveliotou, C., et al. 2005, ApJ, 625, L91 [NASA ADS] [CrossRef] [Google Scholar]
  52. Rees, M. J., & Mészáros, P. 1992, MNRAS, 258, 41 [NASA ADS] [CrossRef] [Google Scholar]
  53. Reynoso, M. M., Romero, G. E., & Sampayo, O. A. 2006, A&A, 454, 11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Riffert, H., & Herold, H. 1995, ApJ, 450, 508 [NASA ADS] [CrossRef] [Google Scholar]
  55. Rosswog, S., Ramirez-Ruiz, E., & Davies, M. B. 2003, MNRAS, 345, 1077 [NASA ADS] [CrossRef] [Google Scholar]
  56. Ruffert, M., Janka, H.-Th., Takahashi, K., & Schäfer, G. 1997, A&A, 319, 122 [NASA ADS] [Google Scholar]
  57. Salmonson, J. D., & Galama, T. J. 2002, ApJ, 569, 682 [NASA ADS] [CrossRef] [Google Scholar]
  58. Sarazin, C. L., Begelman, M. C., & Hatchett, S. P. 1980, ApJ, 238, L129 [NASA ADS] [CrossRef] [Google Scholar]
  59. van Putten, M. H. P. M., & Ostriker, E. C. 2001, ApJ, 552, L31 [NASA ADS] [CrossRef] [Google Scholar]
  60. Waxman, E. 2004, ApJ, 602, 886 [NASA ADS] [CrossRef] [Google Scholar]
  61. Wei, D. M., & Gao, W. H. 2003, MNRAS, 345, 743 [NASA ADS] [CrossRef] [Google Scholar]
  62. Woosley, S.E. 1993, ApJ, 405, 273 [NASA ADS] [CrossRef] [Google Scholar]
  63. Woosley, S. E., & Bloom, J. S. 2006, ARA&A, 44, 507 [NASA ADS] [CrossRef] [Google Scholar]
  64. Yamazaki, R., Yonetoku, D., & Nakamura, T. 2003, ApJ, 594, L79 [NASA ADS] [CrossRef] [Google Scholar]
  65. Yamazaki, R., Ioka, K., & Nakamura, T. 2004, ApJ, 606, L33 [NASA ADS] [CrossRef] [Google Scholar]
  66. Yonetoku, D., Murakami, T., Nakamura, T., et al. 2004, ApJ, 609, 935 [NASA ADS] [CrossRef] [Google Scholar]
  67. Zhang, B., & Mészáros, P. 2002, ApJ, 581, 1236 [NASA ADS] [CrossRef] [Google Scholar]
  68. Zhang, B.,& Mészáros, P. 2004, Int. J. Mod. Phys. A, 19, 2385 [NASA ADS] [CrossRef] [Google Scholar]

All Figures

  \begin{figure} \par\includegraphics[width=8.5cm]{13447f1.eps} \end{figure} Figure 1:

Schematic picture of a precessing system.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7cm,clip]{13447f2.eps} \end{figure} Figure 2:

Illustration of numerical results for P as a function of $\dot{M}$ using different parameter sets as marked in the plot.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7cm,clip]{13447f3.eps} \end{figure} Figure 3:

$\dot{M}$ as a function of M for different parameter sets as marked in the plot. The viscosity parameter is adopted as $\alpha = 0.01$. The two interaction points A nd B indicate estimates of Mand $\dot{M}$ for a given set of (P, L, a, $\alpha $).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13447f4a.eps}\hspace*{2mm} \includegraphics[width=8.7cm,clip]{13447f4b.eps} \end{figure} Figure 4:

Predicted flux F (the solid line) and Ep (the dashed line) with our model for a symmetric pulse (panel a) and a FRED pulse (panel b) with comparisons to the observations (insets).

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.