| Issue |
A&A
Volume 516, June-July 2010
|
|
|---|---|---|
| Article Number | A76 | |
| Number of page(s) | 11 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/200913201 | |
| Published online | 14 July 2010 | |
X-ray spectroscopy and photometry of the
long-period polar AI Trianguli with XMM-Newton![[*]](/icons/foot_motif.png)
I. Traulsen1 - K. Reinsch1 - R. Schwarz2 - S. Dreizler1 - K. Beuermann1 - A. D. Schwope2 - V. Burwitz3
1 - Institut für Astrophysik, Georg-August-Universität Göttingen,
Friedrich-Hund-Platz 1, 37077 Göttingen, Germany
2 - Astrophysikalisches Institut Potsdam, An der Sternwarte 16, 14482
Potsdam, Germany
3 - Max-Planck-Institut für extraterrestrische Physik, Postfach 1312,
85741 Garching, Germany
Received 28 August 2009 / Accepted 6 March 2010
Abstract
Context. The energy balance of cataclysmic variables
with strong magnetic fields is a central subject in understanding
accretion processes on magnetic white dwarfs. With XMM-Newton, we
perform a spectroscopic and photometric study of soft X-ray selected
polars during their high states of accretion.
Aims. On the basis of X-ray and optical observations
of the magnetic cataclysmic variable AI Tri, we derive the
properties of the spectral components, their flux contributions, and
the physical structure of the accretion region in soft polars.
Methods. We use multi-temperature approaches in our XSPEC
modeling of the X-ray spectra to describe the physical conditions and
the structures of the post-shock accretion flow and the accretion spot
on the white-dwarf surface. In addition, we investigate the accretion
geometry of the system by completing a timing analysis of the
photometric data.
Results. Flaring soft X-ray emission from the heated
surface of the white dwarf dominates the X-ray flux during roughly 70%
of the binary cycle. This component deviates from a single black body
and can be described by a superimposition of mildly absorbed black
bodies with a Gaussian temperature distribution between ![]() and
and ![]() ,
and
,
and ![]() .
In addition, weaker hard X-ray emission is visible nearly all the time.
The spectrum from the cooling post-shock accretion flow is most closely
fitted by a combination of thermal plasma MEKAL
models with temperature profiles adapted from prior stationary
two-fluid hydrodynamic calculations. The resulting plasma temperatures
lie between
.
In addition, weaker hard X-ray emission is visible nearly all the time.
The spectrum from the cooling post-shock accretion flow is most closely
fitted by a combination of thermal plasma MEKAL
models with temperature profiles adapted from prior stationary
two-fluid hydrodynamic calculations. The resulting plasma temperatures
lie between ![]() and
and ![]() ;
additional intrinsic, partial-covering absorption is on the order of
;
additional intrinsic, partial-covering absorption is on the order of ![]() .
The soft X-ray light curves show a dip during the bright phase, which
can be interpreted as self-absorption in the accretion stream.
Phase-resolved spectral modeling supports the picture of one-pole
accretion and self-eclipse. One of the optical light curves corresponds
to an irregular mode of accretion. During a short XMM-Newton
observation at the same epoch, the X-ray emission of the system is
clearly dominated by the soft component.
.
The soft X-ray light curves show a dip during the bright phase, which
can be interpreted as self-absorption in the accretion stream.
Phase-resolved spectral modeling supports the picture of one-pole
accretion and self-eclipse. One of the optical light curves corresponds
to an irregular mode of accretion. During a short XMM-Newton
observation at the same epoch, the X-ray emission of the system is
clearly dominated by the soft component.
Key words: novae, cataclysmic variables - stars: individual: AI Tri - X-rays: binaries - accretion, accretion disks
1 Introduction
AI Tri (RX J0203.8+2959) was first
described within a sample of ROSAT-discovered bright soft X-ray sources
by Beuermann & Thomas
(1993). Their classification of AI Tri as an
AM Her type binary (also called a polar) was later confirmed
in a multiwavelength study by Schwarz
et al. (1998), who identified cyclotron humps in
optical spectra obtained during a high state of accretion. The orbital
period of ![]() is one of the longest known among polars, whereas the magnetic field
strength of
is one of the longest known among polars, whereas the magnetic field
strength of ![]() and the amplitude of the long-term brightness variations between
and the amplitude of the long-term brightness variations between ![]() (Schwarz et al. 1998)
lie in the typical parameter range of this class. Based on the
wavelength dependence of the
(Schwarz et al. 1998)
lie in the typical parameter range of this class. Based on the
wavelength dependence of the ![]() light curve minima and the variations in both the linear and the
circular polarization, Katajainen
et al. (2001) suggest that the system has a high
inclination of
light curve minima and the variations in both the linear and the
circular polarization, Katajainen
et al. (2001) suggest that the system has a high
inclination of ![]() and accretes onto two almost equally fed magnetic poles. On the other
hand, Schwarz et al. (1998)
propose that a single dominating accretion region is active at the
epoch of their observations.
and accretes onto two almost equally fed magnetic poles. On the other
hand, Schwarz et al. (1998)
propose that a single dominating accretion region is active at the
epoch of their observations.
AI Tri belongs to a significantly large group of AM Her systems that were found to emit almost entirely at X-ray energies below 0.5 keV during the ROSAT all-sky survey (Beuermann & Thomas 1993; Beuermann et al. 1999; Thomas et al. 1998). Although these systems could play an important role in investigating the energy balance of polars, only a few of them have been studied using high-resolution X-ray spectroscopy (Ramsay et al. 2004; Ramsay & Cropper 2003). We, therefore, initiated dedicated observations with XMM-Newton to perform a detailed study of the spectral components, their flux contributions, and the physical structure of the accretion region of polars selected by their distinct soft X-ray fluxes during high-states of accretion. In the following, we present an analysis of the magnetic cataclysmic variable AI Tri based on new XMM-Newton and optical data, and archival ROSAT data.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13201fig1.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa13201-09/Timg15.png)
|
Figure 1: EPIC/pn X-ray intensity in both the source region (source plus background) and the source-free background region during the 20 ks XMM-Newton observation, binned into time intervals of 10 s. |
| Open with DEXTER | |
2 Observations and data reduction
2.1 X-ray observations
With XMM-Newton, we obtained a 20 ks (5.6 h) exposure during a high state of AI Tri on August 22, 2005 (observation ID 0306841001), which covers for the first time uninterruptedly more than one complete binary orbit. The EPIC instruments were operated in full frame mode with the thin filter. The UV light curve at an effective wavelength of 2310 Å was measured simultaneously using the optical monitor (OM) in fast mode with the UVM2 filter. RGS spectra were not used from this pointing, since the X-ray flux of the object was too low, and the net source count rate measured by the RGS instruments was consistent with zero for more than 80% of the exposure time.
Data were reduced using the XMM-Newton software analysis system SAS v8.0. Large parts of the exposure were affected by an enhanced background signal. We omitted two time intervals from the analysis (Fig. 1): a strong soft proton flare after 15 ks and the last 2 ks of the observation, when the satellite approaches the Van Allen radiation belt. During these intervals, a considerable spectral hardening at energies above 3 keV and spectral softening at energies below 1 keV were detected.
When extracting light curves, spectra, and images, single and
double events were processed in the case of EPIC/pn data, supplemented
by quadruple events in EPIC/MOS data. Phase-resolved spectra were
generated during the four phase intervals defined in Sect. 3. Source data
were collected from an aperture of 25 arcsec around the source
center, background data from a larger source free region close to the
source position. To diminish potential pile-up effects, we excluded the
innermost 5 arcsec of the source region when extracting the
mean EPIC/pn spectrum and the bright-phase spectra, where the peak
count rates (source plus background) reach ![]() for EPIC/pn and
for EPIC/pn and ![]() for EPIC/MOS, respectively. Appropriate spectral response matrices were
generated for the individual instruments and extraction regions
applying calibration files from the July 2008 release. Spectral bins
comprise a minimum of 20 cts (mean EPIC/pn spectrum:
30 cts). Photon arrival times were corrected to the barycenter
of the solar system via the BARYCEN task.
for EPIC/MOS, respectively. Appropriate spectral response matrices were
generated for the individual instruments and extraction regions
applying calibration files from the July 2008 release. Spectral bins
comprise a minimum of 20 cts (mean EPIC/pn spectrum:
30 cts). Photon arrival times were corrected to the barycenter
of the solar system via the BARYCEN task.
Table 1: Log of the ROSAT and XMM-Newton observations and of the optical photometry of AI Tri.
In the soft energy regime below 0.9 keV, where the
calibration is known to be least precise (Stuhlinger et al. 2008;
Mateos
et al. 2009), we use the isolated neutron star
AI Tri to calibrate the EPIC spectra.
RX J1856.4-3754 was established as a low-energy calibration
target for missions such as Chandra, Suzaku, Swift, and XMM-Newton![]() , and exhibits a high soft
X-ray and low optical flux. Its spectrum is free from prominent line
features and described well by two black bodies (Beuermann et al. 2006).
We compare archival XMM-Newton EPIC data of RX J1856.4-3754,
which span more than five years, with the model spectra of Beuermann et al. (2006)
and carefully adjust the instrumental effective areas. In this
approach, we assume that the energy redistribution is independent of
the incident energy when considering only objects with very soft X-ray
spectra. The discrepancies between data and model remain mostly below
5%, with larger excesses up to 20% for EPIC/MOS2.
, and exhibits a high soft
X-ray and low optical flux. Its spectrum is free from prominent line
features and described well by two black bodies (Beuermann et al. 2006).
We compare archival XMM-Newton EPIC data of RX J1856.4-3754,
which span more than five years, with the model spectra of Beuermann et al. (2006)
and carefully adjust the instrumental effective areas. In this
approach, we assume that the energy redistribution is independent of
the incident energy when considering only objects with very soft X-ray
spectra. The discrepancies between data and model remain mostly below
5%, with larger excesses up to 20% for EPIC/MOS2.
A first XMM-Newton observation of AI Tri on August
15, 2005 in the same configuration as described above resulted in
partially corrupted data (observation ID 0306840901) due to technical
problems. During 1.1 to 5 ks (0.3 to 1.4 h), EPIC,
RGS (1st order), and OM data are usable. We apply the same data
reduction steps as applied to the data acquired on August 22, 2005.
With peak count rates of ![]() collected by EPIC/pn and
collected by EPIC/pn and ![]() by the RGS detectors, the source flux was considerably higher than one
week later. Therefore, we extended the EPIC/pn aperture to
30 arcsec, excising the innermost 7 arcsec. The EPIC
spectra were rebinned to at least 20 counts per bin.
by the RGS detectors, the source flux was considerably higher than one
week later. Therefore, we extended the EPIC/pn aperture to
30 arcsec, excising the innermost 7 arcsec. The EPIC
spectra were rebinned to at least 20 counts per bin.
In addition, we used unpublished ROSAT archival data obtained between January 15 and February 5, 1998 with the HRI detector. The total integration time of 35 ks (9.6 h) consisted of nine observation intervals. The individual light curves were extracted with standard tasks of the EXSAS/M IDAS (Zimmermann et al. 1993) software packages, corrected to the barycenter, and combined to a common light curve profile.
2.2 Optical data
At the Göttingen 50 cm, the Potsdam 70 cm, the M ONET/North
(Texas) 1.2 m, and the Tübingen 80 cm telescopes, we
carried out optical V-band and white-light
photometry during ten nights between August 2005 and March 2007.
AI Tri was found in high or intermediate high states at
estimated brightnesses between ![]() and
and ![]() .
For data reduction and differential photometry, we used TRIPP
(Schuh et al. 2003)
and ESO-M IDAS routines. Light curves were
determined using differential aperture photometry. Apparent magnitudes
of the system were calculated against the V-band
magnitudes of the comparison stars USNO-B1.0 1199-0026710 (
.
For data reduction and differential photometry, we used TRIPP
(Schuh et al. 2003)
and ESO-M IDAS routines. Light curves were
determined using differential aperture photometry. Apparent magnitudes
of the system were calculated against the V-band
magnitudes of the comparison stars USNO-B1.0 1199-0026710 (
![]() )
and USNO-B1.0 1199-0026672 (
)
and USNO-B1.0 1199-0026672 (
![]() )
determined by Schwarz (1996).
Fluxes are given relative to their orbital mean, and flux errors were
derived by means of photon statistics. The times were converted to
terrestrial time and corrected to the barycenter on the basis of the
JPL ephemeris (Standish 1998). An
overview of all the data obtained is given in Table 1.
)
determined by Schwarz (1996).
Fluxes are given relative to their orbital mean, and flux errors were
derived by means of photon statistics. The times were converted to
terrestrial time and corrected to the barycenter on the basis of the
JPL ephemeris (Standish 1998). An
overview of all the data obtained is given in Table 1.
3 Optical, UV, and X-ray light curves
3.1 Optical photometry
The optical V-band light curves of AI Tri (e.g. Fig. 2f) during high and intermediate high states of accretion are largely similar to the data presented by Katajainen et al. (2001) and Schwarz et al. (1998). The orbital modulation deviates from a sinusoidal shape and is slightly asymmetric showing a steeper rise and smoother decline. An irregular pattern of narrow small dips is superimposed on the light curves, one dip recurring at photometric phase zero, which has not been seen in earlier data.
The orbital period of AI Tri has not been known
accurately enough to extrapolate the photometric ephemeris given by Schwarz et al. (1998)
to the epochs of our observations. Schwarz
et al. (1998) established photometric phase zero at
the broad minima of the optical high-state light curves, the only
recurrent feature that could be identified in the vast majority of the
light curves. Using timings of six new V-band
minima mapped between August 2005 and March 2007 in addition to the
data published by Schwarz
et al. (1998), we updated their photometric
ephemeris. We determined the minima by performing Gaussian fits to the
light curves, excluding the dips (Table 2). By means of
a least-squares method, the inverse square sum of observed minus
calculated minimum times ![]() was minimized for narrowly spaced trial periods within a
was minimized for narrowly spaced trial periods within a ![]() range of the Schwarz
et al. (1998) value. We derived the improved V-band
ephemeris
range of the Schwarz
et al. (1998) value. We derived the improved V-band
ephemeris
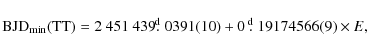
which we use throughout this paper.
In addition, Schwarz
et al. (1998) determined an orbital ephemeris of the
system from long-slit spectroscopy. They defined ![]() at the blue-to-red zero crossing of the radial velocities, which
corresponds to
at the blue-to-red zero crossing of the radial velocities, which
corresponds to ![]() ,
and identified it with the inferior conjunction of the secondary. A
constant relation between photometric and orbital phase can be assumed,
if the system rotates synchronously, as most polars do. Schwarz et al. (1998)
derived a degree of synchronism better than
,
and identified it with the inferior conjunction of the secondary. A
constant relation between photometric and orbital phase can be assumed,
if the system rotates synchronously, as most polars do. Schwarz et al. (1998)
derived a degree of synchronism better than ![]() for AI Tri. We show the orbital phasing as
for AI Tri. We show the orbital phasing as ![]() at the top of Fig. 2,
since it can provide geometrical information about the system
(Sect. 6).
at the top of Fig. 2,
since it can provide geometrical information about the system
(Sect. 6).
Table 2: Barycentric timings of the V-band minima of AI Tri.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13201fig2.eps} \vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/08/aa13201-09/Timg35.png)
|
Figure 2:
X-ray, ultraviolet, and optical light curves of AI Tri folded
over photometric phase. Orbital phase as |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13201fig3.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa13201-09/Timg36.png)
|
Figure 3: Multi-wave-band light curves obtained with XMM-Newton on Aug. 15 (a)-c)) and with the Potsdam 70 cm telescope on Aug. 17, 2005 (d)). The X-ray data are binned into 10 s intervals, the ultraviolet into 30 s, and the hardness ratios into 100 s, respectively. Grey lines indicate the phases of high and low soft X-ray flux in the 20 ks exposure. |
| Open with DEXTER | |
3.2 XMM-Newton light curves
The observation with the optical monitor and the UVM2 filter at an
effective wavelength of 2310 Å presents the first mid
ultraviolet light curve of AI Tri (Fig. 2e). It exhibits
a roughly similar shape but larger amplitude than the optical light
curves, an almost sinusoidal variation, and an additional dip in the
light curve minimum near ![]() .
This dip is shifted by about
.
This dip is shifted by about ![]() in phase relative to the dip within the optical minimum. The UV maximum
at
in phase relative to the dip within the optical minimum. The UV maximum
at ![]() appears to be flattened, but due to the lack of additional UV data it
remains unclear whether this feature recurs or is unique.
appears to be flattened, but due to the lack of additional UV data it
remains unclear whether this feature recurs or is unique.
From the 20 ks exposure performed by the EPIC
instruments, we extracted the first continuous X-ray light curves of
AI Tri over a full binary orbit (Figs. 2b, c).
Two X-ray bright phases during the intervals ![]() and
and ![]() ,
as defined by the ephemeris given above, commence with a steep rise at
,
as defined by the ephemeris given above, commence with a steep rise at ![]() .
They are interrupted by a short soft minimum at
.
They are interrupted by a short soft minimum at ![]() and a larger interval of low flux between
and a larger interval of low flux between ![]() and 1.05 (faint phase). The flux variation is most pronounced in the
soft energy band, the bright phases lasting about 70% of the orbital
period, while hard X-ray emission remains visible at a low level at all
times. The hard X-ray flux increases by a factor of about three at the
beginning of the first bright soft phase and varies slightly during the
second one.
and 1.05 (faint phase). The flux variation is most pronounced in the
soft energy band, the bright phases lasting about 70% of the orbital
period, while hard X-ray emission remains visible at a low level at all
times. The hard X-ray flux increases by a factor of about three at the
beginning of the first bright soft phase and varies slightly during the
second one.
The hardness ratio HR = (H-S)/(H+S), where H and S
represent the counts at energies above and below 0.5 keV,
respectively, correlates largely with the light curves in the soft
energy band, and tends to +1 during faint and to -1 during bright
phases (Fig. 2d).
Throughout the soft minimum at ![]() ,
the hardness ratio levels off around 0 and thus differs from the
faint-phase behavior, where it rises to values around 0.7.
Similar characteristics of the light curves are found from the
ROSAT/HRI data between January 15 and February 5, 1998
(Fig. 2a).
,
the hardness ratio levels off around 0 and thus differs from the
faint-phase behavior, where it rises to values around 0.7.
Similar characteristics of the light curves are found from the
ROSAT/HRI data between January 15 and February 5, 1998
(Fig. 2a).
3.3 Irregular mode on August 17, 2005
The V-band light curve on August 17, 2005
(Fig. 3d)
differs markedly from the majority. At a magnitude around ![]() (close to that during high states of accretion), the light curve is
strikingly variable and more asymmetric than in normal high states; the
photometric minimum appears to be shifted by 0.2 in phase. In
consequence, we did not include this peculiar light curve in the
determination of the new ephemeris. During the next observation on
August 29, the V-band light curve fits in the
prevailing shape again. Schwarz
et al. (1998) described a comparable phase-shift
with an altered light curve shape in their
(close to that during high states of accretion), the light curve is
strikingly variable and more asymmetric than in normal high states; the
photometric minimum appears to be shifted by 0.2 in phase. In
consequence, we did not include this peculiar light curve in the
determination of the new ephemeris. During the next observation on
August 29, the V-band light curve fits in the
prevailing shape again. Schwarz
et al. (1998) described a comparable phase-shift
with an altered light curve shape in their ![]() photometry of
October and November 1992 as an ``irregular mode''.
photometry of
October and November 1992 as an ``irregular mode''.
The irregular light curve was observed only two days after the
curtailed XMM-Newton exposure on August 15, 2005 (Fig. 3a-c). The
EPIC/MOS and RGS1 data cover phases ![]() and EPIC/pn
and EPIC/pn ![]() ,
respectively. This is equivalent to the soft minimum phase and about
the first half of the second bright phase of the August 22 light
curves. The EPIC count rate in the soft energy band, marked by
pronounced flickering, is about a factor of eight higher than one week
later. In contrast, little hard X-ray emission was registered, not
exceeding the low level of hard X-rays on August 22. The hardness
ratios remain almost constant at about -0.87, even during the
,
respectively. This is equivalent to the soft minimum phase and about
the first half of the second bright phase of the August 22 light
curves. The EPIC count rate in the soft energy band, marked by
pronounced flickering, is about a factor of eight higher than one week
later. In contrast, little hard X-ray emission was registered, not
exceeding the low level of hard X-rays on August 22. The hardness
ratios remain almost constant at about -0.87, even during the ![]() interval, where they increase to zero in the August 22 data. The
ultraviolet light curve has similar magnitudes as on August 22. Owing
to the insufficient coverage of the orbital cycle, the appearance of
the soft X-ray minimum and a potential phase shift cannot be
determined.
interval, where they increase to zero in the August 22 data. The
ultraviolet light curve has similar magnitudes as on August 22. Owing
to the insufficient coverage of the orbital cycle, the appearance of
the soft X-ray minimum and a potential phase shift cannot be
determined.
3.4 Short-period variations
The multiwavelength light curves are highly variable and exhibit, on timescales as short as one minute, strong and potentially recurring flickering, which is typical of soft polars. Schwarz et al. (1998) describe possible quasi-periodic oscillations (QPOs) at 6.5-7 min and 13.5-14 min in their optical data. We examine three highly resolved light curves with cycle times below 100 s, obtained between January 25 and 30, 2007, to investigate this feature. Substructure on a timescale of several minutes is clearly identifiable, as demonstrated for instance in Fig. 4. After subtracting a strongly smoothed light curve to remove the low-frequency variations, a Lomb-Scargle analysis (Scargle 1982; Lomb 1976) was performed to search for periodicity. The periodogram in Fig. 5 shows the typical broad maxima, which could be associated with quasi-periodic flickering, but may also arise from a superimposition of different patterns. To exclude false positives, the influence of aperiodic, random brightness variations has to be considered. Such low-frequency flickering or ``red noise'' is caused by unsteady mass transfer and has to be distinguished from the more regular, quasi-periodic oscillations, excited by larger blobs in the accretion stream. To reproduce the red-noise and window effects in the observations, the observed power spectral density (PSD) is fitted with a power law over frequency, and light curves with similar mean count rate, standard deviation, and PSD shape are simulated on the time grid of the observed data. We adopt the Monte Carlo approach of Benlloch et al. (2001), which they use in the search for QPOs from active galactic nuclei, and determine confidence levels from the periodograms of 10 000 fake light curves with the same power-law-shaped PSD. The corresponding levels of 99.9%, 99%, and 95% significance are overplotted in Fig. 5. At two periods around 8 min and 5 min, the power spectrum exceeds 99.9% significance, so the features may be considered to be real. The QPO frequencies found by Schwarz et al. (1998) are not significant at the 99.9% level.
No low-frequency periodicity was found in the XMM-Newton ultraviolet and soft X-ray light curves. All spikes in the periodogram lie well below the 90% confidence level. Rapid variations in the soft X-ray light curves are obvious, but no regular or periodic pattern is detectable.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13201fig4.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa13201-09/Timg49.png)
|
Figure 4: V-band light curve acquired on January 25, 2007 at the 70 cm telescope of the Astrophysical Institute Potsdam. Cycle time is 100 s. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13201fig5.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa13201-09/Timg50.png)
|
Figure 5: Periodogram based on the highest time resolved V-band data from Jan. 2007. In grey, the 95%, 99%, and 99.9% significance levels. |
| Open with DEXTER | |
4 X-ray spectroscopy
With XMM-Newton, we obtained the first well resolved X-ray spectra with
full orbital phase coverage of AI Tri. We used them to constrain the
physical conditions and the structure of the accretion region on the
white dwarf surface and of the post-shock accretion flow, and to
compare the overall flux contributions from both origins. For this
purpose, we analyzed the background-subtracted X-ray spectra by means
of multi-component models using XSPEC v12.5
(Dorman
et al. 2003; Arnaud 1996). Initially, we
modeled the time-averaged spectrum with single-temperature approaches
for the soft and hard X-ray components. More complex and physically
more relevant models were considered to improve the quality and the
validity of the fits. In this context, we investigated separate fits to
the spectra in the energy bands above and below 0.5 keV, and
combined fits to the total spectrum. In a second step, we analyzed the
average spectra of four characteristic phase intervals to constrain the
accretion geometry. In all fits, we described the interstellar
absorption using the TBNEW model![]() with the abundances of Wilms et al. (2000) and
the cross-sections of Verner
& Ferland (1996) and Verner
et al. (1996). EPIC/pn and MOS data were modeled
simultaneously. Treating the different instruments individually does
not improve the fit quality, as tests via F-statistics confirmed. All
errors are given at a 90% level of confidence in the following.
with the abundances of Wilms et al. (2000) and
the cross-sections of Verner
& Ferland (1996) and Verner
et al. (1996). EPIC/pn and MOS data were modeled
simultaneously. Treating the different instruments individually does
not improve the fit quality, as tests via F-statistics confirmed. All
errors are given at a 90% level of confidence in the following.
Table 3: Results of the best XSPEC fits to the total and to the phase-resolved EPIC spectra of AI Tri.
4.1 Soft X-ray component (accretion spot)
The flux contribution of the white dwarf was described by absorbed
black bodies, mainly forming the spectral range below 0.5 keV
and originating in the accretion-heated stellar surface. The spectra
exhibit deviations from a single black body that cannot be explained
merely by uncertainties in the calibration. Within the accretion
region, a wide range of temperatures is expected between the base of
the accretion column and the unheated white-dwarf surface. To
approximate this structure, we fitted multi-component black-body
models, employing different Gaussian and exponential distributions of
temperatures and emitting surface areas. They improved the fit
statistics in the energy range below 0.6 keV to ![]() ,
compared to
,
compared to ![]() for a single absorbed black body. For the final fit over the whole
energy range, we used black bodies with a Gaussian distribution of
temperatures and coupled emitting surface areas, fixing the minimum
temperature at a typical white-dwarf surface temperature of
for a single absorbed black body. For the final fit over the whole
energy range, we used black bodies with a Gaussian distribution of
temperatures and coupled emitting surface areas, fixing the minimum
temperature at a typical white-dwarf surface temperature of ![]() (
(![]() 23 000 K).
A maximum number of fifteen constituents were sufficient to reproduce a
smooth temperature profile with small temperature steps, not exceeding
5 eV between neighboring black-body components. The free
parameters of the model were the temperature and the normalization of
the hottest component. The model spectrum shows a shallower slope than
a single black body. The highest X-ray flux arises from the hottest
components with small effective areas, while the low-temperature black
bodies covering larger surface areas contribute little to the total
soft X-ray emission. The best-fit solution infers temperatures of as
high as
23 000 K).
A maximum number of fifteen constituents were sufficient to reproduce a
smooth temperature profile with small temperature steps, not exceeding
5 eV between neighboring black-body components. The free
parameters of the model were the temperature and the normalization of
the hottest component. The model spectrum shows a shallower slope than
a single black body. The highest X-ray flux arises from the hottest
components with small effective areas, while the low-temperature black
bodies covering larger surface areas contribute little to the total
soft X-ray emission. The best-fit solution infers temperatures of as
high as ![]() ,
which corresponds to a characteristic temperature
,
which corresponds to a characteristic temperature ![]() of a single black-body component. The hydrogen column absorption of
of a single black-body component. The hydrogen column absorption of ![]() is on the same order as the Galactic
is on the same order as the Galactic ![]() of up to
of up to ![]() towards AI Tri listed by Kalberla
et al. (2005) and Dickey
& Lockman (1990).
towards AI Tri listed by Kalberla
et al. (2005) and Dickey
& Lockman (1990).
4.2 Hard X-ray component (post-shock accretion flow)
To reproduce both the diffuse hot plasma and physical structure of the
(post-)shock accretion column, we compared a number of different
emission models (Table 3). Fits
involving several independent plasma components provide a smaller ![]() than those with one mean temperature and, thus, demonstrate that
emission regions at different temperatures influence the spectral
shape. Multi-temperature models in XSPEC
comprise a sum of MEKAL
than those with one mean temperature and, thus, demonstrate that
emission regions at different temperatures influence the spectral
shape. Multi-temperature models in XSPEC
comprise a sum of MEKAL![]() emission model components.
We tested CEMEKL, where the emission
measures are proportional to a power law over temperature, and the
cooling flow MKCFLOW (Table 3). Using
plasma models without considering the accretion physics, however, may
lead to uncertain or erroneous bolometric flux estimates. Flux and
luminosity ratios, used for investigating the energy balance (see
Sect. 5),
depend strongly on the model choice. We employ multi-temperature plasma
models based on the emission region models of Fi-scher
& Beuermann (2001). They calculate the radiative
transfer for bremsstrahlung and cyclotron radiation in a stationary
two-fluid plasma. The local mass flow density is treated as the main
free parameter and determines temperatures and shock height. For a
characteristic primary mass of
emission model components.
We tested CEMEKL, where the emission
measures are proportional to a power law over temperature, and the
cooling flow MKCFLOW (Table 3). Using
plasma models without considering the accretion physics, however, may
lead to uncertain or erroneous bolometric flux estimates. Flux and
luminosity ratios, used for investigating the energy balance (see
Sect. 5),
depend strongly on the model choice. We employ multi-temperature plasma
models based on the emission region models of Fi-scher
& Beuermann (2001). They calculate the radiative
transfer for bremsstrahlung and cyclotron radiation in a stationary
two-fluid plasma. The local mass flow density is treated as the main
free parameter and determines temperatures and shock height. For a
characteristic primary mass of ![]() ,
they derive temperature and density structures. We adopt these to
account for the wide parameter range in the post-shock accretion column
and to establish relations between the temperatures and the emission
measures of several MEKAL components,
assuming that optically thin conditions dominate. The element
abundance, the emission measure, and the temperature of the coolest
component are the free parameters for each
,
they derive temperature and density structures. We adopt these to
account for the wide parameter range in the post-shock accretion column
and to establish relations between the temperatures and the emission
measures of several MEKAL components,
assuming that optically thin conditions dominate. The element
abundance, the emission measure, and the temperature of the coolest
component are the free parameters for each ![]() combination. In addition, a common absorption term is needed for the
total plasma spectrum, which accounts for intrinsic absorption by
material surrounding the emission region in the accretion column. We
employ the partial-covering PCFABS and the
solar metal abundance ratios of Grevesse
et al. (2007) in the plasma models.
combination. In addition, a common absorption term is needed for the
total plasma spectrum, which accounts for intrinsic absorption by
material surrounding the emission region in the accretion column. We
employ the partial-covering PCFABS and the
solar metal abundance ratios of Grevesse
et al. (2007) in the plasma models.
In a single-temperature MEKAL fit
to the accretion-column spectrum of AI Tri, larger residuals
remain around 1 keV and between 3 and 5 keV. The
multi-temperature plasma models describe the emission lines more
precisely and improve the fit accuracy. The CEMEKL
model clearly underestimates the continuum flux at energies above
7 keV, while MKCFLOW and
accretion-flow models yield similar parameters. Closest approximation
of the spectral lines is achieved when using the multi- MEKAL
accretion-flow spectrum with the temperature structure following the
models of Fi-scher &
Beuermann (2001, ``accretion flow'' model in Table 3).
The magnetic field strength was fixed at ![]() ,
referring to the result of Schwarz
et al. (1998). From fits with mass flow densities
between
,
referring to the result of Schwarz
et al. (1998). From fits with mass flow densities
between ![]() and
and ![]() ,
an average
,
an average ![]() is derived. The best-fit solution infers a reduced
is derived. The best-fit solution infers a reduced ![]() at 318 degrees of freedom, plasma temperatures between
at 318 degrees of freedom, plasma temperatures between ![]() and
and ![]() ,
and 1.3+1.0-0.6
times the solar abundances (Fig. 6).
,
and 1.3+1.0-0.6
times the solar abundances (Fig. 6).
Neither of the tested plasma models completely reproduces the spectral slope at energies above 4 keV. The deviations may be caused by remaining unresolved emission lines, which require a modified temperature structure or metal abundances. Alternatively, reflection of the continuum from the white-dwarf surface may harden the spectrum for energies above several keV, as Done et al. (1995) expound for the GINGA spectra of AI Tri. The residuals around 1 keV can indicate photoionization effects. An additional warm absorber model component such as ABSORI (Done et al. 1992; Zdziarski et al. 1995) or XSTAR (García et al. 2005; Kallman & Bautista 2001) accounts more accurately for the spectral shape, but introduces too many free parameters.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13201fig6.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa13201-09/Timg176.png)
|
Figure 6: EPIC spectra extracted from the 20 ks exposure of AI Tri on August 22, 2005. The best-fit model consists of mildly absorbed black bodies, combined with partially absorbed multi- MEKAL plasma emission. |
| Open with DEXTER | |
4.3 Phase-resolved modeling
The 20 ks XMM-Newton exposure was divided into four phase intervals, characterized by the varying amount of soft X-ray emission and the associated hardness ratios (cf. Fig. 2). We extracted and modeled spectra for each of the intervals separately. Since the number of counts are lower than in the complete data set, we used absorbed multi-black body plus single MEKAL models. The element abundances were fixed to those of the solar distribution, which is approximately the orbital mean.
During the two X-ray bright phases, the spectral parameters agree remarkably well. Both the black-body luminosity and emitting surface area exceed the values derived from the fits to the total spectrum, while the contribution of the plasma component remains nearly constant. Owing to the higher background flux during the second bright phase, the fit is affected by larger uncertainties in the mean plasma temperature. On the whole, the two bright-phase spectra are identical within the error bars.
Apart from an intermittent soft flare before ![]() ,
the soft X-ray count rate is consistent with zero during the faint
phase. The hardness ratio reaches a mean value of HR
,
the soft X-ray count rate is consistent with zero during the faint
phase. The hardness ratio reaches a mean value of HR
![]() and a maximum of one. The model temperatures and the intrinsic
absorption overlap with the bright-phase values within the large error
bars and may be considered to be constant. A low signal-to-noise caused
by the high background count rate is the main source of the
uncertainties in the fit.
and a maximum of one. The model temperatures and the intrinsic
absorption overlap with the bright-phase values within the large error
bars and may be considered to be constant. A low signal-to-noise caused
by the high background count rate is the main source of the
uncertainties in the fit.
During the soft minimum phase interval, the low count rate
also leads to a poorer fit accuracy. The black-body flux diminishes,
and the hardness ratio HR
![]() is similar to the orbital mean of HR
is similar to the orbital mean of HR
![]() .
In parallel, the intrinsic absorption increases substantially to
.
In parallel, the intrinsic absorption increases substantially to ![]() ,
and the MEKAL norm rises, such that the
plasma component contributes more significantly to the total X-ray flux
within the XMM-Newton energy range.
,
and the MEKAL norm rises, such that the
plasma component contributes more significantly to the total X-ray flux
within the XMM-Newton energy range.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13201fig7.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa13201-09/Timg182.png)
|
Figure 7: Simultaneous fit to the XMM-Newton EPIC and RGS spectra on August 15, 2005 with the multi-temperature black-body plus single absorbed MEKAL model, as described in the text. |
| Open with DEXTER | |
4.4 XMM-Newton data on August 15, 2005
From the 1.1 to 5 ks XMM-Newton observation on August 15,
2005, EPIC and RGS first order spectra were extracted and fitted
simultaneously (Fig. 7).
Since most of the signal was detected at energies below 1 keV
(
![]() )
and the hard X-ray component almost vanished, we chose an absorbed
multi-temperature black-body model plus a single MEKAL
with fixed solar element abundance. The black-body parameters differ
only marginally from the best fit to the 20 ks exposure on
August 22, 2005. The source flux estimated from the XSPEC
fits, however, was at least a factor of ten higher than that during the
20 ks exposure one week later. The significant increase in the
flux was caused mainly by the dominant soft X-ray component and a
larger emitting surface area.
)
and the hard X-ray component almost vanished, we chose an absorbed
multi-temperature black-body model plus a single MEKAL
with fixed solar element abundance. The black-body parameters differ
only marginally from the best fit to the 20 ks exposure on
August 22, 2005. The source flux estimated from the XSPEC
fits, however, was at least a factor of ten higher than that during the
20 ks exposure one week later. The significant increase in the
flux was caused mainly by the dominant soft X-ray component and a
larger emitting surface area.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13201fig8.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa13201-09/Timg185.png)
|
Figure 8:
Spectral energy distribution of AI Tri. To the right, EPIC/pn
spectra from both the XMM-Newton pointings on August 15 and 22, 2005.
To the left, the corresponding OM/UVM2 spectral points and the V-band
observations on August 17 and 29, respectively, each with orbital
minimum and maximum flux. On August 15, the UV minimum flux is unknown
for lack of phase coverage. Overplotted are the best-fit models (solid
lines) as described in the text, their individual components absorbed
black body (dotted) and MEKAL (dashed) for
each observation, and a non-LTE white-dwarf model spectrum at |
| Open with DEXTER | |
4.5 UV flux
To extend the spectral energy distribution coverage, we
converted photometric measurements obtained at ultraviolet and optical
wavelengths into energy flux units. The total OM/UVM2 flux in the range
between 2050 Å and 2450 Å was calculated from the
corrected count rate using the conversion factor from white dwarf
standards, where 1 count s-1
is equivalent to ![]() Å-1.
It is similar in both the observations. Figure 8 shows the
spectral points from our OM/UVM2 and V-band
photometry, the EPIC/pn spectra, and the best-fit black-body plus MEKAL
models. To be able to compare with the flux contribution of the
unheated primary, a hydrogen-helium non-LTE white-dwarf atmosphere
spectrum was calculated using the modeling package NGRT (Werner & Dreizler 1999),
whose predicted flux can serve as an approximate lower limit to the
low-energy emission of the system. We assume a distance of
Å-1.
It is similar in both the observations. Figure 8 shows the
spectral points from our OM/UVM2 and V-band
photometry, the EPIC/pn spectra, and the best-fit black-body plus MEKAL
models. To be able to compare with the flux contribution of the
unheated primary, a hydrogen-helium non-LTE white-dwarf atmosphere
spectrum was calculated using the modeling package NGRT (Werner & Dreizler 1999),
whose predicted flux can serve as an approximate lower limit to the
low-energy emission of the system. We assume a distance of ![]() (Schwarz et al. 1998)
and a typical effective temperature of
(Schwarz et al. 1998)
and a typical effective temperature of ![]() for the white dwarf (Fig. 8). The
orbital means of optical and UV flux exceed the models by factors up
to 40 at both observational epochs. This is not surprising, as
other system components such as the accretion stream can contribute
significantly to the optical and UV flux. It is also consistent with
the optical spectra presented by Schwarz
et al. (1998), in which no signatures of the white
dwarf could be detected. The emitting surface area of the
low-temperature model components may be, in addition, significantly
larger than derived from the X-ray spectra. The UV data points can thus
be taken to represent an upper limit, which is not violated by the
spectral components required to model the X-ray range.
for the white dwarf (Fig. 8). The
orbital means of optical and UV flux exceed the models by factors up
to 40 at both observational epochs. This is not surprising, as
other system components such as the accretion stream can contribute
significantly to the optical and UV flux. It is also consistent with
the optical spectra presented by Schwarz
et al. (1998), in which no signatures of the white
dwarf could be detected. The emitting surface area of the
low-temperature model components may be, in addition, significantly
larger than derived from the X-ray spectra. The UV data points can thus
be taken to represent an upper limit, which is not violated by the
spectral components required to model the X-ray range.
5 On the soft-to-hard X-ray flux ratios
Several polars have a distinctly higher luminosity at soft than at hard
energies. The true fraction of systems exhibiting this ``soft X-ray
excess'' continues to be a topic of discussion. The phenomenon is
apparently connected to the scenario of inhomogeneous and
time-dependent (``blobby'') column accretion proposed by Kuijpers & Pringle (1982)
and developed further by Frank
et al. (1988). The amount of the excess increases
with magnetic field strength (Ramsay et al. 1994; Beuermann
& Schwope 1994). Beuermann
& Burwitz (1995) point out that at a high field
strength (
![]() )
and a relatively low accretion rate, cyclotron emission rather than
bremsstrahlung becomes the main cooling process, causing an enhanced
soft X-ray flux. Mass flow rate, magnetic field strength, and
white-dwarf mass thus regulate the energy balance in polars (cf. Fi-scher & Beuermann 2001).
Ramsay & Cropper (2004)
examine new XMM-Newton and re-calibrated ROSAT data. Considering
geometrical effects and the influence of accretion blobs, they derive
soft-to-hard ratios close to one for the majority of the observed
systems and conclude that fewer polars than previously understood
exhibit a notable soft X-ray excess. With its strong magnetic field and
known high soft X-ray emission, AI Tri is a suitable target to
investigate the potential connection between system parameters, flaring
signals from blobby accretion, and flux ratio.
)
and a relatively low accretion rate, cyclotron emission rather than
bremsstrahlung becomes the main cooling process, causing an enhanced
soft X-ray flux. Mass flow rate, magnetic field strength, and
white-dwarf mass thus regulate the energy balance in polars (cf. Fi-scher & Beuermann 2001).
Ramsay & Cropper (2004)
examine new XMM-Newton and re-calibrated ROSAT data. Considering
geometrical effects and the influence of accretion blobs, they derive
soft-to-hard ratios close to one for the majority of the observed
systems and conclude that fewer polars than previously understood
exhibit a notable soft X-ray excess. With its strong magnetic field and
known high soft X-ray emission, AI Tri is a suitable target to
investigate the potential connection between system parameters, flaring
signals from blobby accretion, and flux ratio.
5.1 Photometric signs of blobby accretion
Rapid variations characterize the optical as well as the X-ray light curves and are most likely caused by inhomogeneous accretion. Prominent flares may occur, when dense blobs impinge on the white-dwarf atmosphere. In the X-ray light curves, individual accretion events cannot be identified, though their shapes are probably formed by superimposed emission from multiple blobby events. This differs from the situation for the purely blobby accreting long-period polar AI Tri, where Schwarz et al. (2005) distinguished single accretion flares. The possible quasi-periodic oscillations in the optical light curves (Sect. 3.4), which may arise from blob-excited oscillations of the shock front, are in addition indicative of inhomogeneous accretion. Shafter et al. (1995) also report on QPOs at multiple frequencies in optical light curves of V1309 Ori.
5.2 Flux ratios from multi-temperature spectral modeling
The soft-to-hard X-ray flux ratios can be derived from unabsorbed bolometric luminosities. The observed data, however, cover only part of the spectral energy distribution, so the total flux has to be extrapolated and thus strongly depends on the choice of the model and its assumptions. In particular, results from former ROSAT analyses are uncertain, since the hard X-ray component had to be approximated with bremsstrahlung and the temperature could not be constrained from the spectral fits.
Our multi-temperature black-body and MEKAL
model fit to the 2005 August 22 XMM-Newton spectra yields the typical
parameters of the high-energy distribution of CVs. Using the distance
estimate of AI Tri (Schwarz
et al. 1998) ![]() ,
it results in an unabsorbed black-body luminosity of
,
it results in an unabsorbed black-body luminosity of ![]() and an integrated X-ray flux
and an integrated X-ray flux ![]() .
The flux in the soft
.
The flux in the soft ![]() energy band exceeds the hard
energy band exceeds the hard ![]() flux during the whole orbital revolution. The bolometric fluxes of the
individual unabsorbed model components lead to ratios of
flux during the whole orbital revolution. The bolometric fluxes of the
individual unabsorbed model components lead to ratios of ![]() for the orbital mean and of
for the orbital mean and of ![]() for the first bright phase. Owing to the partial-covering absorption
term employed in the spectral fits, the plasma temperatures are lower
than in models that do not account for intrinsic absorption. In
particular, the spectral resolution and range of the ROSAT spectra of
polars was not high enough to derive both a reliable bremsstrahlung
temperature and the absorbing column density. Hence, the cooler plasma
component contributes more significantly to the emission in the soft
X-ray regime, resulting in a lower ratio of the extrapolated fluxes of
the black-body to the MEKAL components.
for the first bright phase. Owing to the partial-covering absorption
term employed in the spectral fits, the plasma temperatures are lower
than in models that do not account for intrinsic absorption. In
particular, the spectral resolution and range of the ROSAT spectra of
polars was not high enough to derive both a reliable bremsstrahlung
temperature and the absorbing column density. Hence, the cooler plasma
component contributes more significantly to the emission in the soft
X-ray regime, resulting in a lower ratio of the extrapolated fluxes of
the black-body to the MEKAL components.
On August 15, 2005, the total integrated flux ![]() was notably governed by an increased black-body component, while the
model flux in the hard band stays at a low level. Due to the low count
rate above energies of 0.8 keV, extrapolating the model flux
to a wider energy range would have produced unacceptably large
uncertainties. We therefore used the flux ratio in the XMM-Newton
bands,
was notably governed by an increased black-body component, while the
model flux in the hard band stays at a low level. Due to the low count
rate above energies of 0.8 keV, extrapolating the model flux
to a wider energy range would have produced unacceptably large
uncertainties. We therefore used the flux ratio in the XMM-Newton
bands, ![]() ,
as a lower limit to the bolometric flux ratio. The black-body flux is
remarkably higher than on August 22, indicating that the mass accretion
rate is higher by a factor of more than one hundred. This may induce a
stronger temporal and spatial inhomogeneity in the accretion stream,
forcing more material into dense blobs. In consequence, the
contribution of the hard X-ray emission will be lower than in states of
lower accretion rates, producing a distinct change in the spectral
shape as seen in Fig. 8. The
pronounced flickering in the X-ray light curves supports the idea of
blobby accretion playing a larger role at that time.
,
as a lower limit to the bolometric flux ratio. The black-body flux is
remarkably higher than on August 22, indicating that the mass accretion
rate is higher by a factor of more than one hundred. This may induce a
stronger temporal and spatial inhomogeneity in the accretion stream,
forcing more material into dense blobs. In consequence, the
contribution of the hard X-ray emission will be lower than in states of
lower accretion rates, producing a distinct change in the spectral
shape as seen in Fig. 8. The
pronounced flickering in the X-ray light curves supports the idea of
blobby accretion playing a larger role at that time.
An extreme dominance of the soft X-ray component was also found in the XMM-Newton spectra of V1309 Ori with a bolometric flux ratio of several thousand (Schwarz et al. 2005) and of the short-period polar AI Tri with a luminosity ratio of 14-2800 (Ramsay et al. 2004). In the few systems lacking distinct soft X-ray emission, such as AI Tri (Vogel et al. 2008) and AI Tri (Ramsay & Cropper 2007), the flux maximum of the reprocessed component appears to be shifted towards the EUV and UV regime. The same could apply to objects that show a detectable, but very weak soft component, such as AI Tri (Ramsay & Cropper 2003). This interpretation implies that single black-body models, adjusted to the X-ray regime, generally give only a lower limit for the reprocessed emission from the accretion region and thus for the flux ratio. To quantify the soft X-ray excess, multi-temperature models are required not only to describe the emission from the post-shock accretion column but also to adequately take into account the soft X-ray emission from the accretion area on the white dwarf.
6 Accretion geometry of the system
Depending on the field topology, the magnetic flux density, and the ram pressure of the free-falling accretion stream, coupling of the accretion plasma onto the field line trajectories can occur at different locations within the binary reference frame, and the infalling material may be channeled into one or more accretion regions on the white-dwarf surface. Constraining the geometry and location of the active X-ray emitting accretion region(s) is important to understanding the origin of X-ray soft and hard components and their flux balance.
Prominent light curve features and phase-resolved spectral
modeling may provide insight into the system geometry. Since it is
crucial to know their orbital phasing, we convert the photometric into
orbital phases as described in Sect. 3.1 and refer
to these values in the following discussion, which is valid based on
the assumption of synchronous rotation. These features are for instance
the two bright phases in our X-ray light curves and the minimum
in-between. The almost identical fits to the bright-phase spectra
strongly indicate that the complete soft X-ray emission originates in
one and the same accretion region. The minima around ![]() and 0.81 (
and 0.81 (
![]() and 0.0) are pronounced mainly in the soft X-ray flux and may
have their origin in a variety of mechanisms. These include a total or
partial self-eclipse of the accretion region by the white dwarf,
absorption in the accretion stream, or random mass-transfer variations
on timescales of several hours. An occultation of the white dwarf by
the secondary star can be excluded, since it would be expected to occur
at inferior conjunction.
and 0.0) are pronounced mainly in the soft X-ray flux and may
have their origin in a variety of mechanisms. These include a total or
partial self-eclipse of the accretion region by the white dwarf,
absorption in the accretion stream, or random mass-transfer variations
on timescales of several hours. An occultation of the white dwarf by
the secondary star can be excluded, since it would be expected to occur
at inferior conjunction.
6.1 Self-eclipse of the accretion region
A self-eclipse occurs when the accretion region passes behind the limb of the white dwarf because of the stellar rotation. Such a feature was found in the X-ray/EUV light curves of several polars such as AI Tri (Szkody et al. 1999), MT Dra (Schwarz et al. 2002), VV Pup (Vennes et al. 1995). The X-ray spectra during phases of self-eclipse are characterized by a vanishing emitting area, at least of the soft X-ray component, while the intrinsic absorption remains nearly constant.
At a system inclination of ![]() (Katajainen et al. 2001),
a partial or total self-eclipse is plausible for AI Tri, if
the colatitude of the accretion region is higher than
(Katajainen et al. 2001),
a partial or total self-eclipse is plausible for AI Tri, if
the colatitude of the accretion region is higher than ![]() .
Of the two phase intervals with reduced X-ray emission detected for
AI Tri, the major faint phase exhibits the characteristic
signatures of a self-eclipse, indicating that larger parts of the
accretion region might disappear behind the horizon of the white dwarf
between
.
Of the two phase intervals with reduced X-ray emission detected for
AI Tri, the major faint phase exhibits the characteristic
signatures of a self-eclipse, indicating that larger parts of the
accretion region might disappear behind the horizon of the white dwarf
between ![]() and
and ![]() .
During the
.
During the ![]() interval, the hardness ratio is not higher than zero, and soft and hard
X-radiation are emitted at a similar level. An eclipse of the accretion
region, hence, is less likely to explain this phase.
interval, the hardness ratio is not higher than zero, and soft and hard
X-radiation are emitted at a similar level. An eclipse of the accretion
region, hence, is less likely to explain this phase.
6.2 Stream absorption
When the accretion column crosses the line of sight, it can obscure
parts of the accretion region. This manifests itself as a sharp dip in
the soft X-ray light curves with a typical duration of ![]() and as significantly enhanced absorption in the X-ray spectrum. Light
curves and spectra of AI Tri display this behavior during the
soft X-ray minimum around
and as significantly enhanced absorption in the X-ray spectrum. Light
curves and spectra of AI Tri display this behavior during the
soft X-ray minimum around ![]() .
The partial-covering absorption term in the spectral models rises
markedly; the hardness ratio of the light curves increases from
.
The partial-covering absorption term in the spectral models rises
markedly; the hardness ratio of the light curves increases from ![]() to values around zero (Fig. 2). The short
ingress and egress times and the duration
to values around zero (Fig. 2). The short
ingress and egress times and the duration ![]() of the light curve dip are also consistent with an origin in stream
absorption. The energy-dependent dip due to stream absorption and the
broad faint phase in the X-ray light curves of AI Tri resemble
the properties of the high-field system AR UMa (Szkody et al. 1999) and
the two-pole accretor MT Dra (Schwarz
et al. 2002). Their X-ray emission can be explained
in the same way.
of the light curve dip are also consistent with an origin in stream
absorption. The energy-dependent dip due to stream absorption and the
broad faint phase in the X-ray light curves of AI Tri resemble
the properties of the high-field system AR UMa (Szkody et al. 1999) and
the two-pole accretor MT Dra (Schwarz
et al. 2002). Their X-ray emission can be explained
in the same way.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{13201fig9.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa13201-09/Timg207.png)
|
Figure 9:
Sketch of the binary geometry on the basis of the spectroscopic phasing
derived by Schwarz et al.
(1998), valid in the case of synchronous rotation, the Roche
lobes being calculated for a mass ratio of |
| Open with DEXTER | |
6.3 A second possible scenario
The faint phase might alternatively be interpreted as stream absorption
and the X-ray light curve dip at ![]() as a self-eclipse of the accretion region. In consequence, the optical
and the UV light curves would then be anti-correlated with the X-ray
data, which would disagree with the standard picture of accretion in
polars (e.g. King
& Lasota 1979; Lamb & Masters 1979) in
which the maximum flux in the UV range is seen when the accretion
region passes the line of sight - just at the phase of the stream
eclipse. If the ultraviolet light curve, however, were dominated by the
revolution of an extended accretion column, we may see its irradiated
surface in anti-phase with the soft X-ray emission. Osborne et al. (1987)
describe an anti-correlation of optical and soft X-ray flux for
AI Tri, another long-period polar, and consider a
possible connection to accretion by means of dense filaments.
as a self-eclipse of the accretion region. In consequence, the optical
and the UV light curves would then be anti-correlated with the X-ray
data, which would disagree with the standard picture of accretion in
polars (e.g. King
& Lasota 1979; Lamb & Masters 1979) in
which the maximum flux in the UV range is seen when the accretion
region passes the line of sight - just at the phase of the stream
eclipse. If the ultraviolet light curve, however, were dominated by the
revolution of an extended accretion column, we may see its irradiated
surface in anti-phase with the soft X-ray emission. Osborne et al. (1987)
describe an anti-correlation of optical and soft X-ray flux for
AI Tri, another long-period polar, and consider a
possible connection to accretion by means of dense filaments.
However, the length of the faint phase, the slow ingress, and
the low intrinsic absorption do not agree well with the characteristics
of a stream dip. The short soft minimum around ![]() cannot be identified in the former ROSAT light curves. A phase of
self-eclipse, however, would be expected to recur on longer timescales.
For both reasons, we consider this second scenario less likely.
cannot be identified in the former ROSAT light curves. A phase of
self-eclipse, however, would be expected to recur on longer timescales.
For both reasons, we consider this second scenario less likely.
6.4 Orientation of the main accretion pole
According to the standard picture of the accretion geometry in polars,
described for example by Cropper
(1988), the magnetic pole of the white dwarf onto which the
major part of the accretion stream is directed is normally found
between longitudes of ![]() and
and ![]() .
In the alternative interpretation of our X-ray light curves presented
in Sect. 6.3,
the accretion region of AI Tri would be visible from
.
In the alternative interpretation of our X-ray light curves presented
in Sect. 6.3,
the accretion region of AI Tri would be visible from ![]() until
until ![]() and, thus, be located around
and, thus, be located around ![]() .
In our favorite scenario (Sects. 6.1
and 6.2),
on the other hand, the bright-phase emission is centered around
.
In our favorite scenario (Sects. 6.1
and 6.2),
on the other hand, the bright-phase emission is centered around ![]() ,
which corresponds to an unusual longitude
,
which corresponds to an unusual longitude ![]() of the dominating pole. But a standard geometry can also be preserved
in this case, if the system rotates asynchronously. Asynchronous
rotation cannot be excluded, as most of our observations (including the
ROSAT and XMM-Newton data) trace solely the spin period. The
information about both the orbital period and the phase shift between
photometric and spectroscopic ephemeris is derived from the optical
spectroscopy of Schwarz
et al. (1998) in 1992/93, who report an upper limit
on the order of 10-4 for the degree of
synchronization. To place the accretion region of AI Tri
within the first quadrant, the orbital phasing at the epoch of the
XMM-Newton observations had to be shifted by
of the dominating pole. But a standard geometry can also be preserved
in this case, if the system rotates asynchronously. Asynchronous
rotation cannot be excluded, as most of our observations (including the
ROSAT and XMM-Newton data) trace solely the spin period. The
information about both the orbital period and the phase shift between
photometric and spectroscopic ephemeris is derived from the optical
spectroscopy of Schwarz
et al. (1998) in 1992/93, who report an upper limit
on the order of 10-4 for the degree of
synchronization. To place the accretion region of AI Tri
within the first quadrant, the orbital phasing at the epoch of the
XMM-Newton observations had to be shifted by ![]() .
A phase shift of this order can be achieved by a small degree of
asynchronism of at least
.
A phase shift of this order can be achieved by a small degree of
asynchronism of at least ![]() .
This is even below the value of
.
This is even below the value of ![]() that Staubert et al.
(2003) derive for AI Tri, the polar
with the slightest non-synchronous rotation determined up to now. Campbell & Schwope (1999)
indeed suggest that a significant number of polars with an undetected
slight asynchronism may exist.
that Staubert et al.
(2003) derive for AI Tri, the polar
with the slightest non-synchronous rotation determined up to now. Campbell & Schwope (1999)
indeed suggest that a significant number of polars with an undetected
slight asynchronism may exist.
6.5 The hard X-ray emission
Low hard X-ray flux remains detectable throughout the orbital cycle. The emission may originate in an extended accretion region that is not totally eclipsed. Another possible explanation is a second accretion pole that is only visible in the high energy range and accretes at a low mass-flow rate. Episodes of accretion onto two poles with different hardness ratios were identified for example in AM Her (e.g. Matt et al. 2000), in AI Tri (Schwarz et al. 2002), and in AI Tri (Ramsay & Cropper 2002), one of the few known asynchronous systems.
6.6 Long-term variation
The X-ray light curves obtained with ROSAT and XMM-Newton between
January 1991 (Schwarz
et al. 1998) and August 2005 (this work) do not
completely repeat themselves. A pronounced faint phase before or around
![]() (
(
![]() ),
though, appears to be common to all X-ray light curves, which is
consistent with the characteristics of a self-eclipse. It largely
coincides with the UV and optical minima and with a peak in the linear
polarization (Katajainen
et al. 2001). The ROSAT HRI light curves taken
between January 15 and February 5, 1998 are similar to the XMM-Newton
light curves, but lack the deep soft X-ray minimum around
),
though, appears to be common to all X-ray light curves, which is
consistent with the characteristics of a self-eclipse. It largely
coincides with the UV and optical minima and with a peak in the linear
polarization (Katajainen
et al. 2001). The ROSAT HRI light curves taken
between January 15 and February 5, 1998 are similar to the XMM-Newton
light curves, but lack the deep soft X-ray minimum around ![]() (
(
![]() ),
identifiable in the XMM-Newton data on August 22, 2005.
),
identifiable in the XMM-Newton data on August 22, 2005.
The accretion scenario described above cannot explain all the
phenomena in the XMM-Newton and archival ROSAT data. In particular, the
emission during the second bright phase is lower than during the first
one; and the count rate changes distinctly between the different X-ray
observations. An expanded accretion curtain along the ballistic
accretion stream might reduce the flux between ![]() and 0.7, as confirmed in the case of AI Tri by Schwope et al. (2001).
Such an accretion curtain would account for the slightly enhanced
absorption inferred by the spectral fits to the XMM-Newton data during
the second bright phase, and be consistent with the finding that the
narrow emission line components in the optical spectra are asymmetric (Schwarz et al. 1998).
By more or less effective shielding, the accretion curtain could induce
the other strong variations detected in the X-ray light curves. Schwope et al. (2001)
report similar effects in the light curves and spectra of
HU Aqr.
and 0.7, as confirmed in the case of AI Tri by Schwope et al. (2001).
Such an accretion curtain would account for the slightly enhanced
absorption inferred by the spectral fits to the XMM-Newton data during
the second bright phase, and be consistent with the finding that the
narrow emission line components in the optical spectra are asymmetric (Schwarz et al. 1998).
By more or less effective shielding, the accretion curtain could induce
the other strong variations detected in the X-ray light curves. Schwope et al. (2001)
report similar effects in the light curves and spectra of
HU Aqr.
Other possible reasons for the long-term evolution of the
light curves are switches between one-pole and two-pole accretion or a
rearrangement of the accretion geometry. The location of the threading
region, where the ionized matter in the accretion stream attaches
itself to the magnetic field lines and is lifted off the orbital plane,
depends on the mass accretion rate ![]() .
A change in
.
A change in ![]() will influence the stream trajectory and thus the region of impact onto
the white dwarf at the footpoints of the magnetic field lines, whose
spread determines the form, extent, and location of the accretion
region. A large number of dense filaments in the stream in addition
affects its structure. The phase shift of the irregular optical light
curve minimum on August 17, 2005 could reflect this modified
accretion geometry. The spectral fits to the 2005 August 15 XMM-Newton
data indicate a highly increased mass accretion rate at this epoch
(Sect. 5.2).
Inhomogeneities and changes in the emission region, hence, are likely.
The irregular mode of the V-band light curves on
October/November 1992 (Schwarz
et al. 1998) could be explained in the same way.
will influence the stream trajectory and thus the region of impact onto
the white dwarf at the footpoints of the magnetic field lines, whose
spread determines the form, extent, and location of the accretion
region. A large number of dense filaments in the stream in addition
affects its structure. The phase shift of the irregular optical light
curve minimum on August 17, 2005 could reflect this modified
accretion geometry. The spectral fits to the 2005 August 15 XMM-Newton
data indicate a highly increased mass accretion rate at this epoch
(Sect. 5.2).
Inhomogeneities and changes in the emission region, hence, are likely.
The irregular mode of the V-band light curves on
October/November 1992 (Schwarz
et al. 1998) could be explained in the same way.
7 Conclusions
By analyzing our phase-resolved X-ray spectroscopy with XMM-Newton, we
have confirmed a strong soft X-ray excess of AI Tri. Both the
emission from the heated accretion spot and the emission from the
post-shock accretion flow depart from single temperature models. From
our multi-temperature approaches, we have found a bolometric flux ratio
of ![]() between the two components during the bright phase of AI Tri
on August 22, 2005. An even higher flux ratio of
between the two components during the bright phase of AI Tri
on August 22, 2005. An even higher flux ratio of ![]() in the XMM-Newton energy bands was observed on August 15, 2005, when
the total source flux was by a factor of at least ten higher. The
distinct soft X-ray excess is probably related to inhomogeneous, blobby
accretion as indicated by the high variability of the optical and X-ray
flux on short timescales.
in the XMM-Newton energy bands was observed on August 15, 2005, when
the total source flux was by a factor of at least ten higher. The
distinct soft X-ray excess is probably related to inhomogeneous, blobby
accretion as indicated by the high variability of the optical and X-ray
flux on short timescales.
From the light-curve characteristics and the spectral variation in the intrinsic absorption with phase, we have inferred the most likely geometry of AI Tri. One main soft X-ray emitting accretion region undergoes a self-eclipse and a short period of accretion-stream absorption during the orbital revolution of the system. In this interpretation, the maxima of the UV and optical light curves occur at the moment that the accretion region passes the line of sight. The finding that hard X-ray emission is present at an almost constant, very low level over the whole orbital cycle, including the faint phase, may imply that a second accretion region with weak hard X-ray emission exists. Changes in the accretion geometry may occasionally occur, possibly in response to significant variations in the mass accretion rate. Signatures of these changes are the irregular light curves on October/November 1992 and on August 17, 2005, and the new minimum dip seen in the V-band light curves from November 2006 onward.
Assuming synchronous rotation of the white dwarf with the
binary orbit, the main accretion region appears to be located around an
unusual longitude of ![]() .
Since we extrapolated the spectroscopic ephemeris from data of Schwarz et al. (1998),
obtained more than ten years before our multiwavelength observations,
we cannot exclude there being a slightly asynchronous rotation of
AI Tri within the accuracy reached. Future optical
spectroscopy is necessary to clarify the ephemeris and to finally
decide on the location of the accretion pole(s).
.
Since we extrapolated the spectroscopic ephemeris from data of Schwarz et al. (1998),
obtained more than ten years before our multiwavelength observations,
we cannot exclude there being a slightly asynchronous rotation of
AI Tri within the accuracy reached. Future optical
spectroscopy is necessary to clarify the ephemeris and to finally
decide on the location of the accretion pole(s).
We thank F. V. Hessman and T. Nagel for carrying out the V-band observations at the M ONET/North and Tübingen telescopes, and the referee for constructive remarks. I.T. gratefully acknowledges helpful discussions with S. Carpano, S. Fritz, D. deMartino, C. Mauche, and J. Wilms. This research is granted by DLR under project numbers 50 OR 0404 and 50 OR 0501.
References
- Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, ed. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [Google Scholar]
- Benlloch, S., Wilms, J., Edelson, R., Yaqoob, T., & Staubert, R. 2001, ApJ, 562, L121 [NASA ADS] [CrossRef] [Google Scholar]
- Beuermann, K., & Burwitz, V. 1995, in Cape Workshop on Magnetic Cataclysmic Variables, ed. D. A. H. Buckley, & B. Warner, ASP Conf. Ser., 85, 99 [Google Scholar]
- Beuermann, K., & Schwope, A. D. 1994, in Interacting Binary Stars, ed. A. W. Shafter, ASP Conf. Ser., 56, 119 [Google Scholar]
- Beuermann, K., & Thomas, H.-C. 1993, Adv. Space Res., 13, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Beuermann, K., Thomas, H., Reinsch, K., et al. 1999, A&A, 347, 47 [NASA ADS] [Google Scholar]
- Beuermann, K., Burwitz, V., & Rauch, T. 2006, A&A, 458, 541 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Campbell, C. G., & Schwope, A. D. 1999, A&A, 343, 132 [NASA ADS] [Google Scholar]
- Cropper, M. 1988, MNRAS, 231, 597 [NASA ADS] [CrossRef] [Google Scholar]
- Dickey, J. M., & Lockman, F. J. 1990, ARA&A, 28, 215 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Done, C., Mulchaey, J. S., Mushotzky, R. F., & Arnaud, K. A. 1992, ApJ, 395, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Done, C., Osborne, J. P., & Beardmore, A. P. 1995, MNRAS, 276, 483 [NASA ADS] [CrossRef] [Google Scholar]
- Dorman, B., Arnaud, K. A., & Gordon, C. A. 2003, in Bull. Am. Astron. Soc., 35, 641 [Google Scholar]
- Fischer, A., & Beuermann, K. 2001, A&A, 373, 211 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frank, J., King, A. R., & Lasota, J.-P. 1988, A&A, 193, 113 [NASA ADS] [Google Scholar]
- García, J., Mendoza, C., Bautista, M. A., et al. 2005, ApJS, 158, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Grevesse, N., Asplund, M., & Sauval, A. J. 2007, Space Sci. Rev., 130, 105 [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kallman, T., & Bautista, M. 2001, ApJS, 133, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Katajainen, S., Scaltriti, F., Piirola, V., Lehto, H. J., & Anderlucci, E. 2001, A&A, 372, 945 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- King, A. R., & Lasota, J. P. 1979, MNRAS, 188, 653 [NASA ADS] [CrossRef] [Google Scholar]
- Kuijpers, J., & Pringle, J. E. 1982, A&A, 114, L4 [NASA ADS] [Google Scholar]
- Lamb, D. Q., & Masters, A. R. 1979, ApJ, 234, L117 [NASA ADS] [CrossRef] [Google Scholar]
- Liedahl, D. A., Osterheld, A. L., & Goldstein, W. H. 1995, ApJ, 438, L115 [NASA ADS] [CrossRef] [Google Scholar]
- Lomb, N. R. 1976, Ap&SS, 39, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Mateos, S., Saxton, R. D., Read, A. M., & Sembay, S. 2009, A&A, 496, 879 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matt, G., de Martino, D., Gänsicke, B. T., et al. 2000, A&A, 358, 177 [NASA ADS] [Google Scholar]
- Mewe, R., Gronenschild, E. H. B. M., & van den Oord, G. H. J. 1985, A&AS, 62, 197 [Google Scholar]
- Osborne, J. P., Beuermann, K., Charles, P., et al. 1987, ApJ, 315, L123 [NASA ADS] [CrossRef] [Google Scholar]
- Ramsay, G., & Cropper, M. 2002, MNRAS, 334, 805 [NASA ADS] [CrossRef] [Google Scholar]
- Ramsay, G., & Cropper, M. 2003, MNRAS, 338, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Ramsay, G., & Cropper, M. 2004, MNRAS, 347, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Ramsay, G., & Cropper, M. 2007, MNRAS, 379, 1209 [NASA ADS] [CrossRef] [Google Scholar]
- Ramsay, G., Mason, K. O., Cropper, M., Watson, M. G., & Clayton, K. L. 1994, MNRAS, 270, 692 [NASA ADS] [CrossRef] [Google Scholar]
- Ramsay, G., Cropper, M., Mason, K. O., Córdova, F. A., & Priedhorsky, W. 2004, MNRAS, 347, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Scargle, J. D. 1982, ApJ, 263, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Schuh, S. L., Dreizler, S., Deetjen, J. L., & Göhler, E. 2003, Balt. Astron., 12, 167 [Google Scholar]
- Schwarz, R. 1996, Diploma Thesis, Humboldt-Universität Berlin [Google Scholar]
- Schwarz, R., Schwope, A. D., Beuermann, K., et al. 1998, A&A, 338, 465 [NASA ADS] [Google Scholar]
- Schwarz, R., Greiner, J., Tovmassian, G. H., Zharikov, S. V., & Wenzel, W. 2002, A&A, 392, 505 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schwarz, R., Reinsch, K., Beuermann, K., & Burwitz, V. 2005, A&A, 442, 271 [Google Scholar]
- Schwope, A. D., Schwarz, R., Sirk, M., & Howell, S. B. 2001, A&A, 375, 419 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shafter, A. W., Reinsch, K., Beuermann, K., et al. 1995, ApJ, 443, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Standish, E. M. 1998, JPL IOM, 312.F-98-048 [Google Scholar]
- Staubert, R., Friedrich, S., Pottschmidt, K., et al. 2003, A&A, 407, 987 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stuhlinger, M., Kirsch, M. G. F., Santos-Lleo, M., et al. 2008, Status of XMM-Newton instrument cross-calibration with SAS v7.1, issue 5.0 edn., ESA, doc. No. XMM-SOC-CAL-TN-0052 [Google Scholar]
- Szkody, P., Vennes, S., Schmidt, G. D., et al. 1999, ApJ, 520, 841 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, H., Beuermann, K., Reinsch, K., et al. 1998, A&A, 335, 467 [NASA ADS] [Google Scholar]
- Vennes, S., Szkody, P., Sion, E. M., & Long, K. S. 1995, ApJ, 445, 921 [NASA ADS] [CrossRef] [Google Scholar]
- Verner, D. A., & Ferland, G. J. 1996, ApJS, 103, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Verner, D. A., Ferland, G. J., Korista, K. T., & Yakovlev, D. G. 1996, ApJ, 465, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Vogel, J., Byckling, K., Schwope, A., et al. 2008, A&A, 485, 787 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Werner, K., & Dreizler, S. 1999, J. Comp. Appl. Math., 109, 65 [Google Scholar]
- Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Zdziarski, A. A., Johnson, W. N., Done, C., Smith, D., & McNaron-Brown, K. 1995, ApJ, 438, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Zimmermann, H. U., Belloni, T., Izzo, C., Kahabka, P., & Schwentker, O. 1993, in Astronomical Data Analysis Software and Systems II, ed. R. J. Hanisch, R. J. V. Brissenden, & J. Barnes, ASP Conf. Ser., 52, 233 [Google Scholar]
Footnotes
- ... XMM-Newton
![[*]](/icons/foot_motif.png)
- Based on observations obtained with XMM-Newton, an ESA science mission with instruments and contributions directly funded by ESA Member States and NASA.
- ... XMM-Newton
![[*]](/icons/foot_motif.png)
- International Astronomical Consortium for High Energy Calibration, http://www.iachec.org
- ... model
![[*]](/icons/foot_motif.png)
- Based on TBVARABS in XSPEC (Wilms et al. 2000), TBNEW provides refined cross-sections. See http://pulsar.sternwarte.uni-erlangen.de/wilms/research/tbabs/
- ... MEKAL
![[*]](/icons/foot_motif.png)
- MEKAL (e.g. Liedahl et al. 1995; Mewe et al. 1985) models include spectral continuum and element lines from a hot, optically thin plasma based on the assumptions of collisional ionization equilibrium and Maxwellian electron and ion energy distributions. Calculating the continuum radiation involves free-free, free-bound, and two-photonemission. Electron impact, radiative and dielectronic recombination, and inner-shell excitation and ionization contribute to the line transitions.
All Tables
Table 1: Log of the ROSAT and XMM-Newton observations and of the optical photometry of AI Tri.
Table 2: Barycentric timings of the V-band minima of AI Tri.
Table 3: Results of the best XSPEC fits to the total and to the phase-resolved EPIC spectra of AI Tri.
All Figures
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13201fig1.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa13201-09/Timg15.png)
|
Figure 1: EPIC/pn X-ray intensity in both the source region (source plus background) and the source-free background region during the 20 ks XMM-Newton observation, binned into time intervals of 10 s. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13201fig2.eps} \vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/08/aa13201-09/Timg35.png)
|
Figure 2:
X-ray, ultraviolet, and optical light curves of AI Tri folded
over photometric phase. Orbital phase as |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13201fig3.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa13201-09/Timg36.png)
|
Figure 3: Multi-wave-band light curves obtained with XMM-Newton on Aug. 15 (a)-c)) and with the Potsdam 70 cm telescope on Aug. 17, 2005 (d)). The X-ray data are binned into 10 s intervals, the ultraviolet into 30 s, and the hardness ratios into 100 s, respectively. Grey lines indicate the phases of high and low soft X-ray flux in the 20 ks exposure. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13201fig4.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa13201-09/Timg49.png)
|
Figure 4: V-band light curve acquired on January 25, 2007 at the 70 cm telescope of the Astrophysical Institute Potsdam. Cycle time is 100 s. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13201fig5.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa13201-09/Timg50.png)
|
Figure 5: Periodogram based on the highest time resolved V-band data from Jan. 2007. In grey, the 95%, 99%, and 99.9% significance levels. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13201fig6.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa13201-09/Timg176.png)
|
Figure 6: EPIC spectra extracted from the 20 ks exposure of AI Tri on August 22, 2005. The best-fit model consists of mildly absorbed black bodies, combined with partially absorbed multi- MEKAL plasma emission. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13201fig7.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa13201-09/Timg182.png)
|
Figure 7: Simultaneous fit to the XMM-Newton EPIC and RGS spectra on August 15, 2005 with the multi-temperature black-body plus single absorbed MEKAL model, as described in the text. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13201fig8.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa13201-09/Timg185.png)
|
Figure 8:
Spectral energy distribution of AI Tri. To the right, EPIC/pn
spectra from both the XMM-Newton pointings on August 15 and 22, 2005.
To the left, the corresponding OM/UVM2 spectral points and the V-band
observations on August 17 and 29, respectively, each with orbital
minimum and maximum flux. On August 15, the UV minimum flux is unknown
for lack of phase coverage. Overplotted are the best-fit models (solid
lines) as described in the text, their individual components absorbed
black body (dotted) and MEKAL (dashed) for
each observation, and a non-LTE white-dwarf model spectrum at |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{13201fig9.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa13201-09/Timg207.png)
|
Figure 9:
Sketch of the binary geometry on the basis of the spectroscopic phasing
derived by Schwarz et al.
(1998), valid in the case of synchronous rotation, the Roche
lobes being calculated for a mass ratio of |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


