| Issue |
A&A
Volume 516, June-July 2010
|
|
|---|---|---|
| Article Number | A44 | |
| Number of page(s) | 9 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/200913167 | |
| Published online | 24 June 2010 | |
Investigating the driving mechanisms of coronal mass ejections
C.-H. Lin - P. T. Gallagher - C. L. Raftery
Astrophysics Research Group, School of Physics, Trinity College Dublin, Dublin 2, Ireland
Received 23 August 2009 / Accepted 2 April 2010
Abstract
Aims. The objective of this study was to examine the
kinematics of coronal mass ejections (CMEs) using EUV and coronagraph
images, and to make a quantitative comparison with a number of
theoretical models. One particular aim was to investigate the
acceleration profile of CMEs in the low corona.
Methods. We selected two CME events for this study, which
occurred on 2006 December 17 (CME06) and 2007 December 31 (CME07).
CME06 was observed using the EIT and LASCO instruments on-board SOHO,
while CME07 was observed using the SECCHI imaging suite on STEREO. The
first step of the analysis was to track the motion of each CME front
and derive its velocity and acceleration. We then compared the
observational kinematics, along with the information of the associated
X-ray emissions from GOES and RHESSI, with the kinematics proposed by
three CME models (catastrophe, breakout and toroidal instability).
Results. We found that CME06 lasted over eight hours while CME07
released its energy in less than three hours. After the eruption, both
CMEs were briefly slowed down before being accelerated again. The peak
accelerations during the re-acceleration phase coincided with the peak
soft X-ray emissions for both CMEs. Their values were ![]() 60 m s-2 for CME06 and
60 m s-2 for CME06 and ![]() 600 m s-2 for CME07. CME07 reached a maximum speed of over 1000 km s-1 before being slowed down to propagate away at a constant, final speed of
600 m s-2 for CME07. CME07 reached a maximum speed of over 1000 km s-1 before being slowed down to propagate away at a constant, final speed of ![]() 700 km s-1.
CME06 did not reach a constant speed but was moving at a small
acceleration by the end of the observation. Our comparison with the
theories suggested that CME06 can be best described by a hybrid of the
catastrophe model and breakout model while the characteristics of CME07
were most consistent with the breakout model. Based on the catastrophe
model, we deduced that the reconnection rate in the current sheet for
CME06 was intermediate, the onset of its eruption occurred at a height
of
700 km s-1.
CME06 did not reach a constant speed but was moving at a small
acceleration by the end of the observation. Our comparison with the
theories suggested that CME06 can be best described by a hybrid of the
catastrophe model and breakout model while the characteristics of CME07
were most consistent with the breakout model. Based on the catastrophe
model, we deduced that the reconnection rate in the current sheet for
CME06 was intermediate, the onset of its eruption occurred at a height
of ![]() 200 Mm, and the Alfvén speed and the magnetic field strength at this height were approximately 130-250 km s-1 and 7 Gauss, respectively.
200 Mm, and the Alfvén speed and the magnetic field strength at this height were approximately 130-250 km s-1 and 7 Gauss, respectively.
Key words: Sun: coronal mass ejections (CMEs) - Sun: flares - magnetic fields - Sun: corona - Sun: atmosphere
1 Introduction
Coronal mass ejections (CMEs) are the ejections of large amount of mass and magnetic flux from the Sun to interplanetary space. The energy released during the process is of the order of 1032-1033 erg. Statistical studies have reported variations in the observed properties and projected kinematics of CMEs (e.g., Cremades & Bothmer 2004; Zhang et al. 2004). Nevertheless, CMEs often rise with a small initial speed of a few kilometers per second, followed by a rapid upward expansion reaching several hundred or several thousand kilometers per second, and, eventually, propagate through the interplanetary space at the ambient solar-wind speed.
Several models have been proposed to explain the driving mechanism and observed properties of the CMEs. A valid model must be able to produce the observed kinematics, dynamics and properties of CMEs. In Sect. 2, we give a review of three representative models: breakout model (BO) (Antiochos et al. 1999), catastrophe model (CA) (see, e.g., Forbes & Isenberg 1991; van Tend & Kuperus 1978; Lin et al. 1998; Forbes & Priest 1995), and toroidal instability model (TI) (see, e.g., Kliem & Török 2006; Chen 1989), which have been investigated in this study. Although the profile of the CME kinematics predicted by each model is qualitatively consistent with the observed three-phase profile (i.e., slow rise, eruption and slow down), the exact profile of each model is different. Several simulations also showed that a same model can produce different kinematic profiles by simply varying the initial conditions and magnetic environment (Schrijver et al. 2008; Lynch et al. 2008; Chen 1989).
In addition to the discrepancies among theoretical predictions,
observational studies that were not based on any model, also reported
different functional forms that best-fitted their respective data.
For instance, Sheeley et al. (1999)
fitted their data by
![]() ;
Gallagher et al. (2003) formulated a double exponential function
;
Gallagher et al. (2003) formulated a double exponential function
![]() to describe the fast rising and decaying acceleration profile; and Alexander et al. (2002) demonstrated that their fast CME was best fitted by the polynomial,
h(t)= h0 + v0t + c tm, with
to describe the fast rising and decaying acceleration profile; and Alexander et al. (2002) demonstrated that their fast CME was best fitted by the polynomial,
h(t)= h0 + v0t + c tm, with
![]() ,
which is consistent with the results by Schrijver et al. (2008).
Although these studies were able to derive how the velocity and
acceleration
evolve through the duration of CMEs, they did not provide a physical
explanation and driving mechanism behind such kinematic profiles.
Besides, while most of these studies chose polynomials or exponential
functions or
a simple combination of the two, there is no guarantee that the chosen
function is the only one
that can fit the observational profile.
,
which is consistent with the results by Schrijver et al. (2008).
Although these studies were able to derive how the velocity and
acceleration
evolve through the duration of CMEs, they did not provide a physical
explanation and driving mechanism behind such kinematic profiles.
Besides, while most of these studies chose polynomials or exponential
functions or
a simple combination of the two, there is no guarantee that the chosen
function is the only one
that can fit the observational profile.
Studies to verify a specific model by comparing observations with models have also been carried out. For example, by selecting only those that can be characterized as flux-rope type CMEs, Krall et al. (2001) showed that the kinematic curves predicted by the TI model matched the kinematics in the higher corona but not the lower coronal region. An extensive examination of a fast CME by Manoharan & Kundu (2003) based on the data from various instruments showed supportive evidence for the BO model. However, Bong et al. (2006) reported that while the magnetic-field configuration and X-ray loop field connectivity in their data indicated a breakout process, the acceleration profile they obtained contradicted the BO model. The studies to verify the CA model (e.g., Schrijver et al. 2008; Alexander et al. 2002), however, often deduced their conclusions by comparing the early-stage expression of CA model with the acceleration phase and/or the late stage of the observed CME kinematic curves. As already been demonstrated in all observational studies, the kinematics of CMEs can change greatly through the duration of the event. Hence, it is unsurprising that the functional form for the early stage does not match with the profiles of the later stages.
The objectives of this paper are first to examine the features and kinematics of CME events, and then to determine the possible mechanism behind the observed phenomena by comparing the observations with various theories. The theory most consistent with the observation can thus provide information on the magnetic environment where the eruption occurs. We have chosen two CME events for this study. We first derived their kinematic profiles and examined the associated X-ray emissions and flares, and then compared the results with those derived from the three different models. The kinematic profiles from the models have been mainly obtained from simulations. The only stage of which an analytical expression of the kinematics is available is the early stage of the eruption. Hence, we first focused on a qualitative comparison of the characteristics between the observations and different models, and then carried out an additional quantitative examination by fitting the observational data with a number of model expressions. The objectives of the quantitative examination were to verify the assumptions employed in the models to derive these expressions, and/or to obtain an empirical expression for the observed kinematics. The values of the fitting parameters may be used to infer the magnetic environment and the initial conditions at the onset of the eruption.
The rest of the paper is organized as follows: the three models are reviewed in Sect. 2. The two selected CME events and how their motions were traced are described in Sect. 3. The qualitative and quantitative comparisons with the models are explained and discussed in Sects. 3.3 and 3.4. We conclude our study in Sect. 5.
2 Review of CME models
2.1 Catastrophe model (CA)
In a two-dimensional CA model (e.g., Forbes & Isenberg 1991; Priest & Forbes 2002),
the flux rope is represented by a ring circling the Sun,
and, hence, does not have anchoring ends.
This flux-rope magnetic-field configuration is generated
by placing two line sources with opposite polarities
on the surface around the Sun.
The magnetic field line connecting the two sources
is initially balanced by a downward force from
the tension of the field line
and a upward force due to the magnetic pressure gradient.
If the photospheric motion moves the two sources closer,
the tension force would increase,
which pulls the field lines downward.
However, the downward movement, compressing the field lines,
subsequently increases the pressure force.
When the sources move closer than a critical distance,
the pressure force takes over
and the flux rope is propelled and accelerated upward,
resulting in the eruption.
The model shows that, at the critical point,
the distance of the sources (d) and the height of the flux rope (h) is
related by
![]() .
After the rope rises to a certain height (
.
After the rope rises to a certain height (
![]() ),
a current sheet begins to form below it,
which acts as a drag force against the rising of the rope.
Using their 2-D model implemented with an isothermal atmosphere,
Lin & Forbes (2000) showed that
the kinematics of CMEs is dependent on
the reconnection rate in the current sheet.
In their study, the reconnection rate is constant along the current sheet,
and is prescribed by the inflow Alfvén Mach number,
),
a current sheet begins to form below it,
which acts as a drag force against the rising of the rope.
Using their 2-D model implemented with an isothermal atmosphere,
Lin & Forbes (2000) showed that
the kinematics of CMEs is dependent on
the reconnection rate in the current sheet.
In their study, the reconnection rate is constant along the current sheet,
and is prescribed by the inflow Alfvén Mach number, ![]() ,
at the midpoint of the current sheet.
They found two critical values of
,
at the midpoint of the current sheet.
They found two critical values of ![]() ,
0.005 and 0.041,
dividing CMEs into three classes:
oscillatory, with and without a deceleration phase.
Since oscillatory CMEs have never been observed,
the first critical value essentially provides
a lower limit of
,
0.005 and 0.041,
dividing CMEs into three classes:
oscillatory, with and without a deceleration phase.
Since oscillatory CMEs have never been observed,
the first critical value essentially provides
a lower limit of ![]() for a CME to happen.
If the reconnection rate is between the two critical values,
the CME in their simulation
first undergoes a fast acceleration phase for
for a CME to happen.
If the reconnection rate is between the two critical values,
the CME in their simulation
first undergoes a fast acceleration phase for ![]() 12 min after
the loss of mechanical equilibrium,
followed by a deceleration period (
t=20-100 min)
and then is re-accelerated again (cf. Fig. 6 in the paper).
For CMEs with a high reconnection rate (
12 min after
the loss of mechanical equilibrium,
followed by a deceleration period (
t=20-100 min)
and then is re-accelerated again (cf. Fig. 6 in the paper).
For CMEs with a high reconnection rate (
![]() ),
the deceleration period would not occur.
To examine the temporal behaviour of the reconnection rate and
the rate of magnetic energy release (d
),
the deceleration period would not occur.
To examine the temporal behaviour of the reconnection rate and
the rate of magnetic energy release (d
![]() /dt),
Priest & Forbes (2000) used the electric field at the X point, E0,
to represent the reconnection rate,
and allowed it to freely evolve.
We can see from their result (Fig. 11.6 in Priest & Forbes 2000) that
the profile of E0 closely follows the profile of d
/dt),
Priest & Forbes (2000) used the electric field at the X point, E0,
to represent the reconnection rate,
and allowed it to freely evolve.
We can see from their result (Fig. 11.6 in Priest & Forbes 2000) that
the profile of E0 closely follows the profile of d
![]() /dtand that the peaks of the two profiles almost coincide.
In other words, we may infer from their result that
the peak of the reconnection rate occur at a similar time as
the peak of d
/dtand that the peaks of the two profiles almost coincide.
In other words, we may infer from their result that
the peak of the reconnection rate occur at a similar time as
the peak of d
![]() /dt.
Based on the above results and
assuming that the rate of thermal-energy change
(d
/dt.
Based on the above results and
assuming that the rate of thermal-energy change
(d
![]() /dt) follows
the rate of magnetic-energy release (Reeves & Forbes 2005)
and that d
/dt) follows
the rate of magnetic-energy release (Reeves & Forbes 2005)
and that d
![]() /dt
can be represented by
the soft X-ray (SXR) emission light curve,
we can deduce that the SXR may reach its emission peak
when the reconnection rate is the highest.
We can also deduce from the CA theory that the SXR and hard X-ray (HXR)
emissions, which are indications of reconnections and flares, should
begin to increase/occur later than the launching of the CME (i.e.,
after the reconnections start in the current sheet).
/dt
can be represented by
the soft X-ray (SXR) emission light curve,
we can deduce that the SXR may reach its emission peak
when the reconnection rate is the highest.
We can also deduce from the CA theory that the SXR and hard X-ray (HXR)
emissions, which are indications of reconnections and flares, should
begin to increase/occur later than the launching of the CME (i.e.,
after the reconnections start in the current sheet).
An analytical expression for the kinematics of a thin flux rope
(i.e., the radius of the flux rope
![]() )
before the formation of the current sheet (i.e.,
)
before the formation of the current sheet (i.e.,
![]() )
can be derived (e.g., Priest & Forbes 2000; Lin & Forbes 2000):
)
can be derived (e.g., Priest & Forbes 2000; Lin & Forbes 2000):
where h is the height of the flux rope, and h0 and
The expression for the ``late'' part was derived by assuming
After the formation of the current sheet, the system becomes too complicated for an analytical expression of the CME kinematics to be derived.
2.2 Toroidal instability model (TI)
The TI model (Kliem & Török 2006; Chen 1989)
considers a pre-existing coronal flux rope
that is initially in a stable equilibrium,
and aims to explain what initiates the eruption of the loop.
There are two dominant forces acting on the flux rope.
One is an outward Lorentz self-force (hoop force) resulting from
the current flowing in the flux rope,
and the other is a compressing Lorentz force due to
the interaction between
the poloidal magnetic fields outside the flux rope and
the current inside the flux rope.
If the external magnetic field (
![]() )
decreases sufficiently fast
from the flux rope and vanishes in the infinity,
the compressing Lorentz force would
not be strong enough to counter-act a sudden increase of the hoop force
resulting from, for instance, a surge of the current in the flux rope.
The flux rope would then rapidly and continuously expand,
leading to a CME eruption.
The condition of
)
decreases sufficiently fast
from the flux rope and vanishes in the infinity,
the compressing Lorentz force would
not be strong enough to counter-act a sudden increase of the hoop force
resulting from, for instance, a surge of the current in the flux rope.
The flux rope would then rapidly and continuously expand,
leading to a CME eruption.
The condition of
![]() for the instability to happen was
derived by Bateman (1978):
for the instability to happen was
derived by Bateman (1978):
![]() ,
where R is the major radius of the flux rope.
We can infer from the above description that
TI theory does not require reconnections to accelerate a CME,
which is a major distinction between TI and the other two models.
Instead, TI proposes that a flux rope can erupt and become CME as long as
the external magnetic fields satisfy the instability condition.
,
where R is the major radius of the flux rope.
We can infer from the above description that
TI theory does not require reconnections to accelerate a CME,
which is a major distinction between TI and the other two models.
Instead, TI proposes that a flux rope can erupt and become CME as long as
the external magnetic fields satisfy the instability condition.
The equation of motion derived from the TI model is too complicated to
be solved analytically (see, e.g., Kliem & Török 2006).
However, by considering only two counter-acting Lorentz forces on the rope,
ignoring temporal changes in the external field and
its resulting flux in the rope, and assuming a simple profile
for the external field (
![]() ),
Kliem & Török (2006) showed that the expression for the beginning stage
of the instability can be approximated as a hyperbolic function:
),
Kliem & Török (2006) showed that the expression for the beginning stage
of the instability can be approximated as a hyperbolic function:
where H and H0 are the height of the rope and the rope height at the on-set of instability;
2.3 Breakout model (BO)
One distinctive requirement for the BO model (Antiochos et al. 1999) is that the flux rope is formed in a multi-polar arcade system, which consists of a low-lying central arcade, two low-lying side arcades (one on each side of the central arcade), and a large arcade overlying the three arcades. The central arcade is what would later become the CME flux rope. The shearing of the central arcade boundaries causes the arcade to rise, which subsequently results in the reconnections with the overlying arcade. As this reconnection (the breakout reconnection) removes some of the overlying magnetic field lines, the rising of central arcade becomes faster, and, in turn, triggers more and faster breakout reconnections. This process manifests as the eruption phase in a BO scenario. As the flux rope rises, it draws the magnetic field lines of the central arcade close to each other to form a current sheet underneath. When the current sheet reaches a certain critical dimension, tearing instability would cause a second set of reconnections, which not only release and further accelerate the CME rope, but also result in post-CME flares. After this set of reconnections cut off the current sheet, the magnetic field lines of the side arcades would move in to form another current sheet, in which a third set of reconnections would happen to reform and restore the magnetic fields after the eruption and also trigger another series of flaring activities, which they identified as the ribbon flares.
Since the breakout reconnection is what allows the flux rope to rise and erupt in a BO picture, we expect that, ideally, significant SXR and HXR emissions should be detected from the very beginning of the loop rising. If the second set of reconnections, responsible for cutting off the tethering force from the current sheet below the CME, can be equated to the reconnection process in the CA model, the temporal behaviour of the reconnection rate during this phase may follow the profile of the corresponding SXR emissions, as we discussed in Sect. 2.1. Because of the reconnections with both the overlying field lines and the trailing current sheets, we can expect indications of flaring activities to be detected both below and on the sides of the CME loop during different stages of the event. However, we must keep in mind that the emissions and flares during some stages might not be detectable due to observational limitations.
Although the BO model does not have an analytical expression
for the kinematics either,
there are three possible profiles produced by
three different simulations
(Lynch et al. 2004; DeVore & Antiochos 2008; Lynch et al. 2008).
While Lynch et al. (2004) showed that
their 2.5 dimensional simulation result can be fitted by
a single, constant-acceleration profile:
the three-dimensional simulation by Lynch et al. (2008) produced a more complex kinematic profile with three phases of constant acceleration: a long interval of low, constant acceleration during the foot-point shearing and breakout reconnection, followed by a short interval of high, constant acceleration during the second set of reconnections (i.e., reconnections in the current sheet formed by the central-arcade magnetic field lines), and finished with a long interval of constant velocity which simply means zero acceleration. DeVore & Antiochos (2008) produced a slightly different three-phase acceleration profile from their simulations: a long interval of slow acceleration during the shearing of the footpoints, a short interval of fast acceleration through the breakout and flare reconnections, and a short interval of fast deceleration at the end indicating the restoration and reformation of the magnetic field configuration.
3 Observations and data analysis
The two CMEs selected for this study were observed on 2006 December 17 (CME06) and 2007 December 31 (CME07). Both events were initiated at the solar limb, which allow their radial motion to be easily observed.
We have utilized observations from EIT (Extreme ultraviolet Imaging Telescope; Delaboudinière et al. 1995) 195 Å wavelength band and LASCO (Large Angle and Spectrometric Coronagraph; Brueckner et al. 1995) for CME06, and STEREO B (Solar TErrestrial RElation Observatory; Howard et al. 2008) instruments (EUVI 171 Å wavelength band, cor1 and cor2) for CME07. The X-ray emission data were obtained from GOES (Geostationary Operational Environmental Satellite; Garcia 1994) and RHESSI (Reuven Ramaty High Energy Solar Spectroscopic Imager; Lin et al. 2002).
We first applied a temporal running difference to the time-series images to enhance the contrast, and then determined the height vs. time relation of the CME by tracing the motion of the CME front. Our determined CME fronts of the two events are plotted as crosses in Fig. 1 for CME06 and Figs. 3 and 4 for CME07. Since the accuracy of the height determination is the most important factor for the accuracy of the rest of the analysis, we repeated the height determination at least ten times, and calculated the standard deviation of the multiple trials. The standard deviations were of the order of 103 km for EIT and EUVI, and 104 - 105 km for LASCO and STEREO cor1 and cor2. We then used the standard deviation plus the spatial resolution of the images as the uncertainties. The observational velocity and acceleration were subsequently calculated by taking the time derivatives of the height. The errors in the derived velocity and acceleration were propagated from the height uncertainties using the IDL function derivsig(). The kinematic profiles of the two CMEs, along with the error bars and the GOES SXR profiles, are plotted in Fig. 2 (CME06) and Fig. 5 (CME07). In the left panels of both figures, we plotted only the results of the lower corona to allow better visibility of the kinematics in this region.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13167fg1.ps} \vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/08/aa13167-09/Timg33.png)
|
Figure 1:
The image sequence of CME06
observed by EIT and LASCO C2 and C3.
The EIT images have been rotated so that the loop top
moves along X axis, as indicated by the dash line.
The pivot of the rotation is plotted as a star,
which is located at |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13167fg2.ps} \vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/08/aa13167-09/Timg34.png)
|
Figure 2: The kinematic profiles of CME06. Different symbols represent the observational results from different instruments, as denoted in the upper right panel. The GOES X-ray emission profile has been scaled to enhance the viewing, and hence the exact magnitude is irrelevant. The right column shows the combined profile of all three instruments. The left column shows only the results from the low corona to give a better view of the kinematics in this region. |
| Open with DEXTER | |
3.1 2006 December 17 CME (CME06)
This CME was highly inclined in the low corona within the field of view of EIT. Hence, we rotated the EIT images with respect to the ``base point''. The base point is the center between the loop footpoints at the limb. The line from the loop top to the base point is called ``base line''. This rotation resulted in the apparent propagation of the loop top along the X-axis. Three examples of the rotated EIT running-difference images are shown in the top row of Fig. 1. The base line is plotted as a dashed line, and the base point is marked as a star. The images of LASCO are not rotated because the CME appears to move in the radial direction at such height.
The CME, initially observed by EIT, was embedded among other loops
until it began to rise shortly after 12:00 UT.
The CME was within the field of view (FOV) of EIT until ![]() 15:12 UT.
It was later observed by LASCO C2 between 15:30 and 19:00 UT and
by C3 between 17:00 and 21:18 UT,
after which it became too faint and diffuse to be reliably identified.
15:12 UT.
It was later observed by LASCO C2 between 15:30 and 19:00 UT and
by C3 between 17:00 and 21:18 UT,
after which it became too faint and diffuse to be reliably identified.
The derived kinematics of the CME (Fig. 2)
shows that the rise of the CME was initially at a constant speed of a few km s-1until ![]() 14:30 UT, when the CME suddenly became eruptive,
indicated by the steep rise of velocity and acceleration.
The eruption was followed by a quick deceleration, reaching
14:30 UT, when the CME suddenly became eruptive,
indicated by the steep rise of velocity and acceleration.
The eruption was followed by a quick deceleration, reaching ![]() -10 m s-2.
Although the exact duration of the eruptive phase is uncertain due to
the gap between the EIT and LASCO C2 FOV, the acceleration profile in
Fig. 2 indicates that
the CME turned from eruption to deceleration in
-10 m s-2.
Although the exact duration of the eruptive phase is uncertain due to
the gap between the EIT and LASCO C2 FOV, the acceleration profile in
Fig. 2 indicates that
the CME turned from eruption to deceleration in ![]() 1.5 h.
After the deceleration, the CME was accelerated again, and then slowed down to propagate away at a small constant acceleration.
1.5 h.
After the deceleration, the CME was accelerated again, and then slowed down to propagate away at a small constant acceleration.
The GOES SXR emissions exhibited two rising phases, an initial steep
rise followed by a more gradual rise. The first rising phase began when
the CME almost reached the boundary of the EIT FOV (![]() 14:50 UT). The second rising phase, as can be seen in Fig. 2,
is where the first CME acceleration peak occurred.
The SXR reached its peak at
14:50 UT). The second rising phase, as can be seen in Fig. 2,
is where the first CME acceleration peak occurred.
The SXR reached its peak at ![]() 17:15 UT,
when the CME reached the re-acceleration peak
and a flaring loop was detected by EIT. We also examined the relevant
Hinode XRT images,
which showed that this flaring loop was located directly below the
erupted loop
and that it contracted slightly before rising to form a cusp-shape loop
top.
By comparing the RHESSI and the EIT images, we found that the sources
of the RHESSI emission (3-6 keV and 6-12 keV) were located
at the top of this post-eruption flaring loop. The GOES SXR emission
finally decreased to a background magnitude after 21:00 UT.
17:15 UT,
when the CME reached the re-acceleration peak
and a flaring loop was detected by EIT. We also examined the relevant
Hinode XRT images,
which showed that this flaring loop was located directly below the
erupted loop
and that it contracted slightly before rising to form a cusp-shape loop
top.
By comparing the RHESSI and the EIT images, we found that the sources
of the RHESSI emission (3-6 keV and 6-12 keV) were located
at the top of this post-eruption flaring loop. The GOES SXR emission
finally decreased to a background magnitude after 21:00 UT.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13167fg3.ps} \vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/08/aa13167-09/Timg36.png)
|
Figure 3: The image sequence to show the formation stage of CME07 as observed by STEREO B EUVI 171 Å. The crosses mark our determined CME front. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13167fg4.ps} \vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/08/aa13167-09/Timg37.png)
|
Figure 4: The image sequence of CME07 observed by STEREO B instruments, EUVI 171 Å, cor1 and cor2. The crosses in all images mark our determined CME front. |
| Open with DEXTER | |
3.2 2007 December 31 CME (CME07)
Figure 3 shows
the early stages of the CME emergence as observed by EUVI.
The figure revealed that
a system of loop arcades appeared at ![]() 00:41 UT,
and quickly rose radially until 00:48 UT,
after which the top of the arcades became visibly connected
to form the front of a balloon-shaped CME,
with a round top and a narrow lower part connected to the solar surface.
EUVI also captured some flaring activities and foot-point brightenings
a few minutes before the emergence of the CME.
After the emergence, Fig. 4 shows that
the CME began to quickly expand sideways while the radial rise became slower than previously.
The CME retained the round-shaped top throughout the EUVI and cor1 FOV,
but changed to a shape resembling conjoined balloons by the time it entered the cor2 FOV.
This suggests that the flux rope may have been turned, by solar rotation and/or footpoint shearing,
to also show part of the farther side of the rope.
00:41 UT,
and quickly rose radially until 00:48 UT,
after which the top of the arcades became visibly connected
to form the front of a balloon-shaped CME,
with a round top and a narrow lower part connected to the solar surface.
EUVI also captured some flaring activities and foot-point brightenings
a few minutes before the emergence of the CME.
After the emergence, Fig. 4 shows that
the CME began to quickly expand sideways while the radial rise became slower than previously.
The CME retained the round-shaped top throughout the EUVI and cor1 FOV,
but changed to a shape resembling conjoined balloons by the time it entered the cor2 FOV.
This suggests that the flux rope may have been turned, by solar rotation and/or footpoint shearing,
to also show part of the farther side of the rope.
The velocity profile of CME07 (second row in Fig. 5)
shows that the first reliable velocity point of the CME is ![]() 200 km s-1.
Unlike CME06, the velocity of the CME07 did not show a clear drop,
but rose monotonically to a peak value of over 1000 km s-1in under 30 min. After reaching the peak, the velocity dropped to a final constant value of
200 km s-1.
Unlike CME06, the velocity of the CME07 did not show a clear drop,
but rose monotonically to a peak value of over 1000 km s-1in under 30 min. After reaching the peak, the velocity dropped to a final constant value of ![]() 700 km s-1. Despite the monotonic rise of the velocity,
the derived acceleration (bottom row of Fig. 5)
exhibited a decrease during the first 15 min,
and then rose to a plateau value of
700 km s-1. Despite the monotonic rise of the velocity,
the derived acceleration (bottom row of Fig. 5)
exhibited a decrease during the first 15 min,
and then rose to a plateau value of ![]() 600 m s-2,
which lasted for
600 m s-2,
which lasted for ![]() 15 min. After that, the acceleration dropped to
15 min. After that, the acceleration dropped to ![]() -150 m s-2
before returning to almost zero at the end. We infer from the high
initial velocity
and the decrease of the acceleration at the beginning that the
observations did not detect the initial eruption phase, during which
the CME may have reached an acceleration peak.
-150 m s-2
before returning to almost zero at the end. We infer from the high
initial velocity
and the decrease of the acceleration at the beginning that the
observations did not detect the initial eruption phase, during which
the CME may have reached an acceleration peak.
The SXR emission from GOES began to rise shortly after 00:40 UT, reached a peak around 01:10 UT, at which time the CME reached its peak velocity, and dropped to background magnitude roughly after 03:00 UT when the acceleration of the CME reduced to almost zero. The analysis of the same event by Raftery et al. (2010), which utilized data from MESSENGER SAX and RHESSI, showed that the flare/SXR emissions actually began much earlier at 00:27 UT and lasted until 03:50 UT. This indicates that the GOES observation was occulted during the beginning stage of this event. A study of the RHESSI HXR data of this event by Krucker et al. (2009a,b) revealed that the RHESSI HXR sources were located above the SXR sources and were detected at 00:48 UT and 01:02 UT. The authors deduced that the HXR sources may indicate the location of particle acceleration. Comparing the timing of these two HXR detections with the kinematics profile of this CME, we found that they occurred respectively at the time of the loop emergence and at the beginning of the re-acceleration.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13167fg5.ps} \vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/08/aa13167-09/Timg38.png)
|
Figure 5: The kinematic profiles of CME07. See the caption of Fig. 2 for the description of the figure. |
| Open with DEXTER | |
3.3 Qualitative examination
The first step of this examination was to identify the properties that can be deduced/derived from and can be used to distinguish different models. These properties must also be derivable and/or detectable from the observation data we have. After these distinctive properties were identified, we then examined the consistency between the features from our observations and the properties of each models.
A CME can be qualitatively identified as CA type if it shows the following features: the CME loop begins to rise before an increase in the X-ray emission is observed; CME-associated flares occur only after the launch of the CME; and the kinematics resemble any profile produced by the CA model (e.g., Lin & Forbes 2000). If there is no flaring activities around the CME launch site and/or if the acceleration profile of a CME resembles any of the TI simulation results, it is likely to be a TI type. However, we would need a quantitative examination (i.e., fitting) to verify whether the profiles proposed by TI indeed match our observational results. To classify a CME as a BO type, we look for the following signs: significant X-ray emissions and flaring activities are detected from the very beginning of a CME event; there are magnetic arcades at the vicinity where the loop is formed; there are flare ribbons after the CME takes off; and/or the kinematic profile resembles any of the simulation results.
3.4 Quantitative examination
The mathematical profiles are often derived by imposing some approximations and assumptions. Changing the initial conditions and assumptions, or using different approximations, can often lead to a different theoretical profile without changing the model itself (e.g., Schrijver et al. 2008). Besides, the analytical expressions derivable from the theories are generally limited to the early stage of a CME process. An expression for the entire process of CME has not been available due to the complexity of the realistic models. Hence, the purpose of this quantitative examination is to verify the mathematical profiles derived from different CME models and, when the theoretical expression is unavailable, to empirically find a functional form for the kinematics of the CME. Our strategy was to first apply several model profiles to fit the height-time data, then calculate the theoretical velocity and acceleration by taking the derivatives of the fitting results, and lastly compare the theoretical and observational kinematic profiles.
We implemented four fitting models for this exercise,
CA, CAlate_e, TI and Poly fits.
CA fit was of the form of Eq. (1),
and the fitting parameters were
the critical height ![]() ,
initial speed v0,
and Alfvén speed at the critical height
,
initial speed v0,
and Alfvén speed at the critical height
![]() .
The profile for CAlate_e fit was Eq. (3)
with a variable exponent, that is,
.
The profile for CAlate_e fit was Eq. (3)
with a variable exponent, that is,
The fitting parameters for CAlate_e fit were the critical height
where t0 corresponds to the time of the first data point. The fitting parameters were h0, v0, a0 and
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13167fg6.ps} \vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2010/08/aa13167-09/Timg42.png)
|
Figure 6: The fitting results of CME06. The best results of applying different fitting models (i.e., CA, CAlate_e and poly) to the height data of EIT and LASCO C2 and C3 are plotted in different line styles. Different symbols represent the observational results of different instruments, as denoted in the figure. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13167fg7.ps} \vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2010/08/aa13167-09/Timg43.png)
|
Figure 7: The fitting results of CME07. The fitting model is a polynomial of the form Eq. (7). Different symbols and continuous lines respectively represent the observational and fitting results from different instruments, as denoted in the figure. |
| Open with DEXTER | |
As explained in Sects. 2.1 and 2.2, the profiles for CA, CAlate_e and TI fits are the profiles for the early stage of the eruption. Nevertheless, all four fitting models were applied to all the data sets. The reason for fitting the higher coronal kinematics with CA, CAlate_e and TI profiles was that we wanted to test the exclusiveness of these profiles to the initial stage. If the kinematics of the later stages can also be well-fitted by these profiles, the physical assumptions and conditions imposed to derive them may not be sufficiently strict. Our strategy of using these profiles to verify and discern different models would thus be inappropriate and unreliable. The data from different instruments were fitted separately because the full kinematics profile of a CME process is too complex to be described by one single function. In addition, by fitting different data sets separately, we avoided possible errors resulting from instrumental differences.
The fitting results of CME06 and CME07 are presented in Figs. 6 and 7, respectively. In the left panels of both figures, we plotted only the results of the lower corona to allow better visibility of the kinematics in this region. The symbols along with the error bars in the figures represent the results from the observational data, and the continuous lines are the results from the fitting, as denoted in the figures.
4 Results
4.1 2006 December 17 (CME06)
The initial part of this CME matches the picture proposed by CA, that is, the CME rose before the SXR emission began to increase. The velocity profile (cf. Fig. 2) also resembles the model profile that corresponds to an intermediate reconnection rate (Fig. 6 in Lin & Forbes 2000). However, a comparison of the kinematics and SXR emission profile appears to indicate that there may be breakout reconnections before the formation of the current sheet. This is explained as follows: if the reconnections in the current sheet were indeed reflected in the re-acceleration of the CME, the rising in the SXR emission before this may appear to be contradictory to the CA model. Although the dissipation of the kinetic energy under an ideal MHD process can result in thermal emissions, the energy is much lower than the energy of X-ray emissions. An explanation we propose to explain this is that there may be reconnections between the rising flux rope and the overlying magnetic fields before the current sheet beneath the flux rope was formed. While TI theory also proposed an ideal MHD process to initiate the instability, most of the kinematic profiles of the CME leading edge from TI simulations did not show a deceleration phase (see, e.g., Schrijver et al. 2008; Török & Kliem 2007; Kliem & Török 2006). However, we need further examinations to determine whether TI may contribute to any part of this CME.
The height-time curve of EIT can be fitted equally well
by CA, CAlate_e and Poly expressions, but not TI.
Hence, only the fitting results of CA, CAlate_e and Poly
were shown in Fig. 6.
The discrepancies among the three fittings only became visible
in the subsequently derived velocity and acceleration profiles.
Although all three fittings were consistent in the early part of the data,
only CAlate_e re-produced the fast rising in the acceleration
seen after ![]() 14:40 UT.
Since the CA-type expressions match the observational data,
we can use the CA theory to deduce that
the eruptive flux rope seen in EIT may be free of current sheet
and that the current sheet may be formed shortly
after the CME went out of the EIT FOV.
The critical height,
14:40 UT.
Since the CA-type expressions match the observational data,
we can use the CA theory to deduce that
the eruptive flux rope seen in EIT may be free of current sheet
and that the current sheet may be formed shortly
after the CME went out of the EIT FOV.
The critical height, ![]() ,
obtained from our CA fit was approximately 200 Mm,
the corresponding Alfvén speed,
,
obtained from our CA fit was approximately 200 Mm,
the corresponding Alfvén speed,
![]() ,
was between 130 and 250 km s-1,
and the initial speed was roughly 3 km s-1.
The observation showed that
the foot-point separation of this CME was approximately 550 Mm
(cf. Fig. 1).
Our fitting-determined critical height,
being roughly half of the foot-point separation,
is consistent with the CA theory (cf. Sect. 2.1).
Assuming the plasma density
,
was between 130 and 250 km s-1,
and the initial speed was roughly 3 km s-1.
The observation showed that
the foot-point separation of this CME was approximately 550 Mm
(cf. Fig. 1).
Our fitting-determined critical height,
being roughly half of the foot-point separation,
is consistent with the CA theory (cf. Sect. 2.1).
Assuming the plasma density
![]() kg km-3and using
kg km-3and using
![]() km s-1, we can estimate the ambient magnetic field strength at the critical height as follows:
km s-1, we can estimate the ambient magnetic field strength at the critical height as follows:
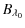
|
= | 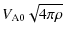
|
|
| (8) |
which is a reasonable value at
The exponent ![]() obtained from our Poly fit,
which gave a good match with the beginning part of the data,
was closer to 2 rather than 3,
which differed from the result by Schrijver et al. (2008).
Hence, the TI expressions produced by Schrijver et al. (2008)
and Kliem & Török (2006) both failed to fit our data.
This Poly fit result, however,
cannot be used to reject either BO or CA because
obtained from our Poly fit,
which gave a good match with the beginning part of the data,
was closer to 2 rather than 3,
which differed from the result by Schrijver et al. (2008).
Hence, the TI expressions produced by Schrijver et al. (2008)
and Kliem & Török (2006) both failed to fit our data.
This Poly fit result, however,
cannot be used to reject either BO or CA because
![]() was mostly scattered between 2 and 2.5.
was mostly scattered between 2 and 2.5.
The best-fit profile of our best CAlate_e fit had an exponent of 5.3.
This leads to the following expression
for the stage just before the formation of the current sheet:
TI, CA and CAlate_e expressions all failed to fit the LASCO data, which is as expected because LASCO only observed the later stage of the CME event. This is a promising indication that the expressions for our quantitative examination are appropriate verification tools. Poly fit was the only one that rendered a close match to the height-time data. However, some differences between the fitting results and the data become visible in the velocity and acceleration profiles. Specifically, Poly fit was incapable of re-producing the dip in the C2 velocity. Hence, Fig. 6 shows the result of fitting only the later, linear part of C2. In addition, the acceleration profile derived from the Poly fit result failed to resemble the profile derived from the data.
The fitting results of EIT and LASCO both revealed that the discrepancies become larger in the higher order derivatives. This suggests that the derived properties (e.g., velocity and accelerations) are more discerning than the directly fitted property (e.g., height) in verifying a model expression.
4.2 2007 December 31 (CME07)
Although the initial eruption phase of this CME was occulted, as we can infer from the derived initial velocity and acceleration profile (cf. Fig. 5), the peak acceleration in this phase is likely to coincide with the maximum of the derivative of the SXR profile (Temmer et al. 2008; Neupert 1968). By a quick visual inspection of Fig. 5, we estimate that the peak occurred approximately between 00:45 and 00:50 UT, which is also when a HXR emission was detected.
The kinematics profile of this CME and the SXR and HXR emission profiles are in good agreement with a BO scenario: the SXR emissions and flaring activities before the emergence of the loop and the HXR signal detected on the top of the emerged loop could be evidence of breakout reconnections. The second HXR signal, coinciding with the beginning of the re-acceleration phase, indicated that the reconnections cut off the drag force from the current sheet beneath the CME loop and accelerated the CME again. However, because the very beginning rising stage of the CME may have been obscured by the magnetic arcades, the CME may have begun to rise earlier than the increase of the SXR emissions, in which case, the timing would be in agreement with the CA theory. Since the reconnection is not a necessary condition to either initiate or accelerate a CME in a TI picture, we cannot use the X-ray emissions and flaring activities to verify the TI model. However, as we explained in Sect. 4.1, most TI simulations of the CME leading-edge kinematics did not show a drop of acceleration in the early phase of the eruption. Based on the above discussion and reasoning, we deduce that this CME was most likely driven by a BO mechanism.
The kinematics of CME07 were well re-produced by the Poly fit, but not the other three models. TI and CA-type expressions failed to fit even the height data. Hence, only the results of Poly fit were plotted in Fig. 7. The unsuccessful fitting using the TI and CA-type expressions is another indication that the CME was driven by neither of the mechanisms and/or that the early stage was not detected, which are both in agreement with the results from our qualitative comparison.
As can be seen in Fig. 7,
despite a few mismatching points in the velocity and acceleration,
overall, the kinematics, both the height and the derived velocity and acceleration,
of the observation and of the fitting were in good agreement.
Hence, we can deduce that each stage of this CME can be approximated
as a polynomial of the form
![]() even though the kinematics of entire process is too complex to be
fitted by one single function.
The fitting results suggest that the order of polynomial (i.e.,
even though the kinematics of entire process is too complex to be
fitted by one single function.
The fitting results suggest that the order of polynomial (i.e., ![]() )
for
the height-time data from the three instruments
were
)
for
the height-time data from the three instruments
were ![]() 3 for EUVI,
3 for EUVI, ![]() 2 for cor1 and
2 for cor1 and ![]() 2.65 for cor2.
2.65 for cor2.
5 Conclusions
One of the main goals of this study was to investigate the possible driving mechanisms behind coronal mass ejections. We have analyzed, both qualitatively and quantitatively, two CME events, and compared them with three CME models for this purpose.
The first CME was observed on 2006 December 17 by EIT and LASCO,
and the associated X-ray emissions were recorded by GOES and RHESSI.
This CME lasted for over eight hours,
and the SXR emission exhibited two rising phases.
A comparison of the SXR emission profile
and the kinematics of the CME showed that
the CME was launched earlier than
the rising of the SXR emissions,
reached an acceleration peak during
the second rising phase of the SXR emission.
The CME was first decelerated after the eruption,
and then re-accelerated to another acceleration peak of ![]() 60 m s-2,
at which time the SXR emissions reached the maximum
and a flare was detected.
The CME propagated away at a small, constant acceleration at the end.
60 m s-2,
at which time the SXR emissions reached the maximum
and a flare was detected.
The CME propagated away at a small, constant acceleration at the end.
Comparing the above information with the three CME models discussed in this paper, CA, TI and BO, we propose that this CME can be best described by a combination of CA and BO models. That is, the CME was initiated by an ideal MHD process (CA), as hinted by the absence of SXR emissions during the initial stage. The rising and expanding of the flux rope against the ambient magnetic fields then led to reconnections with these fields (BO). As it continued to rise, a current sheet was formed underneath, which exerted a dragging force to slow down the rising motion, and, lastly, the current sheet was cut off by reconnections and the CME was re-accelerated. Our quantitative examinations also revealed that the CA-type expressions gave the best fit to the EIT data. From the fitting results, we deduced that the critical height at which the CME erupted was approximately 200 Mm and the Alfvén speed at this height was around 130-250 km s-1, which leads to a magnetic field of about 7 Gauss. They are of reasonable order of magnitude for the low corona. Based on the model results by Lin & Forbes (2000), we can also infer from the occurrence of the deceleration of this CME that the reconnection rate in the current sheet may correspond to a Alfvén Mach number between 0.005 and 0.041.
The second CME was observed on 2007 December 31.
This CME was formed in a magnetic arcade system.
Our analysis indicated that the initial eruption stage might have been
obscured by the arcade system.
After this un-detected eruption, the acceleration of the CME dropped first and
then rose again to a peak value of ![]() 600 m s-2.
The CME remained at this peak acceleration until
its velocity reached a peak value of
600 m s-2.
The CME remained at this peak acceleration until
its velocity reached a peak value of ![]() 1000 km s-1.
The CME then decelerated and eventually propagated away at
a constant speed of
1000 km s-1.
The CME then decelerated and eventually propagated away at
a constant speed of ![]() 700 km s-1.
A comparison between the kinematics of the CME and
the SXR and HXR emission information from
GOES, MESSENGER SAX, and RHESSI
(cf., Fig. 5; Krucker et al. 2009a; Raftery et al. 2010; Krucker et al. 2009b)
showed that the SXR emission began to rise before the emergence of the CME
and peaked around the same time as the peak of the CME velocity,
and that the HXR emission due to particle accelerations
occurred at the time of the CME emergence and at the moment when the acceleration
of the CME began to rise again.
700 km s-1.
A comparison between the kinematics of the CME and
the SXR and HXR emission information from
GOES, MESSENGER SAX, and RHESSI
(cf., Fig. 5; Krucker et al. 2009a; Raftery et al. 2010; Krucker et al. 2009b)
showed that the SXR emission began to rise before the emergence of the CME
and peaked around the same time as the peak of the CME velocity,
and that the HXR emission due to particle accelerations
occurred at the time of the CME emergence and at the moment when the acceleration
of the CME began to rise again.
These observed features can be well described by a BO model as follows: the SXR emission before the CME emerged from the magnetic arcades and the high velocity and acceleration at the beginning of its emergence can be explained as that the breakout reconnections were happening as the CME loop was rising through and breaking the overlying arcade. The reconnections accelerated the CME, and caused the X-ray emissions. By the time the CME broke through the arcades, a trailing current sheet may have been formed to act as a drag force, which was reflected in the decrease of the acceleration. However, we note that some overlying features, such as streamers, could also slow down the CME. The subsequent rising of the acceleration (after 01:00 UT) and the detection of a HXR signal indicated that this drag force was being reduced by the reconnections in the current sheet. After the current sheet was completely cut off, the ambient coronal magnetic fields moved in to reform and settle to a lower potential state. The last stage of the CME indicated that it was being slowed down by the solar wind and/or interstellar medium. To be in agreement with a CA model, which proposes an ideal MHD process to initiate the eruption, a CME should have a beginning rising phase during which there was no X-ray emission. This is inconsistent with the observations of this CME, which detected flares and X-ray emissions from the very beginning of the eruption. However, since the initial rising stage of the CME was occulted, we cannot completely rule out the possibility that an ideal MHD process had taken place. The missing of this ideal MHD process in our data was also reflected in our unsuccessful fitting using CA-type expressions.
Both events exhibited a re-acceleration phase, during which the maximum acceleration coincided with the peak SXR emission. If higher SXR emissions indicate greater reconnection rates, as explained in Sect. 2.1, such coincidence can be explained as that the faster reconnections, which lead to faster reduction of the tethering force, increased the acceleration of the CME.
In conclusion, we have investigated two CME events. Our results showed that the first event, CME06, can be best described by a combination of the CA and BO models while the other event, CME07, can be well explained by the BO model alone. However, it is also possible that CME07 may have been initiated by an ideal MHD process. We conclude that TI model is the least likely driving mechanism for either of the events mainly because our observationally derived kinematic profiles do not match the profiles and expressions from the TI model. Specifically, the decreasing of acceleration in the early stage of our CME events is not seen in TI simulations to-date (Schrijver et al. 2008; Török & Kliem 2007; Kliem & Török 2006). Since our data is a two-dimensional projection of the actual motion, we acknowledge the possibility that this phase be a projection effect. Hence, to improve the accuracy of our analysis, we plan to utilize stereoscopic data to obtain an actual, three-dimensional kinematics of CMEs in our future work. At last, to improve the current CME models, our study suggests that the CA model include the reconnections/interactions between the CME and its ambient magnetic fields, BO model consider the possibility of an ideal MHD process in the early stage, and that TI model provide possible mechanisms for a drag force during the eruptive phase.
AcknowledgementsWe thank the referee for helpful comments that have improved the paper. This work is supported by an ESA/PRODEX grant administered by Enterprise Ireland. C.H.L. is also supported by National Center for Theoretical Sciences, Physics Division, Taiwan.
References
- Alexander, D., Metcalf, T. R., & Nitta, N. V. 2002, Geophys. Res. Lett., 29, 41 [Google Scholar]
- Antiochos, S. K., DeVore, C. R., & Klimchuk, J. A. 1999, ApJ, 510, 485 [Google Scholar]
- Bateman, G. 1978, MHD instabilities (Cambridge, Mass., MIT Press) [Google Scholar]
- Bong, S.-C., Moon, Y.-J., Cho, K.-S., et al. 2006, ApJ, 636, L169 [NASA ADS] [CrossRef] [Google Scholar]
- Brueckner, G. E., Howard, R. A., Koomen, M. J., et al. 1995, Sol. Phys., 162, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, J. 1989, ApJ, 338, 453 [NASA ADS] [CrossRef] [Google Scholar]
- Cremades, H., & Bothmer, V. 2004, A&A, 422, 307 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delaboudinière, J., Artzner, G. E., Brunaud, J., et al. 1995, Sol. Phys., 162, 291 [NASA ADS] [CrossRef] [Google Scholar]
- DeVore, C. R., & Antiochos, S. K. 2008, ApJ, 680, 740 [NASA ADS] [CrossRef] [Google Scholar]
- Forbes, T. G., & Isenberg, P. A. 1991, ApJ, 373, 294 [Google Scholar]
- Forbes, T. G., & Priest, E. R. 1995, ApJ, 446, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Gallagher, P. T., Lawrence, G. R., & Dennis, B. R. 2003, ApJ, 588, L53 [Google Scholar]
- Garcia, H. A. 1994, Sol. Phys., 154, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Howard, R. A., Moses, J. D., Vourlidas, A., et al. 2008, Space Sci. Rev., 136, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Kliem, B., & Török, T. 2006, Phys. Rev. Lett., 96, 255002 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Krall, J., Chen, J., Duffin, R. T., Howard, R. A., & Thompson, B. J. 2001, ApJ, 562, 1045 [NASA ADS] [CrossRef] [Google Scholar]
- Krucker, S., Hudson, H. S., White, S. M., & Lin, R. P. 2009a, in AAS/Solar Physics Division Meeting, 40, 868 [Google Scholar]
- Krucker, S., Hudson, H. S., White, S. M., et al. 2009b, ApJ, submitted [Google Scholar]
- Lin, J., & Forbes, T. G. 2000, J. Geophys. Res., 105, 2375 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, J., Forbes, T. G., Isenberg, P. A., & Demoulin, P. 1998, ApJ, 504, 1006 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, R. P., Dennis, B. R., Hurford, G. J., et al. 2002, Sol. Phys., 210, 3 [Google Scholar]
- Lynch, B. J., Antiochos, S. K., MacNeice, P. J., Zurbuchen, T. H., & Fisk, L. A. 2004, ApJ, 617, 589 [NASA ADS] [CrossRef] [Google Scholar]
- Lynch, B. J., Antiochos, S. K., DeVore, C. R., Luhmann, J. G., & Zurbuchen, T. H. 2008, ApJ, 683, 1192 [NASA ADS] [CrossRef] [Google Scholar]
- Manoharan, P. K., & Kundu, M. R. 2003, ApJ, 592, 597 [NASA ADS] [CrossRef] [Google Scholar]
- Neupert, W. M. 1968, ApJ, 153, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Priest, E., & Forbes, T. 2000, Magnetic Reconnection: MHD Theory and Applications, ed. E. Priest, & T. Forbes, 359, ISBN 0521481791 (Cambridge, UK: Cambridge University Press), 359 [Google Scholar]
- Priest, E. R., & Forbes, T. G. 2002, A&AR, 10, 313 [Google Scholar]
- Raftery, L. C., Gallagher, R. T., McAteer, R. T. J., Lin, C.-H., & Delahunt, G. 2010, ApJ, submitted [Google Scholar]
- Reeves, K. K., & Forbes, T. G. 2005, ApJ, 630, 1133 [NASA ADS] [CrossRef] [Google Scholar]
- Schrijver, C. J., Elmore, C., Kliem, B., Török, T., & Title, A. M. 2008, ApJ, 674, 586 [NASA ADS] [CrossRef] [Google Scholar]
- Sheeley, N. R., Walters, J. H., Wang, Y.-M., & Howard, R. A. 1999, J. Geophys. Res., 104, 24739 [Google Scholar]
- Temmer, M., Veronig, A. M., Vrsnak, B., et al. 2008, ApJ, 673, L95 [Google Scholar]
- Török, T., & Kliem, B. 2007, Astron. Nachr., 328, 743 [NASA ADS] [CrossRef] [Google Scholar]
- van Tend, W., & Kuperus, M. 1978, Sol. Phys., 59, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, J., Dere, K. P., Howard, R. A., & Vourlidas, A. 2004, ApJ, 604, 420 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13167fg1.ps} \vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/08/aa13167-09/Timg33.png)
|
Figure 1:
The image sequence of CME06
observed by EIT and LASCO C2 and C3.
The EIT images have been rotated so that the loop top
moves along X axis, as indicated by the dash line.
The pivot of the rotation is plotted as a star,
which is located at |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13167fg2.ps} \vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/08/aa13167-09/Timg34.png)
|
Figure 2: The kinematic profiles of CME06. Different symbols represent the observational results from different instruments, as denoted in the upper right panel. The GOES X-ray emission profile has been scaled to enhance the viewing, and hence the exact magnitude is irrelevant. The right column shows the combined profile of all three instruments. The left column shows only the results from the low corona to give a better view of the kinematics in this region. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13167fg3.ps} \vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/08/aa13167-09/Timg36.png)
|
Figure 3: The image sequence to show the formation stage of CME07 as observed by STEREO B EUVI 171 Å. The crosses mark our determined CME front. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13167fg4.ps} \vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/08/aa13167-09/Timg37.png)
|
Figure 4: The image sequence of CME07 observed by STEREO B instruments, EUVI 171 Å, cor1 and cor2. The crosses in all images mark our determined CME front. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13167fg5.ps} \vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/08/aa13167-09/Timg38.png)
|
Figure 5: The kinematic profiles of CME07. See the caption of Fig. 2 for the description of the figure. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13167fg6.ps} \vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2010/08/aa13167-09/Timg42.png)
|
Figure 6: The fitting results of CME06. The best results of applying different fitting models (i.e., CA, CAlate_e and poly) to the height data of EIT and LASCO C2 and C3 are plotted in different line styles. Different symbols represent the observational results of different instruments, as denoted in the figure. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13167fg7.ps} \vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2010/08/aa13167-09/Timg43.png)
|
Figure 7: The fitting results of CME07. The fitting model is a polynomial of the form Eq. (7). Different symbols and continuous lines respectively represent the observational and fitting results from different instruments, as denoted in the figure. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\begin{displaymath}\dot{h} \approx \sqrt{\frac{8}{\pi}} V_{\rm A0}
\left[
\ln \l...
...-1}\left(\frac{h}{\lambda_0}\right)
\right]^{1/2}
+ \dot{h_0},
\end{displaymath}](/articles/aa/full_html/2010/08/aa13167-09/img15.png)
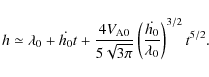
![\begin{displaymath}\dot{h} \approx \sqrt{\frac{8}{\pi}} V_{\rm A0}
\left[
\ln \left(\frac{h}{\lambda_0}\right) - \frac{\pi}{2}
\right]^{1/2}\cdot
\end{displaymath}](/articles/aa/full_html/2010/08/aa13167-09/img25.png)
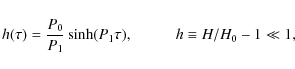
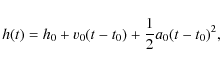
![\begin{displaymath}\dot{h} \approx \sqrt{\frac{8}{\pi}} V_{\rm A0}
\left[
\ln \l...
...rac{h}{\lambda_0}\right) - \frac{\pi}{2}
\right]^{\alpha}\cdot
\end{displaymath}](/articles/aa/full_html/2010/08/aa13167-09/img39.png)
![\begin{displaymath}\dot{h} \approx \sqrt{\frac{8}{\pi}} V_{\rm A0}
\left[
\ln \left(\frac{h}{\lambda_0}\right) - \frac{\pi}{2}
\right]^{5.3}\cdot
\end{displaymath}](/articles/aa/full_html/2010/08/aa13167-09/img50.png)