EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 516 (June-July 2010) A&A, 516 (2010) A111 Full HTML
Free Access
Issue
A&A
Volume 516, June-July 2010
Article Number A111
Number of page(s) 6
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/200912889
Published online 22 July 2010
A&A 516, A111 (2010)

Weak 13CO in the Cloverleaf quasar: evidence for a young, early generation starburst

C. Henkel1 - D. Downes2 - A. Weiß1 - D. Riechers3,4,5 - F. Walter4

1 - Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
2 - Institut de Radio Astronomie Millimétrique, Domaine Universitaire, 38406 St.-Martin-d'Hères, France
3 - California Institute of Technology, Astronomy Department, MC 249-17, 1200 East California Boulevard, Pasadena, CA 91125, USA
4 - Max-Planck-Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
5 - Hubble Fellow

Received 14 July 2009 / Accepted 19 April 2010

Abstract
Observations of 12CO at high redshift indicate rapid metal enrichment in the nuclear regions of at least some galaxies in the early universe. However, the enrichment may be limited to nuclei that are synthesized by short-lived massive stars, excluding classical ``secondary'' nuclei like 13C. Testing this idea, we used the IRAM Interferometer to tentatively detect the 13CO $J=3\rightarrow 2$ line at a level of 0.3 Jy km s-1 toward the Cloverleaf quasar at z = 2.5. This is the first observational evidence for 13C at high redshift. The 12CO/13CO $J=3\rightarrow 2$ luminosity ratio is with 40 +25-8 much higher than ratios observed in molecular clouds of the Milky Way and in the ultraluminous galaxy Arp 220, but may be similar to that observed toward NGC 6240. Large Velocity Gradient models simulating seven 12CO transitions and the 13CO line yield 12CO/13CO abundance ratios in excess of 100. It is possible that the measured ratio is affected by a strong submillimeter radiation field, which reduces the contrast between the 13CO line and the background. It is more likely, however, that the ratio is caused by a real deficiency of 13CO. This is already apparent in local ultraluminous galaxies and may be even more severe in the Cloverleaf because of its young age ($\la$2.5 Gyr). A potential conflict with optical data, indicating high abundances also for secondary nuclei in quasars of high redshift, may be settled if the bulk of the CO emission is originating sufficiently far from the active galactic nucleus of the Cloverleaf.

Key words: galaxies: abundances - galaxies: ISM - galaxies: individual: Cloverleaf quasar - Galaxy: evolution - nuclear reactions, nucleosynthesis, abundances - radio lines: galaxies

1 Introduction

There is evidence for solar or super-solar metallicities in the circumnuclear environments of quasars out to redshifts z>4 (e.g., Hamann & Ferland 1999; Kurk et al. 2007; Jiang et al. 2007; Juarez et al. 2009; Matsuoka et al. 2009). This evidence, mainly from optical lines, is supported by millimeter detections of CO and dust in high-redshift sources, indicating rapid metal enrichment due to starbursts in the circumnuclear regions of at least some galaxies in the early universe (e.g., Solomon & Vanden Bout 2005). This enrichment, however, might apply mainly to atomic nuclei that are synthesized in short-lived massive stars, and not so much to ``secondary'' nuclei like 13C that are thought to be mainly synthesized in longer-lived, less-massive stars (but see, e.g., Hamann et al. 2002, for the mainly secondary element nitrogen).

In the local universe, 12C/13C abundance ratios are sometimes considered to be a diagnostic of deep stellar mixing and a measure of ``primary'' vs. ``secondary'' nuclear processing (e.g., Wilson & Rood 1994). While 12C is produced by He burning on rapid time scales in massive stars, 13C is mainly synthesized by CNO processing of 12C seed nuclei from earlier stellar generations. This processing occurs more slowly, during the red giant phase in low- and intermediate-mass stars or novae. The 12C/13C ratio may therefore depend on the nucleosynthesis history. It could be much higher in high-z galaxies that are too young to have synthesized large amounts of secondary nuclei like 13C.

At optical, near-IR, and UV wavelengths it is difficult to discriminate between an element's isotopes because their atomic lines are blended (e.g., Levshakov et al. 2006). The prospects are better with radio lines from isotopic substitutions in molecules, which are well separated by a few percent of their rest frequency from the main species. This separation allows both the main and rare species to be easily identified, and to be observable with the same radio receivers and spectrometers.

The Cloverleaf quasar (H1413+117), partly because of amplification by gravitational lensing, is a high-z source with exceptional peak flux densities in 12C16O (hereafter 12CO; see Appendix 2 of Solomon & Vanden Bout 2005). This source is therefore one of the best candidates to search for 13C16O (hereafter 13CO) to try to test models of ``chemical'' evolution over a Hubble time. In this paper we report on a search for 13CO(3-2) emission in the Cloverleaf at z=2.5579, when the universe was 2.5 Gyr old.

2 Observations

The measurements were made with the IRAM Interferometer on Plateau de Bure, France, in July, August, and September 2008, with 5 antennas in the compact D-configuration (maximum baseline 97 m) and the new dual-polarization receivers. The receiver and system single-sideband temperatures were 40 and 100 K, respectively. The spectrometers covered 1 GHz in each polarization, and the raw spectral resolution was 2.5 MHz, or 8.1 km s-1. The data were binned to various spectral resolutions; in this paper we present data binned in $19\times160$ km s-1 channels, covering a range of 3040 km s-1, with a noise of 0.22 mJy beam-1 (1$\sigma $) in each channel. The naturally-weighted synthesized beam was 5 $~.\!\!^{\prime\prime}$$6\times4$ $~.\!\!^{\prime\prime}$8 at PA 62$^{\circ}$. Because the four CO spots of the lensed Cloverleaf image are spread over 1 $~.\!\!^{\prime\prime}$7, we included more of the total flux by applying to the u,v data a Gaussian taper that fell to 1/e at a radius of 100 m. The slightly broadened beam then became 6 $~.\!\!^{\prime\prime}$$1\times 5$ $~.\!\!^{\prime\prime}$4, and the noise in the individual channels is 0.23 mJy beam-1.

\begin{figure} \par\includegraphics[angle=0,width=8.5cm]{fig1-12889.eps} \end{figure} Figure 1:

Contour map of continuum plus 13CO $J=3\rightarrow 2$ emission, covering the central 960 km s-1 toward the Cloverleaf QSO. The beam is 6 $~.\!\!^{\prime\prime}$$1\times 5$ $~.\!\!^{\prime\prime}$4 ( lower left) and the contour step is 0.09 mJy (1$\sigma $). The peak value and the spatially-integrated intensity in the central source are both 0.6 mJy.

Open with DEXTER

\begin{figure} \par\includegraphics[angle=0,width=8.5cm]{fig2-12889.eps} \end{figure} Figure 2:

Contour map of the 3.2 mm continuum emission, covering 2080 km s-1in the off-line channels. The beam is 6 $~.\!\!^{\prime\prime}$$1\times 5$ $~.\!\!^{\prime\prime}$4 ( lower left) and the contour step is 0.09 mJy (1.5$\sigma $). The peak and the spatially-integrated flux density of the central source are both 0.3 mJy. Combining this figure with the previous one, we conclude that in the 960 kms-1 band centered on the 13CO $J=3\rightarrow 2$ line, line and continuum each contribute half of the total flux density.

Open with DEXTER

3 Results

Figures 1 through 3 show the data, and Table 1 summarizes the results. In the integrated line + continuum map (Fig. 1), the peak position (Table 1) agrees well with the centroid of previous high-resolution interferometer maps of the source (e.g., Alloin et al. 1997; Yun et al. 1997; Kneib et al. 1998). At 93 GHz, the expected continuum is 0.30-0.35 mJy (from Fig. 3 of Weiß et al. 2003; and the power-law given in Bradford et al. 2009) and a map in the 13 off-line channels at the positive and negative velocity ends of our spectra indeed yields a continuum flux of $0.3\pm0.1$ mJy (Fig. 2). This continuum adds to the line signal, and for this reason, the line appears much broader than the $\sim$430 kms-1 widths of the 12CO and [C I] lines (Weiß et al. 2003). The observed line has a low signal-to-noise ratio, which prevents a clear distinction between line and continuum, and does not allow us to constrain the line shape. Above the 0.3 mJy continuum, a Gaussian fit yields an integrated line flux of ($0.3\pm0.1$) Jy km s-1 (Fig. 3, see also the much higher upper limit given by Barvainis et al. 1997, their Table 1). An alternative Gaussian fit, with the line width fixed to the width of the 12CO line, yields a peak line flux density of ( $0.44\pm0.12$) mJy beam-1, and the same integrated line flux as the fit shown in Fig. 3. This integrated flux, corrected for frequency squared, leads to a 12CO/13CO $J=3\rightarrow 2$ line luminosity ratio (=brightness temperature ratio) of 40 +25-8 (Table 1). This value is conservative. With the line width fixed to the width of the 12CO line and the actual peak flux density of order 0.35 mJy, the ratio would become $\sim$75.

Table 1:   13CO(3-2) Observations and results.

\begin{figure} \par\resizebox{17.8cm}{!}{\rotatebox[origin=br]{-90.00}{\includegraphics{fig3-12889.eps}}} \end{figure} Figure 3:

CO $J=3\rightarrow 2$ from the Cloverleaf QSO, measured with the IRAM interferometer. Left: 12CO(3-2) profile in 10 kms-1 channels from Weiss et al. (2003). Velocity offsets are relative to 97.1928 GHz Right: 13CO(3-2) profile in 160 kms-1 channels, from this paper. Velocity offsets are relative to 92.91816 GHz ( z = 2.55784). The red curves show Gaussian fits above a continuum of 0.3 mJy.

Open with DEXTER

4 Large velocity gradient model calculations

12CO lines have higher optical depths than those of 13CO. Therefore, the measured 12CO/13CO line intensity ratio (Sect. 3) is a lower limit to the 12CO/13CO abundance ratio. To further constrain the 12CO/13CO abundance ratio of the Cloverleaf QSO, Table 2 provides flux densities and brightness temperatures of seven 12CO transitions. To simulate these values, a Large Velocity gradient (LVG) model was used with collision rates from Flower (2001), a cosmic microwave background of 9.7 K, and an ortho-to-para H2 abundance ratio of three (e.g., Weiß et al. 2005, 2007; Riechers et al. 2006b). The latter is, however, not critical for this study.

We calculated a grid for 12CO/13CO with kinetic temperatures of 30-100 K and 12CO fractional abundances per velocity interval of [12CO]/([H2](dv/dr)) = 10 -4...-7 pc (km s-1)-1. Accounting for possible effects of cloud structure, not only a spherical but also a plan-parallel cloud morphology was considered, with escape probabilities $\beta_{\rm spherical} = (1-{\rm e}^{-\tau}$)/$\tau$ and $\beta_{\rm plan-parallel}= (1-3{\rm e}^{-\tau}$)/(3$\tau$), respectively ($\tau$: optical depth). Resulting 12CO/13CO abundance ratios reproducing the six measured 12CO line intensity ratios (Table 2) are given in Figs. 4 and 5 together with reduced $\chi ^2$ ( $\chi ^2_{\rm red}$) values of the best fit. We adopted a 1$\sigma $ error of 15% for each fitted brightness temperature ratio. The dependence of the resulting 12CO/13CO ratios on cloud morphology is caused by the different escape probabilities, related to $\tau$ in the case of a spherical and to 3$\tau$ in the case of a plan-parallel cloud geometry. Therefore, a required amount of excitation through photon trapping is reached at lower 12CO optical depths in the case of a plan-parallel morphology, resulting in smaller 12CO/13CO abundance ratios.

Table 2:   CO line ratios in the Cloverleaf.

The $\chi ^2_{\rm red}$ values displayed in Figs. 4 and 5 indicate that the CO data can be fitted by a single molecular gas component (cf. Bradford et al. 2009). All calculations are also consistent with the (not very stringent) upper limits for the 13CO $J = 7\rightarrow6$ and $8\rightarrow7$ flux densities from Bradford et al. (2009). At first sight, the figures do not strongly reduce the permitted parameter space, providing $\chi ^2_{\rm red}$ values of order 1.25-2. In the upper left corners of each figure, however, the $\chi ^2_{\rm red}$ values rise significantly, becoming too large to provide credible solutions. As a consequence, the overall 12CO/13CO abundance ratio appears to be >100 in the Cloverleaf QSO. There exist further constraints: (1) $T_{\rm kin}$ < 30 K is prohibitive because of the temperatures determined from C I ($\sim$30 K) and the dust ($\sim$50 K, Weiss et al. 2003). Furthermore, such low temperatures would require extreme CO column densities to raise photon trapping to such levels that the emission from the higher J transitions could be reproduced. (2) $T_{\rm kin}$ > 50 K is also not likely because of the temperature deduced from [C I] and the close association of CO and C I, which appears to be independent of the environment (e.g., Ikeda et al. 2002; Zhang et al. 2007).

For $30\leq T_{\rm kin}\leq50$ K and [12CO]/([H2](dv/dr)) = 10-7 pc (km s-1)-1, we obtain 12CO/13CO abundance ratios in the range 200-3000 (Figs. 4 and 5). However, such a low fractional abundance per velocity interval can be firmly excluded. With [C I]/[H2] reaching values in agreement with those of the local galactic disk (Weiß et al. 2005), the [12CO]/[H2] abundance ratio should be of order 10-4 (e.g., Frerking et al. 1982). The resulting velocity gradient of dv/dr = 103 km s-1 pc-1 would be far too large in view of the measured line width (e.g., Weiß et al. 2003) and the kinetic temperature such extreme conditions would induce (e.g., Wiklind & Henkel 2001). A velocity gradient of a few km -1 pc-1 is more realistic as, e.g., obtained from clouds in virial equilibrium for densities of order 104 cm-3 (Goldsmith 2001; his Eq. (2)). Such densities are commonly derived for high z sources (e.g., Weiß et al. 2005, 2007). For diffuse clouds, velocity gradients should be larger (e.g., Papadopoulos et al. 2010). Bradford et al. (2009) suggest that in the Cloverleaf the velocity dispersion may exceed the virial requirement by at least an order of magnitude. Therefore the best choice may be [12CO]/([H2](dv/dr)) = 10 -6...-5 pc (km s-1)-1 (for the higher value see, e.g., Riechers et al. 2006b; Weiß et al. 2007) to simultaneously fit the observed CO transitions from $J=1\rightarrow0$ up to $11\rightarrow10$. Depending on the adopted kinetic temperature (30-50 K) and cloud morphology, and irrespective of the optimal [12CO]/([H2](dv/dr)) value (as long as it is in the wide range displayed by Figs. 4 and 5) we then find a 12CO/13CO abundance ratio in the range 300-10 000. In the following we will discuss whether this estimate can be realistic.

\begin{figure} \par\includegraphics[width=8cm,clip]{fig4-12889.eps} \end{figure} Figure 4:

Results from large velocity gradient (LVG) radiative transfer calculations using a spherical cloud model to simulate the line intensity ratios given in Table 2. The common logarithm of the 12CO/13CO abundance ratio is shown as a function of kinetic temperature in units of Kelvin and of fractional abundance in units of pc (km s-1)-1 for a 12CO/13CO $J=3\rightarrow 2$ line intensity ratio of 40. Resulting reduced $\chi ^2$ values ( $\chi ^2_{\rm red}$) for the simulation of the four 12CO lines given in Table 2 are shaded. Lightest grey: $1.00 \leq \chi ^2_{\rm red} < 1.25$, darker shades of grey at 1.25, 1.50, 1.75 to 4.00 with an increment of 0.25. The maximum value in the upper left corner is $\chi ^2_{\rm red} = 4.07$.

Open with DEXTER

\begin{figure} \par\includegraphics[width=8cm,clip]{fig5-12889.eps} \vspace*{1.5mm}\end{figure} Figure 5:

Same as Fig. 4, but for a plan-parallel cloud geometry. Resulting $\chi ^2_{\rm red}$ values for the simulation of the line intensity ratios given in Table 2 are shaded. Lightest grey: $1.00 \leq \chi ^2< 1.25$, darker shades of grey at 1.25, 1.50, 1.75 to 4.00 with an increment of 0.25. The maximum value in the upper left corner is $\chi ^2_{\rm red} = 6.31$.

Open with DEXTER

5 Discussion

In order to further evaluate our observational result, we have to discuss the correlation between molecular 12CO/13CO and atomic 12C/13C abundance ratios and to summarize relevant observational data from low-redshift galaxies which are, like the Cloverleaf, ultraluminous in the infrared. Finally, we will address some fundamental problems, which are related to the still poorly known morphology of the gas surrounding the Cloverleaf QSO.

5.1 Chemical fractionation and isotope selective photodissociation

Observed isotope ratios may be affected by fractionation. The 12CO/13CO abundance ratio is likely influenced by the reaction

\begin{displaymath}^{13}{\rm C}^+ + ^{12}{\rm CO} \rightarrow\ ^{12}{\rm C}^+ + ^{13}{\rm CO} + \Delta E_{\rm 35~K} \end{displaymath}

(Watson et al. 1976). The process enhances 13CO relative to 12CO in the more diffuse C+ rich parts of molecular clouds. This may be compensated by isotope selective photodissociation. 12CO and 13CO need similar amounts of self-shielding to survive in a hostile interstellar environment. This favors the more abundant isotopologue (e.g., Sheffer et al. 2007).

For the Galaxy, such effects can be quantified. Milam et al. (2005) summarized 12C/13C ratios from the galactic disk, obtained with the three molecules CO, CN, and H2CO. These molecular species are synthesized by quite different chemical reactions. The good agreement between their 12C/13C ratios and a lack of correlation with kinetic temperature suggest that chemical fractionation as well as isotope selective photodissociation do not greatly affect the determined isotope ratios.

Whether this result is also valid in the case of the Cloverleaf QSO may not be obvious at first sight. The ultraviolet radiation field in the vicinity of the quasar might be exceptionally strong, favoring 12CO over 13CO and thus leading to an enhanced molecular abundance ratio with respect to 12C/13C. However, such a scenario is not likely. Firstly, most of the galactic data were obtained toward prominent sites of massive star formation, where the UV radiation field is also exceptionally intense. Secondly, judging from C I, in the Cloverleaf the excitation of the molecular gas is intermediate between conditions found for the starburst galaxy M 82 ( $T_{\rm ex,CI} \sim50$ K) and the central region of the Milky Way ( $T_{\rm ex,CI} \sim 22$ K) (Stutzki et al. 1997; Weiß et al. 2003). Thirdly, polycyclic aromatic hydrocarbon (PAH) features are as strong as expected with respect to the far infrared luminosity when compared with more nearby ultraluminous star-forming galaxies, favoring ``normal'' conditions and a predominantly starburst nature of the Cloverleaf's huge FIR emission (Lutz et al. 2007). Finally, the CO emission from the Cloverleaf appears to be more extended than the effective radius out to which the quasar could dominate the UV field.

Modeling both the source and the lens of the Cloverleaf QSO, Venturini & Solomon (2003) find a characteristic radius of r $\sim$ 800 pc for the CO J=7-6 line, which is higher excited and thus possibly less widespread than the $J=3\rightarrow 2$ transition considered here. If the Cloverleaf's intrinsic far infrared luminosity ( $L_{\rm FIR} \sim 5\times10^{12}$ $L_{\odot}$, Lutz et al. 2007) would entirely originate from 6.2-13.6 eV photons emitted by the active nucleus, we would obtain, at a radius of 800 pc, a UV photon illumination of $\chi \sim 10^5$ $\chi_0$ with respect to the local galactic radiation field, $\chi_0 =2\times10^{-4}$  erg cm-2 s-1 sr-1 (see Draine 1978). The Cloverleaf QSO is a Broad Absorption Line (BAL) quasar which permits at least a partial view onto its nuclear engine. Therefore, taking the Cloverleaf's UV luminosity from Fig. 1 of Barvainis et al. (1995) and accounting for a gravitational amplification by a factor of 11 (Solomon & Vanden Bout 2005), we obtain accordingly $\chi \sim 2.5 \times 10^4$ $\chi_0$. Both $\chi$values are consistent with those encountered in prominent galactic sites of massive star formation and may be upper limits if the Cloverleaf posseses a self-shielding rotating disk. To summarize, physical conditions in the Cloverleaf host galaxy appear to be sufficiently normal so that the 12C/13C isotope ratio should not strongly deviate from the 12CO/13CO molecular abundance ratio.

5.2 12CO/13CO ratios in 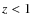$\textit {z} <1$ galaxies

In our Galaxy, the 12CO/13CO line intensity ratios from molecular clouds are typically about 5, probably corresponding to true 12C/13C abundance ratios of $\sim$25 in the galactic Center, $\sim$50 in the inner galactic disk and the LMC, $\sim$70 at the Sun's galactocentric radius, and $\ga$100 in the outer Galaxy. The solar system ratio of 89 may have been typical of the galactic disk at the Sun's galactocentric radius 4.6 Gyr ago (e.g., Wilson & Rood 1994; Wouterloot & Brand 1996; Wang et al. 2009). Within the framework of ``biased infall'', where the galactic disk developed from inside out (Chiappini et al. 2001), there might be a future chance to use 12C/13C ratios as a chronometer for nucleosynthesis.

In nearby galaxies, the 12CO/13CO line intensity ratios are usually measured in the J=1-0 line and have typical values of $\sim$10. They are higher than the values for individual molecular clouds in the Galaxy because they are mostly observed with larger beams. These include not only the dense clouds, where both species are (almost) optically thick, but also the molecular intercloud medium, where 13CO is optically thin. Like the better-resolved CO line ratios in our Galaxy, the ratios in nearby galaxies probably correspond to true 12C/13C abundance ratios between 40 and 90 (e.g., Henkel et al. 1993).

In a presumably ``normal'' spiral galaxy at redshift 0.89, in the lens of the background source PKS 1830-211, Wiklind & Combes (1998), Menten et al. (1999), and Muller et al. (2006) derive, from the optically thin wings of the absorption lines of HCO+, HCN, and HNC, a 12C/13C abundance ratio of $27\pm2$. Apparently, even at an age of the universe of $\sim$6.5 Gyr, it appears that 13C is as abundant with respect to 12C as in the center of our Galaxy at the present epoch. Some low-redshift (ultra)luminous infrared galaxies ((U)LIRGs), however, show peculiarities, which may be more relevant to the Cloverleaf. Local (U)LIRGs are known to reveal 12CO/13CO $J=1\rightarrow0$line intensity ratios which tend to be higher than the canonical value of 10 for ``normal'' galaxies (see, e.g., Aalto et al. 1991; Casoli et al. 1992; Henkel & Mauersberger 1993). According to Taniguchi & Ohyama (1998), there is a tight correlation between L(12CO $J=1\rightarrow0$) and $L_{\rm FIR}$. However, when comparing ``normal'' galaxies with those with a high 12CO/13CO $J=1\rightarrow0$ ratio, the 13CO luminosities show a deficiency by an average factor of $\sim$3, This 13CO deficiency is readily explained by metallicity gradients in the progenitor galaxies and strong interaction- or merger-induced inflow of gas into the luminous cores (e.g., Rupke et al. 2008). Apparently, for ultraluminous galaxies the common luminosity - metallicity correlation is not valid. Ultraluminous galaxies are characterized by a lower metallicity, likely yielding higher 12C/13C isotope ratios. In the early universe, gas from outside the cores of the merging progenitors may have been particularly metal poor, leading to extreme carbon isotope ratios.

For $T_{\rm kin}$ $\ga$20 K, the 12CO $J=3\rightarrow 2$ line is more opaque, typically by a factor of 3, than the corresponding $1\rightarrow 0$line. Thus our conservatively estimated J=3-2 12CO/13CO line intensity ratio of $\ga$40 +25-8 corresponds to a $1\rightarrow 0$ ratio well in excess of 40. So far, only few 12CO/13CO $J=3\rightarrow 2$ line ratios have been measured in luminous mergers of low redshift. Greve et al. (2009) find $8\pm2$ for the ULIRG Arp 220 and $\ga$30 for the LIRG NGC 6240. The latter value might be consistent with that of the Cloverleaf.

5.3 Are there alternatives to a 13C deficiency in the Cloverleaf?

Sects. 5.1 and 5.2 suggest, that our measured 12CO/13CO line intensity ratio (or its lower limit) require a significant 13C deficiency in the Cloverleaf. Are there caveats we may have overlooked when reaching this conclusion?

If the bulk of the CO emission would not arise, as suggested by Venturini & Solomon (2003), from a molecular disk but from a large scale outflow, such gas would not be in virial equilibrium and could arise predominantly from a diffuse gas phase. While this would yield (within the LVG approach) a higher velocity gradient and a lower [12CO]/([H2](dv/dr)) value than what is needed for virialized clouds, required densities would then be well in excess of 104 cm-3, in contradiction with our assumption of predominantly diffuse gas. Furthermore, as long as $T_{\rm kin}$ remains moderate ($\la$50 K; see Figs. 4 and 5), 12C/13C ratios remain larger than those encountered in the galactic disk (Sect. 5.1).

Following White (1977), radiative transfer models with simple geometry, either based on microturbulence or on systematic motions, lead to peak and integrated intensities which agree within the differences (up to a factor of three) caused by an uncertain cloud geometry. A full 3-D model of a rotating circumnuclear disk, computing the radiative transfer through many lines of sight, calculating the LVG level populations within each pixel of the simulated source, and also including continuum radiation from dust (e.g., Downes & Solomon 1998) may be worth doing. In the Cloverleaf, however, the distribution of the molecular gas is still poorly known.

A large 12C/13C ratio, implying an underabundance of 13C, appears to be in direct conflict with optical data. As already mentioned in Sect. 1, solar or super-solar metallicities are common in quasars up to high redshifts. This does not only refer to so-called ``$\alpha$-elements'' being rapidly synthesized in short-lived massive stars but also to iron (e.g., Iwamuro et al. 2004; Kurk et al. 2007; Sameshima et al. 2009), carbon (e.g., Jiang et al. 2007; Juarez et al. 2009), and, even more importantly, nitrogen (Hamann & Ferland 1999; De Breuck et al. 2000; Vernet et al. 2001; Hamann et al. 2002; Nagao et al. 2006; Matsuoka et al. 2009), with 14N being mainly a secondary nucleus produced by CNO burning just like 13C. A possible explanation for the contradictory results obtained at or near optical wavelengths and the microwave data presented here may be different locations. It is well possible that mainly secondary nuclei like 13C and 14N are enriched close to the quasar, in the Broad and Narrow Line Regions and in outflows originating from the active galactic nucleus (AGN). However, CO $J = 7\rightarrow6$ may arise hundreds of pc away from the AGN (Venturini & Solomon 2003) and some of the $J=3\rightarrow 2$ photons may be emitted from locations even farther away.

There exists, however, also the possibility that our measured high 12CO/13CO luminosity ratio is misleading and does not imply a large 12C/13C ratio. As a consequence of different optical depths, 12CO lines are almost thermalized and are characterized by excitation temperatures well above the level of the cosmic microwave background even at z=2.5. 13CO is less thermalized. In our best fitting models, its $J=3\rightarrow 2$ excitation temperature lies in the range 20-30 K. This is significantly above the 9.7 K of the CMB. However, an extreme (and therefore unlikely) enhancement of the background level by dust radiation could reduce the contrast between line and background for 13CO far more efficiently than for 12CO (see Papadopoulos et al. 2010 for the case of Arp 220), thus establishing an apparent 13CO deficiency.

6 Outlook

Molecular lines from galaxies in the distant universe have the potential to reveal the contribution of early stellar generations to the enrichment of the interstellar medium. Our data from the z = 2.5 Cloverleaf QSO are a first step toward studying the isotopic composition of such gas in the distant past. Our data indicate, not unexpectedly, a strong deficiency of 13C with respect to 12C in the host galaxy. However, the weakness of the tentatively detected line, the limited number of observed transitions, the poorly constrained source morphology, and the potential influence of an enhanced submillimeter radiation background do not yet allow us to derive a definite 12C/13C isotope ratio. Significant progress in this field either requires the detection of stronger sources or the higher instrumental sensitivity of the Atacama Large Millimeter Array (ALMA), which will allow us to study the isotopes of C, N, and O in a number of highly redshifted targets. Toward the Cloverleaf, the main isotopologes of HCN, HCO+, and CN (Solomon et al. 2003; Riechers et al. 2006a, 2007) have already been detected.

Acknowledgements
We wish to thank P. P. Papadopoulos, D. Riquelme, S. Veilleux, and an anonymous referee for helpful discussions on ULIRGs and chemical evolution and/or a critical reading of the manuscript. This paper is based on observations taken with the IRAM Plateau de Bure Interferometer. IRAM is supported by INSU/CNRS (France), the MPG (Germany), and the IGN (Spain). D.R. acknowledges support from NASA through Hubble Fellowship grant HST-HF-01212.01-A, awarded by the Space Telescope Science Institute, which is operated by AURA for NASA under contract NAS5-26555. This research has made use of NASA's Astrophysical Data System (ADS).

References

  1. Aalto, S., Johansson, L. E. B., Booth, R. S., & Black, J. H. 1991, A&A, 249, 323 [Google Scholar]
  2. Alloin, D., Guilloteau, S., Barvainis, R., Antonucci, R., & Tacconi, L. 1997, A&A, 321, 24 [NASA ADS] [Google Scholar]
  3. Barvainis, R., Antonucci, R., Hurt, T., Coleman, P., & Reuter, H.-P. 1995, ApJ, 451, L9 [NASA ADS] [CrossRef] [Google Scholar]
  4. Barvainis, R., Maloney, P., Antonucci, R., & Alloin, D. 1997, ApJ, 484, 695 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bradford, C. M., Aguirre, J. E., Aikin, R., et al. 2009, ApJ, 705, 112 [NASA ADS] [CrossRef] [Google Scholar]
  6. Casoli, F., Dupraz, C., & Combes, F. 1992, A&A, 264, 55 [NASA ADS] [Google Scholar]
  7. Chiappini, C., Matteucci, F., & Romano, D. 2001, ApJ, 554, 1044 [NASA ADS] [CrossRef] [Google Scholar]
  8. De Breuck, C., Röttgering, H., Miley, G., van Breugel, W., & Best, P. 2000, A&A, 362, 519 [NASA ADS] [Google Scholar]
  9. Downes, D., & Solomon, P. M. 1998, ApJ, 507, 615 [NASA ADS] [CrossRef] [Google Scholar]
  10. Draine, B. T. 1978, ApJS, 36, 595 [NASA ADS] [CrossRef] [Google Scholar]
  11. Flower, D. R. 2001, J. Phys. B. At. Mol. Opt. Phys., 34, 2731 [Google Scholar]
  12. Frerking, M. A., Langer, W. D., & Wilson, R. W. 1982, ApJ, 262, 590 [NASA ADS] [CrossRef] [Google Scholar]
  13. Goldsmith, P. F. 2001, ApJ, 557, 736 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  14. Greve, T. R., Papadopoulos, P. P., Gao, Y., & Radford, S. J. E. 2009, ApJ, 692, 1432 [NASA ADS] [CrossRef] [Google Scholar]
  15. Hamann, F., & Ferland, G. 1999, ARA&A, 37, 487 [NASA ADS] [CrossRef] [Google Scholar]
  16. Hamann, F., Korista, K. T., Ferland, G. J., Warner, C., & Baldwin, J. 2002, ApJ, 564, 592 [NASA ADS] [CrossRef] [Google Scholar]
  17. Henkel, C., & Mauersberger, R. 1993, A&A, 274, 730 [NASA ADS] [Google Scholar]
  18. Henkel, C., Mauersberger, R., Wiklind, T., et al. 1993, A&A, 268, L17 [NASA ADS] [Google Scholar]
  19. Ikeda, M., Oka, T., Tatematsu, K., Sekimoto, Y., & Yamamoto, S. 2002, ApJS, 139, 467 [NASA ADS] [CrossRef] [Google Scholar]
  20. Iwamuro, F., Kimura, M., Eto, S., et al. 2004, ApJ, 614, 69 [NASA ADS] [CrossRef] [Google Scholar]
  21. Jiang, L., Fan, X., Vestergaard, M., et al. 2007, AJ, 134,1150 [NASA ADS] [CrossRef] [Google Scholar]
  22. Juarez, Y., Maiolino, R., Mujica, R., et al. 2009, A&A, 494, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Kneib, J.-P., Alloin, D., Mellier, Y., et al. 1998, A&A, 329, 827 [NASA ADS] [Google Scholar]
  24. Kurk, J. D., Walter, F., Fan, X., et al. 2007, ApJ, 669, 32 [NASA ADS] [CrossRef] [Google Scholar]
  25. Levshakov, S. A., Centurión, M., Molaro, P., & Kostina, M. V. 2006, A&A, 447, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Lutz, D., Sturm, E., Tacconi, L. J., et al. 2007, ApJ, 661, L25 [NASA ADS] [CrossRef] [Google Scholar]
  27. Matsuoka, K., Nagao, T., Maiolino, R., Marconi, A., & Taniguchi, Y. 2009, A&A, 503, 721 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Menten, K. M., Carilli, C., & Reid, M. J. 1999, in Highly Redshifted Radio Lines, ed. C. Carilli et al., ASP Conf. Ser., 156, 218 [Google Scholar]
  29. Milam, S. N., Savage, C., Brewster, M. A., Ziurys, L. M., & Wyckoff, S. 2005, ApJ, 634, 1126 [NASA ADS] [CrossRef] [Google Scholar]
  30. Muller, S., Guélin, M., Dumke, M., Lucas, R., & Combes, F. 2006, A&A, 458, 417 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Nagao, T., Maiolino, R., & Marconi, A. 2006, A&A, 447, 863 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Papadopoulos, P. P., Isaak, K., & van der Werf, P. 2010, ApJ, 711, 757 [NASA ADS] [CrossRef] [Google Scholar]
  33. Riechers, D., Walter, F., Carilli, C. L., et al. 2006a, ApJ, 645, L13 [NASA ADS] [CrossRef] [Google Scholar]
  34. Riechers, D., Walter, F., Carilli, C., et al. 2006b, ApJ, 650, 604 [NASA ADS] [CrossRef] [Google Scholar]
  35. Riechers, D., Walter, F., Cox, P., et al. 2007, ApJ, 666, 778 [NASA ADS] [CrossRef] [Google Scholar]
  36. Rupke, D. S. N., Veilleux, S., & Baker, A. J. 2008, ApJ, 674, 172 [NASA ADS] [CrossRef] [Google Scholar]
  37. Sameshima, H., Maza, J., Matsuoka, Y., et al. 2009, MNRAS, 395, 1087 [NASA ADS] [CrossRef] [Google Scholar]
  38. Sheffer, Y., Rogers, M., Federman, S. R., Lambert, D. L., & Gredel, R. 2007, ApJ, 667, 1002 [NASA ADS] [CrossRef] [Google Scholar]
  39. Solomon, P. M., & Vanden Bout, P. 2005, ARA&A, 43, 677 [NASA ADS] [CrossRef] [Google Scholar]
  40. Solomon, P. M., Vanden Bout, P., Carilli, C. L., & Guélin, M. 2003, Nature, 426, 636 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  41. Stutzki, J., Graf, U. U., Haas, S., et al. 1997, ApJ, 477, L33 [NASA ADS] [CrossRef] [Google Scholar]
  42. Taniguchi, Y., & Ohyama, Y. 1998, ApJ, 507, L21 [Google Scholar]
  43. Venturini, S., & Solomon, P. M. 2003, ApJ, 590, 740 [NASA ADS] [CrossRef] [Google Scholar]
  44. Vernet, J., Fosbury, R. A. E., Villar-Martín, M., et al. 2001, A&A, 366, 7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Wang, M., Chin, Y.-N., Henkel, C., Whiteoak, J. B., & Cunningham, M. 2009, ApJ, 690, 580 [NASA ADS] [CrossRef] [Google Scholar]
  46. Watson, W. D., Anichich, V. G., & Huntress, W. T. 1976, ApJ, 205, L165 [NASA ADS] [CrossRef] [Google Scholar]
  47. Weiß, A., Henkel, C., Downes, D., & Walter, F. 2003, A&A, 409, L41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Weiß, A., Downes, D., Walter, F., & Henkel, C. 2005, A&A, 440, L45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Weiß, A., Downes, D., Neri, R., et al. 2007, A&A, 467, 955 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. White, R. E. 1977, ApJ, 211, 744 [NASA ADS] [CrossRef] [Google Scholar]
  51. Wiklind, T., & Combes, F. 1998, ApJ 500, 129 [NASA ADS] [CrossRef] [Google Scholar]
  52. Wiklind, T., & Henkel, C. 2001, A&A 375, 797 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Wilson, T. L., & Rood, R. 1994, ARA&A, 32, 191 [NASA ADS] [CrossRef] [Google Scholar]
  54. Wright, E. L. 2006, PASP, 118, 1711 [NASA ADS] [CrossRef] [Google Scholar]
  55. Wouterloot, J. G. A., & Brand, J. 1996, A&AS, 119, 439 [Google Scholar]
  56. Yun, M. S., Scoville, N. Z., Carrasco, J. J., & Blandford, R. D. 1997, ApJ, 479, l9 [Google Scholar]
  57. Zhang, J. S., Henkel, C., Mauersberger, R., et al. 2007, A&A, 465, 887 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

All Tables

Table 1:   13CO(3-2) Observations and results.

Table 2:   CO line ratios in the Cloverleaf.

All Figures

  \begin{figure} \par\includegraphics[angle=0,width=8.5cm]{fig1-12889.eps} \end{figure} Figure 1:

Contour map of continuum plus 13CO $J=3\rightarrow 2$ emission, covering the central 960 km s-1 toward the Cloverleaf QSO. The beam is 6 $~.\!\!^{\prime\prime}$$1\times 5$ $~.\!\!^{\prime\prime}$4 ( lower left) and the contour step is 0.09 mJy (1$\sigma $). The peak value and the spatially-integrated intensity in the central source are both 0.6 mJy.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=0,width=8.5cm]{fig2-12889.eps} \end{figure} Figure 2:

Contour map of the 3.2 mm continuum emission, covering 2080 km s-1in the off-line channels. The beam is 6 $~.\!\!^{\prime\prime}$$1\times 5$ $~.\!\!^{\prime\prime}$4 ( lower left) and the contour step is 0.09 mJy (1.5$\sigma $). The peak and the spatially-integrated flux density of the central source are both 0.3 mJy. Combining this figure with the previous one, we conclude that in the 960 kms-1 band centered on the 13CO $J=3\rightarrow 2$ line, line and continuum each contribute half of the total flux density.

Open with DEXTER
In the text

  \begin{figure} \par\resizebox{17.8cm}{!}{\rotatebox[origin=br]{-90.00}{\includegraphics{fig3-12889.eps}}} \end{figure} Figure 3:

CO $J=3\rightarrow 2$ from the Cloverleaf QSO, measured with the IRAM interferometer. Left: 12CO(3-2) profile in 10 kms-1 channels from Weiss et al. (2003). Velocity offsets are relative to 97.1928 GHz Right: 13CO(3-2) profile in 160 kms-1 channels, from this paper. Velocity offsets are relative to 92.91816 GHz ( z = 2.55784). The red curves show Gaussian fits above a continuum of 0.3 mJy.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{fig4-12889.eps} \end{figure} Figure 4:

Results from large velocity gradient (LVG) radiative transfer calculations using a spherical cloud model to simulate the line intensity ratios given in Table 2. The common logarithm of the 12CO/13CO abundance ratio is shown as a function of kinetic temperature in units of Kelvin and of fractional abundance in units of pc (km s-1)-1 for a 12CO/13CO $J=3\rightarrow 2$ line intensity ratio of 40. Resulting reduced $\chi ^2$ values ( $\chi ^2_{\rm red}$) for the simulation of the four 12CO lines given in Table 2 are shaded. Lightest grey: $1.00 \leq \chi ^2_{\rm red} < 1.25$, darker shades of grey at 1.25, 1.50, 1.75 to 4.00 with an increment of 0.25. The maximum value in the upper left corner is $\chi ^2_{\rm red} = 4.07$.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{fig5-12889.eps} \vspace*{1.5mm}\end{figure} Figure 5:

Same as Fig. 4, but for a plan-parallel cloud geometry. Resulting $\chi ^2_{\rm red}$ values for the simulation of the line intensity ratios given in Table 2 are shaded. Lightest grey: $1.00 \leq \chi ^2< 1.25$, darker shades of grey at 1.25, 1.50, 1.75 to 4.00 with an increment of 0.25. The maximum value in the upper left corner is $\chi ^2_{\rm red} = 6.31$.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.