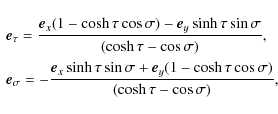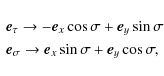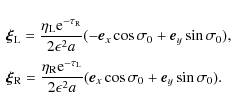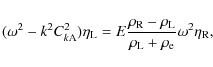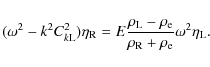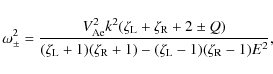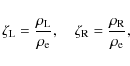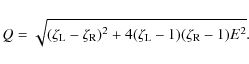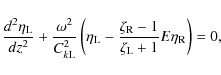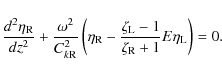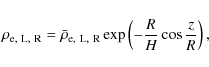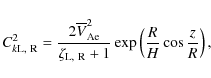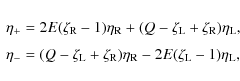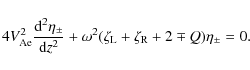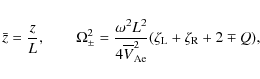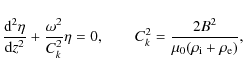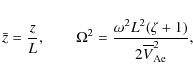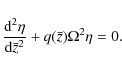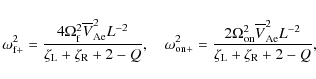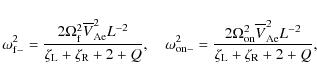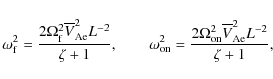| Issue |
A&A
Volume 515, June 2010
|
|
|---|---|---|
| Article Number | A33 | |
| Number of page(s) | 8 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201014055 | |
| Published online | 04 June 2010 | |
The effect of density stratification on the transverse oscillations of two parallel coronal loops
D. Robertson - M. S. Ruderman - Y. Taroyan
Department of Applied Mathematics, University of Sheffield, Hicks Building, Hounsfied Road, Sheffield, S3 7RH, UK
Received 13 January 2010 / Accepted 2 March 2010
Abstract
Transverse oscillations of coronal magnetic loops are routinely observed
during the space missions. Since the first observation these oscillations
were interpreted in terms of kink oscillations of magnetic tubes. Sometimes
collective oscillations of two or more coronal loops are observed. This
makes the development of theory of collective oscillations of a few parallel
magnetic tubes desirable. Another reason for the development of this
theory is that there are evidences that at least some coronal loops are
not monolithic but consist of many thin magnetic threads. In this paper
the linear theory of kink oscillations of two parallel magnetic tubes
with the density varying along the tubes is developed. The asymptotic
method is used to derive the system of equations governing the collective
kink oscillations of two tubes. This system is used to study the effect
of density variation on the eigenfrequencies of collective oscillations.
The implication of the obtained results on coronal seismology is
discussed.
Key words: magnetohydrodynamics (MHD) - methods: analytical - Sun: corona - Sun: oscillations - waves
1 Introduction
The solar corona is a highly non-uniform medium. Its structure is closely related to the magnetic field. In particular, in active regions of the corona there are myriads of coronal magnetic loops, which are the structures elongated in the magnetic field direction with the enhanced plasma temperature and density inside. These structures support many different types of oscillations. One of the particularly important types of coronal loop oscillations are transverse oscillations that were first observed by TRACE on 14 July 1998. The results of this observation were reported by Aschwanden et al. (1999) and Nakariakov et al. (1999), who interpreted these oscillations as standing fast kink waves in a magnetic flux tube.
After this first observation the transverse oscillations of coronal loops remain in the focus of theoretical studies. First theoretical interpretation of the observed transverse coronal loop oscillations were based on the simplest model of a coronal loop. In this model a coronal loop was represented by a straight homogeneous magnetic tube with the magnetic field lines frozen in the dense photospheric plasma at the foot points. Then the theory of oscillations of homogeneous magnetic tubes was used (e.g. Edwin & Roberts 1983). Later theorists started to develop more sophisticated models that took such effects as the loop curvature, non-circular cross-section and magnetic twist into account. For the review of the recent progress in the theory of the transverse coronal loop oscillations see, e.g., a review by Ruderman & Erdélyi (2009).
One particular and very important property of magnetic loops is that the plasma density inside the loop varies along the loop due to gravitational stratification. The theory of transverse oscillations of stratified coronal loops was developed by, e.g., Andries et al. (2005a); Diaz et al. (2006) and Dymova & Ruderman (2006a). This theory was then successfully applied to coronal seismology (e.g., Andries et al. 2005b; Dymova & Ruderman 2006b; McEwan et al. 2008; Morton et al. 2009; Van Doorsselaere et al. 2007; see also a review by Andries et al. 2009).
Sometimes it is observed that a few neighboring coronal loops oscillate simultaneously. When the loops are close enough to each other the observed oscillations should be considered as collective oscillations of loop arrays. It is natural to start studying collective oscillations of loop arrays from studying oscillations of just two loops. This problem was first addressed by Luna et al. (2008) numerically and then by Van Doorsselaere et al. (2008) analytically in the thin tube approximation. This work was extended to studying collective oscillations of four loops by Ofman (2005) and multi-loop systems by Luna et al. (2009).
In this paper we aim to extend the theory of collective oscillations of two loops in another direction. We will take the density variation along the loops into account. The paper is organized as follows. In the next section we describe the equilibrium state and main assumptions, and present the governing equations. In Sect. 3 we introduce bicylindrical coordinates used in our analysis. In Sect. 4 we derive the system of equations governing the kink oscillations of two parallel loops. In Sect. 5 we re-derive the expressions for the frequencies of kink oscillations of two parallel homogeneous tubes previously obtained by Van Doorsselaere et al. (2008). In Sect. 6 we investigate the effect of density variation along the loops on the frequencies of kink oscillations. In Sect. 7 we study the implication of the obtained results on the coronal seismology. Section 8 contains the summary of our results and conclusions.
2 Problem formulation
We start our analysis from describing the equilibrium state. In this state there are two curved parallel coronal loops. They are situated in parallel vertical planes, and the lines connecting their axes at foot points are perpendicular to these planes (see Fig. 1). The plasma density varies along the loops due to gravitational stratification.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{14055fg1.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa14055-10/Timg12.png)
|
Figure 1: Equilibrium with two parallel coronal magnetic loops. |
| Open with DEXTER | |
In what follows we neglect the loop curvature. As a result we obtain a
system of two straight parallel magnetic tubes with the density varying along
the tubes. This system is shown in Fig. 2.
The equilibrium magnetic field is in the z-direction, which
coincides with the direction of the tube axes, and it has constant magnitude.
The radii of the tubes are ![]() and
and ![]() ,
and the distance
between their axes is d. The density is equal to
,
and the distance
between their axes is d. The density is equal to
![]() inside the
left tube,
inside the
left tube,
![]() inside the right tube, and
inside the right tube, and
![]() outside
the tubes. It is assumed that
outside
the tubes. It is assumed that
![]() .
.
![\begin{figure}
\par\includegraphics[angle=270,width=7cm,clip]{14055fg2.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa14055-10/Timg19.png)
|
Figure 2:
The sketch of the equilibrium state with straight magnetic tubes.
The magnetic filed lines are assumed to be frozen in a dense photospheric
plasma at
|
| Open with DEXTER | |
The plasma motion is described by the linearized ideal MHD equations for
cold plasmas,
Here
The normal component of the plasma displacement,
3 Introducing bicylindrical coordinates
To study the oscillations of two-tube system we use bicylindrical
coordinates
![]() ,
where
,
where ![]() varies from
varies from ![]() to
to
![]() ,
and
,
and ![]() varies from 0 to
varies from 0 to ![]() (e.g. Korn & Korn 1961). The
coordinate lines in the
(e.g. Korn & Korn 1961). The
coordinate lines in the
![]() -plane are shown in Van Doorsselaere et al. (2008).
The Cartesian and bicylindrical coordinates are related by
-plane are shown in Van Doorsselaere et al. (2008).
The Cartesian and bicylindrical coordinates are related by
where a is a constant with the dimension of length. The axes of the tubes are parallel to the z-axis. The axes of the left and right tube cross the xy-plane at points x = -d/2 and x = d/2respectively on the x-axis. The boundaries of the left and right tube are defined by
It is shown by Van Doorsselaere et al. (2008) that a,
Here f is an arbitrary function, and
It follows from Eq. (1) that ![]() .
Then we obtain
from Eq. (2) that
.
Then we obtain
from Eq. (2) that
where the square of the Alfvén speed is given by
Equation (1) can be transformed to
where
It follows from Eq. (2) that
Substituting this result in Eq. (10) we obtain
Taking the divergence of this equation and using (8) yields
The conditions that the magnetic pressure perturbation and normal component of displacement are continuous at the tube boundaries are written as
where the square brackets indicate the jump of a quantity across the boundary. It follows from Eqs. (3) and (8) that P satisfies the boundary conditions
Since
Equations (13) and (14) together with the
boundary conditions (15) and the limiting conditions as
![]() and
and
![]() are used in the
next section to derive the governing equations for the tube
oscillations.
are used in the
next section to derive the governing equations for the tube
oscillations.
4 Derivation of governing equations
In this section we derive the system of two equations governing the
kink oscillations of two parallel magnetic tubes in the thin tube
approximation. To do this we use the same asymptotic method that
was used by Dymova & Ruderman (2005) to derive the governing equation for a
single stratified tube, and by Van Doorsselaere et al. (2008) to derive the
dispersion relation for kink oscillations of two parallel
homogeneous tubes. To use this method we assume that the
characteristic spatial scale of the two-tube system in the
transverse direction is much smaller than
L. We can take this characteristic scale to be equal to d,
so that we assume that
![]() .
Since the
characteristic scale in the z-direction is much larger than
d, we introduce the stretching variable
.
Since the
characteristic scale in the z-direction is much larger than
d, we introduce the stretching variable
![]() .
We consider oscillations with periods of the order of
.
We consider oscillations with periods of the order of
![]() ,
where
,
where
![]() is the characteristic value of the Alfvén speed.
The quantity
is the characteristic value of the Alfvén speed.
The quantity
![]() can be considered as the characteristic
time of the problem. Since
can be considered as the characteristic
time of the problem. Since
![]() ,
where
,
where
![]() is the Alfvénic time in the transverse direction,
we also introduce the ``slow'' time
is the Alfvénic time in the transverse direction,
we also introduce the ``slow'' time
![]() .
In the new
variables the Eqs. (13) and (14) are
transformed to
.
In the new
variables the Eqs. (13) and (14) are
transformed to
Neglecting terms of the order of
The general solution to this equation can be looked for in the form of Fourier expansion with respect to
The second term on the right-hand side of this expression is introduced
to satisfy the condition that ![]() as
as
![]() .
Now we easily find that P satisfies Eq. (20), the
conditions that P tends to finite limits when
.
Now we easily find that P satisfies Eq. (20), the
conditions that P tends to finite limits when
![]() ,
and is continuous at the tube boundaries, if
,
and is continuous at the tube boundaries, if ![]() is given by
is given by
where C1 and C2 are arbitrary functions of T and Z satisfying
Substituting the expression for P in Eqs. (17) and (18) we transform them to
where
Using Eq. (22) we obtain that
for
for
for
Let us introduce functions
![]() ,
,
![]() ,
,
![]() and
and
![]() satisfying
satisfying
Then it follows from Eqs. (26) and (27) that
It follows from the second boundary condition in Eqs. (15) and (35) that
where
Substituting these expressions in Eq. (34) we obtain
Eliminating C1 and C2 from Eqs. (32), (33), (39) and (40), and returning to the original independent variables, we arrive at equations for
where the squares of the kink speeds for the left and right tubes are given by
Let us introduce the dimensionless parameters
Obviously
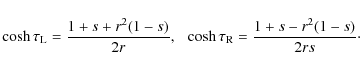
|
(45) |
These relations can be considered as quadratic equations for
When E is fixed, r is a function of s. It is easy to show that r < 1for any value of s > 0,
In the two-tube system the lines that are not perturbed by the fluting modes are not the tube axes, but the lines parallel to the tube axes and crossing the xy-plane at points with coordinates (-a,0) and (a,0). In bicylindrical coordinates these straight lines correspond to
Using the relations
where
as
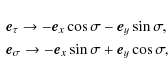
|
(51) |
as
These relations will be used in the discussion of polarization of eigenmodes.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{14055fg3.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa14055-10/Timg144.png)
|
Figure 3:
Dependence of the normalized frequencies on |
| Open with DEXTER | |
5 Eigenmodes of system with constant density
Let us use Eqs. (41) and (42) to study the eigenmodes
of the system of two parallel homogeneous tubes. We will only consider the
fundamental mode with respect to z, and take
![]() and
and
![]() proportional to
proportional to
![]() ,
where
,
where ![]() .
Then the system
of Eqs. (41) and (42) reduces to
.
Then the system
of Eqs. (41) and (42) reduces to
We obtained the system of two linear homogeneous algebraic equations for
This result is in agreement with the result obtained by Van Doorsselaere et al. (2008). In what follows we will call the oscillation mode with the frequency
6 Effect of density stratification
In this section we study the effect of density stratification on the eigenmodes
of the two-tube system oscillations. We look for the solution to the system of
Eqs. (41) and (42) with
![]() and
and
![]() proportional to
proportional to
![]() .
The solution has to satisfy the boundary
conditions
.
The solution has to satisfy the boundary
conditions
Equations (41) and (42) are now reduced to
Equations (59) and (60) together with the boundary condition (58) constitute the eigenvalue problem determining
where H is the atmospheric scale height, and
where
Figure 3 shows the dependence of frequencies of the high-frequency and
low-frequency eigenmodes on the parameter
![]() for
for
![]() .
The left panel corresponds to E =0.188. When s = 2this corresponds to r = 3/4, i.e. for tubes with the radius ratio of two the
distance between the tube axes is twice the larger radius. The right panel
corresponds to E = 1. It follows from Eq. (46) that
r = 1 for any value of s, i.e. we have the limiting case when the tubes
touch each other. In both panels the frequencies of the high-frequency
eigenmodes are shown by dashed lines, and those of the low-frequency eigenmodes
by dotted lines. The frequencies of the fundamental mode, and the first and
second overtones are shown. The frequencies are normalized to the fundamental
Alfvén frequency in the external plasma at the foot point level,
.
The left panel corresponds to E =0.188. When s = 2this corresponds to r = 3/4, i.e. for tubes with the radius ratio of two the
distance between the tube axes is twice the larger radius. The right panel
corresponds to E = 1. It follows from Eq. (46) that
r = 1 for any value of s, i.e. we have the limiting case when the tubes
touch each other. In both panels the frequencies of the high-frequency
eigenmodes are shown by dashed lines, and those of the low-frequency eigenmodes
by dotted lines. The frequencies of the fundamental mode, and the first and
second overtones are shown. The frequencies are normalized to the fundamental
Alfvén frequency in the external plasma at the foot point level,
![]() .
.
Figure 4 shows the dependence of frequencies of the high-frequency and
low-frequency eigenmodes on E for
![]() .
The left panel is
for
.
The left panel is
for
![]() ,
which corresponds to non-stratified tubes. The right panel
is for
,
which corresponds to non-stratified tubes. The right panel
is for
![]() ,
which corresponds to H = R. If we want to find the
values of frequencies for particular values of r and s, then we need to
calculate the corresponding value of E using Eq. (46). For
example, if we take s = 1, i.e.
,
which corresponds to H = R. If we want to find the
values of frequencies for particular values of r and s, then we need to
calculate the corresponding value of E using Eq. (46). For
example, if we take s = 1, i.e.
![]() ,
and r = 4/5, i.e.
,
and r = 4/5, i.e.
![]() ,
then we obtain E = 1/4.
,
then we obtain E = 1/4.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{14055fg4.eps}\vspace*{-1.5mm}
\end{figure}](/articles/aa/full_html/2010/07/aa14055-10/Timg175.png)
|
Figure 4:
Dependence of the normalized frequencies on E for
|
| Open with DEXTER | |
Figure 5 shows the dependence of frequencies of the high-frequency and
low-frequency eigenmodes on the ratio of plasma densities outside and inside
the tubes when the densities inside the tubes are the same,
![]() ,
and
,
and
![]() .
When the
tube radii are equal (s = 1), this value of E corresponds to r = 2/3. The
left panel is for
.
When the
tube radii are equal (s = 1), this value of E corresponds to r = 2/3. The
left panel is for
![]() ,
which corresponds to non-stratified tubes. The
right panel is for
,
which corresponds to non-stratified tubes. The
right panel is for
![]() ,
which corresponds to H = R.
,
which corresponds to H = R.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{14055fg5.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa14055-10/Timg178.png)
|
Figure 5:
Dependence of the normalized frequencies on
|
| Open with DEXTER | |
Let us discuss the mode polarization. It is well known that the kink
oscillations of straight magnetic tubes are infinitely degenerated in the long
wavelength approximation in the sense that the oscillation frequency is
independent of the polarization. Van Doorsselaere et al. (2008) showed that the same is true for
the two-tube system when there is no density stratification. This property
remains valid even when the tubes are stratified. Really, the eigenvalue
problem determining the dependence of ![]() on k does not contain the
parameter
on k does not contain the
parameter ![]() ,
which determines the mode polarization. It follows from
Eq. (52) that the vectors
,
which determines the mode polarization. It follows from
Eq. (52) that the vectors
![]() and
and
![]() have
to be mirror symmetric with respect to the y-direction, otherwise their
directions are arbitrary.
have
to be mirror symmetric with respect to the y-direction, otherwise their
directions are arbitrary.
Van Doorsselaere et al. (2008) pointed out that the degeneracy of kink oscillations is related to
the use of the long wavelength approximation. The account of dispersion related
to the finite thickness of the tubes would remove it. This statement clearly
follows from the numerical results obtained by Luna et al. (2008). These authors
studied kink oscillations of the two-tube system with the tubes having the same
radii and the density inside the tubes being equal. They obtained that there
are four different modes of kink oscillations of this system. The polarization
in these modes corresponds either to
![]() ,
so that the tube
displacements are in the x-direction, or to
,
so that the tube
displacements are in the x-direction, or to
![]() ,
so that the
tube displacements are in the y-direction. Luna et al. (2008) denoted these modes
as Sx and Ax, and as Sy and Ay respectively, where S and A
stay for symmetric and antisymmetric.
,
so that the
tube displacements are in the y-direction. Luna et al. (2008) denoted these modes
as Sx and Ax, and as Sy and Ay respectively, where S and A
stay for symmetric and antisymmetric.
In the symmetric modes the two tubes oscillate in phase, while in the
antisymmetric modes they oscillate in anti-phase. The frequencies of all four
modes are different, however the frequencies of Sx and Ay modes are
smaller than the frequencies of Ax and Sy modes. In fact, the frequencies
of Sx and Ay modes are close to ![]() ,
and the frequencies of
Sy and Ax modes are close to
,
and the frequencies of
Sy and Ax modes are close to ![]() .
.
As we have already mentioned Luna et al. (2008) considered the system of two identical magnetic tubes. Van Doorsselaere et al. (2008) found that the modes Sx, Ax, Sy and Ay exist only for a definite range of parameters corresponding to the standard systems in their terminology. There are also the so-called anomalous systems. In an anomalous system there are two Ax modes, one with the high and one with the low frequency, and two Sy modes, once again one with the high and one with the low frequency. There are no Ay and Sx modes. All systems with equal densities inside the tubes are standard systems.
In our calculations we always took the value of parameters that correspond to
standard systems when the tubes are non-stratified, so that
we anticipated that the system would be standard. The numerical results
confirmed this conjecture. We found that
![]() for the smaller
frequency, and
for the smaller
frequency, and
![]() for the larger frequency. Then it follows
from Eq. (52) that, in the modes with the smaller frequency,
for the larger frequency. Then it follows
from Eq. (52) that, in the modes with the smaller frequency,
![]() and
and
![]() have the same direction when
have the same direction when
![]() ,
and the opposite directions when
,
and the opposite directions when
![]() .
This corresponds to the
Sx and Ay modes. On the other hand, in the modes with the larger
frequency,
.
This corresponds to the
Sx and Ay modes. On the other hand, in the modes with the larger
frequency,
![]() and
and
![]() have the opposite directions when
have the opposite directions when
![]() ,
and the same direction when
,
and the same direction when
![]() .
This
corresponds to the Ax and Sy modes. We see that, similar to the standard
system with non-stratified tubes, the system with stratified tubes have
the Sx and Ay modes oscillating with the smaller frequency, and the Axand Sy modes oscillating with the larger frequency.
.
This
corresponds to the Ax and Sy modes. We see that, similar to the standard
system with non-stratified tubes, the system with stratified tubes have
the Sx and Ay modes oscillating with the smaller frequency, and the Axand Sy modes oscillating with the larger frequency.
7 Implication on coronal seismology
Verwichte et al. (2004) reported two cases of observations of the transverse coronal loop oscillations where, in addition to the fundamental harmonic, the first overtone was also observed. A very important property of these observations was that the ratio of the frequencies of the first overtone and the fundamental harmonic was less than 2. It was equal to 1.81 and 1.64 respectively (note that later Van Doorsselaere et al. (2007) used the improved technique to correct this values to 1.82 and 1.58).
Andries et al. (2005b) suggested to use these observations to estimate the scale height
in the solar corona. They assumed that an oscillating loop has the half-circle
shape and it is in the vertical plane. They also assumed that the atmosphere is
isothermal. In that case the dependence of plasma densities inside and outside
the loop are given by the expressions similar to Eq. (61). Then
they calculated the ratio of frequencies of the first overtone of the loop kink
oscillation to the fundamental harmonic. It turns out that this ratio is a
monotonically decreasing function of
![]() .
Hence, if we know the
ratio of frequencies and R, which is the loop height at the apex point,
then we can determine H. Using the observational data reported by
Verwichte et al. (2004), Andries et al. (2005b) found H = 68 Mm in the first event, and
H = 36 Mm in the second event.
.
Hence, if we know the
ratio of frequencies and R, which is the loop height at the apex point,
then we can determine H. Using the observational data reported by
Verwichte et al. (2004), Andries et al. (2005b) found H = 68 Mm in the first event, and
H = 36 Mm in the second event.
At present there are hot debates about the internal structure of coronal loops. Two competitive models were suggested. In the first model coronal loops are considered as monolithic, while in the second as consisting of a large number of thin threads with different densities and temperatures. Andries et al. (2005b) considered loops as monolithic. Will the estimates of the coronal scale height change if the multi-thread model of coronal loops is used?
To have the first insight in this problem we can use the loop model that
consists of just two threads. Let us consider the two magnetic tubes in the
model studied in this paper not as separate loops, but as two threads of the
same loop. We assume that the threads are in two parallel vertical planes and
have the same shape, so that the equilibrium is similar to one shown in
Fig. 1. We also assume that the threads oscillate in phase. Then, in
accordance with the analysis in the previous section, they oscillate in the
horizontal direction with the frequency ![]() ,
and in the vertical
direction with the frequency
,
and in the vertical
direction with the frequency ![]() .
.
Let us assume that the densities inside the threads are proportional to the
density in the external plasma, so that
![]() and
and
![]() are constant.
Then, introducing new variables,
are constant.
Then, introducing new variables,
we reduce the system of Eqs. (59) and (60) to
We see that now we have two separate equations, one for
we reduce Eq. (64) to
where
where
Eq. (67) is transformed to
We see that Eq. (69) coincides with Eq. (66). Let
where the indices ``f'' and ``o'' indicate the fundamental mode and overtones, and
Andries et al. (2005b) took
![]() in their numerical investigation. It follows
from our analysis that the ratios of the frequencies of the overtones and
the fundamental mode is independent of
in their numerical investigation. It follows
from our analysis that the ratios of the frequencies of the overtones and
the fundamental mode is independent of ![]() .
The only condition that
has to be satisfied is that
.
The only condition that
has to be satisfied is that
![]() .
.
8 Summary and conclusions
In this paper we studied the kink oscillations of two parallel coronal loops with the density varying along the loop. We modelled this two-loop system by the system of two parallel magnetic tubes. Using bicylindrical coordinates we derived the system of equations governing the oscillations of the two-tube system. We then have used this system to study the eigenmodes of kink oscillations. First we re-derived the expressions for the frequencies of kink oscillations of two homogeneous parallel tubes previously derived by Van Doorsselaere et al. (2008). Then we considered the effect of density variation along the tubes. We assumed that the loops are in two parallel vertical planes and have the shape of half-circles with the same radius R. We also assumed that the atmosphere is isothermal and the plasma temperature is the same in the loops and in the surrounding plasma. This implies that the ratios of plasma densities inside the loops to the density of the external plasma are constant. The eigenvalue problem describing the eigenfrequencies of the loop oscillations was solved numerically.
We investigated the implication of our results on coronal seismology. When doing so we concentrated on the problem of determination of the atmospheric scale hight using the ratio of frequencies of the fundamental harmonic and first overtone of the kink oscillations. We compared the results obtained on the basis of two models: one where a coronal loop is assumed to be monolithic, and the other where a coronal loop consists of two threads. We assumed that the ratios of plasma densities inside the loops and in the external plasma are constant. Then we showed that, under this assumption, the two models give exactly the same value of the atmospheric scale height. Moreover, we showed that this value is independent of the density ratios.
AcknowledgementsM.S.R. and Y.T. acknowledge the support by an STFC grant. D.R. acknowledges the support by an STFC postgraduate fellowship.
References
- Andries, J., Goossens, M., Hollweg, J. V., Arregui, I., & Van Doorsselaere, T. 2005a, A&A, 430, 1109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andries, J., Arregui, I., & Goossens, M. 2005b, ApJ, 624, L57 [Google Scholar]
- Andries, J., van Doorsselaere, T., Roberts, B., et al. 2009, Space. Sci. Rev., 149, 3 [CrossRef] [Google Scholar]
- Aschwanden, M. J., Fletcher, L., Schrijver, C. J., & Alexander, D. 1999, ApJ, 520, 880 [NASA ADS] [CrossRef] [Google Scholar]
- Diaz, A. J., Oliver, R., & Ballester, J. L. 2006, ApJ, 645, 766 [NASA ADS] [CrossRef] [Google Scholar]
- Dymova, M. V., & Ruderman, M. S. 2005, Solar Phys., 229, 79 [Google Scholar]
- Dymova, M. V., & Ruderman, M. S. 2006a, A&A, 457, 1059 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dymova, M. V., & Ruderman, M. S. 2006b, A&A, 459, 241 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Edwin, P. M., & Roberts, B. 1983, Solar Phys., 88, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Korn, G., & Korn, T. 1961, Mathematical handbook for scientists and engineers (New York: McGraw-Hill) [Google Scholar]
- Luna, M., Terradas, J., Oliver, R., & Ballester, J. L. 2008, ApJ, 676, 717 [NASA ADS] [CrossRef] [Google Scholar]
- Luna, M., Terradas, J., Oliver, R., & Ballester, J. L. 2009, ApJ, 692, 1582 [NASA ADS] [CrossRef] [Google Scholar]
- McEwan, M. P., Diaz, A. J., & Roberts, B. 2008, A&A, 481, 819 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morton, R. J, & Erdelyi, R. 2009, A&A, 502, 315 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakariakov, V. M., Ofman, L., DeLuca, E. E., Roberts, B., & Davila, J. M. 1999, Science, 285, 862 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ofman, L. 2005, Adv. Space Res., 36, 1572 [NASA ADS] [CrossRef] [Google Scholar]
- Ofman, L. 2009, ApJ, 694, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Ruderman, M. S., & Erdélyi, R. 2009, Space. Sci. Rev., 149, 199 [CrossRef] [Google Scholar]
- Van Doorsselaere, T., Nakariakov, V. M., & Verwichte, E. 2007, A&A, 473, 959 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van Doorsselaere, T., Ruderman, M. S., & Robertson, D. 2008, A&A, 485, 849 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verwichte, E., Nakariakov, V. M., Ofman, L., & Deluca, E. E. 2004, Solar Phys., 223, 77 [Google Scholar]
All Figures
![\begin{figure}
\par\includegraphics[width=7cm,clip]{14055fg1.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa14055-10/Timg12.png)
|
Figure 1: Equilibrium with two parallel coronal magnetic loops. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=270,width=7cm,clip]{14055fg2.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa14055-10/Timg19.png)
|
Figure 2:
The sketch of the equilibrium state with straight magnetic tubes.
The magnetic filed lines are assumed to be frozen in a dense photospheric
plasma at
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{14055fg3.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa14055-10/Timg144.png)
|
Figure 3:
Dependence of the normalized frequencies on |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{14055fg4.eps}\vspace*{-1.5mm}
\end{figure}](/articles/aa/full_html/2010/07/aa14055-10/Timg175.png)
|
Figure 4:
Dependence of the normalized frequencies on E for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{14055fg5.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa14055-10/Timg178.png)
|
Figure 5:
Dependence of the normalized frequencies on
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



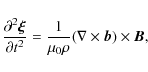
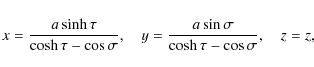
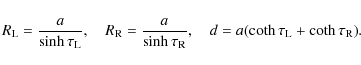
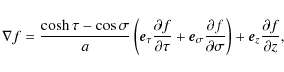
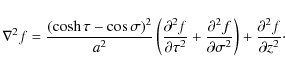
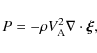
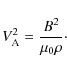
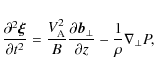
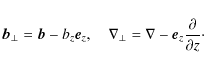
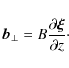
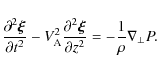
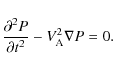
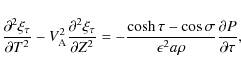
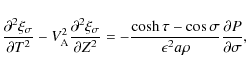
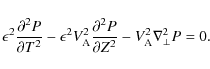
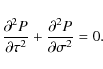
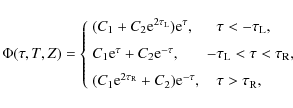

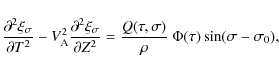
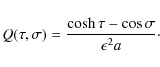
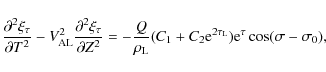
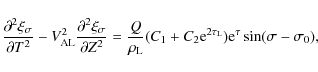
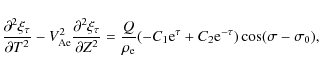

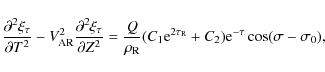

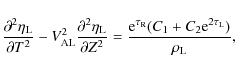
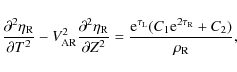
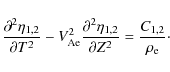
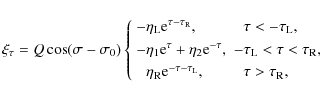
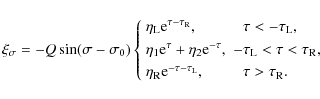
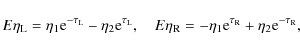
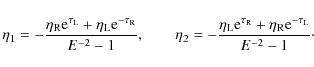
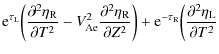
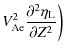
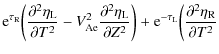
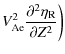
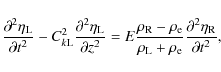
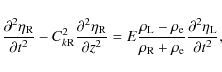
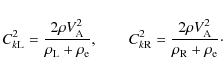
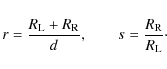
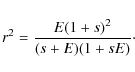
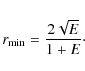
![\begin{displaymath}\begin{array}{l}\displaystyle
\vec{\xi}_{\rm L} = \frac{\eta_...
...igma_0) +
\vec{e}_\sigma\sin(\sigma - \sigma_0)] .
\end{array}\end{displaymath}](/articles/aa/full_html/2010/07/aa14055-10/img137.png)