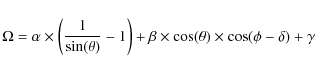| Issue |
A&A
Volume 515, June 2010
|
|
|---|---|---|
| Article Number | A106 | |
| Number of page(s) | 6 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201014005 | |
| Published online | 15 June 2010 | |
Evaluating the stability of atmospheric lines with HARPS![[*]](/icons/foot_motif.png)
P. Figueira - F. Pepe - C. Lovis - M. Mayor
Geneva Observatory, University of Geneva, 51 Ch. des Maillettes, 1290-Sauverny, Switzerland
Received 7 January 2010 / Accepted 17 February 2010
Abstract
Context. When searching for extrasolar systems using the
radial velocity technique, the need for high-precision measurements
implies that a precise wavelength calibration is required. The choice
of the calibrator is a particularly important open question in the
infra-red domain, where precision and achievements remain inferior to
those in the optical.
Aims. We investigate the long-term stability of atmospheric
lines as a precise wavelength reference and analyze their sensitivity
to different atmospheric and observing conditions.
Methods. We use HARPS archival data for three bright stars, Tau Ceti, ![]() Arae, and e Eri,
which span 6 years and include high-cadence measurements performed over
several nights. We cross-correlate this data with an O2 mask and evaluate both radial velocity and bisector variations to a photon noise level of 1 m/s.
Arae, and e Eri,
which span 6 years and include high-cadence measurements performed over
several nights. We cross-correlate this data with an O2 mask and evaluate both radial velocity and bisector variations to a photon noise level of 1 m/s.
Results. We find that the telluric lines in the three data-sets
are stable down to 10 m/s (rms) over the 6 years. We also show
that the radial velocity variations can be modeled by simple
atmospheric models, yielding a final precision of 1-2 m/s.
Conclusions. The long-term stability of atmospheric lines was
10 m/s over six years, in spite of atmospheric phenomena.
Atmospheric lines can be used as a wavelength reference for short
timescale programs, yielding a precision of 5 m/s without any
correction. A higher precision, of 2 m/s, can be reached if the
atmospheric phenomena are corrected for using the simple atmospheric
model described, making it a very competitive method even on long
timescales.
Key words: atmospheric effects - instrumentation: spectrographs - methods: observational - techniques: radial velocities - planetary systems
1 Introduction
The discovery by Mayor & Queloz (1995) of a hot Jupiter orbiting 51 Peg by means of radial velocity (RV) measurements inspired the ongoing search for extrasolar planets. This breakthrough was achievable only by using very precise wavelength calibration systems. Both the Th-Ar emission lamp with the cross-correlation function (CCF) method (Baranne et al. 1996), and the I2 cell with the deconvolution procedure (Butler et al. 1996), were extensively used to detect planets by RV measurements. Technological developments have enabled more advanced spectrographs to be built, such as HARPS (Mayor et al. 2003), and reduction and analysis methods have been perfected through the years (Lovis & Pepe 2007). To this day, HARPS delivers the most precise RV measurements, with sub-m/s precision, which has allowed a succession of ground-breaking detections of the lightest planets known (Lovis et al. 2006; Mayor et al. 2009).
Given the proven stability of these two well-established wavelength references, little investigation was performed of viable alternatives. With time, RV measurements have become possible in the infra-red (IR) domain, where wavelength calibration remains in its infancy and no method has established itself as the paradigm.
In our attempt to measure RV with CRIRES at a very early stage of the instrument's life, we used atmospheric lines as wavelength reference (Huélamo et al. 2008). Figueira et al. (2010) describe an improved data reduction in which a precision of 5 m/s on a timescale of one week is reached. This result was obtained in a RV standard star using CO2 lines as wavelength reference.
Table 1: The summary of the data set properties for the stars used in this paper. Note that the S/N is calculated at the center of order 60.
The usage of telluric lines as a precise wavelength reference dates back to the first attempts to achieve precise RV measurements, by Griffin & Griffin (1973), for Arcturus and Procyon. Balthasar et al. (1982), Smith (1982), and Caccin et al. (1985) also explored adopting atmospheric lines as a viable alternative to wavelength calibration. Using O2 lines, these authors demonstrated that a precision of 5 m/s was possible. This result is particularly significant because they used different RV determination methods (different instrumentation, different line fitting approaches, etc.). Snellen (2004) used the same principle on H2O lines and reached a precision of 5-10 m/s in UVES data. In light of these results, we ask the two following questions:
- What is the stability of atmospheric lines over long timescales?
- What is the sensitivity of atmospheric lines to different observing conditions?
The paper is structured as follows. In Sect. 2, we describe HARPS and the datasets used in our investigation. Section 3 describes the principles of our method and the data reduction. The results are presented in Sect. 4 and discussed in Sect. 5. We conclude in Sect. 6 with the lessons to learn from this campaign.
2 Observations
2.1 Using HARPS as an ``absolute reference''
HARPS (Mayor et al. 2003)
is a fiber-fed cross-dispersed echelle spectrograph installed at the
3.6 m telescope in La Silla. The main dispersion is provided
by an R4 echelle grating in a Littrow configuration. The orders are
then dispersed in a direction perpendicular to the dispersion direction
by a grism and imaged by a ![]() k4k CCD mosaic. This optical design creates 72 orders that span the whole optical range from 3785 to 6915
k4k CCD mosaic. This optical design creates 72 orders that span the whole optical range from 3785 to 6915 ![]() .
The spectral resolution was measured to be R=110 000 and the mean dispersion 0.015
.
The spectral resolution was measured to be R=110 000 and the mean dispersion 0.015 ![]() /pxl
(820 m/s). The sampling is 3.3 pixel per resolution element. The
instrument is located in a vacuum vessel to avoid spectral drift caused
by temperature and air pressure effects, which are kept below
0.01 K and 0.01 mbar, respectively. A Th-Ar emission lamp is
used for wavelength calibration.
/pxl
(820 m/s). The sampling is 3.3 pixel per resolution element. The
instrument is located in a vacuum vessel to avoid spectral drift caused
by temperature and air pressure effects, which are kept below
0.01 K and 0.01 mbar, respectively. A Th-Ar emission lamp is
used for wavelength calibration.
The very high stability of HARPS allows a precision of 1 m/s to be reached routinely. When a precision better than 1 m/s is required, a second channel can be used to image the Th-Ar lamp simultaneously with the science target. The proven intrinsic IP stability of HARPS permits us to study spectral line profile variations as well, which can be done using the well-know bisector technique (BIS) on the cross-correlation function (CCF). We note that long-term precision of HARPS was found to be better than 1 m/s (see previous references), making this study possible for the first time to this level of precision.
2.2 The selection of targets
To perform our study, we selected targets bright enough to allow us to reach a photon noise of ![]() 1 m/s
on the atmospheric lines position error in individual exposures. Out of
these we selected stars which had a high number of points (>1000),
covered a long time span and had, preferably, a very high cadence of
measurements. We payed particular attention to stars followed in
asterosismology campaigns. These campaigns, aiming at studying the
stellar RV variations on a timescale of hours to days, followed the
star across the sky throughout several consecutive nights.
1 m/s
on the atmospheric lines position error in individual exposures. Out of
these we selected stars which had a high number of points (>1000),
covered a long time span and had, preferably, a very high cadence of
measurements. We payed particular attention to stars followed in
asterosismology campaigns. These campaigns, aiming at studying the
stellar RV variations on a timescale of hours to days, followed the
star across the sky throughout several consecutive nights.
By applying the mentioned criteria we pinpointed Tau Ceti (HD 10700), ![]() Ara (HD 160691) and e Eri
(HD 20794) as the most suitable targets for our tests. The details
on the relevant properties of the data sets are provided in Table 1. Tau Ceti and
Ara (HD 160691) and e Eri
(HD 20794) as the most suitable targets for our tests. The details
on the relevant properties of the data sets are provided in Table 1. Tau Ceti and ![]() Ara
were followed in asterosismology campaigns, of 3 and 8 days,
respectively. It is important to note that the beginning of data
acquisition on these targets goes back to 2003, ensuring a long time
span.
Ara
were followed in asterosismology campaigns, of 3 and 8 days,
respectively. It is important to note that the beginning of data
acquisition on these targets goes back to 2003, ensuring a long time
span.
Our objective was simply to provide for a strong background against which the telluric lines can be defined at high signal-to-noise (S/N) and in a short integration time. The stellar spectrum in itself has very little influence on the obtained RV; the only eventual issue is the blending between stellar and atmospheric lines.
3 Methodology and data reduction
A dedicated pipeline was created to reduce HARPS spectra, called Data Reduction Software hereafter DRS. For more details we refer to Mayor et al. (2003). In a nutshell, the pipeline provides the typical bad pixel/column, bias, and dark correction, flat-fielding, and optimal extraction of the spectra. The spectra are then calibrated in wavelength using a Th-Ar lamp. The wavelength-calibrated spectra are cross-correlated (as described in Baranne et al. 1996) with a weighted template mask (Pepe et al. 2002). To calculate the RV of the atmospheric lines in the spectra with the existing pipeline one then needs to construct a telluric mask.
Using the HITRAN database (Rothman et al. 2005), one can locate 11 992 spectral lines within the HARPS wavelength domain. These lines correspond to H2O, OH, and O2
molecules (with 8706, 3060, and 226 lines, respectively) and cover
mainly the red side of the spectra, from 540 to 690 nm. Water
lines span the widest wavelength range, but are of a very high dynamic
range and are strongly blended. Most of the OH lines are too faint to
be detected and are not even visible in Delbouilles FTS spectrum. Out
of the 226 oxygen absorption features, one can find 71 lines
deeper than 1% and some as deep as 95%. These lines are distributed in
2 bands, located at 628-663 and 687-690 nm. The features are
well-separated spectrally by HARPS, exhibiting no clumping neither
among themselves nor with stellar lines, unlike the other two species.
Following the arguments we have presented, we compiled a mask of only O2 lines.
The vacuum wavelengths were drawn from the HITRAN database, and the
corresponding values at standard temperature and pressure were
calculated. The depth of each line could not be estimated accurately by
fitting Gaussian functions to the high S/N spectra; for deep lines
(>90%) the departure from Gaussian profile was too pronounced and
the errors resulting from this assumption were non-negligible. As an
alternative we used the Delbouille FTS spectra![]() .
This high-resolution spectra was convolved with an instrumental profile
representative of HARPS resolution and the resulting spectra were
analyzed. The depth of each line was then estimated by measuring the
depth of the synthetic absorption line. The depth of the corresponding
spectra was found to differ by only 1-2% relative to the normalized
observed spectra depth. The objective of this procedure was to assign
the correct depth and thus the correct weight to each line when
calculating the cross-correlation, as described in Pepe et al. (2002).
.
This high-resolution spectra was convolved with an instrumental profile
representative of HARPS resolution and the resulting spectra were
analyzed. The depth of each line was then estimated by measuring the
depth of the synthetic absorption line. The depth of the corresponding
spectra was found to differ by only 1-2% relative to the normalized
observed spectra depth. The objective of this procedure was to assign
the correct depth and thus the correct weight to each line when
calculating the cross-correlation, as described in Pepe et al. (2002).
![\begin{figure}
\par\includegraphics[width=9cm,clip]{14005fig1.eps}
\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/07/aa14005-10/Timg10.png)
|
Figure 1: The telluric RV variation in all Tau ceti measurements as a function of time. |
| Open with DEXTER | |
The pipeline measures the RV and the associated photon noise error, by analyzing the CCF function as described in Bouchy et al. (2001). In addition to each RV calculation, the bisector inverse slope was computed from the CCF function following the procedure described in Queloz et al. (2001).
4 Results and analysis
From our analysis we excluded spectra which delivered a very low photon
noise precision, superior to 5 m/s. These correspond to a very
small fraction of the measurements, 0.8 % for Tau Ceti, 1.08% for ![]() Ara, and 0.2% for e Eri.
Ara, and 0.2% for e Eri.
The scatter in the RV measurements and the average photon noise for each star are presented in Table 2. The RV variations are very low, roughly 10 m/s for all three stars over 6 years. We plot the RV of Tau Ceti as a function of time in Fig. 1. The low scatter is a remarkable result, especially if we consider that no modeling, correction, or filtering were involved. Nevertheless, the dispersion is much higher than the photon noise, which indicates that there is an additional source in the measured scatter.
Table 2: The dispersion and average photon noise of the stars used in our campaign.
We note that even data subsets covering a short timescale interval, e.g. one night, already exhibit an RV variation larger than the average photon noise. This infers that the measured RV depends on a factor that varies at a timescale of one night. In Fig. 2, we present the atmospheric lines RV variation in the spectra of Tau Ceti over a full night (upper left panel), which clearly illustrates this point.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{14005fig2a.eps}\hspace*{3mm}
\includegraphics[width=8.5cm,clip]{14005fig2b.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa14005-10/Timg13.png)
|
Figure 2: Telluric RV measurements on Tau Ceti over a full night. Note the clear shape drawn by the RV ( left panel, top) and the associated bisector ( left panel, bottom) as function of time. In the right panel we depict the correlation between BIS and airmass ( right panel, top) and FWHM and airmass (right panel, bottom). The plotted errorbars in RV and BIS correspond to photon errors. Photon errors in the BIS are approximated to be twice the RV errors. |
| Open with DEXTER | |
Table 3: The fitted parameters and data properties, before and after the fitted model is subtracted from it.
In this series of measurements the BIS of the CCF clearly varies throughout the night (lower left panel). The BIS seems to be linearly correlated with both the airmass (upper right panel) and the FWHM of the fitted CCF (lower right panel). We omit from this series of plots one showing the correlation between contrast and airmass, which resembles the correlation between FWHM and airmass. Observing a star at different airmasses clearly produces different absorption features, with contrast and FWHM that depend linearly on airmass. The line profile variation is also asymmetric, as the BIS plot ilustrates, and scales with airmass. This asymmetry is therefore expected to have an impact on the measured RV.
These aforementioned properties are consistent with some molecular lines being naturally asymmetric (e.g., Frommhold 2006)![]() .
In observations at different airmasses, the light passes through a
medium with different path lengths. Because absorption does not vary
linearly with geometric path length but exponentially, the line shape
is bound to change. When one observes at higher airmass, the absorption
introduced by the additional molecules is stronger on the wings than in
the core, producing a larger, deeper, and more asymmetric absorption
line. We note that the CCF contrast oscillates around 72%, and many
lines have a contrast greater than 90%. These lines are no longer in
the linear regime. Another possible explanation is that as the line
broadening increases with pressure, the asymmetry becomes detectable.
This was measured for H2 in the Solar System gaseous planets by Cochran & Smith (1983).
.
In observations at different airmasses, the light passes through a
medium with different path lengths. Because absorption does not vary
linearly with geometric path length but exponentially, the line shape
is bound to change. When one observes at higher airmass, the absorption
introduced by the additional molecules is stronger on the wings than in
the core, producing a larger, deeper, and more asymmetric absorption
line. We note that the CCF contrast oscillates around 72%, and many
lines have a contrast greater than 90%. These lines are no longer in
the linear regime. Another possible explanation is that as the line
broadening increases with pressure, the asymmetry becomes detectable.
This was measured for H2 in the Solar System gaseous planets by Cochran & Smith (1983).
However, as seen on Fig. 2, this effect cannot alone explain the shape drawn by the RV, and another effect that operates at a timescale of one night must be present. From our previous discussion about the airmass/bisector influence, this second effect does not have an impact on the line asymmetry; it must therefore shift the center of atmospheric lines.
One possible explanation is a predominant, horizontal wind, constant
during the night. As one follows a star across the sky, the projection
of the wind vector along the line of sight of the telescope changes.
For a given telescope elevation ![]() and azimuth
and azimuth ![]() ,
the projection of an horizontal wind with direction
,
the projection of an horizontal wind with direction ![]() and speed
and speed ![]() along the line of sight of the telescope is given by
along the line of sight of the telescope is given by
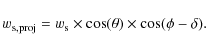
|
(1) |
Unfortunately, both these parameters are unknown
is linearly correlated with the measured RV (note that we used the fact that
We used a weighted linear least squares minimization to determine the best fit parameters for each subset of data. This approach was employed for subsets corresponding to complete nights, for which the hypothesis of a constant wind is a reasonable one. We compared the results yielded by linear least squares with that of non-linear least squares (using a Levenberg-Marquardt algorithm) and we recovered the same results.
If Eq. (2) correctly describes the phenomena affecting the RVs, then the parameter ![]() is
constant with time, by construction. From the same equation we conclude
that this parameter is simply the RV measured at zenith, where the
airmass and wind projection effects are null. One can then fit the
different data sets while imposing the same
is
constant with time, by construction. From the same equation we conclude
that this parameter is simply the RV measured at zenith, where the
airmass and wind projection effects are null. One can then fit the
different data sets while imposing the same ![]() for all. By the same reasoning,
for all. By the same reasoning, ![]() can be fixed. This is justified by the aforementioned assumption that
the bisector effect is caused by the fundamental asymmetry of line and
thus should not vary with time.
can be fixed. This is justified by the aforementioned assumption that
the bisector effect is caused by the fundamental asymmetry of line and
thus should not vary with time.
The results of the fitting are presented in Table 3.
We present the fitted parameters, along with the dispersion before and
after the fitted function is subtracted from the data, and the
![]() for each fit.
for each fit.
We also considered the cases in which ![]() and both
and both ![]() and
and ![]() are allowed to vary. The results are presented in Appendix A in Tables A.1 and A.2, respectively.
are allowed to vary. The results are presented in Appendix A in Tables A.1 and A.2, respectively.
The low chi-squared, within the range 2.5-4.01, attests to the validity of the empirical description of the RV variation. The residuals around the fit are about twice the photon noise, showing that this correction is effective down to roughly 2 m/s. As an example, the fit to the data set corresponding to the first night of the Tau Ceti campaign is presented in Fig. 3.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{14005fig3}
\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/07/aa14005-10/Timg28.png)
|
Figure 3: The fit of the atmospheric lines RV variation for the first night of the asteroseismology run of Tau Ceti. The fitted model is described by Eq. (2) and the parameters are presented in Table A.1. |
| Open with DEXTER | |
5 Discussion
We have demonstrated that O2 telluric lines are stable to 10 m/s (rms) on a timescale of 6 years. This is despite atmospheric phenomena, which introduce variations at the 1-10 m/s level, and can be corrected using simple atmospheric models, as described in Sect. 4.
The properties of the fitted parameters are very insightful in themselves. The imposition of a constant ![]() and
and ![]() for the different data sets lead to
for the different data sets lead to ![]() and
and ![]() values
that vary more smoothly over time and are thus more likely to
correspond to the physical ones. We would expect precisely the opposite
if the model assumptions were wrong because as the number of parameters
were reduced, the remaining ones would have to vary more to compensate
for the observed variations. We conclude therefore that the description
of the phenomena is correct. We cannot, however, discard that our model
cannot be refined. For instance, the airmass effect might depend on a
second order on the wind speed. In any case, the present model provides
good results to twice the photon noise level. Allowing all the fitting
parameters to vary reduces the
values
that vary more smoothly over time and are thus more likely to
correspond to the physical ones. We would expect precisely the opposite
if the model assumptions were wrong because as the number of parameters
were reduced, the remaining ones would have to vary more to compensate
for the observed variations. We conclude therefore that the description
of the phenomena is correct. We cannot, however, discard that our model
cannot be refined. For instance, the airmass effect might depend on a
second order on the wind speed. In any case, the present model provides
good results to twice the photon noise level. Allowing all the fitting
parameters to vary reduces the
![]() ,
but not in a very significant way; we thus consider the approach of fixing the
,
but not in a very significant way; we thus consider the approach of fixing the ![]() and
and ![]() to be the most adequate.
to be the most adequate.
Table 4: The measured dispersion for data-sets with restricted airmass, for time-spans of 1-8 days and the whole data-set.
The fitting delivers commonly ![]() larger than
larger than ![]() ,
i.e., the effect of wind projection on RV is usually of higher
magnitude than the airmass effect. We note that the wind direction is
predominantly from between N and NE and roughly of 40 m/s, which
is a common value for high-altitude winds over La Silla.
,
i.e., the effect of wind projection on RV is usually of higher
magnitude than the airmass effect. We note that the wind direction is
predominantly from between N and NE and roughly of 40 m/s, which
is a common value for high-altitude winds over La Silla.
The constancy of the wind over a short time interval and that the two effects scale with airmass attests that telluric lines can be straightforwardly used as a precise wavelength reference over short time scales, if one observes at low airmass. In Table 4, we present the dispersion in RV on timescales of 1-8 days at restricted airmass, quantifying this conclusion. A precision of 5 m/s can then clearly be routinely obtained without using any atmospheric corrections if one observes in these conditions.
We recall that both O2 and CO2 are abundant species in the atmosphere, with a roughly constant v.m.r. up to 80 km. This implies that these molecules are less sensitive to short timescale weather variations and the assumptions of a constant horizontal wind are realistic hypothesis.
We have not checked whether the correlation with our mask is affected by blending between telluric and stellar lines. The superposition of stellar lines on the telluric spectra varies from star to star, due to the different mean stellar RV and the projection of Earth's motion around the Sun along the line of sight to the star. However, for this to bias the final RV, i.e., introduce a systematic error, the blends would have to be similar for all lines. As a consequence, the superposition of stellar and telluric lines will, if present, only lead to an increase in the scatter of the measured RVs. An extensive study has been initiated to understand the impact of this effect.
6 Conclusions
Our results have proven that O2 telluric lines are stable down to 10 m/s on a timescale of 6 years. Atmospheric phenomena introduce variations at the 1-10 m/s level (rms). These can be accounted for by simple atmospheric models, which allow us to reach a precision of 2 m/s, twice the photon noise.
This work has illustrated the power of atmospheric features as a wavelength calibrator. It is now clear that this approach can compete with gas-cell methods on short timescales (of 1 week) in a straightforward way. A better precision than gas cell can even be achievable on longer timescales if the atmospheric variations are characterized and compensated for by simple modeling.
AcknowledgementsSupport from the Fundação para Ciência e a Tecnologia (Portugal) to P. F. in the form of a scholarship (reference SFRH/BD/21502/2005) is gratefully acknowledged. P.F. thanks to everyone who contributed to Planetary group meetings, and the referee Bill Cochran for his valuable comments on the paper.
Appendix A: Aditional fitting results
In this section we present the parameters for the best fit of Eq. (2), the dispersion of the data before and after the fit correction, the average photon noise and the
![]() .
Note that
.
Note that ![]() corresponds to the South-North direction.
corresponds to the South-North direction.
Table A.1: The fitted parameters and data properties, before and after the fitted model is subtracted from it, when all parameters are left to vary freely.
Table A.2:
The fitted parameters and data properties, before and after the fitted model is subtracted from it, with the ![]() imposed to be the same for all datasets.
imposed to be the same for all datasets.
References
- Balthasar, H., Thiele, U., & Woehl, H. 1982, A&A, 114, 357 [NASA ADS] [Google Scholar]
- Baranne, A., Queloz, D., Mayor, M., et al. 1996, A&AS, 119, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouchy, F., Pepe, F., & Queloz, D. 2001, A&A, 374, 733 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Butler, R. P., Marcy, G. W., Williams, E., et al. 1996, PASP, 108, 500 [NASA ADS] [CrossRef] [Google Scholar]
- Caccin, B., Cavallini, F., Ceppatelli, G., Righini, A., & Sambuco, A. M. 1985, A&A, 149, 357 [NASA ADS] [Google Scholar]
- Cochran, W. D., & Smith, W. H. 1983, ApJ, 271, 859 [NASA ADS] [CrossRef] [Google Scholar]
- Figueira, P., Pepe, F., Melo, C. H. F., et al. 2010, A&A, 511, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frommhold, L. 2006, Collision-Induced Absorption in Gases, ed. L. Frommhold [Google Scholar]
- Griffin, R., & Griffin, R. 1973, MNRAS, 162, 255 [NASA ADS] [Google Scholar]
- Huélamo, N., Figueira, P., Bonfils, X., et al. 2008, A&A, 489, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lovis, C., Mayor, M., Pepe, F., et al. 2006, Nature, 441, 305 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lovis, C., & Pepe, F. 2007, A&A, 468, 1115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
- Mayor, M., Udry, S., Lovis, C., et al. 2009, A&A, 493, 639 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pepe, F., Mayor, M., Galland, F., et al. 2002, A&A, 388, 632 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Queloz, D., Henry, G. W., Sivan, J. P., et al. 2001, A&A, 379, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rothman, L. S., Jacquemart, D., Barbe, A., et al. 2005, J. Quant. Spectrosc. Radiat. Transfer, 96, 139 [Google Scholar]
- Smith, M. A. 1982, ApJ, 253, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Snellen, I. A. G. 2004, MNRAS, 353, L1 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ... HARPS
![[*]](/icons/foot_motif.png)
- Based on observations taken at the 3.6 m telescope at La Silla.
- ... spectra
![[*]](/icons/foot_motif.png)
- The original reference is http://cdsads.u-strasbg.fr/abs/1973apds.book.....D, and the data are also available from the BASS 2000 database at http://bass2000.obspm.fr/solar_spect.php in a much easier way to use.
- ...
##) ![[*]](/icons/foot_motif.png)
- Note that this is the case for homonuclear diatomic molecules, like O2.
- ... unknown
![[*]](/icons/foot_motif.png)
- The weather stations at La Silla monitor the wind at
atmospheric ground layer. It is well known that the wind at the ground
layer is detached from those of high altitude, and as a consequence we
cannot use weather monitor values as a proxy for either
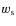 or
or 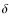 .
.
All Tables
Table 1: The summary of the data set properties for the stars used in this paper. Note that the S/N is calculated at the center of order 60.
Table 2: The dispersion and average photon noise of the stars used in our campaign.
Table 3: The fitted parameters and data properties, before and after the fitted model is subtracted from it.
Table 4: The measured dispersion for data-sets with restricted airmass, for time-spans of 1-8 days and the whole data-set.
Table A.1: The fitted parameters and data properties, before and after the fitted model is subtracted from it, when all parameters are left to vary freely.
Table A.2:
The fitted parameters and data properties, before and after the fitted model is subtracted from it, with the ![]() imposed to be the same for all datasets.
imposed to be the same for all datasets.
All Figures
![\begin{figure}
\par\includegraphics[width=9cm,clip]{14005fig1.eps}
\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/07/aa14005-10/Timg10.png)
|
Figure 1: The telluric RV variation in all Tau ceti measurements as a function of time. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{14005fig2a.eps}\hspace*{3mm}
\includegraphics[width=8.5cm,clip]{14005fig2b.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa14005-10/Timg13.png)
|
Figure 2: Telluric RV measurements on Tau Ceti over a full night. Note the clear shape drawn by the RV ( left panel, top) and the associated bisector ( left panel, bottom) as function of time. In the right panel we depict the correlation between BIS and airmass ( right panel, top) and FWHM and airmass (right panel, bottom). The plotted errorbars in RV and BIS correspond to photon errors. Photon errors in the BIS are approximated to be twice the RV errors. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{14005fig3}
\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/07/aa14005-10/Timg28.png)
|
Figure 3: The fit of the atmospheric lines RV variation for the first night of the asteroseismology run of Tau Ceti. The fitted model is described by Eq. (2) and the parameters are presented in Table A.1. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.