| Issue |
A&A
Volume 515, June 2010
|
|
|---|---|---|
| Article Number | A50 | |
| Number of page(s) | 14 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/200913837 | |
| Published online | 08 June 2010 | |
Low-frequency study of two giant radio galaxies: 3C 35 and 3C 223
E. Orrù1,2 - M. Murgia3,4 - L. Feretti4 - F. Govoni3 - G. Giovannini4,5 - W. Lane6 - N. Kassim6 - R. Paladino1
1 - Institute of Astro- and Particle Physics, University of Innsbruck,
Technikerstrasse 25/8, 6020 Innsbruck, Austria
2 - Radboud University Nijmegen, Heijendaalseweg 135, 6525 AJ Nijmegen,
The Netherlands
3 - INAF - Osservatorio Astronomico di Cagliari, Loc. Poggio dei Pini,
Strada 54, 09012 Capoterra (CA), Italy
4 - INAF - Istituto di Radioastronomia, via Gobetti 101, 40129 Bologna,
Italy
5 - Dipartimento di Astronomia Università degli Studi di Bologna, via
Ranzani 1, 40127 Bologna, Italy
6 - Naval Research Laboratory, Code 7213, Washington DC 20375-5320, USA
Received 9 December 2009 / Accepted 26 February 2010
Abstract
Aims. Radio galaxies with a projected linear size ![]() 1 Mpc
are classified as giant radio sources. According to the current
interpretation these are old sources which have evolved in a
low-density ambient medium. Because radiative losses are negligible at
low frequency, extending spectral aging studies in this frequency range
will allow us to determine the zero-age electron spectrum injected and
then to improve the estimate of the synchrotron age of the source.
1 Mpc
are classified as giant radio sources. According to the current
interpretation these are old sources which have evolved in a
low-density ambient medium. Because radiative losses are negligible at
low frequency, extending spectral aging studies in this frequency range
will allow us to determine the zero-age electron spectrum injected and
then to improve the estimate of the synchrotron age of the source.
Methods. We present Very Large Array images at
74 MHz and 327 MHz of two giant radio sources:
3C 35 and 3C 223. We performed a spectral
study using 74, 327, 608 and 1400 GHz images. The
spectral shape is estimated in different positions along the source.
Results. The radio spectrum follows a power-law in
the hotspots, while in the inner region of the lobe the shape of the
spectrum shows a curvature at high frequencies. This steepening agrees
with synchrotron aging of the emitting relativistic electrons.
In order to estimate the synchrotron age of the sources, the
spectra were fitted with a synchrotron model of emission. They show
that 3C 35 is an old source of 143 ![]() 20 Myr,
while 3C 223 is a younger source of 72
20 Myr,
while 3C 223 is a younger source of 72 ![]() 4 Myr.
4 Myr.
Key words: instrumentation: interferometers - techniques: interferometric - astroparticle physics - radio continuum: galaxies - galaxies: active - radiation mechanisms: non-thermal
1 Introduction
At the center of active galaxies resides a super-massive black hole, according to the standard model of active galactic nuclei (AGNs). The AGN is powered by an accretion disk surrounded by a torus of gas and dust (Blandford & Rees 1974). The powerful radio emission observed in classical double radio sources is produced by a bipolar pair of jets; relativistic outflows of matter which originate in the AGN. They first propagate into the interstellar medium (ISM) and then into the intergalactic medium (IGM) for a typical time of 108 yr (Scheuer 1974). The hotspots are the regions where the energy carried by the jets is diffused into the radio lobes. The observed diffuse radio emission is produced in the ``cocoon'' or lobe, which is formed by the built-up jet material and/or energy in the region between the core and the hotspots. The energy evolution of the cocoon can be traced by observations and spectral studies of the radio lobes. Radio lobes expand, and, assuming the source is in the equipartition regime, the pressure of the relativistic plasma in the lobe equals the pressure of the external environment (Begelman et al. 1984).
The radio spectrum of radio galaxies is initially described by a power-law. The final shape of the spectrum moves away from the power-law showing a steepening at higher frequencies. This is due to the competition between processes of energy injection and losses due to adiabatic expansion, synchrotron emission and inverse Compton scattering with the CMB photons, (Kellermann 1964; Pacholczyk 1970; Kardashev 1962). The initial models developed to interpret these spectra assumed a uniform and constant magnetic field and an isotropic injection of electrons (e.g., Kardashev 1962; Pacholczyk 1970; Jaffe & Perola 1973, hereafter KP and JP). If the former assumptions are satisfied it is possible in theory to use the synchrotron spectrum to estimate the age of the radiating particles.
Many authors (e.g., Eilek et al. 1997; Blundell & Rawlings 2000; Tribble 1993) argue that the observed filamentary structures in the radio lobes (e.g. for Cygnus A, Carilli et al. 1991) can be interpreted as the effect of inhomogeneous magnetic fields on the synchrotron emission. However, Kaiser (2000) demonstrated that the spatial distribution of the synchrotron radio emission can be used to estimate the age for FRII sources (Fanaroff & Riley 1974). Furthermore, based on the dynamical and radiative self-similar models in Kaiser & Alexander (1997) and Kaiser et al. (1997), Kaiser (2000) developed a 3-dimensional model of the synchrotron emissivity of the cocoons of powerful FRII radio sources. The projection along the line of sight (LOS) of the 3D model can be easily compared with radio observations.
X-ray emission related to the lobes has been detected in a
number of radio sources. This is attributed to the inverse
Compton (IC) scattering of microwave background photons. The direct
estimates of the magnetic field (
![]() )
obtained from the combination of the X-ray IC flux and the
radio synchrotron spectrum give values near to those found with the
equipartition (
)
obtained from the combination of the X-ray IC flux and the
radio synchrotron spectrum give values near to those found with the
equipartition (
![]() )
assumption (e.g., Croston
et al. 2005,2004). Moreover,
the above-mentioned comparisons suggest that lobes are not
overpressured at the late stages of the evolution of radio galaxies (Croston
et al. 2005,2004; Konar et al. 2009).
On the other hand, a strong variation of the
X-ray/radio flux ratio across the lobes has been found (Isobe
et al. 2002; Hardcastle & Croston 2005;
Goodger
et al. 2008). This cannot be explained with models
in which either the electron energy spectrum or the magnetic field vary
independently as a function of position in the lobes,
but it is consistent with models in which both vary
together as a function of position.
)
assumption (e.g., Croston
et al. 2005,2004). Moreover,
the above-mentioned comparisons suggest that lobes are not
overpressured at the late stages of the evolution of radio galaxies (Croston
et al. 2005,2004; Konar et al. 2009).
On the other hand, a strong variation of the
X-ray/radio flux ratio across the lobes has been found (Isobe
et al. 2002; Hardcastle & Croston 2005;
Goodger
et al. 2008). This cannot be explained with models
in which either the electron energy spectrum or the magnetic field vary
independently as a function of position in the lobes,
but it is consistent with models in which both vary
together as a function of position.
Among radio galaxies (RG), those with a projected linear size ![]() 1 Mpc
1 Mpc![]() are defined as giant radio
galaxies (GRG). In the complete sample of
3CR radio sources (Laing
et al. 1983) around 6
are defined as giant radio
galaxies (GRG). In the complete sample of
3CR radio sources (Laing
et al. 1983) around 6![]() of the sources are giants; there are about 100 known.
Giant radio galaxies typically have radio powers below 1026.5 W Hz-1 sr-1,
have linear sizes less than 3 Mpc, and are observed
at redshifts z < 0.25,
even though z < 0.5 could
be assumed as an upper limit (Saripalli et al. 2005;
Machalski
et al. 2007; Schoenmakers et al. 2000;
Lara
et al. 2004; Ishwara-Chandra & Saikia
1999). The P-D diagram (Ishwara-Chandra & Saikia
1999; Lara
et al. 2004) shows a dearth of high luminosity GRG,
as predicted by evolutionary models (Kaiser et al. 1997;
Blundell
et al. 1999) and a maximum GRG linear size
cut-off of 3 Mpc. An estimate of the
predominant process of radiative losses, obtained by separating the
contributions of the inverse Compton and synchrotron losses, shows that
the ratio of the estimated
of the sources are giants; there are about 100 known.
Giant radio galaxies typically have radio powers below 1026.5 W Hz-1 sr-1,
have linear sizes less than 3 Mpc, and are observed
at redshifts z < 0.25,
even though z < 0.5 could
be assumed as an upper limit (Saripalli et al. 2005;
Machalski
et al. 2007; Schoenmakers et al. 2000;
Lara
et al. 2004; Ishwara-Chandra & Saikia
1999). The P-D diagram (Ishwara-Chandra & Saikia
1999; Lara
et al. 2004) shows a dearth of high luminosity GRG,
as predicted by evolutionary models (Kaiser et al. 1997;
Blundell
et al. 1999) and a maximum GRG linear size
cut-off of 3 Mpc. An estimate of the
predominant process of radiative losses, obtained by separating the
contributions of the inverse Compton and synchrotron losses, shows that
the ratio of the estimated
![]() /
/
![]() increases with linear size,
and IC losses dominate the
radiative losses in GRG (Ishwara-Chandra
& Saikia 1999).
increases with linear size,
and IC losses dominate the
radiative losses in GRG (Ishwara-Chandra
& Saikia 1999).
As argued by many authors, the observed physical characteristics mentioned above could be the result of selection effects introduced by the selection criteria or by biases due to the low sensitivity of typical radio images. The faintest regions of GRG are well detected, even with a modest angular resolution, only with low frequency interferometric observations. The low-frequency spectral index information is crucial to derive the energy distribution of the radiating electrons and to study the energy transport from the nucleus to the lobes in these exceptionally large radio sources. Multifrequency spectral aging studies of GRG have been recently presented by Jamrozy and collaborators (Jamrozy et al. 2005,2004,2008). The median value for the estimated spectral ages is 23-24 Myr. The injection spectral index ranges from 0.55 to 0.88; it appears to increase with luminosity and redshift but shows an inverse correlation with linear size.
We present a multifrequency spectral analysis of the two classical double giant radio galaxies 3C 35 and 3C 223. In Sect. 2 radio observations and data analysis at 74 and 327 MHz are described. In Sect. 3 we present radio images of 3C 35 and 3C 223 at 74 and 327 MHz. In Sect. 4 we show the spectral index maps and the spectral analysis obtained by combining images at 74, 327, 608 and 1400 MHz. Results are discussed and summarized in Sect. 5.
Table 1: Summary of radio observations and images.
2 Radio data
The two selected giant radio galaxies are 3C 35
and 3C 223. The source 3C 35 is
included in the sample of 47 low redshift (z < 0.4)
GRG obtained by Schoenmakers
et al. (2001) using the Westerbork Northern Sky
Survey (WENSS) of the sky above
![]() of declination at
325 MHz (Rengelink
et al. 1997). The criteria for the sample specified
that a candidate GRG must have i) an angular size larger than
5 arcmin; and ii) a distance to the galactic plane of
more than 12.5 degrees.
of declination at
325 MHz (Rengelink
et al. 1997). The criteria for the sample specified
that a candidate GRG must have i) an angular size larger than
5 arcmin; and ii) a distance to the galactic plane of
more than 12.5 degrees.
The galaxy 3C 223 is included in a complete sample of large scale radio sources selected by Leahy & Perley (1991). The sources are drawn from a subset of the complete radio sample with z less than 0.5 defined by Laing et al. (1983).
Both 3C 35 and 3C 223 have linear sizes of 950 kpc and 780 kpc respectively, with the adopted cosmological parameters.
We observed these two GRG with the Very Large Array at 74 and 327 MHz in several configurations, according to their angular dimensions, in order to avoid the loss of flux. Observational parameters are summarized in Table 1. Because observations were made at slightly different frequencies, we will refer in the text simply to observations at 74 and 327 MHz. The exact frequencies are reported in Sect. 3 and are used for estimates of the physical parameters.
2.1 Observing strategy
Radio Frequency Interference (RFI) strongly affects and corrupts the data in low-frequency observations. In order to permit the RFI excision and to minimize the bandwidth smearing effect, the observations were conducted in spectral line mode. A difference has been established in the nature of the RFI sources in the VLA system: at 74 MHz most of the interference is caused by the 100 kHz oscillators in the bases of each telescope, which generate harmonics at 100 kHz intervals and produce the typical ``100 kHz comb''. This kind of RFI is ``easy'' to predict and eliminate. In the 327 MHz band, the internal electronics of the VLA give rise to harmonics that are multiples of 5 and 12.5 MHz; to avoid these narrow bandwidths are used (Kassim et al. 1993). On the whole, the values of rms sensitivity attained at these frequencies are somewhat higher than the expected thermal noise levels, because of the contribution of several factors: confusion, broad-band RFI, and VLA generated RFI.
2.2 Data reduction
Data were calibrated and reduced with the Astronomical Image Processing System (AIPS). Because the calibration procedures are different for 74 MHz and 327 MHz, the following sections describe the methods employed separately.
2.2.1 74 MHz
The 74 MHz data were calibrated and imaged following the same procedure used for the VLA Low-frequency Sky Survey (VLSS) as described carefully in Kassim et al. (2007) and Cohen et al. (2007).
For both 3C 35 and 3C 223 we made the amplitude and bandpass
calibration using a model of Cygnus A![]() .
.
Careful data editing was used to excise the RFI (Lane et al. 2005);
the percentage of flagged data at the end of this process was
about 13![]() for both sources. Before the final imaging the data were averaged to
8 frequency channels with a resolution
of 170.9 kHz.
for both sources. Before the final imaging the data were averaged to
8 frequency channels with a resolution
of 170.9 kHz.
To produce the final images we used the so-called ``field-based calibration'' method developed for the VLSS (Cotton et al. 2004). The field-based calibration procedure makes a correction for the low order in the ionospheric terms and performs a ``wide-field imaging'' (kindly provided by Cotton). The offsets of the apparent positions of the NRAO VLA Sky Survey (NVSS) sources (Condon et al. 1998) from their expected positions were computed at time intervals of 2 min and corrected in the visibility data. Some data with a too large correction were removed for 3C 35. We corrected the final images for the primary beam effect.
The final image of 3C 35 obtained with VLA data in
B configuration has an rms sensitivity of ![]() 95 mJy/beam
(93
95 mJy/beam
(93
![]()
![]() 64
64
![]() ).
).
For the source 3C 223 we produced a high-resolution
image in A configuration, with rms sensitivity ![]() 43 mJy/beam
(25
43 mJy/beam
(25
![]()
![]() 24
24
![]() ). A low resolution
image was also made with data from the VLA in B configuration;
it has an rms sensitivity
). A low resolution
image was also made with data from the VLA in B configuration;
it has an rms sensitivity ![]() 98 mJy/beam (83
98 mJy/beam (83
![]()
![]() 73
73
![]() ). The image obtained
with the combination of the A and B configuration
data has a sensitivity of 40 mJy/beam (26
). The image obtained
with the combination of the A and B configuration
data has a sensitivity of 40 mJy/beam (26
![]()
![]() 25
25
![]() ). The sensitivity is
different from the theoretical noise because of side-lobe confusion
from other sources in the beam.
). The sensitivity is
different from the theoretical noise because of side-lobe confusion
from other sources in the beam.
2.2.2 327 MHz
We made the amplitude and bandpass calibration with the sources 3C 48 and 3C 286 respectively for 3C 35 and 3C 223.
After careful data editing to remove RFI, 10![]() of
the data were flagged in 3C 35 and 3
of
the data were flagged in 3C 35 and 3![]() for 3C 223.
for 3C 223.
Before imaging, the data of 3C 35 were averaged to five channels with a resolution of 488.3 KHz, and the 3C 223 data were averaged to six channels with a resolution of 781.3 kHz.
The data were mapped with a wide-field imaging technique,
which corrects for distortions in the image caused by the
non-coplanarity of the VLA over a wide field of view
(the ``3D effect'' included in the AIPS task IMAGR).
A set of small overlapping maps was used to cover the central
area of about
![]() in
radius (Cornwell &
Perley 1992). However, at this frequency confusion
lobes of sources far from the center of the field are still present.
Thus, we also imaged strong sources in an area of about
in
radius (Cornwell &
Perley 1992). However, at this frequency confusion
lobes of sources far from the center of the field are still present.
Thus, we also imaged strong sources in an area of about
![]() in radius,
based on positions in the NVSS catalog.
All these ``facets'' were included in the CLEAN and used for several
loops of self-calibration (Perley
1999). The data for each observation and
configuration were calibrated, imaged and then combined. We corrected
the final images for the primary beam effect.
in radius,
based on positions in the NVSS catalog.
All these ``facets'' were included in the CLEAN and used for several
loops of self-calibration (Perley
1999). The data for each observation and
configuration were calibrated, imaged and then combined. We corrected
the final images for the primary beam effect.
In particular, for 3C 35, we obtain a high-resolution
image at 327 MHz with data from the VLA in
B configuration; the rms sensitivity is ![]() 1.3 mJy/beam
(23
1.3 mJy/beam
(23
![]()
![]() 17
17
![]() ). A low resolution
image was made from VLA observations in C configuration, with
an rms sensitivity of
). A low resolution
image was made from VLA observations in C configuration, with
an rms sensitivity of ![]() 2.3 mJy/beam (55
2.3 mJy/beam (55
![]()
![]() 50
50
![]() ). By combining the
B configuration data and data from IF 1 of
the C configuration, we improved the uv-coverage and
sensitivity; the rms in
the combined image is
). By combining the
B configuration data and data from IF 1 of
the C configuration, we improved the uv-coverage and
sensitivity; the rms in
the combined image is ![]() 1.0 mJy/beam
(27
1.0 mJy/beam
(27
![]()
![]() 21
21
![]() ).
).
We obtained a high-resolution image of 3C 223 with
VLA observations in A configuration; the
rms sensitivity is ![]() 0.7 mJy/beam
(6
0.7 mJy/beam
(6
![]()
![]() 5
5
![]() ). A low resolution
image with a sensitivity of
). A low resolution
image with a sensitivity of ![]() 1.3 mJy/beam
was made from VLA data taken in B configuration (19
1.3 mJy/beam
was made from VLA data taken in B configuration (19
![]()
![]() 16
16
![]() ). To improve the
uv-coverage and the sensitivity we combined the datasets. The final
rms sensitivity is
). To improve the
uv-coverage and the sensitivity we combined the datasets. The final
rms sensitivity is ![]() 0.6 mJy/beam
(7
0.6 mJy/beam
(7
![]()
![]() 6
6
![]() ). The final sensitivity
differs from the theoretical noise due to classical confusion.
). The final sensitivity
differs from the theoretical noise due to classical confusion.
3 Results
3.1 3C 35
The source 3C 35 is a classical double radio source with a regular FRII structure (Fanaroff & Riley 1974); its principal characteristics are listed in Table 2. It has been previously studied at frequencies of 608 MHz, 1.4 and 5 GHz with the Westerbork Synthesis Radio Telescope (WSRT) (van Breugel & Jägers 1982; Jägers 1987; Schoenmakers et al. 2000).
The VLA radio images at 74 and 327 MHz of the radio galaxy 3C 35 are shown in the left and the right panel of Fig. 1 respectively; sensitivities and resolutions are listed in Table 1. On the left of Fig. 1 is the image at 73.8 MHz obtained with VLA in B configuration. In the contours map the regular double-lobe structure of the source is clear, as are the two hotspots. The emission is stronger at the head of the northern lobe (N lobe).
On the right panel of Fig. 1 the 327 MHz image is shown. The image is obtained by combining the data of B and C configurations at a frequency of 327.4 MHz. The high and low resolution images (not shown in this paper) were obtained with the B and the C configurations of the VLA respectively. The image at 327 MHz confirms that in the N lobe the radio emission is stronger than in the southern lobe (S lobe). The hot spot South (S hot spot) is slightly shifted with respect to the axis of symmetry of the source. Based on the images at 5 GHz, van Breugel & Jägers (1982) claimed that the S hot spot could be a double. Considering the image at 327 MHz, it seems that the second weak ``hot spot'' is more likely to be a knot of the jet. In the image the core and surrounding low brightness emission have both been detected.
Table 2: Source properties.
![\begin{figure}
\par\includegraphics[width=14cm,clip]{13837fg1.eps}
\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13837-09/Timg29.png)
|
Figure 1:
Radio images of 3C 35, all contours start at (3 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{13837fg2.ps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13837-09/Timg30.png)
|
Figure 2:
Radio images of 3C 223, all contours start at (3 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{13837fg3.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13837-09/Timg31.png)
|
Figure 3:
3C 35: spectral index maps are shown in color; pixels whose
brightness was below 3 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{13837fg4.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13837-09/Timg32.png)
|
Figure 4:
3C 223: spectral index maps are shown in color; pixels whose
brightness was below 3 |
| Open with DEXTER | |
3.2 3C 223
The host galaxy of 3C 223 is in a group of 12 small galaxies (Baum et al. 1988). It is a typical double radio source with a regular FRII structure (Fanaroff & Riley 1974). It was previously studied in with the WRST at 608 MHz, 1.4 and 5 GHz (Hogbom 1979; van Breugel & Jägers 1982; Jägers 1987) and at high resolution with the VLA at 1.4 GHz (Leahy & Perley 1991). The general characteristics of this source are presented in Table 2.
The images at 74 and 327 MHz shown in Fig. 2 were obtained by VLA observations using A and B configurations. The sensitivities and resolutions are listed in Table 1.
The 74 MHz image is shown on the left panel of Fig. 2. A low resolution image was obtained with the VLA in B configuration while the high-resolution image was made with the A configuration (both images are not shown in this paper). To improve the uv-coverage and the sensitivity, we combined the A and B configuration data. The combined image, shown on the left of Fig. 2, is made at an observed frequency of 73.8 MHz.
As can be observed in the higher brightness contours of the
image, the morphology of the source preserves the
FRII structure. An extended low brightness structure
is easily visible to the West of the southern lobe and some faint
extended emission seems also to be present to the East of the northern
lobe. This diffuse structure shows a different orientation axis with
respect to that of
the active lobes. The origin of this structure is not clear,
it could be the remnant of former radio emission,
or a relic lobe. A hint of this low
brightness emission is present at the same position in the existing
image at 1.4 GHz Leahy
& Perley (1991). The estimated spectral index of this
low brightnesses radio structure is ![]()
![]() 1.3
(obtained from the spectral index map between 1.4 GHz and
74 MHz not shown here); this is conspicuously steeper
than the average value measured for the whole radio galaxy
(Sect. 3.3 and Table 5).
1.3
(obtained from the spectral index map between 1.4 GHz and
74 MHz not shown here); this is conspicuously steeper
than the average value measured for the whole radio galaxy
(Sect. 3.3 and Table 5).
The image at 327 MHz is shown on the right panel of Fig. 2. A high-resolution image at 327.3 MHz was obtained with the VLA in A configuration, while the low resolution image was obtained at the observing frequency of 328.9 MHz with the B configuration (both images are not shown in this paper). In the right panel of Fig. 2 the contours of the image obtained by combining the A and B configuration data at the frequency of 327.3 MHz are presented.
Unlike the images at 608 MHz (van Breugel & Jägers 1982), the core was clearly detected at 327 MHz because of the high-resolution achieved. The high-resolution obtained in the image at 327 MHz allows us to confirm the peculiar ``V'' shape of the N hot spot, previously seen in high-resolution images at 1.4 GHz (Leahy & Perley 1991). Moreover, at 327 MHz, as well as in the high-resolution images at 1.4 and 5 GHz (van Breugel & Jägers 1982; Leahy & Perley 1991), the S hot spot seems embedded in the lobe, at the end of which a protuberance is detected.
3.3 Spectral index distribution
By combining the new images at 74 MHz and 327 MHz
with those at 1.4 GHz available in the literature, we
obtained the spectral index![]() distributions of the two radio galaxies 3C 35
and 3C 223. Figures 3 and 4 show the
spectral index maps of 3C 35 and 3C 223,
respectively. Both figures show on the left the spectral index maps
between 74 MHz and 327 MHz, while on the right are
those between 327 MHz and 1.4 GHz. In the
range between 74 MHz and 327 MHz (95
distributions of the two radio galaxies 3C 35
and 3C 223. Figures 3 and 4 show the
spectral index maps of 3C 35 and 3C 223,
respectively. Both figures show on the left the spectral index maps
between 74 MHz and 327 MHz, while on the right are
those between 327 MHz and 1.4 GHz. In the
range between 74 MHz and 327 MHz (95
![]()
![]() 95
95
![]() ), the spectral index
values
of 3C 35 vary from
), the spectral index
values
of 3C 35 vary from ![]()
![]() 0.65
0.65 ![]() 0.04, in the main parts of the source, up to
0.04, in the main parts of the source, up to ![]()
![]() 0.84
0.84 ![]() 0.06 in the region near the core.
0.06 in the region near the core.
Table 3: Resolution and rms of the images used for the spectral index maps.
The spectral index between 327 MHz and
1.4 GHz (45
![]()
![]() 45
45
![]() )
for 3C 35 varies more than the lower frequency index. In the
region of the head of the lobes,
)
for 3C 35 varies more than the lower frequency index. In the
region of the head of the lobes, ![]() is
about 0.72
is
about 0.72 ![]() 0.01,
while it reaches values of
0.01,
while it reaches values of ![]() 1.6
1.6 ![]() 0.04
in the inner region of the lobes around the core. The image at
1.4 GHz used to obtain the spectral index map has been taken
from the NVSS (Condon et al. 1998).
The morphology of this source at 1.4 GHz recalls that
observed at 327 MHz.
0.04
in the inner region of the lobes around the core. The image at
1.4 GHz used to obtain the spectral index map has been taken
from the NVSS (Condon et al. 1998).
The morphology of this source at 1.4 GHz recalls that
observed at 327 MHz.
For the radio galaxy 3C 223, the spectral index
distribution between 74 and 327 MHz (26
![]()
![]() 26
26
![]() )
is slightly more patchy than that of 3C 35. The
average value of
)
is slightly more patchy than that of 3C 35. The
average value of ![]() is about 0.60
is about 0.60 ![]() 0.03. In the North hot spot the
spectral index reaches values of
0.03. In the North hot spot the
spectral index reaches values of ![]() 0.40
0.40 ![]() 0.01, while in the low brightness
regions of the lobes the spectral index steepens up to
0.01, while in the low brightness
regions of the lobes the spectral index steepens up to ![]()
![]() 1.67
1.67 ![]() 0.02.
0.02.
The spectral index map between 327 MHz and
1.48 GHz (7.5
![]()
![]() 7.5
7.5
![]() )
for 3C 223 shows that the spectral index increases from
)
for 3C 223 shows that the spectral index increases from ![]()
![]() 0.72
0.72 ![]() 0.01 in the region of the
head of the lobes, up to values of
0.01 in the region of the
head of the lobes, up to values of ![]()
![]() 1.32
1.32 ![]() 0.09 in the inner regions of the lobes near to the core. The image used
at 1.48 GHz was taken from VLA archive data (Leahy & Perley 1991).
0.09 in the inner regions of the lobes near to the core. The image used
at 1.48 GHz was taken from VLA archive data (Leahy & Perley 1991).
3.4 Measure and estimate of physical parameters
For both sources the flux density at 74 and 327 MHz was measured in the same regions. The values listed in Tables 4 and 5 indicate the flux of the entire source, of the two lobes separately and of the core when detected. For these regions we also calculated the spectral index between 74 and 327 MHz and the equipartition magnetic field (Tables 4 and 5). The measured total flux densities at 327 MHz were compared with the measurements of the WENSS, these agree within the errors for both sources.
Table 4: 3C 35 Flux densities, spectral indices and equipartition magnetic fields.
Table 5: 3C 223 Flux densities, spectral indices and equipartition magnetic fields.
The zero-order estimate of the magnetic field strength, averaged over the entire source volume, can be derived under the assumption of classical equipartition. Here, the radio source is in a minimum energy condition and the relativistic particle energy density equals the magnetic field energy density. In the framework of the equipartition hypothesis, the magnetic field can be determined from the radio synchrotron luminosity and the source volume. We estimated the equipartition magnetic field assuming a magnetic field entirely filling the radio source in a range of frequencies in which the synchrotron luminosity is calculated from a low frequency cutoff of 10 MHz to a high frequency cutoff of 10 GHz. The volume averaged magnetic fields were evaluated within a cylinder. Then we considered two cases: a) one in which the energy is equally divided between relativistic protons and electrons-positrons, and the ratio between protons and electrons k=p/e will be k=1; and b) a case in which all the energy is provided by a plasma of relativistic electrons-positrons and k=0.
In our case we consider a power-law injection spectrum with
index ![]() ,
therefore, since
,
therefore, since ![]() ,
we adopted the measured spectral index
,
we adopted the measured spectral index ![]() for the estimate of the magnetic field.
for the estimate of the magnetic field.
![\begin{figure}
\par\includegraphics[width=14cm,clip]{13837fg5b.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13837-09/Timg45.png)
|
Figure 5b: Similar to 5 for the S lobe of 3C 35. |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{13837fg6b.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13837-09/Timg47.png)
|
Figure 6b: Similar to 6 for the the S lobe of 3C 223. |
Assuming a low-frequency cut-off of 10 MHz in the luminosity
calculation is equivalent to assuming a low-energy cut-off of
![]() in the particle energy spectrum (
in the particle energy spectrum (
![]() in Tables 4 and 5). Therefore we
adopted the revised formalism (Brunetti
et al. 1997; Beck
& Krause 2005) in our estimates of
in Tables 4 and 5). Therefore we
adopted the revised formalism (Brunetti
et al. 1997; Beck
& Krause 2005) in our estimates of
![]() assuming a low-energy cut-off
of
assuming a low-energy cut-off
of ![]() in the particle energy distribution rather than a low-frequency cut-off
in the emitted synchrotron spectrum (
in the particle energy distribution rather than a low-frequency cut-off
in the emitted synchrotron spectrum (
![]() in Tables 4
and 5).
in Tables 4
and 5).
For 3C 35 we considered a cylinder of
190 kpc of radius and height ![]() 1 Mpc. The adopted spectral index of the
electron energy spectrum, between 74 and 327 MHz
(Table 4)
is
1 Mpc. The adopted spectral index of the
electron energy spectrum, between 74 and 327 MHz
(Table 4)
is ![]()
![]() 0.7,
which yields
0.7,
which yields ![]() = 2.4.
The volume of the two lobes respectively is one half of the total
volume. The measure of the fluxes includes the emission of the
hotspots. The estimated equipartition magnetic field strength values
are listed in Table 4.
= 2.4.
The volume of the two lobes respectively is one half of the total
volume. The measure of the fluxes includes the emission of the
hotspots. The estimated equipartition magnetic field strength values
are listed in Table 4.
For the radio source 3C 223, we assumed a cylinder
with radius of ![]() 200 kpc
and height
200 kpc
and height ![]() 900 kpc.
The spectral index of the electron energy spectrum of the entire source
and of the North lobe is
900 kpc.
The spectral index of the electron energy spectrum of the entire source
and of the North lobe is ![]() = 2.2
which corresponds to
= 2.2
which corresponds to
![]()
![]() 0.6,
while for the South lobe we used
0.6,
while for the South lobe we used ![]() = 2.4,
which corresponds to
= 2.4,
which corresponds to ![]()
![]() 0.7.
The contribution of the hotspot emission was included in these
measures. The resulting equipartition magnetic fields strength are
presented in Table 5.
0.7.
The contribution of the hotspot emission was included in these
measures. The resulting equipartition magnetic fields strength are
presented in Table 5.
One of the most important physical properties of GRG, which
distinguishes them from compact and powerful sources like
e.g. CygA, is that the equipartition magnetic field
is far below the inverse
Compton equivalent field over most of the lobes
(see Tables 4
and 5).
This means that the electron energy losses are largely dominated by the
inverse Compton scattering of the CMB photons, which can be
assumed to be fairly uniform and isotropic. Thus the location of the
break energy is mostly unaffected by eventual gradients of the magnetic
field in the lobe. However, very strong negative magnetic field
gradients from the hotspot to the core, if any, could affect
the location of the break frequency and mimic the effect of aging,
i.e. the source would appear older than it really is.
Although, at least in the case of 3C 223, we know from the
X-ray data that the equipartition magnetic field is correct to within a
factor of 2. However, in the hotspots the situation
is different and the magnetic field could be significantly higher
than
![]() ,
where
,
where
![]() is the magnetic field directly
estimated by using X-ray and radio data.
On the other hand, in these regions radiative losses
are balanced by re-acceleration and injection of new particles to form
what we define as ``the zero-age injection spectrum'' (see the
discussion in Carilli
et al. 1991). Unfortunately, we do not have enough
resolution in our images to resolve the hotspots in our GRGs and thus
to address this issue further in detail.
is the magnetic field directly
estimated by using X-ray and radio data.
On the other hand, in these regions radiative losses
are balanced by re-acceleration and injection of new particles to form
what we define as ``the zero-age injection spectrum'' (see the
discussion in Carilli
et al. 1991). Unfortunately, we do not have enough
resolution in our images to resolve the hotspots in our GRGs and thus
to address this issue further in detail.
4 Synchrotron model
4.1 Fitting the spectral shape
The extended size of the two sources and the resolution reached in our
images allowed us to describe the variation of the total intensity at
different frequencies, from the hotspot, where the particles are
injected, up to the inner regions of lobes, where the older
less energetic electrons are supposed to be located. We assumed that
the particles are injected by the jets in the intergalactic medium in a
certain epoch t0
with a power-law energy spectrum
then the jets move further injecting particles into another region. This continues up to the hot spots where particles are injected at the current epoch. The relativistic particles emit a synchrotron radiation and the spectrum is still a power-law with a spectral index
The JP model (Jaffe &
Perola 1973) was used in this analysis. In this model the
pitch angle scattering is very efficient; indeed the isotropization
occurs on a time scale much shorter than the radiative
time-scale. Because the pitch angle is continuously randomized, each
particle of the electron population can assume all possible
orientations with respect to the magnetic field. In the framework of
the JP model, the break frequency
![]() is a time-dependent function
that can be estimated by fitting the
curvature of the radio spectra. If there is no expansion and
the magnetic field is constant, the break frequency depends on
the elapsed time since the injection of
the particles according to this formula (Slee
et al. 2001):
is a time-dependent function
that can be estimated by fitting the
curvature of the radio spectra. If there is no expansion and
the magnetic field is constant, the break frequency depends on
the elapsed time since the injection of
the particles according to this formula (Slee
et al. 2001):
where
For each source we measured the total intensity for the N lobe and S lobe in a grid of boxes placed along the source (top panels of the Figs. 5 and 6). For the source 3C 35 we choose the size of the boxes of half of the beam size for the lobes to have an even number of nearly independent measures, this fine sampling does not affect the age estimate. Because of the poor resolution the boxes of the two hotspots were selected to be of about one beam size to avoid the breaking off of the hotspots in two boxes. For the source 3C 223 boxes are about one beam size.
The plots in Figs. 5 and 6 refer to the N lobes, while Figs. 5 and 6 show the S lobes of the sources 3C 35 and 3C 223 respectively. The contribution of the emission from the core was masked for both sources. Each plot corresponds to a box as shown in the labels on the bottom-left corner. The red dots represent the data, while the blue dashed lines are the fit with the model.
The model used to fit the data is the JP model available in the software package Synage++ (Murgia 2000). For these two radio sources, the choice of the JP model is justified because as the magnetic field is low, the inverse Compton losses are as important as synchrotron losses, therefore the CMB isotropises the electron population.
The spectra of 3C 35 were obtained using cube images
with frequencies of 74, 327, 608 and 1400 MHz at the
resolution of 95
![]() .
To perform this analysis we used the 608 MHz
WSRT image with a resolution of 40
.
To perform this analysis we used the 608 MHz
WSRT image with a resolution of 40
![]()
![]() 20
20
![]() ,
PA = 0
,
PA = 0![]() and rms 1.3 mJy/beam; the 1.4 GHz
image has been taken from the NVSS. The free parameters in the fit are
the break frequency
and rms 1.3 mJy/beam; the 1.4 GHz
image has been taken from the NVSS. The free parameters in the fit are
the break frequency
![]() ,
the injection spectral index
,
the injection spectral index
![]() and the flux normalization,
which is proportional to the
integral along the line of sight of the product N0
and the flux normalization,
which is proportional to the
integral along the line of sight of the product N0 ![]()
![]() .
The resulting fitted parameters obtained for each box and the
reduced
.
The resulting fitted parameters obtained for each box and the
reduced ![]() (
(![]() /ndf, where
ndf is the number of degrees of freedom) are listed in Table 6. The shape of
the hot spots is well described by power-laws; the estimated break
frequencies are >4.71 GHz for the North hot spot and
>3.07 GHz for the South. The injection spectral index
is 0.66
-0.12+0.09
and 0.59
-0.12+0.14
for the North and for the South hot spots respectively. In the inner
part of the lobes
/ndf, where
ndf is the number of degrees of freedom) are listed in Table 6. The shape of
the hot spots is well described by power-laws; the estimated break
frequencies are >4.71 GHz for the North hot spot and
>3.07 GHz for the South. The injection spectral index
is 0.66
-0.12+0.09
and 0.59
-0.12+0.14
for the North and for the South hot spots respectively. In the inner
part of the lobes
![]() is
is ![]() 700-800 MHz.
The fitted spectra are plotted in Figs. 5 and b
and summarized in Fig. 7
as a function of the distance from the core. The central panel
of Fig. 7
shows a variation of the injection spectral index along the source, the
values range from 0.29 to 0.66; on average
700-800 MHz.
The fitted spectra are plotted in Figs. 5 and b
and summarized in Fig. 7
as a function of the distance from the core. The central panel
of Fig. 7
shows a variation of the injection spectral index along the source, the
values range from 0.29 to 0.66; on average
![]()
![]() 0.5.
A variable spectral index could be explained in terms of
deceleration of the relativistic plasma along the jets, following the
subsequently happening of multiple shocks (Meli
et al. 2008). This could be observed with a
steepening of the electron spectra and in parallel of
0.5.
A variable spectral index could be explained in terms of
deceleration of the relativistic plasma along the jets, following the
subsequently happening of multiple shocks (Meli
et al. 2008). This could be observed with a
steepening of the electron spectra and in parallel of
![]() with the aging of the source.
Observations of the electron spectra from
the terminal hotspots to the lobes of the powerful FR-II radio
galaxies showed that
these have not a single and universal power-law form (Rudnick
et al. 1994; Machalski et al. 2007).
with the aging of the source.
Observations of the electron spectra from
the terminal hotspots to the lobes of the powerful FR-II radio
galaxies showed that
these have not a single and universal power-law form (Rudnick
et al. 1994; Machalski et al. 2007).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13837fg7.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13837-09/Timg59.png)
|
Figure 7:
3C 35: plotted with respect to the distance from the core:
the fitted values of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13837fg8.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13837-09/Timg60.png)
|
Figure 8:
3C 223: plotted with respect to the distance from the core:
the fitted values of
|
| Open with DEXTER | |
Nevertheless, is should be considered that our error bars
on
![]() are large, and hence
the injection spectral index could still
be considered fairly constant around a value of
are large, and hence
the injection spectral index could still
be considered fairly constant around a value of ![]() 0.5. Future
observations at possibly higher sensitivity are needed to definitely
confirm the
0.5. Future
observations at possibly higher sensitivity are needed to definitely
confirm the
![]() trend along
the lobes.
trend along
the lobes.
The top panel of Fig. 7 shows the
synchrotron age of 3C 35 calculated with Eq. (2). The values used
for
![]() and
and
![]() (k=1) are
listed in
Tables 6
and 4
respectively. The synchrotron age calculated for the
source 3C 35
138-22+20 Myr
for the North lobe and
147-36+35 Myr
for the South lobe. Therefore, in agreement with Parma et al. (1999),
3C 35 can be considered an old source. Moreover we can
conclude that the source reached this size expanding with a constant
velocity in the
extragalactic medium
(k=1) are
listed in
Tables 6
and 4
respectively. The synchrotron age calculated for the
source 3C 35
138-22+20 Myr
for the North lobe and
147-36+35 Myr
for the South lobe. Therefore, in agreement with Parma et al. (1999),
3C 35 can be considered an old source. Moreover we can
conclude that the source reached this size expanding with a constant
velocity in the
extragalactic medium ![]()
![]() 0.011c
because from the plot we can see that the
0.011c
because from the plot we can see that the
![]() increases linearly with the
distance from the hotspots.
increases linearly with the
distance from the hotspots.
In the analysis of 3C 223 we used images
at 74, 327 and 1400 MHz with a resolution
of 26
![]() .
The 1.4 GHz image is from Leahy
& Perley (1991). We used a fixed
.
The 1.4 GHz image is from Leahy
& Perley (1991). We used a fixed
![]() ,
assumed according to the literature, because the observational data
were only for three frequencies, which restricted us to two free
parameters. These are the break frequency
,
assumed according to the literature, because the observational data
were only for three frequencies, which restricted us to two free
parameters. These are the break frequency
![]() and the flux normalization.
The resulting fitted parameters obtained
for each box and the reduced
and the flux normalization.
The resulting fitted parameters obtained
for each box and the reduced ![]() are listed in Table 7.
In this case the spectral shape of the hot spots drifts away
from a power-law, a
are listed in Table 7.
In this case the spectral shape of the hot spots drifts away
from a power-law, a
![]() of
about 6.0-7.0 GHz was estimated. In the inner
regions of the lobes the spectrum steepens and the
of
about 6.0-7.0 GHz was estimated. In the inner
regions of the lobes the spectrum steepens and the
![]() is
is ![]() 1.5 GHz.
The fitted spectra are plotted in Figs. 6
and b and summarized as a function of the distance from the
core in Fig. 8.
1.5 GHz.
The fitted spectra are plotted in Figs. 6
and b and summarized as a function of the distance from the
core in Fig. 8.
In the top panel of Fig. 8 we plot the
synchrotron age of 3C 223 estimated from the
Eq. (2),
and using the values of
![]() and
and
![]() in Tables 7
and 5.
For the source 3C 223 the
in Tables 7
and 5.
For the source 3C 223 the
![]() is
68-4+4
for the North lobe and
76-5+5 Myr for
the South lobe. As for 3C 35,
the age decreases linearly with the distance from the core,
so we can assume that the lobes advanced with a constant
velocity
is
68-4+4
for the North lobe and
76-5+5 Myr for
the South lobe. As for 3C 35,
the age decreases linearly with the distance from the core,
so we can assume that the lobes advanced with a constant
velocity ![]()
![]() 0.017c.
0.017c.
Table 6:
3C 35: break frequency, alpha injection and reduced ![]() .
.
The 5 GHz archival data were not included in the
spectral aging analysis because the low-surface brightness emission
near the core is not properly imaged by the interferometric
observations at 5 GHz due to the lack of short-space
baselines. However, it should be noted that the fit of the
JP model is able to also recover a break frequency
significantly above the maximum frequency in our data set, because the
spectral shape departs from a pure power law well
before
![]() .
Indeed, although in the JP model all particles have the same
break energy, the break frequency of the particles at small
pitch angle,
.
Indeed, although in the JP model all particles have the same
break energy, the break frequency of the particles at small
pitch angle, ![]() ,
is also smaller:
,
is also smaller:
![]() .
.
4.2 Fit of the spectral index profile
In this section we evaluate the frequency break and the injection
spectral index independently for the two lobes of each source by
fitting with the synchrotron model the two frequency spectral
index,
![]() ,
as a function of the distance from the core. This
method allows an investigation of the spectral index behavior at higher
spatial resolution compared to the previous, multi-frequency analysis
(Sect. 4.1),
which was limited by the resolution of the 74 MHz images.
Following the assumption that the sources are expanding with a constant
velocity, we have
,
as a function of the distance from the core. This
method allows an investigation of the spectral index behavior at higher
spatial resolution compared to the previous, multi-frequency analysis
(Sect. 4.1),
which was limited by the resolution of the 74 MHz images.
Following the assumption that the sources are expanding with a constant
velocity, we have
![]() since t=d/v.
Here t is the age and d is
the distance from the hotspot. We fitted
since t=d/v.
Here t is the age and d is
the distance from the hotspot. We fitted
![]() ,
where
,
where ![]() is a free parameter. If
is a free parameter. If ![]() is 2, this means that the source is expanding with a constant
velocity
and adiabatic losses are negligible. If
is 2, this means that the source is expanding with a constant
velocity
and adiabatic losses are negligible. If ![]() is steeper than 2 either the expansion losses play an
important role in the energetic of the source and/or the radio source
is not expanding with a constant speed.
is steeper than 2 either the expansion losses play an
important role in the energetic of the source and/or the radio source
is not expanding with a constant speed.
The fit for the source 3C 35 (Fig. 9) gives
![]()
![]() 0.7-0.8 GHz, which agrees well with that found
in Sect. 4.1. The slope
0.7-0.8 GHz, which agrees well with that found
in Sect. 4.1. The slope
![]() = 0.7
is slightly steeper with respect to the
= 0.7
is slightly steeper with respect to the
![]() found in Sect. 4.1,
but still consistent within the errors.
For this source the value of the parameter
found in Sect. 4.1,
but still consistent within the errors.
For this source the value of the parameter ![]() is close to a value of about 2.5
is close to a value of about 2.5 ![]() 0.7,
which means that adiabatic losses are negligible
for 3C 35. This can be further
confirmed by the tubular structure of the source.
0.7,
which means that adiabatic losses are negligible
for 3C 35. This can be further
confirmed by the tubular structure of the source.
For the source 3C 223 (Fig. 10) we found
![]()
![]() 1.4-1.9 GHz, which is consistent with that found fitting the
spectral shape in Sect. 4.1. In this case the
injection index of 0.71 is steeper than the assumed
1.4-1.9 GHz, which is consistent with that found fitting the
spectral shape in Sect. 4.1. In this case the
injection index of 0.71 is steeper than the assumed
![]() = 0.5
used previously (Sect. 4.1) and probably reflects both the
higher frequency range of this method and the
non-power-law shape of the hotspots in this source. The
parameter
= 0.5
used previously (Sect. 4.1) and probably reflects both the
higher frequency range of this method and the
non-power-law shape of the hotspots in this source. The
parameter ![]() for this source is about 3.6
for this source is about 3.6 ![]() 1.1. As noted above,
1.1. As noted above, ![]() > 2
indicates either expansion energy losses or a source expanding at a
non-constant speed. A physical motivation for such a value
could be explained as follows. If the inverse Compton
dominates the radiative losses,
> 2
indicates either expansion energy losses or a source expanding at a
non-constant speed. A physical motivation for such a value
could be explained as follows. If the inverse Compton
dominates the radiative losses,
![]()
![]() 1/t
while
1/t
while ![]()
![]()
![]() ,
where
,
where
![]() is
the energy break and B is the magnetic
field. The magnetic field decreases with the lateral expansion of the
lobes as B
is
the energy break and B is the magnetic
field. The magnetic field decreases with the lateral expansion of the
lobes as B ![]() 1/R2,
where R is the radius of the section of the
lobe. Because the source evolves in a self-similar way (Kaiser & Alexander 1997),
R is proportional to d,
which gives B
1/R2,
where R is the radius of the section of the
lobe. Because the source evolves in a self-similar way (Kaiser & Alexander 1997),
R is proportional to d,
which gives B ![]() 1/d2,
and therefore
1/d2,
and therefore ![]()
![]() 1/d4.
That is the value that we found for the free parameter
1/d4.
That is the value that we found for the free parameter ![]() .
In this case the action of expansion losses can be seen in the
arrow structure of the source.
.
In this case the action of expansion losses can be seen in the
arrow structure of the source.
![\begin{figure}
\par\includegraphics[width=14cm,clip]{13837fg9.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13837-09/Timg92.png)
|
Figure 9:
3C 35: left in color the spectral index
map between 327 Mhz and 1.4 GHz; overlayed is the
white array of boxes where the measures were taken. Right
fit of the spectral index
|
| Open with DEXTER | |
5 Summary and conclusions
We present new VLA images of the sources 3C 35 and 3C 223 at the observing frequencies of 327 and 74 MHz.
By combining our images with those at 1.4 GHz
available in the literature, we produced spectral index distribution
maps between 74-327 MHz and 327 MHz-1.4 GHz
for both sources. The spectral
indices across the sources are more constant in the low frequency
range, while in the high frequency range the spectral indices increase
from the hotspots to the inner region of the lobes near to the core.
In particular, for the source 3C 35, ![]() ranges
between 0.6 and 0.8 in the interval of frequencies
74-327 MHz, while between the frequencies
327 MHz-1.4 GHz the values of
ranges
between 0.6 and 0.8 in the interval of frequencies
74-327 MHz, while between the frequencies
327 MHz-1.4 GHz the values of ![]() change from 0.6 in the hotspot's region to 1.7 in the
inner region of the lobes. On the other hand, for the
source 3C 223 the value of
change from 0.6 in the hotspot's region to 1.7 in the
inner region of the lobes. On the other hand, for the
source 3C 223 the value of ![]() is on average 0.6 in the range 74-327 MHz,
but it could reach extreme values, which range
between 0.4 and 1.6. In the range
between 327 MHz-1.4 GHz
is on average 0.6 in the range 74-327 MHz,
but it could reach extreme values, which range
between 0.4 and 1.6. In the range
between 327 MHz-1.4 GHz ![]() varies from 0.7 in the hotspots to 1.5 in the inner
region of the lobes.
varies from 0.7 in the hotspots to 1.5 in the inner
region of the lobes.
![\begin{figure}
\par\includegraphics[width=14cm,clip]{13837fg10.ps}
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13837-09/Timg93.png)
|
Figure 10:
3C 223: left in color the spectral index
map between 327 Mhz and 1.48 GHz; overlayed is the
white array of boxes where the measures were taken. Right
fit of the spectral index
|
| Open with DEXTER | |
Table 7:
3C 223: break frequency and reduced ![]() .
.
By considering the two radio sources in a minimum energy
condition, i.e. in the equipartition regime, we estimated the
magnetic field of the two sources. The estimate was made using two
different approaches often adopted in the literature, a fixed
frequency range and a fixed energy range. Moreover, two different
plasma populations were considered (see Tables 4 and 5): one in
which the energy is equally divided between relativistic protons and
electrons and another one in which all the energy is provided by a
plasma of relativistic electrons-positrons. For both sources the
resulting equipartition magnetic field ranges between values
of 0.5-1.6 ![]() G,
in concordance with typical values of the measured
IC magnetic fields. In particular,
for 3C 223 the value of the equipartition magnetic
field is within a factor of two in agreement with the measured
IC magnetic field (Croston
et al. 2004).
G,
in concordance with typical values of the measured
IC magnetic fields. In particular,
for 3C 223 the value of the equipartition magnetic
field is within a factor of two in agreement with the measured
IC magnetic field (Croston
et al. 2004).
By using our images with those at higher frequencies available in the literature, we obtained the spectral shape of the radio spectrum in many different positions along the lobes. The hot spots of the source 3C 35 are well described by power-laws, while the hot spots of 3C 223 show quite curved spectra. The inner regions of the lobes for the two sources present a break in the range of frequency around 1.0 GHz.
Because for both the sources the magnetic field is low,
the inverse Compton losses are as important as the synchrotron
losses, and we can assume an isotropic electron population. Therefore
we fitted the spectra with a JP (Jaffe
& Perola 1973) model to estimate the frequency
break
![]() ;
for 3C 35 we also estimated
;
for 3C 35 we also estimated
![]() while for 3C 223 we
used a fixed value.
For 3C 35 we found
that
while for 3C 223 we
used a fixed value.
For 3C 35 we found
that ![]()
![]() 800 MHz
and
800 MHz
and
![]() is on average 0.5.
For 3C 223 the
is on average 0.5.
For 3C 223 the
![]() is
about 1.4 GHz with a fixed
is
about 1.4 GHz with a fixed
![]() = 0.5.
= 0.5.
The break frequency
![]() is a time-dependent function. By assuming that there is no
expansion and the magnetic field is constant, we calculated the
radiative age of the source
is a time-dependent function. By assuming that there is no
expansion and the magnetic field is constant, we calculated the
radiative age of the source
![]() from the frequency break. Blundell
& Rawlings (2000) claimed an anomalous diffusion of
relativistic particles which implies that no information about the age
of the source can be inferred from the shape of the emission radio
spectrum. They discussed the discrepancy between the estimates of the
spectral and dynamical ages for sources older then 107 yr.
But Kaiser (2000)
demonstrated that diffusion will not alter the distribution of
relativistic particles, therefore the spatial distribution of the
synchrotron radio emission can be used to estimate the age for
FRII sources (Fanaroff
& Riley 1974). Moreover, as we discussed
above, the magnetic field of these particular sources is low with
respect to the inverse Compton equivalent magnetic field, therefore a
spatially variable magnetic field has a minor impact on the energy
losses of the relativistic electrons. For 3C 35 the
estimated age is about 143
from the frequency break. Blundell
& Rawlings (2000) claimed an anomalous diffusion of
relativistic particles which implies that no information about the age
of the source can be inferred from the shape of the emission radio
spectrum. They discussed the discrepancy between the estimates of the
spectral and dynamical ages for sources older then 107 yr.
But Kaiser (2000)
demonstrated that diffusion will not alter the distribution of
relativistic particles, therefore the spatial distribution of the
synchrotron radio emission can be used to estimate the age for
FRII sources (Fanaroff
& Riley 1974). Moreover, as we discussed
above, the magnetic field of these particular sources is low with
respect to the inverse Compton equivalent magnetic field, therefore a
spatially variable magnetic field has a minor impact on the energy
losses of the relativistic electrons. For 3C 35 the
estimated age is about 143 ![]() 20 Myr while for
3C 223 is about 72
20 Myr while for
3C 223 is about 72 ![]() 4 Myr. The radiative age
confirms that the two sources are rather old. However, these estimates
must be considered upper limits if adiabatic losses cannot be
neglected.
4 Myr. The radiative age
confirms that the two sources are rather old. However, these estimates
must be considered upper limits if adiabatic losses cannot be
neglected.
A high-resolution analysis of the spectral index behavior was
made by fitting the two frequency spectral indices
![]() with the synchrotron model as
a function of the distance from
the core. We fitted with a law
with the synchrotron model as
a function of the distance from
the core. We fitted with a law
![]() .
For the source 3C 35 the frequency break is
about 800 MHz and parameter
.
For the source 3C 35 the frequency break is
about 800 MHz and parameter ![]() is about 2.5
is about 2.5 ![]() 0.7,
in agreement with an expansion with a constant speed and/or
unimportant adiabatic losses. For the source 3C 223,
0.7,
in agreement with an expansion with a constant speed and/or
unimportant adiabatic losses. For the source 3C 223,
![]()
![]() 1.4 GHz,
while the parameter
1.4 GHz,
while the parameter ![]() is about 3.6
is about 3.6 ![]() 1.1;
as discussed before this could be explained if adiabatic losses play an
important role in the energy balance of the source and/or if the
expansion velocity of the source is not constant.
1.1;
as discussed before this could be explained if adiabatic losses play an
important role in the energy balance of the source and/or if the
expansion velocity of the source is not constant.
We thank the anonymous referee for intuitive comments, which improved this manuscript. E.O. acknowledges financial support of Austrian Science Foundation (FWF) through grant number P18523-N16. The National Radio Astronomy Observatory is operated by Associated Universities, Inc., under contract to the National Science Fundation. This research has made use of the NASA/IPAC Extragalactic Database (NED) which operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration and of CATS database Astrophysical CATalogs support System (Verkhodanovet al. 2005).
Appendix A: Faint radio galaxy
![\begin{figure}
\par\includegraphics[width=7cm,clip]{13837fgA1.ps}
\vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13837-09/Timg103.png)
|
Figure A.1:
327 MHz VLA image. The resolution is 7
|
| Open with DEXTER | |
In the field of 3C 223 at 327 MHz, at the
position RA 09![]() 40
40![]() 13.9
13.9![]() Dec +35
Dec +35![]() 57
57![]() 34
34
![]() ,
we detected a small double-lobed radio source. This radio source has
already been detected (see Fig. 6 in Croston et al. 2004)
in the 1.4 GHz VLA data by Leahy
& Perley (1991). In the same position, a bright X-ray
source was found in XMM-Newton by Croston et al. (2004).
This X-ray source, previously detected with ROSAT,
was at first
erroneously identified with a star which is offset by
20 arcsec from the X-ray source (Mason
et al. 2000). A faint optical object
coincident with the X-ray source has been detected in the Sloan Digital
Sky Survey (the u-band magnitude
is
,
we detected a small double-lobed radio source. This radio source has
already been detected (see Fig. 6 in Croston et al. 2004)
in the 1.4 GHz VLA data by Leahy
& Perley (1991). In the same position, a bright X-ray
source was found in XMM-Newton by Croston et al. (2004).
This X-ray source, previously detected with ROSAT,
was at first
erroneously identified with a star which is offset by
20 arcsec from the X-ray source (Mason
et al. 2000). A faint optical object
coincident with the X-ray source has been detected in the Sloan Digital
Sky Survey (the u-band magnitude
is ![]() 22).
Figure A.1
shows the 327 MHz image of the faint radio source with a
resolution of 7
22).
Figure A.1
shows the 327 MHz image of the faint radio source with a
resolution of 7
![]()
![]() 6
6
![]() .
This image points out an extended low brightness emission between the
two lobes in the region around the west side of the core. This implies
low energy electrons in this region, which may possibly contribute
to the IC emission. This emission was weakly detected in the
image at 1.4 GHz. The total flux of the radio source
at 327 MHz is
.
This image points out an extended low brightness emission between the
two lobes in the region around the west side of the core. This implies
low energy electrons in this region, which may possibly contribute
to the IC emission. This emission was weakly detected in the
image at 1.4 GHz. The total flux of the radio source
at 327 MHz is ![]() 93
93 ![]() 2.5 mJy.
The angular extension is about one arcmin. Since there is no redshift
measured for the optical counterpart, we could not provide an estimate
of the linear dimensions or the equipartition magnetic field. The
detection and the study of the low brightness emission of these kinds
of sources, which show most of their emission in the low frequency
range, is one of the main goals of the new generation of radio
telescopes like LOFAR, SKA, LWA etc.
2.5 mJy.
The angular extension is about one arcmin. Since there is no redshift
measured for the optical counterpart, we could not provide an estimate
of the linear dimensions or the equipartition magnetic field. The
detection and the study of the low brightness emission of these kinds
of sources, which show most of their emission in the low frequency
range, is one of the main goals of the new generation of radio
telescopes like LOFAR, SKA, LWA etc.
References
- Abazajian, K. N., Adelman-McCarthy, J. K., Agüeros, M. A., et al. 2009, ApJS, 182, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Baum, S. A., Heckman, T. M., Bridle, A., van Breugel, W. J. M., & Miley, G. K. 1988, ApJS, 68, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, R., & Krause, M. 2005, Astron. Nachr., 326, 414 [NASA ADS] [CrossRef] [Google Scholar]
- Begelman, M. C., Blandford, R. D., & Rees, M. J. 1984, Rev. Mod. Phys., 56, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R. D., & Rees, M. J. 1974, MNRAS, 169, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Blundell, K. M., & Rawlings, S. 2000, AJ, 119, 1111 [NASA ADS] [CrossRef] [Google Scholar]
- Blundell, K. M., Rawlings, S., & Willott, C. J. 1999, AJ, 117, 677 [Google Scholar]
- Brunetti, G., Setti, G., & Comastri, A. 1997, A&A, 325, 898 [NASA ADS] [Google Scholar]
- Burbidge, E. M., & Strittmatter, P. A. 1972, ApJ, 172, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Carilli, C. L., Perley, R. A., Dreher, J. W., & Leahy, J. P. 1991, ApJ, 383, 554 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, A. S., Lane, W. M., Cotton, W. D., et al. 2007, AJ, 134, 1245 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693 [NASA ADS] [CrossRef] [Google Scholar]
- Cornwell, T. J., & Perley, R. A. 1992, A&A, 261, 353 [NASA ADS] [Google Scholar]
- Cotton, W. D., Condon, J. J., Perley, R. A., et al. 2004, in Ground-based Telescopes, ed. J. M. Oschmann, Jr., Proc. SPIE, 5489, 180 [Google Scholar]
- Croston, J. H., Birkinshaw, M., Hardcastle, M. J., & Worrall, D. M. 2004, MNRAS, 353, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Croston, J. H., Hardcastle, M. J., Harris, D. E., et al. 2005, ApJ, 626, 733 [NASA ADS] [CrossRef] [Google Scholar]
- Eilek, J. A., Melrose, D. B., & Walker, M. A. 1997, ApJ, 483, 282 [NASA ADS] [CrossRef] [Google Scholar]
- Fanaroff, B. L., & Riley, J. M. 1974, MNRAS, 167, 31P [Google Scholar]
- Goodger, J. L., Hardcastle, M. J., Croston, J. H., Kassim, N. E., & Perley, R. A. 2008, MNRAS, 386, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Hardcastle, M. J., & Croston, J. H. 2005, MNRAS, 363, 649 [NASA ADS] [Google Scholar]
- Hogbom, J. A. 1979, A&AS, 36, 173 [NASA ADS] [Google Scholar]
- Ishwara-Chandra, C. H., & Saikia, D. J. 1999, MNRAS, 309, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Isobe, N., Tashiro, M., Makishima, K., et al. 2002, ApJ, 580, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Jaffe, W. J., & Perola, G. C. 1973, A&A, 26, 423 [NASA ADS] [Google Scholar]
- Jägers, W. J. 1987, A&AS, 67, 395 [Google Scholar]
- Jamrozy, M., Klein, U., Mack, K.-H., Gregorini, L., & Parma, P. 2004, A&A, 427, 79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jamrozy, M., Machalski, J., Mack, K.-H., & Klein, U. 2005, A&A, 433, 467 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jamrozy, M., Konar, C., Machalski, J., & Saikia, D. J. 2008, MNRAS, 385, 1286 [NASA ADS] [CrossRef] [Google Scholar]
- Kaiser, C. R. 2000, A&A, 362, 447 [NASA ADS] [Google Scholar]
- Kaiser, C. R., & Alexander, P. 1997, MNRAS, 286, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Kaiser, C. R., Dennett-Thorpe, J., & Alexander, P. 1997, MNRAS, 292, 723 [NASA ADS] [CrossRef] [Google Scholar]
- Kardashev, N. S. 1962, Sov. Astron., 6, 317 [NASA ADS] [Google Scholar]
- Kassim, N. E., Perley, R. A., Erickson, W. C., & Dwarakanath, K. S. 1993, AJ, 106, 2218 [NASA ADS] [CrossRef] [Google Scholar]
- Kassim, N. E., Lazio, T. J. W., Erickson, W. C., et al. 2007, ApJS, 172, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Kellermann, K. I. 1964, ApJ, 140, 969 [NASA ADS] [CrossRef] [Google Scholar]
- Konar, C., Hardcastle, M. J., Croston, J. H., & Saikia, D. J. 2009, MNRAS, 400, 480 [NASA ADS] [CrossRef] [Google Scholar]
- Laing, R. A., & Peacock, J. A. 1980, MNRAS, 190, 903 [NASA ADS] [CrossRef] [Google Scholar]
- Laing, R. A., Riley, J. M., & Longair, M. S. 1983, MNRAS, 204, 151 [Google Scholar]
- Lane, W. M., Cohen, A. S., Kassim, N. E., et al. 2005, Radio Science, 40, 5 [CrossRef] [Google Scholar]
- Lara, L., Giovannini, G., Cotton, W. D., et al. 2004, A&A, 421, 899 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leahy, J. P., & Perley, R. A. 1991, AJ, 102, 537 [NASA ADS] [CrossRef] [Google Scholar]
- Machalski, J., Chyzy, K. T., Stawarz, ▯., & Kozie▯, D. 2007, A&A, 462, 43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mason, K. O., Carrera, F. J., Hasinger, G., et al. 2000, MNRAS, 311, 456 [NASA ADS] [CrossRef] [Google Scholar]
- Meli, A., Becker, J. K., & Quenby, J. J. 2008, A&A, 492, 323 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murgia, M., 2000, Ph.D. Thesis, University of Bologna [Google Scholar]
- Pacholczyk, A. G. 1970, Radio astrophysics. Nonthermal processes in galactic and extragalactic sources, Series of Books in Astronomy and Astrophysics (San Francisco: Freeman) [Google Scholar]
- Parma, P., Murgia, M., Morganti, R., et al. 1999, A&A, 344, 7 [NASA ADS] [Google Scholar]
- Perley, R. A. 1999, in Synthesis Imaging in Radio Astronomy II, ed. G. B. Taylor, C. L. Carilli, & R. A. Perley, ASP Conf. Ser., 180, 383 [Google Scholar]
- Rengelink, R. B., Tang, Y., de Bruyn, A. G., et al. 1997, A&AS, 124, 259 [Google Scholar]
- Rudnick, L., Katz-Stone, D. M., & Anderson, M. C. 1994, ApJS, 90, 955 [NASA ADS] [CrossRef] [Google Scholar]
- Saripalli, L., Hunstead, R. W., Subrahmanyan, R., & Boyce, E. 2005, AJ, 130, 896 [NASA ADS] [CrossRef] [Google Scholar]
- Scheuer, P. A. G. 1974, MNRAS, 166, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Schoenmakers, A. P., Mack, K.-H., de Bruyn, A. G., et al. 2000, A&AS, 146, 293 [Google Scholar]
- Schoenmakers, A. P., de Bruyn, A. G., Röttgering, H. J. A., & van der Laan, H. 2001, A&A, 374, 861 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Slee, O. B., Roy, A. L., Murgia, M., Andernach, H., & Ehle, M. 2001, AJ, 122, 1172 [NASA ADS] [CrossRef] [Google Scholar]
- Spergel, D. N., Verde, L., Peiris, H. V., et al. 2003, ApJS, 148, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Tribble, P. C. 1993, MNRAS, 261, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Verkhodanov, O. V., Trushkin, S. A., Andernach, H., & Chernenkov, V. N. 2005, Bull. Spec. Astrophys. Obs., Rusia, 58, 118 [arXiv:0705.2959] [Google Scholar]
- van Breugel, W., & Jägers, W. 1982, A&AS, 49, 529 [NASA ADS] [Google Scholar]
Footnotes
- ...
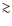 1 Mpc
1 Mpc![[*]](/icons/foot_motif.png)
- Throughout we adopt H0 = 71 km s-1 Mpc-1,
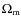 = 0.27,
= 0.27,
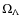 = 0.73 (Spergel et al. 2003). Many radio galaxies have been classified as giant in the past using a different set of cosmological parameters. For this reason some GRG could have a linear size slightly less than 1 Mpc.
= 0.73 (Spergel et al. 2003). Many radio galaxies have been classified as giant in the past using a different set of cosmological parameters. For this reason some GRG could have a linear size slightly less than 1 Mpc.
- ... Cygnus A
![[*]](/icons/foot_motif.png)
- Available from
http://lwa.nrl.navy.mil/tutorial/VLAmodels - ... index
![[*]](/icons/foot_motif.png)
- S(
 )
) 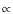
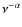 .
.
All Tables
Table 1: Summary of radio observations and images.
Table 2: Source properties.
Table 3: Resolution and rms of the images used for the spectral index maps.
Table 4: 3C 35 Flux densities, spectral indices and equipartition magnetic fields.
Table 5: 3C 223 Flux densities, spectral indices and equipartition magnetic fields.
Table 6:
3C 35: break frequency, alpha injection and reduced ![]() .
.
Table 7:
3C 223: break frequency and reduced ![]() .
.
All Figures
![\begin{figure}
\par\includegraphics[width=14cm,clip]{13837fg1.eps}
\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13837-09/Timg29.png)
|
Figure 1:
Radio images of 3C 35, all contours start at (3 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{13837fg2.ps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13837-09/Timg30.png)
|
Figure 2:
Radio images of 3C 223, all contours start at (3 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{13837fg3.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13837-09/Timg31.png)
|
Figure 3:
3C 35: spectral index maps are shown in color; pixels whose
brightness was below 3 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{13837fg4.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13837-09/Timg32.png)
|
Figure 4:
3C 223: spectral index maps are shown in color; pixels whose
brightness was below 3 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{13837fg5a.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13837-09/Timg44.png)
|
Figure 5a:
3C 35: color map of the source (resolution 95
|
| In the text | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{13837fg5b.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13837-09/Timg45.png)
|
Figure 5b: Similar to 5 for the S lobe of 3C 35. |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{13837fg6a.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13837-09/Timg46.png)
|
Figure 6a:
3C 223: color map of the source (resolution 26
|
| In the text | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{13837fg6b.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13837-09/Timg47.png)
|
Figure 6b: Similar to 6 for the the S lobe of 3C 223. |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13837fg7.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13837-09/Timg59.png)
|
Figure 7:
3C 35: plotted with respect to the distance from the core:
the fitted values of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13837fg8.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13837-09/Timg60.png)
|
Figure 8:
3C 223: plotted with respect to the distance from the core:
the fitted values of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{13837fg9.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13837-09/Timg92.png)
|
Figure 9:
3C 35: left in color the spectral index
map between 327 Mhz and 1.4 GHz; overlayed is the
white array of boxes where the measures were taken. Right
fit of the spectral index
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{13837fg10.ps}
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13837-09/Timg93.png)
|
Figure 10:
3C 223: left in color the spectral index
map between 327 Mhz and 1.48 GHz; overlayed is the
white array of boxes where the measures were taken. Right
fit of the spectral index
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{13837fgA1.ps}
\vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13837-09/Timg103.png)
|
Figure A.1:
327 MHz VLA image. The resolution is 7
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



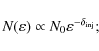
![\begin{displaymath}%
t_{\rm syn}=1590{\frac{B_{\rm eq}^{1/2}}{(B_{\rm eq}^{2}+B^...
...rm CMB}})}}{\frac{1}{[ \nu _{\rm break}(1+z)]^{1/2}}}~\rm Myr,
\end{displaymath}](/articles/aa/full_html/2010/07/aa13837-09/img54.png)