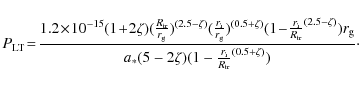| Issue |
A&A
Volume 515, June 2010
|
|
|---|---|---|
| Article Number | A82 | |
| Number of page(s) | 6 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/200913787 | |
| Published online | 11 June 2010 | |
Feasibility study of Lense-Thirring precession in LS I +61 303
303
M. Massi - L. Zimmermann
Max Planck Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
Received 2 December 2009 / Accepted 18 March 2010
Abstract
Context. Very recent analysis of the radio spectral index
and high energy observations have shown that the two-peak
accretion/ejection microquasar model applies for LS I +61![]() 303.
303.
Aims. The fast variations of the position angle observed with
MERLIN and confirmed by consecutive VLBA images must therefore be
explained in the context of the microquasar scenario.
Methods. We calculate what could be the precessional period for the accretion disk in LS I +61![]() 303 under tidal forces of the Be star (
303 under tidal forces of the Be star (
![]() )
or under the effect of frame dragging produced by the rotation of the compact object (
)
or under the effect of frame dragging produced by the rotation of the compact object (
![]() ).
).
Results.
![]() is more than one year.
is more than one year.
![]() depends on the truncated radius of the accretion disk,
depends on the truncated radius of the accretion disk,
![]() .
We determined
.
We determined
![]() for observed QPO at 2 Hz. This value is much above the few
for observed QPO at 2 Hz. This value is much above the few ![]() ,
where the Bardeen-Petterson effect should align the midplane of the disk. For this truncated radius of the accretion disk
,
where the Bardeen-Petterson effect should align the midplane of the disk. For this truncated radius of the accretion disk
![]() for a slow rotator results in a few days.
for a slow rotator results in a few days.
Conclusions. Lense-Thirring precession induced by a slowly
rotating compact object could be compatible with the daily variations
of the ejecta angle observed in LS I +61![]() 303.
303.
Key words: black hole physics - radio continuum: stars - pulsars: general - X-rays: binaries - X-rays: indiviual (LS I +61![]() 303)
303)
1 Introduction
LS I +61![]() 303 is a X-ray binary formed by a compact object and a massive star with an optical
spectrum typical for a rapidly rotating B0 V star (Hutchings & Crampton 1981).
The Be star with a fast polar wind has an equatorial dense, low velocity wind with a
power law density distribution of the form
303 is a X-ray binary formed by a compact object and a massive star with an optical
spectrum typical for a rapidly rotating B0 V star (Hutchings & Crampton 1981).
The Be star with a fast polar wind has an equatorial dense, low velocity wind with a
power law density distribution of the form
![]() ,
where R*is the radius of the primary Be star (Waters et al. 1988; Martí & Paredes 1995).
The real nature of the compact object travelling in this stratified wind on an eccentric
orbit with e=0.54-0.7 is still unknown (Aragona et al. 2009; Casares et al. 2005). In fact, because of the uncertainty in the inclination of the orbit
,
where R*is the radius of the primary Be star (Waters et al. 1988; Martí & Paredes 1995).
The real nature of the compact object travelling in this stratified wind on an eccentric
orbit with e=0.54-0.7 is still unknown (Aragona et al. 2009; Casares et al. 2005). In fact, because of the uncertainty in the inclination of the orbit
![]() ,
the compact object could be either a neutron star or
a black hole of 3-4
,
the compact object could be either a neutron star or
a black hole of 3-4 ![]() .
Two radio periodicities are present (Gregory 2002), one of 26.5 d (phase
.
Two radio periodicities are present (Gregory 2002), one of 26.5 d (phase ![]() ), which corresponds to the orbital period, and a second one of 4.6 yr (phase
), which corresponds to the orbital period, and a second one of 4.6 yr (phase ![]() )
which is related to variations in the equatorial wind of the Be star (Zamanov & Marti 2000).
In the past two scenarios were presented for the system. One is that the
compact object is a young, still very fast rotating, strongly magnetized pulsar,
whose relativistic wind collides with the Be star`s wind and prevents any accretion.
In this scenario the prolonged strong wind interaction during the periastron passage should
continuously accelerate particles to relativistic velocities and
a prolonged optically thin outburst is expected,
as it occurs in the young pulsar PSR B1259-63 (Fig. 3 of Connors et al. 2002).
PSR B1259-63, which clearly is a pulsar, as seen by its
pulses with a period of 48 ms observed by Johnston et al. (1992),
shows a large optically thin radio outburst around the periastron passage.
The other scenario for LS I +61
)
which is related to variations in the equatorial wind of the Be star (Zamanov & Marti 2000).
In the past two scenarios were presented for the system. One is that the
compact object is a young, still very fast rotating, strongly magnetized pulsar,
whose relativistic wind collides with the Be star`s wind and prevents any accretion.
In this scenario the prolonged strong wind interaction during the periastron passage should
continuously accelerate particles to relativistic velocities and
a prolonged optically thin outburst is expected,
as it occurs in the young pulsar PSR B1259-63 (Fig. 3 of Connors et al. 2002).
PSR B1259-63, which clearly is a pulsar, as seen by its
pulses with a period of 48 ms observed by Johnston et al. (1992),
shows a large optically thin radio outburst around the periastron passage.
The other scenario for LS I +61![]() 303 is that the compact object is an accreting black hole or a low magnetic field neutron star. From Bondi (1952) the wind accretion rate is proportional to
303 is that the compact object is an accreting black hole or a low magnetic field neutron star. From Bondi (1952) the wind accretion rate is proportional to
![]() ,
i.e. directly proportional to the wind density and inversely proportional
to the cubic of the relative speed between the compact object and the Be wind.
In an eccentric orbit this different relationship for density and velocity creates
two peaks in the accretion rate curve, one at periastron where the density is at its maximum
and a second one when the drop in density is compensated by the decrease in velocity towards apastron. Taylor et al. (1992)
computed the accretion rate curve for different eccentricities and
showed that two peaks begin to appear for an eccentricity above 0.4.
Whereas the first peak is always toward periastron, the orbital
occurrence of the second accretion peak depends on variations of the
wind of the Be star. Marti & Paredes (1995) computed the accretion rate curve for different wind velocities,
associated with the variability of the Be star, and showed that for a stellar wind velocity of
20 km s-1 the two peaks become rather close to each other, whereas for a wind velocity
of 5 km s-1 they are at their maximum orbital offset of
,
i.e. directly proportional to the wind density and inversely proportional
to the cubic of the relative speed between the compact object and the Be wind.
In an eccentric orbit this different relationship for density and velocity creates
two peaks in the accretion rate curve, one at periastron where the density is at its maximum
and a second one when the drop in density is compensated by the decrease in velocity towards apastron. Taylor et al. (1992)
computed the accretion rate curve for different eccentricities and
showed that two peaks begin to appear for an eccentricity above 0.4.
Whereas the first peak is always toward periastron, the orbital
occurrence of the second accretion peak depends on variations of the
wind of the Be star. Marti & Paredes (1995) computed the accretion rate curve for different wind velocities,
associated with the variability of the Be star, and showed that for a stellar wind velocity of
20 km s-1 the two peaks become rather close to each other, whereas for a wind velocity
of 5 km s-1 they are at their maximum orbital offset of
![]() .
This value, for an orbital period
.
This value, for an orbital period
![]() d, corresponds to almost 11 days, i.e. the second peak may occur almost at apastron.
Bosh-Ramon et al. (2006) showed that around periastron (
d, corresponds to almost 11 days, i.e. the second peak may occur almost at apastron.
Bosh-Ramon et al. (2006) showed that around periastron (![]() )
only a small radio outburst is expected in coincidence with the first
accretion peak. That occurs, because of the severe external inverse
Compton (EIC) losses of the electrons, which upscatter UV stellar
photons of the close Be star to high energies.
In other words, associated with the first accretion/ejection peak a
high energy outburst due to
EIC is expected along with a small radio outburst.
The second displaced accretion/ejection peak, instead, should be
observed in the radio band as
a large outburst.
In particular this large radio outburst,
)
only a small radio outburst is expected in coincidence with the first
accretion peak. That occurs, because of the severe external inverse
Compton (EIC) losses of the electrons, which upscatter UV stellar
photons of the close Be star to high energies.
In other words, associated with the first accretion/ejection peak a
high energy outburst due to
EIC is expected along with a small radio outburst.
The second displaced accretion/ejection peak, instead, should be
observed in the radio band as
a large outburst.
In particular this large radio outburst,
![]() ,
should
follow the characteristics of microquasars:
optically thick emission, i.e.
,
should
follow the characteristics of microquasars:
optically thick emission, i.e.
![]() ,
followed by an optically thin outburst, i.e.
,
followed by an optically thin outburst, i.e.
![]() (Fender et al. 2004).
The first type of emission, the optically thick radio emission, is related
in microquasars to a steady, low velocity jet centered on the orbit.
The following optically thin outburst
is related to a transient jet, associated with shocks quite
displaced from the center (see Fig. 1).
With this transient jet very high energy emission is expected as well,
because of dominating self synchrotron Compton (SSC) losses during the
growing phase of the shock (Marscher & Gear 1985).
(Fender et al. 2004).
The first type of emission, the optically thick radio emission, is related
in microquasars to a steady, low velocity jet centered on the orbit.
The following optically thin outburst
is related to a transient jet, associated with shocks quite
displaced from the center (see Fig. 1).
With this transient jet very high energy emission is expected as well,
because of dominating self synchrotron Compton (SSC) losses during the
growing phase of the shock (Marscher & Gear 1985).
Table 1: Two-peak MQ vs Pulsar Model.
How does LS I +61![]() 303 fit in the two different scenarios? As a matter of fact, radio pulses have
never been observed in LS I +61
303 fit in the two different scenarios? As a matter of fact, radio pulses have
never been observed in LS I +61![]() 303, moreover the large outburst in LS I +61
303, moreover the large outburst in LS I +61![]() 303 is clearly
shifted towards apastron contrary to the case of PSR B1259-63 (Table 1).
In addition, the recent analysis of the radio spectral index,
303 is clearly
shifted towards apastron contrary to the case of PSR B1259-63 (Table 1).
In addition, the recent analysis of the radio spectral index, ![]() ,
by Massi & Kaufman Bernadó (2009)
show the clear sequence typical for microquasars: optically thick
emission (steady jet) and optically thin emission (transient jet). The
quite impressive fact in LS I +61
,
by Massi & Kaufman Bernadó (2009)
show the clear sequence typical for microquasars: optically thick
emission (steady jet) and optically thin emission (transient jet). The
quite impressive fact in LS I +61![]() 303 is that during the maximum of the 4.6 yr periodicity,
i.e
303 is that during the maximum of the 4.6 yr periodicity,
i.e
![]() ,
this sequence (optically thick emission /
optically thin emission) occurs twice along the orbit of 26.5 d.
In Fig. 3 in Massi & Kaufman Bernadó (2009) one sees how
even the small radio peak at periastron, attenuated because of severe EIC losses and nearly
negligible in terms of flux density in comparison to the large
,
this sequence (optically thick emission /
optically thin emission) occurs twice along the orbit of 26.5 d.
In Fig. 3 in Massi & Kaufman Bernadó (2009) one sees how
even the small radio peak at periastron, attenuated because of severe EIC losses and nearly
negligible in terms of flux density in comparison to the large
![]() outburst, presents the same very clear variation in the spectral index, from
outburst, presents the same very clear variation in the spectral index, from
![]() (steady jet) to
(steady jet) to ![]() (transient jet), which proves the two-peak accretion model in the radio band.
(transient jet), which proves the two-peak accretion model in the radio band.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13787fg1.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13787-09/Timg31.png)
|
Figure 1:
X-ray states/radio states vs. hardness. Along with the usual X-ray characteristics (McClintock & Remillard 2006) and radio characteristics (Fender et al. 2004)
of the spectral states, we add for the Steep power-law state also the
X- and gamma-ray characteristics for the shock-in-jet model and for
blazars (Marscher & Gear 1985; Katarzynski et al. 2005; Katarzynski & Walczewska 2010).
The transient radio jet, i.e. ``plasmoids'' displaced from the center,
is related to shocks travelling in the slowly moving preexisting steady
jet established during the previous low hard state. LS I +61 |
| Open with DEXTER | |
In terms of high energy emission as discussed above two peaks are
predicted, each of them formed
by different EIC and SSC contributions. At periastron one expects
dominant EIC contribution to the gamma-ray emission, due to the
proximity of the Be star. Towards apastron one expects the contrary:
Strong gamma-ray emission due to SSC associated with the powerful
transient jet with additional EIC gamma-ray emission that depends on
the distance from the Be star. Two emission peaks are confirmed by
observations at high energies. One data set of EGRET shows evidence of
the periastron peak. A second data set shows a hint of a peak at
periastron and a second peak shifted towards apastron (![]() )
(Massi et al. 2005). The recent Fermi LAT observations confirm the two peaks (Abdo et al. 2009).
The Fermi light curve is characterized by a broad peak after periastron
as well as a smaller peak just before apastron. TeV observations with
VERITAS (Acciari et al. 2009) along with the strong emission at
)
(Massi et al. 2005). The recent Fermi LAT observations confirm the two peaks (Abdo et al. 2009).
The Fermi light curve is characterized by a broad peak after periastron
as well as a smaller peak just before apastron. TeV observations with
VERITAS (Acciari et al. 2009) along with the strong emission at ![]() -0.9, first detected with MAGIC (Albert et al. 2006), also give marginal evidence for emission at
-0.9, first detected with MAGIC (Albert et al. 2006), also give marginal evidence for emission at ![]() -0.3.
-0.3.
LS I +61![]() 303 fits then well the two-peak microquasar scenario. Its radio properties show a
recurrent switch between transient jet and steady jet, the two radio states.
As discussed in Fender et al. (2004)
in microquasars the two radio states, steady and transient jet,
are simultaneous
with two X-ray states: the low/hard state
and the steep power law state respectively (shown in Fig. 1).
This seems to happen also in LS I +61
303 fits then well the two-peak microquasar scenario. Its radio properties show a
recurrent switch between transient jet and steady jet, the two radio states.
As discussed in Fender et al. (2004)
in microquasars the two radio states, steady and transient jet,
are simultaneous
with two X-ray states: the low/hard state
and the steep power law state respectively (shown in Fig. 1).
This seems to happen also in LS I +61![]() 303.
As analysed in Massi & Kaufman Bernadó (2009)
INTEGRAL (keV-MeV) observations
by Chernyakova et al. (2006)
with the typical photon index
303.
As analysed in Massi & Kaufman Bernadó (2009)
INTEGRAL (keV-MeV) observations
by Chernyakova et al. (2006)
with the typical photon index
![]() of the
low/hard state occur
at
of the
low/hard state occur
at ![]() and
and ![]() where optically
thick radio emission is observed, i.e.
where optically
thick radio emission is observed, i.e.
![]() .
INTEGRAL observations with
.
INTEGRAL observations with
![]() ,
are measured
at
,
are measured
at ![]() and
and ![]() where
radio emission with
where
radio emission with
![]() is observed.
Moreover, when TeV emission is detected in LS I +61
is observed.
Moreover, when TeV emission is detected in LS I +61![]() 303 with Cherenkov telescopes
the energy spectrum is always well fitted by a power law with a photon index
303 with Cherenkov telescopes
the energy spectrum is always well fitted by a power law with a photon index
![]() (Albert et al. 2009; Acciari et al. 2009) independently of changes in the flux level
as expected for the steep power law state, where the photon index is
a fundamental property of the state and not the luminosity
(see discussion in Massi & Kaufman Bernadó 2009).
Of particular interest are the recent observations by Anderhub et al. (2009) probing correlated X-ray emission, attributed to synchrotron radiation,
and VHE emission. We note that the corrected X-ray flux of
(Albert et al. 2009; Acciari et al. 2009) independently of changes in the flux level
as expected for the steep power law state, where the photon index is
a fundamental property of the state and not the luminosity
(see discussion in Massi & Kaufman Bernadó 2009).
Of particular interest are the recent observations by Anderhub et al. (2009) probing correlated X-ray emission, attributed to synchrotron radiation,
and VHE emission. We note that the corrected X-ray flux of
![]() erg cm-2 s-1and the VHE flux of
erg cm-2 s-1and the VHE flux of
![]() erg cm-2 s-1 result in
erg cm-2 s-1 result in
![]() with
with ![]() ,
in agreement with the correlation observed in blazars, where
,
in agreement with the correlation observed in blazars, where ![]() is in the range 0.99-3
(Katarzynski & Walczewska 2010). The high energy spectra of TeV blazars are explained
with a model where relativistic electrons accelerated in a shock
emit synchrotron radiation up to X-rays. A fraction of this emission
is upscattered to higher energies by the same population of the electrons (SSC) (Katarzynski et al. 2005).
This agrees with the predictions of the shock-in-jet model invoked for
the optically thin radio outburst of the transient jet described above
and associated to the steep power-law state. Because of the
correspondence between X-ray states and radio states we suggest that
the recurrent switch between transient jet and steady jet observed in
LS I +61
is in the range 0.99-3
(Katarzynski & Walczewska 2010). The high energy spectra of TeV blazars are explained
with a model where relativistic electrons accelerated in a shock
emit synchrotron radiation up to X-rays. A fraction of this emission
is upscattered to higher energies by the same population of the electrons (SSC) (Katarzynski et al. 2005).
This agrees with the predictions of the shock-in-jet model invoked for
the optically thin radio outburst of the transient jet described above
and associated to the steep power-law state. Because of the
correspondence between X-ray states and radio states we suggest that
the recurrent switch between transient jet and steady jet observed in
LS I +61![]() 303 corresponds to a continuous switch between a low/hard state and a steep power-law state (Fig. 1).
The source is therefore pratically frozen in a permanent microquasar
state, in fact it is always radio loud, never reaching, as other X-ray
binaries the high/soft thermal state.
303 corresponds to a continuous switch between a low/hard state and a steep power-law state (Fig. 1).
The source is therefore pratically frozen in a permanent microquasar
state, in fact it is always radio loud, never reaching, as other X-ray
binaries the high/soft thermal state.
The peculiar aspect of LS I +61![]() 303,
that we will deal with in this study, is its short-term variability.
Variability is the main characteristic of blazars and micro-blazars,
where the shock is seen almost face-on and the Doppler factor is large.
LS I +61
303,
that we will deal with in this study, is its short-term variability.
Variability is the main characteristic of blazars and micro-blazars,
where the shock is seen almost face-on and the Doppler factor is large.
LS I +61![]() 303 was indicated since 2002 by Kaufman Bernadó et al. as a microblazar, because of
its one-sided jet radio morphology, typical of blazars,
where the receding jet is Doopler de-boosted whereas the flux density of the approching jet is strongly amplified.
303 was indicated since 2002 by Kaufman Bernadó et al. as a microblazar, because of
its one-sided jet radio morphology, typical of blazars,
where the receding jet is Doopler de-boosted whereas the flux density of the approching jet is strongly amplified.
LS I +61![]() 303
shows strong morphological changes: or the position angle of the
one-sided jet continuosly changes, or at some epochs the receding jet
appears unattenuated (compare the map of Taylor et al. 2000 with that of Dhawan et al. 2006 in Fig. 1 by Massi & Kaufman Bernadó 2009).
Precession of the accretion disk (and therefore of the jet) causing the
jet to point closer to or farther away from the line of sight would
explain variable Doppler boosting and variations in the position angle.
Precessing jets are well known in microquasars, the most spectacular
one being that of SS433, the first microquasar (Dubner et al. 1998).
However, in LS I +61
303
shows strong morphological changes: or the position angle of the
one-sided jet continuosly changes, or at some epochs the receding jet
appears unattenuated (compare the map of Taylor et al. 2000 with that of Dhawan et al. 2006 in Fig. 1 by Massi & Kaufman Bernadó 2009).
Precession of the accretion disk (and therefore of the jet) causing the
jet to point closer to or farther away from the line of sight would
explain variable Doppler boosting and variations in the position angle.
Precessing jets are well known in microquasars, the most spectacular
one being that of SS433, the first microquasar (Dubner et al. 1998).
However, in LS I +61![]() 303 the variations seem to be very rapid compared
to the 164-day precessional period of SS433.
The peculiarity of the variations of LS I +61
303 the variations seem to be very rapid compared
to the 164-day precessional period of SS433.
The peculiarity of the variations of LS I +61![]() 303 is their short timescale.
MERLIN images revealed a surprising variation
of 60
303 is their short timescale.
MERLIN images revealed a surprising variation
of 60
![]() in position angle in only one day (Massi et al. 2004).
Dhawan et al. (2006) measured in VLBA images a rotation of the inner structure of
roughly
in position angle in only one day (Massi et al. 2004).
Dhawan et al. (2006) measured in VLBA images a rotation of the inner structure of
roughly
![]() in 2.5 h, that is again almost 60
in 2.5 h, that is again almost 60
![]() /day.
Indeed, because of the difficulty to explain this puzzling variations in the context of microquasars
the variations were interpreted as due to a cometary tail of a pulsar.
Now, that the radio spectral index analysis and very high energy observations
confirm the two-peak microquasar scenario (see Table 1), an investigation of the physical processes behind these fast variations is necessary. This is the aim of this work.
/day.
Indeed, because of the difficulty to explain this puzzling variations in the context of microquasars
the variations were interpreted as due to a cometary tail of a pulsar.
Now, that the radio spectral index analysis and very high energy observations
confirm the two-peak microquasar scenario (see Table 1), an investigation of the physical processes behind these fast variations is necessary. This is the aim of this work.
The most likely cause for precession of an accretion disk of a compact object is
an assymetric supernova explosion of the progenitor.
As a result the compact object could be tilted (Fragile et al. 2007).
In this case either the accretion disk is coplanar
with the compact object, and therefore subject to the gravitational torque of the Be star or
instead, the accretion disk is coplanar with the orbit, but
tilted in respect to the compact object, which induces Lense-Thirring precession if the
compact object rotates.
In this paper we therefore examine these two possibilities with the
aim to quantify them and
to compare them with the observed short time scale of variations in LS I +61![]() 303.
303.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13787fg2.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13787-09/Timg44.png)
|
Figure 2:
Precession due to tidal torque induced by the Be star as function of
mass ratio, |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13787fg3.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13787-09/Timg46.png)
|
Figure 3:
Precession due to tidal torque induced by the Be star as function of
mass ratio, |
| Open with DEXTER | |
2 Tidal Forces in a binary system
If the accretion disk is tilted with respect to the binary orbital plane, then
its precession can be tidally induced by the companion star. The expression for the
precession period depends, for a given orbital period (P=26.496 d) and semi-major axis (
![]() cm), on the mass ratio
cm), on the mass ratio
![]() ,
the orbital inclination
,
the orbital inclination ![]() with respect to the disk and the accretion disk size
with respect to the disk and the accretion disk size
![]() ,
(Larwood 1998, Eq. (4)):
,
(Larwood 1998, Eq. (4)):
The size of the disk and the orbit can be eliminated, following Larwood (1998), by writing the accretion disc as a fraction
In LS I +61
In our above calculations we assumed a single planar disk.
If, instead, only a portion of the disk is warped out of the binary plane, as could be
likely (Foulkes et al. 2006), a warp at smaller radii would
decrease
![]() in Eq. (1) and further increase
in Eq. (1) and further increase
![]() .
The only way to get a smaller
.
The only way to get a smaller
![]() is therefore to increase
is therefore to increase
![]() .
In Fig. 3 we plot Eq. (1) as a function of
.
In Fig. 3 we plot Eq. (1) as a function of ![]() and
and
![]() for
for
![]() .
The first interesting result
is that the before determined value of
.
The first interesting result
is that the before determined value of
![]() d by using Larwood's (1998) fit for
d by using Larwood's (1998) fit for ![]() ,
which is derived from Paczynski's (1977) values, corresponds to
an already very large disk size,
,
which is derived from Paczynski's (1977) values, corresponds to
an already very large disk size,
![]() (see Fig. 3),
where
(see Fig. 3),
where ![]() is the gravitational radius,
is the gravitational radius,
![]() .
Indeed, Paczynski (1977)
argues that his values constitute upper limits to the disk size
provided that pressure is sufficiently small in the disk. One could
therefore assume larger disks because of higher values of pressure. On
the other hand, if we assume a larger disk size, we get the second
interesting result that one needs to enlarge the disk size one order of
magnitude,
reaching the value of
.
Indeed, Paczynski (1977)
argues that his values constitute upper limits to the disk size
provided that pressure is sufficiently small in the disk. One could
therefore assume larger disks because of higher values of pressure. On
the other hand, if we assume a larger disk size, we get the second
interesting result that one needs to enlarge the disk size one order of
magnitude,
reaching the value of
![]() ,
to finally reduce
,
to finally reduce
![]() to a few days. Such a large
to a few days. Such a large
![]() value is unlikely. Already beyond about 104 gravitational
radii, self-gravitation is larger than central gravitation, and the disk
becomes gravitationally unstable (Collin & Huré 1999).
value is unlikely. Already beyond about 104 gravitational
radii, self-gravitation is larger than central gravitation, and the disk
becomes gravitationally unstable (Collin & Huré 1999).
3 The lense-thirring effect
Whenever a spinning compact object has a misaligned accretion disk, the
Lense-Thirring precession effect will arise with an angular frequency,
![]() ,
given by (Eq. (29) of Caproni et al. 2006; Wilkins 1972):
,
given by (Eq. (29) of Caproni et al. 2006; Wilkins 1972):
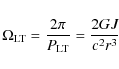
|
(3) |
where J is the angular momentum of the compact object and r the radial distance from the rotating compact object to the accretion disk. The angular momentum, J, can be expressed in terms of the dimensionless spin parameter, a*, such that
In general, the Bardeen-Petterson effect predicts an alignment of the inner accretion disk with the symmetry plane of the compact object. Nelson & Papaloizou (2000) showed that the alignment by the Bardeen-Petterson effect extends only to a few gravitational radii (15-30
Following Stella & Vietri (1998) we can argue that matter inhomogeneities present at an inner
disk boundary cause quasi-periodic oscillations (QPO) at the
Keplerian frequency
![]() .
We can estimate the value for
.
We can estimate the value for
![]() in LS I +61
in LS I +61![]() 303 from observed QPO. During their monitoring with RXTE (2-10 keV) Ray & Hartman (2008)
observed a period of strong variability with a spectrum best fit
by a powerlaw of photon index about 1.5 (i.e. low/hard state);
a power spectral analysis revealed QPO at 2 Hz. The relativistic Keplerian frequency (Eq. (2) in Caproni et al. 2006) is:
303 from observed QPO. During their monitoring with RXTE (2-10 keV) Ray & Hartman (2008)
observed a period of strong variability with a spectrum best fit
by a powerlaw of photon index about 1.5 (i.e. low/hard state);
a power spectral analysis revealed QPO at 2 Hz. The relativistic Keplerian frequency (Eq. (2) in Caproni et al. 2006) is:
![\begin{displaymath}\nu_{\rm K}= {1 \over 2 \pi} {c \over r_{\rm g}} \big[ ({R_{\rm tr}\over r_{\rm g}})^{3/2}+a_* \big ]^{-1}.
\end{displaymath}](/articles/aa/full_html/2010/07/aa13787-09/img70.png)
|
(5) |
By solving for
Equation (6) for
Above, to determine the truncated radius of the accretion disk
we set the QPO frequency of 2 Hz equal to the Keplerian frequency.
Below, we analyse if the resulting
![]() could correspond
to a precessional period of a few days.
This is therefore, different from Ingram et al. (2009) and Ingram & Done (2010),
who associate the low frequency QPO directly to Lense-Thirring precession.
As a matter of fact a truncated radius,
could correspond
to a precessional period of a few days.
This is therefore, different from Ingram et al. (2009) and Ingram & Done (2010),
who associate the low frequency QPO directly to Lense-Thirring precession.
As a matter of fact a truncated radius,
![]() ,
a factor 3 above the value of
100
,
a factor 3 above the value of
100 ![]() determined for X-ray binaries
in low/hard states, is very consistent with the X-ray luminosity value of LS I +61
determined for X-ray binaries
in low/hard states, is very consistent with the X-ray luminosity value of LS I +61![]() 303, which indicates a very low low/hard state.
Moreover, the escape velocity
303, which indicates a very low low/hard state.
Moreover, the escape velocity
![]() for
for
![]() results in v/c=0.08. Following Meier (2005)
the terminal velocity of the steady jet, during the low/hard state, is
approximately equal to the escape speed at the footpoint of the
magnetic field where the jet is launched, that is at the inner
truncated radius of the accretion disk (Meier 2005). The value of v/c=0.08 should therefore be comparable with the velocity of the steady jet. Indeed, when LS I +61
results in v/c=0.08. Following Meier (2005)
the terminal velocity of the steady jet, during the low/hard state, is
approximately equal to the escape speed at the footpoint of the
magnetic field where the jet is launched, that is at the inner
truncated radius of the accretion disk (Meier 2005). The value of v/c=0.08 should therefore be comparable with the velocity of the steady jet. Indeed, when LS I +61![]() 303 was essentially quiescent Peracaula et al. (1998) measured an expansion velocity of
303 was essentially quiescent Peracaula et al. (1998) measured an expansion velocity of
![]() .
Therefore, on the basis of these consistencies we will assume in the following that
the determined value of 300
.
Therefore, on the basis of these consistencies we will assume in the following that
the determined value of 300 ![]() is a good estimate, in terms of order of magnitude,
of the truncated radius during the rather low low/hard state of LS I +61
is a good estimate, in terms of order of magnitude,
of the truncated radius during the rather low low/hard state of LS I +61![]() 303,
even if the Ray and Hartman observations of the QPO during a low/hard state of LS I +61
303,
even if the Ray and Hartman observations of the QPO during a low/hard state of LS I +61![]() 303
are at another epoch than the MERLIN and VLBA observations of the precessing jet.
303
are at another epoch than the MERLIN and VLBA observations of the precessing jet.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{13787fg4.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13787-09/Timg79.png)
|
Figure 4:
Lense-Thirring precession for a test particle
in function of the dimensionless specific angular momentum, a*, (Eq. (4)). The orbit of
|
| Open with DEXTER | |
In Fig. 4 we show the precessional period (Eq. (4)) due to the Lense-Thirring effect as a function of the dimensionless spin parameter a* for the determined radius
![]() .
As a result we deduce a period of a few days for the Lense-Thirring precession
of a slow rotator (
0.001 < a*< 0.01). Therefore, Lense-Thirring precession
could explain the MERLIN and VLBA observations. However, Eq. (4) assumes a single-particle orbit at the truncation radius
.
As a result we deduce a period of a few days for the Lense-Thirring precession
of a slow rotator (
0.001 < a*< 0.01). Therefore, Lense-Thirring precession
could explain the MERLIN and VLBA observations. However, Eq. (4) assumes a single-particle orbit at the truncation radius
![]() ,
how does that change the result when we consider Lense-Thirring
precession of the whole geometrically thick, advection-dominated flow
(ADAF) interior up until the truncated disc? An expression of
Lense-Thirring precession for disks was first given in Liu & Melia (2002) and subsequently reproduced in slightly different forms in Fragile et al. (2007) and Ingram et al. (2009). Equation (2) in Ingram et al. (2009) solved for the precessional period (days) gives:
,
how does that change the result when we consider Lense-Thirring
precession of the whole geometrically thick, advection-dominated flow
(ADAF) interior up until the truncated disc? An expression of
Lense-Thirring precession for disks was first given in Liu & Melia (2002) and subsequently reproduced in slightly different forms in Fragile et al. (2007) and Ingram et al. (2009). Equation (2) in Ingram et al. (2009) solved for the precessional period (days) gives:
The surface density profile through the disk depends on
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{13787fg5.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13787-09/Timg86.png)
|
Figure 5:
Lense-Thirring precession for a geometrically thick accretion flow with inner and outer radii |
| Open with DEXTER | |
4 Conclusions
Two consecutive MERLIN observations of LS I +61![]() 303 showed a rotation
of the position angle of the radio structure of
303 showed a rotation
of the position angle of the radio structure of ![]()
![]() in only 24 h (Massi et al. 2004). Several consecutive VLBA images by Dhawan et al. (2006),
three days apart, have confirmed the fast variations.
In this paper we analyse precession due to the tidal torque induced by the Be star and
to the Lense-Thirring precession induced by the tilted rotating compact object.
in only 24 h (Massi et al. 2004). Several consecutive VLBA images by Dhawan et al. (2006),
three days apart, have confirmed the fast variations.
In this paper we analyse precession due to the tidal torque induced by the Be star and
to the Lense-Thirring precession induced by the tilted rotating compact object.
It is unlikely that the observed days time scale could be created by tidal
precession. In this paper we show that this mechanism would produce too
large a precessional period of
![]() d.
To lower the precessional period to a few days one should increase the disk size above the
limit of any stable disk.
d.
To lower the precessional period to a few days one should increase the disk size above the
limit of any stable disk.
On the contrary, for Lense-Thirring precession for a single-particle orbit we determine
that a slow rotator, with
0.001 < a* < 0.01, induces a
![]() of a few days for a truncated radius
of a few days for a truncated radius
![]() .
The large truncated radius,
.
The large truncated radius,
![]() ,
that we derived from
QPO observed with RXTE (Ray & Hartman 2008), is consistent with the low/hard state of LS I +61
,
that we derived from
QPO observed with RXTE (Ray & Hartman 2008), is consistent with the low/hard state of LS I +61![]() 303 during those observations (spectrum best fit by a powerlaw of photon index about 1.5; Ray & Hartman 2008). Moreover, the escape velocity, that following Meier (2005) is equal to the velocity of the steady jet, for
303 during those observations (spectrum best fit by a powerlaw of photon index about 1.5; Ray & Hartman 2008). Moreover, the escape velocity, that following Meier (2005) is equal to the velocity of the steady jet, for
![]() results in v/c=0.08 and is therefore consistent with the expansion velocity of
results in v/c=0.08 and is therefore consistent with the expansion velocity of
![]() observed by Peracaula et al. (1998) in an epoch when LS I +61
observed by Peracaula et al. (1998) in an epoch when LS I +61![]() 303 was essentially quiescent.
303 was essentially quiescent.
Taking into account the precession of the whole hot, inner thick ADAF disk (between
the Bardeen-Petterson limiting radius of 10![]() and the truncated radius of 300
and the truncated radius of 300![]() )
we obtain an even smaller
)
we obtain an even smaller
![]() .
In order to mantain a precessional period of some days,
as calculated for the single orbit, it is enough to assume a slower rotating compact object, i.e. with lower a*. We conclude that the Lense-Thirring mechanism can be applied to LS I +61
.
In order to mantain a precessional period of some days,
as calculated for the single orbit, it is enough to assume a slower rotating compact object, i.e. with lower a*. We conclude that the Lense-Thirring mechanism can be applied to LS I +61![]() 303 and so explain the observed fast variations.
303 and so explain the observed fast variations.
We are grateful to the anonymous referee for the constructive comments that improved the paper and to Marina Kaufman Bernadó and Johannes Schmid-Burgk for comments and suggestions. The work of L. Zimmermann is partly supported by the German Excellence Initiative via the Bonn Cologne Graduate School.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009, ApJ, 701, L123 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Anton, G., et al. 2009, A&A, 507, 389 [Google Scholar]
- Acciari, V. A., Aliu, E., Arlen, T., et al. 2009, ApJ, 700, 1034 [NASA ADS] [CrossRef] [Google Scholar]
- Albert, J., Aliu, E., Anderhub, H., et al. 2006, Science, 312, 1771 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Albert, J., Aliu, E., Anderhub, H., et al. 2009, ApJ, 693, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Anderhub, H. 2009 ApJ, 706, L27 [Google Scholar]
- Aragona, C., McSwain, M. V., Grundstrom, E. D., et al. 2009, ApJ, 698, 514 [NASA ADS] [CrossRef] [Google Scholar]
- Bondi, H. 1952, MNRAS, 112, 195B [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Bosch-Ramon, V., Paredes, J. M., Romero, G. E., & Ribó, M. 2006, A&A, 459, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casares, J., Ribas, I., Paredes, J. M., Martí, J., & Allende Prieto, C. 2005, MNRAS, 360, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Chernyakova, M., Neronov, A., & Walter, R. 2006, MNRAS, 372, 1585 [NASA ADS] [CrossRef] [Google Scholar]
- Collin, S., & Huré, J.-M. 1999, A&A, 341, 385 [NASA ADS] [Google Scholar]
- Caproni, A., Livio, M., Abraham, Z., & Mosquera Cuesta, H. J. 2006, ApJ, 653, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Connors, T. W., Johnston, S., Manchester, R. N., & McConnell, D. 2002, MNRAS, 336, 1201 [NASA ADS] [CrossRef] [Google Scholar]
- Dhawan, V., Mioduszewski, A., & Rupen, M. 2006, Proceedings of the VI Microquasar Workshop, 52 [Google Scholar]
- Dubner, G. M., Holdaway, M., Goss, W. M., & Mirabel, I. F. 1998, AJ, 116, 1842 [NASA ADS] [CrossRef] [Google Scholar]
- Fender, R. P., Belloni, T. M., & Gallo, E. 2004, MNRAS, 355, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Fragile, P. C., & Anninos, P. 2005, ApJ, 623, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Fragile, P. C., Mathews, G. J., & Wilson, J. R. 2001, ApJ, 553, 955 [NASA ADS] [CrossRef] [Google Scholar]
- Fragile, P. C., Blaes, O. M., Anninos, P., & Salmonson, J. D. 2007, ApJ, 668, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Foulkes, S. B., Haswell, C. A., & Murray, J. R. 2006, MNRAS, 366, 1399 [NASA ADS] [CrossRef] [Google Scholar]
- Gregory, P. C. 2002, ApJ, 575, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Hutchings, J. B., & Crampton, D. 1981, PASP, 93, 486 [NASA ADS] [CrossRef] [Google Scholar]
- Ingram, A., & Done, C. 2010, MNRAS, accepted [arXiv:0907.5485] [Google Scholar]
- Ingram, A., Done, C., & Fragile, P. 2009, MNRAS, 397, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Johnston, S., Lyne, A. G., Manchester, R. N., et al. 1992, MNRAS, 255, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Kaufman Bernadó, M. M., Romero, G. E., & Mirabel, I. F. 2002, A&A, 385, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Katarzynski, K., & Walczewska, K. 2010, A&A, 510, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Katarzynski, K., Ghisellini, G., Tavecchio, F., et al. 2005, A&A, 433, 479 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Larwood, J. 1998, MNRAS, 299, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, S., & Melia, F. 2002, ApJ, 573, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Marscher, A. P., & Gear, W. K. 1985, ApJ, 298, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Martí, J., & Paredes, J. M. 1995, A&A, 298, 151 [NASA ADS] [Google Scholar]
- Massi, M., Ribó, M, Paredes, J. M., et al. 2004, A&A, 414, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Massi, M., Ribó, M., Paredes, J. M., et al. 2005, High Energy Gamma-Ray Astronomy, 745, 311 [NASA ADS] [Google Scholar]
- Massi, M., & Kaufman Bernadó, M. 2009, ApJ, 702, 1179 [NASA ADS] [CrossRef] [Google Scholar]
- McClintock, J. E., & Remillard, R. A. 2006, Compact stellar X-ray sources (Cambridge University Press), 157 [Google Scholar]
- Meier, D. L. 2005, Ap&SS, 300, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, R. P., & Papaloizou, J. C. B. 2000, MNRAS, 315, 570 [NASA ADS] [CrossRef] [Google Scholar]
- Paczynski, B. 1977, ApJ, 216, 822 [NASA ADS] [CrossRef] [Google Scholar]
- Papaloizou, J. C. B., & Pringle, J. E. 1977, MNRAS, 181, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Peracaula, M., Gabuzda, D. C., & Taylor, A. R. 1998, A&A, 330, 612 [NASA ADS] [Google Scholar]
- Ray, P. S., Jacob, M., & Hartman, J. M. 2008, The Astronomer's Telegram, 1730, 1 [NASA ADS] [Google Scholar]
- Stella, L., & Vietri, M. 1998, ApJ, 492, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, A. R., Kenny, H. T., Spencer, R. E., & Tzioumis, A. 1992, ApJ, 395, 268 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, A. R., Dougherty, S. M., Scott, W. K., Peracaula, M., & Paredes, J. M. 2000, proc. of Astrophysical Phenomena Revealed by Space VLBI, ed. H. Hirabayashi, P. G. Edwards, & D. W. Murphy, Pub. ISAS, 223 [Google Scholar]
- Waters, L. B. F. M., Taylor, A. R., van den Heuvel, E. P. J., Habets, G. M. H. J., & Persi, P. 1988, A&A, 198, 200 [NASA ADS] [Google Scholar]
- Wilkins, D. C. 1972, Phys. Rev. D, 5, 814 [NASA ADS] [CrossRef] [Google Scholar]
- Zamanov, R. K., & Martí, J. 2000, A&A, 358, L55 [NASA ADS] [Google Scholar]
All Tables
Table 1: Two-peak MQ vs Pulsar Model.
All Figures
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13787fg1.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13787-09/Timg31.png)
|
Figure 1:
X-ray states/radio states vs. hardness. Along with the usual X-ray characteristics (McClintock & Remillard 2006) and radio characteristics (Fender et al. 2004)
of the spectral states, we add for the Steep power-law state also the
X- and gamma-ray characteristics for the shock-in-jet model and for
blazars (Marscher & Gear 1985; Katarzynski et al. 2005; Katarzynski & Walczewska 2010).
The transient radio jet, i.e. ``plasmoids'' displaced from the center,
is related to shocks travelling in the slowly moving preexisting steady
jet established during the previous low hard state. LS I +61 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13787fg2.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13787-09/Timg44.png)
|
Figure 2:
Precession due to tidal torque induced by the Be star as function of
mass ratio, |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13787fg3.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13787-09/Timg46.png)
|
Figure 3:
Precession due to tidal torque induced by the Be star as function of
mass ratio, |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{13787fg4.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13787-09/Timg79.png)
|
Figure 4:
Lense-Thirring precession for a test particle
in function of the dimensionless specific angular momentum, a*, (Eq. (4)). The orbit of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{13787fg5.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13787-09/Timg86.png)
|
Figure 5:
Lense-Thirring precession for a geometrically thick accretion flow with inner and outer radii |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



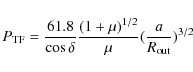
![\begin{displaymath}P_{\rm TF}={61.8\over\cos\delta} {(1+\mu)^{1/2}\over\mu} [{0....
...^{-1/3})\over 0.49 {1.4\over 1+[\ln (1.8 \mu)]^{0.24}}}]^{3/2}
\end{displaymath}](/articles/aa/full_html/2010/07/aa13787-09/img52.png)

![\begin{displaymath}{R_{\rm tr}\over r_{\rm g}}=\big[ {32\times 10^3 \over {{M_{\rm compact~object}\over M_{\odot}} \nu_K}}-a_* \big ]^{2/3}.
\end{displaymath}](/articles/aa/full_html/2010/07/aa13787-09/img72.png)