EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 515 (June 2010) A&A, 515 (2010) A11 Full HTML
Free Access
Issue
A&A
Volume 515, June 2010
Article Number A11
Number of page(s) 9
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/200913559
Published online 28 May 2010
A&A 515, A11 (2010)

The slowing down of galaxy disks in dissipationless minor mergers

Y. Qu1 - P. Di Matteo1 - M. Lehnert1 - W. van Driel1 - C. J. Jog2

1 - GEPI, Observatoire de Paris, CNRS, Université Paris Diderot, 5 place Jules Janssen, 92190 Meudon, France
2 - Department of Physics, Indian Institute of Science, Bangalore 560012, India

Received 27 October 2009 / Accepted 16 February 2010

Abstract
We have investigated the impact of dissipationless minor galaxy mergers on the angular momentum of the remnant. Our simulations cover a range of initial orbital characteristics, and the system consists of a massive galaxy with a bulge and disk merging with a much less massive (one-tenth or one-twentieth) gasless companion that has a variety of morphologies (disk- or elliptical-like) and central baryonic mass concentrations. During the process of merging, the orbital angular momentum is redistributed into the internal angular momentum of the final system; the internal angular momentum of the primary galaxy can increase or decrease depending on the relative orientation of the orbital spin vectors (direct or retrograde), while the initially nonrotating dark matter halo always gains angular momentum. The specific angular momentum of the stellar component always decreases independently of the orbital parameters or morphology of the satellite, the decrease in the rotation velocity of the primary galaxy is accompanied by a change in the anisotropy of the orbits, and the ratio of rotation speed to velocity dispersion of the merger remnant is lower than the initial value, not only because of an increase in the dispersion but also of the slowing-down of the disk rotation. We briefly discuss several astrophysical implications of these results, suggesting that minor mergers do not cause a ``random walk'' process of the angular momentum of the stellar disk component of galaxies, but rather a steady decrease. Minor mergers may play a role in producing the large scatter observed in the Tully-Fisher relation for S0 galaxies, as well as in the increase of the velocity dispersion and the decrease in $v/\sigma $ at large radii as observed in S0 galaxies.

Key words: galaxies: interactions - galaxies: formation - galaxies: evolution - galaxies: kinematics and dynamics - galaxies: structure

1 Introduction

Numerical simulations, as well as observations, show that the final product of a merger between two disk galaxies depends mostly on their mass ratio. Major mergers of spiral galaxies, i.e. of pairs with mass ratios ranging from 1:1 to 3:1, have been known for decades to form pressure-supported elliptical galaxies (Bournaud et al. 2005; Naab et al. 1999; Cretton et al. 2001; Barnes 1992; Bekki & Shioya 1997; Bendo & Barnes 2000; Springel 2000; Barnes & Hernquist 1991; Naab & Burkert 2003), with ``boxy'' or ``disky'' shaped isophotes. Intermediate-mass ratio mergers, with mass ratios from 4.5:1 to 10:1, produce hybrid systems that typically have spiral-like morphologies but elliptical-like kinematics (Bournaud et al. 2005,2004; Jog & Chitre 2002), while minor mergers (mass ratio $\leq$10:1) are much less violent dynamical processes that do not destroy the disk of the more massive galaxy in the merger. However, understanding the impact of minor mergers on galaxies is of particular interest, considering that they occur frequently in the local universe (Carlberg & Couchman 1989; Lacey & Cole 1993; Kaviraj et al. 2009; Gao et al. 2004; Jogee et al. 2009; Frenk et al. 1988) and that they can induce a number of morphological signatures in the final remnant (Newberg et al. 2002; Ibata et al. 1994; Younger et al. 2007; Martínez-Delgado et al. 2001; Ibata et al. 2005; Erwin et al. 2005; Kazantzidis et al. 2009; Ibata et al. 2001; Martínez-Delgado et al. 2008; Yanny et al. 2003; Feldmann et al. 2008; Pohlen & Trujillo 2006; Younger et al. 2008).

The importance of minor mergers in shaping the evolution of galaxies has been supported by detailed numerical simulations. For example, they can induce changes that move late-type spiral galaxies towards earlier Hubble types and contribute to the thickening and heating of the stellar disk (Benson et al. 2004; Walker et al. 1996; Quinn et al. 1993; Velazquez & White 1999; Font et al. 2001; Kazantzidis et al. 2008). The disks of galaxies are generally not fully destroyed by these events, and a remaining kinematically cold and thin component containing $\sim$15 to $25\%$ of the initial stellar disk mass can indeed survive, embedded in a hotter and thicker disk (e.g., Villalobos & Helmi 2008), whereas the presence of gas in the disk galaxy can largely prevent the destruction of its thin stellar disk (Moster et al. 2010).

However, while the role that minor mergers may play in the mass assembly, kinematics, and morphologies of present-day galaxies has been studied extensively both observationally and numerically, much less is known about the way angular momentum is redistributed during these events. Cosmological simulations show that there is a discrepancy between the specific angular momentum of dark matter halos, which have undergone predominantly minor mergers since $z\sim3$, and the observed baryonic component of present-day galaxies. The dark matter halos in cosmological simulations have spin parameters that are a few times smaller than observed in disks of late-type bulgeless dwarf galaxies (D'Onghia & Burkert 2004; van den Bosch et al. 2001). The evolution of the specific angular momentum of dark matter halos as caused by major and minor mergerscan be described as a random walk process, with major mergers contributing to the spin-up of dark halos, and with minor interactions mostly slowing them down (Vitvitska et al. 2002).

The consequence of an interaction is to transfer orbital angular momentum into internal rotation: at the beginning of the interaction, the most extended components first interact tidally, while the more tightly bound components feel the effects of the encounter only in the final phases of the merging process (Barnes 1992; Barnes in Kennicutt et al. 1998). However, little is known about the detailed redistribution of the angular momentum between the baryonic and dark matter components. McMillan et al. (2007) show that, during major mergers of disk galaxies, the dark halos acquire only a small amount of rotation, with the dark component of the final remnant always having a stellar rotation speed to velocity dispersion, or $v/\sigma $, ratio less than 0.2. Jesseit et al. (2009) have discussed the amount of specific angular momentum found in the stellar component of major merger remnants, showing that 1:1 mergers cause the destruction of the ordered rotation of the progenitor disks, while a portion of the original rotation can be preserved during mergers with higher mass ratios. If a dissipative component (gas) is present in the progenitor disks, gravitational torques exerted on it by the stellar disk can extract a significant fraction of its initial angular momentum, causing strong gas inflows into the circumnuclear regions (Barnes & Hernquist 1996). Finally, angular momentum redistribution also occurs during major mergers between spheroidal dissipationless galaxies, leading to a transformation of the orbital angular momentum into the internal angular momentum of both baryons and dark matter, which can be efficient enough to produce fast-rotating ( $v/\sigma > 1$) stellar halos, as recently shown by Di Matteo et al. (2009).

A complete and detailed picture of the angular momentum redistribution during minor mergers is still lacking, even though minor mergers are expected to be much more common than major mergers (Fakhouri & Ma 2008), thereby obviously playing an important role in galaxy mass assembly. For example, Debattista et al. (2006) and Sellwood & Debattista (2006) have suggested that minor mergers could transfer angular momentum to the dark halo through the action of a stellar bar in the disk.

This paper aims to investigate the evolution of the angular momentum in minor mergers and its redistribution between the stellar and the dark matter components of the primary galaxy and its satellite. We investigate this process through the use of dissipationless N-body simulations of minor (mass ratio 10:1 and 20:1) mergers between a disk-plus-bulge primary galaxy and a satellite having either an elliptical or a disk morphology. Specifically, we show that, independent of the morphology of the satellite galaxy or the orbital parameters, minor mergers always cause a slowing down of the stellar disk, as well as a loss of specific angular momentum within the disk, and that this process contributes to moving galaxies towards earlier Hubble types and more slowly rotating systems (Emsellem et al. 2007). The decrease in the specific angular momentum of the stellar component of the disk galaxy is accompanied by an increase in the specific angular momentum of both dark halos (of the primary and of the satellite), as well as of the pressure-supported stellar component that was initially part of the satellite.

2 Models and initial conditions

We studied the coalescence of a massive S0 galaxy and an elliptical having a mass ratio 10:1 or 20:1. The massive S0 galaxy (hereafter called gS0) is composed of a spherical dark matter halo and a spherical stellar bulge, both of which are not rotating initially, and represented by Plummer spheres (Binney & Tremaine 1987) with total masses $M_{\rm H}$ and $M_{\rm B}$ and core radii $r_{\rm H}$ and $r_{\rm B}$, respectively. The stellar disk is represented by a Miyamoto-Nagai density profile (Binney & Tremaine 1987) with mass M*, and vertical and radial scale-lengths of h* and a*, respectively (Table 1). The adopted bulge-to-total baryonic mass ratio of our S0 galaxy model, B/T of 1:5, is based on the most recent estimate for the ratios of S0 galaxies (Laurikainen et al. 2007), which are up to a factor 3 lower than earlier estimates (e.g., Simien & de Vaucouleurs 1986). As the work of Laurikainen et al. (2007) is based on $K_{\rm s}$ band (2.2 $\mu$m) data, it represents more realistic values for the old stellar component than those by Simien & de Vaucouleurs (1986) based on B-band data (the dust extinction being more significant at these wavelengths). The fraction of dark-to-baryonic matter inside R50, the radius containing half of the baryonic matter, is $16\%$, which broadly agrees with observational estimates (Williams et al. 2009), and the resulting rotation curve (see Chilingarian et al. 2009) shows a rapid rise in the center, followed by a decline at larger radii, typical of many S0s (Noordermeer et al. 2007).

This paper is part of a larger program (Di Matteo et al. 2009) whose aim is to systematically study the impact of major and minor mergers on angular momentum redistribution in galaxies. We analyze here the simple case of the impact of minor mergers on early-type, gas poor, S0 galaxies, and we plan in future work to extend this study to the whole Hubble sequence, with a variety of gas fractions and bulge-to-disk ratios. Besides, starting with such simple simulations allows us to compare our results with a well-defined class of objects in order to verify the appropriateness of our simulations and to gain insight into possible evolutionary avenues for relatively simple dynamical systems like S0s.

The satellite elliptical galaxy, which is either ten (dE0, dE0l, dE0h) or twenty (sE0) times less massive than the gS0 galaxy, consists of spherical stellar and dark matter components, both modeled with Plummer profiles and both not rotating initially. The density profile of the satellite galaxy is the same in all simulations, but the central density of the baryonic component is changed to study how changing the density would affect the angular momentum redistribution during the encounter. We thus considered ``reference'' dwarf E0 (dE0) models, as well as galaxies having a central volume density $50\%$higher (dE0h) and lower (dE0l) than the reference dE0 galaxy (see Table 1).

Table 1:   Galaxy parameters for the initial models of the bulge and halo, modeled as Plummer spheres.

To study the dependence of the results on the morphology of the satellite galaxy, we ran twelve additional simulations, modeling mergers of the giant gS0 galaxy with a disk satellite (hereafter called dS0), whose total mass is ten times lower. The dS0 consists of a spherical dark matter halo, a spherical stellar bulge, both of which are not rotating, and a rotating stellar disk. The morphological parameters of the dS0 galaxies are given in Table 1. We refer the reader to Chilingarian et al. (2009) for a more extensive description of these initial models.

All the initial models and their individual components were evolved in isolation for 1 Gyr, before starting the interaction. At this time, the disk had reached a stable configuration, as discussed in the Appendix. The galaxies were initially placed at a relative distance of 100 kpc, with a variety of relative velocities, to simulate different orbits. The orbital initial conditions for the giant-dwarf interactions are given in Table 9 of Chilingarian et al. (2009), so we report here only on the orbital parameters of the gS0-sE0 simulations (Table 2).

We chose a reference frame with its origin at the barycenter of the system and an x-y plane corresponding to the orbital plane. The spin vector of the gS0 galaxy initially defines an angle $i_1=33^{\circ}$or $i_1=60^{\circ}$with respect to the z-axis (see Fig. 3 in Chilingarian et al. 2009). For all simulations involving a dS0 galaxy, we have chosen an initial angle between the dS0 spin and the z-axis of $i_2=130^{\circ}$. The orbital angular momentum can be parallel (direct orbit) or anti-parallel (retrograde orbit) to the z-axis of the reference frame.

Table 2:   Orbital parameters for the gS0-sE0 interactions.

When referring to specific encounters between the spiral and a satellite, the nomenclature adopted is a six(or seven)-character string: the first three characters are the type of the massive galaxy, always ``gS0'', followed by a three(or four)-character string for dE0 (average concentration, dwarf elliptical satellite), dE0l (low concentration dwarf elliptical), dE0h (high concentration dwarf elliptical), dS0 (dwarf spiral satellite) or sE0 (for the two times less massive elliptical satellite). This is followed by a string representing the type of encounter (see first column in Table 2 for the specific types), followed by the suffix ``dir'' or ``ret'', for direct or retrograde orbits. The final two numbers, which are either ``33'' or ``60'', indicate the initial inclination of the gS0 galaxy with respect to the orbital plane. For example, the nomenclature ``gS0dE0h01dir33'' refers to the encounter between the gS0 galaxy (whose initial inclination $i_1=33^{\circ}$) and the high-concentration elliptical satellite dE0h, moving on a direct orbit, whose initial orbital parameters are those corresponding to id = 01dir in Table 9 of Chilingarian et al. (2009).

All simulations (50 in total) were run using the Tree-SPH code described in Semelin & Combes (2002). A total of $N_{\rm TOT}=528~000$ particles was used for all simulations, distributed between the gS0 galaxy and the satellite (see Table 3). We also tested the dependence of the results on the number of particles used in the simulation, running some additional simulations with a total of $N_{\rm TOT}=1~056~000$ particles. A Plummer potential was used to soften gravity on small scales, with constant softening lengths of $\epsilon=200$ pc (or $\epsilon=170$ pc for the high-resolution simulations) for all particles. The equations of motion are integrated using a leapfrog algorithm with a fixed time step of 0.5 Myr. With these choices, the relative error in the conservation of the total energy is close to 10-6 per time step. Since the work presented here only investigates simulated galaxies without any gas, only the part of the code evaluating the gravitational forces acting on the systems has been used.

Table 3:   Particle numbers for disk galaxy and satellites.

3 Results

3.1 Angular momentum evolution

\begin{figure} \par\includegraphics[width=14cm,clip]{13559fg1.ps} \end{figure} Figure 1:

Top panels: evolution of the absolute value of the total (solid line), orbital (dotted line), and internal (dashed line) angular momentum for some of the simulated 10:1 mergers, for both the stellar and dark matter components together. Bottom panels: evolution of the absolute value of the internal angular momentum of the massive gS0 galaxy (red dashed line) and of the dE0 satellite (blue dashed line) for both the stellar and dark matter components together. The angular momentum is in units of $2.3\times10^{11}~M_{\odot}$ kpc km s-1.

Open with DEXTER

As a result of the action of tidal torques and dynamical friction, the satellite loses its orbital angular momentum (hereafter AM) and gradually spirals deeper into the gravitational field of the primary galaxy, where it finally dissolves completely (meaning it does not survive as an entity within the core of the primary galaxy). In this section, we discuss how the orbital AM is converted into internal AM and how it is redistributed among the different components (stars and dark matter) of the two galaxies.

3.1.1 Redistribution of orbital into internal angular momentum

Figure 1 shows the evolution of the absolute value of the total, orbital, and internal angular momenta of the system, for some of our simulations. In all cases, the total (internal + orbital) AM is conserved during the interaction, with an accuracy of $\la$10-6 per time step. The orbital AM is constant until the first pericenter passage of the satellite. At this time, dynamical friction and tidal torques act on the system, converting part of the orbital AM into internal AM. This continues to occur during each successive passage, until the two galaxies finally merge, and the orbital AM has been completely converted into internal rotation of the merged system. Looking at the distribution of the internal AM between the two galaxies (Fig. 1, bottom panels), we can see that the satellite galaxy always gains part of the orbital AM, while the gS0 galaxy either gains or loses angular momentum, depending on the relative orientation of its spin and of the orbital AM (direct and retrograde orbits, respectively). Since the orbital AM in retrograde encounters is anti-parallel to the z-axis of the reference frame, their total AM is systematically lower than that of the corresponding direct encounter.

Changing the baryonic mass concentration of the satellite (Fig. 2) affects the redistribution of the internal AM between the two galaxies, in the sense that, for a given orbit, the denser the satellite, the smaller the amount of AM it absorbs and the larger the variation in the internal AM of the primary galaxy. This trend occurs because a satellite with higher density decays more rapidly in the central regions of the primary galaxy, since it is less susceptible to tidal effects of the primary galaxy, preserves a higher percentage of bound mass, suffers a stronger gravitational drag. Since tidal torques are less effective on denser satellites (see Sect. 3.2 in Di Matteo et al. 2009), the orbital angular momentum is more efficiently redistributed to the dark halo of the primary galaxy, the component that mainly drives its orbital decay through dynamical friction.

3.1.2 Internal angular momentum of the stellar and dark matter components

Here we investigate how the AM is redistributed in each of the two galaxies, between the stellar and the dark matter components. In Fig. 3 we show how the distribution of the internal AM between the baryons and dark matter evolves during the merging process. Near the time of the first barycentric passage, the two dark matter halos (primary and satellite) acquire part of the orbital AM, leading to rotation of a halo that initially was not rotating. In general, the amount of internal AM absorbed by the dark matter component of the primary galaxy is greater (by a factor 2-3) for pairs on direct orbits than for those on retrograde ones. For retrograde orbits, we note that the dark halo of the merger remnant rotates in the direction opposite to that of the stellar disk, because it absorbed part of the orbital AM.

\begin{figure} \par\includegraphics[width=8cm,clip]{13559fg2.ps} \end{figure} Figure 2:

Evolution of the absolute value of the internal angular momentum in minor mergers with different baryonic mass concentrations of the merging satellite. The mass of the satellite is the same, only the central volume density is $50\%$ higher (dotted lines) or $50\%$ lower (solid lines) than in the reference satellite. The internal angular momentum of gS0 galaxy and satellite are shown in red and blue, respectively. Left panel: direct mergers. Right panel: retrograde mergers.

Open with DEXTER

\begin{figure} \par\includegraphics[width=8cm,clip]{13559fg3.ps} \end{figure} Figure 3:

Evolution of the absolute value of the internal angular momentum of the stellar and dark matter components of the gS0 galaxy (solid and dotted red lines) and of its satellite (solid and dotted blue lines) for four 10:1 mergers. The angular momentum is in units of $2.3\times10^{11}~M_{\odot}$ kpc km s-1.

Open with DEXTER
\begin{figure} \par\includegraphics[width=12cm,clip]{13559fg4.ps} \end{figure} Figure 4:

Evolution of the absolute value of the specific angular momentum of the stars in the gS0 galaxy for six of the direct and retrograde merger simulations with a dE0 or a dS0 satellite. The angular momentum is estimated in five different radial regions relative to the half mass radius, R50: $r\le 0.5R_{50}$, $0.5R_{50}<r\le R_{50}$, $R_{50}<r\le 2R_{50}$, $2R_{50}<r\le 5R_{50}$, and $5R_{50}<r\le 10R_{50}$. The specific angular momentum is in units of 100 kpc km s-1.

Open with DEXTER
The stellar component of the satellite also absorbs orbital AM (Fig. 3). For retrograde orbits, this conversion of orbital into internal AM is a mechanism for creating a counter-rotating old stellar component in a merger remnant (as first noted by Kormendy 1984; Balcells & Quinn 1990, for minor mergers involving elliptical galaxies). In contrast to the simulations by Balcells & Quinn (1990), our satellite does not survive as a recognizable entity to the end of the merging process. Its distribution can be described as ``thick disk-like'', encompassing the remaining disk and extending out to $\sim$10 kpc from the center of the remnant. Moreover, less than $4\%$ of the internal stellar AM is transferred to the remnant's bulge by the end of the merger process. Minor mergers do not add significant amounts of angular momentum to the bulges of S0 galaxies.

Although none of the initially pressure supported components were rotating at the beginning of the simulation, they later acquire part of the orbital AM and begin to rotate. The case of the halo component is simple: the more massive and extended, the more AM it absorbs. However, the evolution of the AM of the stellar disk of the primary galaxy is quite different. In all simulated orbits, independent of the orbital parameters and the morphology of the satellite galaxy (whether pressure- or rotationally supported), the disk of the primary galaxy always loses AM during the interaction. Although the decrease in the internal AM of the disk varies depending on orbital parameters and on the internal structure of the satellite (see Fig. 3), on average the relative change of the internal AM is $\Delta L/L\sim 10\%$ for mergers with a mass ratio 10:1. We also find that satellites with higher central stellar densities lead to remnants with a lower internal AM in the stellar component that was formerly part of the disk of the primary.

3.2 The slowing-down of rotating disks

\begin{figure} \par\includegraphics[width=12cm,clip]{13559fg5.ps} \end{figure} Figure 5:

Absolute value of the specific angular momentum, l, of stars in the gS0 galaxy at the start of the simulation, t=0 (dotted lines), and at 3 Gyr (solid lines) after the start of the simulation, as a function of radii containing a fixed percentage of the stellar mass. l was measured at least 1 Gyr after the merger completed. The specific angular momentum is in units of 100 kpc km s-1.

Open with DEXTER

The decrease in the internal AM of the primary stellar disk discussed in the previous section affects the whole of the disk, up to distances of about 5 to 10 times R50[*]. To better demonstrate the loss of angular momentum, in Fig. 4 we show the evolution of the specific internal AM, $l_{\rm int}=\langle\Sigma_{i} \vec{r}_{i}\times \vec{v}_{i}\rangle$, of the stars that were initially part of the primary galaxy. We have evaluated $l_{\rm int}$for five different radial regions of the galaxy: $r\le 0.5R_{50}$, $0.5R_{50}<r\le R_{50}$, $R_{50}<r\le 2R_{50}$, $2R_{50}<r\le 5R_{50}$, and $5R_{50}<r\le 10R_{50}$. In all cases considered here, we find that the stellar component slows down out to at least 5R50, i.e. the radius containing $\sim$$80\%$ of the total stellar mass (Fig. 5), regardless of the initial orbital parameters, inclination angles, or satellite morphologies. The same behavior is also found in the merger with the disky satellite, before it is ultimately destroyed by the tidal field of the primary galaxy.

The question arises as to where this decrease in rotation speed comes from? During the merging process, the variation of the half mass radius, R50, is not more than $10\%$, and what variation there is in the mass distribution is not sufficient to explain the observed decrease. To gain deeper insight, we evaluated the anisotropy parameter, $\beta = 1-\frac{\langle\sigma^{2}_{t}\rangle}{2\langle\sigma^{2}_{\rm r}\rangle}$, where $\sigma_{\rm r}$and $\sigma_{\rm t}$are the velocity dispersions of the radial and tangential components, respectively (Binney & Tremaine 1987). If the velocity distribution is isotropic then $\beta=0$, and if the velocity distribution is dominated by tangential motions, then $\beta<0$, and $\beta>0$if dominated by radial motions. As shown in Fig. 6, the merging process is accompanied by an evolution of the $\beta $ parameter in the stellar component. The change in $\beta $ is particularly large outside of R50. In these outer regions, the stellar orbits, which before the interaction were dominated by tangential orbits, tend to become increasingly radially dominated as the merger advances. While the outermost region, $2R_{50}<r\le 5R_{50}$, of the merger remnant is still dominated by tangential motions, the motion of stars in the region $R_{50}<r\le 2R_{50}$ can become nearly isotropic from the interaction with the satellite (see for example the gS0dE001dir33 simulation shown in Fig. 6). A similar change in the anisotropy was previously noted in simulations of single mergers (Bournaud et al. 2005) and of multiple mergers (Athanassoula 2005; Bournaud et al. 2007). In general, the strongest evolution of the $\beta $ parameter is found in direct encounters.

If the velocity dispersion of a disk increases in a merger, then the effective rotational velocity decreases, because of the asymmetric drift, see, e.g., Sect. 4 of Binney & Tremaine (1987). The anisotropy parameter is a way to represent the conversion of rotational motion into random motions. To confirm that asymmetric drift is the underlying cause, we evaluated the evolution of the radial and tangential components of the velocity dispersions in our simulations. In Fig. 7, their fractional evolution (i.e.,  $\sigma_{\rm r}(t)/\sigma_{\rm r}(t=0)$and $\sigma_{\rm t}(t)/\sigma_{\rm t}(t=0)$) is shown for one of our simulations.

The minor merger is accompanied by an increase in the radial velocity dispersion at all radii, but particularly in the outermost regions. At the same time, the transverse velocity dispersion decreases throughout the whole disk, except in the inner region (inside 0.5R50), where the contribution of bulge stars, which acquire AM during the interaction, leads to an increase of $\sigma_{\rm t}$.

\begin{figure} \par\includegraphics[width=12cm,clip]{13559fg6.ps} \end{figure} Figure 6:

Evolution of the anisotropy parameter, $\beta $, of the stars in the gS0 galaxy for the six merger simulations whose specific internal AM evolutions have been shown in Fig. 4. The anisotropy parameter has been measured in five different radial regions relative to the half mass radius: $r\le 0.5R_{50}$, $0.5R_{50}<r\le R_{50}$, $R_{50}<r\le 2R_{50}$, $2R_{50}<r\le 5R_{50}$, and $5R_{50}<r\le 10R_{50}$.

Open with DEXTER

3.2.1 The effect of increasing the merger mass ratio to 20:1

In the previous sections we discussed the impact of 10:1 mass ratio mergers on the redistribution of AM, focusing particularly on the cause of the decrease in the rotation speed of the primary stellar disk. In this section, we want to focus on the effect that increasing the mass ratio in mergers, specifically from 10:1 to 20:1, has on the evolution of the anisotropy parameter and the decrease in the specific AM of the disk (Fig. 8). Also for 20:1 mass ratio mergers a decrease in the $\beta $ parameter is observed (again especially in the outer regions), indicating that the velocity dispersion is increasing in the radial direction. The overall impact on the disk rotation is, of course, less pronounced than for the 10:1 merger simulations. In this case, we find that the average decrease in the internal AM of the stellar component is $\Delta L/L\simeq 8\%$, which is about $30{-}40\%$ lower than the value found for 10:1 mergers. However, this is an average value, whereas the actual decrease in any particular merger depends on both the morphology and the central density of the satellite galaxy.

3.3 Rotation speeds and v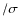$/\sigma $

The decrease in the specific angular momentum of the stellar component during a minor merger is obviously reflected in other dynamical properties of the merger remnant. As shown in Fig. 9 the minor merger reduces the rotation speed of the stellar component of the disk galaxy and increases its velocity dispersion. To evaluate these quantities, we considered all stellar particles 1 kpc above and below the meridional plane of the primary galaxy, including those that were initially part of the satellite galaxy. In the case of a 10:1 direct merger, the rotation speed at r=2R50decreases by about $25\%$, from the initial value of v=200 km s-1 to about v=150 km s-1. At the same time the velocity dispersion increases over the whole disk, e.g. by about $30\%$ at r=2R50. This leads to an overall decrease in the $v/\sigma $ ratio over the entire extent of the disk, e.g. from 2.3 to 1.4 at r=2R50(Fig. 9). The decrease in the rotation speed and $v/\sigma $depends on the merger mass ratio: at the end of the 20:1 merger the remnant shows higher values of both v and $v/\sigma $ than the 10:1 merger. Finally, the decrease in the rotation speed in the remnants of the two retrograde simulations shown in Fig. 9, gS0dE001ret33 and gS0sE001ret33, is due to both a slowing down of stars in the gS0 disk (as discussed previously) and to a negative contribution coming from stars formerly in the satellite galaxy. These stars have acquired part of the orbital AM, which is in the opposite direction to the spin of the gS0, and they form a counter-rotating extended stellar component that contributes to the overall decrease in the line-of-sight velocity of the remnant galaxy and to the increase in its velocity dispersion.

4 Summary and discussion

In this paper, we have studied the redistribution of the angular momentum during dissipationless minor mergers between a massive disk galaxy and an elliptical- or S0-like satellite with masses that are either ten or twenty times smaller than that of the primary galaxy. From an analysis of these simulations, we find that:

\begin{figure} \par\includegraphics[width=7.8cm,clip]{13559fg7.ps} \end{figure} Figure 7:

The evolution of radial and tangential fractional velocity dispersion in different radial regions: $r\le 0.5R_{50}$, $0.5R_{50}<r\le R_{50}$, $R_{50}<r\le 2R_{50}$, $2R_{50}<r\le 5R_{50}$, and $5R_{50}<r\le 10R_{50}$.

Open with DEXTER

  • During the merging process the orbital angular momentum is redistributed into internal angular momentum of both the primary galaxy and the satellite.

  • The total internal angular momentum of the primary galaxy can either increase or decrease, depending on the orientation of the orbital spin (direct or retrograde orbit).

  • While the initially nonrotating dark matter halo of the primary galaxy always acquires angular momentum, the specific angular momentum of the stellar component always decreases, independent of the initial orbital parameters or the morphology of the satellite galaxy.

  • The decrease in the rotation speed of the disk of the main galaxy is accompanied by a change in the distribution of the types of stellar orbits, especially outside of the half mass radius, R50. Generally, the radial component of the velocity dispersion becomes more and more important, as the merger progresses, thus increasing the anisotropy parameter, 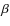$\beta $, from its initially negative value.

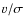  • The ratio of the rotation speed to the velocity dispersion of the disk, $v/\sigma $, decreases at all radii because of both an increase in the velocity dispersion of the disk, which is heated during the merging process, and a decrease in the rotation speed of the disk.

There are a number of astrophysical implications to our results of our (rather idealized) simulations, which we now discuss very briefly. The Tully-Fisher, or T-F, relation between the rotation speed and total luminosity of disk galaxies has, among other possibilities, the following two interpretations. Either the T-F relation originates in the cosmological equivalence between the dark halo mass and the circular velocity (e.g., Mo et al. 1998) or it is due to self-regulated star formation in disks of different masses (e.g., Silk 1997).
\begin{figure} \par\includegraphics[width=7.8cm,clip]{13559fg8.ps} \end{figure} Figure 8:

Upper panels: evolution of the absolute value of the specific angular momentum of stars in the gS0 galaxy undergoing a 20:1 direct ( left panel) and retrograde ( right panel) merger. The specific angular momentum has been measured in five different radial regions, as in Fig. 4. Lower panels: evolution of the anisotropy parameter, $\beta $, for the mergers shown in the upper panels, and measured in the same five radial regions.

Open with DEXTER
The study of S0 galaxies may help to determine which of these hypotheses is correct, and thus to unravel the evolutionary history of S0 galaxies. Studies of the differences between the Tully-Fisher relation of S0s and spirals, while showing some small discrepancies in the offset and scatter, generally find that the S0 galaxies follow the spiral relationship, albeit with a larger scatter (e.g., Bedregal et al. 2006; Hinz et al. 2003, but see Mathieu et al. 2002). The offset and larger scatter have been interpreted as revealing a generally older stellar population in S0 galaxies than in spirals and a range of times during which the S0 galaxies started to evolve passively (Mathieu et al. 2002). However, as noted in Bedregal et al. (2006), there is no strong correlation between the age of the S0 galaxies and the offset from the T-F relation for spiral galaxies. This could stem from a sample that is too small sample size, or it could indicate that other processes may play a role in the larger scatter in the T-F relation among S0 galaxies.

\begin{figure} \par\includegraphics[width=7.8cm,clip]{13559fg9.ps} \end{figure} Figure 9:

Upper panels: line-of-sight velocities and velocity dispersions of stars in the initial gS0 model galaxy (dotted lines) and in the final remnant of a 10:1 (thick solid lines) and a 20:1 (thin solid lines) merger. Direct encounters are shown in the left panel, retrograde encounters on the right. Lower panels: $v/\sigma $ ratio of the initial gS0 model (dotted lines) and of the final remnant of the 10:1 (thick solid lines) and 20:1 (thin solid lines) mergers shown in the upper panels. Distances are in multiples of R50.

Open with DEXTER

We have shown that minor mergers always lead to a decrease in the rotation speed of the primary galaxy. Decreasing its rotation speed while increasing its luminosity will move an S0 galaxy back towards the spiral T-F relation. While it is premature to attempt to quantify this effect in the offset, it is clear that minor mergers would increase the scatter by counteracting, to some extent, passive evolution. In addition to slowing the rotation speed of the disk, we also found that the velocity dispersion of the disk increases, which decreases the $v/\sigma $ of the disk, especially in the outer parts. As we have shown in Fig. 9, this may include an actual decrease with radius in the very outer parts of the disk. This is qualitatively similar to what is observed in the dynamics of planetary nebulae in the outer disks/halos of S0 galaxies (Noordermeer et al. 2008) and it may suggest that, through simulating multiple minor mergers, we may be able to reproduce the velocity structure (e.g., Bournaud et al. 2007).

The models of Vitvitska et al. (2002) have shown that, in mergers of dark matter halos, the specific angular momenta can either increase or decrease. Over time, this would lead to an increase in the dispersion of the specific angular momentum of the halos. Our results for the dark matter halo are consistent with this, but we find systematically a decrease in the specific angular momentum of the stellar component. Instead of a ``random walk'' over time with only an increase in the scatter of the angular momentum, our results appear to suggest a systematic decrease with time in the angular momentum of the stellar component if minor mergers play a large role in the growth of galaxies and the redistribution of angular momentum.

Finally, our results indicate that (single) minor mergers are capable of moving disk galaxies towards earlier types, since they reduce the specific angular momentum and rotation speed, and increase the velocity dispersion of the disk. Bournaud et al. (2007) have shown that a sequence of multiple minor mergers can lead to remnants having global morphological (flattening, Sersic index, etc.) and kinematical ($v/\sigma $ ratio) similar to those observed in real elliptical galaxies. Within this context, it will be interesting to study whether the angular momentum content of the stellar and dark matter components becomes more dispersion-dominated, whether size of this effect depends on the total merged mass rather than on the mass ratio of each merger, and whether successive multiple mergers always slow down the stellar component of the primary galaxy. Many follow-up questions remain - for example, is the specific angular momentum of the stellar component independent of the way mass has been assembled in major and multiple-minor mergers. What role does the dissipative component - gas - play in the way angular momentum is redistributed during the merger and in the remnant? How does the gas content affect the magnitude of the decrease in the rotation speed of the stellar disk? Does each minor merger contribute similarly to the net slowing down, or does each successive merger become less effective in changing the angular momentum and rotation speed? Does the net effect saturate, so that we are ultimately left with nothing but very slow rotators?

Our simulations show that a single dissipationless minor merger is sufficient to considerably reduce the $v/\sigma $ ratio, typically by a factor 1.5-2 at 2R50. Our merger remnants can still be classified as early-type disk galaxies, with a central bulge component and a disk that is thicker and kinematically hotter than that of the progenitor. If the cumulative effect of dissipationless multiple minor mergers leads to systematically slowing down stellar disks, then the final remnants, which should have an elliptical morphology at that point, should not exhibit fast rotation at large radii. The existence of ellipticals with fast rotating halos (Coccato et al. 2009; Rix et al. 1999) may thus require other formation mechanisms, such as major mergers of two elliptical progenitors, as recently suggested by Di Matteo et al. (2009), or dissipationless mergers of disk galaxies with higher mass ratios, typically 3:1 according to Bendo & Barnes (2000); but see also Cretton et al. (2001). However, the presence of a dissipative component, whether in the progenitor disks or accreted after the merger, may change this picture.

We will investigate all these points and their astrophysical implications as discussed above in subsequent papers.

Acknowledgements
Y.Q. and P.D.M. are supported by a grant from the French Agence Nationale de la Recherche (ANR). P.D.M. thanks the Indo-French Astronomy Network for a travel grant, which made a visit to IISc possible, in Bangalore in August 2009. We are grateful to Benoît Semelin and Françoise Combes for developing the code used in this paper and for their permission to use it. These simulations will be made available as part of the GalMer simulation data base (http://galmer.obspm.fr). We wish to thank the referee for the constructive and helpful report that substantially improved this manuscript.

Appendix A: Kinematics of the gS0 galaxy when evolved in isolation

The goal of this paper is to investigate the role minor mergers play in the angular momentum redistribution and kinematics of the massive galaxy. Therefore we must distinguish the impact of minor mergers on the properties of early type disk galaxies from the effects of secular evolution. To make this distinction, it is also important to study the evolution of isolated galaxies. To this end, we ran a control simulation in which the massive S0 galaxy is evolving as an isolated system over 3 Gyr, i.e., the same duration as the merger runs.

As can be seen in Fig. A.1, the kinematics of the isolated S0 galaxy does not change significantly over this period: no increase is found in the velocity dispersion of the central regions or the outer disk, and also the final line-of-sight velocities are remarkably similar to the initial values, apart from some insignificant decrease outside 2R50. Of particular interest is that the final $v/\sigma $ ratio of the isolated massive galaxy differs significantly from that of the massive galaxy even after a minor merger, even in the 20:1 case. Comparing Fig. A.1 with Fig. 9 shows that the minor interaction induces a decrease at all radii, even inside 2R50, which is not found for the galaxy that evolved in isolation. Secular evolution causes only a slight decrease in $v/\sigma $ - the final ratio is $10\%$ lower than the initial one at r=R50, and 23$\%$at r=4R50, whereas even a 20:1 merger induces a much more pronounced slowing down of the disk at all radii, with a final decrease in $v/\sigma $ of $30\%$ at r=R50 and $42\%$ at r=4R50 (see Table A.1). However, it will be interesting to find out at what merger mass ratio the decrease in $v/\sigma $is comparable to that of secular evolution.

\begin{figure} \par\includegraphics[width=6cm,clip]{13559fg10.ps} \end{figure} Figure A.1:

Upper panel: line-of-sight velocities and velocity dispersions of stars in the gS0 galaxy that evolved in isolation, at t=0 (dotted lines) and at t=3 Gyr (solid lines). Lower panel: corresponding $v/\sigma $ ratios at these two times. Distances are in multiples of R50.

Open with DEXTER

Table A.1:   $v/\sigma $ratios at different radii, for the gS0 galaxy which evolved in isolation and after a minor 20:1 and 10:1 merger.

References

  1. Abadi, M. G., Navarro, J., Steinmetz, M., & Eke, V. R. 2003, ApJ, 597, 21 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  2. Athanassoula, E. 2005, in Planetary Nebulae as Astronomical Tools, ed. R. Szczerba, G. Stasinska, & S. K. Gorny, AIP Conf. Ser., 804, 333 [Google Scholar]
  3. Balcells, M., & Quinn, P. J. 1990, ApJ, 361, 381 [NASA ADS] [CrossRef] [Google Scholar]
  4. Barnes, J. E. 1992, ApJ, 393, 484 [NASA ADS] [CrossRef] [Google Scholar]
  5. Barnes, J. E., & Hernquist, L. E. 1991, ApJ, 370, L65 [NASA ADS] [CrossRef] [Google Scholar]
  6. Barnes, J. E., & Hernquist, L. 1996, ApJ, 471, 115 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bedregal, A. G., Aragón-Salamanca, A., & Merrifield, M. R. 2006, MNRAS, 373, 1125 [NASA ADS] [CrossRef] [Google Scholar]
  8. Bekki, K., & Shioya, Y. 1997, ApJ, 478, 17 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bendo, G. J., & Barnes, J. E. 2000, MNRAS, 316, 315 [NASA ADS] [CrossRef] [Google Scholar]
  10. Benson, A. J., Lacey, C. G., Frenk, C. S., Baugh, C. M., & Cole, S. 2004, MNRAS, 351, 1215 [NASA ADS] [CrossRef] [Google Scholar]
  11. Binney, J., & Tremaine, S. 1987, Galactic Dynamics (Princeton: Princeton Univ. Press) [Google Scholar]
  12. Bournaud, F., Combes, F., & Jog, C. J. 2004, A&A, 418, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Bournaud, F., Jog, C. J., & Combes, F. 2005, A&A, 437, 69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Bournaud, F., Jog, C. J., & Combes, F. 2007, A&A, 476, 1179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Carlberg, R. G., & Couchman, H. M. P. 1989, ApJ, 340, 47 [NASA ADS] [CrossRef] [Google Scholar]
  16. Chilingarian, I., Di Matteo, P., Combes, F., Melchior, A.-L., & Semelin, B. 2010, A&A, accepted [Google Scholar]
  17. Coccato, L., Gerhard, O., Arnaboldi, M., et al. 2009, MNRAS, 394, 1249 [NASA ADS] [CrossRef] [Google Scholar]
  18. Cretton, N., Naab, T., Rix, H.-W., & Burkert, A. 2001, ApJ, 554, 291 [NASA ADS] [CrossRef] [Google Scholar]
  19. Debattista, V. P., Mayer, L., Carollo, M. C., et al. 2006, ApJ, 645, 209 [NASA ADS] [CrossRef] [Google Scholar]
  20. Di Matteo, P., Jog, C. J., Lehnert, M. D., Combes, F., & Semelin, B. 2009, A&A, 501, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. D'Onghia, E., & Burkert, A. 2004, ApJ, 612, L13 [NASA ADS] [CrossRef] [Google Scholar]
  22. Emsellem, E., Cappellari, M., Krajnovic, D., et al. 2007, MNRAS, 379, 401 [NASA ADS] [CrossRef] [Google Scholar]
  23. Erwin, P., Beckman, J. E., & Pohlen, M. 2005, ApJ, 626, L81 [Google Scholar]
  24. Fakhouri, O., & Ma, C.-P. 2008, MNRAS, 386, 577 [NASA ADS] [CrossRef] [Google Scholar]
  25. Feldmann, R., Mayer, L., & Carollo, C. M. 2008, ApJ, 684, 1062 [NASA ADS] [CrossRef] [Google Scholar]
  26. Font, A. S., Navarro, J. F., Stadel, J., & Quinn, T. 2001, ApJ, 563, L1 [NASA ADS] [CrossRef] [Google Scholar]
  27. Frenk, C. S., White, S. D. M., Davis, M., & Efstathiou, G. 1988, ApJ, 327, 507 [NASA ADS] [CrossRef] [Google Scholar]
  28. Gao, L., White, S. D. M., Jenkins, A., Stoehr, F., & Springel, V. 2004, MNRAS, 355, 819 [NASA ADS] [CrossRef] [Google Scholar]
  29. Hinz, J. L., Rieke, G. H., & Caldwell, N. 2003, AJ, 126, 2622 [NASA ADS] [CrossRef] [Google Scholar]
  30. Ibata, R., A., Gilmore, G., & Irwin, M. J. 1994, Nature, 370, 194 [NASA ADS] [CrossRef] [Google Scholar]
  31. Ibata, R., Irwin, M., Lewis, G., Ferguson, A. M. N., & Tanvir, N. 2001, Nature, 412, 49 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  32. Ibata, R., Chapman, S., Ferguson, A. M. N., et al. 2005, ApJ, 634, 287 [NASA ADS] [CrossRef] [Google Scholar]
  33. Jesseit, R., Cappellari, M., Naab, T., Emsellem, E., & Burkert, A. 2009, MNRAS, 397, 1202 [NASA ADS] [CrossRef] [Google Scholar]
  34. Jog, C. J., & Chitre, A. 2002, A&A, 393, L89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Jogee, S., Miller, S. H., Penner, K., et al. 2009, ApJ, 697, 1971 [NASA ADS] [CrossRef] [Google Scholar]
  36. Johnston, K. V., Hernquist, L., & Bolte, M. 1996, ApJ, 465, 278 [NASA ADS] [CrossRef] [Google Scholar]
  37. Kaviraj, S., Peirani, S., Khochfar, S., Silk, J., & Kay, S. 2009, MNRAS, 394, 1713 [NASA ADS] [CrossRef] [Google Scholar]
  38. Kazantzidis, S., Bullock, J. S., Zentner, A. R., Kravtsov, A. V., & Moustakas, L. A. 2008, ApJ, 688, 254 [NASA ADS] [CrossRef] [Google Scholar]
  39. Kazantzidis, S., Zentner, A. R., Kravtsov, A. V., Bullock, J. S., & Debattista, V. P. 2009, ApJ, 700, 1896 [NASA ADS] [CrossRef] [Google Scholar]
  40. Kennicutt, R. C., Schweizer, F., Barnes, J. E., et al. 1998, Galaxies: Interactions and Induced Star Formation (Berlin: Springer) [Google Scholar]
  41. Kormendy, J. 1984, ApJ, 287, 577 [NASA ADS] [CrossRef] [Google Scholar]
  42. Lacey, C., & Cole, S. 1993, MNRAS, 262, 627 [NASA ADS] [CrossRef] [Google Scholar]
  43. Laurikainen, E., Salo, H., & Knapen, J. H. 2007, MNRAS, 381, 401 [NASA ADS] [CrossRef] [Google Scholar]
  44. Martínez-Delgado, D., Aparicio, A., Gómez-Flechoso, M., & Carrera, R. 2001, ApJ, 549, L199 [NASA ADS] [CrossRef] [Google Scholar]
  45. Martínez-Delgado, D., Peñarrubia, J., Gabany, R. J., et al. 2008, ASPC, 399, 461 [NASA ADS] [Google Scholar]
  46. Mathieu, A., Merrifield, M. R., & Kuijken, K. 2002, MNRAS, 330, 251 [NASA ADS] [CrossRef] [Google Scholar]
  47. McMillan, P. J., Athanassoula, E., & Dehnen, W. 2007, MNRAS, 376,1261 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  48. Mihos, J. C., Walker, I. R., Hernquist, L., Mendes de Oliveira, C., & Bolte, M. 1995, ApJ, 447, 87 [Google Scholar]
  49. Mo, H. J., Mao, S., & White, S. D. M. 1998, MNRAS, 295, 31 [Google Scholar]
  50. Moster, B. P., Macció, A. V., Somerville, R. S., Johansson, P. H., & Naab, T. 2010, MNRAS, 403, 1009 [NASA ADS] [CrossRef] [Google Scholar]
  51. Naab, T., & Burkert, A. 2003, ApJ, 597, 893 [NASA ADS] [CrossRef] [Google Scholar]
  52. Naab, T., Burkert, A., & Hernquist, L. 1999, ApJ, 523, 133 [NASA ADS] [CrossRef] [Google Scholar]
  53. Newberg, H. J., Yanny, B., Rockosi, C., et al. 2002, ApJ, 569, 245 [NASA ADS] [CrossRef] [Google Scholar]
  54. Noordermeer, E., van der Hulst, J. M., Sancisi, R., et al. 2007, MNRAS, 376, 1513 [NASA ADS] [CrossRef] [Google Scholar]
  55. Noordermeer, E., Merrifield, M. R., Coccato, L., et al. 2008, MNRAS, 384, 943 [NASA ADS] [CrossRef] [Google Scholar]
  56. Pohlen, M., & Trujillo, I. 2006, A&A, 454, 759 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Puerari, I., García-Gómez, C., & Garijo, A. 1998, in Galactic Halos: a UC Santa Cruz Workshop, ed. D. Zaritsky, ASP Conf. Ser., 136, 271 [Google Scholar]
  58. Quinn, P. J., Hernquist, L., & Fullagar, D. P. 1993, ApJ, 403, 74 [NASA ADS] [CrossRef] [Google Scholar]
  59. Rix, H.-W., Carollo, C. M., & Freeman, K. 1999, ApJ, 513, L25 [NASA ADS] [CrossRef] [Google Scholar]
  60. Sellwood, J. A., & Debattista, V. P. 2006, ApJ, 639, 868 [NASA ADS] [CrossRef] [Google Scholar]
  61. Semelin, B., & Combes, F. 2002, A&A, 388, 826 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Silk, J. 1997, ApJ, 481, 703 [NASA ADS] [CrossRef] [Google Scholar]
  63. Simien, F., & de Vaucouleurs, G. 1986, ApJ, 302, 564 [NASA ADS] [CrossRef] [Google Scholar]
  64. Springel, V. 2000, MNRAS, 312, 859 [NASA ADS] [CrossRef] [Google Scholar]
  65. van den Bosch, F. C., Burkert, A., & Swaters, R. A. 2001, MNRAS, 326, 1205 [Google Scholar]
  66. Velazquez, H., & White, S. D. M. 1999, MNRAS, 304, 254 [NASA ADS] [CrossRef] [Google Scholar]
  67. Villalobos, A., & Helmi, A. 2008, MNRAS, 391, 1806 [NASA ADS] [CrossRef] [Google Scholar]
  68. Vitvitska, M., Klypin, A. A., Kravtsov, A. V., et al. 2002, ApJ, 581, 799 [Google Scholar]
  69. Walker, I. R., Mihos, J. C., & Hernquist, L. 1996, ApJ, 460, 121 [NASA ADS] [CrossRef] [Google Scholar]
  70. Williams, M. J., Bureau, M., & Cappellari, M. 2009, MNRAS, 400, 1665 [NASA ADS] [CrossRef] [Google Scholar]
  71. Yanny, B., Newberg, H. J., Grebel, E. K., et al. 2003, ApJ, 588, 824 [NASA ADS] [CrossRef] [Google Scholar]
  72. Younger, J. D., Cox, T. J., Seth, A. C., & Hernquist L. 2007, ApJ, 670, 269 [Google Scholar]
  73. Younger, J. D., Besla, G., Cox, T. J., et al. 2008, ApJ, 676, L21 [NASA ADS] [CrossRef] [Google Scholar]

Footnotes

...R[*]
R50 = 3.3 kpc is the initial half-mass radius of the baryonic component.

All Tables

Table 1:   Galaxy parameters for the initial models of the bulge and halo, modeled as Plummer spheres.

Table 2:   Orbital parameters for the gS0-sE0 interactions.

Table 3:   Particle numbers for disk galaxy and satellites.

Table A.1:   $v/\sigma $ratios at different radii, for the gS0 galaxy which evolved in isolation and after a minor 20:1 and 10:1 merger.

All Figures

  \begin{figure} \par\includegraphics[width=14cm,clip]{13559fg1.ps} \end{figure} Figure 1:

Top panels: evolution of the absolute value of the total (solid line), orbital (dotted line), and internal (dashed line) angular momentum for some of the simulated 10:1 mergers, for both the stellar and dark matter components together. Bottom panels: evolution of the absolute value of the internal angular momentum of the massive gS0 galaxy (red dashed line) and of the dE0 satellite (blue dashed line) for both the stellar and dark matter components together. The angular momentum is in units of $2.3\times10^{11}~M_{\odot}$ kpc km s-1.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13559fg2.ps} \end{figure} Figure 2:

Evolution of the absolute value of the internal angular momentum in minor mergers with different baryonic mass concentrations of the merging satellite. The mass of the satellite is the same, only the central volume density is $50\%$ higher (dotted lines) or $50\%$ lower (solid lines) than in the reference satellite. The internal angular momentum of gS0 galaxy and satellite are shown in red and blue, respectively. Left panel: direct mergers. Right panel: retrograde mergers.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13559fg3.ps} \end{figure} Figure 3:

Evolution of the absolute value of the internal angular momentum of the stellar and dark matter components of the gS0 galaxy (solid and dotted red lines) and of its satellite (solid and dotted blue lines) for four 10:1 mergers. The angular momentum is in units of $2.3\times10^{11}~M_{\odot}$ kpc km s-1.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=12cm,clip]{13559fg4.ps} \end{figure} Figure 4:

Evolution of the absolute value of the specific angular momentum of the stars in the gS0 galaxy for six of the direct and retrograde merger simulations with a dE0 or a dS0 satellite. The angular momentum is estimated in five different radial regions relative to the half mass radius, R50: $r\le 0.5R_{50}$, $0.5R_{50}<r\le R_{50}$, $R_{50}<r\le 2R_{50}$, $2R_{50}<r\le 5R_{50}$, and $5R_{50}<r\le 10R_{50}$. The specific angular momentum is in units of 100 kpc km s-1.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=12cm,clip]{13559fg5.ps} \end{figure} Figure 5:

Absolute value of the specific angular momentum, l, of stars in the gS0 galaxy at the start of the simulation, t=0 (dotted lines), and at 3 Gyr (solid lines) after the start of the simulation, as a function of radii containing a fixed percentage of the stellar mass. l was measured at least 1 Gyr after the merger completed. The specific angular momentum is in units of 100 kpc km s-1.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=12cm,clip]{13559fg6.ps} \end{figure} Figure 6:

Evolution of the anisotropy parameter, $\beta $, of the stars in the gS0 galaxy for the six merger simulations whose specific internal AM evolutions have been shown in Fig. 4. The anisotropy parameter has been measured in five different radial regions relative to the half mass radius: $r\le 0.5R_{50}$, $0.5R_{50}<r\le R_{50}$, $R_{50}<r\le 2R_{50}$, $2R_{50}<r\le 5R_{50}$, and $5R_{50}<r\le 10R_{50}$.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.8cm,clip]{13559fg7.ps} \end{figure} Figure 7:

The evolution of radial and tangential fractional velocity dispersion in different radial regions: $r\le 0.5R_{50}$, $0.5R_{50}<r\le R_{50}$, $R_{50}<r\le 2R_{50}$, $2R_{50}<r\le 5R_{50}$, and $5R_{50}<r\le 10R_{50}$.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.8cm,clip]{13559fg8.ps} \end{figure} Figure 8:

Upper panels: evolution of the absolute value of the specific angular momentum of stars in the gS0 galaxy undergoing a 20:1 direct ( left panel) and retrograde ( right panel) merger. The specific angular momentum has been measured in five different radial regions, as in Fig. 4. Lower panels: evolution of the anisotropy parameter, $\beta $, for the mergers shown in the upper panels, and measured in the same five radial regions.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.8cm,clip]{13559fg9.ps} \end{figure} Figure 9:

Upper panels: line-of-sight velocities and velocity dispersions of stars in the initial gS0 model galaxy (dotted lines) and in the final remnant of a 10:1 (thick solid lines) and a 20:1 (thin solid lines) merger. Direct encounters are shown in the left panel, retrograde encounters on the right. Lower panels: $v/\sigma $ ratio of the initial gS0 model (dotted lines) and of the final remnant of the 10:1 (thick solid lines) and 20:1 (thin solid lines) mergers shown in the upper panels. Distances are in multiples of R50.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=6cm,clip]{13559fg10.ps} \end{figure} Figure A.1:

Upper panel: line-of-sight velocities and velocity dispersions of stars in the gS0 galaxy that evolved in isolation, at t=0 (dotted lines) and at t=3 Gyr (solid lines). Lower panel: corresponding $v/\sigma $ ratios at these two times. Distances are in multiples of R50.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.