Simulations of the cosmic infrared and submillimeter background for future large surveys

N. Fernandez-Conde; G. Lagache; J.-L. Puget; H. Dole

doi:10.1051/0004-6361/200912924

Home

All issues

Volume 515 (June 2010)

A&A, 515 (2010) A48

Full HTML

Free Access

Issue		A&A Volume 515, June 2010


Article Number		A48
Number of page(s)		15
Section		Cosmology (including clusters of galaxies)
DOI		https://doi.org/10.1051/0004-6361/200912924
Published online		08 June 2010

A&A 515, A48 (2010)

II. Removing the low-redshift contribution to the anisotropies using stacking

N. Fernandez-Conde - G. Lagache - J.-L. Puget - H. Dole

Institut d'Astrophysique Spatiale (IAS), Bât. 121, Université Paris-Sud 11 and CNRS (UMR 8617), 91405 Orsay, France

Received 17 July 2009 / Accepted 17 January 2010

Abstract
Context. Herschel and Planck are surveying the sky at unprecedented angular scales and sensitivities over large areas. But both experiments are limited by source confusion in the submillimeter. The high confusion noise in particular restricts the study of the clustering properties of the sources that dominate the cosmic infrared background. At these wavelengths, it is more appropriate to consider the statistics of the unresolved component. In particular, high clustering will contribute in excess of Poisson noise in the power spectra of CIB anisotropies.
Aims. These power spectra contain contributions from sources at all redshift. We show how the stacking technique can be used to separate the different redshift contributions to the power spectra.
Methods. We use simulations of CIB representative of realistic Spitzer, Herschel, Planck, and SCUBA-2 observations. We stack the 24 $\mu$ m sources in longer wavelengths maps to measure mean colors per redshift and flux bins. The information retrieved on the mean spectral energy distribution obtained with the stacking technique is then used to clean the maps, in particular to remove the contribution of low-redshift undetected sources to the anisotropies.
Results. Using the stacking, we measure the mean flux of populations 4 to 6 times fainter than the total noise at 350 $\mu$ m at redshifts z=1 and z=2, respectively, and as faint as 6 to 10 times fainter than the total noise at 850 $\mu$ m at the same redshifts. In the deep Spitzer fields, the detected 24 $\mu$ m sources up to $z \sim 2$ contribute significantly to the submillimeter anisotropies. We show that the method provides excellent (using COSMOS 24 $\mu$ m data) to good (using SWIRE 24 $\mu$ m data) removal of the z<2 (COSMOS) and z<1 (SWIRE) anisotropies.
Conclusions. Using this cleaning method, we then hope to have a set of large maps dominated by high redshift galaxies for galaxy evolution study (e.g., clustering, luminosity density).

Key words: methods: statistical - infrared: galaxies - galaxies: evolution

1 Introduction

The first observational evidence of the cosmic infrared background (CIB) was reported by Puget et al. (1996) and confirmed by Fixsen et al. (1998) and Hauser et al. (1998). The CIB is composed of the relic emission at infrared wavelengths of the formation and evolution of galaxies and consists of contributions from infrared starburst galaxies and to a lesser degree from active galactic nuclei. Deep cosmological surveys of this background have been carried out with ISO (see Elbaz 2005; Genzel & Cesarsky 2000, for reviews) mainly at 15 $\mu$ m with ISOCAM (e.g., Elbaz et al. 2002); at 90 and 170 $\mu$ m with ISOPHOT (e.g., Dole et al. 2001); with Spitzer at 24, 70, and 160 $\mu$ m (e.g., Dole et al. 2004; Papovich et al. 2004) and with ground-based instruments SCUBA (e.g., Blain et al. 2002), LABOCA (e.g., Beelen et al. 2008), and MAMBO (e.g., Bertoldi et al. 2000) at 850, 870, and 1300 $\mu$ m respectively. The balloon-borne experiment BLAST performed the first deep extragalactic surveys at wavelengths 250-500 $\mu$ m capable of measuring large numbers of star-forming galaxies, and their contributions to the CIB (Devlin et al. 2009). These surveys allowed us to obtain a far clearer understanding of the CIB and its sources (see Lagache et al. 2005, for a general review) but many questions remain unanswered such as the evolution of their spatial distribution with redshift.

The spatial distribution of infrared galaxies as a function of redshift is a key component of the scenario of galaxy formation and evolution. However, its study has been hampered by high confusion and instrumental noise and/or by the small size of the fields of observation. Tentative studies, with a small number of sources at 850 $\mu$ m (Blain et al. 2004), found evidence of a relationship between submillimeter galaxies and the formation of massive galaxies in dense environments. Works by Farrah et al. (2006) and Magliocchetti et al. (2008) measured a strong clustering of ultra luminous infrared galaxies (ULIRG) detected with Spitzer at high redshifts. Alternatively, the infrared background anisotropies could also provide information about the correlation between the sources of the CIB and dark matter (Haiman & Knox 2000; Knox et al. 2001; Amblard & Cooray 2007), and its redshift evolution. Lagache et al. (2007) and Viero et al. (2009) reported the detection of a correlated component in the background anisotropies using Spitzer/MIPS (160 $\mu$ m) and BLAST (250, 350, and 500 $\mu$ m) data. These authors found that star formation is highly biased at z > 0.8. The strong evolution of the bias parameter with redshift, caused by the shifting of star formation to more massive halos with increasing redshift, infers that environmental effects influence the vigorous star formation.

To improve our understanding of the formation and evolution of galaxies using CIB anisotropies, we need more information about the redshift of the sources contributing to the CIB. We also need a method that allows to go deeper than the confusion noise level. In this context, an invaluable tool is the stacking technique, which allows a statistical study of groups of sources that cannot be detected individually at a given wavelength. Its requires the knowledge of the positions of the sources being ``stacked'' as inferred from their individual detection at another wavelength. This knowledge is then used to stack the signal of the sources at the wavelength at which they cannot be detected individually. Since the signal of the sources increases with the number of sources N and the noise (if Gaussian) increases with $\sqrt{N}$ , the signal-to-noise ratio will increase with $\sqrt{N}$ . For an additional description of the basics of stacking techniques we refer to for example Dole et al. (2006) and Marsden et al. (2009).

Stacking was used to measure the contribution of 24 $\mu$ m galaxies to the background at 70 and 160 $\mu$ m using MIPS data (Dole et al. 2006). Contribution from galaxies down to 60 $\mu$ Jy at 24 $\mu$ m is at least 79% of the 24 $\mu$ m, and 80% of the 70 and 160 $\mu$ m backgrounds, respectively. At longer wavelengths studies used this technique to determine the contribution of populations selected in the near- and mid-infrared to the FIRB (far-infrared background) background: 3.6 $\mu$ m selected sources to the 850 $\mu$ m background (Wang et al. 2006) and 8 $\mu$ m and 24 $\mu$ m selected sources to the 850 $\mu$ m and 450 $\mu$ m backgrounds (Serjeant et al. 2008; Dye et al. 2006). Finally, Marsden et al. (2009) measured total submillimeter intensities associated with all 24 $\mu$ m sources that are consistent with 24 micron-selected galaxies generating the full intensity of the FIRB. Similar studies with Planck and Herschel will provide even more evidence about the nature of the FIRB sources.

Theoretically, a stacking technique also could be used to study the mean SED (spectral energy distribution) of the stacked sources (e.g., Zheng et al. 2007). The main potential limitations would be caused by the errors in the redshifts of the sources and an insufficiently large number of sources to stack per redshift bin. The observation of sufficiently large fields to which the technique can be applied is now assured by the to Spitzer legacy surveys FIDEL, COSMOS, and SWIRE and Planck and Herschel surveys. Advances in the measurement of the redshift have also been accomplished, although for very small fields for sources up to $z \sim 2$ (e.g. Caputi et al. 2006), and for the larger COSMOS fields up to $z\sim1.3$ with very high accuracy (Ilbert et al. 2009). Future surveys are planned to measure the redshifts in larger fields such as the dark energy survey (DES) or the GAMA spectroscopic survey (e.g. Baldry et al. 2008).

The difficulties in separating the contribution to the signal coming from different redshifts have handicapped the study of CIB anisotropies. However, once the mean SEDs of infrared galaxies per redshift bin are obtained we can use this information to analyze CIB anisotropies. The SEDs obtained with the stacking technique can be used to ``clean'' the low-redshift anisotropies (or at least a significant part of them) from the CIB maps. This can be performed by subtracting the undetected low-redshift (z<1-2) populations from the maps using their mean colors and thus build maps dominated by sources at higher redshifts. This also facilitates the study of the evolution of large-scale structures at high redshift by removing the noise coming from low redshifts.

In this paper, we use the simulations and catalogs presented in Fernandez-Conde et al. (2008) to study the limitations of stacking techniques in CIB anisotropy analysis. We stack 24 $\mu$ m sources detected with MIPS in Planck, Herschel, and SCUBA-2 simulated observations. The catalogs and maps were created for different levels of bias between the fluctuations of infrared galaxy emissivities and the dark matter density field. We use a bias b=1.5, which is very close to that measured by Lagache et al. (2007).

The paper is organized as follows. In Sect. 2, we explain the method used to study the capabilities of the stacking once the redshift of the sources is known. Section 3 details the elements that limit the accuracy of the stacking technique. In Sect. 4, we test the technique for studying the mean SEDs of galaxies. In Sect. 5, the feasibility of using information about the SEDs to clean the observations of low-redshift anisotropies is studied. The results are summarized in Sect. 6. Throughout this paper, the cosmological parameters are assumed to be $h=0.71,\Omega_{\Lambda}=0.73,\Omega_{\rm m}=0.27$ . For the dark-matter linear clustering, we set the normalization to be $\sigma_{8} = 0.8$ .

2 Description of the method

Dole et al. (2006) considered every MIPS 24 $\mu$ m source in selected fields with fluxes >60 $\mu$ Jy and then sorted the 24 $\mu$ m sources by decreasing flux at 24 $\mu$ m (hereafter S₂₄). The sources were placed in 20 bins of increasing flux density. These bins were of equal logarithmic width $\bigtriangleup S_{24}/S_{24}\sim0.15$ , except for the bin corresponding to the brightest flux, to take all the bright sources. They then corrected the average flux obtained by stacking each S₂₄ bin for incompleteness using the correction of Papovich et al. (2004). This allowed them to determine lower limits to the CIB at 70 $\mu$ m and 160 $\mu$ m, and to find the contribution from galaxies down to 60 $\mu$ Jy at 24 $\mu$ m to be at least 79% of the 24 $\mu$ m, and 80% of the 70 and 160 $\mu$ m backgrounds.

While these measurements of the total flux are useful for estimating the overall energy emitted by these populations (see also Marsden et al. 2009), it does little to improve our knowledge of individual sources. To use the average flux efficiently we have to decrease the dispersion in the individual fluxes (at the long wavelength) around the average flux of the population. We can do this by separating large populations of sources into smaller and more homogeneous SED populations.

One of the main sources of flux dispersion is the measurement of the mean flux using galaxies with very different redshifts. The lack of accurate redshifts (up to $z \sim 2$ ) across large fields has so far limited the use of detailed redshift information in stacking analysis. Because of this, the fluxes of sources with different SEDs are averaged together and the mean flux is a poor estimator of the fluxes of individual sources. However advances in the measurement of the redshifts are expected in the coming years with the new generation of spectroscopic and photometric redshift surveys such as GAMA (e.g. Baldry et al. 2008), (Big-)BOSS, DES. We developed a method that assumes that redshifts are known and investigated the limitations of stacking techniques caused by the uncertainties in the redshifts. We assessed the dispersion in the fluxes of individual sources with different redshift errors and the influence of this dispersion on the quality of the results using our simulations since this information will not be available in the real observations.

2.1 Stacking technique

We used our simulations to study the limitations of the stacking technique using 24 $\mu$ m MIPS sources in Planck, Herschel, and SCUBA-2 observations. The choice of this wavelength (24 $\mu$ m) is motivated by several reasons. Firstly, 24 $\mu$ m is a good tracer of infrared galaxies (unlike e.g., near-infrared detections). Secondly, 24 $\mu$ m-selected galaxies emit the bulk of the CIB up to at least 500 $\mu$ m (Dole et al. 2006; Marsden et al. 2009). Thirdly, 24 $\mu$ m Spitzer observations provide large and deep surveys, with redshift distribution of its sources extending up to redshift $z\sim2.5$ . The schematic description of our stacking process follows. The only requirements are knowledge of both the redshifts of the sources and their fluxes at 24 $\mu$ m.

The detected sources at 24 $\mu$ m will be characterized by two parameters S₂₄ and z. We first remove from the long wavelength map (hereafter $\lambda$ map) the sources detected individually, using the criteria described in Fernandez-Conde et al. (2008). These sources are no longer considered in the discussion, so whenever we refer to sources we refer to those detected at 24 $\mu$ m with S₂₄ greater than the detection threshold and not those detected individually in the $\lambda$ map. The sources are then distributed into redshift bins. The width of the redshift bins have to be optimized for each observation. These bins cover the redshift interval between z=0 and $z=z_{\max}$ , where $z_{\max}$ is chosen depending on the goals of the work. We stack independently the sources in each redshift slice. For the sources in a given redshift slice i ( $z_{\rm Slice}^{i}$ ), the process of detection is as follows:

1.: Firstly, we order the sources by decreasing S₂₄. We start by stacking in the $\lambda$ map the sub-images of the two sources with higher S₂₄ (that have not been detected individually). Then we measure the signal-to-noise ratio of the resulting image. A detection is achieved when the signal-to-noise ratio is higher than a certain detection threshold. This detection threshold is optimized for different observations. For the cases discussed in this paper, we use a detection threshold of three. If we do not achieve a detection we stack more sources (always selecting the next brighter sources at 24 $\mu$ m). This is done until we attain the required signal-to-noise ratio.
2.: Once a detection is achieved, we assign to all sources stacked together a flux equal to the total flux measured in the stacked image divided by the number of sources.
3.: After detection, we restart the process starting from the brightest sources that we have not yet stacked.
4.: Sometimes the last (and therefore faintest) group of sources in the redshift slice is not successfully stacked by this algorithm because an insufficient number of faint sources remains to be stacked in this last iteration. To correct for this, we simply carry out the algorithm starting this time from the faintest sources and stacking progressively brighter sources until we achieve a detection. Although in this procedure the last two mean flux bins are not independent, the consequences in terms of systematic errors are negligible (since the sources affected are few, faint, and the relative error in the stacking is small).

Once this process is complete we assign a mean ``stacked'' flux to every source of the redshift slice. The errors in the fluxes of the sources measured by stacking are computed to be the total noise measured in the map (following the method described in Fernandez-Conde et al. 2008) multiplied by $\sqrt{N}/N$ , where N is the number of stacked sources. We repeat this process for all the redshift slices until we have a measurement of the flux at $\lambda$ for all the sources in the catalog. In the 3 dimensional space of $S_{24}-z-S_{\lambda}$ , we then have a set of points $S_{24}^{St}-z^{St}-S_{\lambda}^{St}$ corresponding to different successful stackings. For each successful stacking, the coordinates in each of the three axes are the following:

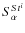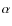$S_{\alpha}^{St^{i}}$ : The mean $S_{\alpha}$ of the sources of the ith stacked population, where $\alpha$ is the reference wavelength (here 24 $\mu$ m).
z^Stⁱ: The mean redshift of the sources of the ith stacked population.
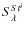$S_{\lambda}^{St^{i}}$ : The mean $S_{\lambda}$ found for the sources using the stacking technique for the ith stacked population.

Redshift slice optimization:

Our algorithm assumes that sources at similar z and of similar S₂₄ have similar characteristics at other wavelengths. Our best option to avoid substantial variance in $S_{\lambda}$ between the stacked sources is to try to avoid stacking together sources of very different S₂₄ or z. In this context, the size of the redshift bins were empirically optimized to ensure that (1) our detections are of high signal-to-noise ratio; (2) we achieve successful detections in each redshift slices without having to stack together sources of very different $S_{\alpha}$ (by more than a factor of three); and (3) the redshift slices are as thin as possible while complying with the first conditions. The redshift slices are chosen differently for each observation to comply with these criteria.

2.2 Color smoothing

The algorithm discussed above is quite simplified because it assumes that all sources detected in the same redshift bin have the same color $S_{\lambda}/S_{\alpha}$ . In contrast we would expect there to be a continuous variation of $S_{\lambda}/S_{\alpha}$ with both $S_{\alpha}$ and z. Following this assumption allows us to interpolate values between detections at different $S_{\alpha}$ for each redshift slice. A more complicated means of correction is to smooth our predictions by interpolating $S_{\lambda}$ through the grid formed by the set of points $S_{\alpha}^{St}-z^{St}-S_{\lambda}^{St}$ found with the stacking algorithm described above for the whole $S_{\alpha}-z$ plane. We do this with the IDL function TRIGRID, which given data points defined by the parameters $S_{\alpha}^{St}-z^{St}-S_{\lambda}^{St}$ and a triangulation of the planar set of points determined by S₂₄^Stand z^St returns a regular grid of interpolated $S_{\lambda}$ values. We tried both approaches and found that the differences between the results for the two different smoothings is very small so from now on we use only the `` $S_{\lambda}$ smoothing''. Figure 1a shows the fluxes at 350 $\mu$ m (with 1.5<z<1.6) before and after the two dimensional smoothing. It shows the real fluxes of the sources (known from the simulations), the recovered fluxes using the smoothing technique, and the recovered fluxes without smoothing. We can see that the smoothing greatly improves the accuracy of the fluxes. After this correction, the results are in very good agreement with the input fluxes.

$\begin{figure} \par\includegraphics[width=6.5cm,clip]{12924_Plot1a}\par\includegraphics[width=6.5cm,clip]{12924_Plot1b} \end{figure}$	Figure 1: Top: input fluxes of the sources in the redshift slice 1.5<z<1.6 (solid line) together with estimates of the fluxes of the sources using the smoothing technique (dashed line) and estimates of the fluxes of the sources without smoothing (diamond). Bottom: the same but zoomed for $0.3~{\rm mJy} < S_{24}<0.47$ mJy.
Open with DEXTER

3 Limitations of the method

We now test the limitations of the method related to the difficulties we expect to face when real data are analyzed (e.g., intrinsic dispersion in the colors of the sources, errors in the measurement of the fluxes and in redshifts, clustering). To illustrate the limitations, in this section we use the simulations at 350 $\mu$ m. We reached the same conclusions using other far-infrared and submillimeter wavelengths. The size of the redshift slices that divide the S₂₄-z space was chosen to be dz=0.1; wider redshift slices would stack together sources with very different fluxes; smaller redshift slices led to too low signal-to-noise ratios.

Two different Spitzer surveys are used, COSMOS and SWIRE. COSMOS is a deep observation with a completeness of $\sim$ 100% up to $S_{24}=80~\mu$ Jy (Sanders et al. 2007). It allows us to test the stacking of faint sources. COSMOS covers a smaller field than SWIRE (2 sq. deg. versus 50 sq. deg.) hence its stacking measurements are less accurate for bright sources. Thus we also use the much larger SWIRE survey (Lonsdale et al. 2004), which is less deep ( $S_{24}>270~\mu$ Jy) but covers $\sim$ 25 times more area. We analyze the stacking of 24 $\mu$ m sources for two study cases: observations in the far-infrared with Herschel at 350 $\mu$ m and (in the next section) observations in the submillimeter with Planck and SCUBA-2 at 850 $\mu$ m. The characteristics of the Herschel/SPIRE, Planck/HFI, and SCUBA-2 observations are the following:

Stacking in the COSMOS field:

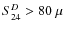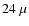Detection limit: $S_{24}^{D}>80~\mu$ Jy at $24~\mu$ m.
Size of the field: 2 sq. deg.
Linear bias: b=1.5.
Type of observation with Herschel: 350 $\mu$ m ``Deep'' (with 1 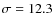$\sigma =12.3$ mJy).
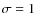Type of observation with SCUBA-2: 850 $\mu$ m (with 1 $\sigma = 1$ mJy).

Stacking in the SWIRE fields:

Detection limit: 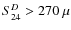$S_{24}^{D}>270~\mu$ Jy at 24 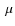$~\mu$ m.

Size of the field: 50 sq. deg.

Linear bias: b=1.5.

Type of observation with Herschel: 350 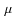$\:\mu$ m ``deep'' (with 1 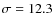$\sigma =12.3$ mJy).

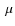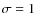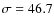Type of observation with SCUBA-2 and Planck: 850 $~\mu$ m (with 1 $\sigma = 1$ mJy and 1 $\sigma =46.7$ mJy - see Table 4 from Fernandez-Conde et al. 2008- respectively).

3.1 Cold and starburst populations

Figure 2 shows the histograms of the fluxes at 350 $\mu$ m for a stacking box with 0.5<z<0.6 and 0.5<S₂₄<1 mJy. The main source of error in the estimate of the fluxes for this case would not be the dispersion in either S₂₄or z but the presence of two different populations, which are indistinguishable using observations at shorter wavelengths. These two populations are the starburst and the normal (cold) populations described in Lagache et al. (2003). Figure 3 shows the number of starburst and normal sources as a function of z for sources with $80<S_{24}<270~\mu$ Jy, 0.27<S₂₄<1 mJy, and S₂₄>1 mJy. For the three afore mentioned cases, the cold sources are the dominant population for z<0.8, z<0.6, and z<0.5 respectively. There are no effective ways of separating these two populations, and this will cause poor estimates of the mean colors of each population. This is particularly important when the number of sources of each type is approximately equal. This is because we add together two populations of very different S₃₅₀(cold sources are in general brighter in the submillimeter than starburst sources at the same redshifts and with similar S₂₄). When one of the populations dominates, this problem becomes negligible.

3.2 Errors caused by intrinsic dispersion in colors

Because of the lack of constraints on SEDs at long wavelengths and their evolution with redshift, the Lagache et al. (2004) model does not take into account that galaxies of the same luminosity and redshift could have different values of $S_{\lambda}$ (apart from the distinction between normal and starburst sources). To assess the effect of this dispersion, we introduce a random Gaussian error into the flux estimated with the stacking for each of the stacked sources. The errors that we make using this procedure are equivalent to those that we would make if we were to use a model with an intrinsic Gaussian dispersion in the $S_{\lambda}$ of the sources. This type of error does not affect the results for the mean of the sources but the average difference between this mean and the fluxes of the individual sources. We test the effect on our results for different levels of dispersion (measured in terms of the standard deviation in the dispersion compared to the mean flux of the sources). In Fig. 4, we can see the histograms of the errors for a dispersion of $0\%$ , $10\%$ , $25\%$ for all sources with $S_{24}>270~\mu$ Jy. As expected, the figure illustrates how the histograms broaden with dispersion. For a standard deviation in the errors of the fluxes associated with the stacking $\sigma_{\rm St}$ and a standard deviation associated with the fluxes $\sigma_{\rm Disp}$ , the final standard deviation in our errors $\sigma_{\rm Tot}$ would be $\sigma_{\rm Tot}=\sqrt{\sigma_{\rm St}^2+\sigma_{\rm Disp}^2}$ . We do not analyze other statistical representations of this effect (i.e., non-Gaussian intrinsic dispersion) since we do not have any strong observational constraints.

$\begin{figure} \par\includegraphics[width=7.cm]{12924_Plot2a} \end{figure}$

Figure 2:

Histogram of the fluxes at 350 $\mu$ m for a stacking box with 0.5<z<0.6 and 0.5<S₂₄<1 mJy. The mean value of the sources is $S_{350}\sim 17$ mJy. The two different populations are the normal cold sources ( left population) and the starburst sources ( right population). It is clear that the main cause of error in our flux measurement comes from us stacking together two different populations. As expected, we checked that reducing the redshift slice does not reduce the dispersion.

Open with DEXTER

$\begin{figure} \par\includegraphics[width=4cm]{12924_Plot3a}\includegraphics[wid... ...space{2cm}\includegraphics[width=4cm]{12924_Plot3c}\hspace{2cm}}\end{figure}$	Figure 3: Histograms of the number of cold (thin line) and starburst (thick line) sources per 24 $\mu$ m flux bin (histograms are normalized to the higher number of sources per histogram). The problematic regions are those where both populations have similar number of galaxies. This is especially important for 0.6<z<0.7 and faint sources.
Open with DEXTER

3.3 Redshift uncertainty

The effect of redshift errors are difficult to evaluate. This is because they combine with the non-linear k-correction, making the variation in $S_{\lambda}$ with z complex. In Sect. 4, we study the effect of redshift errors for two different relative errors $\frac{\triangle z}{z}=3\%$ and $\frac{\triangle z}{z}=10\%$ .

$\begin{figure} \par\includegraphics[width=7cm]{12924_Plot4} \end{figure}$	Figure 4: Ratio of recovered fluxes from stacking ( $S_{350}^{\rm stack}$ ) to input fluxes in the simulation ( $S_{350}^{\rm real}$ ) for sources with S₂₄>270 $~\mu$ Jy, with no additional dispersion in the fluxes at 350 $\mu$ m (thick solid line), and with 10% (dotted-dashed line) and $25\%$ (dashed line) additional dispersion.
Open with DEXTER

3.4 Problematic areas of the S24-z space

Figure 5 shows the errors in the estimate of the mean fluxes in the S₂₄-zspace for a 350 $\mu$ m Herschel observation of the COSMOS field with redshift errors $\frac{\triangle z}{z}=3\%$ and $\frac{\triangle z}{z}=10\%$ . For the estimates of the fluxes, we can easily identify several problematic areas in the S₂₄-z space. These are: data points at very low redshifts (z<0.1), the brightest sources because of small number statistics and the faintest sources because of flux errors.

$\begin{figure} \par\mbox{\includegraphics[width=4.3cm]{12924_Plot5a}\includegrap... ...Plot5c}\hspace{0.2cm} \includegraphics[width=4.cm]{12924_Plot5d} }\end{figure}$

Figure 5:

Accuracy in the mean recovered fluxes at 350 $\mu$ m in a COSMOS-like observation when considering redshift errors of $\frac{\triangle z}{z}=3\%$ ( top) and $\frac{\triangle z}{z}=10\%$ ( bottom). The colors (shading) correspond to different values of the accuracy, while the vertical axis is S₂₄ and the horizontal axis is the redshift bin. Left: relative errors in the mean recovered fluxes ( $\nabla\bar{S}_{350}^{\rm Stack}=(\bar{S}_{350}^{\rm Stack}-\bar{S}_{350}^{\rm Real})/\bar{S}_{350}^{\rm Real}$ ) for all the S₂₄-z space. Right: the same but in absolute values $\left\vert\nabla\bar{S}_{350}^{\rm Stack}\right\vert=\left\vert(\bar{S}_{350}^{\rm Stack}-\bar{S}_{350}^{\rm Real})/\bar{S}_{350}^{\rm Real}\right\vert$ and decreasing the dynamic range of the plot (0-0.5) to illustrate the errors more clearly. The S₂₄-z space is divided linearly in z and logarithmically in S₂₄. Redshifts are given on the bottom-right figure, Log(S₂₄) (in mJy) on the left figures.

Open with DEXTER

4 Application of the method

We now verify the accuracy of the method with realistic simulations of observations including redshift errors and by using existing observations at 24 $\mu$ m with Spitzer.

4.1 Stacking Herschel data in the far-infrared: 350 $\mu$ m

We comment on the main issues and sources of error encountered when stacking 24 $\mu$ m sources in Herschel/Spire observations at 350 $\mu$ m and considering a detection threshold of 3 $\sigma$ . We note that the difficulties faced by the stacking technique at 250 and 500 $\mu$ m are similar. We use a division in the z axis with redshift slices of dz=0.1. We analyze the results for two redshift errors, an optimistic one of $\frac{\triangle z}{z}=3\%$ and a pessimistic one of $\frac{\triangle z}{z}=10\%$ . This illustrates the degradation in the quality of the results with redshift error.

Errors in individual recovered fluxes:

Figure 6 shows the errors in the estimate of the fluxes of the sources with the stacking technique for redshifts 0<z<1 and 1<z<2 for an observation of the COSMOS field at 350 $\mu$ m. Three different estimates are shown: one compiled using stacking without ``smoothing'' and two others created using two different smoothing techniques (in either z or both z and S₂₄, cf. Sect. 2.2). The differences between the estimates obtained using the two smoothing techniques are quite small for most sources. The figures show rather good agreement between the input values of the fluxes and those found by the stacking technique. The results improve for z>1 compared to those at z<1. This is because of the low signal-to-noise ratio at low zand the two-population problem. As expected, the results degrade with the redshift error. The results also improve when either of the two smoothing algorithms are used. Figure 7 shows the results for a SWIRE observation. The recovered fluxes are more accurate because the larger number of sources allows us to obtain higher signal-to-noise ratios for the stacking (but it is limited to $S_{24}>270~\mu$ Jy).

$\begin{figure} \par {\hspace*{4.5mm}\includegraphics[width=6.3cm]{12924_Plot6a}\... ...dth=6.3cm]{12924_Plot6c}\includegraphics[width=7.2cm]{12924_Plot6d} \end{figure}$

Figure 6:

Relative errors in recovered fluxes for individual sources at 350 $\mu$ m in a COSMOS-like observation for redshift errors $\frac{\triangle z}{z}=3\%$ ( top figures) and $\frac{\triangle z}{z}=10\%$ ( bottom figures). Left: for $S_{24}>80~\mu$ Jy and redshifts 0<z<1. Right: for $S_{24}>80~\mu$ Jy and 1<z<2. The zeros represents a perfect estimate. Three estimates are shown: direct values obtained with the stacking (dotted line); values obtained with the stacking and smoothed in z (thin solid line), and smoothed both in z and in S₂₄ (thick solid line).

Open with DEXTER

Limit for faint sources:

Stacking in the COSMOS field allows the detection of sources as faint as $S_{350}=2.1\pm0.7$ mJy at $z \sim 1$ , which is 6 times lower than the noise (1 $\sigma$ ). At $z \sim 2$ , we achieve detections for sources with $S_{350}=3\pm1$ mJy or 4 times lower than the noise. This is equivalent to a gain in the signal-to-noise ratio of a factor of 18 and 12, respectively, with respect to the 3 $\sigma$ detection. If the Spitzer data were complete down to lower fluxes, we should be able to successfully detect those sources too. The stacking method at 350 $\mu$ m is limited by the Spitzer detection limits.

$\begin{figure} \par\includegraphics[width=6.5cm]{12924_Plot7a}\includegraphics[w... ...4_Plot7c}\includegraphics[width=6.5cm]{12924_Plot7d} \vspace*{-4mm} \end{figure}$	Figure 7: Same as Fig. 6 but for an observation at 350 $\mu$ m if the SWIRE fields.
Open with DEXTER

Mean errors:

The final results for the fluxes and colors of the sources obtained using the stacking technique are compared with the real (input) values in Figs. 8 and 9. They are in very good agreement with the input fluxes (called real fluxes in the figures) but to obtain a clearer idea of the errors we show in Fig. 10 two plots of the mean flux relative error per box of S₂₄-z. The left figure shows the relative differences between our mean estimated flux (using the stacking technique) and the flux of the sources introduced in the model. Yellowish colors represent overestimates of the source fluxes compared to their input fluxes. Darker colors represent underestimates. The right figure shows the same relative error but this time in absolute value. We can see that the larger errors, which can be as high as 50%, are made for sources at z<0.1. This is because the small number of sources at these redshifts prevents the stacking from achieving sufficiently high signal-to-noise ratios. For the bulk of sources however, the errors in the mean flux are smaller than 10%. The errors associated with the problem of 2 populations cannot be illustrated by these figures because this problem does not affect the accuracy of the mean value found for a set of sources but the dispersion in the fluxes of individual sources around this mean value.

4.2 Stacking Planck and SCUBA-2 data at 850 $\mu$ m

When applying the same technique to Planck observations at 850 $\mu$ m, we encounter a fundamental limitation of the stacking technique. In the stacked image, we can discern two contributions to the peak, one associated with the stacked sources, which has the shape of the PSF, and another broader peak around it which is associated with the sources correlated with the stacked sources. The method works easily when the PSF width is much smaller than the width of the correlation peak. However, this condition is not fulfilled for Planck observations where the width of the correlation signal around sources is not very different from the width of the PSF. Furthermore, when stacking faint sources, $S_{24}\sim100~\mu$ Jy, the signal associated with the correlations is much stronger than that of the sources: it becomes impossible to distinguish between the signal from the sources being stacked and the signal from the clustering. Figure 11 shows a cut of a stacked image for very faint sources ( $S_{24}\sim100~\mu$ Jy). The figure shows the total signal, the signal coming from both the clustering and the sources. For these faint sources, we can see that the signal from the clustering of the sources is more important than that of the stacked sources and their FWHMs are very similar. Several attempts were made to correct this problem. By far the most effective solution is to use additional observations with a narrower PSF at similar wavelengths to estimate the fraction of the flux that is associated with the clustering. This method is described hereafter. Another possible solution that does not rely on complementary observations is presented in Appendix A.

$\begin{figure} \par\includegraphics[width=4.cm, height=5.35cm]{12924_Plot8a}\includegraphics[width=4.cm, height=5.35cm]{12924_Plot8b} \end{figure}$	Figure 8: Left: real fluxes of the sources at 350 $\mu$ m (in mJy) in the space S₂₄-z. Right: fluxes found by the smoothed stacking technique. The colors correspond to different values of the flux, while the vertical axis is S₂₄ and the horizontal axis is the redshift bin.The S₂₄-z space is divided linearly in z and logarithmically in S₂₄.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=4.cm, height=5.35cm]{12924_Plot9a}\includegraphics[width=4.cm,clip]{12924_Plot9b} \end{figure}$	Figure 9: Left: real S₃₅₀/S₂₄ flux ratio of the sources in the space S₂₄-z. Right: S₃₅₀/S₂₄ flux ratio found by the smoothed stacking technique ( right). The colors correspond to different values of the ratio, while the vertical axis is S₂₄ and the horizontal axis is the redshift bin. The S₂₄-z space is divided linearly in z and logarithmically in S₂₄.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=4.cm]{12924_Plot10a}\includegraphics[width=4.cm]{12924_Plot10b} \end{figure}$	Figure 10: Same as Fig. 5 but with no redshift errors.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=7cm]{12924_Plot11} \end{figure}$	Figure 11: Lateral cut of a stacking image (Planck/HFI at 850 $\mu$ m) for very faint sources ( $S_{24}\sim100~\mu$ Jy). The total signal (normalized to 1 at the peak), the signal from both the clustering and the sources are the solid, dotted, and dashed lines, respectively. One pixel equals 25 arcsec.
Open with DEXTER

The problem caused by the clustering contribution to the flux measured with Planck/HFI makes it difficult to use this instrument alone to estimate the fluxes accurately . It is therefore necessary to use observations with other instruments with smaller FWHM. In the far-infrared, we could use Herschel (for the same channel as Planck at 350 $\mu$ m). For the submillimeter observations, we will have to use ground-based submillimeter instruments (e.g., future camera SCUBA-2 at 850 $\mu$ m or LABOCA at 870 $\mu$ m).

4.2.1 SCUBA-2 observation of the COSMOS field at 850 $\sf\mu$ m

We analyze here the stacking of sources in the COSMOS field observed with SCUBA-2. SCUBA-2 will have a very good sensitivity; we use an estimate of the noise for these observations of $\sigma = 1$ mJy, close to that specified in the SCUBA-2 webpage . Because the signal of the sources at 850 $\mu$ m is much fainter relative to the noise than with Herschel at 350 $\mu$ m, we have to increase the size of the redshift bins to achieve detections. We take the following boundaries for the redshift slices 0, 0.1,0.4,0.8,1.,1.2,1.5,1.8, and 2.2. We use the same detection threshold as that used for Herschel at 350 $\mu$ m ( $D_{\rm thres}=3$ ).

Figure 12 shows the errors in the estimate of individual fluxes of 850 $\mu$ m sources for $S_{24}>80~\mu$ Jy and redshifts 1<z<2with redshift errors of $\frac{\triangle z}{z} =0$ % (top), 3% (middle), and 10% (bottom). The results are poorer than those at 350 $\mu$ m (Fig. 6). This is because the signal of the individual sources is weaker relative to the noise at 850 $\mu$ m than at 350 $\mu$ m. The results are clearly dependent on the redshift errors.

$\begin{figure} \par\includegraphics[width=8.cm]{12924_Plot12a}\\ [4mm] \includeg... ...{12924_Plot12b}\\ [4mm] \includegraphics[width=8.cm]{12924_Plot12c} \end{figure}$

Figure 12:

Relative errors in recovered fluxes for individual sources at 850 $\mu$ m in a COSMOS-like observation for redshift errors $\frac{\triangle z}{z}$ equal to 0 ( top), 3% ( middle), and 10% ( bottom), for $S_{24}>80~\mu$ Jy and 1<z<2. Three estimates are shown: direct values obtained with the stacking (dotted line); values obtained with the stacking and smoothed in z (thin solid line); and values smoothed both in z and in S₂₄ (thick solid line).

Open with DEXTER

The sources detected with the stacking technique at $z \sim 1$ are as faint as $S_{850}=0.10\pm0.03$ mJy, which is 10 times smaller than the noise. At $z \sim 2$ we can achieve detections of sources with $S_{850}=0.17\pm0.05$ mJy, which is 6 times smaller than the noise. This is equivalent to a gain in the signal-to-noise ratio of a factor of 30 and 18, respectively, with respect to the 3 $\sigma$ detection. As for 350 $\mu$ m the stacking method is limited by the Spitzer detection limit.

Figure 13 shows the errors in the estimated mean fluxes at 850 $\mu$ m in the S₂₄-z space for a COSMOS observation stacked with SCUBA-2 at 850 $\mu$ m with redshift error $\frac{\triangle z}{z}=3\%$ before and after the ``smoothing'' correction. It shows the improvement of the accuracy with the ``smoothing'' correction. Figure 13 also shows the errors in the estimate of the mean fluxes for $\frac{\triangle z}{z}=10\%$ (smoothing applied). As at 350 $\mu$ m, we lose accuracy in our predictions when the redshift errors are higher. When comparing with observations at 350 $\mu$ m, we see that our estimates are not as accurate, the mean errors at 850 $\mu$ m being around 15% compared to 5-10% at 350 $\mu$ m. The problems we discussed for 350 $\mu$ m observations are yet greater at 850 $\mu$ m. The problem at low redshift is far more important here because the sources at $z\leq0.9$ are in general fainter than at higher z.

4.2.2 Planck 850 $\sf\mu$ m

The Planck observation is hindered by the clustering problem caused by its large PSF (5'), rendering its flux estimates completely useless unless a correction is applied. The problem is clearly illustrated in Fig. 14, where we show the histograms of the ratio of the flux estimates to the input fluxes for a Planck observation of the SWIRE fields for two selected redshift bins. We developed a simple method to correct this problem.

$\begin{figure} \par\includegraphics[width=0.4\columnwidth,height=0.5\columnwidth... ...aphics[width=0.4\columnwidth,height=0.5\columnwidth]{12924_Plot14d} \end{figure}$

Figure 13:

Accuracy of the mean recovered fluxes at 850 $\mu$ m in a COSMOS-like observation when considering a redshift error of $\frac{\triangle z}{z}=3\%$ and no smoothing ( top), a redshift error of $\frac{\triangle z}{z}=3\%$ and the smoothing ( middle) and a redshift error of $\frac{\triangle z}{z}=10\%$ and the smoothing ( bottom figures). The colors (shading) correspond to different values of the accuracy, while the vertical axis is S₂₄ and the horizontal axis is the redshift bin. The S₂₄-z space is divided linearly in z and logarithmically in S₂₄. Redshifts are given on the right figures, $\log(S_{24})$ (in mJy) on the left figures. Left figures show the relative errors on the mean recovered fluxes ( $\nabla\bar{S}_{850}^{\rm Stack}=(\bar{S}_{850}^{\rm Stack}-\bar{S}_{850}^{\rm Real})/\bar{S}_{850}^{\rm Real}$ ) for all the S₂₄-z space. Right figures show the absolute values $\left\vert\nabla\bar{S}_{850}^{\rm Stack}\right\vert=\left\vert(\bar{S}_{850}^{\rm Stack}-\bar{S}_{850}^{\rm Real})/\bar{S}_{850}^{\rm Real}\right\vert$ .

Open with DEXTER

$\begin{figure} \par\includegraphics[width=4.5cm]{12924_Plot15a}\includegraphics[width=4.5cm]{12924_Plot15b} \end{figure}$

Figure 14:

Ratio of recovered to input fluxes of individual sources at 850 $\mu$ m for an observation of the SWIRE fields, redshift errors $\frac{\triangle z}{z}$ =10%, and two redshift bins, 0<z<1 ( left) and 1<z<2 ( right). Three estimates are shown: direct values obtained with the stacking (dotted line); values obtained with the stacking and smoothed in z (thin solid line); and values smoothed both in z and in S₂₄ (thick solid line). The value 1 represents a perfect measurement. The recovered fluxes have not been corrected from the clustering and are thus highly overestimated.

Open with DEXTER

When stacking sources in a given redshift bin with Planck, we measure the added contribution of the sources and the clustering. To correct the stacked fluxes with Planck for the effects of clustering, we use source fluxes at 850 $\mu$ m obtained by stacking SCUBA-2 data. If we stack sources detected by Planck for which we have an estimate of their fluxes inferred from SCUBA-2 data, we can obtain the contribution of the clustering in the Planck stacking by calculating the difference between the total measured flux and that measured in the SCUBA-2 stacking. For each redshift bin, we therefore stack Planck data for all the sources in a SWIRE observation with fluxes 0.27<S₂₄<1 mJy. We do not use the brighter sources because their flux estimates are poorer. Once we have estimated the effect of the clustering for different redshift bins, we can correct the fluxes found with Planck. Figure 15 shows the effect of applying this correction. We can see that the results are greatly improved. After the correction, the results for the bright sources S₂₄>1 mJy are indeed superior for Planck than with SCUBA-2, because of its larger sky coverage. We note that the correction is assumed to be the same inside a redshift bin for all S₂₄.

$\begin{figure} \par\mbox{\includegraphics[width=4cm]{12924_Plot16a} \includegraphics[width=4cm]{12924_Plot16b} }\end{figure}$

Figure 15:

Relative error in the mean recovered fluxes at 850 $\mu$ m ( $\nabla\bar{S}_{850}^{\rm Stack}=(\bar{S}_{850}^{\rm Stack}-\bar{S}_{850}^{\rm Real})/\bar{S}_{850}^{\rm Real}$ ) for a Planck observations of the SWIRE fields with $\frac{\triangle z}{z}=10\%$ before ( left) and after ( right) correcting from the clustering. The colors (shading) correspond to different values of the relative error, while the vertical axis is S₂₄ and the horizontal axis is the redshift bin.

Open with DEXTER

4.3 Combination of different observations

4.3.1 Observations in the far-infrared (350 $\mu$ m)

We analyzed the Herschel observation of the COSMOS and SWIRE fields. We have seen that the SWIRE stacking is more accurate when estimating the flux of the brightest sources. Figure 16 shows the flux estimates at 350 $\mu$ m when we combine the strengths of both observations. For sources with S₂₄<0.27 mJy, we have only COSMOS estimates, which are therefore compelled to use. Since we know that the SWIRE observations have higher signal-to-noise ratios than COSMOS observations at high fluxes, we chose to use these estimates for sources with S₂₄>0.34 mJy. For the fainter sources stacked in SWIRE 0.27<S₂₄<0.34 mJy data, we obtained errors larger than those of COSMOS since we assume that the colors of the faintest sources are as described in Sect. 3.4. For these sources, the COSMOS estimates have therefore to be used.

$\begin{figure} \par\includegraphics[width=4.5cm]{12924_Plot17a}\includegraphics[... ...h=4.5cm]{12924_Plot17c}\includegraphics[width=4.5cm]{12924_Plot17d} \end{figure}$

Figure 16:

Combined observations at 350 $\mu$ m with redshift errors $\frac{\triangle z}{z}=3\%$ ( top figures) and $\frac{\triangle z}{z}=10\%$ ( bottom figures). Left: relative errors of the estimate of the mean fluxes ( $\nabla\bar{S}_{350}^{\rm Stack}=(\bar{S}_{350}^{\rm Stack}-\bar{S}_{350}^{\rm Real})/\bar{S}_{350}^{\rm Real}$ ) for the S₂₄-z space. Right: absolute values $\left\vert\nabla\bar{S}_{350}^{\rm Stack}\right\vert=\left\vert(\bar{S}_{350}^{\rm Stack}-\bar{S}_{350}^{\rm Real})/\bar{S}_{350}^{\rm Real}\right\vert$ . The colors (shading) correspond to different values of the error, while the vertical axis is S₂₄ and the horizontal axis is the redshift bin.

Open with DEXTER

4.3.2 Observations in the submillimeter (850 $\mu$ m)

As performed at 350 $\mu$ m, we analyzed the COSMOS/SCUBA-2 and SWIRE/Planck observations separately and we now combine their respective strengths. Figure 17 shows the error estimates for these combined observations. For faint sources with S₂₄<0.27 mJy, we use COSMOS/SCUBA-2. For the faintest sources stacked in SWIRE ( 0.27<S₂₄<1 mJy), it is more accurate to use COSMOS/SCUBA-2 than Planck measurements due to the errors induced by the uncertainty in the clustering contribution. For brighter sources (S₂₄>1 mJy), the corrected Planck estimations are more accurate than those of SCUBA-2 and we prefer to use them. Figure 17 shows the relative errors in the mean recovered fluxes with respect to the input fluxes at 850 $\mu$ m, when combining both observations. They are typically of the order of 15% for $\frac{\triangle z}{z}=3\%$ .

$\begin{figure} \par\includegraphics[width=4.3cm, height=6.cm]{12924_Plot18a}\inc... ...24_Plot18c}\includegraphics[width=4.3cm, height=6cm]{12924_Plot18d} \end{figure}$	Figure 17: Same as Fig. 16 for combined observations at 850 $\mu$ m.
Open with DEXTER

4.3.3 Observations at other wavelengths

For observations in the far-infrared and because of the issues discussed in Sect. 4.2 and lower typical noise level, the stacking technique produces more accurate estimates of the fluxes with Herschel than with Planck, although the latter has the advantage of covering the entire sky. We did not present separately the Herschel observations at 250 $\mu$ m or 500 $\mu$ m since the analysis of the results at these two wavelengths are similar to those for 350 $\mu$ m observations. At 550 $\mu$ m, a wavelength where there is a Planck but not a Herschel channel, it is more advisable to use the values found by Herschel at 500 $\mu$ m after applying a small correction than to use the Planck values. At 850 $\mu$ m, we combined the Planck observations with those of SCUBA-2 although other submillimeter data (e.g., LABOCA) could have been used. At 1380 $\mu$ m (Planck/HFI 217 GHz), we tested the same approach using MAMBO/IRAM simulated observations to complement the Planck observations, obtaining similar results as for 850 $\mu$ m.

The complete mean SEDs for the different populations can provide information about the mean galaxy properties, such as star-formation rate and dust content. Figure 18 shows our measurements at 70, 160, 250, 350, 500, and 850 $\mu$ m of the flux of the 800 faintest sources detected in our simulated COSMOS survey at 1<z<1.1 and at 2<z<2.1 relative to both their true fluxes and the SED of a typical source at these fluxes and redshifts. The largest errors are found at 70 $\mu$ m, 160 $\mu$ m, and 850 $\mu$ m. For both redshifts, the errors in our estimates are smaller than 10%. The same method could be applied to fainter populations, if they were detected individually with Spitzer. As mentioned before, the limitation of the method is the detection limit of the Spitzer observations at 24 $\mu$ m.

$\begin{figure} \par\includegraphics[width=4.5cm]{12924_Plot19a}\includegraphics[width=4.5cm]{12924_Plot19b} \end{figure}$

Figure 18:

True mean fluxes (diamonds) compared to the mean fluxes found by stacking (triangles) with the estimated errors at 70, 160, 250, 350, 500, and 850 $\mu$ m of the 800 faintest sources above $80~\mu$ Jy (mean fluxes $S_{24}=110\:\mu$ Jy and $S_{24}=135~\mu$ Jy at redshifts 1<z<1.1 and 2<z<2.1, respectively) in our simulated COSMOS observation. The points at 70 and 160 $\mu$ m are from a Spitzer simulation with instrumental noise taken from Sanders et al. (2007). The solid lines show the Starburst SEDs from the library of Lagache et al. (2004) that has the same mean S₂₄ at those two redshifts.

Open with DEXTER

5 Cleaning maps of undetected source populations

5.1 Contribution to the CIB

An obvious application of the results provided by the stacking technique is the measurement of the total energy emitted by different galaxy populations at wavelengths where they can not be seen directly. This would give us the CIB fraction at those wavelengths coming from the chosen population. We compare the total contribution from sources brighter than $S_{24}=80~\mu$ Jy at redshifts z < 2 in our simulations with that determined using the stacking technique, and obtain very similar results. At 350 $\mu$ m, we find (using our stacking estimates) that these sources account for $35.4\%$ and $35.8\%$ of the CIB when the redshift errors are $3\%$ and $10\%$ , respectively. This is a $0.4\%$ and $0.8\%$ overestimate of their contribution ( $35\%$ ) to the CIB of the underlying model. At 850 $\mu$ m, we estimate that these sources account for $19\%$ and $20\%$ of the CIB when the redshift errors are $3\%$ and $10\%$ , respectively, which is a slight $2{-}3\%$ overestimate of their contribution ( $17\%$ ) to the CIB in the model.

5.2 Removing anisotropies due to low-z infrared galaxies

A more sophisticated use of the present results is the statistical removal of the contribution of these populations at long wavelengths. If we accurately extract a sufficiently large fraction of the background anisotropies at low z, this will allow us to study the CIB anisotropies at high z. For the first time, we could then separate the contributions to the CIB anisotropies at different redshifts. This would allow us to study large-scale structures at high redshift. To remove from the observed maps the contribution of sources up to a certain redshift, we create a map of sources for whose fluxes were estimated using the stacking technique. We subtract this map from the observed maps, which is equivalent to individually subtracting all the stacked sources. We estimate the source fluxes from the colors obtained by combining the different observations, as described in Sect. 4.3. However, we know that the flux estimates have significant errors for very bright sources and sources at redshifts z<0.1at 350 $\mu$ m and z<0.8 at 850 $\mu$ m. These errors will affect the accuracy of our removal of the low-z background anisotropies. We also studied the effect of a Gaussian dispersion in the fluxes of the sources (as described in Sect. 2.2) on the power spectra. For dispersions as high as 25%, the results are equivalent with and without dispersion. This is because of the large number of sources contributing to each bin.

$\begin{figure} \par\includegraphics[width=4.4cm]{12924_Plot20a}\includegraphics[... ...h=4.4cm]{12924_Plot20c}\includegraphics[width=4.5cm]{12924_Plot20d} \end{figure}$

Figure 19:

Power spectra of two maps in which we placed the sources with either their input fluxes from the simulations (dotted line) or their stacked fluxes (dashed line). The results are shown for a SWIRE observation ( left figures) and COSMOS observation ( right figures) at 350 $\mu$ m for stacked sources up to z=2 with redshift errors $\frac{\triangle z}{z}=3\%$ ( top) and $\frac{\triangle z}{z}=10\%$ ( bottom).

Open with DEXTER

$\begin{figure} \par\includegraphics[width=4.5cm]{12924_Plot21a}\includegraphics[... ...h=4.5cm]{12924_Plot21c}\includegraphics[width=4.5cm]{12924_Plot21d} \end{figure}$	Figure 20: Same as Fig. 19 at 850 $\mu$ m.
Open with DEXTER

To assess the importance of these errors, we compare the map compiled using the flux estimates by stacking with a second map where these sources have their true input fluxes. Comparing the power spectrum of both maps gives the accuracy of the anisotropy estimates for the first map. Figure 19 shows the two power spectra at 350 $\mu$ m for sources at z<2 for both a SWIRE observation (with $S_{24}>270~\mu$ Jy) and a COSMOS observation (with $S_{24}>80~\mu$ Jy) and for two redshift errors $\frac{\triangle z}{z}=3\%$ and $\frac{\triangle z}{z}=10\%$ . At $350~\mu$ m, the accuracy of our estimation is superior to $0.5\%$ for both the correlated and Poissonian part of the spectrum in both the SWIRE and COSMOS observations in the case of a small redshift error ( $\frac{\triangle z}{z}=3\%$ ). When the redshift error is greater, our estimate of the Poissonian noise increases moderately with mean errors of 3%. Figure 20 shows the same result at 850 $\mu$ m. Because of the small redshift error in the COSMOS survey, we overestimate the correlated part by $40\%$ and the Poissonian part by $24\%$ . For larger redshift errors, our overestimates increase to $60\%$ and $50\%$ of the correlated and Poissonian part, respectively. In this case, this shows the importance of accurate redshifts. The differences in the overestimates of the Poissonian and correlated part are caused by the populations contributing to these two regimes not being exactly the same, bright sources contributing more in relative terms to the Poissonian fluctuations than to the correlated part.

5.3 High-redshift power spectra of CIB anisotropies

5.3.1 Observations at 350 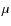$\sf\mu$ m

After analyzing the accuracy of the map that we intend to subtract, we investigate our capabilities to subtract a significant part of the background anisotropies for different redshift limits. Figure 21 compares the power spectra of the total background anisotropies to those at z>1, z>1.5, and z>2 in a SWIRE observation. It also shows the power spectra of the map of CIB anisotropies from which we have subtracted the z<1, z<1.5, and z<2 contribution, which were estimated by stacking. Since our subtraction is rather accurate, the very small difference between these last two sets of power spectra is caused by us not subtracting all the sources but only those above $S_{24}>270~\mu$ Jy. We subtract approximately half the correlated part (k < 8 deg^-1) and two thirds of the Poissonian part (k > 8 deg^-1) independently of redshift errors.

Figure 22 shows the same results for a COSMOS observation. We have the positions of sources with $S_{24}>80~\mu$ Jy which allows us to subtract a larger fraction of the background than in the SWIRE survey. Unfortunately because of the smaller size of the field, we do not have access to the largest scales that we were able to analyze with SWIRE. We subtract approximately $\sim$ 99% of the correlated part and $\sim$ 90% of the Poissonian for the small redshift error. For the large redshift error, these fractions become $\sim$ 85% and $\sim$ 90% of the correlated and Poissonian parts, respectively. For each of the considered redshift limits, the power spectrum of the residual left after our subtraction of the $z<z_{\rm lim}$ stacked source is in close agreement with the power spectrum at high redshifts ( $z>z_{\rm lim}$ ). This remains true when we consider a large redshift error.

$\begin{figure} \par\includegraphics[width=6cm]{12924_Plot22a}\includegraphics[wi... ...idth=6cm]{12924_Plot22d0}\includegraphics[width=6cm]{12924_Plot22d} \end{figure}$

Figure 21:

Power spectra of the map for a SWIRE observation at 350 $\mu$ m. The solid line is the total power spectrum of the background, the dashed line is the power spectrum of the background for $z>z_{\rm lim}$ (where $z_{\rm lim}$ is a redshift limit), and the dotted line is the power spectrum of the total background from which we have subtracted the stacked sources at $z<z_{\rm lim}$ . The redshift limit $z_{\rm lim}$ is $z_{\rm lim}=1$ ( left figures), $z_{\rm lim}=1.5$ ( middle figures), and $z_{\rm lim}=2$ ( right figures). The redshift errors are $\frac{\triangle z}{z}=3\%$ ( top) and $\frac{\triangle z}{z}=10\%$ ( bottom).

Open with DEXTER

$\begin{figure} \par\includegraphics[width=6cm]{12924_Plot23a0}\includegraphics[w... ...width=6cm]{12924_Plot23c}\includegraphics[width=6cm]{12924_Plot23d} \end{figure}$	Figure 22: Same as Fig. 21 but for the COSMOS field.
Open with DEXTER

5.3.2 Observations at 850 $\mu$ m

Figures 23 and 24 show the similar results but at 850 $\mu$ m. For these observations, we needed to use COSMOS data because for SWIRE data we do not subtract a significant fraction of the CIB anisotropies. In terms of power spectra, we are able with SWIRE to subtract only $\sim$ 30% of the correlated part and $\sim$ 50% of the Poissonian part. In the case of COSMOS, we subtract approximately $\sim$ 75% of both the correlated and Poissonian part of the power spectra. Figure 24 (top-right) shows that, for errors of $\frac{\triangle z}{z}=3\%$ , our method is very efficient in subtracting z<2 anisotropies.

6 Summary

We have described a stacking algorithm and illustrated its capabilities using Spitzer observations. We have studied the accuracy of the stacking method as a means of determining the average fluxes of classes of undetectable sources at long wavelengths. The results show that the technique will be capable of measuring accurate fluxes at both far-infrared and submillimeter wavelengths for sources as faint as 80 $\mu$ Jy at 24 $\mu$ m using average colors.

With the successful commissioning of the Planck and Herschel missions, large maps (even all-sky for Planck) from 250 $\mu$ m to the millimeter wavelength range are now available. SCUBA-2 and other submillimeter cameras (e.g., LABOCA) will provide data of higher angular resolution in the submillimeter. We have applied the stacking method to the Herschel, Planck, and SCUBA-2 simulated data and measured the full average SED of populations of sources detected at 24 $\mu$ m. The strong variation in the $S_{24}/S_{\lambda}$ color with redshift requires us to define the populations to which the method will be applied not only in ranges of S₂₄but also in terms of (photometric) redshift. We show we are able to measure the mean flux of populations 4 to 6 times fainter than the total noise at 350 $\mu$ m at redshifts z=1 and z=2, respectively, and 6 to 10 times fainter than the total noise at 850 $\mu$ m, at the same redshifts. We have been able to reproduce the SED at wavelengths 70, 160, 250, 350, 500, and 850 $\mu$ m of a population of sources with mean flux S₂₄=0.11 mJy and S₂₄=0.135 mJy at redshifts z=1 and z=2, respectively.

In the deep Spitzer fields, the detected 24 $\mu$ m sources constitute a large fraction of the anisotropies. We have shown that the method presented in this paper enables an excellent (350-850 COSMOS) to good (350-850 SWIRE) removal of both the Poissonian and correlated low-z anisotropies. The relative contribution of sources to the background anisotropies up to z=2 decreases with wavelength in the model. This property is expected to remain valid independently of the details of the model from 250 $\mu$ m to the millimeter range. Although the accuracy of the subtracted map is lower at 850 $\mu$ m, the cleaning of the power spectrum is quite effective (because the contribution of the low-redshift sources is small at these submillimeter wavelengths).

$\begin{figure} \par\includegraphics[width=4.5cm]{12924_Plot24a}\includegraphics[... ...h=4.5cm]{12924_Plot24c}\includegraphics[width=4.5cm]{12924_Plot24d} \end{figure}$

Figure 23:

Power spectra of the 850 $\mu$ m map of the SWIRE fields. The solid line is the total CIB power spectrum, the dashed line is the CIB power spectrum for $z>z_{\rm lim}$ (where $z_{\rm lim}$ is a redshift limit), and the dotted line is the power spectrum of the total CIB from which we have subtracted the stacked sources at $z<z_{\rm lim}$ . The redshift limit $z_{\rm lim}$ is $z_{\rm lim}=1.5$ ( left) and $z_{\rm lim}=2$ ( right). The redshift errors are $\frac{\triangle z}{z}=3\%$ ( top) and $\frac{\triangle z}{z}=10\%$ ( bottom).

Open with DEXTER

$\begin{figure} \par\includegraphics[width=4.5cm]{12924_Plot25a}\includegraphics[... ...h=4.5cm]{12924_Plot25c}\includegraphics[width=4.5cm]{12924_Plot25d} \end{figure}$	Figure 24: Same as Fig. 23 but for the COSMOS field.
Open with DEXTER

The same technique could also be used to remove from the observations all the contributions from sources for which we have estimated a flux, to decrease the confusion noise caused by infrared galaxies. This would be interesting for the detection of other types of sources (for example, SZ sources in Planck data).

The method allows us to build $z \gtrsim 1{-}2$ CIB maps from the submillimeter to the millimeter. We have found that the method can also be successfully applied at the other Herschel and Planck wavelengths than those tested in this paper. The longer wavelengths at which this can be achieve will depend on the success of the component separation and not on the removal of the z<2 sources. We can then hope to have a set of large CIB maps dominated by high-redshift galaxies. This set of CIB maps at different wavelengths dominated by z>2 sources will be a powerful tool for studying the evolution of the large-scale structure of infrared galaxies. The effect of the K-correction ensures that each of these maps (at different wavelengths) are dominated by particular high-redshift ranges. Methods of independent component separation based on the correlation matrix between these maps (e.g., Delabrouille et al. 2003) should allow us to extract maps and power spectra for a number of redshift ranges equal to the number of maps. This last step will fulfill the main objective of this work. It will allow the study of the evolution of the IR galaxy clustering at high redshifts by means of the power spectrum analysis of CIB anisotropies. These maps may also be used to help us understand the contribution of high-z IR galaxies both to the CIB and the star-formation history.

Appendix A: Alternative correction for the clustering contribution to the stacked fluxes in Planck maps

We developed an alternative method for correcting the photometry of a group of stacked sources for the effects of the clustering. If we consider that the signal measured for a population of stacked sources at a given wavelength is the combination of the signal originating from the sources and from the clustering, we can write the measured flux as:

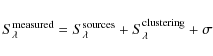
$\begin{displaymath}S_{\lambda}^{\rm measured}=S_{\lambda}^{\rm sources}+S_{\lambda}^{\rm clustering}+{\sigma} \end{displaymath}$

(A.1)

where $S_{\lambda}^{\rm measured}$ is the total measured signal, $S_{\lambda}^{\rm sources}$ is the part of the signal coming from the sources, and $S_{\lambda}^{\rm clustering}$ is the part of the signal coming from the sources correlated with the detected sources that we are stacking, and $\sigma$ is the noise.

If two populations of sources have very similar fluxes at the wavelength of detection (24 $\mu$ m) and are situated at similar redshifts, we can assume that their sources have very similar physical characteristics and hence their colors $S_{\lambda}/S_{24}$ are very similar. In this case, we can write:

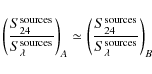
$\begin{displaymath}\left(\frac{S_{24}^{\rm sources}}{S_{\lambda}^{\rm sources}}\... ...ac{S_{24}^{\rm sources}}{S_{\lambda}^{\rm sources}}\right)_{B} \end{displaymath}$

(A.2)

where the A and B subscripts represent the first and second population of sources. We can measure the total flux (from the sources and the clustering) for the stacking of both source populations and express them as:

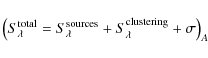
$\begin{displaymath}\left(S_{\lambda}^{\rm total}=S_{\lambda}^{\rm sources}+S_{\lambda}^{\rm clustering}+{\sigma}\right)_{A}\\ \end{displaymath}$

(A.3)

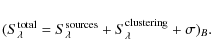
$\begin{displaymath}(S_{\lambda}^{\rm total}=S_{\lambda}^{\rm sources}+S_{\lambda}^{\rm clustering}+{\sigma})_{B}. \end{displaymath}$

(A.4)

If we were to assume that the contribution of the correlated sources to the flux is the same for both populations $(S_{\lambda}^{\rm clustering})_{A} = (S_{\lambda}^{\rm clustering})_{B}$ , as expected for sources with similar spatial distributions, and that the noise is negligible, we would have a system of three equations with three unknowns that we can solve.

The main problem for the applicability of this method is that we need to stack many sources to ensure that the noise becomes negligible compared to the signal. Because of this, it is preferable to combine an observation whose photometry is affected by the clustering with another observation for which this problem does not exist, as illustrated by our present analysis. If the photometry of this second observation is affected by smaller errors (as it is the case of SCUBA-2 data relative to Planck data at 850 $\mu$ m), the results will be improved by combining the two observations. However, the method discussed in this appendix is applicable to cases where we do not have an alternative observation with which we can correct from the clustering problem.

References

Amblard, A., & Cooray, A. 2007, ApJ, 670, 903 [NASA ADS] [CrossRef] [Google Scholar]
Baldry, I., Liske, J., & Driver, S. P. 2008, GAMA: a new galaxy survey, in IAU Symp. 245, ed. M. Bureau, E. Athanassoula, & B. Barbuy, 83 [Google Scholar]
Beelen, A., Omont, A., Bavouzet, N., et al. 2008, A&A, 485, 645 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Bertoldi, F., Menten, K. M., Kreysa, E., Carilli, C. L., & Owen, F. 2000 [arXiv:astro-ph/0010553] [Google Scholar]
Blain, A. W., Smail, I., Ivison, R. J., Kneib, J.-P., & Frayer, D. T. 2002, Phys. Rep., 369, 111 [NASA ADS] [CrossRef] [Google Scholar]
Blain, A. W., Chapman, S. C., Smail, I., et al. 2004, ApJ, 611, 725 [NASA ADS] [CrossRef] [Google Scholar]
Caputi, K. I., Dole, H., Lagache, G., et al. 2006, ApJ, 637, 727 [NASA ADS] [CrossRef] [Google Scholar]
Delabrouille, J., Cardoso, J.-F., & Patanchon, G. 2003, MNRAS, 346, 1089 [NASA ADS] [CrossRef] [Google Scholar]
Devlin, M. J., Ade, P. A. R., Aretxaga, I. 2009, Nature, 458, 737 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Dole, H., Gispert, R., & Lagache, G. 2001, A&A, 372, 364 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Dole, H., Le Floc'h, E., Pérez-González, P. G., et al. 2004, ApJS, 154, 87 [NASA ADS] [CrossRef] [Google Scholar]
Dole, H., Lagache, G., Puget, J.-L., et al. 2006, A&A, 451, 417 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
Dye, S., Eales, S. A., Ashby, M. L. N., et al. 2006, ApJ, 644, 769 [NASA ADS] [CrossRef] [Google Scholar]
Elbaz, D. 2005, Space Sci. Rev., 119, 93 [NASA ADS] [CrossRef] [Google Scholar]
Elbaz, D., Cesarsky, C. J., Chanial, P., et al. 2002, A&A, 384, 848 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Farrah, D., Lonsdale, C. J., Borys, C., et al. 2006, ApJ, 641, L17 [NASA ADS] [CrossRef] [Google Scholar]
Fernandez-Conde, N., Lagache, G., Puget, J.-L., et al. 2008, A&A, 481, 885 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Fixsen, D. J., Dwek, E., Mather, J. C., Bennett, C. L., & Shafer, R. A. 1998, ApJ, 508, 123 [NASA ADS] [CrossRef] [Google Scholar]
Genzel, R., & Cesarsky, C. J. 2000, ARA&A, 38, 761 [NASA ADS] [CrossRef] [Google Scholar]
Haiman, Z., & Knox, L. 2000, ApJ, 530, 124 [NASA ADS] [CrossRef] [Google Scholar]
Hauser, M. G., Arendt, R. G., Kelsall, T., et al. 1998, ApJ, 508, 25 [NASA ADS] [CrossRef] [Google Scholar]
Ilbert, O., Capak, P., Salvato, M., et al. 2009, ApJ, 690, 1236 [NASA ADS] [CrossRef] [Google Scholar]
Knox, L., Cooray, A., Eisenstein, D., et al. 2001, ApJ, 550, 7 [NASA ADS] [CrossRef] [Google Scholar]
Lagache, G., Dole, H., & Puget, J.-L. 2003, MNRAS, 338, 555 [NASA ADS] [CrossRef] [Google Scholar]
Lagache, G., Dole, H., Puget, J.-L., et al. 2004, ApJS, 154, 112 [NASA ADS] [CrossRef] [Google Scholar]
Lagache, G., Puget, J.-L., & Dole, H. 2005, ARA&A, 43, 727 [NASA ADS] [CrossRef] [Google Scholar]
Lagache, G., Bavouzet, N., & Fernandez-Conde, N. 2007, ApJ, 665, L89 [NASA ADS] [CrossRef] [Google Scholar]
Lonsdale, C., Polletta, M. D. C., Surace, J., et al. 2004, ApJS, 154, 54 [NASA ADS] [CrossRef] [Google Scholar]
Magliocchetti, M., Cirasuolo, M., McLure, R. J. 2008, MNRAS, 383, 1131 [NASA ADS] [CrossRef] [Google Scholar]
Mainzer, A. K., Eisenhardt, P., Wright, E. L., Preliminary design of the Wide-Field Infrared Survey Explorer (WISE), in MacEwen, H. A, editor, UV/Optical/IR Space Telescopes: Innovative Technologies and Concepts II, ed. MacEwen, Howard A. Proc. SPIE of Presented at the Society of Photo-Optical Instrumentation Engineers, SPIE Conf., 5899, 262, [Google Scholar]
Marsden, G., Ade, P. A. R., Bock, J. J., et al. 2009, ApJ, 707, 1729 [NASA ADS] [CrossRef] [Google Scholar]
Papovich, C., Dole, H., Egami, E., et al. 2004, ApJS, 154, 70 [NASA ADS] [CrossRef] [Google Scholar]
Puget, J.-L., Abergel, A., Bernard, J.-P., et al. 1996, A&A, 308, L5 [NASA ADS] [Google Scholar]
Sanders, D. B., Salvato, M., Aussel, H., et al. 2007, ApJS, 172, 86 [Google Scholar]
Serjeant, S., Dye, S., Mortier, A., et al. 2008, MNRAS, 386, 1907 [NASA ADS] [CrossRef] [Google Scholar]
Viero, M. P., Ade, P. A. R., & Bock, J. J. 2009, ApJ, 707, 1766 [NASA ADS] [CrossRef] [Google Scholar]
Wang, W.-H., Cowie, L. L., & Barger, A. J. 2006, ApJ, 647, 74 [NASA ADS] [CrossRef] [Google Scholar]
Zheng, X. Z., Dole, H., & Bell, E. F. 2007, ApJ, 670, 301 [NASA ADS] [CrossRef] [Google Scholar]

Footnotes

... SWIRE: http://ssc.spitzer.caltech.edu/legacy/
... (DES: http://www.darkenergysurvey.org/
...Fernandez-Conde et al. (2008): The simulations are publicly available at http://www.ias.u-psud.fr/irgalaxies
... (Big-)BOSS: http://www.sdss3.org/cosmology.php
... DES: http://www.darkenergysurvey.org/
... work: We analyze the stacking up to $z_{\max}=2$ since reliable estimates of the redshift up to that redshift are available (although over quite small areas).
... $\mu$ m): To decrease the computation time, we increase the number of sources to be stacked using a logarithmic step of dN/N= 1.5.
... clustering): The problems associated with errors in the measurement of S₂₄ are considered negligible (see Sanders et al. 2007).
... area: And therefore should have $\sqrt{N}=5$ times more signal-to-noise ratio for similar populations of sources.
... errors: Note that the top right area with no data plotted corresponds to a region where they are no sources at 24 microns; note also that in color representations as in Fig. 5, small differences in estimated value can have a great visual impact due to the variation in colors. A mere 20% change in the estimate can change the color from green to red. The general variation is consistent with our detection threshold of 3 $\sigma$ .
... error: Note that the mean flux relative error is equivalent to the mean color relative error since there is no error in our S₂₄ measurements.
... webpage: http://www.jach.hawaii.edu/JCMT/surveys/Cosmology.html

All Figures

$\begin{figure} \par\includegraphics[width=6.5cm,clip]{12924_Plot1a}\par\includegraphics[width=6.5cm,clip]{12924_Plot1b} \end{figure}$	Figure 1: Top: input fluxes of the sources in the redshift slice 1.5<z<1.6 (solid line) together with estimates of the fluxes of the sources using the smoothing technique (dashed line) and estimates of the fluxes of the sources without smoothing (diamond). Bottom: the same but zoomed for $0.3~{\rm mJy} < S_{24}<0.47$ mJy.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=7.cm]{12924_Plot2a} \end{figure}$	Figure 2: Histogram of the fluxes at 350 $\mu$ m for a stacking box with 0.5<z<0.6 and 0.5<S₂₄<1 mJy. The mean value of the sources is $S_{350}\sim 17$ mJy. The two different populations are the normal cold sources ( left population) and the starburst sources ( right population). It is clear that the main cause of error in our flux measurement comes from us stacking together two different populations. As expected, we checked that reducing the redshift slice does not reduce the dispersion.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=4cm]{12924_Plot3a}\includegraphics[wid... ...space{2cm}\includegraphics[width=4cm]{12924_Plot3c}\hspace{2cm}}\end{figure}$	Figure 3: Histograms of the number of cold (thin line) and starburst (thick line) sources per 24 $\mu$ m flux bin (histograms are normalized to the higher number of sources per histogram). The problematic regions are those where both populations have similar number of galaxies. This is especially important for 0.6<z<0.7 and faint sources.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=7cm]{12924_Plot4} \end{figure}$	Figure 4: Ratio of recovered fluxes from stacking ( $S_{350}^{\rm stack}$ ) to input fluxes in the simulation ( $S_{350}^{\rm real}$ ) for sources with S₂₄>270 $~\mu$ Jy, with no additional dispersion in the fluxes at 350 $\mu$ m (thick solid line), and with 10% (dotted-dashed line) and $25\%$ (dashed line) additional dispersion.
Open with DEXTER
In the text

$\begin{figure} \par\mbox{\includegraphics[width=4.3cm]{12924_Plot5a}\includegrap... ...Plot5c}\hspace{0.2cm} \includegraphics[width=4.cm]{12924_Plot5d} }\end{figure}$	Figure 5: Accuracy in the mean recovered fluxes at 350 $\mu$ m in a COSMOS-like observation when considering redshift errors of $\frac{\triangle z}{z}=3\%$ ( top) and $\frac{\triangle z}{z}=10\%$ ( bottom). The colors (shading) correspond to different values of the accuracy, while the vertical axis is S₂₄ and the horizontal axis is the redshift bin. Left: relative errors in the mean recovered fluxes ( $\nabla\bar{S}_{350}^{\rm Stack}=(\bar{S}_{350}^{\rm Stack}-\bar{S}_{350}^{\rm Real})/\bar{S}_{350}^{\rm Real}$ ) for all the S₂₄-z space. Right: the same but in absolute values $\left\vert\nabla\bar{S}_{350}^{\rm Stack}\right\vert=\left\vert(\bar{S}_{350}^{\rm Stack}-\bar{S}_{350}^{\rm Real})/\bar{S}_{350}^{\rm Real}\right\vert$ and decreasing the dynamic range of the plot (0-0.5) to illustrate the errors more clearly. The S₂₄-z space is divided linearly in z and logarithmically in S₂₄. Redshifts are given on the bottom-right figure, Log(S₂₄) (in mJy) on the left figures.
Open with DEXTER
In the text

$\begin{figure} \par {\hspace*{4.5mm}\includegraphics[width=6.3cm]{12924_Plot6a}\... ...dth=6.3cm]{12924_Plot6c}\includegraphics[width=7.2cm]{12924_Plot6d} \end{figure}$	Figure 6: Relative errors in recovered fluxes for individual sources at 350 $\mu$ m in a COSMOS-like observation for redshift errors $\frac{\triangle z}{z}=3\%$ ( top figures) and $\frac{\triangle z}{z}=10\%$ ( bottom figures). Left: for $S_{24}>80~\mu$ Jy and redshifts 0<z<1. Right: for $S_{24}>80~\mu$ Jy and 1<z<2. The zeros represents a perfect estimate. Three estimates are shown: direct values obtained with the stacking (dotted line); values obtained with the stacking and smoothed in z (thin solid line), and smoothed both in z and in S₂₄ (thick solid line).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=6.5cm]{12924_Plot7a}\includegraphics[w... ...4_Plot7c}\includegraphics[width=6.5cm]{12924_Plot7d} \vspace*{-4mm} \end{figure}$	Figure 7: Same as Fig. 6 but for an observation at 350 $\mu$ m if the SWIRE fields.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=4.cm, height=5.35cm]{12924_Plot8a}\includegraphics[width=4.cm, height=5.35cm]{12924_Plot8b} \end{figure}$	Figure 8: Left: real fluxes of the sources at 350 $\mu$ m (in mJy) in the space S₂₄-z. Right: fluxes found by the smoothed stacking technique. The colors correspond to different values of the flux, while the vertical axis is S₂₄ and the horizontal axis is the redshift bin.The S₂₄-z space is divided linearly in z and logarithmically in S₂₄.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=4.cm, height=5.35cm]{12924_Plot9a}\includegraphics[width=4.cm,clip]{12924_Plot9b} \end{figure}$	Figure 9: Left: real S₃₅₀/S₂₄ flux ratio of the sources in the space S₂₄-z. Right: S₃₅₀/S₂₄ flux ratio found by the smoothed stacking technique ( right). The colors correspond to different values of the ratio, while the vertical axis is S₂₄ and the horizontal axis is the redshift bin. The S₂₄-z space is divided linearly in z and logarithmically in S₂₄.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=4.cm]{12924_Plot10a}\includegraphics[width=4.cm]{12924_Plot10b} \end{figure}$	Figure 10: Same as Fig. 5 but with no redshift errors.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=7cm]{12924_Plot11} \end{figure}$	Figure 11: Lateral cut of a stacking image (Planck/HFI at 850 $\mu$ m) for very faint sources ( $S_{24}\sim100~\mu$ Jy). The total signal (normalized to 1 at the peak), the signal from both the clustering and the sources are the solid, dotted, and dashed lines, respectively. One pixel equals 25 arcsec.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.cm]{12924_Plot12a}\\ [4mm] \includeg... ...{12924_Plot12b}\\ [4mm] \includegraphics[width=8.cm]{12924_Plot12c} \end{figure}$	Figure 12: Relative errors in recovered fluxes for individual sources at 850 $\mu$ m in a COSMOS-like observation for redshift errors $\frac{\triangle z}{z}$ equal to 0 ( top), 3% ( middle), and 10% ( bottom), for $S_{24}>80~\mu$ Jy and 1<z<2. Three estimates are shown: direct values obtained with the stacking (dotted line); values obtained with the stacking and smoothed in z (thin solid line); and values smoothed both in z and in S₂₄ (thick solid line).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=0.4\columnwidth,height=0.5\columnwidth... ...aphics[width=0.4\columnwidth,height=0.5\columnwidth]{12924_Plot14d} \end{figure}$	Figure 13: Accuracy of the mean recovered fluxes at 850 $\mu$ m in a COSMOS-like observation when considering a redshift error of $\frac{\triangle z}{z}=3\%$ and no smoothing ( top), a redshift error of $\frac{\triangle z}{z}=3\%$ and the smoothing ( middle) and a redshift error of $\frac{\triangle z}{z}=10\%$ and the smoothing ( bottom figures). The colors (shading) correspond to different values of the accuracy, while the vertical axis is S₂₄ and the horizontal axis is the redshift bin. The S₂₄-z space is divided linearly in z and logarithmically in S₂₄. Redshifts are given on the right figures, $\log(S_{24})$ (in mJy) on the left figures. Left figures show the relative errors on the mean recovered fluxes ( $\nabla\bar{S}_{850}^{\rm Stack}=(\bar{S}_{850}^{\rm Stack}-\bar{S}_{850}^{\rm Real})/\bar{S}_{850}^{\rm Real}$ ) for all the S₂₄-z space. Right figures show the absolute values $\left\vert\nabla\bar{S}_{850}^{\rm Stack}\right\vert=\left\vert(\bar{S}_{850}^{\rm Stack}-\bar{S}_{850}^{\rm Real})/\bar{S}_{850}^{\rm Real}\right\vert$ .
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=4.5cm]{12924_Plot15a}\includegraphics[width=4.5cm]{12924_Plot15b} \end{figure}$	Figure 14: Ratio of recovered to input fluxes of individual sources at 850 $\mu$ m for an observation of the SWIRE fields, redshift errors $\frac{\triangle z}{z}$ =10%, and two redshift bins, 0<z<1 ( left) and 1<z<2 ( right). Three estimates are shown: direct values obtained with the stacking (dotted line); values obtained with the stacking and smoothed in z (thin solid line); and values smoothed both in z and in S₂₄ (thick solid line). The value 1 represents a perfect measurement. The recovered fluxes have not been corrected from the clustering and are thus highly overestimated.
Open with DEXTER
In the text

$\begin{figure} \par\mbox{\includegraphics[width=4cm]{12924_Plot16a} \includegraphics[width=4cm]{12924_Plot16b} }\end{figure}$	Figure 15: Relative error in the mean recovered fluxes at 850 $\mu$ m ( $\nabla\bar{S}_{850}^{\rm Stack}=(\bar{S}_{850}^{\rm Stack}-\bar{S}_{850}^{\rm Real})/\bar{S}_{850}^{\rm Real}$ ) for a Planck observations of the SWIRE fields with $\frac{\triangle z}{z}=10\%$ before ( left) and after ( right) correcting from the clustering. The colors (shading) correspond to different values of the relative error, while the vertical axis is S₂₄ and the horizontal axis is the redshift bin.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=4.5cm]{12924_Plot17a}\includegraphics[... ...h=4.5cm]{12924_Plot17c}\includegraphics[width=4.5cm]{12924_Plot17d} \end{figure}$	Figure 16: Combined observations at 350 $\mu$ m with redshift errors $\frac{\triangle z}{z}=3\%$ ( top figures) and $\frac{\triangle z}{z}=10\%$ ( bottom figures). Left: relative errors of the estimate of the mean fluxes ( $\nabla\bar{S}_{350}^{\rm Stack}=(\bar{S}_{350}^{\rm Stack}-\bar{S}_{350}^{\rm Real})/\bar{S}_{350}^{\rm Real}$ ) for the S₂₄-z space. Right: absolute values $\left\vert\nabla\bar{S}_{350}^{\rm Stack}\right\vert=\left\vert(\bar{S}_{350}^{\rm Stack}-\bar{S}_{350}^{\rm Real})/\bar{S}_{350}^{\rm Real}\right\vert$ . The colors (shading) correspond to different values of the error, while the vertical axis is S₂₄ and the horizontal axis is the redshift bin.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=4.3cm, height=6.cm]{12924_Plot18a}\inc... ...24_Plot18c}\includegraphics[width=4.3cm, height=6cm]{12924_Plot18d} \end{figure}$	Figure 17: Same as Fig. 16 for combined observations at 850 $\mu$ m.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=4.5cm]{12924_Plot19a}\includegraphics[width=4.5cm]{12924_Plot19b} \end{figure}$	Figure 18: True mean fluxes (diamonds) compared to the mean fluxes found by stacking (triangles) with the estimated errors at 70, 160, 250, 350, 500, and 850 $\mu$ m of the 800 faintest sources above $80~\mu$ Jy (mean fluxes $S_{24}=110\:\mu$ Jy and $S_{24}=135~\mu$ Jy at redshifts 1<z<1.1 and 2<z<2.1, respectively) in our simulated COSMOS observation. The points at 70 and 160 $\mu$ m are from a Spitzer simulation with instrumental noise taken from Sanders et al. (2007). The solid lines show the Starburst SEDs from the library of Lagache et al. (2004) that has the same mean S₂₄ at those two redshifts.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=4.4cm]{12924_Plot20a}\includegraphics[... ...h=4.4cm]{12924_Plot20c}\includegraphics[width=4.5cm]{12924_Plot20d} \end{figure}$	Figure 19: Power spectra of two maps in which we placed the sources with either their input fluxes from the simulations (dotted line) or their stacked fluxes (dashed line). The results are shown for a SWIRE observation ( left figures) and COSMOS observation ( right figures) at 350 $\mu$ m for stacked sources up to z=2 with redshift errors $\frac{\triangle z}{z}=3\%$ ( top) and $\frac{\triangle z}{z}=10\%$ ( bottom).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=4.5cm]{12924_Plot21a}\includegraphics[... ...h=4.5cm]{12924_Plot21c}\includegraphics[width=4.5cm]{12924_Plot21d} \end{figure}$	Figure 20: Same as Fig. 19 at 850 $\mu$ m.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=6cm]{12924_Plot22a}\includegraphics[wi... ...idth=6cm]{12924_Plot22d0}\includegraphics[width=6cm]{12924_Plot22d} \end{figure}$	Figure 21: Power spectra of the map for a SWIRE observation at 350 $\mu$ m. The solid line is the total power spectrum of the background, the dashed line is the power spectrum of the background for $z>z_{\rm lim}$ (where $z_{\rm lim}$ is a redshift limit), and the dotted line is the power spectrum of the total background from which we have subtracted the stacked sources at $z<z_{\rm lim}$ . The redshift limit $z_{\rm lim}$ is $z_{\rm lim}=1$ ( left figures), $z_{\rm lim}=1.5$ ( middle figures), and $z_{\rm lim}=2$ ( right figures). The redshift errors are $\frac{\triangle z}{z}=3\%$ ( top) and $\frac{\triangle z}{z}=10\%$ ( bottom).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=6cm]{12924_Plot23a0}\includegraphics[w... ...width=6cm]{12924_Plot23c}\includegraphics[width=6cm]{12924_Plot23d} \end{figure}$	Figure 22: Same as Fig. 21 but for the COSMOS field.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=4.5cm]{12924_Plot24a}\includegraphics[... ...h=4.5cm]{12924_Plot24c}\includegraphics[width=4.5cm]{12924_Plot24d} \end{figure}$	Figure 23: Power spectra of the 850 $\mu$ m map of the SWIRE fields. The solid line is the total CIB power spectrum, the dashed line is the CIB power spectrum for $z>z_{\rm lim}$ (where $z_{\rm lim}$ is a redshift limit), and the dotted line is the power spectrum of the total CIB from which we have subtracted the stacked sources at $z<z_{\rm lim}$ . The redshift limit $z_{\rm lim}$ is $z_{\rm lim}=1.5$ ( left) and $z_{\rm lim}=2$ ( right). The redshift errors are $\frac{\triangle z}{z}=3\%$ ( top) and $\frac{\triangle z}{z}=10\%$ ( bottom).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=4.5cm]{12924_Plot25a}\includegraphics[... ...h=4.5cm]{12924_Plot25c}\includegraphics[width=4.5cm]{12924_Plot25d} \end{figure}$	Figure 24: Same as Fig. 23 but for the COSMOS field.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

[1] Amblard, A., & Cooray, A. 2007, ApJ, 670, 903 [NASA ADS] [CrossRef] [Google Scholar]

[2] Baldry, I., Liske, J., & Driver, S. P. 2008, GAMA: a new galaxy survey, in IAU Symp. 245, ed. M. Bureau, E. Athanassoula, & B. Barbuy, 83 [Google Scholar]

[3] Beelen, A., Omont, A., Bavouzet, N., et al. 2008, A&A, 485, 645 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[4] Bertoldi, F., Menten, K. M., Kreysa, E., Carilli, C. L., & Owen, F. 2000 [arXiv:astro-ph/0010553] [Google Scholar]

[5] Blain, A. W., Smail, I., Ivison, R. J., Kneib, J.-P., & Frayer, D. T. 2002, Phys. Rep., 369, 111 [NASA ADS] [CrossRef] [Google Scholar]

[6] Blain, A. W., Chapman, S. C., Smail, I., et al. 2004, ApJ, 611, 725 [NASA ADS] [CrossRef] [Google Scholar]

[7] Caputi, K. I., Dole, H., Lagache, G., et al. 2006, ApJ, 637, 727 [NASA ADS] [CrossRef] [Google Scholar]

[8] Delabrouille, J., Cardoso, J.-F., & Patanchon, G. 2003, MNRAS, 346, 1089 [NASA ADS] [CrossRef] [Google Scholar]

[9] Devlin, M. J., Ade, P. A. R., Aretxaga, I. 2009, Nature, 458, 737 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]

[10] Dole, H., Gispert, R., & Lagache, G. 2001, A&A, 372, 364 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[11] Dole, H., Le Floc'h, E., Pérez-González, P. G., et al. 2004, ApJS, 154, 87 [NASA ADS] [CrossRef] [Google Scholar]

[12] Dole, H., Lagache, G., Puget, J.-L., et al. 2006, A&A, 451, 417 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]

[13] Dye, S., Eales, S. A., Ashby, M. L. N., et al. 2006, ApJ, 644, 769 [NASA ADS] [CrossRef] [Google Scholar]

[14] Elbaz, D. 2005, Space Sci. Rev., 119, 93 [NASA ADS] [CrossRef] [Google Scholar]

[15] Elbaz, D., Cesarsky, C. J., Chanial, P., et al. 2002, A&A, 384, 848 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[16] Farrah, D., Lonsdale, C. J., Borys, C., et al. 2006, ApJ, 641, L17 [NASA ADS] [CrossRef] [Google Scholar]

[17] Fernandez-Conde, N., Lagache, G., Puget, J.-L., et al. 2008, A&A, 481, 885 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[18] Fixsen, D. J., Dwek, E., Mather, J. C., Bennett, C. L., & Shafer, R. A. 1998, ApJ, 508, 123 [NASA ADS] [CrossRef] [Google Scholar]

[19] Genzel, R., & Cesarsky, C. J. 2000, ARA&A, 38, 761 [NASA ADS] [CrossRef] [Google Scholar]

[20] Haiman, Z., & Knox, L. 2000, ApJ, 530, 124 [NASA ADS] [CrossRef] [Google Scholar]

[21] Hauser, M. G., Arendt, R. G., Kelsall, T., et al. 1998, ApJ, 508, 25 [NASA ADS] [CrossRef] [Google Scholar]

[22] Ilbert, O., Capak, P., Salvato, M., et al. 2009, ApJ, 690, 1236 [NASA ADS] [CrossRef] [Google Scholar]

[23] Knox, L., Cooray, A., Eisenstein, D., et al. 2001, ApJ, 550, 7 [NASA ADS] [CrossRef] [Google Scholar]

[24] Lagache, G., Dole, H., & Puget, J.-L. 2003, MNRAS, 338, 555 [NASA ADS] [CrossRef] [Google Scholar]

[25] Lagache, G., Dole, H., Puget, J.-L., et al. 2004, ApJS, 154, 112 [NASA ADS] [CrossRef] [Google Scholar]

[26] Lagache, G., Puget, J.-L., & Dole, H. 2005, ARA&A, 43, 727 [NASA ADS] [CrossRef] [Google Scholar]

[27] Lagache, G., Bavouzet, N., & Fernandez-Conde, N. 2007, ApJ, 665, L89 [NASA ADS] [CrossRef] [Google Scholar]

[28] Lonsdale, C., Polletta, M. D. C., Surace, J., et al. 2004, ApJS, 154, 54 [NASA ADS] [CrossRef] [Google Scholar]

[29] Magliocchetti, M., Cirasuolo, M., McLure, R. J. 2008, MNRAS, 383, 1131 [NASA ADS] [CrossRef] [Google Scholar]

[30] Mainzer, A. K., Eisenhardt, P., Wright, E. L., Preliminary design of the Wide-Field Infrared Survey Explorer (WISE), in MacEwen, H. A, editor, UV/Optical/IR Space Telescopes: Innovative Technologies and Concepts II, ed. MacEwen, Howard A. Proc. SPIE of Presented at the Society of Photo-Optical Instrumentation Engineers, SPIE Conf., 5899, 262, [Google Scholar]

[31] Marsden, G., Ade, P. A. R., Bock, J. J., et al. 2009, ApJ, 707, 1729 [NASA ADS] [CrossRef] [Google Scholar]

[32] Papovich, C., Dole, H., Egami, E., et al. 2004, ApJS, 154, 70 [NASA ADS] [CrossRef] [Google Scholar]

[33] Puget, J.-L., Abergel, A., Bernard, J.-P., et al. 1996, A&A, 308, L5 [NASA ADS] [Google Scholar]

[34] Sanders, D. B., Salvato, M., Aussel, H., et al. 2007, ApJS, 172, 86 [Google Scholar]