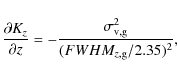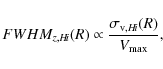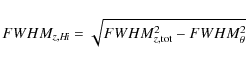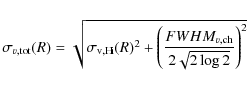| Issue |
A&A
Volume 515, June 2010
|
|
|---|---|---|
| Article Number | A62 | |
| Number of page(s) | 27 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/200912567 | |
| Published online | 09 June 2010 | |
The dark matter halo shape of edge-on disk galaxies
III. Modelling the HI observations: results
J. C. O'Brien1 - K. C. Freeman1 - P. C. van der Kruit2
1 - Research School of Astronomy and Astrophysics, Australian National
University, Mount Stromlo Observatory, Cotter Road, ACT 2611, Australia
2 - Kapteyn Astronomical Institute, University of Groningen, PO Box 800,
9700 AV Groningen, The Netherlands
![]()
Received 25 Mai 2009 / Accepted 5 March 2010
Abstract
This is the third paper in a series in which we attempt to put
constraints on the flattening of dark halos in disk galaxies. We
observed for this purpose the H I in edge-on galaxies, where it is in principle
possible to measure the force field in the halo vertically and radially
from gas layer flaring and rotation curve decomposition respectively.
For this purpose we need to analyse the observed XV diagrams in such a
way as to accurately measure all three functions that describe the
planar kinematics and distribution of a galaxy: the radial H I surface
density, the rotation curve and the H I velocity dispersion.
In this paper, we first present the results of the modelling
of our H I observations of 8 H I rich, late-type, edge-on galaxies. We find that
in all of these we find differential rotation. Most systems display H I velocity
dispersions of 6.5 to 7.5 km s-1 and all except one show radial structure in this property. There is an increase in the mean H I velocity dispersion with
maximum rotation velocity, at least up to 120 km s-1.
Next we analyse the H I observations to derive the radial variation of the thickness of the H I layer. The combination of these gas flaring measurements with the H I kinematics measurements allow us to measure the total vertical force of each galaxy assuming hydrostatic equilibrium. We find that with the exception of the asymmetric IC5052, all of the galaxies in our sample are good candidates for 3D mass modelling to measure the dark halo shape. The flaring profiles are symmetric with respect to the galactic centres and have a common shape, increasing linearly inside the stellar disks and exponential outside where the gravitational potential is dominated by the dark halo. In the best example, UGC 7321, we find in the inner regions small deviations from the midplane and accompanying increases in thickness of the H I layer that are possibly a result of perturbations of the gravitational field by a relatively strong bar.
Key words: galaxies: structure - galaxies: kinematics and dynamics - galaxies: halos - galaxies: ISM
1 Introduction
In Paper I in this series (O'Brien et al. 2010a) we presented H I observations of a sample of 8 edge-on, H I rich, late-type galaxies. The aim of the project has been described there in detail. Briefly, we attempt to put constraints on the flattening of dark halos around disk galaxies by measuring the force field of the halo vertically from the flaring of the H I layer and radially from rotation curve decomposition. For the vertical force field we need to determine in these galaxies both the velocity dispersion of the H I gas (preferably as a function of height from the central plane of the disk) and the thickness of the H I layer, all of these as a function of galactocentric radius. In addition we also need to extract information on the rotation curve of the galaxy and the deprojected H I surface density, also as a function of galactocentric radius. To adequately constrain the halo shape these parameters needed to be measured out to as low surface densities as possible.Here we present the determination of these properties from our H I observations.
In order to resolve the vertical structure, we selected a sample of
nearby, H I rich, late-type edge-on galaxies which are likely to exhibit
large H I flaring expected from high dark matter fractions. From
Paper I, we recall that the gradient of the force field in the vertical
direction for a Gaussian gas layer can be written as
where
In the second paper (O'Brien et al. 2010b, Paper II), we presented a new method to accurately determine the rotation curve, deprojected H I surface density and velocity dispersion at all radii in a edge-on gas disk. The superposition of velocity profiles from many radii in each sightline through an edge-on H I disk tends to cause an overestimate of the velocity dispersion with most measurement methods (see Paper II). Measuring the radial flaring profile requires a model of the galaxy rotation and face-on surface density; this also necessitates high accuracy rotation curve measurement and H I surface density deprojection.
In this third paper we present the rotation curve, H I velocity dispersion and deprojected H I surface density from the XV maps measured using the iterative XV diagram modelling program (see Paper II). Previously, measurement of these parameters in edge-on galaxies has been difficult. Indeed, the gas velocity dispersion has been measured as a function of radius in only one edge-on galaxy NGC 4244 (Olling 1996). If the data have suffiently high S/N, then our iterative XV modelling program is capable of deriving the variation of rotation, velocity dispersion and density as a function of both radius and height z above the equatorial plane of these edge-on galaxies. For the data described in Paper I, the S/N is not high enough to derive the variations in both z and R. We use the XV diagrams integrated over z, and measure the gas surface density distribution and kinematics as a function of radius only, assuming that the gas velocity dispersion is isotropic and vertically isothermal.
![\begin{figure}
\par\includegraphics[width=15cm,clip]{12567fg1.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg14.png)
|
Figure 1:
ESO074-G015 (IC5052).
This figure shows the results of the modelling of the kinematics.
The best fit measurements for each kinematic function are shown in as (red)
crosses for the the H I velocity dispersion in the top left-hand panel
and in the lower left-hand plot for the deprojected H I surface density. The top right-hand panel shows the derived rotation curve (dark/red) overlaid on the observed XV diagram. Also
shown on the XV diagram are the rotation fits obtained using the
less accurate envelope tracing method (dark grey/orange) and the peak flux
method (light grey/yellow). The latter always shows a lower rotation
velocity than the other two fits.
The lower right-hand plot displays the derived rotation
curve with the receding and approaching sides separately
(in the electronic version red and blue respectively).
The FWHM synthesised beam has dimensions
|
| Open with DEXTER | |
2 Results for kinematic modelling
![\begin{figure}
\par\includegraphics[width=15cm,clip]{12567fg2.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg16.png)
|
Figure 2:
ESO109-G021 (IC5249).
This figure shows the results of the modelling of the kinematics. For an
explanation of the figure see the caption of Fig. 1.
The FWHM synthesised beam has dimensions
|
| Open with DEXTER | |
For each galaxy in our sample we present the best fit measurements of the radial kinematics, and show the map of the residuals formed by comparing the model XV diagram to the observed XV map. These XV maps were formed by integrating the observed H I channel maps over the z axis.
2.1 ESO074-G015 (IC5052)
Although ESO074-G015 is one of the nearest edge-on low mass galaxies, it is a galaxy less suitable for dark halo fitting because it is asymmetric in both the H I and optical distribution. Furthermore, it shows a bright star formation region 2 kpc west of the galactic center with associated radio continuum emission, indicating a possible regional deviation from hydrostatic equilibrium. The measured rotation curve (see Fig. 1) also shows a large asymmetry which is unlikely to be solely due to the H I warp. Given the irregular optical distribution, it is more likely to indicate a non-axisymmetric mass distribution commonly found in Magellanic dwarf galaxies. The centre of mass was poorly determined in IC5052 due to the irregular structure of the XV distribution.
Despite the apparent mass asymmetry, the H I velocity dispersion is roughly constant at 6-7 km s-1. Similarly the H I radial profile is reasonably symmetric, although it displays a broad plateau in the bright star formation region on the west side. As the channel maps clearly show vertical flaring of the H I layer, we will proceed with the flaring analysis for this galaxy. However, the gross kinematic asymmetry precludes it from use in the hydrostatic analysis to determine the shape of the dark matter distribution.
![\begin{figure}
\par\includegraphics[width=15cm,clip]{12567fg3.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg18.png)
|
Figure 3:
ESO115-G021.
This figure shows the results of the modelling of the kinematics. For an
explanation of the figure see the caption of Fig. 1.
The FWHM synthesised beam has dimensions
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{12567fg4.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg20.png)
|
Figure 4:
ESO138-G014.
This figure shows the results of the modelling of the kinematics. For an
explanation of the figure see the caption of Fig. 1.
The FWHM synthesised beam has dimensions
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{12567fg5.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg22.png)
|
Figure 5:
ESO146-G014.
This figure shows the results of the modelling of the kinematics. For an
explanation of the figure see the caption of Fig. 1.
The FWHM synthesised beam has dimensions
|
| Open with DEXTER | |
2.2 ESO109-G021 (IC5249)
ESO109-G021 (IC5249) is one of several well-known ``superthin'' galaxies, renowned for the large optical axial ratio. The rotation curve shown in Fig. 2 shows that ESO109-G021 has a maximum rotation speed of 110 km s-1. ESO109-G021 is the only one of the galaxies in our sample with rotation speeds larger than 100 km s-1 that does not show the ``Fig.-8'' signature in the H I distribution indicative of a possible bar.
The measured H I radial surface density has a shallow gradient with dips at around 11-12 kpc in agreement with the features in the deprojected surface density obtained by van der Kruit et al. (2001). However these authors also measured a central H I depression, while we find a small central peak when measuring from the left-hand side and a plateaued central surface density when measuring from the right-hand side. The deprojected surface density was measured after folding the observed surface density calculated from the XV map about the galactic center.
One possible explanation for the discrepancy between our measured
surface density and that of van der Kruit et al. (2001), is the lower
sensitivity of their observations. In addition to the 12 h 6.0C
ATCA observation used by all parties, we acquired an additional 30 h of H I synthesis observations spread over the ATCA EW352, 750D and
6.0A array configurations. This resulted in a peak signal-to-noise of 46.1 and a synthesised beam
![]() of
8
of
8
![]() in the XV map, which appears to be a significantly higher sensitivity and spatial resolution than that acquired by van der Kruit et al. (2001).
in the XV map, which appears to be a significantly higher sensitivity and spatial resolution than that acquired by van der Kruit et al. (2001).
The measured rotation curve is reasonably symmetrical, in agreement with that obtained by van der Kruit et al. (2001) which was derived by modelling the XV distribution using the fixed velocity dispersion XV modelling method of van der Kruit (1981, see also Sect. 2.5 in Paper II). Like that of van der Kruit et al. (2001), our measurement shows a steep inner rise - as opposed to the earlier less accurate measurements by Abe et al. (1999) which appear to have been measured from the peak flux ridge of the XV map.
The measured H I velocity dispersion varies from 5.5 to 8.5 km s-1, falling
to lower values on the right-hand side of the galaxy. The mean H I velocity
dispersion of ![]() km s-1 is in agreement with the best fit value of 7 km s-1 found by van der Kruit et al. (2001).
km s-1 is in agreement with the best fit value of 7 km s-1 found by van der Kruit et al. (2001).
![\begin{figure}
\par\includegraphics[width=15cm,clip]{12567fg6.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg27.png)
|
Figure 6:
ESO274-G001.
This figure shows the results of the modelling of the kinematics. For an
explanation of the figure see the caption of Fig. 1.
The FWHM synthesised beam has dimensions
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{12567fg7.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg29.png)
|
Figure 7:
ESO435-G025 (IC2531).
This figure shows the results of the modelling of the kinematics. For an
explanation of the figure see the caption of Fig. 1.
The FWHM synthesised beam has dimensions
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{12567fg8a.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg30.png)
|
Figure 8a:
UGC 7321.
This figure shows the results of the modelling of the kinematics. For an
explanation of the figure see the caption of Fig. 1.
The FWHM synthesised beam has dimensions
|
2.3 ESO115-G021
The high resolution H I imaging of ESO115-G21 yields an almost solid-body rotation curve flattening out at a radius of 5-6 kpc at a peak rotation speed of approximately 65 km s-1 (see Fig. 3). Like the other small galaxies in our sample it shows steep inner rotation unlike the solid body rotation commonly obtained from low resolution studies of small galaxies. Despite an apparently accurate rotation curve fit there is still significant flux in the residual in the part of the XV diagram containing flux at large radii. This appears to be due to an underestimate of the H I surface density and the velocity dispersion at large radii.
The measured H I velocity dispersion is surprisingly low at only
4.5-6 km s-1 at radii within 5 kpc from the galactic centre. This
galaxy displays particularily bright H I emission in the inner 2-3 kpc, with a brightness temperature
![]() K. The low measured
velocity dispersion and high brightness temperature are consistent with a partially
opaque inner H I disk. In the face-on galaxy NGC 1058,
Petric & Rupen (2006) found regions of H I velocity dispersion as low as
4 km s-1 - indicating cold low velocity dispersion H I on
scales of at least 500 pc which is quite large compared to typical star
formation scales in the ISM. Given the large beamwidth of 1.5 kpc of the NGC 1058 H I observations, it is likely
that smaller regions of even lower velocity dispersion gas exist in
NGC 1058. In ESO115-G021, regions with a H I velocity dispersion of 4.5 km s-1 occur on radial scales of 1 kpc, similar to the cold gas distribution in NGC 1058.
K. The low measured
velocity dispersion and high brightness temperature are consistent with a partially
opaque inner H I disk. In the face-on galaxy NGC 1058,
Petric & Rupen (2006) found regions of H I velocity dispersion as low as
4 km s-1 - indicating cold low velocity dispersion H I on
scales of at least 500 pc which is quite large compared to typical star
formation scales in the ISM. Given the large beamwidth of 1.5 kpc of the NGC 1058 H I observations, it is likely
that smaller regions of even lower velocity dispersion gas exist in
NGC 1058. In ESO115-G021, regions with a H I velocity dispersion of 4.5 km s-1 occur on radial scales of 1 kpc, similar to the cold gas distribution in NGC 1058.
2.4 ESO138-G014
ESO138-G014 is a relatively large Sd galaxy with a H I disk extending to 20 kpc, and a maximum rotation speed of 112 km s-1 (see Fig. 4). The rotation curve is clearly differential, rising steeply in the innermost 5 kpc, then starts to flatten outside of 10 kpc from the galactic centre. As noted in Paper I, the XV map displays a faint ``Fig.-8'' signature, indicating a possible bar.
The H I velocity dispersion is approximately 7 km s-1 at radii outside of 9 kpc. At radii inside of 9 kpc, the H I velocity dispersion rises steeply to a plateau of 10-11 km s-1 within 5 kpc radii.
The H I radial profile is roughly constant within ![]() 9 kpc from the
centre, except for central peak within
9 kpc from the
centre, except for central peak within ![]() 2 kpc radius. The large
central plateau spans the same radial domain as the increased
velocity dispersion and could be explained by radial streaming in the bar
causing redistribution of the gas. As explained in
Sect. 4.4, we will leave this galaxy out of the
discussion because of missing short spacings and a poorly determined flaring
profile of the H I layer.
2 kpc radius. The large
central plateau spans the same radial domain as the increased
velocity dispersion and could be explained by radial streaming in the bar
causing redistribution of the gas. As explained in
Sect. 4.4, we will leave this galaxy out of the
discussion because of missing short spacings and a poorly determined flaring
profile of the H I layer.
2.5 ESO146-G014
ESO146-G014 is another small Sd galaxy similar to ESO115-G021 with a
particularly low H I velocity dispersion of ![]() 4.5 km s-1 at radii
less than 4 kpc. At larger radii, the mean velocity dispersion is
6 km s-1, with a peak of 7.5 km s-1 at 5 kpc west of the
galactic centre. This high velocity dispersion region on the west side
corresponds to a 1 kpc wide bright overdensity in the B-band optical
image, and to a 1 kpc gap between bright H I regions in the H I total intensity map (see Paper I, Fig. 5a).
4.5 km s-1 at radii
less than 4 kpc. At larger radii, the mean velocity dispersion is
6 km s-1, with a peak of 7.5 km s-1 at 5 kpc west of the
galactic centre. This high velocity dispersion region on the west side
corresponds to a 1 kpc wide bright overdensity in the B-band optical
image, and to a 1 kpc gap between bright H I regions in the H I total intensity map (see Paper I, Fig. 5a).
The rotation curve of ESO146-G014 peaks at only 70 km s-1 and is quite symmetric about the galactic centre, particularly within radii of 4.5 kpc. The H I surface density shows a bright central peak, a plateau from 3 to 6 kpc radius, after which it declines steeply on the left-hand side, and less so on the right-hand side.
2.6 ESO274-G001
ESO274-G001 is the closest galaxy in our sample at a distance of only 3.4 Mpc. This allowed the 6 km maximum baseline of the ATCA to yield an exceptionally small H I synthesised beam of 162 pc. Thus despite the small radius of only 7-8 kpc, each side of the galaxy is spanned by over 47 independent beams. Using a beam sampling of 3 pixels per beam, approximately 150 kinematic fits are obtained on each side of the galactic centre.
The measured kinematics shown in Fig. 6
display a differentially rotating galaxy with a maximum rotation
speed of only 86 km s-1. This rotation velocity shows that
ESO274-G001 is a small galaxy with a rotation curve
that continues to rise until the outermost kpc. The ![]() -level envelope fitting method
overestimates the rotation speed by up to 10-15 km s-1, while the peak
flux method dramatically underestimates it by up to
-level envelope fitting method
overestimates the rotation speed by up to 10-15 km s-1, while the peak
flux method dramatically underestimates it by up to
![]() .
The H I surface density is reasonably symmetric,
with a central peak within 2 kpc, and a plateau to 5.5 kpc
on the left-hand side and 4.5 kpc on the right-hand side, declining
to an H I surface density of
.
The H I surface density is reasonably symmetric,
with a central peak within 2 kpc, and a plateau to 5.5 kpc
on the left-hand side and 4.5 kpc on the right-hand side, declining
to an H I surface density of
![]() atoms cm-2. The H I velocity dispersion at 6.5 km s-1 shows no systematic trend with radius, with small oscillations of only 1 km s-1 around this value, throughout the H I disk.
atoms cm-2. The H I velocity dispersion at 6.5 km s-1 shows no systematic trend with radius, with small oscillations of only 1 km s-1 around this value, throughout the H I disk.
2.7 ESO435-G025 (IC2531)
ESO435-G025 is the only Sc galaxy in our sample and more massive than the next largest galaxy by a factor of four. The rotation curve displays an unusual concave shape (see Fig. 7) indicating a dip in the gradient of rotation. ESO435-G025 was one of the first detections of a bar in an edge-on galaxy (Bureau & Freeman 1999). Despite the bar, the measured kinematics are an excellent representation of the galaxy. The inner rotation of IC2531 is similar to that of NGC 891, however lacking gas tracing an inner ring, seen in both H I (Swaters et al. 1997) and CO (Tony Wong, private communication). It is quite possible that like NGC 891, the inner galaxy of ESO435-G025 is largely populated by molecular gas in the inner disk (Wong et al. 2004).
ESO435-G025 is the most distant galaxy in our sample and with a low
peak signal-to-noise of 41.4 in the XV map, and particularly low
signal-to-noise in the parts of the XV diagram with radii less than
7 kpc. Unfortunately, the signal-to-noise in the inner galaxy was
too low to deconvolve for the effect of the H I beam
(
![]() kpc) while modelling the XV diagram. As a result
the H I surface density is probably overestimated at radii within 10 kpc
where the gradient of rotation over each beamwidth
is large. The measured H I velocity dispersion displays a significant peak
and central trough, which is largely an effect of beam smearing.
At radii outside 10 kpc, where the beam smearing effect is minimal,
the H I velocity dispersion has a mean of 7 km s-1. To compensate for the inability to properly measure
the velocity dispersion inside of 10 kpc, we adopt a smooth central
velocity dispersion rising from 8 km s-1 at 10 kpc radius to 10 km s-1 in the centre. Inside of 10 kpc we adopt a
central plateau for the H I surface density, but we flag that the derived
properties within 10 kpc should be treated with caution.
kpc) while modelling the XV diagram. As a result
the H I surface density is probably overestimated at radii within 10 kpc
where the gradient of rotation over each beamwidth
is large. The measured H I velocity dispersion displays a significant peak
and central trough, which is largely an effect of beam smearing.
At radii outside 10 kpc, where the beam smearing effect is minimal,
the H I velocity dispersion has a mean of 7 km s-1. To compensate for the inability to properly measure
the velocity dispersion inside of 10 kpc, we adopt a smooth central
velocity dispersion rising from 8 km s-1 at 10 kpc radius to 10 km s-1 in the centre. Inside of 10 kpc we adopt a
central plateau for the H I surface density, but we flag that the derived
properties within 10 kpc should be treated with caution.
2.8 UGC 7321
The H I bar of UGC 7321 causes a significant distortion in the peak flux of the XV distribution. The effect of non-circular motions in the bar causes a deviation in the projected rotation of gas rotating in the bar. The XV modelling is able to recover the azimuthally averaged surface density, and rotation (Fig. 8); however, it is unable to fit the non-axisymmetric gas in the bar, as can been appreciated from Fig. 8, which shows the observed, model and residual XV diagrams. Orbits in a barred potential have been studied by Contopoulos & Mertzanides (1977), who found that there are two families, where the main orbit family is designated x1 (see also Binney et al. 1991). On the left-hand side of the galactic centre, the x1 orbit showing the near and far side of the bar is clearly apparent in the residual map. The residual structure on the right-hand side of the galactic centre is less clear.
The peak flux in the x1 orbits of the residual is ![]()
![]() of the
peak flux of the observed XV diagram. To ascertain the likely surface mass
density perturbation caused by the bar, we inspected the K band
azimuthal flux profile of the bars in several late-type face-on
galaxies with weak bars. If one assumes a significant fraction of the
brightness variation is biased by young stars contributing to
the bar, galaxies with a relatively weak, diffuse bar are
unlikely to have a difference of stellar surface density between bar and
inter-bar regions greater than
of the
peak flux of the observed XV diagram. To ascertain the likely surface mass
density perturbation caused by the bar, we inspected the K band
azimuthal flux profile of the bars in several late-type face-on
galaxies with weak bars. If one assumes a significant fraction of the
brightness variation is biased by young stars contributing to
the bar, galaxies with a relatively weak, diffuse bar are
unlikely to have a difference of stellar surface density between bar and
inter-bar regions greater than ![]() (for example, the Sc
galaxy NGC 2525). Photometry of UGC 7321 by Pohlen et al. (2003)
shows that the stellar bar is very faint and thin, indicating that
minimal buckling of the bar has occured. The thin stellar bar of
UGC 7321, and the small H I mass fraction in the bar suggest that the
inner mass density perturbation is quite low, and
unlikely to significantly effect the halo mass modelling.
(for example, the Sc
galaxy NGC 2525). Photometry of UGC 7321 by Pohlen et al. (2003)
shows that the stellar bar is very faint and thin, indicating that
minimal buckling of the bar has occured. The thin stellar bar of
UGC 7321, and the small H I mass fraction in the bar suggest that the
inner mass density perturbation is quite low, and
unlikely to significantly effect the halo mass modelling.
3 The flaring of the H I layer
There have been few attempts to directly measure the flaring of the
H I layer in galaxies. With the exception of Olling's study of NGC 4244
(Olling 1996) and an earlier less sensitive study of NGC 5023
(Bottema et al. 1986), all the flaring measurements were undertaken on massive
Sb-Sc galaxies. It is particularly difficult to measure the flaring in
large galaxies, as such galaxies are expected to have higher disk surface densities and
consequently thinner gas layers. For gas in hydrostatic
equilibrium the FWHMz(R) of the H I is inversely proportional to
the maximum rotation velocity ![]() (Eq. (D31) of
Olling 1995)
(Eq. (D31) of
Olling 1995)
so large galaxies with max rotation speeds similar to the Milky Way, will only flare to 1/3 of the height of small galaxies like ESO146-G014, given similar H I vertical velocity dispersions
One of the first measurements of the gas layer thickness in an
external galaxy was the early low resolution WSRT study of NGC 891 by
Sancisi & Allen (1979). This data were re-analyzed by van der Kruit (1981).
These authors found that the vertical thickness of the H I layer was unresolved by the 1.4 kpc beam in the inner parts (R < 8 kpc) and increased to 2 kpc at the outermost measured point of
![]() kpc. Using deeper higher resolution VLA data with
synthesised beam
kpc. Using deeper higher resolution VLA data with
synthesised beam
![]() of 0.4 and 0.9 kpc respectively
for NGC 4565 and NGC 891, Rupen (1989) found that the gas thickness
increased exponentially with radius, although NGC 891 displays
substantial scatter. This is due to a low channel map peak
signal-to-noise of
of 0.4 and 0.9 kpc respectively
for NGC 4565 and NGC 891, Rupen (1989) found that the gas thickness
increased exponentially with radius, although NGC 891 displays
substantial scatter. This is due to a low channel map peak
signal-to-noise of ![]() 13 in the NGC 891 H I cube, compared to
13 in the NGC 891 H I cube, compared to
![]() 64 in the NGC 4565 dataset. This result is consistent with the
thickness of the gas layer in our Galaxy,
which is also found to increase exponentially
from 200 pc near the Galactic Centre to 1.3 kpc at
64 in the NGC 4565 dataset. This result is consistent with the
thickness of the gas layer in our Galaxy,
which is also found to increase exponentially
from 200 pc near the Galactic Centre to 1.3 kpc at ![]() 20 kpc
(Merrifield 1992). Meanwhile, Braun (1991) fitted the gas
thickness of M31 with an exponential z profile and found that the
gas thickness increases roughly linearly from a scale height of 200 pc at 5 kpc radius to 600 pc at 25 kpc.
20 kpc
(Merrifield 1992). Meanwhile, Braun (1991) fitted the gas
thickness of M31 with an exponential z profile and found that the
gas thickness increases roughly linearly from a scale height of 200 pc at 5 kpc radius to 600 pc at 25 kpc.
The most accurate measurement of H I flaring was obtained for the
small Scd galaxy NGC 4244 by Olling (1996) who found that the
FWHMz thickness increased from 400 pc at 5 kpc radius to 1.8 kpc at 14 kpc radius, with uncertainty ranging from ![]() 100 pc
at inner radii to 200-500 pc at the outermost measured point. These
were by far the most sensitive high resolution observations obtained,
with 14 h of VLA data spread over B, C and D arrays, resulting in
a
100 pc
at inner radii to 200-500 pc at the outermost measured point. These
were by far the most sensitive high resolution observations obtained,
with 14 h of VLA data spread over B, C and D arrays, resulting in
a
![]() of 170 pc. The only other small galaxy that has been
observed is the Scd NGC 5023 imaged at the WSRT with a spatial
resolution of
of 170 pc. The only other small galaxy that has been
observed is the Scd NGC 5023 imaged at the WSRT with a spatial
resolution of ![]() 650 pc (Bottema et al. 1986). These authors
find a constant thickness of
650 pc (Bottema et al. 1986). These authors
find a constant thickness of
![]() kpc despite the fact that
their Fig. 4 appears to show an increase of thickness from 1.0 to
1.7 kpc, particularly on the east side. However the spectral
resolution of 16.6 km s-1 available on the WSRT at the time was
a little coarse given the low maximum rotation speed (86 km s-1) of
NGC 5023. This low spectral resolution and the low signal-to-noise of
the observations would have increased the uncertainty in their radial
flaring profile.
kpc despite the fact that
their Fig. 4 appears to show an increase of thickness from 1.0 to
1.7 kpc, particularly on the east side. However the spectral
resolution of 16.6 km s-1 available on the WSRT at the time was
a little coarse given the low maximum rotation speed (86 km s-1) of
NGC 5023. This low spectral resolution and the low signal-to-noise of
the observations would have increased the uncertainty in their radial
flaring profile.
3.1 Methods used to measure the vertical gas thickness
Several methods have been used to measure the vertical flaring of high inclination galaxies. The gas disk thickness must be measured from individual channel maps, rather than from the total H I column density map, as the latter measures the thickness of the integrated flux. If the H I distribution is well resolved by the telescope beam, measuring the gas thickness from channel maps is elementary. The challenge lies in deprojecting the measurements from the projected radius of each measurement to the galactocentric radius. In each method below, the measured FWHMz vertical thicknesses are corrected for the spatial resolution of the beam (see Eq. (3) below).
The most common method used to determine the radial flaring profile is
to fit the vertical thickness of just the extreme velocity channel
maps along each line of sight. This provides an accurate measurement of the flaring in the outer disk if
the rotation curve is flat over this radial domain. If gas in the extreme velocity channel maps is emitted from a
narrow azimuthal range around the line of nodes, then the gas fitted
by a vertical profile at each projected radius
![]() is emitted
from a narrow radial range, allowing the radius of each thickness
measurement to be approximated by the major axis distance
is emitted
from a narrow radial range, allowing the radius of each thickness
measurement to be approximated by the major axis distance
![]() .
This method was used in the early flaring
measurements of NGC 891 (Rupen 1989; Sancisi & Allen 1979), NGC 4565
(Rupen 1989) and NGC 5023 (Bottema et al. 1986).
.
This method was used in the early flaring
measurements of NGC 891 (Rupen 1989; Sancisi & Allen 1979), NGC 4565
(Rupen 1989) and NGC 5023 (Bottema et al. 1986).
Unfortunately this deprojection approximation can often miscalculate the radial shape of the flaring profile. This occurs in less differentially rotating galaxies, as the radial range of gas emission is larger along each line of sight through the extreme channel maps. Also, less massive galaxies with shallower rotation curves will have a smaller major axis extent spanned in the outer velocity channels and the radial domain where the rotation curve is most flattened may not be where the gas disk flares. The other disadvantage is that the vertical thickness at each radius is measured only twice, once on either side of the galaxy. Another problem is that the gas thickness is only measured at radii with flux in the edge channel maps. In a large galaxy with a flat rotation curve, these channel maps will probe most of the radial extent of the galaxy, however in a less massive galaxy with a less steep inner rotation curve, the radial span of the outer channel maps is much less.
The analysis of van der Kruit (1981) of the NGC 891 data of Sancisi & Allen (1979)involves matching the observed XV map to a simulated XV formed with different assumed values of gas thickness and flaring. This study also involved an investigation into the effects of small residual inclinations away from purely edge-on.
The technique used by Braun (1991) to measure the flaring of the inclined galaxy M31 was more complicated. Braun used the fitted inclination and rotation curve to fit the vertical thickness of H I features in the spiral arms.
In the next section, we present the method which we have developed to accurately deproject the projected radius to the galactocentric radius for each vertical thickness measurement, and correct the measured thickess for the spatial resolution of the telescope along the z axis. As our method fits the vertical gas thickness in all channel maps with sufficient flux, the number of measurements at each radius produces a more reliable radial flaring profile, and also allows the flaring profile to be measured at radii much closer to the galactic center. Our method is very similar to that used by Olling (1996); however, we only allow for warps of the H I disk in the plane of the sky.
3.2 Gas flaring measurement by iterative H I cube modelling
The FWHM thickness of the H I disk was determined by fitting a
Gaussian to each vertical slice across the galaxy major axis in each
H I channel map, enabling the gas layer thickness to be measured independently on
each side of the galactic centre. To facilitate vertical thickness
measurements, each H I cube was rotated in the plane of
the sky to align the galaxy major axis with the x axis, i.e. cube
axes (x,z,v), (see Sect. 6 of
Paper I for rotated H I cubes for each galaxy).
The measured FWHM thickness is corrected for the effect of the beam by
to obtain the actual gas thickness
The projected radius was deprojected to the galactocentric radius
using the kinematics measured from the XV map
in Sect. 2
to identify the galactocentric
radius that contributes emission at the projected radius
and line-of-sight velocity of the channel map being measured. This was
facilitated by building a ``face-on'' H I cube that
showed the H I distribution in the equatorial plane
![]() (where
(where ![]() is the projected radius and s is the distance in
the line-of-sight) of the emission in each observed line-of-sight
velocity. For each galaxy a face-on H I cube was built using the radial kinematics determined in
Sect. 2.
is the projected radius and s is the distance in
the line-of-sight) of the emission in each observed line-of-sight
velocity. For each galaxy a face-on H I cube was built using the radial kinematics determined in
Sect. 2.
To simulate the observational effects of the telescope, the face-on
H I cube was convolved by the FWHM of the telescope beam along the
x axis. In order to account for the intrinsic H I velocity
dispersion and the finite spectral resolution, the spectral axis of
the face-on H I cube was convolved by a 1D point-spread-function
with total velocity dispersion
![]() equal to
equal to
where
The intensity-weighted velocity fields of the face-on H I cubes were calculated for each galaxy. These velocity fields provide a representation of the galactocentric radii contributing flux to each major axis slice of the actual observed H I cubes.
Each channel map of the face-on H I cube was masked by the maximum radius of H I emission on each side of the galaxy. Next the galactocentric radius at each projected radius of a channel map was derived by taking the intensity-weighted mean of the galactocentric radii of all points along that projected radius in the face-on channel map, where the intensity weights are the H I flux at those positions. This process was used to find the weighted mean galactocentric radius corresponding to the major axis position of each vertical thickness measured from the actual observed H I cubes.
The FWHMz(R) was determined from the average of all the FWHMz fitted at that galactocentric radius. The number of channel maps with emission from any one galactocentric radius usually ranged from one to 20, as dictated by the galaxy kinematics and the resolution of the observations. Galaxies with flatter rotation curves enabled a greater number of measurements for each galactocentric radius. Higher spectral resolution relative to the H I velocity dispersion caused the H I emission at each galactocentric radius to be spread over more channel maps. However, increasing the spectral resolution resulted in lower signal-to-noise and fewer fits, as fitting was only possible on vertical slices with at least 4 consecutive points with flux greater than two times the rms noise.
To correct for the scatter in the vertical thickness measurements due
to beam-smearing and low signal-to-noise, the whole H I cube fitting process was iterated in a similar manner as that used for
the XV modelling algorithm. The known kinematics (from
Sect. 2) and the newly measured FWHMz(R)flaring fits formed the first model which was used to build a new H I
(x,z,v) H I cube. The effect of the telescope observation was
simulated by convolving the H I cube spatially by the telescope
synthesised beam and spectrally by total velocity dispersion
![]() (defined in Eq. (4)). The model
H I cube was then fitted, and the fits to the model H I cube compared to the fits of the actual observed H I
cube. This cycle was iterated, with all kinematics except the
flaring held fixed, until FWHMz(R) fits to the model H I cube matched the FWHMz(R) fits of the actual observed H I
cube to within 10% of the FWHM of the telescope beam along
the z axis or until the total difference in fits stopped decreasing.
The best fits were usually obtained after 3-4 iterations.
(defined in Eq. (4)). The model
H I cube was then fitted, and the fits to the model H I cube compared to the fits of the actual observed H I
cube. This cycle was iterated, with all kinematics except the
flaring held fixed, until FWHMz(R) fits to the model H I cube matched the FWHMz(R) fits of the actual observed H I
cube to within 10% of the FWHM of the telescope beam along
the z axis or until the total difference in fits stopped decreasing.
The best fits were usually obtained after 3-4 iterations.
This iterative flare fitting method was tested under various conditions on
synthetic galaxy observations. Simulations showed that high
signal-to-noise observations could be corrected for beam smearing to
within 5-10% of the FWHM beam size along z; however, lower
signal-to-noise observations with large beams were somewhat limited
with a FWHMz uncertainty of ![]() 20% of the FWHM beam size
along z. Although the flare fitting algorithm does accurately
correct for the projection and beam-smearing of the H I distribution,
the final FWHMz accuracy is naturally still dependent on the
adequate signal-to-noise of the H I data cube.
20% of the FWHM beam size
along z. Although the flare fitting algorithm does accurately
correct for the projection and beam-smearing of the H I distribution,
the final FWHMz accuracy is naturally still dependent on the
adequate signal-to-noise of the H I data cube.
4 Results for flaring profiles
For each galaxy in our sample we present the best fit measurements of
the FWHMz thickness of the H I disk as a function of radius,
derived independently on each side of the galaxy. The measured
thickness along each major axis slice of the H I channel maps was
undertaken using the kinematics measured by XV modelling in
Sect. 2.
The error bars shown on the flaring profiles in this section are the
1![]() errors of the Gaussian fits.
errors of the Gaussian fits.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{aa12567-fig9.eps}
\vspace*{1cm}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg54.png)
|
Figure 9: ESO074-G015 (IC5052). Top panel: measured FWHMz thickness of the H I gas disks. Lower panels: each of the kinematic functions of the H I reflected about the galactic centre to show both sides of the galaxy, and the average of both sides. Middle left: rotation curve; middle right: H I velocity dispersion; lower left: H I surface density; lower right: H I vertical thickness FWHMz. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{aa12567-fig10.eps}
\vspace*{-3.5mm}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg55.png)
|
Figure 10: ESO109-G021 (IC5249). Measured FWHMz thickness of the H I gas disk and the kinematic functions of the H I. For details see the caption of Fig. 9. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{aa12567-fig11.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg56.png)
|
Figure 11: ESO115-G021. Measured FWHMz thickness of the H I gas disk and the kinematic functions of the H I. For details see the caption of Fig. 9. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{aa12567-fig12.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg57.png)
|
Figure 12: ESO138-G014. Measured FWHMz thickness of the H I gas disk and the kinematic functions of the H I. For details see the caption of Fig. 9. |
| Open with DEXTER | |
We were able to measure the H I flaring to radii within 1-2 kpc of
the maximum radius at which the other H I kinematics were measured.
This was a particularily impressive result considering that the
signal-to-noise of most vertical slices was only 3-5. The average H I cube peak signal-to-noise was only 13.6, except for
UGC 7321, which had almost ![]() 6 times the signal-to-noise of the
other galaxies. Analysis of the vertical shape of the H I distribution in UGC 7321,
facilitated by the high sensitivity observations, found unexpected azimuthal variations
in the gas thickness and midplane displacement of this edge-on galaxy.
These surprising results for UGC 7321 are presented in Sect. 4.8.
6 times the signal-to-noise of the
other galaxies. Analysis of the vertical shape of the H I distribution in UGC 7321,
facilitated by the high sensitivity observations, found unexpected azimuthal variations
in the gas thickness and midplane displacement of this edge-on galaxy.
These surprising results for UGC 7321 are presented in Sect. 4.8.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{aa12567-fig13.eps}
\vspace*{3.5mm} \end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg58.png)
|
Figure 13: ESO146-G014. Measured FWHMz thickness of the H I gas disk and the kinematic functions of the H I. For details see the caption of Fig. 9. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{aa12567-fig14.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg59.png)
|
Figure 14: ESO274-G001. Measured FWHMz thickness of the H I gas disk and the kinematic functions of the H I. For details see the caption of Fig. 9. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{aa12567-fig15.eps}
\vspace*{8mm}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg60.png)
|
Figure 15: ESO435-G025 (IC2531). Measured FWHMz thickness of the H I gas disk and the kinematic functions of the H I. For details see the caption of Fig. 9. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{aa12567-fig16.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg61.png)
|
Figure 16: UGC 7321. Measured FWHMz thickness of the H I gas disk and the kinematic functions of the H I. For details see the caption of Fig. 9. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12567fg17-1.eps}\hspace*{1.5mm}
\includegraphics[width=7.4cm,clip]{12567fg17-2.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg62.png)
|
Figure 17: Left - All the vertical profiles in a sample of galactocentric radial bins in UGC 7321. The radius of the bin is given in the top right-hand corner of each plot. Each radial bin is 145.4 pc wide - the same size as the image pixels along the major and minor axes of UGC 7321. The ordinate axis of each plot shows the H I column density in units of H I atoms cm-2 in each vertical slice. Right - The same as on the left-hand side, but now we show average profiles, which were obtained after aligning the profile centres and vertically rescaling all profiles to a peak of 1. Overlaid in blue is the Gaussian fit to each average profile. |
| Open with DEXTER | |
4.1 ESO074-G015 (IC5052)
The FWHMz vertical thickness of ESO074-G015 expanded from
FWHMz
=0.4 kpc at a galactocentric radius of 1.5 kpc to
FWHMz = 2.5 kpc at ![]() 7.0 kpc, with an additional thicknesses of 3.3and 4.0 kpc measured at the edge of the H I disk at radii 8.0-8.1 kpc (Fig. 9). These outermost two
measurements are consistent with the flaring shape of the disk, but
the measurement has a large uncertainty of 0.5-0.6 kpc and were only measured
in one channel map of the H I data cube. The flaring at 8 kpc comprises the
warped eastward extension at a radius of 4
7.0 kpc, with an additional thicknesses of 3.3and 4.0 kpc measured at the edge of the H I disk at radii 8.0-8.1 kpc (Fig. 9). These outermost two
measurements are consistent with the flaring shape of the disk, but
the measurement has a large uncertainty of 0.5-0.6 kpc and were only measured
in one channel map of the H I data cube. The flaring at 8 kpc comprises the
warped eastward extension at a radius of 4![]() in the H I column density map (see Fig. 1b in Paper I), and is detected as very
diffuse edge emission in the outer channel maps on the receding side. The channel maps show the emission at
in the H I column density map (see Fig. 1b in Paper I), and is detected as very
diffuse edge emission in the outer channel maps on the receding side. The channel maps show the emission at ![]() rms noise of
rms noise of
![]() atoms cm-2.
atoms cm-2.
The integrated flux of ESO074-G015 was ![]() less than that measured
from the H I Parkes All Sky Survey (HIPASS) line spectrum obtained
from the online HIPASS Public Data
Release
less than that measured
from the H I Parkes All Sky Survey (HIPASS) line spectrum obtained
from the online HIPASS Public Data
Release![]() .
This suggested that there is additional extended H I emission that was not
observed with the long ATCA array configurations. Indeed, a low resolution H I column density
map available in the online Local Volume H I Survey
(LVHIS
.
This suggested that there is additional extended H I emission that was not
observed with the long ATCA array configurations. Indeed, a low resolution H I column density
map available in the online Local Volume H I Survey
(LVHIS![]() ),
showed large scale emission around the warped disk extending to
),
showed large scale emission around the warped disk extending to ![]() 12
kpc. The smallest array configuration observations included in our
analysis were low sensitivity snapshot observations with the ATCA 375array configuration. The LVHIS image was
obtained with a 12 h integration using the ATCA EW367 array
configuration. Additional low resolution data of ESO074-G015 may detect H I flaring to thicknesses greater than 4.0 kpc.
12
kpc. The smallest array configuration observations included in our
analysis were low sensitivity snapshot observations with the ATCA 375array configuration. The LVHIS image was
obtained with a 12 h integration using the ATCA EW367 array
configuration. Additional low resolution data of ESO074-G015 may detect H I flaring to thicknesses greater than 4.0 kpc.
Despite the gross asymmetry of the ESO074-G015 rotation curve, the flaring is
remarkably symmetric (see Fig. 9).
This H I disk does thicken by ![]() 200 pc at radii inside 4 kpc
particularly on the east side. This appears to be due to the
increased H I velocity dispersion from
200 pc at radii inside 4 kpc
particularly on the east side. This appears to be due to the
increased H I velocity dispersion from ![]() 6 to 8 km s-1
at the same radii, and is more pronounced on the east side. The inner
west side of the disk from 2-4 kpc shows intense star formation
and radio continuum emission, but the east side is
optically more quiescent. The flaring profile is clearly well-resolved
by the synthesised H I beam FWHM of 292 pc. However,
the low peak signal-to-noise of 14 in the H I data cube restricts measurement of
flaring in the faint outer H I disk.
Despite being well-resolved spatially, the apparent mass asymmetry
indicated by the rotation curve precludes this galaxy from dark halo
flattening modelling.
6 to 8 km s-1
at the same radii, and is more pronounced on the east side. The inner
west side of the disk from 2-4 kpc shows intense star formation
and radio continuum emission, but the east side is
optically more quiescent. The flaring profile is clearly well-resolved
by the synthesised H I beam FWHM of 292 pc. However,
the low peak signal-to-noise of 14 in the H I data cube restricts measurement of
flaring in the faint outer H I disk.
Despite being well-resolved spatially, the apparent mass asymmetry
indicated by the rotation curve precludes this galaxy from dark halo
flattening modelling.
4.2 ESO109-G021 (IC5249)
Like UGC 7321, ESO109-G021 is renowned for being a ``superthin'' galaxy, exhibiting a scalelength-to-scaleheight ratio hR/hz of 11. However, although ESO109-G021 has a similar maximum rotation speed to UGC 7321, its radial scale is approximately 2.5 times larger, with a long scalelength of 7 kpc and a sharp stellar truncation at 17kpc. We find that the H I disk flares from a FWHMz of 800 pc at 2 kpc radius out to 2.8 kpc at 20 kpc (see Fig. 10). The thickness of the gas disk appears to be roughly constant from 2 to 5 kpc and begins to rise exponentially from a radius of 6-7 kpc. The steep flaring of the gas disk at 17-18 kpc is consistent with the edge of the stellar disk.
The gas layer thickness was also been measured by van der Kruit et al. (2001) from the total H I intensity map, as the signal-to-noise of the channel maps was too low as they had only the original 12 h ATCA 6.0C observation by Carignan & Beaulieu. They found the FWHMz thickness rose from 1.3 kpc near the centre to 4.9 kpc at 15 kpc. Our flaring measurements were obtained using an additional 30 h of ATCA time split over EW352, 750D and 6.0A array configurations, yielding a peak channel map signal-to-noise of 10.1
The H I disk was possibly unresolved at radii less than 2 kpc,
as the large synthesis beam of 1.18 kpc made it difficult to
resolve spatial features smaller than ![]() 800 pc. An unresolved
central gas thickness would explain the relatively thick central gas
layer, comparable in thickness to the stellar disk.
800 pc. An unresolved
central gas thickness would explain the relatively thick central gas
layer, comparable in thickness to the stellar disk.
4.3 ESO115-G021
ESO115-G021 shows strong flaring (see Fig. 11) from a central FWHMz thickness of 0.8 kpc to over 2 kpc at the outermost measured point, 6.1 kpc from the galactic centre. The H I emissionof the galaxy extends to a galactocentric radius of 8.2 kpc on the eastward side; however, this emission is very diffuse and too faint for H I thickness measurement.
The peak signal-to-noise of the channel maps used to measure the flaring was only 18.6 and the FWHM beam size was 194 pc. Each radial fit was the average of all vertical thickness fits at major axis positions of a channel map that deprojected to this radius. Some thickness measurements were averaged from measurements to 5-7 channel maps; however, most were obtained from two to three channel maps.
Despite the low average H I velocity dispersion of
![]() km s-1, the H I disk flares to a vertical
HWFMz above the plane of >2 kpc near the H I edge.
km s-1, the H I disk flares to a vertical
HWFMz above the plane of >2 kpc near the H I edge.
4.4 ESO138-G014
ESO138-G014 was the only galaxy in our sample in which it was not
possible to satisfactorily measure the H I gas layer thickness. The measured
flaring thickness are shown in Fig. 12;
however, the derived FWHMz are ballpark estimates only due to
missing large scale structure that was not measured with the large ATCA array
configurations used. ESO138-G014 and ESO274-G001
were the only two galaxies in our sample with extended H I disks
(![]() 10
10![]() diameter) for which we were unable to obtain compact
array H I observations. Although they both had similar peak
channel map signal-to-noise of
diameter) for which we were unable to obtain compact
array H I observations. Although they both had similar peak
channel map signal-to-noise of ![]() 15, the low spatial resolution of
ESO138-G014 prevented correction of the fitted flaring
by iterative modelling. The irregular measured flaring profile, which displays
a decreasing disk thickness at radii outside of 15 kpc, is probably due to
the missing large scale structure.
15, the low spatial resolution of
ESO138-G014 prevented correction of the fitted flaring
by iterative modelling. The irregular measured flaring profile, which displays
a decreasing disk thickness at radii outside of 15 kpc, is probably due to
the missing large scale structure.
Under a constant hydrostatic pressure, a fall in gas thickness of
![]() 0.5-1.0 kpc could be explained by a decrease in H I velocity
dispersion of 15-30% or 1.5-3.0 km s-1. Although a 3 km s-1 decrease in velocity dispersion is observed between 7 and 10 kpc
radius, this decrease is significantly inside the onset radius of the
decline in gas layer thickness. Due to the irregular gas flaring
profile we decided not to model the dark halo of ESO138-G014.
0.5-1.0 kpc could be explained by a decrease in H I velocity
dispersion of 15-30% or 1.5-3.0 km s-1. Although a 3 km s-1 decrease in velocity dispersion is observed between 7 and 10 kpc
radius, this decrease is significantly inside the onset radius of the
decline in gas layer thickness. Due to the irregular gas flaring
profile we decided not to model the dark halo of ESO138-G014.
4.5 ESO146-G014
The H I disk of ESO146-G014 flares dramatically from a FWHMzthickness of 0.4 kpc at radii of 3 kpc, to FWHMz=1.6 kpc at 9.0 kpc from the galactic centre (see Fig. 13). The flaring is highly asymmetric around the galactic centre, probably due to the low peak H I cube signal-to-noise of 11.3 which limited the number of fits at each radius. Despite the noisy data, the measured flaring profile still showed a steep exponential rise from 4 kpc radius to the last measured point at 8 kpc radius. This steep inner flaring, occuring at 1.5 to 2.5 stellar scalelengths, is consistent with a low stellar surface density as inferred from the B-band face-on surface brightness of 23.8mag arcsec-2 and the low rotation speed. The low stellar surface brightness and large flaring make this galaxy an excellent candidate for measuring the shape of the dark halo.
4.6 ESO274-G001
As mentioned above, the H I imaging of ESO274-G001 is also missing some extended large scale structure due to a lack of H I observations using array configurations shorter than 1.5 km. This missing structure was clearly apparent in the flaring measurement process as the measurements of the H I cube modeled with the initial measured flaring were much lower than the flaring measured from the observed H I channel maps. The best fit model displayed in Fig. 14 shows that the flaring rises roughly linearly from a FWHMz thickness of 200 pc at less than 1 kpc radius to 1.9 kpc at 5.5 kpc radius.
4.7 ESO435-G025 (IC2531)
IC2531 displays a very large outer and remarkably symmetric flare (see
Fig. 15), rising from a gas thickness
of 800 pc at 4.5 kpc radius to 3-4 kpc at 30 kpc. The central
gas thickness was initially partially unresolved given the
![]() beamwidth of 1.3, and was decreased to the final
thickness by iterating. The large gas thickness uncertainty of between
100 and 500 pc was due to the low peak channel map signal-to-noise
of 10.9.
beamwidth of 1.3, and was decreased to the final
thickness by iterating. The large gas thickness uncertainty of between
100 and 500 pc was due to the low peak channel map signal-to-noise
of 10.9.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12567fg18.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg68.png)
|
Figure 18: Measured H I FWHMz thickness ( upper panel) and H I midplane location ( lower panel) of UGC 7321 as a function of radius, where the measurements are colour coded by the line-of-sight velocity of each channel map. The most bluewards points were measured from the extreme approaching velocities, and those most redwards were measured from the extreme receding velocities. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12567fg19-1.eps}\par\includegraphics[width=8cm,clip]{12567fg19-2.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg69.png)
|
Figure 19: Measured FWHMz thickness ( upper panel) and midplane displacement ( lower panel) of the H I disk of UGC 7321 deprojected onto the X-Y plane, where the color scale on each plot shows the respective FWHMz or midplane displacement measurements. Measurements in white are off the top end of the color scale. Each line of measurements forming a coloured track shows the measurements from a single H I channel map. The measurements are the same on each side of the Y=0 line, as due to the edge-on orientation of the gas disk, we can't determine if H I emission comes from the near or far side of the disk. |
| Open with DEXTER | |
4.8 UGC 7321
The measured flaring of UGC 7321 is our most accurate determination of the flaring in our sample, rising from a FWHMz thickness of 350pc at a radius of 0.5 kpc to roughly 4 kpc at 11 kpc from the galactic centre. The 16 h of VLA time obtained by Matthews enabled the H I channel maps to be imaged with much better sensitivity than that acquired for the other galaxies observed with the ATCA. As a result the error bars on the UGC 7321 FWHMz thickness measurements are only 15-50 pc, except in the outermost 2-3 kpc. The relatively flat rotation curve also allowed the flaring at most radii to be independently measured in over 10-20 different channel maps.
The flaring profile of UGC 7321 exhibits the high degree of symmetry
of the gas thickness about the galactic center as expected for an
undisturbed, isolated galaxy. At all radii the flaring profiles are symmetric
about the galactic centre to within the bounds of the errors bars
(1![]() errors are
errors are
![]() pc within a radius of 9 kpc). As the H I velocity
dispersion as a function of radius is also very symmetric, this shows
that the total vertical force must also be symmetric.
Given a symmetric luminous density distribution,
this implies that the vertical force and density of the halo are
symmetric about the galaxy centre.
pc within a radius of 9 kpc). As the H I velocity
dispersion as a function of radius is also very symmetric, this shows
that the total vertical force must also be symmetric.
Given a symmetric luminous density distribution,
this implies that the vertical force and density of the halo are
symmetric about the galaxy centre.
The most striking feature of the H I flaring profile of UGC 7321 is the change in the shape of the flaring profile near the edge of the stellar disk. In the inner disk the H I thickness appears to increase linearly with radius, while outside the stellar disk it displays an exponential profile. In UGC 7321, this ``break'' occurs at 7.8 kpc, which is between the stellar truncation radius of 6.7 kpc (Pohlen et al. 2003) and the maximum stellar disk radius of 8.1 kpc (Mattthews & Wood 2003).
The vertical thickness of the H I disk of UGC 7321 has also been studied by Mattthews & Wood (2003) who, as in the study of NGC 2403 by Fraternali et al. (2002), tried to discern the H I flaring from the H I total intensity map. Mattthews & Wood (2003) found that the best fit to the observed H I total intensity map was achieved using a thin H I disk that flares from a FWHMz of 260 pc at the center to 1.64 kpc at 11.8 kpc, and an additional low density halo H I component of constant FWHM z of 3.3 kpc that lagged behind the disk gas rotation. Mattthews & Wood (2003) parameterised the thin H I disk using hf = h1 + hf0 r5/4. This produced a smooth flaring profile, but lacked the steep exponential increase we measured in gas thickness at radii outside of the stellar disk of UGC 7321 and most of the galaxies in our sample (see Sect. 5.4).The addition by Mattthews & Wood (2003) of a low density second gas component with a large constant FWHMz seems to simulate the thick gas layer at the outer radii. The filamentary nature of this structure suggests that it is H I ejecta, originating in the inner disk, rather than a pervasive diffuse thick H I layer. As shown below, our direct flaring measurements of UGC 7321 show that the gas layer can be well represented by a single gaussian gas component with a FWHM that varies smoothly with radius: modelling the gas layer thickness by two gas components appears to be unnecessary.
The high signal-to-noise of these observations allowed
inspection of the intrinsic shape of the vertical gas thickness. The left-hand
panel of Fig. 17 displays the observed vertical
profiles in a sample of galactocentric radial bins on both sides of
the galactic centre. The profiles show the number of independent
measurements in each bin and the flaring of the gas thickness on both
sides of the galaxy. In order to inspect the vertical shape more
closely, we averaged the profiles in each bin after aligning the
profile centres and vertically rescaling all profiles to a peak of 1(see Fig. 17, right-hand panel).
This shows that the profiles are indeed Gaussian in nearly all radii bins, with small high-z wings seen only in annuli at radii of ![]() 4 and
4 and ![]() 8 kpc.
8 kpc.
In Fig. 18 we show the direct FWHMz(upper plot) and midplane position (lower plot) fits of the H I disk.
The FWHMz shows a clear increase in
thickness at radii between 3.5 and 5.5 kpc on both sides
occuring on both sides of the galactic centre. The colors show that
this occurs only in the extreme velocity channels, corresponding to
H I in the line of nodes. The lower plot shows that the H I midplane
also deviates at this radius and azimuth in the X-Y plane, dropping
below ![]() 200 pc below the average midplane position on the left-hand
side, and rising approximately 150 pc above the galactic plane on
the right-hand side.
200 pc below the average midplane position on the left-hand
side, and rising approximately 150 pc above the galactic plane on
the right-hand side.
In Fig. 19 we show the FWHMzthickness (upper panel) and midplane position (lower panel) measurements deprojected onto the X-Y plane, where the color scale on each plot shows the respective FWHMz or midplane displacement measurements. Each line of measurements forming a coloured ``track'' shows the measurements from a single H I channel map. The measurements are the same on each side of the Y = 0 line as, due to the edge-on orientation of the gas disk, we can't determine if H I emission comes from the near or far side of the disk. Below we briefly describe the H I warp of the midplane before discussing the unusual azimuthal variation of both the thickness and midplane displacement mentioned above.
The midplane displacement plot (lower panel) shows that disk plane warps by
300-500 pc in the plane of the sky on the left-hand side centred
around Y=0, while on the right-hand side the warp amplitude is similar,
peaking at a small angle of ![]() 30
30![]() to the line-of-nodes. This
implies that the measured thickness is uneffected by the warp on the
left-hand side of the centre, while on the right-hand side the measured
thickness of the direct loop 1 fit may have been slightly
overestimated due to the projection of the warp. These effects of
warping are corrected by iterating the measurement as explained in
Sect. 3.2.
to the line-of-nodes. This
implies that the measured thickness is uneffected by the warp on the
left-hand side of the centre, while on the right-hand side the measured
thickness of the direct loop 1 fit may have been slightly
overestimated due to the projection of the warp. These effects of
warping are corrected by iterating the measurement as explained in
Sect. 3.2.
Also visible is a pronounced deviation of the midplane and
FWHMz thickness of gas in the line of nodes at
radii between
2.5-5.0 kpc on the left-hand side of the galaxy and at radii from
4-5.5 kpc on the right-hand side. This midplane displacement is
seen most clearly
in the lower plot of Fig. 18; while this
deviation of the gas thickness from the mean flaring can be seen in
both the upper plot of Fig. 18 and the
upper panel of Fig. 19. One
explanation for the increased broadening and tilting of the disk
midplane along the Y = 0 axis at this radius, is that the gas is
responding to the local perturbation of the total potential by the
suspected bar. Peanut-shaped deviations from elliptical isophotes in
the projected R-band image (Pohlen et al. 2003) favour a bar oriented in the
plane of the sky (i.e. along the Y = 0 axis), rather closer to end-on
which would align the bar axis with the line-of-sight. The measured
enhanced local gas thickening along the Y = 0 axis
probably is the best observational evidence of
a bar in an edge-on galaxy![]() . Other explanations for localised regions
of increased thickness are infalling material from a companion or
disruption by a companion, however UGC 7321 is an isolated galaxy. The
high symmetry of the flaring on both sides of the centre, and the high
stellar disk major-to-minor axis ratio (a/b=10.3 at
. Other explanations for localised regions
of increased thickness are infalling material from a companion or
disruption by a companion, however UGC 7321 is an isolated galaxy. The
high symmetry of the flaring on both sides of the centre, and the high
stellar disk major-to-minor axis ratio (a/b=10.3 at
![]() mag arcsec-2, Matthews et al. 1999)
render disruption by an undetected neighbouring galaxy rather implausible.
mag arcsec-2, Matthews et al. 1999)
render disruption by an undetected neighbouring galaxy rather implausible.
Another noticable feature of
Fig. 19 is that the tracks
denoting the location of the measurements in the X-Y plane display
wiggles which systematically vary over a range of azimuthal angles.
As our deprojection method is
based on the velocity field, these wiggles could be due to deviations
from circular rotation in the velocity field causing small errors in
the deprojection![]() .
Kinks are typically seen in the velocity fields
of less inclined galaxies with strong spiral arms (e.g.
M81, Rots 1974) suggesting that, if seen face-on, UGC 7321 may
exhibit weak spiral arms in the gas distribution.
.
Kinks are typically seen in the velocity fields
of less inclined galaxies with strong spiral arms (e.g.
M81, Rots 1974) suggesting that, if seen face-on, UGC 7321 may
exhibit weak spiral arms in the gas distribution.
5 Discussion
5.1 H I rotation curves
In Fig. 20 the rotation curves
of our galaxies are overlaid.
IC 2531 stands out as a massive, large galaxy compared to the rest
of the sample. We have two very slow rotators with maximum rotation
speeds of ![]() 60 km s-1 in our sample, while the others form a group of galaxies rotating at
60 km s-1 in our sample, while the others form a group of galaxies rotating at ![]() 100 km s-1.
The shape of the rotation curves are in good agreement with the
rotation curves of 60 less inclined late-type dwarf galaxies measured
by Swaters (1999). Although low
mass LSB galaxies exhibit a shallower inner rotation gradient, our
high resolution observations clearly resolve differential rotation, in
agreement with other observations by Swaters (1999) and de Blok & Bosma (2002).
100 km s-1.
The shape of the rotation curves are in good agreement with the
rotation curves of 60 less inclined late-type dwarf galaxies measured
by Swaters (1999). Although low
mass LSB galaxies exhibit a shallower inner rotation gradient, our
high resolution observations clearly resolve differential rotation, in
agreement with other observations by Swaters (1999) and de Blok & Bosma (2002).
5.2 H I velocity dispersion
The H I velocity dispersion measurements presented in this paper comprise the highest spatial resolution measurements of velocity dispersion to date and the first measurements using data that span the radial extent of each galaxy by more than 10 H I synthesised beams. Figure 21 shows that the H I velocity dispersion of our galaxies ranges from 4.5 km s-1 to 12.5 km s-1, with most galaxies displaying a H I velocity dispersion of 6.5 to 7.5 km s-1. Of the eight galaxies in our sample, all display radial structure in H I velocity dispersion, except ESO274-G001 which has an approximately constant H I velocity dispersion of 6.5 km s-1.
Figure 22 shows the mean H I velocity dispersion as a function of the maximum rotation velocity of the H I disk. There is a definite increase in the mean velocity dispersion with rotation speed from about 5 to 8 km s-1 for rotation velocities 70 to 120 km s-1, but IC2531 has the same velocity dispersion of approximately 8 km s-1 although its maximum rotation speed is 230 km s-1. Dalcanton et al. (2004) found that edge-on galaxies with rotation velocity greater than 120 km s-1 have well-defined dustlanes, while those with lower rotation do not. Dalcanton et al. suggested that well-defined dust lanes are related to lower gas turbulence and lower scale heights for the dust layer in the more rapidly rotating galaxies. Do our data support this suggestion?
From Eq. (1), the scaleheight h of a Gaussian dust layer is
related to the ISM velocity dispersion ![]() by
by
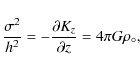
|
(5) |
where
Two of the larger galaxes, IC2531 and ESO138-G014, display H I velocity dispersions 2-3 km s-1 larger at small radii coinciding with the inner stellar disk. IC2531 is a large Sc galaxy with a strong bar, while the H I XV map of ESO138-G014 indicates a possible bar. The other barred galaxy in our sample, UGC 7321, displays the next highest central H I velocity dispersion. These three galaxies have a relatively large standard deviation in the H I velocity dispersion as often observed in more face-on strongly barred galaxies like NGC 1365, presumably caused by gas shocks and increased star formation. Unfortunately, ESO138-G014 was not in our optical sample due to its low galactic latitude, so we were unable to confirm the existence of a bar by investigating the stellar isophotes.
The velocity dispersion profile of UGC 7321 exhibits three broad localised peaks with velocity dispersion 1-2.5 km s-1 higher than the intervening medium. These occur at the galactic centre, and at radii of 6 kpc and 10 kpc. Stellar observations of UGC 7321 by Pohlen et al. (2003) show a central peanut-shaped stellar over-density with a radius of 2.0 kpc, which could be caused by resonant off-plane thickening via bar buckling (e.g. Combes et al. 1990). The rise of H I velocity dispersion from 6.5 km s-1 to 9.5 km s-1 in this region suggests that processes associated with bar buckling could be providing the additional energy heating the gas. The second H I velocity dispersion peak, from 4 kpc to 7 kpc, corresponds to the radius of the bar shown in the ``Fig.-8'' H I signature and the stellar isophotes analysis by Pohlen et al. (2003). The third H I velocity dispersion is of lower amplitude and occurs outside the stellar disk. These results suggest that at least part of the additional gas heating seen in the high inner H I velocity dispersions of barred galaxies in our sample could be due to star formation along radial flows in the bar, and bar buckling.
![\begin{figure}
\par\includegraphics[width=14cm,clip]{12567fg20.eps.old}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg77.png)
|
Figure 20: The H I rotation curves for all galaxies in our sample overlaid on each other for comparison. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{12567fg21.eps.old}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg78.png)
|
Figure 21: The H I velocity dispersion profiles for all galaxies in our sample overlaid on each other for comparison. |
| Open with DEXTER | |
Observations of the face-on galaxies NGC 3938 (van der Kruit & Shostak 1982), NGC 628 (Shostak & van der Kruit 1984), NGC 1058 (van der Kruit & Shostak 1984; Petric & Rupen 2006), NGC 6946 (Boulanger & Viallefond 1992) and NGC 5474 (Rownd et al. 1994) have shown that the H I velocity dispersion ranges from 4 to 16 km s-1, and has generally been assumed to be 6-8 km s-1 in the absence of significant star formation. In NGC 6946, detailed observations by Kamphuis & Sancisi (1993) and Boomsma et al. (2008) indicate the presence of widespread high velocity gas with significant kinetic energy, while the radial H I velocity dispersion profile shows a peak of more than 10 km s-1 within R25, followed by a gradual decline. Large-scale turbulence probably plays a role in this. The cause of the H I velocity dispersions is complicated and not well-understood, but turbulence driven by star formation, supernovae, shearing motions and magnetic instabilities all may play a role (Agertz et al. 2009; Tamburro et al. 2009).
The typical velocity dispersion of 6.5 to 7.5 km s-1 of galaxies in our sample is in agreement with these observations, which is to be expected given the LSB nature of all the galaxies in our sample (except IC2531 and IC5052). On small scales it is assumed that increased H I velocity dispersion is due to heating of the ISM by stellar winds from hot OB stars, supernovae and expanding H II regions (e.g. Spitzer 1978; McKee & Ostriker 1977). Star formation is known to increase the turbulence of the ISM (Oort & Spitzer 1955), as the newly formed stars eject gas from the cloud within which they formed by radiation pressure and stellar winds. Although limited by a small sample size, our results suggest that increased gas velocity dispersion in disk galaxies is linked to the presence or prior formation of bars, which could cause the widespread star formation required to form strong dust lanes. However, it could also be caused by star formation in spiral arms.
The most recent observations of NGC 1058 by Petric & Rupen (2006) are the only
H I velocity dispersion study of a face-on galaxy with high spectral
resolution (2.58 km s-1). They found a general radial trend of a
declining H I velocity dispersion
which was punctuated by many peaks and saddles where
it ranged from 4 to 14 km s-1. Two of
the three regions with high H I velocity dispersion did not coincide
with star formation tracers such as H![]() or radio continuum
emission. For the third one it did, but that region
was located at the galactic center. The high spatial
frequency of H I velocity dispersion variation measured in our sample
also suggests that the small scale velocity structure of the neutral ISM is likely to be quite complex.
or radio continuum
emission. For the third one it did, but that region
was located at the galactic center. The high spatial
frequency of H I velocity dispersion variation measured in our sample
also suggests that the small scale velocity structure of the neutral ISM is likely to be quite complex.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12567fg22.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg80.png)
|
Figure 22:
Mean H I velocity dispersion
|
| Open with DEXTER | |
If the canonical H I velocity dispersion of 7 km s-1 found in the
outer disks of galaxies were due solely to thermal motion, the gas
temperature would need to be
![]() K. In the outer Galaxy
where it is possible to measure the kinetic temperature and the
velocity dispersion, Spitzer (1978) found a thermal
contribution to the H I velocity dispersion of only
K. In the outer Galaxy
where it is possible to measure the kinetic temperature and the
velocity dispersion, Spitzer (1978) found a thermal
contribution to the H I velocity dispersion of only ![]() 1 km s-1,
indicating that most of the broadening is non-thermal in origin.
1 km s-1,
indicating that most of the broadening is non-thermal in origin.
One possible explanation is that differential galactic rotation transforms rotational energy into turbulent motions, perhaps via shocks resulting from disk instabilities (Quiroga 1983; Rohlfs & Kreitschmann 1987; Sellwood & Balbus 1999). Shocks in galactic bars could also generate gas heating. High resolution hydrodynamical simulations, including gaseous self-gravity, realistic radiative cooling, and rotation by Wada et al. (2002) show that large scale rotation combined with gas self-gravity could be the source of the additional non-thermal energy broadening the gas velocity dispersion. Their models of turbulent rotating disks are consistent with the velocity dispersion of the extended H I disk in the dwarf galaxy NGC 2915, which appears to have no prominent star formation. Their numerical simulations also show that the stellar bar in NGC 2915 enhances the H I velocity dispersion, which supports our finding of higher velocity dispersion in the inner disks of IC2531, ESO138-G14 and UGC 7321
5.3 H I radial surface density
Figure 23 shows the measured radial H I surface density of each galaxy in our sample. UGC 7321, ESO274-G001 and ESO115-G021 all show a steep exponential decline at large radii, while IC5052 and ESO138-G014 appear to exhibit a roughly linear decline. With the exception of IC5052, most galaxies appear to show roughly smooth H I surface densities.
5.4 Flaring of H I layers
In Fig. 24 we display a plot of
all the flaring profiles for each galaxy in our sample. The H I flaring profiles appear to obey a typical shape, with the flaring
increasing linearly with radius where the stellar disk dominates the
local gravitational potential, and steepening to an exponential
profile in the outer disk where the potential is probably dominated by
the halo. This break in the change of the flaring profile is seen most clearly in UC7321.
The onset of exponential curvature appears to occur just
outside the stellar truncation radius in the more massive galaxies with
maximum rotation speed
![]() km s-1. In smaller, lower surface
brightness disk galaxies with
km s-1. In smaller, lower surface
brightness disk galaxies with
![]() km s-1, the break possibly occurs
at smaller radii due to dark matter dominating the inner gravitational potential.
km s-1, the break possibly occurs
at smaller radii due to dark matter dominating the inner gravitational potential.
![\begin{figure}
\par\includegraphics[width=14cm,clip]{12567fg23.eps.old}
\vspace{3mm}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg84.png)
|
Figure 23: The face-on surface density profiles for all galaxies in our sample overlaid on each other for comparison. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{12567fg24.eps.old} \vspace{3mm}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg85.png)
|
Figure 24: Measured FWHMz thicknesses of the H I gas disks. ESO 138-G14 has been omitted from this figure, as explained in Sect. 4.4. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{12567fg25.eps.old}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg86.png)
|
Figure 25: Measured FWHMz thicknesses of the H I gas disks. The horizontal axis is radius scaled by the half the H I diameter from Paper I. |
| Open with DEXTER | |
All of the galaxies in our sample display this flaring profile, except
ESO138-G014 which is considered unreliable due to missing large-scale H I structure
(see Sect. 4.4).
Unfortunately, we were unable to detect this radial change in flaring
profile shape in ESO274-G001, the galaxy with the highest spatial
resolution in our sample, as we were unable to measure the gas
thickness at radii outside the stellar disk, due to a lack of
short-spacing observations. Excluding ESO138-G014, all the more
massive galaxies (
![]() km s-1) display a shallower flaring
profile over the inner disk. With the exclusion of ESO146-G014, the
three remaining small disk galaxies (
km s-1) display a shallower flaring
profile over the inner disk. With the exclusion of ESO146-G014, the
three remaining small disk galaxies (
![]() km s-1) all display
steep linear inner flaring profiles.
km s-1) all display
steep linear inner flaring profiles.
The flaring profile of ESO146-G014 shows remarkable similarities to the flaring profile of UGC 7321. Apart from a similar central face-on B-band stellar surface brightness (respectively 23.4 and 23.8 mag arcsec-2), these two galaxies appear quite different - ESO146-G014 has a much lower rotation speed and H I velocity dispersion.
The three well-measured large galaxies (IC2531, IC5249 and UGC 7321) and the unusual ESO146-G014, each display one common profile with a small FWHMz. A common flaring profile in the inner disk suggests a common ratio of the H I velocity dispersion to the stellar density, assuming the stellar density dominates at low radii. The ratio of mean H I velocity dispersion to maximum rotation speed is very similar in IC5249, UGC 7321 and ESO146-G014, the value for IC2531 is roughly half that of the others.
The radial gradient of the flaring is more varied in the smaller galaxies. The coalignment of the inner flaring slopes of UGC 7321, IC5249 and IC2531 is probably a coincidence, as a comparison of IC2531's flaring profile to that of the Galaxy (Olling & Merrifield 2000) shows that the gas disk of IC2531 is approximately twice as thick as the Galactic H I layer.
In Fig. 25 we show the flaring
profiles with the horizontal axis scaled with (half) the diameter of the H I distribution, taken from Paper I. This does make the profiles more comparable
in shape, although still there is quite some variation of the thickness of the
H I in kpc from galaxy to galaxy.
We have done the same by scaling to (half) the optical radius, taken from
NED![]() . Not surprisingly, the
result is similar since the optical and H I diameters do
in general correlate among galaxies,
although the relative positions of the lines with respect to each other is different.
For comparison, the flaring profile of NGC 891 (van der Kruit 1981) would be on
the scale of Fig. 25 run from about 0.3 kpc at
0.2 scaled galactocentric radius to 1.9 kpc at 1.0. This is thinner
than in our systems, but that is not surprising since our sample was
selected to be made up of galaxies with low contributions of the disks to
the gravitational potential and the thickness of the H I layer
is to a larger extent determined
by that of the dark matter halo, which would be less flattened than the disk.
. Not surprisingly, the
result is similar since the optical and H I diameters do
in general correlate among galaxies,
although the relative positions of the lines with respect to each other is different.
For comparison, the flaring profile of NGC 891 (van der Kruit 1981) would be on
the scale of Fig. 25 run from about 0.3 kpc at
0.2 scaled galactocentric radius to 1.9 kpc at 1.0. This is thinner
than in our systems, but that is not surprising since our sample was
selected to be made up of galaxies with low contributions of the disks to
the gravitational potential and the thickness of the H I layer
is to a larger extent determined
by that of the dark matter halo, which would be less flattened than the disk.
In this work we have measured the vertical thickness of the H I disk
by fitting a single Gaussian gas component. We have not attempted to
fit the thickness by a two Gaussian components as others have done,
because the single Gaussian model was a good fit. Earlier higher
resolution VLA observations of NGC 891 yielded an exponentially flaring
thin H I layer. More recent studies of its gas thickness, using
exceptionally sensitive lower resolution WSRT observations
with ![]() 350 h integration time, recover
extended filamentary high latitude H I with unusual velocity
structure comprising
350 h integration time, recover
extended filamentary high latitude H I with unusual velocity
structure comprising ![]() of the total H I mass
(Fraternali et al. 2004; Oosterloo et al. 2007).
By applying this dual gas component modelling process to the initial
144 h of WSRT data on NGC 891, Swaters et al. (1997) found that
the traditional warped and flared gas layer did not simulate the high
latitude inner disk gas. Indeed the best models of NGC 891 tested in
this fashion used two disks each of constant thickness, with
of the total H I mass
(Fraternali et al. 2004; Oosterloo et al. 2007).
By applying this dual gas component modelling process to the initial
144 h of WSRT data on NGC 891, Swaters et al. (1997) found that
the traditional warped and flared gas layer did not simulate the high
latitude inner disk gas. Indeed the best models of NGC 891 tested in
this fashion used two disks each of constant thickness, with
![]() kpc and
kpc and
![]() kpc,
for the thin and thick disk respectively, where the thick disk
rotation lags that of the planar gas, and also displays some radial
infall motion.
kpc,
for the thin and thick disk respectively, where the thick disk
rotation lags that of the planar gas, and also displays some radial
infall motion.
Similar two-component H I modelling has been undertaken on several less-inclined large galaxies: NGC 2403 (Fraternali et al. 2002), NGC 4559 (Barbieri et al. 2005), NGC 253 (Boomsma 2007) and NGC 6946 (Fraternali et al. 2004; Boomsma 2007). Each of these galaxies is actively star-forming with significant fractions of their total H I mass (10-30%) exhibiting anomalous velocities forbidden by circular rotation. As discussed in Sect. 4, Mattthews & Wood (2003) also applied this model to UGC 7321, a low surface brightness galaxy in our sample. In each of these galaxies, modelling has found a thick gas layer combined with a thin constant thickness or flaring thin gas layer. With the exception of UGC 7321, the high stellar density, star formation rate and stellar disk area of these galaxies are all conducive to ejecting a greater H I mass fraction to high latitudes, whether by discrete star formation or large scale galactic fountains. Despite the massive amount of H I in the halos of these galaxies, this inner high latitude H I is probably more akin to Galactic high velocity clouds than a continuous broad H I component.
As discussed in Paper I, a small amount of
high latitude filamentary H I is observed in the larger galaxies in
our sample, with
![]() km s-1, at projected radii corresponding
to the inner disk. However this gas makes up only a small fraction (
km s-1, at projected radii corresponding
to the inner disk. However this gas makes up only a small fraction (![]() 5
5![]() )
of the total gas mass and may not be in hydrostatic
equilibrium. For this reason we have not attempted to measure its mass
distribution.
)
of the total gas mass and may not be in hydrostatic
equilibrium. For this reason we have not attempted to measure its mass
distribution.
5.5 Open issues
As mentioned above, the H I velocity dispersion measured in face-on galaxies were all undertaken with low spatial resolution of 1 kpc, much larger than the scale of most processes in the ISM which are likely to cause local variation in the H I velocity dispersion. Deep high spatial and spectral H I observations of such systems are lacking.
In theory, given high spatial and spectral resolution, it is possible to determine the intrinsic shape of the H I line spectrum, and whether the velocity structure is best represented by one or more Gaussians, or a non-Gaussian function. Petric & Rupen (2006) found that the H I line profile was best fit by a two-Gaussian shape where the ratio of the integrated flux of the thick and thin Gaussians was constant at all radii with good signal-to-noise. The only edge-on galaxy with bright H I that is close enough to image at the required resolution is the small Scd galaxy, NGC 4244, studied by Olling (1996).
It is also important to test the isothermality of the H I distribution by fitting the H I velocity dispersion to XV maps formed from gas at different heights above the galactic plane. This is important; without further information about the z-dependence of the velocity dispersion, we would need to assume z-isothermality when using the equations of hydrostatic equilibrium to derive the vertical potential of the dark matter halo. Although the spatial resolution of ESO274-G001 is sufficient to independently measure the gas at several heights above the plane, additional H I observations in compact array configurations would be needed.
Our H I observations in Paper I show
significant optical depth (assuming H I spin temperatures of 200-400
K) in isolated locations of several galaxies in our sample.
It would be interesting to generalise the XV modelling to also fit the zdirection, as this would allow the H I opacity to be accurately measured
across the galaxy. Such a generalised model would measure the gas
density ![]() .
By integrating over the line of sight, the total
H I column density and H I opacity consistent with the kinematic model
could be calculated and
compared to the observed H I column density to check the calculated
H I opacity. This requires higher spatial resolution data than we have
available in this study.
.
By integrating over the line of sight, the total
H I column density and H I opacity consistent with the kinematic model
could be calculated and
compared to the observed H I column density to check the calculated
H I opacity. This requires higher spatial resolution data than we have
available in this study.
6 Summary and conclusions
Using our new XV modelling method detailed in Paper II we have successfully fit the rotation curves of all eight galaxies in our sample; and the H I velocity dispersion and surface density in all the galaxies except for the inner disk of IC2531. The rotation curve was the most reliably fit achieving an accuracy of roughly 2-4 km s-1. The surface density was also very reliably measured. The H I velocity dispersion was more sensitive to local variations and noise in the XV map, however despite these challenges the uncertainty in the derived H I velocity dispersion is only about 1-1.5 km s-1, which is comparable to the accuracy obtained from NGC 4244 by Olling (1996). The prevalence of bars in the larger galaxies and the increase in the mean velocity dispersion with maximum rotation speed suggests that bar buckling may be a common cause of widespread gas heating in disk galaxies.
The measured rotation curves show that all galaxies in our sample display differential rotation, even the smallest galaxies IC5052 and ESO115-G021 which have peak rotation speeds of only 60 km s-1. The increased velocity dispersion by 1-2.5 km s-1 observed in galaxies with bars suggests that shocks caused by disk instabilities in bars can cause gas heating.
Iterative fitting of the H I layer thickness enabled us to reliably
measure the H I flaring in 7 of the 8 galaxies in our sample, despite
![]() beamwidths of up to 1.3 kpc and a low peak channel
map signal-to-noise of around 13 for most of the galaxies in our
sample. The only galaxy we were unable to reliably fit was ESO138G-014
which was missing large scale H I structure due to an absence of short
baseline observations, and also suffered low peak signal-to-noise
(15) and a large telescope beam (0.965 kpc). For galaxy
observations with only two of these three handicaps it was possible to
iteratively recover a flaring model that fit the observed H I channel
map distribution. UGC 7321 is the most accurately measured flaring
profile in our sample with errors of only 15-50 pc over most of the
radial extent.
beamwidths of up to 1.3 kpc and a low peak channel
map signal-to-noise of around 13 for most of the galaxies in our
sample. The only galaxy we were unable to reliably fit was ESO138G-014
which was missing large scale H I structure due to an absence of short
baseline observations, and also suffered low peak signal-to-noise
(15) and a large telescope beam (0.965 kpc). For galaxy
observations with only two of these three handicaps it was possible to
iteratively recover a flaring model that fit the observed H I channel
map distribution. UGC 7321 is the most accurately measured flaring
profile in our sample with errors of only 15-50 pc over most of the
radial extent.
The flaring profiles show an impressive degree of the symmetry between flaring measurements on either side of the galaxy - this is most clearly seen in UGC 7321. Axial symmetry of the gas layer thickness is expected as in the absence of local variations of the stellar surface density or gas velocity dispersion, the vertical flaring should reflect the smooth symmetric gravitational potential of the dark matter halo. The exceptionally smooth flaring profile of UGC 7321 shows that, on the 0.7 kpc scale of telescope beam, the stellar surface density and dark matter halo gravitational potential are also smooth.
The most remarkable feature of H I flaring
profiles is a common shape displaying a linear
increase at low radii and steepening to an exponential increase in the
outer disk. The steepness of the inner flaring should be dominated by
the radial surface density, while at the stellar disk truncation
radius the flaring becomes exponential and is dominated by the dark
halo shape. This typical flaring shape is found in all of the galaxies
except ESO138-G014 which was incompletely imaged, and ESO274-G001
which appears to have a more linear flaring profile. With the
exception of ESO146-G014, all of the less massive galaxies (
![]() km s-1) display steep inner flaring profiles. The four larger
galaxies (
km s-1) display steep inner flaring profiles. The four larger
galaxies (
![]() km s-1), excluding ESO138-G014, display much
shallower inner flaring profiles.
km s-1), excluding ESO138-G014, display much
shallower inner flaring profiles.
The high sensitivity of the UGC 7321 observations allowed us to discern
variations from azimuthal symmetry of both the H I midplane position
and the H I thickness. We show that at radii from approximately 2.5 to 6 kpc along the Y=0 axis,the FWHMz gas thickness
varies by up to 500 pc from the azimuthally averaged flaring in
those radial annuli. At this same locations along the Y=0 axis the gas midplane tilts, dropping ![]() 200 pc below the average
disk midplane on the left-hand side, and rising
200 pc below the average
disk midplane on the left-hand side, and rising ![]() 200 pc above the
midplane on the right-hand side. These local deviations are considered to
be best observational evidence for a bar in an edge-on disk galaxy.
200 pc above the
midplane on the right-hand side. These local deviations are considered to
be best observational evidence for a bar in an edge-on disk galaxy.
The next paper in this series will be devoted to an analysis of the data on UGC 7321 as a first attempt at deriving constraints on the flattening of a dark halo.
AcknowledgementsWe are very grateful to Albert Bosma who contributed greatly to initiating this project. He pointed out that H I flaring studies are best done on edge-on galaxies with low maximum rotational velocities, and we used an unpublished Parkes H I survey of edge-on galaxies by Bosma and KCF when selecting our galaxies. J.C.O. thanks E. Athanassoula, M. Bureau, R. Olling, A. Petric and J. van Gorkom for helpful discussions. J.C.O. is grateful to B. Koribalski, R. Sault, L. Staveley-Smith and R. Wark for help and advice with data reduction and analysis. We thank the referee, J.M. van der Hulst, for his careful and thorough reading of the manuscripts of this series of papers and his helpful and constructive remarks and suggestions.
References
- Abe, F., Bond, I. A., Carter, B. S, et al., 1999, AJ, 118, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Agertz, O., Lake, G., Teyssier, R. et al. 2009, MNRAS, 392, 284 [Google Scholar]
- Barbieri, C. V., Fraternali, F., Oosterloo, T., et al. 2005, A&A, 439, 947 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Binney, J., Gerhard, O. E., Stark, A. A., Bally, J., & Uchida, K. I. 1991, MNRAS, 252, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Boomsma, R. 2007, Ph.D. Thesis, Groningen [Google Scholar]
- Boomsma, R., Oosterloo, T. A., Fraternali, F., van der Hulst, J. M., & Sancisi, R. 2008, A&A, 490, 555 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bottema, R., Shostak, G. S., & van der Kruit, P. C. 1986, A&A, 167, 34 [NASA ADS] [Google Scholar]
- Boulanger, F., & Viallefond, F. 1992, A&A, 266, 37 [NASA ADS] [Google Scholar]
- Braun, R. 1991, ApJ, 372, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Bureau, M., & Freeman, K. C. 1999, AJ, 118, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Combes, F., Debbasch, F., Friedli, D., et al. 1990, A&A, 233, 82 [NASA ADS] [Google Scholar]
- Contopoulos, G., & Mertzanides, C. 1977, A&A, 61, 477 [NASA ADS] [Google Scholar]
- Dalcanton, J. J., Yoachim, P., & Bernstein, R.A. 2004, ApJ, 608, 189 [NASA ADS] [CrossRef] [Google Scholar]
- de Blok, W. J. G., & Bosma, A. 2002, A&A, 385, 816 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fraternali, F., van Moorsel, G., Sancisi, R. et al. 2002, AJ, 123, 3124 [NASA ADS] [CrossRef] [Google Scholar]
- Fraternali, F., Oosterloo, T., Boomsma, R., Swaters, R. & Sancisi, R. 2004, IAU Symp. 217, ed. P.-A. Duc, J. Braine, & E. Brink (San Francisco: ASP), 136 [Google Scholar]
- Gurovich, S., Freeman, K. C., Jerjen, H., et al. 2010, ApJ, accepted,[arXiv:1004.4365] [Google Scholar]
- Kamphuis, J., & Sancisi, R. 1993, A&A, 273, L31 [NASA ADS] [Google Scholar]
- Kregel, M., & van der Kruit, P. C. 2004, MNRAS, 352, 787 [NASA ADS] [CrossRef] [Google Scholar]
- Kregel, M., van der Kruit, P. C., & de Grijs, R. 2002, MNRAS, 334, 646 [NASA ADS] [CrossRef] [Google Scholar]
- Matthews, L. D., & Wood, K. 2003, ApJ, 593,721 [NASA ADS] [CrossRef] [Google Scholar]
- Matthews, L. D., Gallagher III, J. S., & van Driel, W. 1999, AJ, 118, 2751 [NASA ADS] [CrossRef] [Google Scholar]
- McKee, C. F., & Ostriker, J. P. 1977, ApJ, 218, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Merrifield, M. R. 1992, AJ, 103, 1552 [NASA ADS] [CrossRef] [Google Scholar]
- O'Brien, J. C., Freeman, K. C., van der Kruit, P. C., et al. 2010a, A&A, 515, A60 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- O'Brien, J. C., Freeman, K. C. & van der Kruit, P. C. 2010b, A&A, 515, A61 (Paper II) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Olling, R. P. 1995, AJ, 110, 591 [NASA ADS] [CrossRef] [Google Scholar]
- Olling, R. P. 1996, AJ, 112, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Olling, R. P., & Merrifield, M. R. 2000, MNRAS, 311, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Oort, J. H., & Spitzer, L. 1955, ApJ, 121, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Oosterloo, T., Fraternali, F., & Sancisi, R. 2007, AJ, 134, 1019 [NASA ADS] [CrossRef] [Google Scholar]
- Petric, A. O., & Rupen, M. P. 2007, AJ, 134, 1952 [NASA ADS] [CrossRef] [Google Scholar]
- Pohlen, M., Balcells, M., Lütticcke, R., et al. 2003, A&A, 409, 485 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quiroga, R. J. 1983, Ap&SS, 93, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Rohlfs, K., & Kreitschmann, J. 1987, A&A, 178, 95 [NASA ADS] [Google Scholar]
- Rots, A. H. 1974, Ph.D. Thesis, Groningen [Google Scholar]
- Rownd, B. K., Dickey, J. M., & Helou, G. 1994, AJ, 108, 1638 [NASA ADS] [CrossRef] [Google Scholar]
- Rupen, M. P., Ph.D. Thesis, Columbia [Google Scholar]
- Sancisi, R., & Allen, R. J. 1979, A&A, 74, 73 [NASA ADS] [Google Scholar]
- Sellwood, J. A., & Balbus, S. A. 1999, ApJ, 511, 660 [NASA ADS] [CrossRef] [Google Scholar]
- Shostak, G. S., & van der Kruit, P. C. 1984, A&A, 132, 20 [NASA ADS] [Google Scholar]
- Spitzer, L. 1978, Physical Processes in the Interstellar Medium, (New York: Wiley Interscience) [Google Scholar]
- Swaters, R. S. 1999, Ph.D. Thesis, Groningen [Google Scholar]
- Swaters, R. S., Sancisi, R., & van der Hulst, J. M. 1997, ApJ, 491, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Tamburro, D. Rix, H.-W. Leroy, A. K. et al. 2009, AJ, 137, 4424 [NASA ADS] [CrossRef] [Google Scholar]
- van der Kruit, P. C. 1981, A&A, 99, 298 [NASA ADS] [Google Scholar]
- van der Kruit, P. C & Shostak, G. S. 1982, A&A, 105, 351 [Google Scholar]
- van der Kruit, P. C., & Shostak, G. S. 1984, A&A, 134, 258 [NASA ADS] [Google Scholar]
- van der Kruit, P. C., Jiménez-Vicente, J., Kregel, M., et al. 2001, A&A, 379, 374 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wada, K., Meurer, G., & Norman, C. A. 2002, ApJ, 577, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Wong, T., Blitz, L., & van der Hulst, J. M. 2004, Ap&SS, 289, 211 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ...
![[*]](/icons/foot_motif.png)
- For correspondence contact Ken Freeman or Piet van der Kruit.
- ...
Release
![[*]](/icons/foot_motif.png)
- http://www.atnf.csiro.au/research/multibeam/release
- ...
(LVHIS
![[*]](/icons/foot_motif.png)
- http://www.atnf.csiro.au/research/LVHIS/ic5052/ATCAresults
- ... galaxy
![[*]](/icons/foot_motif.png)
- We thank Lia Athanassoula for pointing this out.
- ... deprojection
![[*]](/icons/foot_motif.png)
- Private communication with Agris Kalnajs.
- ...
NED
![[*]](/icons/foot_motif.png)
- This NASA/IPAC Extragalactic Database is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration.
All Figures
![\begin{figure}
\par\includegraphics[width=15cm,clip]{12567fg1.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg14.png)
|
Figure 1:
ESO074-G015 (IC5052).
This figure shows the results of the modelling of the kinematics.
The best fit measurements for each kinematic function are shown in as (red)
crosses for the the H I velocity dispersion in the top left-hand panel
and in the lower left-hand plot for the deprojected H I surface density. The top right-hand panel shows the derived rotation curve (dark/red) overlaid on the observed XV diagram. Also
shown on the XV diagram are the rotation fits obtained using the
less accurate envelope tracing method (dark grey/orange) and the peak flux
method (light grey/yellow). The latter always shows a lower rotation
velocity than the other two fits.
The lower right-hand plot displays the derived rotation
curve with the receding and approaching sides separately
(in the electronic version red and blue respectively).
The FWHM synthesised beam has dimensions
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{12567fg2.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg16.png)
|
Figure 2:
ESO109-G021 (IC5249).
This figure shows the results of the modelling of the kinematics. For an
explanation of the figure see the caption of Fig. 1.
The FWHM synthesised beam has dimensions
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{12567fg3.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg18.png)
|
Figure 3:
ESO115-G021.
This figure shows the results of the modelling of the kinematics. For an
explanation of the figure see the caption of Fig. 1.
The FWHM synthesised beam has dimensions
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{12567fg4.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg20.png)
|
Figure 4:
ESO138-G014.
This figure shows the results of the modelling of the kinematics. For an
explanation of the figure see the caption of Fig. 1.
The FWHM synthesised beam has dimensions
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{12567fg5.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg22.png)
|
Figure 5:
ESO146-G014.
This figure shows the results of the modelling of the kinematics. For an
explanation of the figure see the caption of Fig. 1.
The FWHM synthesised beam has dimensions
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{12567fg6.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg27.png)
|
Figure 6:
ESO274-G001.
This figure shows the results of the modelling of the kinematics. For an
explanation of the figure see the caption of Fig. 1.
The FWHM synthesised beam has dimensions
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{12567fg7.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg29.png)
|
Figure 7:
ESO435-G025 (IC2531).
This figure shows the results of the modelling of the kinematics. For an
explanation of the figure see the caption of Fig. 1.
The FWHM synthesised beam has dimensions
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{12567fg8a.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg30.png)
|
Figure 8a:
UGC 7321.
This figure shows the results of the modelling of the kinematics. For an
explanation of the figure see the caption of Fig. 1.
The FWHM synthesised beam has dimensions
|
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm]{12567fg8b.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg31.png)
|
Figure 8b:
UGC 7321.
This figure shows the observed XV diagram ( upper panel),
the model XV diagram formed from the best fit kinematics ( middle panel),
and the map with residuals between the two ( lower panel).
The contours are in units of the rms noise, which is
|
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{aa12567-fig9.eps}
\vspace*{1cm}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg54.png)
|
Figure 9: ESO074-G015 (IC5052). Top panel: measured FWHMz thickness of the H I gas disks. Lower panels: each of the kinematic functions of the H I reflected about the galactic centre to show both sides of the galaxy, and the average of both sides. Middle left: rotation curve; middle right: H I velocity dispersion; lower left: H I surface density; lower right: H I vertical thickness FWHMz. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{aa12567-fig10.eps}
\vspace*{-3.5mm}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg55.png)
|
Figure 10: ESO109-G021 (IC5249). Measured FWHMz thickness of the H I gas disk and the kinematic functions of the H I. For details see the caption of Fig. 9. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{aa12567-fig11.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg56.png)
|
Figure 11: ESO115-G021. Measured FWHMz thickness of the H I gas disk and the kinematic functions of the H I. For details see the caption of Fig. 9. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{aa12567-fig12.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg57.png)
|
Figure 12: ESO138-G014. Measured FWHMz thickness of the H I gas disk and the kinematic functions of the H I. For details see the caption of Fig. 9. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{aa12567-fig13.eps}
\vspace*{3.5mm} \end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg58.png)
|
Figure 13: ESO146-G014. Measured FWHMz thickness of the H I gas disk and the kinematic functions of the H I. For details see the caption of Fig. 9. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{aa12567-fig14.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg59.png)
|
Figure 14: ESO274-G001. Measured FWHMz thickness of the H I gas disk and the kinematic functions of the H I. For details see the caption of Fig. 9. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{aa12567-fig15.eps}
\vspace*{8mm}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg60.png)
|
Figure 15: ESO435-G025 (IC2531). Measured FWHMz thickness of the H I gas disk and the kinematic functions of the H I. For details see the caption of Fig. 9. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{aa12567-fig16.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg61.png)
|
Figure 16: UGC 7321. Measured FWHMz thickness of the H I gas disk and the kinematic functions of the H I. For details see the caption of Fig. 9. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12567fg17-1.eps}\hspace*{1.5mm}
\includegraphics[width=7.4cm,clip]{12567fg17-2.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg62.png)
|
Figure 17: Left - All the vertical profiles in a sample of galactocentric radial bins in UGC 7321. The radius of the bin is given in the top right-hand corner of each plot. Each radial bin is 145.4 pc wide - the same size as the image pixels along the major and minor axes of UGC 7321. The ordinate axis of each plot shows the H I column density in units of H I atoms cm-2 in each vertical slice. Right - The same as on the left-hand side, but now we show average profiles, which were obtained after aligning the profile centres and vertically rescaling all profiles to a peak of 1. Overlaid in blue is the Gaussian fit to each average profile. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12567fg18.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg68.png)
|
Figure 18: Measured H I FWHMz thickness ( upper panel) and H I midplane location ( lower panel) of UGC 7321 as a function of radius, where the measurements are colour coded by the line-of-sight velocity of each channel map. The most bluewards points were measured from the extreme approaching velocities, and those most redwards were measured from the extreme receding velocities. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12567fg19-1.eps}\par\includegraphics[width=8cm,clip]{12567fg19-2.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg69.png)
|
Figure 19: Measured FWHMz thickness ( upper panel) and midplane displacement ( lower panel) of the H I disk of UGC 7321 deprojected onto the X-Y plane, where the color scale on each plot shows the respective FWHMz or midplane displacement measurements. Measurements in white are off the top end of the color scale. Each line of measurements forming a coloured track shows the measurements from a single H I channel map. The measurements are the same on each side of the Y=0 line, as due to the edge-on orientation of the gas disk, we can't determine if H I emission comes from the near or far side of the disk. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{12567fg20.eps.old}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg77.png)
|
Figure 20: The H I rotation curves for all galaxies in our sample overlaid on each other for comparison. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{12567fg21.eps.old}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg78.png)
|
Figure 21: The H I velocity dispersion profiles for all galaxies in our sample overlaid on each other for comparison. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12567fg22.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg80.png)
|
Figure 22:
Mean H I velocity dispersion
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{12567fg23.eps.old}
\vspace{3mm}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg84.png)
|
Figure 23: The face-on surface density profiles for all galaxies in our sample overlaid on each other for comparison. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{12567fg24.eps.old} \vspace{3mm}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg85.png)
|
Figure 24: Measured FWHMz thicknesses of the H I gas disks. ESO 138-G14 has been omitted from this figure, as explained in Sect. 4.4. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{12567fg25.eps.old}
\end{figure}](/articles/aa/full_html/2010/07/aa12567-09/Timg86.png)
|
Figure 25: Measured FWHMz thicknesses of the H I gas disks. The horizontal axis is radius scaled by the half the H I diameter from Paper I. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.