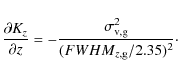| Issue |
A&A
Volume 515, June 2010
|
|
|---|---|---|
| Article Number | A60 | |
| Number of page(s) | 17 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/200912565 | |
| Published online | 09 June 2010 | |
The dark matter halo shape of edge-on disk galaxies
I. HI observations
J. C. O'Brien1 - K. C. Freeman1 - P C. van der Kruit2 - A. Bosma3
1 - Research School of Astronomy and Astrophysics, Australian National
University, Mount Stromlo Observatory, Cotter Road, ACT 2611, Australia
2 - Kapteyn Astronomical Institute, University of Groningen,
PO Box 800, 9700 AV Groningen, The Netherlands ![]()
3 - Laboratoire d'Astrophysique de Marseille, UMR 6110 Université de
Provence/CNRS, 38 rue Frédéric Joliot-Curie, 13388 Marseille Cedex 13,
France
Received 25 May 2009 / Accepted 9 March 2010
Abstract
This is the first paper of a series in which we will attempt to put
constraints on the flattening of dark halos in disk galaxies. We
observe for this purpose the H I in edge-on galaxies, where it is in
principle possible to measure the force field in the halo vertically
and radially from gas layer flaring and rotation curve decomposition
respectively. In this paper, we define a sample of 8 H I rich late-type
galaxies suitable for this purpose and present the H I observations.
Key words: galaxies: structure - galaxies: kinematics and dynamics - galaxies: halos - galaxies: ISM
1 Introduction
Since the 1970's, it has been known that the curvature of the universe
is remarkably flat. This implies that the ratio of the total density
to critical density is ![]() .
At this time, it
was also known from measurements of stars and gas that the mass
density of luminous matter is
.
At this time, it
was also known from measurements of stars and gas that the mass
density of luminous matter is ![]() - less
than
- less
than ![]() of that required for a flat
of that required for a flat ![]() universe.
Indeed, the missing matter controversy had begun in the 1930's when Oort (1932), following Kapteyn (1922), and Zwicky (1937) independently
found evidence for vast amounts of unseen matter on different scales.
Oort's analysis of the spatial and velocity distribution of stars in
the Solar
neighbourhood concluded that luminous stars comprised approximately
half the total mass indicated by their motion, assuming
gravititational equilibrium. Zwicky's analysis of the velocity
dispersions
of rich clusters found that approximately
universe.
Indeed, the missing matter controversy had begun in the 1930's when Oort (1932), following Kapteyn (1922), and Zwicky (1937) independently
found evidence for vast amounts of unseen matter on different scales.
Oort's analysis of the spatial and velocity distribution of stars in
the Solar
neighbourhood concluded that luminous stars comprised approximately
half the total mass indicated by their motion, assuming
gravititational equilibrium. Zwicky's analysis of the velocity
dispersions
of rich clusters found that approximately ![]() of the mass was unseen, if the systems were gravitationally bound.
Later on, the
inventory of the mass in the Solar neighbourhood showed that the dark
matter in the galactic disk at the solar galactocentric radius was
mostly fainter
stars and interstellar gas (e.g. Holmberg
& Flynn 2000). Zwicky's
value of the velocity dispersion in the Coma cluster is close to the
current one (e.g. Colless & Dunn
1996), and, despite the presence of hot X-ray emitting gas,
there must be dark matter to cause
of the mass was unseen, if the systems were gravitationally bound.
Later on, the
inventory of the mass in the Solar neighbourhood showed that the dark
matter in the galactic disk at the solar galactocentric radius was
mostly fainter
stars and interstellar gas (e.g. Holmberg
& Flynn 2000). Zwicky's
value of the velocity dispersion in the Coma cluster is close to the
current one (e.g. Colless & Dunn
1996), and, despite the presence of hot X-ray emitting gas,
there must be dark matter to cause ![]() .
.
Modern dark matter research began in 1970 with several papers
which found that galaxies contain more gravitating matter than can
be accounted for by the stars. Freeman
(1970) noted
that the atomic hydrogen (H I) rotation curves of the late-type disk
galaxies NGC 300 and M 33 peaked at a larger
radius than expected
from the stellar light distribution. This implied that the dark
matter was more extended than the stellar distribution and that its
mass was at least as great as the luminous mass. However, these data
were of poor angular
resolution. At the same time Rubin
& Ford (1970) published a rotation
curve of M 31 based on optical data, which did not seem to
decline in the outer parts.
In the 1970s radio observations of increasingly better angular
resolution and better sensitivity![]() showed that flat rotation curves
are typical in spiral galaxies (Shostak 1971; Bosma 1978;
Rogstad
& Shostak 1972; Roberts & Rots 1973)
and that the HI extent of a spiral galaxy can be far greater than
the extent of the optical image. This, combined with surface
photometry, leads to very high mass-to-light ratios in the outer parts,
as shown clearly for several galaxies in Bosma
(1978) and
Bosma & van der Kruit (1979).
showed that flat rotation curves
are typical in spiral galaxies (Shostak 1971; Bosma 1978;
Rogstad
& Shostak 1972; Roberts & Rots 1973)
and that the HI extent of a spiral galaxy can be far greater than
the extent of the optical image. This, combined with surface
photometry, leads to very high mass-to-light ratios in the outer parts,
as shown clearly for several galaxies in Bosma
(1978) and
Bosma & van der Kruit (1979).
In 1974, dark
matter halos were found to extend even further, when Ostriker et al. (1974)
and Einasto et al. (1974)
tabulated galaxy masses as a function of radius
and found that galaxy mass increased linearly out
to at least 100 kpc and ![]() for normal spirals
and ellipticals. Despite this large dark matter fraction inferred
in galaxies, it was still not sufficient to reach the critical
for normal spirals
and ellipticals. Despite this large dark matter fraction inferred
in galaxies, it was still not sufficient to reach the critical
![]() value of a flat universe. See e.g. Sofue
& Rubin (2001) and Roberts
(2008)
for a brief history of dark matter in galaxies.
value of a flat universe. See e.g. Sofue
& Rubin (2001) and Roberts
(2008)
for a brief history of dark matter in galaxies.
Around the same time, application of nuclear physics to Big
Bang
theory showed that big bang nucleosynthesis (BBNS) in the early
universe produced specific abundances of the light
elements, and predicted the total baryon density was ![]() .
In the last decade, the combined observations of high redshift SNIa,
(Reiss
et al. 1998; Perlmutter et al. 1999),
the 2-Degree Field Galaxy
Redshift Survey (2dFGRS) (Percival
et al. 2001) and WMAP microwave background
measurements (Spergel
et al. 2003) confirmed the baryonic mass density
.
In the last decade, the combined observations of high redshift SNIa,
(Reiss
et al. 1998; Perlmutter et al. 1999),
the 2-Degree Field Galaxy
Redshift Survey (2dFGRS) (Percival
et al. 2001) and WMAP microwave background
measurements (Spergel
et al. 2003) confirmed the baryonic mass density ![]() found by BBNS and established
that dark energy comprises about 75% of the critical density.
Consequently, the scale of the missing
dark matter is now reduced. The mass density
found by BBNS and established
that dark energy comprises about 75% of the critical density.
Consequently, the scale of the missing
dark matter is now reduced. The mass density ![]() is now only
0.25, but the problem remains: the measured baryonic mass density
is still only
is now only
0.25, but the problem remains: the measured baryonic mass density
is still only ![]() 18%
of the total mass density
18%
of the total mass density ![]() .
Thus, dark matter accounts for 82% of mass in the universe, and
baryonic matter is only 4.5% of the total content of the universe
.
Thus, dark matter accounts for 82% of mass in the universe, and
baryonic matter is only 4.5% of the total content of the universe![]() .
.
More than 1000 galactic rotation curves have now been
measured, and
very few display a Keplerian decline with radius. H I and H![]() rotation curves of spiral galaxies show that the total-mass-to-light
ratios are typically
rotation curves of spiral galaxies show that the total-mass-to-light
ratios are typically ![]() /
/![]() ,
and the
luminous matter therefore accounts for only
,
and the
luminous matter therefore accounts for only ![]() of the total
mass inferred from the rotation curves. For low surface brightness
(LSB) disk galaxies (de Blok 1997)
and dwarf irregular (dI)
galaxies (Swaters 1999),
the M/L values increase to 10-100
of the total
mass inferred from the rotation curves. For low surface brightness
(LSB) disk galaxies (de Blok 1997)
and dwarf irregular (dI)
galaxies (Swaters 1999),
the M/L values increase to 10-100 ![]() /
/![]() ,
with an extreme of 220 for ESO215-G009,
a gas-rich LSB galaxy with a very high gas mass to light ratio of
,
with an extreme of 220 for ESO215-G009,
a gas-rich LSB galaxy with a very high gas mass to light ratio of
![]() and low recent star formation (Warren
et al. 2004).
and low recent star formation (Warren
et al. 2004).
Dwarf spheroidal (dSph) galaxies, with typical total masses of
only
![]() 10
10
![]() within radii of a few hundred parsecs,
are even more extreme: several have very large dark matter fractions
with mass-to-light ratios in the range
within radii of a few hundred parsecs,
are even more extreme: several have very large dark matter fractions
with mass-to-light ratios in the range ![]() /
/![]() .
In these faint, small galaxies, the dynamical mass is estimated
from the line-of-sight velocities of individual stars. The Ursa
Major dSph (Willman
et al. 2005), is one of the most dark matter
dominated galaxies known to date with a central mass-to-light ratio
.
In these faint, small galaxies, the dynamical mass is estimated
from the line-of-sight velocities of individual stars. The Ursa
Major dSph (Willman
et al. 2005), is one of the most dark matter
dominated galaxies known to date with a central mass-to-light ratio
![]() /
/![]() ,
which is believed to increase
further at larger radii (Kleyna
et al. 2005). These systems appear to
have only very small baryonic mass fractions.
,
which is believed to increase
further at larger radii (Kleyna
et al. 2005). These systems appear to
have only very small baryonic mass fractions.
The rotation curves of disk galaxies are important probes
of the equatorial halo potential gradient. By decomposing the observed
rotation curve into contributions from the visible mass components, the
radial potential gradient of the
halo can be measured, assuming the system is in centrifugal
equilibrium. The dark halo mass component is typically fitted
by a pseudo-isothermal halo model with density
where the halo is characterised by its central density
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12565fg1a.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg41.png)
|
Figure 1:
ESO074-G015 (IC5052). H I column density map overlaid on the DSS image.
Contours are plotted in |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12565fg1b.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg42.png)
|
Figure 2:
ESO074-G015 (IC5052). Top left: XV map.
XV contours are |
| Open with DEXTER | |
Kormendy & Freeman (2004)
compiled the published dark halo density distributions
for a large sample of Sc-Im and dSph galaxies, and found well-defined
scaling relationships for the dark halo parameters for galaxies
spanning a range of 6 decades of luminosity![]() . They found that halos
of less luminous and massive dwarf spheroidals have higher central
densities,
up to
. They found that halos
of less luminous and massive dwarf spheroidals have higher central
densities,
up to ![]() 1
1 ![]() pc-3
and
core radii of
pc-3
and
core radii of ![]() 0.1 kpc,
compared to
0.1 kpc,
compared to ![]()
![]() pc-3
and
pc-3
and ![]() 30-100 kpc
respectively, for large bright Sc
galaxies. The observed correlations suggest a continuous physical
sequence of dark halo population in which the properties of the
underlying dark halo scale with the baryon luminosity (Kormendy & Freeman 2004).
30-100 kpc
respectively, for large bright Sc
galaxies. The observed correlations suggest a continuous physical
sequence of dark halo population in which the properties of the
underlying dark halo scale with the baryon luminosity (Kormendy & Freeman 2004).
We now consider the flattening of the dark halo density distribution, defined by q=c/a, where c is the halo polar axis and a is the major axis in the galactic plane. The vertical distribution of the halo is much more difficult to measure than the radial distribution in the equatorial plane, as most luminous tracers of the galaxy potential gradient lie in the plane of the galaxy and offer little indication of the vertical gradient of the potential. Past measurements that were obtained with a variety of different methods gave a large range of q from 0.1 to 1.37, with no concentration on any particular value. For our Galaxy, the halo shape has been measured more than ten times by four different methods, that yielded q-values ranging from 0.45 to 1.37.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{12565fg1c.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg44.png)
|
Figure 3:
ESO074-G015 (IC5052). Top: peak brightness
temperature map. Contours are plotted in |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12565fg2a.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg49.png)
|
Figure 4:
ESO109-G021 (IC5249). H I column density map overlaid on the DSS image.
Contours are plotted in |
| Open with DEXTER | |
In this series of papers, we will use the flaring of the HI gas layer to measure the vertical flattening of the dark halo, because we believe this method to be the most promising for late-type disk galaxies. Like all steady state mass components of a galaxy, the gaseous disk of an isolated disk galaxy can be assumed to be in hydrostatic equilibrium in the gravitational potential of the galaxy, unless there are visible signs from the gas distribution and kinematics that the HI layer is disturbed (e.g. by mergers or local starbursts). In the vertical direction, the gradient of gas pressure is balanced by the gravitation force (ignoring any contribution from a magnetic pressure gradient). From the observed distribution of the gas velocity dispersion and the gas density distribution, we can in principle measure the total vertical gravitational force.
Euler's equation for a steady-state fluid of density ![]() ,
velocity
,
velocity
![]() and
pressure p in a gravitational potential
and
pressure p in a gravitational potential ![]() is
is ![]() .
In the case of a vertically Gaussian gas
density distribution with a vertically isothermal gas velocity
dispersion, the gradient of the total vertical force Kz
in the
z-direction can be calculated directly from the gas
velocity
dispersion
.
In the case of a vertically Gaussian gas
density distribution with a vertically isothermal gas velocity
dispersion, the gradient of the total vertical force Kz
in the
z-direction can be calculated directly from the gas
velocity
dispersion ![]() and the gas layer thickness FWHM
and the gas layer thickness FWHM
![]() ,
each of which are functions of radius:
,
each of which are functions of radius:
It is possible to measure the halo shape over the entire H I extent of the luminous disk using the flaring of the H I distribution, which typically extends in radius to 2-3 R25, and by measuring the density distribution of the gas and stellar distributions. For a given vertical gas velocity dispersion, a more flattened dark halo requires decreased flaring and increased gas surface density. The relatively high gas content of late-type galaxies allows measurement of both the halo vertical force field from the gas layer flaring and the halo radial force field from rotation curve decomposition. In this series of papers we will attempt to measure the halo flattening using the flaring of H I disk in eight small late-type disk galaxies.
The main advantage of this method is that it can be used for
all
gas-rich spiral galaxies inclined sufficiently to measure accurate
kinematics, unlike some methods which are applicable only to specific
kinds of galaxies like polar ring galaxies. This minimum inclination
was determined to be ![]() by Olling (1995).
This method was first tried by Celnik
et al. (1979) on the Galaxy, and early development
was undertaken by van der Kruit
(1981), who applied it to low resolution observations of
NGC 891 and
concluded that the halo was
not as flattened as the stellar disk. It was then used for several
galaxies in the 1990's, most notably the careful study of the very
nearby Sc galaxy NGC 4244 which was found to have a highly
flattened halo with q=0.2+0.3-0.1
out to radii of
by Olling (1995).
This method was first tried by Celnik
et al. (1979) on the Galaxy, and early development
was undertaken by van der Kruit
(1981), who applied it to low resolution observations of
NGC 891 and
concluded that the halo was
not as flattened as the stellar disk. It was then used for several
galaxies in the 1990's, most notably the careful study of the very
nearby Sc galaxy NGC 4244 which was found to have a highly
flattened halo with q=0.2+0.3-0.1
out to radii of ![]() 2 R25
(Olling 1996).
2 R25
(Olling 1996).
All applications of the H I flaring method to date have
derived
highly flattened halo distributions (
![]() ). With the exclusion
of NGC 4244, we suspect that the assumption of a
radially-constant
gas velocity dispersion led to errors in the measured total vertical
force, and thereby to the derived flattening of
the halo. The other difficulty for all these galaxies except
NGC 4244 is that they are large galaxies with peak rotation
speeds
>170 km s-1. Given that
(i) spiral galaxies typically have
H I velocity dispersions in the relatively small range
6-10 km s-1(Tamburro et al. 2009);
and (ii) the halo shape q is roughly proportional
to the gradient of the vertical force, we see from
Eq. (2)
that the H I thickness is to first order
inversely proportional to the peak rotation speed. Consequently, the H
I flaring method should work best for small disk galaxies with
relatively low
rotation speeds, as these galaxies should exhibit more H I flaring. Bosma (1994) already showed by
calculations that flaring is relatively more important in galaxies with
low circular velocity.
). With the exclusion
of NGC 4244, we suspect that the assumption of a
radially-constant
gas velocity dispersion led to errors in the measured total vertical
force, and thereby to the derived flattening of
the halo. The other difficulty for all these galaxies except
NGC 4244 is that they are large galaxies with peak rotation
speeds
>170 km s-1. Given that
(i) spiral galaxies typically have
H I velocity dispersions in the relatively small range
6-10 km s-1(Tamburro et al. 2009);
and (ii) the halo shape q is roughly proportional
to the gradient of the vertical force, we see from
Eq. (2)
that the H I thickness is to first order
inversely proportional to the peak rotation speed. Consequently, the H
I flaring method should work best for small disk galaxies with
relatively low
rotation speeds, as these galaxies should exhibit more H I flaring. Bosma (1994) already showed by
calculations that flaring is relatively more important in galaxies with
low circular velocity.
The flaring method has also been applied to the Galaxy by Olling & Merrifield (2000).
However, uncertainty in the position and rotation speed of the Sun
resulted in a large uncertainty of the measured halo shape ![]() .
.
In this first paper we discuss the selection of our sample and present H I observations. In paper II we will review methods to derive the information we need for our analysis from these data, namely the rotation curves and the H I distributions, H I velocity dispersion and the flaring of the H I layer, all as a function of radius in the deprojected galaxy plane. Paper III will be devoted to applying this to our data and presenting the results for each individual galaxy. In Paper IV will analyse the data of one galaxy in our sample, namely UGC 7321 and we will set limits on the flattening of its dark halo.
2 Observations
2.1 Sample selection
We selected a sample of southern disk galaxies, for observation with the Australia Telescope Compact Array (ATCA), that were small, H I-rich and late-type, in order to maximise the expected flaring and the likelihood that the H I brightness would be sufficient to probe the low surface densities needed to measure the vertical structure of disk galaxies.
The galaxies were chosen to be edge-on (optical major-to-minor
axis
ratio ![]() )
to simplify H I modelling and increase the
accuracy of the measured H I density and kinematics. We avoided
galaxies at
Galactic latitude
)
to simplify H I modelling and increase the
accuracy of the measured H I density and kinematics. We avoided
galaxies at
Galactic latitude ![]() to reduce
Galactic extinction in the optical bands. To minimise uncertainties in
the
stellar mass distribution we chose relatively bulgeless galaxies
with Hubble type Scd-Sd. The galaxies were
chosen to be nearer than 30 Mpc to enable the flaring of the H
I to be
resolved with the 6
to reduce
Galactic extinction in the optical bands. To minimise uncertainties in
the
stellar mass distribution we chose relatively bulgeless galaxies
with Hubble type Scd-Sd. The galaxies were
chosen to be nearer than 30 Mpc to enable the flaring of the H
I to be
resolved with the 6
![]() ATCA synthesised beam. At 30 Mpc the FWHM
of the ATCA beam is
ATCA synthesised beam. At 30 Mpc the FWHM
of the ATCA beam is ![]() 1 kpc.
The vicinity of each galaxy was searched
in NED for nearby neighbours to ensure that it was isolated. The
H I masses of all galaxies satisfying these criteria were measured
from the H I Parkes All-Sky survey (HIPASS) online data
release
1 kpc.
The vicinity of each galaxy was searched
in NED for nearby neighbours to ensure that it was isolated. The
H I masses of all galaxies satisfying these criteria were measured
from the H I Parkes All-Sky survey (HIPASS) online data
release![]() .
With a minimum H I flux integral of 15 Jy km s-1,
this limited our
sample to only 5 galaxies.
.
With a minimum H I flux integral of 15 Jy km s-1,
this limited our
sample to only 5 galaxies.
The nearest isolated thin edge-on galaxy, ESO274-G001, was
added to
the sample. Although it had a Galactic latitude of ![]() ,
it is
exceptionally close at 3.4 Mpc in the Centaurus A galaxy
group,
allowing the H I disk to be measured at a resolution of
,
it is
exceptionally close at 3.4 Mpc in the Centaurus A galaxy
group,
allowing the H I disk to be measured at a resolution of ![]() 150 pc.
A search of H I observations
in the VLA archive revealed the superthin northern Sd galaxy
UGC 7321
which we also added to our sample. We also added the Sb
galaxy IC2531 to our sample, since it has an extended H I disk and a
large quantity of archival observations available. The range of
maximum rotation velocity of our sample galaxies in shown in
Col. 7 of Table 4.
With the inclusion of IC2531, a galaxy with a box/peanut
bulge, and hence barred (Bureau
& Freeman 1999), we
attempt to measure the halo shape of galaxies spanning
different mass scales and stages of secular evolution.
150 pc.
A search of H I observations
in the VLA archive revealed the superthin northern Sd galaxy
UGC 7321
which we also added to our sample. We also added the Sb
galaxy IC2531 to our sample, since it has an extended H I disk and a
large quantity of archival observations available. The range of
maximum rotation velocity of our sample galaxies in shown in
Col. 7 of Table 4.
With the inclusion of IC2531, a galaxy with a box/peanut
bulge, and hence barred (Bureau
& Freeman 1999), we
attempt to measure the halo shape of galaxies spanning
different mass scales and stages of secular evolution.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12565fg2b.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg69.png)
|
Figure 5:
ESO109-G021 (IC5249). Top left: XV map.
XV contours are |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{12565fg2c.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg71.png)
|
Figure 6:
ESO109-G021 (IC5249). Top: peak brightness
temperature map. Contours are plotted in |
| Open with DEXTER | |
Table 1: HI observations.
2.2 Observing modes and method
Galaxies were observed with the ATCA in a range of array configurations to obtain high spatial resolution across each galaxy. In addition, available observations from the ATCA and VLA archives were also used. The list of observations is shown in Table 1. Column 8 shows the integration time in hours of each observation. The resulting resolution and sensitivity of the H I observations are shown in Tables 2 and 3, respectively. We have smoothed the data in Right Ascension to match that in Declination, providing the smallest circular beam possible. The spatial resolutions shown in Table 2 correspond to the FWHM of the resulting beams.
Table 2: Resolution of H I observations.
Table 3: Noise of H I channel maps.
At the ATCA the XX and YY polarisations were used, with a spectral channel width of 3.3 km s-1. At the VLA the RR and LL polarizations were used, and the channel width was 5.2 km s-1. Due to the narrow bandwidth available with the VLA correlator at the time of observations, multiple overlapping bandpasses were observed to fully span the velocity width of the target galaxies. For those observations, each bandpass was calibrated and imaged separately, and the resulting subcubes glued together along the spectral axis.
3 Data reduction and imaging
A detailed account and discussion of the data reduction and imaging procedures is given in the online appendix. Here we restrict ourselves to a brief synopsis.
The reduction of the H I data was performed with the radio interferometry data reduction package MIRIAD. The data were calibrated in the usual manner, using primary and secondary flux calibrators. Solar and terrestrial interference peaks in the calibrator scans were inspected, and flagged if necessary. The bandpass calibration was done using either the primary or, in case of sufficient signal-to-noise ratio, the secondary calibrator. After calibration, the target data were inspected for interference, and flagged appropriately. The radio continuum contribution to each channel map was removed in the uv-plane, by using a suitable average of line-free channel maps.
![\begin{figure}
\par\includegraphics[width=9cm,clip=]{12565fg3a.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg97.png)
|
Figure 7:
ESO115-G021. H I column density map overlaid on the DSS image. Contours
are plotted in |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12565fg3b.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg103.png)
|
Figure 8:
ESO115-G021. Top left: XV map. XV contours are |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{12565fg3c.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg105.png)
|
Figure 9:
ESO115-G021. Top: peak brightness temperature map.
Contours are plotted in |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12565fg4a.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg109.png)
|
Figure 10:
ESO138-G014. H I column density map overlaid on the DSS image. Contours
are plotted in |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12565fg4b.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg116.png)
|
Figure 11:
ESO138-G014. Top left: XV map. XV contours are |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{12565fg4c.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg118.png)
|
Figure 12:
ESO138-G014. Top: peak brightness temperture map.
Countours are plotted in |
| Open with DEXTER | |
4 H I emission
4.1 The H I distribution
To make the H I column density map, the intensity of each channel map
was first converted from flux density I(x,y)
in units of Jy beam-1 to
H I column density ![]() in atoms cm-2 using
in atoms cm-2 using
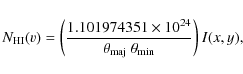
|
(3) |
where
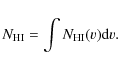
|
(4) |
To exclude any residual sidelobes, a loose region mask was defined interactively for each channel map and then all pixels with flux density above a nominal clip level of 2-3
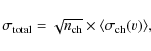
|
(5) |
where
4.2 Global properties
The integrated H I spectrum was measured from the H I data cube using
the H I column density map to mask the cube, and integrating over the
area of the galaxy mask. This flux density spectrum was converted to
units of Jy by dividing by the synthesised beam area
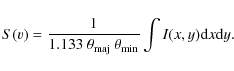
|
(6) |
As the flux was integrated over an equal area in each channel map, the noise of each channel is
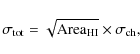
|
(7) |
where Area
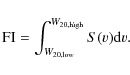
|
(8) |
The restriction of the integration to the velocity range W20 introduces a small but systematic error in the total flux, underestimating it by no more than a few %. However, for our present purposes it is important to examine the integrated profile in order to identify major asymmetries that would make the galaxy unsuitable for our purposes.
Table 4: HI measurements.
The total H I mass, ![]() was then measured from the flux integral
using the formula
was then measured from the flux integral
using the formula
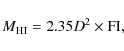
|
(9) |
where the adopted distance D is given in Mpc. These H I measurements are shown in Table 4. These total masses are also underestimated by a few %.
The centre of each galaxy was obtained from the H I column
density map by
rotating the image by ![]() and finding the optimal pixel
offset of the rotated image relative to the original image by
maximising the correlation function of the two images using the IDL
Astronomy User's Library function correl_optimize
and finding the optimal pixel
offset of the rotated image relative to the original image by
maximising the correlation function of the two images using the IDL
Astronomy User's Library function correl_optimize![]() .
Formally this gives the center of the H I disk rather than the
galactic rotational center. Comparison to the coordinates given in the
NASA/IPAC Extragalactic Database
NED
.
Formally this gives the center of the H I disk rather than the
galactic rotational center. Comparison to the coordinates given in the
NASA/IPAC Extragalactic Database
NED![]() , which are derived from
the Two Micron All Sky Survey 2MASS
, which are derived from
the Two Micron All Sky Survey 2MASS![]() ,
show differences of on average only 4 arcsec per coordinate,
except for
ESO074-G015, where it is about 20 arcsec in RA and
30 arcsec in Dec. However,
this galaxy shows some deviations from symmetry, both in optical
appearance as well as in the H I distribution. The position adopted
fits the symmetry of the XV map very well (see Fig. 1)
and is also closer to centers
listed in NED that are derived from photographic and IRAS data.
,
show differences of on average only 4 arcsec per coordinate,
except for
ESO074-G015, where it is about 20 arcsec in RA and
30 arcsec in Dec. However,
this galaxy shows some deviations from symmetry, both in optical
appearance as well as in the H I distribution. The position adopted
fits the symmetry of the XV map very well (see Fig. 1)
and is also closer to centers
listed in NED that are derived from photographic and IRAS data.
The position angle of the galaxy was found by a similar
method.
First a wide range of position angles were trialed around the
estimated position angle. The H I column density map was reflected
over each test position angle about the galaxy center and the
residual of the two maps was calculated. The position angle that
yielded the lowest summed residual was then adopted as the next
position angle estimate. Subsequent rounds spanned smaller and
smaller ranges of the position angle until the position angle was
determined to less than ![]() or until the total residual dropped
below 1% of the summed flux of the H I column density map.
Both
methods worked very well for observations with a near circular
synthesised beam, achieving an accuracy of
or until the total residual dropped
below 1% of the summed flux of the H I column density map.
Both
methods worked very well for observations with a near circular
synthesised beam, achieving an accuracy of ![]() 1 pixel in the
centre position and
1 pixel in the
centre position and ![]() in position angle. However,
observations with a highly elongated beam were poorly fitted, as
the distortion of the image caused by the beam shape biased the
derived PA towards the PA of the synthesised beam. For such
observations the uncertainty of the measured centre and position
angle were larger.
in position angle. However,
observations with a highly elongated beam were poorly fitted, as
the distortion of the image caused by the beam shape biased the
derived PA towards the PA of the synthesised beam. For such
observations the uncertainty of the measured centre and position
angle were larger.
The xzv cube was constructed by rotating
the H I data cube about the galaxy center to align the galaxy major
axis with the X axis. In
Sect. 5
we show the rotated channel maps to
allow the flaring to be viewed directly from the observations. We also
present the H I column density map with the projected major and minor
axis profiles as measured from the H I column density map. The H I
diameter and maximum vertical extent were measured at the ![]() level of the
projected profiles.
level of the
projected profiles.
An XV cube was also produced by reordering the cube axes to form a xvz cube. This cube was then integrated over the z axis to make an XV map using the same method as was used to make the H I column density map. Both the XV map and the H I column density map are shown with their respective noise levels in Sect. 5. The systemic velocity of the galaxy was measured from the XV map by shifting the XV distribution flipped in V with respect to the actual XV map to maximise the correlation function.
Peak brightness temperature maps were also made for each
galaxy,
where the peak brightness temperature is the maximum brightness
temperature over all channel maps at each spatial position. The
brightness temperature ![]() was derived from the H I column density
was derived from the H I column density
![]() in each channel map using
in each channel map using
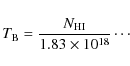
|
(10) |
The major axis profile of the peak brightness map is also shown for each galaxy in Sect. 5. These plots are useful indicators of possible H I self-absorption that could be obscuring the intrinsic H I surface distribution. Section 5 also shows the inferred H I opacity of the brightest H I emission at each major axis position, assuming three different values of the H I spin temperature ( 200, 300, 400 K).
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12565fg5a.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg148.png)
|
Figure 13:
ESO146-G014. H I column density map overlaid on the DSS image. Contours
are plotted in |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12565fg5b.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg153.png)
|
Figure 14:
ESO146-G014. Top left: XV map.
XV contours are |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{12565fg5c.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg155.png)
|
Figure 15:
ESO146-G014. Top: peak brightness temperature map.
Contours are plotted in |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12565fg6a.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg159.png)
|
Figure 16:
ESO274-G001. H I column density map overlaid on the DSS image. Contours
are plotted in |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12565fg6b.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg164.png)
|
Figure 17:
ESO274-G001. Top left: XV map.
XV contours are |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{12565fg6c.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg166.png)
|
Figure 18:
ESO274-G001. Top: peak brightness temperature map.
Contours are plotted in |
| Open with DEXTER | |
5 Results for individual galaxies
In this section we present our data for the galaxies in the sample.
For each galaxy we present the following figures. Part a shows
an H I column density map overlaid on an optical image from the
Digitized Sky Survey (DSS)![]() .
Part b shows the total intensity
position-velocity map (XV map) together with the integrated
spectrum,
and the H I column density map aligned with the major axis of the
galaxy and the corresponding major and minor axis surface density
profiles. Part c shows the peak brightness temperature map
and the corresponding observed major axis profile and compares this
with opacity profiles calculated with some assumed H I spin
temperatures. The individual channel maps were presented
by O'Brien (2007) and
are included in further parts d, e etc.
(depending on how many figures are needed) as online-only material
at the end of this paper.
.
Part b shows the total intensity
position-velocity map (XV map) together with the integrated
spectrum,
and the H I column density map aligned with the major axis of the
galaxy and the corresponding major and minor axis surface density
profiles. Part c shows the peak brightness temperature map
and the corresponding observed major axis profile and compares this
with opacity profiles calculated with some assumed H I spin
temperatures. The individual channel maps were presented
by O'Brien (2007) and
are included in further parts d, e etc.
(depending on how many figures are needed) as online-only material
at the end of this paper.
5.1 ESO074-G015 (IC5052)
ESO074-G015 is a SBd galaxy with a substantial star formation region extending above and below the galactic plane on the west side of the galactic centre. However despite this, the H I column density distribution (shown in Fig. 1) is surprisingly symmetric. Although there is extensive high latitude H I gas extending to 3.7 kpc above and 4.2 kpc below the galactic equator, the distribution of elevated gas appears to be similar on both sides of the galactic centre. Similarly the XV diagram is also fairly symmetric. There is a slight decrease in flux along the line-of-nodes of the west side of the galaxy possibly indicating gas depletion due to a star burst. However there is no apparent localised region of high velocity dispersion gas that could be associated with the star burst.
The H I distribution extends to a maximum radial extent of
281
![]() or 9.1 kpc (for the adopted distance of 6.7 kpc). The
scalelength of the projected distribution hX
is
or 9.1 kpc (for the adopted distance of 6.7 kpc). The
scalelength of the projected distribution hX
is ![]() 120
120
![]() or
3.9 kpc, with the edge of the H I disk at 2.3 hX.
The
exponential scaleheight of the projected minor axis distribution hz
is 20.5
or
3.9 kpc, with the edge of the H I disk at 2.3 hX.
The
exponential scaleheight of the projected minor axis distribution hz
is 20.5 ![]() or 667 pc. The high latitude H I clouds extend to a
height of 3.9 kpc or 6 scaleheights away from the equatorial
plane.
or 667 pc. The high latitude H I clouds extend to a
height of 3.9 kpc or 6 scaleheights away from the equatorial
plane.
The galaxy is well-resolved by the synthesised beam along the
major
axis, extending to 31 FWHM beamwidths on
each side of the galactic
centre, where each FWHM beamwidth is
292 pc. In the vertical
direction the measured scaleheight of the projected distribution is
approximately ![]() beamwidth, indicating that the vertical
H I structure is well-resolved by the synthesised beam. Indeed the
high latitude H I gas extends to
beamwidth, indicating that the vertical
H I structure is well-resolved by the synthesised beam. Indeed the
high latitude H I gas extends to ![]() beamwidth. Vertical
flaring of the gas distribution can be noted in the extreme velocity
channels 499, 509,
657, 667, 677 km s-1 in the
outer part of the
galaxy where the rotation curve inferred from the XV map is roughly
flat.
beamwidth. Vertical
flaring of the gas distribution can be noted in the extreme velocity
channels 499, 509,
657, 667, 677 km s-1 in the
outer part of the
galaxy where the rotation curve inferred from the XV map is roughly
flat.
The H I column density distribution is dominated by two bright
spots
at a projected radius of ![]() 1
kpc from the centre. The brightest
gas emission in the cube with brightness temperatures of approximately
140 K also correspond to this position. The H I disk also
contains
two outer bright points (although less defined on the western side) at
a radius of
1
kpc from the centre. The brightest
gas emission in the cube with brightness temperatures of approximately
140 K also correspond to this position. The H I disk also
contains
two outer bright points (although less defined on the western side) at
a radius of ![]() 5-6 kpc
with a equatorial brightness
distribution similar to that of the barred galaxy UGC 7321,
which also
displays the characteristic ``Fig.-8'' pattern of a bar in its
XV distribution. Although ESO074-G015 is classified as a barred
SBd galaxy in NED, it does not display a ``Fig.-8'' pattern in
the XV map. ESO074-G015 contains only 1/3 of the H I mass of
UGC 7321, and has a lower maximum rotation speed of
90.1 km s-1,
relative to 112.1 km s-1 for
UGC 7321. It is possible that the lower angular
momentum and overall mass of ESO074-G015 restricts gas flow in
the orbital patterns of a barred potential.
5-6 kpc
with a equatorial brightness
distribution similar to that of the barred galaxy UGC 7321,
which also
displays the characteristic ``Fig.-8'' pattern of a bar in its
XV distribution. Although ESO074-G015 is classified as a barred
SBd galaxy in NED, it does not display a ``Fig.-8'' pattern in
the XV map. ESO074-G015 contains only 1/3 of the H I mass of
UGC 7321, and has a lower maximum rotation speed of
90.1 km s-1,
relative to 112.1 km s-1 for
UGC 7321. It is possible that the lower angular
momentum and overall mass of ESO074-G015 restricts gas flow in
the orbital patterns of a barred potential.
5.2 ESO109-G021 (IC5249)
ESO109-G021 is a superthin Sd galaxy with B-band stellar scalelength-to-scaleheight ratio of 11 (van der Kruit et al. 2001). The rotation curve was initially found to be in solid body rotation by Abe et al. (1999), however van der Kruit et al. (2001) pointed out such a rotation curve was inconsistent with the double-horned H I spectrum (see Fig. 2). By modelling the XV diagram van der Kruit et al. (2001) show that ESO109-G21 is differentially rotating.
To improve signal-to-noise and recovery of image structure we obtained two additional 12-h synthesis observations at the ATCA and added these to the earlier observation by Carignan which was used in the rotation curve analysis by Abe et al. (1999) and van der Kruit et al. (2001). The distance of ESO109-G21 is about 30 Mpc distant so the H I beam is relatively large, 1179 pc. The H I column density map in Fig. 2 shows the galaxy to be well-resolved in the radial direction, while perpendicular to the plane the resolution is just sufficient to detect flaring in the extreme velocity channel maps. Comparison of the XV map in Fig. 2 with that measured by van der Kruit et al. (2001) shows significantly improved structure recovery. However the peak signal-to-noise of the H I channel maps is 10.1, which will make measurement of the H I flaring quite difficult.
5.3 ESO115-G021
This Scd galaxy extends to a maximum radial extent of 445
![]() or
9.7 kpc (assuming a Hubble flow distance of 4.5 kpc
inferred from
the
or
9.7 kpc (assuming a Hubble flow distance of 4.5 kpc
inferred from
the ![]() ). The scalelength of the
projected distribution, hX,
is 209
). The scalelength of the
projected distribution, hX,
is 209
![]() or 4.6 kpc, with the edge of the H I disk at
2.1 hX.
This H I column density map
(Fig. 3)
displays a very
symmetric disk which appears to be relatively quiescent with no
obvious H I extensions above and below the inner disk. The vertical
structure is well-resolved, extending to a height of 1.7 kpc,
equivalent to 8.5 FWHM beamwidths or 2.9 hz,
where hz
is the projected scaleheight of 26.7 arcsec or 583 pc . The
flaring
of the vertical H I distribution can clearly be seen in channel
maps at 459,
469, 479, 548, 558, 568 km s-1,
particularily on the eastern
side where the flatter domain of the rotation curve is more extended
(as inferred from the XV map shown in Fig. 3).
or 4.6 kpc, with the edge of the H I disk at
2.1 hX.
This H I column density map
(Fig. 3)
displays a very
symmetric disk which appears to be relatively quiescent with no
obvious H I extensions above and below the inner disk. The vertical
structure is well-resolved, extending to a height of 1.7 kpc,
equivalent to 8.5 FWHM beamwidths or 2.9 hz,
where hz
is the projected scaleheight of 26.7 arcsec or 583 pc . The
flaring
of the vertical H I distribution can clearly be seen in channel
maps at 459,
469, 479, 548, 558, 568 km s-1,
particularily on the eastern
side where the flatter domain of the rotation curve is more extended
(as inferred from the XV map shown in Fig. 3).
The XV diagram does not display barred gas kinematics; however
a small galaxy like ESO115-G021 with a rotation speed of
62 km s-1 is
unlikely to show the strong orbital patterns of a gas bar. The H I
column density distribution is dominated by a plateau within a radius
of 5 kpc, except for a central bright peak with a peak
brightness of ![]() 150 K
in the central 1 kpc.
150 K
in the central 1 kpc.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12565fg7a.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg172.png)
|
Figure 19:
ESO435-G025 (IC2531). H I column density map overlaid on the DSS image.
Contours are plotted in |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12565fg7b.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg177.png)
|
Figure 20:
ESO435-G025 (IC2531). Top left: XV map.
XV contours are |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{12565fg7c.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg179.png)
|
Figure 21:
ESO435-G025 (IC2531). Top: peak brightness
temperature map. Contours are plotted in |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{12565fg8a.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg184.png)
|
Figure 22:
UGC 7321. H I column density map overlaid on the DSS image.
Contours are plotted in |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12565fg8b.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg191.png)
|
Figure 23:
UGC 7321. Top left: XV map.
XV contours are |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{12565fg8c.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg193.png)
|
Figure 24:
UGC 7321. Top: peak brightness
temperature map. Contours are plotted in |
| Open with DEXTER | |
5.4 ESO138-G014
ESO138-G14 is a larger Sd galaxy, with a maximum rotation speed of
120.4 km s-1 and a H I disk
extending to 23 kpc. The H I column
density map in Fig. 4
shows the H I disk
is well-resolved by the H I synthesised beam of 10.7
![]() or
960 pc. The XV diagram in
Fig. 4
shows depressions in the
H I flux at radii of
or
960 pc. The XV diagram in
Fig. 4
shows depressions in the
H I flux at radii of ![]() 10 kpc,
with the indication of a
``Fig.-8'' structure in the gas kinematics. This suggests that the
galaxy is actually barred, as ``Fig.-8'' structures are typically
seen in gas kinematics of barred edge-on systems (Bureau
& Freeman 1999).
10 kpc,
with the indication of a
``Fig.-8'' structure in the gas kinematics. This suggests that the
galaxy is actually barred, as ``Fig.-8'' structures are typically
seen in gas kinematics of barred edge-on systems (Bureau
& Freeman 1999).
We were able to observe this galaxy only in the 1.5A and 6A ATCA array configurations. Due to the lack of short spacing observations we are missing much of the extended structure on large spatial scales. The channel maps show that the H I disk clearly flares vertically with radius, but the missing extended structure will hamper accurate measurement of the flaring.
5.5 ESO146-G014
This Sd galaxy extends to a maximum radial extent of 118
![]() or 12.3 kpc (assuming the distance of 21.5 kpc
determined from
its systemic velocity). The galaxy is well-resolved by the synthesised
beam along the major axis, extending to 15 FWHM
beamwidths on
each side of the galactic centre, where each FWHM
beamwidth is 793 pc. In the vertical direction the measured
scaleheight of the
projected distribution is 2.6 times the HWHM beamwidth,
indicating
that the galaxy is well-resolved in the vertical direction also.
or 12.3 kpc (assuming the distance of 21.5 kpc
determined from
its systemic velocity). The galaxy is well-resolved by the synthesised
beam along the major axis, extending to 15 FWHM
beamwidths on
each side of the galactic centre, where each FWHM
beamwidth is 793 pc. In the vertical direction the measured
scaleheight of the
projected distribution is 2.6 times the HWHM beamwidth,
indicating
that the galaxy is well-resolved in the vertical direction also.
ESO146-G014 has a rotation speed of 70.2 km s-1, typical of low-mass Sd galaxies. The rotation of ESO146-G014 appears solid body from the XV diagram in Fig. 5, however H I modelling (see Paper III) shows a differential inner rotation curve like other small disk galaxies when observed at high resolution (e.g. Swaters 1999). The XV diagram shows no evidence of a H I bar, which is as expected given the low oxygen abundance of 6% of the solar value (Bergvall & Ronnback 1995).
5.6 ESO274-G001
ESO274-G001 is the closest galaxy in our sample, at a distance of
3.4 Mpc in the Centaurus A group. Its proximity allows the H I
disk
to be examined at 160 pc resolution with the 9.8
![]() resolution
of the H I synthesised beam. To image this galaxy we used two partial
observations in 1.5 km ATCA array configurations from the ATCA
archive,
and one new 12-h synthesis observation in the ATCA 6A array
configuration. From the H I total column density map in
Fig. 6
we can see that the vertical axis
is very well-resolved, although it is clear from the diffuse structure
that the significant extended H I emission is not observed due to the
lack
of observations in short array configurations. Comparison of the H I
flux integral with that measured from the H I Parkes All-Sky Survey
(HIPASS) data shows that about 30% of the H I flux is not
measured.
resolution
of the H I synthesised beam. To image this galaxy we used two partial
observations in 1.5 km ATCA array configurations from the ATCA
archive,
and one new 12-h synthesis observation in the ATCA 6A array
configuration. From the H I total column density map in
Fig. 6
we can see that the vertical axis
is very well-resolved, although it is clear from the diffuse structure
that the significant extended H I emission is not observed due to the
lack
of observations in short array configurations. Comparison of the H I
flux integral with that measured from the H I Parkes All-Sky Survey
(HIPASS) data shows that about 30% of the H I flux is not
measured.
From the XV map in Fig. 6 we see that the rotation curve of this small Sd galaxy rises steeply to a radius of 1-2 kpc and then flattens on one side, but continues to rise with a shallower slope on the other side. In these outer velocity channel maps, where the H I spans a larger range along major axis, it is possible to see clear flaring of the gas thickness with radius. However, the galaxy is lopsided kinematically, and also slightly lopsided in its H I distribution with an indication of a warp on the NE side.
5.7 ESO435-G025 (IC2531)
ESO435-G25 is the only large spiral galaxy in our sample. It is an Sb galaxy with a bright peanut-shaped bulge shown to be a bar from the ``Fig.-8'' signature in the optical emission line kinematics (Bureau & Freeman 1999). The line splitting faintly seen as a Fig.-8 signature in the H I XV diagram in Fig. 7 was first detected by Bureau & Freeman (1997). We use the same ATCA H I observations in our study.
The H I column density map shows the galaxy extends to ![]() 25 beamwidths
on either side of the galactic centre, and three beamwidths
on either side of the H I midplane. Above the galactic centre, the H I
column density map in Fig. 7
shows H I filaments extending to
25 beamwidths
on either side of the galactic centre, and three beamwidths
on either side of the H I midplane. Above the galactic centre, the H I
column density map in Fig. 7
shows H I filaments extending to ![]() 3 kpc above and below the
midplane. Like ESO109-G021, the other distant galaxy, the peak
signal-to-noise is quite low at 10.9. Although the H I disk appears
to be flared in the H I column density map (Fig. 7),
the flaring is not visibly
obvious in the H I channel maps due to the low signal-to-noise.
3 kpc above and below the
midplane. Like ESO109-G021, the other distant galaxy, the peak
signal-to-noise is quite low at 10.9. Although the H I disk appears
to be flared in the H I column density map (Fig. 7),
the flaring is not visibly
obvious in the H I channel maps due to the low signal-to-noise.
5.8 UGC 7321
This Sd galaxy extends to a maximum radial extent of 288
![]() or
14.0 kpc (assuming the distance of 10 kpc adopted by
Uson & Matthews 2003).
The scalelength of the projected distribution,
hX, is 112
or
14.0 kpc (assuming the distance of 10 kpc adopted by
Uson & Matthews 2003).
The scalelength of the projected distribution,
hX, is 112
![]() or 5.4 kpc, with the edge of the H I disk at
2.6hX.
This galaxy exhibits substantial high latitude H I extending up to 144
or 5.4 kpc, with the edge of the H I disk at
2.6hX.
This galaxy exhibits substantial high latitude H I extending up to 144
![]() or 7.0 kpc in the inner H I disk. The
scaleheight of the projected minor axis distribution hz
is 11.6
or 7.0 kpc in the inner H I disk. The
scaleheight of the projected minor axis distribution hz
is 11.6
![]() or 560 pc. Thus the high latitude H I clouds extend to a
height of 12 scaleheights above the equatorial plane.
or 560 pc. Thus the high latitude H I clouds extend to a
height of 12 scaleheights above the equatorial plane.
The galaxy is well-resolved by the synthesis beam along the major axis, extending to 19 FWHM beamwidths on each side of the galactic centre, where each FWHM beamwidth is 727 pc. In the vertical direction the measured scaleheight of the projected distribution is similar to the FWHM beamwidth, suggesting that the low latitude vertical structure is dominated by the shape of the synthesised beam. However despite the relatively large synthesised beam, the vertical flaring is clearly visible in most channel maps due to the extended roughly flat rotation curve which is clearly apparent in the XV map (Fig. 8).
The XV diagram (Fig. 8)
also exhibits
the characteristic ``Fig.-8'' shape, which can be indicative of
barred H I dynamics (Athanassoula
& Bureau 1999; Bureau & Freeman 1999; Kuijken &
Merrifield 1995; Athanassoula 2000).
Further evidence for a dynamical bar in UGC 7321 was later
found by
Pohlen who detected the distinctive boxy-bulge shape in the
near-IR distribution (Pohlen
et al. 2003). Pohlen
et al. (2003) measure the
bar length as ![]()
![]() or
or ![]() kpc. This is in
agreement with the bar size inferred from the size of the ``Fig.-8''
kinematics. It also corresponds to the scalelength of the
projected H I profile. The H I column density has a plateau at
radii within 5 kpc, declining steeply at radii outside this
radius.
kpc. This is in
agreement with the bar size inferred from the size of the ``Fig.-8''
kinematics. It also corresponds to the scalelength of the
projected H I profile. The H I column density has a plateau at
radii within 5 kpc, declining steeply at radii outside this
radius.
The peak brightness temperature rises steeply at radii inside
2 kpc
to 94 K. Assuming a H I spin temperature of 200 or
400 K, the
corresponding central H I opacity ![]() is 0.65 or 0.27. The two
outer peak brightness points correspond to radii of 6 kpc
east, and
5.5 kpc west, also aligning with the outer Lindblad resonance
points
of the stellar bar measured by Pohlen
et al. (2003).
is 0.65 or 0.27. The two
outer peak brightness points correspond to radii of 6 kpc
east, and
5.5 kpc west, also aligning with the outer Lindblad resonance
points
of the stellar bar measured by Pohlen
et al. (2003).
6 Discussion and summary
The resolution of our H I data along the major axis is high, with the number of independent beamwidths on each side of the galaxy centre ranging from 15 to over 50 in our galaxies. In the vertical direction all galaxies are spanned by at least 5 beamwidths. Unfortunately three of the galaxies in the sample suffer from incomplete imaging, resulting in missing information about the extended spatial structure due to the lack of observations along short baselines. For two of these galaxies ESO074-G015 and ESO274-G001, the images still contain substantial information due to the small linear size of the beam, 290 pc and 160 pc, respectively. For these galaxies the iterative H I modelling methods used to measure the deprojected H I density distribution and kinematics (Paper II) should provide good measurements of the flaring. But the H I images of ESO138-G014 indicate missing extended H I emission and low spatial resolution which will probably prevent reliable measurement of the flaring in this galaxy. All the other galaxies in our sample are promising candidates for accurate measurement of the H I kinematics and vertical flaring.
The H I column density distribution of the galaxies in our
sample
varies quite substantially. The four galaxies with maximum rotation
speeds ![]() 100 km s-1
all have H I disks that extend to greater than
5 kpc away from the plane. Three of them (ESO435-G25,
UGC 7321 and
ESO138-G14) also have the ``Fig.-8'' signature in the
XV diagram
suggestive of an edge-on bar in the gas distribution. ESO435-G25
(Bureau & Freeman 1999)
and UGC 7321 (Pohlen
et al. 2003) both have boxy-peanut
shaped stellar bulges consistent with a bar seen edge-on. Combined
with the Fig.-8 signature in the H I gas structure this is strong
evidence for a bar (Athanassoula
& Bureau 1999; Bureau & Freeman 1999; Kuijken &
Merrifield 1995; Athanassoula 2000).
E138-G014, IC5249 and IC2531 all have large H I disks with radii
larger than 20 kpc, while UGC 7321 is much smaller
with a radius of
only 14.0 kpc.
100 km s-1
all have H I disks that extend to greater than
5 kpc away from the plane. Three of them (ESO435-G25,
UGC 7321 and
ESO138-G14) also have the ``Fig.-8'' signature in the
XV diagram
suggestive of an edge-on bar in the gas distribution. ESO435-G25
(Bureau & Freeman 1999)
and UGC 7321 (Pohlen
et al. 2003) both have boxy-peanut
shaped stellar bulges consistent with a bar seen edge-on. Combined
with the Fig.-8 signature in the H I gas structure this is strong
evidence for a bar (Athanassoula
& Bureau 1999; Bureau & Freeman 1999; Kuijken &
Merrifield 1995; Athanassoula 2000).
E138-G014, IC5249 and IC2531 all have large H I disks with radii
larger than 20 kpc, while UGC 7321 is much smaller
with a radius of
only 14.0 kpc.
The other four galaxies are not much smaller than UGC 7321 in radial extent, but they are considerably smaller in total mass. They also lack the vertical extensions in the central disk that suggest additional sources of heat in the disk. This suggests that one of the causes of extended high latitude H I filaments is heating related to star formation and other processes associated with the bar.
The peak brightness profiles of each galaxy show that the
inferred H I opacity (assuming a constant H I spin temperature) varies
substantially across the major axis of each galaxy. The high spatial
resolution of our images has made it possible to measure high H I
brightness temperatures. The maximum brightness temperature in our
galaxies ranges from 94.4 K for UGC 7321 to
168.6 K for ESO146-G14.
In addition to ESO146-G14, two other galaxies have high H I brightness
temperatures >150 K. Assuming a mean H I spin
temperature of 300 K, the maximum inferred opacity for these H
I bright galaxies is
![]() 0.7. This is
comparable to the maximum H I opacity of 0.85measured in
NGC 891 (Kregel
et al. 2004). Inspection of the peak
brightness as a function of major axis position for these three
galaxies shows that, in each case, the region of increased opacity is
localised spanning a projected radius of
0.7. This is
comparable to the maximum H I opacity of 0.85measured in
NGC 891 (Kregel
et al. 2004). Inspection of the peak
brightness as a function of major axis position for these three
galaxies shows that, in each case, the region of increased opacity is
localised spanning a projected radius of ![]() 1-2 kpc. In ESO115-G21,
this increased opacity region occurs at the galactic centre. However
for ESO138-G14 and ESO146-G14, the regions of increased opacity occur
in
the outer disk.
Three of our eight galaxies appear to be warped, and one
is lopsided. This is consistent with results from larger samples,
as e.g. mentioned in the review by Sancisi
et al. (2008).
1-2 kpc. In ESO115-G21,
this increased opacity region occurs at the galactic centre. However
for ESO138-G14 and ESO146-G14, the regions of increased opacity occur
in
the outer disk.
Three of our eight galaxies appear to be warped, and one
is lopsided. This is consistent with results from larger samples,
as e.g. mentioned in the review by Sancisi
et al. (2008).
J.C.O. thanks E. Athanassoula, M. Bureau, R. Olling, A. Petric and J. van Gorkom for helpful discussions. J.C.O. is grateful to B. Koribalski, R. Sault, L. Staveley-Smith and R. Wark for help and advice with data reduction and analysis. We thank the referee, J.M. van der Hulst, for his careful and thorough reading of the manuscripts of this series of papers and his helpful and constructive remarks and suggestions.
Appendix A: Data reduction
A.1 Calibration
Reduction of the H I data was performed with the radio interferometry data reduction package MIRIAD. First, the data was loaded into MIRIAD with the task ATLOD, using the barycentric velocity reference frame, and specifying the rest frequency of H I. The visibilities were then split into separate datasets for each source. The primary and secondary calibrators for each source were inspected for the characteristic signs of solar and terrestrial radio frequency interference (RFI) using the task UVPLT and TVFLAG. Visibilities with RFI, Galaxy H I emission, shadowing or during known telescope system problems were flagged bad. The primary calibrator data were flux calibrated using the known flux with the task MFCAL. The secondary calibrator was then used to calibrate the telescope gains, and if sufficient parallactic angle coverage was obtained with the secondary calibrator it was also used to calibrate the bandpass. For observations with low parallactic angle coverage, such as snapshots, the bandpass solution of the primary calibrator was used to calculate the bandpass.
The calibrated flux solution of both primary and secondary calibrators was inspected with UVPLT. New secondary calibrators were calibrated during observations, and then inspected with the task UVFLUX to see if they resembled an unpolarised point source. If the secondary calibrator was too faint, showed polarisation or structure in L band then it was replaced by the next nearest suitable bright calibrator for later calibrator scans throughout the observing run. Gains and bandpass solutions were inspected with the task GPPLT. The flux density of the secondary calibrator was then corrected using the primary calibrator flux solution.
The final calibration tables were copied to the target galaxy visibility dataset. Before applying the calibration, the gains were averaged over the duration of each secondary calibrator pointing (3 minutes) and gains interpolation was limited to the interval between secondary calibrator observations (30-45 min).
The calibrated target galaxy visibilities were then inspected with the tasks TVFLAG, UVPLT, and any data contaminated by RFI or shadowing was flagged bad with the appropriate flagging tool ( TVFLAG, UVFLAG or BLFLAG).
A.2 Continuum subtraction
To identify the presence of radio continuum sources in the field of view, a largeThe radio continuum was then removed by performing a low order polynomial fit to the line-free channels with the task UVLIN. If the observation included a radio continuum source with flux significantly brighter than the channel-averaged H I flux of the target galaxy, then the phase center was shifted to the position of the brightest contaminating continuum source during the continuum subtraction. The continuum-corrected visibility spectra were checked with the task UVSPEC and a new large ch0 image was formed to search for additional fainter residual continuum sources that remained after the first continuum subtraction. If found, continuum subtraction was repeated with the phase center shifted to the next brightest source. The process was repeated until the ch0 image showed no significant contaminating continuum sources. For observations that were taken during daylight hours, the continuum subtraction was performed with the phase center shifted to the position of the Sun. This procedure could be compromised by continuum emission from the galaxy itself or background sources and in all cases it worked satisfactorily.
For the narrow bandpass VLA observations, it was not
possible to span the full galaxy emission in a single bandpass when
using the high spectral resolution correlator configuration. In such
cases, the galaxy was imaged with two overlapping bandpasses. As these
bandpasses included only a few line-free channels on one side of the
bandpass it was not possible to perform an accurate 1st order
polynomial fit to the line-free channels with UVLIN.
Instead any
bright continuum sources were subtracted from each bandpass with the
task UVMODEL using a point source model
with the fitted
flux and position of the radio source. Any residual continuum emission
was removed with a zero-order fit to the few line-free channels in
each bandpass. This performed a satisfactory continuum subtraction for
the three galaxies observed at the VLA.
Appendix B: Imaging
A preliminary dirty H I data cube and dirty beam map was formed using the default gridding where each pixel size is 1/3of the synthesised beam FWHM along the Xand Y axes of the beam. The accurate beam shape was then measured from the central peak of the dirty beam by fitting an elliptical Gaussian to determine the majorThe visibilities were weighted using a robust weighting of 0.4
(Briggs 1995) to
provide a optimal compromise between spatial resolution and
suppression of sidelobes. A positive robust weighting causes the
visibilities in the
more sparsely-sampled parts of the visibility phase space to be
down-weighted relative to uniform weighting. This reduces the
amplitude of the sidelobes, without significantly increasing the size
of the synthesised beam FWHM. The barycentric
velocity reference frame and the
radio definition of velocity was used for the
velocity axis of the
H I data cube. We chose the radio definition because
it yields a constant velocity increment between channels, which was
useful for later modelling of the H I distribution![]() .
.
We used the MIRIAD CLEAN
algorithm to correct for effects
introduced by the sparcity of the visibility sampling. To find the
approximate H I emission region in a each channel, first an initial CLEAN
was performed over the central quarter of each channel
map, and a low resolution data cube was made by restoring the clean
components with a Gaussian of twice the full resolution synthesised
beam size. The noise in each plane of the low resolution cube was then
measured, and inspected to find the region of H I emission in each
plane. Following standard practise, a clean mask
was created by
selecting the region in each plane of the low resolution data cube
with H I emission greater than twice the rms noise (2![]() )
using
the task CGCURS. The noise level of the
full resolution
dirty cube was measured and then the areas defined by the clean
mask were cleaned down to 0.5
)
using
the task CGCURS. The noise level of the
full resolution
dirty cube was measured and then the areas defined by the clean
mask were cleaned down to 0.5![]() using MIRIAD CLEAN.
We realise that this is not the optimal procedure
to find the low level emission as CLEAN components found in a high
resolution image usually do not represent the low level extended
emission properly. Better practice would have been to make low
resolution images from the continuum subtracted u,v data directly and
CLEAN those. In the
case of this study, however, only high resolution images are produced
and
used.
using MIRIAD CLEAN.
We realise that this is not the optimal procedure
to find the low level emission as CLEAN components found in a high
resolution image usually do not represent the low level extended
emission properly. Better practice would have been to make low
resolution images from the continuum subtracted u,v data directly and
CLEAN those. In the
case of this study, however, only high resolution images are produced
and
used.
The final full resolution H I data cube was produced using the task RESTOR which produces a residual map for each channel map by subtracting the transformed clean components, and then adds the restored flux to each residual image by convolving the clean components by the clean beam. A circular Gaussian was used for the clean beam, with the FWHM set by the measured major axis FWHM of the dirty beam. After restoration the full cube was corrected for the effect of the antennae primary beam using the task LINMOS. The size of the restoring beam is shown in Cols. 2 & 3 of Table 2.
As multiple observations in different array configurations were combined to provide the maximum visibility sampling, resolution and sensitivity, some galaxies were observed at slightly different pointing positions. These observations were imaged using the mosaic mode in INVERT, and deconvolved using the task MOSMEM which performs a maximum entropy deconvolution of data with multiple pointings.
In the case of VLA data for which multiple bandpasses were needed to span the galaxy H I emission, the visibility data were split into separate bandpasses prior to imaging, with the overlap region combined using the task UVCAT. Each bandpass was then imaged, cleaned and restored separately, before concatenating the final subcubes with the task IMCAT. Although the channel separation at the joins was not exactly the same as the channel width elsewhere, the difference was less than 1 km s-1, which is unlikely to effect subsequent modelling of the H I distribution. The overlap channels were observed for a longer integration time and consequently these channel maps have a lower rms noise. However as channel maps and moment analysis were made using the noise measured in each channel map, the difference in noise level over the velocity range of the galaxy is handled appropriately and does not cause noise contamination in the derived images. The measured noise levels of the H I data cubes are shown in Table 3.
After forming the full resolution H I data cubes with Miriad, all subsequent imaging, moment analysis and measurements were undertaken using the Interactive Data Language (IDL).
Appendix C: Channel maps
In O'Brien (2007) all the channel maps that contain H I emission have been dispayed as contour diagrams. Interested readers can obtain an electronic .pdf file with these maps upon request from P. C. van der Kruit or K. C. Freeman at the email address given on the first page.
References
- Abe, F., Bond, I. A., Carter, B. S., et al. 1999, AJ, 118, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Athanassoula, E. 2000, ASP Conf. Ser. 221, 243 [Google Scholar]
- Athanassoula, E., & Bureau, M. 1999, ApJ, 522, 699 [NASA ADS] [CrossRef] [Google Scholar]
- Bergvall, N., & Ronnback, J. 1995, MNRAS, 273, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Bosma, A. 1978, Ph.D. Thesis, Groningen [Google Scholar]
- Bosma, A. 1994, ESO/OHP Workshop on Dwarf Galaxies, ESO, 187 [Google Scholar]
- Bosma, A., van der Kruit, P. C. 1979, A&A, 79, 281 [NASA ADS] [Google Scholar]
- Briggs, D. 1995, BAAS, 27, 1444 [NASA ADS] [Google Scholar]
- Bureau, M., & Freeman, K. C. 1997, PASA, 14, 146 [NASA ADS] [Google Scholar]
- Bureau, M., & Freeman, K. C. 1999, AJ, 118, 126 [NASA ADS] [CrossRef] [Google Scholar]
- de Blok, W. J. G. 1997, Ph.D. Thesis, Groningen [Google Scholar]
- Celnik, W., Rohlfs, K., & Braunsfurth, E. 1979, A&A, 76, 24 [NASA ADS] [Google Scholar]
- Colless, M., & Dunn, A. M. 1996, ApJ, 458, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Einasto, J., Kaasik, A., & Saar, E. 1974, Nature, 250, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Freeman, K. C. ApJ, 160, 811 [Google Scholar]
- Holmberg, J., & Flynn, C. 2000, MNRAS, 313, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Kapteyn, J. C. 1922, ApJ, 55, 302 [NASA ADS] [CrossRef] [Google Scholar]
- Kleyna, J. T., Wilkonson, M. I., Evans, N. W., et al. 2005, ApJ, 630, L141 [NASA ADS] [CrossRef] [Google Scholar]
- Kormendy, J., & Freeman, K. C. 2004, IAU Symp. 220, 377 [Google Scholar]
- Kregel, M., van der Kruit, P. C., & de Blok, W. J. G. 2004, MNRAS, 352, 768 [NASA ADS] [CrossRef] [Google Scholar]
- Kuijken, K. H., & Merrifield, M. R. 1995, ApJ, 443, L13 [NASA ADS] [CrossRef] [Google Scholar]
- O'Brien, J. C. 2007, Ph.D. Thesis, Australian National University [Google Scholar]
- Olling, R. P. 1995, AJ, 110, 591 [NASA ADS] [CrossRef] [Google Scholar]
- Olling, R. P. 1996, AJ, 112, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Olling, R. P., & Merrifield, M. R. 2000, MNRAS, 311, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Oort, J. H. 1932, Bull. Inst. Neth., 6, 249 [Google Scholar]
- Ostriker, J. P., Peebles, P. J. E., & Yahil, A. 1974, ApJ, 193, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Percival, W. J., Baugh, C. M., Bland-Hawthorn, J., et al. 2001, MNRAS, 327, 1297 [NASA ADS] [CrossRef] [Google Scholar]
- Perlmutter, S., Aldering, G., Goldhaber, G., et al. 1999, ApJ, 517, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Pohlen, M., Balcells, M., Lütticcke, R., et al. 2003, A&A, 409, 485 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Riess, A. G., Filippenko, A. V., Challis, P., et al. 1998, AJ, 116, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts, M. S. 2008, ASP Conf. Ser., 395, 283 [NASA ADS] [Google Scholar]
- Roberts, M. S., & Rots, A. H. 1973, A&A, 26, 483 [NASA ADS] [Google Scholar]
- Rogstad, D. H., & Shostak, G. S. 1972, ApJ, 176, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Rubin, V., & Ford, W. K. 1970, ApJ, 159, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Sancisi, R., Fraternali, F., Oosterloo, T., et al. 2008, A&AR, 15, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Shostak, G. S. 1971, Ph.D. Thesis, Caltech [Google Scholar]
- Sofue, Y., & Rubin, V. 2001, ARA&A, 39, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Spergel, D. N., Verde, L., Peiris, H. V., et al. 2003, ApJS, 148, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., White, S. D. M., Jenkins, A., et al. 2005, Nature, 435, 629 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Swaters, R. A. 1999. Ph.D. Thesis, Groningen [Google Scholar]
- Tamburro, D., Rix, H.-W., Leroy, A. K., et al. 2009, AJ, 137, 4424 [NASA ADS] [CrossRef] [Google Scholar]
- Uson, J. M., & Matthews, L. D. 2003, AJ, 125, 2455 [NASA ADS] [CrossRef] [Google Scholar]
- van der Kruit, P. C. 1981, A&A, 99, 298 [NASA ADS] [Google Scholar]
- van der Kruit, P. C., Jiménez-Vicente, J., Kregel, M., et al. 2001, A&A, 379, 374 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Warren, B. E., Jerjen, H., & Koribalski, B. S. 2004, AJ, 128, 1152 [NASA ADS] [CrossRef] [Google Scholar]
- Willman, B., Dalcanton, J. J., Martinez-Delgado, D., et al. 2005, ApJ, 626, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Zwicky, F. 1937, ApJ, 86, 217 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ...
![[*]](/icons/foot_motif.png)
- For correspondence contact Ken Freeman or Piet van der Kruit.
- ... sensitivity
![[*]](/icons/foot_motif.png)
- KCF and PCvdK recall influential colloquia and other presentations by Roberts in the early 1970s on a flat H I rotation curve of the Andromeda galaxy which helped to steer the evolution of this subject.
- ...
universe
![[*]](/icons/foot_motif.png)
- For this illustration we used the
parameters adopted in the Millenium Simulation (Springel et al. 2005),
which are
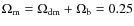 ,
,
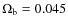 ,
,
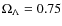 .
.
- ... luminosity
![[*]](/icons/foot_motif.png)
- E-Sbc galaxies were not included to avoid the larger uncertainties associated with stellar bulge-disk decomposition and the relatively larger contribution of the stellar mass of varying stellar ages.
- ...
release
![[*]](/icons/foot_motif.png)
- http://www.atnf.csiro.au/research/multibeam/release
- ... correl_optimize
![[*]](/icons/foot_motif.png)
- http://idlastro.gsfc.nasa.gov/homepage.html
- ...
NED
![[*]](/icons/foot_motif.png)
- nedwww.ipac.caltech.edu
- ... 2MASS
![[*]](/icons/foot_motif.png)
- www.ipac.caltech.edu/2mass/
- ... (DSS)
![[*]](/icons/foot_motif.png)
- The Digitized Sky Surveys were produced at the Space Telescope Science Institute under US Government grant NAG W-2166. The images of these surveys are based on photographic data obtained using the Oschin Schmidt Telescope on Palomar Mountain and the UK Schmidt Telescope. The plates were processed into the present compressed digital form with the permission of these institutions.
- ... distribution
![[*]](/icons/foot_motif.png)
- There are two
common approximations to the relativistic equation describing the
doppler effect - the ``radio definition'' for which equal increments
in frequency translate to equal increments in velocity,
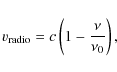
and the ``optical definition'',
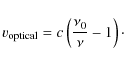
The difference in v for fixed is
is  1% for
2500 km s-1, the
highest radial velocity in our sample.
1% for
2500 km s-1, the
highest radial velocity in our sample.
All Tables
Table 1: HI observations.
Table 2: Resolution of H I observations.
Table 3: Noise of H I channel maps.
Table 4: HI measurements.
All Figures
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12565fg1a.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg41.png)
|
Figure 1:
ESO074-G015 (IC5052). H I column density map overlaid on the DSS image.
Contours are plotted in |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12565fg1b.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg42.png)
|
Figure 2:
ESO074-G015 (IC5052). Top left: XV map.
XV contours are |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{12565fg1c.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg44.png)
|
Figure 3:
ESO074-G015 (IC5052). Top: peak brightness
temperature map. Contours are plotted in |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12565fg2a.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg49.png)
|
Figure 4:
ESO109-G021 (IC5249). H I column density map overlaid on the DSS image.
Contours are plotted in |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12565fg2b.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg69.png)
|
Figure 5:
ESO109-G021 (IC5249). Top left: XV map.
XV contours are |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{12565fg2c.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg71.png)
|
Figure 6:
ESO109-G021 (IC5249). Top: peak brightness
temperature map. Contours are plotted in |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip=]{12565fg3a.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg97.png)
|
Figure 7:
ESO115-G021. H I column density map overlaid on the DSS image. Contours
are plotted in |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12565fg3b.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg103.png)
|
Figure 8:
ESO115-G021. Top left: XV map. XV contours are |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{12565fg3c.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg105.png)
|
Figure 9:
ESO115-G021. Top: peak brightness temperature map.
Contours are plotted in |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12565fg4a.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg109.png)
|
Figure 10:
ESO138-G014. H I column density map overlaid on the DSS image. Contours
are plotted in |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12565fg4b.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg116.png)
|
Figure 11:
ESO138-G014. Top left: XV map. XV contours are |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{12565fg4c.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg118.png)
|
Figure 12:
ESO138-G014. Top: peak brightness temperture map.
Countours are plotted in |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12565fg5a.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg148.png)
|
Figure 13:
ESO146-G014. H I column density map overlaid on the DSS image. Contours
are plotted in |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12565fg5b.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg153.png)
|
Figure 14:
ESO146-G014. Top left: XV map.
XV contours are |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{12565fg5c.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg155.png)
|
Figure 15:
ESO146-G014. Top: peak brightness temperature map.
Contours are plotted in |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12565fg6a.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg159.png)
|
Figure 16:
ESO274-G001. H I column density map overlaid on the DSS image. Contours
are plotted in |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12565fg6b.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg164.png)
|
Figure 17:
ESO274-G001. Top left: XV map.
XV contours are |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{12565fg6c.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg166.png)
|
Figure 18:
ESO274-G001. Top: peak brightness temperature map.
Contours are plotted in |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12565fg7a.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg172.png)
|
Figure 19:
ESO435-G025 (IC2531). H I column density map overlaid on the DSS image.
Contours are plotted in |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12565fg7b.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg177.png)
|
Figure 20:
ESO435-G025 (IC2531). Top left: XV map.
XV contours are |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{12565fg7c.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg179.png)
|
Figure 21:
ESO435-G025 (IC2531). Top: peak brightness
temperature map. Contours are plotted in |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{12565fg8a.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg184.png)
|
Figure 22:
UGC 7321. H I column density map overlaid on the DSS image.
Contours are plotted in |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12565fg8b.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg191.png)
|
Figure 23:
UGC 7321. Top left: XV map.
XV contours are |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{12565fg8c.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa12565-09/Timg193.png)
|
Figure 24:
UGC 7321. Top: peak brightness
temperature map. Contours are plotted in |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\begin{displaymath}
\rho(R) = \rho_0 \left[ 1 + \left(\frac{R}{R_{\rm c}}\right)^2 \right]^{-1},
\end{displaymath}](/articles/aa/full_html/2010/07/aa12565-09/img37.png)