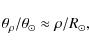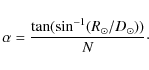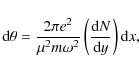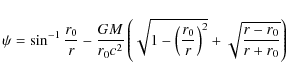EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 515 (June 2010) A&A, 515 (2010) A59 Full HTML
Free Access
Issue
A&A
Volume 515, June 2010
Article Number A59
Number of page(s) 6
Section Astronomical instrumentation
DOI https://doi.org/10.1051/0004-6361/200810357
Published online 09 June 2010
A&A 515, A59 (2010)

Precision effects for solar image coordinates within the FITS world coordinate system

W. T. Thompson

Adnet Systems, Inc., NASA Goddard Space Flight Center, Code 671, Greenbelt, MD 20771, USA

Received 9 June 2008 / Accepted 12 March 2010

Abstract
The FITS world coordinate system (WCS) provides a number of tools for precisely specifying the spatial coordinates of an image. Many of the finer details that the WCS addresses have not historically been taken into account in solar image processing. This paper examines various effects which can affect the expression of coordinates in FITS headers, to determine under what conditions such effects need to be taken into account in data analysis, and under what conditions they can be safely ignored. Effects which are examined include perspective, parallax, spherical projection, optical axis determination, speed-of-light effects, stellar aberration, gravitational deflection, and scattering and refraction at radio wavelengths. Purely instrumental effects, such as misalignment or untreated optical aberrations, are not considered. Since the value of the solar radius is an experimental quantity, the effect of adopting a specific radius value is also examined. These effects are examined in the context of a previous paper outlining a WCS standard for encoding solar coordinates in FITS files. Aspects of that previous paper are clarified and extended in the present work.

Key words: standards - Sun: general - techniques: image processing - astronomical data bases: miscellaneous - methods: data analysis

1 Introduction

In Thompson (2006), hereafter referred to as Paper I, a standard was described for encoding the coordinates of solar images within FITS files, building on the world coordinate system (WCS) described in Greisen & Calabretta (2002) and Calabretta & Greisen (2002). That standard allowed coordinates to be specified to a greater level of precision than had previously been commonly applied to solar image data. Paper I described standards for encoding both heliographic coordinates and coordinates in telescopic images. The latter type of coordinate, labeled helioprojective, included both cartesian and radial forms.

The present work builds on that previous paper by examining various effects which may affect the precision of coordinate calculations, in particular those effects which have often been previously ignored in solar data analysis. The goal of this study is to determine when common simplifying assumptions are valid, or when a more detailed coordinate analysis is necessary. In essence, we aim to ``demystify'' the WCS formalism. In the following sections, we examine the effects of perspective, parallax, spherical projection, optical axis determination, speed of light, stellar aberration, gravitational deflection, and determining the instrument plate scale based on an assumed value of the solar radius. The scattering and refraction effects of the coronal plasma are discussed for radio observations. Purely instrumental effects, such as misalignment, or optical aberrations not handled by the spherical projection, are not considered. Such effects are peculiar to each instrument, and their importance is well established.

2 Perspective

Perspective is the property of observing an object from a given distance. We can characterize the perspective of a solar observation by the ratio of the viewing distance $D_\odot$ to the solar radius $R_\odot$. For some applications it may be appropriate to make the simplifying assumption that $D_\odot \gg R_\odot$, and treat the observer distance as essentially infinite. Thus, one assumes that

\begin{displaymath}\theta_\rho / \theta_\odot \approx \rho / R_\odot, \end{displaymath} (1)

where $\theta_\rho$ is the angular distance of a solar feature from disk center, $\theta_\odot = \sin^{-1}(R_\odot/D_\odot)$ is the angular radius of the solar limb, and $\rho$ is the radial distance from the Sun-observer line. For heliographic coordinates, the assumption of Eq. (1) is equivalent to using the orthographic (SIN) projection in place of the perspective zenithal (AZP) projection, as discussed in Paper I.

The simplifying assumption of Eq. (1) is commonly used within the solar community. However, the perspective effects from a distance of 1 AU are significant. The difference in heliographic coordinates between perspective and non-perspective calculations grows in an almost linear fashion from 0 at disk center to about 16' at the limb. Performing the calculation in reverse, converting heliographic coordinates to either $\theta_\rho$ or $\rho$, the difference reaches a maximum of just over 2'' at about 0.7 solar radii.

For many applications, an error of 2'' is significant. There- fore, we recommend that perspective should routinely be taken into account when converting between helioprojective and heliographic coordinates. Paper I defines the keyword DSUN_OBS to describe the perspective distance from Sun center of an observation, together with the keywords HGLN_OBS and HGLT_OBS to describe the direction that the observation is made from. These keywords are of particular importance when the observation is taken at a significant distance away from Earth.

It's common within solar physics to use the term ``solar radius'' both for the physical radius $R_\odot$, and for the apparent angular radius $\theta_\odot$. However, in Greisen & Calabretta (2002), the units designator ``solRad'' is specifically defined as a measure of distance[*]. Characterizing solar images as being in ``solRad'' units when the coordinates are actually angular implicitly ignores perspective. Such usage is not recommended when an error of ${\sim}2''$ would be important.

Perspective also comes into play when comparing observations made from different solar distances. For any two terrestial observers, the difference in perspective will be miniscule ( ${<}0{\hbox{$.\!\!^{\prime\prime}$ }}0001$). However, the maximum difference between an observer at the Sun-Earth L1 Lagrange point and a terrestrial observation is just over 0 $.\!\!^{\prime\prime}$02.

3 Parallax

Except for the heliographic case, the coordinate systems defined in Paper I are explicitly observer-centric; i.e. topocentric when viewed from Earth. One possible effect on the accuracy of the calculated coordinates is parallax. This can be characterized by the horizontal parallax, which is defined as the pointing difference between two hypothetical observers, one viewing the Sun on the horizon, and the other observing from the geocenter. From a distance of 1 AU, the horizontal parallax of solar disk center is about 9''. Two observers located on diametrically opposite sides of the Earth would see a maximum relative parallax between each other of twice this amount, or ${\sim}18''$.

However, the coordinate systems of Paper I are defined relative to solar disk center, so the potential error source that one needs to consider is the differential parallax between a solar feature and disk center. For example, consider the point on the solar surface that is disk center for a hypothetical geocentric observer. An observer situated on the day-night terminator would define a different point as disk center. The heliographic coordinates of this point would be separated from the previous point by about 0 $.\!\!^{\prime\prime}$04. Foreshortening decreases the importance of parallax as one moves away from disk center along the solar surface. The effect of parallax can be larger in the corona, again with the largest effects occuring along the Sun-Earth line.

Another important case to consider is that of a satellite in geostationary orbit. Given that the semi-major axis of geostationary orbits is about $6.6~R_\oplus$, the photospheric difference between hypothetical geocentric and geostationary observers could be as high as 0 $.\!\!^{\prime\prime}$3.

A third important case is that of a satellite in a halo or Lissajous orbit about the L1 Lagrange point between Earth and the Sun. The effect of parallax for such orbits can be quite large. For example, the maximum parallax for the SOHO satellite is ${\sim}4''$.

These differences between observers are not errors, since each set of coordinates is correct for that observer. The potential for error exists when data from two observers are compared without taking the difference in observer position into account. Greisen et al. (2006) describe the keywords OBSGEO-X, OBSGEO-Y, OBSGEO-Z for specifying the topocentric coordinates of an Earth-based observatory, while Sect. 9.1 of Paper I defines keywords suitable for describing the position of a satellite in a variety of coordinate systems, including HGLN_OBS and HGLT_OBS. Using these keywords removes any potential ambiguity in the interpretation of the data. These keywords become critical for observatories beyond Earth orbit; for example, the STEREO mission uses the parallax differences between two widely separated spacecraft to derive three-dimensional information about the Sun.

The OBSGEO-X, etc. keywords of Greisen et al. (2006) are essentially equivalent to the keywords GEOX_OBS, GEOY_OBS, GEOZ_OBS of Paper I. However, there is one important distinction between these two keyword systems. The OBSGEO keywords are used specifically for terrestrial observatories, and denote not only the position of the observer, but also that the observer takes part in Earth's rotational and orbital motions. The GEOX_OBS, etc. keywords of Paper I denote location only, and have no implications regarding the observer's motion.

Paper I described the Carrington heliographic coordinate system in terms of longitude and latitude, but did not specify a way to express these coordinates in terms of cartesian x,y,z values. We therefore correct that lack by reserving the CUNIT labels CARX, CARY, CARZ. The axes are defined by the following relationships to Carrington heliograph longitude  $\Phi\mbox{$_{\mbox{\tiny C}}$ }$ and latitude  $\Theta\mbox{$_{\mbox{\tiny C}}$ }$:

                $\displaystyle X\mbox{$_{\mbox{\tiny C}}$ }$ = $\displaystyle r \cos\Theta\mbox{$_{\mbox{\tiny C}}$ } \cos\Phi\mbox{$_{\mbox{\tiny C}}$ },$  
$\displaystyle Y\mbox{$_{\mbox{\tiny C}}$ }$ = $\displaystyle r \cos\Theta\mbox{$_{\mbox{\tiny C}}$ } \sin\Phi\mbox{$_{\mbox{\tiny C}}$ },$ (2)
$\displaystyle Z\mbox{$_{\mbox{\tiny C}}$ }$ = $\displaystyle r \sin\Theta\mbox{$_{\mbox{\tiny C}}$ }.$  

We also reserve the keywords CARX_OBS, CARY_OBS, CARZ_OBS to store the observer's position in Carrington coordinates. In keeping with WCS standards, the values of these keywords will be in meters.

4 Projection

Projections are the mechanisms the WCS uses to handle the mapping between the curved space of spherical coordinates, and the flat data space in which the data are stored. The coordinates of any image of the Sun will have some kind of spherical projection associated with it. The selection of the proper projection to use will often depend on the properties of the optics. For example, the optical properties of the Heliospheric Imager telescopes aboard STEREO are well characterized by the AZP projection, with a PVj_1 value customized for each telescope (Brown et al. 2009). (Note that this is a distinctly different use of the AZP projection than the heliographic coordinate case discussed in Paper I.) In the absence of significant spherical aberration, a typical solar image is usually best described by the gnomonic projection, which Calabretta & Greisen (2002) designate with the mnemonic ``TAN'' because the distance from the reference pixel varies as $\tan\theta_\rho$. For many solar images, the effect of such projections is very small, and is often ignored.

A useful metric to characterize the importance of taking projection into account is the difference between the angle $\theta_\rho$ and the $R_\theta$value for the given projection as defined by Calabretta & Greisen (2002). For observations taken from 1 AU, the maximum difference for the TAN projection is about 0 $.\!\!^{\prime\prime}$007. As one moves off the disk into the corona, the difference grows as $\theta_\rho^3$. To a certain extent this effect is mitigated by the fact that instruments with wide fields of view also have large pixels. However, the effect definitely becomes significant at large radial distances, and can no longer be ignored. It's important that solar image data, particular those from instruments with large fields of view, correctly designate the spherical projection, using the mechanism described in Paper I and in Calabretta & Greisen (2002). Aberrations within the optics can often be mitigated by the proper selection of the projection.

5 Optical axis

The azimuthal projections of Calabretta & Greisen (2002) are defined relative to a particular reference pixel. For telescope observations, this pixel represents the optical axis of the instrument. For the purposes of this discussion, we will define the optical axis as that point in the image which, when combined with the selected projection, produces calculated coordinates which best match the true coordinates over the image. Because most solar images are best expressed in the TAN projection, and because this projection tends to be particularly sensitive to errors, we will devote our analysis to the TAN projection.

It's not always possible to determine the precise optical axis, and proxies are often used instead. One common proxy is the center of the detector. On the other hand, instruments which image the full Sun may use solar disk center as a proxy for the optical axis. Depending on the instrument design, either of these may be a good approximation

We define i0,j0 to be the pixel coordinates of the true optical axis, and i0',j0' to be the pixel coordinates of the assumed optical axis. The physical coordinates of each pixel are $\alpha_0,\beta_0$ and $\alpha_0',\beta_0'$ respectively. For simplicity, we assume that the reference values are correct in each case, and only look at the errors that build up as one moves radially away from the reference pixel. Thus, for each pixel i,j we calculate $\alpha,\beta$ and $\alpha',\beta'$ using the true and assumed optical axes, and then calculate the error $\epsilon = \sqrt{(\alpha'-\alpha)^2 + (\beta'-\beta)^2}$.

\begin{figure} \par\includegraphics[width=9cm,clip]{10357fg1.eps} \end{figure} Figure 1:

Maximum coordinate errors as a function of radial distance for optical axis errors of 1'', 10'', 100'', and 1000'' respectively, using the gnomonic (TAN) projection. The vertical dotted line represents the position of the solar limb.

Open with DEXTER

Figure 1 shows how the maximum error varies with solar radii for different cases of optical axis error, ranging from a small 1'' error, to a huge (and unlikely) 1000'' error. (The actual error varies with position; only the maximum error is plotted.) This plot demonstrates that the coordinate determination is relatively insensitive to the optical axis determination. Even a fairly large optical axis error of 100'' produces an error of only $\sim$0 $.\!\!^{\prime\prime}$002 across the solar disk. Off the limb the errors tend to increase as $\theta_\rho^2$ for any given optical axis error, but are still relatively small. At any given radial distance, the error at large distances tends to increase linearly with the optical axis error for the cases studied.

6 Speed of light

The helioprojective coordinates of Paper I are defined relative to apparent solar disk center. However, there's no fiducial on the Sun marking disk center. Instead, one determines disk center by calculating the centroid of a fit to the solar limb. It is this calculated position which defines the origin of the helioprojective coordinate systems of Paper I, as well as the zero longitude of the Stonyhurst heliographic system.

Because of the finite speed of light, radiation from disk center reaches the observer 2.3 s before that from the limb. During that time, the apparent position of the Sun in the sky will have changed, and the Sun will have undergone a certain amount of differential rotation. One must also consider the fact that, overall, the light coming from the Sun is delayed by the light travel time, so that the apparent distance $D_\odot$ is different from the instantaneous distance at the observation time t. However, from Earth, this last effect only amounts to $\pm6$ kilometers over the course of the year - for most applications this is negligable. Therefore, we will only consider the effects arising from the 2.3 s delay between disk center and the limb.

Light coming from the limb travels a distance of $D_\odot \cos\theta_\odot$ before reaching the observer. From a distance of 1 AU, this differs from $D_\odot$ only by 1 part in 105, and for practical purposes can be considered to be the same as $D_\odot$. Light from disk center arrives 2.3 s earlier, when the Sun was at a different apparent location in the sky. From Earth, the average apparent motion in the sky during 2.3 s is $\sim$0 $.\!\!^{\prime\prime}$09, which is how much distortion occurs at disk center due to the differential light travel time effects. An observatory in significantly closer orbit about the Sun would show larger distortions, both because of the smaller distance, and because the orbital speed would be higher.

The latitude of disk center as seen from Earth is restricted to a region within 7$^\circ$ of the equator. At those latitudes, the average synodic rotation rate is 13 $.\!\!^\circ$34/day. From 1 AU over 2.3 s, this amount of rotation works out to $\sim$0 $.\!\!^{\prime\prime}$006.

7 Stellar aberration

Stellar aberration is the deflection of light due to the transverse motion of the observer relative to an inertial reference frame (Stumpff 1979). For terrestrial observations of the Sun, this effect is maximized because Earth's orbital motion is essentially perpendicular to the Sun-Earth line. The average aberration of the Sun as seen from Earth is $\sim$20 $.\!\!^{\prime\prime}$5, with small corrections of a few $\times$ 0 $.\!\!^{\prime\prime}$1 caused by the eccentricity of the orbit, and by Earth's rotational motion at the location of the observatory.

For coordinates defined relative to solar disk center, what is important is not the total amount of aberration, but the change in aberration as one moves away from disk center. On the solar disk, this reaches a maximum of $\sim$0 $.\!\!^{\prime\prime}$0002 at the east and west ecliptic limbs, and can be considered neglible. As one moves further out into the corona, the effect of differential aberration increases roughly as $\theta^2$, primarily along the ecliptic.

Related to stellar aberration is the phenomenon known as ``planetary aberration'', which is the combination of stellar aberration and light travel time effects. Aside from the zeroth-order displacement of $\sim$20 $.\!\!^{\prime\prime}$5, the planetary aberration effects which are important for solar observations are discussed in Sect. 6.

8 Solar radius

For some instruments, the only way to accurately establish the plate scale is to measure the apparent solar radius on the detector. To convert this into degrees, one must know both the observing distance $D_\odot$ and the solar radius $R_\odot$. The latter is an experimental quantity, and is known only to a certain level of precision. The current canonical photospheric value is $R_\odot = 695.508 \pm 0.026$ Mm (Cox 2000), which differs significantly from the previous value of $695.99 \pm 0.07$ Mm (Allen 1976) quoted in Greisen & Calabretta (2002). Other values have been published, e.g. Schou et al. (1997) quotes $695.68 \pm 0.03$ Mm. Individual measurements of the apparent radius can vary by as much as 0.2% (about 1.4 Mm, or 2'') between observatories (Badache-Damiani & Rozelot 2006), and may have a solar cycle dependence (Delmas et al. 2006).

One possible solution to the uncertainty in the value of $R_\odot$ is to set CUNITi=``solRad''. This has the advantage of being ``agnostic'' about the proper value of $R_\odot$, making it a parameter in the data analysis. However, as has already been pointed out in Sect. 2, expressing the coordinates in solRad units ignores the effect of perspective. Also, unless the coordinates are expressed in angular units, projection effects cannot be properly accounted for (Sect. 4). Although projection effects are typically small, they can be significant at the level needed to address questions of solar oblateness and solar cycle variability of $R_\odot$.

We believe that a better approach is to express the coordinates in angular units, but to document the values of $D_\odot$ and $R_\odot$ used in deriving the plate scale, so that they can be backed out if necessary. To that end, we reserve the FITS keyword RSUN_REF to store the value of $R_\odot$ used in deriving the plate scale. The units applied to this keyword will be meters. The value $D_\odot$ is stored in the keyword DSUN_OBS defined in Paper I. For example, one might have the following entries in the FITS header: 

DSUN_OBS=          1.50713E+11
RSUN_REF=          6.95508E+08.
The principal error resulting from applying the wrong solar radius is that the perspective will be slightly different than assumed. Let $R_\odot$ be the true solar radius, and $R_\odot'$ be the assumed radius, with $\theta_\odot$ and $\theta_\odot'$ being the respective angular sizes from the distance $D_\odot$. For our test case, we set $R_\odot'-R_\odot=1$ Mm ($\sim$1 $.\!\!^{\prime\prime}$4), which should be taken as a worst case scenario. The error reaches a maximum of about 0 $.\!\!^{\prime\prime}$003 close to 0.7 solar radii, and scales as the difference $R_\odot'-R_\odot$.

Another effect to consider is that of projection errors. As was done in Sect. 5, we'll concentrate on the gnomonic (TAN) projection. The gnomonic plate scale $\alpha$ is defined such that $\tan\theta = \alpha n$, where n is the radial distance in pixels from the reference pixel. If N is the apparent solar radius in pixels, then the plate scale can be derived as

\begin{displaymath}\alpha = \frac{\tan( \sin^{-1}( R_\odot / D_\odot ) )}{N} \cdot \end{displaymath} (3)

(Other definitions would apply for projections other than TAN.) We thus have two plate scales to consider, $\alpha$ and $\alpha'$, derived from $R_\odot$ and $R_\odot'$ respectively. The error between the derived angles $\theta$ and $\theta'$, defined as

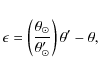
\begin{displaymath}\epsilon = \left( \frac{\theta_\odot}{\theta_\odot'} \right) \theta' - \theta, \end{displaymath} (4)

reaches a maximum of only $7.7 \times 10^{-6}$ arcsec around 0.6 solar radii. From these data, we conclude that the errors in $R_\odot$ have a negligable effect on the projection calculation.

It's not uncommon within solar physics to approximate the plate scale as $\alpha \approx (R_\odot/D_\odot) / N$, with the result interpreted as radians. The difference from the full calculation of Eq. (3) is equivalent to underestimating $R_\odot$ by $\sim$0.0075 Mm ( $0{\hbox{$.\!\!^{\prime\prime}$ }}010$), of which $\sim$0.0025 Mm ( $0{\hbox{$.\!\!^{\prime\prime}$ }}003$) is due to perspective effects, with the rest being due to the projection.

The minuteness of the errors generated by adopting a value for $R_\odot$validates the approach outlined earlier in this section. It's more accurate to express coordinates in angular units, using an adopted value for $R_\odot$specified by RSUN_REF, rather than to use ``solRad'' units. Such an approach allows perspective and projection effects to be taken into account to a high degree of accuracy, but does not preclude the data being used to derive a more accurate measure of the solar radius or shape.

In this discussion we have concentrated on uncertainties in the value of the solar radius. It is assumed that the solar distance is known to a much higher level of accuracy. The important quantity is actually $R_\odot/D_\odot$; it is the combined uncertainty in that ratio which determines the error.

9 Plasma effects

There are several ways that the solar corona can effect the radiation passing through it that are generally only important at radio wavelengths. Bastian (1994) discusses the scattering caused by turbulence, and concludes that this limits the resolution of solar radio observations to a few arc seconds at centimeter wavelengths, with the effect scaling as $\lambda^2$at shorter wavelengths.

The solar corona is also capable of refracting radio waves. For a rarefied plasma, the index of refraction can be approximated as

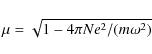
\begin{displaymath}\mu = \sqrt{1 - 4 \pi N e^2/(m \omega^2)} \end{displaymath} (5)

(Lang 1980), where N is the electron number density, e is the electron charge, m is the electron mass, and $\omega$ is the angular frequency. Thus, the deflection ${\rm d}\theta$ of a ray traversing a distance dxis given by

\begin{displaymath}{\rm d}\theta = \frac{2 \pi e^2}{\mu^2 m \omega^2} \left( \frac{{\rm d}N}{{\rm d}y} \right) {\rm d}x, \end{displaymath} (6)

where ${\rm d}N/{\rm d}y$ is the density gradient perpendicular to the wave propagation. In the regime where $\mu \approx 1$, the deflection scales as $\lambda^2$.

The amount of refraction occurring in any given observation will depend on the detailed structure of the corona traversed. However, we can get a rough idea of the importance of refraction at a given wavelength by modeling the corona with the expression

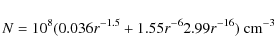
\begin{displaymath}N = 10^8 (0.036 r^{-1.5} + 1.55 r^{-6} 2.99 r^{-16}) \mbox{~cm}^{-3} \end{displaymath} (7)

from Cox (2000), and integrating Eq. (6) for a ray originating at the solar limb towards an observer at 1 AU Near the Sun, where the gradient is strongest, this ray would be mostly perpendicular to the density gradient, and would experience the maximum refraction. For a wavelength $\lambda=10$ cm, this works out to a deflection of about 0 $.\!\!^\circ$5. In other words, a radio source appearing to come from just above the limb would actually be from a source with a heliographic position 0 $.\!\!^\circ$5 degrees behind the limb. The angle of refraction does not translate directly into a shift in the plane of sky position. In the above example, that shift would be ${\sim}2''$.

Refraction is particularly important at wavelengths in the meter to kilometer range. Generally speaking, the term refraction is reserved for the effect of the smoothly varying component of the corona, while the effect of density fluctuations is described as scattering, even though the physical mechanism for both is the same. Thejappa & MacDowall (2009) discuss the refraction effects based on an interplanetary coronal model, and find that refraction is important when determining the source location through triangulation at hectometric to kilometric wavelengths. The same authors also studied the effects of scattering from density fluctuations, and showed that these fluctuations increase the apparent size of the solar diameter by several arc minutes at 50 MHz (Thejappa & MacDowall 2008). Hoang et al. (1998) found that the combined effects of refraction and scattering caused the apparent location of a type II radio burst from Ulysses observations on 8 January 1997 to be off by several AU from the true location.

When a strong magnetic field is applied to the plasma, Eq. (6) is modified to take into account not only the plasma frequency $\omega_{\rm p} = \sqrt{4 \pi N e^2 / m}$, but also the gyrofrequency $\omega_B = \pi e B / (m c)$, where B is the magnetic field strength (Ramaty 1969). A complete discussion of this topic is beyond the scope of this article. However, through most of the corona one can make the symplifying assumption that $\omega_{\rm p} \gg \omega_B$, and use Eq. (6).

\begin{figure} \par\includegraphics[width=8cm,clip]{10357fg2.eps} \end{figure} Figure 2:

Geometry illustrating gravitational deflection of a limb source S. The solar mass has been increased by a factor of 105 for illustrative purposes. The angle O'-P-O represents the total deflection of light, while the much smaller angle L-O-P represents the apparent displacement of the source as seen by the observer.

Open with DEXTER

10 Gravitational deflection

General relativity predicts that star light grazing the solar surface will be deflected by $\sim$1 $.\!\!^{\prime\prime}$75, with the effect dropping as $1/\theta_\rho^2$. VLBI observations have confirmed this result to very high accuracy (Shapiro et al. 2004). However, we are concerned with the behavior of radiation emitted close to the Sun, where as in the case of refraction, the amount of deflection does not translate directly into a shift in the image position. For example, a photon emitted at the solar limb would experience a deflection half that of a star, or $\sim$0 $.\!\!^{\prime\prime}$875. This should be interpreted not as a shift in plane-of-sky coordinates, but primarily as a shift in the heliographic coordinates.

The first order general relativistic solution for the motion of a photon in the Sun's gravitational field is

\begin{displaymath}\psi = \sin^{-1}\frac{r_0}{r} - \frac{GM}{r_0 c^2} \left( \s... ...t(\frac{r_0}{r}\right)^2} + \sqrt{\frac{r-r_0}{r+r_0}}\right) \end{displaymath} (8)

where $r,\psi$ are the polar coordinates of the ray path, and r0 is the point of closest approach (Weinberg 1972). The quantity r0 is related to the impact parameter b, and to first order $r_0 \approx b$. For a source on the limb, we can set $r_0 = R_\odot$, evaluate Eq. (8) in the neighborhood of r = 1 AU, and trace this back to the apparent position of the limb. When this is done, we find that the apparent solar radius is about 0 $.\!\!^{\prime\prime}$002 larger than the geometric value.

The geometry is illustrated in Fig. 2, where the solar mass has been increased by a factor of 105 to allow the effects to be visible. Light emitted by the source S in the direction O' is gravitationally deflected to be seen by the observer O. The point P marks the intersection of the original and final directions of propagation. The angle O'-P-Otherefore is the total amount of deflection. When the actual solar mass is used, this angle is 0 $.\!\!^{\prime\prime}$875 as expected. The point L marks the geometric position of the limb relative to O. The angle L-O-Prepresents the change in apparent position of the limb in the plane of the sky, and is much smaller than the deflection.

11 Conclusions

The relative importance of the various effects discussed in this paper are summarized in Table 1 for the solar disk seen from 1 AU. Most of these effects are only important for high precision measurements, and can be safely ignored when only modest accuracy is required.

Table 1:   Effects which need to be taken into account to achieve photospheric accuracies on the solar disk ranging from 1'' down to 0 $.\!\!^{\prime\prime}$001, as seen by an observer at 1 AU.

Typical solar data analysis is carried out in the small-angle regime where no distinction is made between angular and planar coordinates - in Paper I this was referred to as pseudo-angles. The present work validates that approach when only modest accuracy ( ${>}0{\hbox{$.\!\!^{\prime\prime}$ }}1$) is required, and when the field-of-view doesn't exceed more than a few solar radii. Although the pseudo-angles of Paper I were defined to lie on the plane perpendicular to the Sun-observer line, the analysis of Sect. 5 shows that the results are not significantly affected if the plane used is slightly inclined to that of the formal definition. However, perspective effects are still important when converting between helioprojective and heliographic coordinates.

Some effects which are small for photospheric measurements become more significant as one moves out into the corona. This is particularly true for spherical projection effects, which can become quite important for large-angle coronagraphs.

The precisions of Table 1 can only be achieved if the instrumental effects and cross-instrument coalignments can be determined to comparable or better precision. For high precision work, one must also consider any optical distortions which occur in the image. One way to deal with optical distortion is by a judicious selection of the projection used to describe the observation. There is also a standard in development for how to encode distortions within FITS files (Calabretta et al. 2004).

Table 2 lists the FITS keywords introduced in the present work. Paper I also introduced the keyword CAR_ROT to store the Carrington rotation number, plus a family of keywords ending in ``_OBS'' based on the labels of Tables 1 and 3 in that work.

An important effect on solar coordinates is differential solar rotation. This primarily affects data sets which are a combination of observations over a period of time, such as slit spectrograph raster scans, or synoptic maps. The scope of this topic is very broad, and will be addressed in a future paper.

The coordinate systems of Paper I are based on the WCS formalism established in Greisen & Calabretta (2002) and Calabretta & Greisen (2002). We would also like to bring the reader's attention to Greisen et al. (2006), which further extends the WCS system. The primary focus of that latter work is spectral coordinates, but there are also aspects which apply to all kinds of coordinates. Of particular interest is the table lookup (TAB) projection, which can be used for a wide variety of otherwise difficult to encode data. For example, the TAB projection could be used for storing model calculations using adaptive mesh refinement.

Table 2:   FITS keywords introduced in this paper. Each is expressed in units of meters.

Acknowledgements

The author would like to thank Dean Pesnell for many helpful suggestions, and Gordon Holman and Jeffrey Brosius for useful references on the theory of radio transport through a plasma. The author would also like to thank the referee for many helpful comments and careful criticisms. This work was carried out under NASA grant NNG06EB68C.

References

  1. Allen, C. W. 1976, Astrophysical Quantities, 3rd edn. (London: Athlone) [Google Scholar]
  2. Badache-Damiani, C., & Rozelot, J. P. 2006, MNRAS, 369, 83 [Google Scholar]
  3. Bastian, T. S. 1994, ApJ, 426, 774 [NASA ADS] [CrossRef] [Google Scholar]
  4. Brown, D. S., Bewsher, D., & Eyles, C. J. 2009, Sol. Phys., 254, 185 [NASA ADS] [CrossRef] [Google Scholar]
  5. Calabretta, M. R., & Greisen, E. W. 2002, A&A, 395, 1077 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Calabretta, M. R., Valdes, F., Greisen, E. W., & Allen, S. L. 2004, in Astronomical Data Analysis Software and Systems (ADASS) XIII, ed. F. Ochsenbein, M. G. Allen, & D. Egret, ASP Conf. Ser., 314, 551 [Google Scholar]
  7. Cox, A. N. 2000, Allen's Astrophysical Quantities, 4th edn. (New York: AIP Press, Springer) [Google Scholar]
  8. Delmas, C., Morand, F., Laclare, F., et al. 2006, Adv. Space Res., 37, 1564 [NASA ADS] [CrossRef] [Google Scholar]
  9. Greisen, E. W., & Calabretta, M. R. 2002, A&A, 395, 1061 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Greisen, E. W., Calabretta, M. R., Valdes, F. G., & Allen, S. L. 2006, A&A, 446, 747 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Hoang, S., Maksimovic, M., Bougeret, J.-L., Reiner, M. J., & Kaiser, M. L. 1998, Geophys. Res. Lett., 25, 2497 [NASA ADS] [CrossRef] [Google Scholar]
  12. Lang, K. R. 1980, Astrophysical Formulae, 2nd edn. (New York: Springer-Verlag) [Google Scholar]
  13. Ramaty, R. 1969, ApJ, 158, 753 [NASA ADS] [CrossRef] [Google Scholar]
  14. Schou, J., Kosovichev, A. G., Goode, P. R., & Dziembowski, W. A. 1997, ApJ, 489, L197 [NASA ADS] [CrossRef] [Google Scholar]
  15. Shapiro, S. S., Davis, J. L., Lebach, D. E., & Gregory, J. S. 2004, Phys. Rev. Lett., 92, 121101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  16. Stumpff, P. 1979, A&A, 78, 229 [NASA ADS] [Google Scholar]
  17. Thejappa, G., & MacDowall, R. J. 2008, ApJ, 676, 1338 [NASA ADS] [CrossRef] [Google Scholar]
  18. Thejappa, G., & MacDowall, R. J. 2009, in IAU Symp. 257, ed. N. Gopalswamy, & D. F. Webb, 329 [Google Scholar]
  19. Thompson, W. T. 2006, A&A, 449, 791 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Weinberg, S. 1972, Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity (New York: John Wiley & Sons, Inc.) [Google Scholar]

Footnotes

...distance[*]
Note that this means that one cannot combine units of ``solRad'' with explicitly angular axis labels such as HPLN-TAN, HPLT-TAN.

All Tables

Table 1:   Effects which need to be taken into account to achieve photospheric accuracies on the solar disk ranging from 1'' down to 0 $.\!\!^{\prime\prime}$001, as seen by an observer at 1 AU.

Table 2:   FITS keywords introduced in this paper. Each is expressed in units of meters.

All Figures

  \begin{figure} \par\includegraphics[width=9cm,clip]{10357fg1.eps} \end{figure} Figure 1:

Maximum coordinate errors as a function of radial distance for optical axis errors of 1'', 10'', 100'', and 1000'' respectively, using the gnomonic (TAN) projection. The vertical dotted line represents the position of the solar limb.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{10357fg2.eps} \end{figure} Figure 2:

Geometry illustrating gravitational deflection of a limb source S. The solar mass has been increased by a factor of 105 for illustrative purposes. The angle O'-P-O represents the total deflection of light, while the much smaller angle L-O-P represents the apparent displacement of the source as seen by the observer.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.