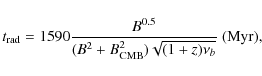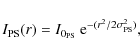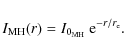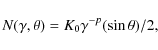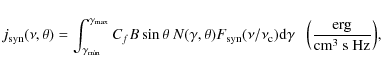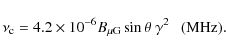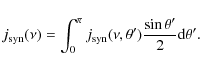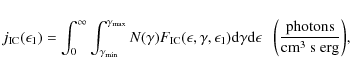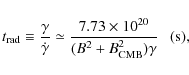EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 514 (May 2010) A&A, 514 (2010) A76 Full HTML
Free Access
Issue
A&A
Volume 514, May 2010
Article Number A76
Number of page(s) 14
Section Cosmology (including clusters of galaxies)
DOI https://doi.org/10.1051/0004-6361/201014126
Published online 26 May 2010
A&A 514, A76 (2010)

GMRT observations of the Ophiuchus galaxy cluster

M. Murgia1 - D. Eckert2 - F. Govoni1 - C. Ferrari3 - M. Pandey-Pommier4 - J. Nevalainen5 - S. Paltani6

1 - INAF - Osservatorio Astronomico di Cagliari, Poggio dei Pini, Strada 54, 09012 Capoterra (CA), Italy
2 - INAF - IASF-Milano, via Bassini 15, 20133 Milano, Italy
3 - UNS, CNRS UMR 6202 Cassiopée, Observatoire de la Côte d'Azur, Nice, France
4 - CRAL - Observatoire de Lyon, 9 avenue Charles André, 69230 Saint-Genis-Laval, France
5 - Department of Physics, PO Box 48, 00014 University of Helsinki, Finland
6 - ISDC, Université de Genève, 16, Ch. d'Ecogia, 1290 Versoix, Switzerland

Received 25 January 2010 / Accepted 10 February 2010

Abstract
Aims. Observations with the Very Large Array telescope at 1477 MHz revealed the presence of a radio mini-halo surrounding the faint central point-like radio source in the Ophiuchus cluster of galaxies. In this work we present a study of the radio emission from this cluster of galaxies at lower radio frequencies.
Methods. We observed the Ophiuchus cluster at 153, 240, and 614 MHz with the Giant Metrewave Radio Telescope.
Results. The mini-halo is clearly detected at 153 and 240 MHz, the frequencies at which we reached the best sensitivity to the low-surface brightness diffuse emission, while it is not detected at 610 MHz because of the too low signal-to-noise ratio at this frequency. The most prominent feature at low frequencies is a patch of diffuse steep spectrum emission located at about 5$^\prime$ south-east from the cluster centre. By combining these images with that at 1477 MHz, we derived the spectral index of the mini-halo. Globally, the mini-halo has a low-frequency spectral index of $\alpha_{240}^{153} \simeq 1.4\pm0.3$ and an high-frequency spectral index of $\alpha_{1477}^{240}\simeq 1.60\pm 0.05$. Moreover, we measure a systematic increase of the high-frequency spectral index with radius: the azimuthal radial average of $\alpha_{1477}^{240}$ increases from about 1.3, at the cluster centre, up to about 2.0 in the mini-halo outskirts.
Conclusions. The observed radio spectral index agrees with that obtained by modelling the non-thermal hard X-ray emission in this cluster of galaxies. We assume that the X-ray component arises from inverse-Compton scattering between the photons of the cosmic microwave background and a population of non-thermal electrons, which are isotropically distributed and whose energy spectrum is a power law with an index p. We derive that the electrons energy spectrum should extend from a minimum Lorentz factor of $\gamma_{\rm min}\lesssim 700$ up to a maximum Lorentz factor of $\gamma_{\rm max}\simeq 3.8 \times 10^{4}$ with an index $p=3.8\pm 0.4$. The volume-averaged strength for a completely disordered intra-cluster magnetic field is $B_{\rm V}\simeq 0.3\pm 0.1~\mu$G.

Key words: galaxies: clusters: individual: Ophiuchus - radio continuum: galaxies

1 Introduction

Galaxy clusters, the largest gravitationally bound structures in the Universe, are still forming at the present epoch by a merging of nearly equal-mass systems or accretion of groups and field galaxies. They are excellent laboratories to study the baryonic cosmic fraction as well as the interplay between baryonic and dark matter in the formation and evolution process of large scale structures (e.g. Arnaud et al. 2009; Kravtsov et al. 2009). In the last twenty years important progress has been made in the study of galaxy clusters, of the thermal intra-cluster medium (ICM) and of their interaction (e.g. Boselli & Gavazzi 2006; Markevitch & Vikhlinin 2007). Much less is known though about the physical properties and the origin of a non-thermal intra-cluster component (relativistic electrons with energies of $\simeq$10 GeV spiralling in magnetic fields of few $\mu$Gauss) that was discovered and studied mostly through deep radio observations (see e.g. Ferrari et al. 2008, and references therein). However, it is now clear that the impact of the non-thermal component in the physics and thermo-dynamical evolution of galaxy clusters cannot be neglected anymore (e.g. Dursi & Pfrommer 2008; Parrish et al. 2009).

Intra-cluster relativistic electrons radiate through synchrotron emission in the radio domain, but also through inverse Compton scattering of cosmic microwave background (CMB) photons in the hard X-ray (HXR) band. The diffuse non-thermal component is now well detected at radio wavelengths in about 30 clusters (Giovannini et al. 2009). Only a few X-ray satellites allowed possible but controversial detection of a hard tail in the X-ray spectrum of about ten clusters (see e.g. Fusco-Femiano et al. 2003; Nevalainen et al. 2004; Rephaeli et al. 2008). Very recent results either agree with an HXR non-thermal detection (e.g. Eckert et al. 2008) or suggest a possible thermal origin of the detected HXR emission (e.g. Kawano et al. 2009).

Table 1:   Details of the GMRT observations.

The Ophiuchus cluster (z=0.028, Johnston et al. 1981) is one of the brightest clusters of galaxies in the X-ray band. It is an extremely interesting target for non-thermal cluster studies, because it shows evidence of both radio and possibly HXR emission (Eckert et al. 2008; Govoni et al. 2009; Murgia et al. 2009; Nevalainen et al. 2009). The dynamical state of the Ophiuchus cluster has been strongly debated in the last years. A recent Chandra study (Million et al. 2009) shows evidence of a recent merger event in the central region of the cluster of $8 \times 8$ arcmin2 (but see also Fujita et al. 2008, for an opposite conclusion based on Suzaku data). In addition several clusters and groups of galaxies have been detected within a distance of 8$^\circ $ from the cluster centre, indicating that Ophiuchus is in a supercluster environment (Wakamatsu et al. 2005).

By analysing Very Large Array (VLA) data of Ophiuchus at 1477 MHz, Govoni et al. (2009) recently detected a radio mini-halo surrounding the faint central point-like radio source. Radio mini-halos are diffuse steep-spectrum ( $\alpha > 1$; $S_{\nu}\propto \nu^{- \alpha}$) sources, permeating the central regions of relaxed, cool-core galaxy clusters. They usually surround a radio galaxy. These diffuse radio sources are extended on a moderate scale (typically $\simeq$500 kpc) and, in common with large-scale halos observed in merging clusters of galaxies, have a steep spectrum and a very low surface brightness. As a consequence of their relatively small angular size and possibly strong radio emission of the central radio galaxy, radio mini-halos are very elusive sources, and our current observational knowledge of mini-halos is limited to only a handful of well-studied clusters.

Based on current observational and theoretical analyses, radio emission from mini-halos would be due to a population of relativistic electrons ejected by the central AGN and re-accelerated by MHD turbulence, whose energy is, in turn, supplied by the cluster cooling-core (Gitti et al. 2004). Recent analysis of the most X-ray luminous cluster (RX J1347-1145) suggests that additional energy for electron re-acceleration in mini-halos might be provided by sub-cluster mergers that have not been able to destroy the central cluster cooling-core (Gitti et al. 2007). Ophiuchus is the second known cluster showing a radio mini-halo, and also a cool-core that has survived a possible recent merging event (Nevalainen et al. 2009; Million et al. 2009). Indeed, Burns et al. (2008) simulated the formation and evolution of galaxy clusters, and showed that cool-core clusters can accrete mass over time and grow slowly via hierarchical mergers; when late mergers occur, the cool-cores survive the collisions.

Eckert et al. (2008) measured a high confidence level (6.4$\sigma $) HXR excess in Ophiuchus through INTEGRAL observations. This emission may be of non-thermal origin, caused presumably by Compton scattering of cosmic microwave background radiation by the relativistic electrons responsible for the mini-halo emission (see e.g., Rephaeli et al. 2008; Petrosian et al. 2008, and references therein for reviews). Alternative explanations have also been put forward (Profumo 2008; Pérez-Torres et al. 2009; Colafrancesco & Marchegiani 2009). The HXR excess detection in Ophiuchus was recently confirmed by Nevalainen et al. (2009). In addition, their joint INTEGRAL and XMM analysis partly reconciled the previous discrepancy between the results by Eckert et al. (2008) and the upper limits on HXR flux obtained by Ajello et al. (2009) through Swift/BAT data.

Ophiuchus is thus one of the few clusters of galaxies in which the non-thermal component is revealed both in the radio and in the HXR bands. For this reason it is particularly interesting to investigate the radio spectrum of the mini-halo. By combining this information with the observed properties of the HXR emission it would be possible to derive important constraints on the energy spectrum of the synchrotron electrons. In particular, by assuming that the synchrotron emission and the HXR excess are co-spatial and produced by the same population of relativistic electrons, their comparison would allow the determination of the cluster magnetic field (Nevalainen et al. 2009).

In this work we present a study of the radio emission from the Ophiuchus cluster of galaxies at low radio frequencies. We observed the Ophiuchus cluster at 153, 240, and 614 MHz with the giant metrewave radio telescope (GMRT). Throughout this paper we assume a $\Lambda$CDM cosmology with H0 = 71 km s-1 Mpc-1, $\Omega_{\rm m} = 0.27$, and $\Omega_{\Lambda} = 0.73$. At the distance of Ophiuchus (z=0.028), 1 $^{\prime\prime}$  corresponds to 0.55 kpc.

2 GMRT observations

We observed the cluster of galaxies Ophiuchus using the GMRT at the frequencies of 153, 240, and 614 MHz (program OJ1712). The GMRT antennas were pointed at RA = 17$^{\rm h}$12$^{\rm m}$28$^{\rm s}$ and Dec = -23$^\circ $ 22$^\prime$06 $^{\prime\prime}$ (J2000). The visibilities were acquired in spectral line mode in order to reduce the bandwidth smearing effect and to facilitate the excision of narrow band radio frequency interferences (RFIs).

We summarize the details of the observations in Table 1, where we provide the frequency and total bandwidth, observation date, total time on source, beamwidth (FWHM) of the full array, and rms level (1$\sigma $) in the full resolution images. Calibration and imaging were performed with the NRAO astronomical image processing system (AIPS).

The Ophiuchus cluster has already been observed with the GMRT at 240 and 610 MHz by Pérez-Torres et al. (2009), who did not detect the diffuse mini-halo emission at the noise level of their images. The observations presented here, however, have on average an exposure time about a factor 4.5 longer and hence they permit us to go deeper in sensitivity.

\begin{figure} \par\includegraphics[width=18.2cm,clip]{14126fg1.eps} \vspace*{-2mm} \end{figure} Figure 1:

Top left: GMRT radio iso-contours at 153 MHz at full resolution overlaid to the ROSAT PSPC X-ray image of the Ophiuchus galaxy cluster. The radio image has an FWHM beam of $37.1\hbox {$^{\prime \prime }$ }\times 22.6\hbox {$^{\prime \prime }$ }$ with PA = 35.1$^\circ $ and a noise level of 5 mJy/beam (1$\sigma $). Contours start at 15 mJy/beam (3$\sigma $) and scale by a factor of $\sqrt {2}$. Top right: iso-contours at the frequency of 1477 from the VLA image by Govoni et al. (2009). The image as an FWHM beam of $91.4\hbox{$^{\prime\prime}$ }~\times~40.3\hbox{$^{\prime\prime}$ }$ with PA =  $-24.4\hbox {$^\circ $ }$. Contours start at 0.3 mJy/beam (3$\sigma $) and increase by $\sqrt {2}$. Bottom panels: finding charts from DSS2 - red for sources A, B, C, and D. No obvious optical identification exists for radio source B.

Open with DEXTER

2.1 153 MHz

The observations were performed using a central frequency of 153 MHz and a bandwidth of 8 MHz for both the upper and lower sideband (USB and LSB). The data were collected in spectral line mode with 128 spectral channels of 62.5 kHz in width. The observations consist of two distinct runs of about 5.2 and 4.7 h on source, performed on 2008 Aug. 21 and 22, respectively. The flux density scale and the bandpass were calibrated for both runs with the primary calibrator 3C 286. An initial amplitude solution for the bandpass calibrators was first obtained for a central channel free of RFIs. This channel was then used as reference in task BPASS to derive a bandpass solution. The bandpass solution was visually inspected and the most obvious RFIs were carefully excised. This procedure was repeated several times until a refined bandpass solution was obtained. Task FLGIT was applied to the whole dataset and about 30% of the data were automatically removed because of the contamination from strong RFIs. We ran task SPLAT to apply the bandpass calibration and to reduce the number of channels from 128 to six channels of 1 MHz width each. We calibrated the final data set in both phase and amplitude. The phase calibration was completed with the secondary calibrators 1830-360 and 1833-210, observed at intervals of $\sim$30 min. Low-level residual RFIs were carefully removed from the six-channels dataset by visual inspection, and finally the Ophiuchus data were extracted with task SPLIT and imaged. Several cycles of self-calibration were applied to remove residual phase variations.

We ran task IMAGR in 3D mode over a mosaic of slightly overlapping fields to account for the non-coplanarity of the incoming wavefront within the large primary beam of $\sim$ $3\hbox{$^\circ$ }$.

\begin{figure} \par\includegraphics[width=17.2cm,clip]{14126fg2.ps}\vspace*{-2.5mm} \end{figure} Figure 2:

Central panel: GMRT radio iso-contours at 240 MHz of the Ophiuchus galaxy cluster at full resolution. The radio image has a FWHM beam of $18.7\hbox{$^{\prime\prime}$ }~\times~15.9\hbox{$^{\prime\prime}$ }$ with PA = -25.7$^\circ $ and a noise level of 1.1 mJy/beam (1$\sigma $). Contours start at 3.3 mJy/beam (3$\sigma $) and scale by a factor of $\sqrt {2}$. The insets show the GMRT image at 614 MHz of sources A, B, C, and D. The 614 MHz has a FWHM beam of $7\hbox{$^{\prime\prime}$ }~\times~7\hbox{$^{\prime\prime}$ }$ and a noise level of 0.25 mJy/beam (1$\sigma $).

Open with DEXTER

We first calibrated the 153 MHz observations from the two runs independently and then combined the two datasets with task DBCON, performing a final self-calibration run. In the left panel of Fig. 1 we present the radio image at 153 MHz resulting from the combination of the data sets from the two observing days. The radio image has a FWHM beam of $37.1\hbox{$^{\prime\prime}$ }~\times ~22.6\hbox{$^{\prime\prime}$ }$ with PA = 35.1$^\circ $ and a noise level of 5 mJy/beam (1$\sigma $).

2.2 240 MHz

The 240 MHz observations consist of two data sets of 4.6 and 4.3 h on source, taken on 2008 Aug. 23 and 28, respectively. The Aug. 23 observations were performed for both the LSB and the USB with a total bandwidth of 8 MHz splitted into 128 channels of 62.5 kHz in width. The Aug. 28 observations were performed for the USB with a total bandwidth of 8 MHz splitted into 64 channels of 125 kHz in width. The flux density scale was calibrated by the source 3C 286. The source 1830-360 was observed at intervals of $\sim$30 min and used as secondary phase and gain calibrator. The bandpass was calibrated using the sources 3C 286 and 1830-360. Task FLGIT was applied to the whole dataset, and about 26% of the data were eliminated because of RFIs. Both data sets were averaged in frequency to six channels of 1 MHz in width to reduce noise while still keeping the bandwidth smearing effect under control. We processed the two data sets separately applying several cycles of imaging and self-calibration. The datasets were then combined with task DBCON, and we performed a final self-calibration run. The contour levels of the full resolution 240 MHz image are shown in the central panel of Fig. 2. The radio image has a FWHM beam of $18.7\hbox{$^{\prime\prime}$ }\times15.9\hbox{$^{\prime\prime}$ }$ with PA = -25.7$^\circ $ and a noise level of 1.1 mJy/beam (1$\sigma $).

2.3 614 MHz

The observations were performed on 2008 Aug. 28 for a total of 4.3 h on source. Data were recorded for both the USB and the LSB with a 16 MHz bandwidth splitted in 128 channels of 125 kHz in width. The central frequencies of the USB and LSB are 606 and 622 MHz, respectively. The flux density scale was calibrated by using the source 3C 286. The phase 1830-360 was observed at intervals of $\sim$30 min. The bandpass was calibrated using the sources 3C 286 and 1830-360. In order to improve the signal to noise ratio, data were averaged in frequency by collapsing the bandwidth to six spectral channels of 2 MHz in width. The six-channels dataset was carefully inspected to excise the RFIs. Several cycles of imaging and self-calibration were applied to remove the residual phase variations.

The USB and the LSB were imaged separately and then averaged together to produce a final image at a frequency of 614 MHz with a FWHM beam of $7\hbox{$^{\prime\prime}$ }\times7\hbox{$^{\prime\prime}$ }$ and a noise level of 0.25 mJy/beam (1$\sigma $). Cut-outs of the 614 MHz image are shown in the insets of Fig. 2.

3 Results

We analyse the results of the GMRT observations with particular emphasis on the determination of the radio spectrum of the cluster discrete sources and of the mini-halo.

3.1 Optical and radio properties

The Ophiuchus cluster is one of the most luminous X-ray galaxy clusters in the local Universe, but its optical properties are not very well known because of its unfortunate line-of-sight. The cluster lies in projection at only about 10$^\circ $  from the Galactic Centre and hence it is highly obscured. Recently, Ophiuchus was studied in the optical band by Wakamatsu et al. (2005), who derived spectroscopic redshifts for about 200 galaxies to within 5$^\circ $ from the cD galaxy at the centre of the cluster core. The velocity dispersion of the Ophiuchus cluster is found to be $1050\pm50$ km s-1. Such a large velocity dispersion is consistent with its high X-ray luminosity. Moreover, several clusters and groups of galaxies are observed to within a distance of 8$^\circ $ from the cluster centre, indicating that the Ophiuchus concentration may be a supercluster comparable in richness to the Coma-A1367 system, as early suggested by Djorgovski et al. (1990).

In the top left panel Fig. 1, the overlay of the GMRT radio iso-contours at 153 MHz to the ROSAT PSPC X-ray image of the Ophiuchus galaxy cluster is shown. The X-ray image is in the 0.1-2.4 keV energy band and has been background subtracted, divided by the exposure image, and smoothed with a Gaussian kernel with $\sigma=30\hbox{$^{\prime\prime}$ }$.

\begin{figure} \par\includegraphics[width=18cm,clip]{14126fg3.eps} % \end{figure} Figure 3:

Radio images of the Ophiuchus cluster of galaxies at $92\hbox {$^{\prime \prime }$ }\times 92\hbox {$^{\prime \prime }$ }$ FWHM beam resolution. Contours start at 3$\sigma $ level and scale by a factor of $\sqrt {2}$. Left to right: 74 MHz (VLSS; $\sigma =280$ mJy/beam), 153 MHz (GMRT; $\sigma =18$ mJy/beam), 240 MHz (GMRT; $\sigma =10$ mJy/beam), 614 MHz (GMRT; $\sigma =5.5$ mJy/beam), 1477 MHz (VLA; $\sigma =0.16$ mJy/beam).

Open with DEXTER

The most relevant radio features we detected are labeled A through E. At the centre of the cluster we detected a faint point-source (labeled A), whose position is coincident with the peak of the X-ray emission. This is the same point source detected with the VLA at 1477 MHz by Govoni et al. (2009), see Fig. 1 top right panel. Radio source A is associated with the prominent cD galaxy, which lies at the centre of the cluster (Fig. 1, bottom left panel). Source A appears point-like at our resolution and sensitivity. The brightest radio source in the field is source B, which is located about 10$^\prime$ north to the centre. Source B is an extended source with an angular size of $174\hbox{$^{\prime\prime}$ }\times 50\hbox{$^{\prime\prime}$ }$, corresponding to a projected linear size of about $100\times 30$ kpc (see top-left inset in Fig. 2). There is no obvious optical identification for this radio source, whose rather peculiar morphology makes its classification very uncertain. In fact, it lacks of any of the typical features observed in ordinary radio galaxies, like core, jets, or lobes. Source B is not a head-tail radio galaxy either. Rather, the source has an amorphous filamentary structure. The south-east part is characterized by several threads of radio emission emerging perpendicular to the source's major axis. The north-west part of the source is composed by a single filamentary feature whose tip bends backwards to form what resembles a vortex-like structure. Instead, sources C and D are the typical cluster tailed radio galaxies. Source C is about 300 $^{\prime\prime}$ long (165 kpc) and is pointing north-east to south-west. Source D has a faint tail about 230 $^{\prime\prime}$ long (127 kpc) pointing from south to north. The apparent difference in radial velocity between sources C and D and the Ophiuchus cluster is $\ga$1000 km s-1. We assume here a mean recession velocity of 9063 km s-1 for the central region of the Ophiuchus cluster (Wakamatsu et al. 2005) and that the two radio sources are associated to galaxies 2MASX J17115542-2309423 (cz = 8050 km s-1) and 2MASX J17120908-2328263 (cz = 7469 km s-1) (Hasegawa et al. 2000). These properties are further confirmed by the spectral ageing analysis presented in Sect. 3.3 and indicate that the ram-pressure model can easily explain the radio jet deflection. The two galaxies could have this high velocity with respect to the ICM either because they are individually infalling towards the cluster centre or because they are part of merging sub-clusters. The merger-induced bulk motion of the galaxies in the ICM would then be responsible for bending the radio jets. The latter scenario would agree with the results by Bliton et al. (1998), who derived that narrow-angle tailed radio galaxies are preferentially found in dynamically complex clusters.

Finally, we detected an extended patch of diffuse emission at about 5$^\prime$ south-west from the cluster centre. This feature, labelled E in Fig. 1, is the only part of the mini-halo visible in the 153 MHz GMRT image at full resolution. This patch is also present in the 240 MHz image at full resolution shown in Fig. 2, where few other ``fragments'' of the mini-halo can be observed all around the cluster centre. At 614 MHz the diffuse emission of the mini-halo is too faint to be detected at full resolution.

The VLA image at 1477 MHz shown in the top-right panel of Fig. 1 has a very good sensitivity to the extended emission. Given the noise level of about 0.1 mJy and the relatively high resolution of $91\hbox{$^{\prime\prime}$ }\times 40\hbox{$^{\prime\prime}$ }$ provided by the VLA in D configuration, the 3$\sigma $ sensitivity level on the mini-halo diffuse emission is of 0.07 $\mu$Jy/arcsec2. For comparison, the sensitivities of the full resolution GMRT images are of 15.8, 8.9, and 13.5 $\mu$Jy/arcsec2 at 153, 240, and 614 MHz. It should be considered that the observed surface brightness at 1477 MHz of the mini-halo is at best $\la$0.5 $\mu$Jy/arcsec2 and hence the minimum spectral index required to detect the mini-halo at 153 and 240 MHz is $\alpha > 1.5$. The detection turns out to be prohibitive at 614 MHz because the required mini-halo spectral index should be as high as $\alpha > 3.8$.

Thus to improve the signal to noise ratio of the GMRT data, we realized a set of images with natural weighting (ROBUST = 5 in IMAGR) and by tapering the longest baselines in order to smooth the angular resolution to $92\hbox {$^{\prime \prime }$ }\times 92\hbox {$^{\prime \prime }$ }$. This is the resolution adopted in the VLA study of the mini-halo at 1477 MHz by Murgia et al. (2009). The radio iso-contours of these images are presented in Fig. 3. The degradation of the resolution of the images results in an improved sensitivity to the diffuse emission. At $92\hbox {$^{\prime \prime }$ }\times 92\hbox {$^{\prime \prime }$ }$ resolution, the 3$\sigma $ sensitivities of the GMRT images are of 5.6, 3.1, and 1.6 $\mu$Jy/arcsec2 respectively at 153, 240, and 614 MHz.

The mini-halo is clearly detected at 153 and 240 MHz, the frequencies at which we reached the best sensitivity to the low-surface brightness diffuse emission, while it is too faint to be detected at 614 MHz even at the $92\hbox {$^{\prime \prime }$ }\times 92\hbox {$^{\prime \prime }$ }$ resolution. The most prominent feature of the mini-halo at low frequencies is still the patch E, which is marginally visible also in the VLSS at 74 MHz. However, the higher signal-to-noise ratio achieved in the 153 and 240 MHz images at low-resolution reveals a bridge of diffuse radio emission, which is aligned along the cluster major axis and connects patch E, the central source A, and the amorphous source B.

Table 2:   Integrated spectra for cluster discrete sources.

3.2 Integrated radio spectra of discrete sources

Determining the radio spectra of the discrete sources is important to understand their nature and, possibly, their connection with the mini-halo. We analysed the integrated radio spectra of sources A, B, C, and D by complementing the GMRT measurements at 153, 240 and 614 MHz with the flux densities available in literature. In particular, we made use of the VLSS at 74 MHz, the WISH survey at 325 MHz, the NVSS at 1400 MHz and the VLA 1477 MHz image by Govoni et al. (2009). The flux density of source A at the different frequencies has been determined by using AIPS task JMFIT. Since sources B, C, and D are extended, we determined the flux density by integrating their radio brightness down to the 3$\sigma $ isophote. All the VLSS flux densities at 74 MHz reported in this work have been corrected for the clean bias, following the prescription of Cohen et al. (2007). The integrated spectra are reported in Table 2. The flux density uncertainties include a 5% absolute calibration error.

In Fig. 4 we present the plots of the integrated radio spectra along with a power law fit to the data. Overall, the GMRT measurements agree both with the fit and with the adjacent data points taken from the literature, thus providing a positive check of the flux density scale in our images.

Source A is a compact source with a steep spectrum. The spectral index of the central source in the considered frequency window is $\alpha\simeq$0.6, a typical value for radio sources.

The amorphous source B presents a power law radio spectrum with a spectral index of about $\alpha=1.01 \pm 0.03$. This is a quite usual value for active radio galaxies, which makes the interpretation of this object even more puzzling. Indeed, although the distorted morphology of this radio source recalls that of extreme relic sources in clusters of galaxies (see e.g. Slee et al. 2001), on the basis of its radio spectrum it cannot be classified as an ultra-steep spectrum source. A 5 GHz archive VLA image (not shown) suggests a very weak point-like source but without kpc-scale jets. Indeed, it is not clear which mechanism is powering the relativistic electrons in this extended radio source. One possibility could be that source B is a relic radio source revived by the adiabatic compression caused by a shock wave or a bulk gas motion propagating thought the ICM (Enßlin & Gopal-Krishna 2001). However, no particular X-ray feature is visible in coincidence of the radio source neither in the ROSAT nor in the XMM-Newton  images and hence the origin of this peculiar radio source as well as its possible relation with the mini-halo remain, at the moment, unclear.

Finally, the tailed sources C and D have similar integrated spectra that are well described by a power law with the index  $\alpha\simeq 0.5$.

\begin{figure} \par\includegraphics[width=17.2cm,clip]{14126fg4.ps}\vspace*{2mm} \end{figure} Figure 4:

Integrated radio spectra for the central source A (top-left), for the amorphous source B (top-right), and for the two tailed sources C and D (bottom panels). The triangles represent the GMRT flux density measurement from this work, while the dots are the data taken from the literature. The lines represent the best fit of a power law with index $\alpha $.

Open with DEXTER

\begin{figure} \par\includegraphics[width=16.5cm,clip]{14126fg5.ps} \end{figure} Figure 5:

Spectral index profile between 153 and 1400 MHz along the tail for radio sources C (left panel) and D (right panel). Data points have been sampled in circular boxes of one beam-width, as shown in the inset. The line is the expected spectral index trend for the case of constant advance speed.

Open with DEXTER

3.3 Spectral ageing analysis of sources C and D

Sources C and D can be classified as narrow-angle-tails (NATs). This morphology is indicative of a strong relative velocity between the host galaxy and the ICM. The ram pressure exerted by the external gas bends the radio jets that merge together forming the characteristic tail of radio plasma. The relativistic electrons at the end of the tail must have been deposited first and hence their radio spectrum should be steeper because they suffered greater energy losses.

In Fig. 5 we present the spectral index profile between 153 MHz (GMRT) and 1400 MHz (NVSS) as a function of distance from the host galaxy for sources C and D. Both the GMRT and the NVSS images were convolved to the same resolution of $45\hbox{$^{\prime\prime}$ }\times 45\hbox{$^{\prime\prime}$ }$ and re-gridded to a common pixel size to ensure a proper comparison.

For both sources, the spectral index increases systematically with the increasing distance from the host galaxy, a typical behaviour observed in many NATs. The spectral steepening can be interpreted in terms of radiative losses of the relativistic electrons. In particular, we assumed that the radio spectrum is described by a JP model (Jaffe & Perola 1972), characterized by a low-frequency zero-age power law with an index $\alpha_{\rm inj}$ and an exponential cut-off beyond a high-frequency break, $\nu_{\rm b}$. The break frequency is related to the radiative age of the relativistic electron, $t_{\rm rad}$, and to the source's magnetic field, B, through

\begin{displaymath}t_{\rm rad}= 1590 \frac{B^{0.5}}{(B^2+B_{\rm CMB}^2) \sqrt{(1+z) \nu_{b}}}~\rm (Myr), \end{displaymath} (1)

where the magnetic field is in $\mu$G and the break frequency in GHz, while $B_{\rm CMB}=3.25(1+z)^{2}~\mu$G is a virtual magnetic field whose energy density equals that of the CMB and accounts for the inverse Compton losses (see also Sect. 4.2).

Following Parma et al. (1999), we assumed that the radio plasma in the tail separates from the host galaxy at a constant speed. In this case, the break frequency scales $\nu_{\rm b}\propto 1/d^2$, where d is the distance along the tail. Given this trend for $\nu_{\rm b}$, we computed the expected spectral index on the basis of the JP model as a function of the distance d. Close to the host galaxy ( $d\rightarrow 0$) the break frequency $\nu_{\rm b}\rightarrow\infty$; the radio spectrum is a power law with the index $\alpha_{\rm inj}$. At an increasing distance from the host galaxy, $\nu_{\rm b}$ shifts to a low frequency and the radio spectrum steepens. By fitting the observed spectral index profile, we derived the injection spectral index and the lowest value for the break frequency. For source C we found $\alpha_{\rm inj}\simeq 0.42\pm 0.03$ and a minimum break frequency of $\nu_{\rm b}\simeq 800 \pm 170$ MHz at a distance of 120 kpc from the host galaxy. By using standard formulas (e.g. Pacholczyk 1970), we estimated the minimum energy magnetic field, $B_{\rm min}$, of the tail by integrating the radio luminosity from 100 MHz to 10 GHz and by assuming a ratio between the energy density of relativistic protons to that of the electrons of k=1. For source C we obtained $B_{\rm min}\simeq 6.7$ $\mu$G and, on the basis of Eq. (1), we calculated a radiative age of $t_{\rm rad}=80 \pm 10$ Myr. The corresponding advancing speed of the tail is $v\gtrsim 1460\pm 160$ km s-1, in agreement with the dispersion velocity of galaxies in the Ophiuchus cluster.

Source D is fainter than source C, and thus the uncertainties on the best-fit parameters are larger. However, we found $\alpha_{\rm inj}\simeq 0.5~\pm ~0.3$ and a lowest break frequency of $\nu_{\rm b}\simeq 400~ \pm ~200$ MHz at a distance of about 40 kpc from the host galaxy. We calculated for the radio source a minimum energy magnetic field of $B_{\rm min}\simeq 8.4$ $\mu$G, and we estimated a radiative age of $t_{\rm rad}=87 \pm 26$ Myr, which corresponds to an advancing speed for the tail of $v\gtrsim 450\pm120$ km s-1, i.e. smaller than that of source C.

It is worth noting that the estimated advancing velocities should be regarded as lower limits if the tail's length has been significantly shortened by projection effects.

3.4 The mini-halo spectral index image

The main goal of this work is to constrain the spectral index of the mini-halo in the Ophiuchus cluster. This is a particularly hard task because the mini-halo is very faint and extended. The best compromise between sensitivity and resolution is obtained in the 240 MHz image at a $92\hbox {$^{\prime \prime }$ }\times 92\hbox {$^{\prime \prime }$ }$ resolution. In the top-left panel of Fig. 6 we present the spectral index image between 240 and 1477 MHz with the 240 MHz radio iso-contours overlaid. The spectral index image is calculated only from those pixels whose brightness is above the $3\sigma$ level at both frequencies. The overall radio spectrum of the mini-halo is steep. The spectral index ranges from about $\alpha\simeq 1.5$, close to the cluster centre, up to about $\alpha\simeq 2.0$ in correspondence of patch E. In the top-right panel of Fig. 6 we show the spectral index uncertainty, which is in the range from 0.05 to 0.2.

The bottom panels of Fig. 6 show the radio spectrum of the mini-halo at four different sample positions. In addition to the GMRT data, the spectra also include the measurements obtained from the VLSS at 74 MHz and the VLA at 1477 MHz. All the images considered were re-gridded to a common geometry and convolved at the same angular resolution of $92\hbox{$^{\prime\prime}$ }~\times~ 92\hbox{$^{\prime\prime}$ }$. The radio spectra between 74 and 1477 MHz indicate no deviation from a power law model, although this could be due to the comparatively small frequency range considered.

Patch E is also detected at 74 MHz in the VLSS and has a spectral index of $\alpha\simeq 2.04\pm0.09$ (see Fig. 6, bottom-left spectrum). Patch E appears as an isolated feature at a comparatively large distance from the centre of the cluster. It is important to stress again though that the VLA image at 1477 MHz has a much higher dynamic range compared to the GMRT image at 240 MHz. Indeed, there are regions of the mini-halo that are clearly detected at 1477 MHz but are not represented in Fig. 6 simply because their spectrum is not steep enough.

3.5 Azimuthally averaged radial profile of the mini-halo emission

The GMRT images at 153 and 240 MHz at $92\hbox {$^{\prime \prime }$ }\times 92\hbox {$^{\prime \prime }$ }$ resolution have enough sensitivity to allow us the analysis of the azimuthally averaged radial profiles of the mini-halo emission. The surface brightness of mini-halos in clusters of galaxies decreases with increasing distance from the cluster centre, eventually falling below the noise level of the radio images. Although deviations of the diffuse emission from spherical symmetry are often observed, the azimuthally averaged radial profiles are indeed quite smooth and regular. We derived the azimuthally averaged brightness of the Ophiuchus mini-halo at 153 and 240 MHz and compare the result with the finding obtained with the VLA at 1477 MHz by Murgia et al. (2009).

\begin{figure} \par\includegraphics[width=15.4cm,clip]{14126fg6.eps} \end{figure} Figure 6:

Spectral index image of the mini-halo in the Ophiuchus cluster. The top left panel shows the spectral index image of the mini-halo in the Ophiuchus cluster between 240 and 1477 MHz at an angular resolution of $92\hbox{$^{\prime\prime}$ }~\times~ 92\hbox{$^{\prime\prime}$ }$. The iso-contours represent the 240 MHz image obtained by tapering the long baselines between the GMRT antennas. Contours start at 30 mJy/beam (3$\sigma $) and increase by a factor of $\sqrt {2}$. The 1477 MHz image is taken from Govoni et al. (2009) and has a noise level of 0.16 mJy/beam (1$\sigma $). The spectral index is calculated only in those pixels whose brightness is above 3$\sigma $ at both frequencies. The top right panel shows the image of the spectral index uncertainty. The bottom panels show the mini-halo spectrum between 74 MHz and 1477 MHz in the four sample positions indicated in the top left panel.

Open with DEXTER

In the top panel of Fig. 7 we show the azimuthally averaged radio halo brightness profiles obtained from the 153, 240 and 1477 MHz images at 92 $^{\prime\prime}$ resolution. Each data point represents the average brightness in concentric annuli of half beam width centred on the X-ray peak. Discrete sources were masked out and excluded from the statistics. We considered only data points whose observed brightness was five times above the error on the radial average. Following Murgia et al. (2009), in order to carefully separate the contribution of the mini-halo from that of the central radio galaxy, we fitted the total brightness profiles with a central point source plus the radio mini-halo diffuse emission

\begin{displaymath}I(r)=I_{\rm PS}(r)+I_{\rm MH}(r). \end{displaymath} (2)

The profile of the central point source was characterized by a Gaussian of the form

\begin{displaymath}% I_{\rm PS}(r)=I_{0_{\rm PS}}~{\rm e}^{-(r^2/2\sigma_{\rm PS}^2)}, \end{displaymath} (3)

while the brightness profile of the mini-halo was characterized by an exponential law of the form

\begin{displaymath}% I_{\rm MH}(r)=I_{0_{\rm MH}}~{\rm e}^{-r/r_{\rm e}}. \end{displaymath} (4)

The best fit of the total model in Eq. (2) is represented by the solid lines in the top panel of Fig. 7. The contribution from the mini-halo exponential disc alone is represented by the dotted lines. The fit was performed in the image plane as described in Murgia et al. (2009). In order to properly take into account the resolution, the exponential model was first calculated in a 2-dimensional image, with the same pixel size and field of view as the observed one, and was then convolved with the same beam by means of a Fast Fourier Transform. The resulting image was masked exactly in the same regions as the observations. Finally, the model was azimuthally averaged with the same set of annuli used to obtain the observed radial profile. All these functions were performed at each step during the fit procedure. As a result, the values of the central brightness, $I_{0_{\rm MH}}$, and the e-folding radius, $r_{\rm e}$, provided by the fit are deconvolved quantities, and their estimate includes all the uncertainties related to the masked regions and to the sampling of the radial profile in annuli of finite width. The best-fit parameters are reported in Table 3.

At 153 MHz the best fit of the exponential model yields a central brightness of $I_{0_{\rm MH}}\simeq 7.0~\mu$Jy/arcsec2 and $r_{\rm e}\simeq 510$ kpc, while at 240 MHz the best fit yields $I_{0_{\rm MH}}\simeq 3.9~\mu$Jy/arcsec2 and $r_{\rm e}\simeq 450$ kpc.

In the bottom panels of Fig. 7 we trace the spectral index radial profile of the mini-halo between 153 and 240 MHz and between 240 and 1477 MHz. The radial profile of the low-frequency spectral index between 153 and 240 MHz is fairly constant to a value of about $\alpha\simeq 1.3 \div 1.5$. On the other hand, the e-folding radius of the mini halo at low frequency is more than four times larger than at 1477 MHz. This results in a progressive steepening of the spectral index with the increase of the distance from the cluster centre. The spectral index between 240 and 1477 MHz increases steadily from $\alpha\simeq 1.3$ at the cluster centre, and up to $\alpha\simeq 2.0$ at the mini-halo periphery.

\begin{figure} \par\includegraphics[width=9cm,clip]{14126fg7.ps} \end{figure} Figure 7:

Azimuthally averaged radial profiles of the mini-halo radio intensity at 153, 240 and 1477 MHz ( top panel). We considered only data points whose observed brightness is five times above the error on the radial average. The solid lines represent the best fit of the exponential disc model plus the contribution by the central point source. The dotted lines represent the exponential disc model alone. The mid and bottom panels show the radial profiles of the spectral index between 153 and 240 MHz and between 240 and 1477 MHz, respectively.

Open with DEXTER

Table 3:   Properties of the Ophiuchus mini halo derived from the fit procedure.

We calculated the model flux densities in an area with a radius of $r=7\hbox{$^\prime$ }$ (corresponding to about 230 kpc) from the cluster centre. This is the extraction region of the HXR emission used by Nevalainen et al. (2009). The mini-halo flux densities were obtained by the formula (Murgia et al. 2009):

\begin{displaymath}S_{\rm MH}= 2\pi \int_{0}^{r^{\prime}} I_{\rm MH}(r) r {\rm d... ...e}}(-r^{\prime}/r_{\rm e}-1)] \cdot r_{\rm e}^2 I_{0_{\rm MH}} \end{displaymath} (5)

where we set $r^{\prime}=7\hbox{$^\prime$ }$.

We obtained S153=2900 mJy, S240=1560 mJy, and S1477=85 mJy. The mini-halo is not detected at 74 and 614 MHz, the upper limit to the flux density in a 7$^\prime$ area are of S74<48 500 mJy and S614<900 mJy, respectively. These limits were calculated with the assumption that the average surface brightness of the diffuse emission is lower than the $3\sigma$ noise level of the corresponding radio image.

The global radio spectrum of the mini-halo is shown in Fig. 8. The low and high frequency spectral indices are $\alpha_{240}^{153}\simeq 1.38\pm 0.27$ and $\alpha_{1477}^{240}\simeq 1.60\pm 0.05$ respectively. Indeed, a hint of spectral steepening is seen at high frequency, although the two values are still compatible to within the errors.

It is worthwhile to note that the global low-frequency radio spectral index is fully consistent with the reported range of 1.2-1.5 obtained in the XMM-Newton/INTEGRAL  analysis by Nevalainen et al. (2009), see the next section for further details.

4 Discussion

The Ophiuchus galaxy cluster is one of the very rare clusters where the non-thermal component is revealed both in the radio and X-ray bands.

Assuming that the X-ray component arises from inverse-Compton (IC) scattering from the non-thermal electrons with the photons of the CMB, the volume-averaged cluster magnetic field, $B_{\rm V}$, can be derived essentially from the ratio between the power emitted through synchrotron and IC (see e.g. Blumenthal & Gould 1970).

Using XMM-Newton and INTEGRAL spectra of the cluster and fixing the spectral index of the power law to 1.4 (this work), we extracted the fluxes of the non-thermal component in five different X-ray energy bands (0.6-2, 2-5, 5-10, 20-40, and 40-80 keV). For the details of the data analysis and the modelling of the different thermal components, we refer to Nevalainen et al. (2009). The total non-thermal flux in the 20-80 keV band is $5.5\times10^{-12}$ ergs s-1 cm-2, in agreement with the upper limits derived from Swift (Ajello et al. 2009) and Suzaku (Fujita et al. 2008) data.

Using these measurements together with the radio fluxes presented in Table 3, we constructed a spectral energy distribution (SED) of the non-thermal emission (see Fig. 8). We also added to the SED the upper limits at 74 MHz (VLSS) and 607 MHz (GMRT), as well as the Swift upper limit (Ajello et al. 2009).

\begin{figure} \par\includegraphics[width=18cm,clip]{14126fg8.ps} \end{figure} Figure 8:

Spectral energy distribution of the non-thermal emission (plotted as $\nu \cdot S_{\nu }$ versus $\nu $) from the Ophiuchus cluster, using data from GMRT (153 and 240 MHz) and VLA (1477 MHz) from Table 3, and data from XMM-Newton and INTEGRAL (see text) in the X-ray range. Upper limits at 74 MHz (VLSS), 614 MHz (this work), and in the 20-60 keV band (Swift, Ajello et al. 2009) are also displayed.

Open with DEXTER

4.1 SED modelling

To model the SED, we used the exact derivation of the synchrotron and IC spectrum for a single electron from Blumenthal & Gould (1970), and numerically convolved the resulting spectrum with the differential distribution of non-thermal electrons $N(\gamma,\theta)$. Here $\gamma$ is the electron's Lorentz factor, while $\theta$ is the pitch angle between its velocity and the local direction of the magnetic field. Indeed, d $N=N(\gamma,\theta)$d$\gamma$d$\theta$ is the number density of non-thermal electrons with a Lorentz factor between $\gamma$ and $\gamma+{\rm d}\gamma$ and a pitch angle between $\theta$ and $\theta+{\rm d}\theta$.

We assumed that the energy spectrum of the non-thermal electrons is described by a power law with the index p, with a high-energy cut-off $m_{\rm e}c^2 \gamma_{\rm max}$ and a low-energy cut-off $m_{\rm e}c^2\gamma_{\rm min}$

\begin{displaymath}N(\gamma,\theta)=K_0 \gamma^{-p}(\sin\theta)/2, \end{displaymath} (6)

where we consider an isotropic distribution of pitch angles.

The radio emissivity as a function of the pitch angle in a uniform magnetic field of strength B is given by

\begin{displaymath}j_{\rm syn}(\nu,\theta)=\int_{\gamma_{\rm min}}^{\gamma_{\rm ... ...c}){\rm d}\gamma ~~~{\rm\left(\frac{erg}{cm^{3}~s~Hz}\right)}, \end{displaymath} (7)

where $F_{\rm syn}(\nu/\nu_{\rm c})$ is the synchrotron kernel (see e.g. Blumenthal & Gould 1970; Rybicki & Lightman 1979), while

\begin{displaymath}\nu_{\rm c}=4.2\times 10^{-6} B_{\rm\mu G} \sin\theta~\gamma^2 ~~~\rm (MHz). \end{displaymath} (8)

The constant $C_{\rm f}=2.3444\times 10^{-22}$ erg Gauss-1 depends only on fundamental physical constants.

Due to the high-beaming of the synchrotron radiation pulses, only relativistic electrons with a pitch angle $\theta\simeq \theta^{\prime}$ will be observed if the magnetic field direction shows an angle $\theta^{\prime}$ with respect to the line-of-sight. In this work, we suppose that the intra-cluster magnetic field is completely tangled in an infinitesimally small scale compared to the mini-halo size. With this assumption, the synchrotron emissivity averaged over all the possible magnetic field directions[*] is

\begin{displaymath}j_{\rm syn}(\nu)=\int_{0}^{\pi} j_{\rm syn}(\nu,\theta^{\prime}) \frac{\sin\theta^{\prime}}{2} {\rm d}\theta^{\prime}. \end{displaymath} (9)

By using standard formulas, we calculated the HXR emission deriving from the inverse Compton scattering of the CMB photons by the same population of relativistic electrons in Eq. (6):

\begin{displaymath}j_{\rm IC}(\epsilon_1)=\int_{0}^{\infty}\int_{\gamma_{\rm min... ... d}\epsilon ~~~{\rm\left(\frac{photons}{cm^{3}~s~erg}\right)}, \end{displaymath} (10)

where $F_{\rm IC}(\epsilon,\gamma,\epsilon_1)$ is the kernel emission of a single electron with the Lorentz factor $\gamma$, scattering to energy $\epsilon_1$ a segment of the distribution of CMB photons with an initial energy $\epsilon$ (see e.g. Eq. (2.48) in Blumenthal & Gould 1970). Here $N(\gamma)=\int_{0}^{\pi}N(\gamma,\theta) {\rm d}\theta$.

The synchrotron and inverse Compton emissivities are converted to flux densities by multiplying Eqs. (9) and (10) by a volume of $V=1.51\times10^{72}$ cm3 (that is the volume of a sphere whose radius corresponds to a projected distance of $r=7\hbox{$^\prime$ }$  from the cluster centre) and then by dividing by the cluster's luminosity distance, DL, i.e. $S_{\nu}=j(\nu) \cdot V/(4\pi D_{L}^2)$.

We then fitted our model to the data and extracted the relevant physical parameters. The resulting best-fit model is shown as a line in Fig. 8, while the best-fit parameters are reported in Table 4 along with their 1$\sigma $ uncertainties. The two upper limits at 74 and 614 MHz and that in the 20-60 keV band were not considered in the fit because they have no influence on the $\chi^2$ statistics.

Unfortunately, the available HXR data did not allow us to precisely constrain the value of the low-energy cut-off, but only to place an upper limit at $\gamma_{\rm min}\lesssim 700$. We indeed decided to fix this parameter to the arbitrary value of $\gamma_{\rm min}=300$, see Sect. 4.2.

Table 4:   Best fit parameters of the spectral energy distribution of the non-thermal emission from the Ophiuchus cluster.

The radio and HXR data are consistent with a slope for the energy spectrum of the relativistic electrons of $p\simeq 3.8\pm 0.4$ and with a high-energy cut off $\gamma_{\rm max}\simeq 3.8 \times 10^{4}$. The power law index p is related to the radio spectral index via the relation $p=2\alpha+1$. Indeed, the global mini-halo radio spectrum can be described by a low-frequency power law spectral index of $\alpha\simeq 1.4$ followed by a high-frequency break at $\nu_{\rm max}\gtrsim 1900$ MHz.

The derived volume-average magnetic field value $B_{\rm V}$ is found to be

\begin{displaymath}B_{\rm V}=0.31^{+0.11}_{-0.07} ~~~(\mu \rm G). \end{displaymath} (11)

This estimate depends only weakly on the values of the spectral parameters $\gamma_{\rm min}$, $\gamma_{\rm max}$, and p. It is very sensitive, however, to the assumptions that the distribution of non-thermal electrons is isotropic and that the magnetic field is completely disordered over the large volume of space we considered. We may for instance consider the simpler, but less realistic situation in which the pitch angle is $\theta=90\hbox{$^\circ$ }$ for all the electrons with a perfectly ordered magnetic field aligned to the plane of the sky. In this case, the synchrotron emission is maximized and the magnetic field strength has to be reduced to $B_{\rm V}\simeq 0.18~\mu$G. This lower value for the volume-average magnetic field strength is consistent to within the statistical uncertainties with that in Nevalainen et al. (2009), who indeed assumed $\theta=90\hbox{$^\circ$ }$ and a perfectly ordered magnetic field.

An important point to discuss is that given a magnetic field strength of $B\simeq 0.3 ~\mu $G, only high-energy electrons with $\gamma> 10^4$ can emit at radio frequencies of 153 MHz and above (see Eq. (8)). On the other hand, the HXR emission would be tracing relativistic electrons of lower energy, with characteristic Lorentz factors in the range 103-104. Indeed, the radio and HXR emissions are not tracing exactly the same particles. Nevertheless, the low-frequency spectral index measured in this work, $\alpha_{240}^{153} \simeq 1.4\pm0.3$, is consistent with the scenario in which the energy spectrum of the synchrotron electrons most probably belongs to the extrapolation at higher energies of the power law energy distribution of the electrons radiating in the HXR band through the inverse Compton process.

4.2 Energetics and particle life-time

The total pressure from the non-thermal electrons is given by

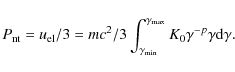
\begin{displaymath}P_{\rm nt}=u_{\rm el}/3 = mc^2/3 \int_{\gamma_{\rm min}}^{\gamma_{\rm max}} K_0 \gamma^{-p} \gamma {\rm d}\gamma. \end{displaymath} (12)

The non-thermal energy pressure depends critically on the low energy cut-off of the particle distribution. With the choice of $\gamma_{\rm min}=300$, it results $P_{\rm nt}\sim2.5\times 10^{-12}$ erg cm-3. Given that the pressure of the thermal plasma is $P_{\rm ther}\sim9.2\times10^{-11}$ erg cm-3 (Nevalainen et al. 2009), the non-thermal electrons are responsible for $\sim$3% of the total energy budget, so the dynamics of the gas are unaffected by the non-thermal electron population. It is worthwhile to mention that at energies lower than $\gamma \lesssim 700$Coulomb collisions with the thermal plasma are the most important energy-loss process for the relativistic electrons in Ophiuchus (see e.g. Sarazin 1999). In particular, we calculated that for $\gamma_{\rm min}=300$ the heating rate of the intra-cluster medium produced by the non-thermal electrons through Coulomb collisions still does not exceed the bremsstrahlung cooling rate of the gas. The heating rate produced by the non-thermal electrons begins to dominate over the gas cooling rate if the low energy cut-off is lower than $\gamma_{\rm min}\lesssim 180$ (see Colafrancesco & Marchegiani 2009, for a detailed discussion). We note that in this limiting case the re-heating of the cluster's cooling core by the non-thermal mini-halo could not be neglected.

Another important consideration is that the energy density of the relativistic electrons is four orders of magnitude higher than the energy density of the magnetic field, $B^2/(8\pi)=3.6\times 10^{-15}$ erg cm-3. This result would imply that the mini-halo is not in a minimum energy condition, which requires instead that the energy densities of particles and field should be nearly equipartited. This result holds even in the case where the energy distribution is truncated at a $\gamma_{\rm min}=700$, that is the upper limit we can place on the basis of the current HXR data.

The radiative life-time of the relativistic electrons can be estimated as

\begin{displaymath}t_{\rm rad}\equiv \frac{\gamma}{\dot\gamma} \simeq \frac{7.73\times 10^{20}}{(B^2+B_{\rm CMB}^2) \gamma} ~~~\rm (s), \end{displaymath} (13)

where the magnetic field is in $\mu$G, while $B_{\rm CMB}=3.25(1+z)^{2}~\mu$G is a virtual magnetic field, whose energy density is equal to that of the CMB and accounts for the inverse Compton losses.

Since $B_{\rm CMB}\gg B$, the radiative losses are dominated by the inverse Compton process, which cools down the high-energy electrons with $\gamma=10^4$ (i.e. those radiating at $\sim$153 MHz) in a time-scale of $t_{\rm rad}\simeq 2\times 10^{8}$ yrs. This is a relatively short time compared to the diffusion time needed by the relativistic electrons to cross the mini-halo. If we suppose (Melrose 1968) that the relativistic electrons diffuse at the Alfvén speed

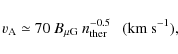
\begin{displaymath}v_{\rm A}\simeq 70 ~ B_{\mu \rm G}~n_{\rm ther}^{-0.5} ~~~\rm (km~s^{-1}), \end{displaymath} (14)

where the thermal gas density is expressed in units of 10-3 cm-3, the characteristic diffusion length of the synchrotron electrons radiating at 153 MHz results in just $L_{\rm diff}\sim 4.4$ kpc, i.e. two orders of magnitude smaller than the mini-halo size. This confirms the well-known results that the non-thermal electrons must be constantly injected and/or re-accelerated in-situ with great efficiency over the cluster volume.

It is important to stress that the interpretation of the SED presented above relies on a simplified cluster model, in which the relevant physical properties, $N(\gamma,\theta)$ and B, represent volume-averaged quantities. It is clear, however, that a much more detailed modelling is needed to explain the spatial variations of the spectral index observed across the mini-halo. Particularly, the systematic increase of the mini-halo spectral index with the radius shown in the bottom panel of Fig. 7 may indicate that the high-frequency break $\nu_{\rm max}$, and hence either $\gamma_{\rm max}$ and/or the magnetic field B (see Eq. (8)), decrease from the cluster centre outward. Another possibility is that just the slope, p, and the normalisation, K0, of the energy spectrum of the non-thermal electrons are changing with radius. This could be supported by the radio spectrum of patch E, which shows no evidence for a strong spectral curvature (see Fig. 7). Disentangling these scenarios is not easy with the current data. Future spatially resolved analyses of both the radio and HXR emissions could shed light on this important issue.

5 Conclusions

In a search for diffuse radio emission in relaxed, cool-core galaxy clusters at 1.4 GHz, Govoni et al. (2009) found the presence of a mini-halo surrounding the faint central point-like radio source in the Ophiuchus cluster of galaxies. Murgia et al. (2009) analysed the radio properties of this diffuse radio source in comparison to other mini-halos and radio halos known in the literature and found that Ophiuchus is characterized by a brightness and size very similar to that of the smaller halos rather than to that of the prototypical mini-halo in the Perseus cluster (e.g. Burns et al. 1992). In this work we presented a study of the radio emission of the Ophiuchus cluster of galaxies at low radio frequencies performed at 153, 240, and 614 MHz with the GMRT.

The mini-halo is clearly detected at 153 and 240 MHz, the frequencies at which we reached the best sensitivity to the low-surface brightness diffuse emission, while at 614 MHz we only derived an upper limit to the mini-halo emission. By combining these images with the VLA data at 1477 MHz from Govoni et al. (2009) and with the VLSS upper limit at 74 MHz, we derived the spectral index of the mini-halo.

Globally, the mini-halo has a low-frequency spectral index of $\alpha_{240}^{153}\simeq 1.4~\pm~0.3$, with a hint of steepening at higher frequencies. Moreover, we found indications that the high-frequency spectral index $\alpha_{1477}^{240}$ increases with the increasing distance from the cluster centre. The most prominent feature at low frequencies is a patch of diffuse steep spectrum emission located at about 5$^\prime$ south-east from the cluster centre.

The observed radio spectral index agrees with that obtained by modelling the non-thermal HXR emission in this cluster of galaxies. We assume that the X-ray component arises from inverse-Compton scattering between the photons of the cosmic microwave background and a population of non-thermal electrons, which are isotropically distributed and whose energy spectrum is a power law with the index p. We derive that the electrons energy spectrum should extend from a minimum Lorentz factor of $\gamma_{\rm min}\lesssim 700$ up to a maximum Lorentz factor of $\gamma_{\rm max}\simeq 3.8 \times 10^{4}$ with an index $p=3.8\pm 0.4$ and that the volume-averaged strength for a completely disordered intra-cluster magnetic field is $B_{\rm V}\simeq 0.3\pm 0.1~\mu$G. Given this magnetic field strength, only high-energy electrons with $\gamma> 10^4$ can emit in the observed radio frequency window, while the HXR emission would be tracing relativistic electrons of lower energy, with characteristic Lorentz factors in the range 103-104. Indeed, the radio and HXR emissions are not tracing exactly the same particles. Nevertheless, the low-frequency radio spectral index measured in this work is consistent with the scenario in which the energy spectrum of the synchrotron electrons most probably belongs to the extrapolation at higher energies of the power law energy distribution of the electrons radiating in the HXR band through the inverse Compton process.

In addition to the mini-halo spectrum, we also analysed the properties of the cluster discrete sources, specifically source A, the radio source associated to the central cD galaxy, source B, the brightest radio source in the field located at about 10$^\prime$ north to the cluster centre, and the two NATs C and D located in the cluster outskirts. Source A is point-like at our highest resolution of 7 $^{\prime\prime}$  (corresponding to about 3.8 kpc) and its spectral index is $\alpha\simeq 0.6$, a typical value for radio sources. Source B is an extended source with no obvious optical identification and a rather peculiar morphology, which makes its classification very uncertain. The global spectral index of the source is $\alpha\simeq 1.01~\pm ~0.05$. This is a quite usual value for active radio galaxies, which makes the interpretation of this object even more puzzling. In fact, although the distorted morphology of this radio source recalls that of extreme relic sources in clusters of galaxies (see e.g. Slee et al. 2001), on the basis of its radio spectrum it cannot be classified as an ultra-steep spectrum source. A possibility could be that source B is a relic radio source revived by the adiabatic compression caused by a shock wave or a bulk gas motion propagating thought the ICM (Enßlin & Gopal-Krishna 2001). However, the relation of this peculiar radio source with the mini-halo remains at the moment unclear. Finally, the analysis of the radio morphology and spectral properties of the tailed sources C and D confirm that their host galaxies are moving at high velocity with respect to the ICM either because they are individually infalling towards the cluster centre or because they are part of merging sub-clusters.

Acknowledgements
We acknowledge the anonymous referee for helpful comments that improved the paper. We thank the staff of the GMRT, who made these observations possible. The GMRT is run by the National Centre for Radio Astrophysics of the Tata Institute of Fundamental Research. This work is part of the ``Cybersar'' Project, which is managed by the COSMOLAB Regional Consortium with the financial support of the Italian Ministry of University and Research (MUR), in the context of the ``Piano Operativo Nazionale Ricerca Scientifica, Sviluppo Tecnologico, Alta Formazione (PON 2000-2006)''. This research was partially supported by ASI-INAF I/088/06/0 - High Energy Astrophysics and PRIN-INAF 2008. C.F. acknowledges financial support by the Agence Nationale de la Recherche through grant ANR-09-JCJC-0001-01. J.N. is supported by the Academy of Finland. The National Radio Astronomy Observatory (NRAO) is a facility of the National Science Foundation, operated under cooperative agreement by Associated Universities, Inc.

References

  1. Ajello, M., Rebusco, P., Cappelluti, N., et al. 2009, ApJ, 690, 367 [NASA ADS] [CrossRef] [Google Scholar]
  2. Arnaud, M., Böhringer, H., Jones, C., et al. 2009, Technical Report, [arXiv:0902.4890] [Google Scholar]
  3. Bliton, M., Rizza, E., Burns, J. O., et al. 1998, MNRAS, 301, 609 [NASA ADS] [CrossRef] [Google Scholar]
  4. Blumenthal, G. R., & Gould, R. J. 1970, Rev. Mod. Phys., 42, 237 [NASA ADS] [CrossRef] [Google Scholar]
  5. Boselli, A., & Gavazzi, G. 2006, PASP, 118, 517 [NASA ADS] [CrossRef] [Google Scholar]
  6. Burns, J. O., Sulkanen, M. E., Gisler, G. R., & Perley, R. A. 1992, ApJ, 388, L49 [NASA ADS] [CrossRef] [Google Scholar]
  7. Burns, J. O., Hallman, E. J., Gantner, B., et al. 2008, ApJ, 675, 1125 [NASA ADS] [CrossRef] [Google Scholar]
  8. Cohen, A. S., Lane, W. M., Cotton, W. D., et al. 2007, AJ, 134, 1245 [NASA ADS] [CrossRef] [Google Scholar]
  9. Colafrancesco, S., & Marchegiani, P. 2009, A&A, 502, 711 [Google Scholar]
  10. Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693 [NASA ADS] [CrossRef] [Google Scholar]
  11. De Breuck, C., Tang, Y., de Bruyn, A. G., Röttgering, H., & van Breugel, W. 2002, A&A, 394, 59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Djorgovski, S., Thompson, D. J., de Carvalho, R. R., & Mould, J. R. 1990, AJ, 100, 599 [NASA ADS] [CrossRef] [Google Scholar]
  13. Dursi, L. J., & Pfrommer, C. 2008, ApJ, 677, 993 [NASA ADS] [CrossRef] [Google Scholar]
  14. Eckert, D., Produit, N., Paltani, S., Neronov, A., & Courvoisier T. J.-L. 2008, A&A, 479, 27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Enßlin, T. A., & Gopal-Krishna 2001, A&A, 366, 26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Ferrari, C., Govoni, F., Schindler, S., Bykov, A. M., & Rephaeli, Y. 2008, SSRv, 134, 93 [Google Scholar]
  17. Fujita, Y., Hayashida, K., Nagai, M., et al. 2008, PASJ, 60, 1133 [NASA ADS] [Google Scholar]
  18. Fusco-Femiano, R., dal Fiume, D., Orlandini, M., et al. 2003, ASP Conf. Ser., 301, 109 [NASA ADS] [Google Scholar]
  19. Gitti, M., Brunetti, G., Feretti, L., & Setti, G. 2004, A&A, 417, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Gitti, M., Ferrari, C., Domainko, W., Feretti, L., & Schindler, S. 2007, A&A, 470, 25 [Google Scholar]
  21. Giovannini, G., Bonafede, A., Feretti, L., et al. 2009, A&A, 507, 1257 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Govoni, F., Murgia, M., Markevitch, M., et al. 2009, A&A, 499, 371 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Jaffe, W. J., & Perola, G. C. 1973, A&A, 26, 423 [NASA ADS] [Google Scholar]
  24. Johnston, M. D., Bradt, H. V., Doxsey, R. E., et al. 1981, ApJ, 245, 799 [NASA ADS] [CrossRef] [Google Scholar]
  25. Kawano, N., Fukazawa, Y., Nishino, S., et al. 2009, PASJ, 61, 377 [NASA ADS] [Google Scholar]
  26. Kravtsov, A., Gonzalez, A., Vikhlinin, A., et al. 2009, Technical Report, [arXiv:0903.0388] [Google Scholar]
  27. Markevitch, M., & Vikhlinin, A. 2007, Phys. Rep., 443, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Melrose, D. B. 1968, Ap&SS, 2, 171 [NASA ADS] [CrossRef] [Google Scholar]
  29. Million, E. T., Allen, S. W., Werner, N., & Taylor, G. B. 2010, MNRAS, in press [arXiv:0910.0025] [Google Scholar]
  30. Murgia, M., Govoni, F., Markevitch, M., et al. 2009, A&A, 499, 679 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Nevalainen, J., Oosterbroek, T., Bonamente, M., & Colafrancesco, S. 2004, ApJ, 608, 166 [NASA ADS] [CrossRef] [Google Scholar]
  32. Nevalainen, J., Eckert, D., Kaastra, J., Bonamente, M., & Kettula, K. 2009, A&A, 508, 1161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Pacholczyk, A. G. 1970, Series of Books in Astronomy and Astrophysics (San Francisco: Freeman) [Google Scholar]
  34. Parma, P., Murgia, M., Morganti, R., et al. 1999, A&A, 344, 7 [NASA ADS] [Google Scholar]
  35. Parrish, I. J., Quataert, E., & Sharma, P. 2009, ApJ, 703, 96 [NASA ADS] [CrossRef] [Google Scholar]
  36. Petrosian, V., Bykov, A., & Rephaeli, Y. 2008, Space Sci. Rev., 134, 191 [Google Scholar]
  37. Pérez-Torres, M. A., Zandanel, F., Guerrero, M. A., et al. 2009, MNRAS, 396, 2237 [NASA ADS] [CrossRef] [Google Scholar]
  38. Profumo, S. 2008, Phys. Rev. D, 77, 103510 [NASA ADS] [CrossRef] [Google Scholar]
  39. Rephaeli, Y., Nevalainen, J., Ohashi, T., & Bykov, A. M. 2008, Space Sci. Rev., 134, 71 [Google Scholar]
  40. Rybicki, G. B., & Lightman, A. P. 1979 (New York: Wiley-Interscience), 393 [Google Scholar]
  41. Sarazin, C. L. 1999, ApJ, 520, 529 [NASA ADS] [CrossRef] [Google Scholar]
  42. Slee, O. B., Roy, A. L., Murgia, M., et al. 2001, AJ, 122, 1172 [NASA ADS] [CrossRef] [Google Scholar]
  43. Wakamatsu, K., Malkan, M. A., Nishida, M. T., et al. 2005, in Nearby Large-Scale Structures and the Zone of Avoidance, ASP Conf. Ser., 329, 189 [Google Scholar]

Footnotes

... directions[*]
From simple geometric considerations it follows that the probability to observe an angle $\theta^{\prime}$ between the local direction of a random magnetic field and the line-of-sight is proportional to $\sin \theta^{\prime}$.

All Tables

Table 1:   Details of the GMRT observations.

Table 2:   Integrated spectra for cluster discrete sources.

Table 3:   Properties of the Ophiuchus mini halo derived from the fit procedure.

Table 4:   Best fit parameters of the spectral energy distribution of the non-thermal emission from the Ophiuchus cluster.

All Figures

  \begin{figure} \par\includegraphics[width=18.2cm,clip]{14126fg1.eps} \vspace*{-2mm} \end{figure} Figure 1:

Top left: GMRT radio iso-contours at 153 MHz at full resolution overlaid to the ROSAT PSPC X-ray image of the Ophiuchus galaxy cluster. The radio image has an FWHM beam of $37.1\hbox {$^{\prime \prime }$ }\times 22.6\hbox {$^{\prime \prime }$ }$ with PA = 35.1$^\circ $ and a noise level of 5 mJy/beam (1$\sigma $). Contours start at 15 mJy/beam (3$\sigma $) and scale by a factor of $\sqrt {2}$. Top right: iso-contours at the frequency of 1477 from the VLA image by Govoni et al. (2009). The image as an FWHM beam of $91.4\hbox{$^{\prime\prime}$ }~\times~40.3\hbox{$^{\prime\prime}$ }$ with PA =  $-24.4\hbox {$^\circ $ }$. Contours start at 0.3 mJy/beam (3$\sigma $) and increase by $\sqrt {2}$. Bottom panels: finding charts from DSS2 - red for sources A, B, C, and D. No obvious optical identification exists for radio source B.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=17.2cm,clip]{14126fg2.ps}\vspace*{-2.5mm} \end{figure} Figure 2:

Central panel: GMRT radio iso-contours at 240 MHz of the Ophiuchus galaxy cluster at full resolution. The radio image has a FWHM beam of $18.7\hbox{$^{\prime\prime}$ }~\times~15.9\hbox{$^{\prime\prime}$ }$ with PA = -25.7$^\circ $ and a noise level of 1.1 mJy/beam (1$\sigma $). Contours start at 3.3 mJy/beam (3$\sigma $) and scale by a factor of $\sqrt {2}$. The insets show the GMRT image at 614 MHz of sources A, B, C, and D. The 614 MHz has a FWHM beam of $7\hbox{$^{\prime\prime}$ }~\times~7\hbox{$^{\prime\prime}$ }$ and a noise level of 0.25 mJy/beam (1$\sigma $).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=18cm,clip]{14126fg3.eps} % \end{figure} Figure 3:

Radio images of the Ophiuchus cluster of galaxies at $92\hbox {$^{\prime \prime }$ }\times 92\hbox {$^{\prime \prime }$ }$ FWHM beam resolution. Contours start at 3$\sigma $ level and scale by a factor of $\sqrt {2}$. Left to right: 74 MHz (VLSS; $\sigma =280$ mJy/beam), 153 MHz (GMRT; $\sigma =18$ mJy/beam), 240 MHz (GMRT; $\sigma =10$ mJy/beam), 614 MHz (GMRT; $\sigma =5.5$ mJy/beam), 1477 MHz (VLA; $\sigma =0.16$ mJy/beam).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=17.2cm,clip]{14126fg4.ps}\vspace*{2mm} \end{figure} Figure 4:

Integrated radio spectra for the central source A (top-left), for the amorphous source B (top-right), and for the two tailed sources C and D (bottom panels). The triangles represent the GMRT flux density measurement from this work, while the dots are the data taken from the literature. The lines represent the best fit of a power law with index $\alpha $.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=16.5cm,clip]{14126fg5.ps} \end{figure} Figure 5:

Spectral index profile between 153 and 1400 MHz along the tail for radio sources C (left panel) and D (right panel). Data points have been sampled in circular boxes of one beam-width, as shown in the inset. The line is the expected spectral index trend for the case of constant advance speed.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=15.4cm,clip]{14126fg6.eps} \end{figure} Figure 6:

Spectral index image of the mini-halo in the Ophiuchus cluster. The top left panel shows the spectral index image of the mini-halo in the Ophiuchus cluster between 240 and 1477 MHz at an angular resolution of $92\hbox{$^{\prime\prime}$ }~\times~ 92\hbox{$^{\prime\prime}$ }$. The iso-contours represent the 240 MHz image obtained by tapering the long baselines between the GMRT antennas. Contours start at 30 mJy/beam (3$\sigma $) and increase by a factor of $\sqrt {2}$. The 1477 MHz image is taken from Govoni et al. (2009) and has a noise level of 0.16 mJy/beam (1$\sigma $). The spectral index is calculated only in those pixels whose brightness is above 3$\sigma $ at both frequencies. The top right panel shows the image of the spectral index uncertainty. The bottom panels show the mini-halo spectrum between 74 MHz and 1477 MHz in the four sample positions indicated in the top left panel.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{14126fg7.ps} \end{figure} Figure 7:

Azimuthally averaged radial profiles of the mini-halo radio intensity at 153, 240 and 1477 MHz ( top panel). We considered only data points whose observed brightness is five times above the error on the radial average. The solid lines represent the best fit of the exponential disc model plus the contribution by the central point source. The dotted lines represent the exponential disc model alone. The mid and bottom panels show the radial profiles of the spectral index between 153 and 240 MHz and between 240 and 1477 MHz, respectively.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=18cm,clip]{14126fg8.ps} \end{figure} Figure 8:

Spectral energy distribution of the non-thermal emission (plotted as $\nu \cdot S_{\nu }$ versus $\nu $) from the Ophiuchus cluster, using data from GMRT (153 and 240 MHz) and VLA (1477 MHz) from Table 3, and data from XMM-Newton and INTEGRAL (see text) in the X-ray range. Upper limits at 74 MHz (VLSS), 614 MHz (this work), and in the 20-60 keV band (Swift, Ajello et al. 2009) are also displayed.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.