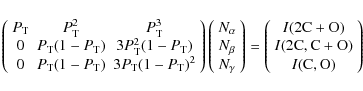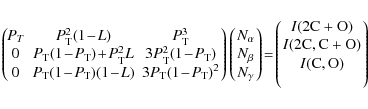EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 514 (May 2010) A&A, 514 (2010) A83 Full HTML
Free Access
Issue
A&A
Volume 514, May 2010
Article Number A83
Number of page(s) 8
Section Atomic, molecular, and nuclear data
DOI https://doi.org/10.1051/0004-6361/200913891
Published online 26 May 2010
A&A 514, A83 (2010)

Experimental studies of the dissociative recombination processes for the dimethyl ether ions CD3OCD2+ and (CD3)2OD+

M. Hamberg1 - F. Österdahl1 - R. D. Thomas1 - V. Zhaunerchyk1 - E. Vigren1 - M. Kaminska2 - M. af Ugglas1 - A. Källberg3 - A. Simonsson3 - A. Paál3 - M. Larsson1 - W. D. Geppert1

1 - Department of Physics, Stockholm University, Alba Nova, 106 91 Stockholm, Sweden
2 - Institute of Physics, Jan Kochanowski University, Swietokrzyska 15, 25406 Kielce, Poland
3 - Manne Siegbahn Laboratory, Frescativägen 26, 114 18 Stockholm, Sweden

Received 16 December 2009 / Accepted 4 February 2010

Abstract
Aims. Determination of branching fractions, cross sections and thermal rate coefficients for the dissociative recombination of CD3OCD2+ (0-0.3 eV) and (CD3)2OD+ (0-0.2 eV) at the low relative kinetic energies encountered in the interstellar medium.
Methods. The measurements were carried out using merged electron and ion beams at the CRYRING storage ring, Stockholm, Sweden.
Results. For (CD3)2OD+ we have experimentally determined the branching fraction for ejection of a single hydrogen atom in the DR process to be maximally 7% whereas 49% of the reactions involve the break up of the COC chain into two heavy fragments and 44% ruptures both C-O bonds. The DR of CD3OCD2+ is dominated by fragmentation of the COC chain into two heavy fragments. The measured thermal rate constants and cross sections are $k(T)=1.7\pm0.5\times 10^{-6}(T/300)^{-0.77\pm0.01}$ cm3 s-1, $\sigma = 1.2\pm0.4\times10^{-15}(E_{\rm cm}{\rm [eV]})^{-1.27\pm0.01}$ cm2 and $k(T)= 1.7~\pm~0.6~\times~ 10^{-6}(T/300)^{-0.70~\pm~0.02}$ cm3 s-1, $\sigma = 1.7~\pm~0.6~\times~10^{-15}(E_{\rm cm}[{\rm eV}])^{-1.20\pm0.02}$ cm2 for CD3OCD2+ and (CD3)2OD+, respectively.

Key words: astrochemistry - molecular processes - plasmas - methods: laboratory - methods: numerical - ISM: molecules

1 Introduction

One of the most important questions in our understanding of the emergence of life in the universe is how complex molecules such as biomolecule precursors are formed from more simple species and from which degree of complexity planetary conditions are necessary.

To date more than 150 molecules and about 20 molecular ions have been detected in the interstellar medium (astrochemistry.net 2009) including molecules with long carbon chains such as HC11N (Bell et al. 1997). Furthermore, laboratory studies of meteoritic material have revealed complex species such as amino acids (Botta 2005). The number of discovered molecules in space is steadily rising, which critically increases the complexity of the chemical models of dark clouds, hot cores and other astronomical objects. These molecules undergo various reactions, e.g. association, ionization, recombination, etc. A small change in the rate of one particular reaction may have a serious impact on the evolution of the environment and significantly change the outcome of a simulation. Therefore, the abundance of important species (e.g. biomolecule precursors) may turn out to be heavily over- or underestimated. Hence, accurate determination of rates and product distributions of astrophysically relevant reactions is a must. Dissociative recombination (DR) reactions have been found to play an especially pivotal role as the final step in the synthesis of many complex molecules in space.

DR is the process where a molecular ion recombines with an electron and the excited neutral molecule formed releases excitation energy by dissociating into neutral fragments. The phenomenon is one of the dominating ion processes in dark interstellar clouds (Thomas 2008; Boger & Sternberg 2006; Florescu-Mitchell & Mitchell 2006), the comae of comets (Haider & Bhardwaj 2005), and also plays an important role in aurorae (Peterson et al. 1994), aeronomical plasmas (Yee et al. 1989), lightning (Smirnova et al. 2002) as well as in man-made plasmas such as those in combustion processes and fusion reactors (Florescu-Mitchell & Mitchell 2006). DR is known to be very efficient at low temperatures and therefore the reaction rates involved have a significant impact on model calculations of interstellar chemistry. The heavy-ion storage ring CRYRING in Stockholm, Sweden is an appropriate tool for investigations of astrophysically relevant DR reactions and has proven successful in doing so for several years, see e.g. Thomas (2008); Al-Khalili et al. (1998); Neau et al. (2000); McCall et al. (2003); Larsson et al. (1995); Hamberg et al. (2005); Larsson et al. (1993); Geppert et al. (2005).

We have undertaken merged ion-electron beam studies into the DR of the fully deuterated isotopologues of the methoxymethyl cation (CD3OCD2+) and the deuteronated dimethyl ether cation ((CD3)2OD+). The unhydronated dimethyl ether (DME) is found in objects known to host complex chemistry such as hot cores and corinos (Cazaux et al. 2003; Sutton et al. 1995; Maret et al. 2004; Groner et al. 1998). On the other hand, it has neither been detected in cold molecular clouds (Peeters et al. 2006; Friberg et al. 1988) nor cometary comae (Crovisier et al. 2004). Both ions also play an important role in alkyl- and proton-transfer reactions between protonated alcohols and ethers (Karpas & Meot-Ner 1989). One example of such reactions is:

$\displaystyle {\ensuremath{{\rm CH_3OH_2^+ + H_2CO \rightarrow CH_3OCH_2^+ + H_2O }} }.$     (1)

Karpas & Meot-Ner (1989) remark that the rate constants for such processes were found to be lower by factors of 10-100 compared with the usual rate constants of $\sim$10-9 cm3 s-1. However, they report indications for negative temperature dependencies which could mean that the reactions are more efficient at the low temperatures encountered in the interstellar medium.

The formation of DME in the interstellar medium has been a subject of ongoing discussion for many years. Blake et al. (1987) and Millar et al. (1991) argue that DME is most likely produced by synthesis from methyl alcohol, in which the precursor molecule is first desorbed from dust particles and then involved in the reaction sequence below to form protonated DME:

    $\displaystyle {\ensuremath{{\rm CH_3^+ + CH_3OH \rightarrow (CH_3)_2OH^+ +}} h\nu}$ (2)
    $\displaystyle {\ensuremath{{\rm CH_3OH_2^+ + CH_3OH \rightarrow (CH_3)_2OH^+ + H_2O}} }$ (3)

DME is finally released by the DR process:
$\displaystyle {\ensuremath{{\rm (CH_3)_2OH^+ + e^- \rightarrow CH_3OCH_3 + H}} }.$   (4)

Although methyl formate and dimethyl ether were hitherto assumed to be formed from their protonated ions via DR, this pathway could be expected as having equally low branching fraction as in the case of protonated methanol (Geppert et al. 2006), where DR is dominated by three-body break-up channels and only 3% of the reactions leads to the unprotonated species (6% for the fully deuterated isotopologue). Such behaviour is not unique and has been observed in many H-rich ions, e.g. H3O+ and CH5+ (Semaniak et al. 1998; Jensen et al. 2000). However, Garrod & Herbst (2006) showed with model calculations that dimethyl ether can be produced in a large abundance during the protostellar switch-on phase even when assuming as low a fraction as 1.5% for the final reaction above (this is much less than the value of 50% used in the model of Peeters et al. 2006). The alternative formation route through \ensuremath{{\rm CH_3 + CH_3O \rightarrow CH_3OCH_3}} on grain surfaces with subsequent evaporation was shown to be relevant only at earlier stages of protostellar switch on and does not contribute much to the final abundance levels. Garrod & Herbst (2006) concluded in their study that the main formation route for DME is that in gas phase starting with self-methylation of methanol.

In this paper we present the results from experimental studies on the DR of the titular ions to shed light on the formation of dimethyl ether in the interstellar medium.

2 Experiment

The experiments were performed using CRYRING, a heavy ion storage ring at the Manne Siegbahn Laboratory in Stockholm, Sweden. CRYRING consists of twelve straight segments with bending magnets in between and has a circumference of $\sim$51.63 m. Details about the experimental procedure can be found elsewhere, e.g. Neau et al. (2000) and, therefore, we only summarize the most essential aspects here.

The ions were produced from a gas mixture of fully deuterated dimethyl ether and pure deuterium using a JIMIS hollow-cathode ion source. They were then accelerated to 40 keV energy from the source platform and mass selected by a bending magnet. After injection into the storage ring the ions were accelerated further with a driven drift-tube system until they reached the maximum energy $\sim$96/ $m_{\rm ion}$ meV (where $m_{\rm ion}$ is the ion mass in amu) after about one second. Due to the low pressure of $\sim$10-11 Torr in the ring, rest-gas collisions are minimized and the ions can be stored for several seconds.

The electron cooler located in one of the straight sections consists of a beam of cold electrons (40 mm diameter with 2 meV transversal energy spread). The electrons are produced by an electron gun before they are bent in to overlap the ion beam for $\sim$85 cm, which is the actual DR interaction region. The neutral products from the reaction are unaffected by the bending magnet and thus leave the ring tangentially and can be detected by an ion-implanted silicon detector (IID). In the electron cooler the ion translational energy spread is slightly reduced since the ions experience a drag-force when they travel faster/slower than the electrons. Practically, the longitudinal electron cooling time for this ion in CRYRING is on the order of minutes, and the transversal cooling time is ten times longer due to the high mass to charge ratio of the ion. Therefore, the translational cooling mechanism is in principle without effect. Cooling of internal degrees of freedom (possibly created in the ion source) proceeds in the electron cooler by electron-induced de-excitation (super elastic collisions) for non IR-active modes and mostly naturally through spontaneous photon emission (typically in a timescale of 0.1-1 s) (Wolf et al. 2003) for IR-active modes. Cooling is very important in order to mimic interstellar conditions, since excited states may have different rate constants than the ground state (Tom et al. 2009). Due to lack of experimental time and limited beam lifetime, experiments with different cooling/storage times were not undertaken.

2.1 Branching fractions measurement

The branching fractions for the different reaction channels were measured at a nominal collision energy of 0 eV, i.e., when the electrons and ions travel at the same average velocity. The ion implanted detector used for detecting the neutral DR fragments records the kinetic energy which, since the ion velocity of the ring is well-defined, is directly proportional to the mass of the fragments. The response time of the detection system is much longer than the difference in arrival times of the fragments and so individual fragments are not identified and only one peak corresponding to the energy of the unfragmented ion is seen in the kinetic energy spectrum. To solve this issue, a transparent grid with a well-determined transmission probability $P_{\rm T} = 0.297 \pm 0.015$ is inserted directly in front of the detector. In this case the signal splits up into several peaks with energies corresponding to the masses of the fragments. Due to very small charge to mass ratio of these ions and the magnetic rigidity of the ring the maximum longitudinal energy per amu is comparatively low. This heavily diminishes the resolution of the recorded spectra since the IID has an ideal resolution limit of $\sim$25 keV (for MeV $\alpha$-particles) and the noise from the preamplifier also contributes to the final width of the peaks. As a result it is difficult to distinguish between fragments which differ in mass by 2 amu or less, e.g. one deuterium atom. Hence we focused on determining the probability of fragmentation of the bonds between the heavier atoms. The experiment consisted of four parts:

i)
measurement of the fragment energy spectrum without the grid and with the electron cooler tuned to $E_{\rm cm}~=~\sim$0 eV;
ii)
a spectrum taken without the grid, with the electron cooler tuned to $E_{\rm cm} = 1$ eV. At that energy the cross section is very small and the count rate is dominated by background events.
iii)
a spectrum taken with the grid inserted in front of the detector and the electron cooler tuned to 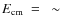$E_{\rm cm}~=~\sim$0 eV;
iv)
a spectrum with the grid inserted in front of the detector, and the electron cooler tuned to 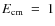$E_{\rm cm}~=~1$ eV. Again the count rate is very low and consists dominantly of products from rest gas collisions.

\begin{figure} \par\includegraphics[width=9cm,clip]{13891fg1.eps} \vspace*{2mm} \end{figure} Figure 1:

A fragment energy spectrum recorded for (CD3)2OD+ when the grid is not inserted. The large peak to the right is due to particles impacting at full beam energy. The two smaller peaks in the middle are due to losses because of fragments with high transverse energy that miss the detector. The sharp peak at the leftmost position is due to noise in the detector system.

Open with DEXTER

Subtracting the background spectra (after normalisation to the ion current in the different measurements) from that recorded at 0 eV yields the pure DR fragment energy distribution. As mentioned earlier, only one peak, corresponding to the sum of fragment kinetic energy, should be visible in the spectrum with the grid removed, see Fig. 1. Signals appearing at lower energies (masses) indicate that some of the fragments miss the detector due to a high kinetic energy release.

Fragment energy spectra with the grid inserted are obtained in a similar way and the background-subtracted result is shown in Fig. 2, where the peaks correspond to fragments containing one (C or O plus deuterium atoms), two (those with 2C or C+O plus deuterium atoms) or three heavy atoms (2C+O plus deuterium atoms). To compute the branching fractions from the peak intensities and the transmission probability, $P_{\rm T}$, the following matrix system was constructed:

\begin{displaymath}\left( \begin{array}{ccc} P_{\rm T} & P_{\rm T}^2 & P_{\rm T}... ... {\rm C}+{\rm O})\\ I({\rm C}, {\rm O})\\ \end{array}\right) \end{displaymath} (5)

\begin{figure} \par\includegraphics[width=9cm,clip]{13891fg2.eps} \vspace*{-2mm} \end{figure} Figure 2:

A fragment energy spectrum recorded for (CD3)2OD+ when the grid is inserted. The three major peaks are due to detection of fragments containing one, two or three heavy atoms, respectively. The sharp peak at the leftmost position is due to noise in the detector system mixed with signal from deuterium fragments.

Open with DEXTER

\begin{figure} \par\includegraphics[width=9cm,clip]{13891fg3.eps} \vspace*{-3mm} \end{figure} Figure 3:

Fragment energy spectrum recorded for CD3OCD2+ with the grid inserted. The three major peaks are due to detection of fragments containing one, two or three heavy atoms respectively. The sharp peak at the leftmost position is due to noise in the detector system mixed with signal from deuterium fragments and was not used in the branching fraction derivation. The second peak from the left stems from signal corresponding 4 amu mass (2D).

Open with DEXTER

where $N_{\alpha-\gamma}$ is the number of counts in each reaction channel, $\alpha-\gamma$ (leading to zero, one and two bond breakages between heavy fragments, respectively), and I is the total number of counts in each peak. For example, each column in the leftmost matrix corresponds to a reaction channel. In the middle column $P_{\rm T}^2$ is the probability that both heavy products from reaction channel $\beta$ pass through the grid and contribute to the full mass energy peak. $P_{\rm T}(1- P_{\rm T})$ in the second and third rows corresponds to the probability that the heavier products (containing C2 or CO) passes through the grid while the lighter products (containing C or O) are stopped by the grid or vice versa. The results of this matrix evaluation are displayed in Table 1 whereas all the energetically plausible channels are found in Tables 2 and 3, respectively.

There exist losses from the DR of (CD3)2OD+, illustrated in Fig. 1, as well as for CD3OCD2+ due to neutral fragments missing the detector. The effect of these losses on the branching fractions is well within the error bars for the matrix system (see Table 1) which have been assessed by varying the integrated area of each peak to extreme values that were still to be considered reasonable and running the matrix evaluation with these values. This was done in conjunction with changing the grid transmission probability within its 3$\sigma$ confidence interval $0.297~\pm~0.015$ (Neau 2002).

To determine upper limits for the losses, Monte Carlo simulations were performed. Assuming that all ions were in their rovibronic ground state and that all the energy released in the DR reactions are transformed into the kinetic energy of the fragments one can calculate the maximum amount of losses for each reaction channel. For a two-body breakup channel this can be solved analytically. For the three-body breakup case a similar approach as Müller & Cosby (1999), Thomas (2008) and Zhaunerchyk (2008) was used. For each reaction channel a large amount of DR events were numerically simulated where the energy distribution as well as the direction of the outgoing fragments are randomized (fulfilling energy and momentum conservation laws). For both the two and three-body breakup cases we extended the simulation to also include an estimated ion beam width (FWHM = 6 mm, assuming Gaussian beam profile) and an IID offset ($\sim$5 mm). We also assumed a synchronous breakup processes where all the reaction products are emitted from the centre of mass at the same time.

The simulations of the losses indicates that the losses of heavy fragments seen in the spectrum taken with the grid out (see Fig. 1) should be from the DR processes splitting up the COC-chain into two parts (see Tables 2 and 3 respectively). A branching fraction matrix system including the effect of the detected losses from the spectra with the grid out (see Fig. 1) were set up.

\begin{displaymath}\left(\!\! \begin{array}{ccc} P_T & P_{\rm T}^2(1\!-\!L) & P_... ...m C}+{\rm O})\\ I({\rm C}, {\rm O})\\ \! \end{array}\!\right) \end{displaymath} (6)

where L, is the loss factor. We have only taken into account losses of one heavy fragment in this system since the amount of losses of two heavy fragments are very small and would not change the outcome substantially. This system is solved iteratively by changing L until the outcome with $P_{\rm T} = 1$ in the matrix system matches the spectra taken with the grid out (the method is described in more detail elsewhere e.g. Hamberg et al. 2005). The results are displayed in Table 1. As can be seen, differences are small and within the error bars.

Table 1:   Branching fraction results for (CD3)2OD+ and CD3OCD2+ respectivelya.

Table 2:   Energetically open and plausible reaction channels for the DR of (CD3)2OD+ including those leading to D2 and 2Da.

Table 3:   Energetically open and plausible reaction channels for the DR of CD3OCD2+a.

2.2 Cross sections and rate constant determination

In this part of the experiment the electron velocity in the electron cooler was linearly ramped relative to the ion velocity during the measurement cycle corresponding to a change in relative kinetic between $\sim$2-2000 meV. The neutral products deriving from the DR reactions were detected with the IID and counted with a multi channel scaler (MCS, divided into time bins of 2 ms) in such a way that each time interval corresponded to a certain relative kinetic energy. The absolute ion current was measured using a capacitive pick up immediately after acceleration (Paal et al. 2006). Neutral particles originating from collisions of the ions with residual gas particles in the ring were counted by a micro channel plate (MCP) detector at the end of a straight section in the ring. Since the intensity of the signals from these background events is directly proportional to the ion current these signals could be scaled to the absolute ion current measurements and fitted by a decay curve to yield the ion current in the ring throughout the whole measurement cycle. This fit could also be used for background subtraction in the cross section measurement. The rate coefficient could then be calculated as:

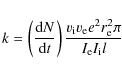
\begin{displaymath}k=\left(\frac{{\rm d}N}{{\rm d}t}\right)\frac{v_{\rm i}v_{\rm e}e^{2}r_{\rm e}^2\pi}{I_{\rm e}I_{\rm i}l} \end{displaymath} (7)

where $I_{\rm i}$, $v_{\rm i}$ and $I_{\rm e}$, $v_{\rm e}$ are the ion and electron currents and velocities (in the laboratory frame), respectively, and ${\rm d}N/{\rm d}t$ is the measured count rate. e, is the elementary charge, $r_{\rm e}$ is the radius of the electron beam and l is the length of the interaction region. Corrections to the data had to be made for:

i)
space charge effects: the electrons experience a drop in the acceleration potential at the gun due to other electrons ahead of them;
ii)
toroidal effects: interaction in the regions where the electron beam is bent into and out from the interaction region correspond to higher 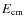$E_{\rm cm}$ due to the extra transversal velocity components (Lampert et al. 1996);
iii)
the rate constant calculated up to now is an averaged value due to the velocity spread amongst the electrons (i.e. 2 meV electron temperature). It can therefore be expressed as the equation below where the actual cross section is found by unfolding it using Fourier methods (Mowat et al. 1995).

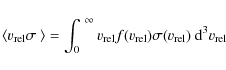
\begin{displaymath}\left\langle v_{\rm rel}\sigma\ \right\rangle = \int^{~\infty... ...\rm rel}f(v_{\rm rel})\sigma(v_{\rm rel})~{\rm d}^3v_{\rm rel} \end{displaymath} (8)

where $f(v_{\rm rel})$ is the electron velocity distribution in center of mass frame. Due to the high mass difference between the electrons and ions, drag force effects were neglected (Neau 2002). The result for the (CD3)2OD+ ion is displayed in Fig. 4 together with the best fit between 1-200 meV giving a cross section of $\sigma= 1.61 \times 10^{-15}(E_{\rm cm}$[eV])-1.20 cm2. Applying the same procedure for the CD3OCD2+ ion gave a best fit of: $\sigma= 1.11 \times 10^{-15}(E_{\rm cm}$[eV])-1.27 cm2. The thermal reaction rate coefficient can be obtained from the cross sections by applying the formula:

\begin{figure} \par\includegraphics[width=9cm,clip]{13891fg4.eps} \end{figure} Figure 4:

Cross section evaluation of (CD3)2OD+. The triangles shows individually measured spots while the line shows the best fit between 1-200 meV.

Open with DEXTER

\begin{displaymath}k(T)=\frac{8\pi m_{\rm e}}{(2\pi m_{\rm e}kT)^{3/2}}\int^{~\i... ...cm}\sigma(E_{\rm cm}){\rm e}^{-E_{\rm cm}/kT}{\rm d}E_{\rm cm} \end{displaymath} (9)

where $m_{\rm e}$ is the electron mass, k is Boltzmann's constant, T is the electron temperature and $E_{\rm cm}$ is the centre of mass energy. Due to losses of some heavy fragments (as can be seen in Fig. 1) and the fact that the MCS signal was discriminated to only consider events with three heavy fragments the obtained values need to be adjusted for the lost percentages. This is done by dividing these values above the discriminator threshold with the actual recording fraction at 0 eV. The possible change in losses of heavy fragments will in each of the affected reaction channels be <1% for the fitted interval of 0-0.2 eV and is not accounted for. We finally obtain, for \ensuremath{{\rm CD_3OCD_2^+}}: $k(T)=1.7\pm0.5\times 10^{-6}(T/300)^{-0.77\pm0.01}$ cm3 s-1 and $\sigma = 1.2\pm0.4\times10^{-15}(E_{\rm cm}{\rm [eV]})^{-1.27\pm0.01}$ cm2; and for \ensuremath{{\rm (CD_3)_2OD^+}}: $k(T)= 1.7~\pm~0.6~\times 10^{-6}(T/300)^{-0.70\pm0.02}$ cm3 s-1 and $\sigma = 1.7\pm0.6 \times 10^{-15}(E_{\rm cm}{\rm [eV]})^{-1.20\pm0.02}$ cm2. In this evaluation errors arise from the uncertainty in the circumference of the ring, the length of the interaction region, the ion and electron currents and the electron density. These combined errors are estimated to be $\sim$25% and $\sim$35% for CD3OCD2+ and (CD3)2OD+, respectively.

3 Discussion

3.1 The structure of the ions

The (CD3)2OD+ ions were produced from DME and deuterium gas. Therefore, the most likely resulting species should be the titular ion ( $\Delta_{\rm f}{\rm H}{\rm (ion)} = 542$ kJ/mol) since formation of the isomeric deuteronated ethanol ( $\Delta_{\rm f}{\rm H}({\rm ion}) = 507$ kJ/mol) would imply heavy restructuring (enthalpy values from Lias et al. 1988). Both isomers are stable and the isomerisation barrier is sufficiently high that they can be considered separate species (Matthews & Adams 1997). The schematic potential diagram by Jarrold et al. (1986) clearly shows that the isomerisation barrier is higher than the dissociation energy.

For C2H5O+ Fairley et al. (1996) reported that the lowest energy isomer is CH3CHOH+ and that CH3OCH2+ is the second lowest lying 73 kJ mol-1 above. Lias et al. (1988) claim that this difference was 74 kJ mol-1 and that the isomer of protonated oxirane energetically lies in between. In the current experiment, the ion is being created from CH3OCH3 (DME) and a substantial reorganization would be necessary to create the ion with the lowest formation enthalpy from the parent substance. Calculations reported by Fairley et al. (1996) also show that there is an isomerisation barrier from CH3OCH2+ to CH2OHCH2+ of 280 kJ mol-1. Investigations by Jarrold et al. (1986) indicated a slightly higher isomerisation barrier and discovered that CH3OCH2+ ions with an internal energy close to the CH3+ + CH2O threshold (and hence less than necessary isomeric conversion energy) would undergo rapid unimolecular dissociation to give mainly HCO+. Therefore it could be concluded that excited ions with sufficient internal energy would mainly undergo fragmentation rather than isomerisation and no significant amounts of other ions than \ensuremath{{\rm CD_3OCD_2^+}} were present in the storage ring.

3.2 Implications of the branching fractions results for (CD3)2OD+

From the fragment energy spectrums of (CD3)2OD+ at $\sim$0 eV nominal $E_{\rm cm}$ (see Fig. 2) it is concluded that channels leading to product masses of 6, 8, 10 and 12 amu (3D, 4D, 5D and C) are not observed which limit the exoergic reaction channels to the ones found in Table 2 (energies calculated from Lias et al. 1988; and NIST 2009).

The signal corresponding to a mass of 4 amu (2D or D2) is close to zero and impossible to distinguish from noise. There are 13 exoergic competing reaction channels (one two-body breakup, eight three-body breakups and four involving four body breakups) that could contribute to the 2D signal. Assuming maximum losses and ignoring the possibility of contribution from the tail of the D peak limit the fraction for the sum of these channels to below $\sim$4%. We therefore conclude that a considerable alteration of the branching fractions of the reactions contributing to this mass cannot be totally excluded but are not likely to severely alter the final result.

The only remaining exoergic channel retaining the COC bonds between the heavy atoms seem to be the one involving the ejection of a single deuterium atom. Hence, we conclude that the branching fraction of 7% obtained for conservation of all heavy atom bonds is in principle due solely to that reaction. This amount is larger than the value of 1.5% assumed by Garrod & Herbst (2006) but much less than the value of 50% used in the model of Peeters et al. (2006).

The overall branching fraction of reactions leading to ejection of one heavy fragment is 49%. There are exoergic reaction channels in which this could occur, although some of these processes would imply considerable rearrangement and they are therefore not deemed plausible. It is assumed that the most important reaction contributing to this fraction is the channel producing \ensuremath{{\rm CD_3OD}} (methanol) and CD3.

Finally, the branching fractions of processes leading to the rupture of both C-O bonds is 44%. Here the most exoergic channel is that leading to CD3 + D2O + CD2. Judging from the structure of the spectrum, the peak corresponding to 16 amu is rather small and channels producing CD2 should not be as important. Therefore the channel leading to CD3 + OD + CD3 seems to be the most likely candidate. A comparison with the D3O+ and CD3OD2+ ions (Jensen et al. 2000; Geppert et al. 2006) shows an interesting similarity: channels leading to three fragments are important in all three ions.

There is an effect of including the losses of one heavy fragment in the analysis, however it is not large and very well within the error bars. The recommended values are those from the analysis including the losses.

3.3 Implications of the branching fractions results for CD3OCD2+

From our resulting spectrum for CD3OCD2+ it is clear that we do not see any fragments with mass 6, 8, 10, 12 or 24 amu which excludes C from the list of possible products as well as channels leading to D2 + D, 3D, 2D2 and 2D2 + D. We are therefore limited to the reaction channels in Table 2, where the energies are calculated from Lias et al. 1988 and NIST 2009). The experiment yields 100% fragmentation of the COC chain into two heavy fragments (CO + C or C2 + O). We can therefore exclude this ion as a source for acetaldehyde but further investigations will have to show if that is also true for the isomeric form CD3CDOD+. The probability of having fragments containing 2C but no O should be significantly smaller than the probability of having resulting fragments containing CO, since the former would imply substantial restructuring of the molecule.

No effect is noticed when extending the analysis to include losses of heavy fragments.

3.4 Implications of rate constants

The thermal rate constants reported here lie at the higher end for DR reaction rates which usually are around $3 \times 10^{-7}$ cm3 s-1 at 300 K. Nevertheless, larger ions have earlier been shown to have thermal reaction rate coefficients of similar magnitude e.g. C3H7+ (Ehlerding et al. 2003), DCCCND+ (Geppert et al. 2004a), POCl+ (Zhaunerchyk et al. 2008) and DOCO+ (Geppert et al. 2004b).

The change of slope appearing at $\sim$0.2 eV in Fig. 4 is likely to be due to the opening of different reaction channels including ones leading to auto ionisation (if it was due to particle losses from the beam it would not likely be so abrupt). The phenomenon has been observed for several polyatomic ions see e.g. Jensen et al. (1999); Vigren et al. (2008); Zhaunerchyk (2008).

To the best of our knowledge other measurements of the titular reactions have not yet been undertaken and we can therefore not compare our results directly. For the isomeric form of CH3OCH2+, CH3CHOH+ a FALP measurement has earlier been performed yielding a rate constant of $3.9\times 10^{-7}$ cm3 s-1 at 300 K with a 30% uncertainty (Geoghegan et al. 1991). Since the authors produced their ions by proton transfer from H3+ to acetaldehyde which therefore resulted in the different isomer the difference in reaction rate coefficients should be adressed to the structure (and possibly to a minor extent to isotopic effects see, below).

3.5 Isotopic effect

The measurements were made with the fully deuterated isotopologue of the ions with the aim of increasing the mass resolution to be able to distinguish peaks that differ by only one deuterium atom. Even with this substitution the resolution is just on the threshold of being insufficient for that purpose. The usage of fully deuterated species instead of their isotopologue is common practice and has been shown to lead in most cases to very similar branching ratios, see e.g. Neau et al. (2000); Jensen et al. (2000); Geppert et al. (2006). But exceptions exist (Larsson et al. 2005; Hamberg et al. 2007), which possibly are due to easier tunneling of hydrogen atoms through exit barriers.

Table 4:   Comparison with UMIST and Ohio State Chemical Network rate constants and their implied branching fractionsa.

3.6 Model implementation

The total reaction rate constant obtained for the (CD3)2OD+ ion are significantly higher than model values summed from viable reaction channels at Woodall et al. (2006); astrochemistry.net (2009), (see Table 4). The implied branching fractions from the models are further compared in Table 4 where the channel leading to CH3OCH3 + H clearly is less than the previous estimates whereas the the reactions leading to CH3OH + CH3 and CH3 + CH4 + O very well could be happening. No reaction leading to fragmentation of the COC-chain into three different particles is included in the UMIST model compared to 44% reported here.

For the CD3OCD2+ ion the total rate constant is higher than in the models (see Table 4). The reaction channels used by the models leading to CO + CH4 + H and H2CO + CH3 are found plausible whereas the CH3CHO + H and H2CCO + H2 + H product channels are not observed. The observed differences could partly be justified by the fact that the models are likely to treat different isomers as one.

Simulation with the new rates in astronomical regions should be undertaken.

4 Conclusion

The DR rate coefficients of the investigated ions are relatively high like it has been the case with other complex ions. For CD3OCD2+the DR exclusively lead to break up of the COC-chain into two fragments, one having one and the other having two heavy atoms. In the DR of deuteronated DME we have found the branching fraction channel leading to the undeuteronated species is only 7%. The impact on astrochemical models needs to be investigated.

Acknowledgements
We thank the staff at the Manne Siegbahn Laboratory for making these experiments possible by excellent technical support. W.D.G. thanks the Swedish Research Council for his Senior Researcher grant (contract No. 2006-427) and the Swedish Space Board (grant No. 76/06).

References

  1. Al-Khalili, A., Danared, H., Larsson, M., et al. 1998, Hyperfine Interact., 114, 281 [NASA ADS] [CrossRef] [Google Scholar]
  2. Angelova, G., Novotny, O., Mitchell, J. B. A., et al. 2004, Int. J. Mass. Spectrom., 232, 195 [Google Scholar]
  3. astrochemistry.net. 2009, http://www.astrochemistry.net [Google Scholar]
  4. Bell, M. B., Feldman, P. A., Travers, M. J., et al. 1997, ApJ, 483, L61 [NASA ADS] [CrossRef] [Google Scholar]
  5. Blake, G. A., Sutton, E. C., Masson, C. R., & Philips, T. G. 1987, ApJ, 315, 621 [NASA ADS] [CrossRef] [Google Scholar]
  6. Boger, G. I., & Sternberg, A. 2006, ApJ, 645, 314 [NASA ADS] [CrossRef] [Google Scholar]
  7. Botta, O. 2005, Astrochemsitry: Recent Successes and Current Challenges Proceedings IAU Symp., 231, 479 [NASA ADS] [Google Scholar]
  8. Cazaux, S., Tielens, A. G. G. M., & Ceccarelli, C. 2003, ApJ, 593, L51 [NASA ADS] [CrossRef] [Google Scholar]
  9. Crovisier, J., Bockelée-Morvan, D., Biver, N., Despois, D., & Lis, D. C. 2004, A&A, 418, 1141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Ehlerding, A., Arnold, S. T., Viggiano, A. A., et al. 2003, J. Phys. Chem. A, 107, 2179 [CrossRef] [Google Scholar]
  11. Fairley, D. A., Scott, G. B. I., Freeman, C. G., Maclagan, R. G. A. R., & McEwan, M. J. 1996, J. Chem. Soc., Faraday Trans., 92, 1305 [Google Scholar]
  12. Florescu-Mitchell, A. I., & Mitchell, J. B. A. 2006, Phys. Rep., 430, 277 [NASA ADS] [CrossRef] [Google Scholar]
  13. Friberg, P., Madden, S., Hjalmarson, A., & Irvine, W. 1988, A&A, 195, 281 [Google Scholar]
  14. Garrod, R. T., & Herbst, E. 2006, A&A, 457, 927 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Geoghegan, M., Adams, N. G., & Smith, D. 1991, J. Phys. B: At. Mol. Opt. Phys., 24, 2589 [NASA ADS] [CrossRef] [Google Scholar]
  16. Geppert, W. D., Ehlerding, A., Hellberg, F., et al. 2004a, ApJ, 613, 1302 [NASA ADS] [CrossRef] [Google Scholar]
  17. Geppert, W. D., Thomas, R., Ehlerding, A., et al. 2004b, Faraday Discuss., 127, 425 [CrossRef] [PubMed] [Google Scholar]
  18. Geppert, W. D., Thomas, R. D., Ehlerding, A., et al. 2005, J. Phys. Conf. Ser., 4, 26 [NASA ADS] [CrossRef] [Google Scholar]
  19. Geppert, W. D., Hamberg, M., Thomas, R. D., et al. 2006, Faraday Discuss., 133, 177 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  20. Groner, P., Albert, S., Herbst, E., & Lucia, F. C. D. 1998, ApJ, 500, 1059 [NASA ADS] [CrossRef] [Google Scholar]
  21. Haider, S. A., & Bhardwaj, A. 2005, Icarus, 177, 196 [NASA ADS] [CrossRef] [Google Scholar]
  22. Hamberg, M., Geppert, W. D., Rosén, S., et al. 2005, PCCP, 7, 1664 [NASA ADS] [CrossRef] [Google Scholar]
  23. Hamberg, M., Geppert, W. D., Thomas, R. D., et al. 2007, Mol. Phys., 105, 899 [NASA ADS] [CrossRef] [Google Scholar]
  24. Jarrold, M. F., Kirchner, N. J., Liu, S., & Bowers, M. T. 1986, J. Phys. Chem., 90, 78 [CrossRef] [Google Scholar]
  25. Jensen, M. J., Bilodeau, R. C., Heber, O., et al. 1999, Phys. Rev. A: At. Mol. Opt. Phys., 60, 2970 [NASA ADS] [Google Scholar]
  26. Jensen, M. J., Bilodeau, R. C., Safvan, C. P., Seiersen, K., & Andersen, L. H. 2000, ApJ, 543, 764 [NASA ADS] [CrossRef] [Google Scholar]
  27. Karpas, Z., & Meot-Ner, M. 1989, J. Phys. Chem., 93, 1859 [CrossRef] [Google Scholar]
  28. Lampert, A., Wolf, A., Habs, D., et al. 1996, Phys. Rev. A, 53, 1413 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  29. Larsson, M., Danared, H., Mowat, J. R., et al. 1993, Phys. Rev. Lett., 70, 430 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  30. Larsson, M., Broström, L., Carlson, M., et al. 1995, Phys. Scr., 51, 354 [NASA ADS] [CrossRef] [Google Scholar]
  31. Larsson, M., Ehlerding, A., Geppert, W. D., et al. 2005, J. Chem. Phys., 122, 156101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  32. Lias, S. G., Bartmess, J. E., Liebman, J. F., et al. 1988, J. Phys. Chem. Ref. Data, 17, Suppl. 1 [Google Scholar]
  33. Maret, S., Ceccarelli, C., & Cauz, E. 2004, A&A, 416, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Matthews, K. K., & Adams, N. G. 1997, Int. J. Mass. Spectrom. Ion. Proc., 163, 221 [Google Scholar]
  35. McCall, B. J., Huneycutt, A. J., Saykally, R. J., et al. 2003, Nature, 422, 500 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  36. Millar, T. J., Herbst, E., & Snyder, L. E. 1991, ApJ, 369, 147 [NASA ADS] [CrossRef] [Google Scholar]
  37. Mowat, J. R., Danared, H., Sundström, G., et al. 1995, Phys. Rev. Lett., 74, 50 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  38. Müller, U., & Cosby, P. C. 1999, Phys. Rev. A, 59, 3632 [NASA ADS] [CrossRef] [Google Scholar]
  39. Neau, A. 2002, Ph.D. Thesis, University of Stockholm, Sweden [Google Scholar]
  40. Neau, A., Al-Khalili, A., Rosén, S., et al. 2000, J. Chem. Phys., 113, 1762 [NASA ADS] [CrossRef] [Google Scholar]
  41. NIST, C. W. 2009, http://webbook.nist.gov/chemistry/ [Google Scholar]
  42. Paal, A., Simonsson, A., Dietrich, J., & Mohos, I. 2006, Proc. EPAC2006, 1196 [Google Scholar]
  43. Peeters, Z., Rodgers, S. D., Charnley, S. B., et al. 2006, A&A, 445, 197 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Peterson, W. K., Abe, T., Fukunishi, H., et al. 1994, J. Geophys. Res., 99, 23257 [NASA ADS] [CrossRef] [Google Scholar]
  45. Semaniak, J., Larson, A., Padellec, A. L., et al. 1998, ApJ, 498, 886 [NASA ADS] [CrossRef] [Google Scholar]
  46. Smirnova, N. V., Lyakhov, A. N., & Kozlov, S. I. 2002, Adv. Space Res., 30, 2597 [NASA ADS] [CrossRef] [Google Scholar]
  47. Sutton, E. C., Peng, R., & Danchi, W. C. 1995, Ap&SS, 97, 455 [Google Scholar]
  48. Thomas, R. D. 2008, Mass Spectrom. Rev., 27, 485 [Google Scholar]
  49. Tom, B. A., Zhaunerchyk, V., Wiczer, M. B., et al. 2009, J. Chem. Phys., 130, 031101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  50. Vigren, E., Kaminska, M., Hamberg, M., et al. 2008, PCCP, 10, 4014 [Google Scholar]
  51. Wolf, A., Krohn, S., Kreckel, H., et al. 2003, Nucl. Instrum. Meth. A, 532, 69 [NASA ADS] [CrossRef] [Google Scholar]
  52. Woodall, A., & Markwick-Kemper, M. 2006, The UMIST Database for Astrochemistry, http://www.udfa.net/ [Google Scholar]
  53. Yee, J. H., Abreu, V. J., & Colwell, W. B. 1989, Dissociative Recombination [Int. Conf.], Meeting 1988, 286 [Google Scholar]
  54. Zhaunerchyk, V. 2008, Ph.D. Thesis, University of Stockholm, Sweden [Google Scholar]
  55. Zhaunerchyk, V., Thomas, R. D., Geppert, W. D., et al. 2008, J. Chem. Phys., 128, 134308 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]

All Tables

Table 1:   Branching fraction results for (CD3)2OD+ and CD3OCD2+ respectivelya.

Table 2:   Energetically open and plausible reaction channels for the DR of (CD3)2OD+ including those leading to D2 and 2Da.

Table 3:   Energetically open and plausible reaction channels for the DR of CD3OCD2+a.

Table 4:   Comparison with UMIST and Ohio State Chemical Network rate constants and their implied branching fractionsa.

All Figures

  \begin{figure} \par\includegraphics[width=9cm,clip]{13891fg1.eps} \vspace*{2mm} \end{figure} Figure 1:

A fragment energy spectrum recorded for (CD3)2OD+ when the grid is not inserted. The large peak to the right is due to particles impacting at full beam energy. The two smaller peaks in the middle are due to losses because of fragments with high transverse energy that miss the detector. The sharp peak at the leftmost position is due to noise in the detector system.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{13891fg2.eps} \vspace*{-2mm} \end{figure} Figure 2:

A fragment energy spectrum recorded for (CD3)2OD+ when the grid is inserted. The three major peaks are due to detection of fragments containing one, two or three heavy atoms, respectively. The sharp peak at the leftmost position is due to noise in the detector system mixed with signal from deuterium fragments.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{13891fg3.eps} \vspace*{-3mm} \end{figure} Figure 3:

Fragment energy spectrum recorded for CD3OCD2+ with the grid inserted. The three major peaks are due to detection of fragments containing one, two or three heavy atoms respectively. The sharp peak at the leftmost position is due to noise in the detector system mixed with signal from deuterium fragments and was not used in the branching fraction derivation. The second peak from the left stems from signal corresponding 4 amu mass (2D).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{13891fg4.eps} \end{figure} Figure 4:

Cross section evaluation of (CD3)2OD+. The triangles shows individually measured spots while the line shows the best fit between 1-200 meV.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.