| Issue |
A&A
Volume 514, May 2010
|
|
|---|---|---|
| Article Number | A50 | |
| Number of page(s) | 18 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/200913872 | |
| Published online | 12 May 2010 | |
Structure of the magnetoionic medium around the Fanaroff-Riley Class I radio galaxy 3C 449
D. Guidetti1,2,3 - R. A. Laing1 - M. Murgia4 - F. Govoni4 - L. Gregorini3 - P. Parma2
1 - European Southern Observatory, Karl-Schwarzschild-Stra![]() e 2, 85748
Garching, Germany
e 2, 85748
Garching, Germany
2 - INAF - Istituto di Radioastronomia, bia Gobetti 101, 40129 Bologna,
Italy
3 - Dipartimento di Astronomia, Univ. Bologna, bia Ranzani 1, 40127
Bologna, Italy
4 - INAF - Osservatorio Astronomico di Cagliari, Loc. Poggio dei Pini,
Strada 54, 09012 Capoterra (CA), Italy
Received 14 December 2009 / Accepted 3 February 2010
Abstract
Aims. The goal of this work is to constrain the
strength and structure of the magnetic field associated with the
environment of the radio source 3C 449 by using observations
of Faraday rotation, which we model with a structure function
technique, and by comparison with numerical simulations. We assume that
the magnetic field is a Gaussian isotropic random variable and that it
is embedded in the hot intra-group plasma surrounding the radio source.
Methods. For this purpose, we present detailed
rotation measure images for the polarized radio source 3C 449,
previously observed with the Very Large Array at seven frequencies
between 1.365 and 8.385 GHz. All of the observations are
consistent with pure foreground Faraday rotation. We quantify the
statistics of the magnetic-field fluctuations by deriving rotation
measure structure functions, which we fit using models derived from
theoretical power spectra. We quantify the errors due to sampling by
making multiple two-dimensional realizations of the best-fitting power
spectrum. We also use depolarization measurements to estimate the
minimum scale of the field variations. We then develop
three-dimensional models with a gas density distribution derived from
X-ray observations and a random magnetic field with this power
spectrum. By comparing our simulations with the observed Faraday
rotation images, we can determine the strength of the magnetic field
and its dependence on density, as well as the outer scale of the
magnetic turbulence.
Results. The rotation measure and depolarization
data are consistent with a broken power-law magnetic-field power
spectrum, with a break at about 11 kpc and slopes of 2.98 and
2.07 at smaller and larger scales respectively. The maximum and minimum
scales of the fluctuations are ![]() 65 and
65 and ![]() 0.2 kpc,
respectively. The average magnetic field strength at the cluster centre
is
0.2 kpc,
respectively. The average magnetic field strength at the cluster centre
is ![]() G, decreasing linearly with
the gas density within
G, decreasing linearly with
the gas density within ![]() 16 kpc
of the nucleus. At larger distances, the dependence of field on density
appears to flatten, but this may be an effect of errors in the density
model. The magnetic field is not energetically important.
16 kpc
of the nucleus. At larger distances, the dependence of field on density
appears to flatten, but this may be an effect of errors in the density
model. The magnetic field is not energetically important.
Key words: magnetic fields - polarization - intergalactic medium - radio continuum: galaxies - X-rays: galaxies
1 Introduction
Magnetic fields in the hot plasma associated with groups and clusters of galaxies are poorly understood, but are thought to play a vital role in regulating thermal conduction (e.g. Balbus 2000; Bogdanovic et al. 2009) and influence the dynamics of cavities formed by radio jets (e.g. Dursi & Pfrommer 2008; O'Neill et al. 2009). The existence of magnetic fields can be demonstrated in several different ways (e.g. Carilli & Taylor 2002; Govoni & Feretti 2004, and references therein). One of these is via the Faraday effect: rotation of the plane of linearly polarized radiation by a magnetized plasma. Synchrotron emission from radio sources (either behind or embedded within the group/cluster medium) can be used to probe the distribution of foreground Faraday rotation. These can be combined with X-ray observations (which provide the thermal gas density profile) to infer the strength and fluctuation properties of the magnetic field.
Faraday rotation studies of clusters have been carried out
with both
statistical samples of background radio sources (e.g. Lawler &
Dennison 1982;
Vallée et al. 1986;
Kim et al. 1990,
1991; Clarke
et al. 2001)
and individual radio
sources within the clusters
(e.g. Taylor & Perley 1993;
Feretti et al. 1995;
Feretti et al. 1999a,b;
Govoni et al. 2001;
Eilek & Owen 2002;
Pollack et al. 2005;
Govoni et al. 2006;
Guidetti
et al. 2008).
The central magnetic field strengths deduced from these data are
usually a few ![]() G,
but can exceed 10
G,
but can exceed 10 ![]() G
in the inner regions of relaxed cool-core clusters (e.g. Taylor
et al. 2002).
The rotation measure (RM) distributions of radio galaxies in both
interacting and relaxed clusters
are generally patchy, indicating that cluster magnetic
fields show a structure on scales
G
in the inner regions of relaxed cool-core clusters (e.g. Taylor
et al. 2002).
The rotation measure (RM) distributions of radio galaxies in both
interacting and relaxed clusters
are generally patchy, indicating that cluster magnetic
fields show a structure on scales ![]() 10 kpc.
10 kpc.
Several studies of Abell clusters (Murgia et al. 2004; Govoni et al. 2006; Guidetti et al. 2008) have shown that detailed RM images of radio galaxies can be used to infer not only the strength of the cluster magnetic field, but also its power spectrum. The analysis of Vogt & Enßlin (2003, 2005) suggests that the power spectrum has a power law form with the slope appropriate for Kolmogorov turbulence and that the auto-correlation length of the magnetic field fluctuations is a few kpc. The deduction of a Kolmogorov slope could be premature, however: there is a degeneracy between the slope and the outer scale, which is difficult to resolve with current Faraday rotation data (Murgia et al. 2004; Guidetti et al. 2008; Laing et al. 2008). Indeed, Murgia et al. (2004) pointed out that shallower magnetic field power spectra are possible if the magnetic field fluctuations have structure on scales of several tens of kpc. Recently, Guidetti et al. (2008) showed that a power-law power spectrum with a Kolmogorov slope, and an abrupt long-wavelength cut-off at 35 kpc gave a very good fit to their Faraday rotation and depolarization data for the radio galaxies in A2382, although a shallower slope extending to longer wavelengths was not ruled out.
While most work until recently has been devoted to rich clusters of galaxies, little attention has been given in the literature to sparser environments, although similar physical processes are likely to be at work. Faraday-rotation fluctuations have previously been detected in galaxy groups (e.g. Perley et al. 1984; Feretti et al. 1999a), but without deriving in detail the geometry and structure of the magnetic field. The first detailed work on galaxy groups was done by Laing et al. (2008), who analysed the radio emission of 3C 31.
They found that the three-dimensional magnetic-field power
spectrum
![]() ,
defined in Sect. 6.1,
can be
described in terms of spatial frequency f by a
broken power-law
,
defined in Sect. 6.1,
can be
described in terms of spatial frequency f by a
broken power-law
![]() with q=11/3
with q=11/3![]() for
f>0.062 arcsec-1
(corresponding to a spatial scale of about 17 kpc) and q=2.32
at lower frequencies, although a
power spectrum with a slope of 2.39 and an abrupt cut-off at
high frequencies could
not be ruled out. Their results are qualitatively similar to those for
sources
in Abell clusters.
for
f>0.062 arcsec-1
(corresponding to a spatial scale of about 17 kpc) and q=2.32
at lower frequencies, although a
power spectrum with a slope of 2.39 and an abrupt cut-off at
high frequencies could
not be ruled out. Their results are qualitatively similar to those for
sources
in Abell clusters.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{13872f1.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13872-09/Timg26.png)
|
Figure 1:
Radio contours of 3C 449 at 1.365 GHz superposed on
the XMM-Newton X-ray image (courtesy of J. Croston,
Croston et al. 2003).
The radio contours start at 3
|
| Open with DEXTER | |
This paper presents a detailed analysis of Faraday rotation in 3C 449, a bright, extended radio source hosted by the central galaxy of a nearby group. With the aim of shedding new light on the environment around this source, we derive the statistical properties of the magnetic field from observations of Faraday rotation, following the method developed by Murgia et al. (2004). We use numerical simulations to predict the Faraday rotation for different strengths and power spectra of the magnetic field.
The paper is organized as follows. In Sect. 2 the general properties of the radio source under investigation are presented. Section 3 presents the radio images on which our analysis is based. In Sect. 4, we discuss the observed Faraday rotation distribution of 3C 449 and assess the contribution from our Galaxy. The observed depolarization and its relation to the RM properties are investigated in Sect. 5. Our two-dimensional analysis of the structure of the RM fluctuations and a three-dimensional model of the magnetic field consistent with these results are presented in Sects. 6 and 7, respectively. Section 8 summarizes our conclusions and briefly compares the Faraday-rotation properties of 3C 449 with those of other sources.
Throughout this paper we assume a cosmology with H0
= 71 km s-1 Mpc-1,
![]() ,
and
,
and ![]() ,
which
implies that 1 arcsec corresponds to 0.342 kpc at the
distance of 3C 449.
,
which
implies that 1 arcsec corresponds to 0.342 kpc at the
distance of 3C 449.
2 The radio source 3C 449: general properties
We image and model the Faraday rotation distribution across the
giant Fanaroff-Riley Class I (FR I; Fanaroff & Riley 1974) radio
source
3C 449, whose environment is very similar to that of
3C 31. The optical counterpart of 3C 449,
UGC 12064, is a dumb-bell galaxy and is the most prominent
member of the group of galaxies 2231.2+3732 (Zwicky & Kowal 1968).
The source is relatively nearby (
z=0.017085,
RC3.9, De Vaucouleurs et al. 1991)
and quite extended, both in angular (30![]() )
and linear size, so it is an
ideal target for an analysis of the Faraday rotation distribution:
detailed
images can be constructed that can serve as the basis of an accurate
study of
magnetic field power spectra.
)
and linear size, so it is an
ideal target for an analysis of the Faraday rotation distribution:
detailed
images can be constructed that can serve as the basis of an accurate
study of
magnetic field power spectra.
The source 3C 449 was one of the first radio galaxies
studied in detail with the VLA![]() (Perley et al. 1979).
High- and low-resolution radio data already exist and the source has
been mapped at many frequencies.
The radio emission of 3C 449 (Fig. 1) is elongated in the
N-S direction and is characterized by long,
two-sided jets with a striking mirror symmetry
close to the nucleus. The jets
terminate in well-defined inner lobes, which fade
into well polarized spurs, of which the southern
one is more
collimated. The spurs in turn expand to form diffuse outer lobes.
(Perley et al. 1979).
High- and low-resolution radio data already exist and the source has
been mapped at many frequencies.
The radio emission of 3C 449 (Fig. 1) is elongated in the
N-S direction and is characterized by long,
two-sided jets with a striking mirror symmetry
close to the nucleus. The jets
terminate in well-defined inner lobes, which fade
into well polarized spurs, of which the southern
one is more
collimated. The spurs in turn expand to form diffuse outer lobes.
The brightness ratio of the radio jets is very nearly 1, implying that they are close to the plane of the sky if they are intrinsically symmetrical and have relativistic flow velocities similar to those derived for other FR I jets (Perley et al. 1979; Feretti et al. 1999a; Laing & Bridle 2002). We therefore assume that the jets lie exactly in the plane of the sky, which simplifies the geometry of the Faraday-rotating medium.
Hot gas associated with the galaxy was detected on both the
group and the galactic scales by X-ray imaging (Hardcastle
et al. 1998;
Croston et al. 2003).
These observations revealed deficits in the X-ray surface brightness
at the positions of the outer radio lobes, suggesting interactions with
the surrounding
material. Figure 1
shows radio contours at 1.365 GHz overlaid on the X-ray
emission as observed by the XMM-Newton satellite (Croston
et al. 2003).
The X-ray radial surface brightness profile
of 3C 449 derived from these data can be fitted with the sum
of a point-source convolved with
the instrumental response and a ![]() model (Cavaliere & Fusco-Femiano 1976),
model (Cavaliere & Fusco-Femiano 1976),
where r,
The source 3C 449 resembles 3C 31 in
environment and in radio morphology: both sources
are associated with the central members of groups of galaxies, and
their
redshifts are very similar.
The nearest neighbours are at a projected distances of about
30 kpc
in both cases. Both radio sources have large angular extents, bending
jets and
long, narrow tails with low surface brightnesses and steep spectra,
although
3C 31 appears much more distorted on large scales. There is
one significant
difference: the inner jets of 3C 31 are thought to be inclined
by
![]() 50
50![]() to the line-of-sight (Laing & Bridle 2002), whereas
those
in 3C 449 are likely to be close to the plane of the sky
(Feretti et al. 1999a).
We therefore expect that the magnetized foreground medium will be very
similar in the two sources, but that the geometry will be significantly
different, leading to a much more symmetrical distribution of Faraday
rotation
in 3C 449 compared with that observed in 3C 31 by
Laing et al. (2008).
to the line-of-sight (Laing & Bridle 2002), whereas
those
in 3C 449 are likely to be close to the plane of the sky
(Feretti et al. 1999a).
We therefore expect that the magnetized foreground medium will be very
similar in the two sources, but that the geometry will be significantly
different, leading to a much more symmetrical distribution of Faraday
rotation
in 3C 449 compared with that observed in 3C 31 by
Laing et al. (2008).
3 Total intensity and polarization properties
The VLA observations and their reduction were presented by Feretti et al. (1999a). The high quality of these data make this source suited for a very detailed analysis of the statistics of the Faraday rotation.
We produced total intensity (I) and
polarization (Q and U) images at
frequencies in the range 1.365-8.385 GHz from the combined,
self-calibrated
u-v datasets described
by Feretti et al. (1999a).
The centre frequencies and
bandwidths are listed in Table 1.
Each frequency channel was imaged
separately, except for those at 8.245 and 8.445 GHz,
which were averaged. The
analysis below confirms that these frequency-bandwidth combinations
lead to
negligible Faraday rotation across the channels, as already noted by
Feretti et al. (1999a).
All of the datasets were imaged with Gaussian tapering in the u-v plane
to give resolutions of 1.25 arcsec and 5.5 arcsec FWHM,
CLEANed
and restored with circular Gaussian beams. The first angular resolution
is the
highest possible at all frequencies and provides good signal-to-noise
for the
radio emission within 150 arcsec (![]() 50 kpc) of the radio
core (the well
defined radio jets and the inner lobes), while minimizing beam
depolarization. The lower resolution of 5.5 arcsec allows
imaging of the
extended emission as far as 300 arcsec (
50 kpc) of the radio
core (the well
defined radio jets and the inner lobes), while minimizing beam
depolarization. The lower resolution of 5.5 arcsec allows
imaging of the
extended emission as far as 300 arcsec (![]() 100 kpc) from the
core at
frequencies from 1.365-4.985 GHz (the 8.385-GHz dataset does
not have
adequate sensitivity to image the outer parts of the source). We can
therefore
study the structure of the magnetic field in the spur regions, which
lie well
outside the bulk of the X-ray emitting gas. Noise levels for both sets
of
images are given in Table 1.
Note that the maximum scales of structure,
which can be imaged reliably with the VLA at 8.4 and 5 GHz are
100 kpc) from the
core at
frequencies from 1.365-4.985 GHz (the 8.385-GHz dataset does
not have
adequate sensitivity to image the outer parts of the source). We can
therefore
study the structure of the magnetic field in the spur regions, which
lie well
outside the bulk of the X-ray emitting gas. Noise levels for both sets
of
images are given in Table 1.
Note that the maximum scales of structure,
which can be imaged reliably with the VLA at 8.4 and 5 GHz are
![]() 180
and
180
and ![]() 300 arcsec,
respectively (Ulvestad et al. 2009). For
this reason, we only use the Stokes I
images for quantitative analysis
within half these distances of the core. The Q and U
images have much less
structure on these large scales and are reliable to distances of
300 arcsec,
respectively (Ulvestad et al. 2009). For
this reason, we only use the Stokes I
images for quantitative analysis
within half these distances of the core. The Q and U
images have much less
structure on these large scales and are reliable to distances of ![]() 150 arcsec
at 8.4 GHz and
150 arcsec
at 8.4 GHz and ![]() 300 arcsec
at 5 GHz, limited by sensitivity rather than
systematic errors due to missing flux as in the case of the I image.
300 arcsec
at 5 GHz, limited by sensitivity rather than
systematic errors due to missing flux as in the case of the I image.
Images of polarized intensity P
= (Q2+U2)1/2
(corrected for Ricean bias, following Wardle &
Kronberg 1974),
fractional polarization p=P/I
and polarization angle ![]() were derived from the I, Q, and
U images.
were derived from the I, Q, and
U images.
Table 1: Parameters of the total intensity and polarization images.
All of the polarization images (P, p,
![]() )
at a given frequency were blanked
where the rms error in
)
at a given frequency were blanked
where the rms error in ![]() at any frequency. We then calculated the scalar mean degree of
polarization
at any frequency. We then calculated the scalar mean degree of
polarization ![]() for each frequency and resolution; the results are listed in
Table 1.
The values of
for each frequency and resolution; the results are listed in
Table 1.
The values of ![]() are higher at 5.5 arcsec resolution than at
1.25 arcsec because of the contribution of the extended and
highly polarized emission, which is not seen at the higher resolution.
At 1.25 arcsec, where the beam depolarization is minimized,
the mean fractional polarization shows a steady increase
from 1.365 to 4.685 GHz, where it reaches an
average value of 0.32 and
then remains roughly constant at higher frequencies, suggesting that
the
depolarization between 4.685 and 8.385 GHz
is insignificant.
are higher at 5.5 arcsec resolution than at
1.25 arcsec because of the contribution of the extended and
highly polarized emission, which is not seen at the higher resolution.
At 1.25 arcsec, where the beam depolarization is minimized,
the mean fractional polarization shows a steady increase
from 1.365 to 4.685 GHz, where it reaches an
average value of 0.32 and
then remains roughly constant at higher frequencies, suggesting that
the
depolarization between 4.685 and 8.385 GHz
is insignificant.
4 The Faraday rotation in 3C 449
4.1 Rotation measure images
A magnetized, ionized medium rotates the plane of polarization of
linearly
polarized radiation passing through it as follows:
where
Images of RM can be obtained for radio sources by fitting to the polarization angle as a function of
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{13872f2.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13872-09/Timg54.png)
|
Figure 2:
a) Image of the rotation measure of
3C 449 at a resolution of 1.25 arcsec FWHM,
computed at the seven
frequencies between 1.365 and 8.385 GHz.
b) Image of the rotation measure of
3C 449 at a resolution of 5.5 arcsec FWHM,
computed at the six frequencies between 1.365
and 4.985 GHz.
In both of the RM images, the sub-regions used for the
two-dimensional analysis of Sect. 6 are labelled.
c) and d) profiles
of |
| Open with DEXTER | |
We produced images of RM and its associated rms error with
resolutions of
1.25 arcsec and 5.5 arcsec (Figs. 2a
and b) using a version of the AIPS task RM
modified by G. B. Taylor.
The 1.25 arcsec-RM map was made by combining the maps
of the polarization ![]() -vector
(
-vector
(![]() )
at all seven
frequencies available to us, so our sampling of
)
at all seven
frequencies available to us, so our sampling of ![]() is very good. The RM map was calculated with a weighted
least-squares fit at pixels with polarization angle uncertainties
<10
is very good. The RM map was calculated with a weighted
least-squares fit at pixels with polarization angle uncertainties
<10 ![]() at
all
frequencies. It is essentially the same as the RM image of
Feretti et al. (1999a),
but with more stringent blanking.
The average fitting error is
at
all
frequencies. It is essentially the same as the RM image of
Feretti et al. (1999a),
but with more stringent blanking.
The average fitting error is ![]() 1.4 rad m-2
and is almost constant over the whole RM image. The image of
RM at 5.5 arcsec resolution
was produced using the polarization position angles at the six
frequencies between
1.365 and 4.985 GHz (see Table 1) with the same
blanking criterion as at higher resolution.
1.4 rad m-2
and is almost constant over the whole RM image. The image of
RM at 5.5 arcsec resolution
was produced using the polarization position angles at the six
frequencies between
1.365 and 4.985 GHz (see Table 1) with the same
blanking criterion as at higher resolution.
Patches with different size are apparent in the
1.25 arcsec resolution map, with
fluctuations down to scales of a few kpc.
The RM values range from about -220 rad m-2
up to
-90 rad m-2, dominated by the
Galactic contribution (see Sect. 4.2). The
RM distribution peaks at -161.7 rad m-2,
with a rms dispersion ![]() = 19.7 rad m-2.
Note that we have not corrected the values of
= 19.7 rad m-2.
Note that we have not corrected the values of ![]() for the
fitting error
for the
fitting error ![]() .
A first order correction would be
.
A first order correction would be ![]() .
Given the low value for
.
Given the low value for ![]() ,
the effect of this correction
would be very small.
,
the effect of this correction
would be very small.
As was noted by Feretti et al. (1999a), the
RM distribution in the inner jets is highly
symmetric about the core with ![]() rad m-2
at distances
rad m-2
at distances ![]() 15 arcsec.
The symmetry of the RM distribution in the jets is broken at
larger distances from the core: while
the RM structure in the southern jet is homogeneous, with
values around -130 rad m-2,
fluctuations on scales of
15 arcsec.
The symmetry of the RM distribution in the jets is broken at
larger distances from the core: while
the RM structure in the southern jet is homogeneous, with
values around -130 rad m-2,
fluctuations on scales of ![]() 10 arcsec
(
10 arcsec
(![]() 3 kpc)
around a
3 kpc)
around a ![]() of -160 rad m-2
are present in the northern jet.
In both lobes, we observe similar patchy RM structures with
mean values
of -160 rad m-2
are present in the northern jet.
In both lobes, we observe similar patchy RM structures with
mean values ![]()
![]() rad m-2
and
rad m-2
and ![]()
![]() 16 rad m-2.
16 rad m-2.
At 5.5 arcsec resolution, more extended polarized
regions of 3C 449 can be
mapped with good sampling in ![]() .
The average fitting error is
.
The average fitting error is ![]() 1.0 rad m-2.
Both spurs are characterized by
1.0 rad m-2.
Both spurs are characterized by ![]()
![]() 160 rad m-2,
with
160 rad m-2,
with ![]() = 15
and 10 rad m-2in the north and
south, respectively. The overall mean and rms for the
5.5 arcsec image,
= 15
and 10 rad m-2in the north and
south, respectively. The overall mean and rms for the
5.5 arcsec image, ![]() =
-160.7 rad m-2 and
=
-160.7 rad m-2 and ![]() = 18.9 rad m-2,
are very close to those determined at higher resolution and are
consistent with the
integrated value of
= 18.9 rad m-2,
are very close to those determined at higher resolution and are
consistent with the
integrated value of
![]() rad m-2
derived by Simard-Normandin et al. (1981).
rad m-2
derived by Simard-Normandin et al. (1981).
It was demonstrated by Feretti et al. (1999a) that
the polarization position
angles at 1.25 arcsec resolution accurately follow the
relation ![]() over a
wide range of rotation. We find the same
effect at lower resolution: plots of
over a
wide range of rotation. We find the same
effect at lower resolution: plots of ![]() -vector position angle
-vector position angle
![]() against
against ![]() at representative points of the 5.5 arcsec-RM image
are shown in Fig. 3.
As at the higher resolution, there are no significant deviations from
the relation
at representative points of the 5.5 arcsec-RM image
are shown in Fig. 3.
As at the higher resolution, there are no significant deviations from
the relation ![]() over a range of rotation
over a range of rotation ![]() of 600
of 600![]() ,
confirming that a foreground magnetized medium is responsible for
the majority of the Faraday rotation and extending this result to
regions of
lower surface brightness.
,
confirming that a foreground magnetized medium is responsible for
the majority of the Faraday rotation and extending this result to
regions of
lower surface brightness.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13872f3.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13872-09/Timg65.png)
|
Figure 3:
Plots of |
| Open with DEXTER | |
In Figs. 2c
and d, we show profiles of ![]() for both low
and
high resolution RM images. The 1.25 arcsec profile
was obtained by averaging
over boxes with lengths ranging from 9
to 13 kpc along the radio axis; for the
5.5 arcsec profile we used boxes with a fixed length of
9 kpc (these sizes were
chosen to give an adequate number of independent points per box).
The boxes extend far enough perpendicular to the source axis to include
all unblanked pixels.
In both plots, there is clear evidence for a decrease in the observed
for both low
and
high resolution RM images. The 1.25 arcsec profile
was obtained by averaging
over boxes with lengths ranging from 9
to 13 kpc along the radio axis; for the
5.5 arcsec profile we used boxes with a fixed length of
9 kpc (these sizes were
chosen to give an adequate number of independent points per box).
The boxes extend far enough perpendicular to the source axis to include
all unblanked pixels.
In both plots, there is clear evidence for a decrease in the observed ![]() towards the
periphery of the source, the value dropping from
towards the
periphery of the source, the value dropping from ![]() 30 rad m-2
close
to the nucleus to
30 rad m-2
close
to the nucleus to ![]() 10 rad m-2
at 50 kpc. This is qualitatively as
expected for foreground Faraday rotation by a medium whose density (and
presumably
also magnetic field strength) decreases with radius. The symmetry of
the
10 rad m-2
at 50 kpc. This is qualitatively as
expected for foreground Faraday rotation by a medium whose density (and
presumably
also magnetic field strength) decreases with radius. The symmetry of
the ![]() profiles is
consistent with our assumption
that the radio source lies in the plane of the sky.
profiles is
consistent with our assumption
that the radio source lies in the plane of the sky.
4.2 The Galactic Faraday rotation
For the purpose of this work, 3C 449 has an unfortunate
line-of-sight within our Galaxy.
Firstly, the source is located at l=95.4![]() ,
b=-15.9
,
b=-15.9 ![]() in Galactic coordinates, where the Galactic magnetic field
is known to be aligned almost along the line-of-sight.
Secondly, there is evidence from radio and optical imaging for a
diffuse,
ionized Galactic feature in front of 3C 449, perhaps
associated with the nearby
HII region S126 (Andernach et al. 1992).
Estimates of the Galactic foreground RM at the position of
3C 449 from observations of other radio sources are uncertain:
Andernach et al. (1992)
found a mean value of
-212 rad m-2 for six nearby
sources, but the spherical harmonic
models of Dineen & Coles (2005), which are
derived by fitting to
the RM values of large numbers of extragalactic sources,
predict
-135 rad m-2. Nevertheless, it
is clear that the bulk of the mean RM
of 3C 449 must be Galactic.
in Galactic coordinates, where the Galactic magnetic field
is known to be aligned almost along the line-of-sight.
Secondly, there is evidence from radio and optical imaging for a
diffuse,
ionized Galactic feature in front of 3C 449, perhaps
associated with the nearby
HII region S126 (Andernach et al. 1992).
Estimates of the Galactic foreground RM at the position of
3C 449 from observations of other radio sources are uncertain:
Andernach et al. (1992)
found a mean value of
-212 rad m-2 for six nearby
sources, but the spherical harmonic
models of Dineen & Coles (2005), which are
derived by fitting to
the RM values of large numbers of extragalactic sources,
predict
-135 rad m-2. Nevertheless, it
is clear that the bulk of the mean RM
of 3C 449 must be Galactic.
In order to investigate the magnetized plasma local to
3C 449, we need to constrain the value and possible spatial
variation of this Galactic
contribution. The profiles of ![]() (Fig. 2) show that the
small-scale fluctuations of RM drop rapidly with distance from
the nucleus. We
might therefore expect the Galactic contribution to dominate on the
largest scales. At low resolution, we could determine the
RM accurately out to
(Fig. 2) show that the
small-scale fluctuations of RM drop rapidly with distance from
the nucleus. We
might therefore expect the Galactic contribution to dominate on the
largest scales. At low resolution, we could determine the
RM accurately out to ![]() 100 kpc
from the core. This is roughly 5 core radii for the X-ray emission and
therefore well outside the bulk of the intra-group gas.
100 kpc
from the core. This is roughly 5 core radii for the X-ray emission and
therefore well outside the bulk of the intra-group gas.
In order to estimate the Galactic RM contribution, we
averaged the 5.5-arcsec RM
image in boxes of length 20 kpc along the radio axis (the box
size has been
increased from that of Fig. 2 to improve the
display of
large-scale variations). The profile of ![]() against
the distance from the
radio core is shown in Fig. 4.
The large deviations from the mean in
the innermost two bins are associated with the maximum in
against
the distance from the
radio core is shown in Fig. 4.
The large deviations from the mean in
the innermost two bins are associated with the maximum in ![]() and are
almost
certainly due to the intra-group medium. The dispersion in
and are
almost
certainly due to the intra-group medium. The dispersion in ![]() is
quite small
in the south and the value of
is
quite small
in the south and the value of ![]() =
-160.7 rad m-2 for the whole
source is very close to that of the outer south jet. There are
significant
fluctuations in the north, however. Given their rather small scale
(
=
-160.7 rad m-2 for the whole
source is very close to that of the outer south jet. There are
significant
fluctuations in the north, however. Given their rather small scale
(![]() 300 arcsec),
it is most likely that these arise in the local environment
of 3C 449, and we include them in the statistical analysis
given below.
300 arcsec),
it is most likely that these arise in the local environment
of 3C 449, and we include them in the statistical analysis
given below.
There is some evidence for linear gradients in Galactic
RM on arcminute scales:
Laing et al. (2006)
found a gradient of 0.025 rad m-2 arcsec-1
along the jets of the radio galaxy NGC 315
(l=124.6 ![]() , b=-32.5
, b=-32.5 ![]() ). They
argued that this gradient is
almost certainly Galactic in origin, since the amplitude of the linear
variation
exceeds that of the small-scale fluctuations associated with
NGC 315. In order
to check the effect of a large-scale Galactic RM gradient on
our results, we
computed an unweighted least-squares fit of a function
). They
argued that this gradient is
almost certainly Galactic in origin, since the amplitude of the linear
variation
exceeds that of the small-scale fluctuations associated with
NGC 315. In order
to check the effect of a large-scale Galactic RM gradient on
our results, we
computed an unweighted least-squares fit of a function ![]()
![]() ,
where a and
,
where a and ![]() are constant and x is measured along the radio
axis. The two innermost bins in Fig. 4 were excluded from
the fit. Our
best estimate for the gradient is very small:
a=0.0054 rad m-2 arcsec-1.
We have
verified that subtraction of this gradient has a negligible effect on
the
structure-function analysis given in Sect. 7.3.
are constant and x is measured along the radio
axis. The two innermost bins in Fig. 4 were excluded from
the fit. Our
best estimate for the gradient is very small:
a=0.0054 rad m-2 arcsec-1.
We have
verified that subtraction of this gradient has a negligible effect on
the
structure-function analysis given in Sect. 7.3.
We therefore adopt a constant value of -160.7 rad m-2 as the Galactic contribution.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13872f4.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13872-09/Timg69.png)
|
Figure 4: Profile of RM averaged over boxes of length 20 kpc along the radio axis for the 5.5 arcsec image. The horizontal bars represent the bin width. The vertical bars are the errors on the mean calculated from the dispersion in the boxes, the contribution from the fitting error is negligible and is not taken into account. Positive distances are in the direction of the north jet. The black vertical dashed line indicates the position of the nucleus; the green dashed line shows our adopted mean value for the Galactic RM. |
| Open with DEXTER | |
5 Depolarization
Faraday rotation generally leads to a decrease of the degree of
polarization
with increasing wavelength, or depolarization (DP).
We define DP
![]() ,
where
,
where ![]() is the degree of polarization at a given wavelength
is the degree of polarization at a given wavelength
![]() .
We adopt the conventional usage, in which higher
depolarization
corresponds to a lower value of DP.
.
We adopt the conventional usage, in which higher
depolarization
corresponds to a lower value of DP.
Laing (1984) summarized the interpretation of polarization data. Faraday depolarization of radio emission from radio sources can occur in three principal ways:
- 1.
- thermal plasma is mixed with the synchrotron emitting material (internal depolarization);
- 2.
- there are fluctuations of the foreground Faraday rotation across the beam (beam depolarization); and
- 3.
- the polarization angle varies across the finite band of the receiving system (bandwidth depolarization).
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{13872f5.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13872-09/Timg73.png)
|
Figure 5:
a) Image of the Burn law k
in rad2 m-4computed
from a fit to the relation |
| Open with DEXTER | |
If ![]() rotation is
observed over a position-angle range
rotation is
observed over a position-angle range ![]() 90
90![]() ,
then a foreground screen must be responsible for
the bulk of the observed RM.
In that case, depolarization can still result from unresolved
inhomogeneities of thermal density or magnetic field
in the surrounding medium.
Our analysis of the depolarization of 3C 449 is based on the
approach of Laing
et al. (2008).
It is still possible to observe
,
then a foreground screen must be responsible for
the bulk of the observed RM.
In that case, depolarization can still result from unresolved
inhomogeneities of thermal density or magnetic field
in the surrounding medium.
Our analysis of the depolarization of 3C 449 is based on the
approach of Laing
et al. (2008).
It is still possible to observe ![]() rotation over a wide range of
polarization angle from a foreground Faraday screen with a small
gradient of RM across the beam. In this case, the wavelength
dependence
of the depolarization is expected to follow the Burn law (Burn 1966)
rotation over a wide range of
polarization angle from a foreground Faraday screen with a small
gradient of RM across the beam. In this case, the wavelength
dependence
of the depolarization is expected to follow the Burn law (Burn 1966)
where p(0) is the intrinsic value of the degree of polarization and
We made images of k at both standard
resolutions by weighted least-squares
fitting to the fractional polarization maps, using the FARADAY code by
M. Murgia. The same frequencies were used as
for the RM images: 8.385-1.365 GHz and
4.985-1.365 GHz at 1.25 and 5.5 arcsec resolution,
respectively.
By simulating the error distributions for p, we
established that the mean values of k were biased
significantly
at low signal-to-noise (cf. Laing et al. 2008), so only
data with ![]() at each frequency are included in the fits.
We estimate that any bias is negligible compared with the fitting
error.
We also derived profiles of k with the same sets of
boxes as for
the
at each frequency are included in the fits.
We estimate that any bias is negligible compared with the fitting
error.
We also derived profiles of k with the same sets of
boxes as for
the ![]() profiles
in Fig. 2.
profiles
in Fig. 2.
The 1.25 arcsec resolution k map
is shown in
Fig. 5a,
together with the profile of the k values
(Fig. 5c).
The fit to a ![]() law is very good everywhere: examples of
fits at selected pixels in the jets and lobes are shown in in
Fig. 6.
The symmetry observed in the
law is very good everywhere: examples of
fits at selected pixels in the jets and lobes are shown in in
Fig. 6.
The symmetry observed in the ![]() profiles is
also seen in the 1.25 arcsec k image
(Fig. 5):
the mean values of kare
profiles is
also seen in the 1.25 arcsec k image
(Fig. 5):
the mean values of kare ![]() 50 rad2 m-4
for both lobes, 107 and 82 rad2 m-4
for the northern and southern jet, respectively. The region with the
highest depolarization is in the northern jet,
very close to the core and along the west side.
The integrated value of k at this resolution is
50 rad2 m-4
for both lobes, 107 and 82 rad2 m-4
for the northern and southern jet, respectively. The region with the
highest depolarization is in the northern jet,
very close to the core and along the west side.
The integrated value of k at this resolution is ![]() 56 rad2 m-4,
corresponding to a mean depolarization
56 rad2 m-4,
corresponding to a mean depolarization ![]() .
.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13872f6.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13872-09/Timg81.png)
|
Figure 6:
Plots of degree of polarization, p (log scale)
against |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13872f7.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13872-09/Timg82.png)
|
Figure 7:
Plots of degree of polarization, p (log scale)
against |
| Open with DEXTER | |
The image and profile of k at 5.5-arcsec resolution
are shown in Figs. 5b
and d.
The fit to a ![]() law is in general good and examples are shown in in Fig. 6.
As mentioned earlier, the maximum scale of structure imaged accurately
in
total intensity at 5 GHz is
law is in general good and examples are shown in in Fig. 6.
As mentioned earlier, the maximum scale of structure imaged accurately
in
total intensity at 5 GHz is ![]() 300 arcsec (100 kpc) and there
are
likely to be significant systematic errors in the degree of
polarization on
larger scales. We therefore show the profile only for the inner
300 arcsec (100 kpc) and there
are
likely to be significant systematic errors in the degree of
polarization on
larger scales. We therefore show the profile only for the inner ![]() 50 kpc.
Over this range, the k profiles are quite
symmetrical, as at higher resolution.
Note also that the
small regions of very high k at the edge of the
northern and southern spurs in
the map shown in Fig. 5
are likely to be spurious.
50 kpc.
Over this range, the k profiles are quite
symmetrical, as at higher resolution.
Note also that the
small regions of very high k at the edge of the
northern and southern spurs in
the map shown in Fig. 5
are likely to be spurious.
The mean values of kare ![]() 184 rad2 m-4
and 178 rad2 m-4
for the northern and southern lobes, respectively; and
184 rad2 m-4
and 178 rad2 m-4
for the northern and southern lobes, respectively; and ![]() 238
and 174 rad2 m-4
in the northern and in the southern spurs.
The integrated value of k is
238
and 174 rad2 m-4
in the northern and in the southern spurs.
The integrated value of k is ![]() 194 rad2 m-4,
corresponding to a depolarization
194 rad2 m-4,
corresponding to a depolarization ![]() .
.
To summarize, we observe depolarization between 20 cm and 3 cm. Since we measure lower values of k at 1.25 arcsec than 5.5 arcsec, there is less depolarization at high resolution, as expected for beam depolarization. The highest depolarization is observed in a region of the northern jet, close to the radio core and associated with a steep RM gradient. Depolarization is significantly higher close to the nucleus, which is consistent with the higher path length through the group gas observed in X-rays. Aside from this global variation, we found no evidence for a detailed correlation of depolarization with source structure. Depolarization and RM data are therefore both consistent with a foreground Faraday screen. We show in Sect. 6.2 that the residual depolarization at 1.25-arcsec resolution can be produced by RM fluctuations on scales smaller than the beamwidth, but higher-resolution observations are needed to establish this conclusively.
6 Two dimensional analysis
6.1 General considerations
In order to interpret the fluctuations of the magnetic field
responsible for the
observed RM and depolarization of 3C 449, we first
discuss the statistics of the
RM fluctuations in two dimensions. We use the notation of
Laing et al. (2008),
in which ![]() is a vector in the spatial frequency
domain, corresponding to the position vector
is a vector in the spatial frequency
domain, corresponding to the position vector ![]() .
We take the
z-axis to be along the line-of-sight, so that the
vector
.
We take the
z-axis to be along the line-of-sight, so that the
vector ![]() is in the plane of the sky and
is in the plane of the sky and ![]() is the
corresponding spatial frequency vector.
Our goal is to estimate the RM power spectrum
is the
corresponding spatial frequency vector.
Our goal is to estimate the RM power spectrum
![]() ,
where
,
where ![]() is the power in
the area
is the power in
the area ![]() and in turn to derive the three-dimensional magnetic-field power
spectrum
and in turn to derive the three-dimensional magnetic-field power
spectrum ![]() ,
defined so that
,
defined so that ![]() is the power in a volume
is the power in a volume ![]() of
frequency space.
of
frequency space.
The relation between the magnetic field statistics and the observed RM distribution is in general quite complicated, depending on the fluctuations in the thermal gas density, the geometry of the source and the surrounding medium, and the effects of incomplete sampling. In order to derive the magnetic-field power spectrum, we make the following simplifying assumptions, as in Guidetti et al. (2008) and Laing et al. (2008).
- 1.
- The observed Faraday rotation is due entirely to a foreground ionized medium (in agreement with our results in Sects. 4 and 5);
- 2.
- the magnetic field is an isotropic, Gaussian random
variable, and can therefore be characterized by a power
spectrum
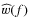 ,
which is a function only of the scalar frequency f;
,
which is a function only of the scalar frequency f;
- 3.
- the form of the magnetic field power spectrum is independent of position;
- 4.
- the magnetic field is distributed throughout the Faraday-rotating medium, whose density is a smooth, spherically symmetric function;
- 5.
- the amplitude of
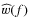 is spatially variable, but is a function only of the thermal electron
density.
is spatially variable, but is a function only of the thermal electron
density.
If the fluctuations are isotropic, the RM power
spectrum ![]() is the Hankel transform of the autocorrelation function
is the Hankel transform of the autocorrelation function ![]() ,
defined as
,
defined as
where
In an ideal case, it would be possible to derive the
RM power spectrum and
consequently that of the magnetic field directly from ![]() .
In
reality, the observations are affected first by the effects of
convolution with
the beam, which modify the spatial statistics of RM, and secondly, by
the
limited size and irregular shape of the sampling region for
3C 449, which results in a
complicated window function (Enßlin & Vogt 2003) and limits
the accuracy
with which the zero-level can be determined. In Sect. 4.2, we showed
that the Galactic contribution to the 3C 449 RM is
substantial and argued that a constant value
of -160.7 rad m-2 is
the best estimate for its value.
Fluctuations in the Galactic magnetic field on scales comparable with
the size of
the radio sources could be present; conversely, the local environment
of the
source might make a significant contribution to the mean RM. Both of
these
possibilities lead to difficulties in the use of the autocorrelation
function.
.
In
reality, the observations are affected first by the effects of
convolution with
the beam, which modify the spatial statistics of RM, and secondly, by
the
limited size and irregular shape of the sampling region for
3C 449, which results in a
complicated window function (Enßlin & Vogt 2003) and limits
the accuracy
with which the zero-level can be determined. In Sect. 4.2, we showed
that the Galactic contribution to the 3C 449 RM is
substantial and argued that a constant value
of -160.7 rad m-2 is
the best estimate for its value.
Fluctuations in the Galactic magnetic field on scales comparable with
the size of
the radio sources could be present; conversely, the local environment
of the
source might make a significant contribution to the mean RM. Both of
these
possibilities lead to difficulties in the use of the autocorrelation
function.
Laing et al. (2008) demonstrated a procedure that takes into account the convolution effects and minimises the effects of uncertainties in the zero-level. In particular, they showed that
- 1.
- in the short-wavelength limit (meaning that changes in Faraday rotation across the beam are adequately represented as a linear gradient), the measured RM distribution is closely approximated by the convolution of the true RM distribution with the observing beam;
- 2.
- the structure function is a powerful and reliable statistical tool to quantify the two dimensional fluctuations of RM, given that it is independent of the zero level and structure on scales larger than the area under investigation.
(Simonetti et al. 1984; Minter & Spangler 1996). It is related to the autocorrelation function
Laing et al. (2008) also derived the effects of convolution with the observing beam on the observed structure function. For the special case of a power-law power spectrum (their Eq. (B2)), they showed that the observed structure function after convolution can be heavily modified even at separations up to a few times the FWHM of the observing beam. This effect must be taken into account when comparing observed and predicted structure functions. Laing et al. (2008) and Guidetti et al. (2008) also showed that numerical simulations of depolarization provide complementary information on RM fluctuations on scales smaller than the beam.
Following the approach of Laing et al. (2008), we
initially used the RM structure
function to determine the form of ![]() (Sect. 6.2),
while for its normalization (determined by global variations of density
and
magnetic field strength), we made use of three-dimensional simulations
(Sect. 7).
(Sect. 6.2),
while for its normalization (determined by global variations of density
and
magnetic field strength), we made use of three-dimensional simulations
(Sect. 7).
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{13872f8.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13872-09/Timg102.png)
|
Figure 8: a)- f) Plots of the RM structure functions for the sub-regions showed in Fig. 2. The horizontal bars represent the bin widths and the crosses the centroids for data included in the bins. The red lines are the predictions for the CPL power spectra described in the text, including the effects of the convolving beam. The vertical error bars are the rms variations for the structure functions derived using a CPL power spectrum with the quoted value of q on the observed grid of points for each sub-region. g)- l) as a)- f), but using a BPL power spectra with fixed slopes and break frequency, but variable normalization. |
| Open with DEXTER | |
6.2 Structure functions
We calculated the structure function for discrete regions of
3C 449, over which
we expected the spatial variations of thermal gas density, rms magnetic
field
strength and path length to be reasonably small. For each of these
regions, we
first made unweighted fits of model structure functions derived from
power
spectra with simple, parameterized functional forms, accounting for
convolution
with the observing beam. We then generated multiple realizations of a
Gaussian,
isotropic, random RM field, with the best-fitting power
spectrum on the
observed grids, again taking into account the effects of the convolving
beam. Finally, we made a weighted fit using the dispersion of the
synthetic
structure functions as estimates of the statistical errors for the observed
structure functions, which are impossible to quantify analytically
(Laing et al. 2008).
These errors, which result from incomplete
sampling, are much larger than those due to noise, but depend only
weakly on the
precise form of the underlying power spectrum. Our measure of the
goodness of fit
is ![]() ,
summed over a range of separations from
,
summed over a range of separations from ![]() to roughly
half of the size of the region: there is no information in the
structure
function for scales smaller than the beam, and the upper limit is set
by
sampling. The errors are, of course, much higher at the large spatial
scales,
which are less well sampled. Note, however, that estimates of the
structure
function from neighbouring bins are not statistically independent, so
it is not
straightforward to define the effective number of degrees of freedom.
to roughly
half of the size of the region: there is no information in the
structure
function for scales smaller than the beam, and the upper limit is set
by
sampling. The errors are, of course, much higher at the large spatial
scales,
which are less well sampled. Note, however, that estimates of the
structure
function from neighbouring bins are not statistically independent, so
it is not
straightforward to define the effective number of degrees of freedom.
We selected six regions for the structure-function analysis, as shown in Fig. 2. These are symmetrically placed about the nucleus, consistent with the orientation of the radio jets close to the plane of the sky. For the north and south jets, we derived the structure functions only at 1.25-arcsec resolution, as the low-resolution RM image shows no additional structure and has poorer sampling. For the north and south lobes, we computed the structure functions at both resolutions over identical areas and compared them. The agreement is very good, and the low-resolution RM images do not sample significantly larger spatial scales, so we show only the 1.25-arcsec results. Finally, we used the 5.5-arcsec RM images to compute the structure functions for the north and south spurs, which are not detected at the higher resolution.
The structure function has a positive bias given by 2
![]() ,
where
,
where ![]() is the uncorrelated random noise in the RM image
(Simonetti et al. 1984).
The mean noise of the 1.25 and 5.5-arcsec RM maps is
<1 rad m2 and is
essentially uncorrelated on scales larger than the
beam. For each region we therefore subtracted 2
is the uncorrelated random noise in the RM image
(Simonetti et al. 1984).
The mean noise of the 1.25 and 5.5-arcsec RM maps is
<1 rad m2 and is
essentially uncorrelated on scales larger than the
beam. For each region we therefore subtracted 2
![]() from the
structure functions, although this correction is always small. The
noise-corrected structure functions are shown in Fig. 8.
from the
structure functions, although this correction is always small. The
noise-corrected structure functions are shown in Fig. 8.
The individual observed structure functions have approximately
power-law
forms. Given that the structure function for a power-law power spectrum
with no
frequency limits is itself a power law (Minter & Spangler 1996; Laing
et al. 2008),
we first tried to fit the observed data with a RM power
spectrum of the
form
over an infinite frequency range. This last assumption allows us to use the analytical solution of the structure function, including convolution (Laing et al. 2008), and therefore to avoid numerical integration.
The fits were quite good, but systematically gave slightly too
much power on
small spatial scales and over-predicted the depolarization. We
therefore fit a cut-off power law (CPL) power
spectrum
Initially, we consider values of
In order to constrain RM structure on spatial scales below the
beamwidth, we
estimated the depolarization expected from the best power spectrum for
each of
the regions with 1.25-arcsec RM images, following the approach
of Laing et al. (2008).
To do this, we made multiple realizations of RM images on
an 81922grid with fine spatial
sampling. We then derived the Q and U images
at our
observing frequencies, convolved to the appropriate resolution and
compared the
predicted and observed mean degrees of polarization. These values are
given in
Table 4.
The uncertainties in the expected ![]() in Table 4
represent statistical errors determined from multiple realizations of
RM images with the same set of power spectrum parameters.
The predicted and observed values are in excellent agreement.
A constant value
of
in Table 4
represent statistical errors determined from multiple realizations of
RM images with the same set of power spectrum parameters.
The predicted and observed values are in excellent agreement.
A constant value
of ![]() arcsec-1
predicts very similar values, also listed
in Table 4.
We have not compared the depolarization data at
5.5-arcsec resolution in the spurs because of limited coverage of large
spatial
scales in the I images (Sect. 3), which is likely to
introduce
systematic errors at 4.6 and 5.0 GHz.
arcsec-1
predicts very similar values, also listed
in Table 4.
We have not compared the depolarization data at
5.5-arcsec resolution in the spurs because of limited coverage of large
spatial
scales in the I images (Sect. 3), which is likely to
introduce
systematic errors at 4.6 and 5.0 GHz.
We performed a joint fit of the CPL power spectra, minimizing
the ![]() summed over all six
sub-regions, giving equal weight to each and allowing the
normalizations to vary
independently. In this case the free parameters of the fit are
the six normalizations (one for each sub-region), the slope, and the
maximum spatial frequency.
The joint best-fitting single power-law power spectrum has q
= 2.68.
summed over all six
sub-regions, giving equal weight to each and allowing the
normalizations to vary
independently. In this case the free parameters of the fit are
the six normalizations (one for each sub-region), the slope, and the
maximum spatial frequency.
The joint best-fitting single power-law power spectrum has q
= 2.68.
Table 2: CPL power spectrum parameters for the six individual sub-regions of 3C 449.
A single power law slope does not give a good fit to all of the regions simultaneously, however. It is clear from Fig. 8 and Table 2 that there is a flattening in the slope of the observed structure functions on the largest scales (which are sampled primarily by the spurs). In order to fit all of the data accurately with a single functional form for the power spectrum, we adopt a broken power law form (BPL) for the RM power spectrum:
We performed a BPL joint fit in the same way as for the CPL power
spectra. In this case the free parameters of the fit are
the six normalizations, D0,
one for each sub-region, the high and low-frequency slopes, ![]() and
and ![]() ,
and the break and maximum spatial frequencies
,
and the break and maximum spatial frequencies ![]() and
and ![]() .
We found best fitting parameters of
.
We found best fitting parameters of ![]() ,
,
![]() ,
,
![]() .
As noted earlier, we
also fixed
.
As noted earlier, we
also fixed ![]() arcsec-1
to ensure consistency with the
observed depolarizations at 1.25-arcsec resolution.
The corresponding structure functions are plotted in Figs. 8g-l
and the normalizations for the individual regions are given in
Table 4.
As for the CPL fits, the errors bars are derived from the rms scatter
of the
structure functions of multiple convolved RM realizations.
arcsec-1
to ensure consistency with the
observed depolarizations at 1.25-arcsec resolution.
The corresponding structure functions are plotted in Figs. 8g-l
and the normalizations for the individual regions are given in
Table 4.
As for the CPL fits, the errors bars are derived from the rms scatter
of the
structure functions of multiple convolved RM realizations.
Table 3: Best-fitting parameters for the joint CPL and BPL fits to all six sub-regions of 3C 449.
Table 4: Normalizations and expected depolarization for the individual CPL, joint CPL and joint BPL fit parameters at 1.25 arcsec.
It is evident from Fig. 8
that the structure functions corresponding to the BPL power spectrum,
which gives less power
on large spatial scales, agree much better with the data.
The joint BPL fit has a ![]() of 17.7, compared with 33.5 for the joint CPL fit (the former
has only
two extra parameters), which confirms this result.
of 17.7, compared with 33.5 for the joint CPL fit (the former
has only
two extra parameters), which confirms this result.
We have so far ignored the effects of any outer scale of the
magnetic-field
fluctuations. This is justified because the structure functions for the
spurs continue to rise at the largest observed separations, indicating
that the
outer scale must be ![]() 10 arcsec
(
10 arcsec
(![]() 30 kpc).
The model structure functions fit to the
observations assume that the outer scale is infinite and the
realizations are
generated on sufficiently large grids in Fourier space that the effects
of the
implicit outer scale are negligible over the range of scales we
sampled. We use
structure-function data for the entire source to determine an
approximate value
for the outer scale in Sect. 7.3.
30 kpc).
The model structure functions fit to the
observations assume that the outer scale is infinite and the
realizations are
generated on sufficiently large grids in Fourier space that the effects
of the
implicit outer scale are negligible over the range of scales we
sampled. We use
structure-function data for the entire source to determine an
approximate value
for the outer scale in Sect. 7.3.
We now adopt the BPL power spectrum with these parameters and investigate the spatial variations of the RM fluctuation amplitude using three-dimensional simulations.
7 Three-dimensional analysis
7.1 Models
We used the software package FARADAY (Murgia et al. 2004) to compare
the
observed RM with simulated images derived from
three-dimensional multi-scale
magnetic-field models. Given a field model and the density distribution
of the
thermal gas, FARADAY calculates an RM image by integrating
Eq. (3)
numerically. As in Sect. 6,
we modelled the fluctuations of RM on the
assumption that the magnetic field responsible for the foreground
rotation is an
isotropic, Gaussian random variable and therefore characterized
entirely by its
power spectrum. Each point in a cube in Fourier space was first
assigned components of the magnetic vector potential. The amplitudes
were
selected from a Rayleigh distribution of unit variance, and the phases
were random
in ![]() .
The amplitudes were then multiplied by the square root of the
power spectrum of the vector potential, which is simply related to that
of the
magnetic field. The corresponding components of the magnetic field
along the
line-of-sight were then calculated and transformed to real space. This
procedure
ensured that the magnetic field was divergence-free. The field
components in real
space were then multiplied by the model density distribution and
integrated along
the line of sight to give a synthetic RM image at the full
resolution of the
simulation, which was then convolved to the observing resolution.
.
The amplitudes were then multiplied by the square root of the
power spectrum of the vector potential, which is simply related to that
of the
magnetic field. The corresponding components of the magnetic field
along the
line-of-sight were then calculated and transformed to real space. This
procedure
ensured that the magnetic field was divergence-free. The field
components in real
space were then multiplied by the model density distribution and
integrated along
the line of sight to give a synthetic RM image at the full
resolution of the
simulation, which was then convolved to the observing resolution.
For 3C 449, we assumed that the source is in a plane
perpendicular to the line-
of-sight, which passes through the group centre and simulated the field
and
density structure using a 20483 cube with a
real-space pixel size of
0.1 kpc. We used the best-fitting BPL power spectrum found in
Sect. 6.2,
but with a spatially-variable normalization, as
described below (Sect. 7.2),
and a low-frequency cut-off ![]() ,
corresponding to a maximum scale of the magnetic field
fluctuations
,
corresponding to a maximum scale of the magnetic field
fluctuations![]() ,
, ![]() (=
(=
![]() ). The power spectrum of
Eq. (9)
was then set to 0 for
). The power spectrum of
Eq. (9)
was then set to 0 for ![]() .
We fixed the minimum scale of the fluctuations
.
We fixed the minimum scale of the fluctuations ![]() kpc.
This is equivalent to the value
kpc.
This is equivalent to the value ![]() arcsec-1
found in Sect. 6.2
and also consistent with
the requirement that the minimum scale can be no larger than twice the
pixel
size for adequate sampling.
arcsec-1
found in Sect. 6.2
and also consistent with
the requirement that the minimum scale can be no larger than twice the
pixel
size for adequate sampling.
We made multiple synthetic RM images at resolutions
of 1.25 and 5.5 arcsec over
the fields of view of the observations for each combination of
parameters. In
order to estimate the spatial variation of the magnetic-field strength,
we first
made a set of simulations with a large, fixed value of ![]() and
compared the predicted and observed profiles of
and
compared the predicted and observed profiles of ![]() (Sect. 7.2). We then
fixed the radial variation of the field at its
best-fitting form and estimated the value of
(Sect. 7.2). We then
fixed the radial variation of the field at its
best-fitting form and estimated the value of ![]() with a
structure-function analysis for the whole source (Sect. 7.3).
with a
structure-function analysis for the whole source (Sect. 7.3).
Table 5: Summary of magnetic field power spectrum and density scaling parameters.
7.2 Magnetic field strength and radial profile
In order to estimate the radial variation of field strength, we first
fixed the
value of the outer scale to be ![]() kpc,
the longest
allowed by our simulation grid. Our approach was to make a large number
of
simulations for each combination of field strength and radial profile
and to
compare the predicted and observed values of
kpc,
the longest
allowed by our simulation grid. Our approach was to make a large number
of
simulations for each combination of field strength and radial profile
and to
compare the predicted and observed values of ![]() evaluated
over the boxes used
in Sect. 4.1
(Fig. 2).
We used
evaluated
over the boxes used
in Sect. 4.1
(Fig. 2).
We used ![]() summed
over the boxes as a measure of the goodness of fit. This
procedure is independent of the precise value of the outer scale,
provided that
it is much larger than the averaging boxes. We express our results in
terms of
summed
over the boxes as a measure of the goodness of fit. This
procedure is independent of the precise value of the outer scale,
provided that
it is much larger than the averaging boxes. We express our results in
terms of ![]() ,
which is the value of
,
which is the value of ![]() divided by the number of degrees of
freedom.
divided by the number of degrees of
freedom.
We initially tried a radial field-strength
variation of the form
as used by Guidetti et al. (2008) and Laing et al. (2008). Here, B0 is the rms magnetic field strength at the group centre and
We produced simulated RM images for each combination
of B0 and ![]() in the ranges
0.5-10
in the ranges
0.5-10 ![]() G
in steps of 0.1
G
in steps of 0.1 ![]() G
and 0-2 in steps of 0.01, respectively.
We then derived the synthetic
G
and 0-2 in steps of 0.01, respectively.
We then derived the synthetic
![]() profiles and, by comparing
them with
the observed one, calculated the unweighted
profiles and, by comparing
them with
the observed one, calculated the unweighted ![]() .
We repeated this procedure 35 times at each angular
resolution,
noting the (B0,
.
We repeated this procedure 35 times at each angular
resolution,
noting the (B0, ![]() )
pair that gave the lowest
)
pair that gave the lowest ![]() in each case.
These values are plotted in Fig. 9.
As in earlier work (Murgia et al. 2004; Guidetti
et al. 2008;
Laing et al. 2008),
we found a degeneracy between the values of B0
and
in each case.
These values are plotted in Fig. 9.
As in earlier work (Murgia et al. 2004; Guidetti
et al. 2008;
Laing et al. 2008),
we found a degeneracy between the values of B0
and
![]() in the sense
that the fitted values are positively correlated, but there
are clear minima in
in the sense
that the fitted values are positively correlated, but there
are clear minima in ![]() at both resolutions. We therefore adopted the mean values of B0
and
at both resolutions. We therefore adopted the mean values of B0
and ![]() ,
weighted by
,
weighted by ![]() ,
as the best overall
estimates. These are also plotted in Fig. 9
as blue crosses.
Although the central magnetic field strengths derived for the two
RM images are
consistent at the 1
,
as the best overall
estimates. These are also plotted in Fig. 9
as blue crosses.
Although the central magnetic field strengths derived for the two
RM images are
consistent at the 1![]() level (
level (
![]() G
and
G
and ![]() G
at 5.5 and 1.25-arcsec resolution, respectively), the
values of
G
at 5.5 and 1.25-arcsec resolution, respectively), the
values of ![]() are not. The best-fitting values are
are not. The best-fitting values are ![]() at 5.5 arcsec FWHM and
at 5.5 arcsec FWHM and ![]() at 1.25 arcsec FWHM.
at 1.25 arcsec FWHM.
We next produced 35 RM simulations at each angular
resolution by fixing B0 and ![]() at their
best values for that resolution. This allowed us to calculate weighted
at their
best values for that resolution. This allowed us to calculate weighted ![]() 's for the
's for the ![]() profiles,
evaluating the errors for
each box by summing in quadrature the rms due to sampling (determined
from the dispersion in
the realizations) and the fitting-error of the observations. These
values are listed in Table 6.
The observed and best-fitting model profiles at both angular
resolutions
are shown in Fig. 10.
profiles,
evaluating the errors for
each box by summing in quadrature the rms due to sampling (determined
from the dispersion in
the realizations) and the fitting-error of the observations. These
values are listed in Table 6.
The observed and best-fitting model profiles at both angular
resolutions
are shown in Fig. 10.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{13872f9.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13872-09/Timg159.png)
|
Figure 9:
a) and b) distributions
of the best-fitting values of B0
and |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{13872f10.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13872-09/Timg160.png)
|
Figure 10:
a) Observed and synthetic radial
profiles for rms Faraday |
| Open with DEXTER | |
The best-fitting model at 1.25-arcsec resolution,
which is characterized by a more physically reliable ![]() ,
gives a very bad
fit to the low resolution profile at almost all distances from the
core (Fig. 10a).
Conversely, the model determined at 5.5-arcsec resolution gives a very
poor fit to the sharp peak in
,
gives a very bad
fit to the low resolution profile at almost all distances from the
core (Fig. 10a).
Conversely, the model determined at 5.5-arcsec resolution gives a very
poor fit to the sharp peak in ![]() observed
within 20 kpc of the nucleus at 1.25-arcsec resolution, where
the radio and
X-ray data give the strongest constraints (Fig. 10b). We
also verified that no single intermediate value of
observed
within 20 kpc of the nucleus at 1.25-arcsec resolution, where
the radio and
X-ray data give the strongest constraints (Fig. 10b). We
also verified that no single intermediate value of ![]() gives an adequate
fit to the
gives an adequate
fit to the ![]() profiles at
all distances from the nucleus.
profiles at
all distances from the nucleus.
A better description of the observed ![]() profile is
provided by the empirical
function
profile is
provided by the empirical
function
where
We fixed ![]() and
and ![]() ,
consistent with
our initial results, in order to reproduce both the inner sharp peak
and the
outer flat decline of the
,
consistent with
our initial results, in order to reproduce both the inner sharp peak
and the
outer flat decline of the ![]() observed at
the two resolutions, keeping
observed at
the two resolutions, keeping ![]() as a free parameter. We made three sets of three-dimensional
simulations
for values of the outer scale
as a free parameter. We made three sets of three-dimensional
simulations
for values of the outer scale ![]() ,
65 and 20 kpc. Anticipating the result of
Sect. 7.3,
we plot the results
only for
,
65 and 20 kpc. Anticipating the result of
Sect. 7.3,
we plot the results
only for ![]() kpc,
but the derived
kpc,
but the derived ![]() profiles are
in any
case almost independent of the value of the outer scale in this range.
The new simulations
were made only at a resolution of 5.5 arcsec, since the larger
field of view at
this resolution is essential to define the change in slope of the
profile.
profiles are
in any
case almost independent of the value of the outer scale in this range.
The new simulations
were made only at a resolution of 5.5 arcsec, since the larger
field of view at
this resolution is essential to define the change in slope of the
profile.
In order to determine the best-fitting break radius, ![]() in
Eq. (11),
we produced 35 sets of synthetic RM images
for a grid of values
of B0 and
in
Eq. (11),
we produced 35 sets of synthetic RM images
for a grid of values
of B0 and ![]() for each outer scale, noting the pair of values which gave the minimum
unweighted
for each outer scale, noting the pair of values which gave the minimum
unweighted ![]() for the
for the ![]() profile for
each set of simulations. These
values are plotted in Fig. 11,
which shows that there is a degeneracy
between the break radius
profile for
each set of simulations. These
values are plotted in Fig. 11,
which shows that there is a degeneracy
between the break radius ![]() and B0. As with the similar
degeneracy
between B0 and
and B0. As with the similar
degeneracy
between B0 and ![]() noted earlier, there is a clear minimum in
noted earlier, there is a clear minimum in ![]() ,
and we therefore adopted the mean values of B0
and
,
and we therefore adopted the mean values of B0
and ![]() weighted by
weighted by
![]() as our best
estimates of the magnetic-field parameters.
as our best
estimates of the magnetic-field parameters.
We then made 35 simulations with the best-fitting values of B0
and
![]() for each
outer scale and evaluated the weighted
for each
outer scale and evaluated the weighted ![]() 's for the
resulting
's for the
resulting ![]() profiles.
All three values of
profiles.
All three values of ![]() we
investigated give reasonable fits to the observed
we
investigated give reasonable fits to the observed ![]() profile
along the whole
radio source. The fit for
profile
along the whole
radio source. The fit for ![]() kpc
is marginally better
than for the other two values (
kpc
is marginally better
than for the other two values (
![]() ),
consistent with the results of
Sect. 7.3
below. In
this case the central magnetic field strength is
),
consistent with the results of
Sect. 7.3
below. In
this case the central magnetic field strength is ![]()
![]() G and the
break radius is
G and the
break radius is ![]() kpc.
For the power spectrum with
kpc.
For the power spectrum with ![]() kpc
and these best-fitting parameters, we also produced three-dimensional
simulations at a resolution of 1.25 arcsec. Even though the
fitting procedure
is based only on the low-resolution data, this model also reproduces
the
1.25-arcsec profile very well (
kpc
and these best-fitting parameters, we also produced three-dimensional
simulations at a resolution of 1.25 arcsec. Even though the
fitting procedure
is based only on the low-resolution data, this model also reproduces
the
1.25-arcsec profile very well (
![]() ).
Combining the values of
).
Combining the values of
![]() for the two
resolutions, using the 1.25-arcsec profile close to the
core and the 5.5-profile at larger distances, we find
for the two
resolutions, using the 1.25-arcsec profile close to the
core and the 5.5-profile at larger distances, we find ![]() .
.
Figure 12
shows a comparison of the observed radial profiles
for rms Faraday ![]() and
and ![]() with
the synthetic ones
derived for this model. The synthetic
with
the synthetic ones
derived for this model. The synthetic ![]() profile
plotted in Fig. 12
is the mean over 35 simulations and may
be compared directly with the observations.
In contrast, the
profile
plotted in Fig. 12
is the mean over 35 simulations and may
be compared directly with the observations.
In contrast, the ![]() profile
is derived from a single example realization.
It is important to emphasize that the latter is one example
of a random process, and is not expected to fit the
observations; rather, we aim to compare the fluctuation
amplitude as a function of position.
profile
is derived from a single example realization.
It is important to emphasize that the latter is one example
of a random process, and is not expected to fit the
observations; rather, we aim to compare the fluctuation
amplitude as a function of position.
The values of B0
and ![]() for all
of the three-dimensional simulations, together with
for all
of the three-dimensional simulations, together with ![]() and
and ![]() for
the single and double power-law profiles, respectively, are summarized
in
Table 6.
for
the single and double power-law profiles, respectively, are summarized
in
Table 6.
Table 6: Results from the three-dimensional fits at both the angular resolutions of 1.25 and 5.5 arcsec.
![\begin{figure}
\includegraphics[width=8.5cm,clip]{13872f11.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13872-09/Timg175.png)
|
Figure 11:
Distribution of the best-fitting values of B0
and |
| Open with DEXTER | |
7.3 The outer scale of the magnetic-field fluctuations
The theoretical RM structure function for uniform field
strength, density and
path length and a power spectrum with a low-frequency cut-off should
asymptotically approach a constant value (
![]() for a large enough averaging
region) at separations
for a large enough averaging
region) at separations ![]()
![]() .
The observed RM structure function
of the whole source is heavily modified from this theoretical one by
the scaling
of the electron gas density and magnetic field at large separations,
which acts to suppress power on large spatial scales.
In Sect. 6
we therefore
limited the study of the structure function to sub-regions of
3C 449 where
uniformity of field strength, density and path length (and therefore of
the
power-spectrum amplitude) is a reasonable assumption, inevitably
limiting our
ability to constrain the power spectrum on the largest scales.
.
The observed RM structure function
of the whole source is heavily modified from this theoretical one by
the scaling
of the electron gas density and magnetic field at large separations,
which acts to suppress power on large spatial scales.
In Sect. 6
we therefore
limited the study of the structure function to sub-regions of
3C 449 where
uniformity of field strength, density and path length (and therefore of
the
power-spectrum amplitude) is a reasonable assumption, inevitably
limiting our
ability to constrain the power spectrum on the largest scales.
Now that we have an adequate model for the variation of ![]() with radius (Eq. (11)),
we can correct for it to derive what we call the pseudo-structure
function - that is the structure function for
a power-spectrum amplitude, which is constant over the source. This can
be
compared directly with the structure functions derived from the Hankel
transform
of the power spectrum. To evaluate the pseudo-structure function, we
divided the observed 5.5-arcsec RM image by the function
with radius (Eq. (11)),
we can correct for it to derive what we call the pseudo-structure
function - that is the structure function for
a power-spectrum amplitude, which is constant over the source. This can
be
compared directly with the structure functions derived from the Hankel
transform
of the power spectrum. To evaluate the pseudo-structure function, we
divided the observed 5.5-arcsec RM image by the function
(Enßlin & Vogt 2003), where the radial variations of
![\begin{figure}
\par\includegraphics[width=12cm,clip]{13872f12.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13872-09/Timg179.png)
|
Figure 12:
Comparison between observed and synthetic profiles of rms and mean
Faraday rotation at resolutions of 5.5 arcsec ( a)
and b)) and 1.25 arcsec (
c) and d)). The synthetic
profiles are derived from the best-fitting model with
|
| Open with DEXTER | |
The pseudo-structure function is shown in Fig. 14a together
with the predictions for the BPL power spectra with ![]() ,
65 and 20 kpc.
As expected, the normalization of the pseudo-structure function is
consistent
with that of the jets (Figs. 8a
and b).
,
65 and 20 kpc.
As expected, the normalization of the pseudo-structure function is
consistent
with that of the jets (Figs. 8a
and b).
The comparison between the synthetic and observed
pseudo-structure functions
indicates firstly that they agree very well at small separations,
independent of
the value of ![]() .
This confirms that the best BPL power
spectrum found from a combined fit to all six sub-regions is a very
good fit
over the entire source. Secondly, despite the poor sampling on very
large scales, the asymptotic values of the predicted structure
functions for the three values
of
.
This confirms that the best BPL power
spectrum found from a combined fit to all six sub-regions is a very
good fit
over the entire source. Secondly, despite the poor sampling on very
large scales, the asymptotic values of the predicted structure
functions for the three values
of ![]() are sufficiently different from each other that we can
determine an approximate outer scale. The model with
are sufficiently different from each other that we can
determine an approximate outer scale. The model with
![]() kpc
gives the best representation of the data. The fit
is within the estimated errors except for a marginal discrepancy at the
very
largest (and therefore poorly sampled) separations. That with
kpc
gives the best representation of the data. The fit
is within the estimated errors except for a marginal discrepancy at the
very
largest (and therefore poorly sampled) separations. That with ![]() kpc
is inconsistent with the observed
pseudo-structure function for any separation
kpc
is inconsistent with the observed
pseudo-structure function for any separation ![]() 20 arcsec (
20 arcsec (![]() 6 kpc) where
the sampling is still very good, and is firmly excluded. The model with
6 kpc) where
the sampling is still very good, and is firmly excluded. The model with
![]() kpc
has slightly, but significantly too much power on
large scales.
kpc
has slightly, but significantly too much power on
large scales.
We emphasize that our estimate of the outer scale of the
RM fluctuations is essentially independent of the functional
form assumed for the variation of field strength with radius in the
central region, which affects the structure function only for small
separations. Our results are almost identical if we fit the
field-strength variation with either the profile of Eq. (10) (with ![]() )
or that of Eq. (11).
)
or that of Eq. (11).
As for the structure functions of individual regions, the
pseudo-structure
function at large separations is clearly affected by poor sampling:
this
increases the errors, but does not produce any bias in the derived
values. At large radii, however, the integral in Eq. (12) becomes
small, so the noise on the RM image is amplified. This is a
potential source of
error, and we therefore checked our
results using numerical simulations.
We calculated the mean and rms structure functions for sets of
realizations of
RM images generated with the FARADAY code, as
in Sect. 7.1,
for different values of ![]() .
These structure functions are plotted in Figs. 14b and c.
.
These structure functions are plotted in Figs. 14b and c.
![\begin{figure}
\includegraphics[width=8.5cm,clip]{13872f13.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13872-09/Timg182.png)
|
Figure 13:
Comparison of observed and representative synthetic distribution of
Faraday RM at 1.25 arcsec and
5.5 arcsec.
The synthetic images have been produced for the best-fitting model with
|
| Open with DEXTER | |
The main difference between the model structure functions derived from simulations and the pseudo-structure functions described earlier is that the former show a steep decline in power on large scales in place of a plateau. This occurs because the smooth fall-off in density and magnetic field strength with distance from the nucleus suppresses the fluctuations in RM on large scales.
The results of the simulations confirm our analysis using the
pseudo-structure
function. The mean model structure function with ![]() kpc
again fits the data very well, except for a marginal discrepancy at the
largest
scales. In view of the deviations from spherical symmetry on large
scales evident in the X-ray emission surrounding 3C 449
(Fig. 1),
we do
not regard this as a significant effect.
kpc
again fits the data very well, except for a marginal discrepancy at the
largest
scales. In view of the deviations from spherical symmetry on large
scales evident in the X-ray emission surrounding 3C 449
(Fig. 1),
we do
not regard this as a significant effect.
In order to check that the best-fitting density and field
model also reproduces the data at small separations, we repeated the
analysis at 1.25-arcsec resolution. The observed pseudo-structure
function is shown in Fig. 14d, together with the predictions for the
BPL power spectrum with ![]() ,
65 and 20 kpc. The observed structure function is
compared with the mean from 35 simulations with
,
65 and 20 kpc. The observed structure function is
compared with the mean from 35 simulations with ![]() kpc
in Fig. 14e. In both cases, the agreement for
kpc
in Fig. 14e. In both cases, the agreement for ![]() kpc
is excellent.
kpc
is excellent.
In Fig. 13, example realizations of this model with the best-fitting field variation are shown for resolutions of 1.25 and 5.5 arcsec alongside the observed RM images.
![\begin{figure}
\par\includegraphics[width=14.5cm,clip]{13872f14.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13872-09/Timg184.png)
|
Figure 14:
a) Comparison of the observed
pseudo-structure function of the
5.5-arcsec RM image as described in the text (points) with the
predictions of the BPL model
(curves, derived using a Hankel transform). The predicted curves are
for
|
| Open with DEXTER | |
8 Summary and comparison with other sources
8.1 Summary
In this work we have studied the structure of the magnetic field associated with the ionized medium around the radio galaxy 3C 449. We have analysed images of linearly polarized emission with resolutions of 1.25 arcsec and 5.5 arcsec FHWM at seven frequencies between 1.365 and 8.385 GHz, and produced images of degree of polarization and rotation measure. The RM images at both the angular resolutions show patchy and random structures. In order to study the spatial statistics of the magnetic field, we used a structure-function analysis and performed two- and three-dimensional RM simulations. We can summarize the results as follows.
- 1.
- The absence of deviations from
 rotation over a wide range of
polarization position angle implies that a pure foreground Faraday
screen with no mixing of radio-emitting and thermal electrons is a good
approximation for 3C 449 (Sect. 4).
rotation over a wide range of
polarization position angle implies that a pure foreground Faraday
screen with no mixing of radio-emitting and thermal electrons is a good
approximation for 3C 449 (Sect. 4).
- 2.
- The dependence of the degree of polarization on wavelength is well fitted by a Burn law. This is also consistent with pure foreground rotation, with the residual depolarization observed at the higher resolution being due to unresolved RM fluctuations across the beam (Sect. 5). There is no evidence for a detailed correlation of radio-source structure with either RM or depolarization.
- 3.
- There is no obvious anisotropy in the RM distribution, consistent with our assumption that the magnetic field is an isotropic, Gaussian random variable.
- 4.
- Our best estimate for the Galactic contribution to the RM of 3C 449 is a constant value of -160.7 rad m-2 (Sect. 4.2).
- 5.
- The RM structure functions for six different regions of the source are consistent with the hypothesis that only the amplitude of the RM power spectrum varies across the source.
- 6.
- A broken power-law spectrum of the form given in
Eq. (9)
with
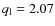 ,
, 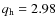 ,
,
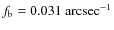 and
and 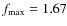 arcsec-1
(corresponding to a spatial scale
arcsec-1
(corresponding to a spatial scale 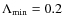 kpc)
is consistent with the observed structure functions and depolarizations
for all six regions. No single power law provides a good fit to all of
the structure functions.
kpc)
is consistent with the observed structure functions and depolarizations
for all six regions. No single power law provides a good fit to all of
the structure functions.
- 7.
- The high-frequency cut-off in the power spectrum is required to model the depolarization data.
- 8.
- The profiles of
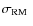 strongly
suggest that most of the fluctuating component of RM is associated with
the intra-group gas, whose core radius is comparable with the
characteristic scale of the profile (Sect. 4.1). The
symmetry of the profile is consistent with the idea that the radio
source axis is close to the plane of the sky.
strongly
suggest that most of the fluctuating component of RM is associated with
the intra-group gas, whose core radius is comparable with the
characteristic scale of the profile (Sect. 4.1). The
symmetry of the profile is consistent with the idea that the radio
source axis is close to the plane of the sky.
- 9.
- We therefore simulated the RM distributions expected for an isotropic, random magnetic field in the hot plasma surrounding 3C 449, assuming the density model derived by Croston et al. (2008).
- 10.
- These three-dimensional simulations show that the
dependence of magnetic field on density is best modelled by a broken
power-law function with
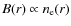 close to the nucleus and
close to the nucleus and 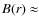 constant at larger distances.
constant at larger distances.
- 11.
- With this density model, our best estimate of the central
magnetic field strength is
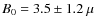 G.
G.
- 12.
- Assuming these variations of density and field strength
with radius, a structure-function analysis can be used to estimate the
outer scale
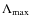 of the magnetic-field fluctuations. We find excellent agreement for
of the magnetic-field fluctuations. We find excellent agreement for 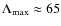 kpc
(
kpc
(
 arcsec-1).
arcsec-1).
8.2 Comparison with other sources
Our results are qualitatively similar to those of Laing et al.
(2008) on
3C 31. The maximum RM fluctuation amplitudes are
similar in the two sources, as
are their environments. For spherically-symmetric gas density models,
the
central magnetic fields are almost the same: ![]() G
for 3C 31
and
G
for 3C 31
and ![]() G
for 3C 449. Both results are consistent with the idea that the
RM fluctuation amplitude in galaxy groups and clusters scales
roughly linearly
with density, ranging from a few rad m-2
in the sparsest
environments (e.g. NGC 315; Laing et al. 2006), through
intermediate values
G
for 3C 449. Both results are consistent with the idea that the
RM fluctuation amplitude in galaxy groups and clusters scales
roughly linearly
with density, ranging from a few rad m-2
in the sparsest
environments (e.g. NGC 315; Laing et al. 2006), through
intermediate values ![]() 30-100 rad m-2
in rich groups such as 3C 31 and 3C 449 to
30-100 rad m-2
in rich groups such as 3C 31 and 3C 449 to ![]() 104 rad m-2
in the centres of clusters with cool cores.
104 rad m-2
in the centres of clusters with cool cores.
The RM distribution of 3C 31 is
asymmetrical, the
northern (approaching) side of the source showing a much lower
fluctuation
amplitude, consistent with the inclination of ![]()
![]() estimated by
Laing & Bridle (2002).
Detailed modelling of the RM profile led Laing et al.
(2008) to
suggest that there is a cavity in the X-ray gas, but this would have
to be significantly larger than the observed extent of the radio lobes
and is,
as yet, undetected in X-ray observations. A broken power-law scaling of
magnetic
field with density, similar to that found for 3C 449 in the
present paper,
would also improve the fit to the
estimated by
Laing & Bridle (2002).
Detailed modelling of the RM profile led Laing et al.
(2008) to
suggest that there is a cavity in the X-ray gas, but this would have
to be significantly larger than the observed extent of the radio lobes
and is,
as yet, undetected in X-ray observations. A broken power-law scaling of
magnetic
field with density, similar to that found for 3C 449 in the
present paper,
would also improve the fit to the ![]() profile for
3C 31; alternatively, the
effects of cavities around the inner lobes and spurs of 3C 449
might be
significant. Deeper X-ray observations of both sources are needed to
resolve
this issue. In neither case is the magnetic field dynamically
important: for
3C 449 we find that the ratio of the thermal and
magnetic-field pressures is
profile for
3C 31; alternatively, the
effects of cavities around the inner lobes and spurs of 3C 449
might be
significant. Deeper X-ray observations of both sources are needed to
resolve
this issue. In neither case is the magnetic field dynamically
important: for
3C 449 we find that the ratio of the thermal and
magnetic-field pressures is ![]() 30 at the nucleus
and
30 at the nucleus
and ![]() 400
at the core radius of the group gas,
400
at the core radius of the group gas, ![]() kpc.
kpc.
The magnetic-field power spectrum in both sources can be fit
by a broken
power-law form. The low-frequency slopes are 2.1
and 2.3 for 3C 449 and 3C 31
respectively. In both cases, the power spectrum steepens at higher
spatial
frequencies, but for 3C 31 a Kolmogorov index (11/3) provides
a good fit,
whereas we find that the depolarization data for 3C 449
require a cut-off below
a scale of 0.2 kpc and a high-frequency slope of 3.0.
The break scales are
![]() 5 kpc
for 3C 31 and
5 kpc
for 3C 31 and ![]() 11 kpc
for 3C 449. It is important to
note that the simple parametrized form of the power spectrum is not
unique, and
that a smoothly curved function would fit the data equally well.
11 kpc
for 3C 449. It is important to
note that the simple parametrized form of the power spectrum is not
unique, and
that a smoothly curved function would fit the data equally well.
The gas-density structure on large scales in the
3C 31 group is uncertain, so
Laing et al. (2008)
could only give a rough lower limit to the outer scale of
magnetic-field fluctuations, ![]() kpc.
For 3C 449, we
find
kpc.
For 3C 449, we
find ![]() kpc.
The projected distance between 3C 449 and
its nearest neighbour is
kpc.
The projected distance between 3C 449 and
its nearest neighbour is ![]() 33 kpc (Birkinshaw
et al. 1981),
similar to
the scale on which the jets first bend through large angles
(Fig. 1).
As
in 3C 31, it is plausible that the outer scale of
magnetic-field fluctuations
is set by interactions with companion galaxies in the group.
33 kpc (Birkinshaw
et al. 1981),
similar to
the scale on which the jets first bend through large angles
(Fig. 1).
As
in 3C 31, it is plausible that the outer scale of
magnetic-field fluctuations
is set by interactions with companion galaxies in the group.
This work is part of the ``Cybersar'' Project, which is managed by the COSMOLAB Regional Consortium with the financial support of the Italian Ministry of University and Research (MUR), in the context of the ``Piano Operativo Nazionale Ricerca Scientifica, Sviluppo Tecnologico, Alta Formazione (PON 2000-2006)''. We thank Luigina Feretti for providing the VLA data for 3C 449, Greg Taylor for the use of his rotation measure code and Marco Bondi for many helpful comments. We also acknowledge the use of HEALPIX package (http://healpix.jpl.nasa.gov) and the provision of the models of Dineen & Coles (2005) in HEALPIX format.
References
- Andernach, H., Feretti, L., Giovannini, G., et al. 1992, A&A, 93, 331 [Google Scholar]
- Balbus, S. A. 2000, ApJ, 534, 420 [NASA ADS] [CrossRef] [Google Scholar]
- Birkinshaw, M., Laing, R. A., & Peacock, J. A. 1981, MNRAS, 197, 253 [NASA ADS] [Google Scholar]
- Bogdanovic, T., Reynolds, C. S., Balbus, S. A., & Parrish, I. J. 2009, ApJ, 704, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Brunetti, G., Setti, G., Feretti, & Giovannini, L. G. 2001, MNRAS, 320, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Burn, B. J. 1966, MNRAS, 133, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Carilli, C. L., & Taylor, G. B. 2002, ARA&A, 40, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Cavaliere, A., & Fusco-Femiano, R. 1976, A&A, 49, 137 [NASA ADS] [Google Scholar]
- Clarke, T. E., Kronberg, P. P., & Böhringer, H. 2001, ApJ, 547, L111 [NASA ADS] [CrossRef] [Google Scholar]
- de Vaucouleurs, G., de Vaucouleurs, A., Corwin, Jr., et al. 1991, Third Reference Catalogue of Bright Galaxies (New York: Springer) [Google Scholar]
- Croston, J. H., Hardcastle, M. J., Birkinshaw, M., & Worrall, D. M. 2003, MNRAS, 346, 1041 [NASA ADS] [CrossRef] [Google Scholar]
- Croston, J. H., Hardcastle, M. J., Birkinshaw, M., & Laing, R. A. 2008, MNRAS, 386, 1709 [NASA ADS] [CrossRef] [Google Scholar]
- Dineen, P., & Coles, P. 2005, MNRAS, 362,403 [NASA ADS] [CrossRef] [Google Scholar]
- Dolag, K. 2006, Astron. Nachr., 327, 575 [Google Scholar]
- Dolag, K., Schindler, S., Govoni, F., & Feretti, L. 2001, A&A, 378, 777 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dursi, L. J., & Pfrommer, C. 2008, ApJ, 677, 993 [NASA ADS] [CrossRef] [Google Scholar]
- Eilek, J. A., & Owen, F. N. 2002, ApJ, 567, 202 [NASA ADS] [CrossRef] [Google Scholar]
- Enßlin, T. A., & Vogt, C. 2003, A&A, 401, 835 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fanaroff, B. L., & Riley, J. M. 1974, MNRAS, 167, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Feretti, L., Dallacasa, D., Giovannini, G., & Tagliani, A. 1995, A&A, 302, 680 [NASA ADS] [Google Scholar]
- Feretti, L., Perley, R., Giovannini, G., & Andernach, H. 1999a, A&A, 341, 29 [NASA ADS] [Google Scholar]
- Feretti, L., Dallacasa, D., Govoni, F., et al. 1999b, A&A, 344, 472 [NASA ADS] [Google Scholar]
- Govoni, F., & Feretti, L. 2004, Inter. J. Mod. Phys. D 13, 1549 [NASA ADS] [CrossRef] [Google Scholar]
- Govoni, F., Taylor, G. B., Dallacasa, D., Feretti, L., & Giovannini, G. 2001, A&A, 379, 807 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Govoni, F., Murgia, M., Feretti, L., et al. 2006, A&A, 460, 425 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guidetti, D., Murgia, M., Govoni, F., et al. 2008, A&A, 483, 699 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hardcastle, M. J., Worrall, D. M., & Birkinshaw, M. 1998, MNRAS, 296, 1098 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, K. T., Kronberg, P. P., Dewdney, P. E., & Landecker, T. L. 1990, ApJ, 355, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, K. T., Kronberg, P. P., & Tribble, C. 1991, ApJ, 379, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Laing, R. A. 1984, in Physics of Energy Transport in Extragalactic Radio Sources, ed. A. H. Bridle, & J. A. Eilek, NRAO Workshop, 9, 90 [Google Scholar]
- Laing, R. A., & Bridle, A. H. 2002, MNRAS, 336, 328 [NASA ADS] [CrossRef] [Google Scholar]
- Laing, R. A., Canvin, J. R., Cotton, W. D., & Bridle, A. H. 2006, MNRAS, 368, 48 [NASA ADS] [Google Scholar]
- Laing, R. A., Bridle, A. H., Parma, P., & Murgia, M. 2008, MNRAS, 391, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Lawler, J. M., & Dennison, B. 1982, ApJ, 252, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Minter, A. H., & Spangler, S. R. 1996, ApJ, 467, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Murgia, M., Govoni, F., Feretti, L., et al. 2004, A&A, 424, 429 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- O'Neill, S. M., De Young, D. S., & Jones, T. W. 2009, ApJ, 694, 1317 [NASA ADS] [CrossRef] [Google Scholar]
- Perley, R. A., Willis, A. G., & Scott, J. S. 1979, Nature, 281, 437 [NASA ADS] [CrossRef] [Google Scholar]
- Perley, R. A., Bridle, A. H., & Willis, A. G. 1984, ApJS, 54, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Pollack, L. K., Taylor, G. B., & Allen, S. W. 2005, MNRAS, 359, 1229 [NASA ADS] [CrossRef] [Google Scholar]
- Simard-Normandin, M., Kronberg, P. P., & Button, S. 1981, ApJS, 45, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Simonetti, J. H., Cordes, J. M., & Spangler, S. R. 1984, ApJ, 284, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, G. B., & Perley, R. A. 1993, ApJ, 416, 554 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, G. B., Fabian, A. C., & Allen, S. W. 2002, MNRAS, 334, 769 [NASA ADS] [CrossRef] [Google Scholar]
- Ulvestad, J. S., Perley, R. A., & Chandler, C. J. 2009, The Very Large Array observational status summary, http://www.vla.nrao.edu/astro/guides/vlas/current/vlas.html [Google Scholar]
- Vallée, J. P., MacLeod, M. J., & Broten, N. W. 1986, A&A, 156, 386 [NASA ADS] [Google Scholar]
- Vogt, C., & Enßlin, T. A. 2003, A&A, 412, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vogt, C., & Enßlin, T. A. 2005, A&A, 434, 67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wardle, J. F. C., & Kronberg, P. P. 1974, ApJ, 194, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Zwicky, F., & Kowal, C. T. 1968, Catalogue of Galaxies and of Clusters of Galaxies, California Institute of Technology, Pasadena, 6 [Google Scholar]
Footnotes
- ...=11/3
![[*]](/icons/foot_motif.png)
- q=11/3is the slope of the three-dimensional power spectrum for Kolmogorov turbulence.
- ... VLA
![[*]](/icons/foot_motif.png)
- The very large array is a facility of the National Science Foundation, operated under cooperative agreement by Associated Universities, Inc.
- ...
fluctuations
![[*]](/icons/foot_motif.png)
- Here we refer to the scale length
 as a complete
wavelength, i.e.
as a complete
wavelength, i.e.
 .
This differs by a factor of 2 from the
definition in Guidetti et al. (2008), where
.
This differs by a factor of 2 from the
definition in Guidetti et al. (2008), where  is the reversal scale of the
magnetic field, so
is the reversal scale of the
magnetic field, so
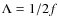 .
.
All Tables
Table 1: Parameters of the total intensity and polarization images.
Table 2: CPL power spectrum parameters for the six individual sub-regions of 3C 449.
Table 3: Best-fitting parameters for the joint CPL and BPL fits to all six sub-regions of 3C 449.
Table 4: Normalizations and expected depolarization for the individual CPL, joint CPL and joint BPL fit parameters at 1.25 arcsec.
Table 5: Summary of magnetic field power spectrum and density scaling parameters.
Table 6: Results from the three-dimensional fits at both the angular resolutions of 1.25 and 5.5 arcsec.
All Figures
![\begin{figure}
\par\includegraphics[width=12cm,clip]{13872f1.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13872-09/Timg26.png)
|
Figure 1:
Radio contours of 3C 449 at 1.365 GHz superposed on
the XMM-Newton X-ray image (courtesy of J. Croston,
Croston et al. 2003).
The radio contours start at 3
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{13872f2.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13872-09/Timg54.png)
|
Figure 2:
a) Image of the rotation measure of
3C 449 at a resolution of 1.25 arcsec FWHM,
computed at the seven
frequencies between 1.365 and 8.385 GHz.
b) Image of the rotation measure of
3C 449 at a resolution of 5.5 arcsec FWHM,
computed at the six frequencies between 1.365
and 4.985 GHz.
In both of the RM images, the sub-regions used for the
two-dimensional analysis of Sect. 6 are labelled.
c) and d) profiles
of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13872f3.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13872-09/Timg65.png)
|
Figure 3:
Plots of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13872f4.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13872-09/Timg69.png)
|
Figure 4: Profile of RM averaged over boxes of length 20 kpc along the radio axis for the 5.5 arcsec image. The horizontal bars represent the bin width. The vertical bars are the errors on the mean calculated from the dispersion in the boxes, the contribution from the fitting error is negligible and is not taken into account. Positive distances are in the direction of the north jet. The black vertical dashed line indicates the position of the nucleus; the green dashed line shows our adopted mean value for the Galactic RM. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{13872f5.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13872-09/Timg73.png)
|
Figure 5:
a) Image of the Burn law k
in rad2 m-4computed
from a fit to the relation |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13872f6.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13872-09/Timg81.png)
|
Figure 6:
Plots of degree of polarization, p (log scale)
against |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13872f7.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13872-09/Timg82.png)
|
Figure 7:
Plots of degree of polarization, p (log scale)
against |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{13872f8.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13872-09/Timg102.png)
|
Figure 8: a)- f) Plots of the RM structure functions for the sub-regions showed in Fig. 2. The horizontal bars represent the bin widths and the crosses the centroids for data included in the bins. The red lines are the predictions for the CPL power spectra described in the text, including the effects of the convolving beam. The vertical error bars are the rms variations for the structure functions derived using a CPL power spectrum with the quoted value of q on the observed grid of points for each sub-region. g)- l) as a)- f), but using a BPL power spectra with fixed slopes and break frequency, but variable normalization. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{13872f9.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13872-09/Timg159.png)
|
Figure 9:
a) and b) distributions
of the best-fitting values of B0
and |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{13872f10.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13872-09/Timg160.png)
|
Figure 10:
a) Observed and synthetic radial
profiles for rms Faraday |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[width=8.5cm,clip]{13872f11.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13872-09/Timg175.png)
|
Figure 11:
Distribution of the best-fitting values of B0
and |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{13872f12.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13872-09/Timg179.png)
|
Figure 12:
Comparison between observed and synthetic profiles of rms and mean
Faraday rotation at resolutions of 5.5 arcsec ( a)
and b)) and 1.25 arcsec (
c) and d)). The synthetic
profiles are derived from the best-fitting model with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[width=8.5cm,clip]{13872f13.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13872-09/Timg182.png)
|
Figure 13:
Comparison of observed and representative synthetic distribution of
Faraday RM at 1.25 arcsec and
5.5 arcsec.
The synthetic images have been produced for the best-fitting model with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14.5cm,clip]{13872f14.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13872-09/Timg184.png)
|
Figure 14:
a) Comparison of the observed
pseudo-structure function of the
5.5-arcsec RM image as described in the text (points) with the
predictions of the BPL model
(curves, derived using a Hankel transform). The predicted curves are
for
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



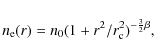
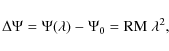
![\begin{displaymath}
{\rm RM_{~[rad/m^2]}}=812\int_{0}^{L_{\rm [kpc]}}n_{\rm e~[cm^{-3}]}B_{\parallel~[\mu G]}{\rm d}l.
\end{displaymath}](/articles/aa/full_html/2010/06/aa13872-09/img51.png)
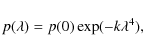
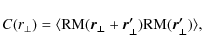
![\begin{displaymath}S(r_\perp)=\rm {\langle[RM({\vec r}_\perp + {\vec r}_\perp^\prime)-RM({\vec r}_\perp^\prime)]^2\rangle}
\end{displaymath}](/articles/aa/full_html/2010/06/aa13872-09/img100.png)
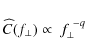
![\begin{displaymath}
\langle B^2(r)\rangle^{1/2} = B_{0} \left[\frac{n_{\rm e}(r)}{n_0}\right]^{~\eta}
\end{displaymath}](/articles/aa/full_html/2010/06/aa13872-09/img149.png)
![$\displaystyle B_{0}\left[\frac{n_{\rm e}(r)}{n_0}\right]^{~\eta_{\rm int}} ~~~~~~~
r\leq{r_{\rm m}}$](/articles/aa/full_html/2010/06/aa13872-09/img165.png)
![$\displaystyle B_{0} \left[\frac{n_{\rm e}(r)}{n_0}\right]^{~\eta_{\rm out}} ~~~~~~
r>r_{\rm m} ,$](/articles/aa/full_html/2010/06/aa13872-09/img166.png)
![\begin{displaymath}
\left [\int_{0}^{L}n_{\rm e}(r)^2B(r)^2{\rm d}l\right ]^{1/2}
\end{displaymath}](/articles/aa/full_html/2010/06/aa13872-09/img178.png)