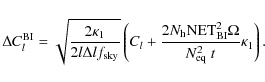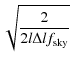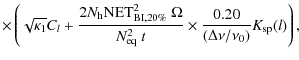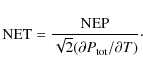| Issue |
A&A
Volume 514, May 2010
|
|
|---|---|---|
| Article Number | A37 | |
| Number of page(s) | 13 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/200913446 | |
| Published online | 07 May 2010 | |
Bandwidth in bolometric interferometry
R. Charlassier1 - E. F. Bunn2 - J.-Ch. Hamilton1 - J. Kaplan1 - S. Malu3
1 - APC, Université Denis Diderot-Paris 7, CNRS/IN2P3, CEA, Observatoire de Paris, 10 rue A. Domon and L. Duquet, Paris, France
2 - Physics Department, University of Richmond, Richmond, VA 23173, USA
3 - Inter-University Centre for Astronomy and Astrophysics (IUCAA), Pune 411 007, India
Received 9 October 2009 / Accepted 13 January 2010
Abstract
Context. Bolometric interferometry is a promising new
technology with potential applications to the detection of B-mode
polarization fluctuations of the cosmic microwave background (CMB). A
bolometric interferometer will have to take advantage of the wide
spectral detection band of its bolometers to be competitive with
imaging experiments. A crucial concern is that interferometers are
assumed to be significantly affected by a spoiling effect known as
bandwidth smearing.
Aims. We investigate how the bandwidth modifies the work
principle of a bolometric interferometer and affects its sensitivity to
the CMB angular power spectra.
Methods. We obtain analytical expressions for the broadband
visibilities measured by broadband heterodyne and bolometric
interferometers. We investigate how the visibilities must be
reconstructed in a broadband bolometric interferometer and show that
this critically depends on hardware properties of the modulation phase
shifters. If the phase shifters produce shifts that are constant with
respect to frequency, the instrument works like its monochromatic
version (the modulation matrix is not modified), while if they vary
(linearly or otherwise) with respect to frequency, one has to perform a
special reconstruction scheme, which allows the visibilities to be
reconstructed in frequency subbands. Using an angular power spectrum
estimator that accounts for the bandwidth, we finally calculate the
sensitivity of a broadband bolometric interferometer. A numerical
simulation is performed that confirms the analytical results.
Results. We conclude that (i) broadband bolometric
interferometers allow broadband visibilities to be reconstructed
regardless of the type of phase shifters used and (ii) for dedicated
B-mode bolometric interferometers, the sensitivity loss caused by
bandwidth smearing is quite acceptable, even for wideband instruments
(a factor of 2 loss for a typical 20% bandwidth experiment).
Key words: instrumentation: interferometers - polarization - cosmic microwave background - submillimeter: diffuse background - cosmology: observations
1 Introduction
The detection of B-mode polarization anisotropies in the cosmic microwave background (CMB) is one of the most exciting challenges of modern cosmology. The weakness of the expected signal requires the development of highly sensitive experiments with an exquisite control of systematic errors. Most experiments or projects dedicated to this quest are based on well-known direct imaging technology. An appealing alternative called bolometric interferometry has been proposed (Tucker et al. 2003). This technology combines the advantages of interferometry in handling systematic effects and those of bolometric detectors in enhancing sensitivity. The two teams that accepted the challenge (Charlassier & the BRAIN coll. 2008; Timbie et al. 2006) have combined their efforts to form the QUBIC collaboration (Kaplan & the QUBIC coll. 2009).
In (Charlassier et al. 2009), hereafter (C09), we introduced a simple formalism for the general design of a bolometric interferometer operating at a monochromatic frequency and showed that its phase shifting scheme must respect a property which we called ``coherent summation of equivalent baselines''. This scheme was optimized further in (Hyland et al. 2009). In (Hamilton et al. 2008), hereafter (H08), we calculated the sensitivity of a bolometric interferometer and showed that this technology can be competitive with imaging experiments and heterodyne interferometers for the measurement of CMB B-mode. For the sake of simplicity, we did not deal with the question of bandwidth in (C09) and (H08).
We know that a dedicated B-mode bolometric interferometer will have to use the wide spectral detection band of its bolometers to be competitive with imaging experiments. On the other hand, the bandwidth is often considered as a crucial issue in radio-interferometry; if the raw sensitivity of radio interferometer detectors increases as the square root of the bandwidth, there is a secondary effect, well known as bandwidth smearing, which can largely degrade the global sensitivity. When the signals originating in a point source interfere after being collected by two broadband receivers, the resulting fringe pattern is smeared by an envelope whose amplitude depends on the bandwidth, consequently leading to a degradation in the signal-to-noise ratio - see for instance (Thompson et al. 2001). We later see that these two main characteristics remain in bolometric interferometry: the bolometers' sensitivity also increases as the square root of the bandwidth, and a bandwidth smearing of the observables, the visibilities, degrades the global sensitivity of the instrument (however, because the observation of CMB angular correlations requires a poorer spatial resolution than the observation of point sources to which classical radio-interferometers are mostly dedicated, this smearing will lead to a less critical sensitivity loss). But we also see that an additional kind of bandwidth issue occurs, because in bolometric interferometry, visibilities are not measured directly but by solving a linear problem.
We investigate how the visibilities are smeared in heterodyne and bolometric interferometers with wide spectral bands and large primary beams in Sect. 2. We investigate how the work principle of bolometric interferometry is affected by bandwidth in Sect. 3. We show in particular that the visibilities can be reconstructed exactly as in the monochromatic case detailed in (C09) if the modulation phase shifts are constant with respect to frequency, while one has to perform the special reconstruction scheme described in Sect. 4 when the modulation phase shifts vary with respect to frequency. In Sect. 5, we introduce an angular power spectrum estimator that accounts for the bandwidth and estimate how the bandwidth smearing results in a degradation of the sensitivity for B-mode experiments. A numerical simulation that confirms our analytical results is presented in Sect. 6.
2 Visibilities measured by generic interferometers with wide spectral bands and large primary beams
2.1 Monochromatic visibilities
The observables measured by a monochomatic interferometer working at a
frequency ![]() and looking at a radiation field of spectral power
and looking at a radiation field of spectral power
![]() ,
in units of [
,
in units of [
![]() ],
are called the visibilities. A monochromatic visibility is
defined for one baseline
],
are called the visibilities. A monochromatic visibility is
defined for one baseline
![]() ,
which is the vector separation
between two horns in units of the electromagnetic wavelength of the
radiation. Its expression is given by
,
which is the vector separation
between two horns in units of the electromagnetic wavelength of the
radiation. Its expression is given by
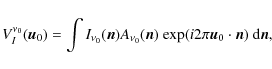
|
(1) |
where
2.2 Broadband visibilities for a generic interferometer
We consider now an interferometer that is sensitive to a finite spectral
band through a bandpass function
![]() ,
centered
,
centered![]() at frequency
at frequency ![]() .
We arbitrarily define
the bandwidth
.
We arbitrarily define
the bandwidth ![]() of the instrument as
of the instrument as![]()
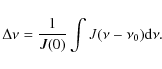
|
(2) |
We define a generic interferometer to be an instrument in which visibilities are directly given by the outputs of the detectors (this is the case in heterodyne interferometry, but not in bolometric interferometry). The expression for a broadband visibility measured by a generic interferometer - in power units, for a baseline
The baselines define a plane usually called the uv-plane. It is better to write the visibility as a convolution in the uv-plane to understand the bandwidth effect,
| |
= | ||
| (4) |
where we have introduced the Fourier transform of the signal and that of the beam (w is the associated transform variable), i.e.,
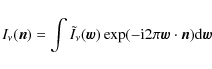
|
(5) |
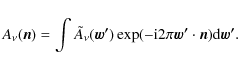
|
(6) |
In the flat-sky approximation, the integral over the field
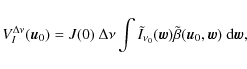
|
(7) |
where we have defined the convolution kernel in the uv-plane
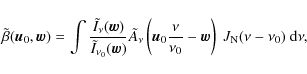
|
(8) |
in which we have introduced the normalized bandpass function
In the following, to allow for complete analytic calculation, we first
ignore the frequency dependence of both the signal and the beam. We
write
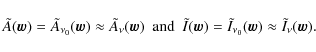
|
(9) |
This defines the approximate form of the convolution kernel
This approximation allows us to obtain an intuitive idea of how the bandwidth smearing acts with good enough accuracy to estimate the sensitivity loss. We discuss in Sect. 2.5 a refined form of the kernel that takes into account the frequency dependence of the beam and the intensity. As shown in Fig. 2, the difference between the approximate kernel, derived in Sect. 2.3, and the refined kernel is small.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13446fig01.ps}\hspace*{4mm}\includegraphics[width=8cm,clip]{13446fig02.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13446-09/Timg42.png)
|
Figure 1:
Left: convolution kernel in the uv-plane for a monochromatic
interferometer, which is actually just the Fourier transform of the
primary beam, for a 90 GHz central frequency and a Gaussian beam with
|
| Open with DEXTER | |
2.3 Approximate analytical form of the kernel
In order to perform the analytical calculation, we also assume a
Gaussian normalized bandpass function
The instrument bandwidth is related to the standard deviation of the Gaussian distribution by
As previously explained, we ignore the frequency dependence of the beam. The integral of the beam over the sky is defined for the central frequency,
This can be analytically integrated (details are given in Appendix A) and written in the form
where we have made the variable substitution
| (15) |
We can define the effective beam in real space for a broadband interferometer
with
We can finally rewrite the kernel as
This
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13446fig03.ps}\hspace*{4mm}\includegraphics[width=8cm,clip]{13446fig04.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13446-09/Timg65.png)
|
Figure 2:
Left: the black full line shows longitudinal profile of the
kernel for monochromatic visibilities, while the color lines show the
longitudinal profile of the convolution kernel for baselines
corresponding to
l0=50, 100, 200, for an instrument with a 20% Gaussian bandwidth
centered at 90 GHz and
|
| Open with DEXTER | |
2.4 Broadband visibilities in temperature units for CMB experiments
It is more convenient to work with visibilities in temperature units
when studying CMB temperature and polarization anisotropies![]() . If
. If ![]() is the intensity of the observed field, in units of
[
is the intensity of the observed field, in units of
[
![]() ], the spectral power collected
by a horn of surface S is
], the spectral power collected
by a horn of surface S is
CMB experiments observe small spatial fluctuations over the sky
| (21) |
The oscillating term of the visibilities washes out the constant part of the spectral power, so the visibilities can be rewritten
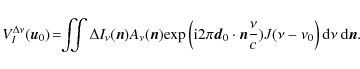
|
(22) |
The temperature fluctuations over the sky are linked to the power fluctuations by
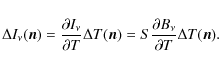
|
(23) |
We can then define the broadband visibilities in temperature units as
Following the same arguments as previously, one can show that
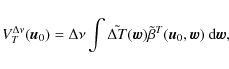
|
(25) |
where we have introduced the Fourier transform of the temperature field,
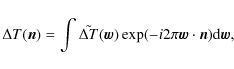
|
(26) |
and a temperature convolution kernel,
If we neglect the dependence of both the signal and the beam on frequency, this kernel actually becomes the one defined in Eq. (10),
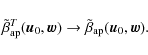
|
(28) |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13446fig05.ps}\hspace*{4mm}\includegraphics[width=8cm,clip]{13446fig06.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13446-09/Timg77.png)
|
Figure 3:
Left: shift of the effective l window function as a function of
l0, dashed lines for a Gaussian bandwidth, solid lines for a
top hat one.
Right: the variation in
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13446fig07.ps}\hspace*{4mm}
\includegraphics[width=8cm,clip]{13446fig08.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13446-09/Timg78.png)
|
Figure 4:
Left: sensitivity degradation on Clextraction due to bandwidth smearing for multipoles between 50 and 200; the quantity
|
| Open with DEXTER | |
2.5 A refined kernel
The intensity ![]() of the observed field actually depends on
frequency for a black body source at temperature T such that
of the observed field actually depends on
frequency for a black body source at temperature T such that
Inside the bandwidth, the frequency dependence of the T derivative of
The beam of the horns also depends on frequency. The surface of the horns S, the solid angle covered
Figure 2 shows for several values of lhow the approximate kernel of Eq. (19) is refined
when one takes into account the above frequency dependences of the
beam and the intensity.
The signal and the beam dependencies largely
compensate each other, and the difference between the two kernels
turns out to be negligible considering the accuracy level required for the
sensitivity loss estimation. The main difference is a shift in the
centroid of the window function shown in the left panel of Fig. 3, which is absent in the approximate kernel. This will
introduce systematics that have to be corrected for. We also
show what happens for a more realistic top-hat-shaped bandwidth (right
panel of Fig. 2, solid lines in Fig. 3). For the data extraction of a given instrument,
the convolution kernel has to be computed numerically; however,
the approximate Gaussian kernel provides a good enough accuracy to estimate
the sensitivity loss. In the remainder of this paper, we use the approximate
analytical form of the kernel, and write
![]() instead
of
instead
of
![]() .
Finally, the right panel of Fig. 3
shows the variation in
.
Finally, the right panel of Fig. 3
shows the variation in
![]() with l0 for a Gaussian
(dashed line) and a top hat (solid line) bandwidth.
with l0 for a Gaussian
(dashed line) and a top hat (solid line) bandwidth.
3 Visibilities measured by broadband bolometric interferometers
The effect of the bandwidth is more subtle in a bolometric
interferometer than in a generic interferometer, because the visibilities
are not measured directly.
As described in (C09), a time-domain modulation of the visibilities is
performed by controlled phase shifters - located behind each
polarization channel (twice the number of horns)- which take some
well-chosen time-sequences of discrete phase values. The corresponding
time-sequences of bolometers' measurements will allow us to recover,
independently for each bolometer, all the different visibilities, by
solving a linear problem of the form
![]() ,
where
X is a vector including the visibilities, S is a vector including a time-sequence
of one bolometer's measurements, and A is a coefficient matrix depending on the
phase shift sequences. In the following, we generalize the (C09)
formalism, taking the bandwidth into account. As in the generic case,
we assume in this section that the detectors (here the bolometers) are sensitive to a
spectral bandwidth
,
where
X is a vector including the visibilities, S is a vector including a time-sequence
of one bolometer's measurements, and A is a coefficient matrix depending on the
phase shift sequences. In the following, we generalize the (C09)
formalism, taking the bandwidth into account. As in the generic case,
we assume in this section that the detectors (here the bolometers) are sensitive to a
spectral bandwidth
![]() ,
by means of a bandpass function
,
by means of a bandpass function
![]() centered on the frequency
centered on the frequency ![]() .
.
3.1 Signal in broadband bolometers
We consider a bolometric interferometer consisting of ![]() horns,
whose beams are defined by the same function
horns,
whose beams are defined by the same function
![]() and
and
![]() bolometers. The electric field at the output of polarization
splitters, corresponding to horn i coming from direction
bolometers. The electric field at the output of polarization
splitters, corresponding to horn i coming from direction ![]() for polarization
for polarization
![]() is
is
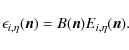
|
(32) |
During a time sample k, each controlled phase shifter adds to its associated input channel the phase
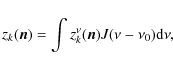
|
(33) |
where
![\begin{displaymath}z_{k}^\nu(\vec{n})=\frac{1}{\sqrt{N_{{\rm out}}}}\sum_{i=0}^{...
...0}^{1}\epsilon_{i,\eta}(\vec{n})\exp[i\Phi^k_{i, \eta}(\nu)].
\end{displaymath}](/articles/aa/full_html/2010/06/aa13446-09/img94.png)
|
(34) |
The power originating in each of the combiner outputs is averaged on timescales given by the time constant of the detector, which is much larger than the EM wave period. The power collected by a given bolometer during a time sample k
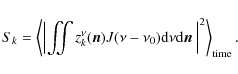
|
(35) |
Signals coming from different directions of the sky are incoherent, as are signals at different frequencies, so their time-averaged correlations vanish to produce
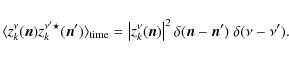
|
(36) |
The signal on the bolometer is finally
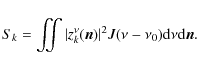
|
(37) |
Developing this expression leads to autocorrelation terms for each input channel and cross-correlation terms between all the possible pairs
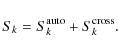
|
(38) |
As in the general case, one can write the visibilities as a convolution in the uv-plane, where we define
We have defined the Fourier transform of the physical signal to be
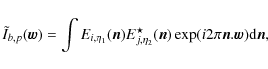
|
(40) |
and the kernel
where
3.2 Phase shifters constant with respect to frequency
We first consider the simplest case where the phase shift values do not depend on the frequency ![]() .
When
.
When
![]() ,
the phase shift term comes outside the integral over
,
the phase shift term comes outside the integral over ![]()
The signal of the cross-correlations on the bolometer is thus the one expressed in (C09), with the broadband visibilities defined in Eq. (24) instead of the monochromatic ones
Following (C09), we can introduce the broadband Stokes visibilities
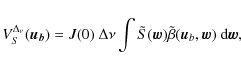
|
(45) |
where S stands for the Stokes parameters I, Q, U or V and
where
![]() is the vector, defined in (C09), encoding the phase shifting values, and
is the vector, defined in (C09), encoding the phase shifting values, and
![]() is a vector including the real and imaginary parts of the broadband
Stokes visibilities. If the phase shift values of a broadband
bolometric interferometer are constant with respect to frequency, the
visibilities should thus be reconstructed exactly as explained in
(C09), by solving a linear problem. In this case, a broadband
bolometric interferometer therefore works exactly as a monochromatic
one, except that the output observables will be broadband visibilities
instead of monochromatic ones.
is a vector including the real and imaginary parts of the broadband
Stokes visibilities. If the phase shift values of a broadband
bolometric interferometer are constant with respect to frequency, the
visibilities should thus be reconstructed exactly as explained in
(C09), by solving a linear problem. In this case, a broadband
bolometric interferometer therefore works exactly as a monochromatic
one, except that the output observables will be broadband visibilities
instead of monochromatic ones.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13446fig09.ps}\hspace*{4mm}\includegraphics[width=8cm,clip]{13446fig10.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13446-09/Timg118.png)
|
Figure 5:
Left: reconstructed temperature and polarization power spectra for a monochromatic (black squares) and a |
| Open with DEXTER | |
3.3 Phase shifters linear with respect to frequency
We now consider the more complicated case where the modulation phase shifters vary linearly with respect to frequency,

|
(47) |
From a technological point of view, this may seem more natural, since it is automatically respected if for instance the phase shifters are just constituted by delay-lines.
For the sake of simplicity, we write
![]() instead of
instead of
![]() in the following. As in
Sect. 2, to carry out the analytical
calculation, we assume both the beam and the intensity
to be independent of frequency,
and we assume a
normalized Gaussian bandpass function JN. We show in
Appendix B that
in the following. As in
Sect. 2, to carry out the analytical
calculation, we assume both the beam and the intensity
to be independent of frequency,
and we assume a
normalized Gaussian bandpass function JN. We show in
Appendix B that
![]() is then
is then
where we have defined
Thus the cross-correlation part of the bolometer signal can be written
where we have introduced some ``phase-dependent'' broadband visibilities
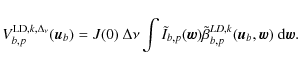
|
(52) |
The new kernel is linked to the generic one by a rotation in the complex plane
This complex factor unfortunately depends on the phase differences: this means that the definition of every visibility will slightly change between two different samples k and k'! This is of course a defect that will corrupt the linear problem.
We will show in a paper in preparation that an error varying with the
modulation will lead to a dramatic leakage from the intensity
visibilities into the polarization ones (which are at least two orders
of magnitudes smaller in CMB observations). This prediction (which is
not trivial and is not proven analytically in this article) is
supported by our Monte-Carlo simulation (cf. Sect. 6): introduction of the ![]() -kernel of
Eq. (48) in the simulation leads to a huge error on
the reconstructed polarization spectrum (typically two orders of
magnitude bigger than the one on temperature spectrum), as shown in
Fig. 5, when the modulation matrix used to solve
the problem is the monochromatic one defined in (C09). Fortunately,
there is a way to get rid of this leakage, as described in Sect. 4, by reconstructing the I visibilities in
sub-bands. Using the extended modulation matrix introduced in
Sect. 4.3, this dramatic error source can be
put under control, and the broadband polarization visibilities can be
reconstructed without loss of sensitivity.
-kernel of
Eq. (48) in the simulation leads to a huge error on
the reconstructed polarization spectrum (typically two orders of
magnitude bigger than the one on temperature spectrum), as shown in
Fig. 5, when the modulation matrix used to solve
the problem is the monochromatic one defined in (C09). Fortunately,
there is a way to get rid of this leakage, as described in Sect. 4, by reconstructing the I visibilities in
sub-bands. Using the extended modulation matrix introduced in
Sect. 4.3, this dramatic error source can be
put under control, and the broadband polarization visibilities can be
reconstructed without loss of sensitivity.
3.4 Geometrical phase shifts
In the quasi-optical combiner design considered for the QUBIC experiment (Kaplan & the QUBIC coll. 2009), some geometrical phase shifts
![]() are automatically introduced by the combiner
are automatically introduced by the combiner![]() .
These phase shifts, stemming from path differences between rays in the
optical combiner, vary linearly with respect to frequency:
.
These phase shifts, stemming from path differences between rays in the
optical combiner, vary linearly with respect to frequency:
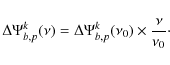
|
(54) |
But as explained in (C09), these geometrical phase shifts ought not to be used to modulate the visibilities
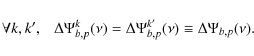
|
(55) |
Hence they do not cause any error during the reconstruction: the
| |
= | ||
| (56) |
3.5 Photon noise error in reconstructed visibilities
We assume here that the modulation matrix used to reconstruct the
visibilities is the monochromatic one defined in (C09); this is
completely true in the case of frequency-independent phase shifters,
and true for the rows concerning the polarization visibilities in the
case of frequency-dependent phase shifters (see
Sect. 4.3). We have shown in (C09) that the
visibility covariance matrix is, where the factor
![]() is caused by the difference in the definitions of the monochromatic
and broadband visibilities,
is caused by the difference in the definitions of the monochromatic
and broadband visibilities,
![\begin{displaymath}N=\frac{\sigma_0^2 N_{\rm h}}{\left[J(0) \ \Delta \nu \right]^2 \ N_{\rm out}} \times \left( A^{\rm t} \cdot A \right)^ {-1},
\end{displaymath}](/articles/aa/full_html/2010/06/aa13446-09/img139.png)
|
(57) |
where A is a matrix including the
where
4 Virtual reconstruction sub-bands in bolometric interferometry
We show that the linear dependence in frequency of the
modulation phase shifts
![]() enables independent reconstruction
of the visibilities in narrower frequency subbands. This
idea was first proposed by (Malu 2007).
We
initially interpretted this method as a way of reducing the smearing
because the sub-band visibilities that are reconstructed are less
smeared
than the broadband ones. However we now demonstrate that its
application produces a loss in signal-to-noise ratio that
thwarts the gain in sensitivity, and thus makes this method
inefficient for decreasing bandwidth smearing. However, as we see, this
method can be succesfully set up to remove the dramatic effect
described in Sect. 3.3, and thus saves the
frequency-dependent option for the modulation phase shifters.
enables independent reconstruction
of the visibilities in narrower frequency subbands. This
idea was first proposed by (Malu 2007).
We
initially interpretted this method as a way of reducing the smearing
because the sub-band visibilities that are reconstructed are less
smeared
than the broadband ones. However we now demonstrate that its
application produces a loss in signal-to-noise ratio that
thwarts the gain in sensitivity, and thus makes this method
inefficient for decreasing bandwidth smearing. However, as we see, this
method can be succesfully set up to remove the dramatic effect
described in Sect. 3.3, and thus saves the
frequency-dependent option for the modulation phase shifters.
4.1 Principle
Before doing the visibility reconstruction, one can choose a number
![]() of virtual reconstruction sub-bands of width
of virtual reconstruction sub-bands of width
![]() .
We emphasize that this division into
subbands is purely virtual in that the hardware design does not
depend on it. The
.
We emphasize that this division into
subbands is purely virtual in that the hardware design does not
depend on it. The
![]() -kernel becomes
-kernel becomes
![\begin{displaymath}\tilde{\eta}^{{\rm BI}, \Delta\nu}_{b,p}(\vec{u}_b, \vec{w}) ...
...{\eta}^{{\rm BI}, \delta\nu}_{b,p}[\vec{u}_b, \vec{w}, \nu_m],
\end{displaymath}](/articles/aa/full_html/2010/06/aa13446-09/img150.png)
|
(60) |
where
| |
= | ||
| (61) |
where
where we have defined
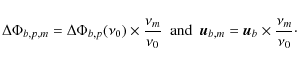
|
(63) |
The sub-band visibilities
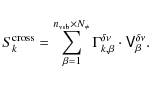
|
(64) |
The problem can thus be inverted exactly as in (C09) to recover the
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13446fig11.ps}\hspace*{4mm}
\includegraphics[width=8cm,clip]{13446fig12.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13446-09/Timg164.png)
|
Figure 6:
Left: phase shifters linear with respect to frequency and
reconstruction with monochromatic modulation matrix. Reconstructed
temperature and polarization power spectra for a monochromatic (black
squares and triangles) and a |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13446fig13.ps}\hspace*{4mm} \includegraphics[width=8cm,clip]{13446fig14.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13446-09/Timg165.png)
|
Figure 7:
Left: phase shifters linear with respect to frequency and
reconstruction with the extended modulation matrix (5 virtual sub-bands
for I visibilities only). Reconstructed temperature and
polarization power spectra for a monochromatic (black squares and
triangles) and a |
| Open with DEXTER | |
4.2 Sensitivity issue
In every time sample k, the signal of the sub-band visibilities is
![]() times weaker than the signal of the broadband visibilities, and consequently their reconstruction variance is
times weaker than the signal of the broadband visibilities, and consequently their reconstruction variance is
One can average offline (i.e., after the reconstruction) the sub-band visibilities derived from the same baseline
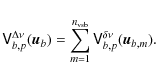
|
(66) |
These broadband visibilities are equivalent to those that would have been reconstructed without subband division but are affected less by bandwidth smearing (
A comparison with Eq. (59) shows that the reconstruction into virtual sub-bands comes along with a loss by a factor
4.3 Reconstruction scheme for instruments with frequency-dependent phase shifters
This method, however, provides a solution for a crucial issue
described in Sect. 3.3. The idea is to estimate at
the same time the intensity visibilities in subbands (Stokes I), and
the polarization visibilities in one single broad band (Stokes Q, U, and V). This can easily be achieved by writing an extended coefficient matrix
based on the decomposition
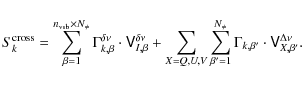
|
(68) |
Practically, this means that the part of the matrix encoding the
polarization visibilities is identical to that of the monochromatic
matrix, while the part encoding the intensity visibilities contains a factor of
![]() more rows. The matrix thus has a total of
more rows. The matrix thus has a total of
![]() rows. The corruption of the linear problem (and
then the leakage of the error in the intensity visibilities into the
polarization ones) can thus be reduced as much as necessary by
increasing the number of subbands, without loss of signal-to-noise
ratio for the polarization visibilities. This reconstruction was performed with our numerical simulation, as described in
Sect. 6; a comparison of Figs. 6
and 7 shows its efficiency. One drawback of
this method is of course that it increases the minimal sequence length
required to invert the problem. Finally, we notice that
this method could in principle apply just as well to phase shifters
with any arbitrary (but known) frequency dependence.
rows. The corruption of the linear problem (and
then the leakage of the error in the intensity visibilities into the
polarization ones) can thus be reduced as much as necessary by
increasing the number of subbands, without loss of signal-to-noise
ratio for the polarization visibilities. This reconstruction was performed with our numerical simulation, as described in
Sect. 6; a comparison of Figs. 6
and 7 shows its efficiency. One drawback of
this method is of course that it increases the minimal sequence length
required to invert the problem. Finally, we notice that
this method could in principle apply just as well to phase shifters
with any arbitrary (but known) frequency dependence.
5 Loss in sensitivity of CMB experiments
We have shown in Sects. 3 and 4 how the broadband visibilities defined in Sect. 2 can be reconstructed, independently of the frequency dependence of modulation phase shifters, from the bolometer sequences measured by a broadband bolometric interferometer. To evaluate the resulting loss in sensitivity for a dedicated CMB experiment, it is important to understand that it is meaningless to compare directly monochromatic visibilities and broadband ones, because they are not the same observables because it is meaningless to directly compare two signals that have been convolved with kernels of different shape and/or size. A correct way to deal with this problem is to compare the sensitivities achieved for the observable of physical interest, here the CMB power spectra. In this section, we generalize the estimator introduced in (H08) and derive new formulae for the sensitivity of the CMB BB power spectrum.
5.1 Generalization of the pseudo-power spectrum estimator
We make the same assumptions and follow exactly the same arguments
as in (H08), substituting the kernel
![]() for
the Fourier transform of the beam
for
the Fourier transform of the beam
![]() .
Assuming perfect E/B separation, one can show that
.
Assuming perfect E/B separation, one can show that
We recall that in the flat-sky approximation,
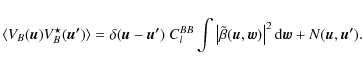
|
(70) |
In Appendix C, we show that the integral of the square modulus of the convolution kernel in the uv-plane actually equals half of the effective beam defined in Eq. (16)
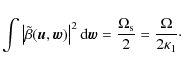
|
(71) |
There is a perfect analogy with the monochromatic case where
where
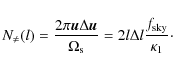
|
(73) |
The variance in the estimator for a broadband interferometer can be derived as in (H08), leading to the error in the power spectrum
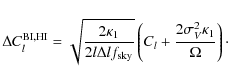
|
(74) |
The only differences from the monochromatic interferometer formula concerns the
Using the expression for ![]() given by Eq. (59),
the error in the angular power spectrum measured by a broadband
bolometric interferometer during a time t can finally be written
given by Eq. (59),
the error in the angular power spectrum measured by a broadband
bolometric interferometer during a time t can finally be written
The
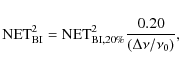
|
(76) |
where
where the smearing penalty factor is defined by
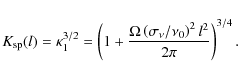
|
(78) |
If we neglect the
![]() penalty on the sample variance,
the factor of sensitivity degradation due to bandwidth smearing for a
bolometric interferometer is indeed given by
penalty on the sample variance,
the factor of sensitivity degradation due to bandwidth smearing for a
bolometric interferometer is indeed given by
![]() .
The physical
interpretation of Eq. (77) is straightforward: the
sensitivity improvement provided by bandwidth broadening (more photons are
collected) is in competition with the sensitivity degradation caused by
bandwidth smearing (the fringes are degraded). Figure 4
(right) shows the evolution of
.
The physical
interpretation of Eq. (77) is straightforward: the
sensitivity improvement provided by bandwidth broadening (more photons are
collected) is in competition with the sensitivity degradation caused by
bandwidth smearing (the fringes are degraded). Figure 4
(right) shows the evolution of
![]() as a function of bandwidth. We see that, for the typical B-mode
experiment considered, the smearing begins to cancel the broadening
for bandwidths larger than
as a function of bandwidth. We see that, for the typical B-mode
experiment considered, the smearing begins to cancel the broadening
for bandwidths larger than ![]() - which is fortunately the typical
bandwidth of bolometers used in CMB experiments
- which is fortunately the typical
bandwidth of bolometers used in CMB experiments![]() . Figure 4 (left)
shows that the total loss in sensitivity on power spectra due to
bandwidth smearing is about 2 for l=150, for a typical dedicated
B-mode experiment with 20% bandwidth. This result, which may seem
unexpected considering the poor reputation of radio-interferometers
in terms of bandwidth, is mainly caused by the spatial
resolution required for the observation of CMB angular correlations being
poorer than that required for the observation of point sources.
. Figure 4 (left)
shows that the total loss in sensitivity on power spectra due to
bandwidth smearing is about 2 for l=150, for a typical dedicated
B-mode experiment with 20% bandwidth. This result, which may seem
unexpected considering the poor reputation of radio-interferometers
in terms of bandwidth, is mainly caused by the spatial
resolution required for the observation of CMB angular correlations being
poorer than that required for the observation of point sources.
5.2 Inefficiency of the reconstruction in sub-bands in preventing bandwidth smearing
If the visibilities were reconstructed into
![]() sub-bands, the smearing would be reduced but the signal-to-noise ratio in each l band would decrease, leading to a
sub-bands, the smearing would be reduced but the signal-to-noise ratio in each l band would decrease, leading to a
![]() additional factor in
additional factor in ![]() as explained in Sect. 4. The smearing penalty factor would be
as explained in Sect. 4. The smearing penalty factor would be
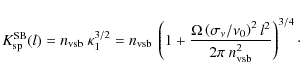
|
(79) |
However, it can be shown that
5.3 Comparison with an imager and a heterodyne interferometer
We now correct the ratio formulae derived in (H08). The comparison
between the sensitivities of a heterodyne and a bolometric
interferometer is not straigthforward since there is an important
difference in hardware design between the two kind of interferometry
in terms of bandwidth. In a radio heterodyne interferometer such as
DASI (Kovac et al. 2002) or CBI (Readhead et al. 2004), the analog correlators only
work at low frequencies (typically below 2 GHz), so the broadband
signal collected by each horn is divided into different channels of
typically 1 GHz bandwidth each and then downconverted before being
correlated. This forced division has prevented past interferometer CMB
experiments from any important bandwidth smearing effects, but the
price to pay was of course the hardware complexity of these
systems. On the other hand, bolometers are naturally broadband, and we
have shown how the monochromatic bolometric
interferometer described in (C09) generalizes almost naturally into a
broadband bolometric interferometer: a broadband instrument only needs
broadband components, e.g., horns, filters. To correct the ratio
formula obtained in (H08), one can neglect the bandwidth smearing for
heterodyne interferometers (for a ![]() bandwidth,
bandwidth, ![]() is
always very close to 1); the formula is then only corrected by the
smearing penalty factor
is
always very close to 1); the formula is then only corrected by the
smearing penalty factor
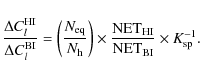
|
(80) |
To be completely fair, one must keep in mind that in the true state of the technological art, it seems difficult to design heterodyne interferometers with bandwidths larger than
The comparison between a bolometric interferometer and an imager is
also only modified by the smearing penalty factor. If the experiment is
dominated by instrumental noise, the ratio of the variances becomes
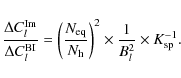
|
(81) |
6 Monte Carlo simulations
We performed a Monte Carlo simulation to check the results obtained in this article. Starting from CMB maps generated from theoretical spectra, the basic principle is to compute the sequences of data measured by a broadband bolometric interferometer, to reconstruct visibilities from these sequences, and to estimate power spectra from these visibilities. The comparison between input and output spectra then allows us to check the analytical calculations (and the associated assumptions) of this article. The code is available upon request; questions or comments can be addressed by e-mail to the authors.
6.1 Simulation overview
We consider a ``standard'' bolometric interferometer (as defined in
Sect. 3) constituted by a square array of ![]() horns, the associated
horns, the associated ![]() polarization splitters, the
polarization splitters, the
![]() modulation phase shifters, a beam combiner and
modulation phase shifters, a beam combiner and
![]() bolometers. In this simulation, we only compute the power measured by
one of the bolometers. We assume that the beams of the horns are all
described by the same perfect Gaussian function of
Eq. (12). We assume that the phase shift values
taken by the modulation phase shifters are equally spaced.
The physical input parameters are then the number of horns
bolometers. In this simulation, we only compute the power measured by
one of the bolometers. We assume that the beams of the horns are all
described by the same perfect Gaussian function of
Eq. (12). We assume that the phase shift values
taken by the modulation phase shifters are equally spaced.
The physical input parameters are then the number of horns ![]() ,
the
horns radius, the distance between two adjacent horns, the FWHM of the
Gaussian beam, the number of phase shift values taken by the
modulation phase shifters
,
the
horns radius, the distance between two adjacent horns, the FWHM of the
Gaussian beam, the number of phase shift values taken by the
modulation phase shifters ![]() ,
the central observation
frequency
,
the central observation
frequency ![]() ,
the bandwidth
,
the bandwidth
![]() ,
the form of the
bandpass function (either Gaussian or top hat) J, and the number of
data samples in one sequence
,
the form of the
bandpass function (either Gaussian or top hat) J, and the number of
data samples in one sequence ![]() .
.
The CMB maps are generated from spectra given by the standard WMAP-5
cosmological model (although the spectra shapes are not really
important to this simulation, the only crucial feature being the
ratio of the amplitude of temperature to polarization spectra). The
question of the E and B mode separation in interferometry is beyond
the scope of both this article and simulation. So we consider only
the TT and EE spectra, which we refer to from now, respectively, as the
temperature and polarization spectra. Computation of the ![]() and
and
![]() kernels involves a numerical integration over the frequency
band, while computation of the samples measured by the bolometer
involves one over the uv-plane. The numerical input parameters are
then the resolution in the uv-plane, the resolution in the frequency
band, and the number of CMB map realisations
kernels involves a numerical integration over the frequency
band, while computation of the samples measured by the bolometer
involves one over the uv-plane. The numerical input parameters are
then the resolution in the uv-plane, the resolution in the frequency
band, and the number of CMB map realisations
![]() .
.
The simulation pipeline is the following:
- 1.
- the position of primary horns and the associated set of baselines are generated;
- 2.
- the
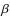 and
and 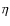 kernels are computed - either from
analytical formulas (given by Eqs. (19) and (43) or numerical integrations (following
Eqs. (10) and (41)), which enables us
to check the analytical formulae - for every different baseline and, in the case of
kernels are computed - either from
analytical formulas (given by Eqs. (19) and (43) or numerical integrations (following
Eqs. (10) and (41)), which enables us
to check the analytical formulae - for every different baseline and, in the case of 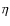 ,
for every phase difference;
,
for every phase difference;
- 3.
- beginning of MAPS loop. CMB temperature and polarization maps are generated from theoretical spectra;
- 4.
- monochromatic and broadband visibilities are computed by
convolving the maps Fourier transforms and the
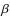 kernels for
every baseline. ``Generalized'' broadband visibilities
(i.e., the convolution of maps Fourier transforms with
kernels for
every baseline. ``Generalized'' broadband visibilities
(i.e., the convolution of maps Fourier transforms with 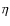 kernels)
are computed for every baseline and every phase
difference;
kernels)
are computed for every baseline and every phase
difference;
- 5.
- random phase sequences are generated for every horn and both polarizations, respecting the coherent summation of equivalent baselines scheme described in (C09). Phase differences are then computed for every baseline;
- 6.
- a sequence of
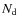 data sets Sk measured by the bolometer is computed (Eq. (39)) by summing ``generalized" broadband visibilities, following the phase sequences;
data sets Sk measured by the bolometer is computed (Eq. (39)) by summing ``generalized" broadband visibilities, following the phase sequences;
- 7.
- the modulation matrix is generated (see (C09) for its explicit expression in the monochromatic case);
- 8.
- the visibilities are reconstructed by solving the linear problem of Eq. (46). End of MAPS loop;
- 9.
- measured spectra are computed from the reconstructed visibilities using the estimators defined in Sect. 5. Relative errors are obtained by comparing with the input theoretical spectra.
6.2 Validation of the work principle of a broadband bolometric interferometer and test of the broadband estimator
In step 9, we do not average the modulus of the reconstructed
visibilities over the different baselines matching the same multipole
as in Eq. (72), but for each different baseline, we
average over all the
![]() maps realisations. Moreover, the power
is actually not flat over the
maps realisations. Moreover, the power
is actually not flat over the ![]() of integration, so it cannot be
taken out of the integral in Eq. (69). Since l2 Cl is nearly flat, we can however
define an unbiased estimator (assuming no instrumental noise) for the broadband interferometer
of integration, so it cannot be
taken out of the integral in Eq. (69). Since l2 Cl is nearly flat, we can however
define an unbiased estimator (assuming no instrumental noise) for the broadband interferometer
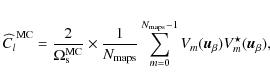
|
(82) |
where
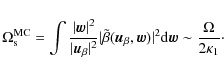
|
(83) |
We thus expect the spectra reconstruction to only be affected by the ``sample'' variance
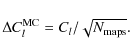
|
(84) |
We execute the simulations for the following input parameters: 16 horns,
15 degrees FWHM primary beam, 12 modulation phase shift values, a 90 GHz central
frequency, 20% bandwidth,
![]() .
We first simulate the case
of phase shifters constant with respect to frequency (the
.
We first simulate the case
of phase shifters constant with respect to frequency (the
![]() -kernels are computed following Eqs. (41) and (43)) and use the monochromatic modulation matrix
defined in (C09) to reconstruct the visibilities. The results, shown
in Fig. 5, validate our study since our
broadband estimator, taking the smearing into account,
reconstructs the generated power spectra well: a broadband bolometric
interferometer with phase shifters that are constant with respect to frequency
operates exactly like a monochromatic interferometer, but the reconstructed
visibilities are the predicted smeared ones. We then simulate the case
of frequency-dependent modulation phase shifters, with kernels
computed following Eqs. (41) and (48). Figure 6 shows the
dramatic effect described in Sect. 3.3 on the
reconstructed polarization spectrum when the monochromatic modulation
matrix is used to reconstruct the
visibilities. Figure 7 shows the efficiency
of using the extended modulation matrix described in
Sect. 4.3 to reconstruct the polarization
visibilities: the intensity visibilities have been reconstructed into 5
sub-bands, completely removing the error in the polarization
visibilities reconstruction in the configuration considered (at the
level of sample variance considered of course).
-kernels are computed following Eqs. (41) and (43)) and use the monochromatic modulation matrix
defined in (C09) to reconstruct the visibilities. The results, shown
in Fig. 5, validate our study since our
broadband estimator, taking the smearing into account,
reconstructs the generated power spectra well: a broadband bolometric
interferometer with phase shifters that are constant with respect to frequency
operates exactly like a monochromatic interferometer, but the reconstructed
visibilities are the predicted smeared ones. We then simulate the case
of frequency-dependent modulation phase shifters, with kernels
computed following Eqs. (41) and (48). Figure 6 shows the
dramatic effect described in Sect. 3.3 on the
reconstructed polarization spectrum when the monochromatic modulation
matrix is used to reconstruct the
visibilities. Figure 7 shows the efficiency
of using the extended modulation matrix described in
Sect. 4.3 to reconstruct the polarization
visibilities: the intensity visibilities have been reconstructed into 5
sub-bands, completely removing the error in the polarization
visibilities reconstruction in the configuration considered (at the
level of sample variance considered of course).
7 Conclusion
We have analytically and numerically studied the work principle of a broadband bolometric interferometer. We have defined its (indirect) observables - the broadband visibilities - and introduced numerical methods to reconstruct them. We have finally calculated the sensitivity of such an instrument dedicated to the B-mode.
Bolometers are naturally broadband, and consequently the design of a broadband bolometric interferometer is identical to the design of the monochromatic one described in (C09), a broadband bolometric interferometer only requiring broadband components, e.g., horns, filters. Nevertheless, we have seen that the modulation matrix that should be used to reconstruct the broadband visibilities depends on some hardware properties of the modulation phase shifters. If these are constant with respect to frequency, the modulation matrix should be that defined in (C09) for a monochromatic instrument. If they are dependent on frequency (this dependence should be known of course), a more complicated scheme involving a reconstruction in sub-bands of the intensity visibilities should be performed. We have verified by using a numerical simulation that in both cases the visibilities can be reconstructed without any additional loss in sensitivity to that caused by the smearing.
Visibilities are defined as the convolution of the Fourier transform of the signal with a kernel, which in the monochromatic case is defined as the Fourier transform of the primary beam. We have shown that the effect of the smearing is to stretch this kernel, in the baseline direction only, and that the amplitude of the smearing depends only on three quantities: the bandwidth, the baseline length, and the size of the primary beam. We have finally defined, as a function of broadband visibilities, a new power spectrum estimator and from this derived a generalized uncertainty formula.
The main conclusion of this article is that for a bolometric interferometer dedicated to CMB B-mode, the sensitivity loss, due to bandwidth smearing, is quite acceptable (a factor of 2 loss for a typical 20% bandwidth experiment).
AcknowledgementsThe authors are grateful to the entire QUBIC collaboration for fruitful discussions.
Appendix A: Analytical derivation of the
 -kernel
-kernel
The kernel of Eq. (13) can be written as a Gaussian integral:
| |
= | (A.1) | |
| = | ![$\displaystyle \frac{\Omega}{\sigma_\nu \sqrt{2\pi}} \exp \left[ \frac{B^2}{4A}-C\right] \sqrt{\frac{\pi}{A}} ,$](/articles/aa/full_html/2010/06/aa13446-09/img215.png)
|
(A.2) |
where we have defined the quantities
| A | = | 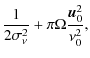
|
(A.3) |
| B | = | 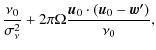
|
(A.4) |
| C | = | 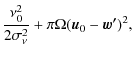
|
(A.5) |
and have made the variable substitution
| (A.6) |
It is straightforward to show that
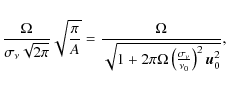
|
(A.7) |
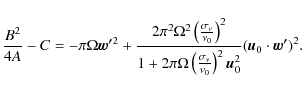
|
(A.8) |
Thus, we can write the kernel as a function of the Fourier transform of the beam as in Eq. (14).
Appendix B: Analytical derivation of the
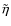 -kernel
-kernel
The kernel of Eq. (41) can be written as the Fourier transform of a Gaussian:
| |
= | (B.1) | |
| = | 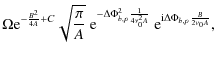
|
(B.2) |
where A, B, and C are the quantities defined in Appendix A. It is straightforward to show that
| G | = | 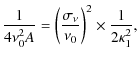
|
(B.3) |
| = | 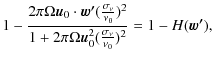
|
(B.4) |
where
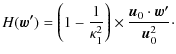
|
(B.5) |
We can finally write the kernel as in Eq. (48).
Appendix C: Integration of the
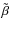 -kernel square modulus in the uv-plane
-kernel square modulus in the uv-plane
We calculate this integral using the approximate kernel of Eq. (18). The variable substitution
![]() does not change the integral
does not change the integral
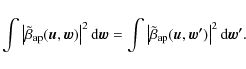
|
(C.1) |
Using Parseval's theorem, one obtains
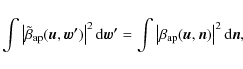
|
(C.2) |
where
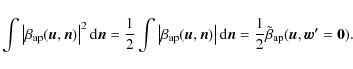
|
(C.3) |
By definition
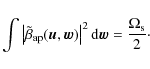
|
(C.4) |
Appendix D: Noise equivalent power and noise equivalent temperature
The spectral power ![]() collected by a horn of surface S is defined in Eq. (20).
We assume for simplicity that the number of bolometers equals the
number of horns. The total power measured by a bolometer is then
collected by a horn of surface S is defined in Eq. (20).
We assume for simplicity that the number of bolometers equals the
number of horns. The total power measured by a bolometer is then
| |
= | (D.1) | |
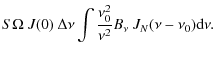
|
(D.2) |
The noise equivalent power (NEP) caused by photon noise in a bolometer, in units of [
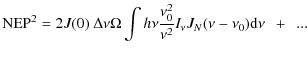
|
|||
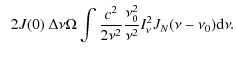
|
(D.3) |
For CMB work, bolometer sensitivity is usually quoted as a noise equivalent temperature in units of [
It is straightforward to show that
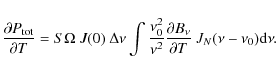
|
(D.5) |
The NET thus scales as the inverse square root of the bandwidth
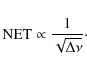
|
(D.6) |
Appendix E: Noise in visibility measurement in Kelvin
We can write the relation between ![]() in units of [
in units of [
![]() ]
and the NEP in units of [
]
and the NEP in units of [
![]() ]
as
]
as
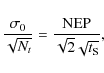
|
(E.1) |
where
![\begin{displaymath}\sigma_V [{\rm in \ W}] = \alpha \ \frac{{\rm NEP}}{\sqrt{2} \sqrt{t} \ J(0) \ \Delta \nu}\cdot
\end{displaymath}](/articles/aa/full_html/2010/06/aa13446-09/img252.png)
|
(E.2) |
The quantity
![\begin{displaymath}\sigma_V [{\rm in \ K}] = \sigma_V [{\rm in \ W}] \times \fra...
...ft. ({\partial B_\nu}/{\partial T}) \right\vert _{\nu_0}}\cdot
\end{displaymath}](/articles/aa/full_html/2010/06/aa13446-09/img255.png)
|
(E.3) |
Using the definition of the NET given in D.4, the noise in a visibility measurement in Kelvin finally becomes
![\begin{displaymath}\sigma_V [{\rm in \ K}] = \alpha \ \frac{{\rm NET} \ \Omega}{\sqrt{t}} \ \kappa_2,
\end{displaymath}](/articles/aa/full_html/2010/06/aa13446-09/img256.png)
|
(E.4) |
where we have introduced the substitution
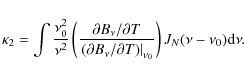
|
(E.5) |
We see in Table E.1 that
![]() is a good approximation.
is a good approximation.
Table E.1:
Values of ![]() for a
for a ![]() bandwidth, for different central frequencies
bandwidth, for different central frequencies ![]() .1
.1
References
- Charlassier, R., Hamilton, J., Bréelle, É., et al. 2009, A&A, 497, 963 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Charlassier, R., & the BRAIN coll. 2008, Proc. 43rd Rencontres de Moriond on Cosmology [Google Scholar]
- Hamilton, J., Charlassier, R., Cressiot, C., et al. 2008, A&A, 491, 923 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hyland, P., Follin, B., & Bunn, E. F. 2009, MNRAS, 393, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Kaplan, J., & the QUBIC coll. 2009, Proc. of the June 2009 Blois conf. Windows on the Universe [Google Scholar]
- Kovac, J. M., Leitch, E. M., Pryke, C., et al. 2002, Nature, 420, 772 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lamarre, J. M. 1986, Appl. Opt., 25, 870 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Malu, S. S. 2007, Ph.D. Thesis, The University of Wisconsin - Madison [Google Scholar]
- Readhead, A. C. S., Myers, S. T., Pearson, T. J., et al. 2004, Science, 306, 836 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Thompson, A. R., Moran, J. M., & Swenson, Jr., G. W. 2001, Interferometry and Synthesis in Radio Astronomy, 2nd edn., ed. A. R. Thompson, J. M. Moran, & G. W., Jr. Swenson, [Google Scholar]
- Timbie, P. T., Tucker, G. S., Ade, P. A. R., et al. 2006, New Astron. Rev., 50, 999 [NASA ADS] [CrossRef] [Google Scholar]
- Tucker, G. S., Kim, J., Timbie, P., et al. 2003, New Astron. Rev., 47, 1173 [NASA ADS] [CrossRef] [Google Scholar]
- White, M., Carlstrom, J. E., Dragovan, M., & Holzapfel, W. L. 1999, ApJ, 514, 12 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ... centered
![[*]](/icons/foot_motif.png)
- The definition of the center is somewhat arbitrary. A convenient definition is the barycenter of J.
- ... as
![[*]](/icons/foot_motif.png)
- This definition is very close to the FWHM for a Gaussian bandwidth.
- ...
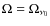
![[*]](/icons/foot_motif.png)
- This solid angle is then related to the rms of the Gaussian beam
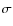 by
by
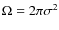 .
.
- ... kernel
![[*]](/icons/foot_motif.png)
- Because JN is normalized to 1, the inverse transform of
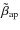 equals 1 at the top of the beam.
equals 1 at the top of the beam.
- ... anisotropies
![[*]](/icons/foot_motif.png)
- Practically, the visibilities measured by a bolometric interferometer will be in power units as defined in Eq. (3).
- ...k
![[*]](/icons/foot_motif.png)
- Recall that this is a sequence of such time samples that will be used to invert the problem and recover the visibilities.
- ... defined
![[*]](/icons/foot_motif.png)
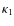 is defined in Eq. (17).
is defined in Eq. (17).
- ... combiner
![[*]](/icons/foot_motif.png)
- As mentioned in (C09), these phase shifters naturally respect the ``coherent summation of equivalent baselines'' scheme.
- ... visibilities
![[*]](/icons/foot_motif.png)
- As geometrical phase shifts depend on the spatial positions of bolometers in the quasi-optical combiner focal plane, using them to invert the problem requires the use of different bolometers; this must be avoided because of intercalibration issues.
- ... equals 1
![[*]](/icons/foot_motif.png)
- A is filled
with elements of the form
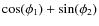 and because we assume that the angles are uniformly distributed, they have an average of zero and a variance of 1.
and because we assume that the angles are uniformly distributed, they have an average of zero and a variance of 1.
- ... (NET
![[*]](/icons/foot_motif.png)
- See Appendix D for definition.
- ... then
![[*]](/icons/foot_motif.png)
- We omit here the correction terms involving G and H to simplify the expression in the case of frequency-dependent phase shifters.
- ... experiments
![[*]](/icons/foot_motif.png)
- For ground-based experiments, atmospheric emission lines exclude the possibility of wider bandwidth.
All Tables
Table E.1:
Values of ![]() for a
for a ![]() bandwidth, for different central frequencies
bandwidth, for different central frequencies ![]() .1
.1
All Figures
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13446fig01.ps}\hspace*{4mm}\includegraphics[width=8cm,clip]{13446fig02.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13446-09/Timg42.png)
|
Figure 1:
Left: convolution kernel in the uv-plane for a monochromatic
interferometer, which is actually just the Fourier transform of the
primary beam, for a 90 GHz central frequency and a Gaussian beam with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13446fig03.ps}\hspace*{4mm}\includegraphics[width=8cm,clip]{13446fig04.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13446-09/Timg65.png)
|
Figure 2:
Left: the black full line shows longitudinal profile of the
kernel for monochromatic visibilities, while the color lines show the
longitudinal profile of the convolution kernel for baselines
corresponding to
l0=50, 100, 200, for an instrument with a 20% Gaussian bandwidth
centered at 90 GHz and
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13446fig05.ps}\hspace*{4mm}\includegraphics[width=8cm,clip]{13446fig06.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13446-09/Timg77.png)
|
Figure 3:
Left: shift of the effective l window function as a function of
l0, dashed lines for a Gaussian bandwidth, solid lines for a
top hat one.
Right: the variation in
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13446fig07.ps}\hspace*{4mm}
\includegraphics[width=8cm,clip]{13446fig08.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13446-09/Timg78.png)
|
Figure 4:
Left: sensitivity degradation on Clextraction due to bandwidth smearing for multipoles between 50 and 200; the quantity
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13446fig09.ps}\hspace*{4mm}\includegraphics[width=8cm,clip]{13446fig10.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13446-09/Timg118.png)
|
Figure 5:
Left: reconstructed temperature and polarization power spectra for a monochromatic (black squares) and a |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13446fig11.ps}\hspace*{4mm}
\includegraphics[width=8cm,clip]{13446fig12.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13446-09/Timg164.png)
|
Figure 6:
Left: phase shifters linear with respect to frequency and
reconstruction with monochromatic modulation matrix. Reconstructed
temperature and polarization power spectra for a monochromatic (black
squares and triangles) and a |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13446fig13.ps}\hspace*{4mm} \includegraphics[width=8cm,clip]{13446fig14.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13446-09/Timg165.png)
|
Figure 7:
Left: phase shifters linear with respect to frequency and
reconstruction with the extended modulation matrix (5 virtual sub-bands
for I visibilities only). Reconstructed temperature and
polarization power spectra for a monochromatic (black squares and
triangles) and a |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



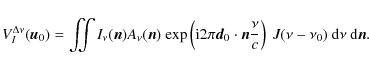
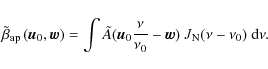
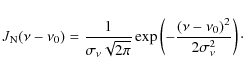
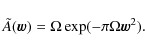
![$\displaystyle \tilde{\beta}_{\rm ap}(\vec{u}_{0},\vec{w})=\frac{\Omega}{\sigma_...
...{w}\right)^{2}-\frac{(\nu-\nu_{0})^{2}}{2\sigma_{\nu}^{2}}\right]}\ {\rm d}\nu.$](/articles/aa/full_html/2010/06/aa13446-09/img49.png)
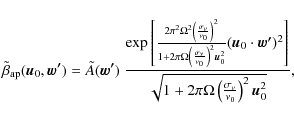
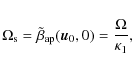
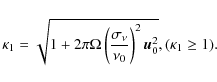
![$\displaystyle \tilde{A}(\vec{w'})\times\frac{1}{\kappa_{1}}\times\exp\left[2\pi...
...nu}}{\nu_{0}}\right)^{2}\Omega_{\rm s}^{2}(\vec{u}_{0}\cdot\vec{w'})^{2}\right]$](/articles/aa/full_html/2010/06/aa13446-09/img58.png)
![$\displaystyle \tilde{A}(\vec{w'})\times\frac{1}{\kappa_{1}}\times\exp\left[\pi\...
...}^{2}}\right)\frac{(\vec{u}_{0}\cdot\vec{w'})^{2}}{\vec{u}_{0}^{2}}\right]\cdot$](/articles/aa/full_html/2010/06/aa13446-09/img59.png)
![\begin{displaymath}V_{T}^{\Delta\nu}(\vec{u}_{0})[{\rm in\
K]}=\frac{V_{I}^{\Del...
...left.(\partial B_{\nu}/\partial T)\right\vert _{\nu_{0}}}\cdot
\end{displaymath}](/articles/aa/full_html/2010/06/aa13446-09/img72.png)
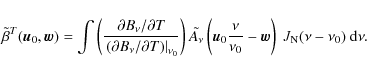
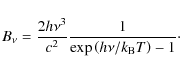
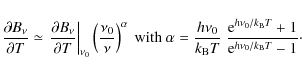
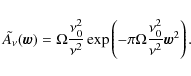
![\begin{displaymath}S_{k}^{\rm cross} = \frac{2 J(0) \ \Delta \nu}{N_{\rm out}} {...
...ta}^{\rm BI}_{b,p}(\vec{u_b}, \vec{w}) {\rm d}\vec{w} \right].
\end{displaymath}](/articles/aa/full_html/2010/06/aa13446-09/img101.png)
![$\displaystyle \int \tilde{A}\left(\frac{\nu}{\nu_0} \vec{u_b} - \vec{w}\right) \! J_N(\nu-\nu_0) \! \exp[i\Delta \Phi^ k_{b,p}(\nu)] \ {\rm d}\nu,$](/articles/aa/full_html/2010/06/aa13446-09/img105.png)
![\begin{displaymath}\tilde{\eta}^{\rm BI}_{b,p}(\vec{u_b}, \vec{w}) = \tilde{\beta}(\vec{u_b}, \vec{w}) \exp[i\Delta \Phi^k_{b,p}(\nu_0)].
\end{displaymath}](/articles/aa/full_html/2010/06/aa13446-09/img110.png)
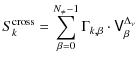
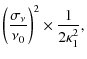
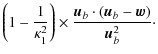
![\begin{displaymath}\tilde{\beta}^{{\rm LD}, k}_{b,p}(\vec{u}_b, \vec{w}) = \tild...
... \vec{w}) \exp \left[-i \Delta\Phi^k_{b,p} H(\vec{w}) \right].
\end{displaymath}](/articles/aa/full_html/2010/06/aa13446-09/img129.png)
![\begin{displaymath}\sigma_{V}[{\rm in \ W}] = \frac{\sqrt{N_{\rm h}}}{N_{\rm eq}...
...sigma_0}{\sqrt{N_{\rm t}}} \times \frac{1}{J(0) \ \Delta \nu},
\end{displaymath}](/articles/aa/full_html/2010/06/aa13446-09/img143.png)
![\begin{displaymath}\sigma_{V}[{\rm in \ K}] = \frac{\sqrt{N_{\rm h}}}{N_{\rm eq}} \frac{{\rm NET} \ \Omega}{\sqrt{t}}\cdot
\end{displaymath}](/articles/aa/full_html/2010/06/aa13446-09/img145.png)
![\begin{displaymath}S_{k}^{\rm cross} = \frac{2}{N_{\rm out}} {\rm Re}\left[ \sum...
...i^k_{b,p} \right] V^{\delta\nu}_{b,p}(\vec{u_{b,m}}) \right],
\end{displaymath}](/articles/aa/full_html/2010/06/aa13446-09/img158.png)
![\begin{displaymath}\sigma^{\delta \nu}_{V}[{\rm in \ K}] = \frac{\sqrt{N_{\rm h}...
...rm vsb}}{N_{\rm eq} } \frac{{\rm NET} \ \Omega}{\sqrt{t}}\cdot
\end{displaymath}](/articles/aa/full_html/2010/06/aa13446-09/img166.png)
![\begin{displaymath}\sigma^{\Delta \nu}_{V}[{\rm in \ K}] = \frac{\sqrt{N_{\rm h}...
...m vsb}}}{N_{\rm eq} } \frac{{\rm NET} \ \Omega}{\sqrt{t}}\cdot
\end{displaymath}](/articles/aa/full_html/2010/06/aa13446-09/img169.png)
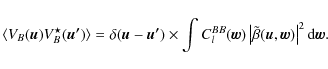
![\begin{displaymath}\widehat{C_l} = \frac{2}{\Omega_{\rm s}} \times \frac{1}{N_{\...
...star}(\vec{u}_\beta) - N(\vec{u}_\beta,\vec{u}_\beta) \right],
\end{displaymath}](/articles/aa/full_html/2010/06/aa13446-09/img179.png)