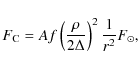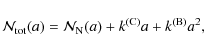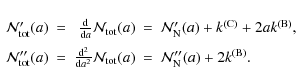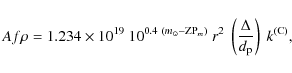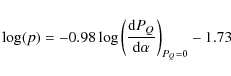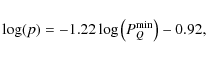EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 514 (May 2010) A&A, 514 (2010) A99 Full HTML
Free Access
Issue
A&A
Volume 514, May 2010
Article Number A99
Number of page(s) 13
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/200913339
Published online 28 May 2010
A&A 514, A99 (2010)

Polarimetry and photometry of the peculiar main-belt object 7968 = 133P/Elst-Pizarro[*]

S. Bagnulo1 - G. P. Tozzi2 - H. Boehnhardt3 - J.-B. Vincent3 - K. Muinonen4,5

1 - Armagh Observatory, College Hill, Armagh BT61 9DG, Northern Ireland, UK
2 - INAF - Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy
3 - Max-Planck-Institut für Sonnensystemforschung, Max-Planck-Strasse 2, 37191 Katlenburg-Lindau, Germany
4 - Observatory, PO Box 14, 00014 University of Helsinki, Finland
5 - Finnish Geodetic Institute, PO Box 15, 02431 Masala, Finland

Received 22 September 2009 / Accepted 26 January 2010

Abstract
Context. Photometry and polarimetry have been extensively used as a diagnostic tool for characterizing the activity of comets when they approach the Sun, the surface structure of asteroids, Kuiper-Belt objects, and, more rarely, cometary nuclei.
Aims. 133P/Elst-Pizarro is an object that has been described as either an active asteroid or a cometary object in the main asteroid belt. Here we present a photometric and polarimetric study of this object in an attempt to infer additional information about its origin.
Methods. With the FORS1 instrument of the ESO VLT, we have performed during the 2007 apparition of 133P/Elst-Pizarro quasi-simultaneous photometry and polarimetry of its nucleus at nine epochs in the phase angle range ${\sim} 0\hbox{$^\circ$ }{-}20\hbox{$^\circ$ }$. For each observing epoch, we also combined all available frames to obtain a deep image of the object, to seek signatures of weak cometary activity. Polarimetric data were analysed by means of a novel physical interference modelling.
Results. The object brightness was found to be highly variable over timescales <1 h, a result fully consistent with previous studies. Using the albedo-polarization relationships for asteroids and our photometric results, we found for our target an albedo of about 0.06-0.07 and a mean radius of about 1.6 km. Throughout the observing epochs, our deep imaging of the comet detects a tail and an anti-tail. Their temporal variations are consistent with an activity profile starting around mid May 2007 of minimum duration of four months. Our images show marginal evidence of a coma around the nucleus. The overall light scattering behaviour (photometry and polarimetry) resembles most closely that of F-type asteroids.

Key words: comets: individual: 7968 133P/Elst-Pizarro - minor planets, asteroids: individual: 7968 133P/Elst-Pizarro - techniques: polarimetric - techniques: photometric

1 Introduction

Light scattering of minor solar system bodies, such as asteroids, comets, and Kuiper-Belt objects, plays a central role in determining global physical parameters such as size and albedo, and the detailed understanding of the surface structure such as micro structure and single scattering albedo of the body surface (Muinonen 2004). This applies to both remote sensing observations from Earth and to in situ measurements during spacecraft encounters. Light scattering is studied by means of photometric and linear polarimetric measurements obtained at different phase angles, i.e., the angle between the Sun, the object, and the observer. The way in which photometry and linear polarization change as a function of the phase angle helps us to characterize the scattering medium, in both the case of solid surfaces and dust ejecta around comets.

The phase angle range between 0$^\circ$ and about 30$^\circ$ is of particular interest. At small phase angles $({\la}10\hbox{$^\circ$ })$, the linear polarization of small bodies in the solar system is usually parallel to the scattering plane, in contrast to what is expected from the simple single Rayleigh-scattering or Fresnel-reflection model, and the intrinsic brightness may increase above the normal linear brightening with phase angle. Both phenomena are a consequence of the surface micro structure and usually attributed to the combined action of the shadowing effect and the coherent backscattering of light. At larger phase angle values, the value of the polarization minimum, the inversion angle at which the polarization changes from being parallel to the scattering plane to becoming perpendicular to it, and the slope of the polarimetric curve at the cross-over point differ for asteroids of different surface taxonomy and may even be used to assess the albedo of the object.

The systematic research and classification of the linear polarimetric and photometric phase functions for the zoo of small bodies in the solar system remains in its infancy, mostly because of a lack of good coverage by measurements for the various objects types to be considered (for instance, asteroids, cometary nuclei, Kuiper-Belt objects, Trojans, minor satellites). Photometric and polarimetric techniques have been used to study asteroids (e.g., Muinonen et al. 2002), Kuiper-Belt objects (e.g., Bagnulo et al. 2008; Boehnhardt et al. 2004; Bagnulo et al. 2006), and the activity of comets while approaching the Sun, (e.g. Penttilä et al. 2005). In contrast, photometric and polarimetric data of cometary nuclei are scarce in the literature. Photometric phase functions of cometary nuclei are available for fewer than a dozen of objects (see Lamy et al. 2007a,c; Boehnhardt et al. 2008; Lamy et al. 2004; Li et al. 2007a,b; Snodgrass et al. 2008; Lamy et al. 2007b; Tubiana et al. 2008). The polarization of cometary nuclei is even less observed and studied than photometry. To the best of our knowledge, only a single comet nucleus, that of 2P/Encke, has been observed in polarized light (Boehnhardt et al. 2008), over an extented phase-angle range. Although the shape of the polarimetric curve of 2P/Encke resembles to those of asteroids, the numerical values of the polarization minimum, slope, and inversion phase-angle differ remarkably from those of other small bodies (including asteroids) in the solar system measured so far.

Here we present new observations of 133P/Elst-Pizarro, an object classified as both a comet and an asteroid (7968 Elst-Pizarro) and seems to be by its nature in between comets and asteroids. It is a small km-size body (Hsieh et al. 2009) that belongs to the type of so-called main-belt comets (MBC, Hsieh & Jewitt 2006) of which only five objects are known so far - P/2005 U1 (Read), 176P/(118401) LINEAR, P/2008 R1 (Garradd), and P/2010 A1 (LINEAR) are the four others. It has an orbit rather typical of main-belt asteroids, for which reason it is also designated as asteroid, is similar to the Themis collision family, or a sub-family of it, called the Beagle family, (Nesvorny et al. 2008). It was discovered in 1996 by Elst et al. (1996) at the European Southern Observatory (ESO) in La Silla (Chile); at that time it displayed a long thin dust tail, which triggered its initial designation as a comet. Although details of the activity's origin are as yet unknown, the activity producing the tail seems to be recurrent and occur close to perihelion passage, while the object may be inactive over the remainder of its orbit around the Sun (Hsieh et al. 2004; Jewitt et al. 2007). Rather than a mostly inactive comet, 133P/Elst-Pizarro is nowadays more commonly regarded as an asteroid with an ice reservoir, which periodically sublimates, with consequent material ejection (Hsieh et al. 2004; Toth 2006; Boehnhardt et al. 1997).

2 Observations

Polarimetric and photometric observations of 133P/Elst-Pizarro were obtained in service mode at the ESO Very Large Telescope (VLT) from May to September 2007, with the FORS1 instrument (Appenzeller et al. 1998), using broadband Bessell R and V filters. Linear polarization measurements were obtained at nine different epochs, one before perihelion (in May 2007), and the remaining eight after perihelion (from July to September 2007). Each series of polarimetric observations consisted of a 30 s acquisition image obtained in the R Bessell filter without polarimetric optics, and a series of images obtained with the half waveplate set at 12 to 24 position angles in the range 0$^\circ$-337.5$^\circ$, in steps of 22.5$^\circ$, both with R and V Bessell filters. We also obtained photometric imaging in R and V Bessell filters (i.e., without polarimetric optics) at the same nine epochs (quasi-simultaneous to the polarimetric series).

We performed a preliminar inspection of the Line of Sight Sky Absorption Monitor[*] (LOSSAM) plots of each observing night showing the atmospheric conditions on site, and we found that for all epochs, except one, sky transparency was close to photometric at the time of the observations. Night 29 to 30 August 2007, corresponding to our target at phase-angle =15.3$^\circ$, was cloudy. For polarimetry, the only impact is in terms of a reduced signal-to-noise ratio, while photometric measurements and tail length measurements obtained during that night should not be considered reliable. Some of the frames obtained on 24 September could not be used because of background objects overlapping the image of 133P/Elst-Pizarro.

3 Data analysis

Both polarimetric and photometric data, including acquisition frames and science frames, were pre-processed in a similar way. Frames were bias-subtracted using a master bias obtained from a series of five frames taken the morning after the observations, then divided by a flat-field obtained by combining four sky flat images taken during twilight with no use of polarimetric optics. From this point, we proceeded with different strategies tailored to the specific analysis that we aimed to perform.

3.1 Deep imaging and tail analysis

Deep imaging of 133P/Elst-Pizarro was obtained by coadding the polarimetric images as follows. For each frame, we considered separately the two images with opposite polarization that are split by the Wollaston prism, from which we subtracted the background using SEXTRACTOR[*] with the mesh option. ``Full resolution'' background images were checked to ensure that they were constant around the target, and that background subtraction neither remove nor added small scale features. We then coadded the two images with opposite polarization for each of the frames obtained at various positions of the retarder waveplate. These frames were corrected for their corresponding airmass values. Extinction coefficients, colour correction terms, and zeropoints were obtained from the observations performed within the framework of the FORS1 instrument calibration plan. For the R filter, we adopted the values of $k_R=0.087 \pm 0.014$ and $k_{V-R} = -0.097 \pm 0.01$ for the extinction and the colour correction, respectively; for the V filter, we adopted $k_V=0.112 \pm 0.012$ and $k_{B-V} = -0.015 \pm 0.007$. For the colour indices of 133P/Elst-Pizarro we adopted V-R=0.41 and B-V=0.60, which are close to solar colours. However, the instrument calibration plan does not include photometric calibration of the images obtained with the polarimetric optics, and the transmission function of the polarimetric optics is documented in neither the FORS user manual nor the literature. We therefore performed a quick photometric calibration of the images obtained with the polarimetric optics by comparing the flux of the same objects observed with and without polarimetric optics. We estimated that the absorption of the polarimetric optics is about 0.60 and 0.54 mag in R, and V, respectively. Instrument zeropoints for the polarimetric mode were thus calculated by subtracting 0.60 or 0.54 from the night zeropoints obtained within the context of the instrument calibration plan in imaging mode. We note that this correction was obtained without accounting for a change in the extinction and colour coefficients caused by the polarimetric optics. The impact of this approximation should be minimal, relative to the uncertainties discussed in Sect. 3.3.

All frames obtained during a single epoch were average-combined using a $\sigma $-clipping algorithm, adopting the pixel median value as a center for clipping, and calculating the average of the non-clipped pixels. These combined images were then calibrated in Af, where A is the albedo and f the filling factor, using Eq. (1) of Tozzi et al. (2007)

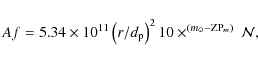
\begin{displaymath}% Af = 5.34 \times 10^{11} \left(r/d_{\rm p}\right)^2 10 \times^{\left(m_\odot - {\rm ZP}_m\right)} \ \mathcal{N}, \end{displaymath} (1)

where r is the heliocentric distance in AU, $m_\odot$ is the absolute magnitude of the Sun in the considered filter, ZPm is the zeropoint in that filter, and $d_{\rm p}$ is the CCD pixel scale in arcsec (0.25 $^{\prime \prime }$in our case), and $\mathcal{N}$ is the number of electrons per pixel.

Images were finally magnified using a scale factor

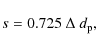
\begin{displaymath}% s = 0.725~ \Delta ~ d_{\rm p}, \end{displaymath} (2)

where $\Delta$ is the geocentric distance in AU at the time of the specific observation. In this way, the pixel coordinates where converted into identical spatial coordinates expressed in 1000 km.

\begin{figure} \par\includegraphics[width=9cm,clip]{aa13339-09-fig1.eps} \end{figure} Figure 1:

Contour plots of Af in R and V Bessell filter ( left and right columns, respectively). North is up, and east to the left. The black arrow and red arrow represent the direction of the Sun, and the negative target velocity as seen from the observer in the plane of the sky, respectively. The x and y axes are in units of 103 km. Contour levels are calibrated in Af (for explanations see text). Contour levels correspond to $Af=7.0 \times 10^{-9}$, $8.3 \times 10^{-9}$, $1.0 \times 10^{-8}$, $1.25 \times 10^{-8}$, $1.65 \times 10^{-8}$, $2.5 \times 10^{-8}$, and $5 \times 10^{-8}$.

Open with DEXTER

Figure 1 shows the contour plots of the coadded polarimetric images of 133P/Elst-Pizarro at the nine observing epochs, i.e., from 38 days before to 87 days after perihelion.

The image of 22 May 2007 shows a marginal indication of a tail in the anti-solar direction. In all images obtained after perihelion, we clearly detected one or two narrow tails, either at position angles PA corresponding to the direction of the Sun, at 180$^\circ$ from it, or in both directions. Since the tails are seen in both V and R filters, we conclude that they represent dust-reflected sunlight (and not so much - or possibly not at all - from gas emission). Table 1 provides geometric information about the two tail features measured from the images.

Table 1:   Geometric information about the dust tails of 133P/Elst-Pizarro.

For comparison purpose, in Fig. 1 we adopted the same contour levels for all epochs, $7\times10^{-9}$ being the one at the smallest Af value. However, we note that in all images, apart from one obtained before perihelion, tails extend to a greater distance than indicated by the $7\times10^{-9}$ contour level (although, below this value, background noise becomes quite significant). The tail was detected with the highest signal-to-noise ratio in the two images obtained in July 2007, extending at least up to 25 000 km from the photometric centre of the object, pointing toward the Sun. We note that because of projection foreshortening, the measured length of the tail in the sky compares to a much longer extension in space. In the images obtained on July 13, and in the regions at projected distance between 6000 and 20 000 km, we estimate that the scattering cross-section of the tail (i.e., the projected surface multiplied by the albedo) is about 0.27 km2 and 0.19 km2 in the R and V filter, respectively. In the images obtained on July 17 for the same regions, we measure about 0.24 km2 and 0.21 km2 in the R and V filter, respectively. Figure 2 shows the contour plot for the combined image obtained on July 17 in the R filter setting for the lower contour level curve of value $Af = 2 \times 10^{-9}$.

\begin{figure} \par\includegraphics[width=8cm,clip]{aa13339-09-fig2.ps}\vspace*{-1mm}\end{figure} Figure 2:

Contour plots of Af in R Bessell filter for the combined image obtained on July 17. Contour levels correspond to $Af = 2 \times 10^{-9}$, $4 \times 10^{-9}$, and $6 \times 10^{-9}$.

Open with DEXTER

In August, we detected, apart from the primary tail, a weak secondary tail, which then prevailed in brightness over the first tail in the two images obtained in September 2007. Hereafter, the primary one will be referred to as ``Tail 1'', the secondary tail as ``Tail 2''. Tail 1 points westward, i.e., close to opposition it is directed towards the Sun. It appears as an anti-tail (a sun-ward pointing dust tail) in our July 2007 image, and thereafter as a normal tail. It is brighter than Tail 2 before about mid-August 2008, then fades away and is no longer detectable in our last exposure series on 24 September 2007. Tail 2 in the eastern hemisphere always appears as an anti-tail. It is first imaged in early August 2007 as a short eastward extension in the isophote pattern in Fig. 1, then brightens above Tail 1 by the end of August, and remains detectable until the end of our observations in late September 2007. The appearance of the two tails in 133P/Elst-Pizarro resembles in terms of its behaviour the dust phenomena observed in this object in 1995 and described by Boehnhardt et al. (1997).

Using the Finson-Probstein (FP) code (Beisser 1990; Beisser & Drechsel 1992), we could develop a qualitative and in part also quantitative understanding of the dust activity of 133P/Elst-Pizarro. The FP code allows one to calculate and display the so-called synchrone-syndyne pattern of cometary dust tails, where synchrones represent the location of the dust emitted from the nucleus at the same time and syndynes represent the dust subject to the same solar radiation pressure characterized by the $\beta_{\rm r}$ parameter, the ratio of the force of solar radiation pressure to that of the gravity of the Sun. During perihelion passage in 2007, the synchrone-syndyne pattern of 133P/Elst-Pizarro shows a very dense and narrow grid of overlapping lines, indicating a very narrow and spiky dust tail. It also suggests that the two observed tails are phenomena of projection caused by a single dust tail, formed by the dust activity of the object that lasted over a certain period around perihelion. Owing to the low orbital inclination of 133P/Elst-Pizarro, the dust tail is seen almost edge-on from Earth during the whole observing interval. Depending on the observing dates, the FP calculations show that the two tails represent different dust grain populations, emitted by the nucleus at different time before the observing epoch and located on different sides of the nucleus as projected onto the sky of the observer on Earth. The projection-induced transition between Tails 1 and 2 happened shortly after opposition passage of the object on 20 July 2007.

From the images, we conclude that the dust activity of 133P/Elst-Pizarro was very low (or even absent) during our first observing night (22 May 2007) 38 days before perihelion (top panels of Fig. 1). However, the presence of Tail 1 on 30 August 2007, and possibly on 19 Sept. 2007, suggests that significant dust activity had started shortly (a few days) after 22 May 2007, since the dust grains seen in this tail region must have been released by the nucleus about 100 days or more before the date of observation, i.e., in late May 2007. On the other side, the existence of Tail 2 in September 2007 is indicative of dust release by the nucleus that was still ongoing by the time of our observations, i.e., almost 90 days after perihelion passage.

The extension of Tail 2 from the nucleus allows us to estimate an approximate maximum $\beta_{\rm r}$ value for grains in the most distant region of this tail: we found a maximum $\beta_{\rm r}$ of about 0.15, which is characteristic for instance of a few $\mu$m or ten $\mu$m size grains from silicate or absorptive materials. On 9 August 2007, the width of Tail 1 is about 1000 km at a projected distance of 5000 km from the nucleus indicating a slow (out-of-plane) expansion speed of the dust of only about 1.5 m/s. The tail width on 13 and 17 July 2007 at the same distance range (4000-5000 km) was measured to be 1750 and 2250 km, respectively, which results in an expansion speed out of the orbital plane of about 1.45 m s-1. Both results support the conclusions of a low expansion velocity of the dust grains in this object.

Finally, to obtain tighter constraints of the tail(s) brightness, we calculated the average Af at different distances along the direction identified by the tail(s). We measured the average flux in rectangular areas of 20 pixels, five along the direction identified by the tail, and four in the direction perpendicular to it[*]. Figure 3 shows the Af in the R and V filters, and the colour index V-R, versus distance from the photometric centre of the object. The points at positive distances refer to Tail 1, and those at negative distances refer to Tail 2. The V-R points of the rightmost panels were plotted only when flux was detected in both filters at the minimum 2$\sigma $ level. The V-R colour of the tails is about 0.4. It is mostly constant along the tail axes, and close to a neutral intrinsic colour typical of a flat spectrum in the visible. It is also in good agreement with the V-R colour of the nucleus itself (see Sect. 3.3). The neutral colour of the dust tails is compatible with light scattering by grains that were much larger than the wavelengths of the filter measurements. It also implies that the surface material and the dust released by 133P/Elst-Pizarro is not ``red'' as frequently observed for cometary dust and considered indicative of the space weathering effects on the surface materials.

\begin{figure} \par\includegraphics[width=16cm,clip]{aa13339-09-fig3.ps} \end{figure} Figure 3:

Tail Af measured along the direction identified by the tail, with respect to the photometric center, and tail colour indices V-R. In the left and middle column panels, green lines show the zero axes (corresponding to the nucleus position). In the right panels, they correspond to the colour index derived for the nucleus.

Open with DEXTER

3.2 Searching for coma activity

We provide a formal description of our approach to evaluate coma contribution from our measurements. This is based on a strategy originally developed by Tozzi & Licandro (2002) and Tozzi et al. (2004). Thereafter, we describe the results of the analysis performed on the combined polarimetric images of 133P/Elst-Pizarro.

We assume that the number of detected electrons e- of the object per unit of time within a circular aperture of radius a, $\ensuremath{\mathcal{N}_{\rm tot}} (a)$, is the sum of the contribution of the nucleus, \ensuremath{\mathcal{N}_{\rm N}}, plus the contribution of the coma, \ensuremath{\mathcal{N}_{\rm C}}  and, possibly, a spurious contribution \ensuremath{\mathcal{N}_{\rm B}}, due to non-perfect background subtraction

\begin{displaymath}% \ensuremath{\mathcal{N}_{\rm tot}} (a) = \ensuremath{\mathc... ...athcal{N}_{\rm C}} (a) + \ensuremath{\mathcal{N}_{\rm B}} (a), \end{displaymath} (3)

where a is the radius of the aperture in pixels. Following A'Hearn et al. (1984), the flux of a (weak) coma around the nucleus in a certain wavelength band can be written as

\begin{displaymath}% \ensuremath{F_{\rm C}} = A f \left(\frac{\rho}{2 \Delta}\right)^2 \frac{1}{r^2} {F_\odot}, \end{displaymath} (4)

where A is the mean albedo (unitless), f is the filling factor (unitless), $\Delta$ is the geocentric distance and $\rho$ is the projected distance from the nucleus (corresponding to the aperture in which the flux \ensuremath{F_{\rm C}} was measured), expressed in identical units, r is the heliocentric distance expressed in AU, $F_\odot$ is the solar flux at 1 AU integrated in the same band as \ensuremath{F_{\rm C}}, and convolved with the filter transmission curve. Equation (4) applies to the reflected light of the dust coma, which in the visible clearly dominates over contributions from gas emission. Based on the hypothesis of uniform and isotropic ejection of dust at constant velocity, A'Hearn et al. (1984) note that the product $Af\rho $ is constant with $\rho$. The background is assumed to be constant in the small region measured around the object, hence, linearly proportional to the aperture area. Equation (3) can thus be written

\begin{displaymath}% \ensuremath{\mathcal{N}_{\rm tot}} (a) = \ensuremath{\mathc... ...) + \ensuremath{k^{\rm (C)}} a + \ensuremath{k^{\rm (B)}} a^2, \end{displaymath} (5)

where \ensuremath{k^{\rm (C)}} and \ensuremath{k^{\rm (B)}} are terms independent of a. We then trivially obtain

\begin{displaymath}% \begin{array}{rcrcl} \ensuremath{\mathcal{N}_{\rm tot}} '(a... ...N}_{\rm N}} ''(a) + 2 \ensuremath{k^{\rm (B)}} .\\ \end{array}\end{displaymath} (6)

Plotting $\ensuremath{\mathcal{N}_{\rm tot}} ''(a)$versus a allows one to estimate whether background subtraction is optimum, as at large apertures compared to the comet image - barring the presence of background objects - $\ensuremath{\mathcal{N}_{\rm tot}} ''(a)$should converge toward the $\ensuremath{k^{\rm (B)}} $ value, which for optimum sky subtraction should be zero.

Assuming that the nucleus is a point source, the term $\ensuremath{\mathcal{N}_{\rm N}} '(a)$ is the point spread function, and, for apertures sizes that are large compared to the seeing, should tend to zero. If an extended coma is present, we expect a contribution from the term $\ensuremath{\mathcal{N}_{\rm C}} '(a)$ constant with a. The coma contribution can then be evaluated by measuring the constant \ensuremath{k^{\rm (C)}} as a weighted average of $\ensuremath{\mathcal{N}_{\rm tot}} '(a)$ in the aperture interval [ai1,ai2], with ai1 < ai2. The \ensuremath{k^{\rm (C)}} value can finally be used in Eq. (5) to distinguish, for each aperture value, the flux due to the coma and that due to the nucleus. In particular, the former one increases linearly with aperture, and the latter should appear constant at the aperture values at which $\ensuremath{\mathcal{N}_{\rm tot}} '(a)$ is constant, and which were used to determine \ensuremath{k^{\rm (C)}}.

The nucleus contribution \ensuremath{\mathcal{N}_{\rm N}} can then be transformed to magnitude m, following the standard recipes for photometry. The coma contribution \ensuremath{\mathcal{N}_{\rm C}} can be transformed into astrophysically meaningful terms using the quantity $Af\rho $ introduced by A'Hearn et al. (1984), using the formula

\begin{displaymath}% A f \rho = 1.234 \times 10^{19} \ 10^{0.4~\left(m_\odot - {... ...t(\frac{\Delta}{d_{\rm p}}\right) \ \ensuremath{k^{\rm (C)}} , \end{displaymath} (7)

where r and $\Delta$ are measured in AU, $d_{\rm p}$ in arcsec per pixel, $\ensuremath{k^{\rm (C)}} $ in e- per pixel, and $Af\rho $ is obtained in cm.

To test this algorithm, we used the frames obtained on 22 May 2007, when 133P/Elst-Pizarro exhibited the least evidence of tail activity, and its image appeared relatively isolated from background objects. We applied our algorithm to both 133P/Elst-Pizarro and an isolated background star of similar brightness. Suitable comparison objects are extremely rare in our images. During a series of exposures, differential tracking causes background objects to shift away from the field of view limited by the 22 $^{\prime \prime }$wide strip mask used in polarimetric mode. However, since individual exposures were short (between 30 s and 100 s), star trailing was limited always to less than 1 pixel size, compared to a typical seeing of 4 pixels.

\begin{figure} \par\includegraphics[width=7.5cm,clip]{aa13339-09-fig4.ps} \end{figure} Figure 4:

From top to bottom: $\mathcal{N}$, $\mathcal{N}'$, and $\mathcal{N}''$ profiles for a background reference star (blue thick lines) and for the object 133P/Elst-Pizarro (red thin lines), observed on 22 May 2007 in the R filter. All profiles are plotted versus the aperture measured in pixels (for 133P/Elst-Pizarro, on 22 May 2007, a 0.25 $^{\prime \prime }$pixel corresponds to 365 km). Together with the $\ensuremath{\mathcal{N}_{\rm tot}} (a)$ profile (solid lines), the top panel shows also the two contributions $\ensuremath{\mathcal{N}_{\rm N}} (a)$ (dashed lines), and $\ensuremath{\mathcal{N}_{\rm C}} (a)$ (lower dotted lines).

Open with DEXTER

The results of our test are illustrated in Fig. 4, which shows that for the background star $\ensuremath{\mathcal{N}_{\rm C}} '(a)$ tends to zero for $a \ga 20$ pixels, while for 133P/Elst-Pizarro $\ensuremath{\mathcal{N}_{\rm C}} '(a)$ converges to a positive constant value. In Fig. 4, the constant used to disentangle the $\ensuremath{\mathcal{N}_{\rm N}} (a)$ and $\ensuremath{\mathcal{N}_{\rm C}} (a)$ profiles was calculated by interpolating with a constant term the $\ensuremath{\mathcal{N}_{\rm tot}} '(a)$ profiles (shown in the middle panel) between 22 and 28 pixels. For both the background star and 133P/Elst-Pizarro, all profiles were normalised imposing that the fluxes integrated within a 15 pixel (=3.75 $^{\prime \prime }$) aperture are equal to 1.

The most critical issue is that the coma region (if a coma is present at all) is contaminated by the tail contribution, which so far we have implicitly neglected. Therefore, we transformed our images into polar coordinates $(a,\theta)$ and removed the regions within those azimuth ranges that were clearly contaminated by tail(s) or background sources. The flux pertaining to a certain annulus $[a,a+{\rm d}a]$was then calculated by integrating the pixel values at the various $\theta$ values contaminated by netiher tail nor background sources, multiplied by a factor ${\ge} 1$ to account for the image trimming. The errorbars in the $\ensuremath{\mathcal{N}_{\rm N}} '$ profiles were estimated by associating with the measured flux the standard deviation of the distribution of the fluxes at the various $\theta$ values. Finally, we applied an algorithm similar to that described in the case of cartesian coordinates. The coma contribution was measured in circular regions between 4500 and 9000 km from the nucleus photo-centre.

The results of this analysis, shown in Fig. 5, are consistent with there being a coma with $Af\rho $ $\la 1$ cm detected at a 2-5$\sigma $ level. This result could well be ascribed to stray light in the instrument (which may mimic a diffuse halo). We therefore repeated the same analysis on the images of a number of background stars at various observing epochs. We found that the ratios $\ensuremath{\mathcal{N}_{\rm C}} (a)/\ensuremath{\mathcal{N}_{\rm tot}} (a)$ were generally substantially higher for 133P/Elst-Pizarro than for background objects. In conclusion, our data exclude the presence of a coma with $Af\rho \ga 3$ cm, but certainly do not allow us to rule out the possibility that a faint coma, with $Af\rho $ of the order of 1 cm or smaller, exists. Data shown in Fig. 5 marginally suggest a change of the colour index, but reaching a firm conclusion in that respect would require higher signal-to-noise ratio data.

This value compares to a dust production rate of the order of 100 g s-1 (Boehnhardt et al. 2008), which would be one of the lowest level ever measured for a comet, although lasting most likely for several months around perihelion. Despite its large uncertainty (order of one magnitude), this dust production rate is still higher than that obtained by Hsieh et al. (2004), which could be caused by temporal variability in the nucleus activity and/or measurement and modeling errors (in both datasets). The most logical explanation of the almost absent coma and the narrow dust tails is low nucleus activity and the small terminal expansion velocity of the dust grains after release by the nucleus of 133P/Elst-Pizarro. Small dust expansion velocities can be concluded from estimations of the tails. Hence, the dust coma is weak and confined very much to the near-nucleus region, which makes it difficult to detect in the atmospheric seeing disk of the latter.

3.3 Nucleus photometry

\begin{figure} \par\includegraphics[width=8cm,clip]{aa13339-09-fig5.ps} \end{figure} Figure 5:

$Af\rho $for the coma on 22 May 2007. Red circles refer to R filter, blue squares to V filter. Dashed lines mark the average $Af\rho $ values in the two filters, obtained neglecting the points marked with empty symbols.

Open with DEXTER

For each observing night, our data set typically consists of an acquisition image in R, a series of 12 to 32 polarimetric images in V, followed by a series of 12 to 32 polarimetric images in R, and a series of two photometric images in R and two in V. Images were taken approximately two or three minutes apart, except for the photometric series, which was occasionally taken ten to thirty minutes before or after the polarimetric series. For each epoch, the set of photometric data consists of the acquisition image of the polarimetric series in R, the averaged frames obtained from all polarimetric images in R and V, and images obtained in R and V with no polarimetric optics.

For all images, we used aperture photometry, adopting an aperture radius of 12 pixels $({=}3\hbox{$^{\prime\prime}$ })$. Our nucleus brightness measurements are contaminated by the emission of a tail and (possibly) a coma. Tail emission was roughly taken into account by subtracting, from the flux integrated in a circular aperture of radius a (in pixels), the amount corresponding to $Af=2.5 \times 10^{-8}$ per pixel, multiplied by an area of 4 (a-2) pixels, both for the R and the V filter, for all observing epochs apart from the one before perihelion, when the tail was very faint. For the adopted 12 pixel aperture, this corresponds typically to a 0.1 mag correction. Coma contribution was subtracted using the results of the previous section. For a 12 pixel aperture, this corresponds to a correction generally of the order of 0.1 mag. Finally, the apparent magnitudes were converted into normalised magnitude using

\begin{displaymath}% H_m(\alpha) = m - 5~\log (r~\Delta), \end{displaymath} (8)

where r and $\Delta$ (the heliocentric and the geocentric distances), are expressed in AU, and $\alpha$ is the phase-angle.

For each observing epoch, we finally obtained a light curve with a typical time baseline of the order of 1 h 15 m to 1 h 30 m. At all the observing epochs, we could clearly note that the object photometry varyed within a short timescale (${\le} 1$ h). The most extreme case, shown in Fig. 6, is night 22 May 2007, during which we measured an amplitude of about 0.5 mag and 0.6 mag in R and V, respectively, to be compared to a variability of ${\la} 0.02$ mag measured for a nearby background star. In the observations obtained on 19 September 2007, which have the shortest time baseline of our dataset (1.1 h), 133P/Elst-Pizarro exhibited the smallest brightness variability ${\la} 0.2$ mag in both filters. While in some cases, the variability of 133P/Elst-Pizarro may be explained by the close presence of background objects or by changes in the sky transparency, in most of the cases the observed variability is intrinsic to the object. Hsieh et al. (2004) estimated a light curve amplitude of the order of 0.4 magnitude in R filter, with a 3.471 h period. Earlier observations reported substantially larger variability (see Hsieh et al. 2004, and references therein), which may indicate changes of the nucleus aspect angle along the orbit (although some results reported previously may be affected by poor calibration).

\begin{figure} \par\includegraphics[width=8.5cm,clip]{aa13339-09-fig6.ps} \end{figure} Figure 6:

Photometry in the R (red circles) and V (blue squares) filters for 133P/Elst-Pizarro as function of time, obtained on 22 May 2007. Filled symbols refer to the photometry obtained from the polarimetric images, empty symbols refer to the photometry obtained from the images with no polarimetric optics in. Asterisks show the photometry obtained from the averaged polarimetric images. Point at t=0 is obtained from the acquisition image of the polarimetric series.

Open with DEXTER

Table 2:   Photometry of comet 133P/Elst-Pizarro.

We note that our observational dataset may possibly be suited to a detailed period analysis based on differential photometry, which is beyond the scope of this paper. The aim of our photometric measurements is to determine, by extrapolating of the brightness measured at various phase angles, an estimate of the absolute brightness of the object nucleus at phase angle 0$^\circ$. With this in mind, the uncertainty introduced by using simple aperture photometry (as opposed to the PSF fitting method), and by a less than optimal photometric characterization of the observing nights, is negligible compared to the variability of the object due to its rotation. The major contribution to the errorbars comes from the uncertainty in the zeropoints, and in both the tail and coma contributions, the sum of which was finally estimated to be 0.1 mag for all points.

Our results are given in Table 2 and plotted in Fig. 7. The slopes of the brightness curves are $0.052 \pm 0.004$ mag/deg in R, and $0.055 \pm 0.005$ mag/deg in V, indicating a phase darkening coefficient in the range typical of cometary nuclei. The extrapolated average brightnesses at phase angle =0$^\circ$ are $15.50 \pm 0.05$ and $15.88 \pm 0.07$ in the R and V filters, respectively, resulting in an average colour index V-R=0.38, which is equivalent to an average spectral gradient of +2%/100 nm in the V and R wavelength range, i.e., the intrinsic color of 133P/Elst-Pizarro appears to be neutral, and a flat solar reflectance spectrum in the visible is expected, at least beyond about 500 nm.

\begin{figure} \par\includegraphics[width=8.4cm,clip]{aa13339-09-fig7.ps} \end{figure} Figure 7:

Photometry in the R (red circles) and V (blue squares) filters for 133P/Elst-Pizarro as function of the phase angle. Solid lines show the corresponding linear best-fits. Points that were not used to calculate the best-fit are represented with empty symbols.

Open with DEXTER

The absolute brightness of 133P/Elst-Pizarro in R and V filter clearly increases towards zero phase angle, but no indication of an opposition brightening is found. Deviations from linearity may be caused by measurement errors and (mostly) rotation variations of the elongated body (Hsieh et al. 2004, give a minimum axis ratio of 1.45 and a rotation period of 3.471 h). The absolute brightnesses at zero phase-angle correspond to an average equivalent radius of 1.6 km (range is 1.64-1.72 km in R to 1.47-1.57 km in V), assuming the 0.07 and 0.06 albedo values (in R and V, respectively) obtained from our polarimetric measurements.

We finally compare our results with those of previous studies, noting that previous photometric measurements were obtained more than four months (Boehnhardt et al. 1997) and more than seven months (Hsieh et al. 2004) after perihelion in 1996 and 2002, respectively, while the measurements presented in this work cover the orbit arc from about one month before to three months after perihelion in 2007.

Hsieh et al. (2004) and Jewitt et al. (2007) found a phase darkening coefficient $\beta_{\rm d} = 0.044~ \pm~ 0.007$ mag/deg and an average V-R color of $0.42~ \pm~ 0.03$, which are fully consistent with our own measurements. We note that colour indices obtained from quasi-simultaneous images in R and V vary between 0.29 and 0.48, which is marginally larger than reported by Hsieh et al. (2004), who measured V-R varying between 0.35 and 0.49.

Table 3:   Polarization measurements of 133P/Elst-Pizarro.

The nucleus size has been previously estimated (neglecting possible contamination from coma and tails) to be about $2.5 \pm 0.1$ km assuming an albedo of 0.04, which is also consistent with our values when applying identical albedo parameters. Hsieh et al. (2009) give an equivalent radius of the nucleus of 133P/Elst-Pizarro of $1.9\pm0.3$ km for a geometric albedo of 0.05.

We note that the variation amplitudes of 0.5 to 0.6 mag seen in our photometric data over time intervals between 1 h and 1.5 h, compare to a minimum aspect ratio (ratio of the long to short axes lengths for a prolate ellipsoid rotating about its small axis) of about 1.6 to 1.7. These values are slightly larger than that measured by Hsieh et al. (2004), which could be due to the different aspect angles of the varying nucleus cross-section along the orbit of the object.

\begin{figure} \par\includegraphics[width=7.8cm,clip]{aa13339-09-fig8.ps} \end{figure} Figure 8:

The measured \ensuremath {P_Q} valuesas a function of the phase angle in the R (red circles) and V (blue squares) filters. The solid lines show the best-fit relation obtained with a second order polynomial expansion constrained to pass through (0, 0).

Open with DEXTER

3.4 Imaging polarimetry

\begin{figure} \par\includegraphics[width=7.8cm,clip]{aa13339-09-fig9.ps} %\end{figure} Figure 9:

Distribution of the \ensuremath {P_U} values expressed in units of errorbar. The vertical dotted lines refer to the 3-$\sigma $ detection level.

Open with DEXTER

Polarimetry was calculated using the method outlined, e.g., by Bagnulo et al. (2006) and Bagnulo et al. (2008). Null parameters (see Bagnulo et al. 2009) were also systematically calculated to check the reliability of the results. The final reduced Stokes parameters \ensuremath {P_Q} and \ensuremath {P_U} were obtained by adopting as a reference direction the perpendicular to the great circle passing through the object and the Sun, using Eq. (5) of Bagnulo et al. (2006). In this way, $\ensuremath{P_Q} $ represents the flux perpendicular to the plane defined by the Sun, Object, and Earth (the scattering plane) minus the flux parallel to that plane, divided by the sum of these fluxes. Our final polarimetric measurements are reported in Table 3. Figure 8 shows \ensuremath {P_Q} results as a function of the phase angle in both filters.

For symmetry reasons, $\ensuremath{P_U} $ values are always expected to be zero, and inspection of their values allows us to perform an indirect quality check of the \ensuremath {P_Q} values. Figure 9 shows the distribution of the \ensuremath {P_U} values in the R and V filters expressed in errorbar units. Since the distribution appears to be peaked at about zero, and none of the \ensuremath {P_U} values exceed a 3-$\sigma $ detection, this test represents a positive quality check of our polarimetric measurements of 133P/Elst-Pizarro.

3.4.1 Polarimetry of the tail

We attempted to measure the polarization of the tail, but, not unexpectedly, the low signal-to-noise ratio prevented us from obtaining accurate measurements. The highest precision was reached in the images obtained on 13 July 2007 and 17 July 2007, where \ensuremath {P_Q} and \ensuremath {P_U} could be measured with a ${\sim} 3$% errorbar. In the R filter, we integrated the signals over an area of 110 and 130 pixels, respectively, and we obtained $\ensuremath{P_Q} =-1.60\pm 3.0$% and $\ensuremath{P_U} =-0.5\pm 3.0$% on 13 July 2007, and $\ensuremath{P_Q} =-1.1\pm 2.5$% and $\ensuremath{P_U} =0.4\pm 2.5$% on 17 July 2007. On the image obtained on 5 August 2007, we integrated over a 40 pixel area of the tail, and we obtained $\ensuremath{P_Q} =-1.0\pm 3.8$% $\ensuremath{P_U} =1.6\pm 3.8$%. In all cases, the null parameters were consistent with zero at the 1.5$\sigma $ level.

3.4.2 Identifying the polarization of the nucleus

We now discuss whether our measurements can be considered representative of the nucleus of 133P/Elst-Pizarro, and to what extent they are contaminated by the coma and tail of the object.

We used the results obtained in the polar coordinate system to estimate the true fluxed produced by the nucleus of 133P/Elst-Pizarro within the aperture used for our polarimetric measurements (see Col. 8 of Table 3), and we found that for the apertures selected for the polarimetric measurements, the contributions from the coma were between 0.05 and 0.1 mag, while the contribution from tail was generally 0.02-0.03 mag. We can therefore assume that, for the aperture values used for polarimetry, at least about 90% of the measured flux is related to the nucleus contribution. Assuming that the flux contribution due to coma and tail is entirely produced by a dust scattering mechanism rather than gas emission, we conclude that the radiation due to coma and tails is either parallel to the light reflected by the nucleus, or perpendicular to it. This hypothesis is supported by all of our \ensuremath {P_U} measurements being consistent with zero. Following Eq. (1) of Bagnulo et al. (2008), we can thus write the nucleus polarization \ensuremath{P^{\rm N}_{Q}} as

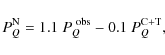
\begin{displaymath}% \ensuremath{P^{\rm N}_{Q}} = 1.1~\ensuremath{P^{\rm ~obs}_{Q}} - 0.1~\ensuremath{P^{\rm C+T}_{Q}} , \end{displaymath} (9)

where \ensuremath{P^{\rm ~obs}_{Q}} is the total observed polarization, and \ensuremath{P^{\rm C+T}_{Q}} is the fraction of linear polarization of the light scattered by coma and tail. For instance, if coma and tail are not polarized ( \ensuremath{P^{\rm C+T}_{Q}}= 0), the nucleus polarization is underestimated (in absolute value) by about 10%; if coma and tails are polarized at a 3% level parallel to the scattering plane ( $\ensuremath{P^{\rm C+T}_{Q}} =-3$%), the observed polarization minimum of about -1.5% would correspond, for the nucleus, to ${\sim} {-}1.35$%; if coma and tails are polarized at a 3% level perpendicular to the scattering plane (for the case of Fresnel-reflection mechanism), the observed polarization minimum will be $\ensuremath{P^{\rm N}_{Q}} =-1.95$%. We note that our direct measurements presented in Sect. 3.4.1, although affected by large errorbars, seem more consistent with a negative value of the tail polarization than a positive one, and infer that the fraction of tail linear polarization is very similar to the fraction of polarization from the nucleus plus tail. Our dataset does not allow us to go beyond these qualitative statements, yet our conclusion is that the observed polarization is representative of the polarization of the nucleus of 133P/Elst-Pizarro. The following analysis will be based on this conclusion.

3.4.3 Characterization of the polarimetric curve

As for the large number of atmosphere-less solar system bodies, the nucleus of the 133P/Elst-Pizarro exhibits the phenomenon of negative polarization: at small phase angles, the electric field vector component parallel to the scattering plane predominates over the perpendicular component, in contrast to what is expected from the simple single Rayleigh-scattering or Fresnel-reflection model. This phenomenon is generally explained in terms of coherent backscattering (e.g., Muinonen 2004). For small bodies of the solar system, the polarization reaches a minimum value generally between phase angle 7$^\circ$ and 10$^\circ$, and becomes positive at phase angles of between 17$^\circ$ and 22$^\circ$ (e.g., Penttilä et al. 2005). In conclusion, for those small bodies for which it is possible to measure the behaviour of the polarization for an extended range of phase angles, three important characteristics can be measured well, and used to perform an empirical classification: the minimum polarization and its corresponding phase angle, the slope of the polarimetric curve in the linear part beyond polarization minimum, and the inversion angle at which the polarization changes from being parallel to the scattering plane and becomes, at larger phase angles, perpendicular to the scattering plane. Following these guidelines, we perform an analysis of our polarimetric data for the nucleus of 133/Elst-Pizarro.

Inspection of Fig. 8 shows that measurements in both the R and V filters agree within the errors (except for a point at phase angle 3$^\circ$). Nevertheless, we perform our basic analysis based on the measurements obtained in the R and V filters separately.

The best-fit relation obtained using a second order polynomial (constrained to pass through the origin) shows that in the R filter, the minimum is reached at phase angle $\alpha_R^{\rm min}=8.8\hbox{$^\circ$ }\pm 0.6\hbox{$^\circ$ }$, for a minimum polarization value of $\ensuremath{P_Q} ^{\rm min}(R)=-1.30 \pm 0.20$%. In the V filter, the minimum is reached at phase angle $\alpha_V^{\rm min}=8.5\hbox{$^\circ$ }\pm 0.5\hbox{$^\circ$ }$, with a minimum polarization value of $\ensuremath{P_Q} ^{\rm min}(V)=-1.57 \pm 0.20$%. The positive crossover, when the observed polarization changes sign from negative to positive, is at phase angle $\alpha_R(\ensuremath{P_Q} =0) = 17.6\hbox{$^\circ$ }\pm 2.1\hbox{$^\circ$ }$ in the R filter, and at phase angle $\alpha_V(\ensuremath{P_Q} =0) = 17.0\hbox{$^\circ$ }\pm 1.6\hbox{$^\circ$ }$ in the V filter.

Using a second order polynomial, the slope of the polarization depends clearly on the phase angle in which it is calculated. With reference to the the crossover point, the polarization slopes are

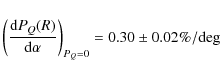
\begin{displaymath}\left(\frac{{\rm d}\ensuremath{P_Q} (R)}{{\rm d}\alpha}\right)_{\ensuremath{P_Q} =0} = 0.30 \pm 0.02\%{\rm /deg} \end{displaymath}

and

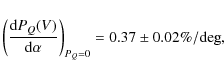
\begin{displaymath}\left(\frac{{\rm d}\ensuremath{P_Q} (V)}{{\rm d}\alpha}\right)_{\ensuremath{P_Q} =0} = 0.37 \pm 0.02\%{\rm /deg}, \end{displaymath}

for the R and the V filter, respectively. We note however that these estimates are obtained based on the assumption that the measurements may be fitted with a second order polynomial.

\begin{figure} \par\includegraphics[width=16cm,clip]{aa13339-09-fig10.ps} \end{figure} Figure 10:

Polarimetric observations of the nucleus of comet 2P/Encke ( left panel) and of 133P/Elst-Pizarro ( right panel), modeled using MCMC for the empirical linear-exponential model. Blue squares refer to V Bessell filter, and red circles to R Bessell filter. For 2P/Encke, red and blue asterisks refer to narrow band filters centred about 834 and 485 nm, respectively. The best-fit models are shown with solid line, while the 3$\sigma $ error envelopes are shown with dashed lines.

Open with DEXTER

3.4.4 Relationships between polarization and albedo

For asteroids, two empirical relationships have been found between the polarization characteristics and the albedo, namely, both slope and polarization minimum seem to be related to the geometric albedo of the body by means of a simple expression as given, e.g., by Lupishko & Mohamed (1996)

\begin{displaymath}% \log(p) = -0.98 \log\left(\frac{{\rm d}\ensuremath{P_Q} }{{\rm d}\alpha}\right)_{\ensuremath{P_Q} =0} - 1.73 \end{displaymath} (10)

and

\begin{displaymath}% \log(p) = -1.22 \log\left(\ensuremath{P_Q} ^{\rm min}\right) - 0.92, \end{displaymath} (11)

where p is the albedo, ${\rm d}\ensuremath{P_Q} /{\rm d}\alpha$ is the derivative of the observed linear polarization with respect to phase angle, and $\ensuremath{P_Q} ^{\rm min}$ is the minimum value of the polarization. Using Eq. (10), from our data we obtain for the albedo the values $p_R = 0.061 \pm 0.004$ in the R filter, and $p_V = 0.049 \pm 0.003$ in the V filter. Using Eq. (11), we obtain $p_R = 0.087 \pm 0.017$ and $p_V = 0.069\pm 0.011$. Their average values correspond to about pR= 0.07 and pV= 0.06, uncertainties being about 0.01.

The average albedo value obtained from our polarization measurements agrees remarkably well with that determined via the classical method of combined visible and thermal flux measurements of 133P/Elst-Pizarro, i.e., $p_R=0.05\pm0.02$ as published by Hsieh et al. (2009). However, it remains to be shown that the albedo-polarization relationships are indeed applicable to our target since they were verified and calibrated using asteroid data for different taxonomic types than those that we have found for 133P/Elst-Pizarro (see Sect. 4).

Table 4:   MCMC parameters for 133P/Elst-Pizarro, 2P/Encke, and (1) Ceres.

4 Discussion

There are two main aspects to the properties of 133P/Elst-Pizarro. On the one hand, it is located in the asteroid belt with an orbit similar to the Themis collision family or a subgroup of it, the Beagle family, and over a large part of its orbital revolution it appears asteroid-like. On the other hand, around and after perihelion it displays activity producing a dust tail, as comets do. In the following, we discuss whether our new polarimetric measurements could help us to identify whether it is an asteroid (with cometary activity) or a comet (scattered into the asteroid belt).

We first compare the polarimetric curve of the nucleus of 133P/Elst-Pizarro with that of the nucleus of comet 2P/Encke (Boehnhardt et al. 2008) by making use of the scattering parametrisation provided in Muinonen et al. (2009b,a). By using lines of electric dipoles with an inverse-gamma distribution for the line lengths, and by estimating the parameters with a Markov-Chain Monte-Carlo (MCMC) method (see, e.g., Muinonen et al. 2009b), we have computed, for 133P/Elst-Pizarro and 2P/Encke, physical interference models. The eight parameters of the full model are: the exponents or shape parameters s1 and s2 and the scale parameters y1 and y2 of the inverse-gamma distributions for the two polarization states (subscripts 1 and 2 are for positive and negative states, respectively); the complex amplitude Z and interdipole distance kd3 ( $k=2\pi/\lambda$is the wave number and d3 the physical distance) for the longitudinal electric-dipole contribution; and the normalized weight w of the Rayleigh-like contribution to the polarization curve.

For 133P/Elst-Pizarro and 2P/Encke, reduced six parameter models already suffice to explain the polarimetric observation. We assume that s1=s2=s and fix $kd_3=\pi$. Least squares fitting analysis and MCMC sampling provide the polarization curve corresponding to the best-fit relations (solid lines), and in the 3$\sigma $ error envelopes (dashed lines) depicted in Fig. 10. Best-fit model parameters and their 3$\sigma $ errors are given in Table 4. Among the parameters, the weights w, exponents s and scale parameters y1 and y2 are of importance for the present study. The weights w obtained realistic values w > 0.5, which, in the physical model, indicate a positive contribution from point-like Rayleigh scatterers in addition to the contributions from the lines of dipoles. The exponents s and the scale parameters y1 and y2 are loosely constrained by the polarimetric data in the current case of considerable observational errors.

In addition to 2P/Encke and 133P/Elst-Pizarro, the physical model has so far been applied only to the polarimetric data of asteroid (1) Ceres (Muinonen et al. 2009b). The corresponding best-fit model parameters are given in Table 4.

We conclude that it is too early to reach definitive conclusions using MCMC models, beyond that the polarization characteristics of 133P/Elst-Pizarro are closer to those of (1) Ceres than those of 2P/Encke. The polarimetric slope at the inversion angle is larger for 133P/Elst-Pizarro than for (1) Ceres. All three weights w can overlap within their 3-$\sigma $ error domains and the same is true for the scale parameter y2. Mainly in terms of the scale parameter y1, 2P/Encke differs from the others.

A more statistically meaningful approach is offered by a straight comparison of the photometric and polarimetric properties of 133P/Elst-Pizarro with those of different types of asteroids, cometary dust, Centaurs and Kuiper-Belt objects. Table 2 of Boehnhardt et al. (2008) lists the typical numerical values for albedo, slope of the photometric phase function, spectral gradient, minimum polarization and the related phase angle, slope of the polarization phase function, inversion angle, and spectral gradient of the polarization for different classes of small bodies of the solar system. A comparison with the values of 133P/Elst-Pizarro derived in this work allows us to conclude that 133P/Elst-Pizarro does not exhibit the typical properties of Kuiper-Belt objects and Centaurs, C, S, E and M type asteroids, cometary dust, while there is a rather good agreement in all parameters with those of F-type asteroids.

F-type asteroids are considered to be primitive (Bus et al. 2002), and they are sometimes claimed to be related to comet-like objects (Weissman et al. 2002). A weakness in this comparison is the meager knowledge of polarimetric parameters of certain types of small bodies, such as cometary nuclei, Centaurs, and also F-type asteroids themselves (although the polarimetric dataset for F-type asteroids is substantially larger than that for Centaurs and cometary nuclei). However, if the parameter similarity between 133P/Elst-Pizarro and F-type asteroids is to be seen as an indicator of the similarity of these objects, one can predict that more objects with cometary activity will be found among asteroids with F-type taxonomy.

Licandro et al. (2007a) assigned 133P/Elst-Pizarro a C- or B-type classification taxonomy classes to which F-type asteroids are closely related to (the water absorption feature around 3 $\mu$m is missing and differences in the continuum below 0.4 $\mu$m exist for F-type objects). Other notable, peculiar C-class objects include 107P/Wilson-Harrington (C- or F-type; Tholen & Barucci 1989), 3200 Phaethon (B- or F-type; Licandro et al. 2007b; Tholen & Barucci 1989), and 2005 UD (B- or F-type; Kinoshita et al. 2007; Jewitt & Hsieh 2006). The former two objects at least have displayed cometary activity in the past. An F-type 133P/Elst-Pizarro would thus have good company with respect to cometary activity.

Comet migration into the asteroid belt does not seem to be a very efficient process dynamically (Levison et al. 2006), and the ``snowline'', i.e., the distance to the Sun at which water vapour in the protoplanetary disk condenses and becomes accreted in forming planetesimal, falls into the (outer) asteroid belt. Therefore, one may be inclined to accept 133P/Elst-Pizarro as a ``child of the inner solar system'', and not of the cold outskirts where cometary nuclei originate. Our observational results are certainly compatible with this scenario, although it implies that cometary activity can also occur in asteroids. The dust activity in 133P/Elst-Pizarro and the other so-called ``main-belt comets'' require a driving mechanism. Ice sublimation is considered a possibility, but is not as yet supported by observational evidence.

5 Conclusions

With the FORS1 instrument of the 8 m ESO VLT, we have carried out imaging observations in polarimetric mode of the object 133P/Elst-Pizarro at nine observing epochs. The first observation was performed in May 2007, about one month before perihelion, and the remaining eight from July to September 2007, up to about three months after perihelion. These observations cover the phase-angle range of 0$^\circ$-20$^\circ$.

Our images have detected one or two tails close to perihelion, and, to a marginal level of evidence, the presence of a coma. We have then performed an analysis of the dust production. The dust release of 133P/Elst-Pizarro may have started about one month before perihelion passage and continued at least until about three months after perihelion. The onset of dust activity in 2007 happened earlier than concluded for the 1996 apparition of the comet by Pravec & Sekanina (1996) and Boehnhardt (1996), although, admittedly, the latter analyses could not really constrain dust release before perihelion passage. However, the dust release in 133P/Elst-Pizarro is clearly repetitive and it starts and extends around perihelion passage. The dust grains that dominate the optical appearance of the tail were of micrometer size and larger, and were released at a relatively low speed. The appearance of the tail in 2007 resembles that seen in 1996, although the two tail patterns refer to different emission periods with respect to perihelion passage. The 1996 tail appearance supports the scenario of dust production that continued for up to half a year after perihelion passage. Considering the results of Hsieh et al. (2004), the active period would even extend to about a year after perihelion. The dust tails seen in 133P/Elst-Pizarro during the 1995, 2002, and 2007 apparitions support the concept that the activity of 133P/Elst-Pizarro is recurrent and that it extends over the same arc of the orbit (from about 1 month before perihelion to at least 1 year after perihelion). A possible yet unproven scenario, described in greater detail by Hsieh et al. (2004) and implicitly assumed also in earlier publications by Pravec & Sekanina (1996) and Boehnhardt et al. (1997), is that a main region of local activity is switched on - possibly due to solar illumination - shortly before perihelion and continues to be active along the orbit over a year or so. The repetitive behaviour of the activity would suggest a rather stable orientation of the rotation axis over the past three apparitions of 133P/Elst-Pizarro. The activity level of the nucleus is not very high and produces micron-size dust at low speed. The true release mechanism could not be constrained from our observations.

We have used our observations to characterize the polarimetric and photometric behaviour of the object as a function of its phase-angle, and we have compared it to that of the nucleus of comet 2P/Encke, and other small bodies of the solar-system. In particular, the comparison with the polarimetric curve of 2P/Encke was performed by adopting a physical classification tool for the polarization phase curves, but our results are not conclusive because current lack of a statistically meaningful sample of objects that have been analysed in a similar fashion. However, a direct comparison of the polarimetric and photometric curves identified several similarities with the observational parameters of F-type asteroids.

Acknowledgements
We thank Dr. H. Hsieh for a useful discussion at the early stages of the work, and the anonymous referee for a very careful review of the original manuscript.

References

  1. Appenzeller, I., Fricke, K., Furtig, W., et al. 1998, The Messenger, 94, 1 [NASA ADS] [Google Scholar]
  2. A'Hearn, M. F., Schleicher, D. G., Feldman, P. D., Millis, R. M., & Thompos, D. T. 1984, AJ, 89, 579 [NASA ADS] [CrossRef] [Google Scholar]
  3. Bagnulo, S., Boehnhardt, H., Muinonen, K., et al. 2006, A&A, 450, 1239 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Bagnulo, S., Belskaya, I., Muinonen, K., et al. 2008, A&A, 491, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Bagnulo, S., Landolfi, M., Landstreet, J. D., et al. 2009, PASP, 121, 993 [NASA ADS] [CrossRef] [Google Scholar]
  6. Boehnhardt, H. 1996, IAUC, 6473 [Google Scholar]
  7. Boehnhardt, H., Sekanina, Z., Fiedler, A., et al. 1997, Highlights Astron., 11A, 233 [Google Scholar]
  8. Boehnhardt, H., Bagnulo, S., Muinonen, K., et al. 2004, A&A, 415, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Boehnhardt, H., Tozzi, G. P., Bagnulo, S., et al. 2008, A&A, 489, 1337 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Beisser, K. 1990, Ph.D. Thesis, Univ. Erlangen [Google Scholar]
  11. Beisser, K., & Drechsel, H. 1992, Ap&SS, 181, 1 [NASA ADS] [CrossRef] [Google Scholar]
  12. Bus, S. J., Vilas, F., & Barucci, M. A. 2002, in Asteroids III, ed. W. F. Bottke, A. Cellino, P. Paolicchi, & R. P. Binzel (Tucson: Univ. Arizona Press), 169 [Google Scholar]
  13. Donati, J.-F., Semel, M., Carter, B. D., et al. 1997, MNRAS, 291, 658 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  14. Elst, E. W., Pizarro, O., Pollas, C., et al. 1997, IAU Circ., 6456 [Google Scholar]
  15. Hsieh, H. H., & Jewitt, D. C. 2006, Science, 312, 561 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  16. Hsieh, H. H., Jewitt, D. C., & Fernandez, Y. R. 2004, AJ, 127, 2997 [NASA ADS] [CrossRef] [Google Scholar]
  17. Hsieh, H. H., Jewitt, D. C., & Fernandez, Y. R. 2009, ApJ, 694, L111 [NASA ADS] [CrossRef] [Google Scholar]
  18. Jewitt, D., & Hsieh, H. H. 2006, AJ, 132, 1624 [NASA ADS] [CrossRef] [Google Scholar]
  19. Jewitt, D. C., Lacerda, P., & Peixinho, N. 2007, IAUC, 8847 [Google Scholar]
  20. Kinoshita, D., Ohtsuka, K., Sekiguchi, T., et al. 2007, A&A, 466, 1153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Lamy, P. L., Toth, I., Fernandez, Y. R., & Weaver, H. A. 2004, in Comets II, ed. M. C. Festou, H. U. Keller, & H. A. Weaver (Tucson: Univ. Arizona Press), 223 [Google Scholar]
  22. Lamy, P. L., Toth, I., A'Hearn, M. F., et al. 2007a, Icarus, 187, 132 [NASA ADS] [CrossRef] [Google Scholar]
  23. Lamy, P. L., Toth, I., A'Hearn, M. F., et al. 2007b, Icarus, 191, 310 [NASA ADS] [CrossRef] [Google Scholar]
  24. Lamy, P. L., Toth, I., Davidsson, B., et al. 2007c, SSRv, 128, 223 [Google Scholar]
  25. Levison, H. F., Terrell, D., Wiegert, P. A., et al. 2006, Icarus, 182, 161 [NASA ADS] [CrossRef] [Google Scholar]
  26. Li, J. Y., A'Hearn, M. F., Belton, M. J. S., et al. 2007a, Icarus, 187, 41 [NASA ADS] [CrossRef] [Google Scholar]
  27. Li, J. Y., A'Hearn, M. F., Belton, M. J. S., et al. 2007b, Icarus, 187, 195 [NASA ADS] [CrossRef] [Google Scholar]
  28. Licandro, J., Pinilla Alonso, N., de Leon J., et al. 2007a, BAAS, 38, 470 [NASA ADS] [Google Scholar]
  29. Licandro, J., Campins, H., Motte-Diniz, T., et al. 2007b, A&A, 461, 751 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Lupishko, D. F., & Mohamed, R. A. 1996, Icarus, 11, 209 [NASA ADS] [CrossRef] [Google Scholar]
  31. Marsden, B. G., 1996, IAU, Circ., 6457 [Google Scholar]
  32. Muinonen, K. 2004, Waves in Random Media, 14, 365 [NASA ADS] [CrossRef] [Google Scholar]
  33. Muinonen, K., Piironen, J., Shkuratov, Y. G., & Ovcharenko, A. 2002, in Asteroids III, ed. W. F. Bottke, A. Cellino, P. Paolicchi, & R. P. Binzel (Tucson: Univ. Arizona Press), 123 [Google Scholar]
  34. Muinonen, K., Tyynelä, J., Zubko, E., & Videen, G. 2009a, Scattering parameterization for interpreting asteroid polarimetric and photometric phase effects, Earth, Planets, and Space, in press [Google Scholar]
  35. Muinonen, K., Tyynelä, J., Zubko, E., & Videen, G. 2009b, Coherent backscattering in planetary regoliths. Light Scattering Reviews, in press [Google Scholar]
  36. Nesvorný, D., Bottke, W. F., Vokrouhlický, D., et al. 2008, ApJ, 679, L143 [NASA ADS] [CrossRef] [Google Scholar]
  37. Penttilä, A., Lumme, K., Hadamcik, E., & Levasseur-Regourd, A. C. 2005, A&A, 432, 1081 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Pravec, P., & Sekanina, Z. 1996, IAUC, 6459 [Google Scholar]
  39. Snodgrass, C., Lowry, S. C., & Fitzsimmons, A. 2008, MNRAS, 385, 737 [Google Scholar]
  40. Shurcliff, W. A. 1962, Polarized Light (Cambridge, Mass: Harward University Press) [Google Scholar]
  41. Tholen, D. J., & Barucci, M. A. 1989, in Asteroids II, ed. R. P. Binzel, T. Gehrels, & M. S. Matthews (Tucson: Univ. Arizona Press), 289 [Google Scholar]
  42. Toth, I. 2006, A&A 446, 333 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Tozzi, G. P., & Lincandro, J. 2002, Icarus, 157, 187 [NASA ADS] [CrossRef] [Google Scholar]
  44. Tozzi, G. P., Lara, L. M., Kolokolova, L., et al. 2004, A&A, 424, 325 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Tozzi, G. P., Boehnhardt, H., Kolokolova, K., et al. 2007, A&A, 476, 979 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Tubiana, C., Barrera, L., Drahus, M., & Boehnhardt, H. 2008, A&A, 490, 377 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Weissman, P. R., Bottke, W. F., & Levison, H. F. 2002, in Asteroids III, ed. W. F. Bottke, A. Cellino, P. Paolicchi, & R. P. Binzel (Tucson: Univ. Arizona Press), 669 [Google Scholar]

Footnotes

... 133P/Elst-Pizarro[*]
Based on observations made with ESO Telescopes at the Paranal Observatory under programme ID 079.C-0653 (PI = Tozzi).
... Monitor[*]
Online data available at the ESO web site.
... SEXTRACTOR[*]
http://astromatic.iap.fr/software/sextractor
... it[*]
We note that the measured tail Af values may be possibly overestimated by up to 10% because of a faint coma (see Sect. 3.2).

All Tables

Table 1:   Geometric information about the dust tails of 133P/Elst-Pizarro.

Table 2:   Photometry of comet 133P/Elst-Pizarro.

Table 3:   Polarization measurements of 133P/Elst-Pizarro.

Table 4:   MCMC parameters for 133P/Elst-Pizarro, 2P/Encke, and (1) Ceres.

All Figures

  \begin{figure} \par\includegraphics[width=9cm,clip]{aa13339-09-fig1.eps} \end{figure} Figure 1:

Contour plots of Af in R and V Bessell filter ( left and right columns, respectively). North is up, and east to the left. The black arrow and red arrow represent the direction of the Sun, and the negative target velocity as seen from the observer in the plane of the sky, respectively. The x and y axes are in units of 103 km. Contour levels are calibrated in Af (for explanations see text). Contour levels correspond to $Af=7.0 \times 10^{-9}$, $8.3 \times 10^{-9}$, $1.0 \times 10^{-8}$, $1.25 \times 10^{-8}$, $1.65 \times 10^{-8}$, $2.5 \times 10^{-8}$, and $5 \times 10^{-8}$.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{aa13339-09-fig2.ps}\vspace*{-1mm}\end{figure} Figure 2:

Contour plots of Af in R Bessell filter for the combined image obtained on July 17. Contour levels correspond to $Af = 2 \times 10^{-9}$, $4 \times 10^{-9}$, and $6 \times 10^{-9}$.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=16cm,clip]{aa13339-09-fig3.ps} \end{figure} Figure 3:

Tail Af measured along the direction identified by the tail, with respect to the photometric center, and tail colour indices V-R. In the left and middle column panels, green lines show the zero axes (corresponding to the nucleus position). In the right panels, they correspond to the colour index derived for the nucleus.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.5cm,clip]{aa13339-09-fig4.ps} \end{figure} Figure 4:

From top to bottom: $\mathcal{N}$, $\mathcal{N}'$, and $\mathcal{N}''$ profiles for a background reference star (blue thick lines) and for the object 133P/Elst-Pizarro (red thin lines), observed on 22 May 2007 in the R filter. All profiles are plotted versus the aperture measured in pixels (for 133P/Elst-Pizarro, on 22 May 2007, a 0.25 $^{\prime \prime }$pixel corresponds to 365 km). Together with the $\ensuremath{\mathcal{N}_{\rm tot}} (a)$ profile (solid lines), the top panel shows also the two contributions $\ensuremath{\mathcal{N}_{\rm N}} (a)$ (dashed lines), and $\ensuremath{\mathcal{N}_{\rm C}} (a)$ (lower dotted lines).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{aa13339-09-fig5.ps} \end{figure} Figure 5:

$Af\rho $for the coma on 22 May 2007. Red circles refer to R filter, blue squares to V filter. Dashed lines mark the average $Af\rho $ values in the two filters, obtained neglecting the points marked with empty symbols.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{aa13339-09-fig6.ps} \end{figure} Figure 6:

Photometry in the R (red circles) and V (blue squares) filters for 133P/Elst-Pizarro as function of time, obtained on 22 May 2007. Filled symbols refer to the photometry obtained from the polarimetric images, empty symbols refer to the photometry obtained from the images with no polarimetric optics in. Asterisks show the photometry obtained from the averaged polarimetric images. Point at t=0 is obtained from the acquisition image of the polarimetric series.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.4cm,clip]{aa13339-09-fig7.ps} \end{figure} Figure 7:

Photometry in the R (red circles) and V (blue squares) filters for 133P/Elst-Pizarro as function of the phase angle. Solid lines show the corresponding linear best-fits. Points that were not used to calculate the best-fit are represented with empty symbols.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.8cm,clip]{aa13339-09-fig8.ps} \end{figure} Figure 8:

The measured \ensuremath {P_Q} valuesas a function of the phase angle in the R (red circles) and V (blue squares) filters. The solid lines show the best-fit relation obtained with a second order polynomial expansion constrained to pass through (0, 0).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.8cm,clip]{aa13339-09-fig9.ps} %\end{figure} Figure 9:

Distribution of the \ensuremath {P_U} values expressed in units of errorbar. The vertical dotted lines refer to the 3-$\sigma $ detection level.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=16cm,clip]{aa13339-09-fig10.ps} \end{figure} Figure 10:

Polarimetric observations of the nucleus of comet 2P/Encke ( left panel) and of 133P/Elst-Pizarro ( right panel), modeled using MCMC for the empirical linear-exponential model. Blue squares refer to V Bessell filter, and red circles to R Bessell filter. For 2P/Encke, red and blue asterisks refer to narrow band filters centred about 834 and 485 nm, respectively. The best-fit models are shown with solid line, while the 3$\sigma $ error envelopes are shown with dashed lines.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.