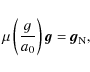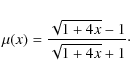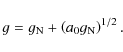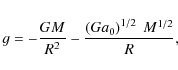| Issue |
A&A
Volume 514, May 2010
|
|
|---|---|---|
| Article Number | A101 | |
| Number of page(s) | 8 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/200913301 | |
| Published online | 28 May 2010 | |
Understanding local dwarf spheroidals and their scaling relations under MOdified Newtonian Dynamics
X. Hernandez1,2 - S. Mendoza1 - T. Suarez1 - T. Bernal1
1 - Instituto de Astronomía, Universidad Nacional
Autónoma de Mexico, AP 70-264, Ciudad Universitaria, Distrito Federal
04510, Mexico
2 - GEPI, Observatoire de Paris, Meudon Cedex, France
Received 15 September 2009 / Accepted 23 November 2009
Abstract
We use a specific form of the interpolation function in the MOND
formalism, which optimally accounts for the internal structure of dwarf
spheroidal (dSph) galaxies, to explore the consequences it has on the
scaling relations seen in these systems.
The particular form of the interpolation function we used leads to a
law of
gravity that does not degrade the good fit
of the MOND proposal on galactic scales, and in fact, slightly
improves the accordance with observations on dSph scales. This
formalism
yields a good description of gravitational phenomena
without the need of invoking any still undetected and
hypothetically dominant dark matter, in the weak field regime probed
by local dSph galaxies.
Isothermal equilibrium density
profiles then yield projected surface density profiles for the local
dSph
galaxies in very good agreement with observational determinations, for
values of the relevant parameters as inferred from recent observations
of these Galactic satellites. The observed scaling relations for these
systems are also naturally accounted for within the proposed scheme,
including a previously unrecognised correlation of the inferred
mass-to-light
ratios of local dSph's with the ages of their stellar populations,
which is natural in modified gravity schemes in the absence of dark
matter.
The results shed some light on the form that the MOND interpolating
function may have in the most challenging regime, which occurs at
moderate accelerations and intermediate mass-weighted lengths.
Key words: gravitation - galaxies: dwarf - galaxies: kinematics and dynamics - dark matter - Local Group
1 Introduction
If one wants to explore options where the existence of dark matter is not a necessity, one must consider variations in the law of gravity on galactic and extra-galactic scales where dark matter has been proposed to account for the observed dynamics. The best-studied such proposal is the MOdified Newtonian Dynamics (MOND) hypothesis of Milgrom (1983), which has been shown to account for the rotation curves of spiral galaxies (e.g. Sanders & McGaugh 2002), naturally incorporating the Tully-Fisher relation, see for example Milgrom (2008a) and references therein.
Abundant recent publications of the velocity dispersion measurements of stars in the local dwarf spheroidal (dSph) galaxies, the extended and flat rotation curves of spiral galaxies, the high dispersion velocities of galaxies in clusters, the gravitational lensing due to massive clusters of galaxies, and even the cosmologically inferred matter content for the universe, are all successfully modelled using MOND, not as indirect evidence of a dominant dark matter component, but as direct evidence of the failure of the current Newtonian and general relativistic theories of gravity, in the large-scale or low-acceleration regimes relevant to the above. Some recent examples of the above are Milgrom & Sanders (2003), Sanders & Noordermeer (2007), Nipoti et al. (2007), Famaey et al. (2007), Gentile et al. 2007), Tiret et al. (2007) and Sanchez-Salcedo et al. (2008).
The range of galactic dynamical problems treated with the MOND formalism has extended from the first-order gravitational effects of rotation curves and velocity dispersion measurements to cover a wide range of more subtle problems. With their role in limiting the sizes of satellites and establishing in MOND escape velocities for satellites or galaxies subject to an external acceleration field, tidal forces were studied by Sanchez-Salcedo & Hernandez (2007). Wu et al. (2008) calculated the escape velocity for the Milky Way using both MOND and dark matter, and conclude that the LMC appears as bound from both points of view, in spite of the recently determined high proper motion for this object, with slightly better fits using the MOND prescription. Sanchez-Salcedo et al. (2008) looked at the thickness of the extended HI disk of the Milky Way from both angles and find a somewhat better fit to observations in the MOND theory. Sanchez-Salcedo et al. (2006) and Nipoti et al. (2008) examined the problem of dynamical friction in dSph galaxies, comparatively assuming Newtonian gravity or MOND, with decay timescales for globular clusters being somewhat shorter in MOND. This is a potential problem, unless one allows large initial orbital radii for the observed globular clusters beyond the current extent of the stellar populations.
Going to cosmological scales, Skordis et al. (2006) have studied the cosmic microwave background, Halle et al. (2008) looked at the problem of the cosmic growth of structure, Zhao et al. (2006) studied gravitational lensing of galaxies, and Angus et al. (2007) and Milgrom & Sanders (2008) studied dynamics of clusters of galaxies. All of the above find the MOND description of the problem to be a viable option within the observational errors of the relevant determinations, despite the need to include some unseen mass on galaxy cluster scales. Options for the above include the cluster baryonic dark matter proposed by Milgrom (2008b), or the inclusion of neutrinos, whether active as studied by Sanders (2003) and Angus et al. (2007) or sterile as proposed by Angus et al. (2010), always within plausible expectations. Also, in spiral galaxies, although within observational errors, rotation curves have been reported by Gentile et al. (2007) and Corbelli & Salucci (2007) to be somewhat less well-fitted assuming the MOND prescription than when using cored dark matter haloes.
Observationally, it appears that MOND fares as well as dark matter in accounting for measured dynamics, in all but the smallest scales, the case of local dSph galaxies remains the most controversial. Published studies using MOND, which typically assume the deep MOND regime, sometimes find a different value for the acceleration scale of the theory for different dSph galaxies, when fitting detailed dynamical models to the data (Lokas 2001), or that M/L ratios remain higher than those of stellar populations, making dark matter necessary even under the MOND formulation, e.g., Sanchez-Salcedo & Hernandez (2007). Still, this last point remains somewhat controversial. Angus (2008) suggests that the MOND proposal will hold for local dSph galaxies, once the effects of tidal disruption are adequately incorporated.
Regarding corresponding theoretical developments, numerous alternative theories of gravity have recently appeared (Bekenstein 2004; Sanders 2005; Sobouti 2007; Mendoza & Rosas-Guevara 2007; Bruneton & Esposito-Farese 2007; Zhao 2007; Arbey 2008), now mostly grounded on geometrical extensions of general relativity and field theory, which lead to laws of gravity in the Newtonian limit that in the large-scale or low-acceleration regime reduce to the MOND prescription fitting formula.
The MOND theory is characterised by: (i) a low acceleration
regime where dynamics mimic the presence of dark matter; (ii) a
high acceleration regime where Newtonian gravity is recovered; and
(iii) a somewhat ill-defined transition region. Variants of MOND
are defined by the form of the interpolation function, ![]() ,
which mediates the transition between the two limit regimes, see Eq. (1).
,
which mediates the transition between the two limit regimes, see Eq. (1).
We show how the MOND prescription with a suitable interpolation function, such as the one used by Bekenstein (2004) and used by Famaey & Binney (2005), can be written as the addition of both low acceleration limit MOND and Newtonian contributions to the acceleration on all scales. The large differences in scales and magnitudes of the two acceleration terms ensure that the addition does not spoil the good match with observations on galactic scales. We are trying to look for a suitable MOND interpolation function for the local dSph galaxies, but not necessarily one that works on all scales.
This, as it is the regime of the local dSph galaxies, the one which has proven most difficult for MOND, and the one where the high-quality recent observations now available allow for a relatively clean test. We find that this interpolation function not only yields acceptable M/Lvalues for all dSph galaxies without the need for any dark matter in all cases, but also provides a natural explanation for all the scalings seen in these Galactic satellites. An interesting correlation between the M / L ratios inferred and the ages of the stellar populations in local dSph galaxies is found, and naturally accounted for in modified gravity schemes where stars alone account for the gravitational force.
However, on solar system scales, Sanders (2006) has shown this particular interpolation function to be incompatible with limits on the variations of Kepler's constant. Thus, the good accordance we find with observations for dSph's must be understood as evidence in favour of the particular interpolation function we test, at the weak field limit relevant for these systems. What a full interpolation function for MOND should be is a more complicated issue. One, however, which has to be addressed bearing in mind the results presented here.
Section 2 gives a brief summary of the interpolation function first explored by Bekenstein (2004) and gives equilibrium isothermal configurations. These are then used in Sect. 3 to model the local dSph galaxies and obtain M/L ratios, which are found to be consistent with those typical of stellar populations, at the ages of the different dSph systems. Section 4 includes an exploration of the most conspicuous scaling relations for local dSph galaxies, finding that Bekenstein's interpolation function naturally accounts for all features found. Our conclusions are summarised in Sect. 5.
2 A particular form of the interpolating function in the MOND prescription
In terms of the acceleration ![]() felt by a test particle, the MOND
proposal is (see e.g. Milgrom 2002)
felt by a test particle, the MOND
proposal is (see e.g. Milgrom 2002)
where
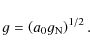
|
(2) |
Strictly speaking, MOND is a theory defined only at the limit values for the acceleration. The value of the constant a0has been reasonably determined by calibrating the deep MOND regime through observations of rotation velocity curves of large spiral galaxies (e.g. Sanders & McGaugh 2002). However, the details of the transition region between the two regimes (i.e. the function
Bekenstein (2004) shows that his relativistic extension of TeVeS in the appropriate non-relativistic limits yields the interpolating function
This particular interpolating function converges to the right limits as
This equation can be thought of as a generalised gravity recipe described by the addition of two terms, the first a standard Newtonian acceleration term and the second the MOND limit acceleration term. Seen in this way, Eq. (4) changes its acceleration behaviour limiting cases to a scale limiting behaviour. Indeed, for the case of a test particle on a gravitational field produced by a central mass M, located at a distance distance R from it, Eq. (4) can be written as
where G is Newton's constant of gravity. Seen in this way, Eq. (5) converges to Newtonian gravity for sufficiently small R / M1/2's and reproduces the MOND strong limit for sufficiently large R / M1/2's, and so the acceleration limits are now ``scale-weighted'' limits. It is worth noting that Eq. (5) is certainly the simplest modification to Newtonian gravity once the weak acceleration MOND regime is known.
Let us now rewrite Eq. (4) in such a way that the
scale weighting becomes clearer. To do so, recall
that
![]() ,
where
,
where
![]() represents the standard
Newtonian potential and
represents the standard
Newtonian potential and
![]() ,
where
,
where ![]() is the scalar
potential of the gravitational field. With this, Eq. (4) can be
written as
is the scalar
potential of the gravitational field. With this, Eq. (4) can be
written as
where
As already mentioned, we are interested in the form of ![]() at scales of the local dSph galaxies. That the particular
at scales of the local dSph galaxies. That the particular ![]() we are testing is incompatible with solar system dynamics implies that a complete
we are testing is incompatible with solar system dynamics implies that a complete ![]() MOND
function is probably complex, that is, if one wants to treat the MOND
formalism as more than just an empirical phenomenological description
of gravitational physics on galactic scales.
On the other hand, some researchers (see e.g. Bekenstein 2006 and references therein) claim that the Pioneer anomaly can be explained by the MOND hypothesis. This assumption
can prove wrong if uneven thermal radiation in the spacecrafts is found
(Toth & Turyshev 2009), which could possibly come from the flyby anomaly
(Turyshev 2009). In other words, the MOND formalism does not appear to be relevant on solar system scales, where General Relativity and
Newtonian Gravity have proven correct (e.g. Turyshev & Toth 2009; Anderson et al. 2002). Still, as discussed by Milgrom (2009),
it is possible that current tests on solar system scales cannot reach
definitive conclusions on the MOND interpolating function.
MOND
function is probably complex, that is, if one wants to treat the MOND
formalism as more than just an empirical phenomenological description
of gravitational physics on galactic scales.
On the other hand, some researchers (see e.g. Bekenstein 2006 and references therein) claim that the Pioneer anomaly can be explained by the MOND hypothesis. This assumption
can prove wrong if uneven thermal radiation in the spacecrafts is found
(Toth & Turyshev 2009), which could possibly come from the flyby anomaly
(Turyshev 2009). In other words, the MOND formalism does not appear to be relevant on solar system scales, where General Relativity and
Newtonian Gravity have proven correct (e.g. Turyshev & Toth 2009; Anderson et al. 2002). Still, as discussed by Milgrom (2009),
it is possible that current tests on solar system scales cannot reach
definitive conclusions on the MOND interpolating function.
For globular clusters, with
![]() ,
,
![]() ,
we get values for
,
we get values for ![]() of between 0.1 and
0.01, and the correction becomes smaller than the errors and
uncertainties in the observational determinations for the values of radii
and masses for globular clusters. For elliptical galaxies and bulges,
with masses going from about 109 to
of between 0.1 and
0.01, and the correction becomes smaller than the errors and
uncertainties in the observational determinations for the values of radii
and masses for globular clusters. For elliptical galaxies and bulges,
with masses going from about 109 to
![]() and radii
of between 0.5 and 10 kpc,
and radii
of between 0.5 and 10 kpc, ![]() is about 0.1. We thus see that
the correction to gravitational dynamics due to the proposed inclusion
of a second term in Eq. (6) is small enough to have remained
undetected in galactic systems where no gravitational anomaly is found and
where dynamics are consistent with Newtonian gravity, in the absence of
any dark matter.
is about 0.1. We thus see that
the correction to gravitational dynamics due to the proposed inclusion
of a second term in Eq. (6) is small enough to have remained
undetected in galactic systems where no gravitational anomaly is found and
where dynamics are consistent with Newtonian gravity, in the absence of
any dark matter.
On the other hand, for systems where the presence of dark matter is
inferred, given that this is always required to be dominant, adding the
Newtonian term onto the MOND proposal generally provides a negligible
contribution. For example, for the Galactic disk at the solar radius,
![]() and
R=8.5 kpc give
and
R=8.5 kpc give ![]() ,
consistent with an inference of about 50% dark matter within the
solar circle. In going to the outskirts of the Milk Way, we go to
R=100 kpc, hence
,
consistent with an inference of about 50% dark matter within the
solar circle. In going to the outskirts of the Milk Way, we go to
R=100 kpc, hence ![]() .
The system is either totally dominated by dark matter, or it is in a regime
where the second term in Eq. (6)
almost fully determines the dynamics. We see that the distinct
power-law dependences ensure that the Newtonian term completely
dominates at small values of
.
The system is either totally dominated by dark matter, or it is in a regime
where the second term in Eq. (6)
almost fully determines the dynamics. We see that the distinct
power-law dependences ensure that the Newtonian term completely
dominates at small values of ![]() ,
while the
opposite holds for large values of
,
while the
opposite holds for large values of ![]() ,
with a necessarily narrow transition region.
,
with a necessarily narrow transition region.
From the form of Eq. (5), it would be tempting to
add the following term of the
![]() series, a further
(perhaps positive) constant term, which would result in an
series, a further
(perhaps positive) constant term, which would result in an ![]() additive term in Eq. (6). If chosen suitably small, for
the same reasons as given above, it would have no measurable effects on all
but the largest scales, perhaps as a tool to model the cosmological
constant. This extension certainly does not correspond to MOND, since
no interpolation function
additive term in Eq. (6). If chosen suitably small, for
the same reasons as given above, it would have no measurable effects on all
but the largest scales, perhaps as a tool to model the cosmological
constant. This extension certainly does not correspond to MOND, since
no interpolation function ![]() can be constructed. However,
in such terms, Eq. (6) might be interpreted as a series
expansion of a more fundamental underlying gravity law, only the first
terms of which we have begun to appreciate empirically as observations
probe increasingly higher
can be constructed. However,
in such terms, Eq. (6) might be interpreted as a series
expansion of a more fundamental underlying gravity law, only the first
terms of which we have begun to appreciate empirically as observations
probe increasingly higher ![]() regimes, typically corresponding to
increasingly larger scales. The introduction of the constant term in
Eq. (5) and its calibration from cosmology, however, must
be done within a generalised GR framework.
regimes, typically corresponding to
increasingly larger scales. The introduction of the constant term in
Eq. (5) and its calibration from cosmology, however, must
be done within a generalised GR framework.
2.1 Equilibrium configurations
To test at the regime which has resulted most troublesome
for the MOND formalism, we go to the now very well studied dSph galaxies of the local group.
To compare against local dSph galaxies, we require the derivation of
equilibrium configurations for a population of self-gravitating stars.
We begin by noting that the validity of Newton's theorems for spherically
symmetric matter distributions, that the contribution to the force felt
by an observer due to external shells vanishes, and that the contribution
of all shells interior to the observer is equivalent to concentrating all
mass interior to the observer at the centre, also holds under the present
proposal. The two theorems depend on the numerator of the
Newtonian term in Eq. (5) for a fixed solid angle fraction of a thin
shell scaling with the second power of distance to the shell, as the
denominator does. For the second term in Eq. (5), the numerator scales
with
![]() ,
as does the denominator, assuring the validity of
Newton's theorems for spherical mass distributions (e.g. see Bekenstein &
Milgrom 1984).
,
as does the denominator, assuring the validity of
Newton's theorems for spherical mass distributions (e.g. see Bekenstein &
Milgrom 1984).
We now write the equation of hydrostatic equilibrium for a polytropic equation of state
![]() :
:
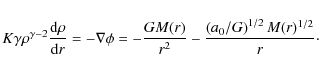
|
(7) |
Since
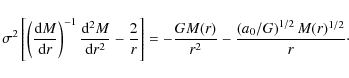
|
(8) |
In the above second-order differential equation for M(r), the constant isotropic velocity dispersion for the population of stars has been written as
Notice that neglecting the first term on the right hand side of Eq. (8),
the limit behaviour for M(r) for large values of r when the weak limit
of the MOND formalism dominates, is characterised by a finite total mass.
In contrast to what happens in Newtonian systems
where isothermal configurations have an infinite total mass,
isothermal self-gravitating configurations will
be naturally bound in mass, under the proposed gravity law.
As a result, there will also be a well-defined
and finite half-mass radius,
![]() ,
to characterise the resulting
equilibrium configurations. Also, as is the case using the MOND
prescription, the total mass of the configuration is expected to scale
with
,
to characterise the resulting
equilibrium configurations. Also, as is the case using the MOND
prescription, the total mass of the configuration is expected to scale
with
![]() .
From the dimensional mass scale
.
From the dimensional mass scale
![]() ,
one is led to expect an analogue to the Tully-Fisher relation for spheroidal galactic systems, down to the dSph regime.
,
one is led to expect an analogue to the Tully-Fisher relation for spheroidal galactic systems, down to the dSph regime.
Figure 1 gives a plot of
![]() vs
vs
![]() for a sample numerical solution to Eq. (8) for
for a sample numerical solution to Eq. (8) for
![]() and
and
![]() .
We obtain a well-defined resulting
total mass,
.
We obtain a well-defined resulting
total mass,
![]() ,
of
,
of
![]() ,
and a final volume
half-mass radius of
0.39 kpc. We see the expected decay
of the density profile at large radii, slightly faster than r-3. It
is this type of density profiles that is used in the next section to
model the local dSph galaxies.
,
and a final volume
half-mass radius of
0.39 kpc. We see the expected decay
of the density profile at large radii, slightly faster than r-3. It
is this type of density profiles that is used in the next section to
model the local dSph galaxies.
![\begin{figure}
\par\includegraphics[height=6.51cm,width=8.01cm]{13301fg1.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13301-09/Timg63.png)
|
Figure 1:
A sample isothermal equilibrium density profile for
|
| Open with DEXTER | |
3 Local dwarf spheroidal galaxies
As discussed above, once values for the velocity dispersion and the
central density are given, numerically solving Eq. (8) yields
the full equilibrium density profile. To now model dSph galaxies, we
take values for the reported velocity dispersions for these systems,
which thus fix one of the two parameters of the model. A resulting
density profile is then integrated along one dimension to yield a
surface density profile, from which the projected half-mass radius is
measured. This provides a second constraint; we then vary the value
of the input central density to ensure that the resulting half-mass
radius
![]() matches the reported half-light radius
matches the reported half-light radius
![]() of a given dSph. Observational determinations of the
velocity dispersion and the half-light radius of a certain dSph galaxy
then fully determine the model. Dividing the total mass for the
resulting model
of a given dSph. Observational determinations of the
velocity dispersion and the half-light radius of a certain dSph galaxy
then fully determine the model. Dividing the total mass for the
resulting model
![]() by the reported total luminosity
by the reported total luminosity
![]() of a dSph, yields a mass to light ratio for the model.
Values of the half-light radii and total luminosities were taken from
Gilmore et al. (2007), who summarise published results from the
references given in Table 1, except for Ursa Minor, where we took the
revised value for
of a dSph, yields a mass to light ratio for the model.
Values of the half-light radii and total luminosities were taken from
Gilmore et al. (2007), who summarise published results from the
references given in Table 1, except for Ursa Minor, where we took the
revised value for
![]() from Palma et al. (2003).
from Palma et al. (2003).
Table 1: Basic properties and resulting M/L ratios for the sample of dSph galaxies.
Although other stellar systems show velocity dispersion profiles that generally decay as the radial coordinate increases, e.g. globular clusters, the case for observed dSph galaxies is different, with these systems showing essentially flat velocity dispersion profiles, e.g. Gilmore et al. (2007). In cases where some drop in the velocity dispersion profile is observed, this typically occurs towards the edge of the galaxy, affecting only a very small percentage of the total mass of the system. The constancy of these observed velocity dispersion profiles validates the use of Eq. (8) under isothermal conditions for modelling local dSph's. We have not at this point attempted a more detailed modelling considering non-isothermal conditions, for example including orbital anisotropy, although such models are now common in models of dSph galaxies under Newtonian (e.g. Lokas 2002) or MOND frameworks (e.g. Angus 2008) and could be included in subsequent analysis. We point to the recent work by Gilmore (2007), in which isothermal conditions are used to model local dSph galaxies assuming Newtonian gravity.
Values of ![]() were taken from adjusting a constant level
to the
were taken from adjusting a constant level
to the ![]() profiles of Angus (2008), which are flat to a very
good approximation, with the exception of Ursa Minor that shows
a significant decrease with increasing radial distances. This galaxy
also shows internal structure in phase space at small radii, which might
partly account for the steep increase in
profiles of Angus (2008), which are flat to a very
good approximation, with the exception of Ursa Minor that shows
a significant decrease with increasing radial distances. This galaxy
also shows internal structure in phase space at small radii, which might
partly account for the steep increase in ![]() seen by Angus (2008) towards the centre. We have taken a value for
seen by Angus (2008) towards the centre. We have taken a value for ![]() representative of the situation at around the half-light radius. If a strong
radial dependence of
representative of the situation at around the half-light radius. If a strong
radial dependence of ![]() in Ursa Minor were confirmed, however, this system would have to be excluded from the present sample, as it would then
conflict with the simple isothermal modelling we are performing here.
in Ursa Minor were confirmed, however, this system would have to be excluded from the present sample, as it would then
conflict with the simple isothermal modelling we are performing here.
Table 1 gives our results for the 8 best-studied local dSph galaxies.
The values we obtain for M/L are mostly comparable to those obtained by
Angus (2008) for the same systems, but a slight systematic decrease
is evident, consistent with having included a further force term, the
Newtonian component, which reduced inferred M/L ratios even further.
In general, the values of the parameter
![]() we found, calculated from the resulting model total mass as
we found, calculated from the resulting model total mass as
![]() ,
explain why the addition of the Newtonian term is required to fully
account for the dynamics. Further, the wide range of values of
,
explain why the addition of the Newtonian term is required to fully
account for the dynamics. Further, the wide range of values of
![]() shown in the table explains why a different a0has sometimes been found for various dSph's, when fitting dynamics using
only the weak acceleration limit of the MOND formalism, e.g. Lokas (2001).
shown in the table explains why a different a0has sometimes been found for various dSph's, when fitting dynamics using
only the weak acceleration limit of the MOND formalism, e.g. Lokas (2001).
The case where the effect of the second term in Eq. (6) is
greatest is that of Draco, where the compact configuration and relatively
high ![]() values allow the Newtonian term to figure somewhat more,
leading to a strong decrease in the inferred M/L of between 8.1 and 30.9, compared to the Angus (2008) results of M/L between 22.6
and 72.9. With the possible exception of Fornax and Sculptor,
cases where the reported King core radius serves only as a lower limit
for the projected
values allow the Newtonian term to figure somewhat more,
leading to a strong decrease in the inferred M/L of between 8.1 and 30.9, compared to the Angus (2008) results of M/L between 22.6
and 72.9. With the possible exception of Fornax and Sculptor,
cases where the reported King core radius serves only as a lower limit
for the projected
![]() ,
the value for the parameter
,
the value for the parameter
![]() for Draco is the lowest in the sample. This naturally explains why it
is here that our results for M/L differ most and show a significant
reduction when contrasting with the results of Angus (2008), who takes a
for Draco is the lowest in the sample. This naturally explains why it
is here that our results for M/L differ most and show a significant
reduction when contrasting with the results of Angus (2008), who takes a ![]() function
that rapidly converges to the low acceleration limit of the MOND
prescription, as this is the parameter that determines the relative
importance of the Newtonian
and low acceleration limit MOND terms in Eq. (6).
function
that rapidly converges to the low acceleration limit of the MOND
prescription, as this is the parameter that determines the relative
importance of the Newtonian
and low acceleration limit MOND terms in Eq. (6).
The ![]() confidence intervals of our results are only lower
bounds, as their calculation includes only uncertainties in the adopted
values of
confidence intervals of our results are only lower
bounds, as their calculation includes only uncertainties in the adopted
values of ![]() and not observational errors in total luminosities
and half-mass radii. Also, freedom in the light profile functional
fitting would increase our confidence intervals slightly, e.g., the
reported
and not observational errors in total luminosities
and half-mass radii. Also, freedom in the light profile functional
fitting would increase our confidence intervals slightly, e.g., the
reported
![]() values for Ursa Minor, Fornax and Sculptor are only
lower bounds, because the quantity available for those galaxies is the core
radius from King profile fits. Still, this last is only a second-order
effect, since our inferred M/L values are not very sensitive to the values
of
values for Ursa Minor, Fornax and Sculptor are only
lower bounds, because the quantity available for those galaxies is the core
radius from King profile fits. Still, this last is only a second-order
effect, since our inferred M/L values are not very sensitive to the values
of
![]() used, provided this does not change by a large factor
(see the following section).
used, provided this does not change by a large factor
(see the following section).
As expected, the main determinant of the resulting total mass of a
numerical solution of Eq. (8), is the input ![]() .
We find, as
expected from the situation of the low acceleration limit of the MOND
prescription, a strong correlation, with the resulting scaling for all
galaxies being well described by
.
We find, as
expected from the situation of the low acceleration limit of the MOND
prescription, a strong correlation, with the resulting scaling for all
galaxies being well described by
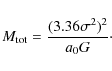
|
(9) |
This could be seen as an extension of the Tully-Fisher relation down to the smallest galactic scales, a natural consequence of the model being explored.
Considering the large M/L values natural for old stellar populations,
e.g., Queloz et al. (1995) and Romanowsky (2003), who find M/L ratios for old
stellar populations as high as 7 or 8, our new results are now at the
limit of compatibility with M/L ratios for old naked stellar populations
for all the well-studied local dSph galaxies. This holds comfortably for
all galaxies except Draco, where compatibility is found only just at the
![]() level for our lower limits on the confidence intervals.
Our model thus yields equilibrium isothermal configurations able to
explain the observed dynamics of the local dSph galaxies, without the
need for dark matter.
level for our lower limits on the confidence intervals.
Our model thus yields equilibrium isothermal configurations able to
explain the observed dynamics of the local dSph galaxies, without the
need for dark matter.
A consistency check of the above interpretation is available from the comparison of the M/L ratios we found and the age of the youngest stellar population found in each of the galaxies, as inferred from the direct studies of the observed CMDs of the galaxies in question, given in the last column of Table 1. It is reassuring that the highest values for our inferred M/L ratios, for Ursa Minor and Draco coincide with the galaxies showing no star formation over the past 10 Gyr, the oldest galaxies in the sample, while the lowest values for M/L are obtained for Leo I and Fornax, the youngest galaxies in the sample with stellar populations as young as 2 Gyr. For the remainder of the sample, galaxies showing their youngest stars at intermediate ages, we find the intermediate values for M/L. The interpretation of the dynamics under the proposed model thus accords with the natural increase in the M/L ratios of stellar populations due to the ageing of stars and the consequent build up of black holes, neutron stars, and white dwarfs. This correspondence is natural in any modified gravity scheme where the stars alone are responsible for the dynamics, but has to be thought of as a fortuitous coincidence under the dark matter hypothesis.
![\begin{figure}
\par\includegraphics[height=6.51cm,width=8.01cm]{13301fg2.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13301-09/Timg98.png)
|
Figure 2:
Comparison of our projected surface density profile for an
equilibrium isothermal solution to Eq. (8), having input |
| Open with DEXTER | |
As a second consistency check, we now show the resulting projected
surface density mass profile for a model of the Leo II galaxy, normalised
by the total luminosity of that system. We construct the surface
brightness profile using our model for an equilibrium isothermal system
having velocity dispersion and projected
![]() (assumed equal to
the observed
(assumed equal to
the observed
![]() ), equal to those observed for Leo II. This is
given in Fig. 2, where we have also plotted the observation for the
actual surface density light profile of Leo II, from the star counts
analysis of Coleman et al. (2007), out to the radius where measurements fall
below the background noise level, both normalised to the same total
luminosity. We note that the error bars of Coleman et al. (2007) are only a
lower estimate of the confidence intervals for this comparison, as they
only refer to the errors in the measured star counts and not to full
surface density profile inferences. A very good agreement is evident,
showing the proposed models are a good, fully self-consistent
representation of the dynamics and both the integral and spatially
resolved light distribution in the well-studied local dSph galaxies.
), equal to those observed for Leo II. This is
given in Fig. 2, where we have also plotted the observation for the
actual surface density light profile of Leo II, from the star counts
analysis of Coleman et al. (2007), out to the radius where measurements fall
below the background noise level, both normalised to the same total
luminosity. We note that the error bars of Coleman et al. (2007) are only a
lower estimate of the confidence intervals for this comparison, as they
only refer to the errors in the measured star counts and not to full
surface density profile inferences. A very good agreement is evident,
showing the proposed models are a good, fully self-consistent
representation of the dynamics and both the integral and spatially
resolved light distribution in the well-studied local dSph galaxies.
4 Scaling relations
We now turn to the scalings shown by the dSph galaxies in our sample.
Firstly, we show in Fig. 3 the behaviour of the equilibrium isothermal
configurations we are solving for, in terms of the resulting projected
![]() as a function of the input value of
as a function of the input value of ![]() ,
at a constant
value of
,
at a constant
value of
![]() .
The remarkable feature of Fig. 3 is that, after decreasing as
.
The remarkable feature of Fig. 3 is that, after decreasing as ![]() increases, when
increases, when ![]() reaches a value of about
reaches a value of about
![]() ,
the resulting
,
the resulting
![]() stops changing and settles at relatively constant value of around
stops changing and settles at relatively constant value of around
![]() ,
below which it does not fall further. This is qualitatively
reproduced at all values of
,
below which it does not fall further. This is qualitatively
reproduced at all values of ![]() ,
with only small changes in the
minimum values of
,
with only small changes in the
minimum values of
![]() ,
for
,
for ![]() in the range of values
observed for local dSph galaxies. This is interesting, as it offers a
natural explanation for local dSph galaxies showing a
minimum lower value for their projected half-light radii of around
in the range of values
observed for local dSph galaxies. This is interesting, as it offers a
natural explanation for local dSph galaxies showing a
minimum lower value for their projected half-light radii of around
![]() ,
with most lying around a factor of 2 above this critical
limit, as noticed by Gilmore et al. (2007) and seen from Table 1. Indeed, all our models constrained by the observational values of
,
with most lying around a factor of 2 above this critical
limit, as noticed by Gilmore et al. (2007) and seen from Table 1. Indeed, all our models constrained by the observational values of ![]() and
and
![]() for the local dSphs, occur within the flat region of
the
for the local dSphs, occur within the flat region of
the
![]() space.
space.
We can now try to understand the assigned Newtonian values of M/L for
local dSph galaxies and the scalings they show with total luminosity or
absolute magnitude, e.g., Mateo (1998). The assigned
Newtonian values of M/L will never be far from (e.g. Gilmore et al. 2007)
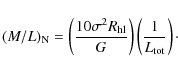
|
(10) |
Given our results in the previous section, or alternatively taking the observed
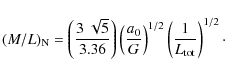
|
(11) |
Introducing the absolute magnitude
| (12) |
Figure 4 now gives a plot of Eq. (12), superimposed on recent determinations of the Newtonian M/L values for a larger sample of local dSph galaxies, using reported values of L to calculate the values plotted on the x-axis, and of L,
![\begin{figure}
\par\includegraphics[height=6.51cm,width=8.01cm]{13301fg3.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13301-09/Timg112.png)
|
Figure 3:
Dependence of the resulting projected half-mass radius in kpc,
against the assumed central density in
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=6.51cm,width=8.01cm]{13301fg4.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13301-09/Timg115.png)
|
Figure 4:
Logarithms of the Newtonian M/L values of local dSph galaxies against total observed V band magnitudes, from data as summarised in Walker et al. (2009a). The straight line is not a fit, but gives the Newtonian M/L values that would be assigned to isothermal equilibrium populations of stars having a constant intrinsic stellar M/L ratio of 5 and a constant half-mass radius of
|
| Open with DEXTER | |
We see that the expectations of the model for the inferred Newtonian
M/L values of local dSph galaxies, which are
modelled as equilibrium isothermal solutions to Eq. (8) and having
typical radii of close to
0.3 kpc, agree very well with independent measurements. The
small scatter in Fig. 4 beyond observational error bars is compatible with the variations in the actual intrinsic M/L values for the individual galaxies, and variations of
![]() around the average 0.3 kpc used in Eq. (12),
which is not a fit to the data, but a first-order estimate within our
prescription. A very simple explanation for the
around the average 0.3 kpc used in Eq. (12),
which is not a fit to the data, but a first-order estimate within our
prescription. A very simple explanation for the
![]() values
assigned to all well-studied dSphs is thus naturally afforded by our
assumptions for the most average intrinsic M/L and
values
assigned to all well-studied dSphs is thus naturally afforded by our
assumptions for the most average intrinsic M/L and
![]() values,
without the need of invoking complex astrophysical processes (e.g. tidal
disruption, strong outflows, etc.) or fine-tuning any parameters.
To first order, one can understand the well-established scalings of Fig. 4 as the extension of the Tully-Fisher relation, which appears in the MOND formalism, down to the dSph regime.
values,
without the need of invoking complex astrophysical processes (e.g. tidal
disruption, strong outflows, etc.) or fine-tuning any parameters.
To first order, one can understand the well-established scalings of Fig. 4 as the extension of the Tully-Fisher relation, which appears in the MOND formalism, down to the dSph regime.
5 Conclusions
We used a MOND interpolation function that can be seen as the
addition of both the Newtonian acceleration and the low acceleration limit of the MOND formalism on all scales (Bekenstein 2004).
For the local dSph galaxies,
where the application of the MOND formalism has been most
controversial, we show that isothermal equilibrium configurations
characterised by well-defined
finite total masses and half-mass radii result, giving M/L values in agreement with naked stellar populations. As a result,
no dark matter is now needed. The observed scalings
in
![]() and assigned
and assigned
![]() values as a function of total
magnitudes are explained naturally, including the previously unrecognised correlation of resulting M/L ratios
with the relative youth of the stellar populations of the individual
dSph galaxies, for the sample studied. This last is a natural
consequence of using the MOND prescription, but an odd coincidence
under the dark matter hypothesis.
values as a function of total
magnitudes are explained naturally, including the previously unrecognised correlation of resulting M/L ratios
with the relative youth of the stellar populations of the individual
dSph galaxies, for the sample studied. This last is a natural
consequence of using the MOND prescription, but an odd coincidence
under the dark matter hypothesis.
Fixing the optimal ![]() for
the MOND prescription in the dSph regime through the arguments
presented here constitutes an interesting condition on this function in
the regime studied, and it provides a constraint on any global
for
the MOND prescription in the dSph regime through the arguments
presented here constitutes an interesting condition on this function in
the regime studied, and it provides a constraint on any global ![]() MOND function.
MOND function.
We would like to thank Benoit Famaey, Moti Milgrom, and Jacob Bekenstein for fruitful comments in connection to a previous version of this article. We thank an anonymous referee for comments that were useful towards reaching a more balanced and complete presentation. This work was supported in part through two DGAPA-UNAM grants (PAPIIT IN-113007-3 and IN-114107). S.M. and T.B. gratefully acknowledge support from DGAPA (IN119203-3) at the Universidad Nacional Autónoma de México (UNAM). S.M. acknowledges financial support by CONACyT (26344). T.B. acknowledges support from CONACyT (207529).
References
- Aden, D., Feltzing, S., Koch, A., et al., A&A 2009, 506, 1147 [Google Scholar]
- Arbey, A. 2008, OAJ, 1, 27 [NASA ADS] [Google Scholar]
- Anderson, J. D., Lau, E. L., Turyshev, S., Williams, J. G., & Nieto, M. M. 2002, in BAAS, 660, 34 [Google Scholar]
- Angus, G. W. 2008, MNRAS, 387, 1481 [NASA ADS] [CrossRef] [Google Scholar]
- Angus, G. W., Shan, H. Y., Zhao, H. S., et al. 2007, ApJ, 654, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Angus, G. W., Famaey, B., & Diaferio, A. 2010, MNRAS, 402, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Aparicio, A., Carrera, R., & Martínez-Delgado, D. 2001, AJ, 122, 2524 [NASA ADS] [CrossRef] [Google Scholar]
- Babusiaux, C., Gilmore, G., & Irwin, M. 2005, MNRAS, 359, 985 [NASA ADS] [CrossRef] [Google Scholar]
- Bekenstein, J. D. 2004, Phys. Rev. D, 70, 083509 [NASA ADS] [CrossRef] [Google Scholar]
- Bekenstein, J. 2006, Contemporary Physics, 47, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Belokurov, V., Walker, M. G., & Evans, N. W., et al. 2008, ApJ, 686, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Belokurov, V., Walker, M. G., Evans, N. W., et al. 2009, MNRAS, 397, 1748 [NASA ADS] [CrossRef] [Google Scholar]
- Bruneton, J. P., & Esposito-Farese, G. 2007, Phys. Rev. D, 76, 124012 [NASA ADS] [CrossRef] [Google Scholar]
- Chapman, S. C., Ibata, R., Lewis, G. F., et al. 2005, ApJ, 632, L87 [NASA ADS] [CrossRef] [Google Scholar]
- Coleman, M. G., Jordi, K., Rix, H.-W., Grebel, E. K., & Koch, A. 2007, AJ, 134, 1938 [NASA ADS] [CrossRef] [Google Scholar]
- Coleman, M. G., & de Jong, J. T. A. 2008, ApJ, 685, 933 [NASA ADS] [CrossRef] [Google Scholar]
- Corbelli, E., & Salucci, P. 2007, MNRAS, 374, 1051 [NASA ADS] [CrossRef] [Google Scholar]
- Côté, P., Mateo, M., Olszewski, E. W., et al. 1999, ApJ, 526, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Famaey, B., & Binney, J. 2005, MNRAS, 363, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Famaey, B., Gentile, G., Bruneton, J.-P., et al. 2007, Phys. Rev. D, 75, 063002 [NASA ADS] [CrossRef] [Google Scholar]
- Fraternali, F., Tolstoy, E., Irwin, M., et al. 2009, A&A, 499, 121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Geha, M., Willman, B., Simon, J. D., et al. 2009, ApJ, 692, 1464 [NASA ADS] [CrossRef] [Google Scholar]
- Gentile, G., Famaey, B., Combes, F., et al. 2007, A&A, 472, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gilmore, G., Wilkinson, M. I., Wyse, R. F. G., et al. 2007, ApJ, 663, 948 [NASA ADS] [CrossRef] [Google Scholar]
- Halle, A., Zhao, H. S., & Li, B. 2008, ApJS, 177, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Hernandez, X., Gilmore, G., & Valls-Gabaud, D. 2000, MNRAS, 317, 831 [NASA ADS] [CrossRef] [Google Scholar]
- Ibata, R. A., & Irwin, M. J. 1997, AJ, 113, 1865 [NASA ADS] [CrossRef] [Google Scholar]
- Ibata, R., Martin, N. F., Irwin, M., et al. 2007, ApJ, 671, 1591 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, M., & Hatzidimitriou, D. 1995, MNRAS, 277, 1354 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, M. J., Belokurov, V., Evans, N. W., et al. 2007, ApJ, 656, L13 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Kleyna, J. T., Wilkinson, M. I., Evans, N. W., et al. 2004, MNRAS, 354, L66 [NASA ADS] [CrossRef] [Google Scholar]
- Koch, A., Wilkinson, M. I., Kleyna, J. T., et al. 2007a, ApJ, 657, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Koch, A., Kleyna, J. T., Wilkinson, M. I., et al. 2007b, AJ, 134, 566 [NASA ADS] [CrossRef] [Google Scholar]
- Koch, A., Wilkinson, M. I., Kleyna, J. T., et al. 2009, ApJ, 690, 453 [NASA ADS] [CrossRef] [Google Scholar]
- Letarte, B., Chapman, S. C., Collins, M., et al. 2009, MNRAS, 400, 1472 [Google Scholar]
- Lee, M. G., Park, H. S., Park, J.-H., et al. 2003, AJ, 126, 2840 [NASA ADS] [CrossRef] [Google Scholar]
- Lewis, G. F., Ibata, R. A., Chapman, S. C., et al. 2007, MNRAS, 375, 1364 [NASA ADS] [CrossRef] [Google Scholar]
- ▯okas, E. L. 2001, MNRAS, 327, L21 [NASA ADS] [CrossRef] [Google Scholar]
- ▯okas, E. L. 2002, MNRAS, 333, 697 [NASA ADS] [CrossRef] [Google Scholar]
- Majewski, S. R., Skruskie, M. F., Weinberg, M. D., et al. 2003, ApJ, 599, 1082 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, N. F., Ibata, R. A., Chapman, S. C., Irwin, M., & Lewis, G. F. 2007, MNRAS, 380, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, N. F., de Jong, J. T. A., & Rix, H. W. 2008, ApJ, 684, 1075 [NASA ADS] [CrossRef] [Google Scholar]
- Mateo, M. L. 1998, ARA&A, 36, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Mateo, M., Olszewski, E. W., & Walker, M. G. 2008, ApJ, 675, 201 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- McConnachie, A. W., & Irwin, M. 2006, MNRAS, 365, 1263 [NASA ADS] [CrossRef] [Google Scholar]
- Mendoza, S., & Rosas-Guevara, Y. M. 2007, A&A, 472, 367 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Milgrom, M. 1983, ApJ, 270, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Milgrom, M., & Sanders, R. H. 2003, ApJ, 599, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Milgrom, M., & Sanders, R. H. 2008, ApJ, 678, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Milgrom, M. 2008a, unpublished [arXiv:0801.3133] [Google Scholar]
- Milgrom, M. 2008b, New Astron. Rev., 51, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Milgrom, M. 2009, MNRAS, 1143 [Google Scholar]
- Nipoti, C., Londrillo, P., Zhao, H., et al. 2007, MNRAS, 379, 597 [NASA ADS] [CrossRef] [Google Scholar]
- Nipoti, C., Ciotti, L., Binney, J., & Londrillo, P. 2008, MNRAS, 386, 2194 [NASA ADS] [CrossRef] [Google Scholar]
- Palma, C., Majewski, S. R., Siegel, M. H., et al. 2003, AJ, 125, 1352 [NASA ADS] [CrossRef] [Google Scholar]
- Queloz, D., Dubath, P., & Pasquini, L. 1995, A&A, 300, 31 [NASA ADS] [Google Scholar]
- Romanowsky, A. J., Douglas, N. G., Arnaboldi, M., et al. 2003, Science, 301, 1696 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Sánchez-Salcedo, F. J., & Hernandez, X. 2007, ApJ, 667, 878 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez-Salcedo, F. J., Reyes-Iturbide, J., & Hernandez, X. 2006, MNRAS, 370, 1829 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez-Salcedo, F. J., Saha, K., & Narayan, C. A. 2008, MNRAS, 385, 1585 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, R. H. 2003, MNRAS, 342, 901 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, R. H. 2005, MNRAS, 363, 459 [NASA ADS] [Google Scholar]
- Sanders, R. H. 2006, MNRAS, 370, 1519 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, R. H., & McGaugh, S. S. 2002, ARA&A, 40, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, R. H., & Noordermeer, E. 2007, MNRAS, 379, 702 [NASA ADS] [CrossRef] [Google Scholar]
- Saviane, I., Held, E. V., & Piotto, G. 1996, A&A, 315, 40 [NASA ADS] [Google Scholar]
- Simon, J. D., & Geha, M. 2007, ApJ, 670, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Skordis, C., Mota, D. F., Ferreira, P. G., & Boehm, C. 2006, Phys. Rev. Lett., 96, 1301 [Google Scholar]
- Sobouti, Y. 2007, A&A, 464, 921 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tiret, O., Combes, F., Angus, G. W., et al. 2007, A&A, 476, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Turyshev, S. G. 2009, Physics Uspekhi, 52, 1 [Google Scholar]
- Toth, V. T., & Turyshev, S. G. 2009a, Phys. Rev. D, 79, 043011 [NASA ADS] [CrossRef] [Google Scholar]
- Turyshev, S. G., & Toth, V. T. 2009b, Space Sci. Rev., 86 [Google Scholar]
- Walker, M. G., Mateo, M., Olszewski, E. W., et al. 2006, AJ, 131, 2114 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, M. G., Mateo, M., Olszewski, E. W., et al. 2007, ApJ, 667, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, M. G., Mateo, M., Olszewski, E. W., et al. 2009a, ApJ, 704, 1274 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, M. G., Belokurov, V., Evans, N. W., et al. 2009b, ApJ, 694, L144 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, M. G., Mateo, M., Olszewski, E. W., Sen, B., & Woodroofe, M. 2009c, AJ, 137, 3109 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, M. G., Mateo, M., Olszewski, E. W., Peñarrubia, J., Evans, N. W., Gilmore, G. 2009d, ApJ, 704, 1274 [NASA ADS] [CrossRef] [Google Scholar]
- Wilkinson, M. I., Kleyna, J. T., Evans, N. W., et al. 2004, ApJ, 611, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Wilkinson, M. I., Kleyna, J. T., Wyn Evans, N., et al. 2006, in EAS Publ. Ser. 20, ed. G. A. Mamon, F. Combes, C. Deffayet, & B. Fort, 105 [Google Scholar]
- Wu, X., Famaey, B., Gentile, G., Perets, H., & Zhao, H. S. 2008, MNRAS, 386, 2199 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, H. S. 2007, ApJ, 671, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, H. S., Bacon, D. J., Taylor, A. N., & Horne, K. 2006, MNRAS, 368, 171 [NASA ADS] [Google Scholar]
All Tables
Table 1: Basic properties and resulting M/L ratios for the sample of dSph galaxies.
All Figures
![\begin{figure}
\par\includegraphics[height=6.51cm,width=8.01cm]{13301fg1.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13301-09/Timg63.png)
|
Figure 1:
A sample isothermal equilibrium density profile for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=6.51cm,width=8.01cm]{13301fg2.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13301-09/Timg98.png)
|
Figure 2:
Comparison of our projected surface density profile for an
equilibrium isothermal solution to Eq. (8), having input |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=6.51cm,width=8.01cm]{13301fg3.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13301-09/Timg112.png)
|
Figure 3:
Dependence of the resulting projected half-mass radius in kpc,
against the assumed central density in
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=6.51cm,width=8.01cm]{13301fg4.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13301-09/Timg115.png)
|
Figure 4:
Logarithms of the Newtonian M/L values of local dSph galaxies against total observed V band magnitudes, from data as summarised in Walker et al. (2009a). The straight line is not a fit, but gives the Newtonian M/L values that would be assigned to isothermal equilibrium populations of stars having a constant intrinsic stellar M/L ratio of 5 and a constant half-mass radius of
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.