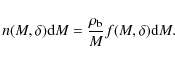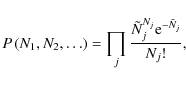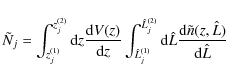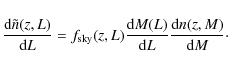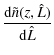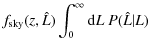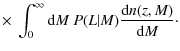| Issue |
A&A
Volume 514, May 2010
|
|
|---|---|---|
| Article Number | A80 | |
| Number of page(s) | 8 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/200913133 | |
| Published online | 26 May 2010 | |
Improvements in the X-ray luminosity function and constraints on the cosmological parameters from X-ray luminous clusters
A. Del Popolo1,2 - V. Costa3 - G. Lanzafame4
1 - Dipartimento di Fisica e Astronomia, Università di Catania, Viale Andrea Doria 6, 95125 Catania, Italy
2 -
Argelander-Institut für Astronomie, Auf dem Hügel 71, 53121 Bonn, Germany
3 -
Dipartimento di Metodologie Chimiche e Fisiche per l'Ingegneria, Univesità di Catania, Viale
A. Doria 6, 95125, Catania, Italy
4 -
Osservatorio Astrofisico di Catania, Istituto Nazionale di Astrofisica, via S. Sofia 78, 95123,
Catania, Italy
Received 17 August 2009 / Accepted 31 December 2010
Abstract
Aims. We improve the current constraints on
![]() ,
the dark-energy equation-of-state parameter, w, and
,
the dark-energy equation-of-state parameter, w, and ![]() ,
obtained from measurements of the X-ray luminosity function of galaxy
clusters, namely MACS, the local BCS, and the REFLEX galaxy cluster
samples with luminosities
,
obtained from measurements of the X-ray luminosity function of galaxy
clusters, namely MACS, the local BCS, and the REFLEX galaxy cluster
samples with luminosities
![]() erg/s in the 0.1-2.4 keV band.
erg/s in the 0.1-2.4 keV band.
Methods. To this aim, we use Tinker and collaborators mass
function instead of Jenkins and collaborators and the mass-luminosity
relationship obtained by Del Popolo and collaborators.
Results. Using the same methods and priors as Mantz and collaborators, we find
![]() and
and
![]() ,
for a
,
for a ![]() CDM universe, while the result of Mantz and collaborators gives less tight constraints
CDM universe, while the result of Mantz and collaborators gives less tight constraints
![]() and
and
![]() .
In the case of a wCDM model, we find
.
In the case of a wCDM model, we find
![]() ,
,
![]() and
w=-1.3+0.3-0.4, while in Mantz and collaborators they are again less tight
and
w=-1.3+0.3-0.4, while in Mantz and collaborators they are again less tight
![]() ,
,
![]() and
w=-1.4+0.4-0.7. Combining the XLF analysis with the
and
w=-1.4+0.4-0.7. Combining the XLF analysis with the
![]() +CMB+SNIa data set results in the constraint
+CMB+SNIa data set results in the constraint
![]() ,
,
![]() and
and
![]() ,
to be compared with Mantz and collaborators,
,
to be compared with Mantz and collaborators,
![]() ,
,
![]() and
and
![]() .
The tightness of the last constraints obtained by Mantz and collaborators, are fundamentally due to the tightness of the
.
The tightness of the last constraints obtained by Mantz and collaborators, are fundamentally due to the tightness of the
![]() +CMB+SNIa constraints and not to their XLF analysis. Our findings, consistent with w=-1, lend additional support to the cosmological-constant model.
+CMB+SNIa constraints and not to their XLF analysis. Our findings, consistent with w=-1, lend additional support to the cosmological-constant model.
Key words: cosmology: theory - cosmological parameters
1 Introduction
Clusters of galaxies are the
largest gravitationally-collapsed structures in the Universe. Even at
the present epoch
they are relatively rare, with only a few percent of all galaxies in
clusters.
In the hierarchical collapse scenario for structure formation in the
universe, the number density of collapsed objects as a function of mass
and cosmic time is a sensitive probe in cosmology. The galaxy clusters
that occupy the
high-mass tail of this population provide a powerful and
relatively clean tool, since their growth is
predominantly determined by linear gravitational processes.
Starting from the 1990s, analyses of massive clusters have consistently
indicated low values for
![]() ,
from the baryonic fraction arguments (White et al. 1993) and measurements of the evolution
in the cluster number density (Eke et al. 1998; Borgani et al. 2001), and from low values of
,
from the baryonic fraction arguments (White et al. 1993) and measurements of the evolution
in the cluster number density (Eke et al. 1998; Borgani et al. 2001), and from low values of
![]()
![]() (Henry & Arnaud 1991; Reiprich & Böringer 2002; Schuecker et al. 2003). A result later
confirmed by cosmic microwave background (CMB) studies, cosmic
shear, and other experiments (Spergel et al. 2007; Komatsu et al. 2008; Dunkley et al. 2008; Benjamin et al. 2007; Fu et al. 2008).
For precision's sake, cluster surveys in the local universe are particularly useful
for constraining a combination of the matter density parameter
(Henry & Arnaud 1991; Reiprich & Böringer 2002; Schuecker et al. 2003). A result later
confirmed by cosmic microwave background (CMB) studies, cosmic
shear, and other experiments (Spergel et al. 2007; Komatsu et al. 2008; Dunkley et al. 2008; Benjamin et al. 2007; Fu et al. 2008).
For precision's sake, cluster surveys in the local universe are particularly useful
for constraining a combination of the matter density parameter
![]() and the normalization of the power spectrum of density fluctuations. Following the evolution of the cluster
space density over a wide redshift baseline, one can break the degeneracy between
and the normalization of the power spectrum of density fluctuations. Following the evolution of the cluster
space density over a wide redshift baseline, one can break the degeneracy between ![]() and
and
![]() (Rosati et al. 2002).
(Rosati et al. 2002).
Recently, X-ray studies (Vikhlinin et al. 2009b) of the evolution of the cluster
mass function at z = 0-0.8 have convincingly demonstrated that the growth of cosmic
structure has slowed down at z
< 1 owing to the effects of dark energy. Thus such measurements
have been used to improve its equation of state parameter.
Although the quoted cosmological test is very powerful, there are two
main problems for practical applications: first, theoretical
predictions provide the number density of clusters of a given mass,
while the mass itself is never the directly observed quantity. Second,
a cluster sample is needed that spans a wide-z baseline and is based on model-independent selection criteria![]() .
.
Determining the evolution of the space density of clusters requires
counting the
number of clusters of a given mass per unit volume at different
redshifts. Therefore, three essential tools are required for its
application as a cosmological test: (a) an efficient method of
finding clusters over a wide redshift range; (b) an observable
estimator of the cluster mass; and (c) a method of computing
the selection function or, equivalently, the survey volume within which
clusters are found.
Observations of clusters in the X-ray band provide an efficient and
physically
motivated method of identification, which fulfills the three
requirements above.
The X-ray luminosity, ![]() ,
provides a very efficient method for identifying clusters down to a
given X-ray flux limit so that, within a known survey volume for
each
,
provides a very efficient method for identifying clusters down to a
given X-ray flux limit so that, within a known survey volume for
each ![]() ,
which uniquely specifies the cluster selection, it is also a good
probe of the depth of the cluster gravitational potential.
,
which uniquely specifies the cluster selection, it is also a good
probe of the depth of the cluster gravitational potential.
For these reasons most of the cosmological studies based on clusters have used X-ray-selected samples. According to the three points quoted above, the recipe for constraining cosmological parameters by means of clusters is composed of three ingredients:
- 1)
- the predicted mass function of clusters, n(M,z), as a function of cosmological parameters (
 ,
,
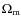 ,
w, etc.);
,
w, etc.);
- 2)
- sky surveys with well-understood selection functions to find
clusters, as well as a relation linking cluster mass with an
observable. A successful solution to the former requirement has been to
identify clusters by the X-ray emission produced by hot intracluster
gas, notably using data from ROSAT
![[*]](/icons/foot_motif.png) ;
;
- 3)
- tight and well-determined scaling relation between survey observable (e.g.
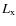 )
and mass, with minimal intrinsic scatter.
)
and mass, with minimal intrinsic scatter.
Until some years ago, the results for
![]() disagree several times. Studies by different authors (Bahcall et al. 1997; Bahcall & Fan 1998; Sadat et al. 1998; Blanchard et al. 1998; Blanchard & Bartlett 1998; Eke et al. 1998; Viana & Liddle 1999; Reichart et al. 1999; Donahue & Voit 1999; Borgani et al. 2001) found values for
disagree several times. Studies by different authors (Bahcall et al. 1997; Bahcall & Fan 1998; Sadat et al. 1998; Blanchard et al. 1998; Blanchard & Bartlett 1998; Eke et al. 1998; Viana & Liddle 1999; Reichart et al. 1999; Donahue & Voit 1999; Borgani et al. 2001) found values for
![]() spanning the entire range of acceptable values:
spanning the entire range of acceptable values:
![]() .
On the basis of the same data set of Eke et al. (1998) with Viana & Liddle (1999),
showed that uncertainties both in fitting local data and in the
theoretical modelling could significantly change the final results.
They found
.
On the basis of the same data set of Eke et al. (1998) with Viana & Liddle (1999),
showed that uncertainties both in fitting local data and in the
theoretical modelling could significantly change the final results.
They found
![]() as a preferred value with a critical density model acceptable at <
as a preferred value with a critical density model acceptable at <![]() c.l., while Eke et al. (1998) found
c.l., while Eke et al. (1998) found
![]() .
.
The reasons leading to the quoted discrepancies have been studied in several papers (Eke et al. 1998; Reichart et al. 1999; Donahue & Voit 1999; Borgani et al. 2001) and can be summarized as coming from:
1) the inadequate approximation given by the mass function used (e.g., Bryan & Norman 1998);
2) inadequacy in the structure formation as described by the
spherical model leading to changes in the threshold parameter
![]() (e.g., Governato et al. 1999); 3) inadequacy in mass-temperature relation (M-T) obtained from the virial theorem (see Voit & Donahue 1998; Del Popolo 2002);
4) effects of cooling flows; 5) determination of the X-ray cluster catalog's selection function;
6) missing high redshift clusters in the data used (e.g., the EMSS); 7) evolution of the luminosity-temperature relation (L-T) (Voit & Donahue 1998); 8) use of different best-fitting procedures to get the constraints (Eke et al. 1998); 9) other effects described in more recent papers (e.g., Mantz et al. 2008, hereafter M08; Vikhlinin et al. 2009b).
(e.g., Governato et al. 1999); 3) inadequacy in mass-temperature relation (M-T) obtained from the virial theorem (see Voit & Donahue 1998; Del Popolo 2002);
4) effects of cooling flows; 5) determination of the X-ray cluster catalog's selection function;
6) missing high redshift clusters in the data used (e.g., the EMSS); 7) evolution of the luminosity-temperature relation (L-T) (Voit & Donahue 1998); 8) use of different best-fitting procedures to get the constraints (Eke et al. 1998); 9) other effects described in more recent papers (e.g., Mantz et al. 2008, hereafter M08; Vikhlinin et al. 2009b).
The situation with the cluster mass function data has been
dramatically improved in past years. A large sample
of sufficiently massive clusters extending to
![]() has been
derived from ROSAT PSPC pointed data covering 400 deg2(Burenin et al. 2007). Distant clusters from
the 400d sample were then observed with Chandra, providing
high-quality X-ray data and much more accurate total mass
indicators (see Vikhlinin et al. 2009b). Chandra coverage has also become available for
a complete sample of low-z clusters originally derived from
the ROSAT All-Sky Survey (see Vikhlinin et al. 2009b).
Results from deep Chandra pointings
to a number of low-z clusters have significantly improved
our knowledge of the outer cluster regions and provided a
much more reliable calibration of the
has been
derived from ROSAT PSPC pointed data covering 400 deg2(Burenin et al. 2007). Distant clusters from
the 400d sample were then observed with Chandra, providing
high-quality X-ray data and much more accurate total mass
indicators (see Vikhlinin et al. 2009b). Chandra coverage has also become available for
a complete sample of low-z clusters originally derived from
the ROSAT All-Sky Survey (see Vikhlinin et al. 2009b).
Results from deep Chandra pointings
to a number of low-z clusters have significantly improved
our knowledge of the outer cluster regions and provided a
much more reliable calibration of the
![]() vs. proxy relations
than was possible before.
On the theoretical side, improved
numerical simulations resulted in better understanding
of measurement biases in the X-ray data analysis (Nagai
et al. 2007; Rasia et al. 2006; Jeltema et al. 2007).
In the present paper, we want to show how tighter constraints
can be obtained in the M08 model, improving the mass function adopted by them, and the scaling laws used (e.g., the M-T and Mass-Luminosity (M-L) relationships).
In this paper, we use the observed X-ray luminosity
function to investigate two cosmological
scenarios, assuming a spatially flat metric
in both cases: the first includes dark energy in
the form of a cosmological constant (
vs. proxy relations
than was possible before.
On the theoretical side, improved
numerical simulations resulted in better understanding
of measurement biases in the X-ray data analysis (Nagai
et al. 2007; Rasia et al. 2006; Jeltema et al. 2007).
In the present paper, we want to show how tighter constraints
can be obtained in the M08 model, improving the mass function adopted by them, and the scaling laws used (e.g., the M-T and Mass-Luminosity (M-L) relationships).
In this paper, we use the observed X-ray luminosity
function to investigate two cosmological
scenarios, assuming a spatially flat metric
in both cases: the first includes dark energy in
the form of a cosmological constant (![]() CDM), and
the second has dark energy with a constant
equation-of-state parameter, w (wCDM). The
theoretical background for this work is reviewed
in Sect. 2. Section 3 presents the results
and Sect. 4 the conclusions.
CDM), and
the second has dark energy with a constant
equation-of-state parameter, w (wCDM). The
theoretical background for this work is reviewed
in Sect. 2. Section 3 presents the results
and Sect. 4 the conclusions.
2 Theory
After discussing the ingredients needed in the recipe used to constrain
cosmological parameters from X-ray observations, now we derive an expression for
the X-ray luminosity function (XLF) (using now the mass function obtained in Del Popolo 2006a,b and M-T, L-T relations obtained in Del Popolo 2002
and Del Popolo et al. 2005, respectively) and then set some constraints on
![]() ,
,
![]() ,
and the dark-energy equation-of-state parameter w,
by using the data (clusters) used in M08, namely MACS (Massive Cluster
Survey), BCS (Brightest Cluster Sample), and REFLEX (ROSAT ESO FLUX
LIMITED X-ray SAMPLE).
Following M08, the constraints are obtained from measurements of the
XLF of the quoted samples. The most straightforward mass-observable
relation to complement these X-ray flux-limited surveys is the
mass-X-ray luminosity relation. For sufficiently massive (hot) objects
at the relevant redshifts, the conversion from X-ray flux to luminosity
is approximately independent of temperature, in which case the
luminosities can be estimated directly from the survey flux and the
selection function is identical to the requirement for detection. A
disadvantage is that there is large scatter in cluster luminosities at
fixed mass; however, having enough data allows this scatter to be
quantified empirically. More recently, a dramatic reduction in
luminosity-mass scatter has been demonstrated when luminosities are
measured by excluding cluster centres (typically
r<0.15 r500; Maughan 2007; Zhang et al. 2007).
Alternative approaches use cluster temperature (Henry 2000; Seljak 2002; Pierpaoli et al. 2003; Henry 2004), gas fraction (Voevodkin & Vikhlinin 2004) or
,
and the dark-energy equation-of-state parameter w,
by using the data (clusters) used in M08, namely MACS (Massive Cluster
Survey), BCS (Brightest Cluster Sample), and REFLEX (ROSAT ESO FLUX
LIMITED X-ray SAMPLE).
Following M08, the constraints are obtained from measurements of the
XLF of the quoted samples. The most straightforward mass-observable
relation to complement these X-ray flux-limited surveys is the
mass-X-ray luminosity relation. For sufficiently massive (hot) objects
at the relevant redshifts, the conversion from X-ray flux to luminosity
is approximately independent of temperature, in which case the
luminosities can be estimated directly from the survey flux and the
selection function is identical to the requirement for detection. A
disadvantage is that there is large scatter in cluster luminosities at
fixed mass; however, having enough data allows this scatter to be
quantified empirically. More recently, a dramatic reduction in
luminosity-mass scatter has been demonstrated when luminosities are
measured by excluding cluster centres (typically
r<0.15 r500; Maughan 2007; Zhang et al. 2007).
Alternative approaches use cluster temperature (Henry 2000; Seljak 2002; Pierpaoli et al. 2003; Henry 2004), gas fraction (Voevodkin & Vikhlinin 2004) or ![]() parameter (Kravtsov et al. 2006)
to achieve tighter mass-observable relations at the expense of reducing
the size of the samples available for analysis. The need to quantify
the selection
function in terms of both X-ray flux and a second observable
additionally complicates these efforts.
parameter (Kravtsov et al. 2006)
to achieve tighter mass-observable relations at the expense of reducing
the size of the samples available for analysis. The need to quantify
the selection
function in terms of both X-ray flux and a second observable
additionally complicates these efforts.
The first ingredient of the quoted recipe (i.e., mass function) used in M08 was the Jenkins et al. (2001, hereafter J01) mass function. J01 writes the mass function of galaxy clusters of mass M at redshift z as a ``universal function'' of
![]()
which is fitted by
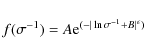
|
(2) |
for cosmological -constant models, with A=0.316, B=0.67, and
As shown in Del Popolo (2006a,b), the theoretical mass function obtained in the quoted papers is in better agreement with high-resolution N-body simulations, namely Reed et al. 2003 (R03), Yahagi et al. (2004) (YNY), Warren et al. 2006 (W06), and Tinker et al. (2008, see the following and Fig. 1b) (T08).
![\begin{figure}
\par\subfigure[]{\hspace*{1.1cm}\includegraphics[width=7.8cm]{131...
...e[]{\includegraphics[width=8.8cm]{13133fig1b.eps} }\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/06/aa13133-09/Timg40.png)
|
Figure 1:
In Panel a): multiplicity function obtained in this paper (solid line), fitting formula proposed by Yahagi et al. (2004) their Eq. (7) (short-dashed line), Sheth & Tormen (2002) (ST) multiplicity function (dotted line), Jenkins et al. (2001)
multiplicity function (long-dashed line). The error bars with open
circles represent the run 140 of YNY, those with filled squares
case 70b, those with open squares case 70a, those with filled circles
case 35b, those with crosses case 35a. Panel b): mass function plotted in redshift-independent form. The measured
|
| Open with DEXTER | |
The mass function is calculated according to the model of Del Popolo (2006a,b).
The multiplicity function, in the quoted model, is given by
where
where i=1 or 2,
The ``multiplicity function'' is correlated with the usual, more
straightforwardly used, ``mass function'' as follows. Following Sheth
& Tormen (2002, hereafter ST) notation, if
![]() denotes the fraction of mass that is contained in collapsed haloes that have mass in the range
denotes the fraction of mass that is contained in collapsed haloes that have mass in the range
![]() ,
at redshift z, and
,
at redshift z, and ![]() is the redshift dependent overdensity,
the associated ``unconditional'' mass function is
is the redshift dependent overdensity,
the associated ``unconditional'' mass function is
In Fig. 1a, we plot the multiplicity function obtained in this paper (symbols are described in the figure caption).
There are some differences between the quoted simulations and the J01 simulations.
First, the multiplicity function of the present paper, similar to that of YNY, in
the low-![]() region of
region of
![]() systematically falls below the J01 functions. In this region the multiplicity function of the
present paper is very close to that of YNY.
Additionally, the numerical multiplicity functions (and that in Del Popolo 2006a,b) have an apparent peak at
systematically falls below the J01 functions. In this region the multiplicity function of the
present paper is very close to that of YNY.
Additionally, the numerical multiplicity functions (and that in Del Popolo 2006a,b) have an apparent peak at
![]() instead of the plateau that is seen in the
J01 function. Similar differences are seen in the high-
instead of the plateau that is seen in the
J01 function. Similar differences are seen in the high-![]() region.
These differences between numerical multiplicity functions (R03; YNY; W05; Del Popolo 2006a,b) and J01, are however within 1-
region.
These differences between numerical multiplicity functions (R03; YNY; W05; Del Popolo 2006a,b) and J01, are however within 1-![]() error bars, and so they agree overall.
The multiplicity function obtained in the present paper peaks
at
error bars, and so they agree overall.
The multiplicity function obtained in the present paper peaks
at
![]() as in YNY numerical multiplicity function, instead of a plateau as in the
J01 function. Differences are also observed in the redshift evolution of the J01 mass function (Del Popolo 2006b). Fitting formulas presented by J01 are accurate to
as in YNY numerical multiplicity function, instead of a plateau as in the
J01 function. Differences are also observed in the redshift evolution of the J01 mass function (Del Popolo 2006b). Fitting formulas presented by J01 are accurate to ![]() 10-20% (Tinker et al. 2008, T08). In our model,
the mass function is given by Eqs. (3)-(5),
which agrees perfectly with the T08 mass function, as shown in Fig. 1b.
The accuracy of the mass function is, as in T08, of
10-20% (Tinker et al. 2008, T08). In our model,
the mass function is given by Eqs. (3)-(5),
which agrees perfectly with the T08 mass function, as shown in Fig. 1b.
The accuracy of the mass function is, as in T08, of ![]()
![]() for
for ![]() CDM
models for the mass and redshift range of interest in this study. In
this way the theoretical uncertainties in the mass function do not
contribute
significantly to the systematic error budget.
In Fig. 1b, we plot the mass function for all of our outputs in the
CDM
models for the mass and redshift range of interest in this study. In
this way the theoretical uncertainties in the mass function do not
contribute
significantly to the systematic error budget.
In Fig. 1b, we plot the mass function for all of our outputs in the
![]() plane. High values of
plane. High values of
![]() correspond to rare haloes of high redshift and/or high mass, while
low values of
correspond to rare haloes of high redshift and/or high mass, while
low values of
![]() describe haloes of low-mass and
redshift combinations.
Figure 1b shows the function
describe haloes of low-mass and
redshift combinations.
Figure 1b shows the function ![]() measured for all simulations in Table 1 of T08.
measured for all simulations in Table 1 of T08.
As previously reported, one of the main problems with using the mass
function to constrain cosmological parameters is that theoretical
predictions provide the number density for clusters of a given mass,
while the mass itself is never the directly observed quantity. One then
needs relations connecting mass with other more easily obtainable
quantities that can be used as a surrogate for cluster mass.
Over the past decade, observations of clusters of galaxies (e.g. ROSAT,
ASCA) have shown the existence of a correlation between the total
gravitating mass of clusters,
![]()
![]() , their X-ray luminosity (
, their X-ray luminosity (![]() ), and the temperature (
), and the temperature (![]() )
of the intracluster medium (ICM) (David et al. 1993; Markevitch 1998; Horner et al. 1999).
By means of the quoted scaling relations, one can obtain
different methods for tracing the evolution of the cluster number density:
(1) the X-ray temperature function (XTF), which has been presented for local (e.g., Henry & Arnaud 1991) and distant clusters (Eke et al. 1998; Henry 2000); and
(2) the evolution of the XLF. In this case, we need a relation between the observed
)
of the intracluster medium (ICM) (David et al. 1993; Markevitch 1998; Horner et al. 1999).
By means of the quoted scaling relations, one can obtain
different methods for tracing the evolution of the cluster number density:
(1) the X-ray temperature function (XTF), which has been presented for local (e.g., Henry & Arnaud 1991) and distant clusters (Eke et al. 1998; Henry 2000); and
(2) the evolution of the XLF. In this case, we need a relation between the observed ![]() and the cluster virial mass.
and the cluster virial mass.
In the present paper, following M08, we use the XLF to constrain cosmological parameters.
Then the next crucial step is to convert it in a XLF. This
can be done by first converting mass into intracluster gas temperature, by means of the
![]() relation, and then converting the temperature into X-ray luminosity, by means of the
relation, and then converting the temperature into X-ray luminosity, by means of the
![]() relation.
M08 used a self-similar relationship between mass and X-ray luminosity for massive clusters (e.g., Bryan & Norman 1998) modified by an additional redshift-dependent factor (see Morandi et al. 2007).
At this point, we must stress that numerical simulations confirm
that the DM component in clusters of galaxies, which represents the
dominant fraction of the mass,
has a remarkably self-similar behaviour, but the baryonic component
does not show the same level of self-similarity. This picture
is confirmed by X-ray observations, see, for instance, the deviation of
the luminosity-temperature (L-T) relation
in clusters, which is steeper than the theoretical
value predicted by the previous scenario.
More precisely, until some years ago, the cluster structure was
considered to be scale-free, which means that the global properties of
clusters,
such as halo mass, L-T relationship, and X-ray luminosity would scale self-similarly (Kaiser 1986; Evrard & Henry 1991).
In particular, the gas temperature would scale with cluster mass as
relation.
M08 used a self-similar relationship between mass and X-ray luminosity for massive clusters (e.g., Bryan & Norman 1998) modified by an additional redshift-dependent factor (see Morandi et al. 2007).
At this point, we must stress that numerical simulations confirm
that the DM component in clusters of galaxies, which represents the
dominant fraction of the mass,
has a remarkably self-similar behaviour, but the baryonic component
does not show the same level of self-similarity. This picture
is confirmed by X-ray observations, see, for instance, the deviation of
the luminosity-temperature (L-T) relation
in clusters, which is steeper than the theoretical
value predicted by the previous scenario.
More precisely, until some years ago, the cluster structure was
considered to be scale-free, which means that the global properties of
clusters,
such as halo mass, L-T relationship, and X-ray luminosity would scale self-similarly (Kaiser 1986; Evrard & Henry 1991).
In particular, the gas temperature would scale with cluster mass as
![]() and the
bolometric X-ray luminosity would scale with temperature as
and the
bolometric X-ray luminosity would scale with temperature as
![]() in the bremsstrahlung-dominated regime above 2 keV.
in the bremsstrahlung-dominated regime above 2 keV.
Studies following that of Kaiser (1986) show that the observed luminosity-temperature relation is closer to
![]() (e.g., Edge & Stewart 1991), indicating that non-gravitational processes should influence the density structure of clusters core,
where most of the luminosity is generated (Kaiser 1991; Evrard & Henry 1991; Navarro et al. 1995; Bryan & Norman 1998).
One way to obtain a scaling law closer to the observational one is
either to inject non-gravitational energy into the ICM before or during
cluster formation, the so-called pre-heating (Ponman et al. 1999; Bower et al. 1997; Cavaliere et al. 1997, 1999; Tozzi & Norman 2001; Borgani et al. 2001; Voit & Brian 2001) or to consider feedback processes that alter the gas characteristics during the evolution of the cluster's (Voit & Bryan 2001) cooling flows (Allen & Fabian 1998).
A similar situation is valid for the M-T relationship, namely that the self-similarity in the
M-T relation seems to break at a few keV (Nevalanien et al. 2000; Xu et al. 2001; Finoguenov et al. 2001; Muanwong et al. 2001; Bialek et al. 2001).
Consequently, if one starts with self-similar scaling laws,
as in M08, in order to have consistent scaling relations one
has to compare the self-similar scaling relations to observations
(Morandi et al. 2007).
(e.g., Edge & Stewart 1991), indicating that non-gravitational processes should influence the density structure of clusters core,
where most of the luminosity is generated (Kaiser 1991; Evrard & Henry 1991; Navarro et al. 1995; Bryan & Norman 1998).
One way to obtain a scaling law closer to the observational one is
either to inject non-gravitational energy into the ICM before or during
cluster formation, the so-called pre-heating (Ponman et al. 1999; Bower et al. 1997; Cavaliere et al. 1997, 1999; Tozzi & Norman 2001; Borgani et al. 2001; Voit & Brian 2001) or to consider feedback processes that alter the gas characteristics during the evolution of the cluster's (Voit & Bryan 2001) cooling flows (Allen & Fabian 1998).
A similar situation is valid for the M-T relationship, namely that the self-similarity in the
M-T relation seems to break at a few keV (Nevalanien et al. 2000; Xu et al. 2001; Finoguenov et al. 2001; Muanwong et al. 2001; Bialek et al. 2001).
Consequently, if one starts with self-similar scaling laws,
as in M08, in order to have consistent scaling relations one
has to compare the self-similar scaling relations to observations
(Morandi et al. 2007).
Unlike the M08 approach, we used models for the L-T, M-T, relationships taking the non-self similarity into account: namely, the
![]() relation obtained analytically using the model of Del Popolo (2002),
while the
relation obtained analytically using the model of Del Popolo (2002),
while the
![]() relation is the one obtained in Del Popolo et al. (2005) based on an improvement of the
punctuated equilibrium model (PEM) of Cavaliere et al. (1997, 1998, 1999).
The drawbacks of using self-similar relationships fitted to the data
(clusters) and the reasons for using a different approach were already
discussed in Del Popolo (2003, their Sect. 3), as well as in this section.
relation is the one obtained in Del Popolo et al. (2005) based on an improvement of the
punctuated equilibrium model (PEM) of Cavaliere et al. (1997, 1998, 1999).
The drawbacks of using self-similar relationships fitted to the data
(clusters) and the reasons for using a different approach were already
discussed in Del Popolo (2003, their Sect. 3), as well as in this section.
Similar to the 2009 study, in Del Popolo (2003) we used the models for the L-T, T-M, relationships
instead of the scaling relations obtained from simulations of Chandra
data (see, e.g., Pierpaoli et al. 2001, 2003, for references)![]() .
Equation (5) in M08, similar to that Eq. (13) of Pierpaoli et al. (2001) or Eq. (4) of Pierpaoli
et al. (2003),
comes from rather simplistic arguments (dimensional analysis and an
assumption that clusters are self-similar),
not taking important physical effects into account, which then gives
rise to a non-self-similar behaviour of the quoted relation,
as previously discussed. The fitting procedure used by M08, trying
to consider the previous physics and the non-self-similar behaviour of
the relationship is complicated by several effects.
In fact, in the fit one uses data that may contain small groups that
can be influential in estimating the slope of the model, and one has
then to carefully choose the data to be used in the fit. This choice
mitigates the possibility of obtaining biased results if the slope of
the mass-luminosity relation is different for massive
clusters than for smaller groups. In M08 the data (clusters) were
fitted with
.
Equation (5) in M08, similar to that Eq. (13) of Pierpaoli et al. (2001) or Eq. (4) of Pierpaoli
et al. (2003),
comes from rather simplistic arguments (dimensional analysis and an
assumption that clusters are self-similar),
not taking important physical effects into account, which then gives
rise to a non-self-similar behaviour of the quoted relation,
as previously discussed. The fitting procedure used by M08, trying
to consider the previous physics and the non-self-similar behaviour of
the relationship is complicated by several effects.
In fact, in the fit one uses data that may contain small groups that
can be influential in estimating the slope of the model, and one has
then to carefully choose the data to be used in the fit. This choice
mitigates the possibility of obtaining biased results if the slope of
the mass-luminosity relation is different for massive
clusters than for smaller groups. In M08 the data (clusters) were
fitted with
![]() erg/s
in the 0.1-2.4 keV band. Moreover, the process of fitting the
model in Eq. (7) of M08 is complicated by the Malmquist bias.
Close to the flux limit for selection, any X-ray-selected sample will
tend to include the most luminous sources for a given mass.
This results in a steepening of the derived mass-luminosity relation
and a bias in the inferred intrinsic scatter in luminosity for a given
mass.
The use of the extended sample of Reiprich & Böringer (2002)
(RB02), rather than only their flux-limited HIFLUGCS sample, partially
mitigates this effect by decreasing the flux limit.
Another problem is that as a consequence of Malmquist bias there is a
strong apparent, but not necessarily physical, correlation between
luminosity and redshift because the flux limit corresponds to higher
luminosities at higher redshifts.
erg/s
in the 0.1-2.4 keV band. Moreover, the process of fitting the
model in Eq. (7) of M08 is complicated by the Malmquist bias.
Close to the flux limit for selection, any X-ray-selected sample will
tend to include the most luminous sources for a given mass.
This results in a steepening of the derived mass-luminosity relation
and a bias in the inferred intrinsic scatter in luminosity for a given
mass.
The use of the extended sample of Reiprich & Böringer (2002)
(RB02), rather than only their flux-limited HIFLUGCS sample, partially
mitigates this effect by decreasing the flux limit.
Another problem is that as a consequence of Malmquist bias there is a
strong apparent, but not necessarily physical, correlation between
luminosity and redshift because the flux limit corresponds to higher
luminosities at higher redshifts.
For what concerns the data (clusters) used in the analysis, they are the same as those used by M08: the following three flux-limited surveys are included in our analysis: the BCS (Ebeling et al. 1998) and REFLEX sample (Böhringer et al. 2004) at low redshifts (z < 0.3), and the MACS (Ebeling et al. 2001) at 0.3 < z < 0.5 (see M08). In the analysis, the sample was chosen to cover the redshift range z<0.5, since at higher redshifts the number of unrelaxed clusters decrease, and the L-T and T-M relations are appropriate for relaxed clusters. In this paper we present an analysis based only on the XLF data described above, along with the priors described in Sect. 4 of M08.
Following M08, we parametrize the full model fitted to the XLF data as h,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
w,
where
,
w,
where
![]() and
and
![]() are the baryon and cold dark matter densities (
are the baryon and cold dark matter densities (
![]() ).
In addition to the assumption of spatial flatness, we adopt the Gaussian priors
).
In addition to the assumption of spatial flatness, we adopt the Gaussian priors
![]() (Freedman et al. 2001) and
(Freedman et al. 2001) and
![]() (Kirkman et al. 2003) from the Hubble Key Project and Big Bang nucleosynthesis studies, respectively.
Since the results are insensitive to the spectral index within a reasonable range (see M08), we fix
(Kirkman et al. 2003) from the Hubble Key Project and Big Bang nucleosynthesis studies, respectively.
Since the results are insensitive to the spectral index within a reasonable range (see M08), we fix
![]() in accordance with (Spergel et al. 2007) for the standard analysis. The dark-energy equation of state was bounded by a uniform prior, -5<w<0.
in accordance with (Spergel et al. 2007) for the standard analysis. The dark-energy equation of state was bounded by a uniform prior, -5<w<0.
The luminosity function likelihood is the same as in M08 (Sect. 4.2).
The likelihood that N clusters with inferred luminosities in a range d![]() exist in a volume dV
can in general be written as a Poisson probability plus a correction
for the clustering of haloes with one another. If the plane of redshift
and inferred luminosity is divided into non-overlapping cells, then the
likelihood of our data is simply
exist in a volume dV
can in general be written as a Poisson probability plus a correction
for the clustering of haloes with one another. If the plane of redshift
and inferred luminosity is divided into non-overlapping cells, then the
likelihood of our data is simply
where Nj and
If the cells are taken to be rectangular, with the jth cell given by
![]() and
and
![]() ,
then
,
then
where V(z) is the comoving volume within redshift z. In the absence of intrinsic scatter in the mass-luminosity relation and measurement errors in the observed luminosities, the derivative of the comoving number density would simply be
Here,
Similar to M08, the presence of scatter requires us to take into account that a cluster detected with inferred luminosity ![]() could potentially have any true luminosity L and mass M,
with some associated probability. To calculate the predicted number
density correctly, we must therefore convolve with these probability
distributions:
could potentially have any true luminosity L and mass M,
with some associated probability. To calculate the predicted number
density correctly, we must therefore convolve with these probability
distributions:
where P(L|M) is a log-normal distribution whose width is like in M08 the intrinsic scatter in the mass-luminosity relation,
3 Results
In Fig. 2, we compare the joint
![]() constraints obtained from the BCS, REFLEX, and MACS data set combination for a
constraints obtained from the BCS, REFLEX, and MACS data set combination for a ![]() CDM.
The marginalized constraints from the combination of the three cluster samples are
CDM.
The marginalized constraints from the combination of the three cluster samples are
![]() and
and
![]() ,
while the result of M08 gives less tight constraints
,
while the result of M08 gives less tight constraints
![]() and
and
![]() .
.
![\begin{figure}
\par\includegraphics[width=7.3cm]{13133fig2.eps}
\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/06/aa13133-09/Timg95.png)
|
Figure 2:
Joint 68.3 and 95.4% confidence constraints on
|
| Open with DEXTER | |
Our previous constraints are in good agreement with recent, independent results from the CMB (Spergel et al. 2007) and cosmic shear, as measured in the 100 Square Degree Survey (Benjamin et al. 2007) and CFHTLS (Canada-France-Hawaii Telescope Legacy Survey) Wide field (Fu et al. 2008).
Our results also agree overall with previous findings based on the
observed X-ray luminosity and temperature functions of clusters (Eke
et al. 1998; Donahue & Voit 1999; Henry 2000; Borgani et al. 2001; Seljak 2002; Allen et al. 2003; Pierpaoli et al. 2003; Schuecker et al. 2003; Henry 2004).
Our result for
![]() is in excellent agreement with current constraints based on cluster
is in excellent agreement with current constraints based on cluster
![]() data (Allen et al. 2008, and references therein) and the power spectrum of galaxies in the 2dF galaxy redshift survey (Cole et al. 2005) and Sloan Digital Sky Survey (SDSS) (Eisenstein et al. 2005; Tegmark et al. 2006; Percival et al. 2007a), as well as the combination of CMB data with a variety of external constraints (Spergel 2007).
data (Allen et al. 2008, and references therein) and the power spectrum of galaxies in the 2dF galaxy redshift survey (Cole et al. 2005) and Sloan Digital Sky Survey (SDSS) (Eisenstein et al. 2005; Tegmark et al. 2006; Percival et al. 2007a), as well as the combination of CMB data with a variety of external constraints (Spergel 2007).
In Fig. 3a, we set constraints for the wCDM model, and we plot the joint constraints on
![]() and
and ![]() from the luminosity function data using our standard priors,
while Fig. 3b displays constraints on
from the luminosity function data using our standard priors,
while Fig. 3b displays constraints on
![]() and w obtained independently of the XLF data.
The marginalized results from the XLF data are
and w obtained independently of the XLF data.
The marginalized results from the XLF data are
![]() ,
,
![]() and
w=-1.3+0.3-0.4,
while in M08 they are again less tight
and
w=-1.3+0.3-0.4,
while in M08 they are again less tight
![]() ,
,
![]() and
w=-1.4+0.4-0.7.
Our new XLF results are consistent
with the cosmological-constant model (w=-1).
and
w=-1.4+0.4-0.7.
Our new XLF results are consistent
with the cosmological-constant model (w=-1).
| Figure 3:
Panel a). Same as Fig. 2 but for a wCDM model. Panel b). Joint 68.3 and 95.4% confidence constraints on
|
|
| Open with DEXTER | |
| Figure 4:
Joint 68.3 and 95.4 per cent confidence constraints on
|
|
| Open with DEXTER | |
An improvement in the previous results can be obtained by adding to the XLF analysis the
![]() +CMB+SNIa data set.
The
+CMB+SNIa data set.
The
![]() +CMB+SNIa combination already provides tight constraints on
+CMB+SNIa combination already provides tight constraints on
![]() ,
h,
,
h,
![]() ,
and
,
and ![]() (so that no priors on these parameters are used in either of the combined analyses), but the degeneracy between w and
(so that no priors on these parameters are used in either of the combined analyses), but the degeneracy between w and ![]() (right panel of Fig. 4)
limits the precision of the dark-energy results. The addition of the XLF data breaks the degeneracy in the
(right panel of Fig. 4)
limits the precision of the dark-energy results. The addition of the XLF data breaks the degeneracy in the
![]() plane (left panel),
resulting in tighter constraints on
plane (left panel),
resulting in tighter constraints on
![]() ,
,
![]() ,
and w. The degeneracy breaking power of
other combinations of data with the CMB is discussed by Spergel et al. (2007).
The resulting constraints are
,
and w. The degeneracy breaking power of
other combinations of data with the CMB is discussed by Spergel et al. (2007).
The resulting constraints are
![]() ,
,
![]() ,
and
,
and
![]() ,
to be compared with M08
,
to be compared with M08
![]() ,
,
![]() ,
and
,
and
![]() .
The previous constraints agree within the errors with the Vikhlinin et al. (2009b) constraints, namely,
.
The previous constraints agree within the errors with the Vikhlinin et al. (2009b) constraints, namely,
![]() ,
,
![]() ,
and
,
and
![]() .
.
The tight constraints obtained by M08 when combining XLF analysis with the
![]() +CMB+SNIa data set are
primarily due to the tightness of the constraints obtained from
+CMB+SNIa data set are
primarily due to the tightness of the constraints obtained from
![]() +CMB+SNIa data itself and not to the precision
of the XLF analysis of M08, as shown by comparing our results for
+CMB+SNIa data itself and not to the precision
of the XLF analysis of M08, as shown by comparing our results for
![]() ,
,
![]() ,
w obtained by the XLF analysis with those of M08.
In our model the improvement in the mass function model and the L-M relationship gives rise to tight constraints even when using only the XLF function.
,
w obtained by the XLF analysis with those of M08.
In our model the improvement in the mass function model and the L-M relationship gives rise to tight constraints even when using only the XLF function.
To understand why the results of our analysis are different from those of M08, we have to stress a key point. The M08 paper, as well as several others papers in the literature, used two different data sets, the first one composed by REFLEX, BCS, and MACS, to constrain cosmological parameters and the second external data set (RB02 data set) to constrain the luminosity-mass relation, which in M08 is a power law with three free parameters, without explicitly accounting for selection bias. Consequently, it was necessary to restrict the external data set (RB02) to low redshifts and high fluxes to minimize the effects of selection bias, making it impossible to test for departures from self-similar evolution in the scaling relation. For a ``self-consistent'' analysis, it is necessary that a single likelihood function be applied to the full data set, which encompasses the entire theoretical model (cosmology + scaling relations) so as to ensure that the covariance among all the model parameters is fully captured and that the effects of the mass function and selection biases are properly accounted for throughout. This kind of analysis has been performed for the first time by Vikhlinin et al. (2009a,b), who used the same cluster sample to constrain the scaling relations, thus obtaining tighter constraints.
In the analysis of the present paper, the L-M relation is a physically motivated relation (not a power law with free parameters) that does not require fits to data, as in M08. Since we do not need the double analysis of M08 and previous papers, the first to get the L-M fitting parameters from RB02 data and the second to obtain the cosmological constraints using BCS, REFLEX, and MACS, we bypass the quoted drawback in the M08 analysis.
A month after the present paper was submitted, two papers, Mantz et al. (2009a,b),
appeared in arXiv
showing that the key point stressed previously,
namely generalizing M08 to allow the quoted simultaneous and
self-consistent fit and using T08 mass function (instead of that in
Jenkins et al. 2001)
result in cosmological constraints that are a factor 2-3 better
than those in M08, based on the same flux-limited sample of clusters.
In the present paper, we have also checked that using the same L-M relation as in M08, we obtain the same set of constraints as derived by M08![]() again.
again.
The use of our non-self-similar L-M relation for clusters of luminosity
![]() erg/s in the 0.1-2.4 keV band. Since the clusters included in the M08 sample have high X-ray luminosity (above
erg/s in the 0.1-2.4 keV band. Since the clusters included in the M08 sample have high X-ray luminosity (above
![]() erg/s), one could think that
the changes in the L-M
relation of the present paper with respect to the classical
self-similar model will not produce significant changes in constraints
on the cosmological parameters. Even if major differences between the L-M model of the present paper and the self-similar model are observed at gas temperatures below 3 keV, the present L-M relation depends on the M-T and L-T relationships,
and especially the second one (based on the modified punctuated
equilibrium model (MPEM)) never behaves in a self-similar way as shown
in Del Popolo et al. (2005,
even at gas temperatures higher than 10 keV). Moreover,
as previously reported, the improvement in the constraints is
strictly connected bypassing the quoted drawback in the M08 analysis by
means of our L-M relation and does not depend on parameters that must be fixed using external data.
erg/s), one could think that
the changes in the L-M
relation of the present paper with respect to the classical
self-similar model will not produce significant changes in constraints
on the cosmological parameters. Even if major differences between the L-M model of the present paper and the self-similar model are observed at gas temperatures below 3 keV, the present L-M relation depends on the M-T and L-T relationships,
and especially the second one (based on the modified punctuated
equilibrium model (MPEM)) never behaves in a self-similar way as shown
in Del Popolo et al. (2005,
even at gas temperatures higher than 10 keV). Moreover,
as previously reported, the improvement in the constraints is
strictly connected bypassing the quoted drawback in the M08 analysis by
means of our L-M relation and does not depend on parameters that must be fixed using external data.
To obtain tighter and tighter constraints, one needs to try to reduce the systematic uncertainties in the analysis to a minimum. Progress is expected over the coming years in refining the ranges of these allowances, both observationally and through improved simulations. A reduction in the size of the required systematic allowances will tighten the cosmological constraints. Improved numerical simulations of large samples of massive clusters, including a more complete treatment of star formation and feedback physics that reproduces both the observed optical galaxy luminosity function and cluster X-ray properties, will be of major importance. Further deep X-ray and optical observations of nearby clusters will provide better constraints on the viscosity of the cluster gas. Improved optical/near infrared observations of clusters should pin down the stellar mass fraction in galaxy clusters and its evolution. Ground and space-based gravitational lensing studies will provide strong, independent constraints on the mass distributions in clusters. A large programme using the Subaru telescope and Hubble Space Telescope is underway, as is similar work by other groups (e.g. Hoekstra 2007).
In the near future, continuing programmes of Chandra and XMM-Newton
observations of known X-ray luminous clusters should allow progress,
both by
expanding the
![]() sample (e.g. Chandra snapshot observations of the entire MACS sample; Ebeling et al. 2001,
2007) and through deeper observations of the current target
list.
A new, large-area X-ray survey such as proposed by the
Spectrum-RG/eROSITA project could make a substantial contribution by
finding hundreds of suitable systems at high redshifts.
sample (e.g. Chandra snapshot observations of the entire MACS sample; Ebeling et al. 2001,
2007) and through deeper observations of the current target
list.
A new, large-area X-ray survey such as proposed by the
Spectrum-RG/eROSITA project could make a substantial contribution by
finding hundreds of suitable systems at high redshifts.
Looking a decade ahead, the International X-ray Observatory (IXO), the
result of the merging of NASA's Constellation-X and ESA/JAXA's XEUS mission concepts,
will offer the possibility to carry out precise studies of dark energy using the
![]() technique
technique![]() .
.
4 Conclusions
We showed how to improve the constraints onThe author acknowledges financial support from the German Research Foundation (DFG) under grant NO. KR 1635/16-1.
References
- Allen, S. W., & Fabian, A. 1998, MNRAS, 297, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Allen, S. W., Schmidt, R. W., Fabian, A. C., & Ebeling, H. 2003, MNRAS, 342, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Allen, S. W., Rapetti, D. A., Schmidt, R. W., et al. 2008, MNRAS, 383, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Bahcall, N. A., & Fan, X. 1998, ApJ, 504, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Bahcall, N. A., Fan, X., & Cen, R. 1997, ApJ, 485, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Bardeen, J. M., Bond, J. R., Kaiser, N., & Szalay, A. S. 1986, ApJ, 304, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Benjamin, J., Heymans, C., Semboloni, E., et al. 2007, MNRAS, 381, 702 [NASA ADS] [CrossRef] [Google Scholar]
- Bialek, J. J., Evrard, A. E., & Mohr, J. J. 2001, ApJ, 555, 597 [NASA ADS] [CrossRef] [Google Scholar]
- Blanchard, A., & Bartlett, J. G. 1998, A&A, 332, L49 [NASA ADS] [Google Scholar]
- Blanchard, A., Bartlett, J. G., & Sadat, R. 1999, CRASB, 327, 313 [NASA ADS] [Google Scholar]
- Böhringer, H., Schuecker, P., Guzzo, L., et al. 2004, A&A, 425, 367 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borgani, S., Rosati, P., Tozzi, P., et al. 2001, ApJ, 561, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Bower, R. G., Castander, F. J., Couch, W., Ellis, R. S., & Böhringer, H. 1997, MNRAS, 291, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Bryan, G. L., & Norman, M. L. 1998, ApJ, 495, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Burenin, R. A., Vikhlinin, A., Hornstrup, A., et al. 2007, ApJS, 172, 561 [NASA ADS] [CrossRef] [Google Scholar]
- Cavaliere, A., Menci, N., & Tozzi, P. 1997, ApJ, 484, L21 (CMT97) [NASA ADS] [CrossRef] [Google Scholar]
- Cavaliere, A., Menci, N., & Tozzi, P. 1998, ApJ, 501, 493 (CMT98) [NASA ADS] [CrossRef] [Google Scholar]
- Cavaliere, A., Menci, N., & Tozzi, P. 1999, MNRAS, 308, 599 (CMT99) [NASA ADS] [CrossRef] [Google Scholar]
- Cash, A. 1979, ApJ, 228, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Cole, S., Percival, W. J., Peacock, J. A., et al. 2005, MNRAS, 362, 505 [NASA ADS] [CrossRef] [Google Scholar]
- David, L. P., Slyz, A., Jones, C., Forman, W., & Vrtilek, S. D. 1993, ApJ, 412, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Del Popolo, A. 2002, MNRAS, 336, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Del Popolo, A. 2003, ApJ, 599, 723 [NASA ADS] [CrossRef] [Google Scholar]
- Del Popolo, A. 2006a, ApJ, 637, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Del Popolo, A. 2006b, AJ, 131, 2367 [NASA ADS] [CrossRef] [Google Scholar]
- Del Popolo, A., Hiotelis, S., & Penarrubia, G. 2005, ApJ, 628, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Donahue, M., & Voit, G. M. 1999, ApJ, 523, L137 [NASA ADS] [CrossRef] [Google Scholar]
- Dunkley, J., Spergel, D. N., Komatsu, E., et al. 2009, ApJ, 701, 1804 [NASA ADS] [CrossRef] [Google Scholar]
- Ebeling, H., Edge, A. C., Bohringer, H., et al. 1998, MNRAS, 301, 881 [NASA ADS] [CrossRef] [Google Scholar]
- Ebeling, H., Edge, A. C., Allen, S. W., et al. 2000, MNRAS, 318, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Ebeling, H., Edge, A. C., & Henry, J. P. 2001, ApJ, 553, 668 [Google Scholar]
- Ebeling, H., Barrett, E., Donovan, D., et al. 2007, ApJ, 661, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Edge, A. C., & Stewart, G. C. 1991, MNRAS, 252, 414 [NASA ADS] [CrossRef] [Google Scholar]
- Eke, V. R., Cole, S., & Frenk, C. S. 1996, MNRAS, 282, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Eke, V. R., Cole, S., Frenk, C. S., & Patrick Henry, J. 1998, MNRAS, 298, 1145 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenstein, D. J., Zehavi, I., Hogg, D. W., et al. 2005, ApJ, 633, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Finoguenov, A., Reiprich, T. H., & Böhringer, H. 2001, A&A, 368, 749 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Freedman, W. L., McClintock, J. E., Narayan, R., et al. 2001, ApJ, 553, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Fu, L., Semboloni, E., Hoekstra, H., et al. 2008, A&A, 479, 9 [Google Scholar]
- Gao, L., Navarro, J. F., Cole, S., et al. 2007, MNRAS, 387, 536 [Google Scholar]
- Governato, F., Babul, A., Quinn, T., et al. 1999, MNRAS, 307, 949 [NASA ADS] [CrossRef] [Google Scholar]
- Gregory, P. C., & Loredo, T. 1992, ApJ, 398, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Henry, J. P. 2000, ApJ, 534, 565 [Google Scholar]
- Henry, J. P. 2004, ApJ, 609, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Henry, J. P., & Arnaud, K. A. 1991, ApJ, 372, 410 [NASA ADS] [CrossRef] [Google Scholar]
- Horner, D. J., Mushotzky, R. F., & Scharf, C. A. 1999, ApJ, 520, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Hoekstra, H. 2007, MNRAS, 379, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, W., & Kravtsov, A. V. 2003, ApJ, 584, 702 [NASA ADS] [CrossRef] [Google Scholar]
- Jenkins, A., Frenk, C. S., White, S. D. M., et al. 2001, MNRAS, 321, 372 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Jeltema, T. E., Hallman, E. J., Burns, J. O., & Motl, P. M. 2008, ApJ, 681, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Kaiser, N. 1986, MNRAS, 222, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Kaiser, N. 1991, ApJ, 383, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Kirkman, D., Tytler, D., Suzuki, N., O'Meara, J. M., & Lubin, D. 2003, ApJS, 149, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, E., Dunkley, J., Nolta, M. R., et al. 2009, ApJS, 180, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Kravtsov, A. V., Vikhlinin, A., & Nagai, D. 2006, ApJ, 650, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Maughan, B. J. 2007, ApJ, 668, 772 [NASA ADS] [CrossRef] [Google Scholar]
- Mantz, A., Allen, S. W., Ebeling, H., & Rapetti, D. 2008, MNRAS, 387, 1179 (M08) [NASA ADS] [CrossRef] [Google Scholar]
- Mantz, A., Allen, S. W., Rapetti, D., & Ebeling, H. 2009a [arXiv:0909.3098] [Google Scholar]
- Mantz, A., Allen, S. W., Ebeling, H., et al. 2009b [arXiv:0909.3099] [Google Scholar]
- Markevitch, M. 1998, ApJ, 503, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Morandi, A., Ettori, S., & Moscardini, L. 2007, MNRAS, 379, 518 [NASA ADS] [CrossRef] [Google Scholar]
- Muanwong, O., Thomas, P. A., Kay, S. T., Pearce, F. R., & Couchman, H. M. P. 2001, ApJ, 552, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Nagai, D., Vikhlinin, A., & Kravtsov, A. V. 2007, ApJ, 655, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1995, MNRAS, 275, 720 [NASA ADS] [CrossRef] [Google Scholar]
- Nevalainen, J., Markevitch, M., & Forman, W. 2000, ApJ, 532, 694 [NASA ADS] [CrossRef] [Google Scholar]
- Percival, W. J., Nichol, R. C., Eisenstein, D. J., et al. 2007a, ApJ, 657, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Percival, W. J., Cole, S., Eisenstein, D. J., et al. 2007b, MNRAS, 381, 1053 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Pierpaoli, E., Scott, D., & White, M. 2001, MNRAS, 325, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Pierpaoli, E., Borgani, S., Scott, D., & White, M. 2003, MNRAS, 342, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Ponman, T. J., Cannon, D. B., & Navarro, J. F. 1999, Nature, 397, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W., & Schechter, P. 1974, ApJ, 187, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Rasia, E., Ettori, S., Moscardini, L., et al. 2006, MNRAS, 369, 2013 [NASA ADS] [CrossRef] [Google Scholar]
- Reed, D., Gardner, J., Quinn, T., et al. 2003, MNRAS, 346, 565 (R03) [NASA ADS] [CrossRef] [Google Scholar]
- Reiprich, T. H., & Böhringer, H. 2002, ApJ, 567, 716 [NASA ADS] [CrossRef] [Google Scholar]
- Reichart, D. E., Nichol, R. C., Castander, F. J., et al. 1999b, ApJ, 518, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Rosati, P., Borgani, S., & Norman, C. 2002, ARA&A, 40, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Sadat, R., Blanchard, A., & Oukbir, J. 1998, A&A, 329, 21 [Google Scholar]
- Schuecker, P., Böhringer, H., Collins, C. A., & Guzzo, L. 2003, A&A, 398, 867 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seljak, U. 2002, MNRAS, 337, 769 [NASA ADS] [CrossRef] [Google Scholar]
- Sheth, R. K., & Tormen, G. 2002, MNRAS, 329, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Spergel, D. N., Bean, R., Doré, O., et al. 2007, ApJS, 170, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Tegmark, M., Eisenstein, D. J., Strauss, M. A., et al. 2006, Phys. Rev. D, 74, 123507 [Google Scholar]
- Tinker, J., Kravtsov, A. V., Klypin, A., et al. 2008, ApJ, 688, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Tozzi, P., & Norman, C. 2001, ApJ, 546, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Trümper, J. 1993, Science, 260, 1769 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Viana, P. T. P., & Liddle, A. R. 1999, MNRAS, 303, 535 [NASA ADS] [CrossRef] [Google Scholar]
- Voit, C. M. 2000, ApJ, 543, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Vikhlinin, A., McNamara, B. R., Forman, W., et al. 1998, ApJ, 502, 558 [NASA ADS] [CrossRef] [Google Scholar]
- Vikhlinin, A., Burenin, R. A., Ebeling, H., et al. 2009a, ApJ, 692, 1033 [NASA ADS] [CrossRef] [Google Scholar]
- Vikhlinin, A., Kravtsov, A. V., Burenin, R. A., et al. 2009b, ApJ, 692, 1060 [NASA ADS] [CrossRef] [Google Scholar]
- Voevodkin, A., & Vikhlinin, A. 2004, ApJ, 601, 610 [NASA ADS] [CrossRef] [Google Scholar]
- Voit, C. M., & Donahue, M. 1998, ApJ, 500, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Voit, G. M., & Bryan, G. 2001, Nature, 414, 425 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Warren, M. S., Abazajian, K., Holz, D. E., & Teodoro, L. 2006, ApJ, 646, 881 [NASA ADS] [CrossRef] [Google Scholar]
- White, S. D. M., Navarro, J. F., Evrard, A. E., & Frenk, C. S. 1993, Nature, 366, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, H., Jing, G., & Wu, X. 2001, ApJ, 553, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Yahagi, H., Nagashima, M., & Yoshii, Y. 2004, ApJ, 605, 709 (YNY04) [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Y. Y., Finoguenov, A., Böhringer, H., et al. 2007, A&A, 467, 437 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Footnotes
- ...
![[*]](/icons/foot_motif.png)
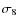 is the amplitude of the mass density fluctuation power spectrum over spheres of radius
is the amplitude of the mass density fluctuation power spectrum over spheres of radius
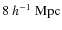 ,
and M8
is the mean mass within these spheres.
,
and M8
is the mean mass within these spheres.
- ... criteria
![[*]](/icons/foot_motif.png)
- This is so that the search volume and the number density associated with each cluster are uniquely identified.
- ...
ROSAT
![[*]](/icons/foot_motif.png)
- The ROSAT Brightest Cluster Sample (BCS; Ebeling et al. 1998, 2000) and ROSAT-ESO Flux Limited X-ray sample (REFLEX; Böhringer et al. 2004) together cover approximately two-thirds of the sky out to redshift
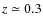 and contain more than 750 clusters. The Massive Cluster Survey (MACS; Ebeling et al. 2001, 2007)
extends these data to
and contain more than 750 clusters. The Massive Cluster Survey (MACS; Ebeling et al. 2001, 2007)
extends these data to
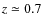 .
The ROSAT 160 sq. degree survey, described for the first time by Vikhlinin et al. (1998)
is a serendipitous cluster catalogue containing 201 groups/clusters, while the ROSAT
400 sq. degree survey is based on 1610 high Galactic latitude ROSAT PSPC pointings (Burenin et al. 2007)
and includes 266 optically confirmed galaxy clusters, groups and individual elliptical galaxies.
.
The ROSAT 160 sq. degree survey, described for the first time by Vikhlinin et al. (1998)
is a serendipitous cluster catalogue containing 201 groups/clusters, while the ROSAT
400 sq. degree survey is based on 1610 high Galactic latitude ROSAT PSPC pointings (Burenin et al. 2007)
and includes 266 optically confirmed galaxy clusters, groups and individual elliptical galaxies.
- ...
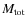
![[*]](/icons/foot_motif.png)
- Since
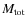 compares with the ICM temperature measurements that can be obtained
through X-ray spectroscopy, this explains the importance of a M-T relation.
compares with the ICM temperature measurements that can be obtained
through X-ray spectroscopy, this explains the importance of a M-T relation.
- ... references)
![[*]](/icons/foot_motif.png)
- Equation (22) in Del Popolo (2003) and Eq. (5) in M08 are very similar.
- ... M08
![[*]](/icons/foot_motif.png)
- Mantz et al. (2009a,b) obtain
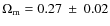 ,
,
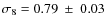 and
and
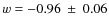 .
.
- ... technique
![[*]](/icons/foot_motif.png)
- The large collecting area and combined
spatial/spectral resolving power of IXO
should permit precise
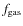 measures. An investment of
measures. An investment of  10 Ms of IXO time to measure
10 Ms of IXO time to measure
 to 5% (corresponding to 3.3% accuracy in distance) in
each of the 500 hottest, most X-ray luminous,
dynamically relaxed clusters detected in future cluster surveys, spanning the redshift range 0 < z < 2 (typical redshift
to 5% (corresponding to 3.3% accuracy in distance) in
each of the 500 hottest, most X-ray luminous,
dynamically relaxed clusters detected in future cluster surveys, spanning the redshift range 0 < z < 2 (typical redshift
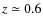 ),
will be sufficient to constrain cosmological parameters with a DETF figure of merit of 2040.
),
will be sufficient to constrain cosmological parameters with a DETF figure of merit of 2040.
All Figures
![\begin{figure}
\par\subfigure[]{\hspace*{1.1cm}\includegraphics[width=7.8cm]{131...
...e[]{\includegraphics[width=8.8cm]{13133fig1b.eps} }\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/06/aa13133-09/Timg40.png)
|
Figure 1:
In Panel a): multiplicity function obtained in this paper (solid line), fitting formula proposed by Yahagi et al. (2004) their Eq. (7) (short-dashed line), Sheth & Tormen (2002) (ST) multiplicity function (dotted line), Jenkins et al. (2001)
multiplicity function (long-dashed line). The error bars with open
circles represent the run 140 of YNY, those with filled squares
case 70b, those with open squares case 70a, those with filled circles
case 35b, those with crosses case 35a. Panel b): mass function plotted in redshift-independent form. The measured
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.3cm]{13133fig2.eps}
\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/06/aa13133-09/Timg95.png)
|
Figure 2:
Joint 68.3 and 95.4% confidence constraints on
|
| Open with DEXTER | |
| In the text | |
| |
Figure 3:
Panel a). Same as Fig. 2 but for a wCDM model. Panel b). Joint 68.3 and 95.4% confidence constraints on
|
| Open with DEXTER | |
| In the text | |
| |
Figure 4:
Joint 68.3 and 95.4 per cent confidence constraints on
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



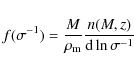
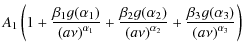
![$\displaystyle \times ~\sqrt{\frac{a\nu }{2\pi }}
{\rm e}^{\left\{\frac{-a \nu}{...
...alpha_2}}+\frac{\beta_3}{\left( a\nu \right) ^{\alpha_3}}
\right] ^{2}\right\}}$](/articles/aa/full_html/2010/06/aa13133-09/img43.png)