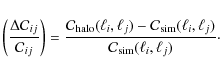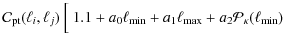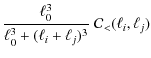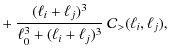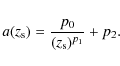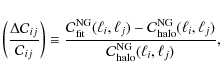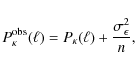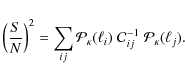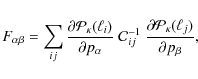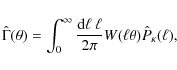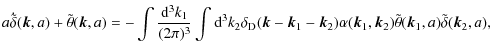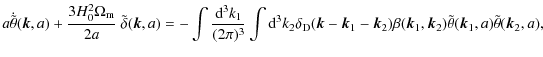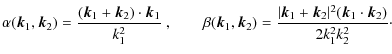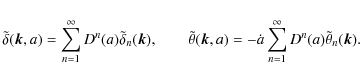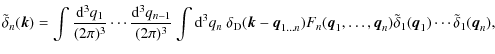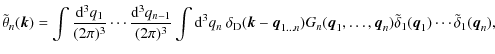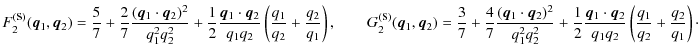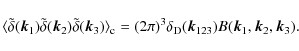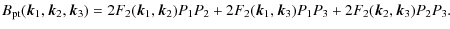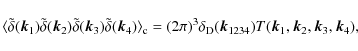| Issue |
A&A
Volume 514, May 2010
|
|
|---|---|---|
| Article Number | A79 | |
| Number of page(s) | 19 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/200912854 | |
| Published online | 26 May 2010 | |
A fitting formula for the non-Gaussian contribution to the lensing power spectrum covariance
J. Pielorz - J. Rödiger - I. Tereno - P. Schneider
Argelander-Institut für Astronomie (AIfA), Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
Received 8 July 2009 / Accepted 10 December 2009
Abstract
Context. Weak gravitational lensing is one of the most
promising tools to investigate the equation-of-state of dark energy.
In order to obtain reliable parameter estimations for current and
future experiments, a good theoretical understanding of dark
matter clustering is essential. Of particular interest is the
statistical precision to which weak lensing observables, such as
cosmic shear correlation functions, can be determined.
Aims. We construct a fitting formula for the non-Gaussian part
of the covariance of the lensing power spectrum. The Gaussian
contribution to the covariance, which is proportional to the lensing
power spectrum squared, and optionally shape noise can be included
easily by adding their contributions.
Methods. Starting from a canonical estimator for the
dimensionless lensing power spectrum, we model first the covariance in
the halo model approach including all four halo terms for one fiducial
cosmology and then fit two polynomials to the expression found. On
large scales, we use a first-order polynomial in the wave-numbers and
dimensionless power spectra that goes asymptotically towards
![]() for
for
![]() ,
i.e., the result for the non-Gaussian part of the covariance using
tree-level perturbation theory. On the other hand, for small scales we
employ a second-order polynomial in the dimensionless power spectra for
the fit.
,
i.e., the result for the non-Gaussian part of the covariance using
tree-level perturbation theory. On the other hand, for small scales we
employ a second-order polynomial in the dimensionless power spectra for
the fit.
Results. We obtain a fitting formula for the non-Gaussian
contribution of the convergence power spectrum covariance that is
accurate to ![]() for the off-diagonal elements, and to
for the off-diagonal elements, and to ![]() for the diagonal elements, in the range
for the diagonal elements, in the range
![]() and can be used for single source redshifts
and can be used for single source redshifts
![]() in WMAP5-like cosmologies.
in WMAP5-like cosmologies.
Key words: cosmology: theory - large-scale structure of Universe - gravitational lensing: weak - methods: numerical
1 Introduction
Weak gravitational lensing by the large-scale structure, or cosmic
shear, is an important tool to probe the mass distribution in the
Universe and to estimate cosmological parameters. The constraints it
provides are independent and complementary to those found by other
cosmological probes such as cosmic microwave background (CMB)
anisotropies, supernovae (SN) type Ia, baryon acoustic
oscillations (BAO) or galaxy redshift surveys. The cosmic shear field
quantifies the distortion of faint galaxy images that is induced by
continuous light deflections caused by the large-scale structure in the
Universe (e.g., Schneider 2006; Bartelmann & Schneider 2001).
Since this effect
is too small to be measured for a single galaxy, large surveys with
millions of galaxies are required to detect it in a statistical way.
The cosmic shear signal has been successfully measured in various
surveys, since the first detections of Kaiser et al. (2000); Bacon et al. (2000); Van Waerbeke et al. (2000); Wittman et al. (2000).
Most recently, shear two-point correlation functions were measured in
the Canada-France-Hawaii Telescope Legacy Survey (CFHTLS) and were used
to constrain the amplitude of dark matter
clustering,
![]() ,
with
,
with ![]() uncertainty (Fu et al. 2008).
uncertainty (Fu et al. 2008).
The next generation of galaxy surveys will greatly improve the precision with which weak lensing effects can be measured (Albrecht et al. 2006) enabling us to obtain, with accurate redshift information and tomographic measurements, precise constraints on the evolution of dark energy. However, the expected improvement in future data only leads to a significant improvement of the precision and accuracy of the cosmological interpretation if the systematic errors, the underlying physics, and the statistical precision of cosmic shear estimators are well understood. Systematics currently identified arise mainly from non-cosmological sources of shear correlations, i.e., intrinsic alignments of galaxies (e.g., Schäfer 2009, for a review), and biases on the shear measurement (Massey et al. 2007; Semboloni et al. 2009). This paper addresses the issue of the statistical precision of cosmic shear estimators, determined by the covariance of the estimator. Since much of the scales probed by cosmic shear lie in the non-linear regime, being affected by non-linear clustering, the covariance depends on non-Gaussian effects and has a non-Gaussian, as well as a Gaussian, contribution. Indeed, even though the non-Gaussianity of the shear field is weaker than that of the matter field due to the projection along the line-of-sight, various studies indicate that the non-Gaussian contribution to the covariance cannot be neglected when constraining cosmological parameters with weak lensing (Kilbinger & Schneider 2005; White & Hu 2000; Cooray & Hu 2001; Semboloni et al. 2007; Takada & Jain 2009; Scoccimarro et al. 1999).
Most cosmic shear results are based on the measurement of two-point
correlation functions of the shear field. Since, in general, the
number of independent measurements is insufficient to infer the
complete covariance directly from observations, one may derive it from
ray-tracing maps of numerical N-body
simulations. This, however, requires a large number of realizations
and, in addition, is very time-consuming if an exploration of
the covariance in the parameter space is needed. An alternative is
to compute the covariance with an analytic approach. For shear
two-point correlation functions, Schneider et al. (2002) derived an expression for the Gaussian contribution to the covariance. Semboloni et al. (2007) fitted the ratio between that expression and a covariance computed with N-body
simulations, containing both Gaussian and non-Gaussian contributions,
providing thus a formula to compute the total covariance from the
Gaussian term. In Fourier space, large-scale modes are independent
and, differently from real space, the Gaussian contribution to the
covariance of the convergence power spectrum (i.e., of the Fourier
transform of the two-point shear correlation function) is diagonal and
can be computed from the convergence power spectrum alone (Kaiser 1992; Joachimi et al. 2008), whereas the non-Gaussian contribution can be computed from the trispectrum of the convergence (Scoccimarro et al. 1999). The trispectrum, on large scales, can be accurately derived in tree-level perturbation theory![]() ,
and, on small scales, is well represented by the one-halo term of
a halo model approach. A non-Gaussian part of the covariance
consisting of a perturbation theory term and a one-halo term was used,
e.g., in Takada & Jain (2009).
,
and, on small scales, is well represented by the one-halo term of
a halo model approach. A non-Gaussian part of the covariance
consisting of a perturbation theory term and a one-halo term was used,
e.g., in Takada & Jain (2009).
This paper aims at producing an accurate expression for the non-Gaussian contribution of the covariance of the convergence power spectrum that is fast to compute, contributing thus to accurate estimates of cosmological parameters. Following Scoccimarro et al. (1999) and Cooray & Hu (2001), we start from a canonical estimator of the dimensionless convergence power spectrum and use it to derive an analytic expression for the corresponding covariance. The various spectra involved are evaluated using the halo model approach of dark matter clustering (Peacock & Smith 2000; Seljak 2000; Ma & Fry 2000; Scoccimarro et al. 2001; Cooray & Sheth 2002). The halo model approach assumes that all dark matter in the Universe is bound in spherical halos, and uses results from numerical N-body simulations to characterize halo properties such as their profile, abundance and clustering behavior.
The evaluation of the covariance of the convergence power spectrum in the halo model approach is time-consuming. In addition, it may be needed to repeat it for different cosmological models for the purpose of parameter estimation. To allow for a faster computation, we construct a fitting formula for the non-Gaussian part of the convergence power spectrum covariance. On small scales, we fit the halo model result with a polynomial in the non-linear dimensionless convergence power spectrum. On large scales, we fit the ratio between the halo model covariance and the perturbation theory covariance. We stress that it is a fit to the halo model covariance, not involving a covariance computed from N-body simulations. The result is, however, calibrated by N-body simulations, since they determine the halo model parameters.
The paper is organized as follows. We define in Sect. 2 the reference cosmology, considering the growth of matter perturbations. We introduce the convergence spectra, construct an estimator for the dimensionless convergence power spectrum, and derive an expression for its covariance in Sect. 3. In Sect. 4, we describe the halo model approach, and compute the covariance of the power spectrum. The covariance depends on the values of halo model parameters, which are also defined here. It also depends on the power spectrum, bispectrum and trispectrum of the correlations of halo centers. Expressions for these spectra, in the framework of perturbation theory, are given in the Appendix. Section 5 tests the accuracy of the halo model predictions, for both the power spectrum and its covariance, against two sets of ray-tracing simulations. Section 6 presents the fitting formula for the non-Gaussian contribution to the covariance where its coefficients are given as function of source redshift. We conclude in Sect. 7.
2 Structure formation in a  CDM cosmology
CDM cosmology
Throughout this work we assume a spatially flat cold dark matter model with a cosmological constant (
![]() ), as supported by the latest 5-year data release of WMAP results (Komatsu et al. 2009). The expansion rate of the Universe,
), as supported by the latest 5-year data release of WMAP results (Komatsu et al. 2009). The expansion rate of the Universe,
![]() ,
in such models is described by the Friedmann equation
,
in such models is described by the Friedmann equation
![]() ,
where
,
where
![]() is the Hubble constant,
is the Hubble constant,
![]() denotes the combined contributions from dark matter and baryons today in terms of the critical density
denotes the combined contributions from dark matter and baryons today in terms of the critical density
![]() ,
and
,
and
![]() is the density parameter of the cosmological constant. The comoving distance to a source at a is then
is the density parameter of the cosmological constant. The comoving distance to a source at a is then
where the scale factor is related to the redshift via the relation 1+z=1/a using the convention a(t0)=1 today.
In structure formation, the central quantity is the Fourier transform of the density contrast
![]() ,
which describes the relative deviation of the local matter density
,
which describes the relative deviation of the local matter density
![]() to the comoving average density of the
Universe
to the comoving average density of the
Universe
![]() at time t. We suppress the time dependence of
at time t. We suppress the time dependence of ![]() in the following. In this way, the mean density contrast is by
definition zero, and we can describe matter perturbations in the early
Universe as zero-mean Gaussian random fields. In this case,
the statistical properties of the Fourier transformed density
field,
in the following. In this way, the mean density contrast is by
definition zero, and we can describe matter perturbations in the early
Universe as zero-mean Gaussian random fields. In this case,
the statistical properties of the Fourier transformed density
field,
are completely characterized by the power spectrum
where
In linear perturbation theory, which is valid on large scales, the power spectrum at a scale factor a is characterized by
where the amplitude A is normalized in terms of
is the growth factor which we normalize as D(a=1)=1. In the non-linear regime, i.e., on small scales, different Fourier modes couple and the Gaussian assumption cannot be maintained. Thus we have to consider higher-order moments of the density field to describe its statistical properties. In perturbation theory, it is possible to find analytic expressions for these moments, which hold up to the quasi-linear regime. In Appendix A, we derive the expressions for the bispectrum and trispectrum in tree-level perturbation theory, which are the Fourier transforms of the three- and four-point-correlation functions, respectively.
3 Covariance of the convergence power spectrum
A central quantity in weak lensing applications is the two-dimensional projection of the density contrast
![]() on the sky, which is known as effective convergence
on the sky, which is known as effective convergence
![]() .
It is obtained by projecting the density contrast along the
backward-directed light-cone of the observer according to
.
It is obtained by projecting the density contrast along the
backward-directed light-cone of the observer according to
where
where H(x) denotes the Heaviside step function. To take advantage of the Fourier properties, we analyze the statistical properties of the Fourier counterpart of
where the subscript ``c'' refers to the connected part of the corresponding moment and
where
We are interested in estimating the dimensionless convergence power spectrum
and the corresponding covariance for wave-vectors of different length
which is unbiased in the limit of infinitesimal small bin sizes, since
The evaluation of the covariance of the estimator, Eq. (13), results in an expression of the form
where
where
We can analytically perform one of the integrations of the bin-averaged trispectrum in Eq. (15). First, note that it only depends on the parallelogram configuration of the convergence trispectrum, i.e., setting
![]() ,
,
![]() and
and
![]() in Eq. (11).
Also, if we choose an appropriate coordinate system for the integration
over the wave-vectors, the problem becomes symmetric under rotations
and we can parametrize the convergence trispectrum by the length of the
two sides of the parallelogram
in Eq. (11).
Also, if we choose an appropriate coordinate system for the integration
over the wave-vectors, the problem becomes symmetric under rotations
and we can parametrize the convergence trispectrum by the length of the
two sides of the parallelogram ![]() and
and ![]() and the angle between them,
and the angle between them,
![]() .
Hence, we define
.
Hence, we define
Making use of the symmetry properties of this problem, one angular integration becomes trivial and the integration in Eq. (15) simplifies to
If the bin-width
Note that if
4 Halo model
We have seen that the covariance of the dimensionless convergence power spectrum estimator consists of two terms: a Gaussian part, which is proportional to the dimensionless convergence power spectrum squared and a non-Gaussian part, which is the bin-averaged dimensionless convergence trispectrum (see Eq. (14)). We will compute these terms using the halo model approach (Peacock & Smith 2000; Scoccimarro et al. 2001; Ma & Fry 2000; Seljak 2000; see also the comprehensive review by Cooray & Sheth 2002).
4.1 Overview
With the assumption that all dark matter is bound in spherically-symmetric, virialized halos, the halo model provides a way to calculate the three-dimensional polyspectra of dark matter in the non-linear regime. In Sect. 4.5 below, we summarize the equations one obtains for the dark matter power spectrum and trispectrum.
In the halo model description, the density field at an arbitrary position ![]() in space is given as a superposition of all N halo density profiles such that
in space is given as a superposition of all N halo density profiles such that
where
where
where n(m) is the halo mass function and p(c|m) is the concentration probability distribution for halos given a mass m.
4.2 Ingredients
The halo model approach provides a scale-dependent description of the statistical properties of the large-scale structure. On small scales, the correlation of dark matter is governed by the mass profiles of the halos, whereas on large scales the clustering between different halos determines the nature of the correlation. As there are a multitude of models to describe the behavior on different scales, and an even larger number of parameters one has to set judiciously, there exists no such thing as a unique halo model. In order to have reproducible results, it is therefore necessary to specify ones choice of parameters. For this work, we will adopt the following parameters for the halo model:
- 1.
- The average mass of a halo is defined as the mass within a sphere of virial radius
 as
as
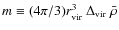 ,
where
,
where
 denotes the overdensity of the virialized halo with respect to the average comoving mass density
denotes the overdensity of the virialized halo with respect to the average comoving mass density  in the Universe. Typically, values for
in the Universe. Typically, values for
 are derived in the framework of the non-linear spherical collapse model (e.g. Gunn & Gott 1972). Expressions valid for different cosmologies are summarized in Nakamura & Suto (1997). In our
implementation, we use the results which are valid for a flat
are derived in the framework of the non-linear spherical collapse model (e.g. Gunn & Gott 1972). Expressions valid for different cosmologies are summarized in Nakamura & Suto (1997). In our
implementation, we use the results which are valid for a flat 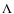 CDM-Universe, i.e.,
CDM-Universe, i.e.,
where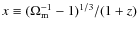 .
We find for our fiducial WMAP5-like cosmology
.
We find for our fiducial WMAP5-like cosmology
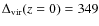 .
.
- 2.
- N-body simulations suggest that the density profile of
a halo follows a universal function. We choose to use the
NFW profile (Navarro et al. 1997), which is in good agreement with numerical results and has an analytical Fourier transform. It is given by
where is the amplitude of the density profile and
is the amplitude of the density profile and 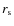 characterizes the scale at which the slope of the density profile changes. For small scales (
characterizes the scale at which the slope of the density profile changes. For small scales (
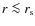 )
the profile scales with
)
the profile scales with
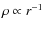 ,
whereas for large scales it behaves as
,
whereas for large scales it behaves as
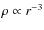 .
The Fourier transform of the NFW profile is
.
The Fourier transform of the NFW profile is
where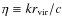 ,
we truncated the integration at
,
we truncated the integration at
 in the second step, and introduced the concentration parameter
in the second step, and introduced the concentration parameter
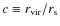 in the third step.
Additionally, we use for the sine- and cosine integrals the definitions
in the third step.
Additionally, we use for the sine- and cosine integrals the definitions
- 3.
- The abundance of halos of mass m at a redshift z is given by
where we introduced the dimensionless variable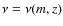 ,
,
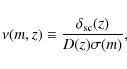
(27)
where D(z) denotes the redshift-dependent growth factor,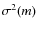 is the smoothed variance of the density contrast, and
is the smoothed variance of the density contrast, and
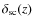 denotes the value of a spherical overdensity that collapses at a redshift z as calculated from linear perturbation theory. In our work, we use the expression from Nakamura & Suto (1997), which is valid for a
denotes the value of a spherical overdensity that collapses at a redshift z as calculated from linear perturbation theory. In our work, we use the expression from Nakamura & Suto (1997), which is valid for a 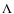 CDM Universe,
CDM Universe,
where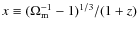 .
The quantity has only a weak dependence on redshift and we find
.
The quantity has only a weak dependence on redshift and we find
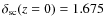 for our fiducial model.
for our fiducial model.
The advantage of introducing
 is that part of the mass function can be expressed by the multiplicity function
is that part of the mass function can be expressed by the multiplicity function
 ,
which has a universal shape, i.e., is independent of cosmological
parameters and redshift. In this work, we employ the Sheth and
Tormen mass function (Sheth & Tormen 1999)
,
which has a universal shape, i.e., is independent of cosmological
parameters and redshift. In this work, we employ the Sheth and
Tormen mass function (Sheth & Tormen 1999)
which is an improvement over the original Press-Schechter formulation (Press & Schechter 1974). We use the parameter values p=0.3, q=0.707, and amplitude A(0.3)=0.322, which follows from mass conservation. - 4.
- The concentration parameter
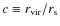 characterizes the form of the halo profile. From N-body simulations one finds that the average,
characterizes the form of the halo profile. From N-body simulations one finds that the average, 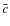 ,
depends on the halo mass (Bullock et al. 2001) like
,
depends on the halo mass (Bullock et al. 2001) like
where m*=m*(z=0) is the characteristic mass defined within the Press-Schechter formalism as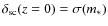 .
In the following, we will use the values c*=10 and
.
In the following, we will use the values c*=10 and
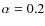 as proposed by Takada & Jain (2003). This implies that more massive halos are less centrally
concentrated than less massive ones. However, results from numerical N-body simulations (Bullock et al. 2001; Jing 2000) indicate that there is a significant scatter in the concentration parameter for halos of the same mass. Furthermore, Jing (2000) proposes that such a concentration distribution can be described by a log-normal distribution
as proposed by Takada & Jain (2003). This implies that more massive halos are less centrally
concentrated than less massive ones. However, results from numerical N-body simulations (Bullock et al. 2001; Jing 2000) indicate that there is a significant scatter in the concentration parameter for halos of the same mass. Furthermore, Jing (2000) proposes that such a concentration distribution can be described by a log-normal distribution
Typical values for the concentration dispersion range from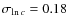 to
to
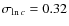 (Wechsler et al. 2002; Jing 2000). Note that the width of the distribution
(Wechsler et al. 2002; Jing 2000). Note that the width of the distribution
 is independent of the halo mass. The variation of the halo
concentration can be attributed to the different merger histories of
the halos (Wechsler et al. 2002). We will analyze the impact of this effect on different spectra in
Sect. 4.7.
When we use only the mean concentration parameter, we have to replace
the probability distribution of the concentration, needed for example
in Eq. (21), by a Dirac delta distribution
is independent of the halo mass. The variation of the halo
concentration can be attributed to the different merger histories of
the halos (Wechsler et al. 2002). We will analyze the impact of this effect on different spectra in
Sect. 4.7.
When we use only the mean concentration parameter, we have to replace
the probability distribution of the concentration, needed for example
in Eq. (21), by a Dirac delta distribution
- 5.
- On large scales, the correlation of the dark matter density
field is governed by the spatial distribution of halos. Since the
clustering behavior of halos and matter density differ,
one introduces the bias factors bi(m,z) such that
In this way, the halo density contrast,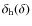 ,
is expressed as a Taylor expansion of the matter density contrast,
,
is expressed as a Taylor expansion of the matter density contrast,
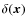 .
The bias parameters are in general derived based on the Sheth-Tormen
mass function introduced above. For the linear halo bias one obtains
then
.
The bias parameters are in general derived based on the Sheth-Tormen
mass function introduced above. For the linear halo bias one obtains
then
where p and q match the values used in the mass function. Expressions for higher-order bias factors can be found, e.g., in Scoccimarro et al. (2001). Since they only have a small impact on the quantities employed here, we take into account only the first-order bias. In Fourier space we may then write
- 6.
- To obtain the final correlation function, one has to perform
integrations along the halo mass and optionally along the halo
concentration, with limits formally extending from 0 to
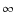 .
In practice, we use the mass limits
.
In practice, we use the mass limits
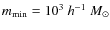 and
and
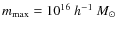 .
Masses smaller than
.
Masses smaller than
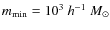 give no significant contribution to the considered quantities, while,
due to the exponential cut-off in mass, masses larger than
give no significant contribution to the considered quantities, while,
due to the exponential cut-off in mass, masses larger than
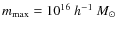 are rare. For the concentration, we employ the integration limits
are rare. For the concentration, we employ the integration limits
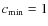 and
and
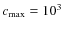 .
.
- 7.
- Due to the cut-off in mass, the consistency relation (Scoccimarro et al. 2001)
does not hold. To cure this problem we consider a rescaled linear bias such that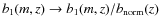 ,
where
,
where
 is the result of the integral in
Eq. (36).
In this way, one ensures that the halo term with the largest
contribution to the correlation equals the perturbation theory
expression on large scales (see
Fig. 1).
is the result of the integral in
Eq. (36).
In this way, one ensures that the halo term with the largest
contribution to the correlation equals the perturbation theory
expression on large scales (see
Fig. 1).
4.3 Building blocks
Using the ingredients described in the previous section, it is
possible to define building blocks, which simplify significantly the
notation for expressing the polyspectra (Cooray & Hu 2001):
In the case i=0, we additionally define
![\begin{figure}
\par\includegraphics[width=12cm,clip]{12854fg1}
\end{figure}](/articles/aa/full_html/2010/06/aa12854-09/Timg194.png)
|
Figure 1:
Square configuration of the dimensionless convergence trispectrum
|
| Open with DEXTER | |
4.4 Power spectrum
We can now compute the power spectrum from Eq. (20). The result consists of two terms, the 1-halo and the 2-halo terms,
![]() (Seljak 2000). They are given by
(Seljak 2000). They are given by
where
| (40) |
The 1-halo term,
4.5 Trispectrum
We compute now the dark matter trispectrum in the halo model approach. As discussed in Sect. 3,
only parallelogram configurations of the trispectrum wave-vectors
contribute to the covariance of the convergence power spectrum.
Restricting our
calculations to these configurations, we obtain four different halo
term contributions,
which are simpler than in the general case. In addition, we neglect terms involving higher-order halo bias factors since, on most scales, they provide only a small correction (Takada & Jain 2003; Ma & Fry 2000). We further note that the perturbative expansion of halo centers, used in the calculations, was shown to become inaccurate on non-linear scales (Smith et al. 2007). The contributions to the trispectrum take the following forms, using the compact notation of the building blocks (see Cooray & Sheth 2002, for the expression of the halo model trispectrum including higher-order bias factors): The 1-halo term, dominant on the smallest scales, is
The 2-halo term has two contributions,
| |
= | ||
| (43) | |||
| = | (44) |
The 3-halo term is given by
Finally, the 4-halo term, dominant on large scales, is
and describes correlations of points distributed in four different halos. Note that, like for the power spectrum, the 2-halo term is computed from the linear power spectrum. On the other hand, the 3- and 4-halo terms depend on
4.6 Convergence spectra
The convergence power spectrum and trispectrum, needed to evaluate the covariance in Eq. (14), are computed by projecting
![]() and
and
![]() ,
according to Eqs. (10) and (11). Figure 1 shows the dimensionless
convergence trispectrum, defined as
,
according to Eqs. (10) and (11). Figure 1 shows the dimensionless
convergence trispectrum, defined as
![]() for a square configuration where all wave-numbers have a
length
for a square configuration where all wave-numbers have a
length ![]() ,
where
,
where
![]() denotes the contribution from the corresponding halo term. The plot
shows the individual contributions to the dimensionless
denotes the contribution from the corresponding halo term. The plot
shows the individual contributions to the dimensionless
![]() (the projections of Eqs. (42)-(46)),
illustrating on which scales the individual terms are important,
as well as the total contribution of all halo terms
(the projections of Eqs. (42)-(46)),
illustrating on which scales the individual terms are important,
as well as the total contribution of all halo terms
![]() .
We show, in addition, the dimensionless projected
.
We show, in addition, the dimensionless projected
![]() ,
which closely follows the 4-halo term. We see that the commonly used approximation
,
which closely follows the 4-halo term. We see that the commonly used approximation
![]() is accurate for large wave-numbers (
is accurate for large wave-numbers (
![]() )
but has a deviation of about
)
but has a deviation of about ![]() from the complete trispectrum
from the complete trispectrum
![]() for small wave-numbers (
for small wave-numbers (
![]() ).
).
4.7 Stochastic halo concentration
The previous results were computed using the deterministic concentration-mass relation of Eq. (30). We now analyze the impact of scatter in the halo concentration parameter c on the covariance of the convergence power spectrum, using the stochastic concentration relation given by the the log-normal concentration distribution of Eq. (31).
Cooray & Hu (2001), analyzed the effect of a stochastic concentration on the three-dimensional power spectrum and trispectrum and found that the behavior of the corresponding 1-halo terms were increasingly sensitive to the width of the concentration distribution for smaller wave-numbers k. Furthermore, the effect of a stochastic concentration relation was more pronounced for the trispectrum than for the power spectrum, since the tail of the concentration distribution is weighted more strongly in higher-order statistics.
Performing the same analysis for the projected power spectrum and
trispectrum, we find a similar trend as in the three-dimensional
case, but with a smaller sensitivity to the concentration width of
the distribution on small scales. For
![]() ,
we find, in the case of the 1-halo
term of the power spectrum, a deviation from a deterministic concentration relation of about
,
we find, in the case of the 1-halo
term of the power spectrum, a deviation from a deterministic concentration relation of about ![]() for wave-numbers larger than
for wave-numbers larger than
![]() ,
whereas, for the 1-halo term of the trispectrum, the deviation is of the order of
,
whereas, for the 1-halo term of the trispectrum, the deviation is of the order of ![]() in the same
in the same ![]() -range.
Thus, when considering the covariance of the convergence power
spectrum, one should take into account the concentration dispersion in
the 1-halo term of the trispectrum but can safely neglect it for the
power spectrum. Additionally, we find that a stochastic concentration
has only a small impact on the 2-halo terms of the power spectrum and
trispectrum (Pielorz 2008).
-range.
Thus, when considering the covariance of the convergence power
spectrum, one should take into account the concentration dispersion in
the 1-halo term of the trispectrum but can safely neglect it for the
power spectrum. Additionally, we find that a stochastic concentration
has only a small impact on the 2-halo terms of the power spectrum and
trispectrum (Pielorz 2008).
From this analysis, we expect the effect of a concentration
distribution to be the strongest on the non-Gaussian part of the
covariance, which depends on the trispectrum. To directly infer
the
impact of a concentration distribution on the covariance, we calculate
the 1-halo contribution to the non-Gaussian covariance, i.e., we
perform the bin averaging of Eq. (15),
for two different concentration dispersions
where
![\begin{figure}
\par\includegraphics[width=12cm,clip]{12854fg2}
\end{figure}](/articles/aa/full_html/2010/06/aa12854-09/Timg243.png)
|
Figure 2:
Contour plots of the ratio
|
| Open with DEXTER | |
5 Comparison with N-body simulations
In Sect. 4, we computed the power spectrum and trispectrum of the dark matter fluctuations. Projecting them according to Eqs. (10) and (11), and inserting the result in Eqs. (12), (14), and (15), we obtained the covariance of the convergence power spectrum estimator.
To test the accuracy of the halo model predictions for the statistics of the dark matter density field, we compare the dimensionless convergence power spectrum and the corresponding covariance, calculated in the halo model approach, with results from two different ray-tracing simulations.
Table 1: Cosmological parameters used to set up the initial power spectrum.
Table 2: Parameters used for generating the two N-body simulations.
5.1 Virgo and Gems simulation
For our comparison, we chose one simulation from Jenkins et al. (1998) and ten simulations from Hartlap et al. (2009),
which we denote in the following as Virgo and Gems simulation,
respectively. The Virgo simulation was carried out in 1997 by the
Virgo-Consortium for a
![]() CDM cosmology (see Table 1) with
CDM cosmology (see Table 1) with
![]() particles in a periodic box of comoving side length
particles in a periodic box of comoving side length
![]() (see Table 2).
It uses the PP-/PM-code HYDRA, which places subgrids of higher
resolution in strongly clustered regions. Structures on scales larger
than
(see Table 2).
It uses the PP-/PM-code HYDRA, which places subgrids of higher
resolution in strongly clustered regions. Structures on scales larger
than
![]() can be considered as well resolved. The Gems simulations were set up in cubic volumes of comoving side length
can be considered as well resolved. The Gems simulations were set up in cubic volumes of comoving side length
![]() with 2563 particles (see Table 2). Note that the simulations employ either the BBKS (Bardeen et al. 1986) or the EH (Eisenstein & Hu 1998) transfer function. The cosmology chosen reflects the WMAP5 results (Komatsu et al. 2009) and thus has a lower value for
with 2563 particles (see Table 2). Note that the simulations employ either the BBKS (Bardeen et al. 1986) or the EH (Eisenstein & Hu 1998) transfer function. The cosmology chosen reflects the WMAP5 results (Komatsu et al. 2009) and thus has a lower value for ![]() than the Virgo simulation (see Table 1). It uses the GADGET-2 code to simulate the evolution of dark matter particles (Springel 2005) and has a softening length of
than the Virgo simulation (see Table 1). It uses the GADGET-2 code to simulate the evolution of dark matter particles (Springel 2005) and has a softening length of
![]() .
.
5.2 Ray-tracing
The output of numerical simulations are three-dimensional distributions of
![]() particles in cubic boxes over a range of redshift values. In order to compare the results with the predicted
convergence power spectrum from the halo model, we make use of the multiple-lens-plane ray-tracing algorithm (see e.g., Jain et al. 2000; Hilbert et al. 2009)
to construct
effective convergence maps. The basic idea is to introduce a series of
lens planes perpendicular to the central line-of-sight of the
observer's backward light cone. In this way, the matter distribution
within the light cone is sliced and can be projected onto the
corresponding lens plane. By computing the deflection of light
rays and its derivatives at each lens plane, one simulates the photon
trajectory from the observer to the source by keeping track of the
distortions of ray bundles. In this way, the continuous deflection
of light rays is approximated by a finite number of deflections at the
lens planes. As a result, one obtains the Jacobian matrix for the
lens mapping from source to observer and can construct convergence
maps.
particles in cubic boxes over a range of redshift values. In order to compare the results with the predicted
convergence power spectrum from the halo model, we make use of the multiple-lens-plane ray-tracing algorithm (see e.g., Jain et al. 2000; Hilbert et al. 2009)
to construct
effective convergence maps. The basic idea is to introduce a series of
lens planes perpendicular to the central line-of-sight of the
observer's backward light cone. In this way, the matter distribution
within the light cone is sliced and can be projected onto the
corresponding lens plane. By computing the deflection of light
rays and its derivatives at each lens plane, one simulates the photon
trajectory from the observer to the source by keeping track of the
distortions of ray bundles. In this way, the continuous deflection
of light rays is approximated by a finite number of deflections at the
lens planes. As a result, one obtains the Jacobian matrix for the
lens mapping from source to observer and can construct convergence
maps.
For both simulations, a similar number of around
200 effective convergence maps were produced, with source galaxies
situated at a single redshift of either
![]() or
or
![]() .
Table 2
summarizes the parameters used for producing the resulting convergence
maps with the multiple-lens-plane-ray-tracing-algorithm. These are: the
side length,
.
Table 2
summarizes the parameters used for producing the resulting convergence
maps with the multiple-lens-plane-ray-tracing-algorithm. These are: the
side length,
![]() ,
of the cubic simulation box, the number of particles,
,
of the cubic simulation box, the number of particles,
![]() ,
used for the simulation, their mass,
,
used for the simulation, their mass,
![]() ,
and the number of available convergence maps,
,
and the number of available convergence maps,
![]() ,
with area
,
with area
![]() .
.
The maps produced with the Gems simulation have an area of 16 ![]() ,
while the ones from Virgo are much smaller, with 0.25
,
while the ones from Virgo are much smaller, with 0.25 ![]() .
.
![\begin{figure}
\par\hspace*{0.25mm}\includegraphics[width=11.9cm,clip]{12854fg3}...
...e*{0.25mm}\vspace*{3mm}
\includegraphics[width=12cm,clip]{12854fg4}
\end{figure}](/articles/aa/full_html/2010/06/aa12854-09/Timg263.png)
|
Figure 3:
Dimensionless convergence power spectrum
|
| Open with DEXTER | |
5.3 Convergence power spectrum
To test the accuracy of the halo model approach in describing the non-linear evolution of dark matter, we compare the dimensionless projected power spectrum, computed in the halo model approach, to the ones estimated from the numerical N-body simulations.
The dimensionless convergence power spectra of the simulations are
measured from the real-space two-dimensional convergence maps of
length
![]() and grid-size
and grid-size
![]() .
For this, we first apply a Fast Fourier Transform
.
For this, we first apply a Fast Fourier Transform![]() to obtain
to obtain
![]() on each grid-point. Then, we estimate the power spectrum at a wave-number
on each grid-point. Then, we estimate the power spectrum at a wave-number ![]() for the kth convergence map by averaging over all Fourier modes in the band
for the kth convergence map by averaging over all Fourier modes in the band
![]() }, i.e.,
}, i.e.,
where
Figure 3 shows a good agreement between the halo model and the N-body simulation convergence power spectra. We also include, in Fig. 3, the convergence power spectra computed using the fitting formulae of Peacock & Dodds (1996) and
Smith et al. (2003). Both, the
halo model and the fitting formulae, show a better agreement with
simulations for the lower source redshift case. On small scales, the
halo model and the Smith et al. fitting formula agree well with
the simulations, whereas the Peacock-Dodds fitting formula has too
little power, in particular in the case of the Gems simulation. On
intermediate scales
(
![]() ),
the halo model is less accurate than the Smith et al. fitting
formula, suggesting that the halo model suffers from the halo exclusion
problem on these scales, as described, e.g., in Tinker et al. (2005).
This means that, while in simulations
halos are never separated by distances smaller than the sum of their
virial radii, this is not accounted for in the framework of our halo
model and is probably the cause for the deviation. The good agreement
of the Smith et al. formula is not surprising, since it is based
on simulations of similar resolution than the ones we consider here.
In contrast, a similar comparison using the convergence power
spectrum estimated with the Millennium Run (Hilbert et al. 2009)
clearly
favors the halo model prediction over of the two fitting formulae, with
both fitting formulae strongly underestimating the power on
intermediate and small scales.
),
the halo model is less accurate than the Smith et al. fitting
formula, suggesting that the halo model suffers from the halo exclusion
problem on these scales, as described, e.g., in Tinker et al. (2005).
This means that, while in simulations
halos are never separated by distances smaller than the sum of their
virial radii, this is not accounted for in the framework of our halo
model and is probably the cause for the deviation. The good agreement
of the Smith et al. formula is not surprising, since it is based
on simulations of similar resolution than the ones we consider here.
In contrast, a similar comparison using the convergence power
spectrum estimated with the Millennium Run (Hilbert et al. 2009)
clearly
favors the halo model prediction over of the two fitting formulae, with
both fitting formulae strongly underestimating the power on
intermediate and small scales.
The good overall accuracy of the halo model results was expected since its ingredients, such as the mass function and the halo profile, were obtained from N-body simulations. We note that, in this analysis, we used a deterministic concentration parameter, since the use of a stochastic one has only a small effect on the small scales of the convergence power spectrum.
5.4 Covariance of the convergence power spectrum
The similarity between simulation and halo model power spectra was to some extent expected. The ability to make an accurate description of higher-order correlations provides a stronger test of the halo model. Due to its important role in calculating the error of the power spectrum and for parameter estimates, we focus in this section on the accuracy of the covariance of the dimensionless convergence power spectrum.
We need an appropriate estimator for the power spectrum covariance of the simulations. As each simulation provides
![]() different
different ![]() -maps, we have
-maps, we have
![]() realizations
of the power spectrum. From these we estimate the covariance by
applying the unbiased sample covariance estimator which has
for our purpose the form:
realizations
of the power spectrum. From these we estimate the covariance by
applying the unbiased sample covariance estimator which has
for our purpose the form:
where
The halo model results,
![]() ,
are calculated as described in Sect. 4
and include all terms of the non-Gaussian covariance. In their
computation, we use our fiducial halo model with the ingredients
summarized in Sect. 4.2, and use the cosmological parameters values corresponding to each simulation, given in Table 1, for the case
,
are calculated as described in Sect. 4
and include all terms of the non-Gaussian covariance. In their
computation, we use our fiducial halo model with the ingredients
summarized in Sect. 4.2, and use the cosmological parameters values corresponding to each simulation, given in Table 1, for the case
![]() .
We consider both, a deterministic concentration-mass relation and a stochastic one, with dispersion
.
We consider both, a deterministic concentration-mass relation and a stochastic one, with dispersion
![]() for the 1-halo term of the trispectrum.
for the 1-halo term of the trispectrum.
![\begin{figure}
\par\includegraphics[width=15cm,clip]{12854fg5}
\end{figure}](/articles/aa/full_html/2010/06/aa12854-09/Timg284.png)
|
Figure 4:
Relative difference
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{12854fg6}
\end{figure}](/articles/aa/full_html/2010/06/aa12854-09/Timg285.png)
|
Figure 5:
Relative difference
|
| Open with DEXTER | |
We compare the halo model with the simulations covariance matrices considering their relative deviation
We note that although the number of available convergence maps for our simulations (
Although the halo model predictions strongly deviate from the
simulation estimates of the covariance on small scales, this analysis
does not necessarily imply a poor accuracy of those predictions.
Indeed, the simulation covariances estimated in this analysis have a
strong scatter. In particular, in the case of the Gems simulation,
we found from bootstrap subsamples of 50 convergence maps that the
resulting covariances can deviate up to ![]() from the average covariance of the complete sample (Pielorz 2008). This is in agreement with the results by Takahashi et al. (2009)
who need to use 5000 simulations to obtain an estimate of the
matter power spectrum covariance at a sub-percent level accuracy.
from the average covariance of the complete sample (Pielorz 2008). This is in agreement with the results by Takahashi et al. (2009)
who need to use 5000 simulations to obtain an estimate of the
matter power spectrum covariance at a sub-percent level accuracy.
There are however very recent indications that Eq. (14) indeed underestimates the covariance of the convergence power spectrum on small scales (Sato et al. 2009). In particular, sample variance in the number of halos in a finite field is not accounted for by
Eq. (14).
Indeed, the mass function yields a mean number density, but there are
fluctuations on the number of halos due to the large-scale mass
fluctuations. Sample variance in the number of clusters in a
volume-limited survey (Hu & Kravtsov 2003) has been considered in cluster abundance studies (e.g., Vikhlinin et al. 2009). In the halo model framework, the
sample variance in the number of halos was derived in Takada & Bridle (2007) and its contribution to the covariance of the convergence power spectrum was found, in Sato et al. (2009), to boost the non-Gaussian errors of a 25 ![]() survey by one order of magnitude on scales
survey by one order of magnitude on scales
![]() .
The increase is reduced for larger survey areas.
.
The increase is reduced for larger survey areas.
6 Fitting formula for the covariance of the convergence power spectrum
Future weak lensing surveys will provide much more precise measurements of the convergence power spectrum. In order to obtain robust constraints on cosmological parameters, accurate estimates of both the power spectrum and its covariance are needed.
6.1 Methodology
The number of measured power spectra is, in general, insufficient to infer the complete covariance directly from observations. One has thus to derive it either from ray-tracing maps of numerical N-body simulations or with an analytic approach. A drawback of the first method is that it requires a large number of realizations and, in addition, is very time-consuming if an exploration of the covariance in the parameter space is needed.
In the previous sections, we derived the covariance, and in
particular its non-Gaussian part, with an analytic approach. This
computation is, however, time-consuming and it might be useful to
obtain an accurate covariance in a faster way. A first approach
would be to rely on stronger approximations. For example,
a commonly used approximation consists on evaluating the
non-Gaussian covariance from
![]() ,
instead of using the full trispectrum. We saw in Sect. 4 that this approximation recovers the full trispectrum for scales
,
instead of using the full trispectrum. We saw in Sect. 4 that this approximation recovers the full trispectrum for scales
![]() but deviates by
but deviates by
![]() on scales
on scales
![]() for square configurations (compare also with Fig. 6).
for square configurations (compare also with Fig. 6).
An alternative approach that we consider in the following, is to
find a fitting formula for the halo model covariance that can be
subsequently used without the need for implementing the halo model. We
will provide a fit only for the non-Gaussian part of the halo model
covariance, since the Gaussian part only depends on the non-linear
convergence power spectrum and can thus be accurately computed without
relying on the halo model. The inclusion of non-Gaussian errors
increases the total covariance and one might think of fitting the ratio
between the non-Gaussian and Gaussian terms. However, this is not
a good quantity to fit, since the Gaussian contribution is diagonal and
binning-dependent. In contrast, a similar ratio was fitted in
the real space, where the Gaussian term is non-diagonal and
binning-independent, using a non-Gaussian contribution measured from
N-body simulations (Semboloni et al. 2007).
In Fourier space, there is some relevant analogous information
contained in the tree-level perturbation theory trispectrum. Indeed,
pursuing the
analogy with the real-space fit,
![]() is
a non-diagonal and binning-independent quantity, with a lower amplitude
than the full trispectrum, approaching it at large scales. We thus
compute
is
a non-diagonal and binning-independent quantity, with a lower amplitude
than the full trispectrum, approaching it at large scales. We thus
compute
![]() ,
the covariance predicted in tree-level perturbation theory on large scales (see Eq. (A.27) and Appendix A for a detailed derivation) and compare it with our covariance computed with the full halo model trispectrum,
,
the covariance predicted in tree-level perturbation theory on large scales (see Eq. (A.27) and Appendix A for a detailed derivation) and compare it with our covariance computed with the full halo model trispectrum,
![]() ,
defined in Eq. (14). The ratio between the two covariances is shown in Fig. 6. In agreement with Fig. 1, the covariance predicted by tree-level perturbation theory contributes only
,
defined in Eq. (14). The ratio between the two covariances is shown in Fig. 6. In agreement with Fig. 1, the covariance predicted by tree-level perturbation theory contributes only
![]() to the complete non-Gaussian covariance along the diagonal. On very large scales
to the complete non-Gaussian covariance along the diagonal. On very large scales
![]() ,
the ratio
,
the ratio
![]() lies between 1.1 and 2. On smaller scales,
lies between 1.1 and 2. On smaller scales,
![]() decreases fast and is no longer useful for fitting purposes.
decreases fast and is no longer useful for fitting purposes.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12854fg7}
\end{figure}](/articles/aa/full_html/2010/06/aa12854-09/Timg303.png)
|
Figure 6:
Ratio
|
| Open with DEXTER | |
This discussion motivates us to use two different fitting formulae to
model the non-Gaussian covariance over the whole range of scales. On
large scales (
![]() ), we model the ratio
), we model the ratio
![]() as a polynomial in the wave-numbers,
as a polynomial in the wave-numbers,
![]() ,
and the dimensionless non-linear convergence power spectrum
,
and the dimensionless non-linear convergence power spectrum
![]() .
More precisely, we assume
.
More precisely, we assume
where
On small scales, i.e. for
![]() ,
we model directly the non-Gaussian covariance amplitude using a second-order polynomial in the power spectrum, such that
,
we model directly the non-Gaussian covariance amplitude using a second-order polynomial in the power spectrum, such that
The scale-dependence of the nonlinear regime of the covariance of the three-dimensional power spectrum is also to some extent captured in powers of the non-linear power spectrum
To ensure a smooth transition from small to large wave-numbers, we
consider a linear combination of the two matrices defined in Eqs. (52) and (53) with weightings of
third-order in the wave-numbers, such that the full non-Gaussian covariance becomes
with the transition scale fixed at
The covariances used in the fitting procedure, both tree-level
perturbation theory and halo model covariance, depend on perturbation
theory polyspectra. These were evaluated from the expressions derived
in Appendix A using a linear matter power spectrum computed with the Eisenstein-Hu transfer function (Eisenstein & Hu 1998) and assuming the WMAP5-like fiducial model shown in Table 3.
The non-linear convergence power spectrum, used in the polynomial
expressions, was evaluated from the same linear power spectrum.
In addition, the halo model non-Gaussian covariance was evaluated
using the input parameters as described in Sect. 4.2, including a stochastic concentration-mass relation with
![]() for the 1-halo term of the trispectrum.
for the 1-halo term of the trispectrum.
Table 3: Fiducial model used for the fitting procedure.
Table 4:
Best-fit values for the parameters
(p0,p1,p2) of the redshift-fit for the set of coefficients
![]() .
.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12854fg8}\vspace*{2mm}
\includegraphics[width=8.5cm,clip]{12854fg9}
\end{figure}](/articles/aa/full_html/2010/06/aa12854-09/Timg346.png)
|
Figure 7:
Coefficients ai of the fitting formula obtained for various source redshifts. Left (right) panel
shows the coefficients of the large (small) scales fitting formula. For
convenience, scaled versions of the coefficients are shown,
as indicated in the key. Note for example that a5, a7 and a8 change sign. The lines show the redshift fit, Eq. (55), with the parameters given in Table 4. They provide a good fit for
|
| Open with DEXTER | |
6.2 Redshift dependence
All quantities,
![]() ,
,
![]() ,
and
,
and
![]() ,
were evaluated for several values of source redshifts (assuming a single source redshift plane), in the range
,
were evaluated for several values of source redshifts (assuming a single source redshift plane), in the range
![]() .
For each redshift, we perform the fit and find a set of best-fit values for the coefficients
.
For each redshift, we perform the fit and find a set of best-fit values for the coefficients
![]() .
Next, we fit the best-fit values of each coefficient as a function of
redshift. Some of the best-fit values are increasing functions of the
source redshift, while others decrease with redshift, and others still
are non-monotonic. They all are, however, monotonic in the redshift
range of interest for current and future weak lensing surveys,
.
Next, we fit the best-fit values of each coefficient as a function of
redshift. Some of the best-fit values are increasing functions of the
source redshift, while others decrease with redshift, and others still
are non-monotonic. They all are, however, monotonic in the redshift
range of interest for current and future weak lensing surveys,
![]() .
In this range, the best-fit values
.
In this range, the best-fit values
![]() are accurately fitted with
are accurately fitted with
Table 4 shows the resulting values of the 27 parameters, which define our fitting formula for the halo model covariance of the convergence power spectrum. To obtain these results we use the 3-parameter fit as defined in Eq. (55) which is valid in the range
![\begin{figure}
\par\mbox{\includegraphics[angle=0,width=8.5cm]{12854fg10}\includ...
....5cm]{12854fg12}\includegraphics[angle=0,width=8.5cm]{12854fg13} }\end{figure}](/articles/aa/full_html/2010/06/aa12854-09/Timg355.png)
|
Figure 8:
Accuracy of the fitting formula for
|
| Open with DEXTER | |
6.3 Accuracy of the fitting formula
To test the performance of the fitting, we calculate the relative
deviation between the non-Gaussian covariance computed with the fitting
formula and the halo model one. The deviation,
is computed for every wave-number pair
The fit works quite well on the off-diagonal elements that are close to the diagonal, showing an average overestimation of ![]() .
When moving along any off-diagonal, from larger to smaller scales, (lower panels of Fig. 8), we move from the first fit, Eq. (52), where the deviation is mostly positive, to the second one, Eq. (53), where the deviation is mostly negative. The transition occurs at the local maximum, which indicates that
none of the fitting formulae should be extrapolated to the other region. The fits break down on the
smallest scales, with the deviation increasing very rapidly when the largest scale reaches
.
When moving along any off-diagonal, from larger to smaller scales, (lower panels of Fig. 8), we move from the first fit, Eq. (52), where the deviation is mostly positive, to the second one, Eq. (53), where the deviation is mostly negative. The transition occurs at the local maximum, which indicates that
none of the fitting formulae should be extrapolated to the other region. The fits break down on the
smallest scales, with the deviation increasing very rapidly when the largest scale reaches
![]() .
Smaller scales would clearly require higher-order terms in Eq. (53).
.
Smaller scales would clearly require higher-order terms in Eq. (53).
As we move away from the diagonal the fit gets increasingly worse, in particular the deviations are larger than ![]() in the region shown in black in the upper left panel of Fig. 8,
which correlates very small with very large scales. The reason for this
is that this region was effectively not fitted, since it is not
contained in any of the two blocks
fitted by Eq. (54). Restricting to the range where both scales are between
in the region shown in black in the upper left panel of Fig. 8,
which correlates very small with very large scales. The reason for this
is that this region was effectively not fitted, since it is not
contained in any of the two blocks
fitted by Eq. (54). Restricting to the range where both scales are between
![]() ,
roughly
,
roughly ![]() of the elements show deviations between
of the elements show deviations between ![]() and
and ![]() ,
with the average of the absolute deviations being
,
with the average of the absolute deviations being ![]() .
This range contains also
.
This range contains also ![]() of outliers where the deviations are larger than
of outliers where the deviations are larger than ![]() .
The outliers occur in the low-amplitude correlations between the largest
.
The outliers occur in the low-amplitude correlations between the largest
![]() and smallest
and smallest
![]() scales.
scales.
The fit is worse on the diagonal than on the first off-diagonals (where
![]() ). On the diagonal, the fit always underestimates the covariance. Scales in the range
). On the diagonal, the fit always underestimates the covariance. Scales in the range
![]() show a deviation between
show a deviation between ![]() and
and ![]() ,
with an average of
,
with an average of ![]() .
The accuracy degrades at larger scales, which is not a problem since for
.
The accuracy degrades at larger scales, which is not a problem since for ![]() the non-Gaussian contribution to the total covariance is negligible, as seen in Fig. 8
(upper right
panel). Adding the Gaussian contribution to the fitted non-Gaussian
one, the underestimation in the diagonal elements is always better
than
the non-Gaussian contribution to the total covariance is negligible, as seen in Fig. 8
(upper right
panel). Adding the Gaussian contribution to the fitted non-Gaussian
one, the underestimation in the diagonal elements is always better
than ![]() ,
with an average of
,
with an average of ![]() .
.
In summary, the fitting formula for the cosmic variance, including
Gaussian and non-Gaussian contributions, has an average accuracy
of ![]() in the off-diagonal and
in the off-diagonal and ![]() in the diagonal.
It is valid when both scales are in the range
in the diagonal.
It is valid when both scales are in the range
![]() ,
corresponding to
,
corresponding to
![]() in real space. This is roughly the range used in the latest results from CFHTLS-Wide (Fu et al. 2008).
This range includes the scales where non-Gaussianity is relevant,
i.e., where the cosmic shear error budget is both dominated by
cosmic variance and has important contributions from non-linear
clustering (see Sect. 6.4).
in real space. This is roughly the range used in the latest results from CFHTLS-Wide (Fu et al. 2008).
This range includes the scales where non-Gaussianity is relevant,
i.e., where the cosmic shear error budget is both dominated by
cosmic variance and has important contributions from non-linear
clustering (see Sect. 6.4).
6.4 Impact of the accuracy of the fitting formula on parameter estimations
We study the impact of the fitting formula accuracy on the estimation
of cosmological parameters, using a Fisher matrix approach. For this,
we need to take into account not only the Gaussian and non-Gaussian
contributions to the covariance, but also the noise in the observed
power spectrum. In practical applications, the convergence field
in Eq. (13)
is obtained
from the observed ellipticities of the source galaxies. The intrinsic
ellipticity field (i.e., in the absence of a gravitational
lensing effect) is assumed to have zero mean and rms of
![]() per
component. This shape noise contaminates the observed power spectrum.
Assuming that the intrinsic ellipticities of different galaxies do not
correlate, the shape
noise contribution to the covariance of the power spectrum is diagonal
and given by the new terms arising in Eq. (14) when replacing the power spectrum, in that expression, by the observed one defined as (Kaiser 1992),
per
component. This shape noise contaminates the observed power spectrum.
Assuming that the intrinsic ellipticities of different galaxies do not
correlate, the shape
noise contribution to the covariance of the power spectrum is diagonal
and given by the new terms arising in Eq. (14) when replacing the power spectrum, in that expression, by the observed one defined as (Kaiser 1992),
where n is the number density of source galaxies.
We consider the following three surveys: a medium-deep weak lensing survey covering an area of
![]() with
with
![]() ,
like the current CFHTLS-Wide, a wider survey of similar depth covering
,
like the current CFHTLS-Wide, a wider survey of similar depth covering
![]() with
with
![]() ,
like the planned Dark Energy Survey
(DES)
,
like the planned Dark Energy Survey
(DES)![]() , and a wide and deep survey with
, and a wide and deep survey with
![]() and
and
![]() ,
like the proposed E UCLID
,
like the proposed E UCLID![]() . For all three we assume
. For all three we assume
![]() and compute the covariance using the halo model and the developed fit formula in the range
and compute the covariance using the halo model and the developed fit formula in the range
![]() .
Additionally, we add the covariance of a Gaussian contribution using a logarithmic binning with 61 bins in a range from
.
Additionally, we add the covariance of a Gaussian contribution using a logarithmic binning with 61 bins in a range from
![]() to
to
![]() .
The wider
surveys will measure correlations on scales larger than
.
The wider
surveys will measure correlations on scales larger than ![]() ,
which we do not consider here for comparison purposes. Note also that
for very large scales the flat-sky approximation breaks down.
,
which we do not consider here for comparison purposes. Note also that
for very large scales the flat-sky approximation breaks down.
![\begin{figure}
\par\hspace*{-2mm}\includegraphics[width=8.1cm,clip]{12854fg14}\vspace*{5mm}
\includegraphics[width=7.7cm,clip]{12854fg15}
\end{figure}](/articles/aa/full_html/2010/06/aa12854-09/Timg383.png)
|
Figure 9:
Left panel: relative contributions to the diagonal of the
convergence power spectrum covariance. The binning-dependent Gaussian
to non-Gaussian ratio (solid line; see caption of Fig. 8 for the employed binning scheme) and the shape noise to cosmic variance ratio for two surveys with
|
| Open with DEXTER | |
The left panel of Fig. 9
compares the different terms contributing to the diagonal of the
covariance, by showing the Gaussian to non-Gaussian ratio and the
shape noise to cosmic variance ratio, where by cosmic variance we
denote the sum of the Gaussian and non-Gaussian
contributions. The ratio between the Gaussian and non-Gaussian terms is
independent of the survey and, for our particular choice of
binning, non-Gaussianity starts to affect the diagonal around
![]() ,
where its amplitude is
,
where its amplitude is ![]() of the Gaussian amplitude, and dominates from
of the Gaussian amplitude, and dominates from
![]() onwards. Shape noise, including both pure shape noise and the coupling
with cosmic variance, also becomes important on small scales,
but in a survey-dependent way. It is as large as the cosmic
variance on
onwards. Shape noise, including both pure shape noise and the coupling
with cosmic variance, also becomes important on small scales,
but in a survey-dependent way. It is as large as the cosmic
variance on
![]()
![]() for surveys with 10 (40) galaxies per arcmin squared. The vertical lines in Fig. 9 (left panel) show, for the E UCLID-like
survey, the range where the non-Gaussian contribution to the diagonal
is non-negligible, i.e., where it accounts for more than
for surveys with 10 (40) galaxies per arcmin squared. The vertical lines in Fig. 9 (left panel) show, for the E UCLID-like
survey, the range where the non-Gaussian contribution to the diagonal
is non-negligible, i.e., where it accounts for more than ![]() of the cosmic variance while having an amplitude of at least
of the cosmic variance while having an amplitude of at least ![]() of the shape noise. This range is roughly
of the shape noise. This range is roughly
![]() ,
or approximately
,
or approximately
![]() .
This is a rough estimate of the minimum range where the fitting formula is required to have a good accuracy.
.
This is a rough estimate of the minimum range where the fitting formula is required to have a good accuracy.
In addition, the accuracy of the off-diagonal terms is crucial, since
the non-Gaussianity is the sole contribution there. To evaluate
the required range of validity of the fitting formula,
in a way that includes the off-diagonal elements and is
independent of bin width, we define the signal-to-noise ratio (Takada & Jain 2009),
For each survey, we compute the signal-to-noise ratio (SNR) using all scales between
We consider now the Fisher information matrix, which to first order,
neglecting the cosmology dependence of the covariance matrix, is
given by
where the derivatives are taken w.r.t. a set of cosmological parameters
We compute Eq. (59)
for both the fit and halo model covariances, for each of the three
surveys. We perform the derivatives at the fiducial model of Table 3, varying only 2 cosmological parameters
![]() .
For each survey, we compare the areas of the two
.
For each survey, we compare the areas of the two ![]() error
ellipses (which defines the inverse of the figure-of-merit) thus
obtained. For all three cases, there is a good agreement between the
two ellipses.
error
ellipses (which defines the inverse of the figure-of-merit) thus
obtained. For all three cases, there is a good agreement between the
two ellipses.
For the two cases with large shape noise, CFHTLS and DES, we
find that the fitting formula underestimates the Fisher ellipse, as
compared to the halo model covariance. This is expected because with an
enhanced diagonal the correlations between bins are weaker, and the
result is dominated by the accuracy of the diagonal, where the fitting
formula underestimates the
covariance, as we saw earlier on. The deviation is however weak,
the areas of the ellipses obtained using the fitting formula are ![]() smaller than the halo model result, and the deviation is uniformly distributed on the parameter space (see Fig. 9, right panel, large ellipses). This implies that the deviation on the marginalized constraints is much smaller,
and we find that the fitting formula underestimates the errors on both
smaller than the halo model result, and the deviation is uniformly distributed on the parameter space (see Fig. 9, right panel, large ellipses). This implies that the deviation on the marginalized constraints is much smaller,
and we find that the fitting formula underestimates the errors on both
![]() and
and ![]() by only
by only ![]() ,
for both surveys. This corresponds to a deviation of
,
for both surveys. This corresponds to a deviation of ![]()
![]() of the parameters values, for CFHTLS (DES). In contrast, for the E UCLID
case, where the covariance has larger correlations, the fitted
covariance produced an ellipse slightly larger than the halo model one,
by about
of the parameters values, for CFHTLS (DES). In contrast, for the E UCLID
case, where the covariance has larger correlations, the fitted
covariance produced an ellipse slightly larger than the halo model one,
by about ![]() (see Fig. 9, right
panel, small ellipses).
(see Fig. 9, right
panel, small ellipses).
6.5 Covariance of real-space estimators
For practical purposes it is sometimes more convenient to study
real-space correlations rather than correlations in Fourier space. We
therefore define an estimator of a general second-order cosmic shear
measure which is related to the convergence power spectrum
estimator by
where W(x) is an arbitrary weight function. A well-known example of this equation are the shear two-point correlation functions
| |
= | 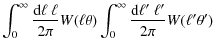
|
|
| (61) |
which is related to the covariance of the dimensionless power spectrum used in the fitting formula by
![$\displaystyle {\rm Cov}\left[\hat{\Gamma}(\theta),\hat{\Gamma}(\theta')\right] ...
...rm d}\ell}{\ell^{3}}~\mathcal{P}_{\kappa}^{2}(\ell)
W(\ell\theta)W(\ell\theta')$](/articles/aa/full_html/2010/06/aa12854-09/img412.png)
|
||
| (62) |
We find that the Gaussian part of the real-space covariance is independent of the binning scheme and is non-diagonal in contrast to the covariance in Fourier space.
7 Conclusions
We present a fitting formula for the halo model prediction of the
non-Gaussian contribution to the covariance of the dimensionless power
spectrum of the weak lensing convergence. The formula was constructed
assuming a ![]() CDM cosmology with WMAP5-like cosmological parameters. In particular, it was obtained for
CDM cosmology with WMAP5-like cosmological parameters. In particular, it was obtained for
![]() ,
,
![]() and other parameter values
as shown in Table 3. It is valid for a scale range of
and other parameter values
as shown in Table 3. It is valid for a scale range of
![]() ,
corresponding to
,
corresponding to
![]() in real space and can be used for surveys with galaxy source redshifts
in real space and can be used for surveys with galaxy source redshifts
![]() .
In this range, it reproduces the results of a full
implementation of the halo model approach, with a scale-averaged
accuracy of
.
In this range, it reproduces the results of a full
implementation of the halo model approach, with a scale-averaged
accuracy of ![]() in the off-diagonal, and
in the off-diagonal, and ![]() in the diagonal elements. The formula also allows us to recover the halo model
in the diagonal elements. The formula also allows us to recover the halo model
![]() error ellipses within
error ellipses within ![]() .
The range of validity of the formula and its level of
accuracy render it applicable to low shape noise scenarios from next generation weak lensing surveys.
.
The range of validity of the formula and its level of
accuracy render it applicable to low shape noise scenarios from next generation weak lensing surveys.
To use the formula, shown in Eq. (54), one needs three quantities:
- The non-Gaussian contribution to the covariance of the convergence power spectrum in tree-level perturbation theory
 ,
shown in Eq. (A.27). This involves the computation of the convergence trispectrum in tree-level perturbation theory, Eq. (A.26), which requires the calculation of the linear power spectrum and of the F2 and F3 coupling functions (Eqs. (A.10) and (A.12)).
,
shown in Eq. (A.27). This involves the computation of the convergence trispectrum in tree-level perturbation theory, Eq. (A.26), which requires the calculation of the linear power spectrum and of the F2 and F3 coupling functions (Eqs. (A.10) and (A.12)).
- The non-linear convergence power spectrum.
- The 9 coefficients of the fit, which are obtained by inserting the 27 values given in Table 4 in Eq. (55), for the required redshift.
The work presented in this paper is based on the assumption that the halo model is a powerful approach to probe non-linear clustering. We tried to test this assumption against results from N-body simulations, but our comparisons were inconclusive. Indeed, such analysis requires ray-tracing simulations with both large number of convergence maps and large convergence map area. Only then it would be possible to minimize the effect of sampling variance in the simulations, which hindered our attempted tests. Such simulations would also allow us to consider error bars for the estimate of the simulation covariance. There are however indications that the halo model approach underestimates the non-Gaussianity of the covariance and there are attempts to include additional contributions (Sato et al. 2009; Takada & Jain 2009).
The reliability of the halo model for higher-order polyspectra also
needs to be studied in more detail. Some work in this direction are the
analyses of the impact of the triaxiality of the halo profiles (Smith et al. 2006; Smith & Watts 2005), and halo exclusion effects (Tinker et al. 2005). Moreover, the issue of halo substructure (Dolney et al. 2004)
and of the effect of a stochastic concentration parameter have to be
understood properly. This paper also addresses this last issue. We
analyze the impact of a stochastic concentration parameter on the
covariance of the convergence power spectrum. We found that the effect
can safely be neglected for the Gaussian contribution, with the
convergence power spectrum varying only slightly, and at small scales,
for concentration scatters of
![]() .
For the non-Gaussian contribution the effect is more pronounced due to
the higher
sensitivity of the trispectrum to a stochastic concentration relation.
In the case of the 1-halo term of the trispectrum, we find it useful to
take into account a concentration dispersion of
.
For the non-Gaussian contribution the effect is more pronounced due to
the higher
sensitivity of the trispectrum to a stochastic concentration relation.
In the case of the 1-halo term of the trispectrum, we find it useful to
take into account a concentration dispersion of
![]() .
The deviation to a deterministic concentration-mass relation is larger than
.
The deviation to a deterministic concentration-mass relation is larger than ![]() for wave-numbers
for wave-numbers
![]() .
.
Although the fitting formula we obtained provides a more thorough
estimate for the non-Gaussian contribution to the power spectrum
covariance than the earlier approximation of Semboloni et al. (2007) (global accuracy of
![]() along the diagonal, which becomes less for the off-diagonals), there is
still room for improvements. One drawback of our approach is that it
requires the computation of the convergence trispectrum in tree-level
perturbation theory. Furthermore, it is only applicable to a small
range of WMAP5-like cosmologies and is only valid in the interval
along the diagonal, which becomes less for the off-diagonals), there is
still room for improvements. One drawback of our approach is that it
requires the computation of the convergence trispectrum in tree-level
perturbation theory. Furthermore, it is only applicable to a small
range of WMAP5-like cosmologies and is only valid in the interval
![]() .
A possible way to avoid these problems and extend the accuracy of
the fitting formula might be to construct it entirely from its
three-dimensional counterpart, the three-dimensional covariance of
the matter power spectrum. This has the advantage that
perturbations of different length scales are not additionally mixed due
to projection effects, which might allow us to cover a wider range of
cosmologies. The desired projected covariance could then be
obtained by performing an additional integration along the
redshift-space. We will address this issue in a future paper.
.
A possible way to avoid these problems and extend the accuracy of
the fitting formula might be to construct it entirely from its
three-dimensional counterpart, the three-dimensional covariance of
the matter power spectrum. This has the advantage that
perturbations of different length scales are not additionally mixed due
to projection effects, which might allow us to cover a wider range of
cosmologies. The desired projected covariance could then be
obtained by performing an additional integration along the
redshift-space. We will address this issue in a future paper.
The authors thank Christoph Lampert for invaluable discussions, and Jan Hartlap for providing his ray-tracing simulations of the Gems and Virgo simulations. Together with Martin Kilbinger both provided useful comments to the manuscript. J.P. would like to thank the TRR33. J.R. is supported by the Deutsche Forschungsgemeinschaft under the project SCHN 342/7-1 within the Priority Programme SPP 1177 ``Galaxy Evolution''. I.T. is supported by the Marie Curie Training and Research Network ``DUEL''.
References
- Albrecht, A., Bernstein, G., Cahn, R., et al. 2006 [arXiv:astro-ph/0609591]
- Bacon, D. J., Refregier, A. R., & Ellis, R. S. 2000, MNRAS, 318, 625
- Bardeen, J. M., Bond, J. R., Kaiser, N., & Szalay, A. S. 1986, ApJ, 304, 15
- Bartelmann, M., & Schneider, P. 2001, Phys. Rep., 340, 291
- Bernardeau, F., Colombi, S., Gaztañaga, E., & Scoccimarro, R. 2002, Phys. Rep., 367, 1
- Bullock, J. S., Kolatt, T. S., Sigad, Y., et al. 2001, MNRAS, 321, 559
- Cooray, A., & Hu, W. 2001, ApJ, 554, 56
- Cooray, A., & Sheth, R. 2002, Phys. Rep., 372, 1
- Dolney, D., Jain, B., & Takada, M. 2004, MNRAS, 352, 1019
- Eisenstein, D. J., & Hu, W. 1998, ApJ, 496, 605
- Fry, J. N. 1984, ApJ, 279, 499
- Fu, L., Semboloni, E., Hoekstra, H., et al. 2008, A&A, 479, 9
- Gunn, J. E., & Gott, J. R. I. 1972, ApJ, 176, 1
- Hartlap, J., Schrabback, T., Simon, P., & Schneider, P. 2009, A&A, 504, 689
- Hilbert, S., Hartlap, J., White, S. D. M., & Schneider, P. 2009, A&A, 499, 31
- Hu, W., & Kravtsov, A. V. 2003, ApJ, 584, 702
- Jain, B., & Bertschinger, E. 1994, ApJ, 431, 495
- Jain, B., Seljak, U., & White, S. 2000, ApJ, 530, 547
- Jenkins, A., Frenk, C. S., Pearce, F. R., et al. 1998, ApJ, 499, 20
- Jing, Y. P. 2000, ApJ, 535, 30
- Joachimi, B., Schneider, P., & Eifler, T. 2008, A&A, 477, 43
- Kaiser, N. 1992, ApJ, 388, 272
- Kaiser, N. 1998, ApJ, 498, 26
- Kaiser, N., Wilson, G., & Luppino, G. A. 2000, unpublished[arXiv:astro-ph/0003338]
- Kilbinger, M., & Schneider, P. 2005, A&A, 442, 69
- Komatsu, E., Dunkley, J., Nolta, M. R., et al. 2009, ApJS, 180, 330
- Ma, C.-P., & Fry, J. N. 2000, ApJ, 543, 503
- Massey, R., Heymans, C., Bergé, J., et al. 2007, MNRAS, 376, 13
- Nakamura, T. T., & Suto, Y. 1997, Prog. Theor. Phys., 97, 49
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493
- Peacock, J. A., & Dodds, S. J. 1996, MNRAS, 280, L19
- Peacock, J. A., & Smith, R. E. 2000, MNRAS, 318, 1144
- Pielorz, J. 2008, Ph.D. Thesis, University of Bonn
- Press, W. H., & Schechter, P. 1974, ApJ, 187, 425
- Sato, M., Hamana, T., Takahashi, R., et al. 2009, ApJ, 701, 945
- Schäfer, B. M. 2009, Int. J. Modern Phys. D, 18, 173
- Schneider, P. 2006, in Gravitational Lensing: Strong, Weak and Micro, Saas-Fee Advanced Courses, ed. P. Schneider, C. S. Kochanek, & J. Wambsganss (Berlin: Springer-Verlag), 33, 269
- Schneider, P., van Waerbeke, L., Kilbinger, M., & Mellier, Y. 2002, A&A, 396, 1
- Scoccimarro, R., Colombi, S., Fry, J. N., et al. 1998, ApJ, 496, 586
- Scoccimarro, R., Sheth, R. K., Hui, L., & Jain, B. 2001, ApJ, 546, 20
- Scoccimarro, R., Zaldarriaga, M., & Hui, L. 1999, ApJ, 527, 1
- Seljak, U. 2000, MNRAS, 318, 203
- Semboloni, E., Tereno, I., van Waerbeke, L., & Heymans, C. 2009, MNRAS, 397, 608
- Semboloni, E., van Waerbeke, L., Heymans, C., et al. 2007, MNRAS, 375, L6
- Sheth, R. K., & Tormen, G. 1999, MNRAS, 308, 119
- Smith, R. E., & Watts, P. I. R. 2005, MNRAS, 360, 203
- Smith, R. E., Peacock, J. A., Jenkins, A., et al. 2003, MNRAS, 341, 1311
- Smith, R. E., Scoccimarro, R., & Sheth, R. K. 2007, Phys. Rev. D, 75, 063512
- Smith, R. E., Watts, P. I. R., & Sheth, R. K. 2006, MNRAS, 365, 214
- Springel, V. 2005, MNRAS, 364, 1105
- Takada, M., & Jain, B. 2003, MNRAS, 340, 580
- Takada, M., & Bridle, S. 2007, New J. Phys., 9, 446
- Takada, M., & Jain, B. 2009, MNRAS, 395, 2065
- Takahashi, R., Yoshida, N., Takada, M., et al. 2009, ApJ, 700, 479
- Tinker, J. L., Weinberg, D. H., Zheng, Z., & Zehavi, I. 2005, ApJ, 631, 41
- Van Waerbeke, L., Mellier, Y., Erben, T., et al. 2000, A&A, 358, 30
- Vikhlinin, A., Burenin, R. A., Ebeling, H., et al. 2009, ApJ, 692, 1033
- Wechsler, R. H., Bullock, J. S., Primack, J. R., Kravtsov, A. V., & Dekel, A. 2002, ApJ, 568, 52
- White, M., & Hu, W. 2000, ApJ, 537, 1
- Wittman, D. M., Tyson, J. A., Kirkman, D., Dell'Antonio, I., & Bernstein, G. 2000, Nature, 405, 143
Appendix A: Cosmological perturbation theory
On large scales, different Fourier modes evolve independently from
each other and thus conserve the Gaussian behavior of the density
perturbation field
![]() .
It is therefore
convenient to work in Fourier space and Fourier transform the fields as
well as the non-linear fluid equations (consisting of continuity, Euler
and Poisson equation) that describe their evolution in an
expanding Universe. Contrary to linear perturbation theory, there is a
coupling between different Fourier modes mediated by the coupling
function
.
It is therefore
convenient to work in Fourier space and Fourier transform the fields as
well as the non-linear fluid equations (consisting of continuity, Euler
and Poisson equation) that describe their evolution in an
expanding Universe. Contrary to linear perturbation theory, there is a
coupling between different Fourier modes mediated by the coupling
function
![]() on smaller scales. In this case, the fluid equations for the density contrast and the irrotational peculiar velocity field
on smaller scales. In this case, the fluid equations for the density contrast and the irrotational peculiar velocity field
![]() in Fourier space are given by (e.g., Bernardeau et al. 2002)
in Fourier space are given by (e.g., Bernardeau et al. 2002)
where we introduced the two fundamental mode coupling functions
For an Einstein-de Sitter (EdS) cosmology it is possible to find a perturbative ansatz that separates the scale- and time dependencies, whereas for a general
Therefore, we find that the whole information on cosmological parameters is encoded in the growth function due to its dependence on the Hubble parameter (see Eq. (5)).
A.1 Coupling functions
The nth order density contrast and the divergence of the peculiar velocity in Eq. (A.4) is given by
and the nth order coupling functions Fn and Gn are obtained by the following recursion relations (Jain & Bertschinger 1994)
![$\displaystyle F_n({\vec q_1},\ldots,{\vec q_n}) = \sum_{m=1}^{n-1}
\frac{G_m({\...
..._n})
+ 2\beta({\vec k_1},{\vec k_2})G_{n-m}({\vec q_{m+1}},\ldots,{\vec q_n})],$](/articles/aa/full_html/2010/06/aa12854-09/img433.png)
|
(A.7) | |
![$\displaystyle G_n({\vec q_1},\ldots,{\vec q_n}) = \sum_{m=1}^{n-1}
\frac{G_m({\...
...n})
+ 2n\beta({\vec k_1},{\vec k_2})G_{n-m}({\vec q_{m+1}},\ldots,{\vec q_n})],$](/articles/aa/full_html/2010/06/aa12854-09/img434.png)
|
(A.8) |
where
where the sum is taken over all possible permutations
The calculation of the second-order coupling functions is straightforward. The result is
The third-order coupling function is given by
![$\displaystyle %
F_3({\vec q_1},{\vec q_2},{\vec q_3}) = \frac{1}{18}\Big\{
7\al...
...vec q_3}) +
2\beta({\vec q}_{12},{\vec q_3})] G_2({\vec q_1},{\vec q_2})\Big\},$](/articles/aa/full_html/2010/06/aa12854-09/img445.png)
|
(A.11) |
where
From now on the symmetry superscript `` (s)'' will be omitted because we will only deal with symmetric coupling functions. For the calculation of the trispectrum in the halo model approach as described in Sect. 4.5, one needs perturbation theory. More precisely, we need the subsequent components
| |
= | ||
| (A.13) |
where we have defined the difference vector
We already mentioned in the previous section that it is possible to
find a solution for an arbitrary cosmology if one makes a small
approximation. In the literature one can find closed solutions for the
second- and third-order coupling functions. The second-order coupling
function changes to
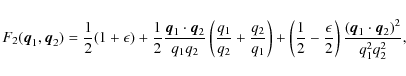
|
(A.14) |
where
A.2 Correlation functions
A.2.1 Bispectrum
The dark matter bispectrum is defined as
Since the connected bispectrum vanishes for Gaussian random fields, it is the first intrinsically non-linear moment. Inserting the perturbative expansion (A.4) for each term results generally in an infinitely large sequence of correlators. The lowest non-vanishing order is the so-called tree-level contribution to the bispectrum. We find for the correlator in tree level
| (A.16) |
Replacing the second-order density contrast with Eq. (A.5) results in
| |
= | 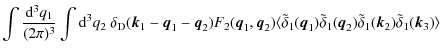
|
|
| = | (A.17) |
where we applied Wick's theorem to express the four-point correlator of Gaussian fields in terms of products of power spectra, and performed the two integrations over the Dirac delta distributions. The results for the other two terms of the tree-level bispectrum are simply obtained by permutations of the arguments. Finally, the tree-level bispectrum is given by
The factor 2 follows from using the symmetrized version of the second-order coupling function.
A.2.2 Trispectrum
The dark matter trispectrum is defined as the connected four-point function in Fourier space:
where
| |
= | ||
| (A.20) |
In total we find 6 terms of the first type and 4 terms for the second type, where the rest is obtained by permutations. All other contributions either vanish or are built of higher-order terms. Note that for the second type of terms we need the results from perturbation theory up to the third order. The calculation of each term is a tedious but straightforward calculation. We obtain for the first term of the expansion
![$\displaystyle %
\langle \tilde\delta_{2}({\vec k}_{1}) \tilde\delta_{2}({\vec k...
...)+ P_{14}F_{2}({\vec k}_{3},-{\vec k}_{23})F_{2}({\vec k}_{4},-{\vec k}_{14})],$](/articles/aa/full_html/2010/06/aa12854-09/img473.png)
|
(A.21) |
where the six-point correlator resolves into 15 terms consisting of power spectra products. Performing the integrations over the arising delta functions yields in the end 8 different terms. Similarly, we find for the second type of terms
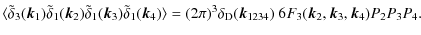
|
(A.22) |
The other terms are easily obtained by permutations, however, we present here the complete result to avoid confusion with a shorthand notation that is introduced afterwards. The trispectrum of cold dark matter is in first non-vanishing order given by (Fry 1984):
where
and
where
For the covariance matrix one only needs the parallelogram configuration. This imposes the condition
![]() and
and
![]() on the wave-vectors. In this case Eq. (A.23) simplifies to
on the wave-vectors. In this case Eq. (A.23) simplifies to
where
where A denotes the survey area,
Footnotes
- ... theory
![[*]](/icons/foot_motif.png)
- We refer by tree-level perturbation theory to the lowest, non-vanishing order of the considered quantity in perturbation theory.
- ... Transform
![[*]](/icons/foot_motif.png)
- For the FFT we use an algorithm from the GNU scientific library (see http://www.gnu.org/software/gsl/ for more details).
- ... spectrum
![[*]](/icons/foot_motif.png)
- Using the hierarchical ansatz, which is approximately valid in the highly nonlinear regime, the three-dimensional dark matter trispectrum is proportional to the power spectrum cubed.
- ...
(DES)
![[*]](/icons/foot_motif.png)
- http://www.darkenergysurvey.org/
- ... UCLID
![[*]](/icons/foot_motif.png)
- http://www.dune-mission.net/
All Tables
Table 1: Cosmological parameters used to set up the initial power spectrum.
Table 2: Parameters used for generating the two N-body simulations.
Table 3: Fiducial model used for the fitting procedure.
Table 4:
Best-fit values for the parameters
(p0,p1,p2) of the redshift-fit for the set of coefficients
![]() .
.
All Figures
![\begin{figure}
\par\includegraphics[width=12cm,clip]{12854fg1}
\end{figure}](/articles/aa/full_html/2010/06/aa12854-09/Timg194.png)
|
Figure 1:
Square configuration of the dimensionless convergence trispectrum
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{12854fg2}
\end{figure}](/articles/aa/full_html/2010/06/aa12854-09/Timg243.png)
|
Figure 2:
Contour plots of the ratio
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\hspace*{0.25mm}\includegraphics[width=11.9cm,clip]{12854fg3}...
...e*{0.25mm}\vspace*{3mm}
\includegraphics[width=12cm,clip]{12854fg4}
\end{figure}](/articles/aa/full_html/2010/06/aa12854-09/Timg263.png)
|
Figure 3:
Dimensionless convergence power spectrum
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{12854fg5}
\end{figure}](/articles/aa/full_html/2010/06/aa12854-09/Timg284.png)
|
Figure 4:
Relative difference
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{12854fg6}
\end{figure}](/articles/aa/full_html/2010/06/aa12854-09/Timg285.png)
|
Figure 5:
Relative difference
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12854fg7}
\end{figure}](/articles/aa/full_html/2010/06/aa12854-09/Timg303.png)
|
Figure 6:
Ratio
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12854fg8}\vspace*{2mm}
\includegraphics[width=8.5cm,clip]{12854fg9}
\end{figure}](/articles/aa/full_html/2010/06/aa12854-09/Timg346.png)
|
Figure 7:
Coefficients ai of the fitting formula obtained for various source redshifts. Left (right) panel
shows the coefficients of the large (small) scales fitting formula. For
convenience, scaled versions of the coefficients are shown,
as indicated in the key. Note for example that a5, a7 and a8 change sign. The lines show the redshift fit, Eq. (55), with the parameters given in Table 4. They provide a good fit for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[angle=0,width=8.5cm]{12854fg10}\includ...
....5cm]{12854fg12}\includegraphics[angle=0,width=8.5cm]{12854fg13} }\end{figure}](/articles/aa/full_html/2010/06/aa12854-09/Timg355.png)
|
Figure 8:
Accuracy of the fitting formula for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\hspace*{-2mm}\includegraphics[width=8.1cm,clip]{12854fg14}\vspace*{5mm}
\includegraphics[width=7.7cm,clip]{12854fg15}
\end{figure}](/articles/aa/full_html/2010/06/aa12854-09/Timg383.png)
|
Figure 9:
Left panel: relative contributions to the diagonal of the
convergence power spectrum covariance. The binning-dependent Gaussian
to non-Gaussian ratio (solid line; see caption of Fig. 8 for the employed binning scheme) and the shape noise to cosmic variance ratio for two surveys with
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



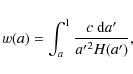
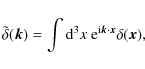
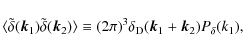
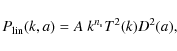
![\begin{displaymath}%
D(a) \propto \frac{H(a)}{H_0} \int_0^a
\frac{{\rm d}a'}{[a'H(a')/H_0]^3}
\end{displaymath}](/articles/aa/full_html/2010/06/aa12854-09/img73.png)
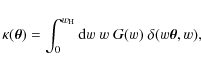
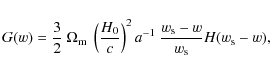
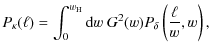
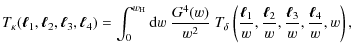
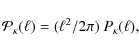
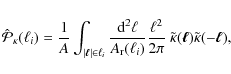
![$\displaystyle \frac{1}{A}\left[ \frac{(2\pi)^{2}}{A_{\rm {r}}(\ell_{i})} 2 {\ca...
...,\ell_{j}) \right]
\equiv \mathcal{C}^{\rm G}_{ij} + \mathcal{C}^{\rm NG}_{ij},$](/articles/aa/full_html/2010/06/aa12854-09/img99.png)
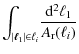
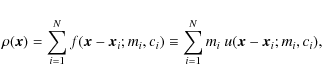
![$\displaystyle %
\langle X \rangle \equiv \int \left[ \prod_{i=1}^{N} {\rm d}^3 ...
...}c_i \right]
~ p({\vec x}_1,\dots,{\vec x}_N, m_1,\dots,m_N,c_1,\dots,c_N) ~ X,$](/articles/aa/full_html/2010/06/aa12854-09/img133.png)
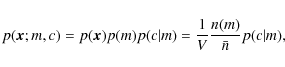
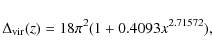
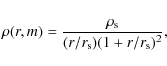
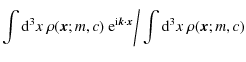
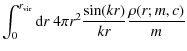
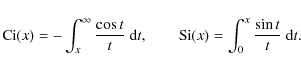
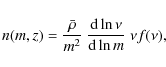
![\begin{displaymath}%
\delta_{\rm sc}(z) = \frac{3(12\pi)^{2/3}}{20} \left[1-0.0123
\ln(1+x^3)\right],
\end{displaymath}](/articles/aa/full_html/2010/06/aa12854-09/img162.png)
![\begin{displaymath}%
\nu f(\nu) = A(p) \left[1+(q\nu^2)^{-p} \right]
\sqrt{\frac{2q}{\pi}} ~ \nu \exp{(-q\nu^2/2)},
\end{displaymath}](/articles/aa/full_html/2010/06/aa12854-09/img166.png)
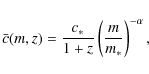
![\begin{displaymath}%
p(c\vert m) {\rm d}c = \frac{1}{\sqrt{2\pi\sigma^2_{\ln c}}...
...ln c -
\ln \bar c)^2}{2\sigma^2_{\ln c}}\right] {\rm d}\ln c.
\end{displaymath}](/articles/aa/full_html/2010/06/aa12854-09/img171.png)

![\begin{displaymath}%
b_1(m,z)= 1 + \frac{q[\nu(m,z)]^{2} -1}{\delta_{\rm sc}(z)} +
\frac{2p}{\delta_{\rm sc}(z)[1+(q[\nu(m,z)]^{2})^p]},~~
\end{displaymath}](/articles/aa/full_html/2010/06/aa12854-09/img179.png)
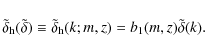
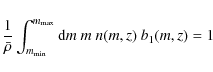
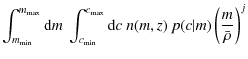
![$\displaystyle \left[ \frac{1}{\bar\rho}\! \int_{m_{\rm min}}^{m_{\rm max}} {\rm...
..._{\rm min}}^{c_{\rm max}} {\rm d}c ~
~ p(c\vert m) ~ \tilde{u}(k;m,c) \right]^2$](/articles/aa/full_html/2010/06/aa12854-09/img199.png)
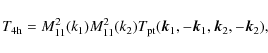
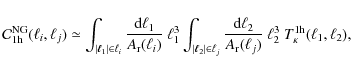
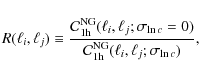
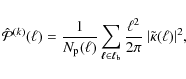
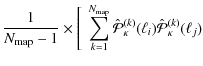
![$\displaystyle - ~ \frac{1}{N_{\rm map}} \Bigg(\sum_{k=1}^{N_{\rm map}} \hat{\ca...
...gg( \sum_{k=1}^{N_{\rm map}}
\hat{\cal P}_\kappa^{(k)}(\ell_j) \Bigg) ~ \Bigg],$](/articles/aa/full_html/2010/06/aa12854-09/img278.png)