| Issue |
A&A
Volume 514, May 2010
|
|
|---|---|---|
| Article Number | A31 | |
| Number of page(s) | 7 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/200911991 | |
| Published online | 06 May 2010 | |
Survival of a convective core in low-mass solar-like pulsator HD 203608
S. Deheuvels1 - E. Michel1 - M. J. Goupil1 - J. P. Marques1 - B. Mosser1 - M. A. Dupret1 - Y. Lebreton1 - B. Pichon2 - P. Morel2
1 - LESIA, CNRS UMR 8109, Observatoire de Paris, Université Paris 6,
Université Paris 7, 92195 Meudon Cedex, France
2 - Laboratoire Cassiopée, CNRS UMR 6202, Observatoire de la Côte
d'Azur, BP 4229, 06304 Nice Cedex 4, France
Received 6 March 2009 / Accepted 15 January 2010
Abstract
Context. A 5-night asteroseismic observation of the
F8V star HD 203608 was conducted in August 2006 with HARPS,
followed by an analysis of the data, and a preliminary modeling of the
star (Mosser et al. 2008). The stellar parameters were
significantly constrained, but the behavior of one of the seismic
indexes (the small spacing ![]() )
could not be fitted with the observed one, even with the best
considered models.
)
could not be fitted with the observed one, even with the best
considered models.
Aims. We study the possibility of improving the
agreement
between models and observations by changing the physical properties of
the inner parts of the star (to which
![]() is sensitive).
is sensitive).
Methods. We show that, in spite of its low mass, it
is possible
to produce models of HD 203608 with a convective core. No such
model was considered in the preliminary modeling. In practice, we
obtain these models here by assuming some extra mixing at the edge of
the early convective core. We optimized the model parameters using the
Levenberg-Marquardt algorithm.
Results. The agreement between the new best model
with a
convective core and the observations is much better than for the models
without. All the observational parameters are fitted within 1-![]() observational error bars. This is the first observational evidence of a
convective core in an old and low-mass star such as HD 203608.
In
standard models of low-mass stars, the core withdraws shortly after the
ZAMS. The survival of the core until the present age of
HD 203608
provides very strong constraints on the size of the mixed zone
associated to the convective core. Using overshooting as a proxy to
model the processes of transport at the edge of the core, we find that
to reproduce both global and seismic observations, we must have
observational error bars. This is the first observational evidence of a
convective core in an old and low-mass star such as HD 203608.
In
standard models of low-mass stars, the core withdraws shortly after the
ZAMS. The survival of the core until the present age of
HD 203608
provides very strong constraints on the size of the mixed zone
associated to the convective core. Using overshooting as a proxy to
model the processes of transport at the edge of the core, we find that
to reproduce both global and seismic observations, we must have
![]() for HD 203608. We revisit the process of the extension of the
core
lifetime due to overshooting in the particular case of
HD 203608.
for HD 203608. We revisit the process of the extension of the
core
lifetime due to overshooting in the particular case of
HD 203608.
Key words: stars: oscillations - stars: interiors - stars: evolution
1 Introduction
For main sequence stars massive enough to show a convective core (
![]() for solar-like metallicity), the associated mixed region plays the role
of a reservoir
for nuclear reactions. The evolution pace of these stars and the time
they spend on the main sequence depend directly on the size of this
reservoir. The imprecise
knowledge we have of the mixing processes, particularly at the boundary
of the core, generates large uncertainties on the extension of the
mixed core and subsequently
on the stellar age and mass for a given set of surface parameters.
Among the processes of transport of chemical elements that could
contribute to the creation of a mixed zone
beyond the edge of the convective core, overshooting is the one invoked
most often.
for solar-like metallicity), the associated mixed region plays the role
of a reservoir
for nuclear reactions. The evolution pace of these stars and the time
they spend on the main sequence depend directly on the size of this
reservoir. The imprecise
knowledge we have of the mixing processes, particularly at the boundary
of the core, generates large uncertainties on the extension of the
mixed core and subsequently
on the stellar age and mass for a given set of surface parameters.
Among the processes of transport of chemical elements that could
contribute to the creation of a mixed zone
beyond the edge of the convective core, overshooting is the one invoked
most often.
In the deep interior, convective elements rise adiabatically.
They are accelerated until they reach the position of convective
stability, i.e.
![]() .
Then, the buoyancy forces cause a braking of the eddies in the
radiative region. It is, however, unlikely that they should stop
abruptly at the boundary between the
two regimes. They might penetrate, over a distance
.
Then, the buoyancy forces cause a braking of the eddies in the
radiative region. It is, however, unlikely that they should stop
abruptly at the boundary between the
two regimes. They might penetrate, over a distance
![]() ,
in the regions of stability owing to their inertia, and generate a
region of mixing beyond the edge
of the core. This phenomenon has been investigated by several authors
(see Zahn
1991,
and references therein), but no satisfying theoretical or
numerical description have been proposed. In practice, this region is
modeled as an adiabatic layer above the core, whose thickness is a
fraction
,
in the regions of stability owing to their inertia, and generate a
region of mixing beyond the edge
of the core. This phenomenon has been investigated by several authors
(see Zahn
1991,
and references therein), but no satisfying theoretical or
numerical description have been proposed. In practice, this region is
modeled as an adiabatic layer above the core, whose thickness is a
fraction ![]() of the pressure scale height
of the pressure scale height ![]() (
(
![]() )
and where the elements are mixed. While it is admitted that
)
and where the elements are mixed. While it is admitted that ![]() is only a crude account for the complex processes of mixing at the
boundary of the
convective core, it is convenient and usual in the modeling of stellar
interiors to adopt a representation of these processes depending on
this parameter alone.
Different studies have led to a wide range of
is only a crude account for the complex processes of mixing at the
boundary of the
convective core, it is convenient and usual in the modeling of stellar
interiors to adopt a representation of these processes depending on
this parameter alone.
Different studies have led to a wide range of
![]() :
between zero (Langer
1986) and about 2 (Xiong 1985).
In fact, it is currently admitted that different values of
:
between zero (Langer
1986) and about 2 (Xiong 1985).
In fact, it is currently admitted that different values of ![]() might be needed to model stars of different masses and ages (see e.g. Claret 2007).
We therefore do not have precise knowledge of the amount of mixing at
the edge of the core, and
it is one of the main goals of asteroseismology to constrain it with
observations (see Lebreton
et al. 1995; Michel
et al. 2006).
might be needed to model stars of different masses and ages (see e.g. Claret 2007).
We therefore do not have precise knowledge of the amount of mixing at
the edge of the core, and
it is one of the main goals of asteroseismology to constrain it with
observations (see Lebreton
et al. 1995; Michel
et al. 2006).
For intermediate-mass and high-mass stars, ![]() is admitted to play an important role (Maeder 1976).
The case of low-mass stars is not as clear. When they reach the ZAMS,
these stars present a small convective core that disappears almost
immediately. It has already been mentioned that an
extra mixing at the edge of this early convective core might increase
its longevity, by providing first more 12C, and
then more 3He
in the center (Roxburgh 1985).
In the specific case of the Sun, core overshooting was added in the
models, but it was concluded that it had no relevant impact on the
Sun's present structure, unless we add an unreasonable amount of extra
mixing. Later on, stellar models of low-mass stars suggested that the
overshooting at the edge of the core could make it survive almost until
the end of the main sequence, although the phenomenon was not explained
(Mowlavi 1993).
is admitted to play an important role (Maeder 1976).
The case of low-mass stars is not as clear. When they reach the ZAMS,
these stars present a small convective core that disappears almost
immediately. It has already been mentioned that an
extra mixing at the edge of this early convective core might increase
its longevity, by providing first more 12C, and
then more 3He
in the center (Roxburgh 1985).
In the specific case of the Sun, core overshooting was added in the
models, but it was concluded that it had no relevant impact on the
Sun's present structure, unless we add an unreasonable amount of extra
mixing. Later on, stellar models of low-mass stars suggested that the
overshooting at the edge of the core could make it survive almost until
the end of the main sequence, although the phenomenon was not explained
(Mowlavi 1993).
In this article, we revisit this phenomenon in the case of
HD 203608, a low-mass F8V star that presents solar-like
oscillations. It was observed with the high-resolution spectrometer HARPS
at the ESO 3.6-m telescope in August 2006 (Mosser et al. 2008,
hereafter M08). The authors analyzed the oscillation spectrum and
identified 15 ![]() and
and ![]() eigenmodes. They found a model that agrees with the physical parameters
and all the seismic parameters but one: the behavior of the small
spacing
eigenmodes. They found a model that agrees with the physical parameters
and all the seismic parameters but one: the behavior of the small
spacing
![]() with frequency. Since HD 203608 is a low-mass star (less than
1
with frequency. Since HD 203608 is a low-mass star (less than
1 ![]() ),
the effect of core overshooting was neglected in the preliminary
modeling performed in M08.
For this range of mass, stars are not expected
to have a convective core on the main sequence, except for a small one
which disappears shortly after the ZAMS. In Sect. 2,
we show that in the case of HD 203608, with a reasonable
amount of
mixing, the early convective core can survive until the present age.
The agreement between observations and models is then greatly improved.
In Sect. 3,
we explain why the convective core of HD 203608 can survive,
even when the burning of 3He is no longer
capable of sustaining it.
),
the effect of core overshooting was neglected in the preliminary
modeling performed in M08.
For this range of mass, stars are not expected
to have a convective core on the main sequence, except for a small one
which disappears shortly after the ZAMS. In Sect. 2,
we show that in the case of HD 203608, with a reasonable
amount of
mixing, the early convective core can survive until the present age.
The agreement between observations and models is then greatly improved.
In Sect. 3,
we explain why the convective core of HD 203608 can survive,
even when the burning of 3He is no longer
capable of sustaining it.
2 Modeling of HD 203608
2.1 Results from previous modeling of HD 203608
For their modeling of HD 203608, M08 adopted the following
stellar parameters: ![]() K
(Jonsell
et al. 2005; del Peloso
et al. 2005),
K
(Jonsell
et al. 2005; del Peloso
et al. 2005),
![]() (from the Hipparcos parallax
(from the Hipparcos parallax ![]() mas,
van Leeuwen
2007) and an observed surface metallicity of
mas,
van Leeuwen
2007) and an observed surface metallicity of ![]() dex, from detailed analysis (see M08). They searched for an optimal
model by adjusting the age of the star, its mass, the initial abundance
of helium
dex, from detailed analysis (see M08). They searched for an optimal
model by adjusting the age of the star, its mass, the initial abundance
of helium ![]() ,
and the initial metallicity [Z/X]
,
and the initial metallicity [Z/X]![]() to fit the following
observational constraints:
to fit the following
observational constraints: ![]() ,
L,
,
L, ![]() ,
,
![]() ,
,
![]() ,
and
,
and ![]() ,
where
,
where ![]() represents a mean value of the large spacing, and
represents a mean value of the large spacing, and ![]() ,
,
![]() are the small spacings defined as
are the small spacings defined as
Their best model fits the observational constraints on the star quite well, except for
2.2 A new modeling including extra mixing at the core boundary
As shown in Appendix A,
the small spacing ![]() is very sensitive to the central part of the stellar interior. The
present disagreement suggests that the way we model these inner regions
should be reconsidered. As already mentioned, the models computed in
M08 have no convective core. We tried to obtain models of
HD 203608 with a convective core here by generating extra
mixing
at the edge of the core, as suggested by Roxburgh (1985).
is very sensitive to the central part of the stellar interior. The
present disagreement suggests that the way we model these inner regions
should be reconsidered. As already mentioned, the models computed in
M08 have no convective core. We tried to obtain models of
HD 203608 with a convective core here by generating extra
mixing
at the edge of the core, as suggested by Roxburgh (1985).
We performed a new modeling of HD 203608 including
mixing beyond the boundary of the convective core
by allowing ![]() in our models. We computed stellar models using CESAM2k (Morel 1997),
and we derived the mode frequencies from these
models with the Liege oscillation code (LOSC, Scuflaire
et al. 2008). We used the same physics as in M08 for
our models, apart from the treatment of convection.
We preferred to use the more realistic formalism of Canuto &
Mazzitelli (1991). For calibration, we computed a solar model
with this treatment of convection and found
in our models. We computed stellar models using CESAM2k (Morel 1997),
and we derived the mode frequencies from these
models with the Liege oscillation code (LOSC, Scuflaire
et al. 2008). We used the same physics as in M08 for
our models, apart from the treatment of convection.
We preferred to use the more realistic formalism of Canuto &
Mazzitelli (1991). For calibration, we computed a solar model
with this treatment of convection and found ![]() .
As in M08, we adopted this value for our modeling.
Overshooting is described, as explained before, as an extension of the
adiabatic and mixed region associated to the convective core, over a
distance
.
As in M08, we adopted this value for our modeling.
Overshooting is described, as explained before, as an extension of the
adiabatic and mixed region associated to the convective core, over a
distance ![]() defined as
defined as
where
2.3 Optimization
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11991fg1.eps}
\end{figure}](/articles/aa/full_html/2010/06/aa11991-09/Timg35.png)
|
Figure 1:
Variations in the small spacing |
| Open with DEXTER | |
Table 1: Physical and seismic parameters of HD 203608.
We looked for an optimal model fitting the global parameters
of HD 203608:
![]() ,
,
![]() ,
and
,
and ![]() (given in Table 1),
as well as its seismic parameters. For the seismic constraints, we
adopted the mode frequencies obtained in the analysis of M08. We used a
mean value of the large separation
(given in Table 1),
as well as its seismic parameters. For the seismic constraints, we
adopted the mode frequencies obtained in the analysis of M08. We used a
mean value of the large separation
![]() and the coefficients of a least-squares linear regression of the small
spacings
and the coefficients of a least-squares linear regression of the small
spacings ![]() and
and ![]() .
The frequency range of the identified modes is indeed small enough to
linearize them in the form:
.
The frequency range of the identified modes is indeed small enough to
linearize them in the form:
with
The best models are obtained by minimizing the ![]() function defined as
function defined as
where
Table 1
gives the physical and seismic parameters of both models. For
model A, parameters a1
and b1 are obtained at
1.2 ![]() and 2.8
and 2.8 ![]() of the observed values, respectively, causing a high value of
of the observed values, respectively, causing a high value of ![]() (see Fig. 1).
In contrast, for model B, a1
and b1 are fitted within 0.8
(see Fig. 1).
In contrast, for model B, a1
and b1 are fitted within 0.8
![]() and 0.2
and 0.2 ![]() ,
respectively. This results in a significant decrease of
,
respectively. This results in a significant decrease of ![]() for model B.
for model B.
3 Discussion of the results
3.1 Results of the fit
When considering an extension of the mixed zone associated to
the
early convective core induced by overshooting, we get a model that fits
all the observational constraints
better than within 1-![]() of the observed values. This decrease in the
of the observed values. This decrease in the ![]() value in fact stems from the survival of the convective core. Indeed,
model B has a convective core that extends over about
value in fact stems from the survival of the convective core. Indeed,
model B has a convective core that extends over about ![]() of the stellar
mass. The withdrawal of this core generates a discontinuity in the
chemical composition gradient, hence in the sound speed gradient (see
Fig. 2).
It has already been established that such a discontinuity induces an
oscillation of the mode frequencies as a function of the radial order
(see Gough
1990). Provost
et al. (1993)
derived the expressions of mode frequencies in the case of a
discontinuous sound speed profile near the center, in the asymptotic
approximation. Using the second-order development they propose, we
obtained (see Appendix A)
the following expression for
of the stellar
mass. The withdrawal of this core generates a discontinuity in the
chemical composition gradient, hence in the sound speed gradient (see
Fig. 2).
It has already been established that such a discontinuity induces an
oscillation of the mode frequencies as a function of the radial order
(see Gough
1990). Provost
et al. (1993)
derived the expressions of mode frequencies in the case of a
discontinuous sound speed profile near the center, in the asymptotic
approximation. Using the second-order development they propose, we
obtained (see Appendix A)
the following expression for ![]() :
:
![\begin{displaymath}\delta\nu_{01}(\nu)=\frac{A}{\nu}-B\sin \left[ 2\pi\frac{n'}{\mathcal{P}}+\varphi(\nu) \right]
\end{displaymath}](/articles/aa/full_html/2010/06/aa11991-09/img78.png)
|
(6) |
where n', A, B, and
where
When the amount of core overshooting increases, the acoustic
radius of
the discontinuity in the chemical composition gradient increases and
the period of the oscillation decreases (see Eq. (7)). Therefore,
the variations in
![]() become steeper. This shows that the behavior of
become steeper. This shows that the behavior of ![]() in the models that have a convective core can be adjusted by modifying
the extension of the core, e.g. by changing the overshooting
coefficient. With an appropriate value of
in the models that have a convective core can be adjusted by modifying
the extension of the core, e.g. by changing the overshooting
coefficient. With an appropriate value of
![]() ,
we can correctly fit the behavior
of
,
we can correctly fit the behavior
of ![]() and therefore reduce the
and therefore reduce the ![]() value.
We find
value.
We find ![]() for HD 203608.
This result provides new input for the studies that seek to establish
how convective core overshooting depends on the stellar mass (e.g. Claret 2007).
for HD 203608.
This result provides new input for the studies that seek to establish
how convective core overshooting depends on the stellar mass (e.g. Claret 2007).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11991fg2.eps}
\end{figure}](/articles/aa/full_html/2010/06/aa11991-09/Timg84.png)
|
Figure 2: Sound speed profile for the best model without overshooting (model A, dotted line), and the one with overshooting (model B, full line). A zoom of the curves shows the discontinuity at the edge of the convective core for model B. |
| Open with DEXTER | |
Stars in a range of mass half way between the presence and the absence
of a convective core, such as HD 203608, are interesting
objects
for studying core overshooting.
Indeed, if the seismic analysis of such a star can establish the
presence of a convective core, we obtain a firm lower bound for the
amount of mixing at the edge of the core.
In this case, the extension of the core can be derived from seismic
parameters, such as ![]() ,
and we get a precise estimate of
,
and we get a precise estimate of ![]() .
And if, on the contrary,
no convective core is found, a strong upper limit for the extent of the
region of extra mixing can be set.
.
And if, on the contrary,
no convective core is found, a strong upper limit for the extent of the
region of extra mixing can be set.
3.2 Survival of the core
The convective core of HD 203608 disappears at about
200 Myr
without overshooting, and survives until about 7 Gyr with
![]() .
We explain here this huge difference of longevity caused by
overshooting.
.
We explain here this huge difference of longevity caused by
overshooting.
3.2.1 Initial core
A convective core exists in main sequence models when the energy per
unit mass ![]() generated by nuclear burning in the center is too high to be
transported radiatively.
When the nuclear flux is larger than the maximum flux
generated by nuclear burning in the center is too high to be
transported radiatively.
When the nuclear flux is larger than the maximum flux ![]() that can be transported radiatively (corresponding to the radiative
flux in the case of critical stability for the Schwarzschild criterion,
i.e.
that can be transported radiatively (corresponding to the radiative
flux in the case of critical stability for the Schwarzschild criterion,
i.e. ![]() ),
convective motions transport part of the energy. To ensure the
existence of a convective core, we must have high values of the flux of
energy F(m) at low m,
i.e. a high value of
),
convective motions transport part of the energy. To ensure the
existence of a convective core, we must have high values of the flux of
energy F(m) at low m,
i.e. a high value of ![]() in the center. This condition is equivalent to having a steep
(negative) gradient
in the center. This condition is equivalent to having a steep
(negative) gradient ![]() in the center. Indeed, the star luminosity is almost entirely produced
in the most central parts. If it is generated with a gentle gradient of
in the center. Indeed, the star luminosity is almost entirely produced
in the most central parts. If it is generated with a gentle gradient of
![]() ,
the value of
,
the value of ![]() in the center will be moderate (which is the case for model A,
see Fig. 3).
Only with a steep gradient of
in the center will be moderate (which is the case for model A,
see Fig. 3).
Only with a steep gradient of ![]() can it reach higher values (see model B in Fig. 3). We
therefore use the gradient of
can it reach higher values (see model B in Fig. 3). We
therefore use the gradient of ![]() hereafter as an indicator of the existence of a convective core.
hereafter as an indicator of the existence of a convective core.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11991fg3.eps}
\end{figure}](/articles/aa/full_html/2010/06/aa11991-09/Timg90.png)
|
Figure 3:
Profile of the total energy production rate |
| Open with DEXTER | |
In most cases, we may assume that the energy production is dominated by
a given nuclear reaction chain. Thus, ![]() is proportional to
is proportional to ![]() ,
where
,
where ![]() is the density, X the hydrogen mass fraction, T
the temperature,
is the density, X the hydrogen mass fraction, T
the temperature, ![]() characterizes the temperature dependence of this specific reaction
chain and W is the mass fraction of the input element corresponding to
the reaction (see e.g. Hansen
& Kawaler 1994, chap. 6). We can then write
characterizes the temperature dependence of this specific reaction
chain and W is the mass fraction of the input element corresponding to
the reaction (see e.g. Hansen
& Kawaler 1994, chap. 6). We can then write
We then see that, to have a steep
For massive and intermediate-mass stars, the gradient of ![]() is steep due to the strong temperature dependence of the CNO cycle (
is steep due to the strong temperature dependence of the CNO cycle (
![]() ,
Hansen
& Kawaler 1994).
For HD 203608, when reaching the ZAMS, the temperature in the
center is of about
,
Hansen
& Kawaler 1994).
For HD 203608, when reaching the ZAMS, the temperature in the
center is of about ![]() (where
(where ![]() )
in our models. At that temperature, the dominant reactions are those of
the ppI chain. Since the pp reaction - 1H(p,e
)
in our models. At that temperature, the dominant reactions are those of
the ppI chain. Since the pp reaction - 1H(p,e![]() )2H
- is the slowest, its generation rate is proportional to that of the
whole ppI chain if it has achieved equilibrium. The temperature
sensitivity of the ppI chain at equilibrium is therefore the same as
that of the pp reaction
)2H
- is the slowest, its generation rate is proportional to that of the
whole ppI chain if it has achieved equilibrium. The temperature
sensitivity of the ppI chain at equilibrium is therefore the same as
that of the pp reaction ![]() .
Based on Caughlan
& Fowler (1988), we estimate
.
Based on Caughlan
& Fowler (1988), we estimate ![]() at our temperature. This is too weak for the star to have a convective
core. However, as pointed out by Roxburgh (1985),
the abundances of 3He and 12C
are in excess
compared to their equilibrium values when the star enters the main
sequence. The temperature sensitivities of the burning of 3He
to 4He and of 12C to 14N
outside of equilibrium are estimated to be
at our temperature. This is too weak for the star to have a convective
core. However, as pointed out by Roxburgh (1985),
the abundances of 3He and 12C
are in excess
compared to their equilibrium values when the star enters the main
sequence. The temperature sensitivities of the burning of 3He
to 4He and of 12C to 14N
outside of equilibrium are estimated to be ![]() and
and ![]() (Caughlan
& Fowler 1988). We therefore obtain a
(Caughlan
& Fowler 1988). We therefore obtain a ![]() about four times steeper than for the equilibrated ppI chain. This
ensures that an initial convective core is present.
about four times steeper than for the equilibrated ppI chain. This
ensures that an initial convective core is present.
3.2.2 Withdrawal of the core
To achieve equilibrium, the ppI chain requires that the ratio [3He]/[H] corresponds to its equilibrium value. This ratio can be computed by assuming that the deuterium is constantly in equilibrium, which is a good approximation since the destruction of D is much faster than the other reactions in the chain (see Clayton 1968). It is inversely proportional to the temperature. In the core, the temperature increases towards the center, and the abundance of 3He should decrease with r to achieve equilibrium. Since the elements are mixed in the convective core, the abundance of 3He is constant with r, and the reactions are kept outside of equilibrium. The temperature sensitivity therefore remains high, which favors convection. One can say that convection is self-sustained here.
However, ![]() also depends on the abundance of the reactant. As the star evolves, the
abundance of 3He in the core decreases since it
is destroyed faster than it is created.
Therefore,
also depends on the abundance of the reactant. As the star evolves, the
abundance of 3He in the core decreases since it
is destroyed faster than it is created.
Therefore, ![]() decreases, until the flux of nuclear energy becomes lower than
decreases, until the flux of nuclear energy becomes lower than ![]() and
the convective core disappears. This happens at an age of about
200 Myr for model A (without overshooting). When the
core
disappears, the ppI chain quickly achieves equilibrium (see
Fig. 4).
The temperature sensitivity becomes that of the ppI chain, which causes
and
the convective core disappears. This happens at an age of about
200 Myr for model A (without overshooting). When the
core
disappears, the ppI chain quickly achieves equilibrium (see
Fig. 4).
The temperature sensitivity becomes that of the ppI chain, which causes
![]() to
be less steep. Besides, the elements are no longer mixed
in the center, and in Eq. (8),
to
be less steep. Besides, the elements are no longer mixed
in the center, and in Eq. (8), ![]() and
and ![]() .
This also contributes to producing
a more gentle
.
This also contributes to producing
a more gentle ![]() .
.
3.2.3 Effect of an extension of the mixed zone associated to the core
The existence of a mixed zone at the boundary of the convective core modifies the abundances of elements in the center, and it was already suggested by Roxburgh (1985) that it should increase the lifetime of the core.
The peak we observe in the profile of the 3He abundance (see Fig. 4) is formed when the star reaches the ZAMS. It can be shown that the time required to achieve equilibrium is inversely proportional to the temperature (see Clayton 1968). To the left of the peak and outside the convective core, the ppI chain is already in equilibrium, and the abundance of 3He decreases towards the center because the temperature increases. To the right of the peak, the reactions are not in equilibrium yet, and the abundance of 3He decreases towards the surface since the nuclear reactions get less efficient because of decreasing temperature.
When adding a mixed zone at the edge of the core, we can see
in Fig. 4
that the abundance of 3He in the core
increases, owing to the peak we just mentioned. Consequently,
![]() increases. The convective core is therefore bigger and survives longer
than in the case without additional mixing. If the peak described above
did not exist, the mixing would not change the abundance of 3He
and would have little effect on the core lifetime.
No such peak exists for the 12C profile, and
its abundance is small because of the low metallicity of
HD 203608. The role of 12C is
negligible compared to that
of 3He in sustaining the core in the case of
HD 203608.
increases. The convective core is therefore bigger and survives longer
than in the case without additional mixing. If the peak described above
did not exist, the mixing would not change the abundance of 3He
and would have little effect on the core lifetime.
No such peak exists for the 12C profile, and
its abundance is small because of the low metallicity of
HD 203608. The role of 12C is
negligible compared to that
of 3He in sustaining the core in the case of
HD 203608.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11991fg4.eps}
\end{figure}](/articles/aa/full_html/2010/06/aa11991-09/Timg107.png)
|
Figure 4: Abundance of 3He in the center for two ages: 50 Myr ( left) and 200 Myr ( right). The dashed line stands for model A (without overshooting) and the solid line for model B (with overshooting). |
| Open with DEXTER | |
When adding overshooting to our models, we indeed observe an extension
of the core's lifetime. However, this extension is quite short. For
example, with ![]() ,
the core
disappears at an age of about 1 Gyr. In model B, the
core is still present at an age of about 7 Gyr with
,
the core
disappears at an age of about 1 Gyr. In model B, the
core is still present at an age of about 7 Gyr with ![]() .
This sudden increase of the
core lifetime for
.
This sudden increase of the
core lifetime for ![]() is in fact caused by the start of the ppII and ppIII reaction chains,
and later by the CNO chain, because of the increase in temperature in
the center
as the star evolves. If the 3He has kept the
convective
core going until the ppII chain begins to compete, the convection
prevents the ppII reactions from achieving equilibrium,
in exactly the same way as described above for the ppI chain.
The star starts burning 7Li through the
reaction 7Li(p,
is in fact caused by the start of the ppII and ppIII reaction chains,
and later by the CNO chain, because of the increase in temperature in
the center
as the star evolves. If the 3He has kept the
convective
core going until the ppII chain begins to compete, the convection
prevents the ppII reactions from achieving equilibrium,
in exactly the same way as described above for the ppI chain.
The star starts burning 7Li through the
reaction 7Li(p,![]() )4He
out of equilibrium, with a temperature sensitivity of
)4He
out of equilibrium, with a temperature sensitivity of ![]() ,
which sustains the core.
This is what happens for model B. If, on the contrary, the
convective core has already disappeared at that time, there is no more
mixing in the center
and the ppII reactions achieve equilibrium without triggering
convection. This is the case for model A.
,
which sustains the core.
This is what happens for model B. If, on the contrary, the
convective core has already disappeared at that time, there is no more
mixing in the center
and the ppII reactions achieve equilibrium without triggering
convection. This is the case for model A.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11991fg5.eps}
\end{figure}](/articles/aa/full_html/2010/06/aa11991-09/Timg113.png)
|
Figure 5:
Energy production rate |
| Open with DEXTER | |
We can see in Fig. 5
that the ppII chain makes a major contribution to the nuclear
production rate ![]() .
The importance of the CNO reactions is still small.
As mentioned above, the energy brought by the ppII chain is almost
entirely due to the burning of 7Li outside
equilibrium, with the other reactions contributing very little to
.
The importance of the CNO reactions is still small.
As mentioned above, the energy brought by the ppII chain is almost
entirely due to the burning of 7Li outside
equilibrium, with the other reactions contributing very little to ![]() .
If the star were only slightly more evolved, the CNO cycle would take
over, causing the convective core to grow.
.
If the star were only slightly more evolved, the CNO cycle would take
over, causing the convective core to grow.
3.3 Influence on the evolution
We notice that, even though the structure of the core is different for
our models with and without overshooting, their age is very comparable
(see Table 1).
This suggests that the survival of the convective core does
not significantly influence the global nuclear energy produced by
HD 203608 during its evolution. This constitutes a striking
difference with higher mass models, where overshooting is known to have
a strong impact on the evolution of the star, especially on its age,
for a given ![]() and L.
For high-mass stars, since the temperature dependence of the dominant
CNO cycle is large, it operates in a narrow area in the center, and the
wider convective core can act as a reservoir. For HD 203608,
the
pp chain is dominant, and its temperature dependence is much lower.
Therefore, the reactions take place in an area wider than the extent of
the convective core, and the mixing has less effect on the evolution.
and L.
For high-mass stars, since the temperature dependence of the dominant
CNO cycle is large, it operates in a narrow area in the center, and the
wider convective core can act as a reservoir. For HD 203608,
the
pp chain is dominant, and its temperature dependence is much lower.
Therefore, the reactions take place in an area wider than the extent of
the convective core, and the mixing has less effect on the evolution.
This means that it would be hopeless to try to characterize an
extension of the convective core in this type of star by classical
fundamental stellar parameters alone (
![]() ,
L, M), as was done by Claret
(2007) for higher masses.
,
L, M), as was done by Claret
(2007) for higher masses.
4 Conclusion
We present here a modeling of HD 203608 based on the analysis
of HARPS data performed in M08. Our main
result is that, on this basis,
we find strong evidence that this old low-mass star has a convective
core.
Models with convective cores enabled us to solve the disagreement with
observations
that was pointed out in M08 for models without convective cores,
bringing the ![]() function
from 9.1 to 0.8. All the observed parameters for HD 203608 are
now fitted within 1-
function
from 9.1 to 0.8. All the observed parameters for HD 203608 are
now fitted within 1-![]() error bars.
error bars.
In the case of our modeling of HD 203608, the value
obtained for the ![]() parameter (
parameter (
![]() )
is strongly constrained. Overshooting was here used as a proxy to model
the complex processes of transport
at the edge of a convective core, as is usually done in the present
state of stellar modeling.
Rather than finding a unique absolute value for
)
is strongly constrained. Overshooting was here used as a proxy to model
the complex processes of transport
at the edge of a convective core, as is usually done in the present
state of stellar modeling.
Rather than finding a unique absolute value for ![]() ,
the current aim is to try to observationally determine which values of
the
,
the current aim is to try to observationally determine which values of
the ![]() parameter
are needed to represent stars of different masses and evolution stages.
In this respect, the value obtained for HD 203608 constitutes
a
valuable input for
low-mass objects.
parameter
are needed to represent stars of different masses and evolution stages.
In this respect, the value obtained for HD 203608 constitutes
a
valuable input for
low-mass objects.
We discussed in detail how the existence of a convective core
in such an evolved
low-mass star can be explained by a reasonable amount of extra mixing
(modeled here as core overshooting) inducing the survival of the early
convective core. For low-mass stars such as HD 203608, an
early
convective core exists because of the burning of 12C
and 3He outside equilibrium. An extra mixing at
the edge of the core increases its lifetime, by bringing more 3He
to the center, as mentioned in Roxburgh (1985).
Here, we showed that, above a certain amount of overshooting (
![]() ),
the burning of 3He
out of equilibrium sustains the core until the ppII and ppIII reactions
take over. Convection prevents these reactions from achieving
equilibrium, and the burning of 7Li outside
equilibrium is currently keeping the core convective.
This is a transitional phase before the CNO cycle takes over.
),
the burning of 3He
out of equilibrium sustains the core until the ppII and ppIII reactions
take over. Convection prevents these reactions from achieving
equilibrium, and the burning of 7Li outside
equilibrium is currently keeping the core convective.
This is a transitional phase before the CNO cycle takes over.
The observation of low-mass stars can play a specific role in
the study
of extra mixing at the edge of stellar cores. Indeed, the presence or
absence of a convective core in these stars, which can be established
by seismic indicators such as the
![]() small spacing, strongly constrains the amount of mixing at the edge of
the core. This stresses the interest in observing this type of star
with ground-based observation campaigns or with the space mission COROT
(Baglin et
al. 2006).
small spacing, strongly constrains the amount of mixing at the edge of
the core. This stresses the interest in observing this type of star
with ground-based observation campaigns or with the space mission COROT
(Baglin et
al. 2006).
We are grateful to A. Noels for useful discussions about the nuclear reactions in the core of low-mass stars.
Appendix A: Expression of the small spacing 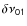 with a discontinuous sound speed profile
with a discontinuous sound speed profile
By neglecting the variations in the gravitational potential (Cowling
approximation) and using the asymptotic development derived in Tassoul
(1980), Provost
et al. (1993) obtained the expression of the
oscillation frequencies in the case of a discontinuous sound speed
profile.
The discontinuity is characterized by the parameter ![]() :
:
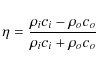
where the subscripts i and o describe the quantities at the edge of the convective core in the inner and outer regions. Provost et al. (1993) showed that under these assumptions and provided
with
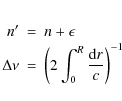
where n is the radial order of the mode and
Based on this, we can derive the following expression for ![]() :
:
As can be seen in Fig. 1, the mean value of the small spacing
where
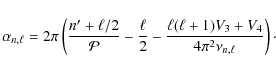
The Vj for j=1,4 are defined in Provost et al. (1993). They are of the same order of magnitude as
This can be rearranged in the form
![\begin{displaymath}\delta\nu_{01}(\nu)=\frac{A}{\nu}+B\sin \left[ 2\pi\frac{n'}{\mathcal{P}}+\varphi(\nu) \right]
\end{displaymath}](/articles/aa/full_html/2010/06/aa11991-09/img136.png)
|
(A.5) |
where
![\begin{eqnarray*}A & = & -\frac{V_1\Delta\nu}{2\pi^2} \\ %
B & = & -\frac{2\eta\...
...ac{V_3}{2\pi\nu} \right) \right] - \frac{V_3+V_4}{2\pi\nu}\cdot
\end{eqnarray*}](/articles/aa/full_html/2010/06/aa11991-09/img137.png)
With a discontinuous sound speed profile, the small spacing
References
- Baglin, A., Auvergne, M., Barge, P. et al. 2006, ESA Special Publication, 1306, 33
- Bevington, P. R., & Robinson, D. K. 2003, Data reduction and error analysis for the physical sciences, ed. P. R. Bevington, & K. D. Robinson, 3rd edn. (Boston, MA: McGraw-Hill)
- Brown, T. M., Christensen-Dalsgaard, J., Weibel-Mihalas, B., & Gilliland, R. L. 1994, ApJ, 427, 1013
- Canuto, V. M., & Mazzitelli, I. 1991, ApJ, 370, 295
- Caughlan, G. R., & Fowler, W. A. 1988, Atomic Data and Nuclear Data Tables, 40, 283
- Claret, A. 2007, A&A, 475, 1019
- Clayton, D. D. 1968, (New York: McGraw-Hill), 1968
- del Peloso, E. F., Cunha, K., da Silva, L., & Porto de Mello, G. F. 2005, A&A, 441, 1149
- Gough, D. O. 1990, Progress of Seismology of the Sun and Stars, 367, 283
- Hansen, C. J., & Kawaler, S. D. 1994, Stellar Interiors. Physical Principles, Structure, and Evolution, XIII
- Jonsell, K., Edvardsson, B., Gustafsson, B. et al. 2005, A&A, 440, 321
- Langer, N. 1986, A&A, 164, 45
- Lebreton, Y., Michel, E., Goupil, M. J., Baglin, A., & Fernandes, J. 1995, Astronomical and Astrophysical Objectives of Sub-Milliarcsecond Optical Astrometry, 166, 135
- van Leeuwen, F. 2007, Astrophysics and Space Science Library, 250,
- Maeder, A. 1976, A&A, 47, 389
- Michel, E., Baglin, A., Auvergne, M. 2006, ESA Special Publication, 1306, 39
- Miglio, A., & Montalbán, J. 2005, A&A, 441, 615
- Monteiro, M. J. P. F. G., Christensen-Dalsgaard, J., & Thompson, M. J. 1994, A&A, 283, 247
- Morel, P. 1997, A&AS, 124, 597
- Mosser, B., Deheuvels, S., Michel, E., et al. 2008, A&A, 488, 635
- Mowlavi, N. 1993, IAU Colloq. 137: Inside the Stars, 40, 454
- Ozel, N., Dupret, M. A., Michel, E., & Baglin, A. 2009, A&A, submitted
- Provost, J., Mosser, B., & Berthomieu, G. 1993, A&A, 274, 595
- Ribas, I., Jordi, C., & Giménez, Á. 2000, MNRAS, 318, L55
- Roxburgh, I. W. 1985, Sol. Phys., 100, 21
- Schaller, G., Schaerer, D., Meynet, G., & Maeder, A. 1992, A&AS, 96, 269
- Scuflaire, R., Montalbán, J., Théado, S., et al. 2008, Ap&SS, 316, 149
- Shaviv, G., & Salpeter, E. E. 1971, ApJ, 165, 171
- Sienkiewicz, R., Bahcall, J. N., & Paczynski, B. 1990, ApJ, 349, 641
- Tassoul, M. 1980, ApJS, 43, 469
- Xiong, D. R. 1985, A&A, 150, 133
- Zahn, J.-P. 1991, A&A, 252, 179
All Tables
Table 1: Physical and seismic parameters of HD 203608.
All Figures
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11991fg1.eps}
\end{figure}](/articles/aa/full_html/2010/06/aa11991-09/Timg35.png)
|
Figure 1:
Variations in the small spacing |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11991fg2.eps}
\end{figure}](/articles/aa/full_html/2010/06/aa11991-09/Timg84.png)
|
Figure 2: Sound speed profile for the best model without overshooting (model A, dotted line), and the one with overshooting (model B, full line). A zoom of the curves shows the discontinuity at the edge of the convective core for model B. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11991fg3.eps}
\end{figure}](/articles/aa/full_html/2010/06/aa11991-09/Timg90.png)
|
Figure 3:
Profile of the total energy production rate |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11991fg4.eps}
\end{figure}](/articles/aa/full_html/2010/06/aa11991-09/Timg107.png)
|
Figure 4: Abundance of 3He in the center for two ages: 50 Myr ( left) and 200 Myr ( right). The dashed line stands for model A (without overshooting) and the solid line for model B (with overshooting). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11991fg5.eps}
\end{figure}](/articles/aa/full_html/2010/06/aa11991-09/Timg113.png)
|
Figure 5:
Energy production rate |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



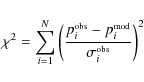
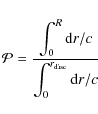
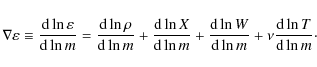
![\begin{displaymath}\nu_{n,\ell}=\left[ n' +\frac{\ell}{2} -\frac{\eta}{\pi}\sin ...
...+\ell/2}{\mathcal{P}} - \frac{\ell}{2}\right) \right]\Delta\nu
\end{displaymath}](/articles/aa/full_html/2010/06/aa11991-09/img119.png)
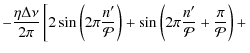
![$\displaystyle \left. \sin \left( 2\pi \frac{n'}{\mathcal{P}} - \frac{\pi}{\mathcal{P}} \right) \right]$](/articles/aa/full_html/2010/06/aa11991-09/img125.png)
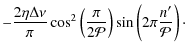
![\begin{displaymath}\nu_{n,\ell}=\left[ n'+\frac{\ell}{2}+\frac{\ell(\ell+1)V_1+V...
...{n,\ell}} -\frac{\eta}{\pi}\sin\alpha_{n,\ell}\right]\Delta\nu
\end{displaymath}](/articles/aa/full_html/2010/06/aa11991-09/img127.png)
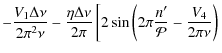
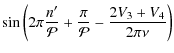
![$\displaystyle \left. \sin \left( 2\pi \frac{n'}{\mathcal{P}} - \frac{\pi}{\mathcal{P}} - \frac{2V_3+V_4}{2\pi\nu}\right) \right]$](/articles/aa/full_html/2010/06/aa11991-09/img132.png)
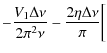
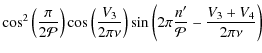
![$\displaystyle \left. \sin^2 \left( \frac{\pi}{2\mathcal{P}} \right) \sin \left(...
...\left( 2\pi\frac{n'}{\mathcal{P}} -\frac{V_3+V_4}{2\pi\nu} \right) \right]\cdot$](/articles/aa/full_html/2010/06/aa11991-09/img135.png)