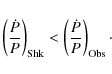EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 514 (May 2010) A&A, 514 (2010) A74 Full HTML
Free Access
Issue
A&A
Volume 514, May 2010
Article Number A74
Number of page(s) 9
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/200911728
Published online 21 May 2010
A&A 514, A74 (2010)

Long-term timing of four millisecond pulsars

G. H. Janssen1,2 - B. W. Stappers1,2,3 - C. G. Bassa1,4,5 - I. Cognard6 - M. Kramer7,1 - G. Theureau6,8

1 - Jodrell Bank Centre for Astrophysics, School of Physics and Astronomy, University of Manchester, Manchester M13 9PL, UK
2 - Astronomical Institute ``Anton Pannekoek'', University of Amsterdam, Postbus 94249, 1090 GE Amsterdam, The Netherlands
3 - Stichting ASTRON, Postbus 2, 7990 AA Dwingeloo, The Netherlands
4 - SRON, Sorbonnelaan 2, 3584 CA Utrecht, The Netherlands
5 - Department of Astrophysics/IMAPP, Radboud University Nijmegen, PO Box 9010, 6500 GL Nijmegen, The Netherlands
6 - Laboratoire de Physique et Chimie de l'Environnement, CNRS, 3A Avenue de la Recherche Scientifique, 45071 Orléans Cedex 2, France
7 - Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
8 - Galaxies, Étoiles, Physique, Instrumentation, CNRS URA 1757, 92195 Meudon Principal Cedex, France

Received 26 January 2009 / Accepted 15 February 2010

Abstract
We have timed four millisecond pulses, PSRs J1721-2457, J1745-0952, J1810-2005, and J1918-0642, for up to a total of 10.5 years each using multiple telescopes in the European Pulsar Timing Array network: the Westerbork Synthesis Radio Telescope in The Netherlands, the Nançay Radio Telescope in France and the Lovell telescope at Jodrell Bank in the UK. The long time span has enabled us to measure the proper motions of J1745-0952 and J1918-0642, indicating that they have transverse velocities of 200(50) and 54(7) km s-1 respectively. We have obtained upper limits on the proper motion of J1721-2457 and J1810-2005, which imply that they have transverse velocities less than 140 and 400 km s-1 respectively. In all cases, the velocities lie in the range typical of millisecond pulsars. We present pulse profiles for each pulsar taken from observations at multiple frequencies in the range of 350 to 2600 MHz, and show that J1810-2005 shows significant profile evolution in this range. Using our multi-frequency observations, we measured the spectral indices for all four pulsars, and for J1810-2005 it appears to be very flat. The flux density of J1918-0642 shows extensive modulation which we attribute to the combined effects of refractive and diffractive scintillation. We discuss the possible use of including J1721-2457 or J1918-0642 in a pulsar timing array, and find that J1918-0642 will be useful to include when the timing precision of this pulsar is improved over the next few years. We have searched archival optical observations to detect companions of the binary pulsars, but none were detected. However, we provide lower limits on the masses of the white dwarf companions of PSRs J1745-0952 and J1918-0642.

Key words: stars: neutron - pulsars: general - pulsars: individual: J1721-2457 - pulsars: individual: J1745-0952 - pulsars: individual: J1810-2005 - pulsars: individual: J1918-0642

1 Introduction

In this paper we present improved timing solutions for four millisecond pulsars (MSPs): PSRs J1721-2457, J1745-0952, and J1918-0642, discovered by Edwards & Bailes (2001), and J1810-2005, that was discovered by Camilo et al. (2001). Long-term timing of MSPs is an important tool to determine masses of the individual stars in binary systems, and by constraining secular effects like proper motion, it can be used to improve statistics on the evolution of these systems.

In general, masses of pulsars are not easy to determine. In some cases, when the pulsar is in a binary with another compact object, high precision pulsar timing observations on extended timescales can allow for detecting post-Keplerian parameters of the systems, which can be used to separately measure the individual masses of the stars. Space velocities derived from proper motion measurements of radio pulsars give clues about the evolution of these systems and their birth supernovae (e.g. Toscano et al. 1999; Hobbs et al. 2005; Lorimer 2008). It is believed that recycled pulsars have lower space velocities than normal, slowly rotating pulsars. However as MSPs are generally the most stable rotators, the effects of their space velocities on their rotational and orbital parameters will be easier to derive from timing measurements of those systems and could be used to deduce the intrinsic properties of the stars.

Table 1:   Timing solutions for the pulsars.

Another interesting and important use of timing MSPs to high precision, is the formation of a pulsar timing array (PTA, e.g. Janssen et al. 2008b; Hobbs et al. 2008). An instrument like this will use an array of MSPs as the endpoints of a Galaxy-scale gravitational wave (GW) detector. Current estimates predict that to detect a GW background, long-term high precision timing of about 20 MSPs is required (Jenet et al. 2005; Van Haasteren et al. 2009). Increasing the number of stable MSPs in the array will improve the detection significance. In order to better understand these systems in general, and to determine their suitability for inclusion in a timing array, their long-term timing behaviour needs to be determined. Moreover, the best frequency at which they should be timed needs to be ascertained. This is a combination of the pulse shape at these frequencies and their intensity. We observed all four pulsars at additional frequencies to find their best possible observing frequency for timing purposes, and discuss their suitability for inclusion in a PTA.

Three of the pulsars that are presented in this paper are in low-eccentricity binary systems with white dwarf companions (see Table 1). These systems are usually classified as low-mass binary pulsars (LMBPs). The LMBPs distinguish themselves from intermediate-mass binary pulsars (IMBPs) in having shorter periods (<10 ms), very low eccentricities (<10-5), and they follow relationships between their orbital period and the eccentricity of their orbit, and their orbital period and the companion mass (Thorsett & Chakrabarty 1999). The origin of the difference between these two classes of binary MSPs is believed to be an evolutionary effect, and mainly due to the progenitor masses of the companion stars. There are now $\sim$65 MSP binary pulsars with probable white dwarf companions known (e.g. Lorimer 2008) and about 16 of these can be regarded as IMBP candidates (Jacoby et al. 2006).

Detecting an optical counterpart to one of the binary pulsars allows to derive properties of their white dwarf companions. Because of differences in the cooling properties of white dwarfs in LMBPs and IMBPs, optical observations can in some cases be used to distinguish between the two classes (e.g. van Kerkwijk & Kulkarni 1995). So far, for all three binary pulsars described in this paper, the most recently published limit on optical magnitude of the companion is R>24 (van Kerkwijk et al. 2005).

2 Pulsar timing observations and data analysis

2.1 Westerbork

The pulsars were observed approximately monthly using the pulsar machines at the Westerbork Synthesis Radio Telescope (WSRT): PuMa (Voûte et al. 2002) since August 1999, and PuMaII (Karuppusamy et al. 2008) since August 2006. The WSRT has three frequency ranges allocated for pulsar timing; for observations centred at 350 MHz we use two bands of 10 MHz wide, and observations centred at 1380 or 2300 MHz use 80 MHz of bandwidth, spread in 8 steps of 10 MHz over a range of 160 MHz. The new pulsar machine uses the full 80 MHz bandwidth at the low frequencies, and all of the available 160 MHz bandwidth at 1380 and 2300 MHz. For all four pulsars presented here, we mainly used the 1380 MHz band as the pulsars were detected in this band, and there are no other reports of detections in other bands. Also this is the best available band for timing at the WSRT as it has the best sensitivity. For completeness, we observed all pulsars for one hour at 350 and 2300 MHz, see Fig. 1.

\begin{figure} \par\includegraphics[width=11cm,angle=270]{11728fg1.ps} \vspace*{1.5mm} \end{figure} Figure 1:

Profiles for the PSRs at multiple frequencies. All profiles were generated from a single 55 min observation using PuMaII, except the 1380 MHz profiles of PSRs J1721-2457, J1745-0952 and J1810-2005 that used 10 to 12 h of PuMaII observations, and the 2600 MHz profile of PSR J1745-0952 was generated from a 50 min Nançay observation. These profiles are to show their appearance; for timing purposes we used high S/N templates as described in the text.

Open with DEXTER

For a complete description of the PuMa data analysis, we refer to Janssen et al. (2008a). Analysis of the PuMaII data was carried out using the PSRCHIVE (Hotan et al. 2004) software suite. For both instruments, each profile was cross-correlated with a standard profile at the corresponding observing frequency (Fig. 1), obtained from the summation of high signal-to-noise (S/N) profiles, to calculate a time of arrival (TOA) for each observation. These were referred to local time using time stamps from a H-maser at WSRT and converted to UTC using global positioning system (GPS) maser offset values measured at the observatory, and GPS to UTC corrections from the Bureau International des Poids et Mesures (BIPM)[*]. The TOAs were converted to the Solar system barycentre using the JPL ephemeris DE405[*]. We used the TEMPO2 timing software package (Hobbs et al. 2006) to analyse the data.

Flux densities were calculated for the WSRT observations by using the aforementioned bandwidth and observing times, the measured S/N ratio for each profile, the gain of the WSRT (1.2 K/Jy), the pulse duty cycle ($\sim$10%), the system temperature and the pulsar specific radiometer equation (Dewey et al. 1985). The total system temperature was determined from the synthesis data that is taken in parallel with the pulsar observations.

2.2 Nançay

PSR J1721-2457, J1745-0952 and J1918-0642 were observed roughly every 3 to 4 weeks with the Nançay Radio Telescope (NRT) since 2006.

Equivalent to a 93-m dish, the Nançay Radio Telescope and the BON (Berkeley-Orléans-Nançay) coherent dedispersor were used for typical integration times of 45 min. Coherent dedispersion of a 64 MHz band centred on 1398 MHz was carried out on sixteen 4 MHz channels using a PC-cluster in the period covered by the observations. The Nançay data are written with timestamps which are directly tied to UTC(GPS) in realtime, using a Thunderbolt receiver (Trimble Inc.), when converting from an analogue to digital signal is performed. Differences between UTC and UTC(GPS) are less than 10 ns at maximum, and therefore no laboratory clock corrections are needed. One TOA was calculated from a cross-correlation with a pulse template for each observation of $\sim$45 min.

The flux densities for the Nançay data were calculated in a similar way to those for the WSRT except that the system temperature was determined from the known receiver temperature and sky temperature in the direction of the source. The gain of the NRT is 1.4 K/Jy.

2.3 Jodrell bank

PSR J1810-2005 was observed at Jodrell Bank since November 1997, and PSR J1918-0642 since February 2008. Both pulsars were observed every two weeks at a centre frequency around 1400 MHz. The gain of the Lovell telescope is 1 K/Jy.

The polarized signals from the receiver were were fed into an analogue filterbank system with $2 \times 32 \times 1$ MHz channels, and filtered and digitised at appropriate sampling intervals and incoherently dedispersed in hardware. The resulting dedispersed timeseries were folded on-line with the topocentric pulsar period and finally written to disc. In the off-line reduction, the two polarisations were summed to form total-intensity profiles. A standard high S/N pulse template was used to determine a TOA for each observation. During this process, TOAs were referred to the local H-maser time-standard and already corrected to UTC using information obtained via the GPS.

3 Pulsar timing results and discussion

We present new timing solutions for the pulsars in Table 1, based on 7.5 to 10.5 years of radio pulsar timing as described in Sect. 2. The vast majority of our timing data were taken using a centre frequency around 1380 MHz, and therefore originally only the timing variation across the observing bandwidth was used to measure the dispersion measure (DM) of the four pulsars. As the combined data sets of WSRT and Nançay or Jodrell Bank together cover more than 200 MHz of bandwidth, the DM was already determined with good accuracy using only that data. However, to allow for refining the DM value even more, and to study the pulse shape and flux densities at other frequencies, we also observed the pulsars at 350 MHz and 2.3 GHz. This resulted in a few detections, see Fig. 1.

For PSRs J1745-0952, J1810-2005 and J1918-0642, all in very low-eccentricity binaries, we have used the ELL1 timing model (Lange et al. 2001) to avoid the high degree of covariance between the epoch and longitude of periastron.

We have measured significant proper motions for PSRs J1918-0642: $\mu_{\rm T} = 9.2(2)$ mas yr-1 and J1745-0952: $\mu_{\rm T} = 24(2)$ mas yr-1. By combining those proper motions with the DM-derived distances from the Cordes & Lazio (2002) model, we have calculated transverse velocities for those systems. For the other two pulsars, we use the marginally significant values from the timing solution to calculate a limit on their transverse velocities, see Sect. 3.1.

3.1 Proper motion and velocity

We use our proper motion measurements to derive transverse velocities, or limits on those, for all four pulsars (see Table 1). We have a highly significant measurement of the proper motion of PSR J1918-0642, and a significant detection in right ascension for PSR J1745-0952. The proper motion values as presented for the other two pulsars are not significant. We note that both PSR J1721-2457 and J1810-2005 have ecliptic latitudes very close to the ecliptic plane ( $\beta=-1\hbox{$.\!\!^\circ$ }8$and $3\hbox{$.\!\!^\circ$ }3$ respectively), and therefore their proper motions may be better and more independently fit in ecliptic parameters. However, as the coordinate systems are nearly parallel because both pulsars are near $\alpha = 18^{\rm h}$, fits in this coordinate system did not result in an improvement of the limits on their proper motions, or the significance of their positions. As both of these pulsars lie quite close to the ecliptic, it may be that they will show effects due to the solar wind (You et al. 2007). However at the present timing precision we see no influence on the observed TOAs.

Due to changes in the projected line of sight, transverse motions of pulsars can affect observed periodicities in the system (Shklovskii 1970). We present the contributions to the spin period derivative of each pulsar in Table 2. For completeness, the contributions to the observed $\dot P$ from accelerations in the Galactic potential are also presented, although those are not important effects for these pulsars. To calculate the magnitude of the Shklovskii term we have used the total proper motion values as presented in Table 1. For PSR J1918-0642, the contribution to its spin period derivatives, $\dot P_{\rm Shk}$, from proper motion is less than $8\%$of the observed value. However for PSR J1745-0952, the effect can be as large as 50% of the observed value, leading to an underestimation of the characteristic age and an overestimation of the magnetic field. Moreover, as the proper motions for the solitary pulsar J1721-2457 and PSR J1810-2005 have not been determined significantly yet, the Shlovskii term may even completely dominate the observed $\dot P$ for those pulsars. To calculate an upper limit for the proper motion, and accordingly a limit to the transverse velocity, we can use the observed $\dot P$ as a maximum:

\begin{displaymath} \left(\frac{\dot P}{P}\right)_{\rm Shk} < \left(\frac{\dot P}{P}\right)_{\rm Obs}\cdot \end{displaymath} (1)

This yields $\mu_{\rm T} < 23$ mas yr-1 and $V_{\rm T} < 140$ km s-1 for PSR J1721-2457 and $\mu_{\rm T} < 22$ mas yr-1 and $V_{\rm T} < 400$ km s-1 for PSR J1810-2005.

Table 2:   Contributions to the period derivative.

About 50% of the known solitary and low-eccentricity binary pulsars have measured transverse velocities (Tables 2 and 4 in Lorimer 2008). Hobbs et al. (2005) quote mean values of 2D speeds of 77(16) km s-1 for solitary MSPs and 89(15) km s-1 for binary MSPs. Compared to those, the (limits on) transverse velocities that we have derived from the proper motion measurements represent normal velocities for recycled pulsars.

3.2 Profiles

Apart from our normal timing observing frequency of 1380 MHz, we have observed all four pulsars at additional frequencies: 350 MHz and 2300 MHz. The results are shown in Fig. 1. It is now standard procedure for WSRT timing observations of MSPs to use both pulsar machines, and as we havetwice the bandwidth available in PuMaII, we present the profile of the detected pulsars at 350 MHz and 2.3 GHz from that data, see Fig. 1. Single observations of 55 min were used to generate the profiles at 350 and 2300 MHz. Where no profile is plotted, the pulsar was not seen at that frequency. The profiles at 1380 MHz were generated using one year of regular timing observations and consist of 10 to 12 observations of 25 min, except for PSR J1918-0642, where again one observation of 55 min. was used. PSR J1745-0952 was detected with NRT at 2600 GHz in an observation of 50 min.

As reported by Kramer et al. (1998), for most MSPs there is very little development of pulse profiles with frequency, which can be explained by MSPs having a very compact magnetosphere. For all pulsars except PSR J1810-2005, we indeed see no changes in the pulse profile with changing frequency, except for changes in the ratios of the heights of some components, within the significance of our detections. Compared to its profile at 1380 MHz, the 2300 MHz profile of PSR J1810-2005 appears to have more components in the main peak. Also the profile appears to show a leading component about 70 degrees before the main peak, although higher S/N will be needed to confirm this. Of all the MSP profiles presented by Kramer et al. (1999) none show more complex profiles at higher frequencies than at lower frequencies. Thus a further study of the profile of PSR J1810-2005 and its polarisation properties could reveal more about MSP emission profiles. The extra features in the peak of the high-frequency profiles of PSR J1810-2005 could be an indication that the profile at 1380 MHz suffers from scattering effects. However, the Cordes & Lazio (2002) model predicts very little scattering for this pulsar at both 1380 MHz (0.26 ms) and 2300 MHz (0.03 ms) suggesting that the features in the main peak of the pulse profile are intrinsic to the pulsar. It may turn out that, when better sensitivity can be achieved at higher frequencies, PSR J1810-2005 will give better timing results compared with the more commonly used 1380 MHz as its profile shows more features at higher frequencies.

3.2.1 Useful for pulsar timing array?

PSR J1721-2457 shows very stable rotational behaviour. All parameters of the timing solution presented in Table 1 are consistent with the original timing solution as published by Edwards & Bailes (2001). However, for the present S/N ratio, the wide profile of this pulsar does not allow for the high timing precision that is required for PTA pulsars (Jenet et al. 2005).

In contrast, despite its relatively long spin period compared to most pulsars considered for PTA studies, PSR J1918-0642 may be worthwile to include. Already at 1380 MHz the profile has a very sharp peak, allowing for very precise timing over 7.5 years (rms = 2.3 $\mu$s). Furthermore, it is possible that better results for pulsar timing arrays may be deduced by including not only the best-timing pulsars, but extending the PTA pulsar set with pulsars that have timing solution with rms $\sim$1 $\mu$s (Jenet et al. 2005; Van Haasteren et al. 2009). The pulse profile as shown in Fig. 1 was generated by the PuMaII machine in WSRT, promising even better timing precision in the ongoing timing programme. Observations with PuMaII use twice the bandwidth of those with PuMaI and so give an increase in the sensitivity. Moreover, because PuMaII uses coherent dedispersion, it yields a sharper profile. The combination of these effects should lead to an improvement in the timing precision of a factorbetween 2 and 4 for this pulsar over the next five years which may bring it to the required level for a PTA pulsar.

3.3 Flux density and scintillation

Table 3:   Flux densities and spectral index.

We calculated flux densities for the four pulsars as described in Sect. 2.1, based on the profiles as shown in Fig. 1, see Table 3. We note that apart from those at 21 cm, the profiles are generated from single observations only, and therefore the resulting flux densities should not be regarded as accurate measurements, but are indicative of the intensities of the pulsars at the observed frequencies. The spectral indices for these pulsars are normal except for PSR J1810-2005, which appears to have a relatively flat spectrum. We observed this pulsar a couple of times at 2.3 GHz, and the resulting flux densities were varying by a factor 2, indicating that the brightness of this pulsar may be affected by scintillation.

Not long after we began our observations of PSR J1918-0642 we noticed that there were a number of occasions when we either did not detect the pulsar at all or it was extremely bright. A plot of the flux densities determined from all observations is shown in Fig. 2.

\begin{figure} \par\includegraphics[angle=-90,width=17cm,clip]{11728fg2} \vspace*{7mm} \end{figure} Figure 2:

Flux density variations of PSR J1918-0642 obtained with the WSRT and NRT from observations made at 21 cm. The left panel shows the distribution of flux densities from the two observatories, where the leftmost column represent all non-detections. In the right panel we show the individual flux density values as a function of time, where the length of the line in each case is proportional to the flux density, as indicated in the legend. Observations where there was no clear detection (ND) of the pulsar and thus only an upper limit on the flux density can be determined, are plotted with a cross.

Open with DEXTER

The left hand panel shows a histogram of flux values from both Nançay and WSRT observations with the non-detections in the WSRT data shown in the far left hand bin. The right hand panel shows the variation in flux density as a function of time indicating the variations are typically on short timescales, although a long period of non-detections can be seen in 2006-2007. We note that the pulsar is not detected in approximately 20% of all WSRT observations. The pulsar is always detected, although sometimes with very low S/N ratio, in the Nançay data. This is not suprising due to the higher gain and longer integration times for the Nançay observations meaning that the NRT is approximately 30% more sensitive than the WSRT for this pulsar.

If these flux variations are due to scintillation then the quite frequent non-detections would suggest that the scintillation bandwidth must be at least as wide as the PuMaI bandwidth of 80 MHz. For the dispersion measure of this pulsar at this observing frequency such a large scintillation bandwidth seemed too large to be diffractive (Rickett 2001). Checking the literature, we found four pulsars with similar dispersion measures which had measured diffractive scintillation bandwidths in the range 15-70 MHz (Wang et al. 2005; Johnston et al. 1998) at 21 cm. While this is a large range the diffractive scintillation bandwidth would need to be above the highest measured value to explain the observed flux variations.

\begin{figure} \par\mbox{\includegraphics[width=8.8cm,clip]{11728f3a} \includegraphics[width=8.8cm,clip]{11728f3b} }\end{figure} Figure 3:

Dynamic spectra of PSR J1918-0642 plotted as a greyscale of intensity as a function of time and frequency. Darker pixels correspond to higher intensity values and the intensity scales linearly with the levels of grey. The dynamic spectra are from two observations made using PuMaII on 23 February 2008 ( left) and 24 March 2008 ( right).

Open with DEXTER

Using the improved bandwidth of our PuMaII measurements we were able to better explain the scintillation properties of PSR J1918-0642. In Fig. 3 we show the dynamic spectra from two observations of PSR J1918-0642, separated by just one month. The left hand side shows a classic case of scintillation with a scintillation bandwidth of approximately 5 MHz. Comparing this value to the range of bandwidths seen for similar dispersion measure pulsars, as discussed earlier, it is a factor of three smaller than the lowest measured scintillation bandwidth. In contrast, the right hand plot shows just a single scintle, which is perhaps somewhat broader than 5 MHz, across the full 160 MHz of bandwidth. It may be possible that these variations are purely statistical in nature, although the lack of any scintles in the band of at least 80 MHz in width, appears to happen about 20% of the time. We note that Gupta et al. (1994) explain variations in the scintillation properties like this as being to the refractive modulation of the diffractive interstellar scintillation pattern. While beyond the scope of this paper, the techniques outlined by Gupta et al. (1994) could be used to further examine the relationship between the velocities in this system and the interstellar medium along the line of sight. We note also that very wide bandwidth observations of this pulsar provide the best opportunity to do high precision timing, as when the pulsar is bright it can be timed to high precision.

\begin{figure} \par\mbox{\includegraphics[width=8.8cm]{11728f4a} \includegraphics[width=8.8cm]{11728f4b} }\end{figure} Figure 4:

$45\hbox {$^{\prime \prime }$ }\times 45\hbox {$^{\prime \prime }$ }$ subsections of the deep images of PSR J1745-0952 (left) and PSR J1810-2005 (right). To retain visibility, the pulsar positions are denoted by a circles with a $1\hbox {$^{\prime \prime }$ }$ radius, even though the actual error ellipses are considerably smaller than this.

Open with DEXTER

4 Optical observations

We have analysed archival observations of PSR J1745-0952 and PSR J1810-2005. These observations were obtained with the ESO Multi-Mode Instrument (EMMI) at the 3.6 m telescope of the European Southern Observatory at La Silla, Chile on March 15th, 2004. The instrument has two 2K $\times$ 4K detectors which were read out with $2\times2$ binning, providing a pixel scale of $0\hbox{$.\!\!^{\prime\prime}$ }33$ pix-1. The observations consisted of two 10 min. R-band exposures of PSR J1745-0952 and two 5 min. R-band exposures for PSR J1810-2005. For both pulsars, these long exposures were preceded by short (10 s) exposures, also in the R-band. The seeing during these observations was about $0\hbox{$.\!\!^{\prime\prime}$ }86$to $0\hbox{$.\!\!^{\prime\prime}$ }88$. All images were bias-subtracted and flat-fielded using twilight flats. The two deep images of each pulsar were averaged and used for further analysis.

The short 10 s observations were astrometrically calibrated against the 2nd version of the USNO CCD Astrograph Catalog (UCAC2, Zacharias et al. 2004). For the PSR J1745-0952 observations, 34 UCAC2 stars overlapped with the chip on which the pulsar was located, of which 26 were not saturated and appeared stellar and unblended, giving rms residuals of $0\hbox{$.\!\!^{\prime\prime}$ }056$ in right ascension and $0\hbox{$.\!\!^{\prime\prime}$ }091$ in declination. A secondary astrometric catalog was created from the stars on the short exposure and used to calibrate the average of the two 10 min exposures. For the transfer, about 300 stars were used, giving residuals of $0\hbox{$.\!\!^{\prime\prime}$ }022$ in right ascension and $0\hbox{$.\!\!^{\prime\prime}$ }025$in declination. Combined with the uncertainty on the timing position of the pulsar, the quadratic uncertainty of the pulsar position on the deep optical image is $0\hbox{$.\!\!^{\prime\prime}$ }060$ in right ascension and $0\hbox{$.\!\!^{\prime\prime}$ }096$in declination. For PSR J1810-2005, we used 23 of the 32 overlapping UCAC2 stars, giving rms residuals of $0\hbox{$.\!\!^{\prime\prime}$ }049$ in right ascension and $0\hbox{$.\!\!^{\prime\prime}$ }091$ in declination. The transfer of the secondary catalog to the deeper average of the two 5 min 180 secondary standards, giving residuals of $0\hbox{$.\!\!^{\prime\prime}$ }028$ in right ascension and $0\hbox{$.\!\!^{\prime\prime}$ }018$ in declination. The final uncertainty on the pulsar position on the deep image is $0\hbox{$.\!\!^{\prime\prime}$ }058$ in right ascension and $0\hbox{$.\!\!^{\prime\prime}$ }220$ in declination. No sources are present in the error circles of both pulsars, as shown in Fig. 4.

In order to determine upper limits on the brightness of the pulsar companions, we performed PSF photometry on the averaged deep images using DAOPHOT II (Stetson 1987). The resulting instrumental magnitudes were calibrated against 47 standard stars in the PG 1525-071 using the calibrated magnitudes of Stetson (2000). Since only R-band observations were taken, only the zeropoint was fitted for the calibration, giving rms residuals of 0.02 mag. The standard La Silla R-band extinction of 0.07 mag per airmass was used to correct for extinction between the standard observations taken at an airmass of 1.08 and the pulsar observations taken at an airmass of 1.34 (for PSR J1745-0952) and 1.25 (for PSR J1810-2005). Based on the magnitudes and uncertainties of faint stars in the images, we estimate the 3$\sigma$ detection limit at R>24.49 for PSR J1745-0952 and R>24.02 for PSR J1810-2005.

4.1 Model predictions

Though no optical counterparts to PSR J1745-0952, PSR J1810-2005 and PSR J1918-0642 (R>24, see van Kerkwijk et al. 2005) were detected, it is still worthwhile to compare the upper limits on the white dwarf magnitudes with those predicted by models. To convert the upper limits on the apparent magnitudes to limits on the absolute magnitude, we need estimates for the distance and absorption. Estimates for the distance to each pulsar using the observed dispersion measure and the Cordes & Lazio (2002) model for the Galactic distribution of electrons are given in Table 1. The V-band absorption AValong the line-of-sight and at the distance of each pulsar was estimated using the Drimmel et al. (2003) model for Galactic extinction and converted to R-band absorption AR using the extinction coefficients of Schlegel et al. (1998) ( AR=0.819AV). We estimate upperlimits on the absolute R-band magnitude of MR>11.3 for PSR J1745-0952, MR>3.3 for PSR J1810-2005 and MR>12.7 for PSR J1918-0642.

\begin{figure} \par\includegraphics[width=8.8cm,clip]{11728fg5} \vspace*{4mm} \end{figure} Figure 5:

Absolute R-band magnitude and cooling age predictions. Shown are helium-core white dwarf cooling tracks by Rohrmann et al. (2002) and carbon-oxygen white dwarf cooling tracks with hydrogen-rich atmospheres by Bergeron et al. (1995) ($\log g=8$ corresponds to $M_{\rm c}\approx0.6~M_\odot$ while $\log g=9$ corresponds to $M_{\rm c}\approx1.2~M_\odot$). Helium-core models with masses below approximately 0.18-0.20 $M_\odot $ have thick hydrogen envelopes and continue to residually burn hydrogen, keeping the white dwarf hot and slowing the cooling. Heavier models have thin hydrogen envelopes and cool much faster, creating a dichotomy in the cooling properties of white dwarf companions to millisecond pulsars. White dwarfs with carbon-oxygen cores cool even faster. Shown with error bars are PSR J0218+4232 (Bassa et al. 2003), PSR J0437-4715 (Danziger et al. 1993), PSR J0751+1807 (Bassa et al. 2006) and PSR J1012+5307 (Lorimer et al. 1995), where the white dwarf cooling age is assumed to be equal to the characteristic age of the pulsar (using braking indices of n=3). Shown with upper limits on the absolute R-band magnitude are the values for PSR J1745-0952 and PSR J1918-0642. For these two pulsars, thick hydrogen envelopes are excluded, indicating the white dwarf companions in these systems are heavier than about 0.2 $M_\odot $.

Open with DEXTER

In Fig. 5 we show predictions of absolute magnitude and cooling ages from the white dwarf cooling tracks by Rohrmann et al. (2002) and Bergeron et al. (1995). The helium-core white dwarf cooling tracks show a dichotomy in the cooling properties of helium-core white dwarfs caused by differences in the thickness of the hydrogen layer surrounding the helium core of these white dwarfs (see, e.g. Althaus et al. 2001; Schönberner et al. 2000). White dwarfs heavier than 0.18-0.20 $M_\odot $ have thin envelopes and cool faster than lighter white dwarfs which have thick envelopes. Cooling tracks appropriate for heavier carbon-oxygen white dwarfs with hydrogen-rich atmospheres are even fainter.

Under the assumption that the characteristic pulsar ages are equal to the white dwarf cooling ages, we plot the upper limits on our white dwarf pulsar companions and detections of others in Fig. 5. Because of the large distance and absorption towards PSR J1810-2005, the limit does not constrain any white dwarf parameters. For PSR J1745-0952 and PSR J1918-0642 the upper limits exclude white dwarfs with thick hydrogen envelopes. As such, the mass of the white dwarf in these systems is constrained to $M_{\rm c}\ga 0.2~M_\odot$. For PSR J1745-0952 this mass limit, combined with the low massfunction of the system, constrains the inclination of the binary orbit to the low value of $i<34\hbox{$^\circ$ }$(assuming $M_{\rm psr}=1.35~M_\odot$). Should this pulsar have a carbon-oxygen white dwarf, which is not excluded by the optical observations, the limit on the inclination will be even lower.

5 Conclusions

Using the WSRT, NRT and Lovell telescopes, we have timed four MSPs for 7.5 to 10.5 years. We have presented updated timing solutions, pulse profiles at multiple frequencies for each pulsar, and scintillation parameters for PSR J1918-0642. We have measured transverse velocities for PSRs J1745-0952 and J1918-0642, and set limits on the velocities of PSRs J1721-2457 and J1810-2005. All velocities are consistent with previously published distributions for solitary and binary MSPs.

We have analysed archival optical observations for the binary MSPs and found no companions to the pulsars. From the magnitude limits we deduce for the companions, we can exclude white dwarfs with thick atmospheres. This indicates that the companions must be heavier than about 0.2 $M_\odot $ . At this point, the mass restrictions as well as the optical magnitude limits give no conclusive information to classify PSRs J1745-0952 or J1810-2005 as either LMBPs or IMBPs.

For low-eccentricity binary pulsars, the only post-Keplerian parameter that is likely to be measurable is the Shapiro delay. The upper limit for inclination of PSR J1745-0952, i < 34, suggests that the effect of Shapiro delay in timing will be very low and therefore we can not expect to use pulsar timing analyis to disentangle the individual masses of this system. However, the expected luminosity of MR>11.3 indicates that using a dedicated optical observation, the companion of this pulsar may be detectable, and this will therefore be the most promising way of deducing the pulsar and companion masses.

Acknowledgements
The Westerbork Synthesis Radio Telescope is operated by ASTRON (Netherlands Foundation for Research in Astronomy) with support from the Netherlands Foundation for Scientific Research NWO. The Nançay radio Observatory is operated by the Paris Observatory, associated to the French Centre National de la Recherche Scientifique (CNRS). The Nançay Observatory also gratefully acknowledges the financial support of the Region Centre in France.

References

  1. Althaus, L. G., Serenelli, A. M., & Benvenuto, O. G. 2001, MNRAS, 324, 617 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bassa, C. G., van Kerkwijk, M. H., & Kulkarni, S. R. 2003, A&A, 403, 1067 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Bassa, C. G., van Kerkwijk, M. H., & Kulkarni, S. R. 2006, A&A, 450, 295 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Bergeron, P., Wesemael, F., & Beauchamp, A. 1995, PASP, 107, 1047 [NASA ADS] [CrossRef] [Google Scholar]
  5. Camilo, F., Lyne, A. G., Manchester, R. N., et al. 2001, ApJ, 548, L187 [NASA ADS] [CrossRef] [Google Scholar]
  6. Cordes, J. M., & Lazio, T. J. W. 2002, unpublished [arXiv:astro-ph/0207156] [Google Scholar]
  7. Danziger, I. J., Baade, D., & Della Valle, M. 1993, A&A, 276, 382 [NASA ADS] [Google Scholar]
  8. Dewey, R. J., Taylor, J. H., Weisberg, J. M., et al. 1985, ApJ, 294, L25 [NASA ADS] [CrossRef] [Google Scholar]
  9. Drimmel, R., Cabrera-Lavers, A., & López-Corredoira, M. 2003, A&A, 409, 205 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Edwards, R. T., & Bailes, M. 2001, ApJ, 553, 801 [NASA ADS] [CrossRef] [Google Scholar]
  11. Gupta, Y., Rickett, B. J., & Lyne, A. G. 1994, MNRAS, 269, 1035 [NASA ADS] [CrossRef] [Google Scholar]
  12. Hobbs, G., Jenet, F., Lommen, A., et al. 2008, in AIP Conf. Ser. 983, ed. C. G. Bassa, Z. Wang, A. Cumming, & V. M. Kaspi, 630 [Google Scholar]
  13. Hobbs, G., Lorimer, D. R., Lyne, A. G., et al. 2005, MNRAS, 360, 974 [NASA ADS] [CrossRef] [Google Scholar]
  14. Hobbs, G. B., Edwards, R. T., & Manchester, R. N. 2006, MNRAS, 369, 655 [NASA ADS] [CrossRef] [Google Scholar]
  15. Hotan, A. W., van Straten, W., & Manchester, R. N. 2004, Proc. Astr. Soc. Aust., 21, 302 [Google Scholar]
  16. Jacoby, B. A., Chakrabarty, D., van Kerkwijk, M. H., Kulkarni, S. R., & Kaplan, D. L. 2006, ApJ, 640, L183 [NASA ADS] [CrossRef] [Google Scholar]
  17. Janssen, G. H., Stappers, B. W., Kramer, M., et al. 2008a, A&A, 490, 753 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Janssen, G. H., Stappers, B. W., Kramer, M., et al. 2008b, in AIP Conf. Ser. 983, ed. C. G. Bassa, Z. Wang, A. Cumming, & V. M. Kaspi, 633 [Google Scholar]
  19. Jenet, F. A., Hobbs, G. B., Lee, K. J., et al. 2005, ApJ, 625, L123 [NASA ADS] [CrossRef] [Google Scholar]
  20. Johnston, S., Nicastro, L., & Koribalski, B. 1998, MNRAS, 297, 108 [NASA ADS] [CrossRef] [Google Scholar]
  21. Karuppusamy, R., Stappers, B. W., & Van Straten, W. 2008, PASP, 120, 191 [NASA ADS] [CrossRef] [Google Scholar]
  22. Kramer, M., Lange, C., Lorimer, D. R., et al. 1999, ApJ, 526, 957 [NASA ADS] [CrossRef] [Google Scholar]
  23. Kramer, M., Xilouris, K. M., Lorimer, D. R., et al. 1998, ApJ, 501, 270 [NASA ADS] [CrossRef] [Google Scholar]
  24. Lange, C., Camilo, F., Wex, N., et al. 2001, MNRAS, 326, 274 [NASA ADS] [CrossRef] [Google Scholar]
  25. Lorimer, D. R. 2008, Living Reviews in Relativity, http://relativity.livingreviews.org/Articles/lrr-2008-8/ [Google Scholar]
  26. Lorimer, D. R., Lyne, A. G., Festin, L., et al. 1995, Nature, 376, 393 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  27. Rickett, B. J. 2001, A&AS, 278, 5 [Google Scholar]
  28. Rohrmann, R. D., Serenelli, A. M., Althaus, L. G., et al. 2002, MNRAS, 335, 499 [NASA ADS] [CrossRef] [Google Scholar]
  29. Schönberner, D., Driebe, T., & Blöcker, T. 2000, A&A, 356, 929 [NASA ADS] [Google Scholar]
  30. Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
  31. Shklovskii, I. S. 1970, Sov. Astron., 13, 562 [NASA ADS] [Google Scholar]
  32. Stetson, P. B. 1987, PASP, 99, 191 [NASA ADS] [CrossRef] [Google Scholar]
  33. Stetson, P. B. 2000, PASP, 112, 925 [NASA ADS] [CrossRef] [Google Scholar]
  34. Thorsett, S. E., & Chakrabarty, D. 1999, ApJ, 512, 288 [NASA ADS] [CrossRef] [Google Scholar]
  35. Toscano, M., Sandhu, J. S., Bailes, M., et al. 1999, MNRAS, 307, 925 [NASA ADS] [CrossRef] [Google Scholar]
  36. Van Haasteren, R., Levin, Y., McDonald, P., et al. 2009, MNRAS, 395, 1005 [NASA ADS] [CrossRef] [Google Scholar]
  37. van Kerkwijk, M., Bassa, C. G., Jacoby, B. A., et al. 2005, in Binary Radio Pulsars, ed. F. Rasio, & I. H. Stairs (San Francisco: ASP), 357 [Google Scholar]
  38. van Kerkwijk, M. H., & Kulkarni, S. R. 1995, ApJ, 454, L141 [NASA ADS] [CrossRef] [Google Scholar]
  39. Voûte, J. L. L., Kouwenhoven, M. L. A., van Haren, P. C., et al. 2002, A&A, 385, 733 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Wang, N., Manchester, R. N., Johnston, S., et al. 2005, MNRAS, 358, 270 [NASA ADS] [CrossRef] [Google Scholar]
  41. You, X. P., Hobbs, G. B., Coles, W. A., Manchester, R. N., & Han, J. L. 2007, ApJ, 671, 907 [NASA ADS] [CrossRef] [Google Scholar]
  42. Zacharias, N., Urban, S. E., Zacharias, M. I., et al. 2004, AJ, 127, 3043 [NASA ADS] [CrossRef] [Google Scholar]

Footnotes

... (BIPM)[*]
http://www.bipm.org
... DE405[*]
ftp://ssd.jpl.nasa.gov/pub/eph/export/DE405/de405iom.ps

All Tables

Table 1:   Timing solutions for the pulsars.

Table 2:   Contributions to the period derivative.

Table 3:   Flux densities and spectral index.

All Figures

  \begin{figure} \par\includegraphics[width=11cm,angle=270]{11728fg1.ps} \vspace*{1.5mm} \end{figure} Figure 1:

Profiles for the PSRs at multiple frequencies. All profiles were generated from a single 55 min observation using PuMaII, except the 1380 MHz profiles of PSRs J1721-2457, J1745-0952 and J1810-2005 that used 10 to 12 h of PuMaII observations, and the 2600 MHz profile of PSR J1745-0952 was generated from a 50 min Nançay observation. These profiles are to show their appearance; for timing purposes we used high S/N templates as described in the text.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=-90,width=17cm,clip]{11728fg2} \vspace*{7mm} \end{figure} Figure 2:

Flux density variations of PSR J1918-0642 obtained with the WSRT and NRT from observations made at 21 cm. The left panel shows the distribution of flux densities from the two observatories, where the leftmost column represent all non-detections. In the right panel we show the individual flux density values as a function of time, where the length of the line in each case is proportional to the flux density, as indicated in the legend. Observations where there was no clear detection (ND) of the pulsar and thus only an upper limit on the flux density can be determined, are plotted with a cross.

Open with DEXTER
In the text

  \begin{figure} \par\mbox{\includegraphics[width=8.8cm,clip]{11728f3a} \includegraphics[width=8.8cm,clip]{11728f3b} }\end{figure} Figure 3:

Dynamic spectra of PSR J1918-0642 plotted as a greyscale of intensity as a function of time and frequency. Darker pixels correspond to higher intensity values and the intensity scales linearly with the levels of grey. The dynamic spectra are from two observations made using PuMaII on 23 February 2008 ( left) and 24 March 2008 ( right).

Open with DEXTER
In the text

  \begin{figure} \par\mbox{\includegraphics[width=8.8cm]{11728f4a} \includegraphics[width=8.8cm]{11728f4b} }\end{figure} Figure 4:

$45\hbox {$^{\prime \prime }$ }\times 45\hbox {$^{\prime \prime }$ }$ subsections of the deep images of PSR J1745-0952 (left) and PSR J1810-2005 (right). To retain visibility, the pulsar positions are denoted by a circles with a $1\hbox {$^{\prime \prime }$ }$ radius, even though the actual error ellipses are considerably smaller than this.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{11728fg5} \vspace*{4mm} \end{figure} Figure 5:

Absolute R-band magnitude and cooling age predictions. Shown are helium-core white dwarf cooling tracks by Rohrmann et al. (2002) and carbon-oxygen white dwarf cooling tracks with hydrogen-rich atmospheres by Bergeron et al. (1995) ($\log g=8$ corresponds to $M_{\rm c}\approx0.6~M_\odot$ while $\log g=9$ corresponds to $M_{\rm c}\approx1.2~M_\odot$). Helium-core models with masses below approximately 0.18-0.20 $M_\odot $ have thick hydrogen envelopes and continue to residually burn hydrogen, keeping the white dwarf hot and slowing the cooling. Heavier models have thin hydrogen envelopes and cool much faster, creating a dichotomy in the cooling properties of white dwarf companions to millisecond pulsars. White dwarfs with carbon-oxygen cores cool even faster. Shown with error bars are PSR J0218+4232 (Bassa et al. 2003), PSR J0437-4715 (Danziger et al. 1993), PSR J0751+1807 (Bassa et al. 2006) and PSR J1012+5307 (Lorimer et al. 1995), where the white dwarf cooling age is assumed to be equal to the characteristic age of the pulsar (using braking indices of n=3). Shown with upper limits on the absolute R-band magnitude are the values for PSR J1745-0952 and PSR J1918-0642. For these two pulsars, thick hydrogen envelopes are excluded, indicating the white dwarf companions in these systems are heavier than about 0.2 $M_\odot $.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.