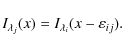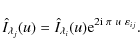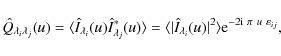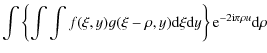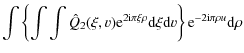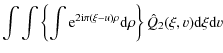EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 514 (May 2010) A&A, 514 (2010) A91 Full HTML
Free Access
Issue
A&A
Volume 514, May 2010
Article Number A91
Number of page(s) 10
Section The Sun
DOI https://doi.org/10.1051/0004-6361/200811455
Published online 27 May 2010
A&A 514, A91 (2010)

Measuring line formation depths by cross-spectral analysis

Numerical simulations for the 630 nm Fe I line pair

C. Grec1 - H. Uitenbroek2 - M. Faurobert1 - C. Aime1

1 - UMR 6525 H. Fizeau, Université de Nice Sophia Antipolis, CNRS, Observatoire de la Côte d'Azur, Campus Valrose, 06108 Nice, France
2 - National Solar Observatory/Sacramento Peak, PO Box 62, Sunspot, NM88349, USA

Received 1 December 2008 / Accepted 2 December 2009

Abstract
Context. Numerical three-dimensional simulations of the solar photosphere have progressed greatly in the last 15 years. Observational tests are needed to independently verify the realism of these simulations.
Aims. We aim to measure the perspective shift between monochromatic images at different wavelengths taken away from disk center. We investigate the feasibility of our method by applying it to simulated spectra of the Fe  I line pair at 630.15 and 630.25 nm calculated from several snapshots of a three-dimensional simulation of solar magneto-convection.
Methods. We present a method to determine line formation depths from spectroscopic observations without relying on assumptions about an atmospheric model. Our method is based on the measurement of a perspective shift, which is detected as a linear phase term in the cross-spectrum of the images. In principle this detection is independent of the spatial resolution of the observations, and provides a valuable test for numerical simulations of the solar photosphere.
Results. To obtain accurate formation heights we need to correct spectra for convective Doppler shifts, and we need to accumulate successive phase shifts between images in nearby wavelengths, rather than compare images from the continuum and core directly. The comparison of images provides large dissimilarities, which result from the temperature contrast inversion in the granulation with height. We verify that the cross-spectrum phase of the simulated images shows the expected linear behavior with spatial frequency when considering two close enough wavelengths in a spectral line profile. This linear behavior is however only obtained at small spatial frequencies, i.e. for large granular structures. Derived line formation heights of the two lines range from 239 and 287 km above the continuum formation height for the 630.15 nm line, and from 138 to 201 km for the 630.25 nm line, with significant variation between snapshots. Formation height estimates from optical depth unity give on average 319 km and 244 km respectively.
Conclusions. Our numerical tests validate measurements of line formation depths from cross-spectra between images at different wavelengths and stress the value of measuring the phase of the cross-spectra as an important test for numerical simulations.

Key words: line: formation - techniques: high angular resolution - techniques: spectroscopic - Sun: photosphere

1 Introduction

Numerical simulations of solar magneto-convection have been successful in reproducing the morphology of granules (Stein & Nordlund 2000,1998), the prediction of solar p-modes (Stein & Nordlund 2001; Nordlund & Stein 2001), and in particular in the reproduction of the space- and time-averaged shapes of photospheric absorption lines (Asplund et al. 2000b,a). Finding observational tests for such simulations that are independent of spatial resolution and that can be compared with theory without prejudice is not straightforward. We describe here a spatial resolution independent method to determine formation depths of spectroscopic lines from observations. More precisely, our method allows us to measure the difference between the formation heights of images obtained in the continuum and at a wavelength within a spectral line, thus providing access to parameters which could be used as constraints in inversion procedures. For this reason we chose to test our method on the line pair of Fe  I at 630 nm, which is widely used for magnetic field measurements. Recently, Martínez González et al. (2006) have shown that inversion methods should take into account the difference in formation height between the pair of lines. This quantity can be directly measured by the inter-spectral method that we present here.

The method was first introduced in a previous paper, referred to as Paper I below (Grec et al. 2007). The basic idea is that when one observes solar structures at two different wavelengths away from the disk center, their difference in formation depth is projected into a spatial shift between the images at the two wavelengths. This spatial shift may be very small, but is detectable by a method inspired by differential interferometry, which we recall briefly here. First of all, two-dimensional images are not required because the perspective shift lies along the radial direction, so one-dimensional spectrograms may be safely used, as long as the slit of the spectrograph is radially oriented (see Appendix A). Let us consider two brightness distributions $I_{{\lambda _i}}(x)$ and $I_{{\lambda _j}}(x)$recorded along the spectrograph slit at two different wavelengths i and j; they reflect the spatial variations of the source function at their respective formation depths. Assuming that the vertical variation scale of the source function is large compared to the formation depth difference, we can write that  $I_{{\lambda _i}}(x)$ and  $I_{{\lambda _j}}(x)$ are similar, but are simply shifted by the perspective effect, i.e.

\begin{displaymath} I_{\lambda_j}(x) = I_{\lambda_i}(x- \varepsilon_{ij}). \end{displaymath} (1)

In the Fourier space this spatial shift gives rise to a phase term with a linear variation with respect to the spatial frequency variable u,

\begin{displaymath} \hat{I}_{\lambda_j}(u) = \hat{I}_{\lambda_i}(u){\rm e}^ {2{\rm i}~\pi~u~\varepsilon_{ij}} . \end{displaymath} (2)

The sequential cross-spectrum ${\hat Q}_{\lambda_i \lambda_j}(u)$between $I_{{\lambda _i}}(x)$ and $I_{{\lambda _j}}(x)$ is given by the ensemble average:

\begin{displaymath} \hat{Q}_{\lambda_i \lambda_j}(u) = \langle \hat{I}_{\lambda_... ...\vert^2 \rangle {\rm e}^ {- 2{\rm i}~\pi~ u~\varepsilon_{ij}}, \end{displaymath} (3)

where the symbol * indicates the complex conjugate. The spatial shift due to the perspective effect, and therefore the difference of the two image formation heights, can then be directly derived from a linear fit of the phase.

There is no fundamental limit for the minimum measurable value of $\varepsilon_{ij}$, which can be much smaller than the telescope resolution. The only limitation is the signal-to-noise ratio (SNR). To increase it, we need to process a large number of spectrograms to be as close as possible to the ensemble average, as in a classical solar speckle interferometric technique. The averaging process applies both to the fluctuations due to the solar granulation itself and the atmosphere-telescope response, if applicable. In the present theoretical study, this latter effect is not of concern. The measurement of the height differences is therefore insensitive to the resolution obtained with the telescope. This follows from the principle of the experiment presented above, but can be further illustrated. Indeed, let us assume that the images $I_{{\lambda _i}}(x)$ and $I_{{\lambda _j}}(x)$ are affected by a blurring effect B(x). Since all measurements are made within a small spectral window (a few angstroms), this blurring will be the same for all images. The image Fourier transforms $\hat{I}_{\lambda_i}(u)$, and $\hat{I}_{\lambda_j}(u)$ will suffer from the same filtering effect $\hat{B}(u)= \vert\hat{B}(u)\vert\exp({\rm i} \varphi(u))$. By virtue of the complex conjugate, this latter phase term disappears in the cross-spectrum, which is only affected by an amplitude term $\langle \vert\hat{B}(u)\vert^{2}\rangle $. This amplitude term can only decrease the SNR of the measurement, but does not bias it. However, as we will see during the course of the paper, a pre-processing of the spectrogram is necessary to get rid of Doppler shifts. To do these corrections, good images are required, but once these corrections are made, the measurement is indeed resolution-independent.

The method outlined here relies on two important conditions: we must compare similar images and we must be able to assign a given formation layer to a given wavelength in the spectrograms. As the line absorption profile is shifted by granular motions in the photosphere, which alters the heights sampled by the different wavelengths in the line, we must correct the spectrograms from velocity distortions. It is not sufficient to correct the spectra for the general shift of the line profile in each location, we also have to correct for line asymmetries in each line profile introduced by gradients of the velocity along the line of sight. These velocity gradients result in the familiar $\mathcal{C}$-shape of the line bisector. In Paper I, we proposed some methods to correct the phase measurement from these velocity effects.

In Paper I we also pointed out that contrast inversion of the granulation between the lower and upper photosphere is detected as a phase jump of $\pi$ in the phase of the cross-spectrum of the images taken in the continuum and at the center of strong enough photospheric lines, violating the similarity condition between two correlated images. In order to recover the difference $\varepsilon$between the continuum and the line core formation depths, therefore, we typically have to sum the shifts $\varepsilon_{ij}$ obtained sequentially through the line:

\begin{displaymath}\varepsilon = \sum_{i,j}{\varepsilon_{ij}} = \sum_{i=0}^{N-1}{\varepsilon_{i,i+1}}, \end{displaymath}

where N denotes the total number of points in the line.

In the present paper we use three-dimensional numerical simulations of the photosphere together with a local thermodynamic equilibrium (LTE) radiative transfer calculation of the iron spectra to test the cross-spectral method and investigate in detail the physical effects which play a role in the determination of the phase of the cross-spectra. We compare the value measured with our method for the line pair of Fe  I at 630 nm with the line formation depth obtained from LTE radiative transfer calculations. This thus allows us to validate the cross-spectral analysis method for the measurement of line formation depths. These results will be exploited in a subsequent article, where we compare observed line formation depths in the 630 nm pair of lines with the theoretical approach presented here. The cross-spectral analysis is applied to slit-spectrograph scans of the granulation, obtained with the SOT instrument on board of the satellite Hinode.

In Sect. 2 we explain how the simulated spectrograms are obtained from three-dimensional radiative transfer calculations, and comment on some physical phenomena we must take into account to perform the cross-spectral analysis. In Sects. 3 and 4 we present the effects of granulation velocities and show how these effects may be corrected to derive the relative formation depth between the continuum and the line core.

2 Numerical simulations

2.1 Multi-dimensional transfer modeling of the 630 nm pair of lines

To verify the validity of the cross-spectral analysis method we applied the same method to a series of three-dimensional snapshots from a magneto-hydrodynamic simulation of solar granulation (Stein & Nordlund 1998). We calculated the emergent intensity at the wavelengths of the iron line pair at an angle of 30 degrees ( $\mu = 0.87$, partial radius of 0.5) to the normal, first by applying this angle in the x-z plane, and also by applying the same angle in the y-z plane, in order to double the number of independent spectra from which the perspective shift can be determined. This viewing angle is optimal for our purposes. Closer to the limb the line of sight crosses too many granules, confusing the perspective shift, while closer to disk center the perspective shift is too small. We assumed LTE source functions and opacities for both lines, and evaluated the emergent intensities using the multi-dimensional transfer code of Uitenbroek (2000). This code uses bi-cubic interpolation in horizontal planes and employs the characteristic method described by Kunasz & Auer (1988) for the formal solution of the transfer equation. The original simulation cubes were interpolated in the vertical dimension to better represent the surface layers and omit the deeper layers at large optical depths (below z = 350 km) that would be irrelevant for the present investigation. The interpolated cubes measured $253\times253\times64$ grid points and had a spacing of 23.7 km in both horizontal directions and 13.9 km in the vertical direction. Each of the two iron lines was sampled with 50 wavelengths spaced equidistantly across the line with a sampling of 1 pm.

\begin{figure} \resizebox{8cm}{!}{\includegraphics[trim = 0mm 0mm 0mm 0mm]{11455f01.eps}} \end{figure} Figure 1:

Demonstration of the inversion of temperature contrast with height in the solar atmosphere between layers where the local continuum forms, and those where the core of the Fe  I 630.25 nm line is formed. This inversion implies important changes in the intensity pattern that we aim to cross-correlate through the photosphere. Axes are labeled with the grid indices, with a grid spacing of 23.7 km in both directions.

Open with DEXTER

2.2 Physics of the granulation: contrast inversion

For each viewing direction we accumulated 253 synthetic spectrograms of $253\times 50 (x,\lambda )$ pixels, just as if we scanned a spectrograph slit across the simulation snapshot in 253 steps. The imaginary slit lies along the y direction for viewing angles in the y-z plane, and along the x direction for viewing angles in the x-z plane. We illustrate in Fig. 1 (left) the characteristic temperature pattern sampled by the continuum near the 630.25 nm Fe  I line, with bright hot rising up-flows surrounded by cooler inter-granular lanes. In the higher layers of the photosphere a reversal in the temperature contrast is visible: the layer above the granules becomes cool, while the layer above the inter-granular lanes becomes relatively hot (see the right panel in Fig. 1). This reversal occurs when up-flow in hot granules has to expand very rapidly when the material ascends into the much more tenuous layers above the photosphere. The resulting expansion work cools the material and provides a mostly horizontal flow. When the horizontal outflow from neighboring granules collides over the inter-granular lanes it causes local compression heating. Obviously, we cannot directly cross-correlate the continuum and line core images since the condition of their similarity is not fulfilled. A sequential cross-spectrum of images at closely spaced wavelengths is more suitable, and allows the perspective shifts to be accumulated more reliably, as we will show below.

3 Correction for the photospheric velocity fields

To investigate the effects of the general line shift and the line asymmetry separately, the correction of line-of-sight (LOS) velocity effects on the spectrograms proceeded in two steps: first we corrected for the overall Doppler displacement of the line, and then for the distortion resulting from velocity gradients. Because of this pre-processing, the wavelength can no longer be used as an indicator of the position within the line. Below we use alternatively the wavelength with respect to the center of the corrected line profiles, and the line depression coefficient $\bar {\delta } = (I_{\lambda_i}- I_{C})/ I_{C}$ (where IC is the intensity in the continuum) to refer to a given position in the line. Wavelength and depression coefficient have a one-to-one correspondence via the spatially averaged line profile (see Fig. 4). Since line profiles are corrected for wavelength shifts at a given line depression, we feel that the latter is often a more truthful indicator of a position in the line.

3.1 Overall line Doppler shift

Several different methods can be employed to determine the line Doppler displacements, such as the center-of-gravity method or the constant-cord method. Here we simply determine the wavelength of the line intensity minimum along the spectrograph slit. In order to assign the same wavelength to the position of the line minimum at each x location along the slit we translate the whole profile to a given reference wavelength. This translation is performed using classic Fourier transform properties. With this correction we obtain 1st-stage spectrograms that can be used to provide indications about the impact of velocity gradients on the observed spectrum.

3.2 Line asymmetries

To account for the photospheric velocity gradients, we have to compensate for the curved bisector shape, i.e. to symmetrize the line for all intensity levels and for all spatial positions along the slit. In the two lines, we determine the line bisector position for different intensity levels, with a constant step $\Delta I=0.01$ (in units of the continuum intensity), sufficient to precisely trace the bisector. We use a routine based on Newton's method to determine the two wavelength solutions (in pixels here) of the equation $I(\lambda)=A$, where A stands for successive intensity levels in the line profile. Thus we get the coordinates ( $\lambda_{s}(A_{s}),~A_{s}$) for positions s in the line profile, where s is a priori real. Then we calculate for each level As the ${\Delta\lambda}_{\rm D}$ Doppler shifts with respect to the mean bisector position. For each position along the slit, we do a linear interpolation of the curve described by the points ( $\lambda_{s}(A_{s})-{\Delta\lambda}_{\rm D}(A_{s}),~A_{s}$) to calculate the new coordinates ( $\lambda_{i},~A_{i}$), where $i \in \{1,...~N\}$ corresponds to the pixel number in the wavelength grid. Finally, we use the same Fourier procedure as described in Sect.  3.1 to correct for any residual line center shift and recenter all of the curves to the same reference position.

Let us comment on some aspects of the LOS velocity corrections. In Fig. 2, we present images of the granulation, corresponding to successive correction levels. First we display in the left column (A) the images resulting from the radiative transfer calculation in the 630.15 nm Fe  I line, which show the granulation pattern observed at different wavelength positions in the blue wing of the line (from the continuum to the line core, top to bottom). The continuum image ( $\bar {\delta }=0.0$, top panels) is not sensitive to velocity effects; it reflects the temperature structure at the base of the photosphere. As we go further along the line, i.e. as we consider higher photospheric levels, the up- and down-flows change the visual impression of the granulation pattern. A contrast inversion starts to appear at a position in the line wing surprisingly close to the continuum ( $\bar {\delta }=0.16$). In fact, the rising granules are blue-shifted and the granular intensity in the blue wing is formed at higher photospheric levels than that of the rest of the image. At such levels, the material runs into the density decrease, where it cools and darkens. The smaller the granule, the more rapid the cooling: the panel shows contrast inversion in small structures, that is rarely seen in larger granules. Then, for higher photospheric levels, this contrast reversal progressively becomes visible in the whole image because the largest granular structures also become relatively cool in the higher layers.

\begin{figure} \resizebox{9cm}{!}{\includegraphics[trim = 0mm 0mm 0mm 0mm]{11455f02.eps}} \end{figure} Figure 2:

The granulation pattern within the 630.15 nm line after each step of the velocity correction procedure. Column (A): emergent intensity derived from the radiative transfer calculation for various line depression levels $\bar {\delta }$ (corresponding to wavelengths ranging from continuum to line center at $\bar {\delta} = 0.66$). Column (B): 1st step correction, line core Doppler shifts compensated. Column (C): 2nd step, velocity gradients in the line corrected. Line depression coefficient is use to refer to the wavelength in the spatially averaged symmetrized line profile. $\Delta \lambda $ (in pm) is relative to the line center of the symmetrized line profile.

Open with DEXTER
\begin{figure} \resizebox{9cm}{!}{\includegraphics[trim = 0mm 0mm 0mm 0mm]{11455f03.eps}} \end{figure} Figure 3:

Comparison of line profiles at 630.25 nm: intensities in granule (gray) and intergranular lane (dark), after the line core Doppler shift correction on the same arbitrary wavelength reference ( $\lambda _{\rm ref}$). Profiles are normalized to the continuum intensity of the granular profile. In the blue wing, the contrast reversal is an artifact caused by the shape and strong asymmetry of the granular line profile. It dramatically affects the granulation pattern shown in Col. B of Fig. 2.

Open with DEXTER

In the middle Col. B the global line Doppler shifts have been corrected. Line profiles coming from granules have been red shifted, whereas profiles coming from inter-granular lanes have been blue shifted, so that their minima are at the same wavelength location. After this first correction, it may still happen when we compare the intensities at a given wavelength of the line wing in granules and inter-granules that the inter-granular intensity is larger than that of the granular profile (see Fig. 3). This produces an artificial contrast inversion. This is likely to happen as typical granular intensity profiles are flatter and broader than inter-granular ones. Actually the contrast inversion is visible for most of the image for a $\bar {\delta }$ of 0.16 or 0.34, whereas that was not the case before any correction. After the global Doppler shift correction, the image still shows structures mainly due to velocity effects not correlated with the structures seen in the continuum.

Finally we present in the third Col. C the monochromatic images after compensation of the bisector $\mathcal{C}$-shape. The structures seen in the wings are now well correlated with those observed in the continuum (compare for example images for $\bar {\delta }$ equal to 0 and 0.16, or 0.16 and 0.34) and reflect temperature fluctuations, rather than motions. Notice that the image at $\bar {\delta } = 0.5$in Col. C shows quite a low contrast. This corresponds to the layer where contrast inversion starts to take place. The inverted contrast increases at higher levels (closer to line center). Note that since all line shifts and asymmetries have now been corrected, the images in the blue and red wings of the line are now the same at corresponding distances from line center.

After line-of-sight velocities have been corrected, we can investigate the systematic displacement of the images with respect to each other as a result from the perspective effect. We keep in mind that it is not possible to directly correlate continuum and line core intensity images to get their perspective shift because the physical conditions are too different (the hypothesis of image similarity is not fulfilled), and we sequentially calculate the cross-spectrum through the line profile. We expect to detect in this only a fraction of pixel displacement between images at successive line depths. Below we examine sequentially the evolution of the cross-spectrum modulus and phase within the line.

4 Getting the relative formation depths

4.1 Computation of the cross-spectra. First properties

We compute the cross spectra ${\hat Q}_{\lambda_i \lambda_j}(u,v)$ between the intensity distributions at two different wavelengths, in the simulated data cubes scanning a region of $8.3''\times8.3''$. The number of structures it represents would not be sufficient to describe the statistical properties of the granulation in the case of real observations, but it is sufficient to calculate the cross-spectrum in ideal conditions (no effect from the terrestrial atmospheric turbulence and no signal-to-noise ratio decreasing in the line profile). However, as we have only a few different granular structures, we have to deal with several difficulties resulting from moving features of granular patterns as a function of depth. The lowest spatial frequency that we can reach with the numerical simulations is given by the inverse of the cube size, i.e. 1/8.3 arcsec-1, and the highest spatial frequency is given by $1/(2~\delta x) = 1/0.066= 15$ arcsec-1.

Let us first consider the cross-spectrum modulus evolution from the lowest photospheric layers to the highest. We show characteristic examples in Fig. 4. The top-left panel represents the symmetrized 630.25 nm line profile, normalized and spatially averaged along the slit direction. Numbers 1,  2,  ...,  12correspond to different nearby wavelengths along the line profile. For two successive levels, we cross-correlate the one-dimensional intensity fluctuations subtracted by their mean value, and we average over the 253 spectra. The cross-spectrum modulus is an even symmetric function, so we can plot its variation only for positive spatial frequencies without losing any information. This is what we have done in Fig. 4. Panels 2-9 show the log-modulus cross-spectrum evolution across the line (abscissa on the right side of the plots). For all line levels, we observe an exponential decrease in a given spatial frequency domain $\Delta u_{\lambda}$, which reduces as we go deeper into the line. It is maximal close to the continuum ( $\Delta u_{\lambda}\in[0,5.6]$ arcsec-1, not shown here), and rapidly decreases as soon as we enter the line wing (for $\lambda_{1} \lambda_{2}$, $\Delta u_{\lambda}\in[0,~5.0]$arcsec-1 ; for $\lambda_{6} \lambda_{7}$ and $\lambda_{7} \lambda_{8}$, $\Delta u_{\lambda}\in[0,~1.5]$ arcsec-1). The reason is that in the line wings the absorption profile varies rapidly with wavelength and so does the formation depth of the monochromatic images. Then only the larger structures remain similar enough on large scales. We already noticed that at the highest photospheric levels only the smallest spatial frequencies subsist in the images of the contrast-inverted granulation (see Fig. 1), because the smaller the structures are, the more rapidly the material extends and cools when the density drops. In the following section we examine the complex coherence between the brightness distributions at two wavelengths in the line profile. This quantity is well suited to estimate their degree of correlation.

\begin{figure} \resizebox{18cm}{!} {\includegraphics[trim = 0mm 0mm 0mm 0mm]{11455f04.eps}}\vspace*{1.4mm} \end{figure} Figure 4:

Panel 1: line depression of the spatially averaged and symmetrized 630.25 nm line profile. Panels 2-9: modulus of the coherency spectrum $\Vert c_{\lambda_i\lambda_j}\Vert(u)$ and log-modulus of the cross-spectra $\log_{10}(\vert\hat{I}_{\lambda_i}\hat{I}^*_{\lambda_j}\vert)(u)$ obtained sequentially through the line profile, as a function of the spatial frequency. Since the quantities are symmetric with respect to spatial frequency, we show the modulus of the coherency spectrum for negative frequencies and the log-modulus of the cross-spectra for positive frequencies. In addition, the left ordinate in each panel refers to the coherency spectrum (plotted at negative frequencies), and the right ordinate refers to the log-modulus of the cross-spectra. The intensities $I_{{\lambda _i}}(x)$ and $I_{{\lambda _j}}(x)$ have a high coherency and thus remain correlated at low spatial frequencies. The dashed lines on the right side of the panels show the exponential decrease of the cross-spectra modulus at small frequencies.

Open with DEXTER
\begin{figure} \resizebox{18cm}{!}{\includegraphics[trim = 0mm 0mm 0mm 0mm]{11455f05.eps}} \end{figure} Figure 5:

Phase of the cross-spectra of brightness distributions at nearby wavelengths along the line profile, for the same wavelength points as in Fig. 4. Top- left: spatially averaged line profile, wavelength scale in pm centered on the wavelength reference $\lambda _{0} = 630.25$ nm. Other panels from the top to the bottom and the left to the right: phase (radians) as a function of spatial frequency in arcsec-1.

Open with DEXTER

4.2 Variation of resemblance with frequency

The degree of correlation between two brightness distributions at two different wavelengths may be measured by calculating the so-called complex coherence (see Brillinger 1981; Koopmans 1974; Priestley 1981), here denoted by $c_{\lambda_i \lambda_j}$. It gives the degree of correlation between $\hat{I}_{\lambda_i}(u)$ and $\hat{I}_{\lambda_j}(u)$. At a spatial frequency u, we have:

\begin{eqnarray*}c_{\lambda_i\lambda_j}(u) ={{\hat{Q}_{\lambda_i\lambda_j}(u)} \... ...}_{\lambda_i\lambda_i}(u)\hat{Q}_{\lambda_j\lambda_j}(u)}}}\cdot \end{eqnarray*}


We remark that this quantity is the cross-spectrum, normalized by the spectral densities respectively calculated at positions i and j in the line profile. The coherence $\Vert c_{\lambda_i\lambda_j}\Vert(u)$ takes values between 0 and 1; it is an even function. The form of the coherence spectrum over all udetermines the extent to which the images observed at line positions i and j are linearly related. We calculate the coherence along the line profiles. In Fig. 4, we plot the coherence calculated within the 630.25 nm line (only for negative spatial frequencies, see the left part of panels 2-9). From position 1 to position 8 in the line, the coherence spectrum shows its maximum at low spatial frequencies, in the domain that we consider for the phase slope evaluation, and then decreases with increasing u. We notice that for the wavelength where the contrast of the images is quite low, the degree of coherence shows a dip at small frequencies and increases at high spatial frequencies (top right panel). For deeper line positions, the coherence spectrum surprisingly increases at high spatial frequencies. At the same time the modulus of the cross-spectrum remains constant and its phase goes to zero (consider Fig. 4 in positive frequencies and Fig. 5 respectively). We suspect that an under sampling of the simulated monochromatic images in the line core, leading to aliasing in Fourier space, could produce such spurious effects. This should be investigated further.

4.3 Different phase frequency regimes

Figure 5 presents the phases $\varphi_{~i~j}$, where $i\in\{1,~...,~11\}$and $j\in\{2,~...,~12\}$ correspond to the same wavelength points as in Fig. 4. Let us first stress that the interpretation of any non-linear behavior of a cross-spectrum phase is far from straightforward. Considering the results shown in Fig. 5 we can identify three different situations. Near the continuum, we compare close-by layers, so we expect the perspective displacement to be very small; the linear approximation of the phase is valid at frequencies where the cross-spectrum modulus shows significant signal and where the coherence modulus is higher than 0.8. As an example, we magnify the figure of the phase $\varphi_{~1~2}$ in Fig. 5; the slope of the phase gives a shift on the order of 1 km.

In the line wings, the line depression coefficient increases rapidly, and we cross-correlate two images that show quite different small scale structures (see for example fast change in intensity at granular edges and in inter-granular lanes in Fig. 2 (panel C) for line depression levels $\bar {\delta }\in\{ 0.0,~ 0.16,~ 0.34\}$). The phase figures obtained for such levels ( $\varphi_{~3~4}$ or $\varphi_{~4~5}$ for example) are difficult to interpret. There is a general trend of the phase, combined with a linear variation for small spatial frequencies that gives the perspective displacement. We also observe breaks for frequencies $u\in[2.5,4.0]$arcsec-1.

Further in the line profile, we correlate layers located in the upper photosphere where the reversal of contrast becomes the dominant phenomenon. However, this contrast inversion does not occur at the same photospheric level for all of the structures. The smallest granules will expand and cool more rapidly than bigger ones, so from one photospheric level to the next, the temperature fluctuations will still be correlated for small spatial frequencies, but not for larger ones. As a consequence the phase shows a linear behavior at small spatial frequencies, but different regimes exist in different spatial frequency ranges.

Deeper in the line, a stabilization of the phase seems to occur: we compare smoothed images that tend to be identical (but shifted), because the reversal of contrast happened everywhere (see $\varphi_{~8~9}$ in Fig. 5 and images for $\bar {\delta }=0.51$, $\bar {\delta }=0.61$ in Fig. 6). Two regimes are visible in the panel corresponding to  $\varphi_{~8~9}$: a linear approximation of the phase can be done for frequencies $u\in[0.0,1.5]$ arcsec-1, and another one for frequencies $u\in[3.0,6.8]$ arcsec-1. The first frequency range corresponds to the domain where the cross-spectrum modulus shows an exponential decrease and where the coherence modulus is maximal. In this small frequency regime, the phase is quite noisy. We interpret this as a consequence of the low contrast of the monochromatic images at these wavelengths, which are formed in the contrast inversion layer. But a tentative estimate of the slope gives a perspective displacement on the order of 24 km; for intermediate frequencies the shift is smaller (about 14 km). This is consistent with the fact that the vertical scale of structures depends on their typical size. It may happen that different structures co-exist, typically the first ones being large, well-identified for all photospheric depths we can reach with the 630 nm line pair, and the other ones smaller and localized, disappearing or changing within a few tens of kilometers. Figure 6 illustrates such a situation. Its shows monochromatic images of the granulation for line depression level values from 0.25 to 0.68. Due to the density drop, the granules expand and the material is compressed in inter-granular lanes. But in some places, granules are also affected: when the increase of pressure around small adjacent granules reaches a critical level, it may force them to be joined, as we can see in Fig. 6, following the evolution of granules through the line wing (example stressed in the white square). To simply interpret the phase behavior as the signature of a unique displacement is obviously not possible here. In fact, the use of the perspective effect on photospheric structures is possible as long as the structures can be well identified over a large range of photospheric heights. In that respect large structures are better suited to perspective measurements than small structures.

\begin{figure} \par\resizebox{9cm}{!}{\includegraphics[trim = 2mm 0mm 2mm 0mm]{11455f06.eps}} \end{figure} Figure 6:

Comparison of structures observed for increasing line depression coefficients $\delta $ across the 630.25 nm line wing. From one level to the next, large structures maintain and are tightly shifted by the perspective effect. This shift indicates the depth difference between two successive photospheric levels. Small granules may disappear or conglomerate within a vertical range smaller that the depth difference between the two levels (example in white square), because they are compressed by larger granules that are expanding due to the density decrease in the higher layers. Since they exist across a smaller depth range, they will be less displaced by the perspective effect.

Open with DEXTER
Finally, let us consider displacements extracted from the phases we get around the line core, i.e. for example $\varphi_{~9~10}$ or $\varphi_{~11~12}$. We see a systematic variation at low frequencies. As we approach the line core, we compare more and more similar structures and the phase becomes less noisy. Similarly, we can consider that the depth range between two successive levels decreases, as the phase slope is smaller too. On the other hand, the phase behaves strangely for frequencies higher than 10 arcsec-1: instead of varying between $\pm$$\pi$ as it does when there is no significant signal in the cross-spectrum, it remains equal to zero. As said previously, we suspect numerical problems such as spatial undersampling of the images in the core of the lines to be responsible for this behavior.

The main conclusion of this analysis of the cross-spectra and coherency spectra in the different regimes is that large granular structures (i.e. small spatial frequencies), which can be well identified over a large depth range, may be used to detect the perspective effect. The radial shift of the structures seen at nearby wavelengths along the line profile is then detected as a linear phase term at small spatial frequencies in the cross-spectra of the corresponding monochromatic images. However, the contrast inversion of the granulation, which takes place in the mid-photosphere, reduces the contrast of the monochromatic images in the line wings. At these wavelengths the phase of the cross-spectrum becomes noisy and the determination of the slope of the phase is difficult.

4.4 The 630 nm pair of lines: formation depths

We present here the line formation depths derived for the 630 nm Fe  I line pair. In Fig. 7 (left panel) we plot the shifts $\varepsilon_{~i~j}$ sequentially calculated between two layers i and j of the photosphere (gray line) and the perspective displacement $\varepsilon$ integrated over the 630.15 nm line profile (dark line). The maximum value of $\varepsilon$represents the perspective shift measured between the continuum formation layer and line core formation layer. Similarly, the right panel gives the results for the 630.25 nm line. The ``layer-by-layer" displacement $\varepsilon_{~i~j}$ is anti-symmetric with respect to the line center; that is expected since we always compare the intensity fluctuations measured for successive and increasing wavelengths. In the blue wing of the line, going from the continuum towards the line center, we compare lower layers to higher ones, so the sign of $\varepsilon_{~i~j}$ is positive, while the opposite occurs in the red part of the line. The scaling factor used for the conversion is 718 km arcsec-1. The line formation depths are derived for the position $\mu = 0.87$ on the solar disk. For the 630.25 nm line the cross-spectral method was applied to three different snapshots of the granulation. By using different snapshots, we increase in a substantial way the statistics of the granulation pattern. The phase of the cross-spectra computed by using the three simulation snapshots gives {193, 163, 138} kilometers for the maximum perspective shift $\varepsilon_{\max}$. The average over all snapshots is $\varepsilon_{\max}=165$ km. For the 630.15 nm line, with two different snapshots, we obtain two values for the difference of formation levels between the continuum and the line core, namely $\varepsilon_{\max} = \{239, 287\}$ kilometers. The average over two images is thus $\varepsilon_{\max} =263$ km.

\begin{figure} \mbox{\resizebox{8.8cm}{!}{\includegraphics[trim = 0mm 0mm 0mm 0m... ...}{!}{\includegraphics[trim = 0mm 0mm 0mm 0mm]{11455f7b.eps}} }\par\end{figure} Figure 7:

Run of the difference in formation height of the 630.15 line ( left) and 630.25 line ( right) with their respective continuum for one snapshot. Crosses show the line profile, gray polygons rthe perspective effect measured between successive layers, dark diamonds represent the perspective effect integrated across each line profile.

Open with DEXTER
On the average we find that the core of the strongest line ( $\lambda_{0}=630.15$ nm) is formed 98 km higher in the photosphere than the core of the 630.25 nm line, but this may fluctuate significantly from one snapshot to an other. This indicates that we would probably need more snapshots to get more significant average values.
\begin{figure} \center\resizebox{8.5cm}{!}{\includegraphics[trim = 5mm 0mm 5mm 0... ...{8.5cm}{!}{\includegraphics[trim = 5mm 0mm 5mm 0mm]{11455f8b.eps}} \end{figure} Figure 8:

Complex coherence obtained in the 630 nm Fe  I line pair, by comparing line core images at 630.15 nm and 630.25 nm. Top panel: modulus of the coherence, bottom panel: phase of the coherence. Difference of depth core formation (49 km) given by low-frequency phase slope (|u|<3 arcsec-1).

Open with DEXTER

Alternatively, the difference in line center formation depths may be measured directly by comparing the monochromatic images in the two line cores. Note that the monochromatic images at line centers are corrected for line center Doppler displacements only; line bisector correction is not needed in this case. The coherence spectrum calculated between the two line centers shows that the coherence is maximum at low spatial frequencies, and close to 1, which validates the approximation of a linear displacement (see Fig. 8, top panel). We notice that the coherence spectrum decreases at high frequency, as expected. The phase of the coherence derived between the two line cores is shown in the bottom panel of Fig. 8. Low-frequency linear variation (|u|<3 arcsec-1) gives a line core depth difference of 49 km. The discrepancy between this result and the one obtained from deriving the core formation heights in the lines separately is likely a consequence of inaccuracy in the latter. Even when we compare images at successive wavelengths the phase of the cross-spectra does not show a clear linear trend (see Fig. 5), because the images are not sufficiently similar. In the next section we present a way of improving the estimate of the line core formation heights by combining the two lines allowing us to make smaller step in depression coefficient.

4.5 Combining the two lines

By using the information provided by the 630.15 nm and 630.25 nm line profiles together, we can cross-correlate images with a higher degree of coherency and determine the two line formation depths. We do this by calculating the cross-spectra for successive values of the line depression by alternating between the two lines as illustrated in Fig. 9, which shows the two spatially averaged line profiles.

In Fig. 10, we compare the shifts that we obtain by using this method (dotted lines), with the shifts determined by using separately the two lines (plain lines), as a function of the line depression coefficient $\bar {\delta }$. Perspective shifts have been computed for the 630.15 nm line (white diamonds) and for the 630.25 nm line (dark diamonds). The difference mainly lies in the shifts determined in the line wings ( $\bar {\delta }<0.5$), where the low-frequency sequential phase determined using a single line is noisy (see $\varphi_{8 9}$ in Fig. 5). With both lines, we obtain new values for the difference of formation levels between the continuum and the two line cores, namely 270 km for the 630.15 nm line and 201 km for the 630.25 nm line. The difference in line core formation depths is thus 69 km, lower than the estimate of 98 km derived from the perspective effect in the lines individually, but higher than the 49 km derived from direct measurement of the perspective shift between images in the line cores.

\begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics[trim = 5mm 0mm 5mm 0mm]{11455f09.eps}} \end{figure} Figure 9:

Principle of combining information in the two lines by sampling the successive depression levels between them.

Open with DEXTER
\begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics[trim = 5mm 0mm 5mm 0mm,clip]{11455f10.eps}} \end{figure} Figure 10:

Difference of continuous formation depth and line core formation depth for the 630.15 nm (white diamonds) and for the 630.25 nm Fe  I lines (dark diamonds), determined using each line separately (plain line) and both lines iteratively (dotted line).

Open with DEXTER

Finally, in the simulation cubes we can estimate the formation height of the Fe  I line pair by calculating the height for which the optical depth in the line core reaches unity. We do this for each column in the cube while accounting for Doppler shifts (i.e., we measure the optical depth at the actual wavelength of the emergent line absorption minimum, and not at the fixed wavelength of the line at rest). In this manner we find that the formation height difference between continuum and line core of the 630.15 nm line is 319 km, and that of the slightly weaker 630.25 nm line is 244 km. The difference in theoretical formation height between the two lines is therefore 75 km, close to the estimate of 69 km derived from successive perspective in the two lines combined.

It is no surprise that estimates of the line formation height with respect to that of the continuum as derived from the location of optical depth unity give higher values than those obtained from either perspective shift measurement. Optical depth unity estimates typically lie above estimates like for instance those obtained from the maximum of the intensity contribution function. However, since the optical depth unity determination over-estimates the formation height of both the continuum and the line, although not necessarily by precisely the same amount, the difference between the two is not affected, and neither is the estimate of the difference between the formation heights of the two lines. In this light it is reassuring for the validity of the perspective shift determination that the optical depth unity derived difference of 75 km is so close to the value of 69 km that was derived from the perspective shift of the two lines combined. It is disconcerting that it is considerably larger than the value determined from direct comparison of the two line core images, which is arguably the most accurate perspective measurement, as it involves only a line shift, no asymmetry correction, and a comparison of two very similar images. Most importantly, however, the relevance of our method is that observations and simulations can be directly compared using the same analysis on both.

5 Conclusion

The numerical experiment described here confirms that it should be possible to measure the perspective shifts between images taken at different wavelength positions through a spectral line profile, by measuring the phase of their cross-spectra. But this requires the correction of the images for the effects of velocity fields on the line profile. This correction procedure requires quite good spatial resolution of the images together with a high spectral frequency resolution of the line profile.

The numerical simulations show that the phase of the cross-spectra between images (or brightness distributions) at successive wavelengths through the line profile shows a linear behavior with respect to spatial frequency only over a limited spatial frequency range at low frequencies. Typically the frequency range where the phase varies linearly with spatial frequency corresponds to the domain where the degree of coherence of the monochromatic images is close to one. This is clearly related to the fact that large structures in the photosphere tend to maintain their identity over a broader range of depths than smaller structures, which vary more rapidly with height.

Numerical simulations also show that the contrast inversion of the granulation observed in the core of strong lines, such as the Fe  I pair of lines at 630 nm, leads to difficulties in the measurement of the phase of the cross-spectra. We follow the phase of the cross-spectra for nearby wavelengths through the line profile and observe a decrease of the degree of coherence at low frequency in the wavelength domain, where the granulation contrast changes its sign. In this low contrast domain the measurement of the phase is delicate, and uncertainties of the integrated shift between the line core and the continuum images are to be expected. This problem does not arise when we directly compare the images taken at the centers of the two lines of the doublet, or when we cross-correlate images formed at successive photospheric levels between the two lines.

The solar images that we observe result from integrating contributions over a range of heights along the line-of-sight. We cannot exclude that variations in the optical path between closely spaced viewing directions might result in slightly different sampled heights, even at the same wavelength. This effect will introduce noise in our phase measurements. The question is whether this noise is random, or if it is biased towards or away from the limb. Given the asymmetric appearance of granular shapes in the radial direction on the disk, with better defined edges limbward and fuzzier outlines towards disk center, such a bias might seem likely. However, since we compare perspective shifts between images at two wavelengths, and since the possible bias should be similar at both wavelengths, the differential shift should not be affected. The noise resulting from opacity fluctuations should then be random.

Finally, even if it is difficult to unambiguously assign a specific perspective shift and thus a formation height to a specific wavelength in a spectral line, given the problems in determining the cross-spectrum phases, the behavior of these phases in simulated spectra can be directly compared with observed ones if the same method of correction for Doppler shift is applied in both cases. This comparison is independent of spatial resolution, although better resolution obviously will give more reliable results. The cross-spectral method therefore provides a powerful test for numerical simulations of solar magneto-convection simulations that needs to be explored for different spectral lines.

Acknowledgements
We thank the referee for his careful reading of the manuscript and suggestions that improved its presentation. Han Uitenbroek thanks the University of Nice - Sophia Antipolis for financial support.

6 Appendix

6.1 Equivalence of 1D and 2D analysis

In this paper we derived the displacement $\varepsilon$ from the phase of the 1D cross-spectrum $\hat{Q}_{1}(u)$ computed by comparing the emergent intensity observed at two successive wavelengths in a spectrogram, denoted here by $S(x, \lambda)$. We followed the approach of Grec et al. (2007). In the present theoretical approach we could have computed the 2D cross-spectrum $\hat{Q}_{2}(u,v)$ between monochromatic images of $S(x,y,\lambda)$provided by the transfer calculations. But we show here that when the displacement lies exactly along the x-axis, the 1D analysis is sufficient and that the 1D cross-spectrum is given by:

$\displaystyle \hat{Q}_{1}(u)= \int \hat{Q}_{2}(u,v){\rm d}v = \hat{Q}(u) {\rm e}^{-2{\rm i} \pi \varepsilon u}.$     (4)

Let us first express the 1D cross-spectrum $\hat{Q}_{1}(u)$calculated in the general case that consists in comparing two images f(x,y) and g(x,y). We obtain:
$\displaystyle \hat{Q}_{1}(u)=\int\{\int f(x,y){\rm e}^{-2 {\rm i}\pi u x}{\rm d}x \int g(x,y){\rm e}^{2{\rm i}\pi ux}{\rm d}x\}{\rm d}y.$     (5)

This expression indicates that we compute the Fourier transform of f(x,y) along the x-axis, then multiply it by the complex conjugate of the corresponding transform of g(x,y), and finally improve the statistics of the result by summing along the y-axis. By expressing the product of simple sums as a double sum, we have:
$\displaystyle \hat{Q}_{1}(u)=\int \int \int f(\xi,y) g(\eta,y) {\rm e}^{-2 {\rm i} \pi (\xi- \eta)u } {\rm d}\xi {\rm d}\eta dy.$     (6)

With the change of variable $\eta=\xi-\rho$, we get :
                         $\displaystyle \hat{Q}_{1}(u)$ = $\displaystyle \int \left\{\int \int f(\xi,y) g(\xi-\rho,y){\rm d}\xi {\rm d}y \right\} {\rm e}^{-2 {\rm i} \pi \rho u } {\rm d}\rho$  
  = $\displaystyle \int C_{2}(\rho,0) {\rm e}^{-2 {\rm i} \pi \rho u } {\rm d}\rho,$ (7)

where we recognize the cross-correlation function $C_{2}(\rho,\sigma)$, with $\sigma$ set to 0. It is the 2D Fourier transform of $\hat{Q}_{2}(u,v)$, and is generally expressed as:
                   $\displaystyle C_{2}(\rho,\sigma)$ = $\displaystyle \int \int f(x,y) g(x-\rho,y-\sigma){\rm d}x {\rm d}y$  
  = $\displaystyle \int \int \hat{Q}_{2}(u,v) {\rm e}^{2 {\rm i} \pi (\rho u + \sigma v) } {\rm d}u {\rm d}v.$ (8)

By substituting the result of Eq. (8) in Eq. (7), we obtain:

                          $\displaystyle \hat{Q}_{1}(u)$ = $\displaystyle \int \left\{ \int \int \hat{Q}_{2}(\xi,v) {\rm e}^{2 {\rm i} \pi ... ...rho } {\rm d}\xi {\rm d}v \right\} {\rm e}^{-2 {\rm i} \pi \rho u } {\rm d}\rho$  
  = $\displaystyle \int \int \left\{ \int {\rm e}^{2 {\rm i} \pi (\xi-u) \rho } {\rm d}\rho \right\}\hat{Q}_{2}(\xi,v) {\rm d}\xi {\rm d}v$  
  = $\displaystyle \int \int \left\{\delta (\xi-u) \right\}\hat{Q}_{2}(\xi,v) {\rm d}\xi {\rm d}v$  
  = $\displaystyle \int \hat{Q}_{2}(u,v){\rm d}v.$ (9)

In our particular case, f(x,y) stands for the first monochromatic image $S(x,y,\lambda_{i})$ and $g(x,y)=f(x-\varepsilon,y)$represents the image $S(x,y,\lambda_{j})$ observed further along the line. Equation (4) results simply by replacing f and g.

References

  1. Asplund, M., Ludwig, H.-G., Nordlund, Å., & Stein, R. F. 2000a, A&A, 359, 669 [NASA ADS] [Google Scholar]
  2. Asplund, M., Nordlund, Å., Trampedach, R., Allende Prieto, C., & Stein, R. F. 2000b, A&A, 359, 729 [NASA ADS] [Google Scholar]
  3. Brillinger, D. 1981, Time Series Data Analysis and Theory (McGraw-Hill, expanded edition) [Google Scholar]
  4. Grec, C., Aime, C., Faurobert, M., Ricort, G., & Paletou, F. 2007, A&A, 463, 1125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Koopmans, L. H. 1974, The spectral analysis of time series (Probability and Mathematical Statistics, New York: Academic Press) [Google Scholar]
  6. Kunasz, P., & Auer, L. H. 1988, J. Quantitative Spectrosc. Radiat. Transf., 39, 67 [Google Scholar]
  7. Martínez González, M. J., Collados, M., & Ruiz Cobo, B. 2006, A&A, 456, 1159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Nordlund, Å., & Stein, R. F. 2001, ApJ, 546, 576 [Google Scholar]
  9. Priestley, M. B. 1981, Spectral Analysis and Time Series (Academic Press limited) [Google Scholar]
  10. Stein, R. F., & Nordlund, Å. 1998, ApJ, 499, 914 [Google Scholar]
  11. Stein, R. F., & Nordlund, Å. 2000, Sol. Phys., 192, 91 [NASA ADS] [CrossRef] [Google Scholar]
  12. Stein, R. F., & Nordlund, Å. 2001, ApJ, 546, 585 [NASA ADS] [CrossRef] [Google Scholar]
  13. Uitenbroek, H. 2000, ApJ, 531, 571 [NASA ADS] [CrossRef] [Google Scholar]

All Figures

  \begin{figure} \resizebox{8cm}{!}{\includegraphics[trim = 0mm 0mm 0mm 0mm]{11455f01.eps}} \end{figure} Figure 1:

Demonstration of the inversion of temperature contrast with height in the solar atmosphere between layers where the local continuum forms, and those where the core of the Fe  I 630.25 nm line is formed. This inversion implies important changes in the intensity pattern that we aim to cross-correlate through the photosphere. Axes are labeled with the grid indices, with a grid spacing of 23.7 km in both directions.

Open with DEXTER
In the text

  \begin{figure} \resizebox{9cm}{!}{\includegraphics[trim = 0mm 0mm 0mm 0mm]{11455f02.eps}} \end{figure} Figure 2:

The granulation pattern within the 630.15 nm line after each step of the velocity correction procedure. Column (A): emergent intensity derived from the radiative transfer calculation for various line depression levels $\bar {\delta }$ (corresponding to wavelengths ranging from continuum to line center at $\bar {\delta} = 0.66$). Column (B): 1st step correction, line core Doppler shifts compensated. Column (C): 2nd step, velocity gradients in the line corrected. Line depression coefficient is use to refer to the wavelength in the spatially averaged symmetrized line profile. $\Delta \lambda $ (in pm) is relative to the line center of the symmetrized line profile.

Open with DEXTER
In the text

  \begin{figure} \resizebox{9cm}{!}{\includegraphics[trim = 0mm 0mm 0mm 0mm]{11455f03.eps}} \end{figure} Figure 3:

Comparison of line profiles at 630.25 nm: intensities in granule (gray) and intergranular lane (dark), after the line core Doppler shift correction on the same arbitrary wavelength reference ( $\lambda _{\rm ref}$). Profiles are normalized to the continuum intensity of the granular profile. In the blue wing, the contrast reversal is an artifact caused by the shape and strong asymmetry of the granular line profile. It dramatically affects the granulation pattern shown in Col. B of Fig. 2.

Open with DEXTER
In the text

  \begin{figure} \resizebox{18cm}{!} {\includegraphics[trim = 0mm 0mm 0mm 0mm]{11455f04.eps}}\vspace*{1.4mm} \end{figure} Figure 4:

Panel 1: line depression of the spatially averaged and symmetrized 630.25 nm line profile. Panels 2-9: modulus of the coherency spectrum $\Vert c_{\lambda_i\lambda_j}\Vert(u)$ and log-modulus of the cross-spectra $\log_{10}(\vert\hat{I}_{\lambda_i}\hat{I}^*_{\lambda_j}\vert)(u)$ obtained sequentially through the line profile, as a function of the spatial frequency. Since the quantities are symmetric with respect to spatial frequency, we show the modulus of the coherency spectrum for negative frequencies and the log-modulus of the cross-spectra for positive frequencies. In addition, the left ordinate in each panel refers to the coherency spectrum (plotted at negative frequencies), and the right ordinate refers to the log-modulus of the cross-spectra. The intensities $I_{{\lambda _i}}(x)$ and $I_{{\lambda _j}}(x)$ have a high coherency and thus remain correlated at low spatial frequencies. The dashed lines on the right side of the panels show the exponential decrease of the cross-spectra modulus at small frequencies.

Open with DEXTER
In the text

  \begin{figure} \resizebox{18cm}{!}{\includegraphics[trim = 0mm 0mm 0mm 0mm]{11455f05.eps}} \end{figure} Figure 5:

Phase of the cross-spectra of brightness distributions at nearby wavelengths along the line profile, for the same wavelength points as in Fig. 4. Top- left: spatially averaged line profile, wavelength scale in pm centered on the wavelength reference $\lambda _{0} = 630.25$ nm. Other panels from the top to the bottom and the left to the right: phase (radians) as a function of spatial frequency in arcsec-1.

Open with DEXTER
In the text

  \begin{figure} \par\resizebox{9cm}{!}{\includegraphics[trim = 2mm 0mm 2mm 0mm]{11455f06.eps}} \end{figure} Figure 6:

Comparison of structures observed for increasing line depression coefficients $\delta $ across the 630.25 nm line wing. From one level to the next, large structures maintain and are tightly shifted by the perspective effect. This shift indicates the depth difference between two successive photospheric levels. Small granules may disappear or conglomerate within a vertical range smaller that the depth difference between the two levels (example in white square), because they are compressed by larger granules that are expanding due to the density decrease in the higher layers. Since they exist across a smaller depth range, they will be less displaced by the perspective effect.

Open with DEXTER
In the text

  \begin{figure} \mbox{\resizebox{8.8cm}{!}{\includegraphics[trim = 0mm 0mm 0mm 0m... ...}{!}{\includegraphics[trim = 0mm 0mm 0mm 0mm]{11455f7b.eps}} }\par\end{figure} Figure 7:

Run of the difference in formation height of the 630.15 line ( left) and 630.25 line ( right) with their respective continuum for one snapshot. Crosses show the line profile, gray polygons rthe perspective effect measured between successive layers, dark diamonds represent the perspective effect integrated across each line profile.

Open with DEXTER
In the text

  \begin{figure} \center\resizebox{8.5cm}{!}{\includegraphics[trim = 5mm 0mm 5mm 0... ...{8.5cm}{!}{\includegraphics[trim = 5mm 0mm 5mm 0mm]{11455f8b.eps}} \end{figure} Figure 8:

Complex coherence obtained in the 630 nm Fe  I line pair, by comparing line core images at 630.15 nm and 630.25 nm. Top panel: modulus of the coherence, bottom panel: phase of the coherence. Difference of depth core formation (49 km) given by low-frequency phase slope (|u|<3 arcsec-1).

Open with DEXTER
In the text

  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics[trim = 5mm 0mm 5mm 0mm]{11455f09.eps}} \end{figure} Figure 9:

Principle of combining information in the two lines by sampling the successive depression levels between them.

Open with DEXTER
In the text

  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics[trim = 5mm 0mm 5mm 0mm,clip]{11455f10.eps}} \end{figure} Figure 10:

Difference of continuous formation depth and line core formation depth for the 630.15 nm (white diamonds) and for the 630.25 nm Fe  I lines (dark diamonds), determined using each line separately (plain line) and both lines iteratively (dotted line).

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.