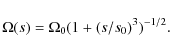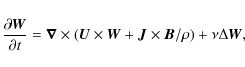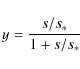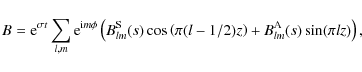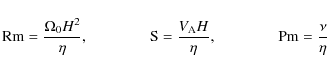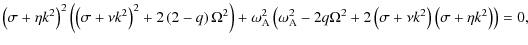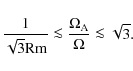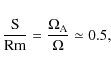EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 513 (April 2010) A&A, 513 (2010) L1 Full HTML
Free Access
Issue
A&A
Volume 513, April 2010
Article Number L1
Number of page(s) 4
Section Letters
DOI https://doi.org/10.1051/0004-6361/201014294
Published online 14 April 2010
A&A 513, L1 (2010)

LETTER TO THE EDITOR

Nonaxisymmetric modes of MRI in dissipative Keplerian disks

L. L. Kitchatinov1,2,3 - G. Rüdiger1

1 - Astrophysikalisches Institut Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany
2 - Institute for Solar-Terrestrial Physics, PO Box 291, Irkutsk 664033, Russia
3 - Pulkovo Astronomical Observatory, St. Petersburg 196140, Russia

Received 19 February 2010 / Accepted 17 March 2010

Abstract
Aims. Deviations from the axial symmetry are necessary to maintain self-sustained MRI-turbulence by a dynamo mechanism. We define the parameter region where the nonaxisymmetric MRI modes are excited and study their geometries and growth rates.
Methods. The linear eigenvalue problem for global nonaxisymmetric modes of standard-MRI in Keplerian disks is solved numerically with allowance for finite diffusion.
Results. For small magnetic Prandtl numbers the microscopic viscosity completely drops out of the analysis so that the stability maps and the growth rates expressed in terms of the magnetic Reynolds number Rm and the Lundquist number S do not depend on the magnetic Prandtl number Pm. The minimum magnetic field for the onset of nonaxisymmetric MRI grows with the rotation rate. For a given S all nonaxisymmetric modes disappear for a sufficiently large Rm. This is a consequence of the radial fine-structure of the nonaxisymmetric modes resulting from the winding effect of differential rotation. It is this fine-structure which also provides serious resolution problems for the numerical simulation of MRI at large Rm.
Conclusions. For weak magnetic fields slightly above the critical value for the onset of MRI only axisymmetric modes are unstable. Nonaxisymmetric modes need stronger fields and not too large Rm. If Pm is small its real value does not play any role in MRI.

Key words: instabilities - magnetohydrodynamics (MHD) - magnetic fields - accretion, accretion disks

1 Introduction

Currently the leading mechanism for the origin of turbulence in accretion disks is the magnetorotational instability (MRI). The instability can be excited by even a very weak magnetic field provided that there is a rotation with outward decreasing angular velocity (see Balbus & Hawley 1998).

The MRI is expected to possess the remarkable property of being self-sustained, i.e. to support the destabilizing magnetic field via its own dynamo (Brandenburg et al. 1995; Hawley et al. 1996). Deviations from the axial symmetry are necessary for any dynamo (Cowling 1933; Elsasser 1946) which in this case have to be produced by the MRI itself. An excitation of nonaxisymmetric modes of MRI is thus necessary for the self-sustained turbulence.

The present paper focuses on the nonaxisymmetric modes of the MRI. A model of a Keplerian disk with finite diffusivities and an axial background field is used in a linear analysis of global stability. As in the axisymmetric case, the nonaxisymmetric MRI exists in a range between some minimum $B_{\rm min}$ and maximum $B_{\rm max}$ values of the background field. The instability range depends on the rotation rate (parameterized by the magnetic Reynolds number ${\rm Rm}$). In contrast to the axisymmetric case, however, the $B_{\rm min}$ for nonaxisymmetric modes does not approach a (low) constant value for an increasing rotation rate, but grows with ${\rm Rm}$. The larger the ${\rm Rm}$, therefore, the stronger is the axial field required to maintain the nonaxisymmetric instability.

This behavior is extremely difficult to follow numerically because of the winding effect of differential rotation. The shearing of nonaxisymmetric fields by differential rotation produces radial fine structures when the field is too weak to resist the winding. This shearing effect must be the reason for the increase of $B_{\rm min}$ with ${\rm Rm}$ and also for the high resolution required to resolve the nonaxisymmetric MRI numerically (see Fromang & Papaloizou 2007).

2 The model

The model of Kitchatinov & Mazur (1997) of a rotating disk of constant thickness, 2H, threaded by a uniform axial magnetic field is used. The rotation axis is normal to the disk plane and the angular velocity, $\Omega$, varies only with the distance s to the axis, i.e.

\begin{displaymath}\Omega(s) = \Omega_0( 1 +({s}/{s_0})^{3})^{-1/2} . \end{displaymath} (1)

This profile describes an almost uniform rotation with the angular velocity $\Omega_0$ up to the distance s0 and Keplerian rotation for s>s0. The aspect ratio is fixed to s0/H = 5. We assume incompressibility, ${\rm div}\ \vec{U} = 0$. The motion equation is curled to exclude the pressure. This results in the equation for vorticity, ${\vec W} = {\vec\nabla}\times{\vec U}$,

\begin{displaymath}\frac{\partial{\vec W}}{\partial t} = {\vec\nabla}\times\lef... ... W} + {\vec J}\times{\vec B}/\rho\right) + \nu\Delta{\vec W}, \end{displaymath} (2)

where ${\vec B}$ is the magnetic field, ${\vec J} = \mu_0^{-1}{\vec\nabla}\times{\vec B}$ is the current density and $\nu$ is the viscosity. The magnetic field obeys the induction equation

\begin{displaymath}\frac{\partial{\vec B}}{\partial t} = {\vec\nabla}\times \left( {\vec U}\times{\vec B}\right) + \eta\Delta{\vec B} . \end{displaymath} (3)

The equations are linearized about the basic state of rotational motion (1) and uniform axial magnetic field ${\vec B}_0 = \hat{\vec z} B_0$, where $\hat{\vec z}$ is the unit vector along the rotation axis. Pseudovacuum conditions for the magnetic field, $ \hat{\vec z}\times\vec{B}^\prime = 0, $ are applied on the disk surfaces at $ z = \pm H, $ where the prime signifies the small disturbances. For the flow we assume impenetrable and stress-free boundaries. To treat the large radial distances we change to the new variable

\begin{displaymath}y = \frac{s/s_*}{1+ s/s_*} \end{displaymath} (4)

with $0 \leq y \leq 1$ and use a uniform numerical grid in y with s* = 3s0. We did not compute up to y=1 but imposed a side boundary at y = 0.99 with the condition that all disturbances there vanish.

The magnetic and velocity disturbances are expressed in terms of scalar potentials, e.g.

$\displaystyle \vec{B}^\prime = \hat{\vec z}\times\vec{\nabla} B + \vec{\nabla}\times\left(\hat{\vec z}\times\vec{\nabla}A\right) ,$   (5)

so that the disturbances are automatically divergence-free. Then Fourier expansions in z and in the azimuthal coordinate $\phi$ of the cylinder coordinate system,

\begin{displaymath}B = {\rm e}^{\sigma t}\sum_{l,m}{\rm e}^{{\rm i}m\phi} \left(... ...\pi(l -1/2)z\right) + B_{lm}^{\rm A}(s)\sin (\pi lz)\right) , \end{displaymath} (6)

are applied. The summation in (6) runs over l = 1,2,3,...and m=0,1,2,... The mathematical treatment of the velocity and vorticity disturbances is quite similar.

The equation system for the disturbances splits into a set of independent equations for different l and m. It is also important that the terms marked by the upper indexes S and A in (6) are not mixed by the equations. These indexes mark the magnetic modes symmetric and antisymmetric relative to the midplane of the disk. We shall use the notation Sm and Am for the symmetric and antisymmetric modes where m is the azimuthal wave number. Note that Sm and Am represent families of modes that can be further distinguished by the vertical wave number l. For a fixed m, l, and a given symmetry type we have an eigenvalue problem for ordinary differential equations in the variable y, which is solved numerically.

The problem has three governing parameters, i.e. the ${\rm Rm}$, the Lundquist number (${\rm S}$) and the magnetic Prandtl number (${\rm Pm}$)

\begin{displaymath}{\rm Rm} = \frac{\Omega_0 H^2}{\eta}, \ \ \ \ \ \ \ \ \ \ \ \... ...ta}, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {\rm Pm}=\frac{\nu}{\eta} \end{displaymath} (7)

with $V_{\rm A} = B_0/\sqrt{\mu\rho}$ as the Alfvén velocity. The Reynolds number ${\rm Re} = {\rm Rm}/{\rm Pm}$ and the Hartmann number ${\rm Ha} = {\rm S}/\sqrt{{\rm Pm}}$ are other possible choices. We shall see however that the parameter set (7) is most convenient for the analysis with small ${\rm Pm}$. With the Alfvén angular frequency $\Omega_{\rm A}= V_{\rm A}/H$ it follows that $\rm S/Rm=\Omega_{\rm A}/\Omega$.

3 Local analysis for axisymmetric modes

For disturbances of a small spatial scale compared to the local radius the differential rotation can be approximated by a plane-shear flow which leads to the local approximation (Hawley & Balbus 1991). For the simplest case of plane-wave disturbances with ${\vec k}\Vert \hat{\vec z}$ one finds the dispersion relation

$\displaystyle \left(\sigma + \eta k^2\right)^2\left( \left(\sigma + \nu k^2\rig... ...a^2 + 2\left(\sigma + \nu k^2\right)\left(\sigma +\eta k^2\right) \right) = 0 ,$   (8)

where $\sigma$ is the eigenvalue, $\omega_{\rm A} = kV_{\rm A}$ is the Alfvén frequency and $q = -{\rm d}\log\Omega /{\rm d}\log s$ is the local shear. An instability for the considered case can come only as a change of stability (Chandrasekhar 1961). Therefore we can put $\sigma =0$ in Eq. (8) to get the neutral stability equation defining the boundary between stability and instability and obtain for q=1.5

\begin{displaymath}{\rm Rm}^2 = \frac{\left({\rm Pm} + {\rm S}^2\right)^2} {3{\rm S}^2 - 1} \end{displaymath} (9)

(Kitchatinov & Rüdiger 2004). The dimensionless quantities (7) have been redefined in terms of the wave number ( $H \rightarrow k^{-1}$).

Equation (9) shows that the instability requires sufficiently large ${\rm Rm}$ exceeding ${\rm Rm}_{\rm min} = \frac{2}{3} \sqrt{1+ 3{\rm Pm}}$ corresponding to ${\rm S} = \sqrt{{\rm Pm} +2/3}$. For ${\rm Rm}\gg {\rm Rm}_{\rm min}$, the instability only exists for ${\rm S}$between a lower and an upper limits, i.e. $ 1/\sqrt{3} \la {\rm S} \la \sqrt{3}\ {\rm Rm}$ or, in other terms,

\begin{displaymath}\frac{1}{\sqrt{3} {\rm Rm}} \la \frac{\Omega_{\rm A}}{\Omega} \la \sqrt{3}. \end{displaymath} (10)

For a small ${\rm Pm}$, Eq. (9) loses its dependence on the ${\rm Pm}$ so that the viscosity drops completely from the analysis. The instability in this limit is fully controlled by ${\rm Rm}$ and ${\rm S}$ both defined in terms of the magnetic diffusivity. The computations of the most unstable axisymmetric modes of MRI for our global model confirm these results. Figure 1 shows that for small ${\rm Pm}$ the entire stability map in the ${\rm Rm}$-${\rm S}$ plane does not depend on the ${\rm Pm}$ (Rüdiger & Kitchatinov 2005). The growth rates of the linear instability for small ${\rm Pm}$ are also fully controlled by the ${\rm Rm}$ and ${\rm S}$.

\begin{figure} \par\includegraphics[width=7.5cm,clip]{14294fg1.eps} \end{figure} Figure 1:

Neutral stability lines for the most easily excited S0 modes and various ${\rm Pm}\leq 1$. The lines do not depend on ${\rm Pm}$ provided that ${\rm Pm}$ is small.

Open with DEXTER

We shall see that the instability condition for nonaxisymmetric modes also is independent of the Pm when the Pm is small though basically different from condition (10) for axisymmetric modes.

4 Nonaxisymmetric modes

The magnetic Prandtl number is very small for cool protostellar and protoplanetary disks; it is also small for the liquid metals used in laboratory experiments, but it is very large for galaxies (cf. Brandenburg & Subramanian 2005). Some of the properties of MRI might be expected to vary strongly between the two cases of small and large ${\rm Pm}$ (see Lesur & Longaretti 2007; Fromang et al. 2007). The linear theory, however, shows that for $\rm Pm<1$ the viscosity does not play any role.

4.1 Small Pm

The results for the nonaxisymmetric modes confirm that the MRI for small ${\rm Pm}$ does not feel the viscosity. The neutral stability lines for m=1 given in Fig. 2 approach a certain limit for decreasing ${\rm Pm}$. The growth rates show the same tendency (Fig. 3). The cases of $\rm Pm = 0.01$ and $\rm Pm = 0.001$are indistinguishable from their growth rates or stability maps.

\begin{figure} \par\includegraphics[width=7.3cm,clip]{14294fg2.eps} \end{figure} Figure 2:

Neutral stability lines for the nonaxisymmetric S1 modes with the lowest vertical wave number (l = 1) and for various ${\rm Pm}$. The lines are marked by the corresponding Pm values.

Open with DEXTER

This small-Pm scaling is important for numerical simulations. The magnetic Prandtl numbers in astrophysical bodies can be too small for simulations. Computations for moderately small magnetic Prandtl number ( ${\rm Pm}\simeq 0.1$) can closely reproduce the results for indefinitely small ${\rm Pm}$ though (provided that the results are expressed in terms of ${\rm Rm}$ and ${\rm S}$or other parameters not including the viscosity). This scaling means that MRI at small ${\rm Pm}$ does not develop a fine enough structure for the viscosity to be important.

\begin{figure} \par\includegraphics[width=7.3cm,clip]{14294fg3.eps} \end{figure} Figure 3:

Growth rates of nonaxisymmetric S1 modes of the lowest vertical wave number (l = 1) for various ${\rm Pm}$. The plot shows the growth rates in the range of magnetic fields producing the instability for ${\rm Rm}=150$.

Open with DEXTER

The strong-field limit of the instability domain in Fig. 2 behaves like

\begin{displaymath}\frac{\rm S}{\rm Rm}= \frac{\Omega_{\rm A}}{\Omega}\simeq 0.5, \end{displaymath} (11)

i.e. the rotation is slightly super-Alfvénic. The new feature in Fig. 2 is that the minimum field, $B_{\rm min}$, for the instability also grows with ${\rm Rm}$. This positive slope is in contrast to the axisymmetric modes of Fig. 1, for which $B_{\rm min}$ approaches a low but constant value as ${\rm Rm}$grows. For a given field strength the nonaxisymmetric modes are suppressed by too fast rotation. The relation ${\Omega_{\rm A}}/\Omega\simeq 0.1$ provides an estimation for the weakest possible field to excite the S1 modes. For ${\Omega_{\rm A}}/\Omega< 0.1$ the unstable S1 modes with l=1 do not exist so that

\begin{displaymath}0.1 \la \frac{\Omega_{\rm A}}{\Omega} \la 0.5 \end{displaymath} (12)

is found as the instability condition. On its LHS this relation strongly differs from the relation (10) for the axisymmetric modes. With a plasma-$\beta$ defined by $\beta\simeq {\rm Rm}^2/{\rm S}^2$ one finds $4 \la \beta \la 100$ as the instability condition for S1 modes with the axial wave number l=1. Hence the magnetic field must be strong enough for the excitation of nonaxisymmetric modes, i.e. for the operation of a hydromagnetic dynamo. We shall demonstrate below however that for ${\Omega_{\rm A}}/\Omega< 0.1$ the realization of the stability of the modes requires an extremely high numerical resolution in radial direction.

The nonaxisymmetric modes are necessary for self-sustained MRI-turbulence. A self-sustained turbulence in the high ${\rm Rm}$-regime is thus not possible. Another possibility for dynamo excitation is the nonaxisymmetric instability of an imposed azimuthal magnetic field (``AMRI'', Rüdiger et al. 2007; Simon & Hawley 2009; Hollerbach et al. 2010).

The increase of $B_{\rm min}$ with ${\rm Rm}$ for nonaxisymmetric MRI is a consequence of the winding effect of differential rotation. Because the pitch-angle of unstable disturbances near $B_{\rm min}$ is small, the winding is strong (Kitchatinov & Rüdiger 2004). The differential rotation converts the azimuthal inhomogeneity of the nonaxisymmetric modes into a fine radial structure, which is finally destroyed by diffusion.

The increase of $B_{\rm min}$ with ${\rm Rm}$ also appears for large ${\rm Pm}$. In this case it is reasonable to use ${\rm Re}$and ${\rm S/Pm}$ to parameterize the rotation and the background field. The lines show little dependence on large ${\rm Pm}$ when plotted in the plane of these parameters, which now do not depend on the magnetic diffusion $\eta$.

4.2 Overtones

Another new feature of the nonaxisymmetric instability is that modes with vertical wave numbers l > 1 are preferred for certain parameter domains. In contrast, for an axial symmetry the region of parameters where the S0 mode with l=1 is unstable includes the instability regions of all other axisymmetric modes.

\begin{figure} \par\includegraphics[width=7.5cm,clip]{14294fg4.eps} \end{figure} Figure 4:

Stability map of the S0 mode and several nonaxisymmetric modes of different vertical structure. The S1 mode is preferred only on the strong-field side of the plot. On the weak-field side the neutral stability lines of the nonaxisymmetric modes intersect. ${\rm Pm} =1$.

Open with DEXTER

Figure 4 shows the neutral stability lines for nonaxisymmetric modes together with the line for the most unstable axisymmetric S0 mode. The lines for the nonaxisymmetric modes intersect so that the modes with finer vertical structure are preferred on the weak-field side of the stability map. This is again related to the winding effect of differential rotation. The modes with finer vertical structure produce a larger Lorentz force to resist the winding. Note that only the S1 mode with l=1 can compete with S0 mode. There is a narrow region on the strong-field side of Fig. 4 where the mode S0 is stable but S1 is not.

\begin{figure} \mbox{ \includegraphics[width=4.2cm,clip]{14294fg5a.eps} \hspace{0.1cm} \includegraphics[width=4.2cm,clip]{14294fg5b.eps} } \end{figure} Figure 5:

Vector plots of magnetic disturbances in the midplane of the disk for the unstable S1 modes (l=1) for ${\rm Rm}=100$ and ${\rm Pm} =1$. The left plot is for the weak field slightly exceeding $B_{\rm min}$ and the right plot is for the strong field slightly below $B_{\rm max}$. The dashed circle shows s = s0.

Open with DEXTER

The positive slope of the upper ${\rm Rm}({\rm S})$ curve of the stability map also exists if higher l modes are included. The existence of nonaxisymmetric magnetic instability is necessary for any form of MRI-dynamo. The preference of nonaxisymmetry for strong fields is promising for the dynamo concept of the self-sustained turbulence. The field strength must increase sufficiently fast with ${\rm Rm}$, or the plasma-$\beta$ of shearing box simulations must be small enough to probe this possibility (Fromang et al. 2007). Otherwise, the nonaxisymmetric modes do not appear for too large $\beta$, or, which is the same, for too weak fields.

4.3 The resolution problem

The upper branches of the neutral stability lines for the nonaxisymmetric modes in Fig. 4 are terminated because of a numerical resolution problem. The resolution needed to follow the lines for higher ${\rm Rm}$ rapidly increases. The shearing by differential rotation is again the reason. Figure 5 gives vector plots of unstable nonaxisymmetric modes for weak (close to $B_{\rm min}$) and strong (close to $B_{\rm max}$) background fields. Obviously the disturbances in the strong-field case resist the shearing by the differential rotation. On the other hand, the shearing of weak fields produces tightly wound spirals to increase demands for the numerical resolution.

\begin{figure} \mbox{ \includegraphics[width=4.4cm]{14294fg6a.eps} \hspace{0.08cm} \includegraphics[width=4.3cm]{14294fg6b.eps} } \end{figure} Figure 6:

Growth rates of S1 modes (l=1) for ${\rm Re}=150$, ${\rm Pm} =1$ (left), and ${\rm Pm}=10$ (right) computed with different resolutions. The dotted, dashed, full, and dashed-dotted lines were obtained with 100, 150, 200, and 300 grid points in radius, respectively.

Open with DEXTER

Figure 6 shows the MRI growth rates for the S1 mode computed with different numbers of radial grid points. All the lines overlap on the strong field side of the plots indicating real instability with growth rates independent of the numerical resolution. For weak fields, however, a too low resolution produces an unreal instability. This numerical artifact can be suppressed by increasing resolution. For a fixed Reynolds number it is harder to do for than for larger ${\rm Pm}$.

The resolution problem also occurred in nonlinear shearing box simulations (Fromang & Papaloizou 2007). If our interpretation of the problem as a result of rotational shearing is correct, only an increase of resolution in the radial direction is necessary to solve the problem. Also their value of the plasma-$\beta$ of the order of 400, which lead to the relation $\rm Rm/{\rm S} \simeq 20\cdot{\rm S} $, indicates too weak magnetic fields to excite the nonaxisymmetric MRI.

Our results for a disk penetrated by a uniform and axial external field suggest that a self-sustained MRI-turbulence can only be found with sufficiently strong initial fields. The minimum field for the turbulence exceeds by at least one order of magnitude the minimum external field required for axisymmetric MRI and its amplitude linearly grows with growing rotation rates.

Acknowledgements
This work was supported by the Alexander von Humboldt Foundation and by the Russian Foundation for Basic Research (project 09-02-91338).

References

  1. Balbus, S. A., & Hawley, J. F. 1998, Rev. Mod. Phys., 70, 1 [Google Scholar]
  2. Brandenburg, A., & Subramanian, K. 2005, Phys. Rep., 417, 1 [NASA ADS] [CrossRef] [Google Scholar]
  3. Brandenburg, A., Nordlund, Å., Stein, R. F., & Torkelsson, U. 1995, ApJ, 446, 741 [NASA ADS] [CrossRef] [Google Scholar]
  4. Chandrasekhar, S. 1961, Hydrodynamic and Hydromagnetic Stability (Oxford: Clarendon Press) [Google Scholar]
  5. Cowling, T. G. 1933, MNRAS, 94, 39 [NASA ADS] [Google Scholar]
  6. Elsasser, W. M. 1946, Phys. Rev., 69, 106 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  7. Fromang, S., & Papaloizou, J. 2007, A&A, 476, 1113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Fromang, S., Papaloizou, J., Lesur, G., & Heinemann, T. 2007, A&A, 476, 1123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Hawley, J. F., & Balbus, S. A. 1991, ApJ, 376, 223 [NASA ADS] [CrossRef] [Google Scholar]
  10. Hawley, J. F., Gammie, C. F., & Balbus, S. A. 1996, ApJ, 464, 690 [NASA ADS] [CrossRef] [Google Scholar]
  11. Hollerbach, R., Teeluck, V., & Rüdiger, G. 2010, , 104, 044502 [Google Scholar]
  12. Kitchatinov, L. L., & Mazur, M. V. 1997, A&A, 324, 821 [NASA ADS] [Google Scholar]
  13. Kitchatinov, L. L., & Rüdiger, G. 2004, A&A, 424, 565 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Lesur, G., & Longaretti, P.-Y. 2007, MNRAS, 378, 1471 [NASA ADS] [CrossRef] [Google Scholar]
  15. Rüdiger, G., & Kitchatinov, L. L. 2005, A&A, 434, 629 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Rüdiger, G., Hollerbach, R., Schultz, M., & Elstner, D. 2007, MNRAS, 377, 1481 [NASA ADS] [CrossRef] [Google Scholar]
  17. Simon, J. B., & Hawley, J. F. 2009, ApJ, 707, 833 [NASA ADS] [CrossRef] [Google Scholar]

All Figures

  \begin{figure} \par\includegraphics[width=7.5cm,clip]{14294fg1.eps} \end{figure} Figure 1:

Neutral stability lines for the most easily excited S0 modes and various ${\rm Pm}\leq 1$. The lines do not depend on ${\rm Pm}$ provided that ${\rm Pm}$ is small.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.3cm,clip]{14294fg2.eps} \end{figure} Figure 2:

Neutral stability lines for the nonaxisymmetric S1 modes with the lowest vertical wave number (l = 1) and for various ${\rm Pm}$. The lines are marked by the corresponding Pm values.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.3cm,clip]{14294fg3.eps} \end{figure} Figure 3:

Growth rates of nonaxisymmetric S1 modes of the lowest vertical wave number (l = 1) for various ${\rm Pm}$. The plot shows the growth rates in the range of magnetic fields producing the instability for ${\rm Rm}=150$.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.5cm,clip]{14294fg4.eps} \end{figure} Figure 4:

Stability map of the S0 mode and several nonaxisymmetric modes of different vertical structure. The S1 mode is preferred only on the strong-field side of the plot. On the weak-field side the neutral stability lines of the nonaxisymmetric modes intersect. ${\rm Pm} =1$.

Open with DEXTER
In the text

  \begin{figure} \mbox{ \includegraphics[width=4.2cm,clip]{14294fg5a.eps} \hspace{0.1cm} \includegraphics[width=4.2cm,clip]{14294fg5b.eps} } \end{figure} Figure 5:

Vector plots of magnetic disturbances in the midplane of the disk for the unstable S1 modes (l=1) for ${\rm Rm}=100$ and ${\rm Pm} =1$. The left plot is for the weak field slightly exceeding $B_{\rm min}$ and the right plot is for the strong field slightly below $B_{\rm max}$. The dashed circle shows s = s0.

Open with DEXTER
In the text

  \begin{figure} \mbox{ \includegraphics[width=4.4cm]{14294fg6a.eps} \hspace{0.08cm} \includegraphics[width=4.3cm]{14294fg6b.eps} } \end{figure} Figure 6:

Growth rates of S1 modes (l=1) for ${\rm Re}=150$, ${\rm Pm} =1$ (left), and ${\rm Pm}=10$ (right) computed with different resolutions. The dotted, dashed, full, and dashed-dotted lines were obtained with 100, 150, 200, and 300 grid points in radius, respectively.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.