| Issue |
A&A
Volume 513, April 2010
|
|
|---|---|---|
| Article Number | L12 | |
| Number of page(s) | 5 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201014197 | |
| Published online | 29 April 2010 | |
LETTER TO THE EDITOR
Confirmation of the occurrence of the Hall instability in the non-linear regime
J. A. Pons1 - U. Geppert2
1 - Departament de Física Aplicada, Universitat d'Alacant,
Ap. Correus 99, 03080 Alacant, Spain
2 - German Aerospace Center, Institute for Space Systems, Rutherfordstr. 2, 12489 Berlin, Germany
Received 4 February 2010 / Accepted 1 April 2010
Abstract
Context. The non-linear Hall term present in the induction
equation in the electron-magneto-hydrodynamics limit is responsible for
the Hall drift of the magnetic field and, in some cases, for the
so-called Hall instability.
Aims. We investigate whether or not the growth rates and
eigenfunctions found in the linear analysis are consistent with the
results of non-linear numerical simulations.
Methods. Following the linear analysis of Rheinhardt &
Geppert, we study the same cases for which the Hall instability was
predicted by solving the non-linear Hall induction equation using a
two-dimensional conservative and divergence-free finite difference
scheme that overcomes intrinsic difficulties of pseudo-spectral methods
and can describe situations with arbitrarily high magnetic Reynolds
numbers.
Results. We show that unstable modes can grow to the level of
the background field without being overwhelmed by the Hall cascade, and
cause a complete rearrangement of the field geometry. We confirm both
the growth rates and eigenfunctions found in the linearized analysis
and hence the instability. In the non-linear regime, after the unstable
modes grow to the background level, the naturally selected modes become
stable and oscillatory. Later on, the evolution tends to select the
modes with the longest possible wavelengths, but this process occurs on
the magnetic diffusion timescale.
Conclusions. We confirm the existence of the Hall instability.
We argue against using the misleading terminology that associates the
non-linear Hall term with a turbulent Hall cascade, since small-scale
structures are not created everywhere. The field evolves instead in a
Burgers-like manner, forms local structures with strong gradients which
become shocks in the zero resistivity limit, and Hall waves are
launched and propagated through the entire domain.
Key words: magnetohydrodynamics (MHD) - stars: neutron - stars: magnetic field - stars: evolution
1 Introduction
The influence of the Hall term on the magnetic field evolution of a neutron star (NS) has been debated for many years. By analogy with the vorticity equation in ordinary hydrodynamics, Goldreich & Reisenegger (1992) conjectured that the transfer of magnetic energy from large to small scales proceeds in a similar way to ordinary turbulence. However, the analogy of the Hall induction equation with the vorticity equation is not complete, and the conjecture remained to be confirmed by multidimensional numerical simulations. Vainshtein et al. (2000) proposed a mechanism for the fast dissipation of magnetic field based on the Hall drift in stratified media. They correctly pointed out that Hall currents are able to create current sheets (which are sites for efficient dissipation) and that the evolution of the toroidal field resembles the Burgers equation. The same Burgers-like equation is applicable even to non-stratified media, but in a spherical shell (Pons & Geppert 2007), in which the Hall term in the induction equation tends to create current sheets instead of ordinary turbulence. Rheinhardt & Geppert (2002, hencefort RG) showed by a linear analysis that, in a one-component (electron) plasma, a large-scale background magnetic field may become unstable to smaller scale perturbations. This Hall-drift induced instability (H I) occurs when the magnetization parameter is high and the background field has enough curvature. Since these conditions may be realized in the crust of a NS, the problem of the H I became interesting not only from the MHD point of view but also for the astrophysics community. Although the Hall-drift is a non-dissipative process, the growth of small-scale magnetic field components modifies the overall magnetic field structure and opens the possibility of more rapid field decay than pure ohmic dissipation would predict. This effect may be relevant, at least, in relatively young neutron stars. Determining its effect on the long-term evolution, and which configurations are stable on long time-scales are different issues. A review by Reisenegger (2009) discusses the main properties of stable magnetic configurations emphasizing the importance of a non-barotropic stratification in neutron stars, and provides insight into the expected long-lived magnetic field structures. Some observational implications of rapid magnetic field decay were also discussed by Pons et al. (2007); Aguilera et al. (2008b,a); Geppert & Rheinhardt (2002). Other attempts to understand the long-term evolution of neutron star magnetic fields by numerical simulations were performed by Hoyos et al. (2008), but were restricted to 1-dimensional geometries.
The appearance of the H I was disputed by Hollerbach & Rüdiger (2002): they did not find any evidence of the instability in their numerical study of field decay under the influence of the Hall drift in a constant density spherical shell. The study was later extended to include density gradients (Hollerbach & Rüdiger 2004). However, it was clear that they could not find the H I because of numerical limitations of their code, which is unable to handle situations with sufficiently high magnetic Reynolds number. The relevance of the H I to astrophysical scenarios had already been questioned by RG. Later Cumming et al. (2004) conjectured that the gap in the energy spectrum created by the H I could be rapidly filled in by the Hall cascade. They also computed Hall-wave eigenfunctions, including the effect of density gradients across the crust, and found agreement with the results of RG. An important component of their study was their estimate of the response of the crust to the magnetic stresses induced by Hall waves. Pons & Geppert (2007) performed 2D simulations by solving the non-linear Hall-induction equation in a realistic NS crust and found some evidence for a rapid reorganization of the field during a relatively short period, but no clear confirmation of the H I could be concluded. The code again had numerical limitations that avoided additional exploration of extreme limits to confirm or rule out the existence of the H I. Wareing & Hollerbach (2009, hereafter WH) used their 3D pseudo-spectral code and concluded that the H I proposed by RG is a consequence of particular initial conditions and irrelevant compared to the Hall cascade. They considered a similar, but not identical, geometry as RG and used a code limited to employing periodic boundary conditions in all directions.
In this Letter, we solve the non-linear induction equation using a new code (Pons et al. 2010, in prep.) based on a divergence-free, conservative, finite-difference scheme that resembles numerical methods widely employed in astrophysical MHD problems to handle situations where shocks are present. It solves problems caused by the transition from a parabolic equation to the hyperbolic regime as the magnetic resistivity vanishes. Since the code is designed by following methods developed to solve hyperbolic equations, which are similar to standard techniques used in perfect fluid hydrodynamics and ideal MHD (Antón et al. 2006), it is able to deal with zero physical resistivity, therefore extending all previous studies to the limit of arbitrary high magnetic Reynolds numbers. Our numerical scheme leads to a fourth order numerical hyper-resistivity, in a similar way to other studies on the basis of which we developed our own algorithm (O'Sullivan & Downes 2006; Tóth et al. 2008). We performed a number of tests including the purely diffusive case and the exactly non-resistive case (e.g., propagation of whistler waves on a homogeneous background). In all cases where analytical solutions are available, the correct modes, decay times, and wave propagation speeds were reproduced.
This allows us to study the same model originally analyzed by RG and answer open questions about the occurrence of the H I and its interplay with the so-called Hall cascade.
2 Basic equations and model set up
To be able to compare with the results of RG, we restrict ourselves to the case of constant density
and electric conductivity. In dimensionless variables (for details, see RG),
the Hall induction equation is given by
which must be solved with the constraint
Following RG, we consider a slab that is infinitely extended in both x- and y-directions.
The upper boundary is located at z=+1 in contact to vacuum, while the lower boundary, located at z=-1,
forms the interface with a perfect conductor.
The background (initial) magnetic field is assumed to have only the x-component and depends only on the z-coordinate
![]() ,
where
,
where ![]() is the unit vector in the x-direction, B0 is a constant fixing the maximum field strength, and f(z)
is an arbitrary function. The reason for this choice is that we must
start with a background field that is not affected by the non-linear
Hall term. Note that this is not an arbitrary choice: in any problem
where one wants to study the evolution of perturbations on a
background, the first important requirement is that the background has
to be an equilibrium solution. Any other choice of
background field, will cause rapid dynamical evolution.
After all, nobody would attempt, for instance, to study perturbations
within a star starting with a fluid configuration in which gravity is
not balanced by the gradient of pressure. Thus, imposing the condition
is the unit vector in the x-direction, B0 is a constant fixing the maximum field strength, and f(z)
is an arbitrary function. The reason for this choice is that we must
start with a background field that is not affected by the non-linear
Hall term. Note that this is not an arbitrary choice: in any problem
where one wants to study the evolution of perturbations on a
background, the first important requirement is that the background has
to be an equilibrium solution. Any other choice of
background field, will cause rapid dynamical evolution.
After all, nobody would attempt, for instance, to study perturbations
within a star starting with a fluid configuration in which gravity is
not balanced by the gradient of pressure. Thus, imposing the condition
![]() ,
which was criticized by WH, is a pre-requisite for a linear analysis, not just a special choice.
,
which was criticized by WH, is a pre-requisite for a linear analysis, not just a special choice.
A different question is whether or not this background is an accurate choice and how this affects the astrophysical relevance of the conclusions. Naively, since a NS at birth is fluid, one would expect that an MHD equilibrium is reached before the crust is formed, and thus that the initial configuration may be closer to an MHD equilibrium than to a Hall equilibrium. But the conditions for reaching these two equilibria are similar (not identical) and one may expect that the initial model is not far from a Hall equilibrium. Another astrophysically interesting scenario could be relatively old NS, with an age of about 106 years. During the photon cooling era, the temperature can become so low that the magnetization parameter becomes high even for moderate magnetic fields ( 1012-1013 G), but it does take time for the temperature to reach such low values. The system slowly approaches the non-resistive case, for a relatively long period not being affected by the H I. It is reasonable to assume that the crustal magnetic field has enough time to steadily adjust itself to a Hall equilibrium until the conditions for triggering the instability can be reached in a similar manner as described above.
The choice of the function f(z) is of course not unique. To be able to compare with RG, we use
for which the modes with the most rapid growth rate correspond to horizontal wavenumbers ky=0 and kx of order 1 for
All quantities are assumed to depend periodically on x with period L(that is, the length of the numerical domain in the x-direction), and periodic boundary conditions are applied in terms of the x-coordinate.
For the inner boundary condition, as in former studies, we mimic the conditions in a NS's crust by
assuming that the matter beneath the lower surface at z=-1 is a perfect conductor. In that case, the
Meissner-Ochsenfeld effect prevents the magnetic field from penetrating into the superconducting matter.
This requires that the normal component of the magnetic field and the tangential components of the electric field
have to vanish (Pons & Geppert 2007), i.e., we assume that
Bz=Ex=Ey=0 at that interface.
At the transition to a vacuum (z=+1), the analog to the toroidal component By
has to vanish, but the boundary conditions for the other components are
not so simple.
In terms of individual modes with fixed wavenumber, a spectral
representation that matches the vacuum solution needs to satisfy a
simple relation between the Stokes function and its derivative (RG).
However, in real space and using the components of the magnetic field,
we have to employ a non-local boundary condition. By using Green's
representation formula to solve the Laplace equation in a bounded
domain, and
considering that we reduce the problem to 2D, one can derive an
explicit form for the outer boundary condition (Rheinhardt 2009,
private communication) given by
| Bx(x) | 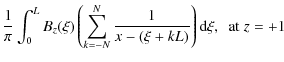
|
(3) |
where the integer N>0 must be chosen to be high enough to ensure that the sum converges.
With the same initial model and physically motivated boundary conditions, RG found that the H I appears for
![]() ,
and
that some small-scale structures must grow quickly. Since there is some confusion in the literature about the
interpretation of the term small scales, we briefly review their results and make some remarks.
For sufficiently strong and curved background fields, there is always a region in the wavenumber space where unstable
modes appear. The highest growth rates correspond to ky=0 and
the range of kx allowing for unstable modes changes depending on both the form of f(z) and
the value of B0 but, in dimensionless units and with
the slab defined in the region z=[-1,+1], it is in all cases of order 1, or even smaller.
This means that the most rapidly growing unstable mode has a typical
wavelength of the order of the slab height. Thus, in some sense, it cannot be rigorously assumed to be
small-scale mode. However, we note that the typical crust size of a NS is about 1 km, compared to its radius
of about 10 km. Thus, if the H I occurs, one would expect structures of a typical size of one km to grow within the crust, with a typical area of
,
and
that some small-scale structures must grow quickly. Since there is some confusion in the literature about the
interpretation of the term small scales, we briefly review their results and make some remarks.
For sufficiently strong and curved background fields, there is always a region in the wavenumber space where unstable
modes appear. The highest growth rates correspond to ky=0 and
the range of kx allowing for unstable modes changes depending on both the form of f(z) and
the value of B0 but, in dimensionless units and with
the slab defined in the region z=[-1,+1], it is in all cases of order 1, or even smaller.
This means that the most rapidly growing unstable mode has a typical
wavelength of the order of the slab height. Thus, in some sense, it cannot be rigorously assumed to be
small-scale mode. However, we note that the typical crust size of a NS is about 1 km, compared to its radius
of about 10 km. Thus, if the H I occurs, one would expect structures of a typical size of one km to grow within the crust, with a typical area of ![]() 103 km2. In this respect, the field geometry will
differ considerably from a typical dipolar field, consisting instead of tens or hundreds of smaller structures,
and that is what RG meant by small-scale structures. In addition, the toroidal field (here By)
may grow rapidly in a very narrow region of 10-100 m beneath the
surface. This is far from the typical picture of turbulence in fluid
dynamics, where multiple small-scale substructures grow in a large
region at the same time. In the H I, there are a few small-scale structures, which can be very localized, in particular close to the boundaries,
or wherever the toroidal field changes sign, because the Burgers-like term in the evolution equation will produce a sharp
discontinuity.
This qualitative difference is easy to visualize when one follows the evolution of the field components in the real space.
It becomes, however, more difficult to distinguish when working in wave-number space with pseudo-spectral
methods if we only consider the power-law in the spectrum.
We think that most of the disagreement and confusion in the past few years has been caused by an inaccurate use
of language, terms such as Hall cascade or small scale being interpreted differently by different readers.
103 km2. In this respect, the field geometry will
differ considerably from a typical dipolar field, consisting instead of tens or hundreds of smaller structures,
and that is what RG meant by small-scale structures. In addition, the toroidal field (here By)
may grow rapidly in a very narrow region of 10-100 m beneath the
surface. This is far from the typical picture of turbulence in fluid
dynamics, where multiple small-scale substructures grow in a large
region at the same time. In the H I, there are a few small-scale structures, which can be very localized, in particular close to the boundaries,
or wherever the toroidal field changes sign, because the Burgers-like term in the evolution equation will produce a sharp
discontinuity.
This qualitative difference is easy to visualize when one follows the evolution of the field components in the real space.
It becomes, however, more difficult to distinguish when working in wave-number space with pseudo-spectral
methods if we only consider the power-law in the spectrum.
We think that most of the disagreement and confusion in the past few years has been caused by an inaccurate use
of language, terms such as Hall cascade or small scale being interpreted differently by different readers.
3 Results
![\begin{figure}
\par\includegraphics[width=15.5cm,clip]{14197_fig1.ps}
\end{figure}](/articles/aa/full_html/2010/05/aa14197-10/Timg11.png)
|
Figure 1: Evolution of the initial configuration defined by Eq. (2) with a kx=0.5 perturbation at four different times. The left panels show transverse cuts of the By (dashes) and Bz (solid line) components at x=0, while the right panels show the field structure. Arrows show the Bx,Bz-components and the color scale the By component (red/black positive, yellow/white negative). Note the different scales in the left panels. |
| Open with DEXTER | |
WH claimed that any instabilities are always overwhelmed by a turbulent Hall cascade.
To either confirm or reject these conclusions, we performed simulations following the
non-linear evolution of the initial model described above. We assumed that B0=1000,
which, according to the linear analysis, should be affected by the H I. The wavenumber of unstable modes is in the range
kx=[0.3,3] and growth rates in the range
![]() ohmic decay times. We
perturbed the background field with small perturbations (0.1-1% in
amplitude) of different wavenumbers in that range, and followed the
time evolution for many growth times, until a quasi-stationary
diffusion regime was
reached.
In most cases, we found that the growth of the structures closely
resembled the eigenfunctions obtained in
RG with the correct timescales.
Figure 1 shows the results for an initial perturbation of kx=0.5 and maximum amplitude 1.
This mode should be unstable and its growth time is about
ohmic decay times. We
perturbed the background field with small perturbations (0.1-1% in
amplitude) of different wavenumbers in that range, and followed the
time evolution for many growth times, until a quasi-stationary
diffusion regime was
reached.
In most cases, we found that the growth of the structures closely
resembled the eigenfunctions obtained in
RG with the correct timescales.
Figure 1 shows the results for an initial perturbation of kx=0.5 and maximum amplitude 1.
This mode should be unstable and its growth time is about
![]() .
As predicted, the initial perturbation
(which is not a pure mode eigenfunction) quickly reaches the typical form of the eigenfunctions, and begins
to grow rapidly on the expected timescale.
.
As predicted, the initial perturbation
(which is not a pure mode eigenfunction) quickly reaches the typical form of the eigenfunctions, and begins
to grow rapidly on the expected timescale.
We note the similarity of the field structure at
t=0.01-0.02 with Figs. 3 and 4 in RG, which delineate the
structure of the most rapidly growing mode. During the linear stage (a
few Hall times), the unstable modes grow exponentially retaining their
structure, as expected, until they reach amplitudes large enough for
non-linear
effects to be important. At that point (![]() 0.02),
the evolution becomes non-linear, there is a drift towards the inner
boundary,
and the global shape of the field is completely reorganized. After a
stationary configuration is adopted, we enter
the diffusion regime and observe long-lived, damped oscillatory modes
with smaller scale modes that dissipate faster. During the late
evolution (bottom panel of Fig. 1), only the longest wavelength modes survive
0.02),
the evolution becomes non-linear, there is a drift towards the inner
boundary,
and the global shape of the field is completely reorganized. After a
stationary configuration is adopted, we enter
the diffusion regime and observe long-lived, damped oscillatory modes
with smaller scale modes that dissipate faster. During the late
evolution (bottom panel of Fig. 1), only the longest wavelength modes survive![]() .
The evolution of the field in terms of the power spectra is shown in Fig. 2. The fast growth of the initial perturbation (kx=0.5) and other unstable modes (
kx=1.0, 1.5, ...) at early times is evident.
After the unstable-mode energy has grown several orders of magnitude,
non-linear coupling fills the full spectrum by t=0.03,
but the dominant mode (besides kx=0) is always the kx=0.5 mode, which has drained more than 10% of the background
energy. Collapsed onto the kz axis, the spectra only shows the ordinary cascade filling short wavelength modes, but this only indicates
that the field has drifted vertically, been compressed into a narrower region, and should not be interpreted as
extended turbulence over the whole domain.
.
The evolution of the field in terms of the power spectra is shown in Fig. 2. The fast growth of the initial perturbation (kx=0.5) and other unstable modes (
kx=1.0, 1.5, ...) at early times is evident.
After the unstable-mode energy has grown several orders of magnitude,
non-linear coupling fills the full spectrum by t=0.03,
but the dominant mode (besides kx=0) is always the kx=0.5 mode, which has drained more than 10% of the background
energy. Collapsed onto the kz axis, the spectra only shows the ordinary cascade filling short wavelength modes, but this only indicates
that the field has drifted vertically, been compressed into a narrower region, and should not be interpreted as
extended turbulence over the whole domain.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14197_fig2.ps}
\end{figure}](/articles/aa/full_html/2010/05/aa14197-10/Timg15.png)
|
Figure 2: Evolution of the power spectrum. Spectra are shown at times t=0, 0.01, 0.02 and 0.03 with asterisks, solid lines, dots, and dashes, respectively. The total energy is collapsed onto the kx axis ( top) and kz axis ( bottom). The upper dotted line marks the initial power in the kx=0 background field, from which the energy of the unstable modes is drained. |
| Open with DEXTER | |
In contrast to WH, who never detected the growth of the initial
perturbation and thus concluded that it is always subsumed into the
standard Hall cascade, we observed the same unstable behavior shown in
Figs. 1 and 2
in a number of other models with different amplitude and kx of the initial perturbation. The same result is obtained with
different grid resolutions.
We also explored other initial choices for f(z), (e.g.
![]() )
and replaced the outer boundary condition with the simpler condition Bx=By=0 obtaining qualitatively similar results.
What then is the origin of this discrepancy?
We note that the finite size (L) of the grid fixes the lower
limit of kx. Periodic boundary conditions result in numerical truncation of all modes with
)
and replaced the outer boundary condition with the simpler condition Bx=By=0 obtaining qualitatively similar results.
What then is the origin of this discrepancy?
We note that the finite size (L) of the grid fixes the lower
limit of kx. Periodic boundary conditions result in numerical truncation of all modes with
![]() .
In the models in which we restricted the horizontal grid to the interval
.
In the models in which we restricted the horizontal grid to the interval ![]() (the typical size in WH models), we observed that unstable modes grew initially but the poloidal
perturbations reached only a few percent of the total energy and the toroidal component saturated even earlier.
Although the linear analysis predicted a few unstable modes with
(the typical size in WH models), we observed that unstable modes grew initially but the poloidal
perturbations reached only a few percent of the total energy and the toroidal component saturated even earlier.
Although the linear analysis predicted a few unstable modes with ![]() ,
in this restricted domain that does not
allow modes with kx<1 the non-linear coupling together with the truncation of long wavelength modes somehow
resulted in the artificial damping of unstable modes much earlier than expected. However, a simple increase in the grid size L by a factor of 2, allowing for
extra modes to exist (kx=0.5 but also
kx=1.5,2.5 ...), immediately changed the picture, allowing the
perturbations to grow to
,
in this restricted domain that does not
allow modes with kx<1 the non-linear coupling together with the truncation of long wavelength modes somehow
resulted in the artificial damping of unstable modes much earlier than expected. However, a simple increase in the grid size L by a factor of 2, allowing for
extra modes to exist (kx=0.5 but also
kx=1.5,2.5 ...), immediately changed the picture, allowing the
perturbations to grow to ![]() B0.
WH included a large number of modes but with
B0.
WH included a large number of modes but with ![]() ,
thus
the truncation of longer wavelength modes seems to be the reason for the artificial damping of the H I. We note that, as the magnetic field
geometry deviates from its initial shape, either due to the finite resistivity (the background field is not affected
by the Hall drift) or because of the growth of the perturbations, the linear analysis is not longer valid.
As the field changes, the kx-window of instability may shift to lower values, and in that case the instability
will be suppressed unless modes with longer wavelengths are permitted.
Another important feature confirming the validity of our results is that the linear stage always proceeds
similarly, irrespectively of the size of the initial perturbation (if models are compared with the appropriate
scaling factor).
,
thus
the truncation of longer wavelength modes seems to be the reason for the artificial damping of the H I. We note that, as the magnetic field
geometry deviates from its initial shape, either due to the finite resistivity (the background field is not affected
by the Hall drift) or because of the growth of the perturbations, the linear analysis is not longer valid.
As the field changes, the kx-window of instability may shift to lower values, and in that case the instability
will be suppressed unless modes with longer wavelengths are permitted.
Another important feature confirming the validity of our results is that the linear stage always proceeds
similarly, irrespectively of the size of the initial perturbation (if models are compared with the appropriate
scaling factor).
4 Conclusions
We have proven that there are cases in which the H I dominates the early evolution of the magnetic field and completely reorganizes the field structure in a few Hall times. It is not always subsumed by the Hall cascade, as argued by other authors. We have found that the finite size of the computational domain, and the use of different boundary conditions significantly affect the outcome. Since the H I is not entirely a scale-free problem and, when a slab geometry is considered, the relative sizes of the length and thickness of the slab make a difference, our findings raise new and interesting questions. In simple terms, a thin slab is easier subject to the H I than a thicker one but, what happens in a real NS crust?
The crust of a NS is not an infinite slab, but a finite-size, curved domain.
To gain insight into realistic scenarios,
one can mimic the axially symmetric case with a plane parallel model of a longitudinal size ![]() 70 km
and a thickness of 1 km (but with reflecting boundary conditions instead of periodic boundaryconditions at the
poles as used in this work).
This resembles one of our
models that has the largest grid size and therefore for which the
H I occurs.
By analogy with this toy model, one may be tempted
to claim that the H I is truly
relevant and will affect the evolution of the magnetic field in NSs.
When we compare the structures and evolutions of the models shown in this paper with those of Pons & Geppert (2007),
both the qualitative shape of the field and the typical evolution are very similar, despite important differences in
the physical model.
Perhaps the octupolar structures that survive to late times in the realistic NS crust simulations
of Pons & Geppert (2007) originate from the H I.
However, caution is required in accepting this interpretation. Given
the sensitivity of the results to details such as the size of the grid
(which allows only a finite number of unstable modes)
and the existence of non-linear couplings between modes,
it becomes necessary to perform multidimensional simulations in a
spherical shell with a realistic crust model before we can make any
claim about the relevance of the H I in NSs.
In addition, toy models that have constant density and cubic boxes with
periodic boundary conditions, such as those studied in WH, cannot be used to argue against the
relevance of the H I
in NSs, which is a global, more complex problem, that also depends on
the true dimensions and the nature of the physical boundaries. As we
have proven, the numerical truncation of some modes due to the
computational domains being too small can suppress the
instability. An extension of our present code to spherical coordinates
and to contain a realistic NS model is under development. Very
preliminary results seem to indicate that an active Hall stage exists,
but only a more detailed
analysis will provide a definitive answer.
70 km
and a thickness of 1 km (but with reflecting boundary conditions instead of periodic boundaryconditions at the
poles as used in this work).
This resembles one of our
models that has the largest grid size and therefore for which the
H I occurs.
By analogy with this toy model, one may be tempted
to claim that the H I is truly
relevant and will affect the evolution of the magnetic field in NSs.
When we compare the structures and evolutions of the models shown in this paper with those of Pons & Geppert (2007),
both the qualitative shape of the field and the typical evolution are very similar, despite important differences in
the physical model.
Perhaps the octupolar structures that survive to late times in the realistic NS crust simulations
of Pons & Geppert (2007) originate from the H I.
However, caution is required in accepting this interpretation. Given
the sensitivity of the results to details such as the size of the grid
(which allows only a finite number of unstable modes)
and the existence of non-linear couplings between modes,
it becomes necessary to perform multidimensional simulations in a
spherical shell with a realistic crust model before we can make any
claim about the relevance of the H I in NSs.
In addition, toy models that have constant density and cubic boxes with
periodic boundary conditions, such as those studied in WH, cannot be used to argue against the
relevance of the H I
in NSs, which is a global, more complex problem, that also depends on
the true dimensions and the nature of the physical boundaries. As we
have proven, the numerical truncation of some modes due to the
computational domains being too small can suppress the
instability. An extension of our present code to spherical coordinates
and to contain a realistic NS model is under development. Very
preliminary results seem to indicate that an active Hall stage exists,
but only a more detailed
analysis will provide a definitive answer.
We are grateful to M. Rheinhardt and Juan A. Miralles for providing the vacuum boundary condition and for many enlightening discussions. This work was partly supported by CompStar, a Research Networking Programme of the European Science Foundation and the Spanish MEC grant AYA 2007-67626-C03-02.
References
- Aguilera, D. N., Pons, J. A., & Miralles, J. A. 2008a, A&A, 486, 255 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aguilera, D. N., Pons, J. A., & Miralles, J. A. 2008b, ApJ, 673, L167 [NASA ADS] [CrossRef] [Google Scholar]
- Antón, L., Zanotti, O., Miralles, J. A., et al. 2006, ApJ, 637, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Cumming, A., Arras, P., & Zweibel, E. 2004, ApJ, 609, 999 [NASA ADS] [CrossRef] [Google Scholar]
- Geppert, U., & Rheinhardt, M. 2002, A&A, 392, 1015 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldreich, P., & Reisenegger, A. 1992, ApJ, 395, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Hollerbach, R., & Rüdiger, G. 2002, MNRAS, 337, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Hollerbach, R., & Rüdiger, G. 2004, MNRAS, 347, 1273 [NASA ADS] [CrossRef] [Google Scholar]
- Hoyos, J., Reisenegger, A., & Valdivia, J. A. 2008, A&A, 487, 789 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- O'Sullivan, S., & Downes, T. P. 2006, MNRAS, 366, 1329 [NASA ADS] [CrossRef] [Google Scholar]
- Pons, J. A., & Geppert, U. 2007, A&A, 470, 303 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pons, J. A., Link, B., Miralles, J. A., et al. 2007, Phys. Rev. Lett., 98, 071101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Reisenegger, A. 2009, A&A, 499, 557 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rheinhardt, M., & Geppert, U. 2002, Phys. Rev. Lett., 88, 101103 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Tóth, G., Ma, Y., & Gombosi, T. I. 2008, J. Comput. Phys., 227, 6967 [CrossRef] [Google Scholar]
- Vainshtein, S. I., Chitre, S. M., & Olinto, A. V. 2000, Phys. Rev. E, 61, 4422 [NASA ADS] [CrossRef] [Google Scholar]
- Wareing, C. J., & Hollerbach, R. 2009, A&A, 508, L39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Footnotes
- ... survive
![[*]](/icons/foot_motif.png)
- Animations of the long-term simulations are available at http://www.ua.es/personal/jose.pons/movies.html, where the evolution is visualized in much more detail than a figure can show.
All Figures
![\begin{figure}
\par\includegraphics[width=15.5cm,clip]{14197_fig1.ps}
\end{figure}](/articles/aa/full_html/2010/05/aa14197-10/Timg11.png)
|
Figure 1: Evolution of the initial configuration defined by Eq. (2) with a kx=0.5 perturbation at four different times. The left panels show transverse cuts of the By (dashes) and Bz (solid line) components at x=0, while the right panels show the field structure. Arrows show the Bx,Bz-components and the color scale the By component (red/black positive, yellow/white negative). Note the different scales in the left panels. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14197_fig2.ps}
\end{figure}](/articles/aa/full_html/2010/05/aa14197-10/Timg15.png)
|
Figure 2: Evolution of the power spectrum. Spectra are shown at times t=0, 0.01, 0.02 and 0.03 with asterisks, solid lines, dots, and dashes, respectively. The total energy is collapsed onto the kx axis ( top) and kz axis ( bottom). The upper dotted line marks the initial power in the kx=0 background field, from which the energy of the unstable modes is drained. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\begin{displaymath}\frac{\partial\vec B}{\partial t}=\Delta\vec{B} - \nabla\times\left[(\nabla\times\vec{B})\times\vec{B}\right],
\end{displaymath}](/articles/aa/full_html/2010/05/aa14197-10/img1.png)