EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 513 (April 2010) A&A, 513 (2010) A55 Full HTML
Free Access
Issue
A&A
Volume 513, April 2010
Article Number A55
Number of page(s) 7
Section Atomic, molecular, and nuclear data
DOI https://doi.org/10.1051/0004-6361/200913571
Published online 27 April 2010
A&A 513, A55 (2010)

Electron-impact excitation of Ni II

Collision strengths and effective collision strengths for low-lying fine-structure forbidden transitions[*]

C. M. Cassidy - C. A. Ramsbottom - M. P. Scott - P. G. Burke

Department of Applied Mathematics & Theoretical Physics, The Queen's University of Belfast, Belfast BT7 1NN, Northern Ireland

Received 29 October 2009 / Accepted 18 January 2010

Abstract
Context. Considerable demand exists for electron excitation data for Ni II, since lines from this abundant ion are observed in a wide variety of laboratory and astrophysical spectra. The accurate theoretical determination of these data can present a significant challenge however, due to complications arising from the presence of an open 3d-shell in the description of the target ion.
Aims. In this work we present collision strengths and Maxwellian averaged effective collision strengths for the electron-impact excitation of Ni II. Attention is concentrated on the 153 forbidden fine-structure transitions between the energetically lowest 18 levels of Ni II. Effective collision strengths have been evaluated at 27 individual electron temperatures ranging from 30-100 000 K. To our knowledge this is the most extensive theoretical collisional study carried out on this ion to date.
Methods. The parallel R-matrix package RMATRX II has recently been extended to allow for the inclusion of relativistic effects. This suite of codes has been utilised in the present work in conjunction with PSTGF to evaluate collision strengths and effective collision strengths for all of the low-lying forbidden fine-structure transitions. The following basis configurations were included in the target model - $3{{\rm d}}^{9}$, $3{{\rm d}}^{8}4{{\rm s}}$, $3{{\rm d}}^{8}4{{\rm p}}$, $3{{\rm d}}^{7}4{{\rm s}}^{2}$ and $3{{\rm d}}^{7}4{{\rm s}}4{{\rm p}}$ - giving rise to a sophisticated 295 jj-level, 1930 coupled channel scattering problem.
Results. Comprehensive comparisons are made between the present collisional data and those obtained from earlier theoretical evaluations. While the effective collision strengths agree well for some transitions, significant discrepancies exist for others.

Key words: atomic data - atomic processes - scattering - plasmas - methods: numerical - binaries: symbiotic

1 Introduction

Reliable atomic data for the highly abundant Fe-peak elements are of crucial importance in astrophysics. In this new era of high resolution astrophysical spectroscopy, a wealth of observations of these species in low ionization stages have been found to dominate the spectra of numerous astronomical sources. Emission lines of singly ionized nickel (Ni II), the heaviest and second most abundant Fe-peak element, are commonly observed in nebular spectroscopy. Recent spectroscopic Space Telescope Imaging Spectrograph (STIS) observations from both the Homunculus and strontium filament of $\eta$ Carinae, the luminous blue variable (LBV) symbiotic star, have revealed a rich spectrum of emission lines including forbidden lines of Ni II (Davidson et al. 2001; Hartman et al. 2004). The more recent work of Vreeswijk et al. (2007) presents high-resolution spectroscopic observations of the $\gamma$-ray burst GRB 060418, obtained with VLT/UVES. These spectra show clear evidence for time variability of allowed transitions involving metastable levels of both Fe II and Ni II. This is the first report of absorption lines arising from metastable levels of Ni II along any GRB sightline. In addition, the observations of Véron-Cetty et al. (2006) have shown that the spectrum of the narrow-line Seyfert galaxy IRAS 07598+6508 is dominated by lines of the Fe-peak elements, including Ni II. In order to facilitate the interpretation of such observations, an ability to properly understand and meticulously model these spectral lines is imperative. There is therefore an overwhelming need for accurate and extensive atomic data for collisional processes in Ni II in order to determine a reliable spectral synthesis.

Until recently, the accurate theoretical determination of these atomic data has remained one of the major outstanding problems in atomic collision physics. Complications arise from the presence of an open 3d-shell in the description of the target ion - a universal problem when dealing with Fe-peak elements. This complex open d-shell structure engenders a number of difficulties. It gives rise to hundreds of target state energy levels and thousands of closely coupled channels which need to be accurately incorporated into the model. These target states require large configuration interaction expansions for their accurate representation. In addition, the low-energy electron scattering region is dominated by an infinite number of Rydberg resonances, converging onto each target state threshold. In order to fully resolve these complex structures, calculations have to be carried out over a very fine mesh of incident electron energies, typically involving thousands of energy points. What ensues is a highly intensive computational challenge. Despite this however, a number of theoretical studies on the electron-impact excitation of Ni II have been performed, each gradually increasing in sophistication alongside the development of more powerful computing resources.

An early calculation by Nussbaumer & Storey (1982) reported the first computation of electron excitation rates for Ni II. However, this calculation was limited to a distorted wave approximation and did not include contributions from resonances, which are known to significantly enhance the astrophysically important effective collision strengths.

Huge advances in computing capabilities and codes in more recent years resulted in the parallel R-matrix calculation of Bautista & Pradhan (1996). This calculation was performed using the early parallelised R-matrix codes of Hummer et al. (1993). Electron-impact excitation rates were limited to the low-lying even parity levels which give rise to some important infrared and optical lines. A 7 LS term expansion was adopted for the complex Ni II target, dominated by the basis configurations $3{{\rm d}}^{9}$ and $3{{\rm d}}^{8}4{{\rm s}}$. This was then transformed into a 17 jj-level fine-structure scattering calculation using an algebraic transformation of the S-matrices to the pair coupling scheme using a parallelised version of the code STGFJ. Collision strengths were computed for a total of 136 transitions and Maxwellian averaged effective collision strengths were obtained for temperatures ranging from 500 K to 50 000 K. The collision strengths were found to differ significantly from the earlier work of Nussbaumer & Storey (1982), although the agreement between both sets of data is reasonable for some of the strong transitions. The discrepancies in the collision strengths of the weaker transitions have been attributed to the coupling effects and resonance structures which were neglected in the previous work.

The subsequent work of Watts et al. (1996) presented the first application of the RMATRX II R-matrix package (Burke et al. 1994) to electron-impact excitation of a lowly ionized open d-shell system. An extensive LS collision study was carried out including 27 doublet and quartet levels arising from the $3{{\rm d}}^{9}$, $3{{\rm d}}^{8}4{{\rm s}}$ and $3{{\rm d}}^{8}4{{\rm p}}$ Ni II basis configurations, a much larger close coupling (CC) expansion than that adopted by Bautista & Pradhan (1996). LS collision strengths were computed using the external region R-matrix package FARM (Burke & Noble 1995). Although fine-structure collision strengths were not computed in this work, the presence of prominent and complex resonance structures would undoubtedly enhance the effective collision strengths, suggesting that they should be greater than those previously calculated by both Nussbaumer & Storey (1982) and Bautista & Pradhan (1996).

To date, the most extensive calculation of collisional data for Ni II is the CC calculation of Bautista (2004). The RMATRX I suite of codes (Berrington et al. 1995) were utilised to perform a comprehensive LS collision calculation incorporating 32 states corresponding to the $3{{\rm d}}^{9}$, $3{{\rm d}}^{8}4{{\rm s}}$, $3{{\rm d}}^{8}4{{\rm p}}$ and $3{{\rm d}}^{7}4{{\rm s}}^{2}$ basis configurations. Fine-structure collision strengths were then generated using the intermediate-coupling frame transformation (ICFT) method of Griffin et al. (1998). Collision strengths were computed at 10 000 energy points ranging from 0 to 11 Rydbergs and effective collision strengths were determined for a total of 2926 transitions among the lowest 77 levels of the Ni II ion. A total of 11 electron temperatures ranging from 1000 to 30 000 K were considered in this work. This collisional data was used in the analysis of the Ni II emission spectra emanating from the strontium filament of $\eta$ Carinae (Bautista et al. 2006). The computed fine-structure collision strengths and associated effective collision strengths were not published however, and the effective collision strengths only have been obtained from the author for comparative purposes in this study.

In the present work, we embark upon the largest theoretical study of fine-structure collisional data for Ni II and report the first application of the recently extended RMATRX II R-matrix package (Burke et al. 1994) in the internal region which now accounts for relativistic fine-structure effects via FINE (Burke, V. M., private communication). The PSTGF program (Ballance & Griffin 2004) is utilised in the external region. We extend the work of Bautista (2004) by including a further basis configuration, $3{{\rm d}}^{7}4{{\rm s}}4{{\rm p}}$, in our theoretical model. All 113 LS terms corresponding to the configurations $3{{\rm d}}^{9}$, $3{{\rm d}}^{8}4{{\rm s}}$, $3{{\rm d}}^{8}4{{\rm p}}$, $3{{\rm d}}^{7}4{{\rm s}}^{2}$ and $3{{\rm d}}^{7}4{{\rm s}}4{{\rm p}}$ are incorporated. This corresponds to a 295 jj-level, 1930 coupled channel scattering calculation, involving a total of 43 365 forbidden and allowed transitions. Thanks to the new generation of powerful parallel codes and state of the art computing facilities, such an involved calculation is now computationally tractable. Maxwellian averaged effective collision strengths are evaluated at much lower and higher temperatures in the current study than in any previous theoretical works. While collision strengths and corresponding effective collision strengths have been calculated for all 43 365 forbidden and allowed transitions, we confine the present evaluation to the 153 fine-structure forbidden transitions between the energetically lowest 18 levels of Ni II. This is sufficient to encompass some of the infrared, optical and near ultraviolet lines of interest.

In the next section we describe the atomic calculation in detail. Section 3 is devoted to a graphical and qualitative synopsis of the results and detailed comparisons are made with previous theoretical works. Conclusions are inferred in Sect. 4.

2 Atomic calculations

2.1 Target data

The initial objective of the present work was to determine accurate representations for both the target and collision wavefunctions. This precursory work was carried out in LS-coupling. The 113 LS target states, including all doublet, quartet and sextet terms arising from the 5 basis configurations - $3{{\rm d}}^{9}$, $3{{\rm d}}^{8}4{{\rm s}}$, $3{{\rm d}}^{8}4{{\rm p}}$, $3{{\rm d}}^{7}4{{\rm s}}^{2}$ and $3{{\rm d}}^{7}4{{\rm s}}4{{\rm p}}$, are optimally represented by configuration interaction type expansions in terms of nine orthogonal basis orbitals, eight spectroscopic - 1s, 2s, 2p, 3s, 3p, 3d, 4s, 4p - and one non-physical $\overline{4{{\rm d}}}$ pseudo orbital included to model additional electron correlation effects, thereby improving the accuracy of the target eigenstate energies. The radial functions, necessary for the R-matrix programs, are expressed as a linear combination of Slater-type orbitals

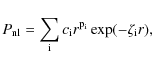
\begin{displaymath}P_{{\rm nl}} = \sum_{{\rm i}}c_{{\rm i}}r^{{\rm p_{{\rm i}}}}\exp(-\zeta_{{\rm i}}r), \end{displaymath} (1)

and the orbital parameters ( $c_{i}, p_{i}, \zeta_{i}$) utilised in the present calculation are those adopted by Watts et al. (1996). The CIV3 configuration interaction package of Hibbert (1975) was used to optimise 4s and 4p excited orbitals, together with a suitable $\overline{4{{\rm d}}}$ pseudo orbital. The remaining Hartree-Fock orbitals were taken from the analysis of Clementi & Roetti (1974).

Together with the aforementioned basis configurations, an additional 9 correlation functions were included in the configuration interaction expansion of the complex ionic target. These correlation functions are listed as: $3{\rm d}^{7}4{\rm p}^{2}$, $3{\rm d}^{6}4{\rm s}^{2}4{\rm p}$, $3{\rm d}^{6}4{\rm s}4{\rm p}^{2}$, $3{\rm d}^{8}{\bar{4{\rm d}}}$, $3{\rm d}^{7}{\bar{4{\rm d}}}^{2}$, $3{\rm d}^{7}4{\rm s}{\bar{4{\rm d}}}$, $3{\rm d}^{7}4{\rm p}{\bar{4{\rm d}}}$, $3{\rm d}^{6}4{\rm s}^{2}{\bar{4{\rm d}}}$ and $3{\rm d}^{6}4{\rm s}{\bar{4{\rm d}}}^{2}$.

Table 1 displays the calculated target state energies in Rydbergs relative to the $3{{\rm d}}^{9}$ $^{2}{{\rm D}}^{{\rm e}}$ ground state. For conciseness, only the lowest 10 LS states are presented. The present theoretical energies are compared with the experimental values of Sugar & Corliss (1985) as presented in the NIST database, and the most recent theoretical data of Bautista (2004). Although Bautista (2004) presents 6 CC calculations, it is the largest target model that he adopts in the computation of his fine-structure collision strengths. The energies for this particular target model are displayed in Table 1. Bautista's energies (2004) in general exhibit good agreement with the observed values. In his work, single-electron orbitals and CI target state eigenfunctions were generated using the atomic structure code AUTOSTRUCTURE (Badnell 1997) which employs a statistical Thomas-Fermi-Dirac model potential ${V(\lambda_{nl})}$ (Eissner & Nussbaumer 1969; Nussbaumer & Storey 1978) with scaling parameter ${\lambda_{nl}}$. This scaling parameter can be adjusted and determined variationally for each orbital and hence very favourable target models, and in particular, target state energies can be determined. However, the present theoretical model improves upon the energies of the awkward lowest-lying states. The $3{{\rm d}}^{8}4{{\rm s}}$ 4F $^{{\rm e}}$ and 2F $^{{\rm e}}$ states lie approximately 26% and 8% respectively closer to the observed data in the present approximation, than in that adopted by Bautista (2004). Furthermore, the energies of the $3{{\rm d}}^{8}4{{\rm p}}$ 4D $^{{\rm o}}$ and 4G $^{{\rm o}}$ odd parity states lie approximately 3% above the observed thresholds, whereas the predicted values of Bautista (2004) lie approximately 13% and 12% lower respectively. This good agreement between the present theoretical predictions and the observed values is consistent for the higher-lying 4p levels. Unfortunately Bautista (2004) only presents the two lowest-lying 4p levels in his latest works so a comparison beyond this is not possible. Although satisfied with the current target representation, the present scattering calculation has been performed with the energies of the spectroscopic target states shifted during diagonalisation of the Hamiltonian so as to agree with the experimental thresholds indicated by the NIST databank. Such adjustments are made to ensure that thresholds lie in their exact positions - crucial to the accurate computation of effective collision strengths. Bautista (2004) adopts exactly the same adjusting procedure. The present thresholds are shifted by approximately ${20\%}$ consistently for the even states, whereas the levels of Bautista (2004) are shifted by differing amounts. These range from ${10\%}$ for some levels, to ${13\%}$ for the lowest-lying $3{{\rm d}}^{8}4{{\rm p}}$ levels, to a substantial ${39\%}$ and ${64\%}$ for the lowest-lying ${3{{\rm d}}^{8}4{{\rm\bf s}}}$ ${^{2}{{\rm F}}^{{\rm e}}}$ and $3{{\rm d}}^{8}4{{\rm s}}$ ${^{4}{{\rm F}}^{{\rm e}}}$ levels respectively. These inaccuracies at low energies are inevitable for such a complex system as Ni II and the only alternative would be to include considerably more terms in the CI expansion of the target and collision wave functions which would greatly extend the present very large calculation.

Table 1:   LS target state energies in Rydbergs relative to the $3{{\rm d}}^{9}$ $^{2}{{\rm D}}^{{\rm e}}$ Ni II ground state.

2.2 Collision calculation

The collision calculation has been performed using powerful parallel codes, currently exploiting the rapidly increasing power and availability of state of the art parallel computing facilities. The RMATRX II R-matrix package (Burke et al. 1994) was used to complete the internal region calculations. This suite of codes allows for a more complete treatment of correlation effects in the internal region than would be possible with other packages. RMATRX II (Burke et al. 1994) utilises LS-coupling in the internal region. Working in LS at this stage ultimately results in more available computing memory and this in turn permits the inclusion of more sophisticated CI wavefunctions representing both the target and the (N + 1)-scattering system. For this particular range of Z-values, it is deemed that correlation effects play a more significant role than relativistic effects and thus their inclusion is paramount. The parallel PSTGF program (Ballance & Griffin 2004) was utilised in the external region. The code framework adopted in the present calculation is detailed in Fig. 1.

RMATRX II (Burke et al. 1994) comprises three main stages - RAD computes the radial integrals, ANG computes the angular integrals and these are combined in HAM to form the Hamiltonian matrix elements. It is also possible to diagonalise the Hamiltonian matrix within HAM, however if the dimensions of this matrix become too large another parallel diagonalisation code is utilised. An LS calculation is performed up to this point. We now turn our attention to the new FINE code (Burke, V. M., private communication) and the inclusion of relativistic fine-structure effects. For atoms or ions with ${\rm Z} < 30$ we can transform the R-matrix in LS-coupling at energy E, $\underline{R}^{LS\pi}(E)$, into an R-matrix in pair coupling, $\underline{R}^{J\pi}(E)$. This is carried out on the R-matrix boundary between the internal and external regions. However, instead of carrying out this transformation at each energy, we can transform the energy independent surface amplitudes. Hence the re-coupling is performed only once for each $LS\pi$ and $J\pi$ symmetry rather than for each scattering energy E. This is performed by the new program FINE. To take account of term splitting in the target, the $\underline{R}^{J\pi}$ can be further transformed using term coupling coefficients which are the mixing coefficients for the individual $L_{i}S_{i}\pi_{i}$ states forming a $J_{i}\pi_{i}$ state. Following the FINE transformation, the fine-structure levels agree well with the observed splittings.

The advantages of this particular transformation method are twofold over existing approaches. Firstly, using LS-coupling in the internal region allows for the inclusion of sophisticated CI wavefunctions for both the target and scattering complex. Secondly, transforming the R-matrix on the R-matrix boundary, as opposed to the asymptotic boundary, allows fine-structure channels to be included in the external region. The FINE approach has been tested against the RMATRX I Breit-Pauli (Berrington et al. 1995) approach for a number of ions including Cr II and Ni V. The results were found to be of a similar accuracy. A test against the ICFT method of Griffin et al. (1998) is currently underway. However, it should be noted that the use of the FINE code includes relativistic effects in the external and asymptotic regions whereas the ICFT method includes these effects only asymptotically.

\begin{figure} \par\includegraphics[width=6cm,clip]{13571fg1.eps} \vspace*{2mm} \end{figure} Figure 1:

Code framework of the present collision calculation.

Open with DEXTER

The theoretical target model discussed previously was adopted to compute converged total collision strengths and Maxwellian averaged effective collision strengths for all of the fine-structure forbidden transitions in this study. The effective collision strengths, $\Upsilon_{{ij}}$, are obtained by averaging the finely resolved collision strengths over a Maxwellian distribution of electron velocities to yield

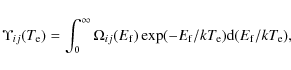
\begin{displaymath}\Upsilon_{{ij}}(T_{{\rm e}}) = \int_{0}^{\infty} \Omega_{{ij}... ...p(-E_{{\rm f}}/kT_{{\rm e}}){\rm d}(E_{{\rm f}}/kT_{{\rm e}}), \end{displaymath} (2)

where $\Omega_{{ij}}$ is the collision strength corresponding to the excitation from level i to level j, $E_{{\rm f}}$ is the final kinetic energy of the electron, $T_{{\rm e}}$ is the electron temperature in Kelvin and k is Boltzmann's constant.

The present 295 jj-level calculation included all incident partial waves with angular momentum $J \leq 12$, for all singlet, triplet, quintet and septet multiplicities and both even and odd parities, giving rise to a total of 104 (N+1)-electron symmetry contributions. This representation is sufficient to ensure convergence of the collision strengths for the optically forbidden transitions with which we are primarily concerned in this work. A total of 20 continuum orbitals were included per orbital angular momentum and the R-matrix boundary radius was set at 10 au to ensure convergence in the electron-impact energy range of interest from 0 to 10 Rydbergs. Following thorough testing of collision strength convergence with decreasing increment, a very fine mesh of incident electron energies ( $2.0 \times 10^{-4}$ Rydbergs) was used in the external region in order to ensure the proper resolution of the complex autoionising resonance structures which dominate the low-enery scattering region as far as the highest-lying target threshold. Approximately 12 000 individual energy points were considered in this region. Above this, where no resonances occur, a much coarser mesh can be adopted. Approximately 200 points were considered above the highest-lying target threshold to the final energy of interest at 10 Rydbergs. Maxwellian averaged effective collision strengths were evaluated at 27 individual electron temperatures ranging from 30 to 100 000 K. This temperature range is sufficient to encompass all temperatures significant to both astrophysical and plasma applications.

\begin{figure} \par\includegraphics[width=9cm,clip]{13571fg2.eps}\vspace*{4mm} \end{figure} Figure 2:

Effective collision strength as a function of log electron temperature in Kelvin for the $3{{\rm d}}^{9}$ $^{2}{{\rm D}}^{{\rm e}}_{5/2}$ - $3{{\rm d}}^{9}$ $^{2}{{\rm D}}^{{\rm e}}_{3/2}$ fine-structure transition: diamonds - present 295 level calculation, circles - 77 level calculation of Bautista (2004), stars - 17 level calculation of Bautista & Pradhan (1996).

Open with DEXTER

\begin{figure} \includegraphics[width=9cm,clip]{13571fg3.eps}\vspace*{3mm} \end{figure} Figure 3:

Effective collision strength as a function of log electron temperature in Kelvin for the $3{{\rm d}}^{9}$ $^{2}{{\rm D}}^{{\rm e}}_{5/2}$ - $3{{\rm d}}^{8}4{{\rm s}}$ $^{4}{{\rm F}}^{{\rm e}}_{9/2}$ fine-structure transition: diamonds - present 295 level calculation, circles - 77 level calculation of Bautista (2004), stars - 17 level calculation of Bautista & Pradhan (1996).

Open with DEXTER
\begin{figure} \includegraphics[width=9cm,clip]{13571fg4.eps}\vspace*{3mm} \end{figure} Figure 4:

Effective collision strength as a function of log electron temperature in Kelvin for the $3{{\rm d}}^{9}$ $^{2}{{\rm D}}^{{\rm e}}_{5/2}$ - $3{{\rm d}}^{8}4{{\rm s}}$ $^{4}{{\rm F}}^{{\rm e}}_{7/2}$ fine-structure transition: diamonds - present 295 level calculation, circles - 77 level calculation of Bautista (2004), stars - 17 level calculation of Bautista & Pradhan (1996).

Open with DEXTER

\begin{figure} \par\includegraphics[width=9cm,clip]{13571fg5.eps}\vspace*{2mm} \end{figure} Figure 5:

Effective collision strength as a function of log electron temperature in Kelvin for the $3{{\rm d}}^{9}$ $^{2}{{\rm D}}^{{\rm e}}_{5/2}$ - $3{{\rm d}}^{8}4{{\rm s}}$ $^{4}{{\rm F}}^{{\rm e}}_{3/2}$ fine-structure transition: diamonds - present 295 level calculation, circles - 77 level calculation of Bautista (2004), stars - 17 level calculation of Bautista & Pradhan (1996).

Open with DEXTER

3 Results and discussion

Collision strengths and Maxwellian averaged effective collision strengths have been computed for a total of 43 365 transitions. However, in this particular study we focus solely on the 153 forbidden transitions of interest between the energetically lowest 18 levels of Ni II. It is not feasible to tabulate the collision strengths due to the large number of incident electron energies involved. These data are available in electronic form at the CDS. We focus our attention in this section on both a graphical and qualitative synopsis.

Figures 2-5 present the total effective collision strength as a function of log electron temperature in Kelvin for a number of fine-structure forbidden transitions. Comparisons are made with all of the currently available effective collision strength data, including the rates corresponding to the 17 level calculation of Bautista & Pradhan (1996) and the rates affiliated with the more sophisticated 77 level approximation of Bautista (2004). Agreement between the early work of Bautista & Pradhan (1996) and the latter works is exceptionally poor for all of the transitions presented, with the values of Bautista & Pradhan (1996) lying an order of magnitude lower than the present values for the majority of temperatures. Agreement between the present rates and the most recent theoretical work of Bautista (2004) is excellent for some transitions, particularly across the entire temperature range for the transition between the ground state terms, $3{{\rm d}}^{9}$ $^{2}{{\rm D}}^{{\rm e}}_{5/2}$ - $3{{\rm d}}^{9}$ $^{2}{{\rm D}}^{{\rm e}}_{3/2}$, as illustrated in Fig. 2, and for some high temperatures for the transition from the ground state, $3{{\rm d}}^{9}$ $^{2}{{\rm D}}^{{\rm e}}_{5/2}$, to the excited state, $3{{\rm d}}^{8}4{{\rm s}}$ $^{4}{{\rm F}}^{{\rm e}}_{3/2}$, as presented in Fig. 5. While agreement is still considered to be good for transitions $3{{\rm d}}^{9}$ $^{2}{{\rm D}}^{{\rm e}}_{5/2}$ - $3{{\rm d}}^{8}4{{\rm s}}$ $^{4}{{\rm F}}^{{\rm e}}_{9/2}$ and $3{{\rm d}}^{9}$ $^{2}{{\rm D}}^{{\rm e}}_{5/2}$ - $3{{\rm d}}^{8}4{{\rm s}}$ $^{4}{{\rm F}}^{{\rm e}}_{7/2}$, as illustrated in Figs. 3 and 4 respectively, the values of Bautista (2004) are somewhat larger than the current values in each case. The predicted rates of Bautitsta (2004) are on average ${10\%}$ higher than the present values at comparable temperatures for the $3{{\rm d}}^{9}$ $^{2}{{\rm D}}^{{\rm e}}_{5/2}$ - $3{{\rm d}}^{8}4{{\rm s}}$ $^{4}{{\rm F}}^{{\rm e}}_{9/2}$ transition presented in Fig. 3. This increases to an average of approximately $21\%$ for the $3{{\rm d}}^{9}$ $^{2}{{\rm D}}^{{\rm e}}_{5/2}$ - $3{{\rm d}}^{8}4{{\rm s}}$ $^{4}{{\rm F}}^{{\rm e}}_{7/2}$ transition presented in Fig. 4. This satisfactory agreement is not retained throughout however.

Two particular transitions were singled out for discussion in the early work of Bautista & Pradhan (1996). Fine-structure collision strengths and the associated effective collision strengths were computed for the two transitions from the ground state to consecutive excited levels. It should be noted at this point that this is the only fine-structure collision strength data in the present literature available for comparative purposes.

\begin{figure} \par\includegraphics[width=9cm,clip]{13571fg6.eps} \end{figure} Figure 6:

Collision strength for the $3{{\rm d}}^{9}$ $^{2}{{\rm D}}^{{\rm e}}_{5/2}$ - $3{{\rm d}}^{8}4{{\rm s}}$ $^{2}{{\rm F}}^{{\rm e}}_{7/2}$ fine-structure transition: solid - present 295 level calculation, dashed - 17 level calculation of Bautista & Pradhan (1996).

Open with DEXTER

In Fig. 6 we present the collision strength as a function of incident electron energy in Rydbergs, for the forbidden transition from the ground state, $3{{\rm d}}^{9}$ $^{2}{{\rm D}}^{{\rm e}}_{5/2}$, to the excited state, $3{{\rm d}}^{8}4{{\rm s}}$ $^{2}{{\rm F}}^{{\rm e}}_{7/2}$. Although collision strengths have been computed for energies up to 10 Rydbergs in the present calculation, attention is concentrated here on the low-energy scattering region where the masses of Rydberg resonances converging onto each target state threshold are abundantly clear. Comparisons are made between the present 295 level approximation and the early 17 level calculation of Bautista & Pradhan (1996). The entire background cross section of Bautista & Pradhan (1996) appears to lie higher than the present dataset, with minimal resonance activity observed. By considering only 1000 points in the low-energy scattering region, this early calculation has not allowed for the proper delineation of complex resonance features. These structures are known to significantly enhance the Maxwellian averaged effective collision strengths. The extent of this enhancement in this particular case is clearly demonstrated in Fig. 7, where we consider the corresponding effective collision strength. Comparisons are made with the earlier evaluation of Bautista & Pradhan (1996) and the most recent data of Bautista (2004). Agreement between the present rates and the predicted values of Bautista & Pradhan (1996) is at it's best for this particular transition. However, the differences are still considerable. The calculation of Bautista & Pradhan (1996) yields effective collision strengths which are up to $37\%$ higher than the present values at comparable low temperatures, and up to $65\%$ lower at higher temperatures. The predictions of Bautista (2004) present a substantially different rate profile to that obtained in the present 295 level approximation, most notably apropos to shape. Analogous to some of the previous transitions considered in this paper, the values of Bautista (2004) appear to overestimate the current effective collision strength across the entire temperature range. This overestimation is particularly sizable at the lowest and highest temperatures considered in Bautista's (2004) study, where differences of up to $40\%$ are observed at comparable temperatu

\begin{figure} \par\includegraphics[width=9cm,clip]{13571fg7.eps}\vspace*{-2mm} \end{figure} Figure 7:

Effective collision strength as a function of log electron temperature in Kelvin for the $3{{\rm d}}^{9}$ $^{2}{{\rm D}}^{{\rm e}}_{5/2}$ - $3{{\rm d}}^{8}4{{\rm s}}$ $^{2}{{\rm F}}^{{\rm e}}_{7/2}$ fine-structure transition: diamonds - present 295 level calculation, circles - 77 level calculation of Bautista (2004), stars - 17 level calculation of Bautista & Pradhan (1996).

Open with DEXTER
res.

In Fig. 8 we present the collision strength as a function of incident electron energy in Rydbergs, for the fine-structure forbidden transition, $3{{\rm d}}^{9}$ $^{2}{{\rm D}}^{{\rm e}}_{5/2}$ - $3{{\rm d}}^{8}4{{\rm s}}$ $^{2}{{\rm F}}^{{\rm e}}_{5/2}$. Again the present 295 level approximation is compared with the earlier 17 level calculation of Bautista & Pradhan (1996). A similar trend to that noted in Fig. 6 is observed. The background cross section of Bautista & Pradhan (1996) lies somewhat lower than the present across the entire energy range, with little resonance activity discerned. The effect of these differing collision strengths on the corresponding Maxwellian averaged values is illustrated in Fig. 9. Comparisons are once again made with the same theoretical works previously acknowledged. The values of Bautista & Pradhan (1996) present a very different rate formation when compared with the present data. They underestimate the present predictions across the entire temperature range by factors of three to seven. The data of Bautista (2004) is considerably different to that obtained in the present study, significantly underestimating the current rates at the lowest temperatures considered in this 2004 evaluation. The present work predicts these values to be up to twice as large. Unfortunately it is difficult to understand the differing rate profiles of Bautista (2004) and those obtained using the present evaluation as we do not have the fine-structure collision strengths computed by Bautista (2004) which were used to obtain the associated Maxwellian averaged effective collision strengths. The conflicting rate profiles presented in both Figs. 7 and 9 will undoubtedly influence any astrophysical or plasma modelling applications which depend on these effective collision strength data. The importance of properly resolving low-energy resonance structures is imperative in the calculation of Maxwellian averaged effective collision strengths. Today's new generation of parallel codes and computing resources permits calculations of the desired sophistication, enabling the computation of effective collision strengths of the highest degree of accuracy attainable.

The effective collision strengths computed in the present 295 jj-level approximation for each of the 153 low-lying forbidden fine-structure transitions of particular interest to this study. Maxwellian averaged values for each of the 27 individual electron temperatures considered are tabulated.

\begin{figure} \par\includegraphics[width=9cm,clip]{13571fg8.eps} \vspace*{3mm} \end{figure} Figure 8:

Collision strength for the $3{{\rm d}}^{9}$ $^{2}{{\rm D}}^{{\rm e}}_{5/2}$ - $3{{\rm d}}^{8}4{{\rm s}}$ $^{2}{{\rm F}}^{{\rm e}}_{5/2}$ fine-structure transition: solid - present 295 level calculation, dashed - 17 level calculation of Bautista & Pradhan (1996).

Open with DEXTER

\begin{figure} \par\includegraphics[width=9cm,clip]{13571fg9.eps}\vspace*{3mm} \end{figure} Figure 9:

Effective collision strength as a function of log electron temperature in Kelvin for the $3{{\rm d}}^{9}$ $^{2}{{\rm D}}^{{\rm e}}_{5/2}$ - $3{{\rm d}}^{8}4{{\rm s}}$ $^{2}{{\rm F}}^{{\rm e}}_{5/2}$ fine-structure transition: diamonds - present 295 level calculation, circles - 77 level calculation of Bautista (2004), stars - 17 level calculation of Bautista & Pradhan (1996).

Open with DEXTER

4 Conclusions

We have come a long way in the last 30 years with electron-impact excitation calculations for key Fe-peak elements such as Ni II, gradually increasing in sophistication alongside the development of more powerful codes and computing capabilities. In the present work we report the computation of collision strengths and effective collision strengths for the 153 fine-structure forbidden transitions among the energetically lowest 18 levels of the complex Ni II ion, encompassing the infrared, optical and ultraviolet lines of interest. The collision calculations were carried out using the new parallel RMATRX II (Burke et al. 1994) R-matrix packages, which have been recently extended to account for relativistic fine-structure effects via the FINE code (Burke, V. M., private communication). To our knowledge, this is the first application of this innovative program. The theoretical target model included the $3{{\rm d}}^{9}$, $3{{\rm d}}^{8}4{{\rm s}}$, $3{{\rm d}}^{8}4{{\rm p}}$, $3{{\rm d}}^{7}4{{\rm s}}^{2}$ and $3{{\rm d}}^{7}4{{\rm s}}4{{\rm p}}$ basis configurations, giving rise to a sophisticated 295 jj-level, 1930 coupled channel scattering complex - the most extensive theoretical study undertaken to date. The astrophysically important effective collision strengths were computed for 27 individual electron temperatures. The comparison with the work of Bautista (2004) yields a mixed bag. For some transitions, the agreement with the present rates is impressive, while for others there are large discrepancies. It is difficult to determine where the main differences lie - structure, code, CI or resonance resolution. The earlier work of Bautista & Pradhan (1996) exhibits poor agreement with the present rates for all transitions. The present work further emphasises the paramount importance of properly resolving the complex auto-ionising resonance features dominating the low-energy scattering region. Thousands of energy points have been considered in the current evaluation to ensure this accurate delineation, thereby obtaining Maxwellian averaged effective collision strengths of the highest degree of accuracy.

Acknowledgements
The authors wish to acknowledge the years of work of V. M. Burke and C. J. Noble at Daresbury Laboratory (UK) who have been responsible for the development of the internal region codes. Special acknowledgement is extended to M. Bautista for supplying unpublished data for comparison purposes. The authors wish to thank the referee for their constructive comments and suggestions. The work presented in this paper is supported by STFC and C. M. Cassidy is supported by a DEL Studentship. The computations were carried out on the IBM HPCx facility at the CLRC Daresbury Laboratory.

References

  1. Badnell, N. R. 1997, J. Phys. B: At. Mol. Opt. Phys., 30, 1 [Google Scholar]
  2. Ballance, C. P., & Griffin, D. C. 2004, J. Phys. B, 37, 2943 [NASA ADS] [CrossRef] [Google Scholar]
  3. Bautista, M. A. 2004, A&A, 420, 763 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Bautista, M. A., & Pradhan, A. K. 1996, A&ASS, 115, 551 [NASA ADS] [Google Scholar]
  5. Bautista, M. A., Hartman, H., Gull, T. R., Smith, N., & Lodders, K. 2006, MNRAS, 370, 1991 [NASA ADS] [CrossRef] [Google Scholar]
  6. Berrington, K. A., Eissner, W., & Norrington, P. H. 1995, Comput. Phys. Commun., 92, 290 [NASA ADS] [CrossRef] [Google Scholar]
  7. Burke, V. M., & Noble, C. J. 1995, Comput. Phys. Commun., 85, 471 [NASA ADS] [CrossRef] [Google Scholar]
  8. Burke, P. G., Burke, V. M., & Dunseath, K. M. 1994, J. Phys. B: At. Mol. Opt. Phys., 27, 5341 [Google Scholar]
  9. Clementi, E., & Roetti, C. 1974, At. Data Nucl. Data Tables, 14, 3 [Google Scholar]
  10. Davidson, K., Smith, N., Gull, T. R., Ishibashi, K. & Hillier, D. J. 2001, AJ, 121, 1569 [NASA ADS] [CrossRef] [Google Scholar]
  11. Eissner, W., & Nussbaumer, H. 1969, J. Phys. B, 2, 1028 [Google Scholar]
  12. Griffin, D. C., Badnell, N. R., & Pindzola, M. S. 1998, J. Phys. B: At. Mol. Opt. Phys., 31, 3713 [Google Scholar]
  13. Hartman, H., Gull, T., Johansson, S., Smith, N., & HST Eta Carinae Treasury Project Team 2004, A&A, 419, 215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Hibbert, A. 1975, Comput. Phys. Comm., 9, 141 [Google Scholar]
  15. Hummer, D. G., Berrington, K. A., Eissner, W., et al. 1993, A&A, 279, 298 [NASA ADS] [Google Scholar]
  16. NIST Atomic Spectra Database, http://physics.nist.gov/PhysRefData [Google Scholar]
  17. Nussbaumer, H., & Storey, P. J. 1978, A&A, 64, 139 [NASA ADS] [Google Scholar]
  18. Nussbaumer, H., & Storey, P. J. 1982, A&A, 110, 295 [NASA ADS] [Google Scholar]
  19. Sugar, J., & Corliss, C. 1985, J. Phys. Chem. Ref. Data, 14, Supplement, 2 [Google Scholar]
  20. Sunderland, A. G., Noble, C. J., Burke, V. M., & Burke, P. G. 2002, Comput. Phys. Commun., 145, 311 [NASA ADS] [CrossRef] [Google Scholar]
  21. Véron-Cetty, M. P., Joly, M., Véron, P., Boroson, T., Lipari, S., & Ogle, P. 2006, A&A, 451, 851 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Vreeswijk, P. M., Ledoux, C., Smette, A., et al. 2007, A&A, 468, 83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Watts, M. S. T., Berrington, K. A., Burke, P. G., & Burke, V. M. 1996, J. Phys. B: At. Mol. Opt. Phys., 29, L505 [NASA ADS] [CrossRef] [Google Scholar]

Footnotes

... transitions[*]
Table 2 is only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/513/A55
Copyright ESO 2010

All Tables

Table 1:   LS target state energies in Rydbergs relative to the $3{{\rm d}}^{9}$ $^{2}{{\rm D}}^{{\rm e}}$ Ni II ground state.

All Figures

  \begin{figure} \par\includegraphics[width=6cm,clip]{13571fg1.eps} \vspace*{2mm} \end{figure} Figure 1:

Code framework of the present collision calculation.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{13571fg2.eps}\vspace*{4mm} \end{figure} Figure 2:

Effective collision strength as a function of log electron temperature in Kelvin for the $3{{\rm d}}^{9}$ $^{2}{{\rm D}}^{{\rm e}}_{5/2}$ - $3{{\rm d}}^{9}$ $^{2}{{\rm D}}^{{\rm e}}_{3/2}$ fine-structure transition: diamonds - present 295 level calculation, circles - 77 level calculation of Bautista (2004), stars - 17 level calculation of Bautista & Pradhan (1996).

Open with DEXTER
In the text

  \begin{figure} \includegraphics[width=9cm,clip]{13571fg3.eps}\vspace*{3mm} \end{figure} Figure 3:

Effective collision strength as a function of log electron temperature in Kelvin for the $3{{\rm d}}^{9}$ $^{2}{{\rm D}}^{{\rm e}}_{5/2}$ - $3{{\rm d}}^{8}4{{\rm s}}$ $^{4}{{\rm F}}^{{\rm e}}_{9/2}$ fine-structure transition: diamonds - present 295 level calculation, circles - 77 level calculation of Bautista (2004), stars - 17 level calculation of Bautista & Pradhan (1996).

Open with DEXTER
In the text

  \begin{figure} \includegraphics[width=9cm,clip]{13571fg4.eps}\vspace*{3mm} \end{figure} Figure 4:

Effective collision strength as a function of log electron temperature in Kelvin for the $3{{\rm d}}^{9}$ $^{2}{{\rm D}}^{{\rm e}}_{5/2}$ - $3{{\rm d}}^{8}4{{\rm s}}$ $^{4}{{\rm F}}^{{\rm e}}_{7/2}$ fine-structure transition: diamonds - present 295 level calculation, circles - 77 level calculation of Bautista (2004), stars - 17 level calculation of Bautista & Pradhan (1996).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{13571fg5.eps}\vspace*{2mm} \end{figure} Figure 5:

Effective collision strength as a function of log electron temperature in Kelvin for the $3{{\rm d}}^{9}$ $^{2}{{\rm D}}^{{\rm e}}_{5/2}$ - $3{{\rm d}}^{8}4{{\rm s}}$ $^{4}{{\rm F}}^{{\rm e}}_{3/2}$ fine-structure transition: diamonds - present 295 level calculation, circles - 77 level calculation of Bautista (2004), stars - 17 level calculation of Bautista & Pradhan (1996).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{13571fg6.eps} \end{figure} Figure 6:

Collision strength for the $3{{\rm d}}^{9}$ $^{2}{{\rm D}}^{{\rm e}}_{5/2}$ - $3{{\rm d}}^{8}4{{\rm s}}$ $^{2}{{\rm F}}^{{\rm e}}_{7/2}$ fine-structure transition: solid - present 295 level calculation, dashed - 17 level calculation of Bautista & Pradhan (1996).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{13571fg7.eps}\vspace*{-2mm} \end{figure} Figure 7:

Effective collision strength as a function of log electron temperature in Kelvin for the $3{{\rm d}}^{9}$ $^{2}{{\rm D}}^{{\rm e}}_{5/2}$ - $3{{\rm d}}^{8}4{{\rm s}}$ $^{2}{{\rm F}}^{{\rm e}}_{7/2}$ fine-structure transition: diamonds - present 295 level calculation, circles - 77 level calculation of Bautista (2004), stars - 17 level calculation of Bautista & Pradhan (1996).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{13571fg8.eps} \vspace*{3mm} \end{figure} Figure 8:

Collision strength for the $3{{\rm d}}^{9}$ $^{2}{{\rm D}}^{{\rm e}}_{5/2}$ - $3{{\rm d}}^{8}4{{\rm s}}$ $^{2}{{\rm F}}^{{\rm e}}_{5/2}$ fine-structure transition: solid - present 295 level calculation, dashed - 17 level calculation of Bautista & Pradhan (1996).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{13571fg9.eps}\vspace*{3mm} \end{figure} Figure 9:

Effective collision strength as a function of log electron temperature in Kelvin for the $3{{\rm d}}^{9}$ $^{2}{{\rm D}}^{{\rm e}}_{5/2}$ - $3{{\rm d}}^{8}4{{\rm s}}$ $^{2}{{\rm F}}^{{\rm e}}_{5/2}$ fine-structure transition: diamonds - present 295 level calculation, circles - 77 level calculation of Bautista (2004), stars - 17 level calculation of Bautista & Pradhan (1996).

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.