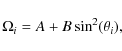EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 513 (April 2010) A&A, 513 (2010) A48 Full HTML
Free Access
Issue
A&A
Volume 513, April 2010
Article Number A48
Number of page(s) 7
Section The Sun
DOI https://doi.org/10.1051/0004-6361/200913193
Published online 23 April 2010
A&A 513, A48 (2010)

Solar active regions: a nonparametric statistical analysis

J. Pelt1 - M. J. Korpi2,3 - I. Tuominen2

1 - Tartu Observatory, 61602 Tõravere, Estonia
2 - Observatory, PO Box 14, 00014 University of Helsinki, Finland
3 - NORDITA, AlbaNova University Center, Roslagstullsbacken 23, 10691 Stockholm, Sweden

Received 27 August 2009 / Accepted 1 February 2010

Abstract
Context. The sunspots and other solar activity indicators tend to cluster on the surface of the Sun. These clusters very often occur at certain longitudes that persist in time. It is of general interest to find new and simple ways to characterize the observed distributions of different indicators and their behaviour in time.
Aims. In the present work we use Greenwich sunspot data to evaluate the statistical but not totally coherent stability of the sunspot distribution along latitudes as well as longitudes. The aim was to obtain information on the longitudinal distribution of the underlying spot-generating mechanism rather than on the distribution and migration of sunspots or sunspot groups on the solar surface. Therefore only sunspot groups were included in the analysis, and only the time of their first appearance was used.
Methods. We used a simple nonparametric approach to reveal sunspot migration patterns and their persistency.
Results. Our analysis shows that regions where spots are generated tend to rotate differentially as the spots and spot groups themselves do. The spatial correlations in activity, however, tend to break down relatively fast, during 7-15 solar rotations.
Conclusions. This study provides a challenge for solar dynamo models, as our results indicate that the non-axisymmetric spot-generating mechanism experiences differential rotation (known as phase mixing in dynamo theory). The new nonparametric method introduced here, completely independent of the choice of the longitudinal distribution of sunspots, was found to be a useful tool for spatio-temporal analysis of surface features.

Key words: Sun: activity - magnetic fields - sunspots - methods: statistical

1 Introduction

Modern observations of the Sun are so rich in detail that astronomers are eventually facing an embarrassment of riches. When spatio-temporal properties of the smaller features - say spots, flares, etc. - are treated with well-established vigour, the analysis of spatially larger or temporarily longer patterns is very complicated. Even the nomenclature of the phenomena is not well established - for instance the time-space cluster of the local phenomena can be called ``active longitude'' (Losh 1938; Vitinskij 1969), ``Sonnefleckenherd'' (``flock of sunspots'', Becker 1955), ``active region'' (Bumba & Howard 1965), ``sunspot nest'' (Castenmiller et al. 1986), ``complex of activity'' (Gaizauskas et al. 1983) or ``hot spot'' (Bai 1988). There is, in addition, a problem with the proper definition of such extended patterns.

It is generally thought that the tracers of solar activity - sunpots, flares, etc. - are randomly generated manifestations of the larger scale mean magnetic field of the Sun generated by a hydromagnetic dynamo process. An analogy with a submerged animal blowing out bubbles is quite appropriate in this context (see Bai 2003). What can we tell about the swimming speed and size of the animal, if only random bubbles are observable? How deep in water is the animal?

The answers to these kinds of questions depend very much on the method of analysis used. Very often subjective judgement is involved, either through steps of visual processing or through involvement of freely chosen procedure parameters (bin sizes, number of longitudinal modes, detection limits, preselection criteria etc.).

From the statistical analysis point of view we can divide the previously used methods along two lines: how the input data is transformed before computing final statistics and what kind of statistics are used. Some typical but random examples:

  • aggregated data (daily Wolf numbers) and correlation analysis (Bogart 1982);
  • raw heliographic longitudes and longitude-wise binning (Trotter & Billings 1962; Warwick 1965);
  • transformed (using trial rotation velocity) longitudes and 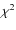$\chi ^2$ statistic (Bai 1987);
  • transformed (using latitude-dependent rotation velocities) longitudes and pattern matching (Usoskin et al. 2005; Pelt et al. 2006, hereafter PBKT);
  • spherical harmonic decomposition and time series analysis of mode amplitudes, phases and phase-walks (Juckett 2003).
The third important aspect of the analysis is the time coverage of the observations. It is quite easy to find recurrent patterns in short time series, but coherence tends to break down very fast for longer datasets.

We try here to return to the square one in a certain sense, back to the very basics. By very simple considerations and avoiding all freely chosen parameters we try to get answers to these questions:

  • is there a tendency for surface elements to occur at certain longitudes that persist over time?
  • how are this persistence and the differential rotation of the surface elements connected?
  • how long do typical correlations in activity persist?
Our aim is not so much to perform another statistical analysis of the well-known and already extensively analysed data, but to introduce a new nonparametric method of analysis involving no physical, geometrical or statistical prior assumptions. In Sect. 2 we introduce our method of analysis, in Sect. 3 we present the results obtained for the Greenwich sunspot data set, and finally in Sects. 4 and 5 we discuss our results in the light of previous statistical analyses.

2 Method of analysis

2.1 Nonparametric method

Let us assume that we have two sets of longitudes: $\lambda_{i}^{(1)},i=1,\dots,N$ and $\lambda_{j}^{(2)},j=1,\dots,M$. Their values belong to the interval $0^{\circ}\le \lambda \le 360^{\circ}$ and we assume that N<=M (if otherwise, we can always swap the sets). We aim to characterize the similarity or the difference between the two longitude distributions somehow. The general theory of directional measurements is considered in mathematical statistics (see for instance the latest monograph by Mardia & Jupp 2000, and references therein), but here we need a more specific method, namely one without any underlying statistical assumptions or parametric models for the distributions involved.

We propose the following very simple nonparametric method: The circular distance between two longitudes $\lambda_k$ and $\lambda_l$ we define as usually done

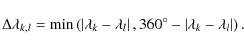
\begin{displaymath}\Delta \lambda _{k,l} = \min \left(\left\vert {\lambda _k - \... ...rc - \left\vert {\lambda _k - \lambda _l } \right\vert\right). \end{displaymath} (1)

Let us take a particular longitude $\lambda_{k}^{(1)}$ from the first set. Among the longitudes of the second set there is always a value whose circular distance from the selected value is the smallest, let us denote this distance as $\Delta \lambda_k$. All together we can compute N such values - for each longitude in the first set. Now we compute a mean of these distances and denote it simply as $\Delta$. It is quite clear that for the particular case when the first set is just a subset of the second one, $\Delta= 0$. If the sets differ, then $\Delta>0$. In principle this distance between two longitude sets is already a useful statistic; its full power, however, is revealed if we properly normalize it.

For the particular set sizes N and M we can compute the mathematical expectation of $\Delta$ for completely random distributions of longitudes in both sets. Let us denote this expectation as  $\bar \Delta$. Our final statistic, which measures the statistical distance between the two sets of longitudes, is then

\begin{displaymath}D = \frac{\Delta }{{\bar \Delta }}\cdot \end{displaymath} (2)

If we wish to stress that the distance D is computed for two particular indexed longitude sets, say for index n (N longitudes) and index m (M longitudes) we use the notation

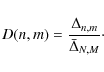
\begin{displaymath}D(n,m) = \frac{{\Delta _{n,m} }}{{\bar \Delta _{N,M} }}\cdot \end{displaymath} (3)

The mathematical expectations ${\bar \Delta _{N,M}}$ depend only on the integers N and M, and can be pretabulated. In our calculations we used approximations obtained from randomly generated longitudes for 10 000 statistically independent runs.

It is quite obvious that for absolutely random pairs of longitude sets our distance will have a value around 1. For weakly correlated sets values are less than 1, and values higher than 1 can occur when the longitude sets involved are constrained in a certain way due to which they cannot form all the patterns that occur for randomly generated sets. For sunspot groups, for instance, the distributions are constrained by group sizes. Randomly generated points can fall arbitrarily close, which is not true for sunspot longitudes, because for them the group centres are separated by definition.

Now that we have the statistic to measure distances between different distributions of longitudes we can go further. For a sequence of longitude sets counted by k we can compute a mean distance between neighbouring sets

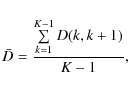
\begin{displaymath}\bar D = \frac{{\sum\limits_{k = 1}^{K - 1} {D(k,k + 1)} }}{{K - 1}}, \end{displaymath} (4)

where K is the number of the sets. We can also investigate how the distance depends on the mutual positions of particular sets

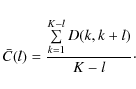
\begin{displaymath}\bar C(l) = \frac{{\sum\limits_{k = 1}^{K - l} {D(k,k + l)} }}{{K - l}}\cdot \end{displaymath} (5)

Obviously $\bar D = \bar C(1)$. The statistic $\bar D$ allows us to investigate the rotational properties of the sunspot groups, and the statistic $\bar C(l)$ will be used to estimate how persistent the longitudinal correlations are.

2.2 Rotation and frames

Heliographic longitudes are measured using the so called Carrington frame, which rotates against fixed stars with the exact period of $P_{\rm C}=25.38$days. The mean rotation period if observed from the Earth is PO=27.2753 days. The Carrington frame is a formal construct and real features on the Sun need not follow it exactly.

Let us fix a certain longitude $\lambda^{(C)}$ of a particular persistent feature on the Sun rotating with the Carrington angular velocity. Then its longitude for different Carrington rotations i will be fixed: $\lambda_i^{(C)} = \left[ {\lambda^{(C)} + i \times 360^{\circ}} \right] = \lambda^{(C)}$, angular brackets denoting here and below reduction to the interval $(0,360^{\circ})$. Because the angular velocity of the Carrington frame is $\Omega_{\rm C} = \frac{{360^{\circ}}}{{P_{\rm C} }}$ degrees per day, we can rewrite the cycle-dependent sequence of longitudes as

\begin{displaymath}% \lambda_i^{(C)} = \left[ {\lambda^{(C)} + i \times \Omega _{\rm C} P_{\rm C} } \right], \quad i = 0,1, \ldots \end{displaymath} (6)

The actual angular velocity of an arbitrary feature on the Sun need not to be exactly $\Omega_{\rm C}$. Let the longitude of the first occurrence of a such feature be $\lambda$. Then its cyclic reoccurrences can be described by a correcting term $\Delta \Omega$:

\begin{displaymath}% \lambda _i = \left[ {\lambda + i \times (\Omega _{\rm C} + \Delta \Omega )P_{\rm C} } \right], \quad i = 0,1, \ldots \end{displaymath} (7)

The corrected frame rotates against the Carrington frame with an angular velocity of $\Delta \Omega$ degrees per day. For convenience we introduce also a notion for sidereal angular velocity of the accelerated or decelerated frames $\Omega=\Omega_{\rm C}+\Delta \Omega$.

Below we measure the angular velocity in degrees per day, latitude in degrees, and periods in days, and give the values in these units.

2.3 Algorithms

To analyse different frames and the corresponding distributions of modified longitudes we use the statistics described above.

As an input data we take a set of time-tagged longitudes $t_l,\lambda_l,l=1,\dots,L$, amounting to L items of data. Using the time points tl we divide the records into subintervals with the length 27.2753 (Carrington rotations). This procedure is not absolutely exact because the observation timing depends on the somewhat excentric orbit of the Earth. Fortunately the errors involved are small and we can ignore them. From the point of generality and objectivity our choice is quite natural. Historical observations are all done from Earth and consequently the features can be observed only half the time. However, during the Carrington rotation we can record what happens at all longitudes. As far as timing is considered, due to the rotation some processes can actually start earlier than observed. This excludes short-lived processes (shorter than Carrington rotation) from our analysis.

It is also possible to divide observations into longer subintervals. Then we increase the statistical stability of our estimates (more observations in subsets), but lose resolution in time. We consider a time step with the length of one Carrington rotation to be optimal.

We assume that the features on the surface of the Sun rotate with angular velocity, which is different from the Carrington velocity $\Omega_{\rm C}$. For a certain trial angular velocity $\Omega$ and for each Carrington cycle i we can compute longitude corrections:

\begin{displaymath}% \Lambda_i = i \times \Delta \Omega P_{\rm C} = i \times (\Omega - \Omega _{\rm C} )P_{\rm C} , \quad i = 0,1, \ldots \end{displaymath} (8)

By substracting rotation-number dependent corrections from measured longitudes and properly reducing results to an interval (0,360) we build transformed longitudes:

\begin{displaymath}% \lambda^{(T)}_i=\left [ \lambda_i-\Lambda_i \right ], \quad i=0,1,\ldots \end{displaymath} (9)

They can be analysed with the statistics introduced above. We can also say that we transform longitudes in the Carrington frame into longitudes in the comoving frame. The frame rotation velocity $\Omega$ is a free parameter of the procedure to be estimated. We expect that the distributions of the transformed longitudes depend on $\Omega$ and the highest level of correlation in the longitude distribution will show up as a minimum of the distance statistic $\bar D$.

First we compute how the mean distance between neighbouring rotations $\bar D$ depends on the angular velocity $\Omega$. Then we can use the best value (producing the highest level of correlation) for the angular velocity to compute how distances depend on the interval between rotations (with the statistic $\bar C(l)$).

3 Data analysis

Here we describe how we applied the presented statistical method to study the particular case of sunspots.

The most comprehensive (in time) compilation of sunspot data was downloaded from the Science at NASA web site[*]. The same minor corrections as in PBKT were introduced. We used the full data set covering the years 1874-2008, or in terms of Carrington rotations, the rotations 275-2074. From all the database records we chose only sunspot groups, leaving out single spots. In this way all the entries in the final set have equal statistical weight. For each sunspot group we selected only the record of its first occurence. This is an important aspect of our analysis. We do not track sunspots as they rotate, but are interested in the movement of the underlying spot-generating structures. The final compiled data sets cover rotations 275-2076 with 16057 records for the Northern hemisphere and 275-2075 rotations with 15859 records for the Southern hemisphere; the compiled data sets are available on the web[*].

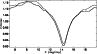
\begin{figure} \par\resizebox{8.5cm}{!}{\includegraphics{13193fg1.eps}} \end{figure} Figure 1:

Statistic $\bar D(\Omega)$ for the full dataset of the Northern hemisphere (thick line) and for the full dataset of the Southern hemisphere (thin line). Minima indicate the best fitting comoving velocities.

Open with DEXTER

3.1 Mean angular velocity

For the first approximation we can assume that the mechanism generating the sunspots rotates as a rigid body. Then we can measure its angular velocity using $\bar D$ statistic by comparing different longitude correction schemes, and choosing the one that produces the lowest value of the statistic. The results can be best illustrated by displaying $\bar D$ as a function of $\Omega$ - the actual sidereal angular velocity of the frame. In Fig. 1 such functions are displayed for both solar hemispheres. As we see both curves show very clear and indicative minima. The absolute mininimum for the Northern data is positioned at 14.338 and for the Southern data at 14.342. The $\bar D(\Omega)$ curves themselves are somewhat fluctuating, so that we found it useful to estimate the minima using local fits of the polynomials. For instance the fifth degree fit performed in the minimum centered interval 13.84-14.84 gave 14.326 for the Northern hemisphere and 14.340 for the Southern hemisphere. For other polynomial degrees the results were quite similar.

To evaluate the significance of our results, we needed a proper method to calculate the error estimates. It is relatively easy to compute the errors of the polynomial fitting procedure. Depending on the degree of the fitted polynomial and hemisphere at hand, the typical standard errors are in the interval 0.001-0.002. Correspondingly we can state that for the particular data run the estimated mean rotation velocity for the Northern hemisphere is somewhat faster than the velocity for the Southern hemisphere.

To obtain a rough estimate of the sampling errors in our nonparametric context we used an approach which is known as a moving block bootstrap (Künsch  1989; Liu & Singh 1992; see also Lahiri 2003). In this method a large number (in our case 500) bootstrap samples are compiled from random sub-blocks of the original data sets. The block length is a defining parameter of the procedure. It must be long enough to take into account dependencies in the data and short enough to allow a proper reshuffling. The underlying theory of the method is developped for stationary sequences. Due to the cyclical nature of the solar activity we do not have a strictly stationary process and must therefore use general results with caution. This is why we calculated our error bars with three different block lengths: 10, 20 and 140. The first is a typical value, which is derived from the general theory, the second is chosen so that it is longer than the typical decorrelation time (see below), and the third one is essentially the mean length of the activity cycle.

Table 1:   Results of the bootstrap claculations.

The results of the bootstrap calculations are presented in Table 1. Higher variance for short block length bootstrap runs can be explained by extra scatter, which results from inter-cycle sampling. For long blocks all phases of the cycle are equally well presented in every block. For shorter blocks the number of, say, sparsely populated blocks can be more fluctuating. This effect is smaller for the minima, which are computed using polynomial fitting.

It is evident from Table 1 that if we consider the data for the two hemispheres as two separate samples, it is not possible to reliably say which one rotates faster.

We also see from the table that the scatter of minima, which are calculated with polynomial fits, is significantly lower than scatter obtained for absolute minima. However, to be consistent with our nonparametric approach we will proceed below using absolute minima.

3.2 Differential rotation

Sunspots and other activity indicators rotate with different angular velocities at different latitudes. By tracking particular objects in time it is possible to build a smooth curve to reveal the overall pattern of this differential, latitude dependent, rotation. Our statistic $\bar D(\Omega)$ does not track single sunspots or the actual movement of sunspot groups, as we include only the first appearance of the sunspot groups. This way we can check whether the spot-generating mechanism itself rotates differentially or not. For that purpose we divided the observed groups into four subsets along latitudes (per hemisphere) and computed $\bar D(\Omega)$ for every group. The latitude limits for the subsets where chosen to make them as equal in size as possible. The typical curves are shown in Fig. 2. The exact determination of the minima for the curves is somewhat complicated. If we locally fit polynomials into the curves as we did above, we can get estimates with high formal precision (0.001-0.002). The differences between the absolute numerical minima and the fitted minima, however, can be quite considerable (up to 0.045). Error estimates from bootstrap calculations depend on the chosen block lengths and are in the range of 0.04-0.12.

\begin{figure} \par\resizebox{8.5cm}{!}{\includegraphics{13193fg2.eps}} \end{figure} Figure 2:

Statistic $\bar D(\Omega)$ for the latitude strip 0.0-9.8. Thick line - Northern hemisphere, thin line Southern hemisphere. Minima indicate the best fitting comoving velocities.

Open with DEXTER

Table 2:   Differential rotation and break down times.

The full set of the absolute minima for all the eight curves is given in Table 2.

\begin{figure} \par\resizebox{8.5cm}{!}{\includegraphics{13193fg3.eps}} \end{figure} Figure 3:

Differential rotation curve.

Open with DEXTER
In Fig. 3 the traditional least squares fit of the obtained angular velocities $\Omega_i$ is presented. We estimated parameters A and B for a simple model:

\begin{displaymath}\Omega_i = A + B\sin ^2 (\theta_i ), \end{displaymath} (10)

where $\theta_i$-s are mid-latitudes of the eight belts. The estimated parameters were $A=14.428\pm 0.023$ and $B=-1.16\pm 0.11$ correspondingly. The standard deviation of the fitting residuals is 0.046 and this is consistent with the rough error estimates above. For both hemispheres the latitude dependence of the angular velocity is monotonically decreasing polewards and resembles quite well the curves obtained from sunspot tracking (see for instance Tuominen & Virtanen 1988; Zappalà & Zuccarello 1991; Pulkkinen & Tuominen 1998; and Beck 1999). Detailed comparison and interpretation in the context of helioseismological investigations will be presented elsewhere.

The results obtained in this section clearly demonstrate that the simple nonparametric method can be succesfully used to study the differential rotation of the solar activity tracers.

3.3 Break-down times

The results of the previous section clearly show that the longitudinally concentrated spot-generating mechanism is subject to differential rotation (to put this result into historical context see the review part in the paper by Usoskin et al. 2007). Kinematic mean-field dynamo theory predicts (e.g. Krause & Rädler 1980) that in the parameter regime where nonaxisymmetric dynamo modes can be excited, the nonaxisymmetric modes are non-oscillatory and rotate rigidly with angular velocity different from the overall rotation period. The phenomenon of phase-mixing, i.e. the nonaxisymmetric modes becoming affected by differential rotation, is against these predictions; our results, however, are consistent with the phase-mixing effect.

Let us now try to quantify the effect of the differential rotation on the nonaxisymmetric structures by calculating the characteristic time needed to break down a longitudinally elongated stucture for different latitude strips. With the estimated B values from Eq. (10) we can define a break-down time for the strip of latitudes $(\theta_1,\theta_2)$ in the number of rotations

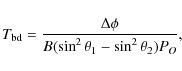
\begin{displaymath}T_{\rm bd} = \frac{{\Delta \phi }}{{B(\sin ^2 \theta _1 - \sin ^2 \theta _2 )P_{O}}}, \end{displaymath} (11)

where $\Delta \phi$ is the phase distance over which the hypothetical longitudinal pattern can be regarded as destroyed. A reasonable value for the parameter $\Delta \phi$ comes from a following simple observation. Let us assume that at the latitudes $\theta_1$ and $\theta_2$ we have K observations. Let the longitudes coincide for the starting point in time. The statistics introduced above are based on finding the nearest ``neighbours''. To break the ties between the neighbours we require that the shear between two bordering latitudes of the strip is large enough. That means we need to have relative shifts that are longer than half the distance between two consequtive observations, or formally $\Delta \phi=0.5 \times {360}^{\circ}/\bar K$, where $\bar K$ is a mean number of observations per Carrington rotation. Applying all this to the same latitude intervals as in Sect. 3.2, we obtain the break-down times listed in Table 2.

3.4 Decorrelation time

So far we have demonstrated that the sunspot group distributions along longitudes for sequential Carrington rotations are correlated. We also computed the best fitting mean angular velocity $\Omega$ for several latitude strips, and as a result found out a clear differential rotation pattern. Next we were interested in estimating the approximate lifetimes of the correlated features found from the sunspot data. For that purpose we used the obtained mean angular velocities for each latitude strip and computed $\bar C(l)$ curves to learn how fast the correlation between appropriately rotated longitude sets fades off.

\begin{figure} \par\resizebox{8.5cm}{!}{\includegraphics{13193fg4.eps}} \end{figure} Figure 4:

Statistic $\bar C(l)$ computed for the four Northern latitude strips. The thicker the line - the nearer to the equator it is. The horizontal line is the asymptotic level for 0.0-9.8 strip (mean value of the $\bar C(26) \dots \bar C(50)$).

Open with DEXTER

\begin{figure} \par\resizebox{8.5cm}{!}{\includegraphics{13193fg5.eps}} \end{figure} Figure 5:

Statistic $\bar C(l)$ computed for the Southern latitude strips. See above.

Open with DEXTER

The results of this analysis are displayed on Figs. 4 and 5. In these plots the thick horizontal lines indicate the asymptotic level of the $\bar C(l)$ curves (mean value of the $\bar C(26) \dots \bar C(50)$) computed for the strips nearest to the equator. As is evident from the plots, the inherent scatter of the $\bar C(l)$ curves is quite large; this is due to the physical variability of the activity level and the roughness of the statistic. Therefore it is hard to fix the point where the asymptotic level is achieved. Some aspects of the curves, however, are quite indicative. First - the shortest decorrelation time is obtained for the highest latitudes. This is obvious because the width (in degrees) of the high altitude strips is more extended and covers very differently rotating spot groups. Secondly - the strips nearest to the equator show the longest correlations. We can quite safely claim that a certain level of correlation is visible up to a time span of 10-15 rotations.

Comparing the estimated decorrelation times for different latitude strips with the break-down times from Table 1 we can see that for lower latitudes the decorrelation times obtained from our analysis are much shorter than the estimated break-down times. For the highest latitude strip the decorrelation time is of the same order of magnitude than the break-down time. Part of this effect could be due to the enhanced diffusion of the field due to the stretching by the shear in angular velocity; the latitude dependence (shorter decorrelation times at high latitudes with the largest relative shear) would support this interpretation. It seems likely, however, that at least at lower latitudes stretching and enhanced turbulent diffusion acting on the magnetic field due to differential rotation are not the only effects at play.

4 Discussion

To put our results in a general context we will compare them with a sample of previous analyses.

To a great extent the solar variability research is not based on a full set of sunspot observations, but on some aggregated form of data. Most typically the daily Wolf sunspot numbers are used. For instance Bogart (1982) analysed these numbers using autocorrelation functions and power spectra. The major results were quite similar to ours - the rotation period around 27 days was detected and the persistence of activity zones was claimed to be of the order of 10 solar rotations. In principle correlation functions and power spectra can be considered to be parameter-free statistics. The aggregated nature of the Wolf numbers, however, does not allow the analysis of the latitude dependence of active clusters.

There is a number of analyses that use longitudinal phase binning of the surface features. For instance in a series of papers Bai (1987, 1988) used comoving frames (as in our work) to seek rotation velocities, which enhance the statistical contrast of the longitudinal distribution of solar flares. The transformed longitudes for each trial rotation velocity were binned into 12 bins and the variance of obtained distributions was computed. The possibility of differential rotation was not taken into account. To study the persistence of particular active regions they were visually tracked and displayed as ``family trees''. In describing his results the author proposed a general scheme to characterize hierarchical patterns of solar activity:

  • single events (sunpots, flares);
  • active regions;
  • activity complexes;
  • active zones.
The lifetimes of the activity centres increase with hierarchy - from days to several years. In a later work Bai (2003) used Rayleigh-type statistics to analyse transformed longitudes. He computed standard spectra, which are sensitive to unimodal distributions, and spectra that are sensitive to bimodal distributions. As a result he found that some characteristics of the longitude distributions are rather persistent in time, even up to decades. Our results describe the average behaviour of the solar activity, and consequently some long-lived elements do not have a strong influence, as they are mixed with other elements whose lifetimes are shorter. It should be also stressed that $\bar D$ and $\bar C(l)$ statistics do not depend on any assumption about the modality of the underlying variability. All the ``modes'' are automatically accounted for.

Probably the most popular method to study the kinematics of the solar surface features is a standard power spectrum analysis and its variants (just an example - Temmer et al.  2004; Giordano 2008). This kind of analysis can be applied to latitude strips and in this way the differential rotation can be taken into account. At a first glance the Fourier analysis seems to be essentially nonparametric. However, because it uses single harmonics as base functions, it prescribes a certain form of preferred activity distributions. The results of the Fourier method are often given as a list of certain periods, which show up in power spectra or on wavelet plots. The periodicity claim itself is quite a strong statement, as it is often very hard to find physically solid timing mechanisms for periods, which strongly differ from the obvious one - that of the solar rotation.

We wish to stress here that in the proposed statistical method no assumptions about the particular form of the activity indicator distributions are made. Even more - the statistics $\bar D$ and $\bar C(l)$ are not seeking certain clusters or other kind of patterns, they are just used to check whether the origins of surface elements are correlated or not. This makes the new method somewhat similar to the method of ``family trees'' (Bai 2003) or longitude-time diagrams (Brouwer & Zwaan 1990).

The literature about the longitudinal distribution of solar activity indicators is so divers that it is not reasonable to compare our results with all of them. It suffices to state that the general patterns revealed so far are quite similar to those described above. The major shortcomings of the previously used methods include the dependence of the results on some prefixed parameters or on the choice of a particular distribution model.

5 Conclusions

When introducing a new method to analyse solar activity patterns we started from certain methodological principles:
  • Input data must be homogeneous, comprehensive and cover as long a time-base as possible.
  • The analysis method must be free from any prefixed constants.
  • The method must not depend on the model of the activity indicator distributions (unimodal, bimodal etc.).
  • The computations must be as simple as possible.
The results obtained with the new method can be ranked employing these underlying principles. We start from the most evident and methodologically ``clean'' facts and proceed towards statements that can be doubted or refined using additional devices.
  • The distribution of sunspots is determined by the underlying large-scale mechanism that is more persistent than sunspots themselves. This shows up as a tendency of new sunspots to occur near the places where the previous sunspots were observed.
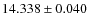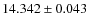  • The mean rotation velocity of the large-scale features for the Northern hemisphere is $14.338\pm 0.040$ deg/days and for the Southern hemisphere $14.342\pm 0.043$ deg/days.
  • The large-scale patterns of activity take part in differential rotation. The differential rotation curve is somewhat shallower if compared with curves obtained from sunspot tracking (see Zappalà & Zuccarello 1991).
  • The strong tendency for the spot groups to cluster on a certain longitude peters out with time. The longest observable correlations can reach 10-15 Carrington rotations.
  • The correlations between rotations are more pronounced for lower latitudes.
  • The observation of the spot-generating mechanism being affected by differential rotation is suggestive of phase mixing occurring in the solar convection zone; such a phenomenon is not predicted by conventional mean-field dynamo theory.
The new method can be applied also to analyse other activity indicators (flares, CMEs etc.).

Acknowledgements
We would like to thank the referee for useful suggestions. Part of this work was supported by the Estonian Science Foundation grant No. 6813 and Academy of Finland grant No. 112020. The authors thank the hospitality of NORDITA during the programme ``Solar and stellar dynamos and cycles''.

References

  1. Bai, T. 1987, ApJ, 314, 795 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bai, T. 1988, ApJ, 328, 860 [NASA ADS] [CrossRef] [Google Scholar]
  3. Bai, T. 2003, ApJ, 585, 1114 [NASA ADS] [CrossRef] [Google Scholar]
  4. Beck, J. G. 1999, Sol. Phys., 191, 47 [NASA ADS] [CrossRef] [Google Scholar]
  5. Becker, U. 1955, Z. Astrophys., 37, 47 [Google Scholar]
  6. Bogart, R. S. 1982, Sol. Phys., 76, 155 [NASA ADS] [CrossRef] [Google Scholar]
  7. Brouwer, M. P., & Zwaan, C. 1990, Sol. Phys., 129, 221 [Google Scholar]
  8. Bumba, V., & Howard, R. 1965, ApJ, 141, 1502 [NASA ADS] [CrossRef] [Google Scholar]
  9. Castenmiller, M. J. M., Zwaan, C., & van der Zalm, E. B. J. 1986, Sol. Phys., 105, 237 [NASA ADS] [CrossRef] [Google Scholar]
  10. Gaizauskas, V., Harvey, K. L., Harvey, J. W., & Zwaan, C. 1983, ApJ. 265, 1056 [NASA ADS] [CrossRef] [Google Scholar]
  11. Giordano, S., & Mancuso, S. 2008, ApJ, 688, 656 [NASA ADS] [CrossRef] [Google Scholar]
  12. Juckett, D. 2003, A&A, 399, 731 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Krause, F., & Rädler, K.-H. 1980, Mean-field magnetohydrodynamics and dynamo theory (Berlin: Akademie-Verlag) [Google Scholar]
  14. Künsch, H. R. 1989, The Annals of Statistics, 17, 1217 [Google Scholar]
  15. Lahiri, S. N. 2003, Resampling Methods for Dependent Data (New-York, Inc.: Springer-Verlag) [Google Scholar]
  16. Liu, R. Y., & Singh, K. 1992, in Exploring the Limits of the Bootstrap, ed. R. Lepage, & L. Billard (New York: Wiley), 225 [Google Scholar]
  17. Losh, N. M. 1938, Publ. Observ. Michigan, 7, 127 [Google Scholar]
  18. Mardia, K. V., & Jupp, P. 2000, Directional Statistics, 2nd edn. (John Wiley and Sons Ltd.) [Google Scholar]
  19. Pelt, J., Brooke, J., Korpi, M., & Tuominen, I. 2006, A&A, 460, 875 (PBKT) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Pulkkinen, P., & Tuominen, I. 1998, A&A, 332, 748 [NASA ADS] [Google Scholar]
  21. Temmer, M., Veronig, A., Rybák, J., Brajsa, R., & Hanslmeier, A. 2004, Sol. Phys., 221, 325 [NASA ADS] [CrossRef] [Google Scholar]
  22. Trotter, D. E., & Billings, D. E. 1962, ApJ, 136, 1140 [NASA ADS] [CrossRef] [Google Scholar]
  23. Tuominen, I., & Virtanen, H. 1988, Adv. Space Res., 8, 141 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  24. Usoskin, I. G., Berdyugina, S. V., & Poutanen, J. 2005, A&A, 441, 347 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Usoskin, I. H., Berdyugina, S. V., Moss, D., & Sokoloff, D. D. 2007, Adv. Space Res., 40, 951 [NASA ADS] [CrossRef] [Google Scholar]
  26. Vitinskij, Ju. I. 1969, Sol. Phys., 7, 210 [NASA ADS] [CrossRef] [Google Scholar]
  27. Warwick, C. S. 1965, ApJ, 141, 500 [NASA ADS] [CrossRef] [Google Scholar]
  28. Zappalà, R. A., & Zuccarello, F. 1991, A&A, 242, 480 [NASA ADS] [Google Scholar]

Footnotes

... site[*]
http://solarscience.msfc.nasa.gov/greenwch.shtml
... web[*]
http://www.aai.ee/ pelt/soft.htm

All Tables

Table 1:   Results of the bootstrap claculations.

Table 2:   Differential rotation and break down times.

All Figures

  \begin{figure} \par\resizebox{8.5cm}{!}{\includegraphics{13193fg1.eps}} \end{figure} Figure 1:

Statistic $\bar D(\Omega)$ for the full dataset of the Northern hemisphere (thick line) and for the full dataset of the Southern hemisphere (thin line). Minima indicate the best fitting comoving velocities.

Open with DEXTER
In the text

  \begin{figure} \par\resizebox{8.5cm}{!}{\includegraphics{13193fg2.eps}} \end{figure} Figure 2:

Statistic $\bar D(\Omega)$ for the latitude strip 0.0-9.8. Thick line - Northern hemisphere, thin line Southern hemisphere. Minima indicate the best fitting comoving velocities.

Open with DEXTER
In the text

  \begin{figure} \par\resizebox{8.5cm}{!}{\includegraphics{13193fg3.eps}} \end{figure} Figure 3:

Differential rotation curve.

Open with DEXTER
In the text

  \begin{figure} \par\resizebox{8.5cm}{!}{\includegraphics{13193fg4.eps}} \end{figure} Figure 4:

Statistic $\bar C(l)$ computed for the four Northern latitude strips. The thicker the line - the nearer to the equator it is. The horizontal line is the asymptotic level for 0.0-9.8 strip (mean value of the $\bar C(26) \dots \bar C(50)$).

Open with DEXTER
In the text

  \begin{figure} \par\resizebox{8.5cm}{!}{\includegraphics{13193fg5.eps}} \end{figure} Figure 5:

Statistic $\bar C(l)$ computed for the Southern latitude strips. See above.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.