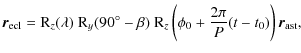| Issue |
A&A
Volume 513, April 2010
|
|
|---|---|---|
| Article Number | A46 | |
| Number of page(s) | 13 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/200912693 | |
| Published online | 23 April 2010 | |
DAMIT: a database of asteroid models
J. Durech1 - V. Sidorin2 - M. Kaasalainen3
1 - Astronomical Institute, Faculty of Mathematics
and Physics, Charles University in Prague, V Holesovickách 2,
18000 Prague, Czech Republic
2 - Astronomical Institute, Academy of Sciences, Bocní II, 14131 Prague, Czech Republic
3 - Tampere University of Technology, PO Box 553, 33101 Tampere, Finland
Received 15 June 2009 / Accepted 20 January 2010
Abstract
Context. Apart from a few targets that were directly imaged
by spacecraft, remote sensing techniques are the main source of
information about the basic physical properties of asteroids, such as
the size, the spin state, or the spectral type. The most widely used
observing technique - time-resolved photometry - provides us with data
that can be used for deriving asteroid shapes and spin states. In the
past decade, inversion of asteroid lightcurves has led to more than a
hundred asteroid models. In the next decade, when data from all-sky
surveys are available, the number of asteroid models will increase.
Combining photometry with, e.g., adaptive optics data produces more
detailed models.
Aims. We created the Database of Asteroid Models from Inversion
Techniques (DAMIT) with the aim of providing the astronomical community
access to reliable and up-to-date physical models of asteroids - i.e.,
their shapes, rotation periods, and spin axis directions. Models from
DAMIT can be used for further detailed studies of individual objects,
as well as for statistical studies of the whole set.
Methods. Most DAMIT models were derived from photometric data by
the lightcurve inversion method. Some of them have been further refined
or scaled using adaptive optics images, infrared observations, or
occultation data. A substantial number of the models were derived also
using sparse photometric data from astrometric databases.
Results. At present, the database contains models of more than
one hundred asteroids. For each asteroid, DAMIT provides the polyhedral
shape model, the sidereal rotation period, the spin axis direction, and
the photometric data used for the inversion. The database is updated
when new models are available or when already published models are
updated or refined. We have also released the C source code for the
lightcurve inversion and for the direct problem (updates and extensions
will follow).
Key words: minor planets, asteroids: general - astronomical data bases: miscellaneous
1 Introduction
The knowledge of basic physical characteristics of asteroids - the spin rate, the spin axis orientation, the shape, the size, the mass, the spectral type, etc. - is important for understanding the history and the current state of the asteroid population. Apart from a few asteroids directly imaged by spacecraft, our knowledge about asteroid physical properties is based on remote sensing techniques. And from all these techniques, time-resolved photometry is by far the most important source of information because it is in principle available for all known asteroids. The lightcurve inversion method developed by Kaasalainen & Torppa (2001) and Kaasalainen et al. (2001) is a powerful tool for deriving asteroid shapes and spins from their lightcurves observed over several apparitions.
So far, the lightcurve inversion method has led to models of about one hundred asteroids. The models have been published in several papers (Durech et al. 2009; Kaasalainen et al. 2002b; Torppa et al. 2003; Kaasalainen et al. 2004, for example). As has been shown by Kaasalainen et al. (2004) or Durech et al. (2005) and demonstrated on real targets by Durech et al. (2009), physical models of asteroids can also be derived from photometry that only sparsely samples brightness variations. This kind of photometric data will be provided by all-sky surveys like Pan-STARRS (Panoramic Survey Telescope and Rapid Response System), LSST (Large Synoptic Survey Telescope), or Gaia (Mignard et al. 2007), and we expect an avalanche of new asteroid models in the next decade.
Models obtained by lightcurve inversion are interesting as such, but their main importance is that, by using the lightcurve inversion, we can reveal new physical phenomena. For example, it was used when the alignment of spins of the Koronis family members was revealed (Slivan et al. 2003) or when the YORP (Yarkovsky-O'Keefe-Radzievskii-Paddack) effect was detected (Kaasalainen et al. 2007). In general, the analysis of spin states and shapes of asteroids has been always related to the inversion of disk-integrated lightcurves (see review papers Magnusson et al. 1989; Pravec et al. 2002, for example). Lightcurve inversion has become a standard tool for revealing asteroids' nature from photometry. Moreover, lightcurves can be combined with other data (Kaasalainen & Lamberg 2006; Kaasalainen 2009). For example, adaptive optics images can provide us with nonconvex details (Descamps et al. 2009), and thermal infrared observations can determine the correct absolute size of the object, its thermal inertia, and albedo (Delbo & Tanga 2009). The reliability of models derived from photometry has been proven by comparison with the real shapes revealed by spacecraft (Lamy et al. 2008; Müller et al. 2005) and by laboratory experiments (Kaasalainen et al. 2005).
To provide an easy access to most of the published lightcurve inversion models we set up the Database of Asteroid Models from Inversion Techniques (DAMIT). DAMIT is an MySQL database accessible via a web interface. In the following section, we describe the structure of DAMIT and the format and physical meaning of individual database items.
2 Database description
The aim of the database is to provide the community access to all published asteroid models derived by the lightcurve and other inversion methods, as well as to source codes for solving direct and inverse problems. For each asteroid in the database, the basic physical parameters are given: the shape model, the spin axis orientation, and the rotation period. DAMIT also contains information about the light-scattering model used in the inversion. The lightcurves from which the model was derived can be downloaded as a data file. Other data sources, such as adaptive optics images, are cited and the data included as auxiliary files when appropriate. The reference to the paper where the model (or its update) was published is always given. However, a number of DAMIT solutions are significantly different from those published in the original papers. This is mainly due to the updated data set or to a range too narrow for the sidereal period search used in the original work. In some cases, photometric data files have been corrupted or misread, and rechecks and data corrections have led to some updates.
In principle, there can be more models for one asteroid,
usually because of a limited geometry (an asteroid orbiting too close
to the
ecliptic, see Kaasalainen & Lamberg 2006 for details) that
introduces an ambiguity
![]() in the ecliptic longitude of the pole.
Or there can be more models corresponding to a different inversion method being applied, e.g., a convex and a nonconvex model
for the same asteroid. So far, DAMIT contains
in the ecliptic longitude of the pole.
Or there can be more models corresponding to a different inversion method being applied, e.g., a convex and a nonconvex model
for the same asteroid. So far, DAMIT contains ![]() 180 models
for more than one hundred asteroids. Usually, the models have similar
values for the rms residual. If one of the models is preferred - either
due to a lower rms residual or for another reason - a comment is added
to it.
180 models
for more than one hundred asteroids. Usually, the models have similar
values for the rms residual. If one of the models is preferred - either
due to a lower rms residual or for another reason - a comment is added
to it.
2.1 Shape models
Asteroid shape models are represented by polyhedrons with triangular surface facets (see an example in Fig. 1). A single file with the list of x,y,z Cartesian coordinates of the polyhedron vertices followed by the list of facets represents each model. Vertices of the corresponding triangle are listed as seen from outside the body in the counterclockwise sense. Because we cannot infer size information from photometry alone, most of the models are scale-free and are arbitrarily scaled to have a unit volume. If a model is scaled to its real dimensions (when, e.g., occultation data, high-angular-resolution data, or infrared measurements are available), this is stated in the corresponding tag, and the x,y,z coordinates are given in kilometres. The model always rotates around its z axis, which is usually close, but not exactly identical, to the maximum principal axis of the inertia tensor (assuming a uniform density distribution). If these two axes differ significantly, the model formally fits the data well, but the rotation around the z axis is physically impossible. Such cases are discussed. There is only one such model in the current database - 167 Urda. The x axis has no special orientation with respect to the minimum principal axis of the inertia tensor. It is usually defined implicitly by setting t0 in Eq. (1) to the minimum JD epoch in the lightcurve data set (or to the nearest lower integer value).
So far, DAMIT does not contain any model of a ``tumbling'' asteroid,
i.e., an asteroid in an excited rotation state.
However, we plan to include such models in the future. The first
example will be the model of asteroid 2008 TC3 derived from
photometry (Scheirich et al., in prep.). DAMIT also does not contain
models of binary asteroids. In cases where the satellite is much
smaller than the primary, DAMIT contains models of primary components
of binary or multiple systems (87 Sylvia and 121 Hermione,
for example). For synchronous binaries, there is only one period in the
lightcurves and it should be possible to create a convex model that
fits the data well. We usually do not include those asteroids in DAMIT
for which a detailed model derived from radar delay-Doppler echoes or
from direct spacecraft imaging is available. These high-resolution
models can be found in the Planetary Data System (PDS) archive![]() .
.
Each shape model is visualized and shown from three directions. There are two views from the asteroid's equator and one from its pole. The three views correspond to the views from the positive x,y,z axes, respectively. The light-scattering model used for rendering has no physical meaning and was chosen just for visualization purposes using Matlab software.
The vast majority of DAMIT asteroid shape models are convex. As shown by Durech & Kaasalainen (2003), disk-integrated lightcurves contain very little information about shape nonconvexities. To reveal nonconvex features from lightcurves, observations at very high phase angles (when shadowing effects are important) are necessary. Moreover, nonconvex solutions lack the stability and uniqueness properties of the convex solutions. Reliable nonconvex shape models can be derived only when lighcurves are combined with high-resolution data (adaptive optics images, for example). This also means that we cannot properly determine the nonconvexity errors of a convex shape model. The match between a convex model and the real shape can be very good for almost-convex bodies (2 Pallas) or can be poor for highly nonconvex bodies (624 Hektor).
The errors of the shape determination were discussed in Kaasalainen & Torppa (2001) and Kaasalainen et al. (2001). They showed that the formal errors are worthless in practice because the effect of random noise is usually negligible compared to systematic and model errors. The only practical way of estimating real errors is to perform a series of optimizations with different methods, scattering laws, and initial values to see how the results differ. However, such detailed investigation of errors is usually not included in those papers where the shape models are published. In general, shape models are much better constrained in the equatorial plane than in the direction of the pole.
![\begin{figure}
\par\includegraphics[width=\textwidth,clip]{12693fg1.eps}
\end{figure}](/articles/aa/full_html/2010/05/aa12693-09/Timg7.png)
|
Figure 1:
An example of the rotational sequence described by Eq. (1).
The four subsequent rotations transform the model from the body-fixed
coordinate frame ``ast'' to the ecliptic coordinate frame ``ecl''. Here
|
| Open with DEXTER | |
2.2 Spin
The rotation state of an asteroid is described by its sidereal rotation period P, the fixed orientation of its spin axis (the z axis in the body frame) expressed by means of
the ecliptic coordinates
![]() ,
and the initial rotation angle
,
and the initial rotation angle ![]() for some epoch t0.
The orientation of the model
in the inertial frame is then obtained by applying a set of rotations
on the model. The transformation from the body-fixed coordinate frame
for some epoch t0.
The orientation of the model
in the inertial frame is then obtained by applying a set of rotations
on the model. The transformation from the body-fixed coordinate frame
![]() to the ecliptic coordinate frame
to the ecliptic coordinate frame
![]() for the time t is given by the equation
for the time t is given by the equation
where
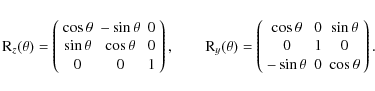
An example illustrating the four subsequent rotations and the definition of the rotation angles is shown in Fig. 1.
For some asteroids in the database, the rotation period is not constant in time but changes secularly
from the YORP effect (Durech et al. 2008a; Kaasalainen et al. 2007). In such
cases, the corresponding rotation matrix has the form
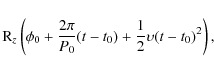
where
The orientation of a model given by Eq. (1) is expressed in the asteroid-centric reference frame.
When computing, for example, the sky-plane projection of a model for a given time
![]() ,
one has to take
the light travel time from the asteroid to the observer into account.
Then
,
one has to take
the light travel time from the asteroid to the observer into account.
Then
![]() ,
where
,
where ![]() is the asteroid-observer distance and c the speed of light.
is the asteroid-observer distance and c the speed of light.
The description of the spin-state given above does not follow the recommendation of the IAU as defined by Seidelmann et al. (2007), mainly
because the rotation angles ![]() and
and ![]() in Eq. (1) are
(contrary to the equatorial reference frame angles
in Eq. (1) are
(contrary to the equatorial reference frame angles ![]() and
and ![]() recommended by the IAU) directly related to the
spin-orbital dynamics. For low-inclination asteroids,
recommended by the IAU) directly related to the
spin-orbital dynamics. For low-inclination asteroids,
![]() is the obliquity.
However, for each model in the database, we also give the rotation elements according to the IAU recommendation:
the direction of the positive spin axis in the equatorial coordinates
is the obliquity.
However, for each model in the database, we also give the rotation elements according to the IAU recommendation:
the direction of the positive spin axis in the equatorial coordinates ![]() ,
,
![]() ,
the rotational rate
,
the rotational rate
![]() ,
and the position of the prime meridian W0 for time t0. The position of the prime meridian W at
time t can be computed as
,
and the position of the prime meridian W0 for time t0. The position of the prime meridian W at
time t can be computed as
![]() .
.
The rotation parameters listed in the database can also be downloaded as a file. This file can be used directly as input for the direct-problem software that enables one to generate lightcurves for a given shape and spin (see Sect. 2.6).
The relative accuracy of the rotation period depends mainly on the total time span of the observations. The higher the number of revolutions in the interval of observations, the higher the accuracy of the length of one revolution, i.e, of the rotation period. The accuracy of the period P corresponds to the order of the last decimal place of P. The typical relative error ranges from 10-5 to 10-6.
Contrary to the database of asteroid spin vector determinations maintained by Kryszczynska at the Poznan Observatory (Kryszczynska et al. 2007)
that compiles all available spin vector solutions derived by various
techniques, all DAMIT spin vector solutions were derived using one
inversion method. The typical uncertainty of the spin axis direction is
about
![]() .
.
2.3 Light-scattering model
Lightcurve inversion models are usually derived under the assumption that the light-scattering behaviour of asteroids can be
described as a combination of Lommel-Seeliger and Lambert models (Kaasalainen et al. 2002a). The surface reflectance S as a function of the angle of incidence i and the angle of emergence e is then
![\begin{displaymath}S(\mu, \mu_0, \alpha) = f(\alpha) \left[ S_{\rm LS}(\mu, \mu_0) + c S_{\rm L}(\mu, \mu_0) \right],
\end{displaymath}](/articles/aa/full_html/2010/05/aa12693-09/img25.png)
where
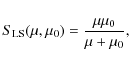
the Lambert term is
and c is the weight factor. Function
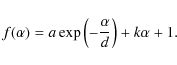
The parameters c, a, d, and k are listed in the database. However, if there are not enough calibrated lightcurves to cover a sufficiently wide range of phase angles,
In some cases, when accurate calibrated photometry covering a wide
range of phase angle was available, instead of the simple model above,
the Hapke scattering model (Hapke 1984,1986,1981) was used during the inversion.
In such cases, DAMIT lists the five parameters of Hapke's model:
the single-particle scattering albedo w, the asymmetry parameter of the single-particle function g, the opposition surge
amplitude B0, the opposition surge width h, and the macroscopic roughness
![]() .
.
2.4 Lightcurves
The photometric data used in the inversion can be downloaded from DAMIT as data files. The lightcurve file contains brightness in intensity units for given epochs (light-time corrected) and the viewing and illumination geometry. The Cartesian ecliptic coordinates of the Sun and the Earth with respect to the asteroid are given for each data point.A tag at the beginning of each lightcurve states whether the lightcurve is relative - i.e., can be shifted on the magnitude scale with respect to other relative lightcurves - or if the brightness measurements are calibrated and no shift with respect to other calibrated curves is allowed. The lightcurve files can be directly used as input for the inversion software (see Sect. 2.6). For each lightcurve, the reference to the original paper where the data were published is given. References to papers in which the original photometric data used for inversion were published are listed in the Appendix A.
2.5 Realization
DAMIT is accessible online at http://astro.troja.mff.cuni.cz/projects/asteroids3D. The core of DAMIT is an MySQL database served by the MySQL server, which ensures high stability and reliability, as well as flexibility for future development. The web interface of DAMIT is written in PHP and allows users to either browse or search the database. Records from the database can be downloaded as text files suitable for further processing. The shape solutions are also provided in the form of computer-generated images in PNG (Portable Network Graphics) format. DAMIT with all its components is hosted and operated by the Astronomical Institute of the Charles University. We plan to set up a mirror site to minimize all negative impacts of a possible hardware failure.
2.6 Software
DAMIT also contains source codes of inversion programs and a tool for lightcurve generation along with the user's manuals. The formats of input and output files are identical to the formats of lightcurve and shape files in DAMIT. The software is available under the General Public Licence, and we encourage all potential users to use it for inversion of their own data and to develop it further. The software will be described in detail in a forthcoming paper.3 Conclusions
The number of asteroid models derived from lightcurves and other sources by inversion techniques is continuously growing, so we expect a dramatic increase of the number of models in the next few years with the dawn of all-sky surveys. The number of observers who use their own data for shape modelling is also growing, mainly thanks to the availability of the Windows-based user-friendly version of the inversion softwareTo increase the scientific attractivity of DAMIT, we will connect it with the IMCCE Virtual Observatory Solar System portal![]() .
The service will compute physical ephemerides of models stored in
DAMIT, for example, sky-plane projections of models for a given epoch
with a realistic brightness distribution (Berthier et al. 2008).
.
The service will compute physical ephemerides of models stored in
DAMIT, for example, sky-plane projections of models for a given epoch
with a realistic brightness distribution (Berthier et al. 2008).
The work of J.D. was supported by grants GACR 205/07/P070 of the Czech grant agency and by the Research Program MSM0021620860 of the Ministry of Education. The work of MK was supported by the Academy of Finland.
Appendix A: Lightcurve references
Below we list the references to papers in which the original
photometric data used for inversion were published. For some asteroids,
DAMIT contains also unpublished lightcurves. USNO stands for the US
Naval Observatory in Flagstaff - the photometry obtained at this
observatory as a by-product of astrometric observations was downloaded
from the AstDys page![]() and used for modelling.
and used for modelling.
(2) Pallas
Binzel (1984)Burchi (1972)
Burchi & Milano (1983)
Burchi et al. (1985)
Carlsson & Lagerkvist (1983)
Groeneveld & Kuiper (1954b)
Chang & Chang (1963)
Chang et al. (1981)
Lagerkvist et al. (1988)
Lupishko et al. (1989)
Lustig & Hahn (1976)
Schober et al. (1994)
Schroll et al. (1976)
van Houten-Groeneveld (1981)
Wood & Kuiper (1963)
(3) Juno
Birch & Taylor (1989)di Martino et al. (1987b)
Gehrels & Owings (1962)
Groeneveld & Kuiper (1954b)
Harris et al. (1989a)
Millis et al. (1981)
Schroll et al. (1981)
(5) Astraea
Gehrels & Owings (1962)Harris et al. (1999)
Chang & Chang (1962)
Lagerkvist et al. (1989)
Melillo (1987a)
Pavlovski et al. (1981)
Taylor (1978)
USNO
Weidenschilling et al. (1990)
(6) Hebe
Ahmad (1954)di Martino & Cacciatori (1984a)
Dotto et al. (1995)
Erikson et al. (1991)
Gehrels & Taylor (1977)
Hutton & Blain (1988)
Hainaut-Rouelle et al. (1995)
Lagerkvist et al. (1995)
Wamsteker & Sather (1974)
Yang et al. (1965)
Zhou et al. (1982)
(7) Iris
Foglia (1992)Gehrels & Owings (1962)
Groeneveld & Kuiper (1954a)
Chang & Chang (1963)
Lagerkvist & Williams (1987)
Taylor (1977)
van Houten-Groeneveld & van Houten (1958)
Zhou et al. (1982)
(8) Flora
Ahmad (1954)Debehogne et al. (1990)
di Martino et al. (1989)
Harris & Young (1989)
Hollis et al. (1987)
Piironen et al. (1998)
Pilcher (2009)
van Houten-Groeneveld & van Houten (1958)
Vesely & Taylor (1985)
Veverka (1971)
Zappala et al. (1983b)
Zhou et al. (1982)
(9) Metis
di Martino & Cacciatori (1984a)di Martino et al. (1987b)
Gehrels & Owings (1962)
Groeneveld & Kuiper (1954a)
Groeneveld & Kuiper (1954b)
Harris & Young (1989)
Chang & Chang (1962)
Melillo (1987b)
Schober & Surdej (1979)
Weidenschilling et al. (1987)
Weidenschilling et al. (1990)
Yang et al. (1965)
Zappala & van Houten-Groeneveld (1979)
Zeigler & Florence (1985)
(15) Eunomia
Foglia (1995)Groeneveld & Kuiper (1954a)
Chang et al. (1959)
Chang et al. (1981)
Lagerkvist & Williams (1987)
Lagerkvist et al. (1989)
Melillo (1986)
Piironen et al. (1985)
Scaltriti & Zappala (1975)
van Houten-Groeneveld & van Houten (1958)
Vesely & Taylor (1985)
Weidenschilling et al. (1987)
(16) Psyche
Dotto et al. (1992)Chang et al. (1981)
Lupishko et al. (1980)
Lupishko et al. (1982)
Lupishko et al. (1989)
Neely (1992)
Taylor et al. (1976)
Tedesco & Taylor (1985)
Tedesco et al. (1983)
van Houten-Groeneveld & van Houten (1958)
Weidenschilling et al. (1987)
Zhou & Yang (1981)
Zhou et al. (1982)
(17) Thetis
Denchev et al. (1998)Groeneveld & Kuiper (1954a)
Harris et al. (1992)
Lagerkvist et al. (1995)
Lupishko et al. (1979)
Lupishko et al. (1989)
Michaowski et al. (1995)
USNO
van Houten-Groeneveld & van Houten (1958)
(19) Fortuna
Denchev (2000, private comm.)Harris et al. (1992)
Harris et al. (1999)
Lagerkvist et al. (1987)
Lupishko et al. (1981)
Lupishko et al. (1989)
van Houten-Groeneveld et al. (1979)
Weidenschilling et al. (1987)
Weidenschilling et al. (1990)
(20) Massalia
Barucci et al. (1985)Dotto et al. (1995)
Gehrels (1956)
Gehrels & Owings (1962)
Hainaut-Rouelle et al. (1995)
Chang & Chang (1962)
McCheyne et al. (1985)
(21) Lutetia
Denchev (2000, private comm.)Denchev et al. (1998)
Dotto et al. (1992)
Chang & Chang (1963)
Lagerkvist et al. (1995)
Lupishko et al. (1983)
Lupishko et al. (1987a)
Zappala et al. (1984)
(22) Kalliope
Gehrels & Owings (1962)Lupishko et al. (1982)
Lupishko et al. (1989)
Melillo (1987a)
Michaowski & Velichko (1990)
Scaltriti et al. (1978)
Surdej et al. (1986)
Weidenschilling et al. (1987)
Weidenschilling et al. (1990)
Zappala & van Houten-Groeneveld (1979)
(23) Thalia
Hainaut-Rouelle et al. (1995)Harris & Young (1983)
Lagerkvist et al. (1995)
Pilcher - unpublished data
Tancredi & Gallardo (1991)
van Houten-Groeneveld et al. (1979)
Vesely & Taylor (1985)
Yang et al. (1965)
Ziegler & Florence (1985)
(29) Amphitrite
Debehogne et al. (1978)Chang & Chang (1963)
McCheyne et al. (1984)
McCheyne et al. (1985)
Polishook (2009)
Tedesco & Sather (1981)
van Houten-Groeneveld et al. (1979)
Weidenschilling et al. (1987)
(30) Urania
Gehrels & Owings (1962)Harris & Young (1980)
USNO
Wisniewski et al. (1997)
(32) Pomona
di Martino et al. (1987b)Dotto et al. (1995)
Erikson et al. (1991)
Chang et al. (1981)
Schober (1976)
(34) Circe
Durech et al. (2009)Lagerkvist et al. (1987)
Lagerkvist et al. (1995)
Magnusson & Lagerkvist (1991)
USNO
Vesely & Taylor (1985)
(39) Laetitia
di Martino et al. (1987b)Gehrels & Owings (1962)
Groeneveld & Kuiper (1954a)
Groeneveld & Kuiper (1954b)
Chang et al. (1981)
McCheyne et al. (1985)
Sather (1976)
van Houten-Groeneveld & van Houten (1958)
Vesely & Taylor (1985)
Wamsteker & Sather (1974)
Weidenschilling et al. (1987)
Weidenschilling et al. (1990)
(41) Daphne
Barucci (1983)Barucci et al. (1985)
Scaltriti & Zappala (1977b)
Weidenschilling et al. (1987)
Weidenschilling et al. (1990)
(43) Ariadne
Barucci et al. (1986)Burchi & Milano (1974)
di Martino & Cacciatori (1984a)
di Martino et al. (1987b)
Dotto et al. (1995)
Lustig & Dvorak (1975)
McCheyne et al. (1984)
Shevchenko et al. (1992)
van Houten-Groeneveld et al. (1979)
Weidenschilling et al. (1987)
Weidenschilling et al. (1990)
(44) Nysa
Birch et al. (1983)di Martino et al. (1987b)
Gehrels & Owings (1962)
Groeneveld & Kuiper (1954b)
Harris & Young (1983)
Harris et al. (1989b)
Chang & Chang (1962)
Shatzel (1954)
Shevchenko et al. (1992)
Taylor & Tedesco (1983)
Weidenschilling et al. (1990)
Yang et al. (1965)
Zappala & van Houten-Groeneveld (1979)
(45) Eugenia
Debehogne & Zappala (1980)Hutton (1989)
Harris & Young (1979)
Harris et al. (1999)
Lebofsky et al. (1988)
Shevchenko et al. (1992)
Tancredi & Gallardo (1991)
Taylor et al. (1988)
Weidenschilling et al. (1987)
(52) Europa
Barucci et al. (1986)Dotto et al. (1995)
Michaowski et al. (1995)
Michaowski et al. (2004)
Scaltriti & Zappala (1977c)
Zappala et al. (1983a)
(54) Alexandra
Belskaya et al. (1993)di Martino et al. (1987b)
Haupt & Hanslmeier (1985)
Tancredi & Gallardo (1991)
USNO
van Houten-Groeneveld et al. (1979)
Warner et al. (2008)
(55) Pandora
Barucci et al. (1985)di Martino & Cacciatori (1984a)
di Martino et al. (1987b)
Lagerkvist et al. (1995)
Shevchenko et al. (1993)
Schober (1978)
Weidenschilling et al. (1987)
Weidenschilling et al. (1990)
(63) Ausonia
di Martino & Cacciatori (1984a)Hainaut-Rouelle et al. (1995)
Lagerkvist (1981)
Lagerkvist & Williams (1987)
Lagerkvist et al. (1989)
Scaltriti & Zappala (1977a)
Zappala et al. (1983b)
(73) Klytia
Hainaut-Rouelle et al. (1995)Marciniak et al. (2008)
Szabo (1998)
Weidenschilling et al. (1990)
(80) Sappho
Burchi et al. (1985)Debehogne et al. (1990)
Harris & Young (1983)
Scaltriti & Zappala (1978)
USNO
(82) Alkmene
Harris et al. (1984)USNO
(87) Sylvia
Blanco et al. (1989)Harris & Young (1980)
Prokof'eva et al. (1992)
Schober & Surdej (1979)
Weidenschilling et al. (1987)
Weidenschilling et al. (1990)
(88) Thisbe
di Martino & Cacciatori (1984a)di Martino et al. (1987b)
Harris et al. (1992)
Choloniewski (1979)
Schober et al. (1979)
Weidenschilling et al. (1987)
Weidenschilling et al. (1990)
(107) Camilla
di Martino et al. (1987a)Harris & Young (1989)
Polishook (2009)
Weidenschilling et al. (1987)
Weidenschilling et al. (1990)
(110) Lydia
Dotto et al. (1992)Durech et al. (2007)
Lagerkvist et al. (1995)
Taylor et al. (1971)
(115) Thyra
Dotto et al. (1995)Chang et al. (1981)
Magnusson & Lagerkvist (1991)
McCheyne et al. (1985)
Michaowski et al. (2004)
Scaltriti et al. (1981)
(121) Hermione
Debehogne et al. (1978)Descamps et al. (2009)
di Martino et al. (1987b)
Hutton (1990b)
Piironen et al. (1994)
(125) Liberatrix
Durech et al. (2007)Hutton (1991)
Harris et al. (1992)
Lagerkvist et al. (1986)
Weidenschilling et al. (1987)
Weidenschilling et al. (1990)
Zappala et al. (1982)
(129) Antigone
Barucci et al. (1985)di Martino & Cacciatori (1984a)
di Martino et al. (1987b)
Dotto et al. (1992)
Scaltriti & Zappala (1977b)
Torppa et al. (2003)
Vesely & Taylor (1985)
Weidenschilling et al. (1987)
Weidenschilling et al. (1990)
(130) Elektra
Danforth & Ratcliff (1994)Debehogne et al. (1990)
Durech et al. (2007)
Harris & Young (1989)
Harris et al. (1999)
Shevchenko et al. (1996)
Weidenschilling et al. (1987)
(132) Aethra
USNOWeidenschilling et al. (1990)
Wisniewski et al. (1997)
(135) Hertha
Dotto et al. (1992)Harris & Young (1980)
Harris et al. (1992)
Lagerkvist (1981)
Lagerkvist et al. (1986)
Lagerkvist et al. (1995)
Tancredi & Gallardo (1991)
Torppa et al. (2003)
(146) Lucina
Harris & Young (1983)Harris & Young (1989)
Harris et al. (1999)
Piironen et al. (1998)
Schober (1983b)
USNO
(152) Atala
Schober (1983b)USNO
(158) Koronis
Binzel (1987)Slivan & Binzel (1996)
Slivan et al. (2003)
(160) Una
di Martino et al. (1994a)Harris et al. (1999)
Marciniak et al. (2009b)
(167) Urda
Slivan & Binzel (1996)Tedesco (1979)
USNO
Warner et al. (2008)
(182) Elsa
Harris et al. (1980)Harris et al. (1992)
Pilcher et al. (2009)
USNO
(184) Dejopeja
Hutton (1995)Marciniak et al. (2007)
Tedesco (1979)
(192) Nausikaa
Dotto et al. (1995)Lagerkvist et al. (1995)
Scaltriti & Zappala (1976)
Yang et al. (1965)
(196) Philomela
Durech et al. (2007)Erikson et al. (1991)
Kryszczynska et al. (1996)
Yang et al. (1965)
Zappala et al. (1983b)
(201) Penelope
Harris & Young (1989)Lagerkvist et al. (1981)
Pfleiderer et al. (1987)
Surdej et al. (1983)
Weidenschilling et al. (1987)
Weidenschilling et al. (1990)
(208) Lacrimosa
Binzel (1987)Slivan & Binzel (1996)
(218) Bianca
Carlsson & Lagerkvist (1981)Denchev et al. (1998)
Durech et al. (2007)
Harris & Young (1989)
Kryszczynska et al. (1996)
(230) Athamantis
Harris & Young (1980)Harris & Young (1989)
Harris et al. (1992)
Harris et al. (1999)
Yang et al. (1965)
Zeigler & Florence (1985)
(250) Bettina
di Martino & Cacciatori (1984a)Dotto et al. (1992)
Lagerkvist & Rickman (1981)
Lagerkvist et al. (1986)
Lagerkvist et al. (1995)
Weidenschilling et al. (1990)
(276) Adelheid
di Martino et al. (1995)Marciniak et al. (2007)
Piironen et al. (1994)
(277) Elvira
Binzel (1987)Slivan & Binzel (1996)
Slivan et al. (2003)
(278) Paulina
Barucci et al. (1994)USNO
(283) Emma
Fauerbach - unpublished dataMichaowski et al. (2006)
Stanzel (1978)
(306) Unitas
Durech et al. (2007)Hainaut-Rouelle et al. (1995)
Harris & Young (1983)
Piironen et al. (1998)
(311) Claudia
Binzel (1987)Slivan & Binzel (1996)
Slivan et al. (2003)
(321) Florentina
Frey (2000)Slivan & Binzel (1996)
Slivan et al. (2003)
Thizy - unpublished data
van Houten-Groeneveld & van Houten (1958)
Warner (2000)
(349) Dembowska
di Martino et al. (1987b)Haupt (1980)
Chang & Chang (1963)
McCheyne et al. (1985)
Weidenschilling et al. (1987)
Zappala et al. (1979)
(350) Ornamenta
Marciniak et al. (2009a)Schober et al. (1993)
(360) Carlova
di Martino et al. (1987a)Dotto et al. (1995)
Harris & Young (1983)
USNO
(377) Campania
di Martino et al. (1994a)Hainaut-Rouelle et al. (1995)
Lagerkvist et al. (1987)
Marciniak et al. (2008)
Schober et al. (1994)
Tedesco (1979)
(378) Holmia
di Martino et al. (1994b)Marciniak et al. (2008)
(382) Dodona
di Martino (1986)Lagerkvist et al. (1986)
Michaowski et al. (2004)
(409) Aspasia
di Martino & Cacciatori (1984b)Hainaut-Rouelle et al. (1995)
Hanslmeier (1981)
Lagerkvist (1981)
Piironen et al. (1998)
USNO
Warner et al. (2008)
(416) Vaticana
Durech et al. (2009)Erikson et al. (1991)
Lagerkvist et al. (1987)
Miles (1990)
Schober et al. (1994)
USNO
(423) Diotima
di Martino & Cacciatori (1984b)Dotto et al. (1995)
Durech et al. (2007)
Hutton (1990a)
Hainaut-Rouelle et al. (1995)
Schober (1983a)
(484) Pittsburghia
Binzel (1987)USNO
(511) Davida
di Martino et al. (1987a)Gehrels & Owings (1962)
Groeneveld & Kuiper (1954a)
Chang & Chang (1963)
Vesely & Taylor (1985)
Weidenschilling et al. (1987)
(516) Amherstia
Dotto et al. (1992)Harris & Young (1980)
Lagerkvist et al. (1987)
USNO
(532) Herculina
Cunnigham (1983)Drummond et al. (1985)
Erikson et al. (1991)
Groeneveld & Kuiper (1954b)
Harris & Young (1979)
Chang & Chang (1963)
Kaasalainen et al. (2002b)
Lebofsky et al. (1988)
Michaowski et al. (1995)
Shevchenko et al. (1992)
Taylor et al. (1987)
Weidenschilling et al. (1990)
(534) Nassovia
Binzel (1987)Slivan & Binzel (1996)
Tedesco (1979)
(556) Phyllis
Harris et al. (1992)Marciniak et al. (2007)
Zappala et al. (1983b)
(584) Semiramis
Hainaut-Rouelle et al. (1995)Harris et al. (1992)
Magnusson (1990)
Weidenschilling et al. (1987)
Weidenschilling et al. (1990)
(595) Polyxena
Hainaut-Rouelle et al. (1995)USNO
Warner (2008)
(614) Pia
di Martino et al. (1994b)USNO
(624) Hektor
Dahlgren et al. (1991)Detal et al. (1994)
Dunlap & Gehrels (1969)
Hainaut-Rouelle et al. (1995)
Hartmann & Cruikshank (1978)
(628) Christine
Stephens (2003)USNO
(665) Sabine
Hainaut-Rouelle et al. (1995)Michaowski et al. (2006)
Riccioli et al. (1995)
(675) Ludmilla
Bernasconi - unpublished dataChang et al. (1981)
Schober & Dvorak (1975)
Velichko et al. (1995)
(690) Wratislavia
Denchev (2000, private comm.)Hutton (1988)
Hutton (1995)
Michaowski et al. (2006)
(694) Ekard
Hainaut-Rouelle et al. (1995)Weidenschilling et al. (1987)
Weidenschilling et al. (1990)
Zeigler & Florence (1985)
(714) Ulula
Schober & Stadler (1990)USNO
(720) Bohlinia
Binzel (1987)Slivan & Binzel (1996)
Slivan et al. (2003)
(747) Winchester
Harris & Young (1980)Marciniak et al. (2009b)
Vesely & Taylor (1985)
Zappala et al. (1983b)
(770) Bali
USNOWisniewski et al. (1997)
(771) Libera
Binzel (1987)Marciniak et al. (2009a)
Warner (2000)
(776) Berbericia
Debehogne et al. (1983)di Martino et al. (1987b)
Durech et al. (2007)
Hainaut-Rouelle et al. (1995)
Harris et al. (1992)
Schober (1979)
(849) Ara
Harris et al. (1992)Marciniak et al. (2009b)
(915) Cosette
di Martino et al. (1994b)USNO
(984) Gretia
di Martino (1984)Marciniak et al. (2009a)
Piironen et al. (1994)
van Houten (1962)
(1012) Sarema
Binzel (1987)USNO
(1022) Olympiada
USNOWarner et al. (2008)
(1036) Ganymed
Hahn et al. (1989)Lupishko et al. (1987b)
(1088) Mitaka
USNOWisniewski et al. (1997)
(1223) Neckar
Binzel (1987)Michaowski et al. (2000)
Slivan & Binzel (1996)
Tedesco (1979)
(1270) Datura
Székely et al. (2005)Vokrouhlický et al. (2009)
Wisniewski et al. (1997)
(1580) Betulia
Erikson et al. (1991)Lagerkvist (1977)
Tedesco et al. (1978)
Wisniewski et al. (1997)
(1600) Vyssotsky
Higgins (2008)Warner (1999)
Warner et al. (2006)
(1620) Geographos
Dunlap (1974)Durech et al. (2008a)
Magnusson et al. (1996)
Michaowski et al. (1994)
Weidenschilling et al. (1990)
(1627) Ivar
Hahn et al. (1989)Hoffmann & Geyer (1990)
Chernova et al. (1995)
Kaasalainen et al. (2004)
Pravec et al. (1996)
Velichko et al. (1990)
(1862) Apollo
Durech et al. (2008b)Hahn (1983)
Harris et al. (1987)
Kaasalainen et al. (2007)
(1980) Tezcatlipoca
Kaasalainen et al. (2004)Wisniewski et al. (1997)
(2100) Ra-Shalom
Harris et al. (1992)Kaasalainen et al. (2004)
Ostro et al. (1984)
Pravec et al. (1998)
(3908) Nyx
Drummond & Wisniewski (1990)Kaasalainen et al. (2004)
(5587) 1990 SB
Kaasalainen et al. (2004)Koff et al. (2002)
Polishook (2009)
Pravec et al. (1998)
(6053) 1993 BW3
Pravec et al. (1997)
References
- Ahmad, I. I. 1954, ApJ, 120, 551 [NASA ADS] [CrossRef] [Google Scholar]
- Barucci, M. A. 1983, A&AS, 54, 471 [NASA ADS] [Google Scholar]
- Barucci, M. A., Fulchignoni, M., Burchi, R., et al. 1985, Icarus, 61, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Barucci, M. A., Bockelee-Morvan, D., Lecacheux, J., Brahic, A., & Clairemidi, S. 1986, A&A, 163, 261 [NASA ADS] [Google Scholar]
- Barucci, M. A., di Martino, M., Dotto, E., et al. 1994, Icarus, 109, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Belskaya, I. N., Dovgopol, A. N., Erikson, A., Lagerkvist, C.-I., & Oja, T. 1993, A&AS, 101, 507 [NASA ADS] [Google Scholar]
- Berthier, J., Hestroffer, D., Carry, B., et al. 2008, LPI Contributions, 1405, 8374 [NASA ADS] [Google Scholar]
- Binzel, R. P. 1984, Icarus, 59, 456 [NASA ADS] [CrossRef] [Google Scholar]
- Binzel, R. P. 1987, Icarus, 72, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Birch, P. V., & Taylor, R. C. 1989, A&AS, 81, 409 [NASA ADS] [Google Scholar]
- Birch, P. V., Tedesco, E. F., Taylor, R. C., et al. 1983, Icarus, 54, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Blanco, C., di Martino, M., Gonano, M., Jaumann, R., & Mottola, S. 1989, Mem. Soc. Astron. Itali., 60, 195 [NASA ADS] [Google Scholar]
- Burchi, R. 1972, Mem. Soc. Astron. Ital., 43, 27 [NASA ADS] [Google Scholar]
- Burchi, R., & Milano, L. 1974, A&AS, 15, 173 [NASA ADS] [Google Scholar]
- Burchi, R., & Milano, L. 1983, Moon and Planets, 28, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Burchi, R., D'Ambrosio, V., Tempesti, P., et al. 1985, A&AS, 60, 9 [Google Scholar]
- Carlsson, M., & Lagerkvist, C.-I. 1981, A&AS, 44, 15 [NASA ADS] [Google Scholar]
- Carlsson, M., & Lagerkvist, C.-I. 1983, A&AS, 53, 157 [NASA ADS] [Google Scholar]
- Chang, Y. C., & Chang, C. S. 1962, Acta Astron. Sinica, 10, 101 [Google Scholar]
- Chang, Y. C., & Chang, C. S. 1963, Acta Astron. Sinica, 11, 139 [Google Scholar]
- Chang, Y. C., Wan-Tsing, H., & Fu-Yuan, K. 1959, Acta Astron. Sinica, 7, 204 [NASA ADS] [Google Scholar]
- Chang, Y. C., Zhou, X.-H., Yang, X.-Y., et al. 1981, Acta Astron. Sinica, 22, 169 [NASA ADS] [Google Scholar]
- Chernova, G. P., Kiselev, N. N., Krugley, Y. N., et al. 1995, AJ, 110, 1875 [NASA ADS] [CrossRef] [Google Scholar]
- Choloniewski, J. 1979, Acta Astron., 29, 105 [NASA ADS] [Google Scholar]
- Cunnigham, C. J. 1983, Minor Planet Bulletin, 10, 26 [NASA ADS] [Google Scholar]
- Dahlgren, M., Lagerkvist, C.-I., Fitzsimmons, A., et al. 1991, MNRAS, 250, 115 [NASA ADS] [Google Scholar]
- Danforth, C. W., & Ratcliff, S. J. 1994, Minor Planet Bulletin, 21, 1 [NASA ADS] [Google Scholar]
- Debehogne, H., & Zappala, V. 1980, A&AS, 40, 257 [Google Scholar]
- Debehogne, H., Surdej, A., & Surdej, J. 1978, A&AS, 32, 127 [NASA ADS] [Google Scholar]
- Debehogne, H., de Sanctis, G., & Zappala, V. 1983, Icarus, 55, 236 [NASA ADS] [CrossRef] [Google Scholar]
- Debehogne, H., Lagerkvist, C.-I., Magnusson, P., et al. 1990, in Asteroids, Comets, Meteors III, ed. C. I. Lagerkvist, H. Rickman, & B. A. Lindblad, 45 [Google Scholar]
- Delbo, M., & Tanga, P. 2009, Planet. Space Sci., 57, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Denchev, P., Magnusson, P., & Donchev, Z. 1998, Planet. Space Sci., 46, 673 [Google Scholar]
- Descamps, P., Marchis, F., Durech, J., et al. 2009, Icarus, 203, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Detal, A., Hainaut, O., Pospieszalska-Surdej, A., et al. 1994, A&A, 281, 269 [NASA ADS] [Google Scholar]
- di Martino, M. 1984, Icarus, 60, 541 [NASA ADS] [CrossRef] [Google Scholar]
- di Martino, M. 1986, in Asteroids, Comets, Meteors II, ed. C.-I. Lagerkvist, H. Rickman, B. A. Lindblad, & H. Lundstedt, 81 [Google Scholar]
- di Martino, M., & Cacciatori, S. 1984a, Icarus, 60, 75 [NASA ADS] [CrossRef] [Google Scholar]
- di Martino, M., & Cacciatori, S. 1984b, A&A, 130, 206 [NASA ADS] [Google Scholar]
- di Martino, M., Zappala, V., de Campos, J. A., Debehogne, H., & Lagerkvist, C.-I. 1987a, A&AS, 67, 95 [NASA ADS] [Google Scholar]
- di Martino, M., Zappala, V., de Sanctis, G., et al. 1987b, Icarus, 69, 338 [NASA ADS] [CrossRef] [Google Scholar]
- di Martino, M., Zappala, V., Cellino, A., et al. 1989, A&A, 223, 352 [NASA ADS] [Google Scholar]
- di Martino, M., Blanco, C., Riccioli, D., et al. 1994a, Icarus, 107, 269 [NASA ADS] [CrossRef] [Google Scholar]
- di Martino, M., Dotto, E., Barucci, M. A., Fulchignoni, M., & Rotundi, A. 1994b, Icarus, 109, 210 [NASA ADS] [CrossRef] [Google Scholar]
- di Martino, M., Dotto, E., Cellino, A., Barucci, M. A., & Fulchignoni, M. 1995, A&AS, 112, 1 [NASA ADS] [Google Scholar]
- Dotto, E., Barucci, M. A., Fulchignoni, M., et al. 1992, A&AS, 95, 195 [NASA ADS] [Google Scholar]
- Dotto, E., de Angelis, G., di Martino, M., et al. 1995, Icarus, 117, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Drummond, J. D., & Wisniewski, W. Z. 1990, Icarus, 83, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Drummond, J. D., Hege, E. K., Cocke, W. J., et al. 1985, Icarus, 61, 232 [NASA ADS] [CrossRef] [Google Scholar]
- Dunlap, J. L. 1974, AJ, 79, 324 [NASA ADS] [CrossRef] [Google Scholar]
- Dunlap, J. L., & Gehrels, T. 1969, AJ, 74, 796 [NASA ADS] [CrossRef] [Google Scholar]
- Durech, J., & Kaasalainen, M. 2003, A&A, 404, 709 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Durech, J., Grav, T., Jedicke, R., Kaasalainen, M., & Denneau, L. 2005, Earth, Moon, and Planets, 97, 179 [Google Scholar]
- Durech, J., Kaasalainen, M., Marciniak, A., et al. 2007, A&A, 465, 331 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Durech, J., Vokrouhlický, D., Kaasalainen, M., et al. 2008a, A&A, 489, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Durech, J., Vokrouhlický, D., Kaasalainen, M., et al. 2008b, A&A, 488, 345 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Durech, J., Kaasalainen, M., Warner, B. D., et al. 2009, A&A, 493, 291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Erikson, A., Lagerkvist, C.-I., Lindgren, M., et al. 1991, A&AS, 91, 259 [Google Scholar]
- Foglia, S. 1992, Minor Planet Bulletin, 19, 19 [Google Scholar]
- Foglia, S. 1995, Minor Planet Bulletin, 22, 36 [NASA ADS] [Google Scholar]
- Frey, G. 2000, Minor Planet Bulletin, 27, 29 [NASA ADS] [Google Scholar]
- Gehrels, T. 1956, ApJ, 123, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, T., & Owings, D. 1962, ApJ, 135, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, T., & Taylor, R. C. 1977, AJ, 82, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Groeneveld, I., & Kuiper, G. P. 1954a, ApJ, 120, 200 [NASA ADS] [CrossRef] [Google Scholar]
- Groeneveld, I., & Kuiper, G. P. 1954b, ApJ, 120, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Hahn, G. 1983, in Asteroids, comets, meteors; Proceedings of the Meeting, Uppsala, Sweden, June 20-22, ed. C.-I. Lagerkvist, & H. Rickman, (A85-26851 11-89), Uppsala, Sweden, Astronomiska Observatoriet, 35, [Google Scholar]
- Hahn, G., Magnusson, P., Harris, A. W., et al. 1989, Icarus, 78, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Hainaut-Rouelle, M.-C., Hainaut, O. R., & Detal, A. 1995, A&AS, 112, 125 [NASA ADS] [Google Scholar]
- Hanslmeier, A. 1981, Mitt. Univ. Graz., 85 [Google Scholar]
- Hapke, B. 1981, J. Geophys. Res., 86, 3039 [Google Scholar]
- Hapke, B. 1984, Icarus, 59, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Hapke, B. 1986, Icarus, 67, 264 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, A. W., & Young, J. 1979, Icarus, 38, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, A. W., & Young, J. W. 1980, Icarus, 43, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, A. W., & Young, J. W. 1983, Icarus, 54, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, A. W., & Young, J. W. 1989, Icarus, 81, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, A. W., Young, J. W., Scaltriti, F., et al. 1980, Icarus, 41, 316 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, A. W., Young, J. W., Scaltriti, F., et al. 1984, Icarus, 57, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, A. W., Young, J. W., Goguen, J., et al. 1987, Icarus, 70, 246 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, A. W., Young, J. W., Bowell, E., et al. 1989a, Icarus, 77, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, A. W., Young, J. W., Contreiras, L., et al. 1989b, Icarus, 81, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, A. W., Young, J. W., Dockweiler, T., et al. 1992, Icarus, 95, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, A. W., Young, J. W., Bowell, E., et al. 1999, Icarus, 142, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Hartmann, W. K., & Cruikshank, D. P. 1978, Icarus, 36, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Haupt, H. 1980, Mitt. Univ. Graz., 69 [Google Scholar]
- Haupt, H., & Hanslmeier, A. 1985, Mitt. der Univ. Sternwarte Graz., 107 [Google Scholar]
- Higgins, D. 2008, Minor Planet Bulletin, 35, 30 [NASA ADS] [Google Scholar]
- Hoffmann, M., & Geyer, E. H. 1990, Acta Astron., 40, 389 [NASA ADS] [Google Scholar]
- Hollis, A. J., Bembrick, C. S., Dumont, M., et al. 1987, Journal of the British Astronomical Association, 97, 220 [NASA ADS] [Google Scholar]
- Hutton, R. G. 1988, Minor Planet Bulletin, 15, 21 [Google Scholar]
- Hutton, R. G. 1989, Minor Planet Bulletin, 16, 16 [NASA ADS] [Google Scholar]
- Hutton, R. G. 1990a, Boletin de la Asociacion Argentina de Astronomia La Plata Argentina, 36, 193 [NASA ADS] [Google Scholar]
- Hutton, R. G. 1990b, Minor Planet Bulletin, 17, 41 [NASA ADS] [Google Scholar]
- Hutton, R. G. 1991, Minor Planet Bulletin, 18, 39 [NASA ADS] [Google Scholar]
- Hutton, R. G. 1995, Rev. Mex. Astron. Astrofis, 31, 19 [Google Scholar]
- Hutton, R. G., & Blain, A. 1988, Minor Planet Bulletin, 15, 3 [NASA ADS] [Google Scholar]
- Kaasalainen, M. 2009, Inverse Problems and Imaging, submitted [Google Scholar]
- Kaasalainen, M., & Lamberg, L. 2006, Inverse Problems, 22, 749 [Google Scholar]
- Kaasalainen, M., & Torppa, J. 2001, Icarus, 153, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Kaasalainen, M., Torppa, J., & Muinonen, K. 2001, Icarus, 153, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Kaasalainen, M., Mottola, S., & Fulchignomi, M. 2002a, in Asteroids III, ed. W. F. Bottke, A. Cellino, P. Paolicchi, & R. P. Binzel (Tucson: University of Arizona Press), 139 [Google Scholar]
- Kaasalainen, M., Torppa, J., & Piironen, J. 2002b, Icarus, 159, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Kaasalainen, M., Pravec, P., Krugly, Y. N., et al. 2004, Icarus, 167, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Kaasalainen, S., Kaasalainen, M., & Piironen, J. 2005, A&A, 440, 1177 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaasalainen, M., Durech, J., Warner, B. D., Krugly, Y. N., & Gaftonyuk, N. M. 2007, Nature, 446, 420 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Koff, R. A., Pravec, P., Sarounová, L., et al. 2002, Minor Planet Bulletin, 29, 51 [Google Scholar]
- Kryszczynska, A., Colas, F., Berthier, J., Micha▯owski, T., & Pych, W. 1996, Icarus, 124, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Kryszczynska, A., La Spina, A., Paolicchi, P., et al. 2007, Icarus, 192, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Lagerkvist, C.-I. 1977, Icarus, 32, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Lagerkvist, C.-I. 1981, A&AS, 44, 345 [NASA ADS] [Google Scholar]
- Lagerkvist, C.-I., & Rickman, H. 1981, Moon and Planets, 24, 437 [NASA ADS] [CrossRef] [Google Scholar]
- Lagerkvist, C.-I., & Williams, I. P. 1987, A&AS, 68, 295 [NASA ADS] [Google Scholar]
- Lagerkvist, C.-I., Rickman, H., Scaltriti, F., et al. 1981, A&A, 104, 148 [NASA ADS] [Google Scholar]
- Lagerkvist, C.-I., Hahn, G., Magnusson, P., Rickman, H., & Hammarback, G. 1986, in Asteroids, Comets, Meteors II, ed. C.-I. Lagerkvist, H. Rickman, B. A. Lindblad, & H. Lundstedt, 67 [Google Scholar]
- Lagerkvist, C.-I., Hahn, G., Magnusson, P., et al. 1987, A&AS, 70, 21 [NASA ADS] [Google Scholar]
- Lagerkvist, C.-I., Magnusson, P., Williams, I. P., Buontempo, M. E., & Gibbs, P. 1988, A&AS, 73, 395 [NASA ADS] [Google Scholar]
- Lagerkvist, C.-I., Magnusson, P., Williams, I. P., et al. 1989, A&AS, 78, 519 [NASA ADS] [Google Scholar]
- Lagerkvist, C.-I., Erikson, A., Debehogne, H., et al. 1995, A&AS, 113, 115 [NASA ADS] [Google Scholar]
- Lamy, P. L., Kaasalainen, M., Lowry, S., et al. 2008, A&A, 487, 1179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lebofsky, L. A., Greenberg, R., Tedesco, E. F., et al. 1988, Icarus, 75, 518 [NASA ADS] [CrossRef] [Google Scholar]
- Lupishko, D. F., Kiselev, N. N., & Chernova, G. P. 1979, Pisma Astronomicheskii Zhurnal, 5, 201 [NASA ADS] [Google Scholar]
- Lupishko, D. F., Kiselev, N. N., Chernova, G. P., et al. 1980, PismaAstronomicheskii Zhurnal, 6, 184 [Google Scholar]
- Lupishko, D. F., Tupieva, F. A., Velichko, F. P., Kiselev, N. N., & Chernova, G. P. 1981, Astronomicheskii Vestnik, 15, 25 [NASA ADS] [Google Scholar]
- Lupishko, D. F., Belskaya, I. N., Tupieva, F. A., et al. 1982, Astronomicheskii Vestnik, 16, 101 [Google Scholar]
- Lupishko, D. F., Belskaya, I. N., & Tupieva, F. A. 1983, Pisma Astronomicheskii Zhurnal, 9, 691 [NASA ADS] [Google Scholar]
- Lupishko, D. F., Velichko, F. P., Belskaya, I. N., et al. 1987a, Kinematika i Fizika Nebesnykh Tel, 3, 36 [NASA ADS] [Google Scholar]
- Lupishko, D. F., Velichko, F. P., Kazakov, V. V., et al. 1987b, Kinematika i Fizika Nebesnykh Tel, 3, 92 [NASA ADS] [Google Scholar]
- Lupishko, D. F., Tupieva, F. A., Velichko, F. P., et al. 1989, Bjull. Inst. Astrofizikii, 80, 13 [NASA ADS] [Google Scholar]
- Lustig, G., & Dvorak, R. 1975, Acta Physica Austriaca, 43, 89 [NASA ADS] [Google Scholar]
- Lustig, G., & Hahn, G. 1976, Acta Physica Austriaca, 44, 199 [Google Scholar]
- Magnusson, P. 1990, Icarus, 85, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Magnusson, P., & Lagerkvist, C.-I. 1991, A&AS, 87, 269 [NASA ADS] [Google Scholar]
- Magnusson, P., Barucci, M. A., Drummond, J. D., et al. 1989, in Asteroids II, ed. R. P. Binzel, T. Gehrels, & M. S. Matthews (Tucson: University of Arizona Press), 66 [Google Scholar]
- Magnusson, P., Dahlgren, M., Barucci, M. A., et al. 1996, Icarus, 123, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Marciniak, A., Micha▯owski, T., Kaasalainen, M., et al. 2007, A&A, 473, 633 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marciniak, A., Micha▯owski, T., Kaasalainen, M., et al. 2008, A&A, 478, 559 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marciniak, A., Micha▯owski, T., Hirsch, R., et al. 2009a, A&A, 508, 1503 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marciniak, A., Micha▯owski, T., Hirsch, R., et al. 2009b, A&A, 498, 313 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McCheyne, R. S., Eaton, N., Green, S. F., et al. 1984, Icarus, 59, 286 [NASA ADS] [CrossRef] [Google Scholar]
- McCheyne, R. S., Eaton, N., & Meadows, A. J. 1985, Icarus, 61, 443 [NASA ADS] [CrossRef] [Google Scholar]
- Melillo, F. J. 1986, Minor Planet Bulletin, 13, 21 [NASA ADS] [Google Scholar]
- Melillo, F. J. 1987a, Minor Planet Bulletin, 14, 42 [NASA ADS] [Google Scholar]
- Melillo, F. J. 1987b, Minor Planet Bulletin, 14, 21 [NASA ADS] [Google Scholar]
- Micha▯owski, T., & Velichko, F. P. 1990, Acta Astron., 40, 321 [NASA ADS] [Google Scholar]
- Micha▯owski, T., Kwiatkowski, T., Borczyk, W., et al. 1994, Acta Astron., 44, 223 [NASA ADS] [Google Scholar]
- Micha▯owski, T., Velichko, F. P., di Martino, M., et al. 1995, Icarus, 118, 292 [NASA ADS] [CrossRef] [Google Scholar]
- Micha▯owski, T., Pych, W., Berthier, J., et al. 2000, A&AS, 146, 471 [Google Scholar]
- Micha▯owski, T., Kwiatkowski, T., Kaasalainen, M., et al. 2004, A&A, 416, 353 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Micha▯owski, T., Kaasalainen, M., Polinska, M., et al. 2006, A&A, 459, 663 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mignard, F., Cellino, A., Muinonen, K., et al. 2007, Earth Moon and Planets, 101, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Miles, R. 1990, Minor Planet Bulletin, 17, 25 [NASA ADS] [Google Scholar]
- Millis, R. L., Wasserman, L. H., Bowell, E., et al. 1981, AJ, 86, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, T. G., Sekiguchi, T., Kaasalainen, M., Abe, M., & Hasegawa, S. 2005, A&A, 443, 347 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neely, A. W. 1992, Minor Planet Bulletin, 19, 28 [Google Scholar]
- Ostro, S. J., Harris, A. W., Campbell, D. B., Shapiro, I. I., & Young, J. W. 1984, Icarus, 60, 391 [NASA ADS] [CrossRef] [Google Scholar]
- Pavlovski, K., Knezevic, Z., & Muminovic, M. 1981, Publ. Astron. Obs. Sarajevo, 1, 1, 225 [Google Scholar]
- Pfleiderer, J., Pfleiderer, M., & Hanslmeier, A. 1987, A&AS, 69, 117 [NASA ADS] [Google Scholar]
- Piironen, J., Bowell, E., Erikson, A., et al. 1994, A&AS, 106, 587 [NASA ADS] [Google Scholar]
- Piironen, J., Lagerkvist, C.-I., Erikson, A., et al. 1998, A&AS, 128, 525 [Google Scholar]
- Piironen, J. O., Poutanen, M., di Martino, M., et al. 1985, A&AS, 61, 299 [Google Scholar]
- Pilcher, F. 2009, Minor Planet Bulletin, 36, 133 [Google Scholar]
- Pilcher, F., Benishek, V., & Krajewski, R. 2009, Minor Planet Bulletin, 36, 40 [NASA ADS] [Google Scholar]
- Polishook, D. 2009, Minor Planet Bulletin, 36, 119 [NASA ADS] [Google Scholar]
- Pravec, P., Sarounová, L., & Wolf, M. 1996, Icarus, 124, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Pravec, P., Wolf, M., & Sarounová, L. 1998, Icarus, 136, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Pravec, P., Wolf, M., Sarounová, L., Harris, A. W., & Davies, J. K. 1997, Icarus, 127, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Pravec, P., Harris, A. W., & Micha▯owski, T. 2002, in Asteroids III, ed. W. F. Bottke, A. Cellino, P. Paolicchi, & R. P. Binzel (Tucson: University of Arizona Press), 113 [Google Scholar]
- Prokof'eva, V. V., Demchik, M. I., Karachkina, L. G., et al. 1992, Astronomicheskii Vestnik, 26, 3 [NASA ADS] [Google Scholar]
- Riccioli, D., Blanco, C., di Martino, M., et al. 1995, A&AS, 111, 297 [NASA ADS] [Google Scholar]
- Sather, R. E. 1976, AJ, 81, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Scaltriti, F., & Zappala, V. 1975, A&AS, 19, 249 [NASA ADS] [Google Scholar]
- Scaltriti, F., & Zappala, V. 1976, A&AS, 23, 167 [NASA ADS] [Google Scholar]
- Scaltriti, F., & Zappala, V. 1977a, Icarus, 31, 498 [NASA ADS] [CrossRef] [Google Scholar]
- Scaltriti, F., & Zappala, V. 1977b, A&A, 56, 7 [NASA ADS] [Google Scholar]
- Scaltriti, F., & Zappala, V. 1977c, A&AS, 30, 169 [NASA ADS] [Google Scholar]
- Scaltriti, F., & Zappala, V. 1978, Icarus, 34, 428 [NASA ADS] [CrossRef] [Google Scholar]
- Scaltriti, F., Zappala, V., & Stanzel, R. 1978, Icarus, 34, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Scaltriti, F., Zappala, V., & Harris, A. W. 1981, Icarus, 46, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Schober, H. J. 1976, A&A, 53, 115 [NASA ADS] [Google Scholar]
- Schober, H. J. 1978, A&AS, 34, 377 [NASA ADS] [Google Scholar]
- Schober, H. J. 1979, A&AS, 38, 91 [NASA ADS] [Google Scholar]
- Schober, H. J. 1983a, A&A, 127, 301 [NASA ADS] [Google Scholar]
- Schober, H. J. 1983b, A&AS, 53, 71 [NASA ADS] [Google Scholar]
- Schober, H. J., & Dvorak, R. 1975, A&A, 44, 81 [NASA ADS] [Google Scholar]
- Schober, H. J., & Stadler, M. 1990, A&A, 230, 233 [NASA ADS] [Google Scholar]
- Schober, H. J., & Surdej, J. 1979, A&AS, 38, 269 [Google Scholar]
- Schober, H. J., Scaltriti, F., & Zappala, V. 1979, A&AS, 36, 1 [NASA ADS] [Google Scholar]
- Schober, H. J., Erikson, A., Hahn, G., Lagerkvist, C. I., & Oja, T. 1993, A&AS, 101, 499 [NASA ADS] [Google Scholar]
- Schober, H. J., Erikson, A., Hahn, G., et al. 1994, A&AS, 105, 281 [NASA ADS] [Google Scholar]
- Schroll, A., Haupt, H. F., & Maitzen, H. M. 1976, Icarus, 27, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Schroll, A., Schober, H. J., & Lagerkvist, C. I. 1981, A&A, 104, 296 [NASA ADS] [Google Scholar]
- Seidelmann, P. K., Archinal, B. A., A'Hearn, M. F., et al. 2007, Celestial Mechanics and Dynamical Astronomy, 98, 155 [Google Scholar]
- Shatzel, A. V. 1954, ApJ, 120, 547 [NASA ADS] [CrossRef] [Google Scholar]
- Shevchenko, V. G., Cherny, V. G., Krugly, Y. N., et al. 1992, Icarus, 100, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Shevchenko, V. G., Chiorny, V. G., Kalashnikov, A. V., et al. 1996, A&AS, 115, 475 [NASA ADS] [Google Scholar]
- Shevchenko, V. G., Krugly, Y. N., Lupishko, D. F., Harris, A. W., & Chernova, G. P. 1993, Astronomicheskii Vestnik, 27, 75 [Google Scholar]
- Slivan, S. M., & Binzel, R. P. 1996, Icarus, 124, 452 [NASA ADS] [CrossRef] [Google Scholar]
- Slivan, S. M., Binzel, R. P., Crespo da Silva, L. D., et al. 2003, Icarus, 162, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Stanzel, R. 1978, A&AS, 34, 373 [NASA ADS] [Google Scholar]
- Stephens, R. D. 2003, Minor Planet Bulletin, 30, 69 [NASA ADS] [Google Scholar]
- Surdej, J., Louis, B., Cramer, N., et al. 1983, A&AS, 54, 371 [NASA ADS] [Google Scholar]
- Surdej, J., Pospieszalska-Surdej, A., Micha▯owski, T., et al. 1986, A&A, 170, 167 [NASA ADS] [Google Scholar]
- Szabo, G. 1998, Acta Physica Polonica A, 93, 23 [NASA ADS] [Google Scholar]
- Székely, P., Kiss, L. L., Szabó, G. M., et al. 2005, Planet. Space Sci., 53, 925 [NASA ADS] [CrossRef] [Google Scholar]
- Tancredi, G., & Gallardo, T. 1991, A&A, 242, 279 [NASA ADS] [Google Scholar]
- Taylor, R. C. 1977, AJ, 82, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, R. C. 1978, AJ, 83, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, R. C., & Tedesco, E. F. 1983, Icarus, 54, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, R. C., Gehrels, T., & Silvester, A. B. 1971, AJ, 76, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, R. C., Gehrels, T., & Capen, R. C. 1976, AJ, 81, 778 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, R. C., Birch, P. V., Drummond, J., Pospieszalska-Surdej, A., & Surdej, J. 1987, Icarus, 69, 354 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, R. C., Birch, P. V., Pospieszalska-Surdej, A., et al. 1988, Icarus, 73, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Tedesco, E., Drummond, J., Candy, M., et al. 1978, Icarus, 35, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Tedesco, E. F. 1979, Ph.D. Thesis, A&A (New Mexico State Univ., University Park) [Google Scholar]
- Tedesco, E. F., & Sather, R. E. 1981, AJ, 86, 1553 [NASA ADS] [CrossRef] [Google Scholar]
- Tedesco, E. F., & Taylor, R. C. 1985, Icarus, 61, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Tedesco, E. F., Taylor, R. C., Drummond, J., et al. 1983, Icarus, 54, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Torppa, J., Kaasalainen, M., Micha▯owski, T., et al. 2003, Icarus, 164, 346 [NASA ADS] [CrossRef] [Google Scholar]
- van Houten, C. J. 1962, Bull. Astron. Inst. Netherlands, 16, 160 [Google Scholar]
- van Houten-Groeneveld, I. 1981, A&A, 98, 203 [NASA ADS] [Google Scholar]
- van Houten-Groeneveld, I., & van Houten, C. J. 1958, ApJ, 127, 253 [NASA ADS] [CrossRef] [Google Scholar]
- van Houten-Groeneveld, I., van Houten, C. J., & Zappala, V. 1979, A&AS, 35, 223 [NASA ADS] [Google Scholar]
- Velichko, F. P., Krugly, Y. N., Lupishko, D. F., et al. 1990, Astronomicheskij Tsirkulyar, 1546, 39 [NASA ADS] [Google Scholar]
- Velichko, F. P., Michalowski, T., Erikson, A., et al. 1995, A&AS, 110, 125 [Google Scholar]
- Vesely, C. D., & Taylor, R. C. 1985, Icarus, 64, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Veverka, J. 1971, Icarus, 15, 454 [NASA ADS] [CrossRef] [Google Scholar]
- Vokrouhlický, D., Durech, J., Micha▯owski, T., et al. 2009, A&A, 507, 495 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wamsteker, W., & Sather, R. E. 1974, AJ, 79, 1465 [NASA ADS] [CrossRef] [Google Scholar]
- Warner, B. 2000, Minor Planet Bulletin, 27, 4 [Google Scholar]
- Warner, B. D. 1999, Minor Planet Bulletin, 26, 31 [NASA ADS] [Google Scholar]
- Warner, B. D. 2008, Minor Planet Bulletin, 35, 171 [NASA ADS] [Google Scholar]
- Warner, B. D., Pray, D. P., Dyvig, R., et al. 2006, Minor Planet Bulletin, 33, 45 [NASA ADS] [Google Scholar]
- Warner, B. D., Durech, J., Fauerbach, M., et al. 2008, Minor Planet Bulletin, 35, 167 [NASA ADS] [Google Scholar]
- Weidenschilling, S. J., Chapman, C. R., Davis, D. R., et al. 1987, Icarus, 70, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Weidenschilling, S. J., Chapman, C. R., Davis, D. R., Greenberg, R., & Levy, D. H. 1990, Icarus, 86, 402 [NASA ADS] [CrossRef] [Google Scholar]
- Wisniewski, W. Z., Micha▯owski, T. M., Harris, A. W., et al. 1997, Icarus, 126, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Wood, X. H. J., & Kuiper, G. P. 1963, ApJ, 137, 1279 [Google Scholar]
- Yang, X. Y., Zhang, Y. Y., & Li, X.-Q. 1965, Acta Astron. Sinica, 13, 66 [Google Scholar]
- Zappala, V., & van Houten-Groeneveld, I. 1979, Icarus, 40, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Zappala, V., van Houten-Groeneveld, I., & van Houten, C. J. 1979, A&AS, 35, 213 [NASA ADS] [Google Scholar]
- Zappala, V., Debehogne, H., Lagerkvist, C.-I., et al. 1982, A&AS, 50, 23 [NASA ADS] [Google Scholar]
- Zappala, V., di Martino, M., & Cacciatori, S. 1983a, Icarus, 56, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Zappala, V., Scaltriti, F., & di Martino, M. 1983b, Icarus, 56, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Zappala, V., di Martino, M., Knezevic, Z., et al. 1984, A&A, 130, 208 [NASA ADS] [Google Scholar]
- Zeigler, K. W., & Florence, W. B. 1985, Icarus, 62, 512 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, X.-H., & Yang, X.-Y. 1981, Acta Astron. Sinica, 22, 378 [Google Scholar]
- Zhou, X. H., Yang, X. Y., & Wu, Z. X. 1982, Acta Astron. Sinica, 23, 349 [Google Scholar]
- Ziegler, K. W., & Florence, W. B. 1985, Minor Planet Bulletin, 12, 21 [NASA ADS] [Google Scholar]
Footnotes
- ... archive
![[*]](/icons/foot_motif.png)
- http://www.psi.edu/pds/
- ... software
![[*]](/icons/foot_motif.png)
- http://www.minorplanetobserver.com
- ... portal
![[*]](/icons/foot_motif.png)
- http://vo.imcce.fr/webservices
- ... page
![[*]](/icons/foot_motif.png)
- http://hamilton.dm.unipi.it/astdys/
All Figures
![\begin{figure}
\par\includegraphics[width=\textwidth,clip]{12693fg1.eps}
\end{figure}](/articles/aa/full_html/2010/05/aa12693-09/Timg7.png)
|
Figure 1:
An example of the rotational sequence described by Eq. (1).
The four subsequent rotations transform the model from the body-fixed
coordinate frame ``ast'' to the ecliptic coordinate frame ``ecl''. Here
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.