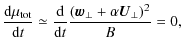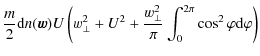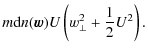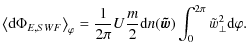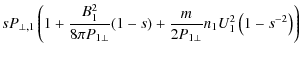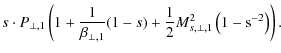EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 512 (March-April 2010) A&A, 512 (2010) A64 Full HTML
Free Access
Issue
A&A
Volume 512, March-April 2010
Article Number A64
Number of page(s) 6
Section Astrophysical processes
DOI https://doi.org/10.1051/0004-6361/200913805
Published online 02 April 2010
A&A 512, A64 (2010)

Upstream ions converting into downstream pick-up ions: the effect of shock-decelerated frozen-in fields

H.-J. Fahr - M. Siewert

Argelander Institut für Astronomie der Universität Bonn, Abteilung f. Astrophysik und Extraterrestrische Forschung, Auf dem Huegel 71, 53121 Bonn, Germany

Received 4 December 2009 / Accepted 30 December 2009

Abstract
Context. Observations by Voyager-2 at the crossing of the solar wind termination shock have led to unexpected discoveries, such as the downstream solar wind protons still having Mach numbers higher than 1 and temperatures, though increased by a factor of about 30, nevertheless being much lower than those expected from classical MHD shock theory. Though our earlier semi-kinetic theories of the ion passage over the termination shock, in which the conservation of the magnetic ion moment was required, provided interesting insights into the detailed microphysics occurring at the shock, our predictions for the downstream ion pressure and temperature in view of observations were both too low.
Aims. Here we improve on our earlier theoretical approach by introducing a so-called ``effective magnetic moment'' by which we not only take into account the increase in the magnetic field magnitude over the shock, but we also respect that the ions comoving with the bulk of the plasma flow gyrate around a decelerated frozen-in field.
Methods. We derive a differential equation for the behaviour of the perpendicular pressure across the shock, which accounts for the conservation of the newly derived effective magnetic moment, and generalises the results of earlier studies. The resulting differential equation is then solved analytically.
Results. With this new concept of conservation of the newly introduced ``effective magnetic moment'' we arrive at interesting new relations between upstream and downstream ion pressures and temperatures which now nicely represent the recent Voyager-2 results.

Key words: shock waves - magnetohydrodynamics (MHD) - plasmas - solar wind

1 Introduction

For a complete description of the ion passage over the solar wind termination shock the standard set of MHD shock relations as given, e.g., by Baumjohann & Treumann (1996), Gombosi (1998), or Diver (2001) is insufficient, because the entropy generation at the shock is not specified. If anisotropic temperatures are admitted in the shock relations (Hudson 1970), this clearly becomes evident from the corresponding set of MHD shock relations being unclosed and does not permit the determination of unequivocal downstream MHD plasma properties (see Vogl et al. 2003; Liu et al. 2007; Erkaev et al. 2000; Génot 2008 or Treumann 2009). Thus, as a way out of this problem, several papers theoretically studied the passage of the solar wind ions over the heliospheric termination shock in a semikinetic treatment (Fahr & Siewert 2006; Siewert & Fahr 2008; Fahr & Verscharen 2008; Verscharen & Fahr 2008).

Starting with the additional requirement that ions at the shock passage have to conserve two CGL-typical invariants (Chew et al. 1956), Siewert & Fahr (2008) demonstrated that the kinetic properties of the downstream plasma flow can be fixed and the set of corresponding MHD shock relations can be closed (Siewert & Fahr 2009; Fahr & Siewert 2007,2008). Based on these results, Fahr & Chalov (2008) demonstrated that these kinetic aspects of the plasma passage over the termination shock can be used to arrive at a multi-fluid MHD description of the shock transition in which all downstream plasma properties are fixed. In their two-fluid approach describing solar wind ions and pick-up ions as separate fluids, they were able to show that the conservation of the first CGL invariant (i.e., the ion magnetic moment) is already sufficient to understand the Voyager-2 observations performed at the shock crossing events (Richardson et al. 2008), namely that the downstream solar wind ions remain supersonic, while the entropized upstream kinetic solar wind energy predominantly reappears in the downstream energy of suprathermal ions (i.e., pick-up ions). This theory nevertheless has a small shortcoming reducing its beauty, namely it delivers too small a temperature increase in the downstream solar wind protons by a factor of about 3, which according to Voyager-2 temperature measurements, however, should be of the order of 10.

To more adequately describe this temperature increase one seriously needs to consider that at the passage of the upstream ions to the downstream side of the shock, gyrating ions convected with the plasma bulk flow and the frozen-in magnetic field do not only recognize the increase in the magnitude of the condensed magnetic field in the bulk flow direction, but also the deceleration of comoving field lines, i.e. of their gyrocenters, which clearly brings them into an overshoot condition. The particle's velocity modification caused by magnetic moment conservation was studied by both Fahr & Siewert (2008) and Siewert & Fahr (2008), while the additional effect of the gyrocenter deceleration is studied in this publication. Focusing on an MHD approach to the problem, the particles will gain the overshoot velocity of $\Delta \vec{U}=\vec{U}_{1}-\vec{U}$ in the form of additional gyrating speed, meaning that the bulk of the upstream ions have to compensate for this velocity loss by an additional increase in downstream gyrational motions. However, this simple approach does not yet take into account the local gyrophase, which, because of the vector properties of the velocities, may lead to a smaller acceleration in a gyroaveraged description. In this paper, we study a more detailed approach to this overshoot effect.

The physics behind this is very similar to the conventional pick-up ion physics in the inner heliosphere (see e.g., Fahr 1973; Rucinski et al. 1993; Paresce et al. 1973; Holzer & Leer 1973; Vasyliunas & Siscoe 1976; Moebius et al. 1998 or Mall 2000), where ions newly created in the inner heliosphere from slow interplanetary atoms start gyrating with keV-energies around the wind-convected magnetic field lines, simply because these frozen-in lines pass over them with solar wind velocities of the order of 400 km s-1. A comparable system related to the heliospheric bowshock and astrophysical boundary layers was studied by Bzowski et al. (2006), who e.g., described overshooting of oxygen ions at the outer bow shock of the solar system.

Therefore, if the shock represents a sufficiently abrupt spatial structure, there appears a need to conserve the - what one could call - ``total magnetic moment'', $\mu_{\rm tot}$, connected with the total perpendicular ion motion, adequately including overshoot velocities (see also Bzowski et al. 2006). As we consider further below, this could perhaps best be respected by requiring that (see also Bzowski et al. 2006)

$\displaystyle % \frac{{\rm d}\mu_{\rm tot}}{{\rm d}t} \simeq \frac{\rm d}{{\rm d}t} \frac{(\vec{w}_{\perp} + \alpha \vec{U}_\perp)^{2}}{B} = 0,$   (1)

where $\alpha$ is a parameter that needs to be determined. This generalised formulation should hold at least under conditions when the ion gyroperiod $\tau_{\rm g}=2\pi mc/(eB)$ is short with respect to the typical time of convective changes $\tau_{\rm c}=2D/U_{1}$ at the shock, where D and U1 denote the shock transition scale and the upstream solar wind velocity, respectively.

2 Magnetic moment conservation in an accelerated reference frame

2.1 The magnetic moment

Throughout literature, there is a large amount of different derivations of the conservation of the magnetic moment, some of which depend on quite restricted physical asumptions. Therefore, we begin by laying out our arguments by noting that the magnetic moment conservation is a very general concept, which is not restricted to single particle plasma physics or even MHD.

We begin by assuming a system composed of one individual charged particle of mass m, charge e and velocity $\vec{w}$, gyrating in a background magnetic field. In the reference frame of the ``guiding center'' (i.e., the center of the circular gyrational motion), the following equation of motion is valid:

$\displaystyle % m\frac{{\rm d}\vec{w}}{{\rm d}t} = \frac{e}{c} \left( \vec{w} \times \vec{B} \right) + e\vec{E}_{\rm ind}.$   (2)

In this equation, the induced electric field $\vec{E}_{\rm ind}$ is given by
$\displaystyle % {\rm rot} \vec{E}_{\rm ind} = -\frac{{\rm d}\vec{B}}{{\rm d}t}\cdot$   (3)

This relation follows directly from Maxwells equations.

To derive the specific form of the induced electric field, we consider the contour integral

$\displaystyle % \oint \vec{E}_{\rm ind} \cdot {\rm d}\vec{s} = \oint {\rm rot}\... ...ot {\rm d}\vec{O} = -\oint \frac{{\rm d}\vec{B}}{{\rm d}t}\cdot {\rm d}\vec{O},$   (4)

which may be expressed using the gyroradius $r_{\rm g}$, and making use of Stokes theorem, then leads to
$\displaystyle % 2\pi r_{\rm g} E_{\rm ind} = - \pi r_{\rm g}^{2} \frac{{\rm d}B}{{\rm d}t}\cdot$   (5)

This finally leads to the expression
$\displaystyle % E_{\rm ind} = -\frac{1}{2}r_{\rm g} \frac{{\rm d}B}{{\rm d}t}\cdot$   (6)

Therefore, the energy gain per unit of time provided by the induced electric field is given by
$\displaystyle % \frac{m}{2}\frac{{\rm d}w_{\perp}^{2}}{{\rm d}t} = eE_{\rm ind} w_{\perp } = -\frac{e}{2} r_{\rm g} w_{\perp} \frac{{\rm d}B}{{\rm d}t},$   (7)

and the mass-normalised force acting on the gyrating particle is given by
$\displaystyle % \frac{{\rm d}w_{\perp}}{{\rm d}t} = -\frac{e}{2m} r_{\rm g} \frac{{\rm d}B}{{\rm d}t} = -\frac{1}{2} w_{\perp }U\frac{{\rm d}}{{\rm d}s} \ln B.$   (8)

Taking the classical magnetic moment conservation
$\displaystyle % \frac{{\rm d}}{{\rm d}t} \mu \propto \frac{{\rm d}}{{\rm d}t} \frac{w_\perp^2}{B} = 0$   (9)

and evaluating the differentiation trivially leads to the same result, i.e. the conservation of the magnetic moment may be interpreted as the energy gain of an individual charged particle gyrating in a bulk-convected magnetic field due to an induced electric field modifying the gyrational motion. This identification does not require any specific plasma-physical assumptions and is therefore valid in MHD, gas-kinetic theory and even for single particles without the explicit presence of any kind of many-particle theory.

In the remaining parts of this study, we use various reference frames, including one that is not inertial, but co-convected with the ion plasma across an MHD shock. In this configuration, the magnetic field is co-convected with the plasma flowing with a velocity U, which allows us to introduce a spatial gradient,

$\displaystyle % \frac{{\rm d}w_\perp}{{\rm d}t} = U \frac{{\rm d}w_{\perp }}{{\rm d}s} = \frac{w_\perp}{2} U \frac{{\rm d}}{{\rm d}s} \ln B.$   (10)

Because of the frozen-in field property of MHD, this approach allows the bulk motion of ions perpendicular to the magnetic field, caused by a separation between the bulk flow velocity U and the perpendicular velocity $w_\perp$. In this configuration, the magnetic moment is defined in the rest frame comoving with U. The behaviour of particles in an accelerated reference frame (i.e., where $\dot{U} \neq 0$) was studied by Siewert & Fahr (2008) for the deceleration at MHD shock waves, while in this study, we focus on modifications to the magnetic moment concept.

2.2 The generalised magnetic moment and the transition layer of MHD shock waves

An MHD shock wave has a rather unique configuration. Despite being classified as an MHD phenomenon that appears in the solutions of the MHD equations, it is a physical region where a pure MHD approach fails. This is because the MHD equations predict a discontinuous behaviour, where all classical MHD properties spontaneously (and discontinuously) jump to different quantities. This abrupt behaviour strongly suggests that the magnetic moment - which is strongly tied to gyrational motion - may not be conserved due to the characteristic timescale for the plasma crossing from the upstream to the downstream sides of the shock most probably being much shorter than the gyrational timescale, $\tau_{\rm cross} \ll \tau{g}$.

Instead of a slow modification of the individual particle velocities governed by the magnetic field (as required by MHD), the local gyrating particles are suddenly faced with an overshooting configuration, where a deceleration of the magnetic field lines by $-\Delta \vec{U}$ needs to lead to a similar increase in the individual gyrating particle velocites by the order of $+\Delta \vec{U}$ to conserve the total momentum flow. This will automatically modify the two velocity components associated with the gyrational motion, $w_\perp$ and $\phi$ in a very nonlinear way, invalidating the concept of gyrational motion, since the particle trajectories will no longer be closed until they reach the downstream side of the shock where MHD again takes over. In addition, this will also modify the bulk energy flow, which, however, is more complicated to evaluate since the bulk kinetic energy is proportional to the square of the individual particle velocities. To summarise, it may be expected that, unlike assumed earlier by e.g., Fahr & Siewert (2006) and Siewert & Fahr (2008), the magnetic moment may need to be replaced by a different quantity that also takes into account overshooting contributions.

This idea is strongly supported by Voyager-2 observations of the solar wind termination shock obtained by Richardson et al. (2008), where it was found that, although the overall MHD compression ratio x may be reproduced well by a kinetically modified two-component model (Fahr & Chalov 2008), the observed temperature (or pressure) increase in solar wind protons was larger by about one magnitude than the temperature increase predicted by a kinetic model based on the conservation of the magnetic moment. Since temperature is equivalent to internal particle motion, this strongly implies that a much larger amount of energy is converted into thermal degrees of freedom, for which the idea presented earlier in this section provides a very probable and straightforward physical explanation.

2.3 Differential kinetic energy flux conservation in the plasma bulk frame

A full treatment of the overshoot condition requires a kinetic, per-particle approach, followed by an MHD limit of the resulting equations. Since we are mainly interested here in the MHD side of the problem, we begin by studying this problem with a different approach, based on simpler physical concepts. In a first step, independent the shock structure, we simply consider gyrating ions in the solar rest frame (SF, i.e., a frame at rest with respect to the Sun), a plasma bulk flow with a velocity $\vec{U}$ and a frozen-in magnetic field $\vec{B}$ perpendicular to $\vec{U}$ (i.e., the Archimedian interplanetary field at solar distances greater than 5 AU).

We begin by considering the differential number density of gyrotropically distributed ions,

$\displaystyle % {\rm d}n(\vec{w}) = f(\vec{w}) {\rm d}w_{\parallel} w_{\perp} {\rm d}w_{\perp}.$   (11)

In the SF, these ions possess an instantaneous velocity vector of $\vec{v} = \vec{U} + \vec{w}$, for which the gyro-averaged local energy flux, neglecting for the moment thermal energies stored in the degree of freedom parallel to the field, is given by
                      $\displaystyle % \left< {\rm d}\Phi_E \right>_\varphi$ = $\displaystyle \frac{1}{2\pi} \frac{m}{2} \int_{0}^{2\pi} {\rm d}n(\vec{w}) \left( (w_{\perp }\cos \varphi + U)^{2} + (w_{\perp }\sin \varphi )^{2} \right)$  
    $\displaystyle \times\left( w_{\perp }\cos \varphi + U \right) {\rm d}\varphi.$ (12)

Assuming a gyrotropic distribution function in the bulk frame (i.e., $\frac{{\rm d}f}{{\rm d}\varphi} = 0$), we may trivially integrate over the gyroangle $\varphi$ and obtain the ``perpendicular'' energy flow
                        $\displaystyle % \left< {\rm d}\Phi_E \right>_\varphi$ = $\displaystyle \frac{1}{2\pi} \frac{m}{2} {\rm d}n(\vec{w}) \int_{0}^{2\pi} \left( U (w_\perp^2 + U^2) + 2 U w_\perp^2 \cos^2 \varphi \right) {\rm d}\varphi$  
  = $\displaystyle \frac{m}{2} {\rm d}n(\vec{w}) U \left( w_\perp^2 + U^2 + \frac{w_\perp^2 }{\pi} \int_{0}^{2\pi} \cos^2 \varphi {\rm d}\varphi \right)$  
  = $\displaystyle \frac{m}{2} {\rm d}n(\vec{w}) U \left( 2 w_\perp^2 + U^2 \right).$  
  = $\displaystyle m {\rm d}n(\vec{w}) U \left( w_\perp^2 + \frac{1}{2} U^2 \right).$ (13)

This is the relevant amount of energy stored in the perpendicular degrees of freedom. In the absence of pitch-angle particle-particle scattering processes, this kinetic energy may only be coupled to the magnetic field, for example via the conservation of the magnetic moment.

In a rest frame comoving with the solar wind (SWF), the energy flow is given by

$\displaystyle % \left< {\rm d}\Phi_{E,SWF} \right>_\varphi = \frac{1}{2\pi} U \... ...{2} {\rm d}n(\vec{\tilde{w}}) \int_{0}^{2\pi} \tilde{w}_\perp^2 {\rm d}\varphi.$   (14)

Now, in an inertial plasma flow (i.e., a SWF that is neither accelerated nor decelerated), the difference between these two energy flows may be normalized away. However, in a decelerated SWF (which appears in the presence of shock waves or general bulk velocity fluctuations), a mechanism must be introduced to convert energy from the bulk to thermal kinetic energies, as well as to electromagnetic field energy. This suggests that Eqs. (13) and (14) are connected by the relation
$\displaystyle % \tilde{w}_{\perp }^{2} = w_{\perp }^{2} + \frac{1}{2}U^{2}.$   (15)

On the other hand, this suggests that, in an accelerated reference frame with $\dot{U} \neq 0$, the ``effective magnetic ion moment'', which should be conserved in the SF, is given by
$\displaystyle % \tilde{\mu}_{\rm tot} = \frac{m \tilde{w}_{\perp }^{2}}{2B} = \mu(w_\perp) + \mu(U),$   (16)

where the functions $\mu(v)$ are defined as the classical magnetic moment using a gyrational velocity v.

We note that the bulk-velocity-related term does not correspond to a separate gyrational motion. It must instead be interpreted as a completing term that takes into account complicated microphysical configurations such as the overshooting condition, which may locally break the closed gyational motions into epicyclic motions.

2.4 Total energy flux conservation in the plasma bulk frame

In the SF, two types of energy fluxes need to be taken into account. First, there is the total kinetic energy flux (Eq. (13)), and integration of this fraction leads to the total contribution

$\displaystyle % C_{\rm kin} = \frac{m}{2} U \cdot \int f(w_\parallel, w_\perp) ... ...perp^2 + \frac{1}{2} U^2 \right) {\rm d}w_\parallel w_{\perp} {\rm d}w_{\perp}.$   (17)

Integrating this expression leads to
$\displaystyle % C_{\rm kin} = U \left( p_\perp + \frac{1}{2} \rho U^2 \right).$   (18)

This is the total kinetic energy flux produced by the velocity components perpendicular to the magnetic field. Formally, one should also require to add the energy flow connected with motions parallel to the magnetic field (Hudson 1970),
$\displaystyle % C_{{\rm kin},2} = U p_\parallel;$     (19)

however, this expression is constant because of the conservation of the second CGL invariant, which leads to $U p_\parallel = {\rm const}.$ (Siewert & Fahr 2008). This relation is not modified by the overshooting condition in the case of a perpendicular shock.

The final participating, relevant energy flow term is the magnetic energy flux of the frozen-in magnetic field,

$\displaystyle % C_{B} = U \frac{B_{\perp}^{2}}{8\pi},$   (20)

which, taken together with Eq. (18), then leads to the conserved total energy flux $\Phi_{E}$,
$\displaystyle % \Phi_E = C_{\rm kin} + C_B = {\rm const.}$   (21)

This result may be interpreted as a Rankine-Hugoniot-like relation,
   
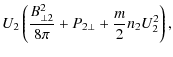
$\displaystyle U_{1}\left(\frac{B_{\perp 1}^{2}}{8\pi }+P_{1\perp }+\frac{m}{2}n_{1}U_{1}^{2}\right)$ = $\displaystyle U_{2}\left(\frac{B_{\perp 2}^{2}}{8\pi }+P_{2\perp }+\frac{m}{2} n_{2}U_{2}^{2}\right),$ (22)

that is not restricted to shocks only but also applies to general plasma flows with a varying bulk velocity in the bulk flow direction. We now solve this equation for $p_{\perp,2}$ at the termination shock; by introducing the compression ratio $s = U_1/U_2 = \rho_2/\rho_1$, we obtain
                                 $\displaystyle % P_{\perp,2}$ = $\displaystyle s \left(P_{\perp,1} + \frac{B_{\perp,1}^{2}}{8\pi}(1-s) + \frac{m}{2} n_{1} U_{1}^{2} \left(1 - s^{-2}\right) \right)$  
  = $\displaystyle s P_{\perp,1} \left( 1 + \frac{B_{1}^{2}}{8\pi P_{1\perp }}(1-s) +\frac{m}{2P_{1\perp }} n_{1}U_{1}^{2}\left(1-s^{-2}\right) \right)$  
  = $\displaystyle s\cdot P_{\perp,1} \left( 1 + \frac{1}{\beta _{\perp,1}}{(1-s)} + \frac{1}{2}M_{s,\perp,1}^{2} \left(1-{\rm s}^{-2} \right) \right).$ (23)

Where $\beta_\perp$ is the classical plasma beta value for the perpendicular pressure defined as
$\displaystyle % \beta_\perp = \frac{8 \pi n k_B T_\perp}{B^2} = \frac{8 \pi p_\perp}{B^2},$   (24)

and $M_{\rm s}$ is the sonic Mach number.

To evaluate Eq. (23) for the case of the Voyager-2 crossing of the solar wind termination shock in quantitative terms, we start from observational data provided by Richardson et al. (2008) and Burlaga et al. (2008). On the basics of both papers, one can conclude that during the VOY-2 TS1 crossing, an upstream proton Mach number in the range $8.8\leq M_{{\rm s},\perp,1}\simeq M_{{\rm s},1}\leq 10.0$ is most likely observationally. In addition, the upstream plasma beta-value (including pick-up ions) is indicative of a low beta plasma with $\beta_{\perp,1}\simeq \frac{1}{2}\beta_{1}\simeq 0.2$ (see Burlaga et al. 2008). Furthermore, the compression ratio at the shock-ramp (not including the shock precursor compression) leads to values in the range 2.4 $\leq s\leq 2.6$. With these values, i.e., s=2.5, $M_{{\rm s},1}=10$, and $\beta_{1}=0.2$ , Eq. (23) predicts that

$\displaystyle % P_{\perp,2} = 2.5 P_{\perp,1}\left( 1 + \frac{1}{0.2}(-1.5) + \frac{1}{2}100 \left(1 - \frac{1}{6.25} \right) \right).$   (25)

For the corresponding downstream/upstream proton temperatures, one finds
                            $\displaystyle % T_{\perp ,2}$ = $\displaystyle \left(\frac{n_{1}}{n_{2}} \right) \cdot P_{\perp ,1} \left( 1+\frac{1}{0.2}(-1.5)+% \frac{1}{2}100 \left(1-\frac{1}{6.25} \right) \right)$  
  $\textstyle \simeq$ $\displaystyle 35 T_{\perp 1}.$ (26)

Taking the proton temperatures found just upstream of the shock ramp of $T_{\perp,1} = T_{1} \simeq 7\times 10^{3}~{\rm K}$, and downstream proton temperatures $T_{\perp 2}=T_{2}\simeq 10^{5}~{\rm K}$, the Voyager data indicates that T2/T1=(1/7)102=14.5. Because upstream pick-up ion pressures cannot be estimated well, the theory developed above provides a rather solid description of the observed plasma properties.

Interestingly, this result is very similar to a relation given by Erkaev et al. (2000), who used the perpendicular momentum flow conservation to derive the downstream perpendicular pressure. They found that

$\displaystyle % p_{\perp,2} = p_{\perp,1} + \frac{B_{t,1}^2}{8\pi} (1 - s^2) + \rho_1 U_{n,1}^2 (1 - s^{-1}),$     (27)

which may be transformed into similar nomenclature as Eq. (23). Using the definition $p_\perp = \rho U_1^2 A_{\rm s}$ (Erkaev et al. 2000), we obtain
                           $\displaystyle % p_{\perp,2}$ = $\displaystyle p_{\perp,1} \left( + \frac{B_{t,1}^2}{8\pi \rho_1 U_1^2 A_{{\rm s},1}} (1 - x^2) + \frac{1}{A_{{\rm s},1}} (1 - x^{-1}) \right)$  
  = $\displaystyle p_{\perp,1} \left( 1 + \frac{1}{\beta_{\perp,1}} (1 - x^2) + M_{{\rm s},\parallel,1}^2 (1 - x^{-1}) \right).$ (28)

This result differs from Eq. (23), which is unsurprising, since Erkaev et al. (2000) did not use any conservation properties to close the set of MHD jump conditions; instead, they pointed out that the anisotropic jump conditions are underdetermined, and that one of the downstream properties had to be kept as a free parameter. Therefore, it would have been more surprising if no difference between both approaches would have emerged.

2.5 Properties of the modified pressure relation

We now perform a parameter study, extracting information on how the pressure jump depends upon the upstream parameters. Equation (23) shows the dependence on the three parameters $M_{{\rm s},\perp,1}$, $\beta_{\perp,1}$, and the downstream compression ratio s, the third of which in turn is an implicit function of the two previous upstream parameters. Therefore, the pressure jump depends only upon two parameters, while the compression ratio as a function of the upstream parameters must be derived separately. For the perpendicular shock, Fahr & Siewert (2009) derived an analytical relation for a configuration where the classical magnetic moment is conserved, and that does not apply to this case. We instead follow a different approach based on the newly derived relations.

Using the Voyager compression ratio of $s_{\rm VOY}=2.5$, we vary the remaining parameters to study the possible range of physical upstream parameters for this specific compression ratio. Since both the plasma beta and the sonic Mach number are not derivable from the Voyager plasma data (Richardson et al. 2008), this will allow us to study how much variation is allowed by the theoretical modeling of the problem. Using Eqs. (23) and (26), it follows that

$\displaystyle % \frac{T_{\perp,2}}{T_{\perp,1}} = 1 + \frac{1}{\beta _{\perp,1}}{(1-s)} + \frac{1}{2}M_{{\rm s},\perp,1}^{2} \left(1-s^{-2} \right).$   (29)

Inserting the observed compression ratio then leads to
$\displaystyle % \frac{T_{\perp,2}}{T_{\perp,1}} = 1 - \frac{1.5}{\beta _{\perp,1}} + 0.42 M_{{\rm s},\perp,1}^{2}.$   (30)

Representative plots of this equation are given in Fig. 1, which clearly exhibits multiple points. First, a significant temperature increase requires rather large plasma beta values and large sonic Mach numbers. The overall temperature increase easily reaches values greater than 10, smaller gains being restricted to a very narrow region in parameter space. In this figure, we have also indicated the observed solar wind temperature jump ( T2/T1)VOY2 and the sonic Mach number inferred from Richardson et al. (2008) ( $M_{\rm s} \simeq 15$), which allows us to estimate the overall plasma beta to $\beta \simeq 0.11$. This result is considerably higher than expected. However, Fig. 1 also proves the high sensitivity to the plasma beta value, suggesting that the uncertainities in these values need to be reduced dramatically to obtain a more accurate result. Nevertheless, this result proves that a mechanism is necessary to increase the overall Mach number and the plasma beta, such as taking the suprathermal pick-up ions on the upstream side into account, which strongly contribute to the energies of the system (Fahr & Chalov 2008; Chalov & Fahr 2009).

Physically, the Mach number sensitivity corresponds to a strongly supersonic plasma, which in turn may be interpreted as a large amount of bulk kinetic energy being available for conversion into internal (thermal) degrees of freedom. In contrast, the other requirement which corresponds to $\beta_1$, is less trivial. Since the plasma beta is defined as the ratio of thermal pressure to magnetic pressure, i.e., $\beta = p_{\rm th}/p_{B}$, its influence corresponds to a comparably weak magnetic field, which may be in conflict with the basic requirements of MHD related to the assumption of frozen-in fields and field-controlled bulk flows. On the other hand, the transition layer of any shock wave is not an ideal MHD system, and therefore, this result infers that the mechanism by which MHD is broken inside the transition layer might actually result in a locally increased plasma beta value, which would allow particle-particle scattering processes to gain dominance.

\begin{figure} \par\includegraphics[width=8cm,clip]{aa13805-09-fig1.eps} \end{figure} Figure 1:

The downstream/upstream temperature ratio for an observed compression ratio of s=2.5, the temperature ratio $(T_2/T_1)\simeq 15$ indicated by Voyager-2 and a Mach number of 8-10.

Open with DEXTER

2.6 A per-particle interpretation of the energy conservation request

From the integrated energy flow invariant (Eq. (17)), one may choose to introduce a per-particle invariant using the following procedure. We begin by introducing a per-particle variant of the total constant energy flow $\Phi_{\rm E}$,

$\displaystyle % \Phi_{\rm E}/n = U (\frac{B^{2}}{8\pi n} + P_{\perp}/n + \frac{m}{2}U^{2}) = U \tilde{\mu}_{\rm E},$   (31)

where $\tilde{\mu}_{\rm E}$ is given by
                   $\displaystyle % \tilde{\mu}_{{\rm E}}$ = $\displaystyle \left(\frac{B^{2}}{8\pi n} + P_{\perp }/n + \frac{m}{2}U^{2} \right)$  
  = $\displaystyle \frac{m}{2} \left(\frac{B^{2}}{4\pi \rho} + <w_\perp^2> + U^{2} \right).$ (32)

The property $\tilde{\mu}$ is constant, since
$\displaystyle % \tilde{\mu}_{\rm E} = \frac{\Phi_{\rm E}}{U n} = \frac{\Phi_{\rm E}}{\Phi_{\rm m}} = {\rm const.},$   (33)

where $\Phi_{\rm m}$ is the (constant) mass flow of the system. After deriving the total temporal derivative of $\tilde{\mu}_{\rm E}$, we obtain
$\displaystyle % \frac{{\rm d}}{{\rm d}t} \tilde{\mu}_{\rm E} = \frac{{\rm d}}{{... ...{{\rm d}}{{\rm d}t} \frac{B^{2}}{4\pi \rho} + \frac{{\rm d}}{{\rm d}t} U^2 = 0.$   (34)

Rearranging this equation then infers that
$\displaystyle % 2 w_\perp \dot{w}_\perp = - \frac{2 B \dot{B}}{4\pi \rho} + \frac{B^2 \dot{\rho}}{4\pi \rho^2} - 2 U \dot{U},$   (35)

and further that
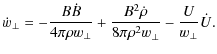
$\displaystyle % \dot{w}_\perp = - \frac{B \dot{B}}{4\pi \rho w_\perp} + \frac{B^2 \dot{\rho}}{8\pi \rho^2 w_\perp} - \frac{U}{w_\perp} \dot{U}.$   (36)

At a perpendicular shock with strictly frozen-in fields, there are multiple relations that allow us to simplify this expression, namely $B \dot{B} = -\frac{B^2}{U} \dot{U}$ and $\dot{\rho} = -\frac{\rho}{U} \dot{U}$, leading to
                     $\displaystyle % \dot{w}_\perp$ = $\displaystyle \frac{\dot{U}}{w_\perp} \left( \frac{B^2}{4\pi \rho U} - \frac{B^2}{8\pi \rho U} - U \right)$  
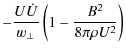
  = $\displaystyle -\frac{U \dot{U}}{w_\perp} \left( 1 - \frac{B^2}{8\pi\rho U^2} \right)$  
  = $\displaystyle -\frac{U \dot{U}}{w_\perp} \left( 1 - \frac{1}{2 M_A^2} \right)\cdot$ (37)

Comparing this with Eq. (8), one can immediately see that this new result does not result in a term proportional to $w_\perp$, i.e., the magnetic moment is no longer conserved; not even a term corresponding to Eq. (8) can be found any longer in the decomposition of this expression. This may be interpreted in multiple ways. Either the terms used in the energy flux conservation (Eq. (21)) do not contain all relevant contributions to the energy flow, and more terms, e.g. plasma wave contributions ( $\propto \delta B^2$), need to be added (the relevance of these terms was previously indicated in Fahr & Siewert 2007). The other possible explanation would be that the microphysics on the downstream side of a classical MHD shock is considerably less trivial than predicted by the MHD approach.

One point worth noting is that these two explanations do not conflict with each other; numerical studies of MHD shocks (Chalov & Fahr 2009) infer that after the classical MHD transition layer (which may produce a downstream pressure anisotropy), a consecutive second layer might follow where the initially generated pressure anisotropy is reduced by mirror or firehose instabilities. This second layer demonstrates all kind of nonlinear processes, such as plasma-wave scattering; since plasma waves are completely absent from the conventional MHD description of the shock, this would offer a natural way of introducing the additional physics seemingly required by the system (see Fahr & Siewert 2007).

To compare this result with the more intuitive approach presented in the introduction (Eq. (1)), we now study the message from this generalised invariant, by deriving

$\displaystyle % \frac{{\rm d}}{{\rm d}t} \frac{w_\perp^2 + \frac{1}{2} U^2}{B} = 0.$   (38)

After evaluating this expression, we obtain
$\displaystyle % \frac{2 w_\perp \dot{w}_\perp}{B} - \frac{w_\perp^2 \dot{B}}{B^2} + \frac{U \dot{U}}{B} - \frac{U^2 \dot{B}}{2 B^2} = 0$   (39)

and further
                   $\displaystyle % \dot{w}_\perp$ = $\displaystyle \frac{B}{2 w_\perp} \left( \frac{U^2 \dot{B}}{2 B^2} - \frac{U \dot{U}}{B} + \frac{w_\perp^2 \dot{B}}{B^2} \right)$  
  = $\displaystyle \frac{1}{2 w_\perp} \left( \frac{U^2}{2} \frac{\dot{B}}{B} - U \dot{U} + w_\perp^2 \frac{\dot{B}}{B} \right)\cdot$ (40)

Making use again of the conservation of the magnetic flux ( $U B = {\rm const.}$), we obtain the simplified expression
$\displaystyle % \dot{w_\perp} = -\frac{U \dot{U}}{2 w_\perp} \left( \frac{3}{2} + \frac{w_\perp^2}{U^2} \right)\cdot$   (41)

Substituting back the expression $-U \dot{U} = -U^2 \frac{{\rm d}}{{\rm d}t} \ln B$, we obtain the alternative representation
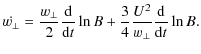
$\displaystyle % \dot{w_\perp} = \frac{w_\perp}{2} \frac{{\rm d}}{{\rm d}t} \ln B + \frac{3}{4} \frac{U^2}{w_\perp} \frac{{\rm d}}{{\rm d}t} \ln B.$   (42)

In this equation, the first term is equivalent to the classical magnetic moment conservation, while the second term is a correction for the non-ideal physics applicable to the transition layer of the shock.

3 Conclusions

In our theoretical description of the plasma passage from the upstream to the downstream side of the solar wind termination shock developed here, it has not explicitly been taken into account that the plasma close to the shock is a multi-fluid plasma and that to correctly predict the downstream plasma properties it is of strong relevance which Alfvenic Mach numbers $M_{{\rm A}1}$, sonic Mach numbers $M_{{\rm S}1}$, and beta values $\beta_1$ prevail on the upstream side. All of these characteristic numbers, however, are strongly influenced by the presence of suprathermal ions, such as pick-up ions in the keV-energy range.

These ions unfortunately cannot be observationally monitored by the Voyager-1/-2 instrumentations due to a lack of 1-keV energy detectors. Our shock relation derived in Eq. (23) thus cannot be reliably evaluated, but must be kept open with respect to the uncertainties in the knowledge of suprathermal ion properties.

One way of improving on this momentarily disappointing scientific situation is to choose instead a multi-fluid description of the shock in which ion populations centered around different thermal energies are treated as independent fluids. These multi-fluid approaches can at least show, how much influence higher-energetic populations have in forming the main shock ramp profile. In their two-fluid description of the shock passage, Fahr & Chalov (2008) demonstrated that the relatively low compression ratio seen at the Voyager-2 TS crossing, i.e., $s\simeq 2.5$, is easily understood with the effect of suprathermal pick-up ions (PUIs) in lowering the effective upstream sonic Mach number. That the solar wind protons at the passage over this PUI-modulated shock also reappear on the downstream side still as a supersonic fluid, can be understood in the framework of a thermodynamical and dynamical coupling of different ion fluids. Chalov & Fahr (2009) extended their earlier two-fluid shock model to a three-fluid model including shock-generated anomalous cosmic ray ions as an additional fluid. In the framework of this extended MHD approach, the well documented precursor phenomenon seen at the Voyager-2 shock crossing (see Richardson et al. 2008) also has a natural explanation.

However, whenever one can start from a predetermined knowledge of the shock compression ratio s, taken directly from either Voyager data or a multifluid theory which delivers s as a function of the upstream Alfvenic Mach numbers $M_{{\rm A}1}$, sonic Mach numbers $M_{{\rm S}1}$, and beta values $\beta_1$, it is possible to derive the ion temperature jump presented in Eq. (26). This is the proof that different ion populations behave separately at their passage over a predetermined shock. However, the structure of the transition layer is determined by the joint action of all ion populations that count in terms of momentum and energy carriers.



References

  1. Baumjohann, W., & Treumann, R. A. 1996, Basic space plasma physics (London: Imperial College Press) [Google Scholar]
  2. Burlaga, L. F., Ness, N. F., Acuna, M. H., et al. 2008, Nature, 454, 75 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  3. Bzowski, M., Fahr, H.-J., & Grzedzielski, S. 2006, ASTRA, 2, 1 [NASA ADS] [Google Scholar]
  4. Chalov, S. V., & Fahr, H.-J. 2009, solar Wind 12, Saint Malo, in print [Google Scholar]
  5. Chew, G. F., Goldberger, M. L., & Low, F. E. 1956, Proc. R. Soc. London A, 236, 112 [Google Scholar]
  6. Diver, D. A. 2001, A Plasma Formulary for Physics, Technology and Astrophysics (Hoboken, New Jersey: John Wiley) [Google Scholar]
  7. Erkaev, N. V., Vogl, D. F., & Biernat, H. K. 2000, J. Plasma Physics, 64, 561 [Google Scholar]
  8. Fahr, H.-J., 1973, Sol. Phys., 30, 193 [NASA ADS] [CrossRef] [Google Scholar]
  9. Fahr, H.-J., & Chalov, S. V. 2008, A&A, 490, L35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Fahr, H.-J., & Siewert, M. 2006, A&A, 458, 13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Fahr, H.-J., & Siewert, M. 2007, ASTRA, 3, 21 [NASA ADS] [CrossRef] [Google Scholar]
  12. Fahr, H.-J., & Siewert, M. 2008, A&A, 484, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Fahr, H.-J., & Siewert, M. 2009, ApJ, 693, 281 [NASA ADS] [CrossRef] [Google Scholar]
  14. Fahr, H.-J., & Verscharen, D. 2008, A&A, 487, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Génot, V. 2008, ApJ, 687, L119 [NASA ADS] [CrossRef] [Google Scholar]
  16. Gombosi, T. I. 1998, Physics of the Space Environment (New York: Cambridge University Press) [Google Scholar]
  17. Holzer, T. E., & Leer, E. 1973, Ap&SS, 24, 335 [NASA ADS] [CrossRef] [Google Scholar]
  18. Hudson, P. D. 1970, Planet. Space Sci., 18, 1611 [NASA ADS] [CrossRef] [Google Scholar]
  19. Liu, Y., Richardson, J. D., Belcher, J. W., & Kasper, J. C. 2007, ApJ, 659, L65 [NASA ADS] [CrossRef] [Google Scholar]
  20. Mall, U. 2000, in The Outer Heliosphere: Beyond the Planets (Copernicus Society), 156 [Google Scholar]
  21. Moebius, E., Rucinski, D., Lee, M. A., & Isenberg, P. A. 1998, J. Geophys. Res., 103, 257 [NASA ADS] [CrossRef] [Google Scholar]
  22. Paresce, F., Fahr, H.-J., & Lay, G. 1973, J. Geophys. Res., 86, 1038 [Google Scholar]
  23. Richardson, J. D., Kasper, J. C., Wang, C., Belcher, J. W., & Lazarus, A. J. 2008, Nature, 454, 63 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  24. Rucinski, D., Fahr, H.-J., & Grzedzielski, S. 1993, Planet. Space Sci., 41, 773 [NASA ADS] [CrossRef] [Google Scholar]
  25. Siewert, M., & Fahr, H.-J. 2008, A&A, 485, 327 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Siewert, M., & Fahr, H.-J. 2009, A&A, 501, 407 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Treumann, R. A. 2009, A&ARv, 17, 409 [NASA ADS] [Google Scholar]
  28. Vasyliunas, V. M., & Siscoe, G. L. 1976, J. Geophys. Res., 81, 1247 [NASA ADS] [CrossRef] [Google Scholar]
  29. Verscharen, D., & Fahr, H.-J. 2008, A&A, 487, 723 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Vogl, D. F., Langmayr, D., Erkaev, N. V., et al. 2003, Planet. Space Sci., 51, 715 [NASA ADS] [CrossRef] [Google Scholar]

All Figures

  \begin{figure} \par\includegraphics[width=8cm,clip]{aa13805-09-fig1.eps} \end{figure} Figure 1:

The downstream/upstream temperature ratio for an observed compression ratio of s=2.5, the temperature ratio $(T_2/T_1)\simeq 15$ indicated by Voyager-2 and a Mach number of 8-10.

Open with DEXTER
In the text
Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.