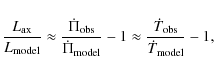EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 512 (March-April 2010) A&A, 512 (2010) A86 Full HTML
Free Access
Issue
A&A
Volume 512, March-April 2010
Article Number A86
Number of page(s) 4
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/200913716
Published online 09 April 2010
A&A 512, A86 (2010)

Axions and the pulsation periods of variable white dwarfs revisited
(Research Note)

J. Isern1,2 - E. García-Berro2,3 - L. G. Althaus3,4 - A. H. Córsico4,5

1 - Institut de Ciències de l'Espai (CSIC), Facultat de Ciències, Campus UAB, 08193 Bellaterra, Spain
2 - Institut d'Estudis Espacials de Catalunya, c/ Gran Capità 2-4, 08034 Barcelona, Spain
3 - Departament de Física Aplicada, Escola Politècnica Superior de Castelldefels, Universitat Politècnica de Catalunya, Avda. del Canal Olímpic s/n, 08860 Castelldefels, Spain
4 - Facultad de Ciencias Astronómicas y Geofísicas, Universidad Nacional de la Plata Paseo del Bosque, s/n, (1900), La Plata, Argentina
5 - Instituto de Astrofísica La Plata, CONICET, Argentina

Received 23 November 2009 / Accepted 16 January 2010

Abstract
Context. Axions are the natural consequence of the introduction of the Peccei-Quinn symmetry to solve the strong CP problem. All the efforts to detect such elusive particles have failed up to now. Nevertheless, it has been recently shown that the luminosity function of white dwarfs is best fitted if axions with a mass of a few meV are included in the evolutionary calculations.
Aims. Our aim is to show that variable white dwarfs can provide additional and independent evidence about the existence of axions.
Methods. The evolution of a white dwarf is a slow cooling process that translates into a secular increase of the pulsation periods of some variable white dwarfs, the so-called DAV and DBV types. Since axions can freely escape from such stars, their existence would increase the cooling rate and, consequently, the rate of change of the periods as compared with the standard ones.
Results. The present values of the rate of change of the pulsation period of G117-B15A are compatible with the existence of axions with the masses suggested by the luminosity function of white dwarfs, in contrast with previous estimations. Furthermore, it is shown that if such axions indeed exist, the drift of the periods of pulsation of DBV stars would be noticeably perturbed.

Key words: elementary particles - white dwarfs - stars: oscillations

1 Introduction

One of the long-standing problems of the standard model of particles is the question of why charge and parity can be violated in weak interactions and not in strong interactions. This is the so-called strong CP problem. One of the possible solutions consists in the introduction of a new symmetry, the Peccei-Quinn symmetry or PQ symmetry, which automatically accounts for the problem (Peccei & Quinn 1977a,b). The spontaneous breaking of this symmetry gives rise to the existence of a new particle called axion, which can couple to photons, electrons and baryons with a strength that depends on their mass and on the specific way in which the PQ symmetry is implemented. The two most popular implementations are the KVSZ model (Kim 1979; Shifman et al. 1980), where the axions couple with photons and hadrons, and the DFSZ model (Dine et al. 1981; Zhitnisky 1980) where they also couple to electrons.

From the first moment that the problem was formulated, a huge effort aimed to directly detect these elusive particles, or at least to constrain their properties using astrophysical and cosmological arguments, was undertaken. Among the experiments looking for a direct detection we mention ADMX and CAST - see Steffen (2009) for a synthetic description. Excellent reviews about the properties of axions and the corresponding astrophysical and cosmological searches can be found in Kim & Carosi (2010), Raffelt (2007, 1996, 1990), Khlopov (1999) and Turner (1990).

White dwarfs represent the final evolutionary stages of low- and intermediate-mass stars. Since they are strongly degenerate and do not have nuclear sources, their evolution is just a gravothermal process of cooling. The simplicity of these objects, the fact that the physical processes necessary to understand them are well identified, although not always well known, and the impressive existing observational background make these stars extremely useful laboratories to test new ideas in physics (Isern & García-Berro 2008). In particular, Isern et al. (2008, 2009) found that the best fit to their luminosity function is obtained when axions of the appropriate mass are included in the calculations. We note that in this case only DFSZ axions were taken into account, since electron bremsstrahlung is the dominant process in white dwarf interiors.

The axion emission rate under these conditions is given by (Nakagawa et al. 1987, 1988):

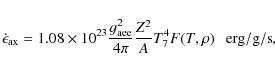
\begin{displaymath}\dot{\epsilon}_{\rm ax} = 1.08\times 10^{23}\frac{g^2_{\rm aee}}{4\pi} \frac{Z^2}{A}T^4_7 F(T,\rho) ~~~ {\rm erg/g/s}, \end{displaymath} (1)

where F takes into account the Coulomb plasma effects, T7 is the temperature in units of 107 K, Z and A are the atomic and mass numbers of the plasma components, respectively, and  $g_{\rm aee}$ is the strength of the axion-electron Yukawa coupling, which is not defined by the theory and determines the total axion luminosity of the white dwarf. The value of this parameter that best fits the luminosity function of white dwarfs is $1.1\times 10^{-13}$, but variations of a factor two are still compatible with the observations (Isern et al. 2008, 2009).

Notice that strictly speaking, the shape of the white dwarf luminosity function can be equally well fitted invoking the existence of any hypothetical light boson or axion-like particle able to couple to electrons with a strength $g_{\rm aee} \approx 10^{-13}$. However, since axions have a solid theoretical justification, we will use this term all along the paper. The relationship between this coupling constant and the mass of the axion is given by

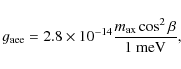
\begin{displaymath}g_{\rm aee} = 2.8 \times 10^{-14} \frac{m_{\rm ax}\cos^2 \beta}{1~ {\rm meV}}, \end{displaymath} (2)

where $\cos^2 \beta$ is an essentially free parameter that probably takes a value ranging from 0.5 to 1 and comes from the ratio of the two Higgs fields that characterize the DFSZ axion models. Therefore, the axion mass necessary to fit the white dwarf luminosity function mass is $m_{\rm ax}\cos^2 \beta \sim 4$ meV where, as previously mentioned, variations of $\sim $2 meV are compatible with the observational uncertainties. For simplicity we will assume $\cos^2 \beta =1$ and will express our results in terms of the mass of the axion, as it is usually done.

Taken at face value, the result of Isern et al. (2009) can be considered as the first indirect proof that axions of the DFSZ type indeed exist. However, before accepting this asseveration some conditions have to be fullfiled: i) Different and independent evolutionary codes must provide the same result; ii) there is no conventional way to account for the presently observed slope of the white dwarf luminosity function; iii) there is no contradiction with other well established astrophysical or cosmological phenomena; and iv) there are some phenomena that are better explained if the axion hypothesis is adopted. Concerning this last point, it is important to realize that the value of the mass of the axion found in Isern et al. (2009) is close to the upper limit obtained from astrophysical constraints. This means that axions with this mass will not dramatically change our current understanding of stellar evolution, but instead some subtle changes that accurate observations could detect and quantify would be apparent. The case of the white dwarf luminosity function is just an example. The drift of the pulsation periods of variable white dwarfs, the topic of this paper, is another one that will be discussed in the following sections. We note however that this is not the case of core collapse supernovae, where axions with this mass can drain an important amount of gravitational energy and modify the process of collapse/explosion. Unfortunately, the nucleon-axion interaction, which is dominant in supernovae, is not well understood and deserves additional work that is out of the scope of this paper. Finally note as well that if $\cos^2 \beta$ was small, the mass of the axion would be higher than the values quoted here and, consequently, the interaction axion-photon would be strengthened. This could be used to rule out our results or to constrain the values that $\cos^2 \beta$ can adopt.

2 Results and discussion

During the process of cooling, white dwarfs experience several phases of pulsational instability powered by the $\kappa$-mechanism and the ``convective driving'' mechanism (Winget & Kepler 2008). Depending on their location in the Hertzsprung-Russell diagram and their atmospheric composition they are called pulsating PG1159 or GW Vir stars, which includes stars with a surrounding nebula (the PNNV stars) and stars without nebula (the DOV stars) at $T_{\rm eff} \sim 70~000 {-}170~000$ K and He-, C-, and O-dominated atmospheres, DBV or V777 Her stars, with $T_{\rm eff} \sim 25~000$ K and He-dominated atmospheres, and DAV or ZZ Ceti stars, with $T_{\rm eff} \sim 12~000$ K and H-dominated atmospheres. All of them display multiperiodic pulsations with periods in the range of 100 to 1000 s, although PNNV stars can pulsate with periods as long as 3000 s. The length of these periods clearly indicates that these objects are experiencing g-mode non-radial pulsations, where the main restoring force is gravity - see Winget & Kepler (2008) for a recent review.

One of the main characteristics of g-mode pulsations is that they experience a secular drift that can be used to test the white dwarf cooling theory. This secular drift can be approximately described by

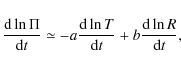
\begin{displaymath}\frac{{\rm d}\ln \Pi}{{\rm d}t} \simeq -a \frac{{\rm d}\ln T}{{\rm d}t} + b \frac{{\rm d}\ln R}{{\rm d}t}, \end{displaymath} (3)

where a and b are constants of the order of unity that depend on the details of the model, and R and T are the stellar radius and the temperature at the region of period formation, respectively (Baglin & Heyvaerts 1969; Winget et al. 1983). This equation reflects the fact that as the star cools down, the degeneracy of the plasma increases, the buoyancy decreases, the Brunt-Väisälä frequency becomes lower and, as a consequence, the spectrum of pulsations gradually shifts to lower frequencies. At the same time, since the star contracts, the radius decreases and the frequency tends to increase. In general, DAV and DBV stars are already so cool that the radial term is negligible and the change of the period of pulsation can be directly related to the change in the core temperature of the star. The timescales involved are of the order of $\sim $10-11 s/s for DOVs, $\sim $10-13 to $\sim $10-14 s/s for DBVs and $\sim $10-15 to $\sim $10-16 s/s for DAVs. The measurement of such drifts is a difficult task but, as was proved, it is feasible (Winget & Kepler 2008).

These properties allow us to build a simple relationship (Isern et al. 1992; Isern & García-Berro 2008) to estimate the influence of an extra sink of energy, like axions, on the period drift of variable white dwarfs:

\begin{displaymath}\frac{L_{\rm ax}}{L_{\rm model}} \approx \frac{\dot{\Pi}_{\rm... ...-1 \approx \frac{\dot{T}_{\rm obs}}{\dot{T}_{\rm model}} -1 , \end{displaymath} (4)

where the suffix ``model'' refers to those models built using standard physics.

G117-B15A is a ZZ Ceti star (McGraw & Robinson 1976) with a dominant period of pulsation of $\sim $215 s. This star, in an exceptional observational effort, has been observed for more than 30 years to obtain the secular evolution of the pulsation period. Kepler et al. (1991a,b), after $\sim $15 years of observations, found a secular drift of $\dot{\Pi}_{\rm obs} = (12.0 \pm 3.5) \times 10^{-15}$ s/s that was more than a factor of two larger than the expected value in the case of a normal carbon-oxygen white dwarf. In order to account for this discrepancy, Isern et al. (1992) proposed the introduction of an extra cooling term due to axions. The mass of the axions necessary to fit this discrepancy was 8.5 meV. Later on, the analysis of additional ten years of observations provided a value of $\dot{\Pi}_{\rm obs} = (2.3 \pm 1.4) \times 10^{-15}$ s/s (Kepler et al. 2000), closer to the value predicted by the standard theory of evolution of white dwarfs. A detailed seismological analysis (Córsico et al. 2001) found a drift $\dot{\Pi}_{\rm model} = (3.9 \pm 2.3) \times 10^{-15}$ s/s, where the main sources of uncertainty were due to the mode identification, the mass of the star, the chemical profile and the effective temperature. This value suggested that it was no longer necessary to invoke axions to account for the observed cooling rate of white dwarfs, but at the same time the uncertainties were large enough to prevent ruling out their existence. It is important to realize here that the values obtained with Eq. (4) agreed well with those obtained from the accurate numerical calculations of Córsico et al. (2001). A new analysis including additional five years of observations gave $\dot{\Pi} = 3.57 \pm 0.82 \times 10^{-15}$ s/s (Kepler et al. 2005), a value that overlaps with the theoretical values obtained by Córsico et al. (2001) and is marginally compatible with the axion luminosity obtained if the axion mass suggested by the luminosity function of white dwarfs, $\sim $4 meV is adopted. Finally, in a recent release that includes yet another five years of observations, Kepler (2009) obtained $\dot{\Pi} = 4.77 \pm 0.59 \times 10^{-15}$ s/s. Adopting the proper motion correction of Kepler et al. (2005), we obtain $\dot{\Pi} = 4.07 \pm 0.61 \times 10^{-15}$ s/s, a value that is consistent with the existence of the extra cooling term suggested by the luminosity function. Figure 1 displays the evolution of the measured value of $\dot\Pi$ with time. The jumps between the different observational values reflect the introduction of corrections, like the proper motion correction, and the fact that the phase of the periodicity is affected by a jitter caused by low-amplitude modes, contamination by G117-B15B, the companion star, use of different telescopes and apertures...that are not well understood yet (Kepler, private communication).

\begin{figure} \par\vspace{7cm} \special{psfile=13716fg1.eps hscale=55 vscale=55 voffset=-105 hoffset=-25} \end{figure} Figure 1:

Evolution of the measurement of the period drift of G117-B15A. Lines represent the theoretical values obtained by Córsico et al. (2001) - solid line - and Bischoff-Kim et al. (2008) - dashed-dotted line (for the case of a thin envelope) and dashed line (for the case of a thick envelope). The nominal uncertainties of these models are 1.15, 0.26 and 0.17 respectively, in the units of the figure.

Open with DEXTER

Table 1 displays the axion luminosity and mass necessary to fit the observations when several white dwarf pulsational models are adopted (the values in brackets correspond to the observational uncertainties). The values of the first row, labeled model C, were obtained using Eq. (4), the model of G117-B15A that best fits the data (Córsico et al. 2001) and the previously mentioned axion emission rates of Nakagawa et al. (1987, 1988). It is important to realize here that in a completely independent analysis, Bischoff-Kim et al. (2008) identified two possible asteroseismological models of G117-B15A, one with a thin hydrogen envelope and the other with a relatively thick hydrogen envelope, with $\dot{\Pi} = 2.98 \pm 0.17 \times 10^{-15}$ s/s and $1.92\pm 0.26 \times 10^{-15}$ s/s, respectively. Both values are smaller than the measured ones and indicate that an additional sink of energy is necessary. Table 1 shows the luminosity and the mass of the axions necessary to account for the most recent data of Kepler (2009) assuming a temperature of the core of $T_{\rm c}=1.2\times 10^7$ K in both cases.

Recently, Mukadam et al. (2009) analyzed R 548 (ZZ Ceti itself) and found that its mass lies between 0.55 and $0.58~ M_{\odot}$, while the mass of the hydrogen envelope is $\log M_{\rm H}\simeq -5.0$ and that the best prediction for the rate of change of the period is $\dot{\Pi} =(8.3 \pm 0.046) \times 10^{-15}$ s/s. These results are fully consistent with the values obtained for G117-B15A and with those displayed in Table 1.

The pulsation properties of DBV stars can provide an additional test to the axion hypothesis. Since these stars have a hotter core than that of DA white dwarfs, the neutrino luminosity can no longer be neglected. and the influence of axions on the pulsation period drift is smaller than that expected for DA white dwarfs. For instance, a DB white dwarf of $ M \sim 0.59~ M_{\odot}$, an effective temperature $T_{\rm eff}\sim 25~200$ K and a core temperature $\log T_{\rm c} = 7.61$ has a luminosity of $L \sim 6.3 \times 10^{-2}~ L_{\odot}$ and a neutrino luminosity $L_\nu \sim 5.1 \times 10^{-2}~L_{\odot}$. If an axion mass of 5 meV is assumed, the axion luminosity amounts $L_{\rm ax} = 6.0 \times 10^{-2}~ L_{\odot}$ and the corresponding secular change of the pulsation period would be

\begin{displaymath}\frac{\dot{\Pi}_{\rm ax}}{\dot{\Pi}_{\rm no-ax}}\simeq 1.5 . \end{displaymath} (5)

Note that because of the strong dependence of the different luminosities on the core temperature, this prediction is very sensitive to the position in the instability strip and on the particular parameters of the star under study. The only case of DB variable white dwarf that is currently being studied is EC20058-5234 (Sullivan 2009), but unfortunately a rate of period change is not yet available for this star.

Table 1:   Axion luminosities and axion masses necessary to account for the observed drift of the period of pulsation of G117-B15A.

3 Conclusions

It has been shown that white dwarf variable G117-B15As present value of the secular rate of change of the period of pulsation, $4.07 \pm 0.61 \times 10^{-15}$ s/s (Kepler 2009), is consistent with the predictions of the theoretical models, as was anticipated by Isern et al. (1992), if an additional source of cooling like axion emission is included. This result is corroborated by the completely independent analysis of the same star done by Bischoff-Kim et al. (2008), using the measured rate of period change ( $3.57 \pm 0.82 \times 10^{-15}$ s/s) obtained previously (Kepler et al. 2005). This means that the conclusion of Córsico et al. (2001) that it was unnecessary to introduce an additional cooling source is no longer valid when the new observational data are taken into account. This is an important result, as asteroseismological observations of white dwarfs seem to give additional and independent support to the claim of Isern et al. (2008, 2009) that the white dwarf luminosity function is better fitted if an additional cooling provided by axions with a mass of a few meV is included in the calculations.

It has also been shown that since the core temperatures of DBV stars are higher, the secular drift of the pulsation period of these stars is strongly enhanced by the axion emission. In particular, if axion emmisivity is computed using the mass obtained from the best fit to the luminosity function of white dwarfs and included in the calculations, the secular rate of period change increases by $\sim $50%, although the exact value depends on the core temperature and, consequently, on their position in the DB variability strip.

Finally, it is worthwhile to emphasize the importance of continued obervations of G117-B15A and R 548. It is also important to enlarge the number of stars with observed period drifts and the measurement of these drifts in hotter variables like DBV white dwarfs. Finally, it is also important to improve the asteroseismological models. All these actions would undoubtely contribute to solve the problem of axions.

Acknowledgements
This work was supported by the MCINN grants AYA08-1839/ESP and AYA2008-04211-C02-01 and the AGAUR grants SGR1002/2009 and SGR315/2009 of the Generalitat de Catalunya and by the European Union FEDER funds. LGA also acknowledges a PIV grant of the AGAUR of the Generalitat de Catalunya.

References

  1. Baglin, A., & Heyvaerts, J. 1969, Nature, 222, 1258 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bischoff-Kim, A., Montgomery, M. H., & Winget, D. E. 2008, ApJ, 675, 1512 [NASA ADS] [CrossRef] [Google Scholar]
  3. Córsico, A. H., Benvenuto, O. G., Althaus, L. G., Isern, J., & García-Berro, E. 2001, New Astr., 6, 197 [Google Scholar]
  4. Dine, M., Fishler, W., & Srednicki, M. 1981, Phys. Lett. B, 104, 199 [NASA ADS] [CrossRef] [Google Scholar]
  5. Isern, J., & García-Berro, E. 2008, Mem. SAIT, 79, 545 [NASA ADS] [Google Scholar]
  6. Isern, J., Hernanz, M., & García-Berro, E. 1992, ApJ, 392, L23 [NASA ADS] [CrossRef] [Google Scholar]
  7. Isern, J., García-Berro, E., Torres, S., & Catalán, S. 2008, ApJ, 682, L109 [NASA ADS] [CrossRef] [Google Scholar]
  8. Isern, J., Catalán, S., & García-Berro, E. 2009, J. Phys. Conf. Ser., 172, 012005 [Google Scholar]
  9. Kepler, S. O. 2009, in New Advances in Helio an Asteroseismology, IAU Joint Discussion 11, XXVII IAU General Assembly (Rio de Janeiro) [Google Scholar]
  10. Kepler, S. O., Kanaan, A, Winget, D. et al. 1991a, in White Dwarfs, ed. G. Vauclair, & E. Sion (Dordrecht: Kluwer), NATO Adv. Sci. Institutes (ASI) Ser. C, 336, 143 [Google Scholar]
  11. Kepler, S. O., Winget, D. E., Nather, R. E., et al. 1991b, ApJ, 378, L45 [NASA ADS] [CrossRef] [Google Scholar]
  12. Kepler, S. O., Mukadam, A., Winget, D. E., et al. 2000, ApJ, 534, L185 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  13. Kepler, S. O., Costa, J. E. S., Castanheira, B. G., Mukadam, A. S., & Sullivan, D. J. 2005, ApJ, 634, 1311 [Google Scholar]
  14. Khlopov, M. Yu. 1999, Cosmoparticle Physics (Singapore: World Scientific) [Google Scholar]
  15. Kim, J. E. 1979, Phys. Rev. Lett., 43, 103 [NASA ADS] [CrossRef] [Google Scholar]
  16. Kim, J. E., & Carosi, G. 2010, Rev. Mod. Phys., 82, 557 [NASA ADS] [CrossRef] [Google Scholar]
  17. McGraw, J. T., & Robinson, E. L. 1976, ApJ, 205, L155 [NASA ADS] [CrossRef] [Google Scholar]
  18. Mukadam, A. S., et al. 2009, J. Phys. Conf. Ser., 172, 012074 [NASA ADS] [CrossRef] [Google Scholar]
  19. Nakagawa, M., Kohyama, Y., & Itoh, N. 1987, ApJ, 322, 291 [NASA ADS] [CrossRef] [Google Scholar]
  20. Nakagawa, M., Adachi, T., Kohyama, Y., & Itoh, N. 1988, ApJ, 326, 241 [NASA ADS] [CrossRef] [Google Scholar]
  21. Peccei, R. D., & Quinn, H. 1977a, Phys. Rev. D, 16, 1791 [NASA ADS] [CrossRef] [Google Scholar]
  22. Peccei, R. D., & Quinn, H. 1977b, Phys. Rev. Lett., 38, 1440 [NASA ADS] [CrossRef] [Google Scholar]
  23. Raffelt, G. G. 1990, Phys. Rep., 198, 1 [NASA ADS] [CrossRef] [Google Scholar]
  24. Raffelt, G. G. 1996, Stars as Laboratories for Fundamental Physics (Cambridge: Cambridge University Press) [Google Scholar]
  25. Raffelt, G. G. 2007, J. Phys. A: Math. Theor., 40, 6607 [NASA ADS] [CrossRef] [Google Scholar]
  26. Shifman, M. A., Vainshtein, A. I., & Zakharov, V. I. 1980, Nucl. Phys. B, 166, 43 [Google Scholar]
  27. Steffen, F. D. 2009, Eur. Phys. J., C59, 557 [Google Scholar]
  28. Sullivan, D. J. 2009, J. of Phys: Conf. Ser., 172, 012070 [NASA ADS] [CrossRef] [Google Scholar]
  29. Turner, M. S. 1990, Phys. Rev., 197, 67 [Google Scholar]
  30. Zhitniskii, A. P. 1980, Sov. J. Nucl., 31, 260 [Google Scholar]
  31. Winget, D. E., Hansen, C. J., & Van Horn, H. M. 1983, Nature, 303, 781 [NASA ADS] [CrossRef] [Google Scholar]
  32. Winget, D. E., & Kepler, S. O. 2008, ARA&A, 46, 157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

All Tables

Table 1:   Axion luminosities and axion masses necessary to account for the observed drift of the period of pulsation of G117-B15A.

All Figures

  \begin{figure} \par\vspace{7cm} \special{psfile=13716fg1.eps hscale=55 vscale=55 voffset=-105 hoffset=-25} \end{figure} Figure 1:

Evolution of the measurement of the period drift of G117-B15A. Lines represent the theoretical values obtained by Córsico et al. (2001) - solid line - and Bischoff-Kim et al. (2008) - dashed-dotted line (for the case of a thin envelope) and dashed line (for the case of a thick envelope). The nominal uncertainties of these models are 1.15, 0.26 and 0.17 respectively, in the units of the figure.

Open with DEXTER
In the text
Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.