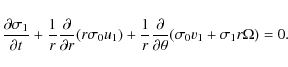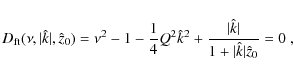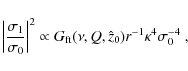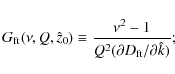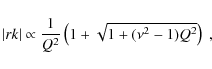EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 512 (March-April 2010) A&A, 512 (2010) A17 Full HTML
Free Access
Issue
A&A
Volume 512, March-April 2010
Article Number A17
Number of page(s) 6
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/200913611
Published online 23 March 2010
A&A 512, A17 (2010)

Prominent spiral arms in the gaseous outer galaxy disks

G. Bertin1 - N. C. Amorisco2,[*]

1 - Dipartimento di Fisica, Università degli Studi di Milano, via Celoria 16, 20133 Milano, Italy
2 - Dipartimento di Fisica, Università di Pisa, Largo Bruno Pontecorvo 3, 56127 Pisa, Italy

Received 5 November 2009 / Accepted 11 December 2009

Abstract
Context. Several spiral galaxies, as beautifully exhibited by the case of NGC 6946, display a prominent large-scale spiral structure in their gaseous outer disk. Such structure is often thought to pose a dynamical puzzle, because grand-design spiral structure is traditionally interpreted as the result of density waves carried mostly in the stellar disk.
Aims. Here we argue that the outer spiral arms in the cold gas outside the bright optical disk actually have a natural interpretation as the manifestation of the mechanism that excites grand-design spiral structure in the main, star-dominated body of the disk: the excitation is driven by angular momentum transport to the outer regions through trailing density waves outside the corotation circle that can penetrate beyond the Outer Lindblad Resonance in the gaseous component of the disk.
Methods. Because of conservation of the density wave action, these outgoing waves are likely to become more prominent in the outer disk and eventually reach nonlinear amplitudes. To calculate the desired amplitude profiles, we make use of the theory of dispersive waves.
Results. If the conditions beyond the optical radius allow for an approximate treatment in terms of a linear theory, we show that fitting the observed amplitude profiles leads to a quantitative test on the density of the disk material and thus on the dark matter distribution in the outer parts of the galaxy.
Conclusions. This study is thus of interest to the general problem of the disk-halo decomposition of rotation curves.

Key words: galaxies: spiral - galaxies: structure - galaxies: halos - galaxies: kinematics and dynamics

1 Introduction

Deep HI observations of nearby galaxies have led to the discovery of a number of important phenomena that are changing our views of the structure and dynamics of galaxies. These include the existence in early-type galaxies of regular and radially extended HI disks (Oosterloo et al. 2007a), the presence in spiral galaxies of extraplanar gas characterized by slow rotation (for NGC 891 see Oosterloo et al. 2007b; for NGC 2403, see Fraternali et al. 2002), and the properties of small-scale structures in the HI distribution (for NGC 6946, see Boomsma et al. 2008). One interesting related discovery is the existence of regular and prominent spiral arms in the gaseous outer disk, well outside the bright optical disk (Shostak & van der Kruit 1984; Dickey et al. 1990; Kamphuis 1993; for NGC 2915, see Meurer et al. 1996; for NGC 3741, see Begum et al. 2005). In this respect, a particularly impressive example is given by the case of NGC 6946 (Boomsma 2007; Boomsma et al. 2008, see Fig. 1), where a spectacular set of gaseous arms can be traced all the way out, with a significant degree of regularity and symmetry even if the outer disk is clearly lopsided and characterized by a fragmentary structure; the outer arms also appear to contain stars (see Ferguson et al. 1998, who also analyze the interesting cases of NGC 628 and NGC 1058; and Sancisi et al. 2008).

The study of spiral structure in galaxies has received great attention in the past. It is now generally thought that grand-design structure is the manifestation of density waves, mostly carried by the stellar component of galaxy disks. A general framework for the interpretation of the observed morphologies, based on a density wave theory, has received significant support from the observations of spiral galaxies in the near-infrared (see Bertin & Lin 1996, and references therein). It might thus appear as a puzzle to find well-organized spiral patterns in the outer disk, in a region where stars are practically absent.

The above-mentioned deep HI studies also serve as interesting probes in view of defining an appropriate visible matter - dark halo decomposition of the gravitational field in galaxies. In particular, the studies of prominent spiral arms in the gaseous outer disks have raised two issues that separately point to the question of whether the outer disk is light or heavy. On the one hand, concerns have been raised about the applicability in this region of the criterion for the onset of star formation proposed by Kennicutt (1989), which relies on a threshold on the axisymmetric stability parameter $Q = c \kappa/\pi G \sigma$. Accordingly, light disks with low $\sigma$ should be unable to make new stars; but in the outer parts the disk might be flared and three-dimensional effects may change the picture significantly (in this regard, see also the comments by Ferguson et al. 1998). On the other hand, there is widespread belief (see Sancisi et al. 2008, p. 212) that light disks should be unable to support a spiral structure (see Toomre 1981; Athanassoula et al. 1987; criticism against this belief can be found e.g. in the article by Bertin et al. 1989a).

In general, the arguments often put forward in favor of a maximum-disk decomposition of the rotation curves of spiral galaxies (starting with van Albada & Sancisi 1986) still await a decisive measurement to remove the remaining degeneracy that characterizes such a decomposition. Some projects, like the ``disk mass project'' (Verheijen et al. 2004, 2007), aim at making full use of three-dimensional gas and stellar dynamical data so as to decompose the field, much like in the classical problem of the disk thickness in the solar neighborhood (Oort 1932; Bahcall 1984; Kuijken & Gilmore 1989; Crézé et al. 1998; Holmberg & Flynn 2000, 2004). Dark halos are generally thought to be made of collisionless dark matter and to have spheroidal shape, but it would be important to have direct proof that the outer disk of spiral galaxies is indeed light, as opposed to the possibility that the disk is heavy because of large amounts of molecular material (Pfenniger et al. 1994; see also Revaz et al. 2009).

One interesting aspect of galactic dynamics is that models for the interpretation of observed structures generally offer independent diagnostics of the overall mass distribution. In this paper we will present one more example of this general aspect of dynamics. Indeed, we will propose a model for the observed spiral structure in the outer disk and then will show how the model can be tested and applied to probe the structure of the outer disk in relation with the problem of the amount and distribution of dark matter.

\begin{figure} \par\includegraphics[width=8.8cm,clip]{13611fg1.eps} \end{figure} Figure 1:

Total HI distribution of NGC 6946 superimposed to its optical image; courtesy of Filippo Fraternali (see Boomsma et al. 2008).

Open with DEXTER

In passing we note that in principle one might test the properties of the final model (i.e., disk-dark matter decomposition) identified by our technique in specific cases against the expectations of non-Newtonian theories of gravity such as MOND; but of course, a discussion within MOND of the full problem including the behavior of density waves is currently not available.

The picture presented in this paper is the following. Global spiral modes are driven by the transfer of angular momentum to the outer regions (see Bertin et al. 1989a,b and references therein; see also Lynden-Bell & Kalnajs 1972; Bertin 1983). Outside the corotation circle, the transfer is performed by short trailing waves. At the outer Lindblad resonance, these outgoing waves are fully absorbed in the stellar disk (Mark 1971, 1974), but only partially absorbed in the gaseous component (Pannatoni 1983; Haass 1983), so that the signal can penetrate beyond this resonance and propagate in the HI disk, if present. The outer spiral arms are thus interpreted as the natural extension in the outer disk of the short trailing waves that are responsible for exciting the global spiral structure in the star-dominated main body of the galaxy disk. The amplitude profile of these outer arms should simply follow the requirements dictated by the conservation of wave action (Shu 1970; Dewar 1972). Because of this conservation, the amplitude of the outer arms is expected to increase with radius in the regions where the inertia of the disk becomes smaller and smaller, much like ocean waves can reach high amplitudes when moving close to the shore. In these outer regions the density wave is thus carried by the gas, but the stars present would collectively respond and some new stars may be born because of the gas compression which follows the gaseous arms.

Of course, galaxies such as NGC 6946 or NGC 628 and the blue compact dwarf NGC 2915 are very different objects; each case should thus be studied separately in detail, and each individual object may have its own special character. Here we wish to offer one quantitative reference frame for a common mechanism that should operate in general in the outer parts of galaxy disks.

A fully nonlinear, three-dimensional analysis of the properties of density waves in the HI outer disk is not available, but we can hope that under suitable conditions an approximate description based on the laws of conservation of wave action for low-amplitude density waves is viable. In any case, it should be tested against the observations. Since fitting the data requires assumptions on the density associated with the spiral arms and the density associated with the fluid basic state, a test of this scenario would be able to tell how much mass in the outer disk is present in the form of molecular gas.

2 Physical model and calculation of the amplitude profiles

We refer to a grand-design spiral galaxy dominated by a global mode with m arms and a pattern frequency $\Omega_{\rm p}$ and consider for simplicity a barotropic fluid model of an infinitesimally thin disk as an idealized representation of the gaseous outer regions of the galaxy. In terms of standard polar cylindrical coordinates $(r, \theta)$, let $\sigma = \sigma_0 + \sigma_1$ be the disk mass density, $(r \Omega + v_1){\vec e}_{\theta} + u_1 {\vec e}_r$ the fluid velocity field, and c the effective sound speed of the fluid. The quantity $\Omega = \Omega (r)$ is the differential rotation. As a measure of the distance from the corotation radius, we then refer to the dimensionless quantity $\nu = m (\Omega_{\rm p} - \Omega)/\kappa$, where $\kappa$ is the epicyclic frequency. Below subscript 0 refers to the axisymmetric basic state of the disk and subscript 1 to the perturbation on this equilibrium associated with the large-scale spiral structure. In the notation just introduced, the relevant axisymmetric stability parameter is defined as $Q = c \kappa/(\pi G \sigma_0)$.

According to the general picture of the modal theory of spiral structure (see Bertin & Lin 1996, and references therein), the global mode is associated with an outgoing (short) trailing wave outside the corotation circle. In general, for a normal spiral mode the corotation circle is expected to occur at the edge of the optical disk (i.e., at $r_{\rm co} \approx 3 - 4 h$, with h the exponential scale of the stellar disk), while for a barred spiral mode the corotation circle is expected to occur just outside the tip of the bar, in the middle of the optical disk, at $r_{\rm co} \approx 2 h$. In the gaseous outer disk the outgoing trailing wave can penetrate beyond the outer Lindblad resonance (which occurs at the radius $r_{\rm OLR}$ where $\nu = 1$). This section is aimed at calculating the amplitude profile of the spiral arms in the outer regions for $r > r_{\rm OLR}$. In this region the calculation of the amplitude profile is particularly simple, while the properties of the spiral structure out to $r \approx r_{\rm OLR}$ are determined by the processes that govern the main body of the disk (see Bertin & Lin 1996).

In the linear theory of density waves, the calculation can be performed in a straightforward manner by imposing the conservation of the density of wave action (see Shu 1970; Dewar 1972; Bertin 1983). Mathematically this is equivalent to carrying out the analysis that leads to the standard algebraic dispersion relation for density waves $D(\nu,\vert\hat{k}\vert) = 0$, with $D(\nu,\vert\hat{k}\vert) = \nu^2 - 1 - Q^2 \hat{k}^2/4 + \vert\hat{k}\vert$ (where the radial wavenumber $k = \hat{k} \kappa^2/(2 \pi G \sigma_0)$ is associated with the pitch angle of the spiral arms, $\tan i = m/(rk)$), to the next order in the WKB expansion (e.g., see Bertin 2000, Chapter 17.3; see Eqs. (17.2), (17.22), (17.28), (17.30), and (17.42)).

In particular, the linear density wave analysis of a zero-thickness barotropic fluid disk is best carried out in terms of the enthalpy perturbation $h_1 = (c^2/\sigma_0)\sigma_1$. The WKB asymptotic analysis then leads to a Schroedinger-like equation of the form

\begin{displaymath} u'' + g(r,\omega)u = 0, \end{displaymath} (1)

where for tightly wound density waves the function g is given approximately by

\begin{displaymath} g(r,\omega) = \frac{\kappa^2}{c^2}\left( \frac{1}{Q^2} -1 + \nu^2\right). \end{displaymath} (2)

The function u in Eq. (1) is defined in terms of the function h1 in such a way that the amplitudes of the two functions are related as

\begin{displaymath} \vert h_1\vert^2 = \frac{\kappa^2\vert 1 - \nu^2\vert}{r\sigma_0}\vert u\vert^2 ~. \end{displaymath} (3)

The WKB analysis of the turning-point equation for u shows that away from the turning points the amplitude of u must scale as $\vert u\vert \sim \vert g\vert^{-1/4}$, which is interpreted as the conservation of the density of wave action. A little algebra then shows that such relation is equivalent to the condition

\begin{displaymath} \left\vert\frac{\sigma_1}{\sigma_0}\right\vert^2 \propto G(\nu,Q) r^{-1}\kappa^{4}\sigma_0^{-4}~, \end{displaymath} (4)

where

\begin{displaymath}G(\nu,Q) \equiv \frac{\nu^2 - 1}{Q^2 \sqrt{1 + (\nu^2 - 1)Q^2}}\cdot \end{displaymath} (5)

The proportionality constant is independent of r. Thus Eq. (4) provides the desired expression for the amplitude profile of the density wave in the outer regions.

In order to complete the description of the amplitude profiles of the spiral arms, we may then consider the linearized continuity equation:

\begin{displaymath} \frac{\partial \sigma_1}{\partial t} + \frac{1}{r} \frac{\pa... ...tial}{\partial \theta} (\sigma_0 v_1 + \sigma_1 r \Omega) = 0. \end{displaymath} (6)

Since the vorticity equation shows that $v_1 = (i/\nu) [\kappa/(2 \Omega)] u_1$, so that v1 and u1 have the same order of magnitude, we can neglect the v1 contribution in the continuity equation consistent with the present WKB approximation and obtain:

\begin{displaymath}\sigma_0 k u_1 \sim \nu \kappa \sigma_1~. \end{displaymath} (7)

By inserting here the solution for k associated with the (short) trailing wave branch,

\begin{displaymath} k = - \left( \frac{\kappa^2}{2 \pi G \sigma_0}\right) \frac{2}{Q^2}\left(1 + \sqrt{1+ (\nu^2 - 1)Q^2}\right)~, \end{displaymath} (8)

we find

\begin{displaymath} \left\vert\frac{u_1}{r \Omega}\right\vert =\nu \left(\frac{\... ...\frac{\kappa}{\Omega}\right) H(\nu,Q) r^{-3/2} \sigma_0^{-1}~, \end{displaymath} (9)

with

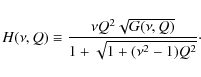
\begin{displaymath}H(\nu,Q) \equiv \frac{\nu Q^2 \sqrt{G(\nu,Q)}}{1+ \sqrt{1 + (\nu^2 - 1)Q^2}}\cdot \end{displaymath} (10)

Again, the proportionality factor is independent of r. Note that the first part of Eq. (9) is an equality, not a proportionality relation. In other words, the scale in the velocity amplitude u1 is uniquely determined by the scale in the amplitude of the density wave $\sigma_1$ in the context of the linear WKB theory. Note also that the perturbation u1 together with v1 will generate the ``wiggles'' in the velocity field which are characteristic of density waves (for M81, see Visser 1977); in the observed cases where the amplitudes are large, a nonlinear theory is required for a quantitative comparison with the observations.

2.1 Effects of the flaring of the outer disk

The analysis described previously can be generalized to include the effects of the finite thickness of the disk. In the discussion of the dynamics of selfgravitating disks, these effects are often ignored, but may actually play an important role; in our case, significant effects would be naturally expected if the disk is flared in the outer parts, as often observed. Qualitatively, these effects should become significant for short waves when the wavelength of the density wave becomes comparable to the thickness of the disk; in terms of local stability, finite-thickness effects are known to be stabilizing, because they effectively ``dilute'' the gravity field. Quantitatively, they are approximately incorporated by the following dispersion relation (see Vandervoort 1970; Yue 1982):

\begin{displaymath} D_{\rm ft}(\nu,\vert\hat{k}\vert, \hat{z}_0) = \nu^2 - 1 - \... ...+\frac{\vert\hat{k}\vert}{1+ \vert\hat{k}\vert\hat{z}_0} = 0~, \end{displaymath} (11)

where z0 represents the disk thickness (defined in a way that the disk surface density $\sigma_0$ is related to the volume density $\rho_0$ on the equatorial plane by the expression $\sigma_0 = 2 \rho_0 z_0$) and

\begin{displaymath} \hat{z}_0 \equiv \frac{\kappa^2 z_0}{2 \pi G \sigma_0}\cdot \end{displaymath} (12)

The modification of the dispersion relation with respect to the standard one used earlier in Sect. 2 changes the expression of the trailing wave-branch that carries angular momentum outwards $k = k_{\rm ST} = \hat{k}_{\rm ST} \kappa^2/(2 \pi G \sigma_0)$ with respect to Eq. (8). But the calculation of this wavebranch is straightforward, because the new dispersion relation (11) is just a cubic in |k|. Here $\hat{k}_{\rm ST} = \hat{k}_{\rm ST} (\nu, Q, \hat{z}_0)$.

From the general theory of dispersive waves, we know that the flux of density wave action is $\mathcal{F} = c_{\rm g} \mathcal{A}$, with the group velocity $c_{\rm g} \equiv -(\partial \omega / \partial k)$ and the wave action density $\mathcal{A} \propto \sigma_1^2 (\partial D/\partial \omega)$. Thus we have $\mathcal{F} \propto (\partial D/ \partial k)$. In the derivation reported in the first part of the section the factor $(\partial D/ \partial k)$ enters in the conservation Eq. (4) as $(\partial D/ \partial \hat{k}) = \sqrt{1 +(\nu^2 - 1)Q^2}$, with the latter derivative evaluated from the zero-thickness dispersion relation on the short trailing wave-branch (8).

Therefore, the desired conservation equation in the finite thickness case becomes

\begin{displaymath} \left\vert\frac{\sigma_1}{\sigma_0}\right\vert^2 \propto G_{\rm ft}(\nu,Q, \hat{z}_0)r^{-1}\kappa^{4}\sigma_0^{-4}~, \end{displaymath} (13)

where now we have

\begin{displaymath}G_{\rm ft}(\nu,Q, \hat{z}_0) \equiv \frac{\nu^2 - 1}{Q^2 (\partial D_{\rm ft}/\partial \hat{k})}; \end{displaymath} (14)

here the partial derivative is evaluated at $\hat{k} = \hat{k}_{\rm ST}$.

The corresponding expression for the amplitude profile in the velocity field is obtained from Eq. (9) by replacing $H(\nu, Q)$ with $H_{\rm ft}(\nu, Q, \hat{z}_0)$, with

\begin{displaymath}H_{\rm ft}(\nu,Q, \hat{z}_0) \equiv \frac{\nu \sqrt{G_{\rm ft... ...\hat{z}_0)}}{\vert\hat{k}_{\rm ST}(\nu,Q,\hat{z}_0)\vert}\cdot \end{displaymath} (15)

In the following subsection it will be shown that flaring effects are under control and do not significantly change the general predictions of the zero-thickness theory.

2.2 A simple reference model

To test the overall picture we may consider the following simple reference model. We refer to a two-armed spiral structure (m = 2) in an outer disk characterized by a flat rotation curve, so that $\kappa = \sqrt{2} \Omega$, $\Omega /\Omega_{\rm p} = r_{\rm co}/r$, and $\nu = \sqrt{2}(r/r_{\rm co} - 1)$. To be specific, we will assume that $r_{\rm co} = 3 h$, in terms of the exponential scale h of the (inner) stellar disk. Thus the outer Lindblad resonance will occur at $r_{\rm OLR} \approx 5.12 h$. Therefore, at $r_{\rm in} = 6 h$ we are outside the circle associated with the outer Lindblad resonance, in a region where we expect the disk to be gas dominated, so that beyond this radius we may proceed to apply our fluid model.

As a further simplification, we take the conservative case in which $\sigma_0 = \sigma_0 (r_{\rm in} )(6 h/r)$. This corresponds to a very gentle decline of the gas density profile. (For faster declining profiles we expect that the relative strength of the spiral amplitude should be more pronounced as we move outwards (cf. Eq. (4)) and thus give rise to a stronger effect.) In our simple reference model, the gas density is then proportional to the differential rotation, so that we find $\vert\sigma_1/\sigma_0\vert^2 \propto G(\nu, Q)/r$ and $\vert u_1/(r\Omega)\vert \propto H(\nu, Q)/r^{1/2}$.

In a zero-thickness disk the pitch angle of the spiral arms depends only on $\nu$ and Q within the adopted reference model, because (cf. Eq. (8))

\begin{displaymath} \vert r k\vert \propto \frac{1}{Q^2}\left(1 + \sqrt{1+(\nu^2 - 1)Q^2}\right)~, \end{displaymath} (16)

where the proportionality constant is independent of the radius. In this case we are thus left to discuss the dependence Q = Q(r). There are observational indications (cf. Boomsma et al. 2008, Fig. 6) that the gas velocity dispersion is steadily declining in the outer disk, while in the present simple model the quantity $\kappa/\sigma_0$ is r-independent. So we could argue that a declining Q-profile would be realistic. However, the observed decline in the gas velocity dispersion is just likely to reflect that because of the stabilizing role of thickness (see previous subsection) the disk can get colder and colder (in terms of the standard Q) and still remain on the margin of local axisymmetric instability. Then we think it appropriate to consider $Q \approx $ constant for the present zero-thickness reference model and for simplicity we take Q = 1. Note that this condition of marginal stability is not strictly necessary, because in the outer disk short trailing waves can propagate even at higher values of Q.

In conclusion, the present simple zero-thickness model is characterized by $G(\nu, Q) = (\nu^2-1)/\nu$, $H(\nu, Q) = \sqrt{\nu(\nu^2 - 1)}/(1+\nu)$, and $rk \propto (1 + \nu)$. By applying Eqs. (8), (4), and (9) we can proceed to calculate the desired profiles i(r), $\vert\sigma_1/\sigma_0\vert$, and $\vert u_1/(r \Omega)\vert$.

In the finite thickness case, the wavenumber for short trailing waves $k_{\rm ST}(\nu, Q, \hat{z}_0)$ is obtained from the dispersion relation Eq. (11), which can also be used to calculate the two relevant quantities $G_{\rm ft}(\nu, Q,\hat{z}_0)$and $H_{\rm ft}(\nu, Q, \hat{z}_0)$. The remaining point that requires discussion is the radial dependence of the two functions $\hat{z}_0=\hat{z}_0(r)$ and Q = Q(r).

As to the vertical thickness of the outer disk, it can be shown (see Appendix A in Bertin & Lodato 1999) for our reference model, which is characterized by $\Omega \sim 1/r$ and $\sigma_0 \sim 1/r$, that in each of the two opposite limits of a totally selfgravitating disk and of a non-selfgravitating layer the thickness behaves as $z_0 \sim r$, so that taking $\hat{z}_0=$constant is a reasonable choice. In addition, since we refer to a fluid, the relevant velocity dispersion tensor is isotropic ( cr = cz = c), so that there is a one-to-one relation between the value of Q and the value of $\hat{z}_0$ that we are going to take; let us denote this relation by $Q = Q_{\rm fluid}(\hat{z}_0)$. On the other hand we should assume that the disk is at marginal stability, i.e. $Q = Q_{\rm max}(\hat{z}_0)$(see Eq. (15.22) in Bertin 2000) for a proper comparison with the zero-thickness reference model described earlier in this subsection. By combining the above requirements into $Q_{\rm fluid}(\hat{z}_0) = Q = Q_{\rm max}(\hat{z}_0)$we get a unique value for the pair $(\hat{z}_0, Q)$, as demonstrated in Fig. 2. With this determination we can calculate the desired profiles i(r), $\vert\sigma_1/\sigma_0\vert$, and $\vert u_1/(r \Omega)\vert$ for the finite thickness model from Eqs. (11), (14), (15), and (13).

\begin{figure} \par\includegraphics[width=9cm,clip]{13611fg2.eps} \end{figure} Figure 2:

For our simple reference fluid model with $\sigma _0 \propto 1/r$ and $\Omega \propto 1/r$, the thick solid line represents the marginal stability condition $Q = Q_{\rm max}(\hat{z}_0)$and the dashed curve the corresponding condition for the case in which the dilution of the gravity field (associated with the finite thickness of the disk) in the relevant dispersion relation is described by an exponential factor (instead of the rational factor used in Eq. (11)). The thin rising curves represent the function $Q = Q_{\rm fluid}(\hat{z}_0)$ for the two cases of a fully selfgravitating layer (upper curve) and for a non-selfgravitating layer (lower curve).

Open with DEXTER

The results of this analysis are illustrated in Fig. 3 in the radial interval 6 h < r < 10 h. In this figure we assumed that at r = 6 h the relative amplitude of the density wave is $\sigma_1/\sigma_0 = 0.15$ and that the pitch angle of the spiral structure at this inner location is 15 degrees. The figure shows that even for the presently assumed very gentle decline of the gas density distribution the amplitude of the spiral wave steadily increases with the radius. Note that in the two limits of a totally selfgravitating disk and a non-selfgravitating disk the finite-thickness effects do not change the general picture; similar results and a similar conclusion have been checked to hold using a dispersion relation alternative to Eq. (11), in which the dilution of the gravitational term $\left\vert\hat{k}\right\vert$ is exponential rather than rational.

\begin{figure} \par\includegraphics[width=9cm,clip]{13611fg3.eps} \end{figure} Figure 3:

Relative amplitude profiles of the spiral arms in terms of density $\sigma _1/\sigma _0$ and of radial velocity $u_1/(r\Omega )$ (dimensionless, left axis) and pitch angle i of spiral structure (degrees, right axis), for three cases of the simple reference model described in Sect. 2.2: zero-thickness disk (thick lines), finite-thickness totally selfgravitating disk (dashed lines), finite-thickness non-selfgravitating disk (dash-dotted lines).

Open with DEXTER

3 Discussion and conclusions

HI observations of the gaseous outer regions provide measurements of the HI gas density $\sigma_{\rm HI}$, of the rotation curve $\Omega$, and of the turbulent velocity $c_{\rm HI}$, which we identify with c. We argue that the actual disk density is traced by the atomic hydrogen, so that $\sigma = f \sigma_{\rm HI}$. In the simplest model we take $f \approx 1.4$, i.e. take that the outer disk just contains the relevant proportion of helium. For the following discussion, we assume that the thickness z0 of the gaseous outer disk is not well constrained by the observations, since we wish to consider objects with prominent observed spiral arms and therefore galaxies that are not edge-on. On the other hand, instead of considering the thickness profile z0 = z0(r) as an additional free function of the problem, we refer to a self-consistent estimate of such profile, which is readily available (e.g., see Appendix A in Bertin & Lodato 1999 and Sect. 2.2 in the present paper).

Clearly, if the linear theory is viable, the basic relations are over-constrained by the data, since we only have some leverage on the precise value of $\Omega_{\rm p}$ (which then sets the form of the function $\nu(r)$) and basically no other free parameters. Note that the morphology, or a suitable Fourier decomposition of the observed structure, would identify the dominant value of m and the pitch angle i(r), i.e., the function k(r). The linear theory makes specific predictions like Eqs. (8), (4), and (9) (or the corresponding equations recorded in Sect. 2.1 for the study that includes the effects of finite thickness). Much as for the classical tests of the density wave theory (for M81, see Visser 1977), we hope that the various observed quantities all agree reasonably well with the theoretical expectations.

Suppose that we started from a straightforward comparison with the observations on the basis of the linear theory described in the first part of Sect. 2. If this attempt turned out to be unsatisfactory, we would have three possibilities to interpret the data.

(i)
One possibility would be to make use of an HI fraction fconstant, but significantly larger than unity. Physically, a choice of this kind would correspond to imagining a heavier outer gaseous disk, which would still be in proportion to the observed HI disk and thus have little relevance for the overall problem of dark matter. 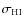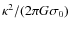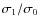For given values of $\sigma_{\rm HI}$ and $c_{\rm HI}$, this would allow us to reduce the value of the wavenumber scale $\kappa^2/(2 \pi G \sigma_0)$ and of the axisymmetric stability parameter Q while leaving the relative density amplitude $\sigma _1/\sigma _0$unchanged on the left hand side of Eq. (4). Except for a small adjustment through the functions G and H, such a constant f would have little or no effect on the fits to the observed amplitude profiles dictated by Eqs. (4) and (9).
(ii)
A second possibility would be to make use of a free function f = f(r) with the general requirement that f > 1.4. This would correspond to imagining that significant amounts of dark matter would be in the thin disk, possibly in molecular form, with a distribution different from that of the cold atomic hydrogen. This leads in the direction of an alternative picture (with respect to the standard picture of a spheroidal halo) for the general problem of dark matter (e.g., see Pfenniger et al. 1994). Clearly a nonconstant HI fraction f(r) would change the character of the observed amplitude profiles predicted by Eqs. (4) and (9).
(iii)
Finally, it may well be that the model developed above, which relies on the predictions of a linear theory, turns out to be inadequate. In other words, we should develop a model in which the role of the nonlinearities associated with the finite amplitude observed in the prominent spiral arms is properly taken into account.
While a more advanced model of the kind outlined in item (iii) above is being developed, we argue here that a first test of the simple picture presented is worth trying. If a satisfactory agreement with the linear theory could be obtained with $f \approx 1.4$, we would have one additional convincing argument that the picture of a spheroidal dark halo indeed holds also for the outermost regions of spiral galaxies. In any case, the considerable effort required by setting up such a test on a specific case, e.g. for NGC 6946, would prepare the ground for a test of the more realistic nonlinear theory that we plan to investigate soon.

Finally, given the picture provided by the simple reference model described in Sect. 2.2, we argue that for those galaxies in which the outer gaseous disk density declines too sharply, the nonlinear effects that would rapidly take place because of the sharp increase in relative amplitude of the density waves may actually tend to break the grand design outer structure and result in turbulent dissipation, as often argued in the physical discussion of the outer boundary condition for the establishment of global spiral modes (e.g., see Bertin & Lin 1996, p. 222).

Acknowledgements

We wish to thank Renzo Sancisi, Rosemary Wyse, and Jay Gallagher for pointing out the interest in this problem and for several stimulating discussions, and Filippo Fraternali and Giuseppe Lodato for a number of useful comments. Special thanks to Filippo Fraternali for providing us with Fig. 1.

References

  1. Athanassoula, E., Bosma, A., & Papaioannou, S. 1987, A&A, 179, 23 [NASA ADS] [Google Scholar]
  2. Bahcall, J. N. 1984, ApJ, 276, 156 [NASA ADS] [CrossRef] [Google Scholar]
  3. Begum, A., Chengalur, J. N., & Karachentsev, I. D. 2005, A&A, 433, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Bertin, G. 1983, A&A, 127, 145 [NASA ADS] [Google Scholar]
  5. Bertin, G. 2000, Dynamics of Galaxies (Cambridge: Cambridge University Press) [Google Scholar]
  6. Bertin, G., & Lin, C. C. 1996, Spiral structure in galaxies: a density wave theory (Cambridge: The MIT Press) [Google Scholar]
  7. Bertin, G., & Lodato, G. 1999, A&A, 350, 694 [NASA ADS] [Google Scholar]
  8. Bertin, G., Lin, C. C., Lowe, S. A., & Thurstans, R. P. 1989a, ApJ, 338, 78 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bertin, G., Lin, C. C., Lowe, S. A., & Thurstans, R. P. 1989b, ApJ, 338, 104 [NASA ADS] [CrossRef] [Google Scholar]
  10. Boomsma, R. 2007, PhD Thesis, Groningen University [Google Scholar]
  11. Boomsma, R., Oosterloo, T. A., Fraternali, F., van der Hulst, J. M., & Sancisi, R. 2008, A&A, 490, 555 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Crézé, M., Chereul, E., Bienaymé, O., & Pichon, C. 1998, A&A, 329, 920 [NASA ADS] [Google Scholar]
  13. Dewar, R. L. 1972, ApJ, 174, 301 [NASA ADS] [CrossRef] [Google Scholar]
  14. Dickey, J. M., Hanson, M. M., & Helou, G. 1990, ApJ, 352, 522 [Google Scholar]
  15. Ferguson, A. M. N., Wyse, R. F. G., Gallagher, J. S., & Hunter, D. A. 1998, ApJ, 506, L19 [Google Scholar]
  16. Fraternali, F., van Moorsel, G., Sancisi,R., & Oosterloo, T. 2002, AJ, 123, 3124 [NASA ADS] [CrossRef] [Google Scholar]
  17. Haass, J. 1983, ed. E. Athanassoula (Dordrecht: Reidel), IAU Symp., 100, 121 [Google Scholar]
  18. Holmberg, J., & Flynn, C. 2000, MNRAS, 313, 209 [NASA ADS] [CrossRef] [Google Scholar]
  19. Holmberg, J., & Flynn, C. 2004, MNRAS, 352, 440 [NASA ADS] [CrossRef] [Google Scholar]
  20. Kamphuis 1993, PhD Thesis, Groningen University [Google Scholar]
  21. Kennicutt, R. C. Jr. 1989, ApJ, 344, 685 [NASA ADS] [CrossRef] [Google Scholar]
  22. Kuijken, K. H., & Gilmore, G. 1989, MNRAS, 239, 571 [NASA ADS] [CrossRef] [Google Scholar]
  23. Lynden-Bell, D., & Kalnajs, A. J. 1972, MNRAS, 157, 1 [NASA ADS] [CrossRef] [Google Scholar]
  24. Mark, J. W-K. 1971, Proc. Natl. Acad. Sci. USA, 68, 2095 [NASA ADS] [CrossRef] [Google Scholar]
  25. Mark, J. W-K. 1974, ApJ, 193, 539 [NASA ADS] [CrossRef] [Google Scholar]
  26. Meurer, G. R., Carignan, C., Beaulieu, S. F., & Freeman, K. C. 1996, AJ, 111, 1551 [NASA ADS] [CrossRef] [Google Scholar]
  27. Oort, J. H. 1932, Bull. Astron. Inst. Netherlands, 6, 249 [Google Scholar]
  28. Oosterloo, T. A., Morganti, R., Sadler, E. M., van der Hulst, T., & Serra, P. 2007a, A&A, 465, 787 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Oosterloo, T., Fraternali, F., & Sancisi, R. 2007b, AJ, 134, 1019 [NASA ADS] [CrossRef] [Google Scholar]
  30. Pannatoni, R. F. 1983, Geophys. Astrophys. Fluid Dyn., 24, 165 [Google Scholar]
  31. Pfenniger, D., Combes, F., & Martinet, L. 1994, A&A, 285, 79 [NASA ADS] [Google Scholar]
  32. Revaz, Y., Pfenniger, D., Combes, F., & Bournaud, F. 2009, A&A, 501, 171 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Sancisi, R., Fraternali, F., Oosterloo, T., & van der Hulst, T. 2008, A&ARv, 15, 189 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Shostak, G. S., & van der Kruit, P. C. 1984, A&A, 132, 20 [NASA ADS] [Google Scholar]
  35. Shu, F. H. 1970, ApJ, 160, 99 [Google Scholar]
  36. Toomre, A. 1981, The structure and evolution of normal galaxies, ed. S. M. Fall & D. Lynden-Bell (Cambridge: Cambridge University Press), 111 [Google Scholar]
  37. van Albada, T. S., & Sancisi, R. 1986, Phil. Trans. R. Soc. London A. 320, 447 [Google Scholar]
  38. Vandervoort, P. O. 1970, ApJ, 161, 87 [NASA ADS] [CrossRef] [Google Scholar]
  39. Verheijen, M. A. W., Bershady, M. A., Andersen, D. R., et al. 2004, Astron. Nachr., 325, 151 [NASA ADS] [CrossRef] [Google Scholar]
  40. Verheijen, M. A. W., Bershady, M. A., Swaters, R. A., Andersen, D. R., & Westfall, K. B. 2007, Island Universes, ed. R. S. de Jong (Berlin: Springer) , 95 [Google Scholar]
  41. Visser, H. C. D. 1977, PhD Thesis, Groningen University [Google Scholar]
  42. Yue, Z. Y. 1982, Geophys. Astrophys. Fluid Dyn., 20, 1 [NASA ADS] [CrossRef] [Google Scholar]

Footnotes

...[*]
also at Scuola Normale Superiore, Piazza dei Cavalieri 7, 56125 Pisa, Italy; as of October 2009, at Institute of Astronomy, Madingley Road, Cambridge CB3 0HA, UK

All Figures

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{13611fg1.eps} \end{figure} Figure 1:

Total HI distribution of NGC 6946 superimposed to its optical image; courtesy of Filippo Fraternali (see Boomsma et al. 2008).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{13611fg2.eps} \end{figure} Figure 2:

For our simple reference fluid model with $\sigma _0 \propto 1/r$ and $\Omega \propto 1/r$, the thick solid line represents the marginal stability condition $Q = Q_{\rm max}(\hat{z}_0)$and the dashed curve the corresponding condition for the case in which the dilution of the gravity field (associated with the finite thickness of the disk) in the relevant dispersion relation is described by an exponential factor (instead of the rational factor used in Eq. (11)). The thin rising curves represent the function $Q = Q_{\rm fluid}(\hat{z}_0)$ for the two cases of a fully selfgravitating layer (upper curve) and for a non-selfgravitating layer (lower curve).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{13611fg3.eps} \end{figure} Figure 3:

Relative amplitude profiles of the spiral arms in terms of density $\sigma _1/\sigma _0$ and of radial velocity $u_1/(r\Omega )$ (dimensionless, left axis) and pitch angle i of spiral structure (degrees, right axis), for three cases of the simple reference model described in Sect. 2.2: zero-thickness disk (thick lines), finite-thickness totally selfgravitating disk (dashed lines), finite-thickness non-selfgravitating disk (dash-dotted lines).

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.