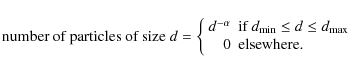| Issue |
A&A
Volume 512, March-April 2010
|
|
|---|---|---|
| Article Number | A60 | |
| Number of page(s) | 8 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/200913418 | |
| Published online | 02 April 2010 | |
A numerical model of cometary dust coma structures
Application to comet 9P/Tempel 1
J.-B. Vincent1 - H. Böhnhardt1 - L. M. Lara2
1 - Max-Planck-Institut für Sonnensystemforschung, Max-Planck-Strasse 2, 37191 Katlenburg-Lindau, Germany
2 -
Instituto de Astrofísica de Andalucía, CSIC, PO Box 3004, 18080 Granada, Spain
Received 7 October 2009 / Accepted 10 December 2009
Abstract
Aims. The purpose of this study is to test our numerical
model of cometary dust coma structures and to use the results to infer
information about the nucleus surface activity of comet 9P/Tempel 1.
Methods. Parameters on the activity were first estimated from
simulations of ground-based observation acquired during the
pre-perihelion period (January to June 2005) and compared with
published results for the same period. The parameters retrieved were
then used to simulate previously unpublished images of the comet
acquired during the post-perihelion period (in July and August 2005).
Results. Our model was able to retrieve the spin axis
orientation of comet 9P/Tempel 1 as well as information on active
regions at the surface of the nucleus. We could localize at least six
active areas and characterize them with parameters such as the velocity
of the dust particles, grain size, and activity profile. Our model
confirms published results from spacecraft measurements but is also
able to make realistic predictions on the evolution of the coma
morphology during the post-perihelion period.
Key words: methods: numerical - comets: general - comets: individual: 9P/Tempel 1
1 Introduction
Studying the surface of a comet is challenging because either the nucleus is too far to be resolved in detail, or it is close enough but its own activity hides all the features we would like to investigate. One of the topic of interest is the localization of active regions on the nucleus.
In principle this determination can be done from a spacecraft, but it is not always a straightforward analysis as it requires a precise understanding of the flyby geometry and the spin state of the nucleus. Even with this information available, it can be still difficult to link the observed activity with geological features. Moreover, the jets of gas and dust represent a hazard for any probe passing at close distance from the nucleus, for example Rosetta which is supposed to orbit the nucleus of comet 67P/Churyumov-Gerasimenko for at least an entire year. Therefore any hint on the local activity should be taken into consideration to constrain the approach.
So far, only six comets have been visited by spacecraft, with imaging of the nucleus for four of them. The last one was comet 9P/Tempel 1 during the Deep Impact mission in July 2005. The main purpose of this mission was to extract information about the structure and composition of the nucleus by crashing a probe into it while observing the impact with a second spacecraft. Many images of the coma were taken during the approach phase and showed dust structures that were later used to estimate the location of active regions on the surface of the nucleus. The results of this study are presented in Farnham et al. (2007).
Different methods have been applied to several comets (e.g. Sekanina 1987; Vasundhara 2002) to simulate ground-based observations of cometary dust activity. This techniques are mainly based on the assumption of point sources of dust emission on the surface of a rotating spherical nucleus. However, from the different cometary flybys, we know that the cometary dust activity is more complex. Active regions can be extended and the nucleus shape is often far from a spherical one.
In this paper we introduce a new model of dust coma structures applied to the test case of comet 9P/Tempel 1 as observed from April to August 2005, around the period of the Deep Impact flyby. Using the shape model of the nucleus, obtained from the spacecraft measurements (Thomas et al. 2007), we try to match accurately the ground based observations to extract useful information from it like the orientation of the spin axis and the localization of active regions.
2 Model description
Our model aims at reproducing dust coma structures of comets, in the first place using ground based-observations. These patterns appear as linear features, spirals, arcs, or shells around the nucleus, embedded in the general dust coma. They have been described in detail by Sekanina (1987) and are considered to be produced by active dust-emitting sources on the rotating nucleus.
Although the final goal is the retrieval of information on the surface activity, our model does not perform a direct inversion of the images but tries to reproduce the observed geometric structures through forward calculations, using as much as possible realistic modeling of the properties:
- the nucleus: orbital elements, size, spin axis orientation, rotational period, 3D shape model, position of the active regions, activity profile;
- the dust particles properties: size,
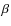 parameter
(ratio between the solar radiation pressure on the grains and solar
gravity), initial velocities and direction of emission,
parameter
(ratio between the solar radiation pressure on the grains and solar
gravity), initial velocities and direction of emission,
As discussed below, some of these parameters are not necessarily known a-priori or well enough. They must be approximated through educated guesses first, and can be refined iteratively later on depending on the results of the simulations.
2.1 Nucleus parameters
2.1.1 Position, spin orientation, and rotation period
To reproduce ground-based observations, one needs to know the position of the comet with respect to the Sun and the observer. This is easily calculated from the orbital elements of the comet.
The orientation of the spin axis is more difficult to obtain and is often unknown for cometary nuclei but it is one of the key parameters for the simulation. We can retrieve it from a first analysis of the coma structures orientations (Vincent et al. 2010). A detailed description of this process will be given in Sect. 3.2.
The rotation period is provided by other means, for example measurement of the light curve.
2.1.2 Shape
As we learnt from spacecraft images, cometary nuclei are far from being spherical. This can lead to a misinterpretation of observed activity. Indeed with the spherical model, one can hardly distinguish between two sources at different locations on the nucleus and two sources close by but with different emission geometries. In this case we would need to introduce a free parameter to infer the original direction of emission at the surface.
Attempts of using a non spherical model of the nucleus have been tried already, for example in Belton et al. (1991) to link observations of CN-jets and shells to activity at the surface of comet 1P/Halley an infer the nucleus spin state. A general conclusion of this paper states that although the ellipsoid model is better than a spherical one, a more realistic description of the shape is needed in order to fully constrain the activity and spin state of the nucleus.
Indeed, by using a realistic 3-dimensional shape to define the surface of the nucleus, we intend to constrain better the emission geometry, but also to calculate a more realistic illumination profile of the active regions during a rotation phase. Our model can use any kind of 3-dimensional shape, from a sphere to a complex body with irregular features (see Fig. 1). As the surface is represented with a mesh of polygons (typically squares or triangles), illumination can be calculated with a basic raytracing algorithm. This approach provides a realistic estimation of the amount of light received by each surface element. If the nucleus is a pure sphere, the illumination profile is equivalent to a cosine function.
| Figure 1: 3D shape model of the nucleus of comet 9P/Tempel 1, adapted from Thomas et al. (2007) showing the illumination with respect to the geographic features on the surface. The red line represents the spin axis and points towards the positive pole. The yellow line points towards the Sun. The blue patch indicates the localization of an active region. |
|
| Open with DEXTER | |
2.1.3 Definition of active regions
Usually, active regions are identified by their local coordinates (latitude & longitude) on the surface. Our model includes the possibility to consider such areas as point source or extended surfaces. It is important to be able to model both hypothesis as the precise mechanism leading to the formation of dust jets is still not completely understood and several unknowns remains regarding the real extension of the activity. The jets are undoubtedly related to sublimation of ices but whether this process occurs at the surface, in the shallow subsurface, or deeper inside the nucleus is still unknown. Most models describe the activity creating the jets through the sublimation of a large region directly from the surface (see for example Keller et al. 1994, for 1P/Halley) but some authors have proposed an other type of activity where the sublimation would take place in a subsurface cavity, with the gas escaping through a narrow vent (see Yelle et al. 2004, for a description of this phenomenon in the case of comet 19P/Borrelly).
Therefore a model using solely point source regions or extended areas can be useful as a first order approximation but may be unrealistic as different situations can be present. In principle a large area can still be approximated by a point source with a large emission cone but this approach is inaccurate in case of strong geometric variations of the surface.
In our model we combine the two approaches, by defining the regions either as point sources either as large areas through the shape model. As stated in Sect. 2.1.2, the 3-dimensional shape of the nucleus is defined by a collection of vertices and facets, each facet having a rough size of a few hundred meters. Given the boundaries of the active region (in latitude and longitude) we define whether a facet is active or not. If a facet is labeled as active, it is then filled with sources according to a density defined by the user. The total activity of the region is distributed among these elementary sources, with the real emission intensity modulated by the illumination.
2.2 Dust parameters
Our model does not simulate the initial acceleration phase of the
dust particles, when they are lifted from the surface and accelerated
by the gas. The model assumes the motion of the dust grains can be
decoupled from the gas, which is typically the case after a few radii
from the surface. After this limit, the acceleration of the grains can
be described by the ratio ![]() between two forces: the gravitational attraction from the Sun,
and the solar radiation pressure, the latter acting in the opposite
direction, both varying with the square of the distance to the Sun. We
assume also that the initial acceleration does not affect the expansion
direction of the dust. We will show later that this assumption is
realistic, at least in the case of comet 9P/Tempel 1.
Trajectories of the dust grains are calculated in a cometocentric frame
and then projected on the plane of sky. The orbits can be fully
constrained from a few parameters:
between two forces: the gravitational attraction from the Sun,
and the solar radiation pressure, the latter acting in the opposite
direction, both varying with the square of the distance to the Sun. We
assume also that the initial acceleration does not affect the expansion
direction of the dust. We will show later that this assumption is
realistic, at least in the case of comet 9P/Tempel 1.
Trajectories of the dust grains are calculated in a cometocentric frame
and then projected on the plane of sky. The orbits can be fully
constrained from a few parameters: ![]() ratio, initial velocity, and ejection geometry.
ratio, initial velocity, and ejection geometry.
2.2.1 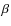 parameter
parameter
The ![]() ratio has been described by Finson & Probstein (1968) and can be written as
ratio has been described by Finson & Probstein (1968) and can be written as

where
The above formula is valid when the grains are observed at a wavelength
![]() .
This is the case in all our observations as we observe the dust structures with a R Johnson filter (visible light) and the size of the visible grains goes typically from micron to millimeter.
.
This is the case in all our observations as we observe the dust structures with a R Johnson filter (visible light) and the size of the visible grains goes typically from micron to millimeter.
The ![]() parameter has been measured for different kind of material. Examples can be found in Burns et al. (1979).
parameter has been measured for different kind of material. Examples can be found in Burns et al. (1979).
For grains bigger than 0.1 micrometers, ![]() can be approximated as
can be approximated as
where k is a constant depending on the material. For cosmically relevant material, Burns et al. (1979) showed that
2.2.2 Initial velocity
As written before, the initial velocity depends on how the grain is
dragged by the gas during the acceleration phase but also on the
radiation pressure. Fulle (1987) derived an equation for the terminal velocity (i.e. speed acquired during the acceleration phase), which can be written as

where v0 is constant for a given heliocentric distance.
This formula assumes an isotropic distribution of dust velocities in the inner coma, which might be unrealistic due to the complexity of this environment. A better model needs to consider a multi fluid approach for the gas, combined with a Monte Carlo modeling of the dust as in Crifo et al. (2005). However, the simplistic approach has been proven to be sufficient in first order approximation to simulate the dust structures in ground-based observations (e.g. Vasundhara et al. 2007).
2.2.3 Grain size distribution
The exact dust size distribution in cometary comae and jets is not
known. However, empirical model based on spacecraft observations can
give a good approximation. It is generally observed that the size
distribution follows an inverse power law defined as:
2.2.4 Ejection geometry
The emission geometry is a very important parameter for the simulation of the observed structures. Whether we have a collimated jet or an emission cone depends on many parameters like the dynamics of the gas lifting up the dust, the size of the active region, the roughness of the terrain, which are mainly unknown. However during spacecraft flybys of several comets, it has been observed that most of the dust is emitted in collimated jets (see for example 9P/Borelly, Thomas et al. 2001; or 82P/Wild 2, Sekanina et al. 2004). While it might not be true for all comets, it is good enough for the simulation of our ground-based images. Concerning the initial direction of motion, the first idea when implementing this model was to allow the emission angle to take any value pointing outside of the local surface, starting with an initial assumption of a maximum of emission in the direction orthogonal to the surface of the local facet. As we will see in the discussion of the results obtained for 9P/Tempel 1 (Sect. 3), this initial guess was enough to constrain very well the location of the active regions, supporting the idea that most of the dust particles present in the jets escape from the nucleus orthogonally to the local surface of emission. However, one has to be cautious with this hypothesis: it provided good results in the case of 9P/Tempel 1 but there is no indication that it would be the case for other cometary nuclei. Hence our model allows the testing of alternative directions of emission.
2.3 Simulation
Given these parameters, our model calculates the orbit of the dust particles, along with the orbital geometry of the comet, the Sun, and the Earth, and projects these positions into a simulated sky plane as seen by the observer on Earth. Particle positions are then converted into intensity through a simple photometric model which considers the luminosity as proportional to the illuminated surface of the grains, seen as perfect spheres. This approach is sufficient as we are mainly interested in the dynamics of the grains, but a more complex one, including Mie theory, needs to be used if we want to simulate the real photometry of the jets.
The final image is then adjusted to fit the observation
parameters (size, field of view, resolution) and convolved with a
Gaussian to simulate the point spread function of the imaging optics
used for the observations. The Gaussian is defined by
![]() ,
parameter that can be adjusted to represent different imaging instruments.
,
parameter that can be adjusted to represent different imaging instruments.
3 Application to comet 9P/Tempel 1, pre-impact period
3.1 Motivation
![\begin{figure}
\par\includegraphics[width=12cm,clip]{13418fg2.eps}\vspace{4mm}
\end{figure}](/articles/aa/full_html/2010/04/aa13418-09/Timg21.png)
|
Figure 2:
Images of the coma structures of comet 9P/Tempel 1 for two different days from Lara et al. (2006).
The left panels
show Laplace filtered images of the coma, where the filter enhances
shortscale brightness features while removing longscales variations.
The random irregular pattern seen in the background is due to the noise
structure in the original images. Labels identify the coma structures
as described in the text. The orientation is given in the lower left of
the images. Field of view is
|
| Open with DEXTER | |
The motivation behind this work was first to test the model described in Sect. 2 and see if our simulation could reproduce and predict ground-based observations of cometary dust comae, and then to compare these results with other techniques, especially information retrieved from in-situ spacecraft measurements. A good test comet for the model requires an extended sequence of ground-based observation of dust coma structures, and a shape model of the nucleus as input of the analysis. We also need to compare the parameters we retrieved for the dust and the active regions with independent published results for the same comet. Six comets have been visited by a space probe in the past, four of them had imaging data returned to Earth. Among them the best choice for our simulation was 9P/Tempel 1 because of the large amount of data available, both ground- and space-based. As we wanted to test our model we decided for a ``blind'' approach, i.e. we did not consider any information published, apart from the required input: ground-based images published and described in detail by Lara et al. (2006), rotation period estimation of 41.85 h from Belton et al. (2005), and a shape model as published by Thomas et al. (2007).
Information on the rotation axis and on the active regions was not considered, but is used in the discussion of our results.
3.2 Determination of the spin axis orientation
The first step was to estimate the orientation of the spin axis. We used a technique described by Sekanina (1987) which we had already applied to determine the spin axis of comet 73P/Schwassmann-Wachmann 3, components B & C (Vincent et al. 2010).
To summarize the process: Given images of dust coma structures, we
consider the observed patterns as produced by active dust-emitting
sources on a rotating nucleus. Single sources create emission cones but
when we observe them side-on, we detect only the borderlines of these
cones, which form straight features in the enhanced images (see Fig. 2 for example).
Following this approach, the projected position of the rotation axis falls in between the borders of the fans.
We first estimate this position from our set of observations. Then, using a trial and error approach
varying the rotation axis systematically over the ![]() sphere of the nucleus, we determine the orientation of the spin axis as
the one which provides the best fit to the estimated projected
orientation for all observing epochs.
Our simulation led us to conclude about a spin model given by a right
ascension (RA) of 293
sphere of the nucleus, we determine the orientation of the spin axis as
the one which provides the best fit to the estimated projected
orientation for all observing epochs.
Our simulation led us to conclude about a spin model given by a right
ascension (RA) of 293![]() and a declination (DEC) of 73
and a declination (DEC) of 73![]() with
with
![]() of uncertainty. This value is in very good agreement with the one retrieved by the Deep Impact team (RA = 294
of uncertainty. This value is in very good agreement with the one retrieved by the Deep Impact team (RA = 294![]() and Dec = 73
and Dec = 73![]() ,
,
![]() )
from the flyby images, see Thomas et al. (2007).
)
from the flyby images, see Thomas et al. (2007).
3.3 Modeling of the pre-perihelion activity
With the spin axis orientation determined, we ran our model to find which parameters for the dust grains and the active regions would allow us to reproduce the activity as observed by Lara et al. (2006) between January and June 2005. An example of our results is shown Fig. 2. This figure shows two different observations of comet 9P/Tempel 1, 14 May 2005 and 5 June 2005, processed with an adaptive Laplace filter, and the result of our simulation. As always when processing images, one has to be aware of the strengths and flaws of a given technique to avoid a misinterpretation of the observed features. Our usual approach to this problem is to always analyze the set of images with at least three independent methods. Here we processed the data not only with a Laplace filter but also with a rotational-shift-difference filter (the so-called Larson-Sekanina filter), and we compared the filtered images with distortions observed in the isophotes of the original exposures. The structures described in the following are clearly identified with all different techniques, therefore they cannot be interpreted as artifacts due to the processing. The images display several patterns labeled with capital letters in alphabetical order, starting from North and turning in an anti-clockwise direction. We kept the same labels of the structures as in the paper already published by Lara et al. Notice that the structure labeled B in our images is identified as dust tail signature and was thus not included in our simulations using the dust emission model.
In order to reproduce the observed features, the model requires several active regions (labeled AR1,2,... in the text) with well constrained parameters. Patterns D & E are present in the images for several months, with their bisector aligned on the spin axis. This is a clear case predicted by the theory where an emission cone is view from the side and appears as a fan, hence the jets D & E were linked to a single active region. The other patterns A, F, G, & H are more difficult to analyze, however it arises from our simulations that they must be linked to separate areas on the surface. The main reason for this is that any attempt to give a common origin to several of these jets and simulate the structures failed whatever the parameters chosen for the localization of the region or the description of the dust particles. In this respect, we do believe that all these jets have a different origin at the surface.
The most active area (AR1) is located on the southern hemisphere, at latitude
![]() and longitude
and longitude
![]() .
Notice than in all this paper, longitudes are counted positive towards the East to be consistent with Thomas et al. (2007).
The region should be extended and shows strong activity, emitting
millimeter-sized particles with a terminal velocity of 12 to
15 m s-1. The activity is constant over the
rotation cycle, with no noticeable variation of intensity between day
and night. From the orbital elements and the determination of the spin
axis, we can estimate that the subsolar position at that time remained
around latitude +15
.
Notice than in all this paper, longitudes are counted positive towards the East to be consistent with Thomas et al. (2007).
The region should be extended and shows strong activity, emitting
millimeter-sized particles with a terminal velocity of 12 to
15 m s-1. The activity is constant over the
rotation cycle, with no noticeable variation of intensity between day
and night. From the orbital elements and the determination of the spin
axis, we can estimate that the subsolar position at that time remained
around latitude +15![]() ,
which means that the southern hemisphere of the nucleus was spending
about 20 h in the night during each rotation.
Hence the activity must be driven by sublimation of a supervolatile ice
that does not require instantaneous illumination to evaporate.
In that respect CO2 ice might be a good candidate. This scenario is enforced by the results from Feaga et al. (2007) showing a strong assymetry between H2O and CO2 in the coma of 9P/Tempel 1, with the CO2 pattern matching the dust morphology more than H2O (the latter being concentrated in the sunward direction). This active region creates structures D & E in Fig. 2.
,
which means that the southern hemisphere of the nucleus was spending
about 20 h in the night during each rotation.
Hence the activity must be driven by sublimation of a supervolatile ice
that does not require instantaneous illumination to evaporate.
In that respect CO2 ice might be a good candidate. This scenario is enforced by the results from Feaga et al. (2007) showing a strong assymetry between H2O and CO2 in the coma of 9P/Tempel 1, with the CO2 pattern matching the dust morphology more than H2O (the latter being concentrated in the sunward direction). This active region creates structures D & E in Fig. 2.
The second area of the nucleus we identified as a possible source for
the dust jets is located in the equatorial region. The orientation of
the jets suggests that the activity is confined to the day side of the
nucleus. The structures produced at this latitude (F, G & H) are
oriented in sunward direction and they are straight or slightly curved
towards the tail direction. This indicates a low sensitivity of the
dust to the radiation pressure. Our simulation reproduced these jest
with particles similar to the ones observed in the southern fan
(100 ![]() m
to mm size particles with low velocity), thus confirming the initial
conclusion.
Using the shape model, we were able to estimate the coordinates of the
active regions corresponding to structures FG & H. The latitude of
m
to mm size particles with low velocity), thus confirming the initial
conclusion.
Using the shape model, we were able to estimate the coordinates of the
active regions corresponding to structures FG & H. The latitude of
![]() is very well constrained due to the favorable geometry of the
observation (nucleus seen almost side-on). Using the 3D shape model, we
could also infer the longitude of these sources. Although the
uncertainty is much larger than for the latitude, we estimate the
following positions:
is very well constrained due to the favorable geometry of the
observation (nucleus seen almost side-on). Using the 3D shape model, we
could also infer the longitude of these sources. Although the
uncertainty is much larger than for the latitude, we estimate the
following positions:
- region AR2: latitude
 ,
longitude 0
,
longitude 0 ,
creating jet F;
,
creating jet F;
- region AR3: latitude
 ,
longitude 90
,
longitude 90 ,
creating jet G;
,
creating jet G;
- region AR4: latitude +5
 ,
longitude 90
,
longitude 90 ,
creating jet H.
,
creating jet H.
The last area of activity identified (AR5) is close to the north pole
of the nucleus and is responsible for structure A in Fig. 2.
The strong counterclockwise curvature of the jet, with respect to the
other ones, implies smaller particles, more sensitive to the ![]() parameter. We estimated grain sizes smaller than 10
parameter. We estimated grain sizes smaller than 10 ![]() m and emission velocities around 30 m s-1. From the images in Lara et al. (2006) it is not possible to conclude about the diurnal profile of activity for this region.
m and emission velocities around 30 m s-1. From the images in Lara et al. (2006) it is not possible to conclude about the diurnal profile of activity for this region.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{13418fg3.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa13418-09/Timg31.png)
|
Figure 3:
Laplace filtered images showing the evolution of the dust coma
structures of 9P/Tempel 1 in the post impact period. The morphology is
fairly constant, and one can identify some of the structures observed
in the pre-impact period as for instance the northern jet (A), the dust
tail (B), and the equatorial activity (G). The southern fan does not
appear clearly in these images. The feature labeled (S) on 26 July 2005
is a background star passing through the field of view. We observed a
new jet (I) which was not detected in the pre-impact observations.
Field of view
|
| Open with DEXTER | |
Table 1: Observations Logs.
3.4 Comparison with existing results
After conducting this simulation, we compared our results with the one already published by the Deep Impact team (Farnham et al. 2007),
as obtained from the fly-by images of the spacecraft. We found a very
good agreement for all the retrieved parameters, in particular similar
values for the dust size and velocity, and for the position of the
active regions. Farnham mentioned the existence of a jet originating at
+40![]() of latitude, and observed during the approach phase of the Deep Impact
mission. This jet does not appear in our ground-based images of the
pre-impact period, probably due to a lower signal-to-noise (S/N) ratio
in the data set. As we will see in the next section, this jet is real
and was observed in an other dataset but we cannot conclude about its
existence from the images by Lara et al. (2006) only.
of latitude, and observed during the approach phase of the Deep Impact
mission. This jet does not appear in our ground-based images of the
pre-impact period, probably due to a lower signal-to-noise (S/N) ratio
in the data set. As we will see in the next section, this jet is real
and was observed in an other dataset but we cannot conclude about its
existence from the images by Lara et al. (2006) only.
4 Application to post impact images
4.1 Data acquisition and processing
After successfully retrieving information on the various active regions of comet 9P/Tempel l, from the pre-impact period, we applied our model to predict the evolution of these structures in the post-perihelion period. The data used for this study consists of broadband images, acquired in the European Southern Observatory of La Silla (Chile). The exposures were taken in service mode from 17 July to 12 August 2005 with the Wild Field Imager (WFI) on the 2.2 m MPG/ESO telescope. This instrument is a half degree camera for the visible wavelength range (see http://www.eso.org/sci/facilities/lasilla/ instruments/wfi/ for details). In order not to smear image details due to the motion of the comet, and to avoid saturation of the central coma part, exposure series ofIn the reduced images, it is usually not possible to distinguish dust structures, apart from the tail, because of their low intensity with respect to the coma background. Different enhancing techniques can be used to display inherent features. We applied two independent methods: (1) adaptive Laplace filtering as described in Boehnhardt & Birkle (1994) and references therein, and (2) Larson-Sekanina filtering (Larson & Sekanina 1984). The first filter applies a Laplacian kernel to a logarithmized image, removing all the gradual variations (linear and second order gradients) while keeping the fine variations of different scale depending on the width of the numerical filter. The second technique is a direct subtraction between the original image and a rotated/shifted version of it.
4.2 Morphology
Figure 3
presents images from the post-impact data set. As the morphology of the
dust coma was mainly constant during the whole observation period, we
describe only selected images representative for the whole data set
(see Fig. 3 and Table 1).
From the Laplace filtered images we can clearly recognize features
observed during the pre-impact period like the dust tail (B), two
equatorial jets (F, G), and the north pole structure (A). The
equatorial jet H is not detected in any of our images.
The southern fan does not appear with this processing but is observed
with the other enhancement technique. For example the comparison with
the Larson-Sekanina filter is shown Fig. 4.
It appears much weaker in August 2005 than before perihelion but we
cannot conclude whether this is due to a poor S/N ratio of the original
images or a real decrease in intensity. We notice however a strong
curvature of this fan (jets D & E) in the anti-sunward direction.
We detected a new structure (labeled I in Fig. 3) at a position angle of ![]() 340
340![]() that is present in all post impact images and that was not seen in the Lara et al. data set.
that is present in all post impact images and that was not seen in the Lara et al. data set.
![\begin{figure}
\par\includegraphics[width=18cm,clip]{13418fg4.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa13418-09/Timg35.png)
|
Figure 4: Comparison between the Laplace filtered image ( left) and the Larson-Sekanina filtered one ( middle). More structures are detected in the latter. The right image shows an overlay of our simulation on top of the Larson-Sekanina processed image. Again we find a good agreement between our model and the observation of the geometric patterns of the dust features. |
| Open with DEXTER | |
4.3 Simulation results
We applied our simulation model to this new set of images, keeping the parameters for the description of the active regions as determined from the pre-impact images. The simulated pictures match well the observations for the equatorial part (structures F & G), and our simulation reproduces the respective features created by regions AR2 and AR3 without changing any parameter.
The situation is different for the southern fan (structures D & E).
Keeping the same parameters as before we reproduce the orientation of
the fan but not the curvature.
In order to match the latter in the images, we need to introduce
smaller particles in our model (10 to 100 ![]() m).
As said before, the southern fan is more difficult to detect in our
images, and this was first interpreted as a lower S/N. However, the
simulation shows that we have smaller particles, which can also
indicate a decrease of activity in region AR1. The geometrical
conditions for the illumination of this region are almost the same as
during the pre-impact phase, which makes an explanation of this change
of activity by a sudden change of illumination of the southern
hemisphere unlikely.
m).
As said before, the southern fan is more difficult to detect in our
images, and this was first interpreted as a lower S/N. However, the
simulation shows that we have smaller particles, which can also
indicate a decrease of activity in region AR1. The geometrical
conditions for the illumination of this region are almost the same as
during the pre-impact phase, which makes an explanation of this change
of activity by a sudden change of illumination of the southern
hemisphere unlikely.
The northern jet originating from region AR5 looks also similar to the one observed in June 2005. However, in order to fully reproduce the observed feature, we need to change the diurnal profile of activity and allow the region to emit particles during the night, in a similar way as it was observed for the southern region.
The jet at a position angle of +340![]() (labeled I) could be reproduced easily by an active region AR6 at +45
(labeled I) could be reproduced easily by an active region AR6 at +45![]() of latitude, emitting millimeter size particles with low velocity (12 m s-1)
during day time. This structure could relate to the jet observed by the
Deep Impact team already during the pre-impact phase, but not seen in
the images from Lara et al. (2006). Our
model could not constrain the longitude for this region, but images of
the surface show a smooth patch in the northern hemisphere around
latitude 45
of latitude, emitting millimeter size particles with low velocity (12 m s-1)
during day time. This structure could relate to the jet observed by the
Deep Impact team already during the pre-impact phase, but not seen in
the images from Lara et al. (2006). Our
model could not constrain the longitude for this region, but images of
the surface show a smooth patch in the northern hemisphere around
latitude 45![]() and longitude 270
and longitude 270![]() similar to the one observed in the southern hemisphere. It is not clear
if those patches are the source of activity, or a product of it (i.e. a
redeposit of material lifted by the sublimation) but the southern fan
is clearly connected to the observed activity in this hemisphere
(region AR1) and it might be similar for the northern patch.
similar to the one observed in the southern hemisphere. It is not clear
if those patches are the source of activity, or a product of it (i.e. a
redeposit of material lifted by the sublimation) but the southern fan
is clearly connected to the observed activity in this hemisphere
(region AR1) and it might be similar for the northern patch.
5 Conclusions and outlook
The model, albeit simple, allows us to retrieve important parameters on active regions of comet 9P/Tempel 1, summarized here.
- 1.
- Spin axis orientation determined from the ground-based observation: RA = 293
 and a Dec = 73
and a Dec = 73 (
(
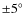 ), unchanged between January and August 2005 and in good agreement with flyby imaging results.
), unchanged between January and August 2005 and in good agreement with flyby imaging results.
- 2.
- Identification of 6 active regions on the nucleus:
- (a)
- a southern region AR1 at
 latitude and
latitude and
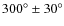 longitude,
close to a smooth area on the nucleus. Its activity does not change
with day/night time, indicating a different material than H2O for the sublimation. This region gives rise which gives rise to the fan (D, E) in the observed images;
longitude,
close to a smooth area on the nucleus. Its activity does not change
with day/night time, indicating a different material than H2O for the sublimation. This region gives rise which gives rise to the fan (D, E) in the observed images;
- (b)
- 3 strong equatorial regions are identified in the pre-perihelion period emitting millimeter size particles at low velocity (
 12 m s-1) during day time. These areas are located at the following coordinates (latitude, longitude): AR2 (
12 m s-1) during day time. These areas are located at the following coordinates (latitude, longitude): AR2 ( ,
0
,
0 ), AR3 (
), AR3 ( ,
90
,
90 ), AR4 (0
), AR4 (0 ,
90
,
90 ). The latitude values have an uncertainty of
). The latitude values have an uncertainty of
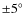 ,
longitudes are only roughly estimated. They are responsible for the jets (F, G, H) in the pre-perihelion exposures;
,
longitudes are only roughly estimated. They are responsible for the jets (F, G, H) in the pre-perihelion exposures;
- (c)
- a region close to the north pole (AR5), emitting particles smaller than 10
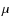 m, also active during night time. This area produces the jet (A);
m, also active during night time. This area produces the jet (A);
- (d)
- an active region in the northern hemisphere (AR6) located at latitude

 ,
creating the jet (I) in the post-impact images.
,
creating the jet (I) in the post-impact images.
- 3.
- In comparison with the pre-impact observations, we noticed a
decrease of activity in the southern hemisphere, which can not be
explained by a difference in illumination, the conditions being fairly
the same.
Table 2: Local coordinates of the active regions and associated jets.
Our results obtained from modelization of ground-based observations agree well with those from in-situ measurement and the model is able to make realistic predictions for the evolution of the structures. This can be of interest in the planning of future missions like Rosetta for which any information on the position of active regions must be known long enough in advance in order to adjust the trajectory of the probe and avoid any hazard. An other outlook of this study would be to combine the simulations with a good photometric model of the coma in order to estimate not only the dynamical parameters of the dust but also the flux and photometry of the jets.
Acknowledgements
We would like to thank Peter Thomas and collaborators for providing us the shape model of 9P/Tempel 1. We also wish to thank the observers at the Calar Alto and La Silla observatories who have performed the service mode observations used in our analysis. Without their dedication and care the images would not be available. It should be noted that the determination of the orientation of the rotation axis of 9P/Tempel 1 using ground-based observations has benefit from the relatively long time interval and from the regular sampling of the telescope imaging the comet. In particular, this time period had covered a significant part of the perihelion arc of the orbit, when the activity is the highest and the changes in viewing geometry of the comet are the largest.
L. M. Lara acknowledges the Ministry of Science and Innovation in Spain for having funded this work through project ESP2006-02934.
References
- Belton, M. J. S., Mueller, B. E. A., Julian, W. H., & Anderson, A. J. 1991, Icarus, 93, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Belton, M. J. S., Meech, K. J., A'Hearn, M. F., et al. 2005, Space Sci. Rev., 117, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Boehnhardt, H., & Birkle, K. 1994, A&AS, 107, 101 [NASA ADS] [Google Scholar]
- Burns, J. A., Lamy, P. L., & Soter, S. 1979, Icarus, 40, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Crifo, J.-F., Loukianov, G. A., Rodionov, A. V., & Zakharov, V. V. 2005, Icarus, 176, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Farnham, T. L., Wellnitz, D. D., Hampton, D. L., et al. 2007, Icarus, 187, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Feaga, L. M., A'Hearn, M. F., Sunshine, J. M., Groussin, O., & Farnham, T. L. 2007, Icarus, 190, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Finson, M. L., & Probstein, R. F. 1968, ApJ, 154, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Fulle, M. 1987, A&A, 171, 327 [NASA ADS] [Google Scholar]
- Fulle, M. 1999, Adv. Sp. Res., 24, 1087 [Google Scholar]
- Keller, H., Knollenberg, J., & Markiewicz, W. 1994, Planet. Space Sci., 42, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Lara, L. M., Böhnhardt, H., Gredel, R., et al. 2006, A&A, 465, 1151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Larson, S. M., & Sekanina, Z. 1984, AJ, 89, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Markovich, M. Z., & Markovich, N. M. 2001, Solar System Research, 35, 320 [NASA ADS] [CrossRef] [Google Scholar]
- Min, M., Hovenier, J. W., de Koter, A., Waters, L. B. F. M., & Dominik, C. 2005, Icarus, 179, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Sekanina, Z. 1987, ESA SP-278, 315 [Google Scholar]
- Sekanina, Z., Brownlee, D. E., Economou, T. E., Tuzzolino, A. J., & Green, S. F. 2004, Science, 304, 1769 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Thomas, N., A'Hearn, M. F., Boice, D. C., et al. 2001, in BAAS, 33, 1074 [Google Scholar]
- Thomas, P. C., Veverka, J., Belton, M. J. S., et al. 2007, Icarus, 187, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Vasundhara, R. 2002, A&A, 382, 342 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vasundhara, R., Chakraborty, P., Muneer, S., Masi, G., & Rondi, S. 2007, AJ, 133, 612 [NASA ADS] [CrossRef] [Google Scholar]
- Vincent, J., Böhnhardt, H., Bertini, I., et al. 2010, Earth Moon and Planets, 106, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Yelle, R., Soderblom, L., & Jokipii, J. 2004, Icarus, 167, 30 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Table 1: Observations Logs.
Table 2: Local coordinates of the active regions and associated jets.
All Figures
| |
Figure 1: 3D shape model of the nucleus of comet 9P/Tempel 1, adapted from Thomas et al. (2007) showing the illumination with respect to the geographic features on the surface. The red line represents the spin axis and points towards the positive pole. The yellow line points towards the Sun. The blue patch indicates the localization of an active region. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{13418fg2.eps}\vspace{4mm}
\end{figure}](/articles/aa/full_html/2010/04/aa13418-09/Timg21.png)
|
Figure 2:
Images of the coma structures of comet 9P/Tempel 1 for two different days from Lara et al. (2006).
The left panels
show Laplace filtered images of the coma, where the filter enhances
shortscale brightness features while removing longscales variations.
The random irregular pattern seen in the background is due to the noise
structure in the original images. Labels identify the coma structures
as described in the text. The orientation is given in the lower left of
the images. Field of view is
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{13418fg3.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa13418-09/Timg31.png)
|
Figure 3:
Laplace filtered images showing the evolution of the dust coma
structures of 9P/Tempel 1 in the post impact period. The morphology is
fairly constant, and one can identify some of the structures observed
in the pre-impact period as for instance the northern jet (A), the dust
tail (B), and the equatorial activity (G). The southern fan does not
appear clearly in these images. The feature labeled (S) on 26 July 2005
is a background star passing through the field of view. We observed a
new jet (I) which was not detected in the pre-impact observations.
Field of view
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{13418fg4.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa13418-09/Timg35.png)
|
Figure 4: Comparison between the Laplace filtered image ( left) and the Larson-Sekanina filtered one ( middle). More structures are detected in the latter. The right image shows an overlay of our simulation on top of the Larson-Sekanina processed image. Again we find a good agreement between our model and the observation of the geometric patterns of the dust features. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.