EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 512 (March-April 2010) A&A, 512 (2010) A37 Full HTML
Free Access
Issue
A&A
Volume 512, March-April 2010
Article Number A37
Number of page(s) 7
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/200913368
Published online 25 March 2010
A&A 512, A37 (2010)

On the kinematic age of brown dwarfs: radial velocities and space motions of 43 nearby L dwarfs[*]

A. Seifahrt1,2 - A. Reiners1 - K. A. M. Almaghrbi1 - G. Basri3

1 - Universität Göttingen, Institut für Astrophysik, Friedrich-Hund-Platz 1, 37077 Göttingen, Germany
2 - Physics Department, University of California, Davis, CA 95616, USA
3 - Astronomy Department, University of California, Berkeley, CA 94720, USA

Received 29 September 2009 / Accepted 23 November 2009

Abstract
We present radial velocity measurements of a sample of L0-L8 dwarfs observed with VLT/UVES and Keck/HIRES. We combine these measurements with distance and proper motion from the literature to determine space motions for 43 of our targets. We identify nine candidate members of young moving groups, which have ages of 50-600 Myr according to their space motion. From the total velocity dispersion of the 43 L dwarfs, we calculate a kinematic age of $\sim$5 Gyr for our sample. This age is significantly higher than the $\sim$3 Gyr age known for late M dwarfs in the solar neighbourhood. We find that the distributions of the U and V velocity components of our sample are clearly non-Gaussian, placing the age estimate inferred from the full space motion vector into question. The W-component exhibits a distribution more consistent with a normal distribution, and from W alone we derive an age of $\sim$3 Gyr, which is the same age found for late-M dwarf samples. Our brightness-limited sample is probably contaminated by a number of outliers that predominantly bias the U and V velocity components. The origin of the outliers remain unclear, but we suggest that these brown dwarfs may have gained their high velocities by means of ejection from multiple systems during their formation.

Key words: stars: low-mass - brown dwarfs - stars: kinematics and dynamics - techniques: radial velocities

1 Introduction

Early- and mid-L dwarfs encompass a mass range that includes very low mass stars as well as more massive brown dwarfs around the hydrogen-burning minimum mass ( ${\it HBMM}\approx0.07$- $0.08~M_\odot$, Chabrier & Baraffe 1997). The kinematics of these stars, especially within the solar neighbourhood, are important because the intrinsic velocity dispersion of the stars can be used to determine their age (Fuchs et al. 2001; Wielen 1977). Brown dwarfs may then serve in turn as Galactic chronometers (Burgasser 2009), given that they constantly cool over time and never reach a stable state on the main sequence.

While an age of $\sim$3 Gyr for the nearby late-M dwarfs is now well established (Reiners & Basri 2009; Reid et al. 2002a), kinematic ages of L and T dwarfs remain preliminary. Zapatero Osorio et al. (2007) derive an age $\sim$1 Gyr for 21 L and T dwarfs based on space motions of these objects, while Faherty et al. (2009) derive an age of 3-6 Gyr for a large sample of L and T dwarfs, based on their distance and proper motion. The discrepancy between these results is probably due to differences between the age computations but may also be attributed to the small number of objects with measured radial velocities, and thus, 3D space motions.

Kinematic studies of brown dwarfs have been predominantly based on proper motion measurements (see, e.g., Casewell et al. 2008; Jameson et al. 2008; Faherty et al. 2009; Schmidt et al. 2007). Absolute radial velocities of brown dwarfs have been obtained for small samples by, e.g., Basri et al. (2000), Bailer-Jones (2004), Blake et al. (2007), or Zapatero Osorio et al. (2007). In this paper, we measure radial velocities and provide space motions for 43 L0-L8 dwarfs, thus for a much larger sample than obtained before.

2 Sample and analysis

Reiners & Basri (2008, hereafter RB08) present high resolution ( $R \ga 30~000$) optical spectra of 45 L dwarfs[*] obtained with VLT/UVES and Keck/HIRES. They measure rotational velocities and chromospheric activity to investigate rotational braking in M and L dwarfs. The sample selection and observations are presented in Sect. 2 of RB08, the targets being essentially the brightest L dwarfs distributed over the whole sky (Martín et al. 1999; Cruz et al. 2003; Reid et al. 2008; Kirkpatrick et al. 2000; Kendall et al. 2004). No preselection of any other parameter was made.

We use Gl 406 as our primary radial velocity standard (M6V, $v_{\rm rad} = 19\pm1$ km s-1, Mohanty & Basri 2003) and employ a cross-correlation technique to measure the radial velocity of each star for various spectral orders (see, e.g., Mohanty & Basri 2003; and Basri et al. 2000, for a detailed description of the method). We focused on the resonance lines of Cs I and Rb I as well as the prominent features of TiO, VO and, most importantly, FeH. Telluric absorption lines of the O2 A-band as well as strong H2O lines around $\lambda\lambda$ 930-960 nm were used to correct for shifts in the wavelength solution of each spectrum with respect to our radial velocity standard. We followed the conservative approach of adopting the standard deviation of the radial velocities obtained in different spectral orders as the intrinsic error of our final radial velocities. The intrinsic uncertainties range from 0.2 km s-1 for the earliest L dwarfs up to 4 km s-1 for the latest and most rapidly rotating targets. The final uncertainty in most cases is dominated by the uncertainty in the absolute radial velocity of Gl406, which we added in quadrature to the intrinsic uncertainty of each target. All radial velocities were finally corrected for barycentric motion.

\begin{figure} \par\includegraphics[width=9cm,clip]{13368f1.eps} \end{figure} Figure 1:

Example of the distribution of radial velocities obtained in different spectral orders from stellar lines ( left) and telluric lines ( right) in the spectrum of 2M1645-1319 (L1.5V). See text for details.

Open with DEXTER

As an example, we show in Fig. 1 the results obtained for the L1.5 dwarf 2M1645-1319. The radial velocities obtained from stellar lines in 11 different orders show a nearly Gaussian distribution with a mean of 26.6 km s-1and a standard deviation of 0.21 km s-1. The telluric lines in 4 different orders show an offset of $0.2\pm0.16$ km s-1. Hence, we determined a radial velocity of $26.4\pm1.0$ km s-1.

For all L dwarfs later than L2, we also used the spectra of 2MASS1645-1319 (L1.5) and 2MASS1045-0149 (L1.0) as secondary radial velocity standards. Absolute radial velocities for both objects were determined against Gl406 with a precision of $\sim$0.3 km s-1. Both targets are relatively slow rotators ( $v\sin{i}=9$ km s-1 and <3 km s-1, respectively, RB08) and their respective VLT/UVES and Keck/HIRES spectra have a high signal-to-noise ratio, making them well suited as cross-correlation templates. Radial velocities of all targets measured relative to Gl406 and our L dwarf templates are always identical, but the latter correlation produced more robust results with smaller uncertainties since the L dwarf templates are a closer match to the spectral features of the targets. Thus, we adopted the radial velocities obtained from the cross-correlation with our secondary velocity standards for all targets later than L2 as our final results.

3 Results


3.1 Radial velocities

We present the final results from our radial velocity measurements in Table 2. Twelve targets were observed with VLT/UVES and Keck/HIRES at different epochs. In all cases, the radial velocities obtained from both runs were fully consistent within their individual uncertainties, showing no sign of significant radial velocity variability on a km s-1 level. We also compared our results to radial velocities reported in the literature (Zapatero Osorio et al. 2007; Blake et al. 2007; Basri et al. 2000; Bailer-Jones 2004). We found good agreement with our values in 16 cases. However, we found two cases, namely 2M0255-47 and 2M1305-25, where our radial velocities are inconsistent with other measurements. We discuss these objects in Sect. 3.5.

3.2 Space motions

To calculate the space motions of our sample, we combine our radial velocity measurements with distance and proper motion data collected from the literature, mainly from the extensive database of Faherty et al. (2009). Distances are based mostly on spectrophotometric estimates and have a typical uncertainty of 1 pc. A few L dwarfs in our sample have measured trigonometric parallaxes, which notably reduces their distance errors. We compared the reported proper motions and distances in Faherty et al. (2009) with other sources and used the values with the smallest uncertainties. Details are provided in Table 2.

Space motions were computed using the IDL routine gal_uvw[*]. All space motions are relative to the sun. We adopt a sign convention for U that is positive towards the Galactic Center. We determine errors in distance, proper motion, and radial velocity in a Monte Carlo fashion to compute error estimates in U, V, and W. In this computation, we derive space motions for all possible combinations of input parameters and their $1\sigma$uncertainties. We then calculate the standard deviation in U, V, and W for each target from this distribution and adopt these values as the $1\sigma$ uncertainties in U, V, and W. The calculated space motions and their respective errors are given in Table 2 along with the distance and proper motion data obtained from the literature.

\begin{figure} \par\includegraphics[width=7.8cm,clip]{13368f2a.eps}\hspace*{2mm} \includegraphics[width=7.8cm,clip]{13368f2b.eps}\vspace*{1mm} \end{figure} Figure 2:

Space velocities in the U-V ( left) and W-V ( right) plane. The velocity ellipsoids for the young disk as well for some young moving groups are shown. Moving groups considered in the analysis but without members in our sample are not shown for clarity. Objects in colour are candidate members of the respective moving groups, as indicated in Table 2.

Open with DEXTER

3.3 Membership in young moving groups

Young moving groups are associations of coeval and comoving stars. Members of moving groups can be identified either on the basis of proper motion and position on the sky, using the moving cluster method (see, e.g., Bannister & Jameson 2007) or by comparing the 3D space motions of individual objects with the mean space motion of the moving group. We found members of four young moving groups (MG), namely of the Hyades, the Pleiades MG, the AB Dor MG, and the UMa MG, with ages ranging from 50-600 Myr. All these moving groups are close-by and located in or near the velocity ellipsoid of the young (thin) disk (-50<U<+20 km s-1, -30<V<0 km s-1, and -25<W<+10 km s-1; see, e.g., Leggett 1992, and references therein). No members were found for other young and close moving groups considered in our analysis, such as the TW Hydrae Association, the $\beta$ Pictoris MG, and the Tucana/Horologium Association (see, e.g., Zuckerman & Song 2004). While their UVW velocity ellipsoids are close to those of the Pleiades MG and the AB Dor MG, we excluded memberships based on distance or position on the sky in all cases where confusion in the UVW space limited our ability to assign memberships based on space motions only.

The space motion of our targets are shown in Fig. 2. We overplot the velocity ellipsoids of the young moving groups in the same figure, adopting a typical dispersion of 10 km s-1 for the Hyades and 7 km s-1 for the Pleiades, AB Dor, and UMa in accordance with Chen et al. (1997) and Chereul et al. (1999). We compare the computed space motion of our targets to the typical space motion of both the young disk and the young moving groups listed in Zuckerman & Song (2004). We found a total of 11 objects that belong to the galactic young disk population (see Table 2) and another 9 objects that belong to the young moving groups (see Table 1). Comments on individual targets are given in Sect. 3.5.

We note that only five out of 43 targets ($\sim$12%) are candidate members of the Hyades. This is in notable contrast to the $\sim$40% (8 out of 21 targets) of L and T dwarfs reported by Zapatero Osorio et al. (2007) that are within or close to the 2$\sigma $ ellipsoid of the Hyades. While this membership criterion is weaker than that applied by ourselves, the space motion of our sample have a much wider dispersion in UVW than the sample of Zapatero Osorio et al. (2007) and significantly fewer objects fall in or near the velocity ellipsoid of the Hyades in our case.

Table 1:   Candidate members of young moving groups based on our UVW analysis.

Table 2:   Radial velocities and space motions of our targets. Data on distance and proper motions are obtained from the literature.

3.4 Kinematic age of the sample

3.4.1 General considerations

The computation of kinematic ages is based on the dispersion of true space motions and requires a complete set of 3D velocity information. The translation of the total velocity dispersion ( $\sigma_{\rm tot}$) to tangential velocities by means of $\sigma_{\rm tot}=(3/2)^{1/2}\sigma_{\rm tan}$ assumes that the dispersions in $v_{\rm tan}$ are spread equally between UVW. Even for a large sample of objects, this assumption might introduce a bias in the age determination from tangential velocities alone, and radial velocity measurements are needed to complete the full set of velocity vectors.

The velocity dispersion of a statistically significant sample of stars allows an estimate of the age of the sample, given the dynamical evolution of the Galaxy (see, e.g., Wielen 1977; or Fuchs et al. 2001). Examples of age estimations for samples including L dwarfs are given in Schmidt et al. (2007), Zapatero Osorio et al. (2007), and Faherty et al. (2009). While the results of Schmidt et al. (2007) and Faherty et al. (2009) are based on large samples of tangential velocities only, Zapatero Osorio et al. (2007) present radial velocities and thus true space motions of 21 L and T dwarfs. We revisit the population of early- to mid-L dwarfs and estimate its age based on the total velocity dispersion of the space motions in our larger sample.

To compute the age of a sample of stars based on the work of Wielen (1977), one has to calculate the velocity dispersion in U, V, and W according to Eqs. (1)-(3) in Wielen (1977), i.e., one must apply a weight of |W| to all data points when calculating the dispersions in each dimension. The weights account for the fact that we are limited to objects within a small volume close to the midplane of the Galactic disk, and enable us to infer ages from the kinematical heating of the whole disk.

We briefly summarise the results from three papers dealing with the kinematic age of low-mass objects. Schmidt et al. (2007) infer an age estimate of 3.1 Gyr for their sample of M 7-L8 L dwarfs, which agrees with the value reported by Faherty et al. (2009) and appears consistent with results for late-M samples (Reiners & Basri 2009; Reid et al. 2002a). On the other hand, Zapatero Osorio et al. (2007) report an age of only $\sim$1 Gyr for their sample of L and T dwarfs. We note that an important difference with respect to our work is that Schmidt et al. (2007), Zapatero Osorio et al. (2007), and Faherty et al. (2009) calculate the total velocity dispersion as the dispersion of $v_{\rm tot}$ instead of $\sigma_{\rm tot} = \left(\sigma_U^2+\sigma_V^2+\sigma_W^2\right)^{1/2}$, which may underestimate the dispersion and thus the age. Unfortunately, an error introduced in the formula computing age from velocity spread had the effect of almost eliminating this offset, so that in two of the papers, an age of 3 Gyr is computed[*]. A more detailed discussion of the computations of kinematic age by Schmidt et al. (2007), Zapatero Osorio et al. (2007), and Faherty et al. (2009) is given in Reiners & Basri (2009).

We reanalyse the space motions of the sample of 21 brown dwarfs of spectral type L4V-T8V of Zapatero Osorio et al. (2007) and calculate |W|-weighted velocity dispersions of $\left(\sigma_U,\sigma_V,\sigma_W\right) = (35.0,15.1,15.3)$ km s-1 from the values given in Tables 3 and 4 of their paper. The |W|-weighted total velocity dispersion is $\sigma_{\rm tot}=41.1$ km s-1. This dispersion is indicative of an age of $\sim$3.0 Gyr, which is in good agreement with ages derived for late-M dwarfs. Reid et al. (2002a) infer an age of 3 Gyr from the velocity distribution of a sample of 31 M 7.5-M 9 dwarfs, and Reiners & Basri (2009) find the same age for a volume-limited sample of 63 M 7.5-M 9 dwarfs in the solar neighbourhood.

3.4.2 Kinematic age of our sample

We now turn to our new sample of L dwarfs; we find that the velocity dispersion of our 43 targets is $\left(\sigma_U,\sigma_V,\sigma_W\right) = (33.8,28.0,16.3)$ km s-1 and calculate a total velocity dispersion of $\sigma_{\rm tot} = 46.8$ km s-1. Our |W|-weighted velocity dispersions are $\left(\sigma_U,\sigma_V,\sigma_W\right) = (39.8,29.7,17.4)$ km s-1 and the |W|-weighted total velocity dispersion is $\sigma_{\rm tot}=52.7$ km s-1. From this value and Eq. (16) of Wielen (1977), we derive an age of $\sim$5.1 Gyr for our sample.

Our result of $\sim$5.1 Gyr is much higher than the $\sim$3 Gyr we derived for the 21 L and T dwarfs in the sample of Zapatero Osorio et al. (2007). This value also seems counterintuitive compared to the age of $\sim$3 Gyr for late-M dwarfs. If anything, one would expect a sample of L0-L8 dwarfs to be younger than a sample of M 7.5-M 9 dwarfs: the hydrogen-burning minimum mass (HBMM) divides late-type objects into low mass stars and brown dwarfs. Comparing the effective temperatures of the lowest mass stars at 1-10 Gyr given in Chabrier & Baraffe (1997) with the temperature scale of Vrba et al. (2004) for L and T dwarfs, this boundary occurs at spectral type L1-L2. Brown dwarfs below the HBMM cool over time and move to much later spectral types than early-L. This causes a depletion of old brown dwarfs with masses just below the HBMM in a sample of early- to mid-L dwarfs (see Burgasser 2004). Given this depletion of old brown dwarfs with spectral types of early- to mid-L, the average age of a sample of L0-L8 dwarfs as presented here might be younger, not older, than a sample of late-M dwarfs.

Since we can expect this to affect early-L dwarfs close to the HBMM differently from the mid to late-L dwarfs, we divided our sample in half and computed the velocity dispersion and age for objects for spectral types L0V-L1.5V and L2V-L8V separately. We found no statistically significant difference between the dispersions and ages of these two groups, nor did we notice any velocity outliers related to only one of the groups. This is consistent with a similar analysis by Schmidt et al. (2007), who analyse the tangential velocity of a sample of M 7-L8 dwarfs and find no significant differences in the velocity dispersion and number of outliers between subsamples of M 7V-L2V and L3V-L8V.

\begin{figure} \par\includegraphics[width=15.7cm,clip]{13368f3.eps} \end{figure} Figure 3:

Top row: histograms of the space motion components in U, V, and W ( from left to right). Bottom row: probability plots for in U, V, and W ( from left to right). Data are shown with their uncertainties as error bars. The dashed line marks the 1.5$\sigma $ cutoff for the fit shown as a solid red line. The slope of the linear fit is the $\sigma $ of the closest matching Gaussian distribution.

Open with DEXTER

3.4.3 Potential explanations of the old age

We can speculate about the reason for this result:

(1)
The velocity dispersion of our sample might not allow us to determine an age of our sample because of the non-Gaussianity of the distribution. While a dispersion can be formally obtained for any distribution of velocities, the dispersion can only be used as an age indicator if the distribution is normal. We show the distributions of U, V, and W velocities in our sample in the top row of Fig. 3. In the bottom row of the same figure, we show probability plots (see, e.g., Reid et al. 2002b; Lutz & Upgren 1980) to help assess how closely a single Gaussian distribution fits our data. As can be seen in the plots, a straight line, corresponding to a single Gaussian distribution, is only marginally consistent with our data. The closest fit is obtained for the distribution of the W component, while the U and V components show notable deviations from a Gaussian distribution. 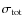Using our measured velocity dispersion $\sigma_W$ and the relation between $\sigma_W$ and $\sigma_{\rm tot}$ given in Wielen (1977), we compute an age of 3.2 Gyr from $\sigma_W$ alone, which is indeed consistent with the age of late-M dwarf samples.

The non-Gaussian distribution of the space motion is probably not due to the limited size of our sample. Reiners & Basri (2009) show probability plots for their sample of 63 late-M dwarfs, which are very well reproduced by a single Gaussian distribution. Our sample is only $\sim$30% smaller but exhibits strong deviations from a Gaussian distribution. The particular choice of the targets for the sample might instead produce a bias. Since our sample comprises the brightest objects per spectral bin, the sample should be biased towards younger objects. This is, however, not what we found. 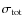From $\sigma_{\rm tot}$, the sample appears much older. 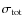On the other hand, the derived age from $\sigma_W$ alone is substantially younger than the one inferred from $\sigma_{\rm tot}$. In fact, the 3 Gyr derived from $\sigma_W$ is similar to the age of the late-M samples, which may be expected to be of comparable age. Because the dispersions in U and V do not follow a Gaussian distribution while the one in W does, one might argue that the age from W alone is a more reliable estimate of the true age of our sample. Unfortunately, at this point we have no explanation of why the distributions in U and V differ from the one in W.

(2)
The lowest mass stars and brown dwarfs might have a different initial velocity dispersion at the time of formation from higher mass stars (v0=10 km s-1 in Wielen 1977). Bihain et al. (2006) find that the velocity dispersion of the brown dwarf members in the Pleiades is about four times the dispersion of solar-type members of the cluster. A higher v0 would naturally lead to a different velocity dispersion as a function of time without invoking a different feedback by the lowest mass stars and brown dwarfs on the Galactic potential. This effect, however, should have identical influences on U, V, and W. We see no reason why only U and V should be affected by such a mechanism.

(3)
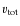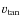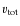Individual kinematical outliers can significantly bias the velocity dispersions of small samples. This effect would be enhanced by the |W|-weighting, as discussed in Reid et al. (2002b). However, we find no clear correlation of |W| with either $v_{\rm tot}$ or $v_{\rm tan}$ in our sample, and the removal of five objects with the highest $v_{\rm tot}$ only marginally lowers the age of the sample. 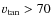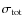On the other hand, the removal of six objects with the highest tangential velocity ( $v_{\rm tan} > 70$ km s-1) lowers the mean age of the sample to 3.0 Gyr, as computed from $\sigma_{\rm tot}$. This effect may be expected but a removal of those objects can only be justified if the distribution of tangential velocities identifies them as clear outliers. This is not evident for our sample. We note that the error in the spectrophotometric distances of some targets might be much larger than the 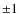$\pm1$ pc given in Faherty et al. (2009), which could contribute to a few moderate 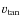$v_{\rm tan}$ outliers. In any case, it remains true that even 43 objects must be considered too small a sample when robustness to kinematic outliers is important, especially when the sample is not volume-limited and prone to selection effects.
In summary, an age of $\sim$3 Gyr for our sample seems likely given the non-Gaussian distribution of the U and V velocities and the age determined from $\sigma_W$ alone. Furthermore, that the removal of the most significant outliers in the distribution of tangential velocities reduces the age of the sample to a similar value may indicate that a handful of fast moving outliers are contained in the sample. These outliers may have been accelerated during a very early phase of their evolution, perhaps by ejection from multiple systems.

3.5 Notes on individual objects

  • 2MASS 0036+18 and 2MASS 0825+21 are both listed in Bannister & Jameson (2007) as belonging to the Hyades Moving Group based on the moving cluster method. We are unable to confirm this finding. Although both objects belong to the young disk population, their space motions are inconsistent with the space vector of the Hyades in V and W (2MASS 0036+18) and U and W (2MASS 0825+21), respectively.

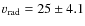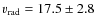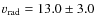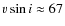  • 2MASS 0255-47: we report a radial velocity for this object of $v_{\rm rad}=25\pm4.1$ km s-1, which is inconsistent with $v_{\rm rad}=17.5\pm2.8$ km s-1 reported in Zapatero Osorio et al. (2007), and $v_{\rm rad}=13.0\pm3.0$ km s-1 in Basri et al. (2000). Given the late spectral type, ranging from L6 to L8, and the high rotational velocity of the system ( $v\sin{i}\approx67$ km s-1, RB08) the uncertainties in all the reported radial velocity values - including ours - might be underestimated. Nevertheless, we note a slight trend with time in the radial velocity that should be verified with additional observations.

  • 2MASS 1045-01 and 2MASS 1047-18: Jameson et al. (2008) list both objects as probable Hyades members, based on new proper motion measurements. We can confirm their membership based on the full space motions of both objects.

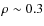
  • 2MASS 1305-25: this object, also known as Kelu 1, is a tight binary ( $\rho\sim0.3$ $^{\prime\prime}$, Liu & Leggett 2005) consisting of a L1.5-L3 and a L3-L4.5 component. Its orbit is highly eccentric and the orbital period is estimated to be $\sim$38 yrs (Stumpf et al. 2008). Using the orbital elements of Stumpf et al. (2008), we estimate that our radial velocity measurement might be affected by the orbital motion of the binary at a level of a few km s-1 depending on the fractional light contribution from each component in our optical spectra. 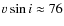Because of the high rotational velocity of the components in the system ( $v\sin{i}\approx76$ km s-1, RB08), we are unable to identify the individual components in the spectrum. We note that Basri et al. 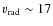(2000) report a radial velocity of $v_{\rm rad}\sim17$ km s-1 measured in June 1997. 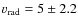This value differs significantly from the $v_{\rm rad}=5\pm2.2$ km s-1 that we measure in our spectrum from May 2006, although the difference seems too large to be explained by the orbital motion only.

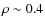
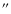  • 2MASS 1441-09: Bouy et al. (2003) found this object to be a close binary ( $\rho\sim0.4$ $^{\prime\prime}$) composed of two L1 dwarfs. Bouy et al. (2008) present follow-up astrometric observations and estimate the orbital period to be 120-230 yr. This period is too long and the brightness difference in the two components too small to bias our radial velocity measurement in any significant way. Seifahrt et al. (2005) demonstrate that this L dwarf binary forms a common proper motion pair with the M4.5V star G124-62. The radial velocity of G124-62 reported by the same authors is $v_{\rm rad}=-29.3$ km s-1, which is in close agreement with our radial velocity for the L dwarf binary. Seifahrt et al. (2005) argue that the system is a probable member of the Hyades supercluster, which we confirm with improved proper motion for the system.

  • 2MASS 1854+84: this object has no published proper motion and distance. Hence, we have to exclude it from our analysis of space motions, reducing the original sample size to 43 objects. We obtain a radial velocity of 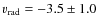$v_{\rm rad}=-3.5\pm1.0$ km s-1 for this target.

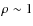
  • 2MASS 2200-30: Burgasser & McElwain (2006) resolve this target into a close binary (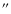$\rho\sim1$ $^{\prime\prime}$) with spectral types of M9V+L1V and estimate the orbital period to be 750-1000 yrs. Hence, our radial velocity measurement should be unaffected by the binarity, given the long period and similar brightness of both components.

4 Summary

We have measured the radial velocities of 44 L0-L8 dwarfs in the solar neighbourhood from high resolution optical VLT/UVES and Keck/HIRES spectra. We combined these measurements with distance and proper motion data to compute space motions for 43 of our targets. For one target (2M1854+84), no proper motion and distance was available in the literature and we had to exclude the target from the sample. We formally derived an age of 5.1 Gyr from the |W|-weighted total velocity dispersion of the sample and the age-velocity relation of Wielen (1977). However, the space motion components U and V of our sample are not normally distributed, compromising the age computation from $\sigma_{\rm tot}$. We found that the distribution in W is, however, quite consistent with a Gaussian shape. From W alone, we compute an age of $\sim$3 Gyr.

We note that the formally derived age of 5.1 Gyr from $\sigma_{\rm tot}$for the whole sample is in disagreement with the mean age of the lowest mass stars in the solar neighbourhood ($\sim$3 Gyr, Reiners & Basri 2009; Reid et al. 2002a) and the expectation that early- to mid-L dwarfs should be younger than the lowest mass stars of spectral type M7.5-M9. We speculate that either the initial velocity dispersion of brown dwarfs is notably different from that of solar-type and lower-mass stars, or that our particular sample is biased towards older and/or kinematically peculiar objects. The latter seems the most likely explanation since a few high-velocity objects could bias our statistics. Such a bias would be enhanced by the |W|-weighting of the dispersions when calculating $\sigma_{\rm tot}$ and thus the mean age of our sample.

The most likely age of nearby early- to mid-L type dwarfs is of the order of 3 Gyr, and we have found no evidence of an age lower than this. However, a statistically clearly defined, and perhaps larger sample of L and T dwarfs with accurate radial velocities would be necessary to robustly determine the mean age of brown dwarfs from a kinematic analysis.

Acknowledgements
This work is based on observations obtained from the European Southern Observatory, PIDs 077.C-0449 and 078.C-0025, and on observations obtained from the W. M. Keck Observatory, which is operated as a scientific partnership among the California Institute of Technology, the University of California and the National Aeronautics and Space Administration. Based on observations made with the European Southern Observatory telescopes obtained from the ESO/ST-ECF Science Archive Facility. This research has benefitted from the M, L, and T dwarf compendium housed at DwarfArchives.org and maintained by Chris Gelino, Davy Kirkpatrick, and Adam Burgasser. We thank the referee, Kelle Cruz, for her constructive report. A.S. and A.R. acknowledge financial support from the Deutsche Forschungsgemeinschaft under DFG RE 1664/4-1. A.S. further acknowledges financial support from NSF grant AST07-08074. G.B. thanks the NSF for grant support through AST06-06748.

References

  1. Bailer-Jones, C. A. L. 2004, A&A, 419, 703 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Bannister, N. P., & Jameson, R. F. 2007, MNRAS, 378, L24 [NASA ADS] [Google Scholar]
  3. Basri, G., Mohanty, S., Allard, F., et al. 2000, ApJ, 538, 363 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bihain, G., Rebolo, R., Béjar, V. J. S., et al. 2006, A&A, 458, 805 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Blake, C. H., Charbonneau, D., White, R. J., Marley, M. S., & Saumon, D. 2007, ApJ, 666, 1198 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bouy, H., Brandner, W., Martín, E. L., et al. 2003, AJ, 126, 1526 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bouy, H., Martin, E. L., Brandner, W., et al. 2008, A&A, 481, 757 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Burgasser, A. J. 2004, ApJS, 155, 191 [Google Scholar]
  9. Burgasser, A. J. 2009, IAU Symp., 258, 317 [NASA ADS] [Google Scholar]
  10. Burgasser, A. J., & McElwain, M. W. 2006, AJ, 131, 1007 [NASA ADS] [CrossRef] [Google Scholar]
  11. Casewell, S. L., Jameson, R. F., & Burleigh, M. R. 2008, MNRAS, 390, 1517 [NASA ADS] [Google Scholar]
  12. Chabrier, G., & Baraffe, I. 1997, A&A, 327, 1039 [NASA ADS] [Google Scholar]
  13. Chen, B., Asiain, R., Figueras, F., & Torra, J. 1997, A&A, 318, 29 [NASA ADS] [Google Scholar]
  14. Chereul, E., Crézé, M., & Bienaymé, O. 1999, A&AS, 135, 5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Costa, E., Méndez, R. A., Jao, W.-C., et al. 2006, AJ, 132, 1234 [NASA ADS] [CrossRef] [Google Scholar]
  16. Cruz, K. L., Reid, I. N., Liebert, J., Kirkpatrick, J. D., & Lowrance, P. J. 2003, AJ, 126, 2421 [NASA ADS] [CrossRef] [Google Scholar]
  17. Cruz, K. L., Kirkpatrick, J. D., & Burgasser, A. J. 2009, AJ, 137, 3345 [NASA ADS] [CrossRef] [Google Scholar]
  18. Faherty, J. K., Burgasser, A. J., Cruz, K. L., et al. 2009, AJ, 137, 1 [NASA ADS] [CrossRef] [Google Scholar]
  19. Fuchs, B., Dettbarn, C., Jahreiß, H., & Wielen, R. 2001, Dynamics of Star Clusters and the Milky Way, 228, 235 [Google Scholar]
  20. Henry, T. J., Jao, W.-C., Subasavage, J. P., et al. 2006, AJ, 132, 2360 [NASA ADS] [CrossRef] [Google Scholar]
  21. Jameson, R. F., Casewell, S. L., Bannister, N. P., et al. 2008, MNRAS, 384, 1399 [NASA ADS] [CrossRef] [Google Scholar]
  22. Kendall, T. R., Delfosse, X., Martín, E. L., & Forveille, T. 2004, A&A, 416, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Kirkpatrick, J. D., Reid, I. N., Liebert, J., et al. 2000, AJ, 120, 447 [NASA ADS] [CrossRef] [Google Scholar]
  24. Leggett, S. K. 1992, ApJS, 82, 351 [NASA ADS] [CrossRef] [Google Scholar]
  25. Liu, M. C., & Leggett, S. K. 2005, ApJ, 634, 616 [NASA ADS] [CrossRef] [Google Scholar]
  26. Lodieu, N., Scholz, R.-D., McCaughrean, M. J., et al. 2005, A&A, 440, 1061 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Lutz, T. E., & Upgren, A. R. 1980, AJ, 85, 1390 [NASA ADS] [CrossRef] [Google Scholar]
  28. Martin, E. L., Basri, G., Delfosse, X., & Forveille, T. 1997, A&A, 327, L29 [NASA ADS] [Google Scholar]
  29. Martín, E. L., Delfosse, X., Basri, G., et al. 1999, AJ, 118, 2466 [NASA ADS] [CrossRef] [Google Scholar]
  30. Mohanty, S., & Basri, G. 2003, ApJ, 583, 451 [NASA ADS] [CrossRef] [Google Scholar]
  31. Perryman, M. A. C., Lindegren, L., Kovalevsky, J., et al. 1997, A&A, 323, L49 [NASA ADS] [Google Scholar]
  32. Reid, I. N., Kirkpatrick, J. D., Liebert, J., et al. 2002a, AJ, 124, 519 [NASA ADS] [CrossRef] [Google Scholar]
  33. Reid, I. N., Gizis, J. E., & Hawley, S. L. 2002b, AJ, 124, 2721 [NASA ADS] [CrossRef] [Google Scholar]
  34. Reid, I. N., Cruz, K. L., Kirkpatrick, J. D., et al. 2008, AJ, 136, 1290 [NASA ADS] [CrossRef] [Google Scholar]
  35. Reiners, A., & Basri, G. 2008, ApJ, 684, 1390 (RB08) [NASA ADS] [CrossRef] [Google Scholar]
  36. Reiners, A., & Basri, G. 2009, ApJ, 705, 1416 [NASA ADS] [CrossRef] [Google Scholar]
  37. Schmidt, S. J., Cruz, K. L., Bongiorno, B. J., Liebert, J., & Reid, I. N. 2007, AJ, 133, 2258 [NASA ADS] [CrossRef] [Google Scholar]
  38. Seifahrt, A., Guenther, E., & Neuhäuser, R. 2005, A&A, 440, 967 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Johnson, D. R. H., & Soderblom, D. R. 1987, AJ, 93, 864 [NASA ADS] [CrossRef] [Google Scholar]
  40. Stumpf, M. B., Brandner, W., Henning, T., et al. 2008, unpublished [arXiv:0811.0556] [Google Scholar]
  41. Vrba, F. J., Henden, A. A., Luginbuhl, C. B., et al. 2004, AJ, 127, 2948 [NASA ADS] [CrossRef] [Google Scholar]
  42. Wielen, R. 1977, A&A, 60, 263 [NASA ADS] [Google Scholar]
  43. Zapatero Osorio, M. R., Martín, E. L., Béjar, V. J. S., et al. 2007, ApJ, 666, 1205 [NASA ADS] [CrossRef] [Google Scholar]
  44. Zuckerman, B., & Song, I. 2004, ARA&A, 42, 685 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]

Footnotes

... dwarfs[*]
Table 2 is also available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/512/A37
... dwarfs[*]
One of the targets (2MASS J1159+00) has too low a signal-to-noise ratio to compute a robust radial velocity, reducing the initial sample size to 44. One more target (2MASS J1854+84) has no published proper motion and distance, reducing the number of final targets in our sample to 43.
...gal_uvw[*]
Written by Landsman and Koposov, based on Johnson & Soderblom (1987).
... computed[*]
This can be illustrated when considering, e.g., the total velocity dispersions in Table 5 of Zapatero Osorio et al. (2007). For G-type stars, the dispersion peaks at 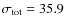$\sigma_{\rm tot}=35.9$ km s-1, which should yield an age lower than $\sim$2.2 Gyr (see Fig. 1 in Fuchs et al. 2001; and tables in Wielen 1977). An age of 9 Gyr is reported in Table 5 of Zapatero Osorio et al. (2007).
Copyright ESO 2010

All Tables

Table 1:   Candidate members of young moving groups based on our UVW analysis.

Table 2:   Radial velocities and space motions of our targets. Data on distance and proper motions are obtained from the literature.

All Figures

  \begin{figure} \par\includegraphics[width=9cm,clip]{13368f1.eps} \end{figure} Figure 1:

Example of the distribution of radial velocities obtained in different spectral orders from stellar lines ( left) and telluric lines ( right) in the spectrum of 2M1645-1319 (L1.5V). See text for details.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.8cm,clip]{13368f2a.eps}\hspace*{2mm} \includegraphics[width=7.8cm,clip]{13368f2b.eps}\vspace*{1mm} \end{figure} Figure 2:

Space velocities in the U-V ( left) and W-V ( right) plane. The velocity ellipsoids for the young disk as well for some young moving groups are shown. Moving groups considered in the analysis but without members in our sample are not shown for clarity. Objects in colour are candidate members of the respective moving groups, as indicated in Table 2.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=15.7cm,clip]{13368f3.eps} \end{figure} Figure 3:

Top row: histograms of the space motion components in U, V, and W ( from left to right). Bottom row: probability plots for in U, V, and W ( from left to right). Data are shown with their uncertainties as error bars. The dashed line marks the 1.5$\sigma $ cutoff for the fit shown as a solid red line. The slope of the linear fit is the $\sigma $ of the closest matching Gaussian distribution.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.